An Inter-Comparison of Dynamic, Fully Coupled, Electro-Mechanical, Models of Tidal Turbines

Abstract

Production of electricity using hydrokinetic tidal turbines has many challenges that must be overcome to ensure reliable, economic and practical solutions. Kinetic energy from flowing water is converted to electricity by a system comprising diverse mechanical and electrical components from the rotor blades up to the electricity grid. To date these have often been modelled using simulations of independent systems, lacking bi-directional, real-time, coupling. This approach leads to critical effects being missed. Turbulence in the flow, results in large velocity fluctuations around the blades, causing rapid variation in the shaft torque and generator speed, and consequently in the voltage seen by the power electronics and so compromising the export power quality. Conversely, grid frequency and voltage changes can also cause the generator speed to change, resulting in changes to the shaft speed and torque and consequently changes to the hydrodynamics acting on the blades. Clearly, fully integrated, bi-directional, models are needed. Here we present two fully coupled models which use different approaches to model the hydrodynamics of rotor blades. The first model uses the Blade Element Momentum Theory (BEMT), resulting in an efficient tool for turbine designers. The second model also uses BEMT, combines this with an actuator line model of the blades coupled to an unsteady computational fluid dynamics simulation by OpenFOAM (CFD/BEMT). Each model is coupled to an OpenModelica model of the electro-mechanical system by an energy balance to compute the shaft speed. Each coupled system simulates the performance of a 1.2 m diameter, three-bladed horizontal axis tidal turbine tested in the University of Edinburgh FloWave Ocean Energy Research Facility. The turbulent flow around the blades and the mechanical-electrical variables during the stable period of operation are analysed. Time series and tabulated average values of thrust, torque, power, and rotational speed, as well as, electrical variables of generator power, electromagnetic torque, voltage and current are presented for the coupled system simulation. The relationship between the mechanical and electrical variables and the results from both tidal turbine approaches are discussed. Our comparison shows that while the BEMT model provides an effective design tool (leading to slightly more conservative designs), the CFD/BEMT simulations show the turbulence influence in the mechanical and electrical variables which can be especially important in assessing an additional source of stresses in the whole electro-mechanical system (though at an increased computational cost).

1. Introduction

With increasing awareness of the rise in global temperatures due to carbon emissions, there is a conscious need to meet electricity demand using renewable energy and reduce the consumption of fossil fuels. Tidal turbines have shown the potential to generate vast amounts of clean electricity from the world’s oceans and have been in continuous technological development for many years. Despite many of its technical characteristics being inherited from and inspired by offshore wind turbines, tidal turbines are entirely surrounded by water and face significantly different challenges. The surrounding sea presents dynamic and unpredictable behaviour, which can impose undesirable dynamic loads against the turbine structure, particularly the rotor blades. Turbulent flow results in more energy dissipation and less kinetic energy captured by the turbine for power generation.

Numerical simulation of the surrounding sea is a challenging task as it is characterized by its unstable behaviour and its intrinsic physical properties like turbulence. Ideal models based on momentum balance can be used for the simulation of the surrounding sea. They have low computational cost but the intrinsic flow characteristics are lost. On the other hand, models based on a domain discretization and solution of the fluid conversation equations for each control volume can also be used. They involve the use of higher computational resources but simulate the fluid dynamic behaviour and keep the fluid physical properties. The performance of these type of models is discussed in this work.

Another point to be considered is the complexity of the whole system under study: the chain of energy conversion, from capturing the kinetic energy of the tidal flow through to the generation of electrical power for transmission, involves considerable development in a number of individual systems. Firstly, the ocean environment in which kinetic energy is to be harvested. Next, the turbine which converts kinetic energy from the flow to mechanical energy through rotor blades rotation. The turbine rotor is connected by a shaft to an electrical generator for conversion of mechanical energy to electrical energy. The electrical generator is managed by a control system to maintain operation at the optimal point. Subsequently, electricity at a fixed voltage and frequency is stepped up by a transformer for power transmission.

Despite the complexity and interaction between different systems within this process of energy conversion, they have so far been studied separately as stand-alone systems; only a few works have started to model it as a coupled system. A study of synthetic turbulence flow models applied to a flume-scale Blade Element Momentum Theory (BEMT) tidal turbine model was carried out by Togneri et al. [1]. Turbulent three-dimensional flow fields were produced by the synthetic turbulence models spectral Sandia and synthetic eddy. The study found a no full reflection of the velocity field spectral properties in the load spectra of the tidal turbine, and a direct relationship between the variability of the tidal turbine loads and the turbulence intensity of the inflow. Using the model of a laboratory-scale three-blades tidal turbine built using Computational Fluid Dynamics/Large Eddy Simulation (CFD/LES) coupled with Actuator Line Model (ALM), Ahmadi and Yang [2] determined a transition zone located shortly behind the simulated tidal turbine with a peak of turbulence intensity. It was found after tracking the streamwise variation of turbulence intensity and turbulent kinetic energy, removing the deterministic velocity fluctuations risen from the tidal turbine rotation.

For the control scheme of the generator side of a tidal turbine system, Zhou et al. [3] proposed an Active Disturbance Rejection Control (ADRC) approach to replace the conventional PI controllers. Under current velocity and turbine torque disturbances, ADRC strategies were tested and compared to achieve Maximum Power Point Tracking (MPPT). The study demonstrated that cascaded ADRC approach slightly improved a tidal turbine system production during swell wave disturbance periods in contrast with the conventional PI controllers. An investigation about the mitigation of undesired torque pulsations by changing the generator speed was presented by Sousounis et al. [4]. The authors propose that the DC link voltage spikes, the electrical components stress increment, and the hazard to grid connection produced by increasing the variation of the generator rotational speed can be overcome by installing a supercapacitor module at the DC link.

The literature also presents electro-mechanical designs and analyses of tidal turbines using uncoupled models. Li et al. [5] designed and tested a 600 kW two-blade horizontal axis tidal turbine. The design included the rotor, a two-stage gearbox and a medium speed permanent magnet synchronous generator (PMSG). It was connected to the grid by a back-to-back converter from alternating current (AC) to direct current (DC) and from DC to AC grid. Its control system was based on an MPPT strategy and a controller which loaded torque to the PMSG. The tidal turbine was built and an onshore and offshore trial campaign was carried out. The performance of the electro-mechanical system was assessed by verifying its efficiency using a mathematical model based on the actuator-disc theory and analytical formulations for power coefficient and electrical power. The work also studied the fluctuations of power and rotational speed occurred during the trial campaign. Alvarez et al. [6] designed an electro-mechanical system of a hydrokinetic microturbine for smart grids connection. A turbine rotor, a permanent magnet generator, a rectifier and boost converter, as well as a microcontroller composed the system. A control strategy was proposed setting three operating regions: cut-in, MPPT and maximum power, which define different values of direct current set points. This control strategy was validated using dynamic simulation where the electro-mechanical system was modelled using a design tool for power electronics. The validation stage was carried out setting arbitrary water speed to feed the turbine rotor and controlling the maximum power of the generator aims to protect the microturbine components. Vasquez et al. [7] presented a mathematical model that describes the response of a tidal turbine electro-mechanical system. The model included a horizontal axis turbine rotor connected to a PMSG by mechanical transmission of known efficiency. Its PMSG model, obtained by a Park’s transform, was connected to resistive and inductive loads. The work also presented a strategy that controls the rotor rotational speed modifying the resistive loads. Thus, a correlation for the resistive load aims to keep the turbine working at optimal rotational speed was also presented. Test cases varying the resistive loads and the stream speed were carried out verifying the system drive line response.

A coupled system model which involves the surrounding sea, modelled by CFD/LES, a tidal turbine, modelled by ALM/BEMT, and its control system, modelled by MPPT, was presented by Ortega et al. [8]. The simulations showed energy balance between the surrounding sea, the tidal turbine, and the torque controller as the tidal turbine starts to work from the rest up to reach optimal rotational speed. The simulations showed that the turbulence in the inflow is reflected in the time-series output of thrust, torque and rotor power. The results presented good agreement when validated against a laboratory-scale tidal turbine. Sousounis et al. [9] implemented a tide-to-wire model for a tidal current conversion system. BEMT was used to model the mechanical performance of a tidal turbine and it was coupled with an electrical system developed using a design tool based on the Modelica language. The rotor torque calculated by the BEMT is sent to the electrical system which feedback is the generator rotational speed calculated using an MPPT strategy.

Despite the efforts made to improve the technological development of the tidal turbines from the perspectives of design, construction, deployment, operation, maintenance and energy supply assurance, it is not yet in the commercial stage; and therefore more efforts have to be done to improve those aspects and so that it becomes attractive to governmental and private investments. The objective of this work is to study the variables that involve the transformation of energy from the sea resource to the energy consumption centre from a holistic perspective. It means a tidal turbine rotor blades model is fully coupled to a complete electrical system model. The coupling is carried out by mutual feedback of information balancing their torque over time-domain (torque controller). For the tidal turbine rotor blades model, two approaches are used. The first approach is based on BEMT, and the second approach is also based on BEMT plus CFD to simulate the surrounding sea and body forces to simulate the interaction of the rotor blades with the sea. Each of these tidal turbine rotor blades approaches is coupled to a full electrical system which besides the generator and its controllers, it considers the distribution lines and the grid consumer.

2. Numerical Models

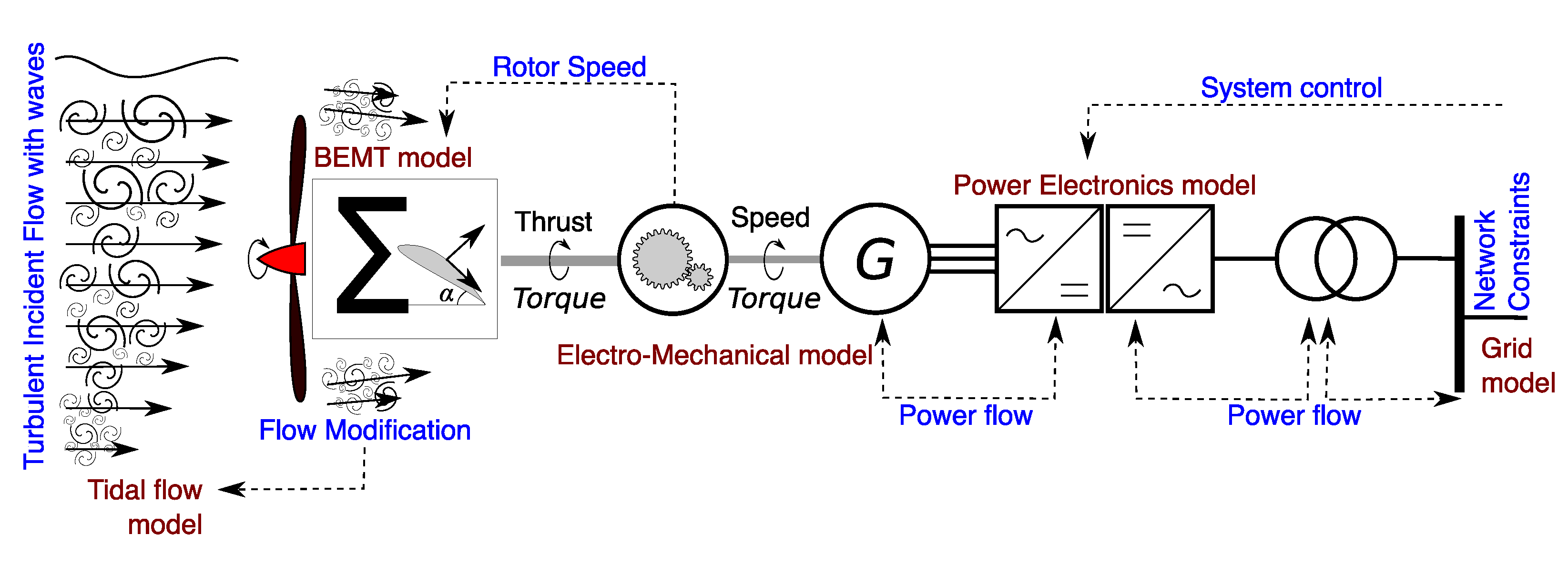
In this section, an introduction to the numerical models and approaches used in this work are presented. They are the models used to represent the tidal turbine rotor blades (BEMT and CFD/BEMT), as well as the model which characterises the electrical system, and the approach used to couple the rotor blades with the electrical system. A layout of the models used in this work, and their integration are represented in Figure 1.

2.1. BEMT Model

Blade Element Momentum Theory (BEMT) provides the most simplified numerical model of tidal turbine rotor blades [10], based on classical laws of physics such as Newton’s Laws of Motion and conservation of momentum. The flow modification by the rotating turbine is modelled in terms of axial and tangential induction factors. The axial induction factor represents the change in the magnitude of axial velocity in the flow while passing through the turbine; the tangential induction factor represents the same for the tangential velocity component. These induction factors are then computed by applying the principles of conservation of linear and angular momentum.

The BEMT tool StarBlades was developed by Bureau Veritas based on those concepts [11]. Unsteady hydrodynamics models have been included to improve on the assumptions and limitations of classical BEMT [12]. These models include a modified Beddoes-Leishamn model for dynamic stall [13]. A solution approach based on the work of Ning [14] has been implemented for the solution of the BEMT equations. The sequence of calculation of the BEMT equations is as follow: It starts computing the equations for each blade element, integrates the forces for each blade, and then for each time-step belonging to a determined operational condition [9].

The flow domain considered for the BEMT computations is a 2D rectangular plane at the rotor axis. In the BEMT model, the blade geometry is represented as 1D line elements, with each blade element corresponding to a foil section. For each time step, the model calculates the angle of attack at each blade element of the resultant velocity vector, combining the axial and tangential velocity vectors. The lift and drag coefficients are then interpolated from a tabulated list, for the corresponding angle of attack. Equating the resultant axial force and tangential force to the changes in axial and angular momentum respectively provides a solution to the BEMT equations.

StarBlades has been validated against experimental measurements from Bahaj and Sabella D10 as well as against numerical results from Hobit [11,15]. The validation presented performance coefficients assessment under diverse operation conditions. The dynamic stall model has been validated versus experimental results from the S814 aerofoil tested in a wind tunnel [16]. The validation verified lift coefficient—angle of attack cycles. StarBlades validation campaign showed a reasonably accurate estimation.

2.2. CFD/BEMT Model

For the CFD/BEMT model, the NREL SOWFA [17] was used. The SOWFA was created to simulate wind turbines applications, however it can be adapted to simulate tidal turbines rotor blades [18,19]. The rotor blades representation used in SOWFA is developed based on the Actuator Line Model (ALM) [20], embedded into the OpenFOAM CFD toolbox [21].

The flow domain is simulated using an OpenFOAM solver for the incompressible Navier-Stoke continuity and momentum equations. During turbine operation, the flow upstream of, around and in the wake of the turbine is turbulent with large, dynamic and unstable, structures; thus to capture these characteristics of the flow, Large Eddy Simulation (LES) is used to model the turbulence [22]. At the upstream boundary, a synthetic turbulence model is imposed as a custom boundary condition of the OpenFOAM toolbox. The turbulent inflow generator produces a turbulence time-series that evolves inside the flow domain. The boundary condition calculations are based on a specified turbulence length scale, reference velocity, and the Reynolds stress tensor [23].

The actuator line model is used to represent the rotor blades and account for their interaction with the surrounding flow. Similar to the BEMT model (Section 2.1), the turbine rotor blades are discretized into a sequence of equally spaced blade elements. As before, in each element, the lift and drag forces are calculated using a-priori airfoil lift and drag data, twist angle, chord length, and incoming flow velocity. The torque and thrust acting on each blade is calculated by integrating these quantities along an actuator line. The locations of the actuator lines change in time, so as to represent the rotation of the blades. An important difference between the BEMT model and the ALM is that as the lines move they sample different parts of the local flow field, in the same way that a blade resolved calculation would.

To achieve this, the hydrodynamic forces are projected on to the control volumes using a Gaussian formulation which considers the blades as equivalent elliptic plan-forms. The body forces, which are used as a source term for the Navier-Stokes momentum equations, are equivalent and opposite to the lift and drag forces applied on each of the blade elements [24].

In the presented work, the behaviour of a 1:15 laboratory scale tidal turbine have been simulated in SOWFA. Comparisons are made against the mechanical variables (thrust, torque, etc) measured using a fully instrumented, controllable, three bladed, horizontal axis, tidal turbine deployed in the Flowave Ocean Energy Research Facility, The University of Edinburgh (see [8] for details).

2.3. Electrical System Model

The electrical system converts mechanical power from the drive shaft into electrical power and conditions it to make it compatible with the grid connection. This electro-mechanical model used was developed at the University of Edinburgh [25] and has been implemented in OpenModelica [26] and then encapsulated using the Functional Mock-up Interface standard (FMI) [27] to be used as a plug-in. The principal components of the model are the electrical generator and power converter. 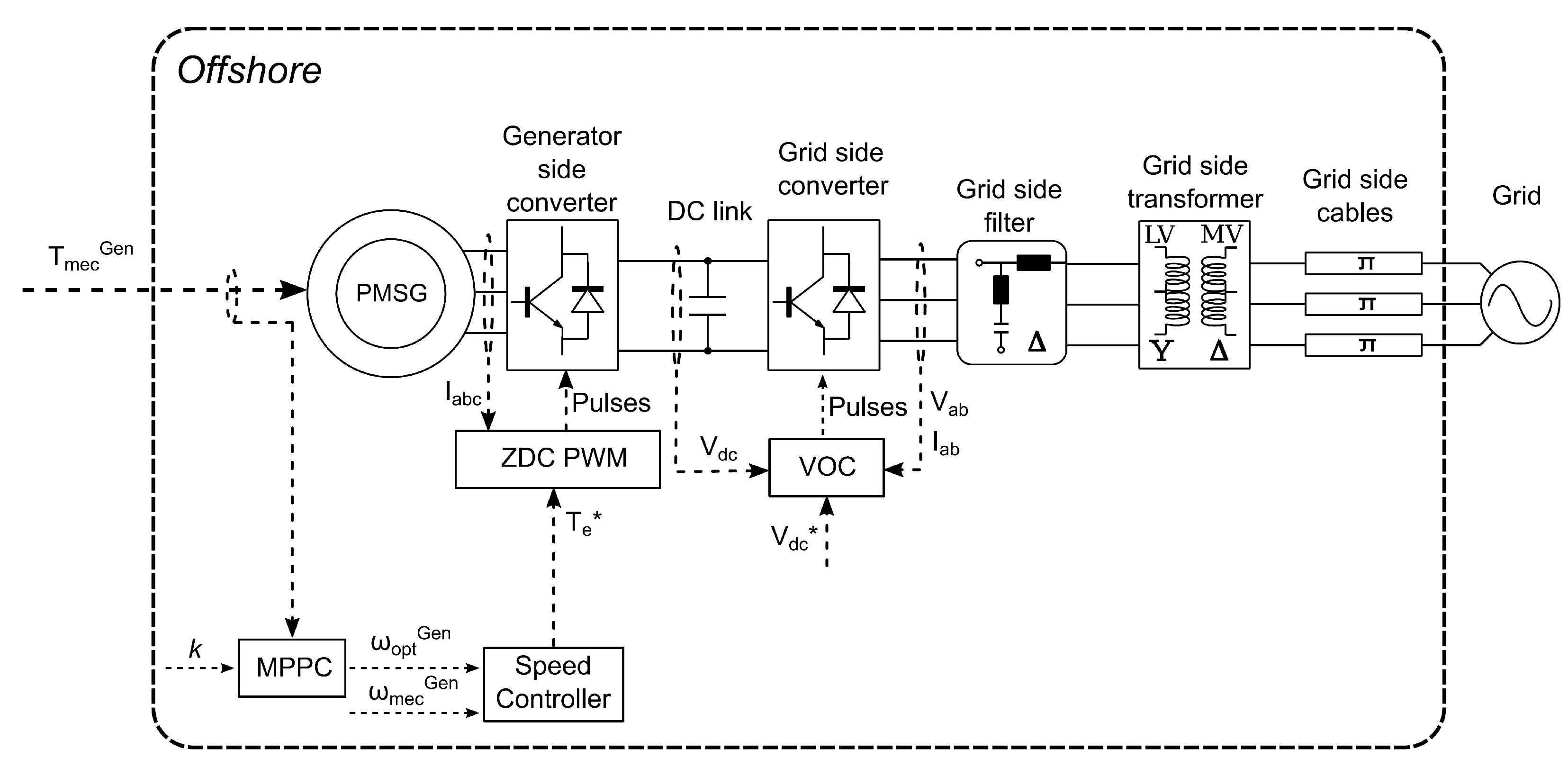The input to the electrical system model is the mechanical torque of the rotor, $T_{mec}^{Gen}$, which is calculated using the hydrodynamic model of the turbine rotor blades, presented in Section 2.1 and Section 2.2. The generator used is a permanent magnet synchronous generator (PMSG). Both the voltage and frequency of the electricity produced vary with changes in shaft speed. The generator’s output is conditioned by passing through two back-to-back voltage-source converters connected by DC link. The generator side converter is also used to control the rotation speed of the generator. Speed is controlled using Maximum Power Point Tracking (MPPT) and zero direct-axis current (ZDC) controllers. On the export side, 3-phase AC power is produced at a fixed frequency. The grid side converter is managed using a voltage-oriented controller (VOC). Figure 2 shows a block diagram of the electrical system model used in this work [9].

The PMSG implemented in the electrical system model is a direct drive (DD) type and operates at low speed and high torque, so there is no gearbox between the generator and the turbine rotor [28]. ZDC control aims to set the electromagnetic torque of the generator $T_e$ equal to an ideal electromagnetic torque $T_e^{*}$ by controlling the active power of the generator. In addition to $T_e^{*}$, the three-phase current $i_{abc}$ at the output of the generator and the generator rotor angle are also required as inputs for ZDC control [29,30]. MPPT aims to control the tip speed ratio in order to achieve the highest possible power at the turbine rotor. It uses a predefined maximum power point curve (MPPC) at which the power of the turbine rotor is maximised for varying tidal flow velocities at a specific optimal rotor rotational speed. The predefined maximum power point curve is characterized by the constant k. The speed controller is responsible for comparing the optimal generator speed ${\omega }_{opt}^{Gen}$ and the actual generator speed ${\omega }_{mec}^{Gen}$ to produce the ideal electromagnetic torque reference $T_e^{*}$ to be used as input to the ZDC controller.

The grid side converter is managed by the VOC using decoupled controllers to ensure: a constant DC link voltage; a constant frequency output that synchronised with the grid voltage; and, control over the amount of reactive power flow depending on the grid requirements [31]. Additionally, the electrical system includes harmonic power filters installed in the nacelle of the tidal turbine to reduce grid side harmonics at the switching frequency of the grid side converter. A step-up transformer is also used to increase the voltage levels for power transmission to the shore. The grid side cables for power transmission are modelled as a network of $\pi$-sections towards the onshore grid. The validation of the electrical system model has been carried out using data from the Andritz Hydro Hammerfest AH1000 MK1 turbine deployed at European Marine Energy Centre’s (EMEC) Falls of Warness tidal test site. The AH1000 is 16 m diameter seabed mounted turbine. AH1000 turbines have also been deployed as part of the MeyGen tidal energy project where they feed into an onshore power conversion unit building at the Ness of Quoys, where the low voltage supply transformed to 33 kV for export to the local distribution network. Full details are given in Sousounis’ Ph.D thesis [25].

2.4. Coupling of Systems

In this section we discuss the bi-directional coupling of the electro-dynamic model (Section 2.3) and turbine rotor models described in the Section 2.1 and Section 2.2. Coupling is achieved using an energy balance between the rotor and electromagnetic torques, Figure 1.

The upstream dynamic, turbulent, flow is disturbed by the body forces imposed by the turbine rotor blades. This means that the flow around and downstream close to the turbine is highly disturbed. This flow becomes more stable as it moves further away from the turbine. The hydrodynamic forces, distributed along the actuator lines (rotor blades), generate a resultant mechanical torque (rotor torque) imposed on the shaft, which connects the rotor of the tidal turbine to the generator of the electrical system. The electrical system responds to this perturbation by applying an opposing electromagnetic torque. This torque balance generates a shaft angular acceleration, so modifying the angular velocity of the turbine rotor, shown in Equation (1):

$$J\frac{d\omega }{dt}=T_e-T_m-B·\omega$$

(1)

where $T_e$ is the electromagnetic torque (Nm), $T_m$ is the mechanical rotor torque (Nm), $\omega$ is the rotor angular speed (rad/s), J is the turbine and rotor inertia (kg-$m^2$), and B is the viscous friction (N-m-s/rad), which is assumed to be negligible in this work.

At each stage, the updated angular velocity of the rotor modifies the dynamic behaviour of the flow surrounding the turbine. At the next stage, the sequence starts again calculating new values of hydrodynamic forces, mechanical torque, electromagnetic torque, angular rotor speed, and velocity field around the turbine. Therefore, the interaction of the fully coupled tidal turbine rotor blades—electrical system, is demonstrated.

3. Cases Setup

The tidal turbine used is a generic, three-bladed, horizontal axis, model scale device. One of three identical turbines originally developed for the UK’s Supergen Marine programme [32] which have been extensively tested in the FloWave Ocean Energy Research Facility [33]. FloWave is a circular wave and current basin, 25 m in diameter and 2 m deep able to create multi-directional waves, with a significant wave height of 0.5 m, and currents, of up to 1.2 ms⁻¹, in any relative direction simultaneously.

The characteristics of the turbine are presented in

Table 1. Geometrical characteristic of the FloWave generic turbine.

Number of blades	3
Rotor diameter (m)	1.2
Hub diameter (m)	0.12
Hub location over tank bed (m)	1

. For the numerical experiment, two cases have been selected with mean flow velocities of 0.6 m/s and 1.0 m/s imposed at the inlet. The turbine and generator inertia have been assumed as 1 kg-m² to test the performance of the mechanical—electrical coupled system.

The BEMT model has been setup as follows. Eleven blade elements were used for the BEMT discretization. The foil lift and drag coefficients were obtained from [34]. The 2D rectangular domain considered for computations has a water depth of 2 m and width of 1 m. For these simulations, There were assumed no variation of velocity over the depth and width of the tank, and no temporal variations of the input velocity field. There is no turbulence model included.

In the case of the CFD/BEMT model, the tank domain was considered as a parallelepiped with a downstream length equal to nine rotor diameters, a water depth of 2 m, and a transversal length of 4 m. The domain was discretized uniformly, with a grid spacing of 0.018 m. Forty blade elements were used for the blade discretization. Both, the tank domain and rotor blades discretization were set up according to the criterion for volume force distributions within ALM on LES. The tidal turbine is located three rotor diameters downstream of the inlet to allow flow development from the synthetic turbulence generated at inflow. Slip wall boundary condition are imposed on the bottom, top and lateral sides of the domain. At the outlet, the flow is considered fully developed. The stream flow velocities are imposed uniformly at inlet together with synthetic turbulence, generating a turbulent intensity equivalent to 10%. For both models, BEMT and CFD/BEMT, a time step of 0.002 s was selected based on the Courant-Friedrichs-Lewy (CFL) criterion for the rotor tip velocity. This was done to avoid numerical instability.

The time step required for the electrical system is in order of $200\mathsf{\mu }\mathrm{s}$ which is much smaller than that used by the mechanical simulation. Consequently, at each mechanical time step, $\Delta T$, the electrical solver performs a number of integration steps. Both simulations synchronize at the end of the mechanical time step. In the present simulations the MPPT constant, $k=0.3134$, a value calculated from the FloWave experiments. The parameters describing the electrical generator are given in

Table 2. Electrical generator model parameters.

Rated speed (rad/s)	15.7
Pole pairs	20
Nominal frequency (Hz)	50
Phase resistance (Ω)	10.5
D-axis phase inductance (H)	0.0785
Q-axis phase inductance (H)	0.0785

.

4. Results and Analysis

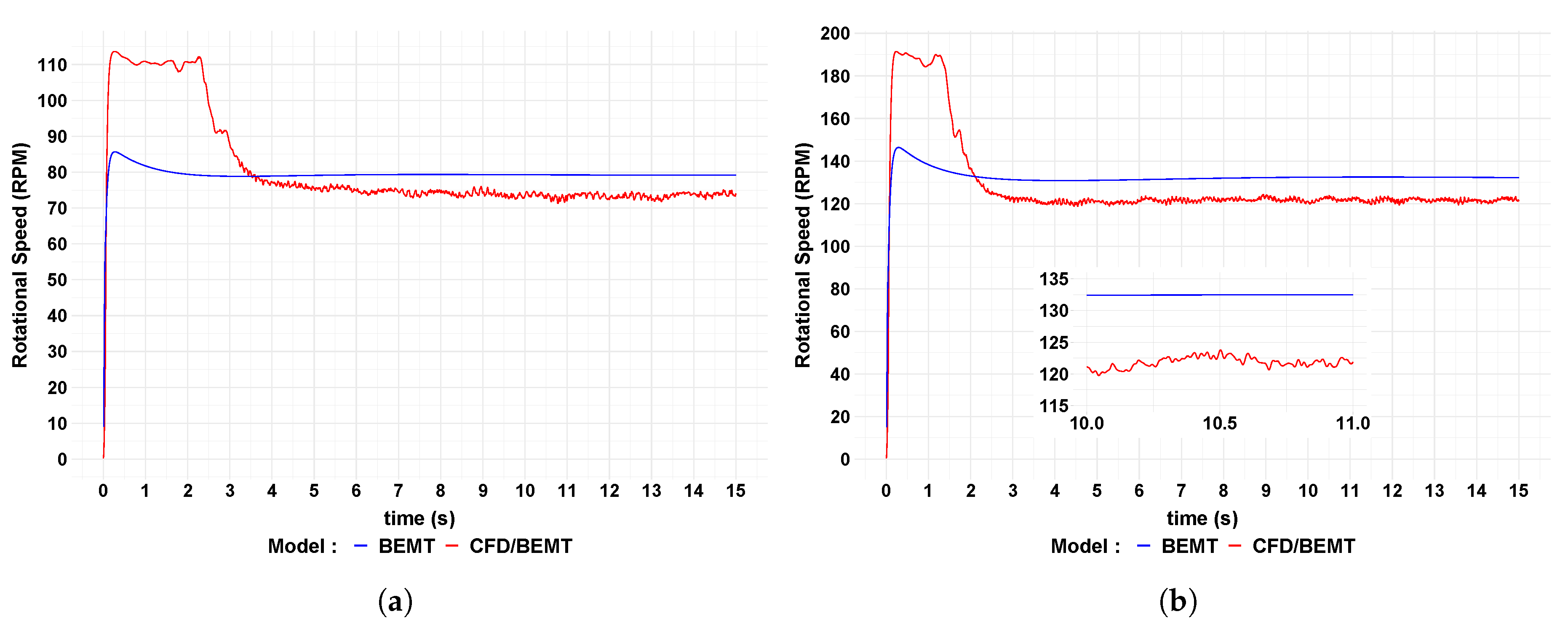
Figure 3 presents the turbine rotational speed time-series for the two approaches. The time-series are divided into two parts. The shortest part is the transient period as the turbine rotor starts from rest. Once the turbine, which works connected to the electrical system, reaches an energy balance between the rotor torque and the electromagnetic torque, produced by the generator, a more stable period is presented. The BEMT model reached the stable period faster than the CFD/BEMT model as BEMT is a steady-state program. Whereas, in the CFD/BEMT model, the interaction between the surrounding sea and the turbine rotor blades is managed by an energy balance, between the imposed hydrodynamic forces (sea against the rotor blades) and the reacted body forces (rotor blades against the sea), and OpenFOAM resolves the Navier-Stoke equations. Thus, the CFD/BEMT model tries to reach a stable behaviour more naturally. The fluctuation of the variable in the CFD/BEMT model is due to the presence of the turbulence. As the free stream velocity increase, higher values of rotational speeds are predicted.

Table 3. Average turbine rotational speed.

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(RPM)	(RPM)	(RPM)	(%)
0.6	79.2	73.5	5.7	7.8
1.0	132.1	121.7	10.4	8.5

shows the average values of the turbine rotational speed calculated by the two approaches. Slightly higher values were calculated by the BEMT model and the difference in the results increase as the free stream velocity increase. It is due to more turbulence is generated around the turbine. The percentage difference presented in the table is with reference to the CFD/BEMT model.

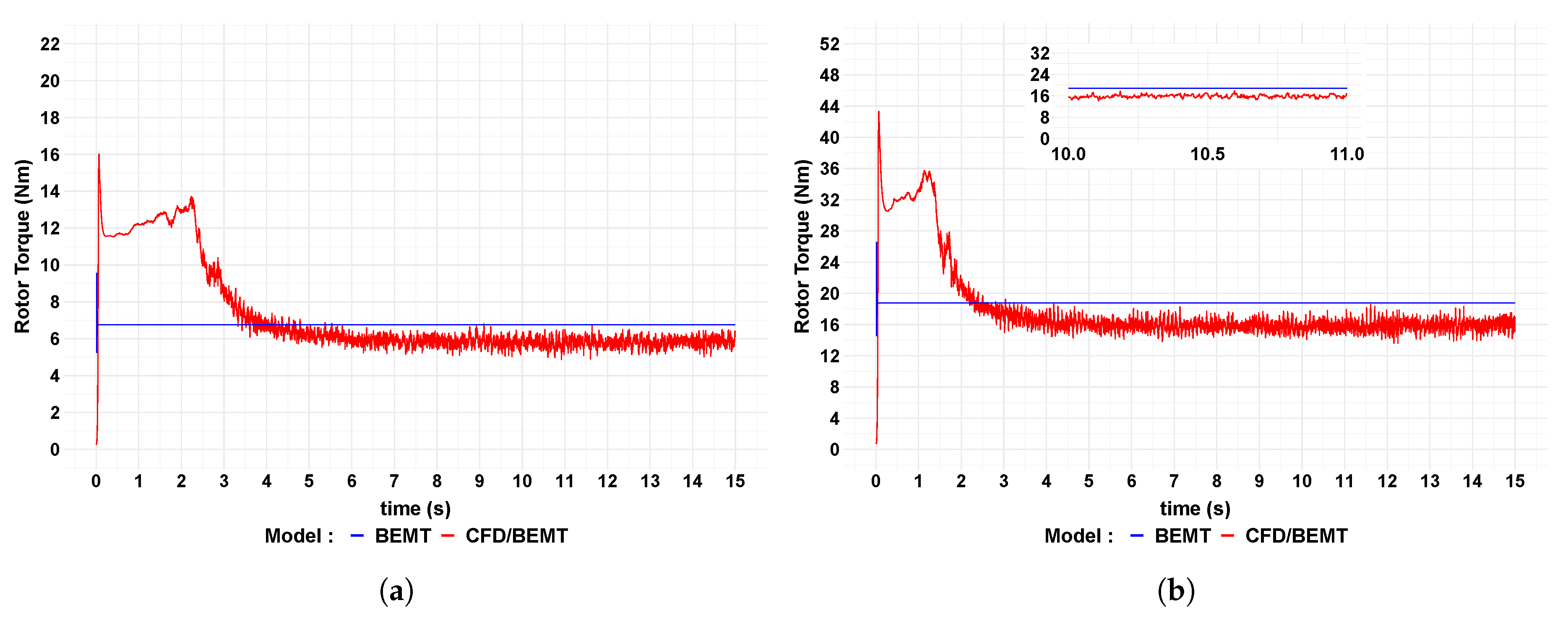
Figure 4 presents the time-series of the rotor torque predicted by two approaches. Transient and stable periods are presented which is more evident for the CFD/BEMT model in contrast to the steady-state approach of the BEMT model. The level of turbulence is also more evident as the fluctuation of the variable in the CFD/BEMT model. As the free stream velocity is increased, the torque balance between the rotor torque and the electromagnetic torque also increases.

Table 4. Average turbine rotor torque.

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(Nm)	(Nm)	(Nm)	(%)
0.6	6.8	5.8	0.9	16.0
1.0	18.8	15.9	2.9	18.3

presents the average values of the rotor torque during the stable period. Higher values are calculated by the BEMT approach as it does not consider the dissipation of energy caused by the turbulence. Again, increasing the free stream velocity meaning more level of turbulence generated around the turbine. That situation is not captured by the BEMT approach, so increasing the free stream velocity, the difference between the values calculated by two approaches also suffer increment.

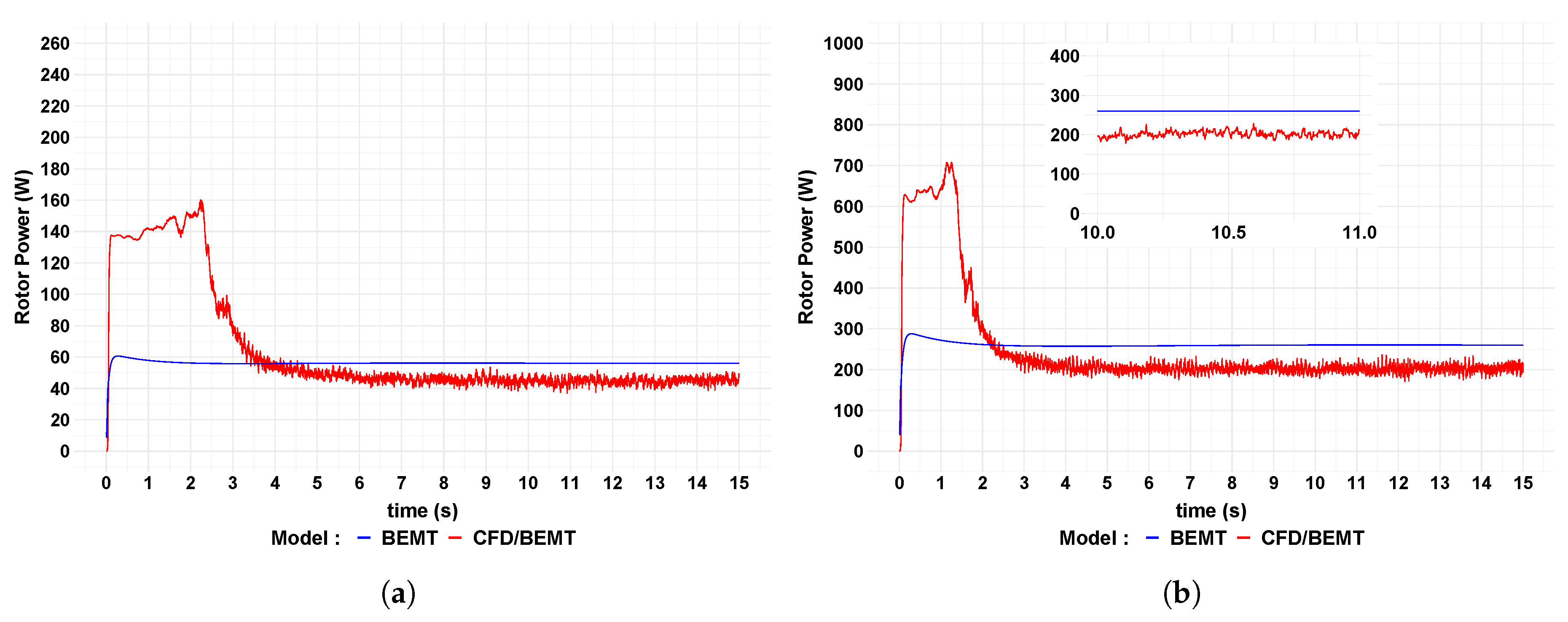
Figure 5 shows time-series for rotor power by two approaches. The time-series behaviour is similar to the previous figures as the rotor power is calculated by the rotor torque times the turbine rotational speed. There is a stable period after an initial transient as the rotor started from rest. The CFD/BEMT model took more time to reach a more stable behaviour than the BEMT model which reached quickly a converged solution. The CFD/BEMT model resolves the time-domain Navier-Stoke equations in contrast to the steady-state solution of the BEMT approach. Turbulence generation is synonymous of energy dissipation. The BEMT model is not able to capture the energy dissipation and so more kinetic energy is transformed to rotor power. In contrast, the CFD/BEMT model considers the production of turbulence which energy is dissipated in the flow around and downstream of the turbine, and so less kinetic energy is captured by the rotor turbine.

Table 5. Average turbine rotor power.

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(W)	(W)	(W)	(%)
0.6	56.1	44.8	11.2	25.0
1.0	259.6	202.3	57.3	28.4

shows the average values of the rotor power calculated by two approaches. Higher values were calculated by the BEMT model as it does not consider the energy dissipation by the turbulence. As explained before, the increase of the free stream velocity means more generation of turbulence and less kinetic energy captured to transform in rotor power.

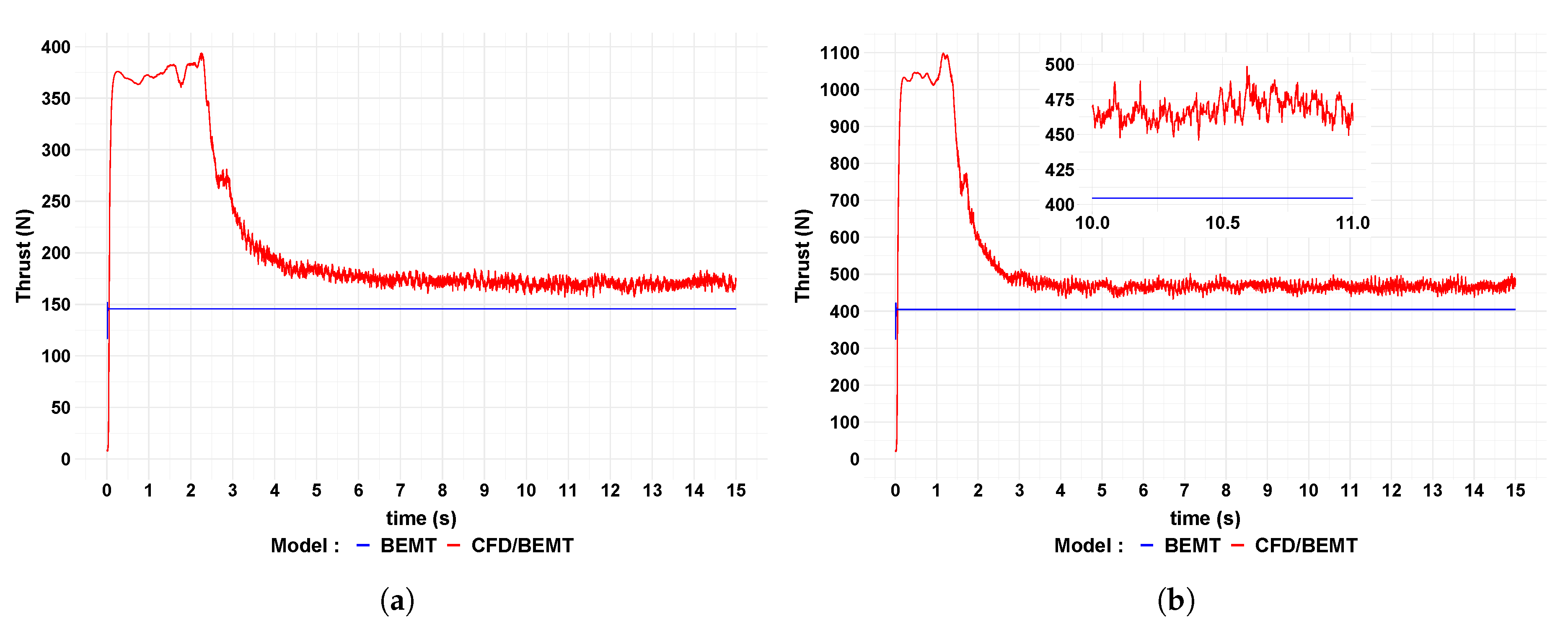
The behaviour of the thrust over the time domain is presented in Figure 6. Differently to previous mechanical variables, the values of thrust predicted by the CFD/BEMT model during the stable period are slightly higher to those calculated by the BEMT model. As the BEMT model does not consider the influence of the turbulence, it is simulating a slightly more “efficient” turbine, i.e., higher values of rotor torque and power and lower values of thrust in contrast to the BEMT/CFD model. The turbulence impact is also reflected in the results shown in

Table 6. Average turbine thrust.

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(N)	(N)	(N)	(%)
0.6	145.7	170.3	−24.6	14.4
1.0	404.7	467.0	−62.3	13.3

. The difference in the average thrust calculated between the two models increases according to the increment of the free stream velocity. Higher free stream velocity means a higher turbulent flow.

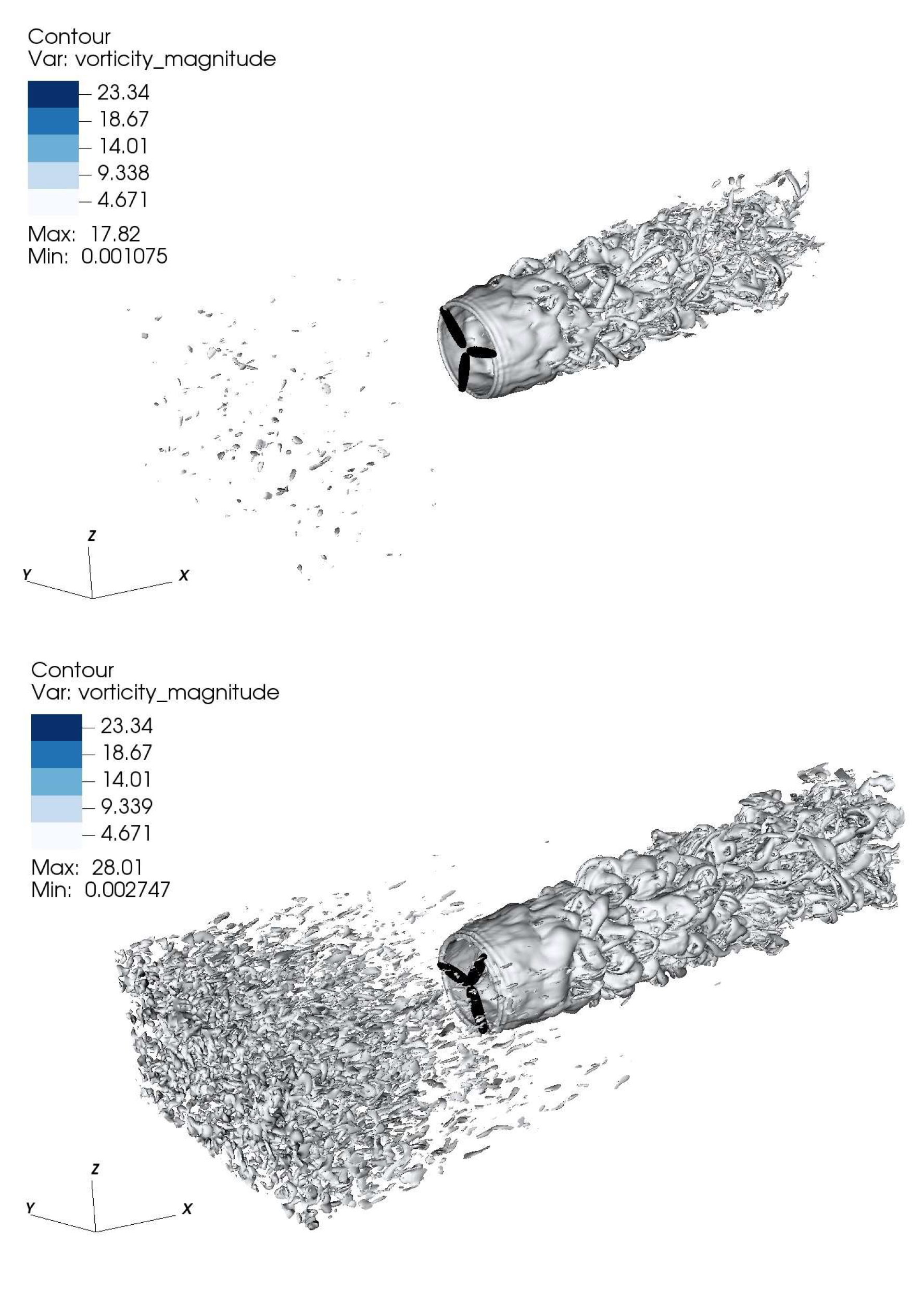
CFD allows a deep understanding of the flow behaviour inside the domain and the impact of this in the tidal turbine variables response. The next figures show snapshots of flow development around the tidal turbine during the stable period generated by the CFD/BEM model. In the figures, the top corresponds to the free stream velocity of 0.6 m/s and the bottom to the free stream velocity of 1.0 m/s. Figure 7 shows the vorticity magnitude contours. It is possible to note, as the free stream velocity increases, more synthetic turbulence is generated at the inlet. Similarly, downstream the turbine, the larger and stronger wake is generated for the higher free stream velocity case.

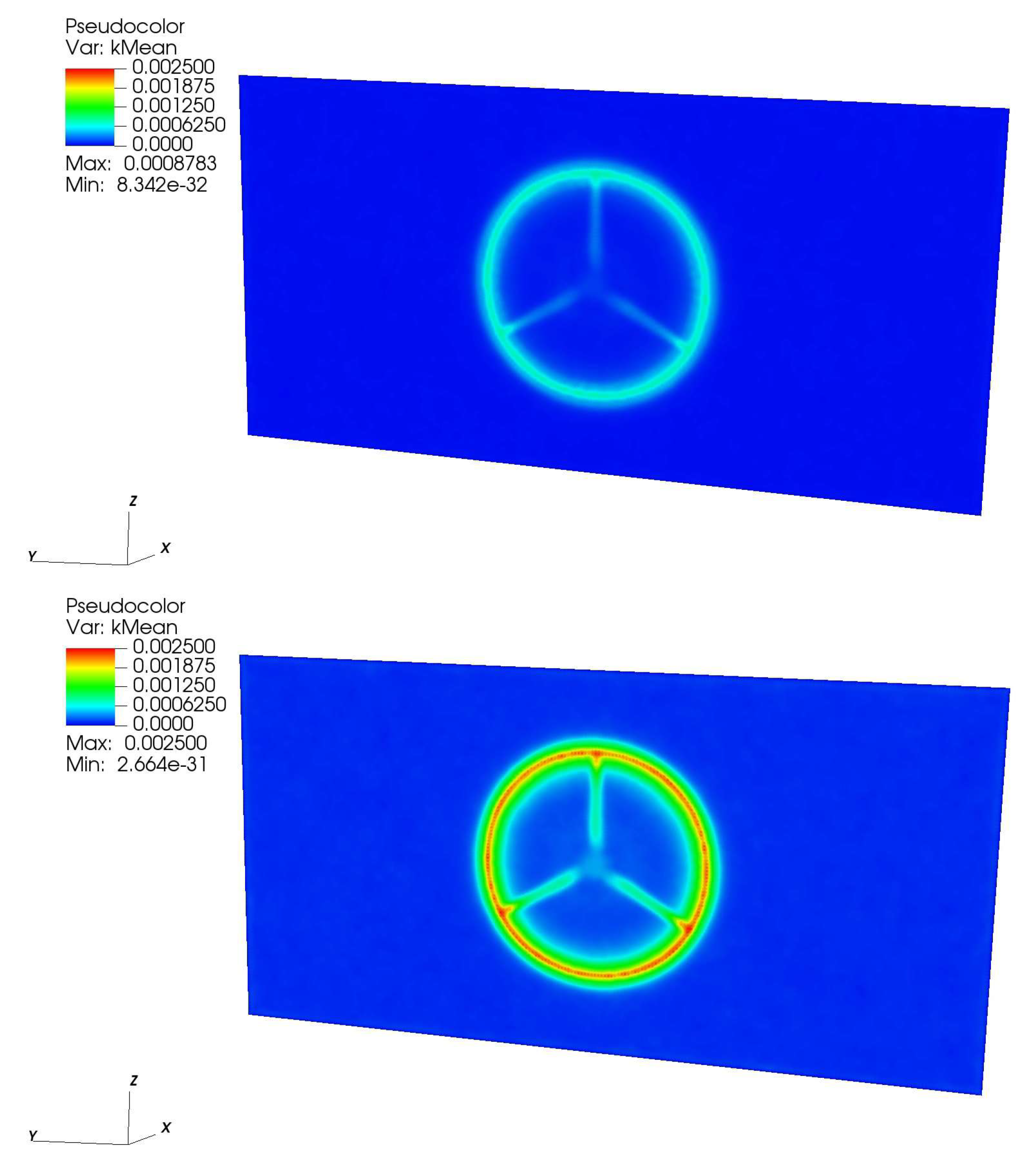
Figure 8 presents the turbulent kinetic energy at the rotor cross-section. The figure shows the highest turbulence generated at the tip of the rotor blades. A “turbulent ring” is generated as the blades rotate around the rotor axis. These Figure 7 and Figure 8 confirm our previous statement about higher free stream velocity means more generation of turbulence and more dissipation of turbulent kinetic energy around and downstream the turbine.

Distribution of velocity magnitude along a longitudinal plane cut at the rotor hub level of the CFD domain is presented in Figure 9. The magnitude of the velocity field is according to the value of the free stream velocity at inlet. The case with lower values of velocity magnitude at the top and the case with higher values of velocity magnitude at the bottom of the figure. For both free stream velocity cases, the lowest values of velocities are those located inside the wake downstream the turbine. It is possible to note a shorter generated wake for the lower free stream velocity case (top).

Next, the results computed by the electrical system are presented. The input to the electrical system model is the time-domain rotor torque at the shaft calculated by the BEMT or CFD/BEMT approaches. As mentioned previously, the rotor torque is a result of an energy balance when the angular shaft acceleration tries to reach zero.

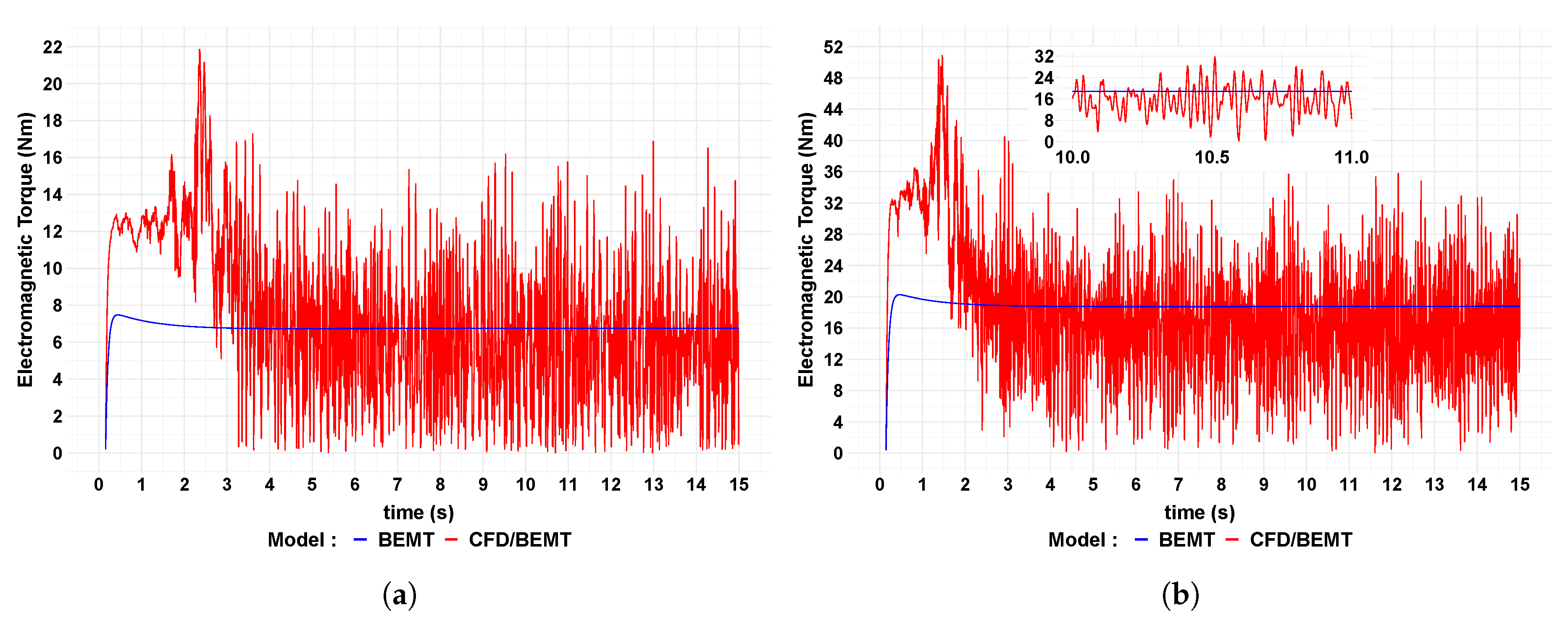
Figure 10 shows the time-series of the electromagnetic torque produced by the generator that is managed by the MPPT and ZDC controllers to reach maximum values of power generation. Similar to the turbine rotor blades results, the time-series comprises a transient and a stable region. Large fluctuations of the electromagnetic torque were predicted in the case where the CFD/BEMT model was used for the coupled-system. In addition to hydrodynamic effects such as turbulence, large fluctuations are also due to the fast response of the controller to maintain optimum generator speed.

Table 7. Average turbine electromagnetic torque.

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(Nm)	(Nm)	(Nm)	(%)
0.6	6.8	5.8	1.0	16.5
1.0	18.8	15.8	2.9	18.5

presents the average values of the electromagnetic torque calculated using the two approaches for the turbine rotor blades. The values are similar to those calculated for the mechanical rotor torque, in Table 4, where the torque balance is reached during the stable period, in Equation (1), and the angular rotational acceleration tries to reach zero. Similar to the results for the mechanical system, if the free stream velocity increases, the difference in the results between the two approaches also increases. Hence, the influence of the hydrodynamic characteristics, like turbulence, also influences the electrical variables.

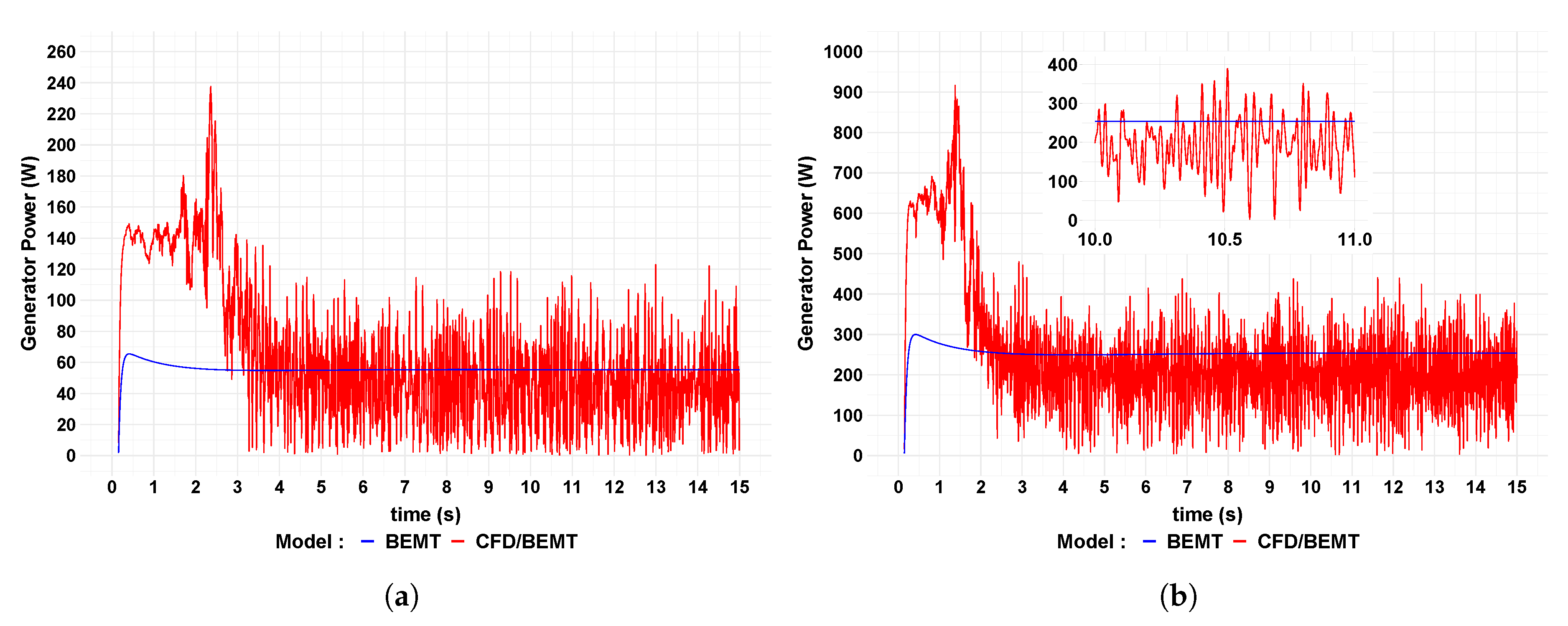
Figure 11, shows the power output from the generator for the two different flow speeds. Since the generator power is a multiplication of generator speed and electromagnetic torque, it follows a similar profile to that of the electromagnetic torque.

Table 8. Average turbine generator power.

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(W)	(W)	(W)	(%)
0.6	55.2	43.7	11.5	26.3
1.0	253.4	196.2	57.2	29.2

shows the average values for generator power calculated using the two different methods. The results are very similar to the average values for turbine rotor power, shown in Table 5, with the difference attributed to the losses within the generator.

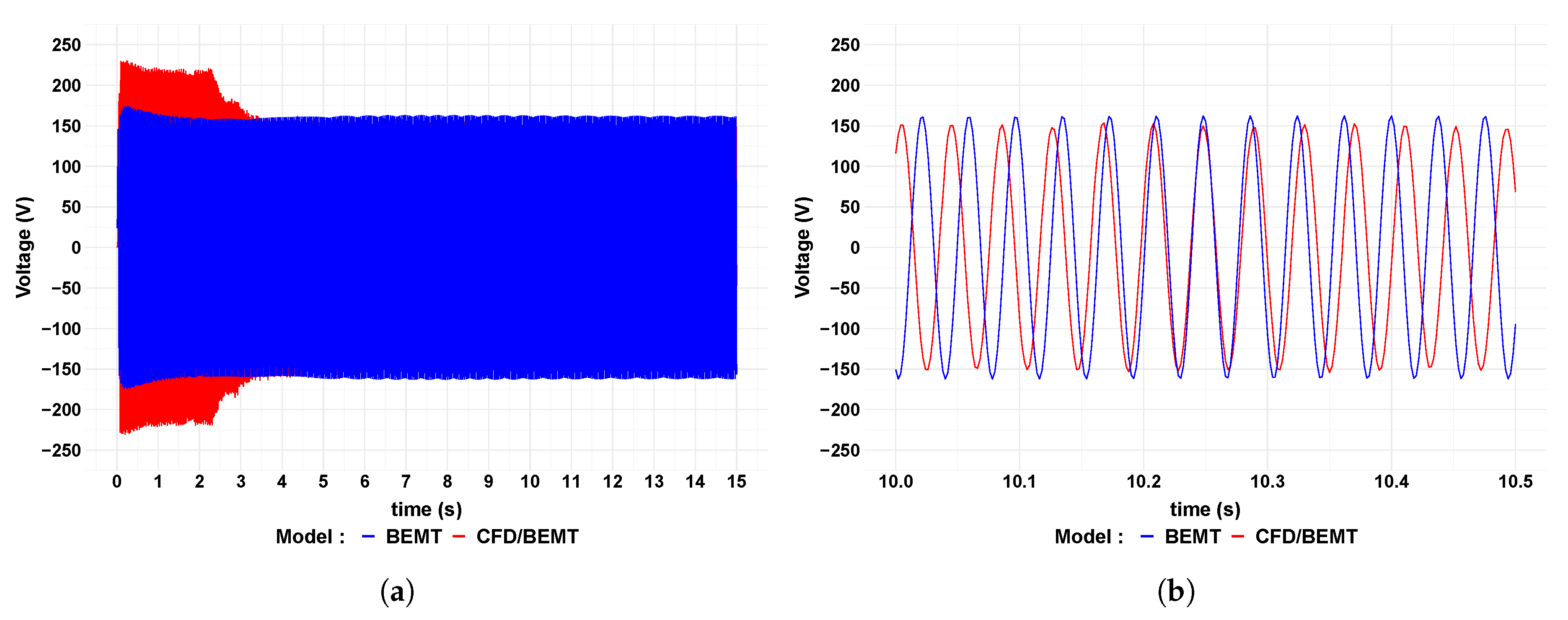
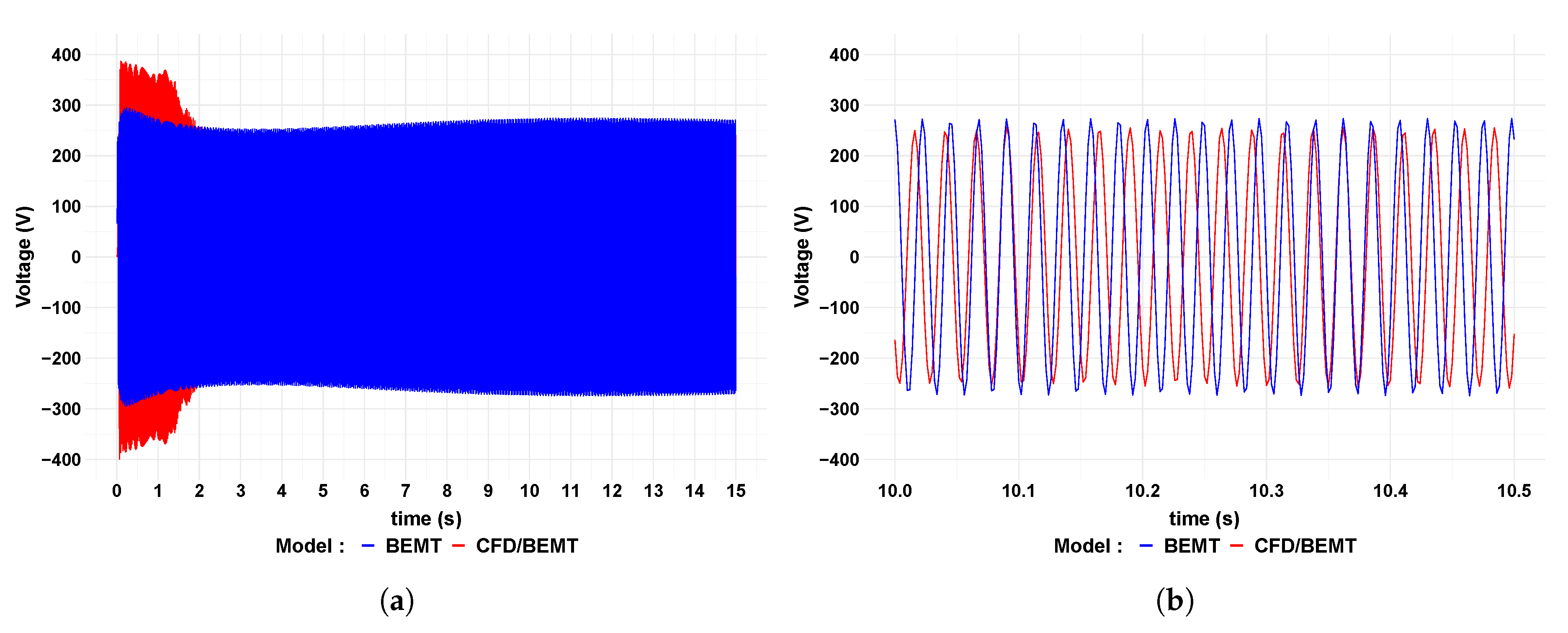
The phase voltage at the generator terminals for flow velocities of 0.6 m/s and 1.0 m/s are shown in Figure 12 and Figure 13 respectively. In both figures, the red and blue wave forms can be seen to move in and out of phase with each other. It is due to the voltage predicted by the BEMT model has a slightly higher frequency than that calculated by the CFD/BEMT model. This situation is related to the turbine rotational speed difference calculated by the two models, Figure 3. The voltage amplitudes, however, are very closely matched between the two modelling approaches after the initial transient period.

Table 9. Generator phase voltage (RMS).

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(V)	(V)	(V)	(%)
0.6	114.6	106.2	8.4	7.9
1.0	190.3	176.7	13.5	7.7

shows a very consistent average voltage difference of just below 8% between the two modelling approaches at both flow velocities.

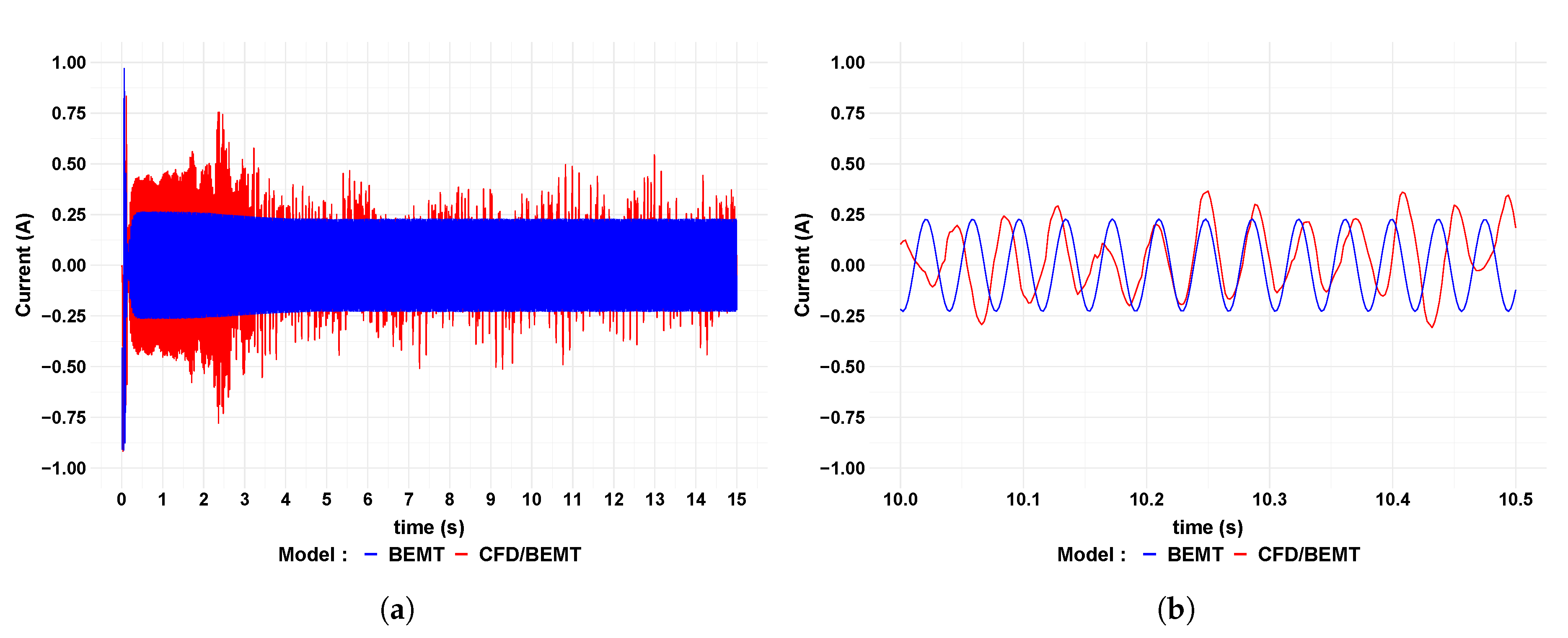
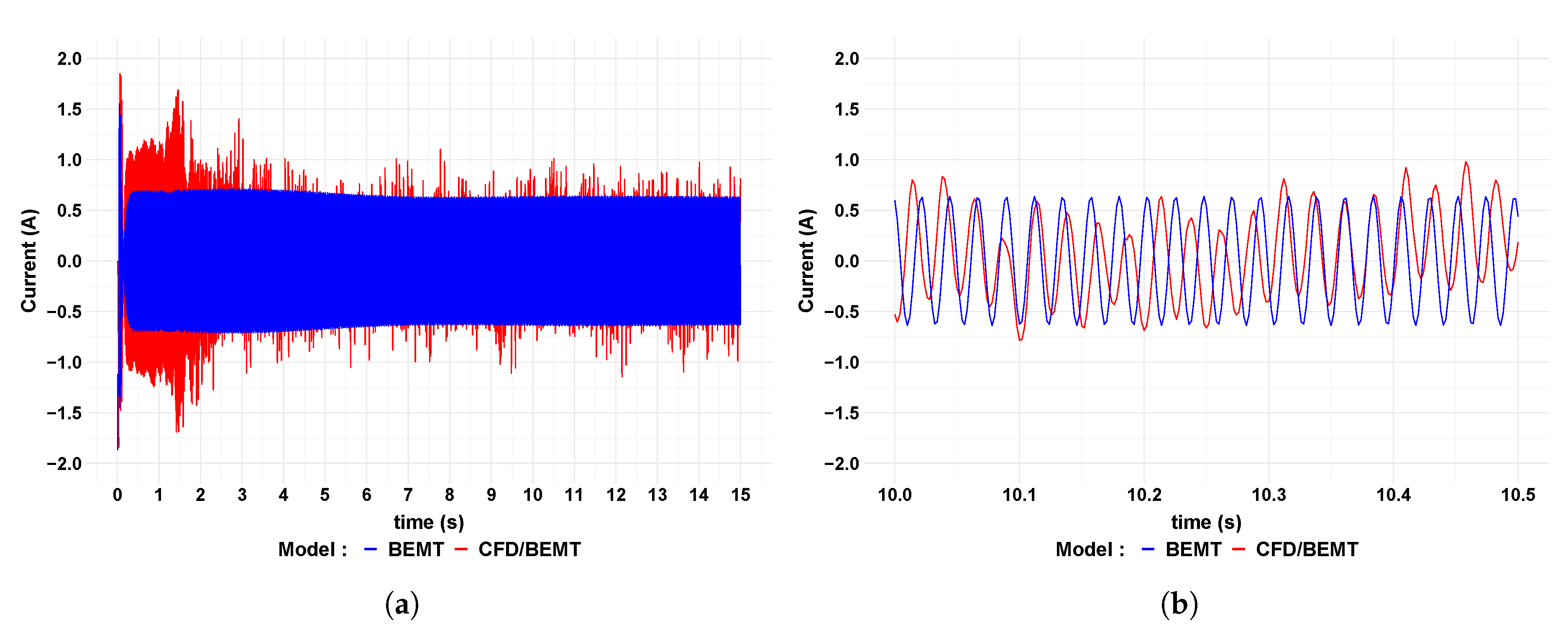
The current at the generator terminals for flow velocities of 0.6 m/s and 1.0 m/s are shown in Figure 14 and Figure 15 respectively. It can be seen that the amplitude of the current for the BEMT model is relatively constant with only a slight increase during the transient period. The CFD/BEMT modelling approach shows more variation in current amplitude; this is particularly noticeable in the wave forms shown in part (b) of both figures. As with the voltage, there is a slight difference in frequency between the two models. The BEMT model predicts a slightly higher frequency than the CFD/BEMT model.

Table 10. Generator phase current (RMS).

Uo	BEMT	CFD/BEMT	Difference	Difference
(m/s)	(A)	(A)	(A)	(%)
0.6	0.161	0.170	−0.009	5.338
1.0	0.448	0.425	0.023	5.491

shows that there is no difference in RMS current, to one decimal place, between the BEMT and CFD/BEMT modelling approaches.

Table 11. Standard deviation of the mechanical and electrical variables using the BEMT/CFD approach.

Uo	Rotational	Thrust	Rotor	Rotor	Electrical	Electrical
	Speed		Torque	Power	Torque	Power
(m/s)	(RPM)	(N)	(Nm)	(W)	(Nm)	(W)
0.6	0.6	3.9	0.2	2.0	3.4	25.7
1.0	0.8	9.7	0.7	9.0	6.5	79.9

shows the standard deviation of the main mechanical and electrical variables operation of the coupled system at flow velocities of 0.6 m/s and 1.0 m/s using the BEMT/CFD model. For the mechanical variables (thrust, torque and power) and rotational speed, the rise in the standard deviation as increasing the free stream velocity is a consequence of the increase of the turbulence. It means the turbine rotor blades have to gather kinetic energy from a more unstable flow. Although average values for rotor and electrical torque are similar, there is significantly more standard deviation variation in electrical torque, which can be attributed to the fast response of the MPPT controller which tries to maintain maximum power by rapidly adjusting the torque produced by the generator.

5. Conclusions

In this work, a coupled system, formed by a mechanical and electrical system, was presented. The mechanical system involves the turbine rotor blades and its surrounding sea. A first approach using Blade Element Momentum Theory (BEMT) was used for the calculation of the hydrodynamics forces at rotor location after approximating the free stream velocity by the use of inductions factors. A second approach called CFD/BEMT was also used. This approach uses CFD and Large Eddy Simulation (LES) to model the ocean environment and an Actuator Line Model (ALM) to simulate the operational blades (BEMT and body forces). The electrical system is composed of a PMSG, harmonic filters, a step-up transformer, lines for power transmission, and an electrical grid. Controllers are also installed in the electrical system to keep the maximum power production and assure the power delivery according to grid requirements. A torque balance allowed the coupling between the mechanical and electrical system. There was a full coupling between the involved systems, as the torque balance generates an angular acceleration at the shaft updating the rotational speed of the turbine rotor and so modifying the velocity field and turbulence generation surrounding the rotor blades.

Thus, the time-series of the results present two defined periods, the transient and the stable period. For the CFD/BEMT model, the transient period is characterized by an irregular behaviour of the turbine variables as the rotor starts to work at rest, progressing trying to reach an energy balance over time. This transient period is followed by a “stable period” where the turbine variables oscillate around a constant average value. The fluctuations presented during the stable period indicate that turbulence continuously influences the behaviour of the mechanical turbine variables (thrust, torque, rotor angular speed, root bending moment, etc.). The BEMT model simulations are not as noisy, since this model does not consider the effects of turbulence and other intrinsic properties of the surrounding sea flow.

The lack of the dynamic flow behaviour in the BEMT model is also reflected in the fact that this model over predicts rotational speed, torque and power and under predicts thrust compared with the CFD/BEMT model. Part of the total kinetic energy in the tidal stream is not captured by the turbine but is instead dissipated by turbulence. Whilst this process is modelled by the LES solver, it is not accounted for the the BEMT model. Consequently this model over predicts the conversion of mechanical power.

The electrical variables (torque, power, current and voltage) behave in a similar way to their mechanical counterparts. The results from the CFD/BEMT model demonstrated that the electrical variables also are affected by the turbulent flow, as well as being perturbed by the fast response of the controllers used to keep the turbine working at high levels of power production. In both the approaches used for the rotor blades (BEMT and CFD/BEMT) similar regular behaviour for the generator phase voltage is observed. However, an irregular curve behaviour was predicted by the CFD/BEMT model for the generator phase current also due to the turbulence and the controller response.

The effect of the turbulence is also reflected when the free stream velocity is increased. Higher free stream velocity means more captured kinetic energy by the turbine and more dissipated kinetic energy by turbulence. This additional dissipation of turbulent kinetic energy is not considered by the BEMT and so it is reflected in the increment of the difference when compared with the CFD/BEMT model results. Rise of turbulence according to the increase of free stream velocity is also manifested in the rise of the standard deviation of mechanical and electrical variables using the BEMT/CFD model. Higher standard deviation during the stable period means a more unstable flow surrounding the turbine.

The BEMT model demonstrated to be an efficient computational tool. It is able to compute turbine characteristic variables like thrust, torque and power with a low computational effort. On the other hand, the CFD/BEMT model, which needs High-Performance Computing, can give insights into the flow dynamics around the turbine and can calculate turbine characteristic variables considering intrinsic flow properties like turbulence. The use of BEMT models in the design process of a turbine can mean to have a slightly more conservative design, with the advantage of lower computational cost. The use of more complete models like CFD/BEMT can lead to more accurate predictions of the blade loads, like those generated by the presence of turbulence, which are especially important in the fatigue-related design process of a turbine. However, the computational cost necessary to carry out the simulations also needs to be weighed up.

A next step in the study of the coupled system for tidal turbines is to analyse abnormal behaviour during operational conditions. That means any abnormal behaviour in the rotor blades can be reflected in the components of the electrical system. For example, large fluctuation of the electromagnetic torque due to the rotor blades operating under a high level of turbulent flow. This situation is a source of additional stresses that are undergone by the generator, like in this work. Similarly, any unexpected failure in an electrical component can compromise the reliability of a mechanical part. For instance, a failure in the generator control system can produce incorrect electromagnetic torque values, so the shaft angular velocity can speed-up compromising the integrity of the rotor and blades. Therefore, failure effects can be propagated through the whole coupled system.