Development of Decision-Making Tool and Pareto Set Analysis for Bi-Objective Optimization of an ORC Power Plant
Abstract
1. Introduction
2. Analysis and Modeling
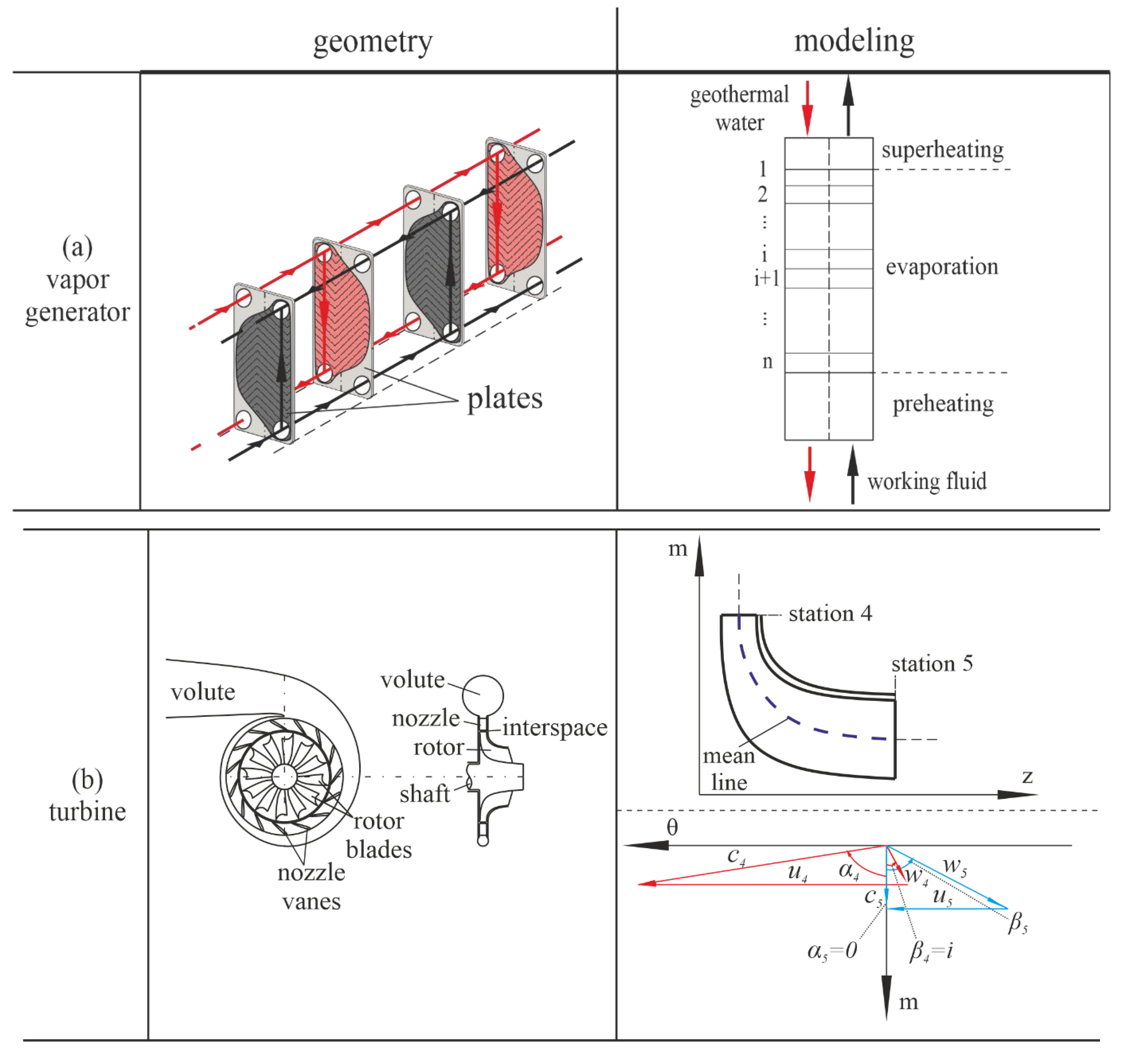
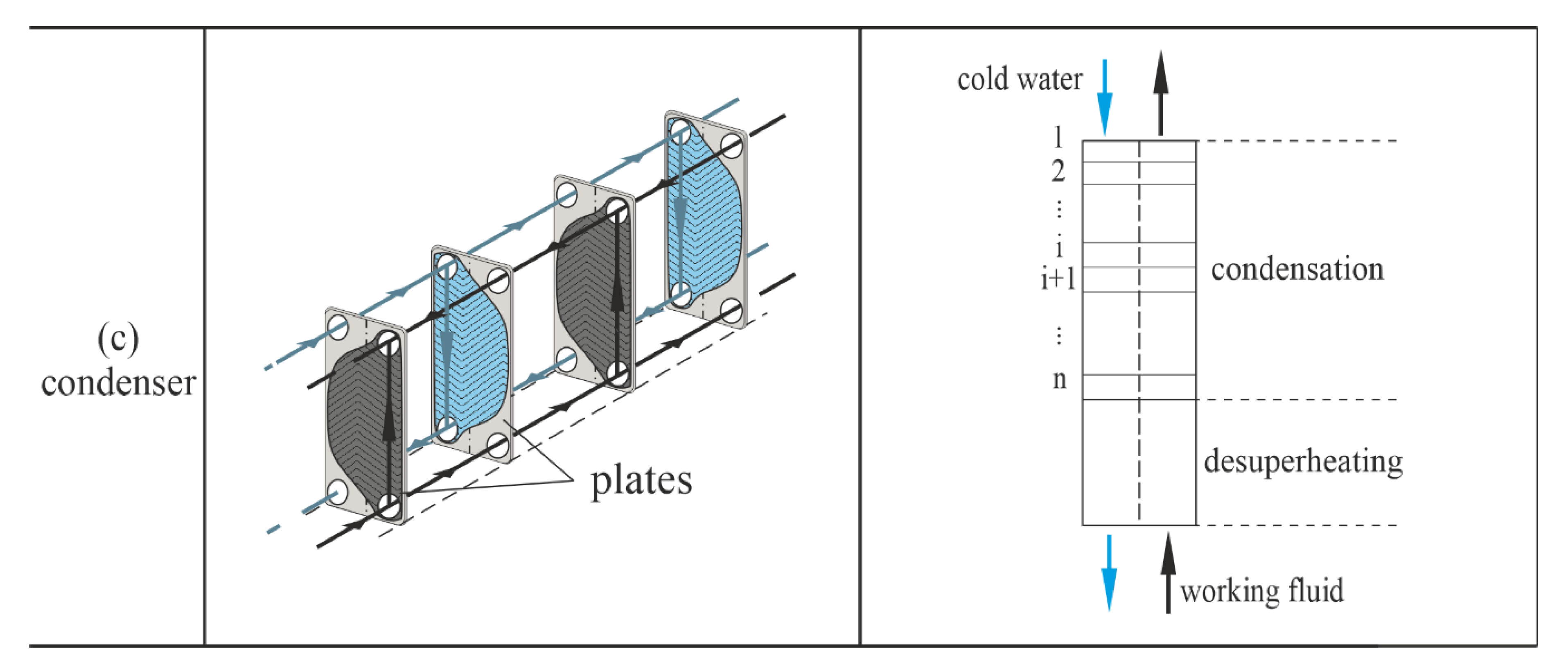
2.1. System Description
2.2. Modeling of ORC Components
2.3. Assumptions and Calculation Steps
2.4. Validation of the Calculation Model
3. Bi-Objective Optimization
Optimization Problem
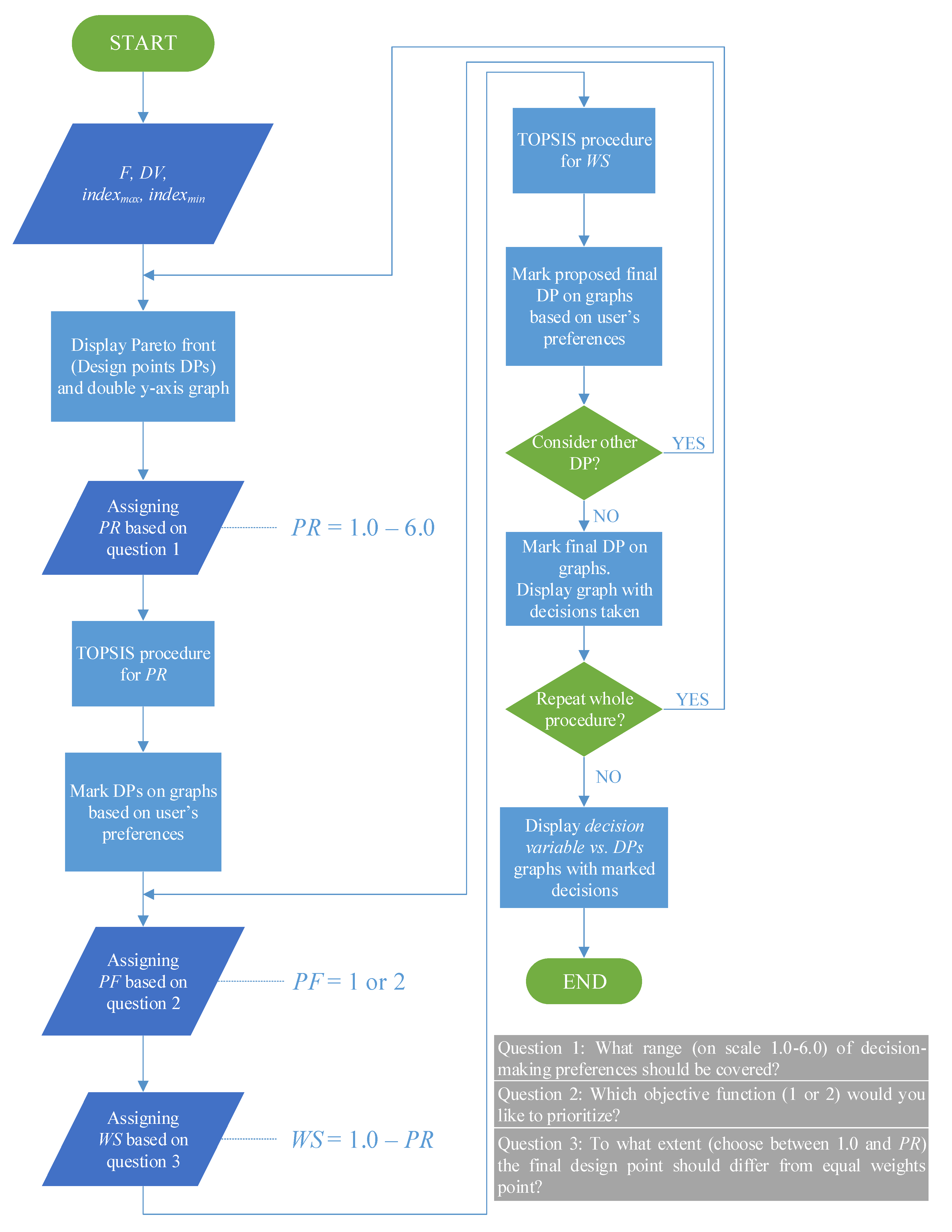
4. Development of Decision-Making Tool
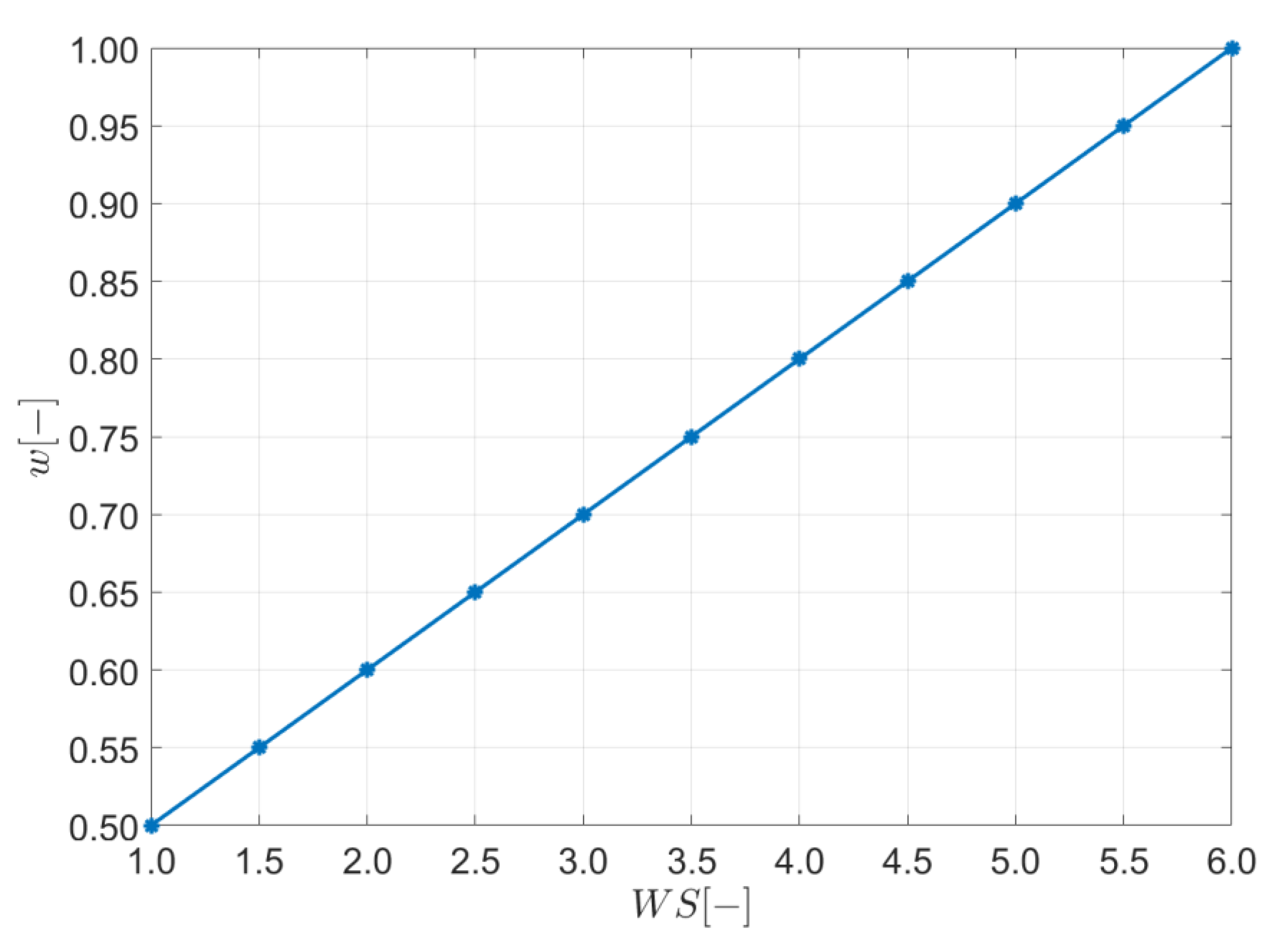
4.1. General Concept and Weighting Technique
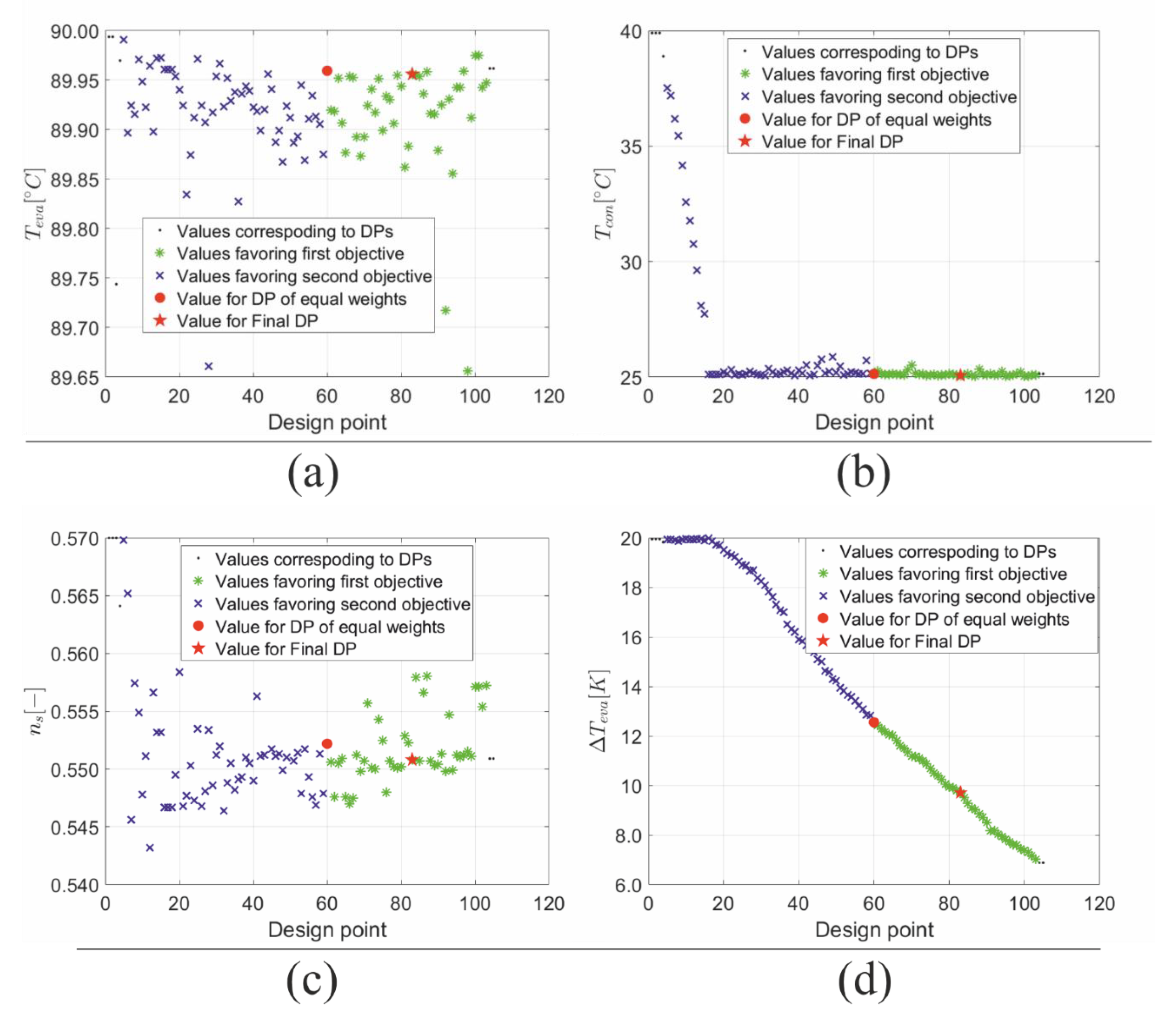
4.2. Description of the Procedure
5. Results and Discussion
5.1. Decision-Making Analysis
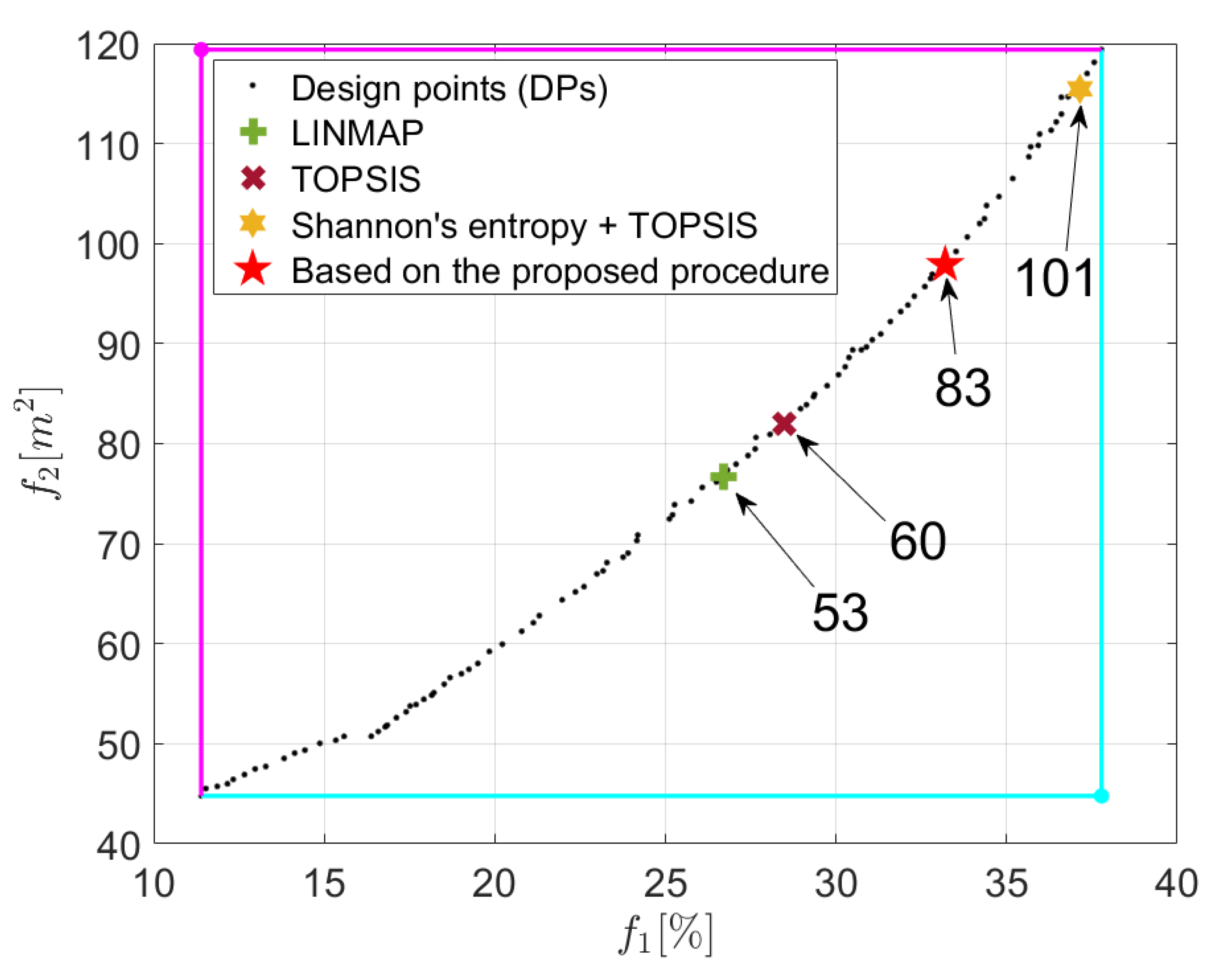
5.2. Comparative Analysis with other Decision-Making Methods
6. Conclusions
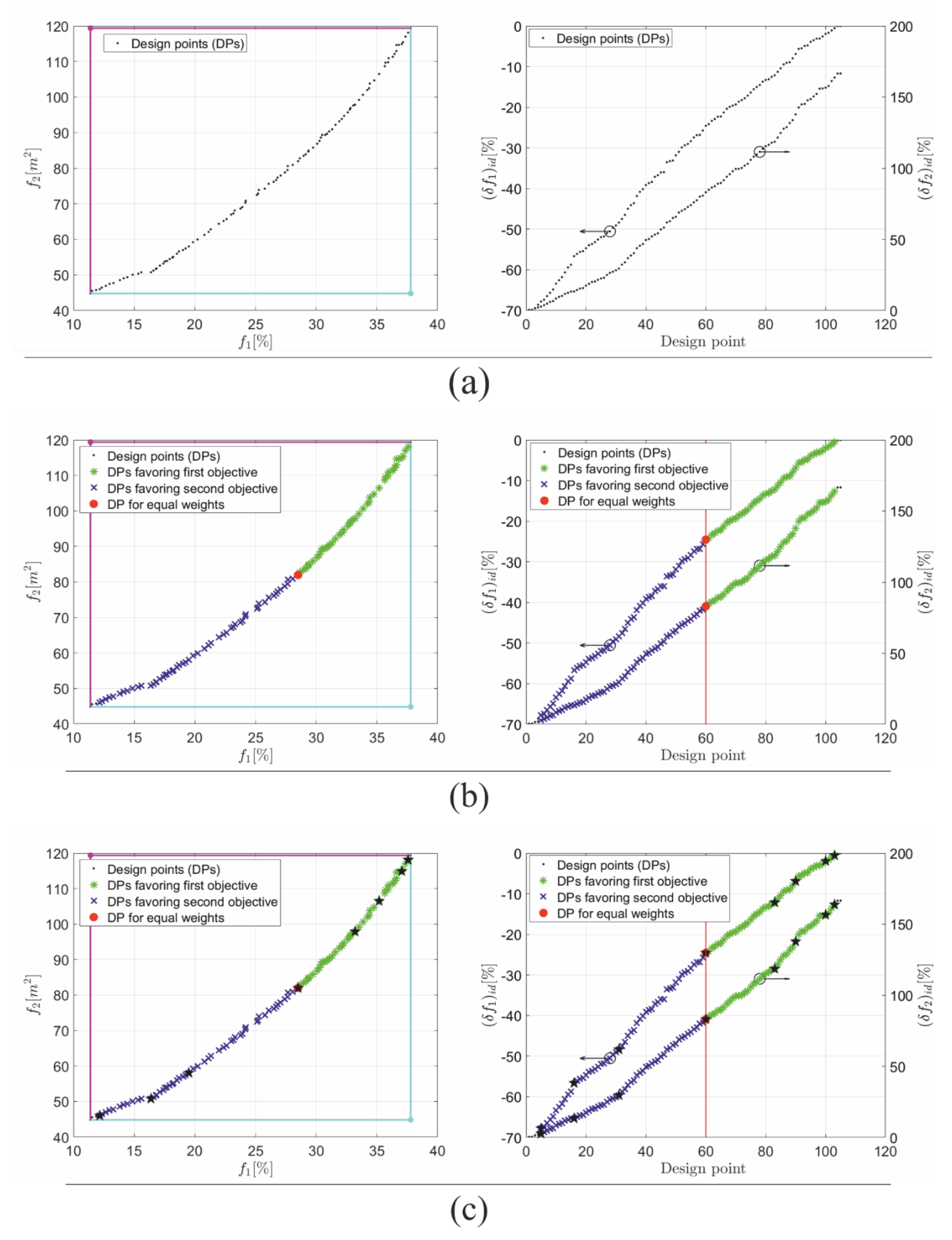
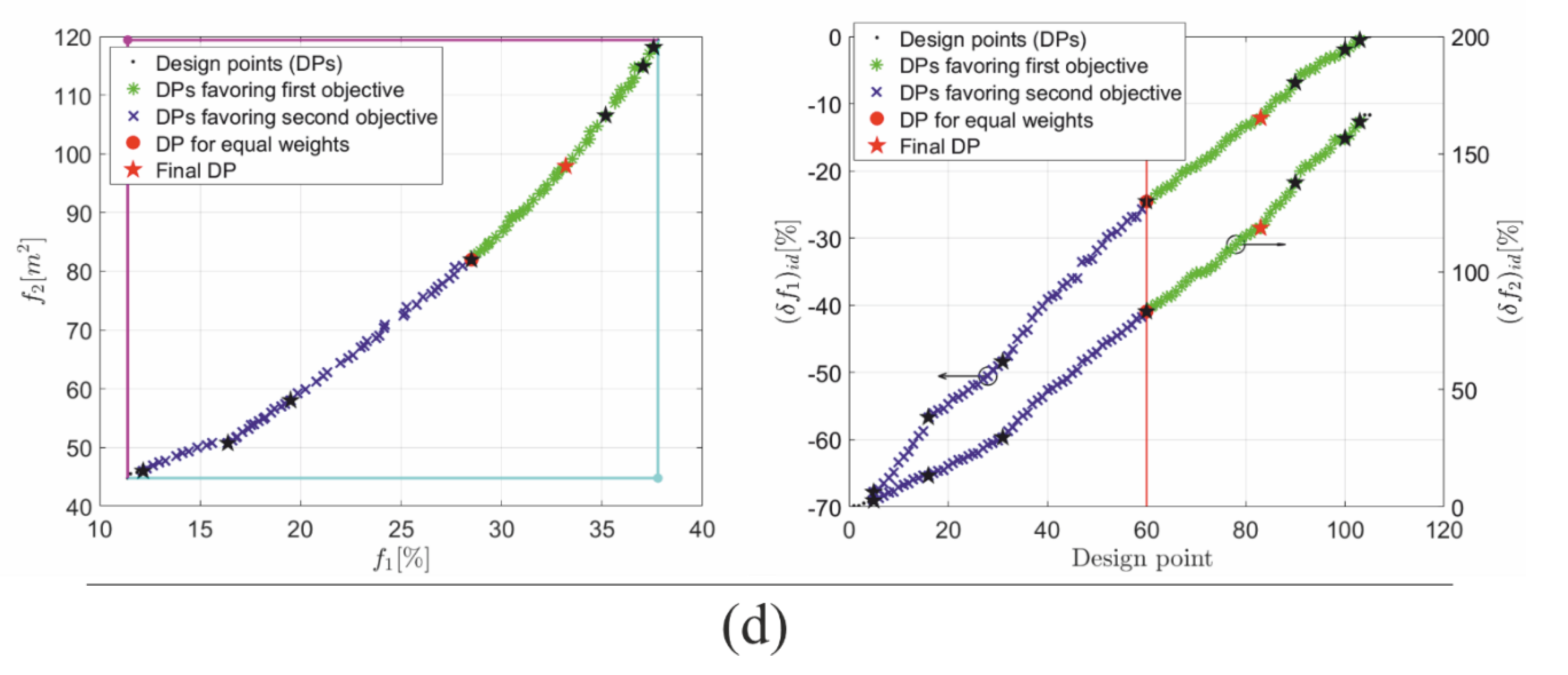
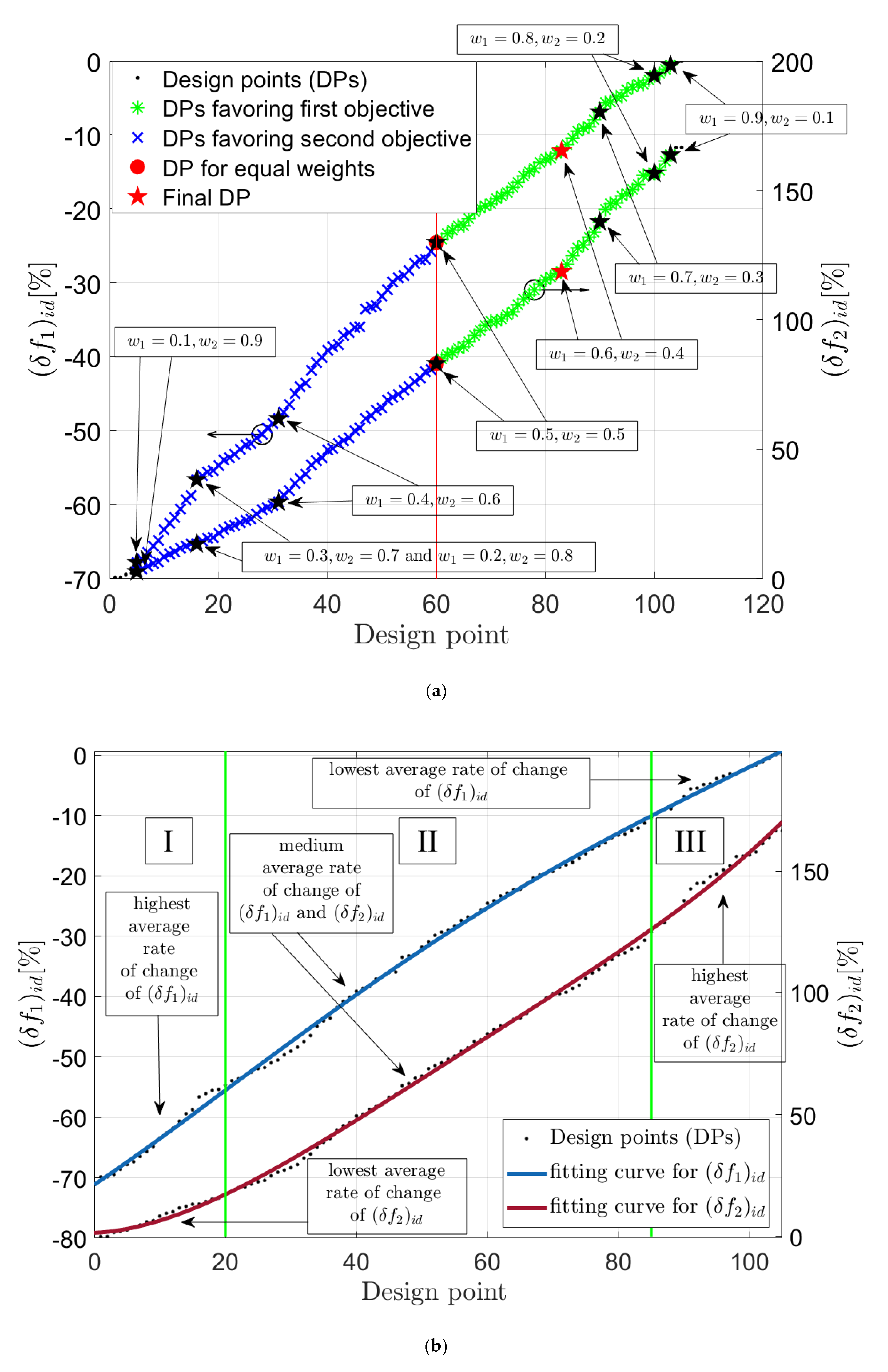
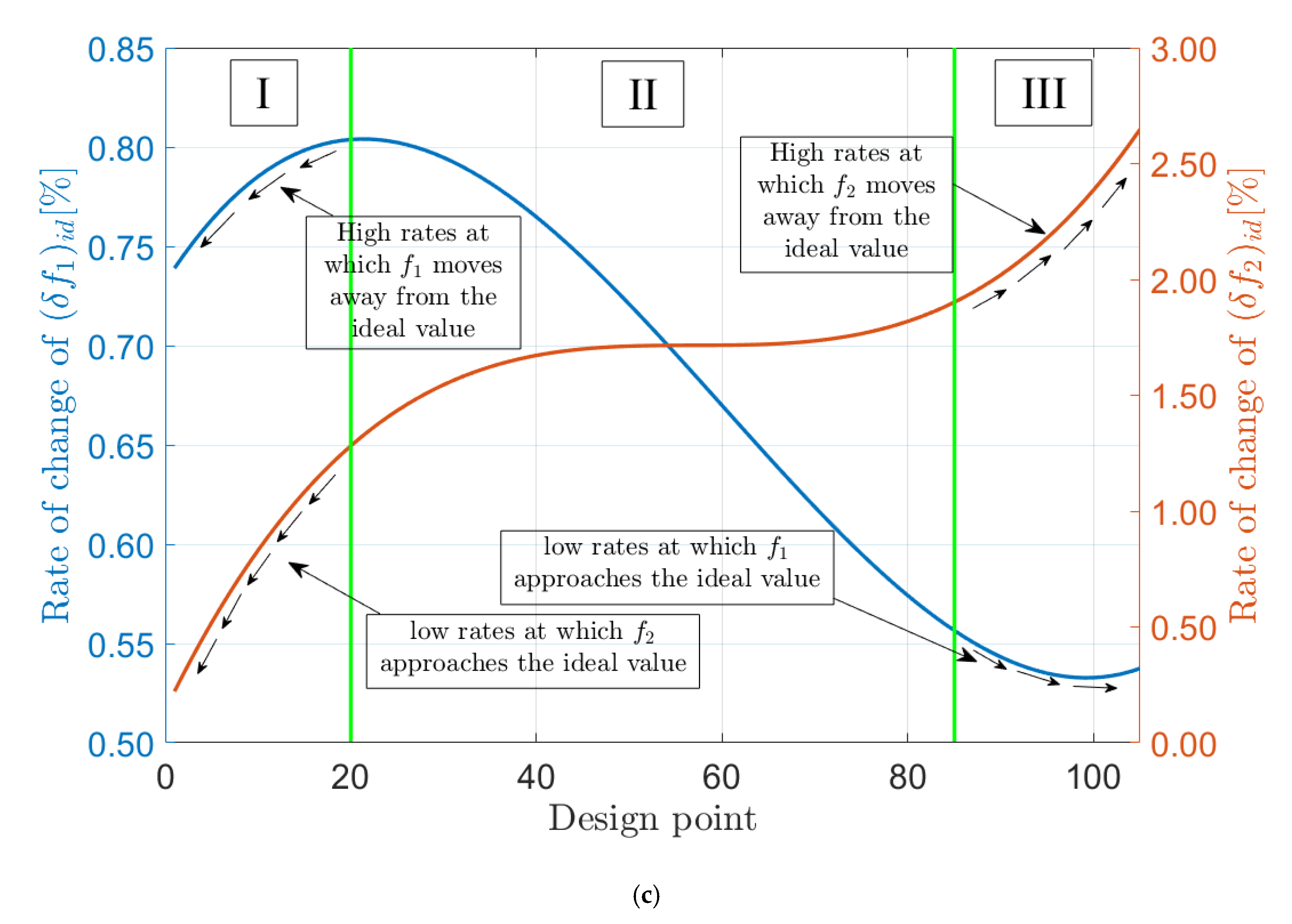
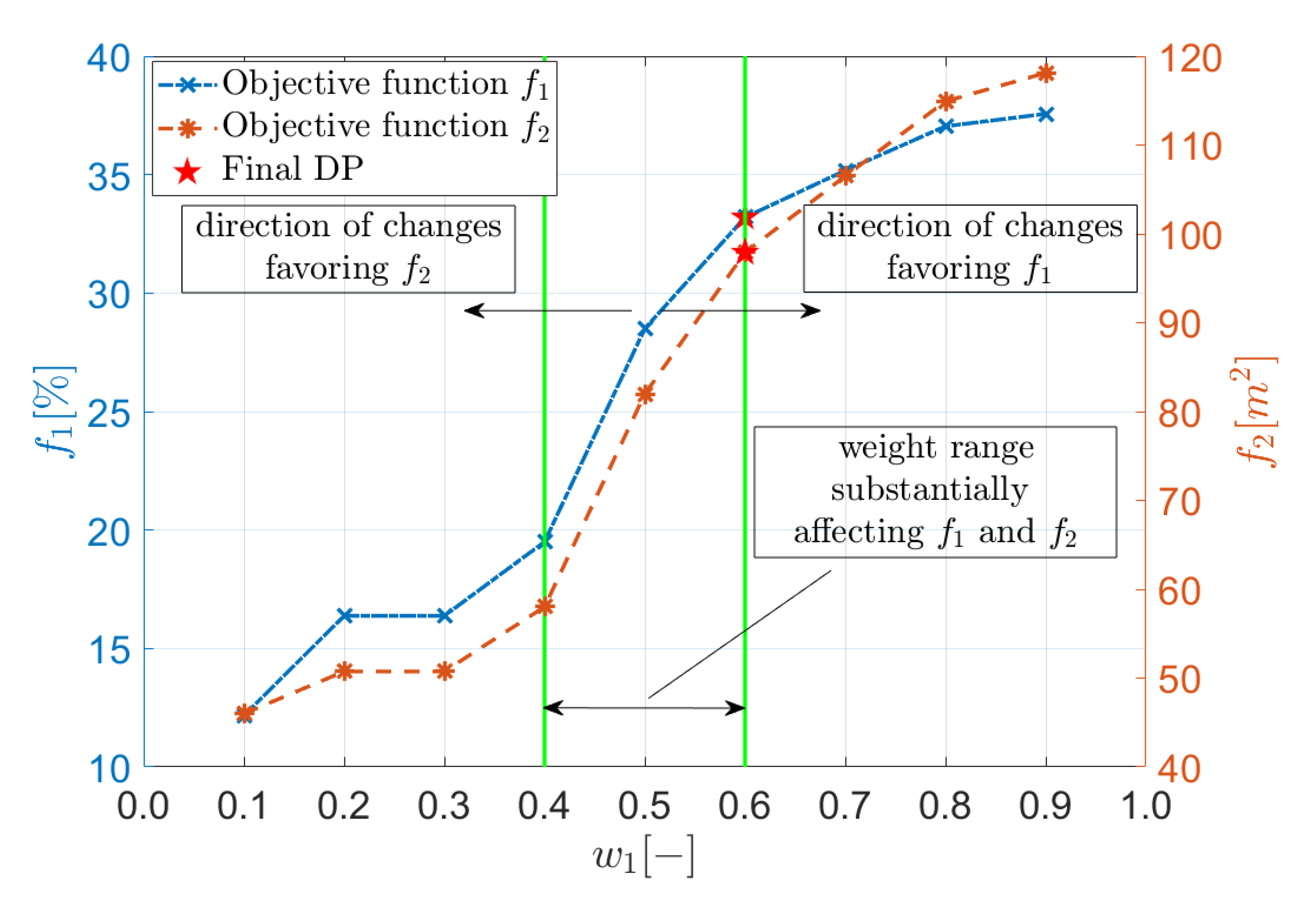
- while analyzing the rates at which the criteria approach their ideal solutions, it was found that there are regions of design points in which an intensified deterioration of one of the objectives is combined with a slight improvement of the second criterion. For this reason, from among the 105 design points, these numbered as lower than 20 and higher than 85 have been excluded from the set of potential final design points;
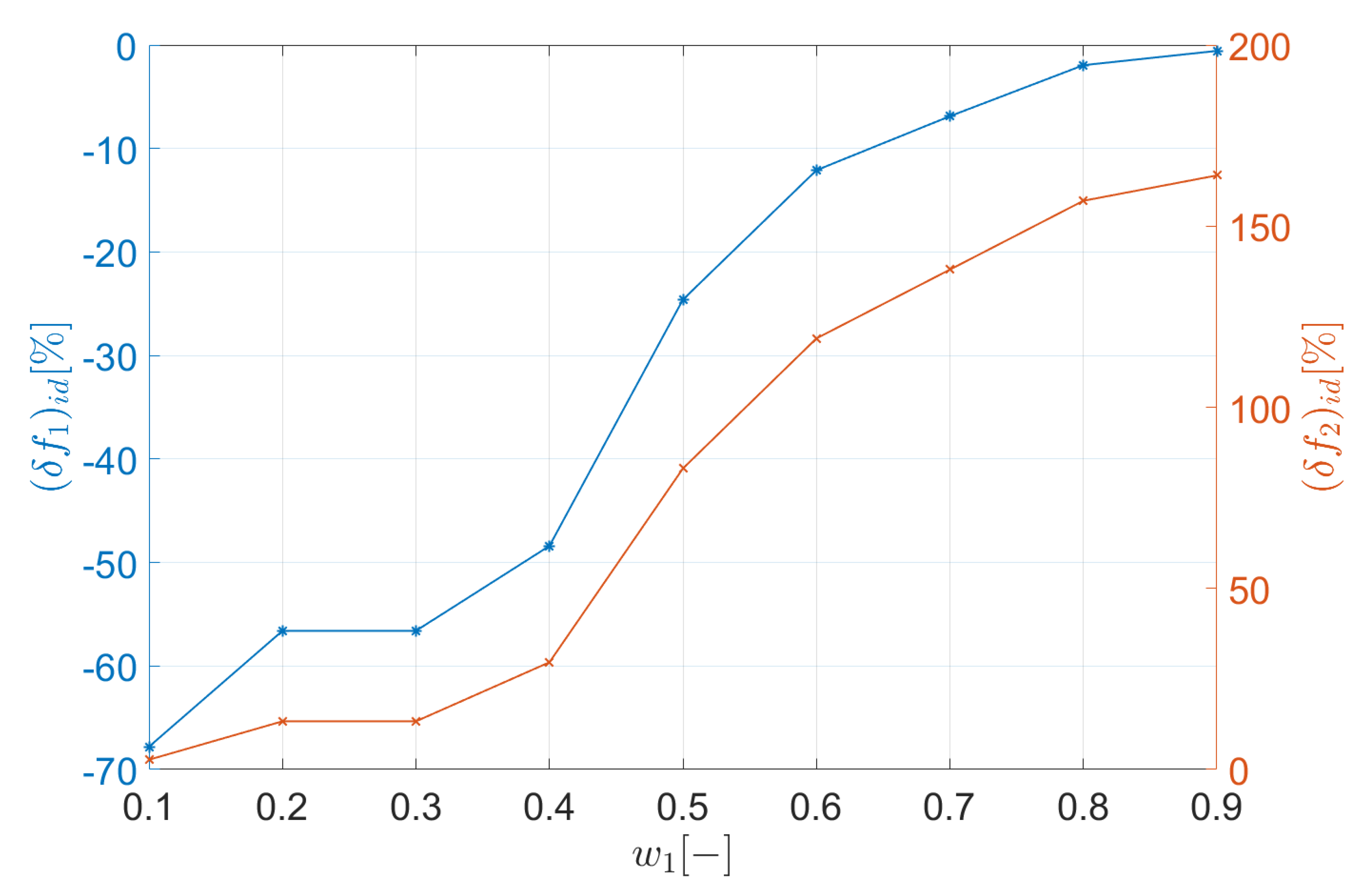
- while considering the final design point, it was highlighted to discard the weights and as values corresponding to excluded Pareto set points;
- most commonly applied forms of decision-making techniques, such as LINMAP or TOPSIS, are appropriate for inexperienced designers as they do not require specifying the decision-maker preferences. As a tool allowing for a careful examination of the criteria weights, the proposed program provides a more conscious and comprehensible choice of the final optimal configuration for the examined system.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | heat transfer area [m2] |
| exergy flow rate [kW] | |
| B | blade width [m] |
| c | absolute velocity [m s−1] |
| f | objective function [m2] or [%] |
| h | specific enthalpy [J kg−1] |
| i | incidence angle [°] |
| k | overall heat transfer coefficient [W m−2 K−1] |
| low | lower bound [-] |
| Ma | Mach number [-] |
| m | meridional direction [-] |
| mass flow rate [kg s−1] | |
| n | number of finite subprocesses [-] |
| ns | specific speed [-] |
| Pout | net power output [kW] |
| PF | priority function parameter |
| PR | preference range parameter |
| heat transfer rate [kW] | |
| R | reaction degree [-] |
| r | radius [m] |
| s | specific entropy [kJ kg−1 K−1] |
| sal | salinity [kgkg−1] |
| T | temperature [K] or [°C] |
| u | peripheral velocity [m s−1] |
| up | upper bound [-] |
| volume flow rate [m3 h−1] | |
| WS | weight superiority parameter |
| w | weight [-] or relative velocity [m s−1] |
| vector of decision variables | |
| ZR | axial length of rotor [m] |
| z | axial direction [-] |
| Greek Symbols | |
| α | absolute flow angle [°] |
| β | relative flow angle [°] |
| ΔHid | isentropic enthalpy drop [kJ kg−1] |
| Δhloss | enthalpy loss [kJ kg−1] |
| ΔT | temperature difference [K] |
| (δf)id | deviation from ideal solution |
| η | efficiency [%] |
| θ | tangential direction [-] |
| ω | rotation speed of a turbine rotor [rad s−1] |
| Sub- or Superscripts | |
| con | condensation |
| cw | cold water |
| eva | evaporation |
| ex | exergy |
| gw | geothermal water |
| hub | hub |
| in | inlet |
| log | logarithmic |
| out | outlet |
| P | pump |
| pre | preheating |
| sh | shroud |
| sup | superheating |
| T | turbine or transposition |
| tot | total |
| VG | vapor generator |
| wf | working fluid |
| Abbreviations | |
| BOO | bi-objective optimization |
| DP | design point |
| LINMAP | Linear Programming Technique for Multidimensional Analysis of Preference |
| MOO | multi-objective optimization |
| NSGA-II | Non-dominated Sorting Genetic Algorithm-II |
| ORC | organic Rankine cycle |
| pp | percentage point |
| RIT | radial-inflow turbine |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| TRADeS | Tracking and Recognizing Alternative Design Solutions |
| WD | weight distribution |
References
- Altun, A.F.; Kilic, M. Thermodynamic performance evaluation of a geothermal ORC power plant. Renew. Energy 2020, 148, 261–274. [Google Scholar] [CrossRef]
- Roumpedakis, T.C.; Loumpardis, G.; Monokrousou, E.; Braimakis, K.; Charalampidis, A.; Karellas, S. Exergetic and economic analysis of a solar driven small scale ORC. Renew. Energy 2020, 157, 1008–1024. [Google Scholar] [CrossRef]
- Kalina, J.; Świerzewski, M.; Strzałka, R. Operational experiences of municipal heating plants with biomass-fired ORC cogeneration units. Energy Convers. Manag. 2019, 181, 544–561. [Google Scholar] [CrossRef]
- Wang, L.; Bu, X.; Li, H. Multi-objective optimization and off-design evaluation of organic rankine cycle (ORC) for low-grade waste heat recovery. Energy 2020, 203, 117809. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Neofytou, P. Investigating the performance and cost effects of nanorefrigerants in a low-temperature ORC unit for waste heat recovery. Energy 2020, 204, 117966. [Google Scholar] [CrossRef]
- Sadreddini, A.; Ashjari, M.A.; Fani, M.; Mohammadi, A. Thermodynamic analysis of a new cascade ORC and transcritical CO2 cycle to recover energy from medium temperature heat source and liquefied natural gas. Energy Convers. Manag. 2018, 167, 9–20. [Google Scholar] [CrossRef]
- Hu, S.; Li, J.; Yang, F.; Yang, Z.; Duan, Y. Multi-objective optimization of organic Rankine cycle using hydrofluorolefins (HFOs) based on different target preferences. Energy 2020, 203, 117848. [Google Scholar] [CrossRef]
- Dai, X.; Shi, L.; An, Q.; Qian, W. Screening of hydrocarbons as supercritical ORCs working fluids by thermal stability. Energy Convers. Manag. 2016, 126, 632–637. [Google Scholar] [CrossRef]
- Oyekale, J.; Haberle, F.; Petrollese, M.; Brüggemann, D.; Cau, G. Thermo-economic evaluation of actively selected siloxane mixtures in a hybrid solar-biomass organic Rankine cycle power plant. Appl. Therm. Eng. 2020, 165, 114607. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Performance comparison of low-grade ORCs (organic Rankine cycles) using R245fa, pentane and their mixtures based on the thermoeconomic multi-objective optimization and decision makings. Energy 2015, 93, 2018–2029. [Google Scholar] [CrossRef]
- Srinivasan, V.; Shocker, A. Linear programming techniques for multidimensional analysis of preference. Psychometrica 1973, 38, 337–369. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K.P. Multiple Attributes Decision making Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Sensitivity analysis and thermoeconomic comparison of ORCs (organic Rankine cycles) for low temperature waste heat recovery. Energy 2015, 82, 664–677. [Google Scholar] [CrossRef]
- Behzadi, A.; Arabkoohsar, A.; Gholamian, E. Multi-criteria optimization of a biomass-fired proton exchange membrane fuel cell integrated with organic rankine cycle/thermoelectric generator using different gasification agents. Energy 2020, 201, 117640. [Google Scholar] [CrossRef]
- Oyekale, J.; Petrollese, M.; Cau, G. Multi-objective thermo-economic optimization of biomass retrofit for an existing solar organic Rankine cycle power plant based on NSGA-II. Energy Rep. 2020, 6, 136–145. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Sheng, Y. Energy, exergy, economic (3E) analysis and multi-objective optimization of a novel dual functional integration system. Energy Convers. Manag. 2019, 199, 111962. [Google Scholar] [CrossRef]
- Pourrahmani, H.; Moghimi, M. Exergoeconomic analysis and multi-objective optimization of a novel continuous solar-driven hydrogen production system assisted by phase change material thermal storage system. Energy 2019, 189, 116170. [Google Scholar] [CrossRef]
- Shen, G.; Yuan, F.; Li, Y.; Liu, W. The energy flow method for modeling and optimization of Organic Rankine Cycle (ORC) systems. Energy Convers. Manag. 2019, 199, 111958. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Y.; Xia, X.; Zuo, Q.; Zhao, B.; Li, Z. Thermo-economic selection criteria of working fluid used in dual-loop ORC for engine waste heat recovery by multi-objective optimization. Energy 2020, 197, 117053. [Google Scholar] [CrossRef]
- Shao, M.; Han, Z.; Sun, J.; Xiao, C.; Zhang, S.; Zhao, Y. Review of multi-criteria decision making applications for renewable energy site selection. Renew. Energy 2020, 157, 377–403. [Google Scholar] [CrossRef]
- Odu, G.O. Weighting Methods for Multi-Criteria Decision Making Technique. J. Appl. Sci. Environ. Manag. 2019, 23, 1449–1457. [Google Scholar] [CrossRef]
- Bina, S.M.; Jalilinasrabady, S.; Fujii, H. Thermo-economic evaluation of various bottoming ORCs for geothermal power plant, determination of optimum cycle for Sabalan power plant exhaust. Geothermics 2017, 70, 181–191. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Bu, X. Multi-objective optimization of Binary Flashing Cycle (BFC) driven by geothermal energy. Appl. Therm. Eng. 2020, 166, 114693. [Google Scholar] [CrossRef]
- Detchusananard, T.; Sharma, S.; Maréchal, F.; Arpornwichanop, A. Generation and selection of Pareto-optimal solution for the sorption enhanced steam biomass gasification system with solid oxide fuel cell. Energy Convers. Manag. 2019, 196, 1420–1432. [Google Scholar] [CrossRef]
- Jankowski, M.; Borsukiewicz, A.; Wiśniewski, S.; Hooman, K. Multi-objective analysis of an influence of a geothermal water salinity on optimal operating parameters in low-temperature ORC power plant. Energy 2020, 202, 117666. [Google Scholar] [CrossRef]
- Da Lio, L.; Manete, G.; Lazzaretto, A. A Mean-line model to predict the design efficiency of radial inflow turbines in organic Rankine cycle (ORC) systems. Appl. Energy 2017, 205, 187–209. [Google Scholar] [CrossRef]
- Whitfield, A.; Baines, N.C. Design of Radial Turbomachines; Longman Scientific & Technical: New York, NY, USA, 1990. [Google Scholar]
- Aungier, R.H. Turbine Aerodynamics; ASME Press: New York, NY, USA, 2006. [Google Scholar]
- Fiaschi, D.; Manfrida, G.; Maraschiello, F. Design and performance prediction of radial ORC turboexpanders. Appl. Energy 2015, 138, 517–532. [Google Scholar] [CrossRef]
- Bekiloğlu, H.E.; Bedir, H.; Anlaş, G. Multi-objective optimization of ORC parameters and selection of working fluid using preliminary radial inflow turbine design. Energy Convers. Manag. 2019, 183, 833–847. [Google Scholar] [CrossRef]
- Gullapalli, V.S. Modeling of brazed plate heat exchangers for ORC systems. Energy Procedia 2017, 129, 443–450. [Google Scholar] [CrossRef]
- Li, J.; Ge, Z.; Duan, Y.; Yang, Z.; Liu, Q. Parametric optimization and thermodynamic performance comparison of single-pressure and dual-pressure evaporation organic Rankine cycles. Appl. Energy 2018, 217, 409–421. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, version R2019a; The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Reference Thermodynamic and Transport Properties—Refprop NIST Standard Reference Base 23, version 9.1; NIST: Gaithersburg, MD, USA, 2013.
- Bahadormanesh, N.; Rahat, S.; Yarali, M. Constrained multi-objective optimization of radial expanders in organic Rankine cycles by firefly algorithm. Energy Convers. Manag. 2017, 148, 1179–1193. [Google Scholar] [CrossRef]
- Jankowski, M.; Borsukiewicz, A. A Novel Exergy Indicator for Maximizng Energy Utilization in Low-Temperature ORC. Energies 2020, 13, 1598. [Google Scholar] [CrossRef]
- Tomków, Ł.; Cholewiński, M. Modelling of a novel power-generating cycle for the utilization of the cold exergy of liquid natural gas with the adjustable parameters of working fluid. Energy Convers. Manag. 2019, 201, 112178. [Google Scholar] [CrossRef]
- Li, P.; Han, Z.; Jia, X.; Mei, Z.; Han, X.; Wang, Z. Analysis and comparison on thermodynamic and economic performances of an organic Rankine cycle with constant and one-dimensional dynamic turbine efficiency. Energy Convers. Manag. 2019, 180, 665–679. [Google Scholar] [CrossRef]
- Jankowski, M.; Borsukiewicz, A.; Szopik-Depczyńska, K.; Ioppolo, G. Determination of an optimal pinch point temperature difference interval in ORC power plant using multi-objective approach. J. Clean Prod. 2019, 217, 798–807. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Jankowski, M.; Borsukiewicz, A. Multi-objective approach for determination of optimal operating parameters in low-temperature ORC power plant. Energy Convers. Manag. 2019, 200, 112075. [Google Scholar] [CrossRef]
- Chang, K.-H. Design Theory and Methods Using CAD/CAE; Elsevier Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Wang, M.; Jing, R.; Zhang, H.; Meng, C.; Li, N.; Zhao, Y. An innovative Organic Rankine Cycle (ORC) based on Ocean Thermal Energy Conversion (OTEC) system with performance simulation and multi-objective optimization. Appl. Therm. Eng. 2018, 145, 743–754. [Google Scholar] [CrossRef]
- Arora, J.S. Introduction to Optimum Design; Elsevier Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Greco, S.; Ehrgott, M.; Figueira, J.R. (Eds.) Multiple Criteria Decision Analysis; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Dordrecht, The Netherlands; London, UK, 2016. [Google Scholar]


| Parameter | Unit | Value | Type of Variable |
|---|---|---|---|
| [m3 h−1] | 30.0 | constant value | |
| Tgw1 | [°C] | 120 | constant value |
| sal | [kgkg−1] | 0.00 | constant value |
| fluid | [-] | R1234yf | constant value |
| ΔTsup | [K] | 5.00 | constant value |
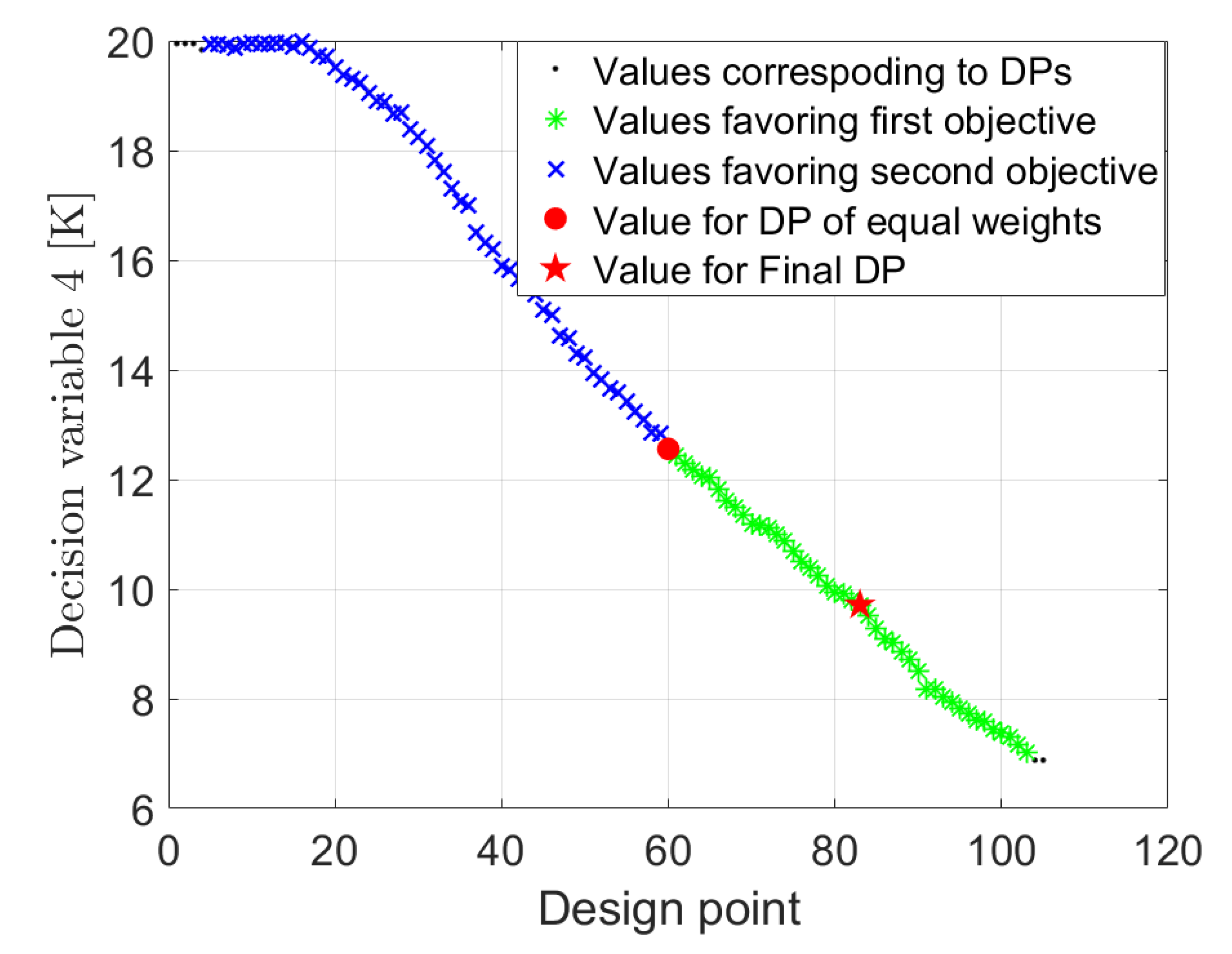
| ΔTeva | [K] | see Equation (15) | decision variable |
| ΔTcon | [K] | 5.00 | constant value |
| Tcw1 | [°C] | 15.0 | constant value |
| ηT | [%] | 75.0 | design variable |
| ns | [-] | see Equation (14) | decision variable |
| ηP | [%] | 75.0 | constant value |
| Teva | [°C] | see Equation (12) | decision variable |
| Tcon | [°C] | see Equation (13) | decision variable |
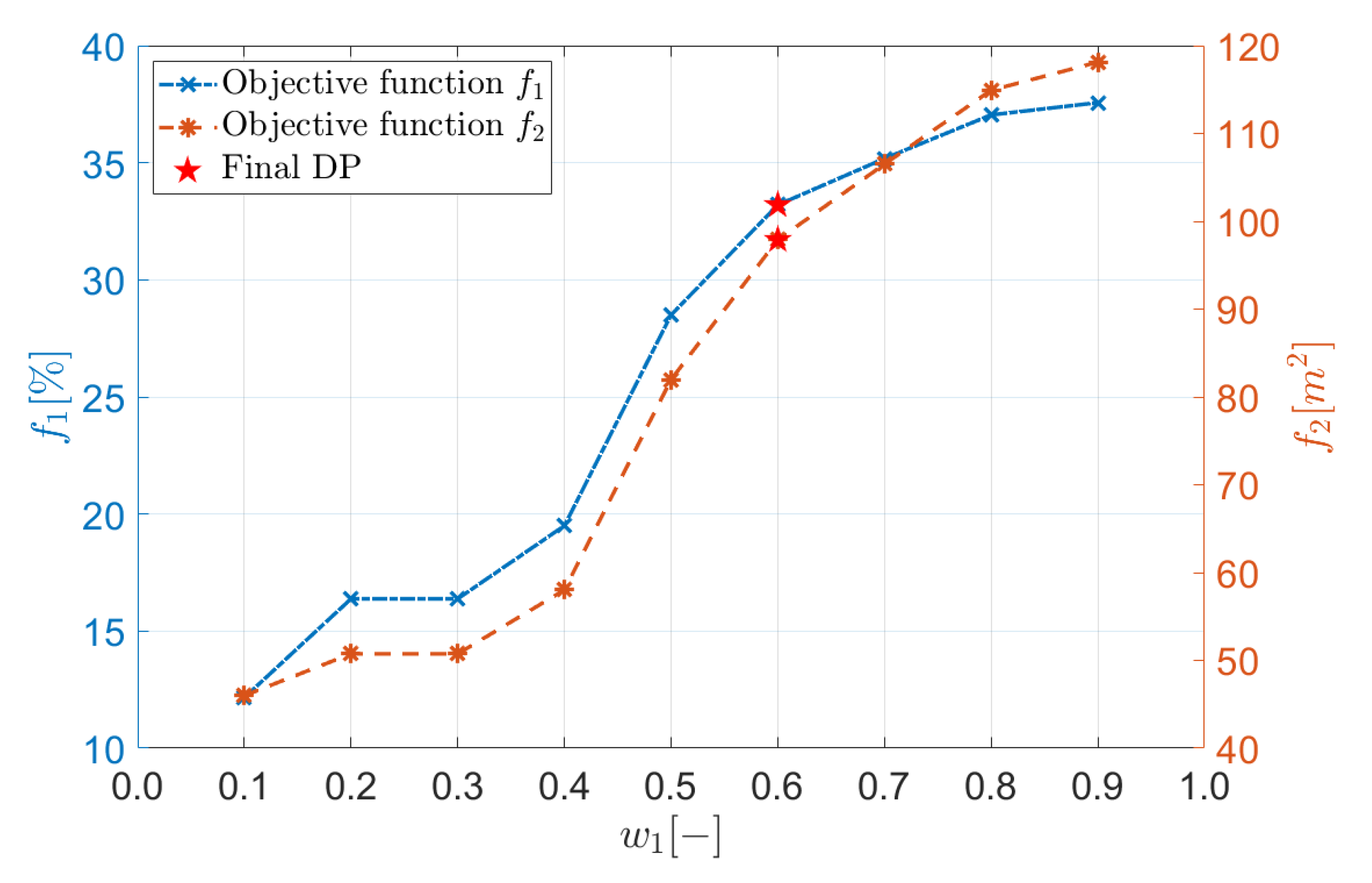
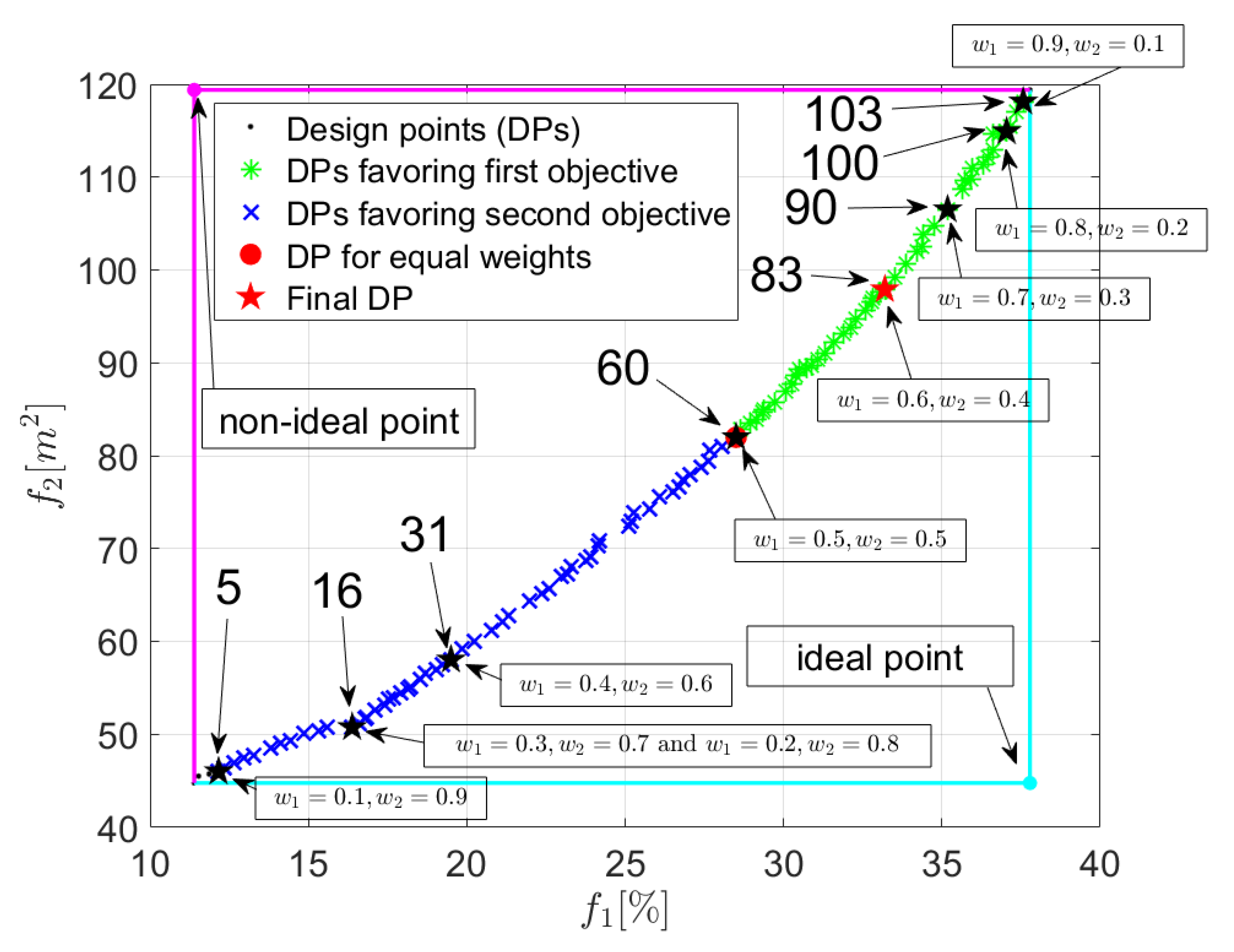
| Parameter | No. of WD | PR | PF | WS | w1 | w2 | No. of DP | f1 | (δf1)id | f2 | (δf2)id |
|---|---|---|---|---|---|---|---|---|---|---|---|
| unit | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [%] | [%] | [m2] | [%] |
| value | 1 | 5.0 | 1 | 5.0 | 0.9 | 0.1 | 103 | 37.6 | −0.57 | 118 | 164 |
| 2 | 5.0 | 1 | 4.0 | 0.8 | 0.2 | 100 | 37.0 | −1.95 | 115 | 157 | |
| 3 | 5.0 | 1 | 3.0 | 0.7 | 0.3 | 90 | 35.2 | −6.88 | 107 | 138 | |
| 4 | 5.0 | 1 | 2.0 | 0.6 | 0.4 | 83 | 33.2 | −12.1 | 97.9 | 119 | |
| 5 | 5.0 | 1 | 1.0 | 0.5 | 0.5 | 60 | 28.5 | −24.6 | 82.0 | 83.1 | |
| 6 | 5.0 | 2 | 2.0 | 0.4 | 0.6 | 31 | 19.5 | −48.4 | 58.0 | 29.6 | |
| 7 | 5.0 | 2 | 3.0 | 0.3 | 0.7 | 16 | 16.4 | −56.6 | 50.7 | 13.3 | |
| 8 | 5.0 | 2 | 4.0 | 0.2 | 0.8 | 16 | 16.4 | −56.6 | 50.7 | 13.3 | |
| 9 | 5.0 | 2 | 5.0 | 0.1 | 0.9 | 5 | 12.2 | −67.8 | 46.0 | 2.70 |
| Average Rate of Change of the Deviations from Ideal Solution | ||
|---|---|---|
| (δf1)id [%] | (δf2)id [%] | |
| region I | 0.78 | 0.82 |
| region II | 0.70 | 1.67 |
| region III | 0.54 | 2.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankowski, M.; Borsukiewicz, A.; Hooman, K. Development of Decision-Making Tool and Pareto Set Analysis for Bi-Objective Optimization of an ORC Power Plant. Energies 2020, 13, 5280. https://doi.org/10.3390/en13205280
Jankowski M, Borsukiewicz A, Hooman K. Development of Decision-Making Tool and Pareto Set Analysis for Bi-Objective Optimization of an ORC Power Plant. Energies. 2020; 13(20):5280. https://doi.org/10.3390/en13205280
Chicago/Turabian StyleJankowski, Marcin, Aleksandra Borsukiewicz, and Kamel Hooman. 2020. "Development of Decision-Making Tool and Pareto Set Analysis for Bi-Objective Optimization of an ORC Power Plant" Energies 13, no. 20: 5280. https://doi.org/10.3390/en13205280
APA StyleJankowski, M., Borsukiewicz, A., & Hooman, K. (2020). Development of Decision-Making Tool and Pareto Set Analysis for Bi-Objective Optimization of an ORC Power Plant. Energies, 13(20), 5280. https://doi.org/10.3390/en13205280






