Optimal Design of a Multibrid Permanent Magnet Generator for a Tidal Stream Turbine
Abstract
1. Introduction
2. System Modeling
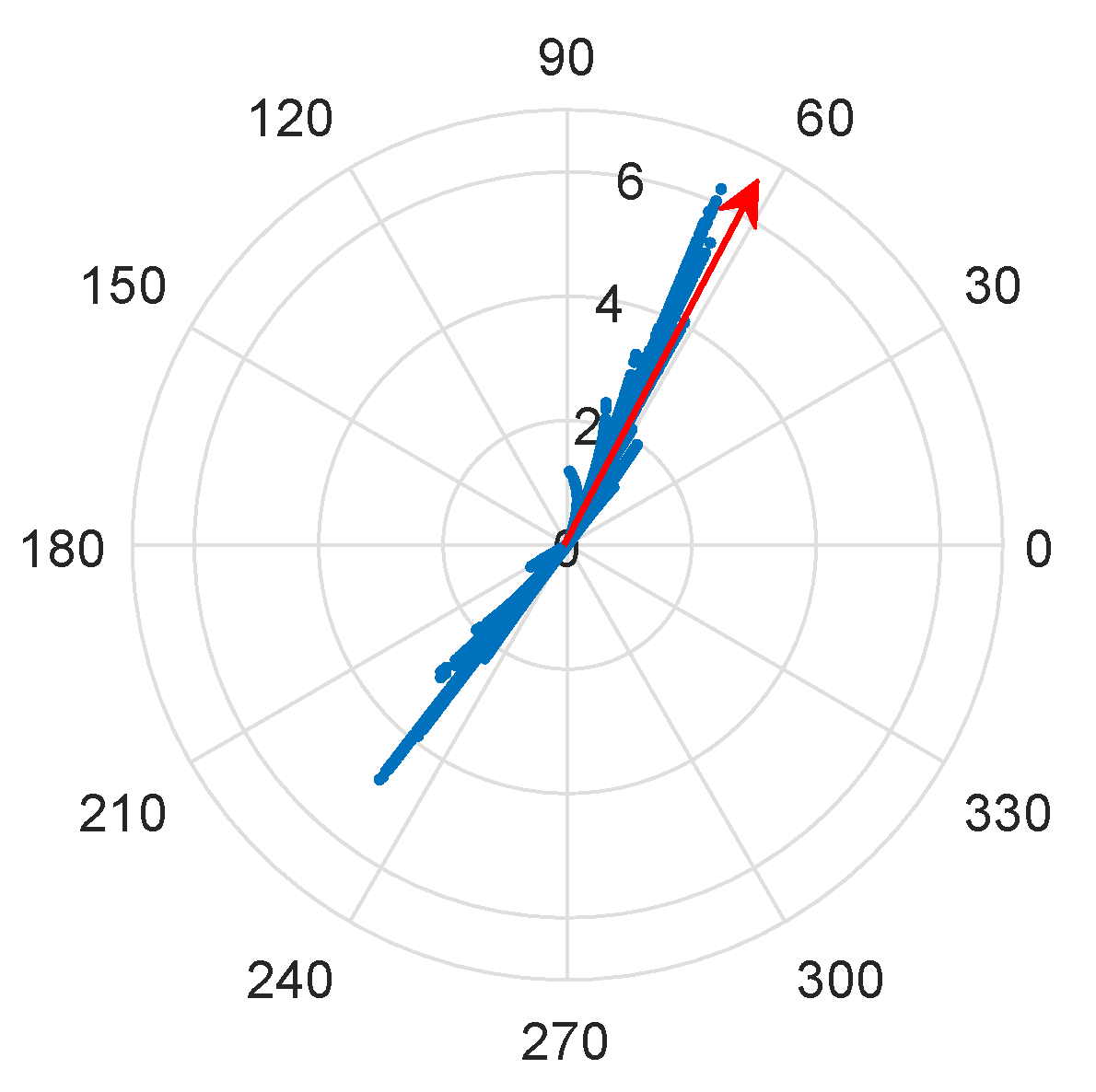
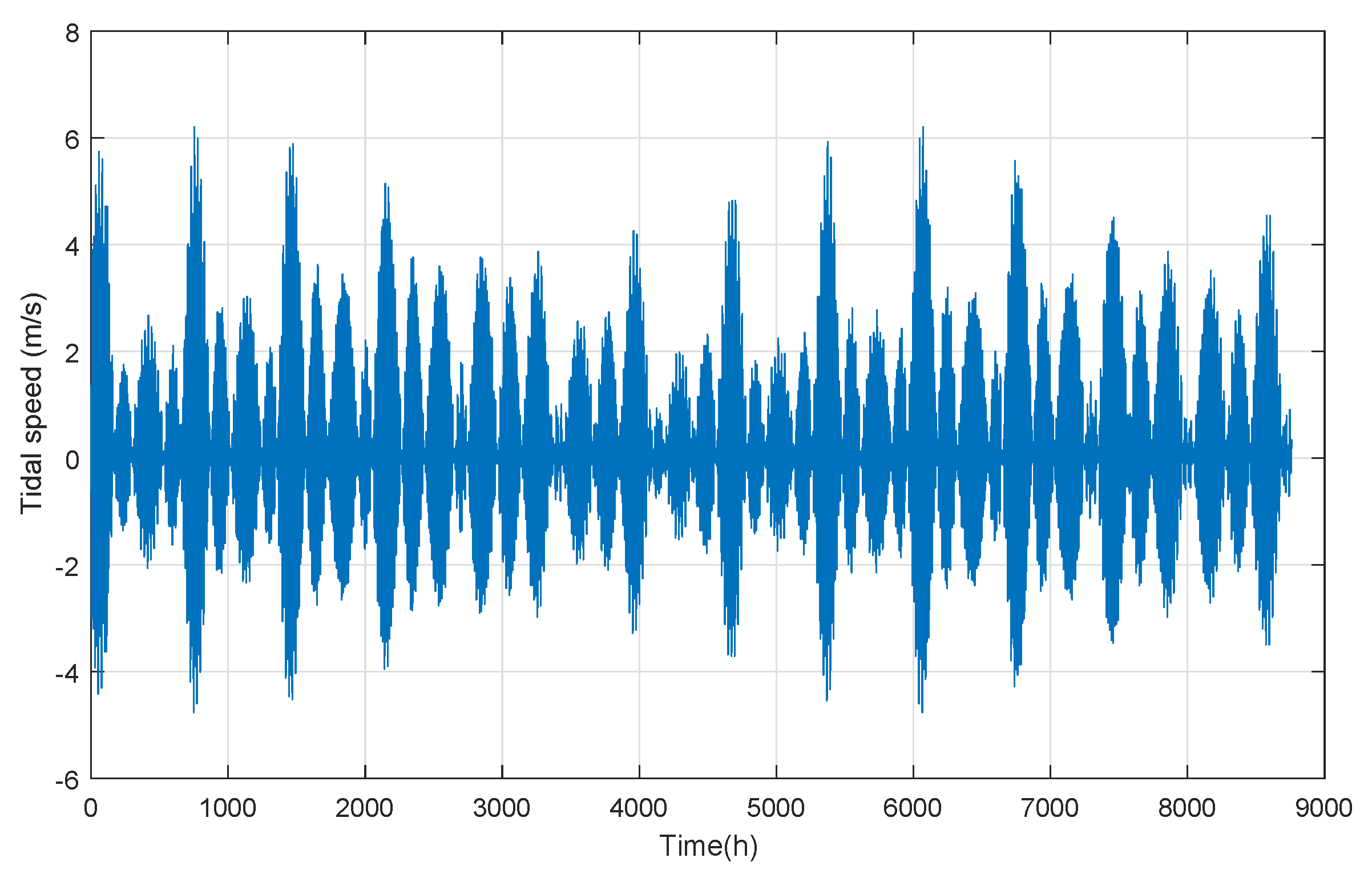
2.1. Renewable Resource and Tidal Turbine Modeling
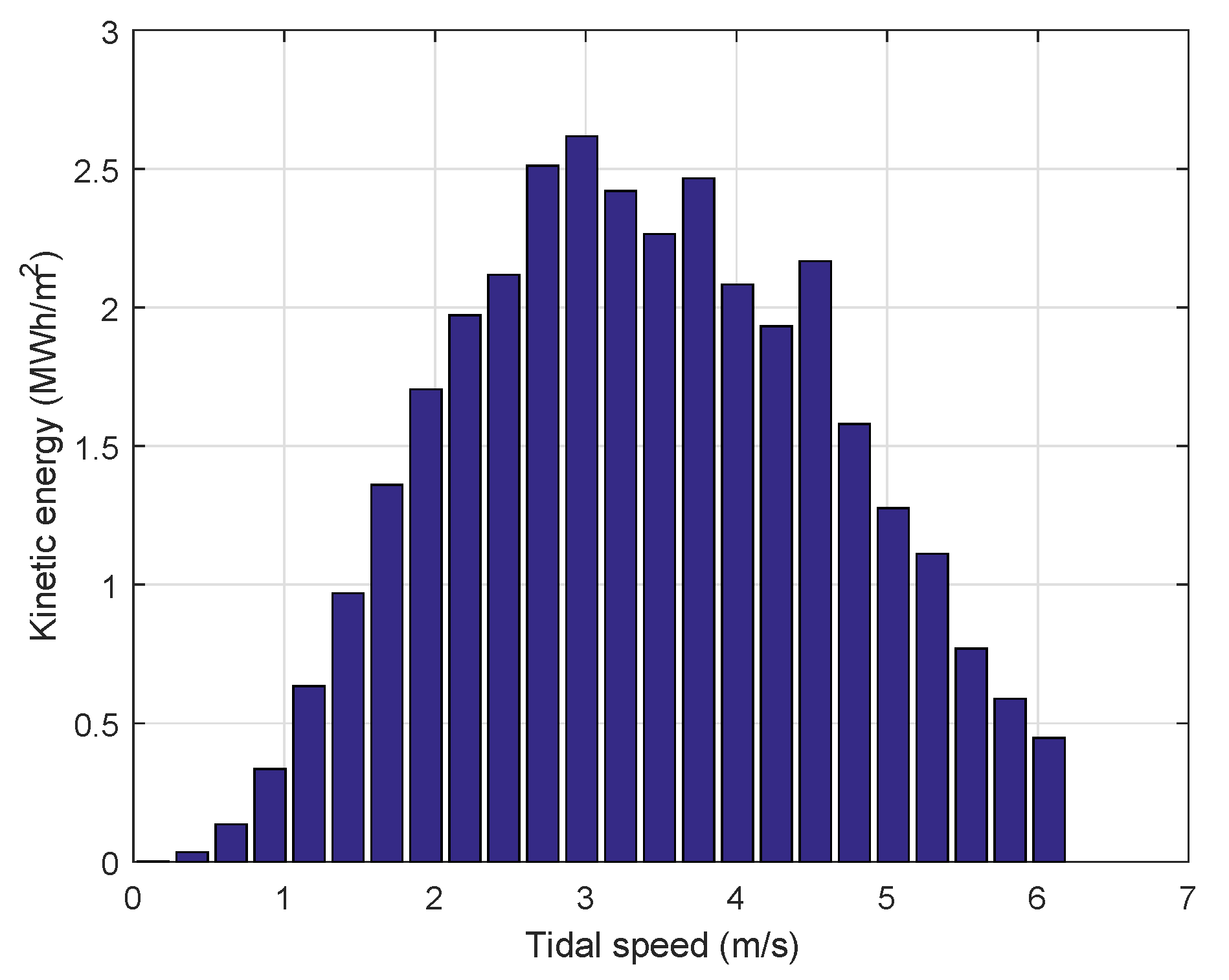
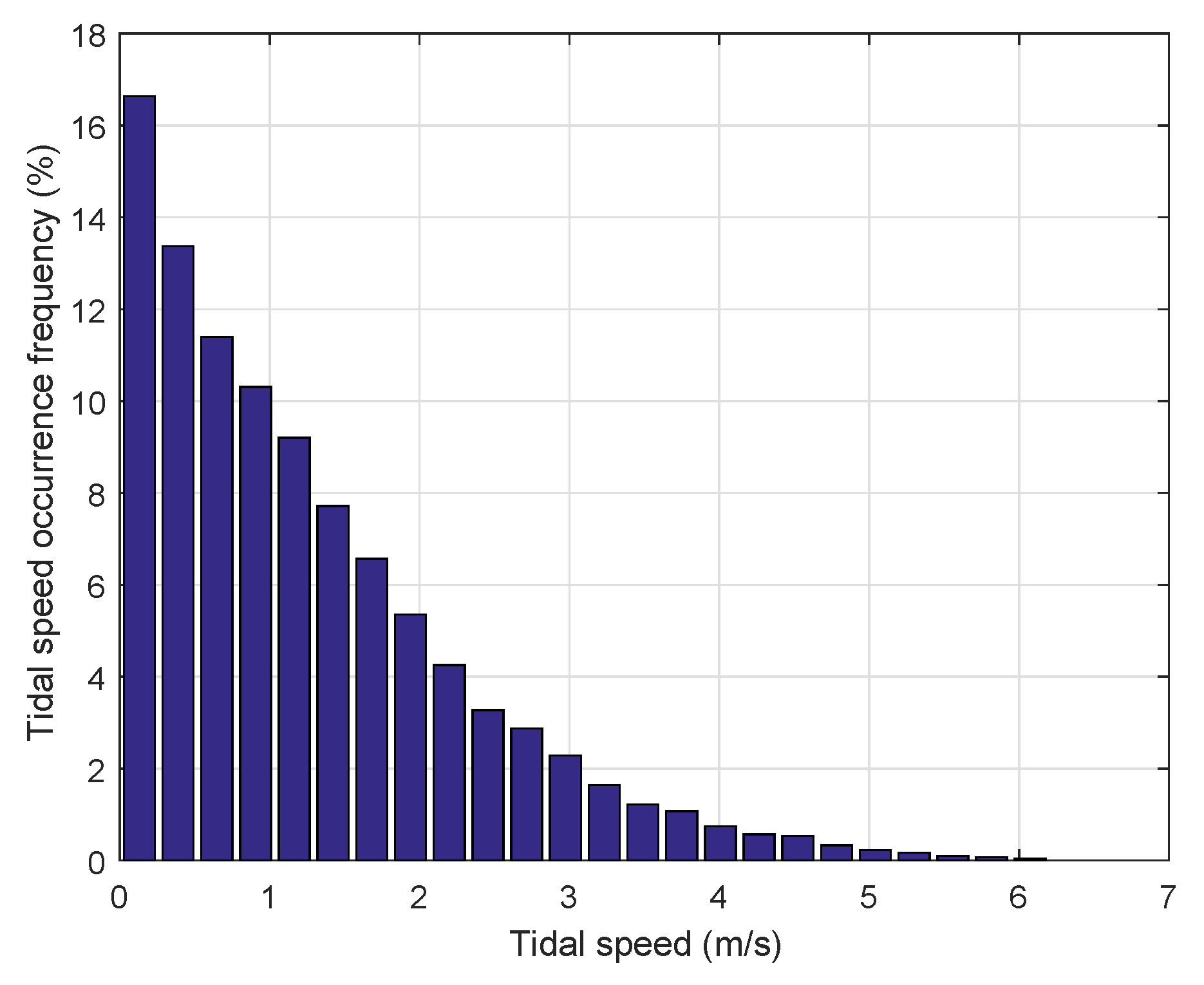
2.1.1. Power and Energy Calculation
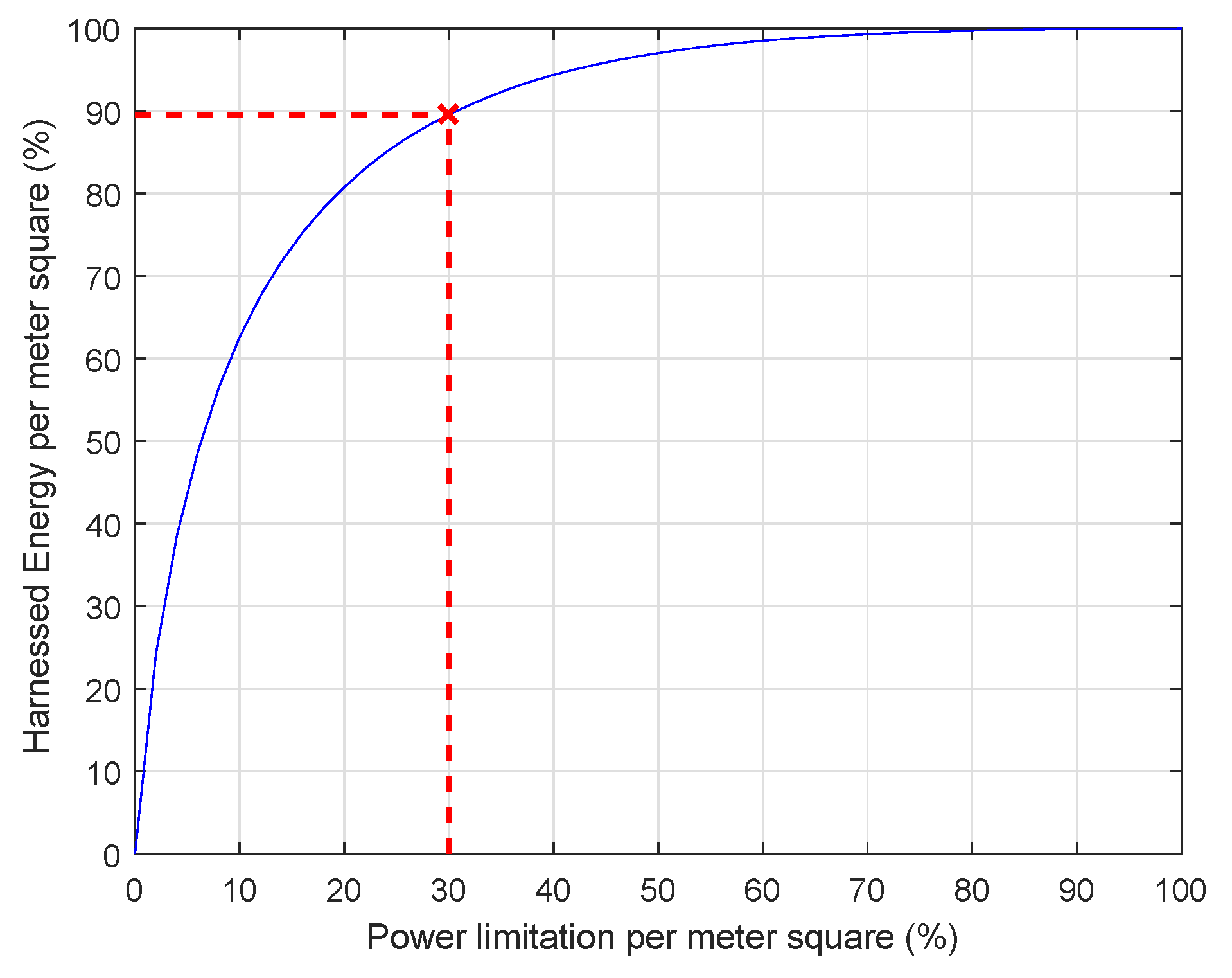
2.1.2. Power Rating Choice
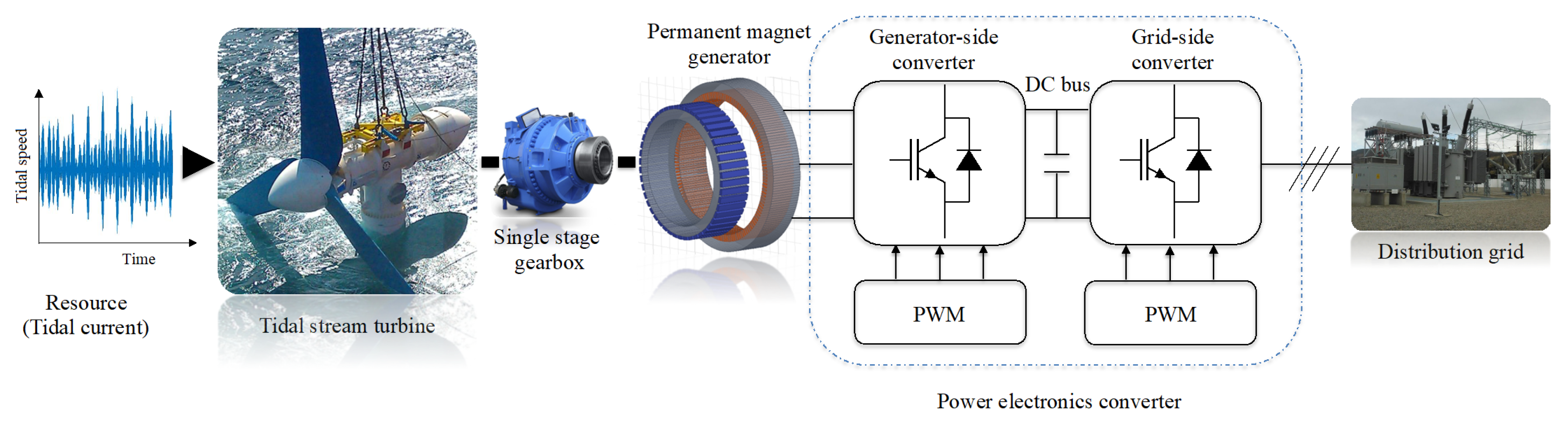
2.2. Gearbox Modeling
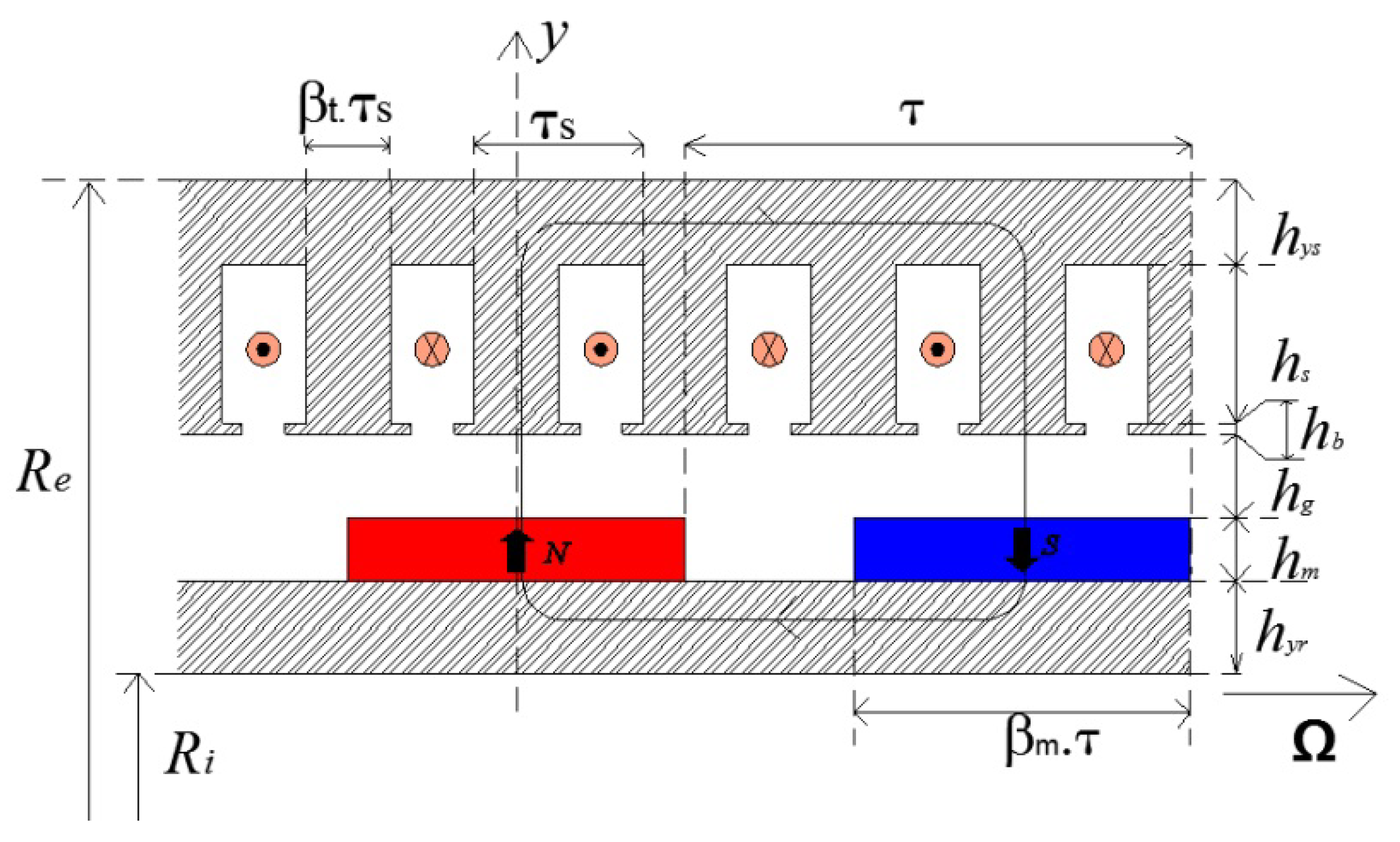
2.3. Single Stage Geared PMG Design
2.3.1. Electromagnetic Torque
2.3.2. Air-Gap
2.3.3. Magnet Height
2.3.4. Slot Height
2.3.5. Stator and Rotor Yoke Height
2.3.6. Teeth Pitch Ratio
2.3.7. Maximum Magnetic Field
2.3.8. Iron Losses
2.3.9. Synchronous Inductance
2.4. Power Electronic Converter Design
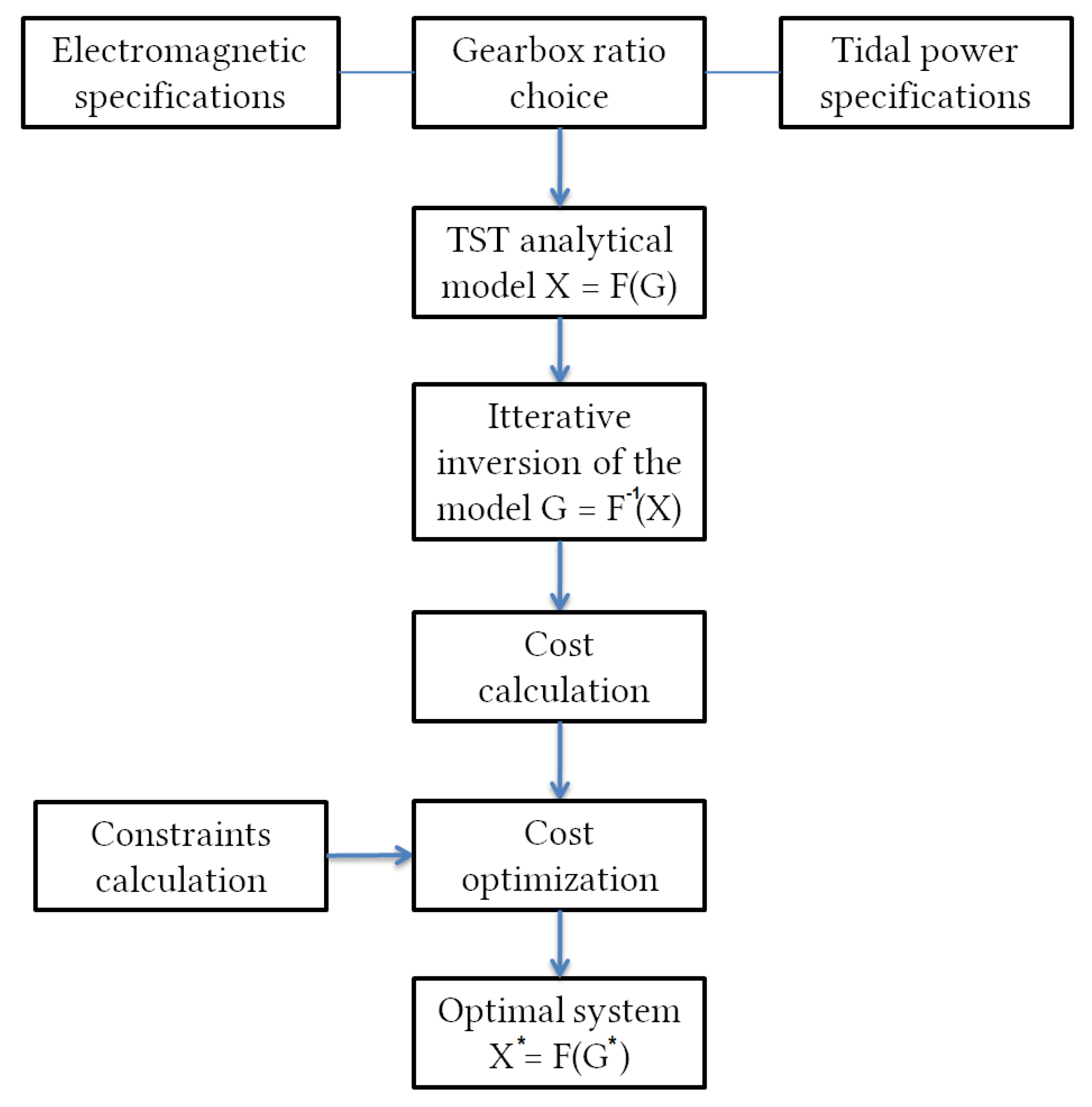
3. Design Optimization
3.1. Cost-Function
3.2. Optimization Constraints
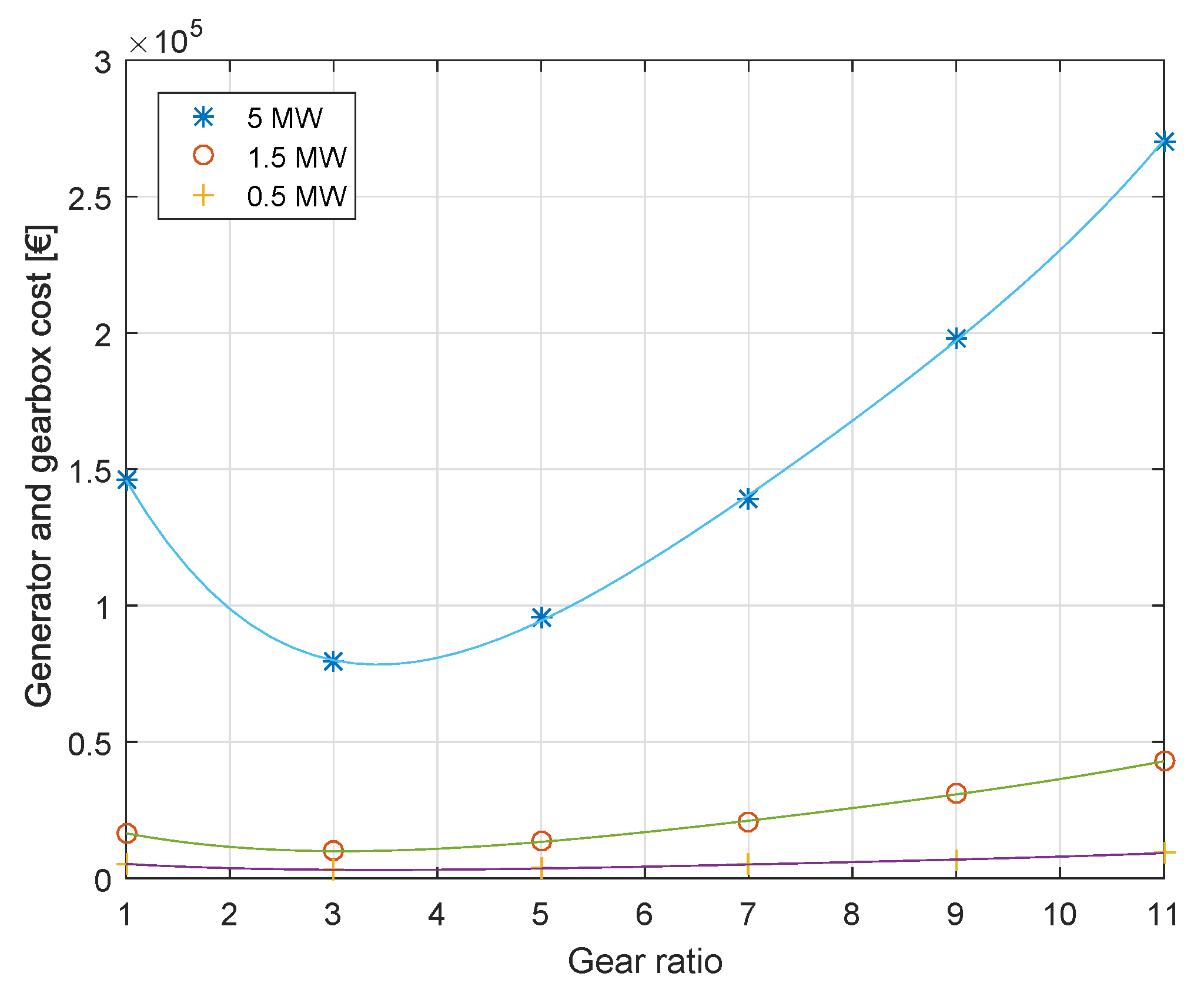
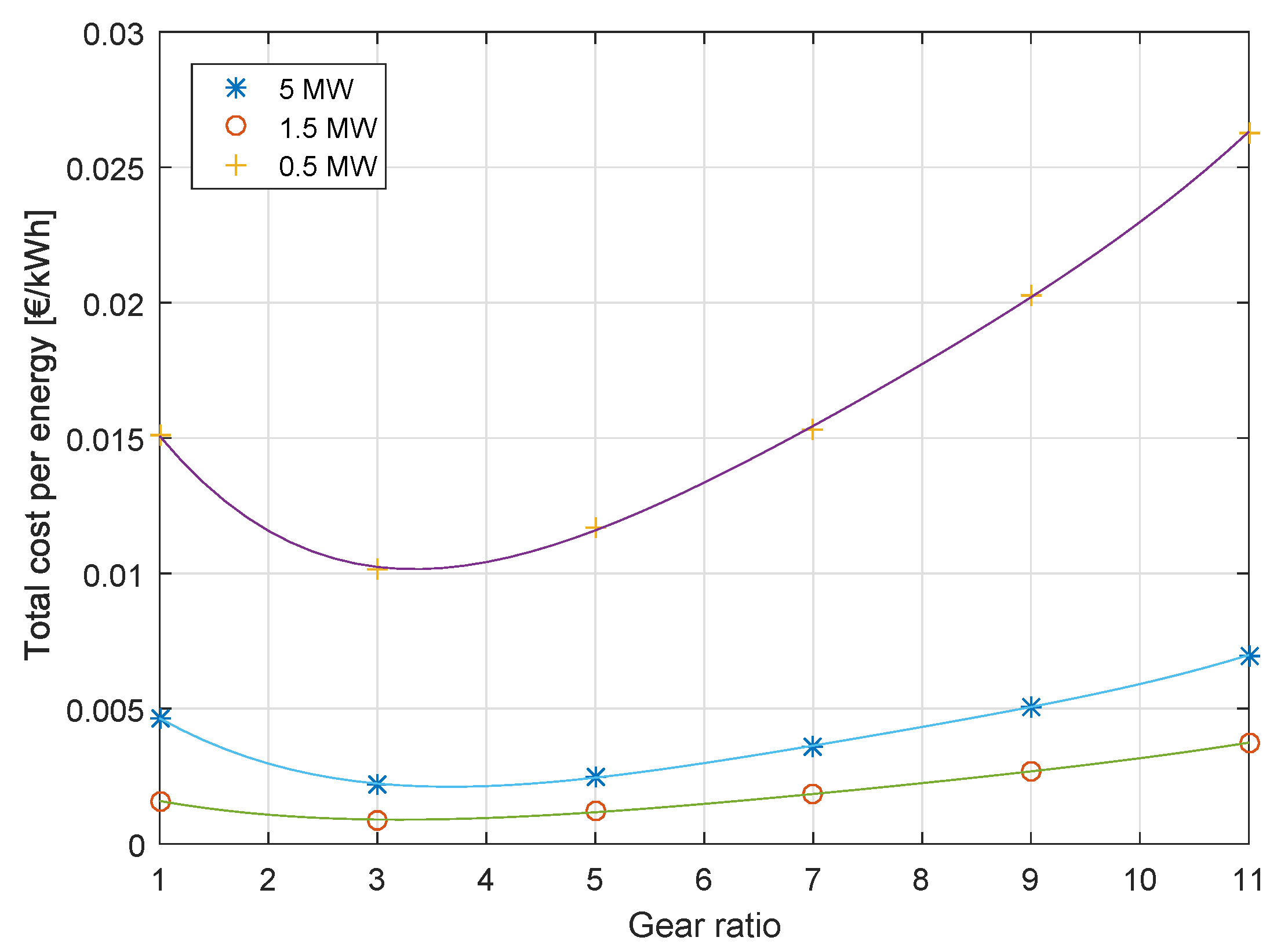
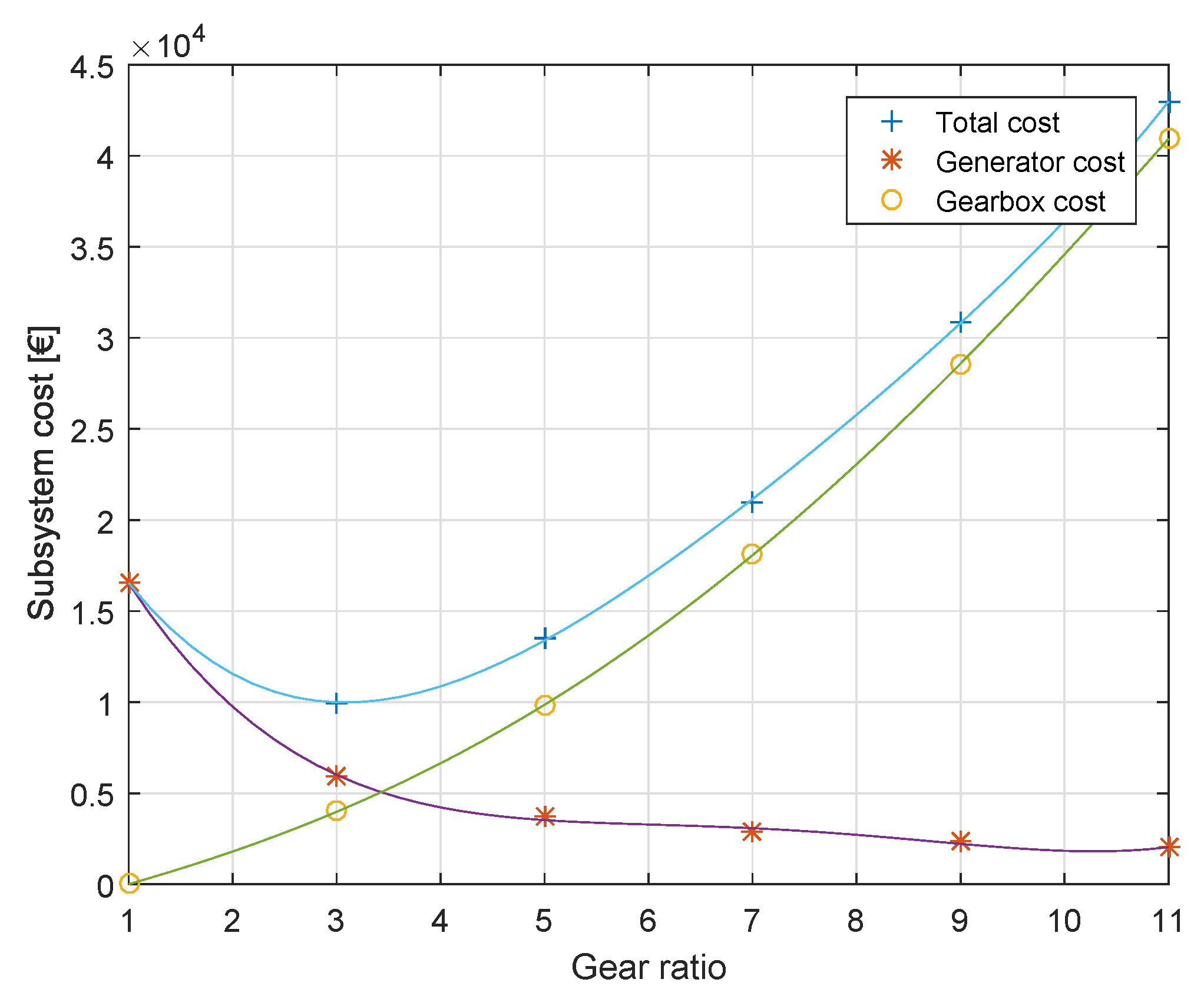
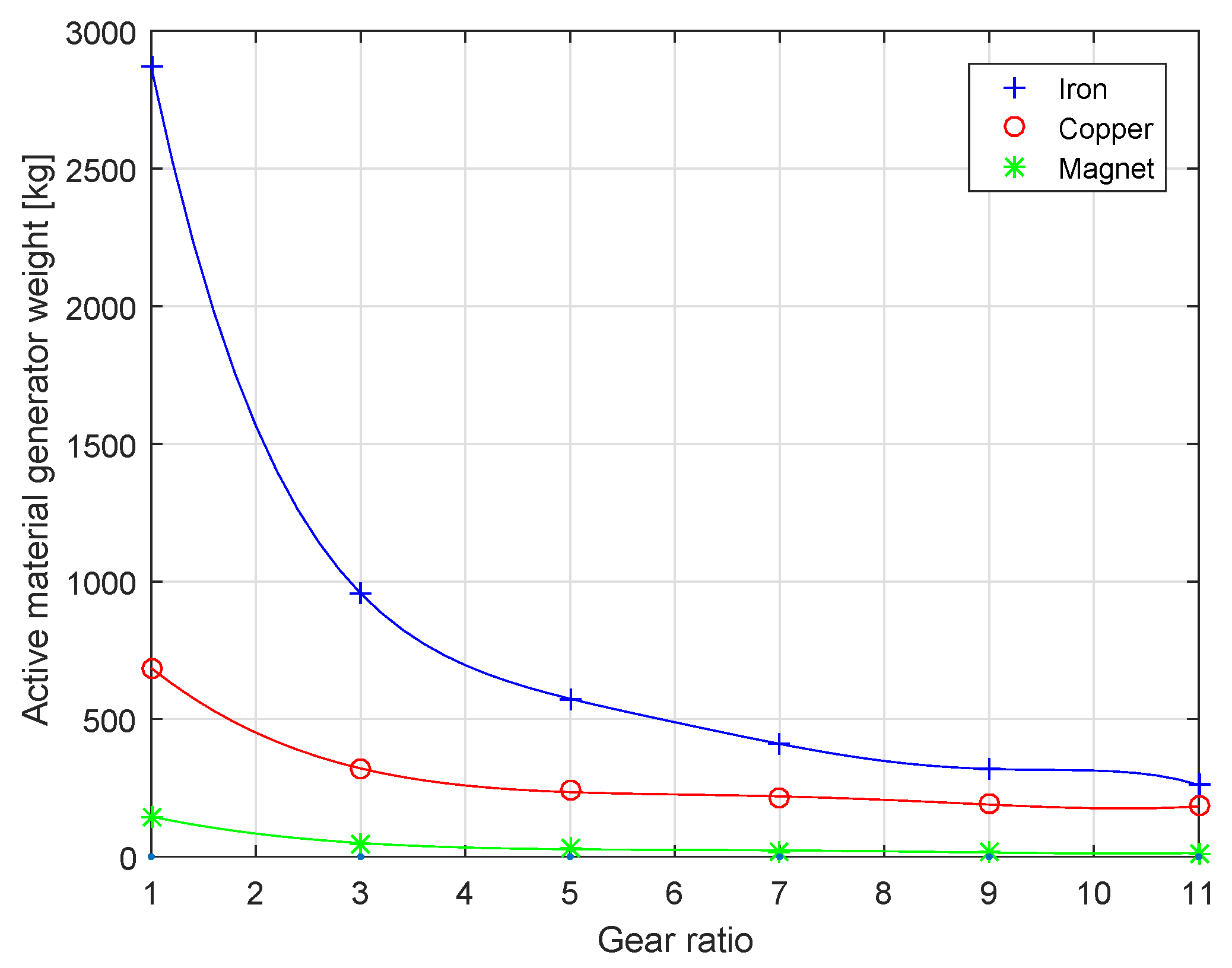
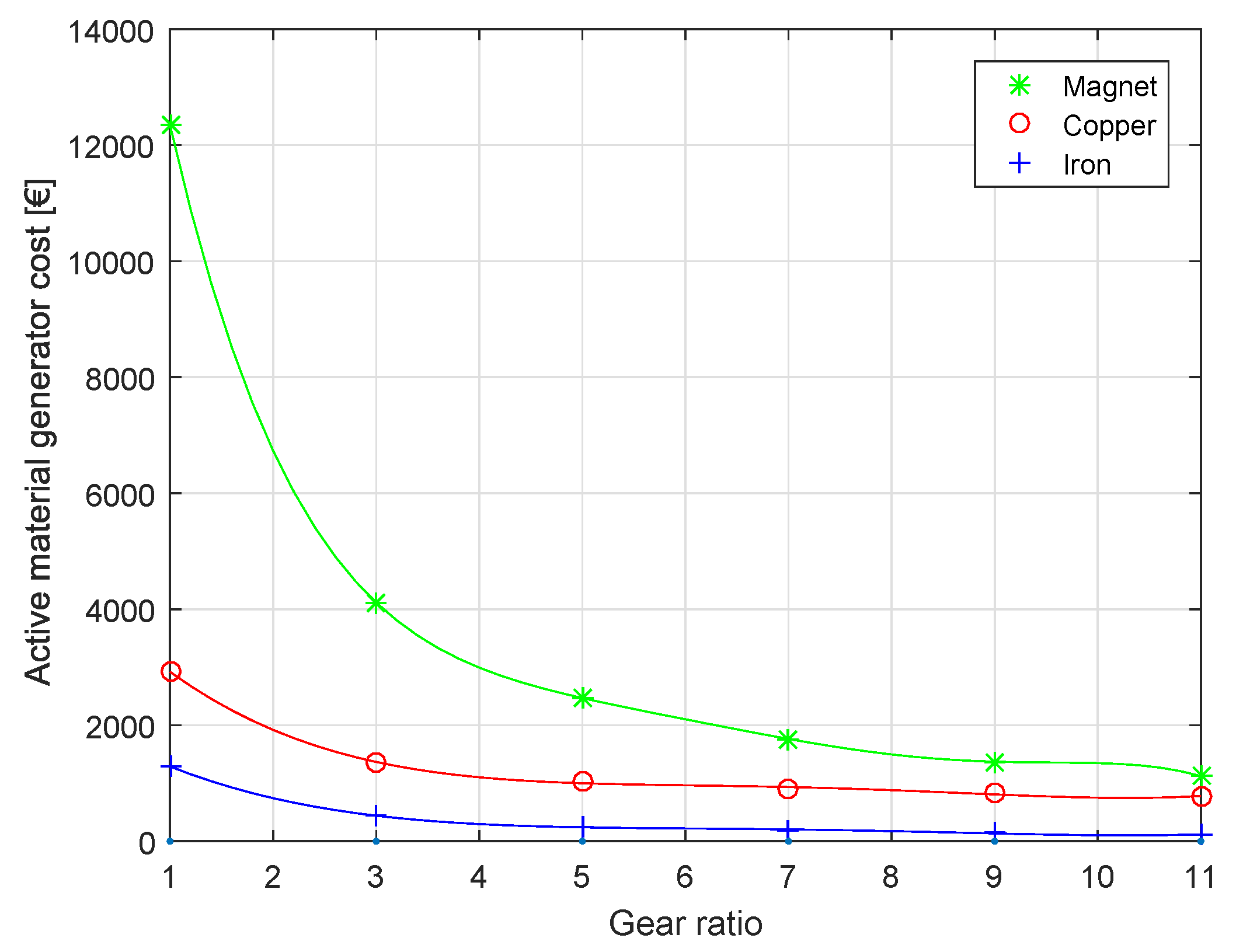
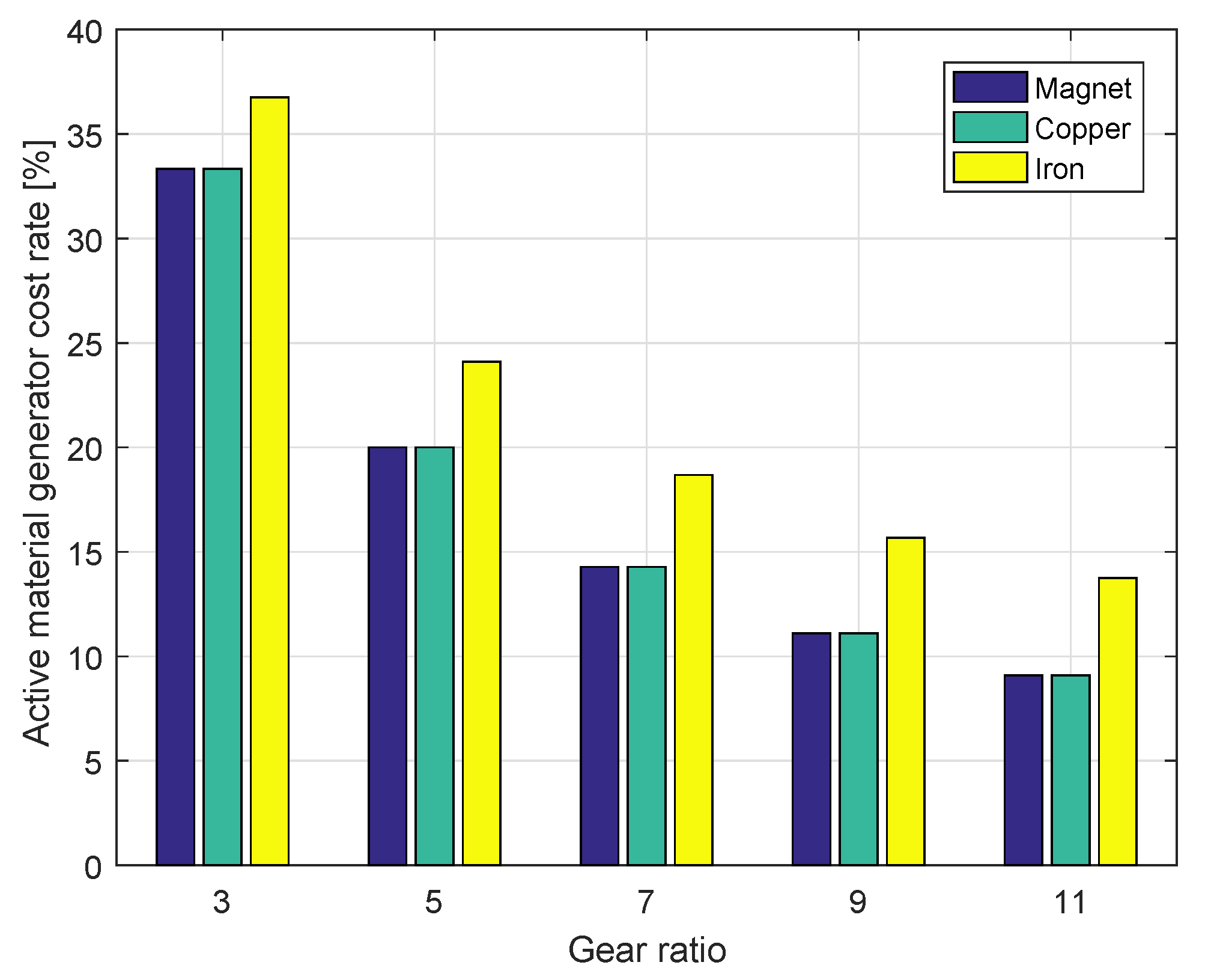
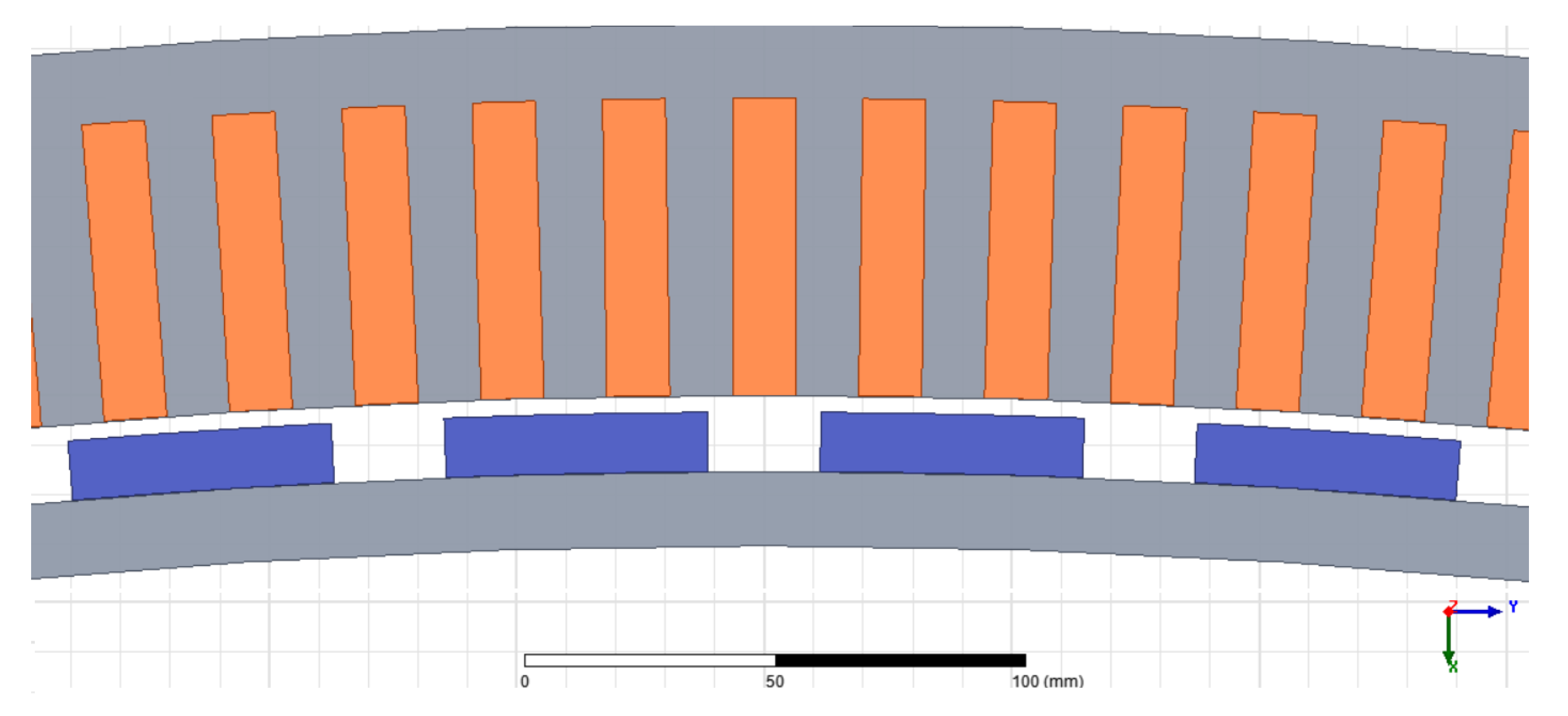
4. Design Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TST | Tidal stream turbine |
| DD | Direct drive |
| 2D | Two-dimensional |
| PMG | Permanent magnet generator |
| 3D | Three-dimensional |
| AEP | Annual energy production |
| PWM | Pulse width modulation |
Nomenclature
| Input shaft power | |
| Turbine blade swept area | |
| Sea water density | |
| Power coefficient | |
| Tip speed ratio | |
| Optimum tip speed ratio | |
| Pitch angle | |
| Cut-in tidal current speed | |
| Cut-out tidal current speed | |
| Rated tidal current speed | |
| Rated input shaft power | |
| Occurrence frequency | |
| Gear face width | |
| Sun gear diameter | |
| Planet gear diameter | |
| Ring gear diameter | |
| Scaling factor | |
| Gearbox output shaft torque | |
| Application factor | |
| Tooth loads intensity index | |
| Gearbox weight constant | |
| Gearbox ratio | |
| Gear ratio between sun and planet gears | |
| Z | Planet gears number |
| Gearbox specific cost | |
| Gearbox weight | |
| Gearbox estimated cost | |
| Gearbox losses | |
| Speed-dependent losses constant | |
| Tidal stream turbine rated power | |
| Rotor speed | |
| Rated rotor speed | |
| Electromagnetic torque | |
| Stator current loading | |
| Maximum air-gap flux density | |
| Air-gap flux density | |
| Saturation flux density | |
| First harmonic winding factor | |
| Phase shift between the electromotive force and the current | |
| Stator radius | |
| Equivalent core length | |
| 3D flow leakage corrective coefficient | |
| Air-gap coefficient | |
| Mechanical air-gap | |
| Additional Carter air-gap | |
| Carter factor | |
| Magnet height | |
| Vacuum permeability constant | |
| Magnets relative permeability | |
| Magnets remanent flux density | |
| Maximum air-gap flow density | |
| Pole pitch | |
| Stator yoke height | |
| Rotor yoke height | |
| Slot height | |
| Fill factor | |
| Teeth pitch ratio | |
| p | Pole pairs number |
| Slots per pole per phase number | |
| m | Phases number |
| Maximum magnetic field in the magnet | |
| Permanent magnet coercive magnetic field | |
| Iron losses | |
| Magnetic field frequency in the iron | |
| Specific hysteresis loss | |
| Specific eddy current loss | |
| Phase winding number of turns | |
| Leakage inductance | |
| Power electronics cost | |
| Permanent magnet generator cost | |
| Tidal stream turbine cost | |
| Copper specific costs | |
| Iron specific costs | |
| Permanent magnet specific costs | |
| Copper specific weight | |
| Iron specific weight | |
| Permanent magnet specific weight | |
| Set of possible solutions | |
| Maximum electrical frequency |
References
- Benbouzid, M.; Titah-Benbouzid, H.; Zhou, Z. Ocean Energy Technologies; Abraham, M.A., Ed.; Encyclopedia of Sustainable Technologies; Elsevier: Amsterdam, The Netherlands, 2017; pp. 73–85. ISBN 978-0-128-04677-7. [Google Scholar]
- Selin, N.E. Tidal Power. April 2019. Available online: https://www.britannica.com/science/tidal-power (accessed on 6 June 2019).
- Flambard, J.; Amirat, Y.; Feld, G.; Benbouzid, M.; Ruiz, N. River and Estuary Current Power Overview. J. Mar. Sci. Eng. 2019, 7, 365. [Google Scholar] [CrossRef]
- Zhou, Z.; Benbouzid, M.; Charpentier, J.F.; Scuiller, F.; Tang, T. Developments in large marine current turbine technologies–A review. Renew. Sustain. Energy Rev. 2017, 71, 852–858. [Google Scholar] [CrossRef]
- Djebarri, S.; Charpentier, J.F.; Scuiller, F.; Benbouzid, M. Comparison of direct-drive PM generators for tidal turbines. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 474–479. [Google Scholar]
- Zeinali, R.; Keysan, O. A Rare-Earth Free Magnetically Geared Generator for Direct-Drive Wind Turbines. Energies 2019, 12, 447. [Google Scholar] [CrossRef]
- Keysan, O.; McDonald, A.S.; Mueller, M. A direct drive permanent magnet generator design for a tidal current turbine (SeaGen). In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 224–229. [Google Scholar]
- Djebarri, S.; Charpentier, J.F.; Scuiller, F.; Benbouzid, M. Design methodology of permanent magnet generators for fixed-pitch tidal turbines with overspeed power limitation strategy. J. Ocean. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Ozturk, S.; Fthenakis, V.; Faulstich, S. Failure Modes, Effects and Criticality Analysis for Wind Turbines Considering Climatic Regions and Comparing Geared and Direct Drive Wind Turbines. Energies 2018, 11, 2317. [Google Scholar]
- Touimi, K.; Benbouzid, M.; Tavner, P. A Review-based Comparison of Drivetrain Options for Tidal Turbines. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Touimi, K.; Benbouzid, M.; Tavner, P. Tidal stream turbines: With or without a Gearbox? Ocean. Eng. 2018, 170, 74–88. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Polinder, H. Optimization of multibrid permanent-magnet wind generator systems. IEEE Trans. Energy Convers. 2009, 24, 82–92. [Google Scholar] [CrossRef]
- Detailed Technical-Specification WWD-3. Available online: http://www.ecosource-energy.bg/uploads/Technical_Specification_WWD3.pdf (accessed on 6 June 2019).
- Multibrid M5000. Available online: https://en.wind-turbine-models.com/turbines/22-multibrid-m5000 (accessed on 6 June 2019).
- Xu, Q.; Li, W.; Lin, Y.; Liu, H.; Gu, Y. Investigation of the performance of a stand-alone horizontal axis tidal current turbine based on in situ experiment. Ocean. Eng. 2016, 113, 111–120. [Google Scholar] [CrossRef]
- Polinder, H.; Van der Pijl, F.F.; De Vilder, G.J.; Tavner, P.J. Comparison of direct-drive and geared generator concepts for wind turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef]
- Hart, K.; McDonald, A.; Polinder, H.; Corr, E.J.; Carroll, J. Improved cost energy comparison of permanent magnet generators for large offshore wind turbines. In Proceedings of the European Wind Energy Association 2014 Annual Conference, Barcelona, Spain, 10–13 March 2014. [Google Scholar]
- Djebarri, S.; Charpentier, J.F.; Scuiller, F.; Benbouzid, M. Design and performance analysis of double stator axial flux PM generator for rim driven marine current turbines. IEEE J. Ocean. Eng. 2015, 41, 50–66. [Google Scholar]
- Titah-Benbouzid, H.; Benbouzid, M. Biofouling issue on marine renewable energy converters: A state of the art review on impacts and prevention. Int. J. Energy Convers. 2017, 5, 67–78. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- SHOM (Service Hydrographique et Ocanographique de la Marine), 3D Marine Tidal Currents in Fromveur (Ouessant island). 2014. Available online: https://diffusion.shom.fr/pro (accessed on 6 June 2019).
- El Tawil, T.; Charpentier, J.F.; Benbouzid, M. Tidal energy site characterization for marine turbine optimal installation: Case of the Ouessant Island in France. Int. J. Mar. Energy 2017, 18, 57–64. [Google Scholar] [CrossRef]
- Radzevich, S.P. Dudley’s Handbook of Practical Gear Design and Manufacture; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Guo, Y.; Parsons, T.; King, R.; Dykes, K.; Veers, P. Analytical Formulation for Sizing and Estimating the Dimensions and Weight of Wind Turbine Hub and Drivetrain Components; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2015.
- Harrison, R.; Hau, E.; Snel, H. Large Wind Turbines: Design and Economics; Wiley: Chichester, UK, 2000; Volume 1. [Google Scholar]
- Rourke, F.O.; Boyle, F.; Reynolds, A. Marine current energy devices: Current status and possible future applications in Ireland. Renew. Sustain. Energy Rev. 2010, 14, 1026–1036. [Google Scholar] [CrossRef]
- Dubois, M.R. Review of electromechanical conversion in wind turbines. Rep. EPP00 2000, 3, 4–10. [Google Scholar]
- Djebarri, S. Contribution à la Modelisation et à la Conception Optimale de Generatrices à Aimants Permanents Pour Hydroliennes. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2015. [Google Scholar]
- Djebarri, S.; Charpentier, J.F.; Scuiller, F.; Benbouzid, M.; Guemard, S. Rough design of a double-stator axial flux permanent magnet generator for a rim-driven marine current turbine. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1450–1455. [Google Scholar]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines; John Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Böhmeke, G. Development and Operational Experience of the Wind Energy Converter WWD-1. In Proceedings of the 2003 Europ Wind Energy Conference, Madrid, Spain, 16–19 June 2003. [Google Scholar]
- Boldea, I. The Electric Generators Handbook-2 Volume Set; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Grauers, A. Efficiency of three wind energy generator systems. IEEE Trans. Energy Convers. 1996, 11, 650–657. [Google Scholar] [CrossRef]
- Xue, Y.S.; Han, L.; Li, H.; Xie, L.D. Optimal design and comparison of different PM synchronous generator systems for wind turbines. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 2448–2453. [Google Scholar]





| Tidal Stream Turbine | |||
| Rated power [MW] | 0.5 | 1.5 | 5 |
| Rated rotor speed [rpm] | 80.3 | 47.0 | 25.8 |
| Rotor diameter D [m] | 6 | 10.3 | 18.8 |
| Cut it tidal current speed [m/s] | 1.0 | ||
| Cut out tidal current speed [m/s] | 6.2 | ||
| Maximum power coefficient | 0.455 | ||
| Optimum tip speed ratio | 5.90 | ||
| Sea water density [kg/m3] | 995.6 | ||
| Single Stage Planetary Gearbox | |||
| Gearbox application factor | 1.5 | ||
| K-factor [N/mm2] | 2.76 | ||
| Gearbox weight constant | 0.6 | ||
| Planet gears number Z | 6 | ||
| Gearbox specific cost [€/kg] | 6 | ||
| Speed dependent losses constant [%] | 1.5 | ||
| PMG System | |||
| Hysteresis losses at 1.5 T and 50 Hz pFe0h [W/kg] | 2 | ||
| Eddy-current losses at 1.5 T and 50 Hz pFe0e [W/kg] | 0.5 | ||
| Specific cost of electrical steel cFe [€/mT] | 449.77 | ||
| Specific cost of copper cCu [€/mT] | 4259.18 | ||
| Specific cost of NdFeB magnet cm [€/mT] | 84,538.60 | ||
| Specific cost of power electronics cconv [€/kW] | 40 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Touimi, K.; Benbouzid, M.; Chen, Z. Optimal Design of a Multibrid Permanent Magnet Generator for a Tidal Stream Turbine. Energies 2020, 13, 487. https://doi.org/10.3390/en13020487
Touimi K, Benbouzid M, Chen Z. Optimal Design of a Multibrid Permanent Magnet Generator for a Tidal Stream Turbine. Energies. 2020; 13(2):487. https://doi.org/10.3390/en13020487
Chicago/Turabian StyleTouimi, Khalil, Mohamed Benbouzid, and Zhe Chen. 2020. "Optimal Design of a Multibrid Permanent Magnet Generator for a Tidal Stream Turbine" Energies 13, no. 2: 487. https://doi.org/10.3390/en13020487
APA StyleTouimi, K., Benbouzid, M., & Chen, Z. (2020). Optimal Design of a Multibrid Permanent Magnet Generator for a Tidal Stream Turbine. Energies, 13(2), 487. https://doi.org/10.3390/en13020487







