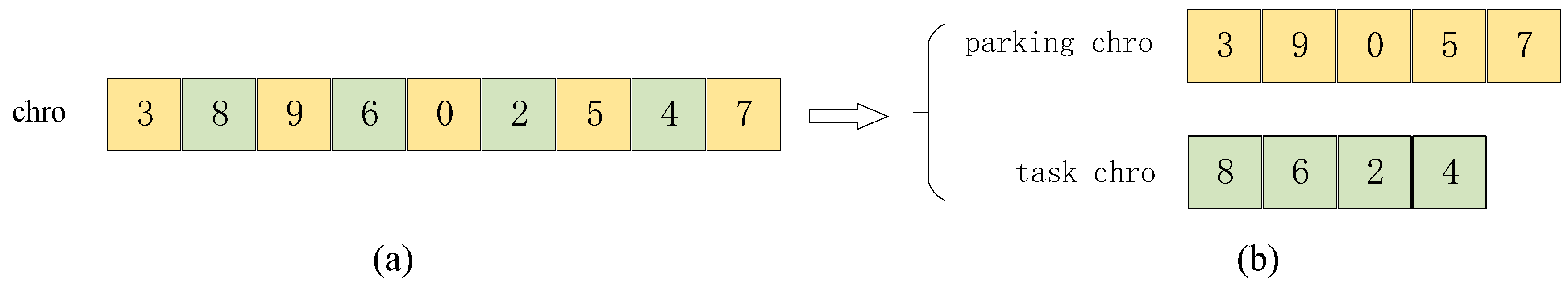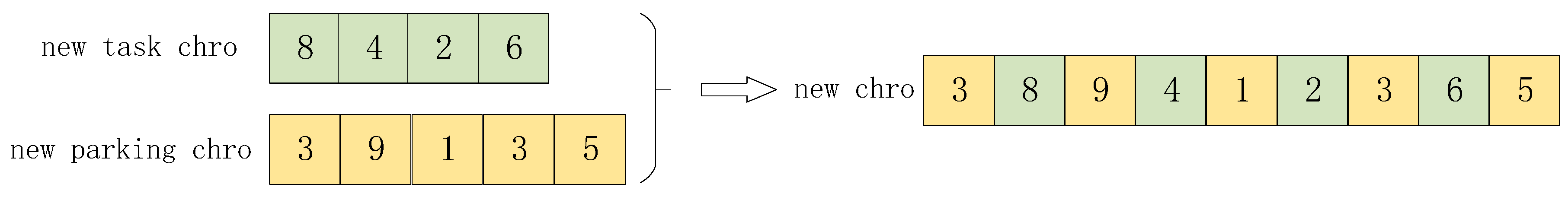1. Introduction
To meet the needs of the rapidly developing society, the total length of China’s 10 KV overhead transmission lines reached 383.54 million km in 2017, an increase of 5.06% over the same period of the previous year, and the scale is still expanding. However, power accidents caused by natural disasters, animal and plant invasion, and human impacts often occur [
1,
2,
3,
4], resulting in serious losses. Therefore, regular inspection of transmission lines is of significant importance for the safety of power supply [
5].
At present, transmission line inspection is mainly conducted via human inspection, which exhibits the following major problems: (1) the personal safety of inspectors is at risk [
6]; (2) the accuracy is low [
7]; (3) the cost is high [
8]; and (4) the level of automation is low. Due to the unique characteristics of a low weight, small size, good flexibility, and low cost [
9], the unmanned aerial vehicle (UAV) has emerged as a promising solution for transmission line inspection. Compared with traditional manual methods, inspection by remotely controlled UAVs reduces the workload of inspectors to a certain extent but also puts forward higher requirements for the ability of inspectors and has not truly achieved automated inspection yet. Therefore, autonomous inspection using UAVs is an inevitable trend of transmission line inspection.
The existing UAV inspection mission can be divided into two typical modes: transmission line corridors [
10,
11] and transmission towers [
12,
13]. In the former mode, mainly high trees, illegal dangerous buildings, and birds’ nests or other foreign objects in transmission line corridors are inspected [
14]. Due to the wide-range and long-distance inspection requirements, fixed-wing UAVs with a high speed and long endurance range are chosen for transmission line corridor inspection.
In the latter mode, mainly the status of parts and components of transmission towers and presence of foreign objects are inspected, such as explosion and breakage of insulator strings [
15], defect and deformation of shock hammers, breakage of lightning protection facilities, and honeycomb interferences [
16]. Due to the large number of parts and complex structures, UAVs are required to fly flexibly and hover smoothly to collect high-quality image information from key parts. Multi-rotor UAVs are chosen for carrying out condition inspections of transmission towers. However, the endurance of multi-rotor UAVs is relatively poor [
17]. Generally, inspectors need to carry numerous batteries to the operation site to ensure the completion of inspection of multiple transmission towers, which brings an additional heavy workload to the inspectors.
The distribution of transmission towers in cities is often concentrated (e.g., urban high-voltage corridors), and the surrounding road network is developed. The advantage of long-distance driving vehicles can compensate for the disadvantage of the limited endurance of multi-rotor UAVs. Therefore, we propose a new urban transmission tower inspection mode, which is the cooperative tower inspection mode with a vehicle and a UAV. That is, a vehicle is employed to launch and recycle the UAV, serving as a mobile platform. In this way, the UAV can change its battery on the vehicle and continue to perform inspection tasks while the vehicle is moving along the road network. This mode can greatly reduce the workload of inspectors.
Based on the new inspection mode, we study the cooperative path planning problem of a UAV and a vehicle to further improve the efficiency of UAV inspection. First, aimed at the characteristics whereby a UAV can inspect several towers consecutively in its range of endurance and different types of towers require different times, inspired by the traveling salesman problem with drones (TSP-D), we propose a transmission tower inspection-TSP-D (TTI-TSP-D). Then, an odd-even layered genetic algorithm (O-ELGA) is proposed to achieve the effective expression of the solution space and efficient solution of the model, taking into account the different constraints of the vehicle and UAV paths.
The remainder of this paper is structured as follows:
Section 2 provides a comprehensive review of the state-of-the-art development.
Section 3 describes the improved TSP-D, TTI-TSP-D. The O-ELGA is proposed in
Section 4. Numerical results and related analyses are presented in
Section 5. Finally,
Section 6 concludes this paper and provides discussions for future research.
2. Literature Review
At present, studies on UAV transmission line inspection mainly focus on image analysis [
18,
19,
20], autonomous navigation [
21], three-dimensional modeling [
22], etc. To achieve autonomous and efficient transmission line inspection using UAVs, it is necessary to plan the UAV inspection path effectively to minimize the cost of inspection. Zhou et al. [
23] established corresponding energy consumption models for different links of the UAV transmission line inspection process and developed a joint optimization method to describe the UAV energy consumption minimization problem and then obtain the optimal path by dynamic programming. Cui et al. [
24] analyzed the different characteristics of multi-rotor UAV transmission tower inspection and fixed-wing UAV transmission line corridor inspection and proposed two heuristic algorithms to obtain the shortest inspection path of the two UAV inspection methods. These works mainly focus on autonomous transmission line inspection, which only utilizes UAVs and does not consider their endurance limitations. These studies cannot be well applied to long-distance and multitask transmission line inspection.
The cooperative mode of a UAV and a vehicle was originally proposed for last-mile parcel delivery, wherein each customer is regarded as a task point. A UAV and a vehicle must traverse all of the task points collaboratively and then return to the starting point together. The execution efficiency of the task can be improved by collaboratively optimizing the vehicle path on the road and the UAV path in the air. This new cooperative optimization problem is called the TSP-D problem, a variant of the TSP problem [
25]. Agatz et al. [
26] modeled the problem as an integer programming model and developed several fast route-first, cluster-second heuristic algorithms to obtain the solution with the shortest delivery time. Murray et al. [
27] established a mixed integer linear programming model, and two heuristic algorithms were proposed for two delivery-by-drone problems to achieve the shortest delivery time. Ferrandez et al. [
28] proposed an algorithm based on K-means clustering and genetic algorithms to determine the optimal launch UAV locations and vehicle paths, respectively. Ha et al. [
29] proposed a greedy random adaptive search algorithm (GRASP) to complete delivery at the lowest operational costs, which first splits TSP tour into a TSP-D solution and then improves the solution by local search operators. Chiang et al. [
30] proposed a mixed integer green path model and designed a genetic solution algorithm, aiming to finish delivery at the lowest cost and carbon emissions. To a certain extent, the abovementioned TSP-D is similar to the transmission tower inspection path planning problem studied in this paper, but the following differences also exist:
- (1)
The former does not consider the time consumption of the UAV and vehicle at the task point because there is little time consumed at the task point of delivery; however, the latter must consider the time consumption of the UAV at the task point of inspection because the UAV spends time to inspect transmission towers.
- (2)
For the former, the UAV must return to the vehicle to obtain the package for the next task after completing the previous task because the UAV can only carry one package during flight. However, for the latter, the UAV can perform multiple tasks consecutively in the range of endurance. When the power level becomes insufficient, the UAV returns to the vehicle for a battery change to perform the follow-up tasks.
In addition to parcel delivery, the cooperative UAV and vehicle path planning problem for inspection has also been studied, such as geographic mapping, reconnaissance, and sensor data gathering. Maini et al. [
31] proposed a cooperative UAV and vehicle routing method for mapping, aiming to minimize the flying distance of the UAV, and there is no time consumption at the task points. Manyam et al. [
32] studied the UAV and vehicle path planning problem for reconnaissance and data gathering under communication constraints, in which both the UAV and vehicle can access task points, and no time is consumed at the points, and the researchers developed a branch-and-cut algorithm to obtain the shortest distance of the UAV and vehicle. Savuran et al. [
33] proposed a path optimization method for a carrier-deployed UAV system based on a genetic algorithm to allow the UAV to accomplish as many tasks as possible within its range of endurance when the vehicle path is fixed. Luo et al. [
34] solved a two-echelon cooperative routing problem for a UAV and a vehicle where the vehicle can visit points in the road network no more than once by developing two heuristic algorithms. The first heuristic algorithm constructs a complete path for all task points and then splits the path by the vehicle path, while the second algorithm constructs a complete vehicle path and then assigns the UAV path to it.
Notice that all of these papers focus on the path planning problem for vehicle-UAV cooperative applications and that our problem is quite different in terms of the task type, optimization objective, and vehicle-UAV cooperative constraints. For these reasons, their proposed solutions are inappropriate for the cooperative path planning problem of UAV-vehicle cooperative inspection of transmission towers, so we establish the TTI-TSP-D model and develop the corresponding solution algorithm.
3. Problem Description and Model Development
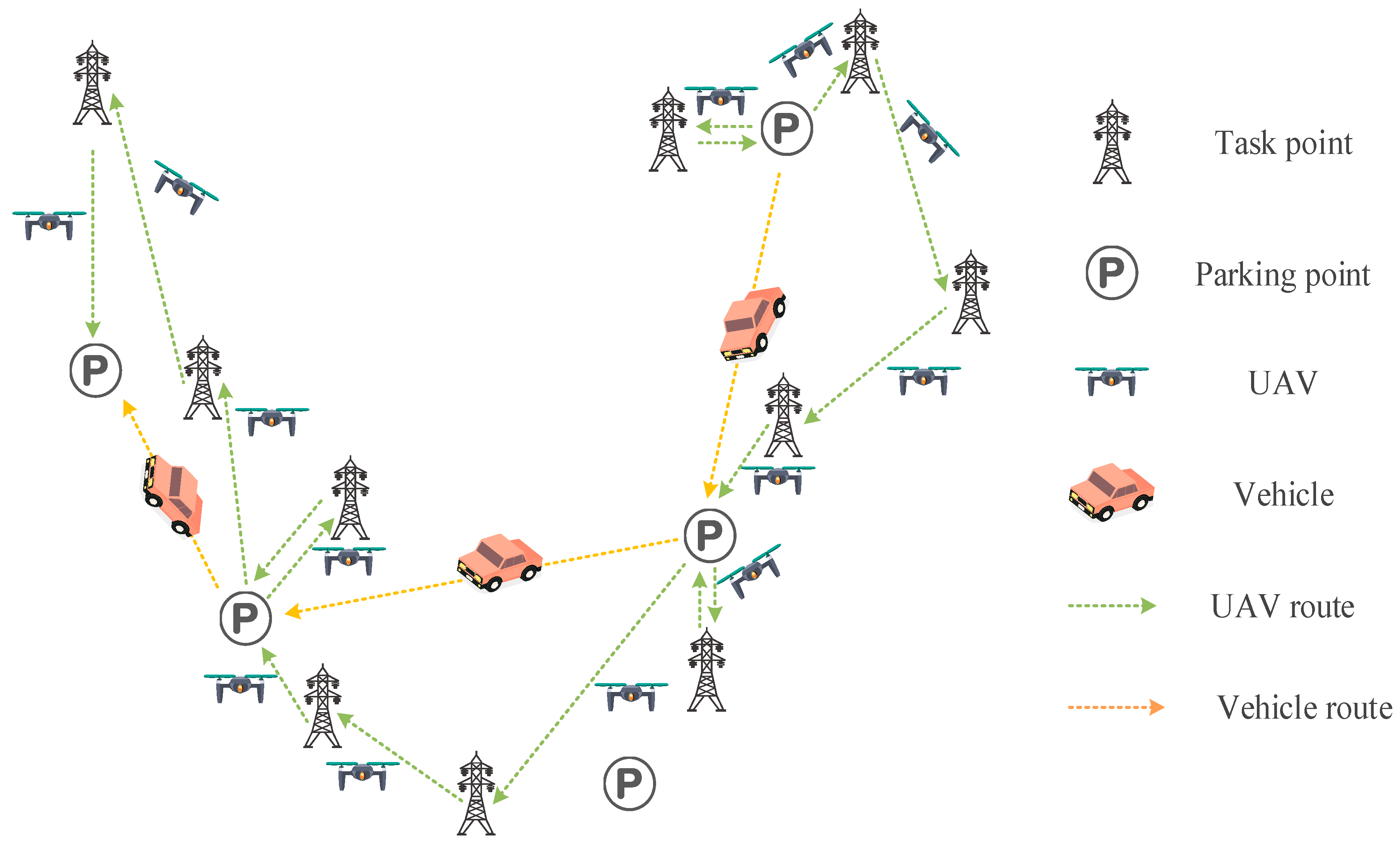
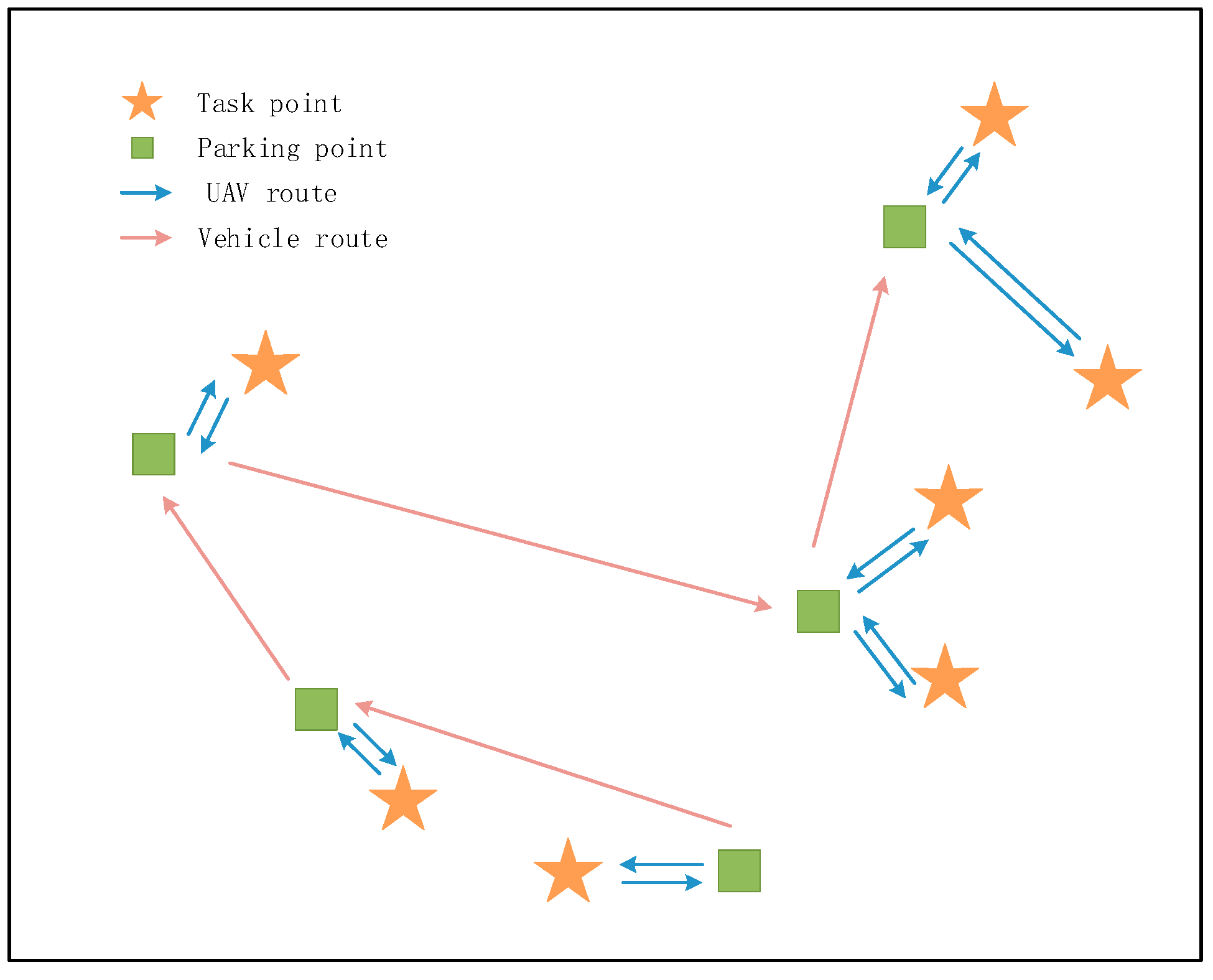
In our scenario, there are several transmission towers distributed across a region in the urban area to be inspected, as shown by the task points in
Figure 1. Every tower must be inspected once by a UAV. A vehicle-carried multi-rotor UAV and a vehicle are employed to inspect these transmission towers, as shown by the vehicle and UAV in
Figure 1. The UAV can sequentially visit and perform multiple tasks in a single flight. For each transmission tower, as the type, volume, structure, and key inspection position are not all the same, the UAV has to spend different times on each to accomplish the inspection tasks. The vehicle drives along roads and releases the UAV at appropriate locations. The UAV flies to the towers to perform the inspection tasks, and the vehicle continues to drive to the next position to rendezvous with the UAV as the UAV is in flight.
When the UAV’s power supply is insufficient to continue to perform the next task, the UAV will return to the vehicle, and the battery is replaced before performing the next task. As the technology of UAVs taking off and landing on mobile vehicles is not mature enough at present [
35] and considering that vehicles cannot park along the roads at will, we define a number of allowed parking spots along the road, as shown by the parking points in
Figure 1. The UAV can take off or land on the vehicle only when the vehicle is parked at one of these spots.
For the convenience of study, the following reasonable assumptions are made:
- (1)
The endurance range of the UAV is limited, and the vehicle’s endurance range can meet the requirements of its own mission; that is, the study does not consider the vehicle’s range constraint;
- (2)
All task points must be visited by the UAV only once, while the parking points can be selectively visited by the vehicle, thus allowing repeated visits.
- (3)
The battery replacement time of the UAV is very short and negligible.
- (4)
As the UAV takes a long time at the task point to inspect, the vehicle can arrive at the corresponding parking point earlier than the UAV and wait for the UAV each time, and the time consumed by the UAV in takeoff and landing can be negligible.
The TTI-TSP-D can be defined as an undirected graph , where is the set of all points, and is the set of all parking points, while is the set of all task points. is the set of edges for the vehicle and UAV, and let denote the shortest path between points and . represents the maximal endurance time of the UAV, and is the distance of . denotes the speed of the UAV, and represents the inspection time at task point . To formulate the problem, we define the following variables:
: a binary variable that is equal to 1 if edge is traversed by the UAV.
: a binary variable that is equal to 1 if is the first task point and is the last task point visited by the UAV in one flight. is the set of task points performed between points and (including and ).
The TTI-TSP-D can be formulated as the following integer programming model:
Objective function (1) minimizes the total time spent on the path for the UAV, which is equivalent to minimizing the total inspection time spent by UAV because the time spent on the task points is fixed. Constraint (2) ensures that every task point is visited once and only once by the UAV. Constraint (3) implies that the starting point of the UAV path can only be a parking point; that is, the UAV can only start from a parking point. Constraint (4) illustrates that the UAV will not travel along the edges in the road network, and constraint (5) ensures that the number of takeoffs is the same as the number of landings. Constraint (6) illustrates that every subset of task points (denoted as ) is incapable of forming a closed loop. Constraint (7) guarantees that when the power supply is insufficient to continue to perform the next task, the UAV can return to the vehicle to have the battery replaced. The time of one flight must not exceed the maximal endurance time. Constraint (8) imposes a simple graph, and constraint (9) defines the decision variables.
4. Solution Algorithm
With the increase in task and parking points, the solution space of our problem exhibits combinatorial explosion characteristics, and it is difficult to solve the problem effectively by exact algorithms. Genetic algorithm (GA) is a classical heuristic algorithm that has been proven to have the advantages of less computing time and better results in solving UAV task allocation and path planning problems [
36,
37]. In this paper, an O-ELGA is proposed to solve the TTI-TSP-D, which can map the solution space to the coding space intuitively and accurately and reduce the difficulty and complexity of the subsequent genetic operations. The main algorithm is shown in Algorithm 1.
In the process of Algorithm 1, the initial population (line 2) is first generated, which is the chromosome set expressed by odd-even coding, and each chromosome represents a cooperative path planning solution of a UAV and a vehicle. Then, the population begins to iterate (line 3). In an iteration, the fitness of each chromosome in the population is calculated (line 4). First, some gene fragments in certain chromosomes do not conform to the constraints in the model and need to be evaluated and corrected until the constraints are met (line 5). The chromosome with the best fitness is directly retained in the next generation population (line 6) and does not participate in the subsequent genetic operations. Then, the population is updated by selection (line 7), layered crossover (line 8), and layered mutation (line 9). Thereafter, a new iteration process begins and continues until the maximum number of iterations, Gen (which is a preset number), is reached.
| Algorithm 1: Odd-Even Layered Genetic Algorithm |
| 1 | Gen: the number of iterations |
| 2 | Initialize the population by odd-even encoding |
| 3 | FOR i = 0 to Gen DO |
| 4 | Calculate the fitness of the population |
| 5 | Check the feasibility of the solutions and correct the unfeasible solutions |
| 6 | Keep the optimal solution of this generation |
| 7 | Perform the selection operation on the population |
| 8 | Perform the layered crossover operation on the population |
| 9 | Perform the layered mutation operation on the population |
| 10 | END FOR |
The computational complexity of an algorithm is dependent mainly on its structure and implementation. The O-ELGA mainly consists of an evaluation and updating of chromosomes and an improvement of the best chromosome through iterations. We let be the scale of the population, be the number of iterations, and be the number of task points. Since the algorithm-related parameters, such as and , are preset, that is, they do not change with the scale of the problem, they can be regarded as constants when performing the algorithm analysis. The complexity of the O-ELGA depends on the steps shown in lines 2, 4, 5, 6, 7, 8, and 9. The complexity of each step is analyzed as follows:
- (1)
The complexity of line 2 is .
- (2)
The complexity of line 4 is .
- (3)
The complexity of line 5 is .
- (4)
The complexity of line 6 is .
- (5)
The complexity of line 7 is .
- (6)
The complexity of line 8 is .
- (7)
The complexity of line 9 is .
Above all, the complexity of the O-ELGA is .
The odd-even encoding in line 2 is described in
Section 4.1, correction of the unfeasible solutions in line 5 is specified in
Section 4.5, selection operation in line 7 is described in
Section 4.2, layered crossover operation in line 8 is specified in
Section 4.3, and layered mutation operation in line 9 is described in
Section 4.4.
4.1. Encoding
The chromosome designed for the TTI-TSP-D is a sequence of task and parking points, which represent a path for the UAV and vehicle to cooperatively conduct the inspection. To formulate the solution space of our problem effectively, the task points are encoded by even numbers, and the numbers belong to set . Each task point number must appear at the even-numbered gene positions of the chromosome only once, while the parking points are encoded with 0 and odd numbers, and the numbers belong to set . Each parking point number can only appear at the odd-numbered gene positions of the chromosome but can appear repeatedly or not. Number 0 is a special parking point number, indicating that the two task points adjacent to it in the chromosome are performed consecutively by the UAV in one flight. To ensure that the UAV takes off and lands at a parking point and traverses all task points, it is required that the number 0 cannot appear at the first and last gene positions of the chromosome and that the length of the chromosome must be . When the flight time of the UAV between any two adjacent parking points in the chromosome is no more than its endurance time, the chromosome represents a feasible solution of the TTI-TSP-D.
A chromosome, as shown in
Figure 2, represents a feasible solution in the case of four task points and several parking points. The UAV takes off from the vehicle at parking point 1, first visits task point 2, then visits task point 8, and thereafter lands on the vehicle coming from parking point 1 and waiting at parking point 5. After the battery is replaced, the UAV takes off from the vehicle and visits task points 6 and 4 consecutively. Finally, the UAV lands on the vehicle coming from parking point 5 and waiting at parking point 9. At this time, all tasks have been completed.
4.2. Fitness Function and Selection Operation
In this paper, we use objective function (1) as the fitness function of the algorithm. In addition, we use the roulette wheel method to perform the selection operation on the population; that is, the better the fitness of the chromosome becomes, the greater the probability that it will be selected into the parental population.
4.3. Layered Crossover Operation
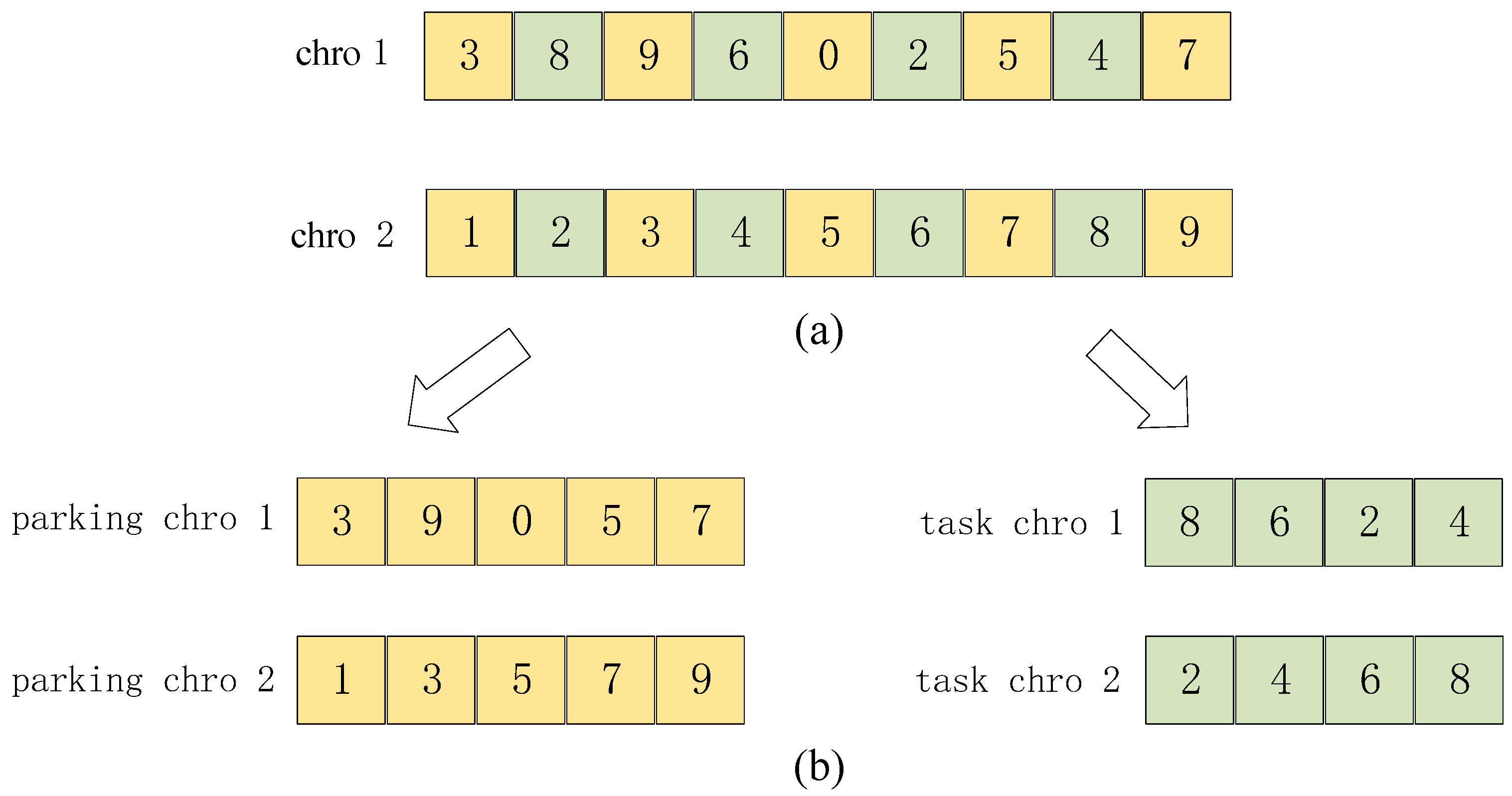
As each chromosome has two kinds of coding that express the task and parking points, to prevent too many unreasonable produced chromosomes by the crossover operation, the chromosomes need to be layered first in the crossover operation. Specifically, each chromosome is divided into a task chromosome (task chro) containing only task points and a parking chromosome (parking chro) containing only parking points. An example is shown in
Figure 3.
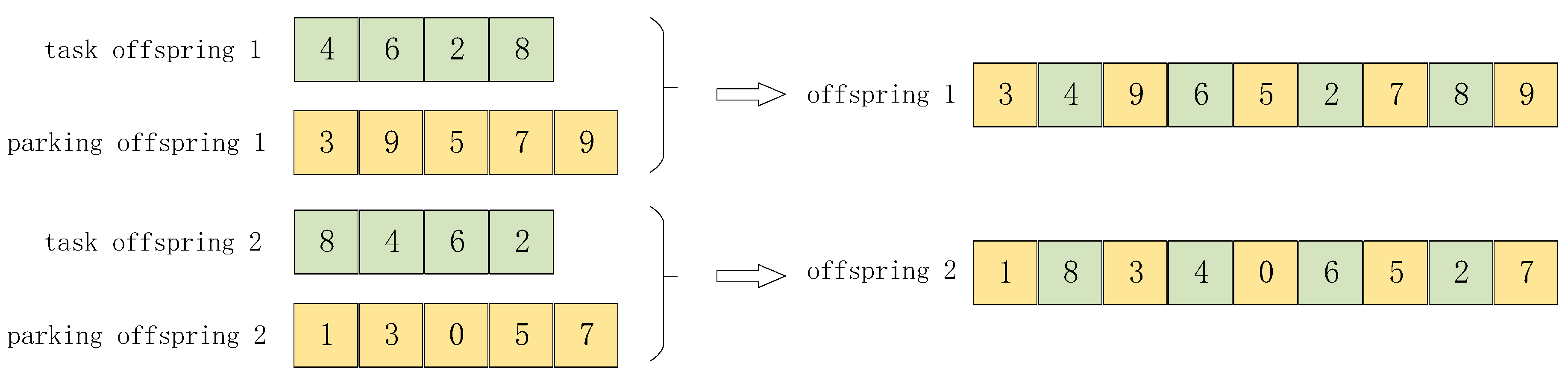
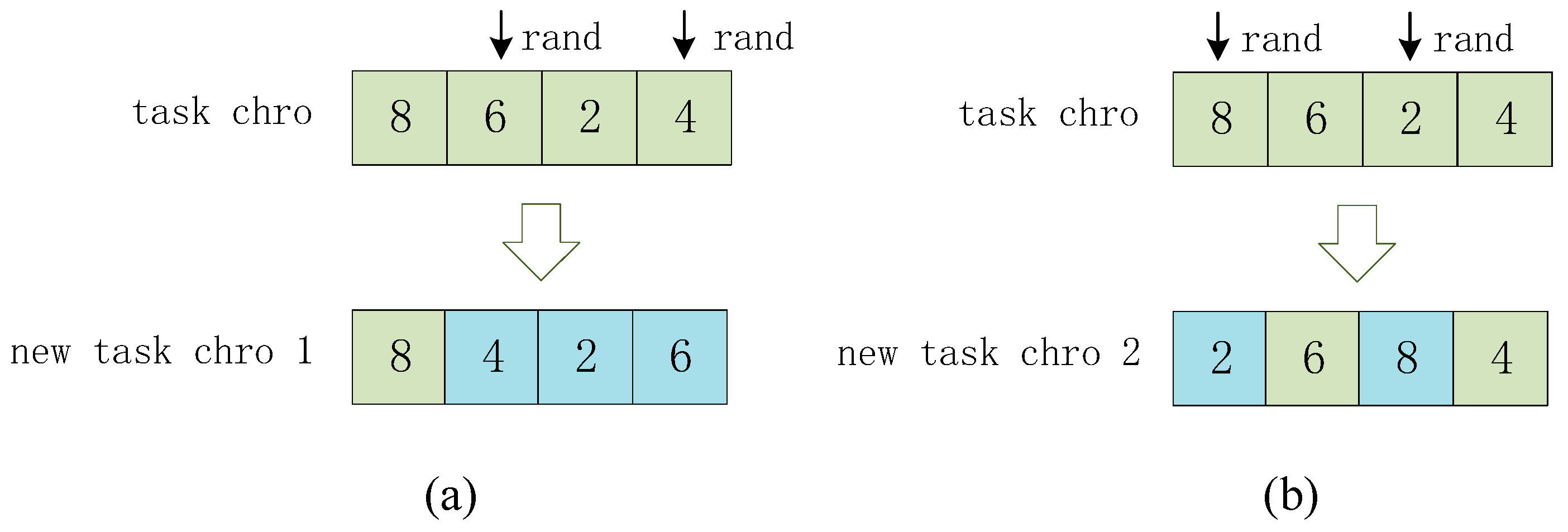
Task Chromosome. Since each task point needs to be visited only once, the task chromosome after the crossover operation cannot contain duplicate genes or lack any gene. We perform the order crossover operation on the task chromosome. That is, any two parent task chromosomes are selected, task parent 1 and task parent 2, and task offspring 1 first randomly inherits a gene fragment from task parent 1 at the same position, and the missing genes of task offspring 1 are obtained sequentially from another parent task chromosome, task parent 2. Then, task offspring 2 is obtained in a similar way. For example, in
Figure 4a, the gene fragment of task parent 1 “6 2” is randomly selected, and task offspring 1 inherits the gene fragment. Genes “4” and “8”, which task offspring 1 does not possess, are sequentially acquired from task parent 2, and task offspring 2 can be obtained by using the above similar operations, as shown in
Figure 4b.
Parking Chromosome. As each parking point can be visited several times or not, and the parking chromosome after the crossover operation is allowed to contain duplicate genes or even not contain certain genes, we perform the one-point crossover operation on the parking chromosome. First, any two parent parking chromosomes are selected, e.g., parking parent 1 and parking parent 2. Second, the same position on parking parent 1 and parking parent 2 is randomly selected. Finally, parking parent 1 and parking parent 2 exchange all the genes after the selected position, thereby obtaining two offspring parking chromosomes, i.e., parking offspring 1 and parking offspring 2. For example, in
Figure 5, we randomly select position 2, and parking parent 1 and parking parent 2 exchange the gene fragments that follow after the selected position to obtain parking offspring 1 and parking offspring 2.
After the crossover operation of the task and parking chromosomes, the offspring chromosomes are paired to form a new chromosome according to their position in the chromosome. For example, in
Figure 6, task offspring 1 and parking offspring 1 are paired to form a new chromosome offspring 1, and offspring 2 is obtained in a similar way.
4.4. Layered Mutation Operation
To prevent too many unreasonable chromosomes, the chromosome in the mutation operation also needs to be layered first as was done in the crossover operation, thus obtaining task (task chro) and parking (parking chro) chromosomes. The example is illustrated in
Figure 7.
According to the difference between the task and parking chromosomes, different mutation operations are proposed in this paper, which are as follows.
Task Chromosome. Since the task chromosomes after the mutation operation cannot contain duplicate genes or lack any gene, inversion and exchange mutations are used in the algorithm. One of these mutation options is randomly selected according to the probability before mutation to increase the population diversity.
Inversion mutation: First, a fragment of the task chromosome (task chro) is randomly selected, and then the genes in this fragment are arranged in reverse order to obtain a new task chromosome (new task chro). For example, as shown in
Figure 8a, the new task chro “8 4 2 6” is obtained by randomly selecting fragment “6 2 4” in task chro “8 6 2 4” and arranging “6 2 4” in reverse order.
Exchange mutation: Two genes in the task chromosome (task chro) are randomly selected, and a new task chromosome (new task chro) is obtained by exchanging the two genes. For example, as shown in
Figure 8b, the “8” and “2” genes in task chro “8 6 2 4” are selected for exchange, and a new task chro, “2 6 8 4”, is obtained.
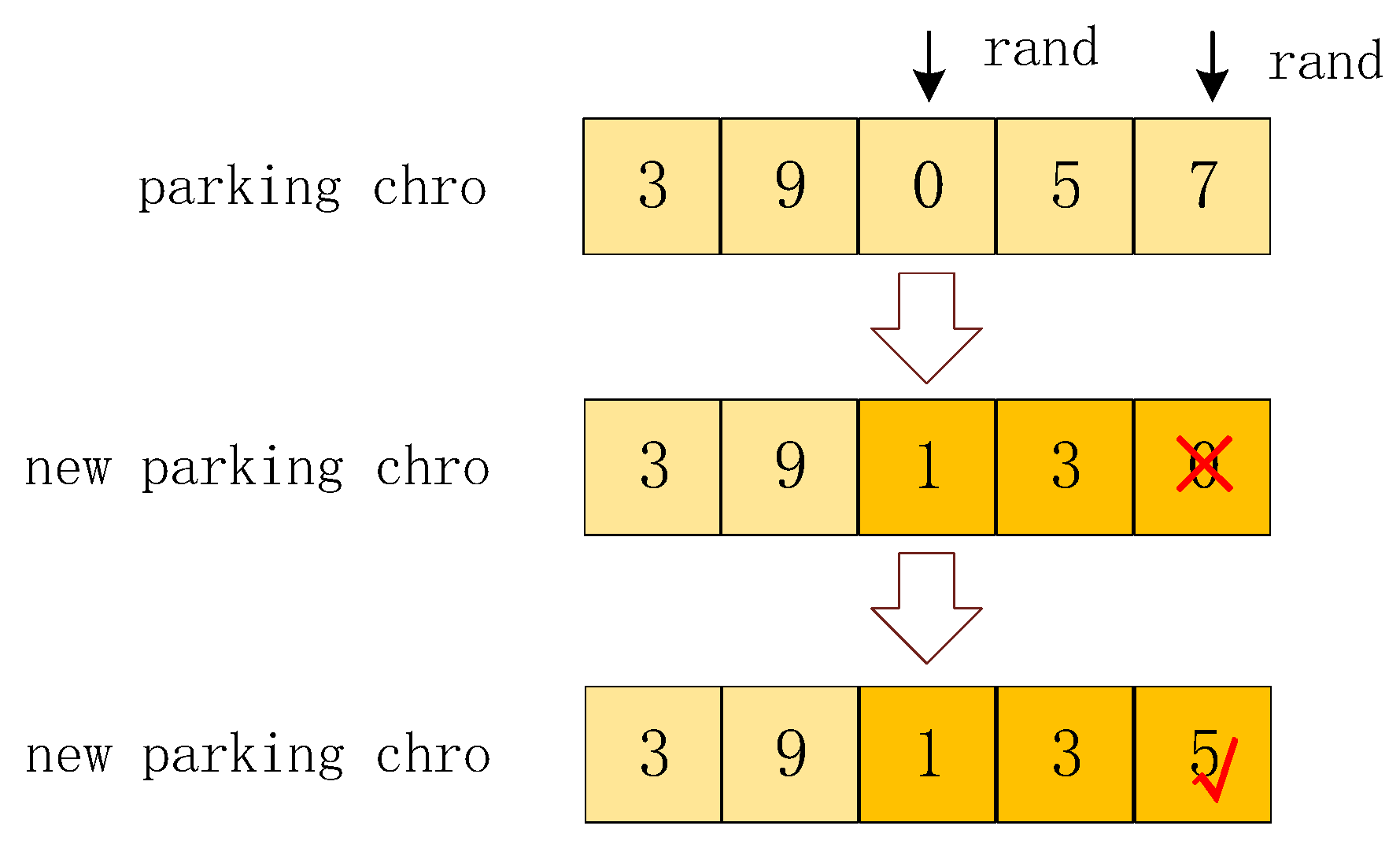
Parking Chromosome. As the parking chromosomes after the mutation operation may contain duplicate genes or even not contain certain genes, we adopt continuous random mutations. A fragment in the parking chromosome (parking chro) is randomly selected, and the genes in the fragment are replaced in turn by randomly selecting a gene from the parking point gene set. If there is a “0” gene at the first or last gene positions after replacement, a replacement gene will be randomly selected until no “0” gene is obtained, thus obtaining new parking chro. For example, in
Figure 9, the “0 5 7” fragment is randomly selected and replaced by “1 3 0”. As “0” appears at the last gene position, a replacement gene for the last position is randomly selected again, and “0” is replaced by “5”.
Finally, new task chro and new parking chro form a new chromosome, new chro, according to their respective positions in the chromosome, as shown in
Figure 10.
4.5. Correction of the Unfeasible Solutions
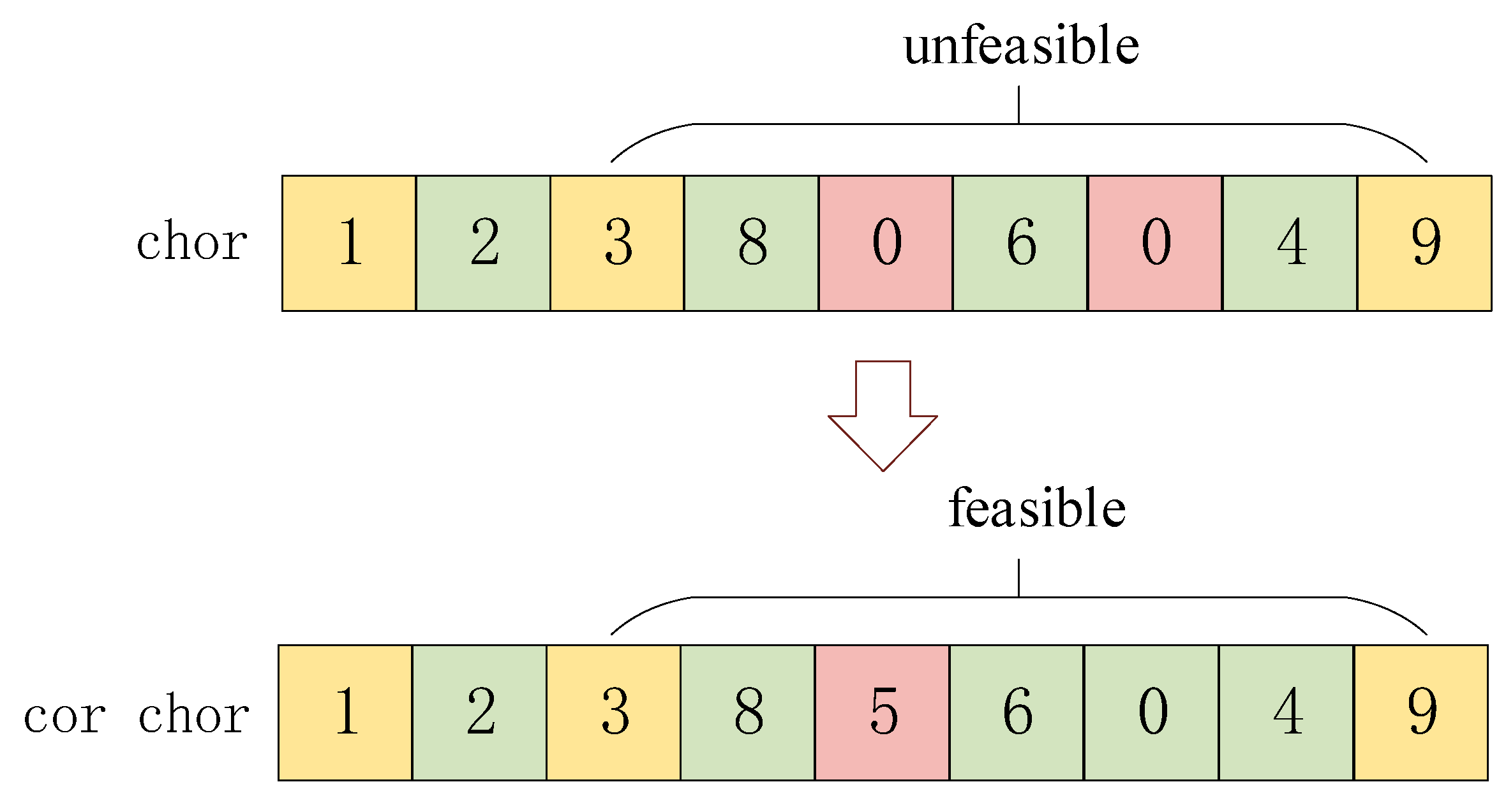
After the crossover and mutation operations, if the parking chromosome has too many consecutive “0” genes, that is, the UAV carries out too many tasks consecutively, with the result that the flight time of the UAV is longer than its endurance, the solution expressed by this chromosome is unfeasible. For this reason, we take the following measures to transform the chromosome into a feasible solution: for the fragments in the chromosome that exceed the endurance constraint, we first transform the first “0” gene into a random parking point gene, and then recalculate the time to consecutively execute the tasks in the fragment, and determine whether the time required meets the endurance constraint. If the constraint is not satisfied, the next “0” gene will be transformed until the continuous execution time after transformation meets the endurance constraint. For example, as shown in
Figure 11, for the “3 8 0 6 0 4 9” fragment, the UAV performs tasks 8, 6, and 4 consecutively, and this solution is unfeasible. Therefore, the first “0” gene is transformed into parking point 5, and the UAV performs tasks 6 and 4 consecutively; the solution is feasible and the transformation of “0” genes is stopped.
5. Experiment Analysis
To verify the performance of the proposed algorithm, three experiments were designed. Experiment 1 verifies the correctness of the algorithm by comparing it with the enumeration algorithm in a small-scale case. Experiment 2 verifies the quality of the algorithm by comparing it with a rule-based path planning algorithm in test instances with different scales. Experiment 3 obtains the optimal combination of crossover and mutation probabilities by comparing the fitness under different crossover and mutation probabilities. The experiment program is coded in C++ in the Microsoft Visual Studio Ultimate 2013 environment. All experiments were run on a 64-bit PC with 16.0 GB RAM and a 3.60 GHz processor. All of the results are the average results of the same experiment that was run 10 times. The relevant parameters of the experiments are as shown in
Table 1.
5.1. Verification of the Correctness
The scenario of this experiment is shown in
Figure 12. There are six task points and four parking points in a 500 × 500 m region. The task execution time of each task point is 5, 7, 6, 6, 5, and 5 min. The results of the proposed and enumeration algorithms are shown in
Table 2.
The experimental results show that the objective function value of the enumeration algorithm is 2.4914, and the optimal solution of the problem can be obtained in 100 runs of our algorithm. Further, the objective function values are the same as the values obtained by the enumeration algorithm, as shown in
Table 2.
5.2. Verification of the Quality
In this experiment, four test instances are designed according to the number of task points, the number of parking points, and the size of the area, as shown in
Table 3.
In each test instance, each task point and each parking point are randomly generated in the corresponding area, and the weight of each task point is an integer randomly generated between 1 and 5. The specific distributions of the points in the four test instances are shown in
Figure 13.
To verify the solution quality of O-ELGA in the different test instances, this paper designed a rule-based path planning (RBPP) algorithm and compared the solution quality of O-ELGA with that of the RBPP algorithm.
The basic idea of the RBPP algorithm is as follows. Firstly, the UAV takes off from the vehicle and inspects the nearest task point. Then, the vehicle parks at the parking point and waits for the UAV to fly back. After inspecting the previous task point, the UAV will fly back to the vehicle and the vehicle will carry the UAV to the parking point nearest to the next task point, where the next task point is the task point closest to the previous task point and has not been visited. Thereafter, the UAV will take off from the vehicle and inspect the next task point. The above steps are repeated until all of the task points are visited. The vehicle driving distance in RBPP is Manhattan distance [
30]. The process is shown in
Figure 14. The experimental results are shown in
Table 4.
The experimental results in
Table 2 show that the objective function values obtained by O-ELGA are better than those obtained by the RBPP algorithm in the different-scale test instances, and the average optimization efficiency is higher than almost 20%. When the scale is not larger than test instance 3, the optimization efficiency is higher than 18%. On the whole, when the scale of the test instances is large, the optimization efficiency decreases but still remains above 12%.
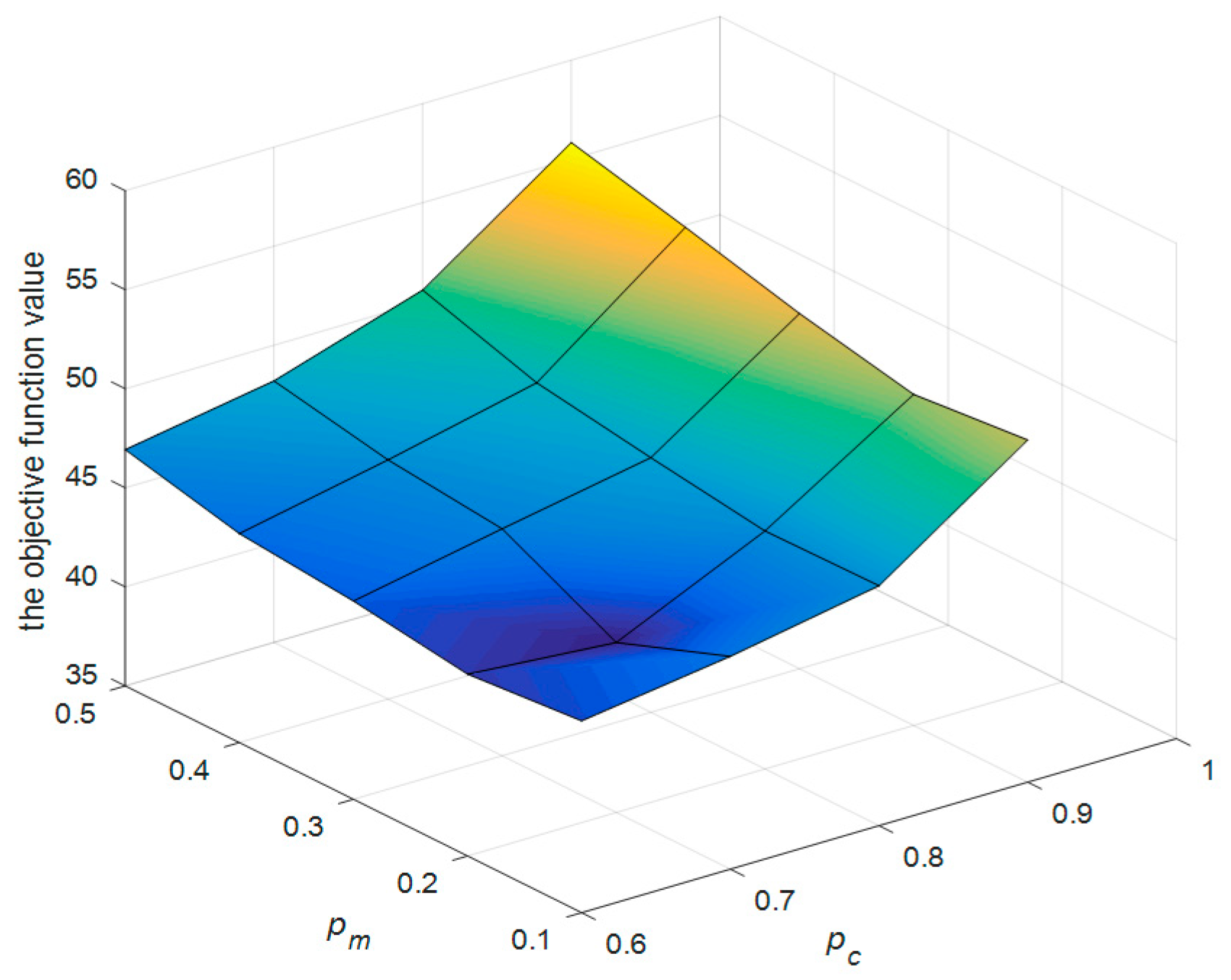
5.3. Sensitivity Analysis of the Parameters
In this experiment, the effect of the algorithm is further analyzed for different combinations of the crossover and mutation probabilities. In this experiment, test instance 3 in
Table 2 is used as the experiment scenario. The crossover probability
is selected from 0.6, 0.7, 0.8, and 0.9, and the mutation probability
is selected from 0.1, 0.2, 0.3, 0.4, and 0.5. For each combination of the probabilities, the algorithm is run 10 times, and the best, average, and worst values of the 10 results are selected. The experimental results are shown in
Table 5.
From the above experimental results, it can be seen that the TTI-TSP-D solved by O-ELGA is relatively stable on the whole, but there are also differences in the effect of the solution for the different combinations of the crossover and mutation probabilities, as shown in
Figure 15.
When the crossover probability is fixed, the objective function value of the experiment increases in general with increasing crossover probability, and when the crossover probability is 0.7 and the mutation probability is 0.2, the objective function value is optimal. When the mutation probability is fixed, the objective function value also shows an increasing trend as a whole with increasing crossover probability. Therefore, in the process of solving the TTI-TSP-D, the crossover and mutation probabilities should be set to 0.7 and 0.2, respectively.
6. Conclusions
In this paper, we proposed a new inspection mode for the cooperation of a UAV and a vehicle for transmission tower inspection (one vehicle and one UAV). The vehicle is employed as a platform for launching and recycling UAV, and at the same time, the vehicle can provide a replacement battery for the UAV when it returns. In this way, the vehicle can launch and recycle the UAV at different locations, and the UAV can perform as many tasks as possible in a single flight, thus minimizing the time wasted in the process of inspection and improving the inspection efficiency. According to the characteristics of this mode, we proposed the TTI-TSP-D, which minimizes the time required to complete the inspection tasks as the optimization goal. To solve the TTI-TSP-D, we developed the O-ELGA in which special odd-even coding and corresponding genetic operations, such as layered crossover and layered mutation operations, were designed to obtain a satisfactory solution. In the experiment process, we not only verified the correctness of the algorithm by comparing it with the enumeration algorithm in a small-scale case but also further verified the superiority of the algorithm by comparing it with the RBPP algorithm in cases with different scales. At the same time, the optimal combination of crossover and mutation probabilities of the algorithm was obtained through parameter sensitivity analysis.
In future research, we will further expand the current study to include multi-UAV and multivehicle cooperative path planning on the basis of this paper and study the task allocation and path planning process of multiple cooperative UAVs and vehicles for transmission tower inspection.
Author Contributions
Conceptualization, G.W. and H.L.; Methodology, J.W. and G.W.; Software, J.W., X.H. and H.X.; Validation, J.W. and G.W.; Formal Analysis, J.W., G.W. and H.L.; Investigation, J.W. and G.W.; Resources, X.H., H.L. and H.X.; Data Curation, J.W.; Writing—Original Draft Preparation, J.W. and G.W.; Writing—Review and Editing, J.W. and G.W.; Visualization, J.W. and G.W.; Supervision, X.H.; Project Administration, X.H. and H.L.; Funding Acquisition, X.H., H.L. and H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 71971075, Grant 71871079, Grant 71671059, and Grant 71401048, in part by the Anhui Provincial Natural Science Foundation under Grant 1808085MG213 and Grant 1508085MG140, and in part by the Fundamental Research Funds for the Central Universities under Grant JZ2018HGBZ0128 and Grant PA2019GDPK0082.
Acknowledgments
The authors also wish to thank American Journal Experts (
https://www.aje.com/) for its linguistic assistance during the preparation of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Kim, J.W.; Yoo, C.W. Analysis of ground control system for a Smart UAV. In Proceedings of the 2009 IEEE International Systems Conference, Vancouver, BC, Canada, 23–26 March 2009. [Google Scholar]
- Ariyur, K.B.; Fregene, K.O. Autonomous tracking of a ground vehicle by a UAV. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008. [Google Scholar]
- Maharjan, S.; Zhu, Q.Y.; Zhang, Y.; Gjessing, S.; Basar, T. Dependable Demand Response Management in the Smart Grid: A Stackelberg Game Approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Z.; Wang, G.; Guo, L.; Wang, X.; Wang, P.; Bao, Z. Analysis of tower foundation stability along the Qinghai–Tibet Power Transmission Line and impact of the route on the permafrost. Cold Reg. Sci. Tech. 2015, 121, 205–213. [Google Scholar] [CrossRef]
- Sampedro, C.; Martinez, C.; Chauhan, A.; Campoy, P. A supervised approach to electric tower detection and classification for power line inspection. In Proceedings of the 2014 International Joint Conference On Neural Networks (IJCNN), Beijing, China, 6–11 July 2014. [Google Scholar]
- Jones, D.I.; Whitworth, C.C.; Earp, G.K.; Duller, A. A laboratory test-bed for an automated power line inspection system. Control Eng. Pract. 2005, 13, 835–851. [Google Scholar] [CrossRef]
- Deng, C.; Wang, S.; Huang, Z.; Tan, Z. Unmanned Aerial Vehicles for Power Line Inspection: A Cooperative Way in Platforms and Communications. J. Commun. 2014, 9, 687–692. [Google Scholar] [CrossRef]
- Tseng, C.Y.; Zheng, X.Y.; Liu, C.Y.; Su, L.K.; Fan, L.W.; Jiang, J.A. A seismic assessment algorithm for smart grid safety monitoring. In Proceedings of the 2015 International Conference On Smart Grid And Clean Energy Technologies (ICSGCE), Offenburg, Germany, 20–23 October 2015; pp. 211–216. [Google Scholar]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Polonen, I.; Hakala, T.; Litkey, P.; Pesonen, L. Processing and assessment of spectrometric, stereoscopic imagery collected using a lightweight UAV spectral camera for precision agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Fang, Y.; Chen, S. UAV Low Altitude Photogrammetry for Power Line Inspection. ISPRS Int. J. Geo-Inf. 2017, 6, 14. [Google Scholar] [CrossRef]
- Nguyen, V.N.; Jenssen, R.; Roverso, D. Automatic autonomous vision-based power line inspection: A review of current status and the potential role of deep learning. Int. J. Electr. Power Energy Syst. 2018, 99, 107–120. [Google Scholar] [CrossRef]
- Bian, J.; Huie, X.; Zhao, X.; Tan, M. A monocular vision-based perception approach for unmanned aerial vehicle close proximity transmission tower inspection. Int. J. Adv. Robot. Syst. 2019, 16. [Google Scholar] [CrossRef]
- Hui, X.; Bian, J.; Zhao, X.; Tan, M. Vision-based autonomous navigation approach for unmanned aerial vehicle transmission-line inspection. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Zhen, Y.; Chen, X.; Zeng, L.; Ou, Q.; He, Q. Method and System for Monitoring Power Transmission Line of Power Grid. U.S. Patent 9158036, 13 October 2015. [Google Scholar]
- Prostejovsky, A.M.; Gehrke, O.; Kosek, A.M.; Strasser, T.; Bindner, H.W. Distribution Line Parameter Estimation under Consideration of Measurement Tolerances. IEEE Trans. Ind. Inform. 2016, 12, 726–735. [Google Scholar] [CrossRef]
- Wilson, T.M.; Stewart, C.; Sword-Daniels, V.; Leonard, G.S.; Johnston, D.M.; Cole, J.W.; Barnard, S.T. Volcanic ash impacts on critical infrastructure. Phys. Chem. Earth 2012, 45–46, 5–23. [Google Scholar] [CrossRef]
- Ersue, E.; Wienand, S. Method for Planning an Inspection Path for Determining Areas that are to be Inspected. U.S. Patent 8059151, 15 November 2011. [Google Scholar]
- Ramesh, K.N.; Murthy, A.S.; Senthilnath, J.; Omkar, S.N. Automatic detection of power lines in UAV remote sensed images. In Proceedings of the 2015 International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Bangalore, India, 10–12 December 2015. [Google Scholar]
- Varghese, A.; Gubbi, J.; Sharma, H.; Balamuralidhar, P. Power infrastructure monitoring and damage detection using drone captured images. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Cheng, H.; Zhai, Y.; Chen, R.; Wang, D.; Dong, Z.; Wang, Y. Self-Shattering Defect Detection of Glass Insulators Based on Spatial Features. Energies 2019, 12, 543. [Google Scholar] [CrossRef]
- Hui, X.; Bian, J.; Zhao, X.; Tan, M. Deep-learning-based autonomous navigation approach for UAV transmission line inspection. In Proceedings of the 2018 Tenth International Conference on Advanced Computational Intelligence (ICACI), Xiamen, China, 29–31 March 2018; pp. 455–460. [Google Scholar]
- Jiang, S.; Jiang, W.; Huang, W.; Yang, L. UAV-Based Oblique Photogrammetry for Outdoor Data Acquisition and Offsite Visual Inspection of Transmission Line. Remote Sens. 2017, 9, 278. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C.; Xu, C.; Xiong, F.; Zhang, Y.; Umer, T. Energy-Efficient Industrial Internet of UAVs for Power Line Inspection in Smart Grid. IEEE Trans. Ind. Inform. 2018, 14, 2705–2714. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, Y.; Ma, S.; Yi, Y.; Xin, J.; Liu, D. Path planning algorithms for power transmission line inspection using unmanned aerial vehicles. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 2304–2309. [Google Scholar]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. ERIM Report Series Reference No. ERS-2015-011-LIS. Transp. Sci. Available online: https://ssrn.com/abstract=2639672 (accessed on 27 June 2016). [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Ferrandez, S.M.; Harbison, T.; Weber, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. J. Ind. Eng. Manag. 2016, 9, 374. [Google Scholar] [CrossRef]
- Quang, M.H.; Deville, Y.; Quang, D.P.; Minh, H.H. On the Min-cost Traveling Salesman Problem with Drone. Transp. Res. Part C Emerg. Technol. 2015, 86, 597–621. [Google Scholar]
- Chiang, W.; Li, Y.; Shang, J.; Urban, T.L. Impact of drone delivery on sustainability and cost: Realizing the UAV potential through vehicle routing optimization. Appl. Energy 2019, 242, 1164–1175. [Google Scholar] [CrossRef]
- Maini, P.; Sujit, P.B. On cooperation between a fuel constrained UAV and a refueling UGV for large scale mapping applications. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 09–12 June 2015; pp. 1370–1377. [Google Scholar]
- Manyam, S.G.; Casbeer, D.W.; Sundar, K. Path Planning for Cooperative Routing of Air-Ground Vehicles. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 4630–4635. [Google Scholar]
- Savuran, H.; Karakaya, M. Efficient route planning for an unmanned air vehicle deployed on a moving carrier. Soft Comput. 2016, 20, 2905–2920. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Z.; Shi, J. A Two-Echelon Cooperated Routing Problem for a Ground Vehicle and Its Carried Unmanned Aerial Vehicle. Sensors 2017, 17, 1144. [Google Scholar]
- Orphanides, K.G. Drones can Now Land on Moving Cars. Wired, 2016. Available online: http://www.wired.co.uk/article/drone-lands-on-moving-car (accessed on 15 October 2018).
- Tian, J.; Shen, L.; Zheng, Y. Genetic algorithm based approach for multi-UAV cooperative reconnaissance mission planning problem. In Proceedings of the 16th International Symposium on Methodologies for Intelligent Systems, Bari, Italy, 27–29 September 2006; pp. 101–110. [Google Scholar]
- Sahingoz, O.K. Generation of bezier curve-based flyable trajectories for multi-UAV systems with parallel genetic algorithm. J. Intell. Robot. Syst. 2014, 74, 499–511. [Google Scholar] [CrossRef]
Figure 1.
Illustration of the transmission tower inspection traveling salesman problem with drone (TTI-TSP-D).
Figure 1.
Illustration of the transmission tower inspection traveling salesman problem with drone (TTI-TSP-D).
Figure 2.
Chromosome encoding and example.
Figure 2.
Chromosome encoding and example.
Figure 3.
An illustration of chromosome layering: (a) chromosomes before layering; (b) chromosomes after layering.
Figure 3.
An illustration of chromosome layering: (a) chromosomes before layering; (b) chromosomes after layering.
Figure 4.
Crossover of the task chromosomes. (a) the first chromosome produced by crossover; (b) the second chromosome produced by crossover.
Figure 4.
Crossover of the task chromosomes. (a) the first chromosome produced by crossover; (b) the second chromosome produced by crossover.
Figure 5.
Crossover of the parking chromosomes.
Figure 5.
Crossover of the parking chromosomes.
Figure 6.
Paired combinations of the chromosomes after the crossover operation.
Figure 6.
Paired combinations of the chromosomes after the crossover operation.
Figure 7.
An illustration of chromosome layering before the mutation operation: (a) chromosome before layering; (b) chromosome after layering.
Figure 7.
An illustration of chromosome layering before the mutation operation: (a) chromosome before layering; (b) chromosome after layering.
Figure 8.
Task chromosome mutation: (a) inversion mutation and (b) exchange mutation.
Figure 8.
Task chromosome mutation: (a) inversion mutation and (b) exchange mutation.
Figure 9.
Mutation of the parking chromosome.
Figure 9.
Mutation of the parking chromosome.
Figure 10.
Paired combination of the chromosomes after the mutation operation.
Figure 10.
Paired combination of the chromosomes after the mutation operation.
Figure 11.
An illustration of chromosome correction.
Figure 11.
An illustration of chromosome correction.
Figure 12.
Distribution of the task and parking points in a small-scale test.
Figure 12.
Distribution of the task and parking points in a small-scale test.
Figure 13.
Distribution of the task and parking points in the four test instances. (1) instance of 20 task points and 10 parking points; (2) instance of 30 task points and 15 parking points; (3) instance of 50 task points and 20 parking points; (4) instance of 70 task points and 30 parking points.
Figure 13.
Distribution of the task and parking points in the four test instances. (1) instance of 20 task points and 10 parking points; (2) instance of 30 task points and 15 parking points; (3) instance of 50 task points and 20 parking points; (4) instance of 70 task points and 30 parking points.
Figure 14.
An illustration of the rule-based path planning (RBPP) algorithm.
Figure 14.
An illustration of the rule-based path planning (RBPP) algorithm.
Figure 15.
The objective function value for different crossover and mutation probabilities.
Figure 15.
The objective function value for different crossover and mutation probabilities.
Table 1.
Relevant parameters of the experiments.
Table 1.
Relevant parameters of the experiments.
| Parameter | Value |
|---|
| (the maximum endurance of the UAV) | 30 min |
| (the speed of the UAV) | 5 m/s |
| (the speed of the vehicle) | 10 m/s |
| (the crossover probability) | 0.7 |
| (the mutation probability) | 0.2 |
| (the scale of the population) | 800 |
| (the number of iterations) | 2000 |
Table 2.
The objective function values of the different algorithms.
Table 2.
The objective function values of the different algorithms.
| Algorithm | Path Sequence | Objective Function Value |
|---|
| Enumeration | (7,12,0,4,0,2,3,6,0,10,0,8,5) | 2.4914 |
| O-ELGA | (7,12,0,4,0,2,3,6,0,10,0,8,5) | 2.4914 |
Table 3.
Test instances with different scales.
Table 3.
Test instances with different scales.
| Test Instance | The Number of Task Points | The Number of Parking Points | The Size of the Area |
|---|
| 1 | 20 | 10 | 1500 × 1500 m |
| 2 | 30 | 15 | 1500 × 1500 m |
| 3 | 50 | 20 | 2500 × 2500 m |
| 4 | 70 | 30 | 2500 × 2500 m |
Table 4.
Comparison of odd-even layered genetic algorithm (O-ELGA) and the RBPP algorithm in the different test instances.
Table 4.
Comparison of odd-even layered genetic algorithm (O-ELGA) and the RBPP algorithm in the different test instances.
| Test Instance | The Objective Function Value | Average Improvement (%) |
|---|
| O-ELGA | RBPP |
|---|
| Average | Best | Worst |
|---|
| 1 | 28.714 | 26.180 | 30.403 | 39.597 | 27.48% |
| 2 | 43.578 | 37.735 | 46.811 | 55.001 | 20.77% |
| 3 | 164.278 | 157.586 | 168.170 | 201.890 | 18.63% |
| 4 | 227.070 | 216.722 | 235.233 | 258.828 | 12.27% |
Table 5.
The objective function values obtained by O-ELGA for different crossover and mutation probabilities.
Table 5.
The objective function values obtained by O-ELGA for different crossover and mutation probabilities.
| | Objective Function Value |
|---|
| Best | Average | Worst |
|---|
| 0.6 | 0.1 | 40.725 | 44.685 | 47.729 |
| 0.2 | 38.820 | 44.181 | 46.521 |
| 0.3 | 42.785 | 45.008 | 47.867 |
| 0.4 | 43.487 | 45.551 | 47.712 |
| 0.5 | 43.363 | 46.927 | 48.591 |
| 0.7 | 0.1 | 41.061 | 45.744 | 46.877 |
| 0.2 | 37.735 | 43.578 | 46.811 |
| 0.3 | 42.740 | 46.461 | 48.191 |
| 0.4 | 44.011 | 47.076 | 48.488 |
| 0.5 | 46.306 | 48.200 | 49.752 |
| 0.8 | 0.1 | 43.249 | 47.111 | 49.492 |
| 0.2 | 44.139 | 47.017 | 49.122 |
| 0.3 | 45.111 | 47.851 | 49.744 |
| 0.4 | 46.704 | 48.768 | 50.792 |
| 0.5 | 44.594 | 50.589 | 53.386 |
| 0.9 | 0.1 | 49.989 | 52.276 | 53.537 |
| 0.2 | 47.995 | 51.712 | 53.098 |
| 0.3 | 48.537 | 52.933 | 54.331 |
| 0.4 | 49.807 | 54.423 | 56.002 |
| 0.5 | 52.357 | 55.836 | 57.938 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).