1. Introduction
Wind energy is one of the most promising renewable alternatives available for exploitation in Brazil today [
1]. It is a mature technology, and the resource is significant and cost-competitive compared with other energy sources. Until now, all wind farms have been situated in continental areas, where they account for 15.52 GW or 9% of the national installed capacity [
2]. It is expected that wind power will reach 19 GW by 2024, an increase of 22.7% in installed wind capacity [
3].
There are still vast areas available for continental exploitation in Brazil, although conflicts over land use have been reported [
4,
5]. The exploitation of offshore wind energy appears to be an alternative to wind energy development [
6]. Although offshore turbines incur larger installation and operational costs, the force of winds is of a stronger magnitude over the ocean [
7,
8,
9]. Offshore wind farms generally operate at larger capacity factors and the investment in these projects tends to have similar return periods to those of onshore wind farms.
The power of Brazil’s offshore wind is estimated to be between 1300 GW and 1800 GW for installations up to 100 m in depth [
10,
11]. However, there is a very limited meteorological buoy network and the country lacks a program for long-term monitoring of coastal winds at the height of wind turbines. Despite this, the quality of its winds has aroused considerable interest in the energy sector. In 2018, Petrobras announced that the first Brazilian offshore wind turbine would be installed in Guamaré, Rio Grande do Norte [
12]. Until January 2020, Brazil had six projects for offshore wind farms with applications for environmental licensing underway at the Brazilian Institute of the Environment and Renewable Natural Resources (IBAMA) for the States of Rio Grande do Sul, Rio de Janeiro, Rio Grande do Norte, and Ceará [
11]. There are notable resources that lie in the north, northeast, southeast, and southern regions of Brazil [
10,
11,
13].
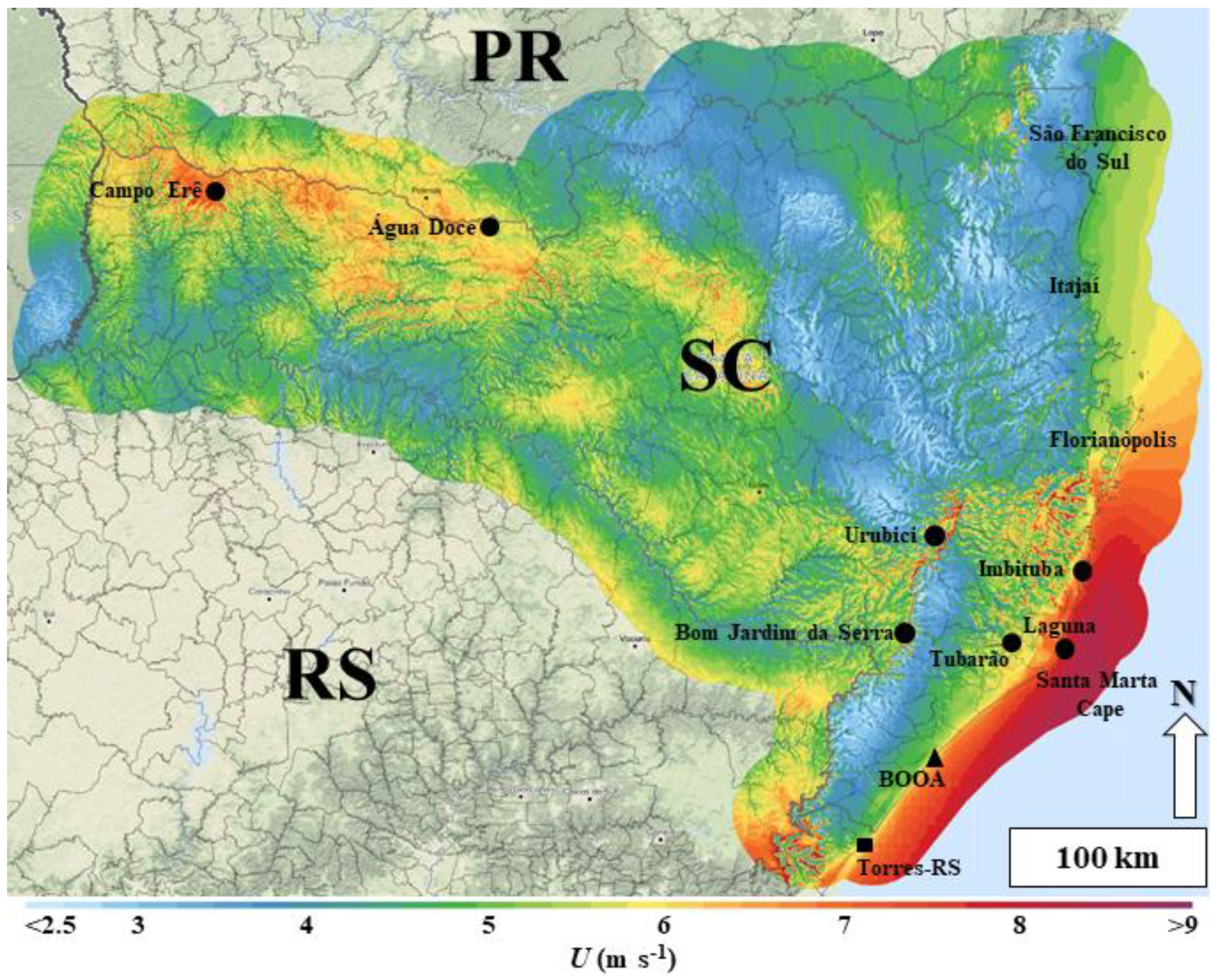
The State of Santa Catarina has promising regions for development in continental and offshore areas, as illustrated by the wind speed fields derived from the Global Wind Atlas [
14] which shows the average wind climatology for the height of 100 m above the terrain/sea surface (
Figure 1). Here the red colors indicate high wind speeds, exceeding 8 m s
−1. Shades in blue indicate weaker winds, below 4 m s
−1.
As shown, there are continental wind resources present in the western highlands of the state, the central region, the coastal mountains, and the coastal plain near Laguna and Santa Marta Cape.
The state contribution to the national generation of energy is 4803.7 MW, where 3415.2 MW comes from hydropower [
2]. The wind-installed capacity is only 245.5 MW with all its farms being located in continental areas: Água Doce (146.8 MW), Bom Jardim da Serra (93.6 MW), Laguna (3.0 MW), and Tubarão (2.1 MW) [
16] (see wind farm locations in
Figure 1).
Offshore wind resources are significant. The map illustrates large changes of ocean wind speeds in different latitudes. Average winds vary from 5 m s
−1 in the north of the state off São Francisco do Sul to more than 9 m s
−1 offshore of Cape Santa Marta (
Figure 1). The estimated offshore potential in a depth of between 0 and 500 m is around 184 GW, based on the analysis of outputs from the statistical downscaling model [
17].
There is a serious lack of wind observational studies for Santa Catarina. In the continental region, Dalmaz (2007) conducted an analysis of winds from six anemometric towers of 48 m, installed in Água Doce, Bom Jardim da Serra, Campo Erê, Imbituba, Laguna, and Urubici (see sites of towers in
Figure 1) [
15]. Here we analyze a new dataset obtained with a Light Detection and Ranging (LIDAR) wind profiler installed in the Ocean and Atmosphere Observation Base (BOOA) coastal laboratory (
Figure 1). BOOA was built over a fishing platform about 250 m from the beach of Balneário Arroio do Silva, in Southern Santa Catarina. The laboratory provides electrical power and support for the LIDAR and has a meteorological tower (
Figure 2).
A preliminary analysis of the first 6 months of LIDAR wind data was conducted by Correa (2018) [
17], Nassif et al. (2020) [
18] and Pires (2019) [
19]. Here we extend the period of analysis, and cover two years of data from January 2017 to December 2018. This study describes the average power, mean capacity factor and energy generated by modern wind turbines at BOOA. It also makes a comparison of the LIDAR data with the statistical parameters derived from the towers, as reported by Dalmaz (2007).
Thus, the aim of this study is to describe the estimated wind power from a coastal site in Southern Brazil using LIDAR profiler measurements between 2017 and 2018. It takes account of the synoptic behavior, its monthly and interannual variability, estimations for a hypothetical wind farm, and comparisons with wind resources from other locations of Santa Catarina State.
Although other studies have employed LIDAR in the world’s coastal and offshore regions to assess wind resources [
20,
21,
22,
23,
24,
25,
26,
27,
28], few studies have investigated LIDAR observations in Brazil. Two pioneer studies monitored winds on the coast of Piauí [
29,
30], one for Espírito Santo State [
31]. Thus, this dataset represents the longest period of LIDAR wind monitoring conducted for the southern coast of the country. The present paper comes at an opportune moment to foster and support the current process of offshore wind energy planning, and underlines the importance of long-term wind profile monitoring for the Brazilian coast.
3. Results and Discussion
LIDAR measurements at the BOOA covered a period of approximately two years, from January 2017 to December 2018. Our analyses first address wind speed and direction, wind power density, turbine power, and generated energy for each year. The probability curves are shown and, in sequence, the interannual variability is explained from the perspective of the South Atlantic Atmospheric Circulation. Finally, a detailed analysis of the monthly variability is conducted, along with a comparison with other localities in the State.
3.1. Wind Variability in 2017–2018
3.1.1. Wind Speed and Direction
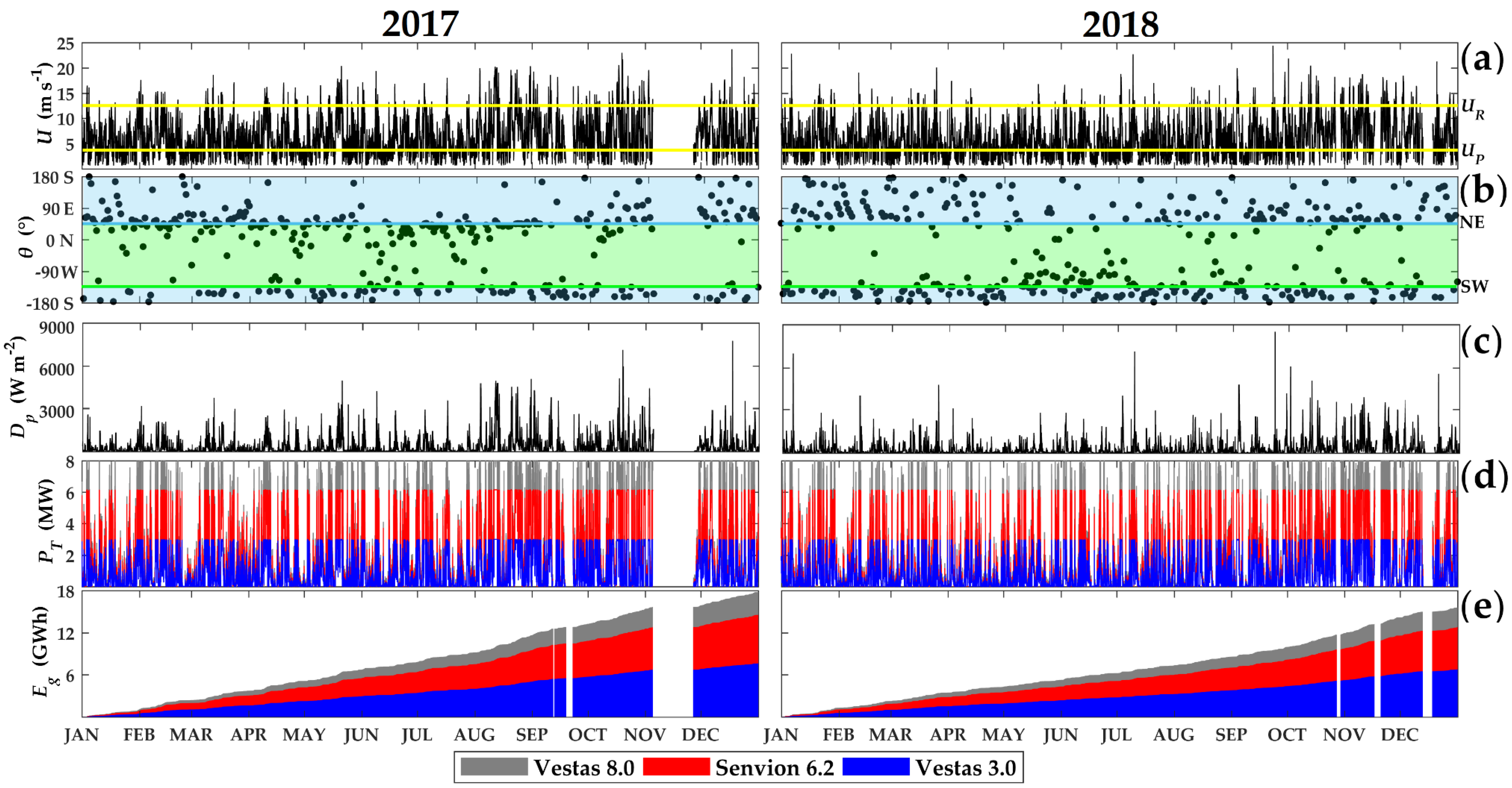
Figure 3 illustrates the LIDAR wind speed
U and direction
θ, the corresponding power density
Dp, turbine output
PT, and generated energy
Eg for 2017 and 2018. All the variables refer to a height of 110 m.
The wind speed graphs for 2017 and 2018 are displayed in
Figure 3a with 10 min time resolution. In these panels, the upper yellow solid line represents the mean rated speed
UR for the selected turbines (12.3 m s
−1), and the lower line represents the mean cut-in speed
UP (3.5 m s
−1). In 2017,
= 6.3 m s
−1 and
σ = 3.8 m s
−1 and, in 2018,
= 5.8 m s
−1 and
σ = 3.6 m s
−1, resulting in
8.3% lower than 2017. As illustrated, around 70% of the time, the wind speed was within the turbine’s operational range, and several times exceeded the rated speed (~7%). These periods of activity will be examined in further detail in
Section 3.2.
The wind direction time series
θ is shown in
Figure 3b. Here the daily averages of the wind direction are included for a better visualization. The blue line represents the northeast direction (NE) and the green line the southwest direction (SW). The light blue and light green shades represent the ocean and continental sectors, respectively. There are two predominant wind patterns in the region [
41]. The main pattern is from the NE quadrant (30°–60°), which is found approximately 23.5% of the time with the mean wind direction
= 45.2° and speed
= 8.4 m s
−1 in 2017. In the case of 2018, winds from the NE quadrant were less frequent and intense, blowing 12.9% of the time with
= 45.9° and
= 6.9 m s
−1 (
Figure 3b). These winds are a manifestation of the average circulation induced by the South Atlantic subtropical high-pressure system (SASH) [
42] and the reasons for the variability between these years will be explored in
Section 3.3.
The second predominant directional sector is linked to southwesterly winds (−150° to −120°), mostly cold front passages. The winds came from the SW quadrant during 11.1% of the time and resulted in
= −135.4° and
= 7.1 m s
−1 during 2017. In 2018,
= −135.2° and
= 7.1 m s
−1 with a time fraction of 16.5%. Cold fronts accompany the displacement of mobile cyclones and anticyclones in the southern region of Brazil [
43] and originate from three cyclogenetic regions in the western sector of the South Atlantic Ocean, near the South American east coast [
44]. In this studied region, there is usually a passage of up to four cold fronts per month with an increase in the spring [
45]. During the passages, the winds tend to intensify and change their direction [
46]. This intensification leads to an increase in turbine production.
The winds were less intense in the NE quadrant and had a larger influence on the SW continental sector in 2018 (
Figure 3b). There was a 10.6% decrease in the frequency of northeasterly winds from 2017 to 2018, while southwesterly winds increased by approximately 5.4%. The bimodal directional distribution and its interannual wind variability are well represented in the directional wind speed histograms (
Figure 4a,b).
Directional statistical parameters were estimated for each year from the LIDAR data at 110 m height (
Table 2). The parameters were calculated by taking account of all the wind directions in BOOA, and also specific sectors denoted as
where
δθ is 90° and
= 45° for the NE sector and
= −135° for the SW sector. The mean wind direction
, their confidence limits (range
d) and the resultant vector length (
R) were estimated by following Berens (2009) [
47] (
Table 2). Here,
R represents a measure of the circular spreading, which is related to variance by
S = (1 −
R). If all samples point in the same direction,
R is close to 1 and
S is small. Correspondingly, if the samples are spread out evenly in all directions,
R is small and
S is close to 1.
is not defined for
R = 0 [
47,
48].
The mean direction was = 40.15° in 2017, with a 95% confidence interval range of d = ±2.15°. In 2018, = 172.25° with d = ±3.70°. These results corroborate the degree of interannual variability, with a greater dominance of NE winds in 2017 and more influence of SW winds in 2018. R is low for both years, but relatively larger for 2017, which is evidence of the dominance of the NE winds.
When the same parameters were applied to the NE sector, it showed that, in 2017, the winds blew in a direction more parallel to the coastline, with mean direction
= 43.40° ± 0.48°, while in 2018, the winds were slightly displaced offshore with
= 51.63° ± 0.58°. Winds from the SW sector showed
= −134.82° ± 0.65° in 2017 and a more offshore component with
= −140.00° ± 0.54° in 2018. The resultant vector length
R for the NE- and SW sectors was above 0.74 in both years, which suggests there was a reduced directional spread. The largest
R = 0.8 was observed in 2017 for the NE sector (
Table 2).
Owing to the bimodal nature of wind directions at BOOA, the circular-linear correlation
ρcl between wind direction and speed was evaluated separately for both sectors, resulting in mild correlations
ρcl = 0.40 for the NE sector and
ρcl = 0.35 for the SW sector. Finally, the LIDAR direction at 20 m correlated with the Sonic anemometer direction at 19.7 m, which yielded a very good circular-circular correlation
ρcc = 0.81 for BOOA using 21,557 10 min paired means of wind direction [
19,
47].
3.1.2. Wind Power Density
The 10 min mean time series of
Dp is illustrated in
Figure 3c. In 2017 and 2018, the mean power density
was 333.4 W m
−2 and 272.2 W m
−2, respectively. In 2017, the maximum
Dp (7760.4 W m
−2) occurred on December 17 at 6:40 p.m. However, in 2018, the maximum
Dp (8509.1 W m
−2) occurred on September 23 at 9:30 a.m. In both years, the
Dp peaks are higher and more frequent in the second semester, with some peaks exceeding 6000 W m
−2.
The directional mean distribution of
Dp is examined in further detail in
Figure 4c,d, through the calculation of average power density for 10° directional sectors. As seen earlier, winds from ocean sectors (NE and SW) have higher
Dp for both years. In the NE sector, the peak was
= 826.4 W m
−2 between 50° and 60° in 2017. In 2018, the peak was
= 681.6 W m
−2 between 60° and 70°. In the case of the SW sector, the peak was
= 615.3 W m
−2 between −160° and −150° in 2017. In 2018, the peak was
= 546.7 W m
−2 between −130° and −120°. The average power density of these sectors tends to be much greater than for other directions. This demonstrates that the bulk of the power is found in winds that blow nearly parallel to the coastline, but predominantly from the ocean sectors (NE and SW). Winds perpendicular to the coast have very low energy content.
Figure 4 shows the importance of ocean winds to coastal wind power generation. The estimated power density from satellite data and numerical modeling, suggest that offshore resources vary seasonally from 600 to 900 W m
−2 [
13,
14,
17].
3.1.3. Turbine Output
The time series for turbine output is illustrated in
Figure 3d for the Vestas 3.0 (blue), Senvion 6.2 (red), and Vestas 8.0 (gray) turbines. The key features of the turbines are described in
Table 1. In 2017, turbine mean output
(
CF) was 2.2 MW for Vestas 8.0 turbine (
CF = 27.5%). In the case of Senvion 6.2, this output was 1.8 MW (
CF = 29.2%), while for Vestas 3.0, 0.9 MW (
CF = 31.5%) (
Table 3). The percentage of time without power generation was 32.8% for Vestas 8.0, 26.8% for Senvion 6.2, and 20.6% for Vestas 3.0. The rated output (maximum turbine capacity) was reached 6.2% of the time for Vestas 8.0, 10.7% for Senvion 6.2, and 7.7% for Vestas 3.0.
In 2018, the
was 1.9 MW (
CF = 23.3%) for Vestas 8.0 turbine. This production was 1.5 MW (
CF = 24.8%) for Senvion 6.2 and 3.0, 0.8 MW for Vestas (
CF = 26.9%) (
Table 4), while the period without turbine production was 38.7% for Vestas 8.0, 32.1% for Senvion 6.2, and 25.5% for Vestas 3.0. Rated output reached 4.8% of the time for Vestas 8.0, 8.3% for Senvion 6.2, and 6.0% for Vestas 3.0. All these calculations were made from the series with a temporal resolution of 10 min.
and CF were also estimated for sectors with the highest wind power densities (NE sector and SW sector), In 2017, the NE sector showed = 3.7 MW (CF = 46.7%) for Vestas 8.0, = 3.1 MW (CF = 49.9%) for Senvion 6.2, and = 1.6 MW (CF = 52.2%) for Vestas 3.0. On the other hand, for the SW sector = 2.8 MW (CF = 35.0%) for Vestas 8.0, = 2.3 MW (CF = 37.6%) for Senvion 6.2, and = 1.2 MW (CF = 40.0%) for Vestas 3.0. In 2018, winds from NE sector showed = 2.6 MW (CF = 32.6%) for Vestas 8.0, = 2.2 MW (CF = 35.2%) for Senvion 6.2 while Vestas 3.0 estimated = 1.1 MW (CF = 37.8%). Winds from SW sector in 2018 showed = 2.7 MW (CF = 34.1%) for Vestas 8.0, = 2.2 MW (CF = 36.2%) for Senvion 6.2, and = 1.2 MW (CF = 38.7%) for Vestas 3.0. In summary, the winds from NE and SW sectors had higher capacity factors, between CF = 34 and 52%.
PT time series (MW) was used for estimating the generated energy
Eg (GWh) at the end of each period, from Equation (3). Thus,
Figure 3e represents the accumulated energy over 2017 and 2018 respectively. The generated energy in 2017 was
Eg = 17.8 GWh for Vestas 8.0 turbine,
Eg = 14.6 GWh for Senvion 6.2, and
Eg = 7.6 GWh for Vestas 3.0. In 2018, the generated energy by the Vestas 8.0 turbine was
Eg = 15.7 GWh, Senvion was
Eg = 12.8 GWh, and Vestas 3.0,
Eg = 6.8 GWh. These can be treated as conservative estimates, as the calculation does not include the power production for periods without LIDAR measurements (
Table 3 and
Table 4).
An estimate of the yearly production can be calculated as Eg* = (365 Eg)/M, where M is the total number of days covered by the LIDAR in each year (M = 337.3 for 2017 and M = 349.6 for 2018). On the basis of this calculation, in 2017 Vestas 8.0 generated Eg* = 19.30 GWh, while Eg* = 15.75 GWh for Senvion 6.2 and Eg* = 8.27 GWh for Vestas 3.0. On the other hand, in 2018, Eg* = 16.35 for Vestas 8.0, Eg* = 13.37 for Senvion 6.2, and Eg* = 7.10 GWh for Vestas 3.0.
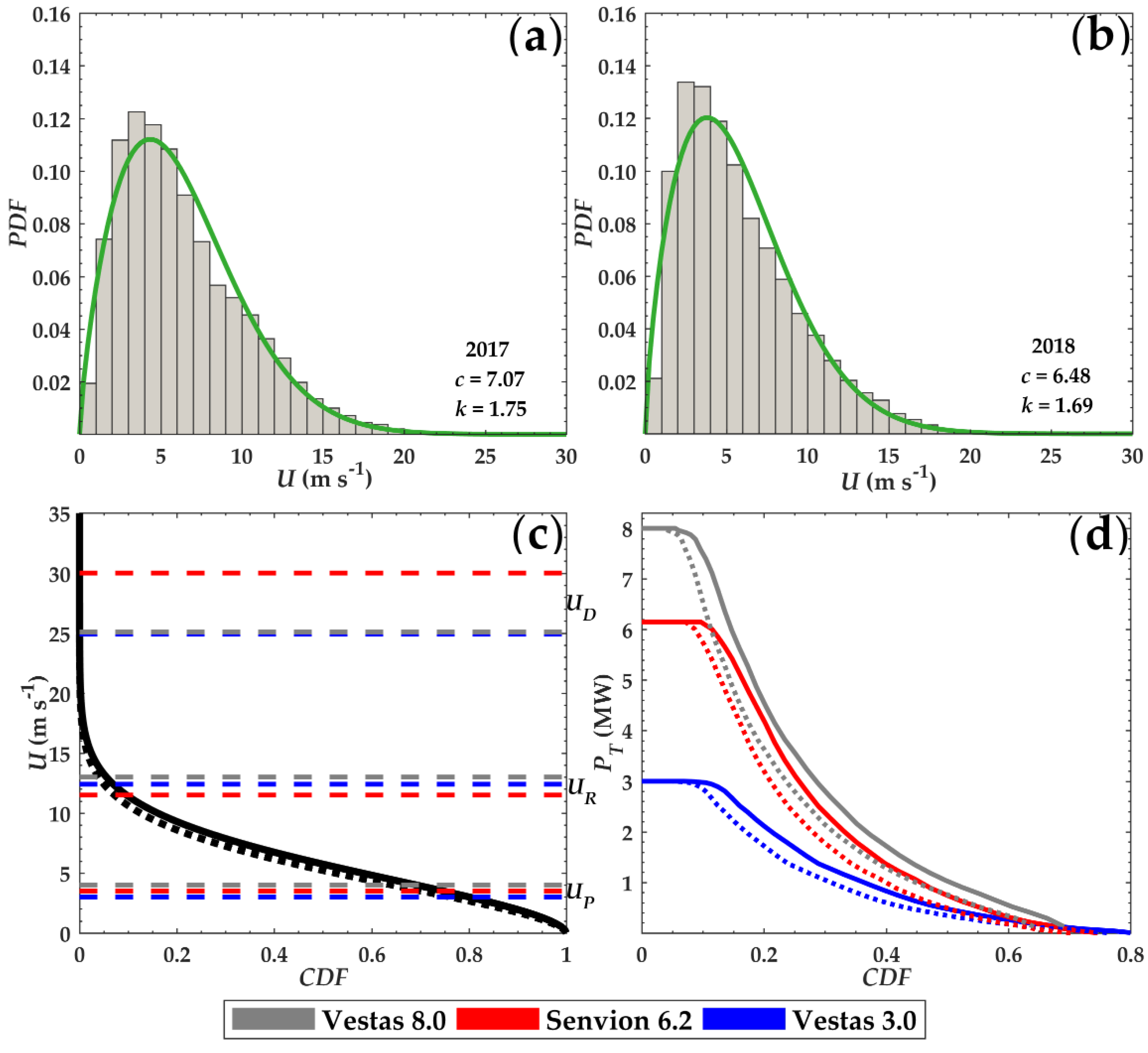
3.2. Analysis of Probability Distributions
An analysis of BOOA wind speeds for the studied period was conducted using the Weibull probability distribution functions (PDF) (Equations (4) and (5)).
Figure 5a,b displays wind speed histograms (gray bars) for 2017 and 2018, respectively. The height for the observation is 110 m. The Weibull probability distribution is represented on these graphs by green lines. When both graphs are compared, it can be seen that there is a lower frequency of winds below 5 m s
−1 for 2017 (42.05%) than 2018 (47.59%). With a wind range between 5 and 10 m s
−1, there is a higher frequency of occurrence in 2017 (41.95%) than 2018 (39.95%). When there are speeds higher than 10 m s
−1, the 2017 frequency (16.00%) is also higher than 2018 (12.46%). This pattern is reflected in the Weibull shape parameter
k and Weibull scale parameter
c, which shows higher values for 2017.
Weibull cumulative distribution curves are shown in
Figure 5c by a continuous line for 2017 and a dotted line for 2018. The right-hand side of the 2017 curve is above the 2018 curve, which shows that the winds were stronger that year. The wind turbine cut-in speed
UP, the rated speed
UR, and cut-out speed
UD are illustrated by the gray (Vestas 8.0), red (Senvion 6.2), and blue dashed lines (Vestas 3.0).
The curves show that for between 64% and 80% of the time, the wind speed was above the cut-in speed for these wind turbines. More specifically, by 2017 (2018), the Vestas 3.0 turbine was producing power at a rate of 80% (76%) of the time, while Senvion 6.2 was at 75% (70%) and Vestas 8.0 at 69% (64%) of the time.
Similarly,
Figure 5d shows cumulative probability distribution curves in terms of turbine output. These turbines achieved maximum output from 3.9% to 9.6% of the time. Vestas 3.0 reached rated capacity in 2017 (2018) by 6.7% (4.8%), Senvion 9.6% (7.2%), and Vestas 8.0 by 5.5% (3.9%).
3.3. Interannual Variability of the SASH
Wind variability in this coastal region is predominantly controlled by the South Atlantic subtropical high (SASH) pressure geographical position [
49]. The center, wind magnitude, and position vary from monthly to interannual timescales, which affects the strength and persistence of northeast winds and the trajectory of storms over Santa Catarina.
During the winter, the SASH is generally stronger, more widespread and displaced in the northwest, close to the South American coast [
50,
51]. During the summer, this system moves southeast and farther away from the South American coast. Throughout the year, the SASH longitudinal variability is around 14° and the latitudinal variability is about 6° [
51]. Southward migrations are usually accompanied by an intensification of SASH [
50].
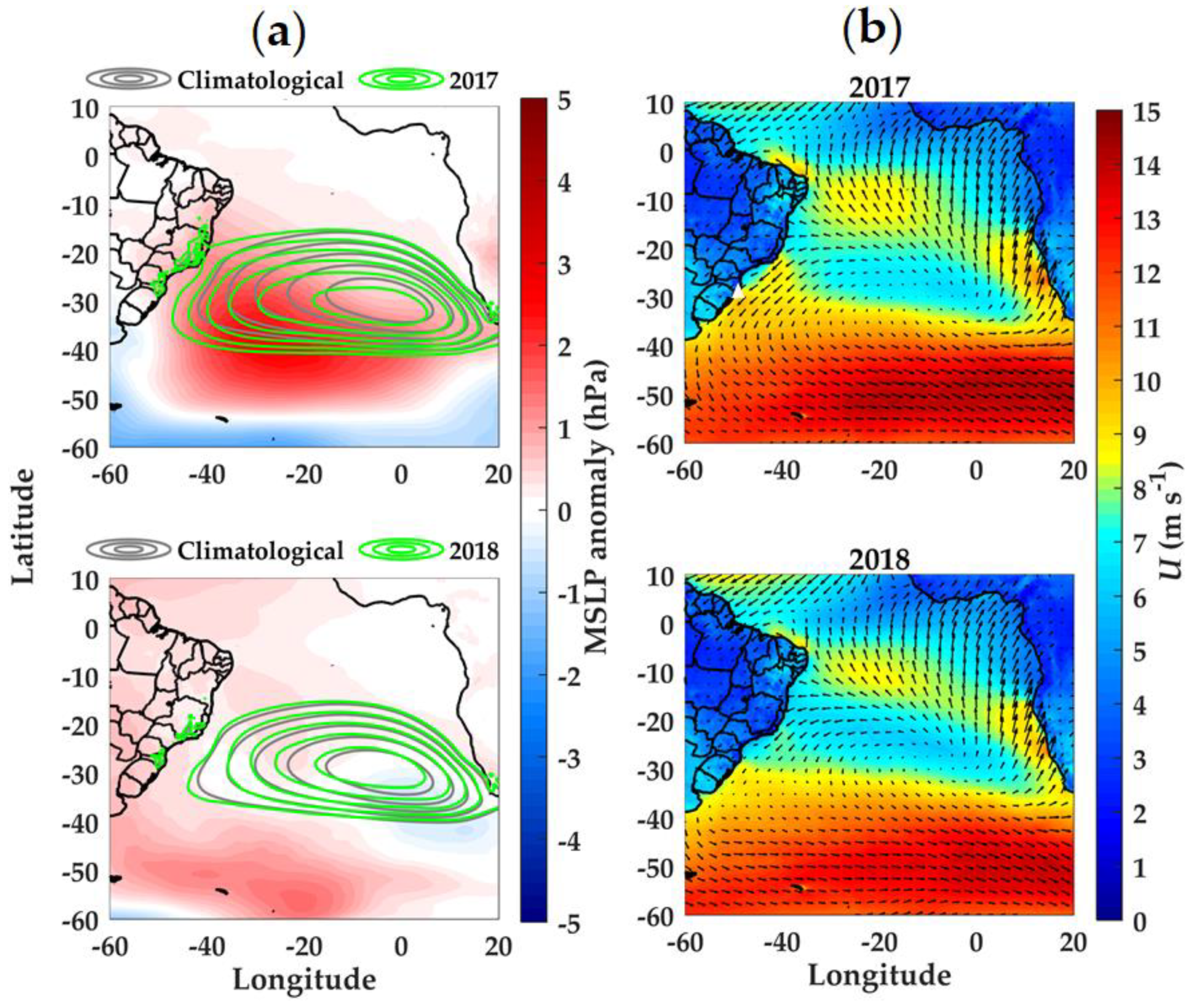
The SASH pressure central position also shows a subtle interannual variability.
Figure 6a illustrates the mean sea level pressure (MSLP) derived from the ERA5 Reanalysis product [
52]. Climatological (1979–2019) MSLP fields are defined by gray contours, that are centered around 5° W and 30° S. The MSLP for the years of 2017 (upper panel) and 2018 (lower panel) are defined by green contours. When these fields are compared, it is clear that the SASH was wider, more intense and displaced southwest of its climatological position in 2017. In 2018 the SASH was closer to its climatological position. The MSLP anomaly fields, which are colored, denote that positive anomalies were found in the Southwest Atlantic, which indicates an intensification of the SASH in 2017 (
Figure 6a).
The average wind speeds at a height of 100 m derived from evidence based on the ERA5 reanalysis, led to stronger northeast winds on the south and southeast coasts of Brazil in 2017, than in 2018 (
Figure 6b). This corroborates the findings of Gillilland and Keim (2018) [
49], who describe spatial correlations of wind speeds with SASH latitudinal and longitudinal migrations. Southward and westward migrations of SASH are accompanied by an increase of wind speeds in Southern Brazil.
SASH interannual migrations might be combined with different large-scale climate phenomena. SASH was correlated with the Southern Annular Mode [
50,
51]. When the mode is negative (positive), SASH tends to shift to the north (south), which means the cyclone trajectories move northward (southward) [
53]. The same occurs when SASH is displaced to the west (east) of its climatological position; the passage of frontal systems near the east coast of South America becomes less frequent (more frequent) [
51]. This partially explains why southwest winds were less frequent in 2017, as many cold fronts might have been blocked by the SASH position. Generally, the largest number of cold front passages along the Santa Catarina coast occur between winter and spring, owing to the increased cyclogenetic activity in these seasons [
46,
54,
55,
56,
57].
With regard to the El Niño–Southern Oscillation (ENSO) phenomenon, the SASH tends to be displaced to the south during periods of La Niña. There are also other phenomena that can affect the SASH and cause atmospheric blocking, such as the Madden Julian Oscillation and the Interdecadal Pacific Oscillation [
58,
59]. However, the identification of each of these climatological patterns is beyond the scope of this study.
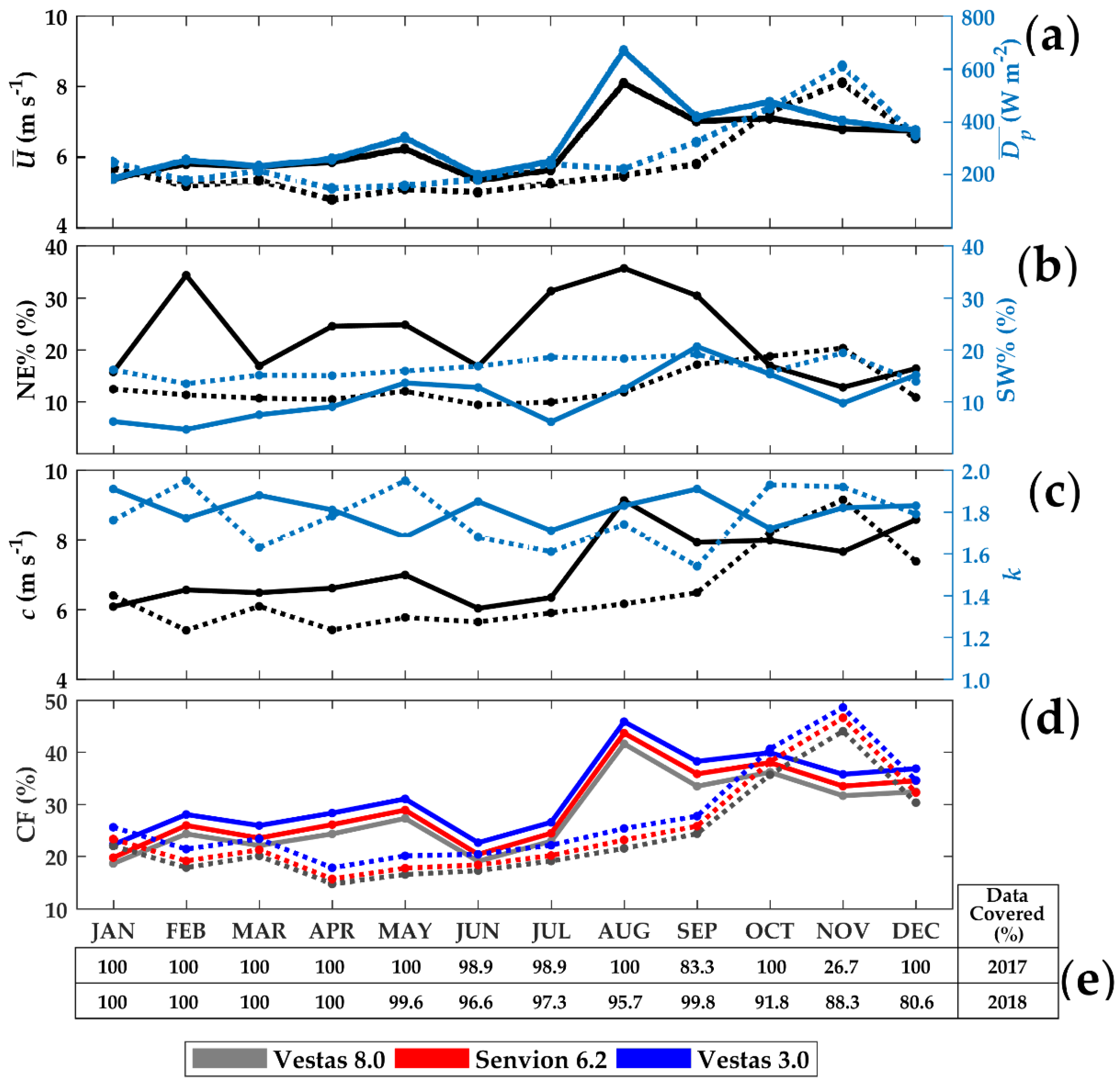
3.4. Monthly Variability
Figure 7 shows the monthly variability for 2017 (solid lines) and 2018 (dotted lines). Wind speed and power density are shown in panel (a). The incidence of winds from the northeast (45° ± 15°) and southwest (−135° ± 15°) sectors are shown in panel (b). Panel (c) shows the Weibull
c and
k parameters. The capacity factors of the three turbines are displayed in panel (d). Finally, the data coverage provided by the LIDAR for each month is shown in panel (e). These monthly statistics are also set out in
Table 3 and
Table 4 for the years of 2017 and 2018, respectively.
In 2017, the highest speeds (
U > 6.7 m s
−1) were observed between August and December (late winter, spring, and early summer) (
Figure 7a). However, 2018 did not show a similar pattern. The most intense winds (
U > 6.6 m s
−1) occurred from October to December (spring and early summer). The maximum monthly values were 8.1 m s
−1 in August 2017 and 8.1 m s
−1 in November 2018.
Throughout the year, there are cold fronts that influence this region, but there is usually an increase in the number of passages of these systems and in the intensity of events from June to September [
46,
54]. The increase of cold fronts between winter and spring can be attributed to the favorable conditions for cyclogenesis over the South American continent [
55]. The passage of cyclones induces strong atmospheric pressure gradients and these events are usually combined with strong pre- and post-frontal winds [
56]. In summer, there is a tendency for extratropical cyclones to be less frequent [
57].
With regard to the density variability of the monthly wind power, the monthly pattern generally follows the speed for the two years. The monthly averages were higher than the annual average for August to December in 2017 and from September to December 2018 (
Figure 7a). The maximum monthly power density was 668.7 W m
−2 in August 2017 and 611.3 W m
−2 in November 2018. These higher
values are caused by the northeasterly winds from the ocean sector.
In light of the monthly frequency of occurrence for northeasterly (30° to 60°) and southwesterly (−150° to −120°) winds, northeasterly winds were more frequent than the southwesterly winds, in 2017 (
Figure 7b). In 2017, the four northeasterly winds with the highest frequency were in February (34.3%), July (31.3%), August (35.7%), and September (30.4%), which is evidence that the persistent northeasterly winds not only blow during the spring and summer, but also during the winter. In 2018, most months had southwesterly winds more often than northeasterly winds. The northeasterly winds were only more frequent than the southwesterly winds in October and November 2018. These months also had the highest average wind speeds during 2018. The highest percentages of northeasterly winds occurred in 2018 for September (17.1%), October (18.7%), and November (20.3%). Several studies have identified wind patterns with northeast and southwest wind directions [
17,
18,
19,
60,
61].
The
c and
k parameters averaged 7.07 and 1.75 in 2017, respectively. In 2018, these parameters were 6.48 and 1.69, respectively. The larger
k implies less variability of wind speeds. The monthly values of
c follow the pattern of
, with higher values found in the second half of both years, during the months of August 2017 (
c = 9.13 m s
−1) and November 2018 (
c = 9.15 m s
−1). In the case of
k, the values did not follow a clear pattern, but ranged from 1.5 to 2 (
Figure 7c).
Accordingly, the turbine output followed the same pattern of monthly variability for wind speed (
Table 3 and
Table 4).
and
Eg increase with the size of the turbine, but the capacity factor (
CF) decreases with the turbine rated power (
Figure 7d). 2017 had an overall higher
CF than 2018, with the exception of the month of November (
Figure 7d). In August 2017, which had the highest production of the year, the figures were as follows: Vestas 3.0 turbine yield
= 1.4 MW,
Eg = 1.02 GWh, and
CF = 45.8%. Vestas 8.0 results in
= 3.3 MW,
Eg = 2.48 GWh, and
CF = 41.6%. In November, the month with the highest turbine output of 2018, the figures were: Vestas 3.0 results in
= 1.5 MW,
Eg = 0.93 GWh, and
CF = 48.6%, while Vestas 8.0 displayed
= 3.5 MW,
Eg = 2.25 GWh, and
CF = 44.0%.
3.5. A Hypothetical Wind Farm
This section makes an evaluation of the electricity generation from a hypothetical wind farm. Assuming a hypothetical farm has
NT = 50 turbines, the total wind farm generation is estimated by
Tg =
NT Eg*, where
Eg* represents the energy generated by a single wind turbine throughout the year (see details in
Section 3.1.3). The calculation is oversimplified, as it does not take account of any factors that might result in losses for an actual wind farm, such as turbine wake effects, operational availability, electrical efficiency, transmission losses, and environmental issues [
62].
In 2017, a farm with Vestas 3.0 would generate a Tg = 413.6 GWh. On the other hand, Senvion 6.2 would generate Tg = 787.7 GWh while a Vestas 8.0 farm would generate Tg = 965.0 GWh. In 2018, a wind farm formed of Vestas 3.0 would generate a Tg = 354.8 GWh, Senvion 6.2 would generate Tg = 668.7 GWh, and Vestas 8.0 farm would generate Tg = 817.5 GWh. When both years are compared, 2017 was 16–18% higher in wind generation than 2018. These are significant year-to-year differences, which will require long-term measurements and climate projections for wind farm planning and operations.
The contribution made by these hypothetical wind farms can be compared to the consumption provided by the State electricity distribution company CELESC, which takes account of the electricity load from residential, industrial, commercial, rural, public power, public lighting, and public service sectors.
The State of Santa Catarina has an estimated population of 7,164,788 inhabitants [
63] and consumed 22,103.46 GWh in 2017 and 22,632.64 GWh in 2018 [
64]. Thus, assuming a farm has
NT = 50 turbines, a Vestas 3.0 wind farm would have generated 1.9% of the State’s total consumption in 2017. A Senvion 6.2 wind farm would have generated 3.6%, while a Vestas 8.0 farm would have generated 4.4%. In 2018, a Vestas 3.0 farm would have generated 1.6%. A Senvion 6.2 farm would have generated 2.9%, while a Vestas 8.0 wind farm would have generated 3.6%.
On the other hand, the southern region of Santa Catarina covers 22 municipalities including Balneário Arroio do Silva, with 589,310 inhabitants [
63], or nearly 8.22% of the state’s population. The consumption in this region was 987.76 GWh in 2017 and 1017.14 GWh in 2018 [
64]. Regarding the southern region alone, a Vestas 3.0 wind farm with
NT = 50 turbines would have generated 41.9% of the region’s consumption in 2017, Senvion 6.2 would have generated 79.7%, while Vestas 8.0 would have generated 97.7%. In 2018, Vestas 3.0 would have generated 34.9%, Senvion 6.2 would have generated 65.7%, and Vestas 8.0 would have generated 80.4%.
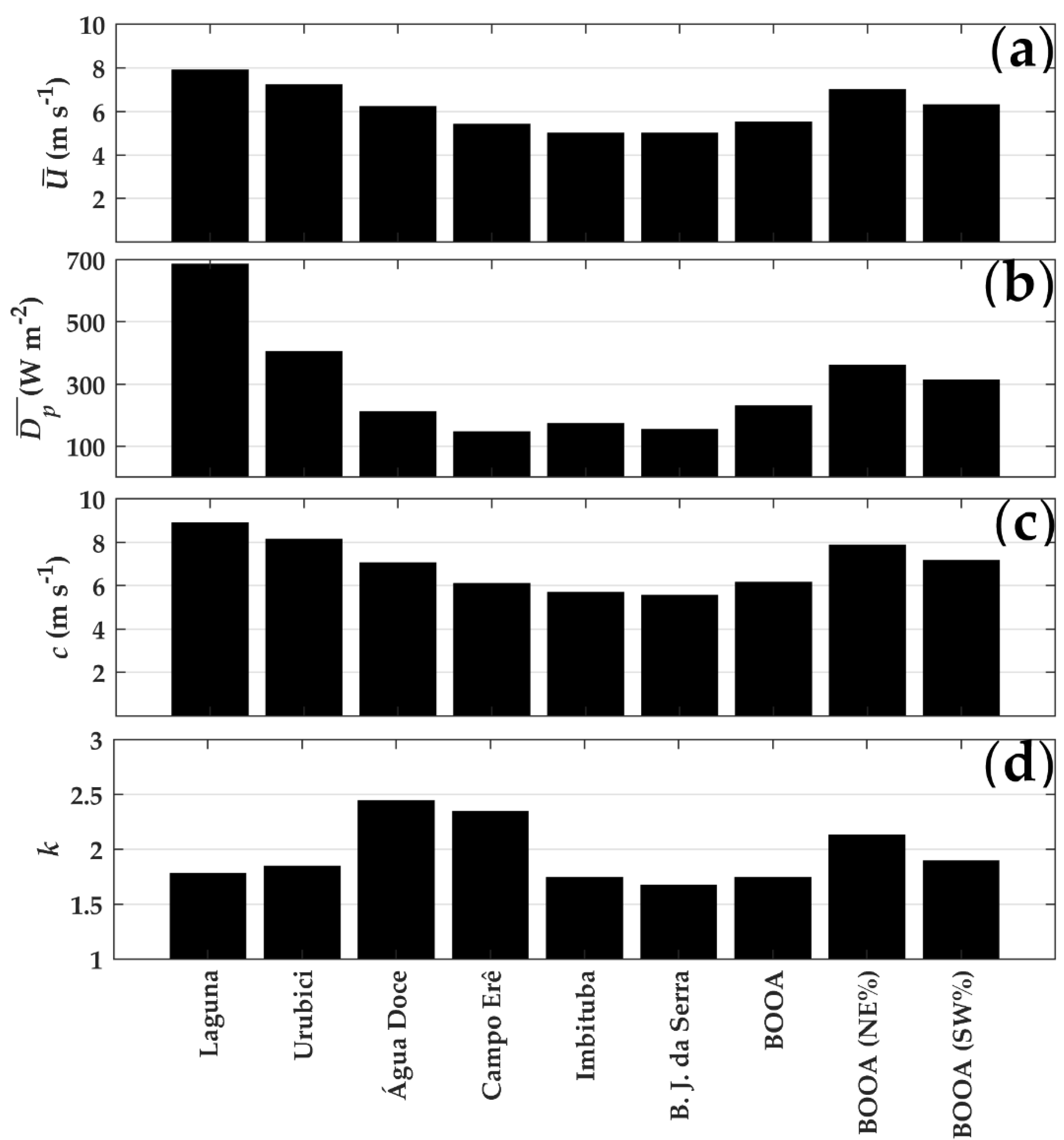
3.6. Comparisons with Other Locations in Santa Catarina
Dalmaz (2007) [
15] analyzed data from meteorological towers in several towns and cities of Santa Catarina State. These included the municipalities of Água Doce, Bom Jardim da Serra, Campo Erê, Imbituba, Laguna, and Urubici. Campo Erê is the only place where the meteorological tower was 30 m high; all the other towers were 48 m. The locations of these meteorological towers are listed on
Table 5 and shown in
Figure 1. The results of
,
,
c, and
k from Dalmaz (2007) [
15] are reproduced in
Table 5 and
Figure 8 and
Figure 9. Dalmaz (2007) employed the two-parameter Weibull distribution and estimated
c and
k by means of the so-called power density or energy pattern factor method [
39,
40,
65,
66].
Table 5 also shows the percentages and periods of data coverage.
LIDAR data at a height of 49 m from BOOA were selected for direct comparison with the results obtained by Dalmaz (2007) [
15] (
Table 5,
Figure 4c,d and
Figure 9). Statistics for BOOA are reported that take account of all the directions, and also winds from the NE (45° ± 15°) and SW sectors (−135° ± 15°).
The towers of Laguna and Imbituba were respectively located 12 and 42 km north of Santa Marta Cape (
Figure 1). BOOA is 70 km south of Santa Marta. Urubici and Bom Jardim da Serra are in the coastal mountain ridges of the State. Campo Erê and Água Doce are in the western region of Santa Catarina.
The highest values of
occur in Laguna (7.9 m s
−1) and Urubici (7.2 m s
−1) (
Figure 8a). The geographical locations of these towns and cities shown in
Figure 1, help to explain these results. The location of Laguna is very close to Santa Marta Cape, where offshore winds are of a significant intensity (
Figure 1). As the tower is located over a prominent coastal cape, winds tend to be less affected by topographical wakes or land roughness for a larger range of wind directions. The Laguna tower was also placed on a rocky hill of 50 m near the ocean, which means that the winds are probably increased by orographic influence.
The location of Urubici benefits from the acceleration of the wind flow over the mountain ridge at a height of 1000 m. Other cities show ranging from 5.0 to 6.2 m s−1. Campo Erê has a probably underestimated , , and c, since the measurements are at a lower height than in the other places. BOOA had the = 5.5 m s−1 at 49 m high for all directions, but higher average values were obtained when account was taken of winds from the NE (7.0 m s−1) and SW (6.3 m s−1) sectors.
The average wind speed for Imbituba tower was
= 5.0 m s
−1 which was less than that of Laguna. These differences can be attributed to offshore variations in the wind field, terrain effects, and coastal orientation. The global wind map illustrates that offshore winds become considerably stronger in a southward direction (
Figure 1), with differences of up to 0.75 m s
−1 between these locations. Imbituba tower was also installed in a coastal plain close to a small residential area, while Laguna tower was placed on top of a rocky hill. Finally, as winds tend to blow in directions that are close to the coastline orientation, there are small changes of wind orientation inland that might have a significant effect on the development of internal boundary layers. Model-derived maps suggest regions of strong wind speed with cross-shelf gradients in the vicinity of Santa Marta Cape (
Figure 1) (see [
17]).
The average power density
and the Weibull c parameter generally follows the changes of average speed
(
Figure 8b,c). These parameters for Laguna are
= 684.3 W m
−2 and
c = 8.89 m s
−1. In the case of Urubici,
= 404.2 W m
−2 and
c = 8.13 m s
−1 had the highest values. In other locations
was smaller than 250 W m
−2 and
c ranged from 7.04 m s
−1 to 5.54 m s
−1.
and
c were higher for northeasterly winds
= 360.3 W m
−2 and
c = 7.86 m s
−1) and southwesterly winds (
= 314.0 W m
−2 and
c = 7.16 m s
−1) at BOOA when compared with the total averages (
= 227.8 W m
−2 and
c = 6.15 m s
−1).
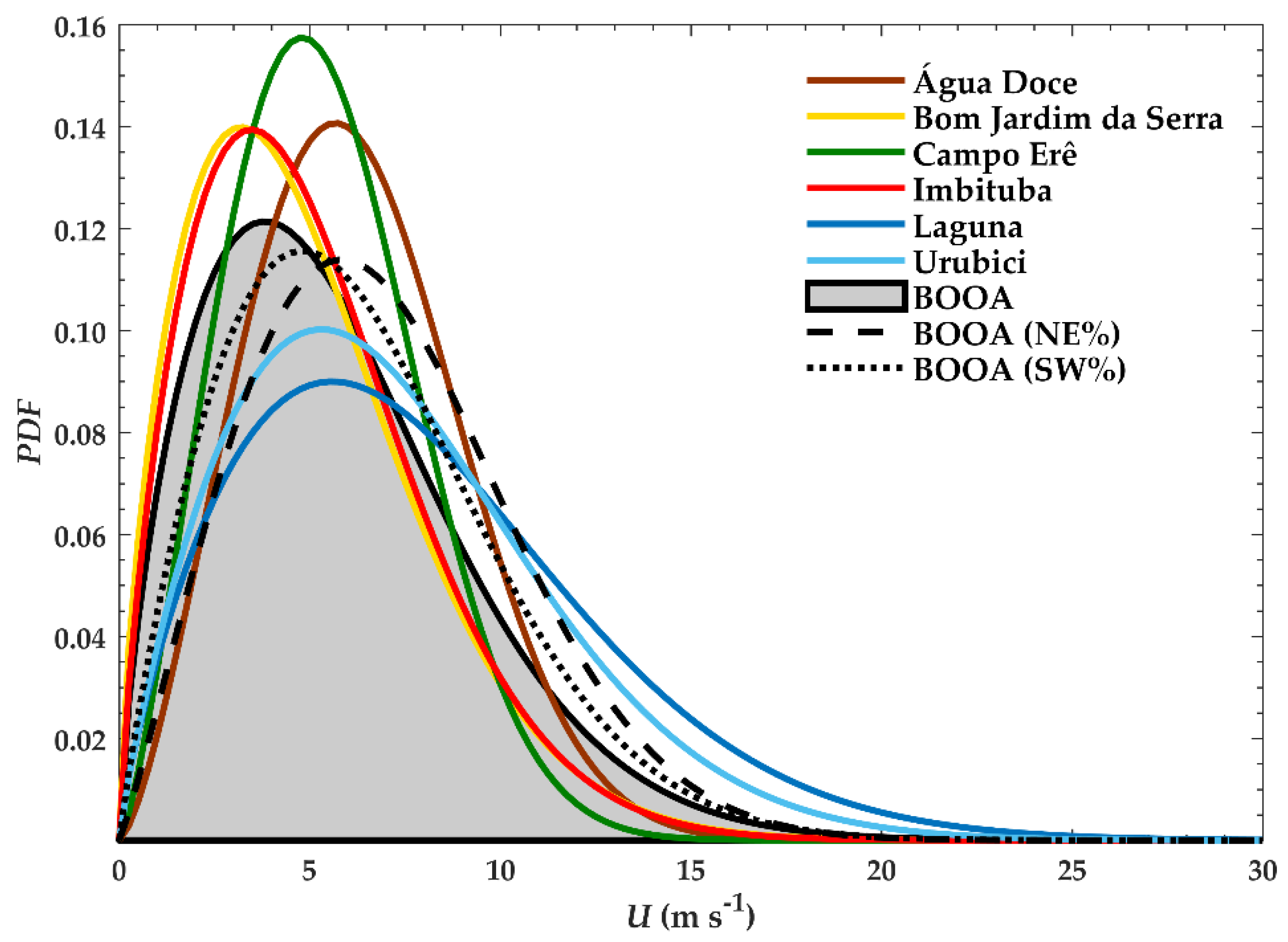
Figure 9 displays the Weibull distribution curves derived from the
c and
k parameters shown in
Table 5. As expected, the highest scale parameters
c and lowest
k parameters are those of Laguna (blue solid line) and Urubici (light blue solid line), featuring PDF curves with peaks and tails displaced to higher wind speeds. The percentage of wind speeds above the rated speeds (
U > 11 m s
−1) is significant in these locations. Imbituba (red solid line) and Bom Jardim da Serra (yellow solid line) had the lowest scale parameter
c with
PDF peaks displaced toward the lowest wind speeds.
The towns and cities located in the west and midwest regions of Santa Catarina had the highest k values (k > 2), and showed narrower PDFs. The other cities, as well as BOOA, had values of k less than 2. With regard to the northeasterly and southwesterly winds at the BOAA, k was 2.13 and 1.89, respectively. Thus, when the winds from the NE and SW sectors at BOOA are included, the PDF curves are closer to those reported for Laguna and Urubici, which increases the probability of high wind speeds.
Note that the two-parameter Weibull probability density functions employed here do not represent wind distributions for every region and situation. In cases where a null wind frequency is significant or bimodal speed distributions are observed, the three-parameter Weibull or the mixture of gamma and Weibull distributions might achieve a much better performance [
67,
68].
4. Summary and Conclusions
This study analyzed data from a LIDAR wind profiler installed over the “Ocean and Atmosphere Observation Base” (BOOA), a laboratory constructed over a fishing platform in Southern Santa Catarina, Brazil. Wind data at 110 m high were first analyzed to describe the monthly variability of the wind magnitude, wind direction, and turbine output for the years 2017–2018. A hypothetical wind farm was simulated to analyze the wind output for the state of Santa Catarina and its southern region in practical terms. Wind data from BOOA at a height of 49 m were compared with statistical parameters derived from meteorological towers installed in other locations of the state.
Winds tend to blow predominantly along the coast from either the NE or SW directions at BOOA. Cross-shore winds are less frequent and have lower energy content. The higher wind speeds, power density magnitudes, and turbine outputs are caused by oceanic winds from northeast and southwest directions.
During 2017, the intensification and southwest displacement of the South Atlantic subtropical high (SASH) pressure center, resulted in persistent northeasterly winds, with a higher wind power density and energy generation than 2018. In 2018, SASH was closer to its climatological position, with cold front passages more common and the southwesterly wind component more dominant. In both years, wind intensity and turbine outputs were larger in the second semester (i.e., from July to December).
The power output from three modern wind turbines was estimated. The Vestas 3.0 was the turbine with the smallest rated capacity and most likely to have the lowest installation and operating costs. A single turbine could produce less electricity than the others (Eg = 7.64 GWh in 2017 and Eg = 6.80 GWh in 2018), but proved to be more active (79.4% in 2017 and 74.5% in 2018) and had the best capacity factors (CF = 31.5% in 2017 and CF = 26.9% in 2018).
A hypothetical wind farm with
NT = 50 turbines would have generated 413.6 GWh (Vestas 3.0) in 2017 compared with 354.8 GWh (Vestas 3.0) in 2018. This output is equivalent to between 34 and 42% of the average electricity demand of Santa Catarina’s southern region, when including the Vestas 3.0 turbines. Generation in 2017 was 16% higher than in 2018. These are significant year-to-year differences, which will require long-term measurements and climate projections for wind farm and operational planning. However, these effects could be mitigated by electric transmission from wind farms located in geographically remote regions or by complementary sources of energy, such as hydropower [
13,
69].
In comparison with other locations, the towns of Laguna and Urubici had the highest average wind speed, power densities, and scale parameters. Owing to its prominent location in a coastal cape, Laguna is less influenced by continental winds, while Urubici benefits from the acceleration of winds at the top of the mountains. The most westerly cities, Água Doce and Campo Erê, had the highest shape parameters. The values found for BOOA are similar to those of the southern stations, such as Imbituba and Bom Jardim da Serra. The results were encouraging, and demonstrate that the southern region of Santa Catarina has a significant potential for coastal and offshore exploitation.
The coastline curvature south of the cape, combined with topographical and terrain effects generate strong cross-shore gradients of wind speed in distances of the order of 10 km. Modeling works suggest that this potential power should grow offshore, as illustrated in
Figure 1 and by the work of Correa (2018) [
17].
The wind variability in Southern Brazil has significant interannual amplitude and the LIDAR data highlighted the importance of long-term monitoring of wind profiles. It is recommended that the state and federal policymakers for the offshore sector continue with the BOOA measurements and the expansion of the LIDAR network in Brazil. The use of the LIDAR data, combined with model downscaling, will assist in the investigation of many aspects of the wind flow.