Aggregation of Households in Community Energy Systems: An Analysis from Actors’ and Market Perspectives
Abstract
1. Introduction
- ▪
- Neglecting the plurality of actors in the community, i.e., considering a single household type, for example, prosumers.
- ▪
- Simplified modeling of electricity market prices or energy demand. For example, [25] assumes that the unit electricity price of the grid has a variable component, which is proportional to the total grid load.
- ▪
- Considering the electricity production costs as the only component of the electricity tariff and modeling the electricity tariffs modeled without considering the influence of the regulatory frameworks.
- ▪
- We propose a bottom-up model to investigate the aggregation of households in a community energy system. To model the interactions between the actors of the community energy system, we employ a Stackelberg game approach. Stackelberg games are widely used to model hierarchical competitions in the energy system such as the one between a retailer and households [25,26,27,28]. By integrating a Stackelberg game structure in our model, we implement a real-time pricing tariff for the community. In contrast to the existing literature, we focus on the heterogeneity of actors in the community energy system and distinguish between households with an inflexible load and those with flexibility options, i.e., battery storage and heat pumps. Moreover, we avoid modeling of electricity market prices. Instead, we use real wholesale market prices and, by taking the regulatory influences into account, model the end-user prices endogenously.
- ▪
- We introduce an indicator to evaluate the market alignment of community energy systems. This indicator can assess the behavior of communities with decentralized generation potential with respect to the electricity wholesale market. We then use this indicator to evaluate the relative economic efficiency of an energy community compared to an idealized benchmark case that is completely aligned with wholesale market price signals.
2. Analysis Procedure
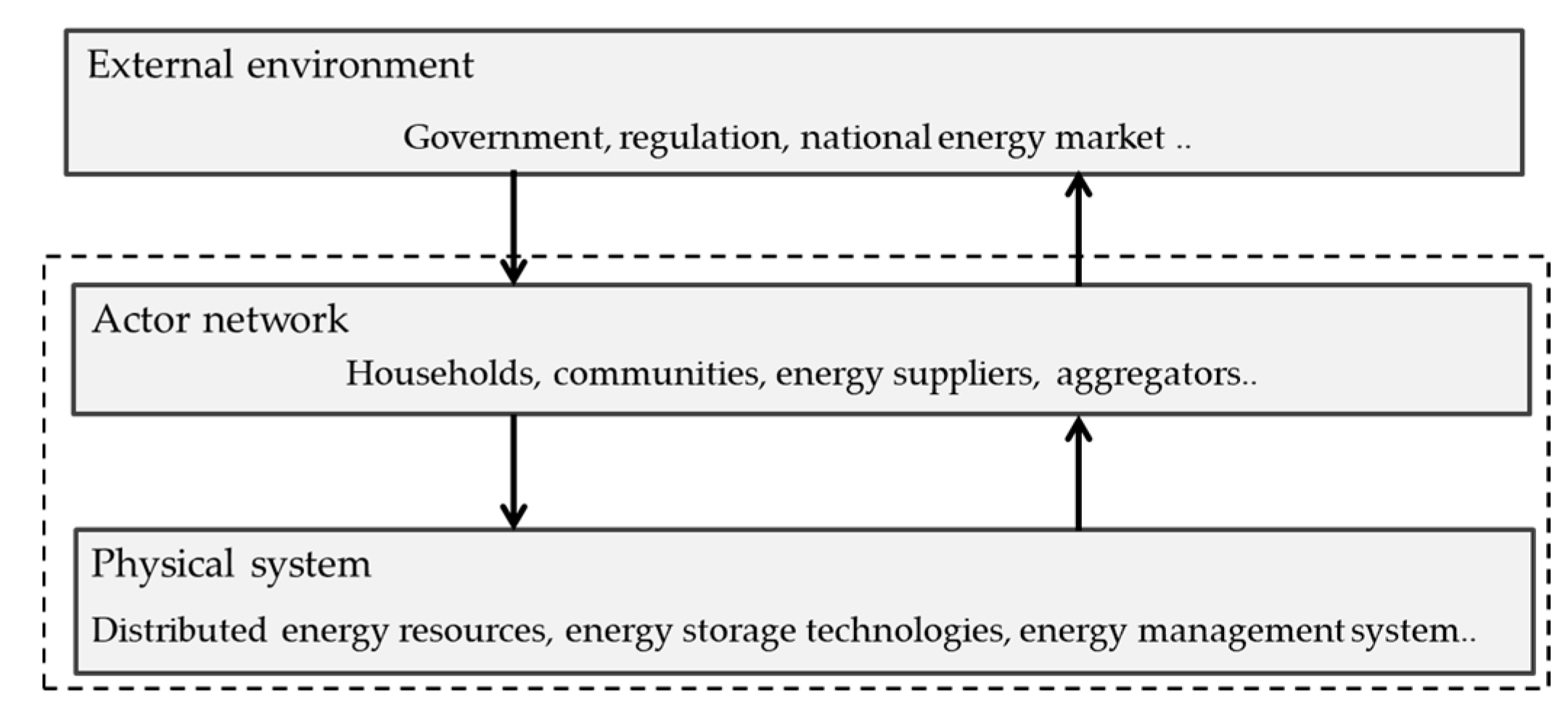
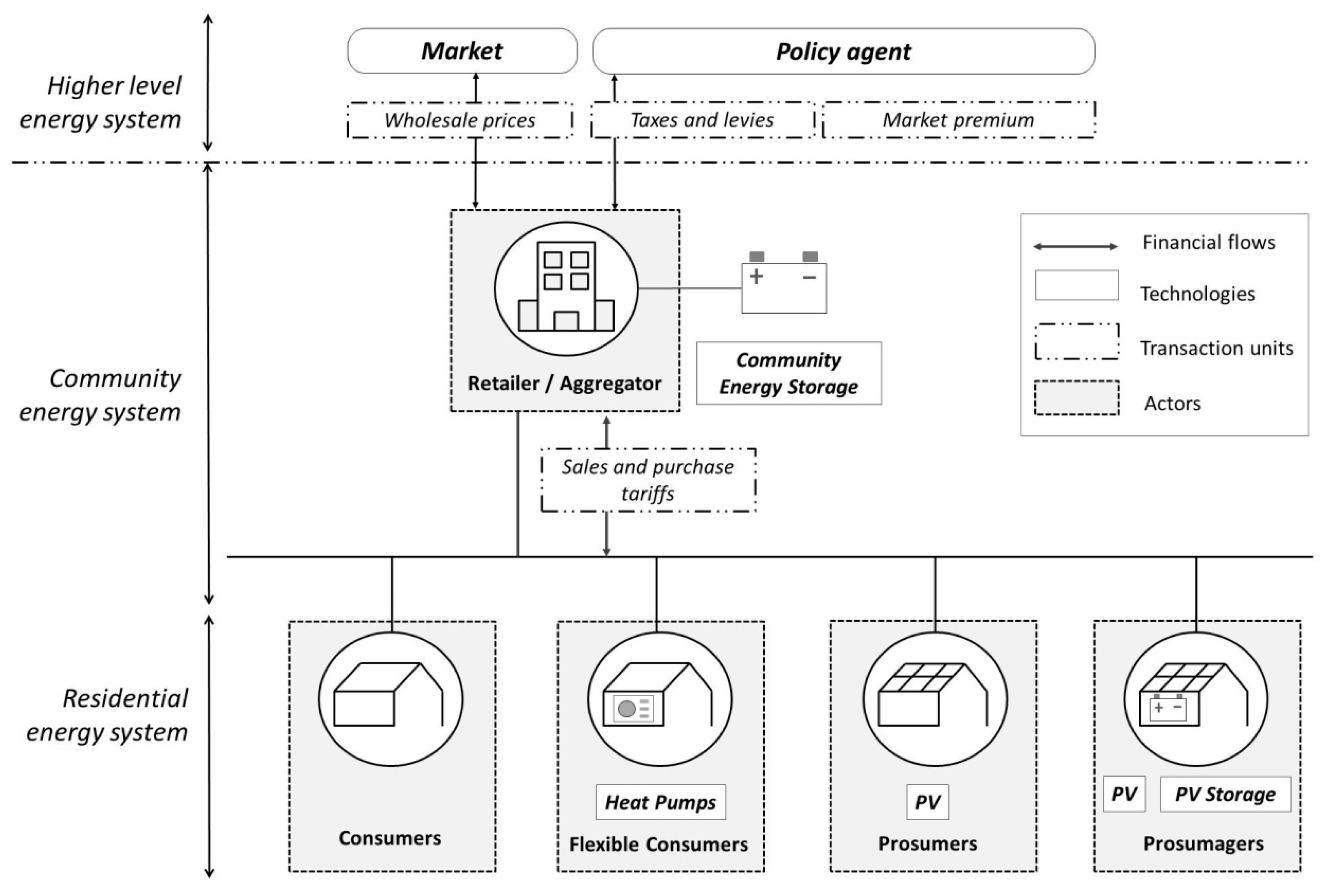
2.1. Community Energy System Structure
2.1.1. Actors and Physical System
- Inflexible households are households that do not operate any storage system and are, therefore unable to shift their electricity load or feed-in at any time of the day. In this category, we distinguish between the consumers and prosumers. Consumers are actors, who own neither a PV system nor a flexibility option. Similar to the consumers, prosumers do not have a flexibility option but they operate a PV system. Prosumers may generate electricity and cover part of their electricity demand themselves.
- Flexible households are actors with load and feed-in shifting potential. These actors are assumed to be equipped with smart meters, which enable them to receive price signals and manage their load and feed-in accordingly. We divide these actors into flexible consumers and prosumagers. Prosumagers are households, who are not only equipped with PV rooftop systems but also own battery storage systems. Prosumagers can use their battery capacity to shift both their grid electricity usage and grid feed-in. Flexible consumers are households that own heat pumps and thermal storage systems, which give them the potential to shift a part of their electricity load.
2.1.2. External Environment: Market and Regulations
2.2. Aggregation Scenarios
- (1)
- Electricity procurement charges, which denote the retailer’s average per unit cost of buying electricity on the market. These charges are part of the retailer’s business model.
- (2)
- Community grid charges ( as a fixed per-unit component of the electricity tariffs that cover the costs due to investment and maintenance of the community grid. We assume that these charges are also part of the business model (in the reality, the grid charges in Germany are a regulated part of the electricity tariff).
- (3)
- Value-added tax () that is collected by the retailer and passed on to the policy agent (see also Figure 3). is a regulated component of the electricity tariff and, in contrast to the other building blocks, it is not part of the business model.
- ▪
- Static Pricing (SP): The SP tariff structure follows the status quo pricing logic in Germany. Charges regarding the procurement of the electricity are based on the mean cost of acquiring electricity from the market, which we assume to be the annual average value of the market prices (). Therefore, this tariff contains no hourly varying component and the electricity prices for the customers are constant at any time of the day.
- ▪
- Market Real-Time Pricing (M-RTP): In this tariff, an hourly forecast of the market prices () of the following day is used as a per-unit charge of acquiring electricity. The electricity prices in this tariff contain a real-time price component, which represents the market price signals.
- ▪
- Community Real-Time Pricing (C-RTP): This tariff consists of optimized real-time procurement charges (), determined by the retailer. The values of these elements may be influenced not only by hourly market prices, but also by the level of local electricity generation and demand in each hour. These charges may fluctuate between and and adopt values higher or lower than market prices in each hour. The calculation of variable procurement elements in this tariff is discussed in Section 3.3.
2.3. Evaluation Indicators
2.3.1. Actor’s Perspective
2.3.2. System Perspective
3. Community Energy System Model
3.1. Data and Model Parameterization
3.2. Actors’ Rationale
3.2.1. Inflexible Households
3.2.2. Flexible Households
3.2.3. Retailer
3.3. Endogenous Calculation of the Real-Time Pricing Components in the C-RTP Tariff
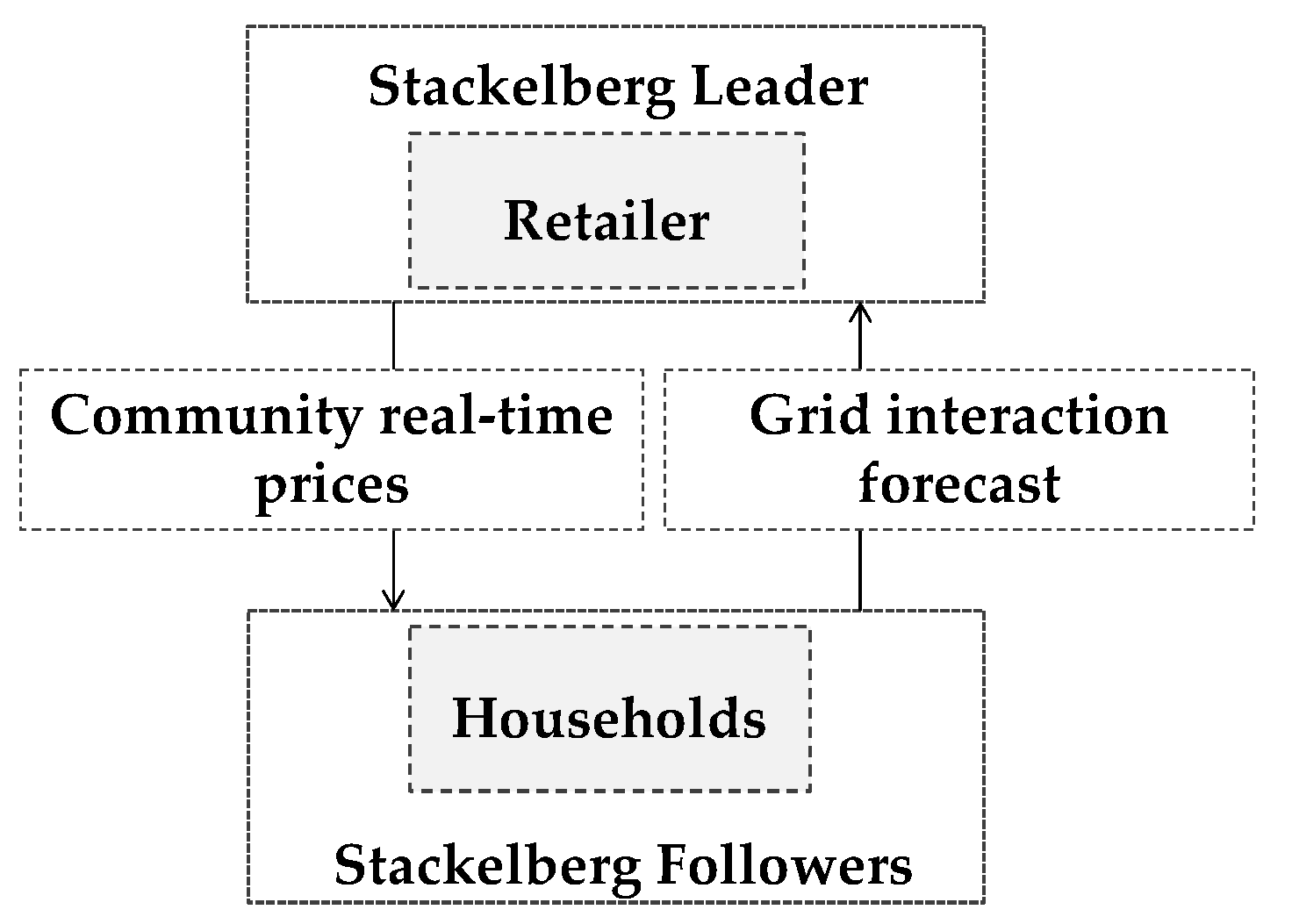
3.3.1. Formulation of the Non-Cooperative Stackelberg Game
- is the set of actors, where the households in the set act as followers in response to the prices set by the retailer ( as the game leader.
- is the set of strategies of households, at time, from which they select their strategy. This strategy represents the grid interaction of households in each time step.
- is the strategy set of the retailer at time, which consists of electricity tariffs and purchase prices.
- is the set of households’ utilities at time as presented.
- in the community competition scenario is the net income of the retailer for trading with users and the market at time , , calculated from cost and revenue functions described in Equations (21) and (22). in the self-sufficiency scenario represents the electricity exchange with the market at time , , calculated from Equation (27).
3.3.2. Solving the Stackelberg Game
| Algorithm 1 retailer’s side GA based real-time pricing algorithm |
| 1: Population initialization, i.e., generating a population of chromosomes randomly; each chromosome denotes an electricity acquiring price set for the optimization period. 2: for to do 3: The retailer decodes the th chromosome (representing the and ) and by adding the other electricity tariff building blocks, i.e., and , calculates its strategy (and ) for the. The prices are then announced to the households. 4: The retailer receives the optimal strategies of the households including the grid interaction forecasts for the optimization period: . 5: Considering the constraints in Equation (29), at this stage the retailer optimizes the CES using the dynamic programming model and then, depending on the aggregation goal, evaluates its net-income () or the amount of traded electricity() for the optimization period ( as the fitness value of its strategy based on the chromosome . 6: end for 7: A new generation of chromosomes is created by using the crossover and mutation operations of the GA. 8: Steps 2–7 are repeated until the convergence condition is reached. 9: The retailer announces the finalized prices to the households at the beginning of the scheduling horizon. |
| Algorithm 2 Households’ side grid interaction optimization |
| 1: Households receive electricity prices from the retailer. 2: Each household calculates its strategy, i.e., the grid interactions in response to prices, by solving the followers’ problem using the dynamic programming model. 3: Households send back the predicted grid interactions during the optimization period to the retailer. |
4. Results
4.1. Actor’s Perspective
- ▪
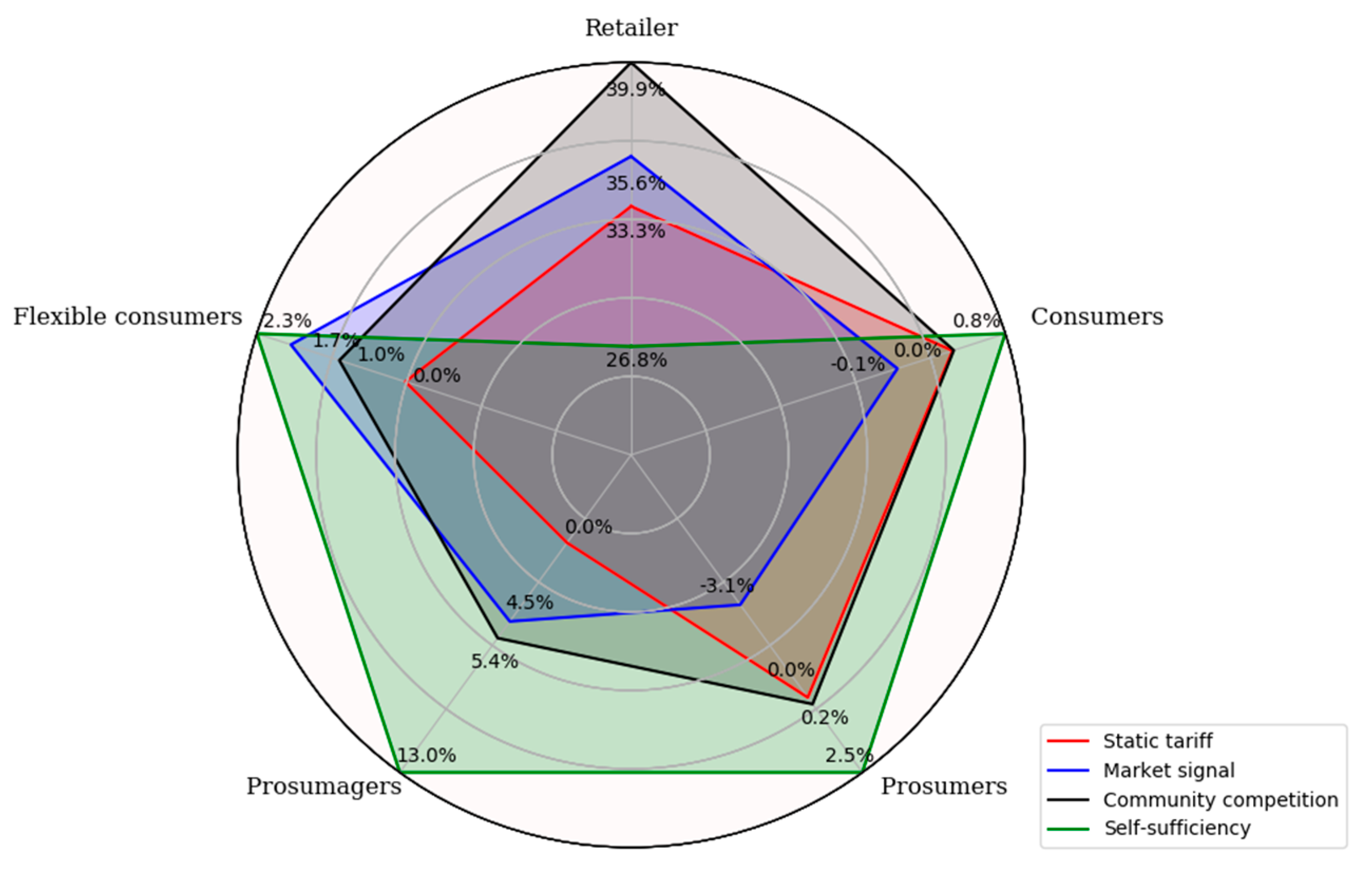
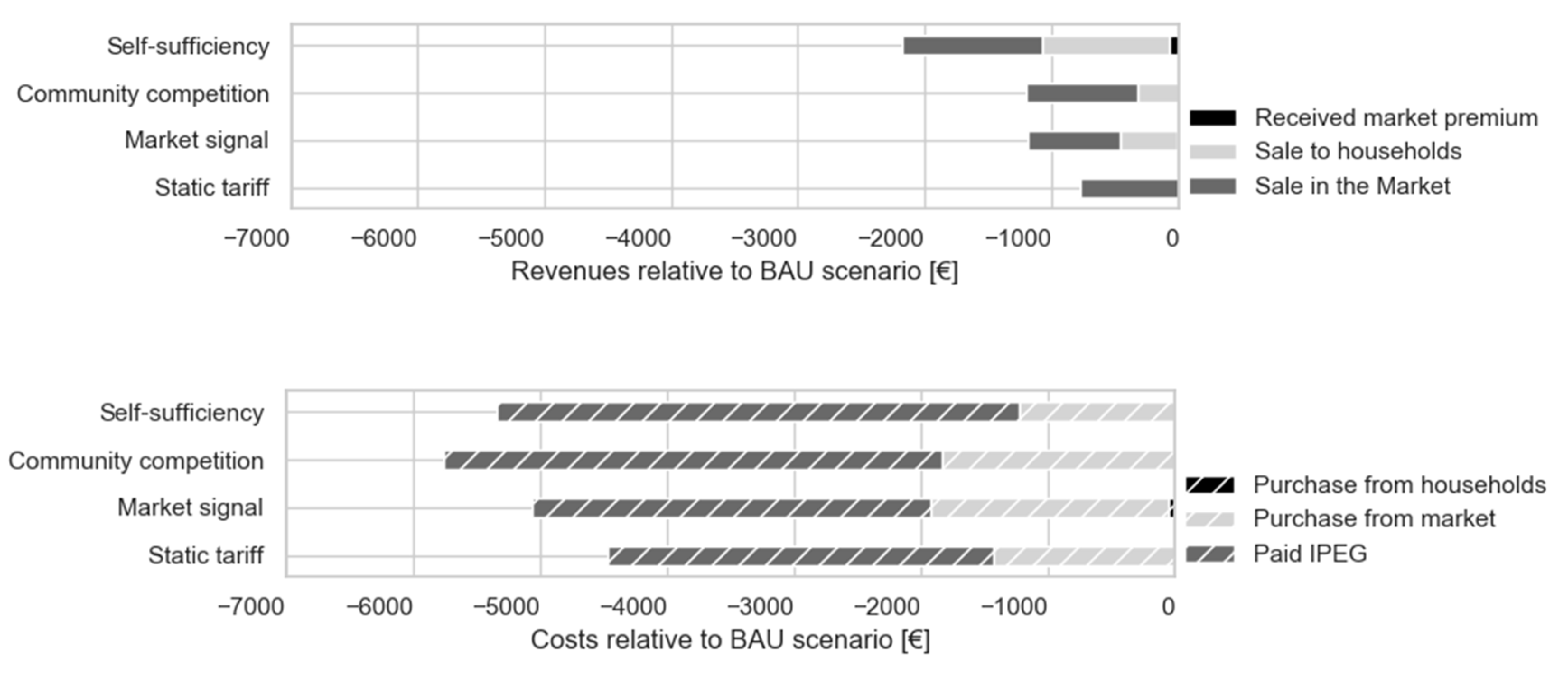
- The most prominent change in the retailer’s cost and revenue streams belongs to the imposed costs due to IPEG. These savings are proportional with reduced electricity imports to the community energy system (Table 7). The exemption from IPEG inside the community energy system gives the retailer an incentive to balance the electricity generation and consumption inside the community and reduce the exchange with the higher-level energy system.
- ▪
- The higher level of self-consumption inside the community lowers the retailer’s cost for electricity acquisition as well as the revenues from selling the electricity in the market. The lower accrued costs due to acquiring electricity from the market also results from the use of flexibility options for efficient market trading, i.e., purchasing electricity at lower prices. Besides CES, in the market signal and community competition scenarios, the flexibility of households is also used for more efficient electricity acquisition.
- ▪
- From the retailer’s perspective, the purchase prices offered to the prosumagers did not seem to have a significant effect on the performance of different scenarios. Similar results were observed when the range for and in the C-RTP tariff is expanded to [0, 10] cents/kWh. The reason for this observation is the high difference between the electricity tariff and purchase prices in this electricity tariff (due to community grid charges and value-added tax) that makes the self-consumption using the PV-storage system for the prosumagers more attractive than selling it to the retailer.
- ▪
- The retailer’s revenue from electricity sales to the households in all scenarios that involve real-time pricing is reduced. These losses can be traced back to the changes in the electricity consumption of flexible households in response to real-time pricing tariffs. The optimization of real-time prices by the profit-maximizing retailer in the community competition scenario reduces these revenue losses in comparison to the market signal scenario. The highest revenue losses appear in the self-sufficiency scenario, since the real-time prices in this scenario are optimized to minimize the interaction with the market and the prices are lower on average than in other scenarios (see Table 6).
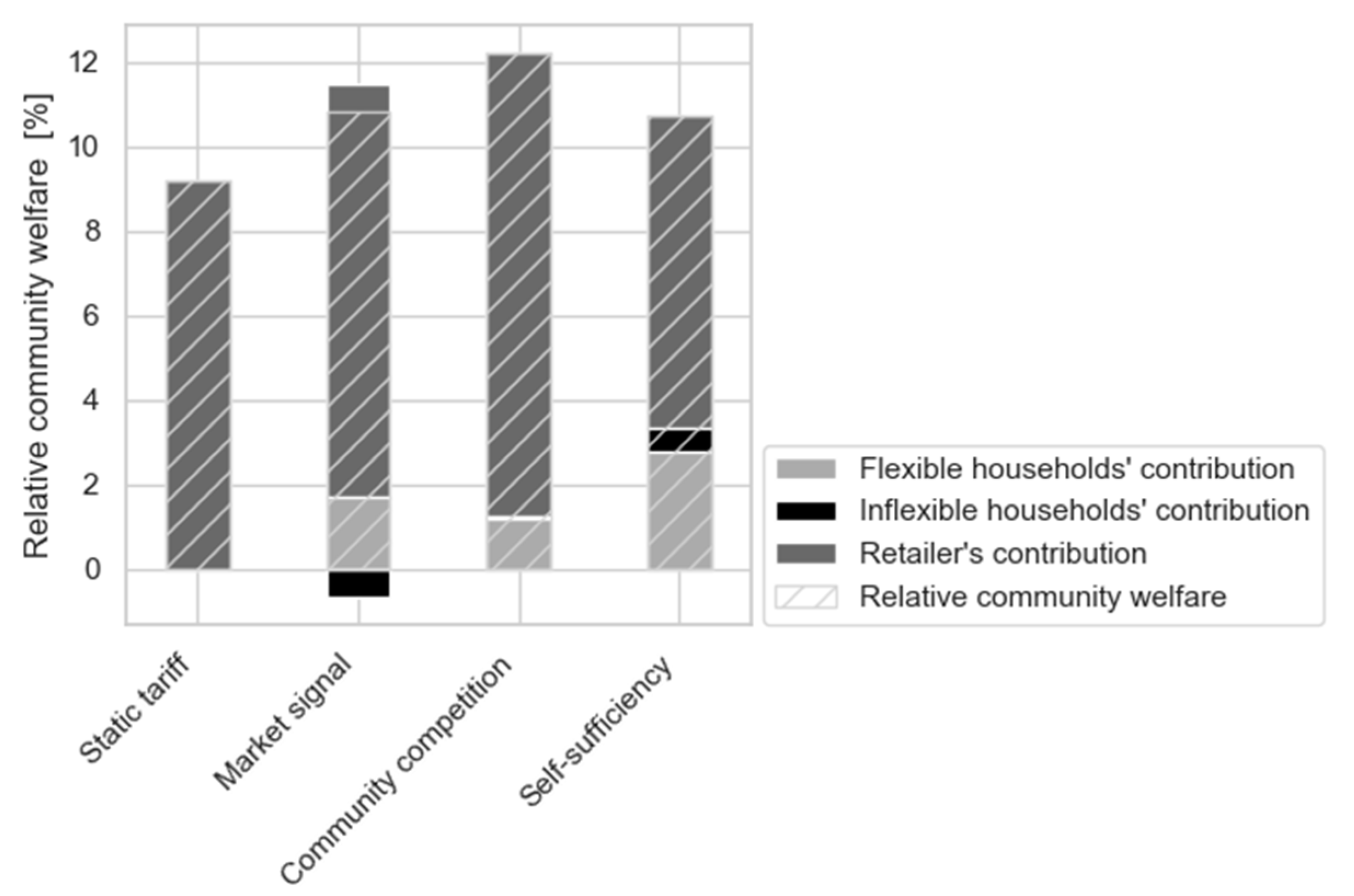
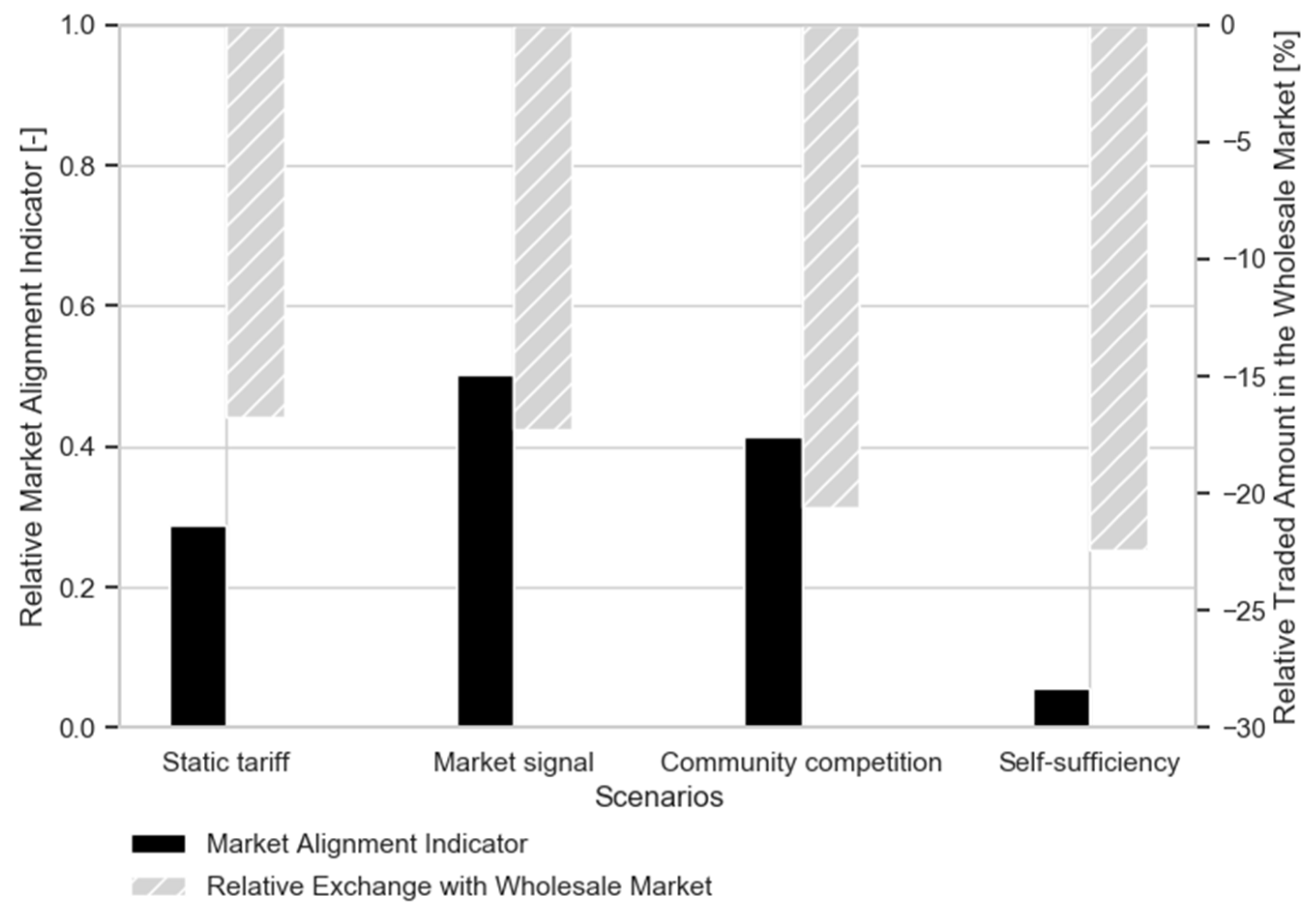
4.2. System Perspective
5. Discussion and Conclusions
5.1. Policy Interpretation
5.2. Limitations and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A. Table of Notation
| Parameter | Meaning |
|---|---|
| Set of actors: retailer (, consumers (, flexible consumers (, prosumers ( and prosumagers ( | |
| Set of households: consumers, flexible consumers, prosumers and prosumagers | |
| Set of households with generation potential: prosumers and prosumagers | |
| Retailer | |
| Number of households in the category | |
| Base electricity demand of the households at time [kWh] | |
| Heat demand of the flexible consumers at time [kWh] | |
| Electricity generation of the households at time [kWh] | |
| Residual load of the households at time [kWh] | |
| Electricity flow by actor at time t from grid to with ={Demand: D, Heat pump: HP, Battery: B, Electricity market: M} [kWh] | |
| Grid feed-in by actor from at time t from with ={Battery: B, PV systems: PV, Electricity market: M} [kWh] | |
| Energy inflow from heat pumps to thermal storage systems at time [kWh] | |
| Total grid feed-in by all prosumers and prosumagers at time [kWh] | |
| Total grid usage by all households at time [kWh] | |
| Revenue of actor in the scenario at time [cents] | |
| Costs of actor in the scenario at time [cents] | |
| Net income of actor in the scenario at time [cents] | |
| Net income of actor in the scenario for the simulation period [cents] | |
| Net income of actor in the scenario relative to BAU scenario for the simulation period [-] | |
| Amount of traded electricity in the market by the retailer at time [kWh] | |
| Peak power of PV system [kW] | |
| Performance ratio of PV system [-] | |
| Battery storage capacity in PV storage systems [kWh] | |
| Peak power of heat pump [kW] | |
| Heat pump COP [-] | |
| Thermal storage capacity in the heat pump systems [kWh] | |
| CES capacity [kWh] | |
| Battery discharge efficiency in CES and PV storage systems [-] | |
| Battery charge efficiency in CES and PV storage systems [-] | |
| Battery energy to power ratio in CES and PV storage systems [-] | |
| CES operation and maintenance costs expressed as a ratio of initial investment costs [%] | |
| CES-specific investment cost [€/kWh] | |
| Discount rate [%] | |
| Battery lifetime [years] | |
| Feed-in tariff [cents/kWh] | |
| EEG and other support levies [cents/kWh] | |
| Public grid charges [cents/kWh] | |
| Community grid charges [cents/kWh] | |
| Electricity tax [cents/kWh] | |
| Value added tax [cents/kWh] | |
| VAT | Value added tax [%] |
| Annual mean value of market prices [cents/kWh] | |
| Market price in time [cents/kWh] | |
| Market premium in the month [cents/kWh] | |
| Market value of PV electricity in the month [cents/kWh] | |
| Retailer’s electricity tariff in time [cents/kWh] | |
| Retailer’s electricity purchase price in time [cents/kWh] | |
| Electricity procurement price component in [cents/kWh] | |
| Electricity procurement price component in [cents/kWh] | |
| Welfare of retailer in the scenario for the simulation period [cents] | |
| Welfare of community in the scenario for the simulation period [cents] | |
| Welfare of community in the scenario for the simulation period relative to BAU scenario [cents] | |
| Market alignment indicator for scenario relative to BAU scenario [-] | |
| Market alignment indicator for scenario [-] | |
| Optimization period [Hours] | |
| Simulation period [Hours] | |
| Strategy set of households in time | |
| Strategy set of the retailer in time |
Appendix B. Dispatch Optimization
Appendix B.1. Constraints for Flexible Consumers’ Optimization Model
Appendix B.2. Constraints for Prosumagers Optimization Model
Appendix B.3. Constraints for Community Energy Storage Optimization Model
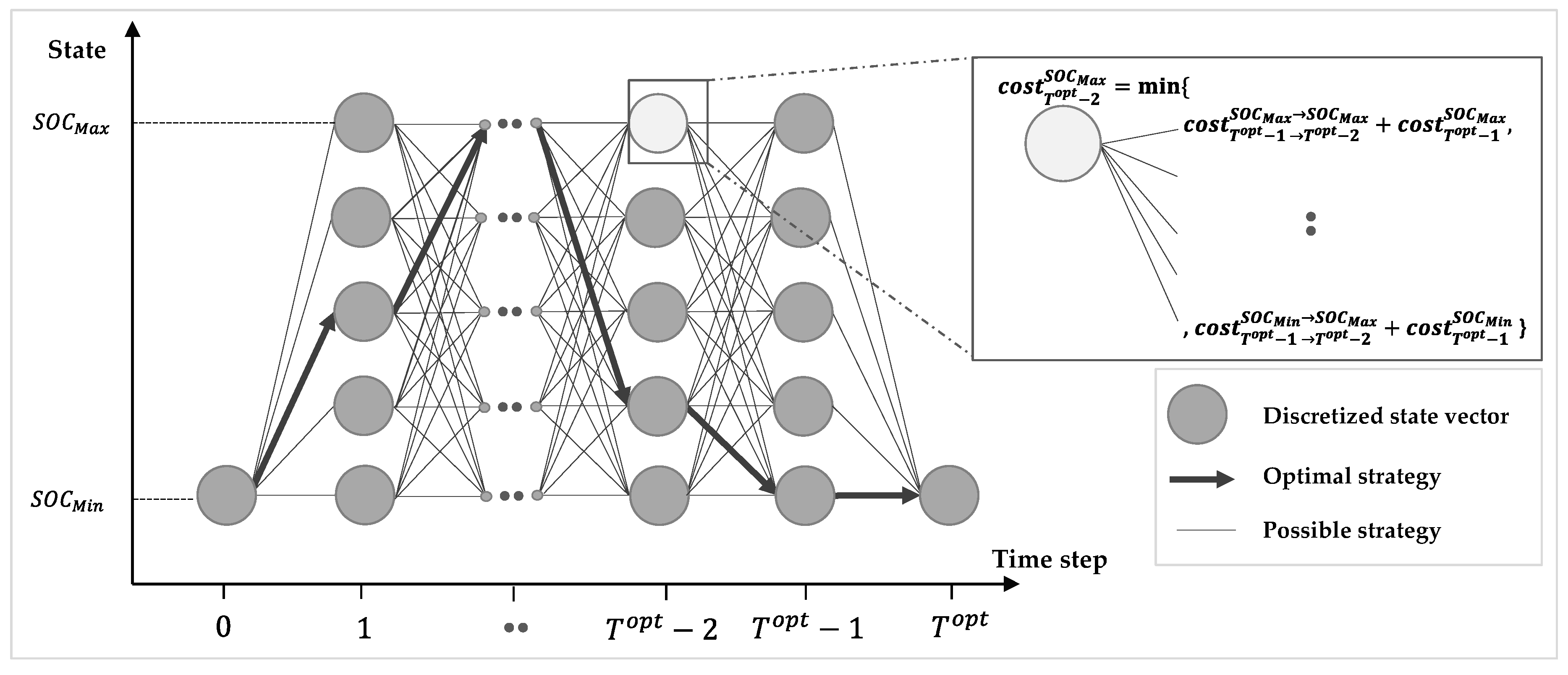
Appendix C. Dynamic Programming Model
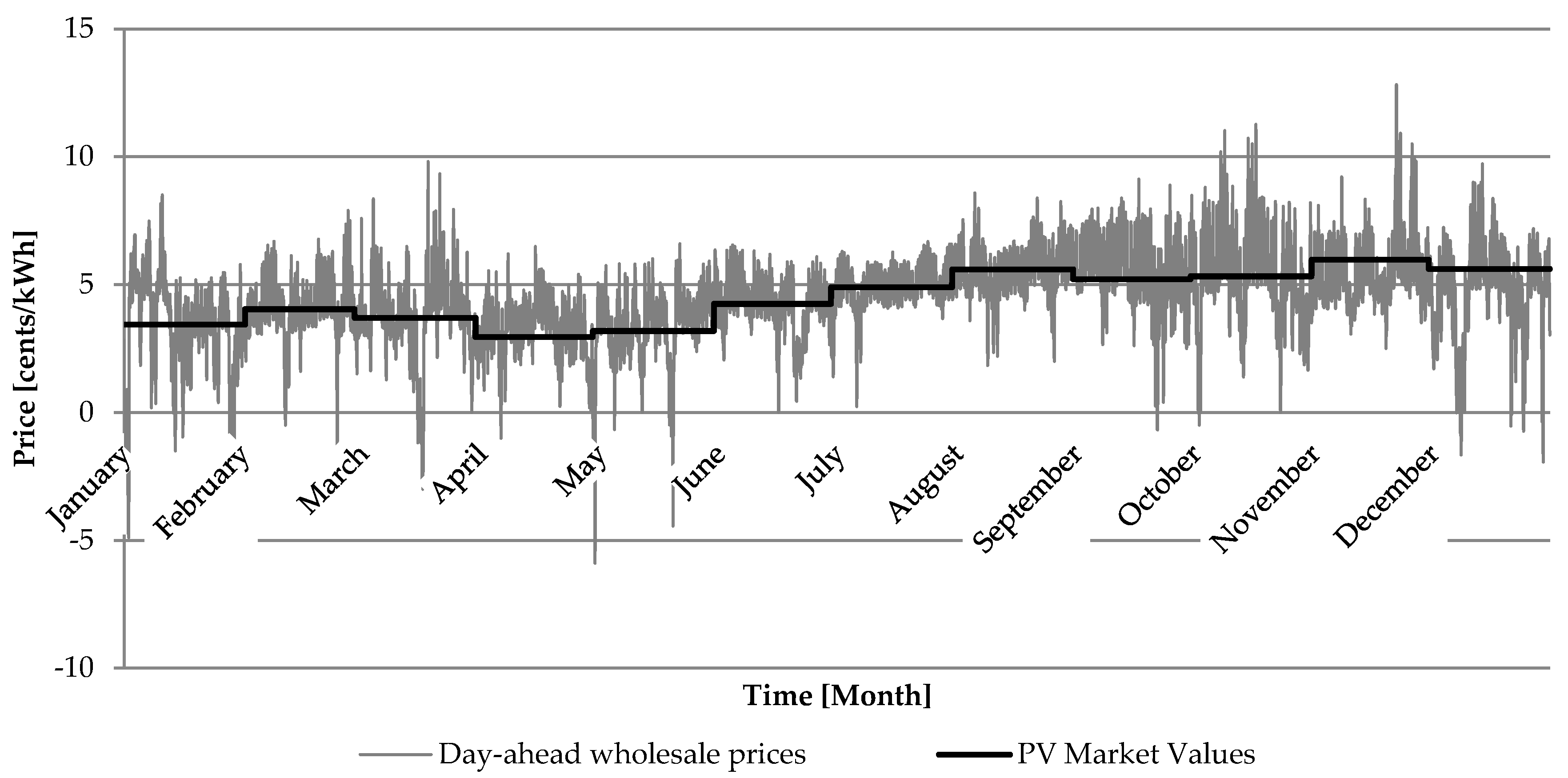
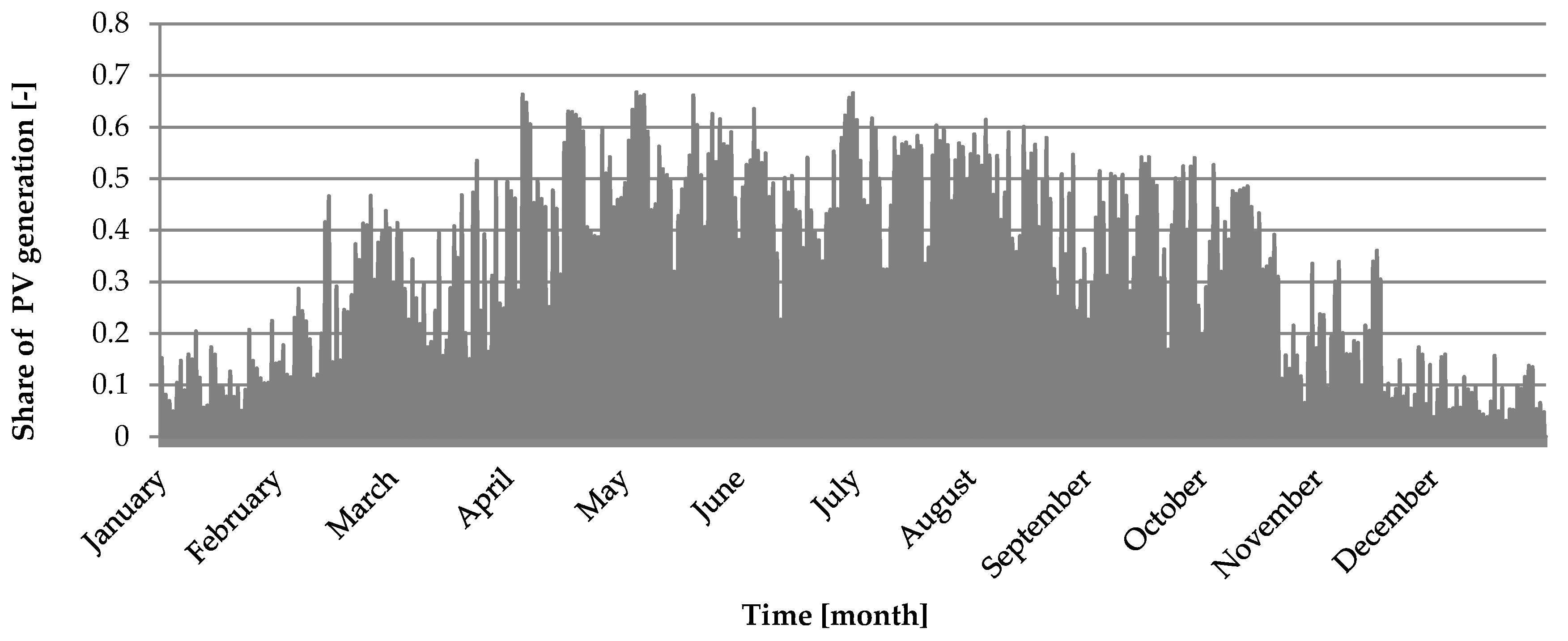
Appendix D. Preparation of the Model’s Input Data
Appendix E. Electricity Prices in Different Tariffs
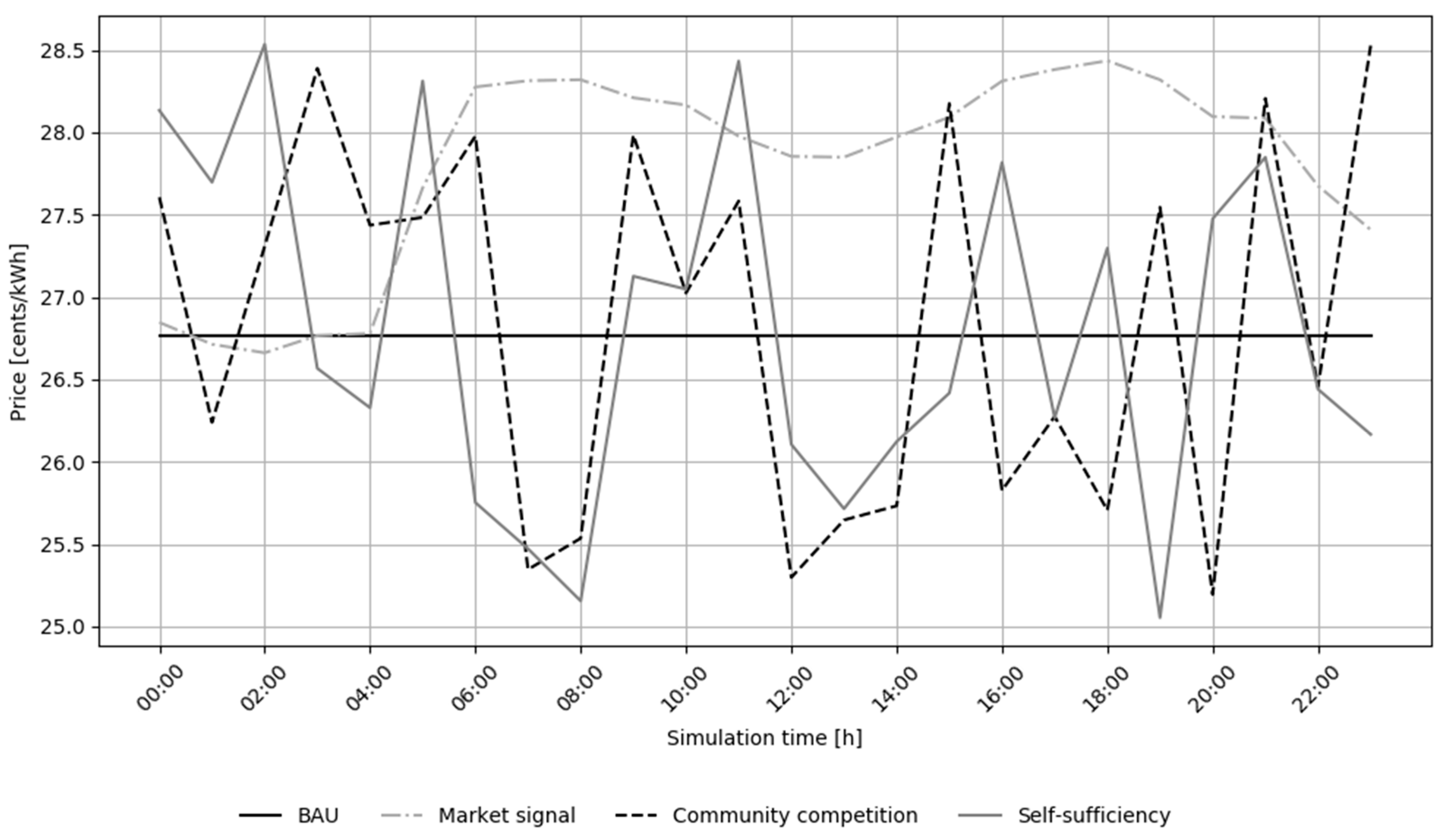
| Scenario | Jan–Mar | Apr–Jun | Jul–Sep | Oct-Dec |
|---|---|---|---|---|
| Market signal | 25.85 | 25.77 | 27.80 | 27.66 |
| Community competition | 26.86 | 26.84 | 26.82 | 26.83 |
| Self-sufficiency | 26.60 | 26.58 | 26.61 | 26.59 |
| Scenario | Jan–Mar | Apr–Jun | Jul–Sep | Oct–Dec |
|---|---|---|---|---|
| Market signal | 1.98 | 1.81 | 1.48 | 2.19 |
| Community competition | 0.92 | 0.95 | 1.04 | 0.90 |
| Self-sufficiency | 0.98 | 1.00 | 1.03 | 1.01 |
Appendix F. Exemplary Dispatch Optimization Results
Appendix F.1. 48 h Flexible Consumers’ Schedule in Response to M-RTP Tariff
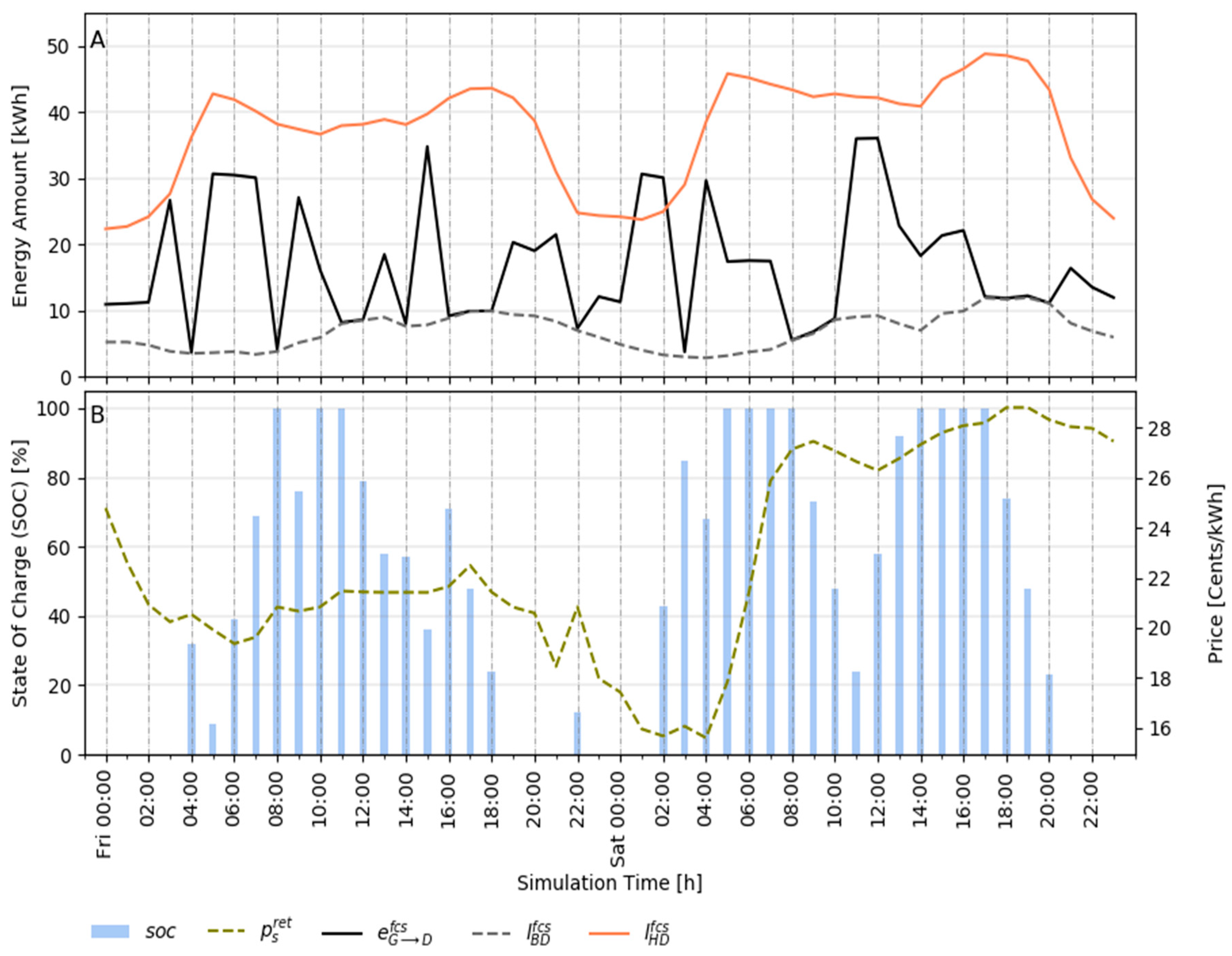
Appendix F.2. 48 h Prosumagers’ Schedule in Response to M-RTP Tariff
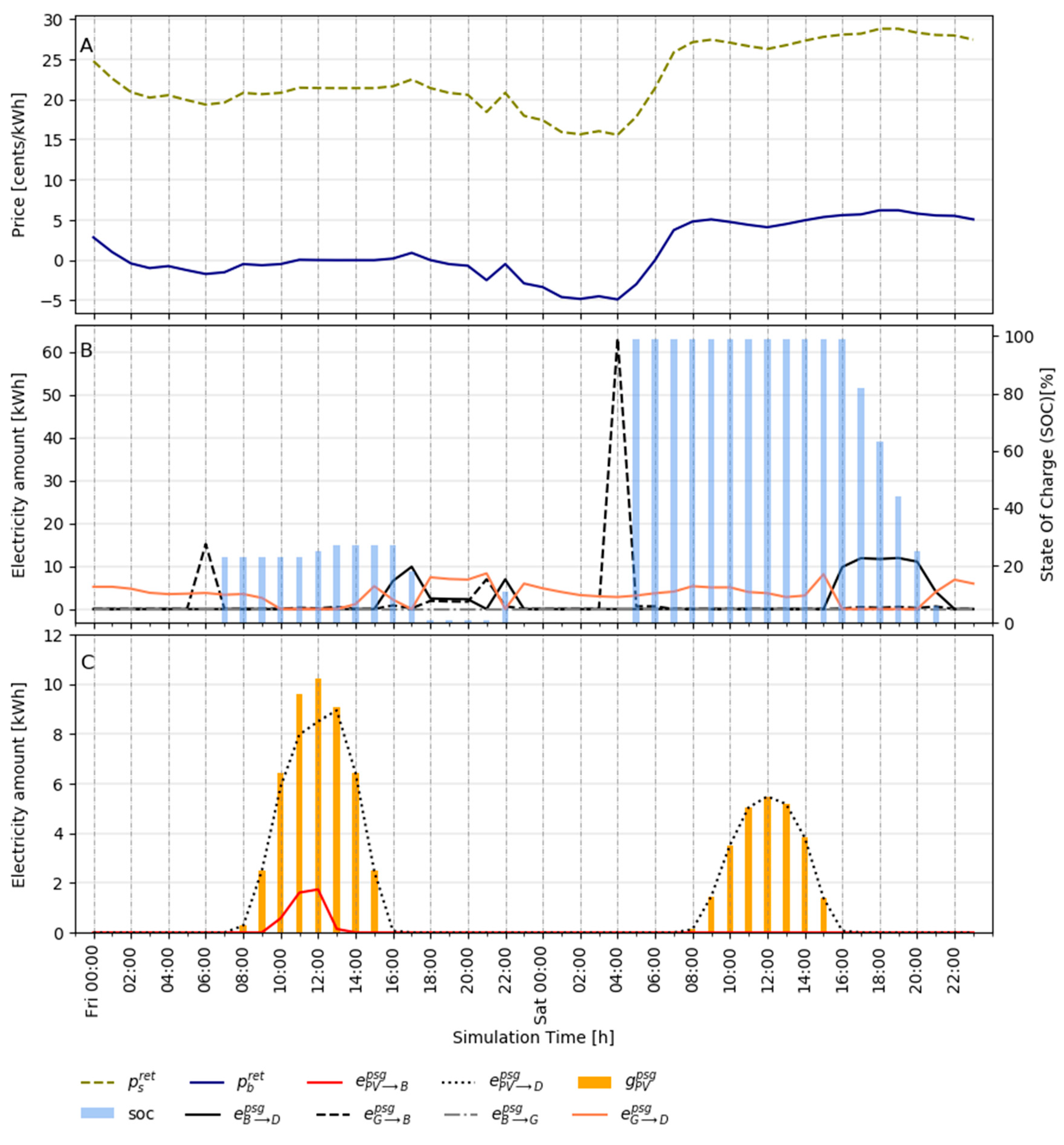
Appendix G. NPV Calculations
References
- Lang, T.; Ammann, D.; Girod, B. Profitability in absence of subsidies: A techno-economic analysis of rooftop photovoltaic self-consumption in residential and commercial buildings. Renew. Energy 2016, 87, 77–87. [Google Scholar] [CrossRef]
- Bazilian, M.; Onyeji, I.; Liebreich, M.; MacGill, I.; Chase, J.; Shah, J.; Gielen, D.; Arent, D.; Landfear, D.; Zhengrong, S. Re-considering the economics of photovoltaic power. Renew. Energy 2013, 53, 329–338. [Google Scholar] [CrossRef]
- Agnew, S.; Dargusch, P. Effect of residential solar and storage on centralized electricity supply systems. Nat. Clim. Chang. 2015, 5, 315. [Google Scholar] [CrossRef]
- Cole, W.J.; Frazier, A. Cost Projections for Utility-Scale Battery Storage; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2019.
- Hoppmann, J.; Volland, J.; Schmidt, T.S.; Hoffmann, V.H. The economic viability of battery storage for residential solar photovoltaic systems–A review and a simulation model. Renew. Sustain. Energy Rev. 2014, 39, 1101–1118. [Google Scholar] [CrossRef]
- Bertsch, V.; Geldermann, J.; Lühn, T. What drives the profitability of household PV investments, self-consumption and self-sufficiency? Appl. Energy 2017, 204, 1–15. [Google Scholar] [CrossRef]
- Ruhnau, O.; Bannik, S.; Otten, S.; Praktiknjo, A.; Robinius, M. Direct or indirect electrification? A review of heat generation and road transport decarbonisation scenarios for Germany 2050. Energy Build. 2019, 166, 989–999. [Google Scholar] [CrossRef]
- Dehler, J.; Keles, D.; Telsnig, T.; Fleischer, B.; Baumann, M.; Fraboulet, D.; Faure-Schuyer, A.; Fichtner, W. Self-consumption of electricity from renewable sources. In Europe’s Energy Transition-Insights for Policy Making; Elsevier: Amsterdam, The Netherlands, 2017; pp. 225–236. [Google Scholar]
- Schill, W.-P.; Zerrahn, A.; Kunz, F. Prosumage of Solar Electricity: Pros, Cons, and the System Perspective. 2017. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2912814 (accessed on 7 February 2017). [CrossRef]
- Klein, M.; Ziade, A.; De Vries, L. Aligning prosumers with the electricity wholesale market–The impact of time-varying price signals and fixed network charges on solar self-consumption. Energy Policy 2019, 134, 110901. [Google Scholar] [CrossRef]
- Pudjianto, D.; Ramsay, C.; Strbac, G. Virtual power plant and system integration of distributed energy resources. IET Renew. Power Gener. 2007, 1, 10–16. [Google Scholar] [CrossRef]
- Frieden, D.; Tuerk, A.; Roberts, J.; D’Hebermont, S.; Gubina, A. Collective Self-Consumption and Energy Communities: Overview of Emerging Regulatory Approaches in Europe. 2019. Available online: https://www.compile-project.eu/wp-content/uploads/COMPILE_Collective_self-consumption_EU_review_june_2019_FINAL-1.pdf (accessed on 15 July 2020).
- Roberts, J.; Frieden, D.; d’Herbemont, S. Energy Community Definitions. Deliverable Developed Under the Scope of the COMPILE Project: Integrating Community Power in Energy Islands. 2019. Available online: https://www.compile-project.eu/wp-content/uploads/Explanatory-note-on-energy-community-definitions.pdf (accessed on 5 December 2019).
- Koirala, B.P.; Koliou, E.; Friege, J.; Hakvoort, R.A.; Herder, P.M. Energetic communities for community energy: A review of key issues and trends shaping integrated community energy systems. Renew. Sustain. Energy Rev. 2016, 56, 722–744. [Google Scholar] [CrossRef]
- Deutscher Genossenschafts-und Raiffeisenverband e. V. (DGRV). Energy Cooperatives: Results of the DGRV-Survey (at 31 December 2018). Available online: https://www.dgrv.de/weben.nsf/web/annualsurveyenergycooperatives (accessed on 5 June 2019).
- Gaudchau, E.; Resch, M.; Zeh, A. Quartierspeicher: Definition, rechtlicher Rahmen und Perspektiven. Ökologisches Wirtsch.-Fachz. 2016, 31, 26–27. [Google Scholar] [CrossRef]
- Koirala, B.P.; van Oost, E.; van der Windt, H. Community energy storage: A responsible innovation towards a sustainable energy system? Appl. Energy 2018, 231, 570–585. [Google Scholar] [CrossRef]
- van der Stelt, S.; AlSkaif, T.; van Sark, W. Techno-economic analysis of household and community energy storage for residential prosumers with smart appliances. Appl. Energy 2018, 209, 266–276. [Google Scholar] [CrossRef]
- Gissey, G.C.; Dodds, P.E.; Radcliffe, J. Market and regulatory barriers to electrical energy storage innovation. Renew. Sustain. Energy Rev. 2018, 82, 781–790. [Google Scholar] [CrossRef]
- Scheller, F.; Götz, M.; Burgenmeister, B.; Seim, S.; Haberland, R.; Kondziella, H.; Bruckner, T. Legal Framework and Economic Feasibility of Neighborhood Energy Storage Systems. In Proceedings of the 10th Internationale Energiewirtschaftstagung Conference, Wien, Austria, 15 February 2017. [Google Scholar]
- Parra, D.; Swierczynski, M.; Stroe, D.I.; Norman, S.A.; Abdon, A.; Worlitschek, J.; O’Doherty, T.; Rodrigues, L.; Gillott, M.; Zhang, X. An interdisciplinary review of energy storage for communities: Challenges and perspectives. Renew. Sustain. Energy Rev. 2017, 79, 730–749. [Google Scholar] [CrossRef]
- Arghandeh, R.; Woyak, J.; Onen, A.; Jung, J.; Broadwater, R.P. Economic optimal operation of Community Energy Storage systems in competitive energy markets. Appl. Energy 2014, 135, 71–80. [Google Scholar] [CrossRef]
- Lombardi, P.; Schwabe, F. Sharing economy as a new business model for energy storage systems. Appl. Energy 2017, 188, 485–496. [Google Scholar] [CrossRef]
- Chakraborty, P.; Baeyens, E.; Poolla, K.; Khargonekar, P.P.; Varaiya, P. Sharing storage in a smart grid: A coalitional game approach. IEEE Trans. Smart Grid 2018, 10, 4379–4390. [Google Scholar] [CrossRef]
- Mediwaththe, C.P.; Stephens, E.R.; Smith, D.B.; Mahanti, A. Competitive energy trading framework for demand-side management in neighborhood area networks. IEEE Trans. Smart Grid 2017, 9, 4313–4322. [Google Scholar] [CrossRef]
- Liu, N.; Cheng, M.; Yu, X.; Zhong, J.; Lei, J. Energy-sharing provider for PV prosumer clusters: A hybrid approach using stochastic programming and stackelberg game. IEEE Trans. Ind. Electron. 2018, 65, 6740–6750. [Google Scholar] [CrossRef]
- Tushar, W.; Chai, B.; Yuen, C.; Smith, D.B.; Poor, H.V. Energy management for a user interactive smart community: A Stackelberg game approach. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA) of Conference, Kuala Lumpur, Malaysia, 20–23 May 2014. [Google Scholar]
- Liu, N.; Yu, X.; Wang, C.; Wang, J. Energy sharing management for microgrids with PV prosumers: A Stackelberg game approach. IEEE Trans. Ind. Inform. 2017, 13, 1088–1098. [Google Scholar] [CrossRef]
- BDEW—Bundesverband der Energie- und Wasserwirtschaft e. V. Strompreisanalyse Januar 2020. Available online: https://www.bdew.de/media/documents/20200107_BDEW-Strompreisanalyse_Januar_2020.pdf (accessed on 1 February 2020).
- Purkus, A.; Gawel, E.; Deissenroth, M.; Nienhaus, K.; Wassermann, S. Der Beitrag der Marktprämie zur Marktintegration Erneuerbarer Energien–Erfahrungen aus dem EEG 2012 und Perspektiven der Verpflichtenden Direktvermarktung; Helmholtz-Zentrum für Umweltforschung—UFZ: Leipzig, Germany, 2017; Available online: http://hdl.handle.net/10419/102740 (accessed on 5 June 2020).
- Sterner, M.; Stadler, I. Energiespeicher-Bedarf, Technologien, Integration; Springer: Berlin, Germany, 2014. [Google Scholar]
- Winkler, J.; Sensfuß, F.; Pudlik, M. Leitstudie Strommarkt Arbeitspaket 4 Analyse Ausgewählter Einflussfaktoren auf den Marktwert Erneuerbarer Energien. 2015. Available online: https://www.bmwi.de/Redaktion/DE/Publikationen/Studien/leitstudie-strommarkt_analyse-ausgewaehlter-einflussfaktoren-auf-den-martkwert-erneuerbarer-energien.pdf?__blob=publicationFile&v=3 (accessed on 27 March 2020).
- Gawel, E.; Purkus, A. EEG 2017—Mehr Markt bei der Erneuerbare-Energien-Förderung? Wirtschaftsdienst 2016, 96, 910–915. [Google Scholar] [CrossRef][Green Version]
- Maly, D.K.; Kwan, K.-S. Optimal battery energy storage system (BESS) charge scheduling with dynamic programming. IEE Proc. Sci. Meas. Technol. 1995, 142, 453–458. [Google Scholar] [CrossRef]
- Open Power System Data: Data Package Time Series. 2019. Available online: https://windenergyscience.com/learn-and-thrive/time-series-data/ (accessed on 27 March 2020). [CrossRef]
- Netztransparenz, Marktwertübersicht. Available online: https://www.netztransparenz.de/EEG/Marktpraemie/Marktwerte (accessed on 5 May 2019).
- Bundesverband Solarwirtschaft eV Feste Einspeise-Vergütungen im Überblick. 2017. Available online: https://www.solarwirtschaft.de/fileadmin/user_upload/Verguetungsuebersicht-Basis.pdf (accessed on 12 January 2020).
- Tjaden, T.; Bergner, J.; Weniger, J.; Quaschning, V. Repräsentative Elektrische Lastprofile für Wohngebäude in Deutschland auf 1-sekündiger Datenbasis; Hochschule für Technik und Wirtschaft HTW Berlin: Berlin, Germany, 2015. [Google Scholar]
- Hayn, M.; Zander, A.; Fichtner, W.; Nickel, S.; Bertsch, V.J.E.S. The impact of electricity tariffs on residential demand side flexibility: Results of bottom-up load profile modeling. Energy Syst. 2018, 9, 759–792. [Google Scholar] [CrossRef]
- Ruhnau, O. When2Heat Heating Profiles. Open Power Syst. Data 2019. [Google Scholar] [CrossRef]
- Ruhnau, O.; Hirth, L.; Praktiknjo, A. Time series of heat demand and heat pump efficiency for energy system modeling. Sci. Data 2019, 6, 189. [Google Scholar] [CrossRef]
- Engelken, M.; Römer, B.; Drescher, M.; Welpe, I. Why homeowners strive for energy self-supply and how policy makers can influence them. Energy Policy 2018, 117, 423–433. [Google Scholar] [CrossRef]
- Förster, H.; Kunert, D.; Hünecke, K.; Schumacher, K.; Siemons, A.; Zell-Ziegler, C. Hintergrundpapier: 50 Jahre Mehrwertsteuer–Ein Blick durch die Klimaschutzbrille. Available online: https://www.oeko.de/fileadmin/oekodoc/Hintergrundpapier_Mehrwertsteuer_2018.pdf (accessed on 18 April 2020).
- Khalid, A.M.; Mitra, I.; Warmuth, W.; Schacht, V. Performance ratio–Crucial parameter for grid connected PV plants. Renew. Sustain. Energy Rev. 2016, 65, 1139–1158. [Google Scholar] [CrossRef]
- Forsén, M.; Boeswarth, R.; Dubuisson, X.; Sandström, B. Heat Pumps: Technology and Environmental Impact. Swedish Heat Pump Association (SVEPR). 2005. Available online: https://ec.europa.eu/environment/ecolabel/about_ecolabel/reports/hp_tech_env_impact_aug2005.pdf (accessed on 3 November 2019).
- Thomann, R.; Lachmann, Y.; Prahl, O. Strombank: Innovatives Betreibermodell für Quartierspeicher. 2016. Available online: https://www.mvv.de/fileadmin/user_upload/Ueber_uns/de/Strombank_Abschlussbericht_2016.pdf (accessed on 12 June 2020).
- Schick, C.; Blesl, M.; Borggrefe, F.; Brand, H.; Buchmann, T.; Fahl, U.; Fuchs, A.-L.; Gils, H.; Hufendiek, K.; Münkel, A.; et al. Energiesystemanalyse Baden-Württemberg; Ministerium für Umwelt, Klima und Energiewirtschaft Baden-Württemberg: Stuttgart, Germany, 2018. [Google Scholar]
- Meng, F.-L.; Zeng, X.-J. An optimal real-time pricing for demand-side management: A Stackelberg game and genetic algorithm approach. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN) of Conference, Beijing, China, 6–11 July 2014. [Google Scholar]
- Hejazi, S.R.; Memariani, A.; Jahanshahloo, G.; Sepehri, M.M. Linear bilevel programming solution by genetic algorithm. Comput. Oper. Res. 2002, 29, 1913–1925. [Google Scholar] [CrossRef]
- Wilhelmstötter, F. JENETICS Library User’s Manual 4.3. 2016. Available online: http://jenetics.io/ (accessed on 20 July 2020).
- Braeuer, F.; Kleinebrahm, M.; Naber, E. Effects of the tenants electricity law on energy system layout and landlord-tenant relationship in a multi-family building in Germany. In Proceedings of the IOP Conference Series: Earth and Environmental Science of Conference, Graz, Austria, 11–14 September 2019. [Google Scholar]
- Gährs, S.; Knoefel, J.; Cremer, N. Politische Zielsetzungen und Rechtlicher Rahmen für Quartierspeicher. 2017, p. 2019. Available online: https://www.esquire-projekt.de/data/esquire/Datein/Arbeitspapier_Politische_Zielsetzungen_und_rechtlicher_Rahmen_f%C3%BCr_Quartierspeicher.pdf (accessed on 25 January 2020).
- Schwarz, H.; Schermeyer, H.; Bertsch, V.; Fichtner, W. Self-consumption through power-to-heat and storage for enhanced PV integration in decentralised energy systems. Solar Energy 2018, 163, 150–161. [Google Scholar] [CrossRef]
- Neuteleers, S.; Mulder, M.; Hindriks, F. Assessing fairness of dynamic grid tariffs. Energy Policy 2017, 108, 111–120. [Google Scholar] [CrossRef]
- Förderer, K.; Lösch, M.; Növer, R.; Ronczka, M.; Schmeck, H. Smart Meter Gateways: Options for a BSI-Compliant Integration of Energy Management Systems. Appl. Sci. 2019, 9, 1634. [Google Scholar] [CrossRef]
- Gesetz Über Den Messstellenbetrieb und Die Datenkommunikation in Intelligenten Energienetzen (Messstellenbetriebsgesetz–MsbG). 2016, Volume 2, p. 48. Available online: https://www.gesetze-im-internet.de/messbg/MsbG.pdf (accessed on 7 February 2020).
- Khalilpour, R.; Vassallo, A. Leaving the grid: An ambition or a real choice? Energy Policy 2015, 82, 207–221. [Google Scholar] [CrossRef]
- Kaschub, T.; Jochem, P.; Fichtner, W. Solar energy storage in German households: Profitability, load changes and flexibility. Energy Policy 2016, 98, 520–532. [Google Scholar] [CrossRef]
- Simshauser, P. Distribution network prices and solar PV: Resolving rate instability and wealth transfers through demand tariffs. Energy Econ. 2016, 54, 108–122. [Google Scholar] [CrossRef]
- Parra, D.; Gillott, M.; Norman, S.A.; Walker, G.S. Optimum community energy storage system for PV energy time-shift. Appl. Energy 2015, 137, 576–587. [Google Scholar] [CrossRef]
- Ensslen, A.; Ringler, P.; Dörr, L.; Jochem, P.; Zimmermann, F.; Fichtner, W. Incentivizing smart charging: Modeling charging tariffs for electric vehicles in German and French electricity markets. Energy Res. Soc. Sci. 2018, 42, 112–126. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S.; Basar, T. Dependable demand response management in the smart grid: A Stackelberg game approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Alabdullatif, A.M.; Gerding, E.H.; Perez-Diaz, A.J.E. Market Design and Trading Strategies for Community Energy Markets with Storage and Renewable Supply. Energies 2020, 13, 972. [Google Scholar] [CrossRef]
- ALSalloum, H.; ELMasri, A.; Merghem-Boulahia, L.; Rahim, R. Demand side management in smart grids: A stackelberg multi period multi provider game. In Proceedings of the 2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS) of Conference, Paris, France, 26–28 February 2018. [Google Scholar]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
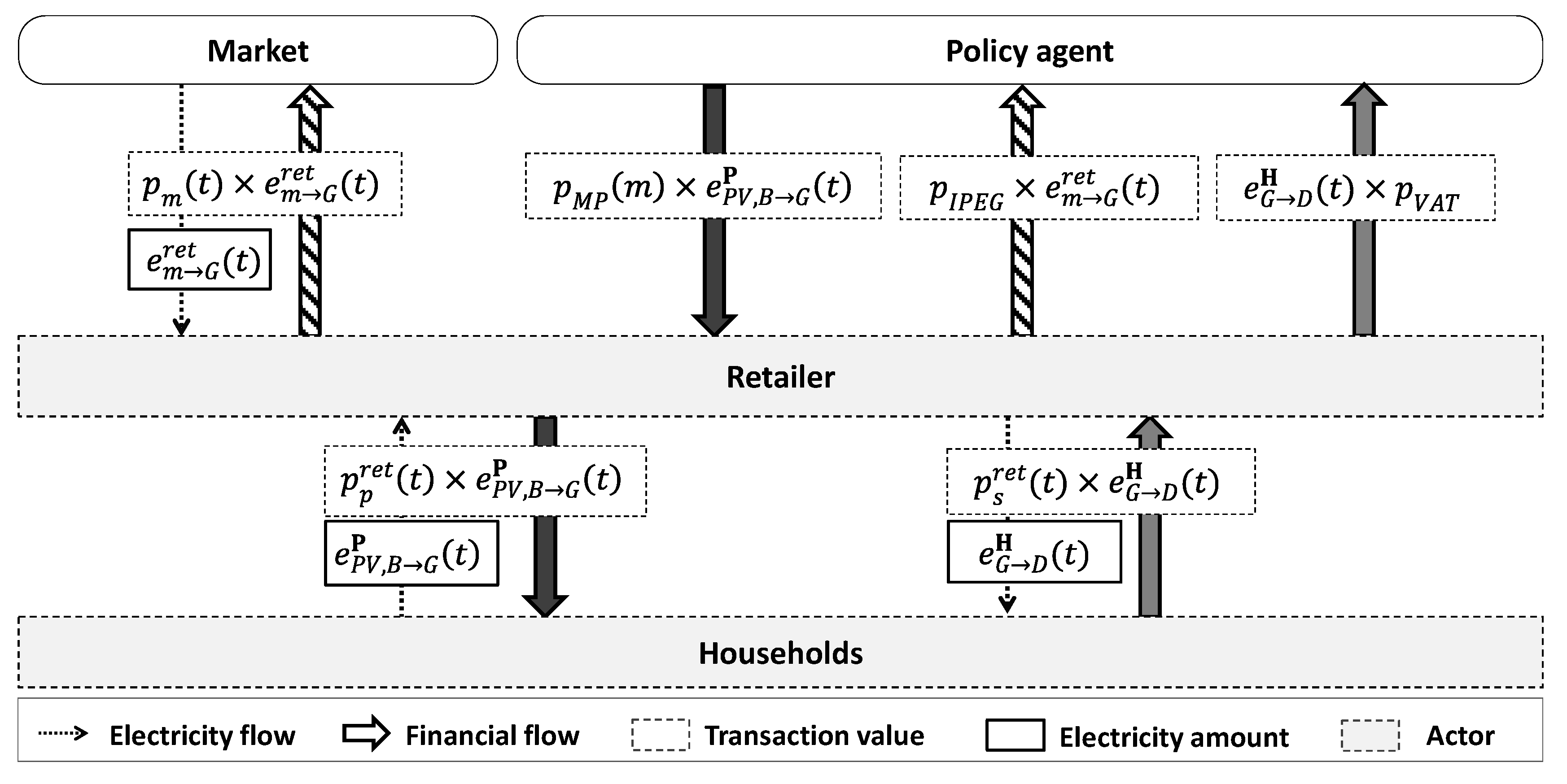


| Tariff | Real-Time Component | |
|---|---|---|
| SP | None | |
| M-RTP | , exogenous model input | |
| C-RTP | , derived endogenously (See Section 3.3) |
| Scenario | Tariff | Aggregation Goal |
|---|---|---|
| Business As Usual (BAU)—no storage | SP | None |
| Static tariff | SP | Maximum profit |
| Market signal | M-RTP | Maximum profit |
| Community competition | C-RTP | Maximum profit |
| Self-sufficiency | C-RTP | Maximum self-sufficiency |
| Input Parameter | Unit | Resolution | Mean | Min | Max | Total |
|---|---|---|---|---|---|---|
| Electricity demand () | kWh | Hour | 0.53 | 0.19 | 1.33 | 4685 |
| Heat demand ( | kWh | Hour | 2.28 | 0.12 | 7.17 | 19,996 |
| Parameter | Unit | Value | Source |
|---|---|---|---|
| cent/kWh | 12.3 | German Solar Association [37] | |
| cent/kWh | 7.68 | BDEW [29] | |
| cent/kWh | 7.3 | BDEW [29] | |
| cent/kWh | 3.71 | BDEW [29] | |
| cent/kWh | 18 | Model assumption | |
| VAT | % | 19 | Förster et al. [43] |
| kW | 6 | Model assumption | |
| % | 84 | Khalid et al. [44] | |
| kWh | 6 | Model assumption | |
| kW | 8 | Model assumption | |
| - | 3 | Forsén et al. [45] | |
| kWh | 14 | Model assumption | |
| kWh | 100 | Thorman et al. [46] | |
| % | 95 | Klein et al. [10] | |
| % | 95 | Klein et al. [10] | |
| - | 1 | Thorman et al. [46] | |
| % | 1 | Klein et al. [10] | |
| % | 4 | Model assumption | |
| years | 20 | Model assumption | |
| €/kWh | 510 and 250 | Schick et al. [47] | |
| hours | 24 | Model assumption | |
| hours | 8760 | Model assumption |
| Parameter | Value |
|---|---|
| Population size | 60 |
| Offspring fraction | 0.2 |
| Mutation | 0.6 |
| Single point crossover | 1 |
| Population convergence threshold | 0.01% |
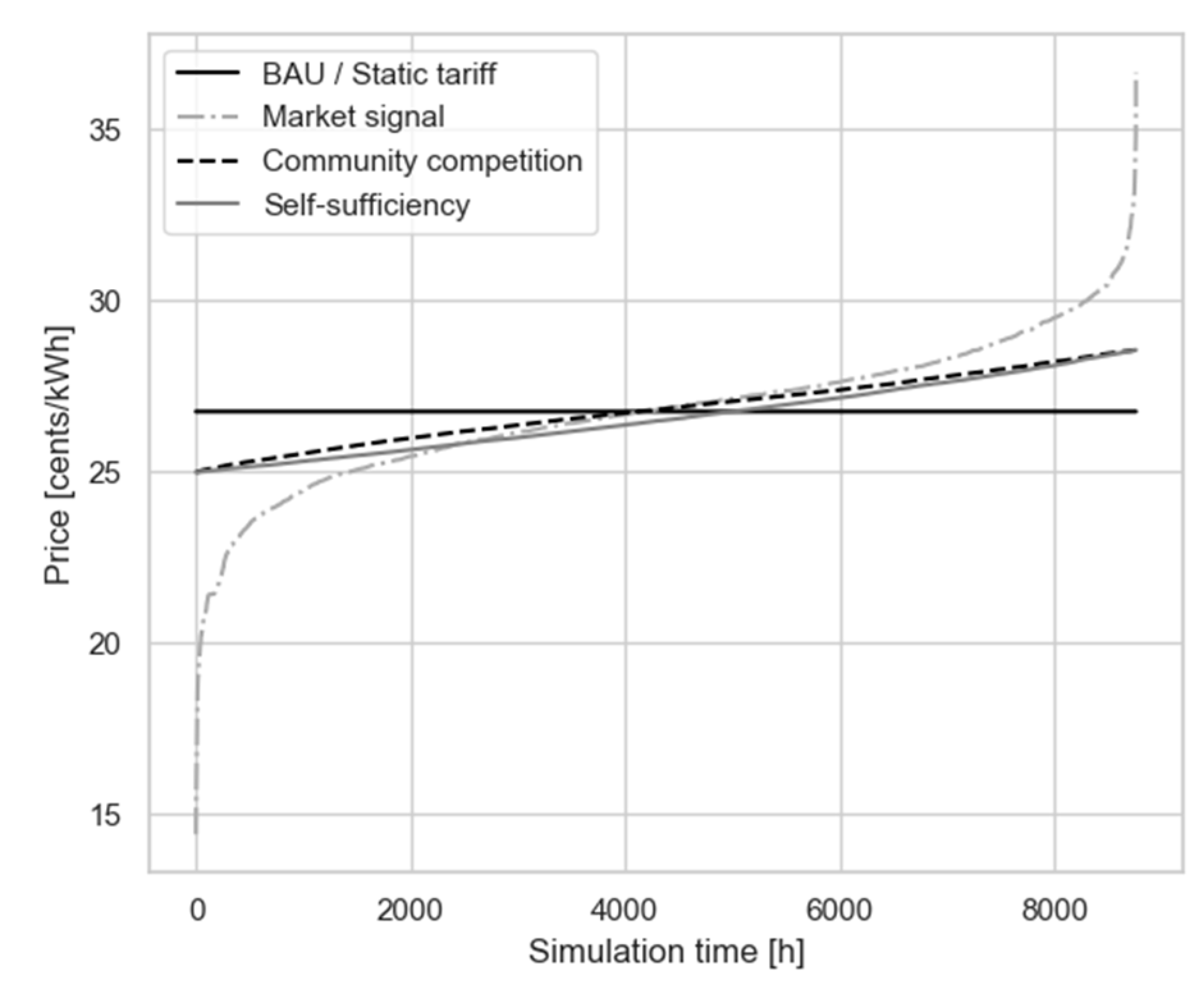
| Scenario | Tariff | Mean Value [cents] | Standard Deviation [-] | Price Range 1 [cents] |
|---|---|---|---|---|
| BAU/Static tariff | SP | 26.76 | 0 | [26.76, 26.76] |
| Market signal | M-RTP | 26.76 | 2.09 | [14.40, 36.68] |
| Community competition | C-RTP | 26.83 | 0.96 | [24.99, 28.56] |
| Self-sufficiency | C-RTP | 26.58 | 1.01 | [24.99, 28.56] |
| Scenario | Relative Import (%) | Relative Export (%) |
|---|---|---|
| Static tariff | −9.6 | −45.0 |
| Market signal | −9.9 | −46.3 |
| Community competition | −12.4 | −53.1 |
| Self-sufficiency | −13.0 | −59.5 |
| Scenario | Unit | NPV_510 | NPV_250 |
|---|---|---|---|
| Static tariff | € | −17,280.1 | 16,512.9 |
| Market signal | € | −13,795.8 | 19,997.2 |
| Community competition | € | −11,671.7 | 22,121.4 |
| Self-sufficiency | € | −27,043.5 | 6749.5 |
| Scenario | Grid Charges (€) | EEG Levy (€) |
|---|---|---|
| Static tariff | −1202.51 | −1120.15 |
| Market signal | −1242.57 | −1157.46 |
| Community competition | −1551.29 | −1445.03 |
| Self-sufficiency | −1628.25 | −1516.72 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarfarazi, S.; Deissenroth-Uhrig, M.; Bertsch, V. Aggregation of Households in Community Energy Systems: An Analysis from Actors’ and Market Perspectives. Energies 2020, 13, 5154. https://doi.org/10.3390/en13195154
Sarfarazi S, Deissenroth-Uhrig M, Bertsch V. Aggregation of Households in Community Energy Systems: An Analysis from Actors’ and Market Perspectives. Energies. 2020; 13(19):5154. https://doi.org/10.3390/en13195154
Chicago/Turabian StyleSarfarazi, Seyedfarzad, Marc Deissenroth-Uhrig, and Valentin Bertsch. 2020. "Aggregation of Households in Community Energy Systems: An Analysis from Actors’ and Market Perspectives" Energies 13, no. 19: 5154. https://doi.org/10.3390/en13195154
APA StyleSarfarazi, S., Deissenroth-Uhrig, M., & Bertsch, V. (2020). Aggregation of Households in Community Energy Systems: An Analysis from Actors’ and Market Perspectives. Energies, 13(19), 5154. https://doi.org/10.3390/en13195154