Variable Bandwidth Adaptive Course Keeping Control Strategy for Unmanned Surface Vehicle
Abstract
1. Introduction
2. Problem Formulation and Preliminaries
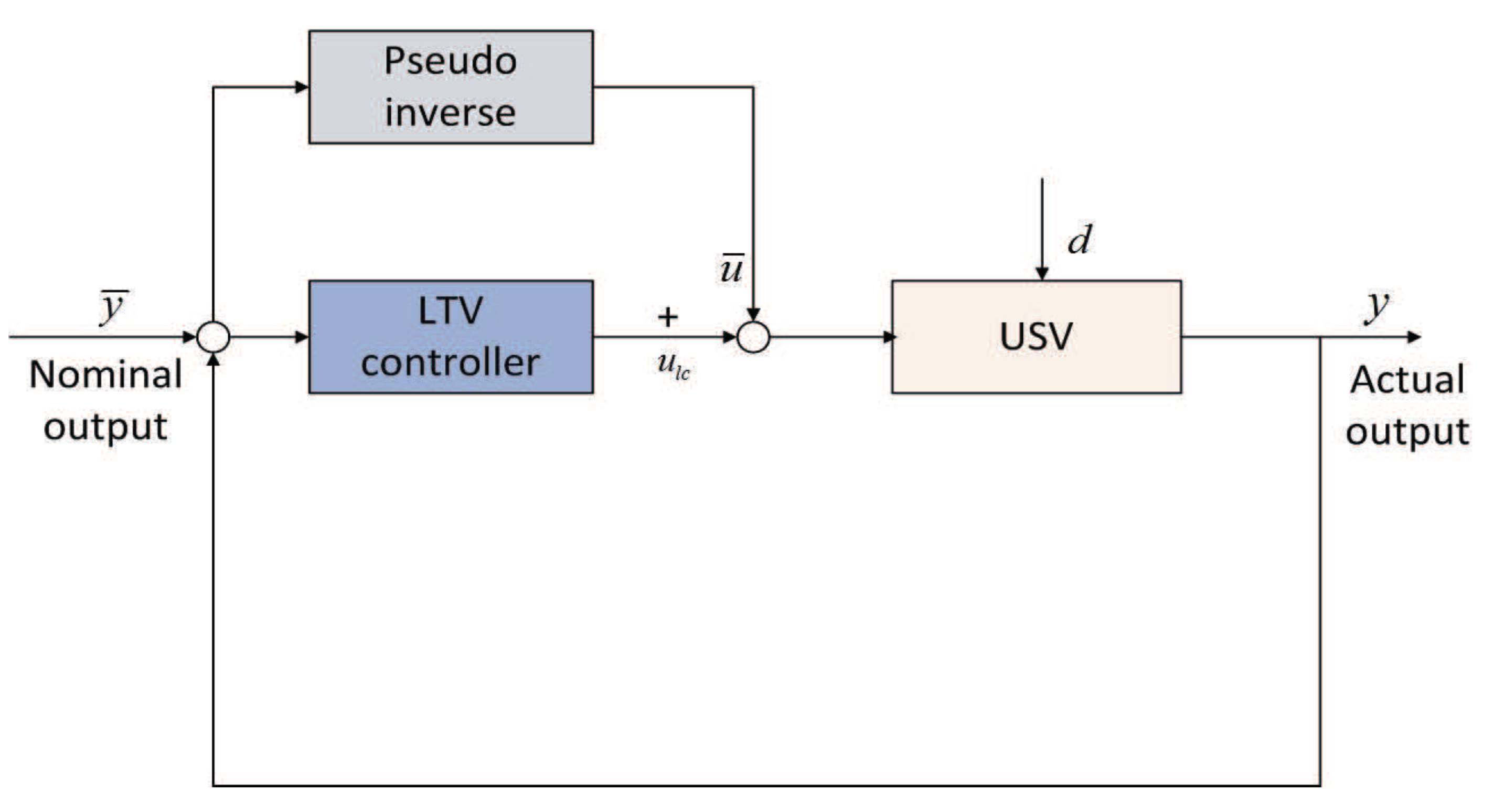
2.1. Problem Formulation
2.2. Trajectory Linearization Control
2.3. Neural Shunting Model
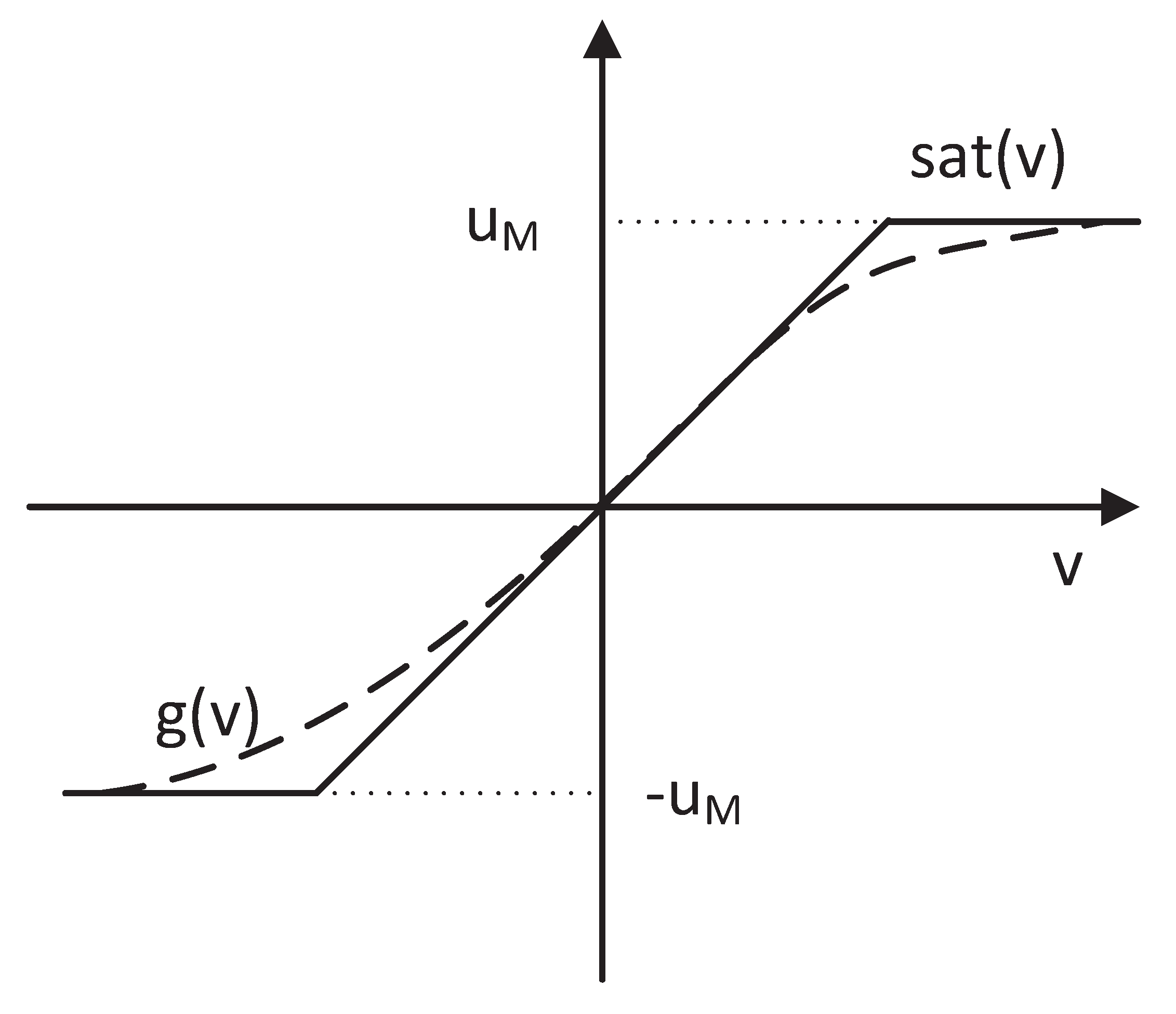
2.4. Input Saturation
2.5. Nussbaum Function
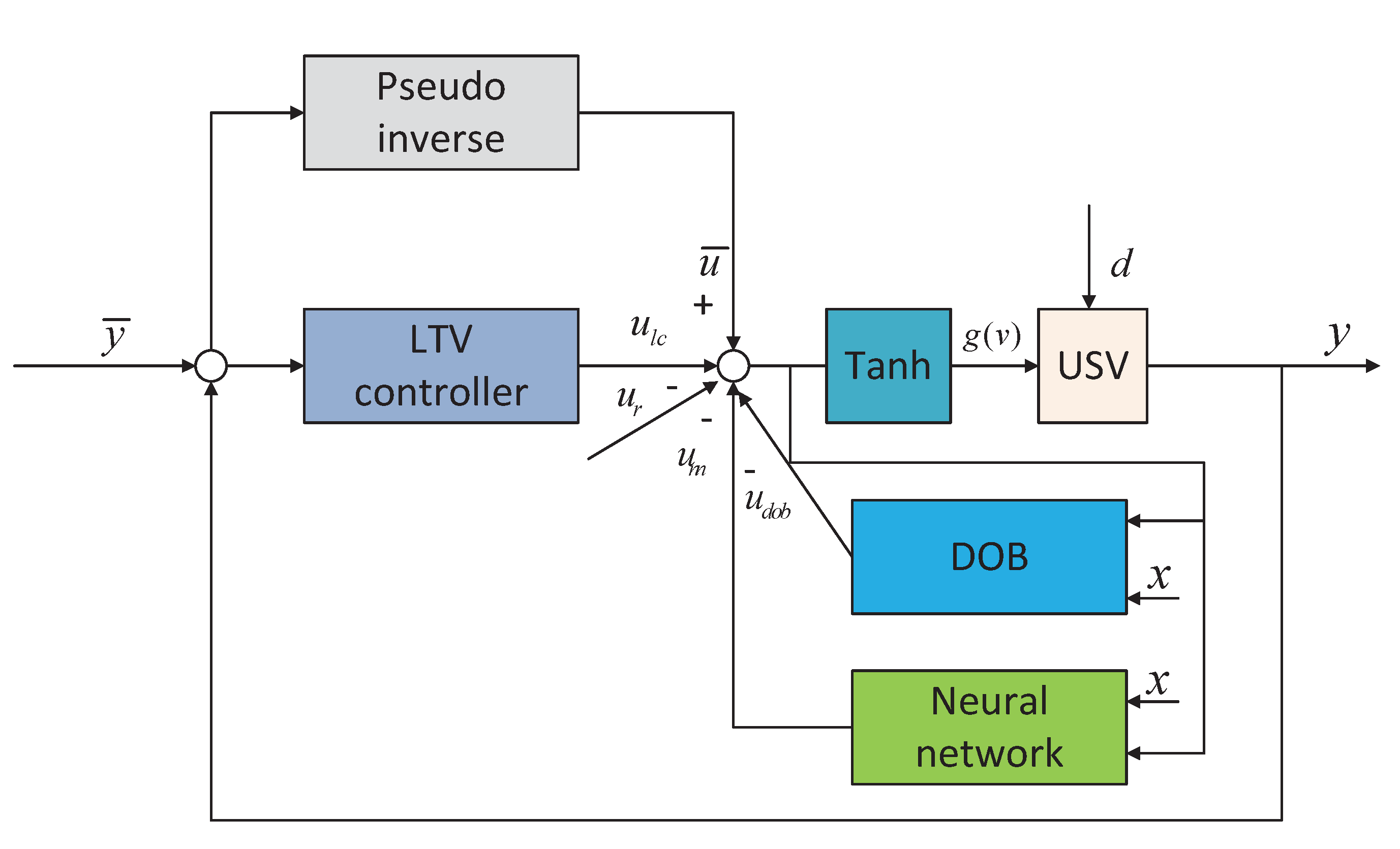
3. Design of Control Strategy
4. Stability Analysis
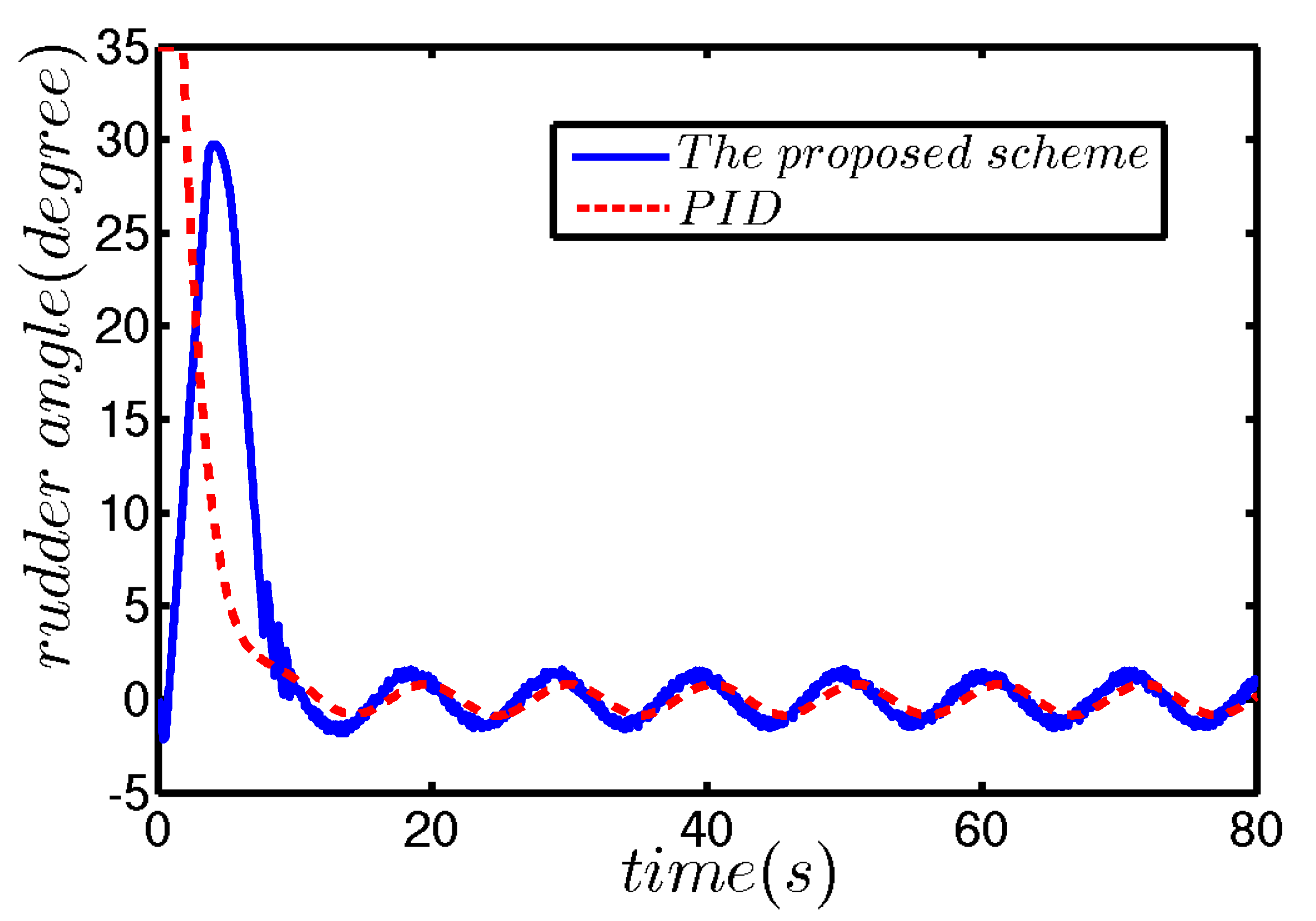
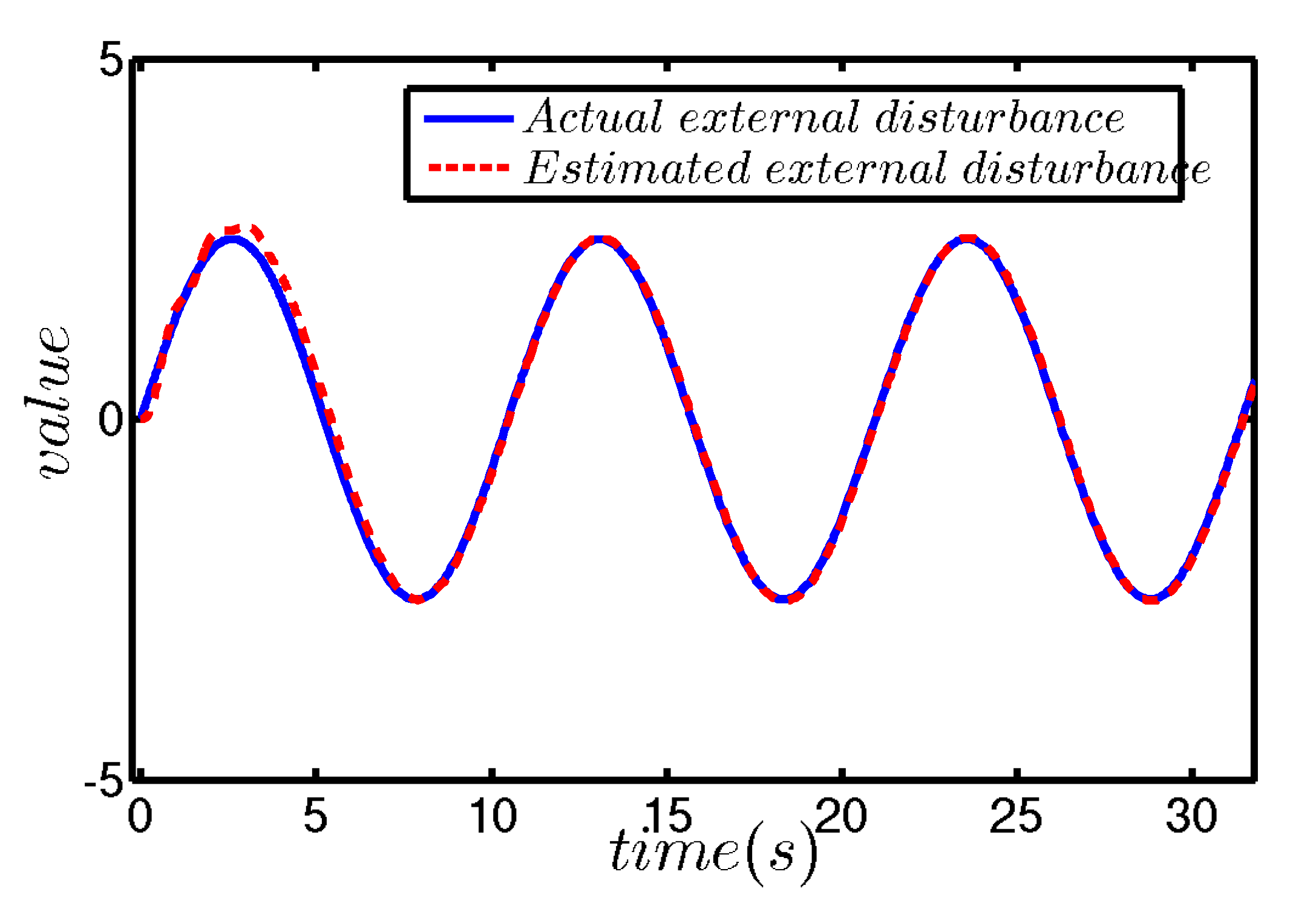
5. Numerical Simulations
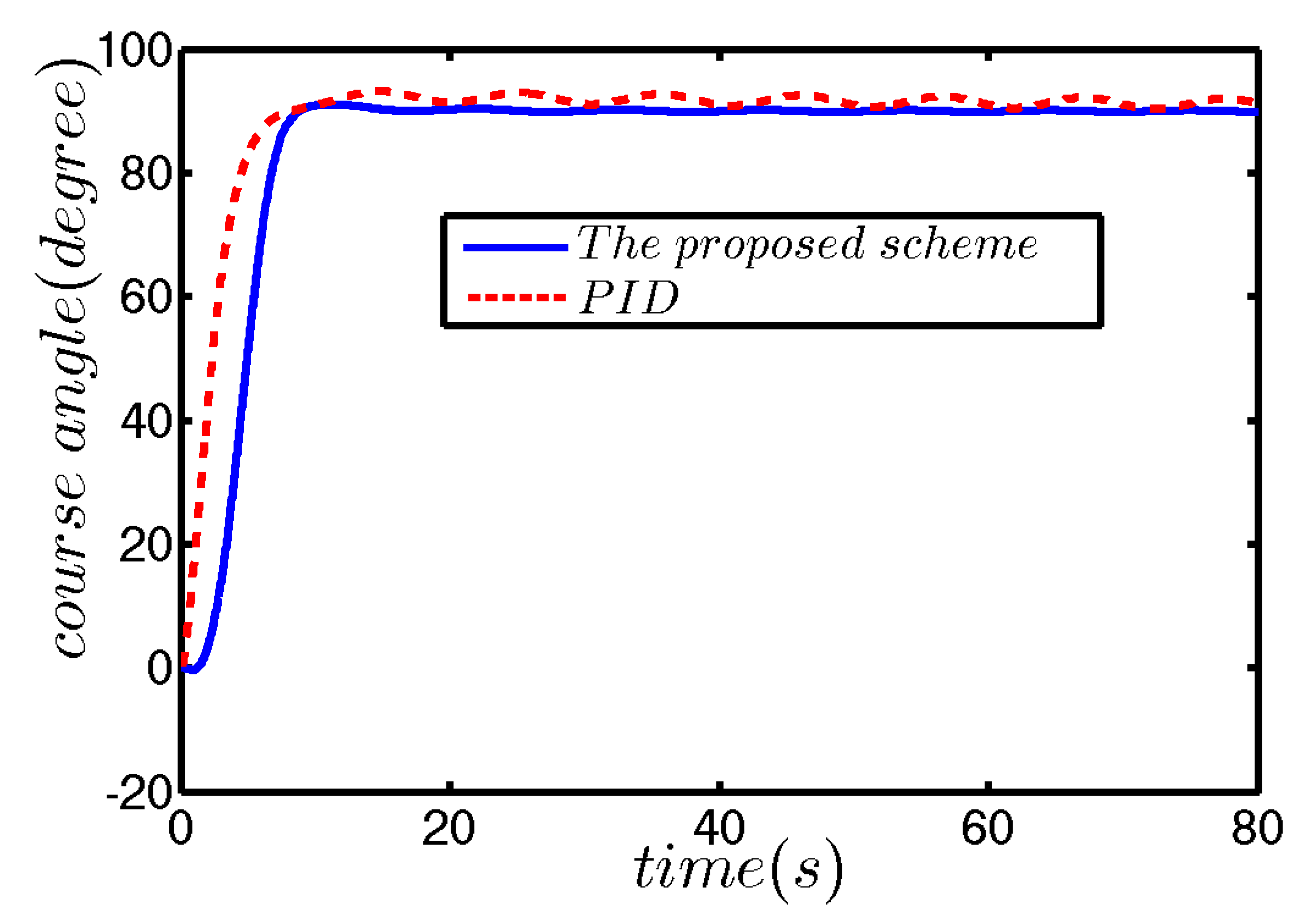
5.1. Weak External Disturbance
5.2. Strong External Disturbance
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| USV | unmanned surface vehicle |
| UTM | unmanned three musketeers |
| UAV | unmanned aerial vehicles |
| PID | proportional integral derivative |
| RBF | radial basis function |
| TLC | trajectory linearization control |
| DOB | disturbance observer |
| UUB | uniformly ultimately bounded |
| ITAE | integrated time and absolute error |
References
- Zaghi, S.; Dubbioso, G.; Broglia, R.; Muscari, R. Hydrodynamic characterization of USV vessels with innovative SWATH configuration for coastal monitoring and low environmental impact. Transp. Res. Procedia 2016, 14, 1562–1570. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Fan, Y.; Mu, D.; Qiu, B. Collision Avoidance Using Finite Control Set Model Predictive Control for Unmanned Surface Vehicle. Appl. Sci. 2018, 926. [Google Scholar] [CrossRef]
- Han, J.; Xiong, J.; He, Y.; Gu, F.; Li, D. Nonlinear Modeling for a Water-Jet Propulsion USV: An Experimental Study. IEEE Trans. Ind. Electron. 2017, 64, 3348–3358. [Google Scholar] [CrossRef]
- Brossard, J.; Bensoussan, D.; Landry, R.; Hammami, M. Robustness studies on quadrotor control. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS 2019), Atlanta, GA, USA, 11–14 June 2019; pp. 344–352. [Google Scholar]
- Mystkowski, A. An application of mu-synthesis for control of a small air vehicle and simulation results. J. Vibroeng. 2012, 14, 79–86. [Google Scholar]
- Tunik, A.A.; Nadsadnaya, O.I. A Flight Control System for Small Unmanned Aerial Vehicle. Int. Appl. Mech. 2018, 54, 239–247. [Google Scholar] [CrossRef]
- Wang, Y.L.; Han, Q.L. Network-based heading control and rudder oscillation reduction for unmanned surface vehicles. IEEE Trans. Control Syst. Technol. 2017, 25, 1609–1620. [Google Scholar] [CrossRef]
- Miao, R.; Dong, Z.; Wan, L.; Zeng, J. Heading Control System Design for a Micro-USV Based on an Adaptive Expert S-PID Algorithm. Pol. Marit. Res. 2018, 25, 6–13. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley: New York, NY, USA, 2011; ISBN 978-1119991496. [Google Scholar]
- Zhang, X.K.; Zhang, Q.; Ren, H.X.; Yang, G.P. RLinear reduction of backstepping algorithm based on nonlinear decoration for ship course-keeping control system. Ocean Eng. 2018, 147, 1–8. [Google Scholar] [CrossRef]
- Witkowska, A.; Śmierzchalski, R. Adaptive dynamic control allocation for dynamic positioning of marine vessel based on backstepping method and sequential quadratic programming. Ocean Eng. 2018, 163, 570–582. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Qiu, B.; Sun, X. Stereovision-based target tracking system for USV operations. Appl. Sci. 2018, 8, 547. [Google Scholar] [CrossRef]
- Mizuno, N.; Saka, N.; Katayama, T. A ship’s automatic maneuvering system using optimal preview sliding mode controller with adaptation mechanism. IFAC-PapersOnLine 2016, 49, 576–581. [Google Scholar] [CrossRef]
- Liu, Z. Ship adaptive course keeping control with nonlinear disturbance observer. IEEE Access 2017, 5, 17567–17575. [Google Scholar] [CrossRef]
- Videcoq, E.; Girault, M.; Bouderbala, K.; Nouira, H.; Salgado, J.; Petit, D. Parametric investigation of Linear Quadratic Gaussian and Model Predictive Control approaches for thermal regulation of a high precision geometric measurement machine. Appl. Therm. Eng. 2015, 78, 720–730. [Google Scholar] [CrossRef]
- Mu, D.; Zhao, Y.; Wang, G.; Fan, Y. USV model identification and course control. In Proceedings of the 2016 IEEE Sixth International Conference on Information Science and Technology (ICIST), Dalian, China, 6–8 May 2016; pp. 263–267. [Google Scholar]
- Lei, Z.; Guo, C. Disturbance rejection control solution for ship steering system with uncertain time delay. Ocean Eng. 2015, 95, 78–83. [Google Scholar] [CrossRef]
- Kahveci, N.E.; Ioannou, P.A. Adaptive steering control for uncertain ship dynamics and stability analysis. Automatica 2013, 49, 685–697. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Wang, W.; Liu, L. Neural adaptive steering of an unmanned surface vehicle with measurement noises. Neurocomputing 2016, 186, 228–234. [Google Scholar] [CrossRef]
- Zhang, X.K.; Zhang, G.Q. Design of Ship Course-Keeping Autopilot using a Sine Function-Based Nonlinear Feedback Technique. J. Navig. 2016, 69, 246–256. [Google Scholar] [CrossRef]
- Fan, Y.; Mu, D.; Zhang, X.; Guo, C.; Wang, G. Course keeping Control Based on Integrated Nonlinear Feedback for a USV with Pod-like Propulsion. J. Navig. 2018, 71, 878–898. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Zhao, Y. Modeling and identification of podded propulsion unmanned surface vehicle and its course control research. Math. Probl. Eng. 2017, 2017, 3209451. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; Ren, B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica 2011, 47, 452–465. [Google Scholar] [CrossRef]
- Norrbin, N.H. Ship manoeuvring with application to shipborne predictors and real-time simulators. Arch. J. Mech. Eng. Sci. 1972, 14, 1959–1982. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, J.J. Car-Like Ground Vehicle Trajectory Tracking by Using Trajectory Linearization Control. In Proceedings of the ASME 2017 Dynamic Systems and Control Conference. American Society of Mechanical Engineers, Tysons, VA, USA, 11–13 October 2017; p. V002T21A014. [Google Scholar]
- Liu, Y.; Wu, X.; Zhu, J.J.; Lwe, J. Omni-directional mobile robot controller design by trajectory linearization. In Proceedings of the IEEE American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 4, pp. 3423–3428. [Google Scholar]
- Zhao, Y.; Zhu, J.J. Automatic Aircraft Loss-of-Control Prevention by Bandwidth Adaptation. J. Guid. Control Dyn. 2016, 40, 878–889. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, J.J. Aircraft loss-of-control autonomous recovery: Mission trajectory tracking restoration. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 801–810. [Google Scholar]
- Liu, Y.; Zhu, J.J.; Williams, R.L., II; Wu, J. Omni-directional mobile robot controller based on trajectory linearization. Robot. Auton. Syst. 2008, 56, 461–479. [Google Scholar] [CrossRef]
- Yali, X.; Changsheng, J. Trajectory linearization control of an aerospace vehicle based on RBF neural network. J. Syst. Eng. Electron. 2008, 19, 799–805. [Google Scholar] [CrossRef]
- Grossberg, S. Nonlinear neural networks: Principles, mechanisms, and architectures. Neural Netw. 1988, 1, 17–61. [Google Scholar] [CrossRef]
- Pan, C.Z.; Lai, X.Z.; Yang, S.X.; Wu, M. A biologically inspired approach to tracking control of underactuated surface vessels subject to unknown dynamics. Expert Syst. Appl. 2015, 42, 2153–2161. [Google Scholar] [CrossRef]
- Wen, C.; Zhou, J.; Liu, Z.; Su, H. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Autom. Control 2011, 56, 1672–1678. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Z.; Zhang, Y.; Chen, C.L.P.; Xie, S. Saturated Nussbaum Function Based Approach for Robotic Systems with Unknown Actuator Dynamics. IEEE Trans. Cybern. 2016, 46, 2311–2322. [Google Scholar] [CrossRef]
- Xudong, Y.; Jingping, J. Adaptive nonlinear design without a priori knowledge of control directions. IEEE Trans. Autom. Control 1998, 43, 1617–1621. [Google Scholar] [CrossRef]
- Han, S.S.; Wang, H.P.; Tian, Y.; Christov, N. Time-delay estimation based computed torque control with robust adaptive RBF neural network compensator for a rehabilitation exoskeleton. ISA Trans. 2020, 97, 171–181. [Google Scholar] [CrossRef]
- Shi, X.Y.; Cheng, Y.H.; Yin, C.; Huang, X.G. Design of adaptive backstepping dynamic surface control method with RBF neural network for uncertain nonlinear system. Neurocomputing 2019, 30, 490–503. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Nikou, A.; Dimarogonas, D.V. Robust Trajectory Tracking Control for Underactuated Autonomous Underwater Vehicles in Uncertain Environments. IEEE Trans. Autom. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Noninear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Xu, J.X.; Li, C.; Hang, C.C. Tuning of fuzzy PI controllers based on gain/phase margin specifications and ITAE index. ISA Trans. 1996, 35, 79–91. [Google Scholar]
- Mu, D.; Wang, G.; Fan, Y.; Sun, X.; Qiu, B. Modeling and Identification for Vector Propulsion of an Unmanned Surface Vehicle: Three Degrees of Freedom Model and Response Model. Sensors 2018, 18, 1889. [Google Scholar] [CrossRef]



| ITAE | Value |
|---|---|
| The proposed scheme | 1500 |
| PID | 5345 |
| ITAE | Value |
|---|---|
| The proposed scheme | 1950 |
| PID | 6788 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, D.; Wang, G.; Fan, Y. Variable Bandwidth Adaptive Course Keeping Control Strategy for Unmanned Surface Vehicle. Energies 2020, 13, 5091. https://doi.org/10.3390/en13195091
Mu D, Wang G, Fan Y. Variable Bandwidth Adaptive Course Keeping Control Strategy for Unmanned Surface Vehicle. Energies. 2020; 13(19):5091. https://doi.org/10.3390/en13195091
Chicago/Turabian StyleMu, Dongdong, Guofeng Wang, and Yunsheng Fan. 2020. "Variable Bandwidth Adaptive Course Keeping Control Strategy for Unmanned Surface Vehicle" Energies 13, no. 19: 5091. https://doi.org/10.3390/en13195091
APA StyleMu, D., Wang, G., & Fan, Y. (2020). Variable Bandwidth Adaptive Course Keeping Control Strategy for Unmanned Surface Vehicle. Energies, 13(19), 5091. https://doi.org/10.3390/en13195091







