On Stability of Perturbed Nonlinear Switched Systems with Adaptive Reinforcement Learning
Abstract
1. Introduction
- (1)
- (2)
- The Neural Network training law with optimization principle is developed to achieve the ARL-based optimal control strategy.
- (3)
- The strict proof concerning UUB stability of the closed system and the convergence of the controller to optimal control input are given based on Lyapunov stability theory and reinforcement learning scheme.
2. Problem Statement and Preliminaries
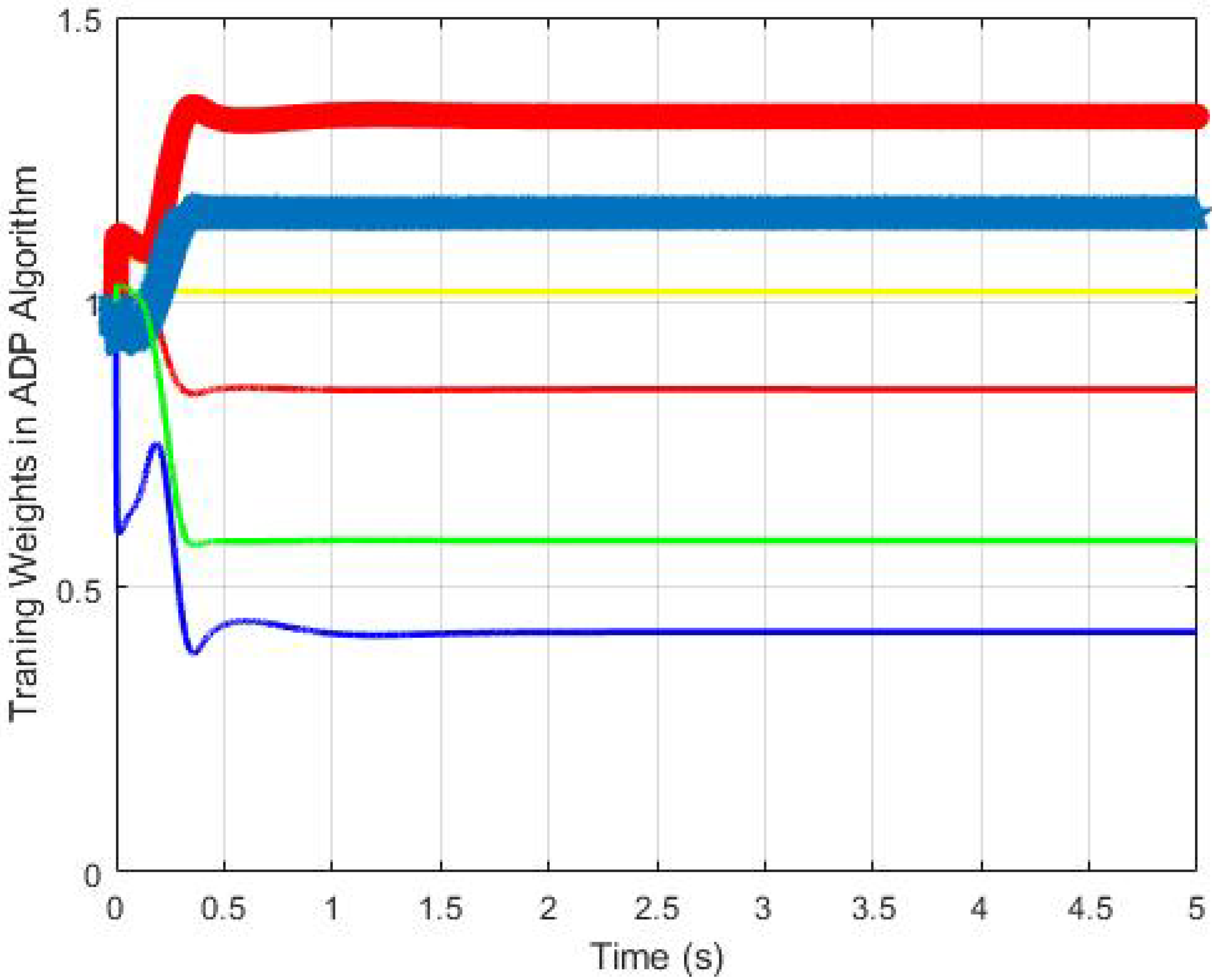
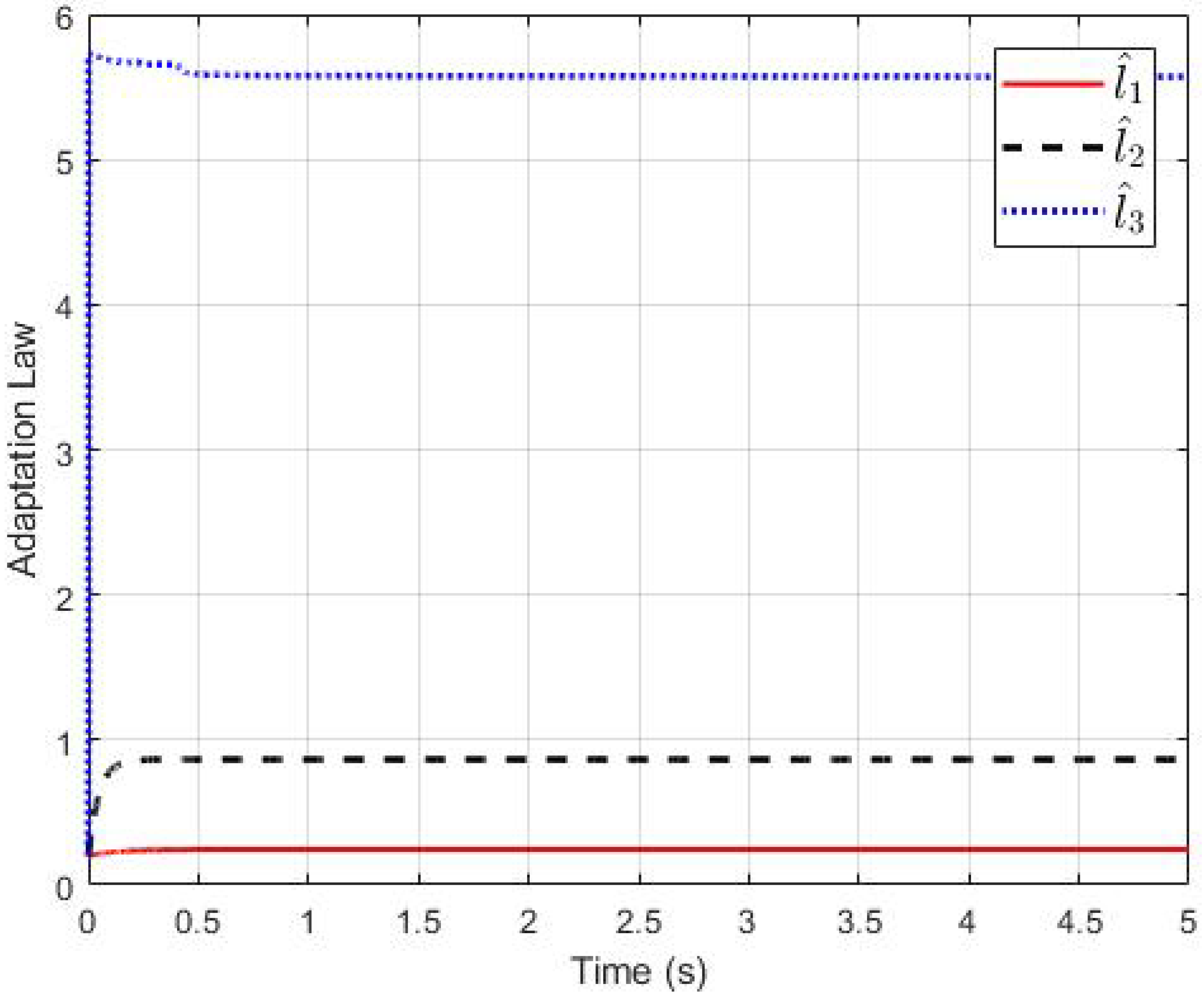
3. Adaptive Reinforcement Learning-Based Control Design
4. Simulation Results
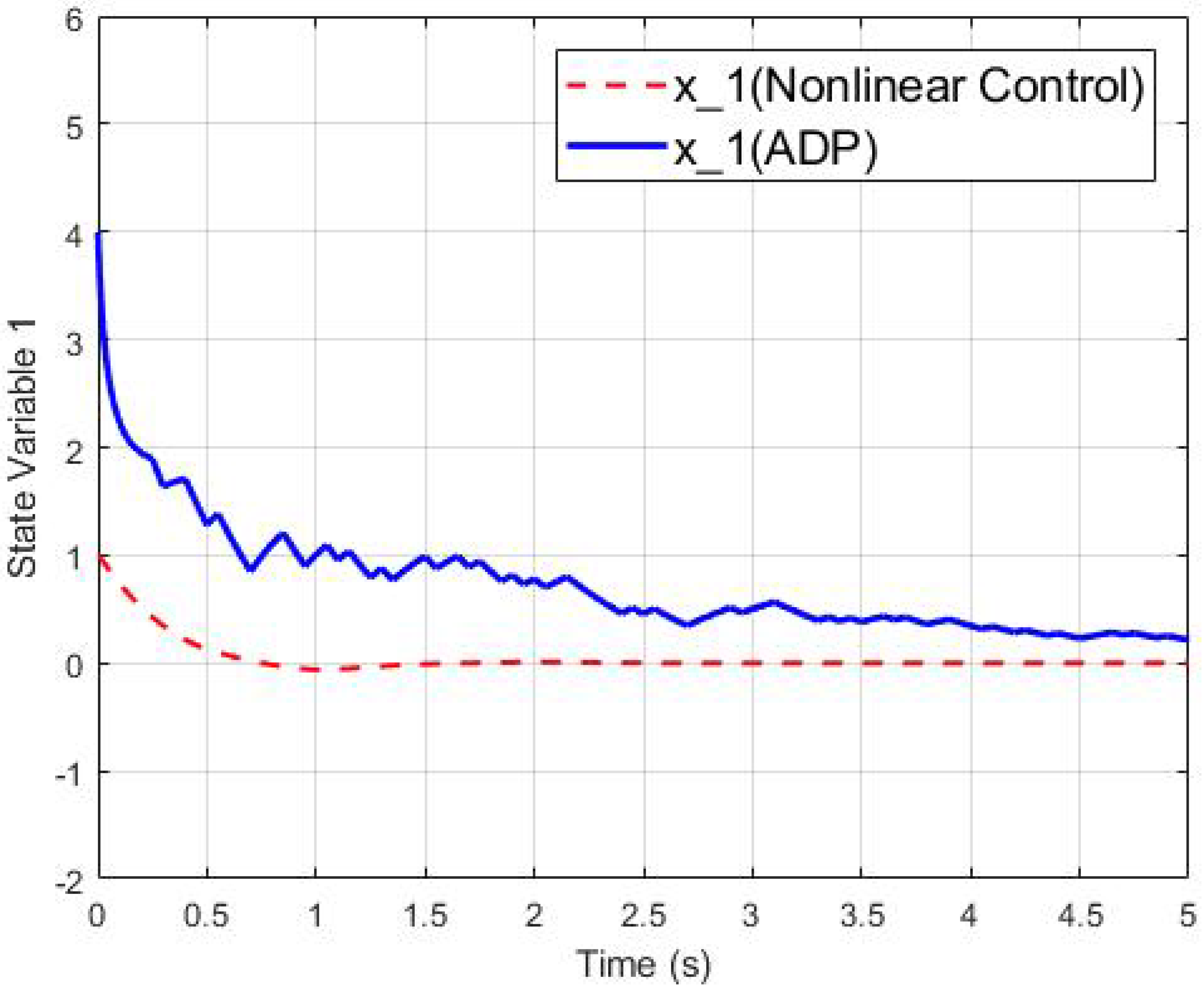
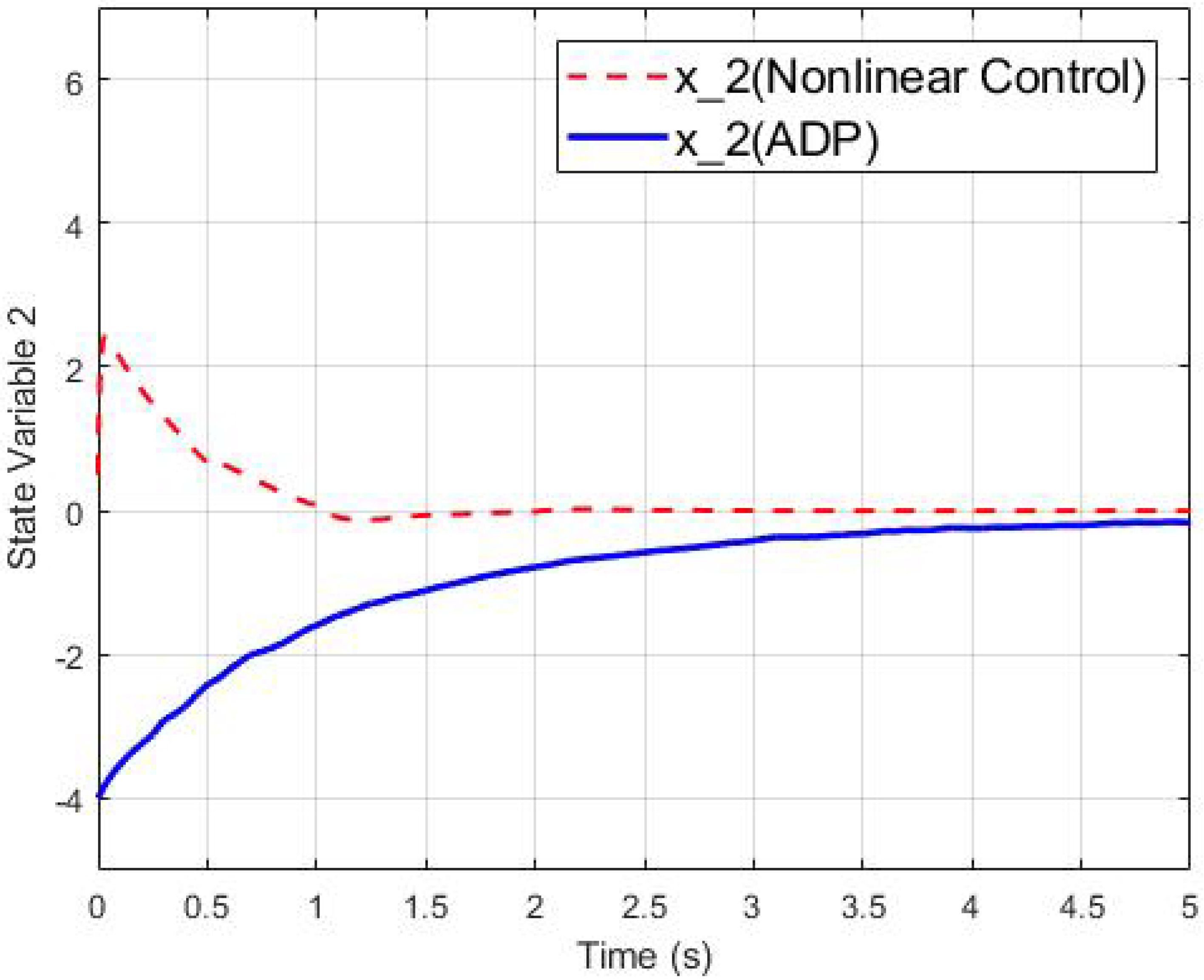
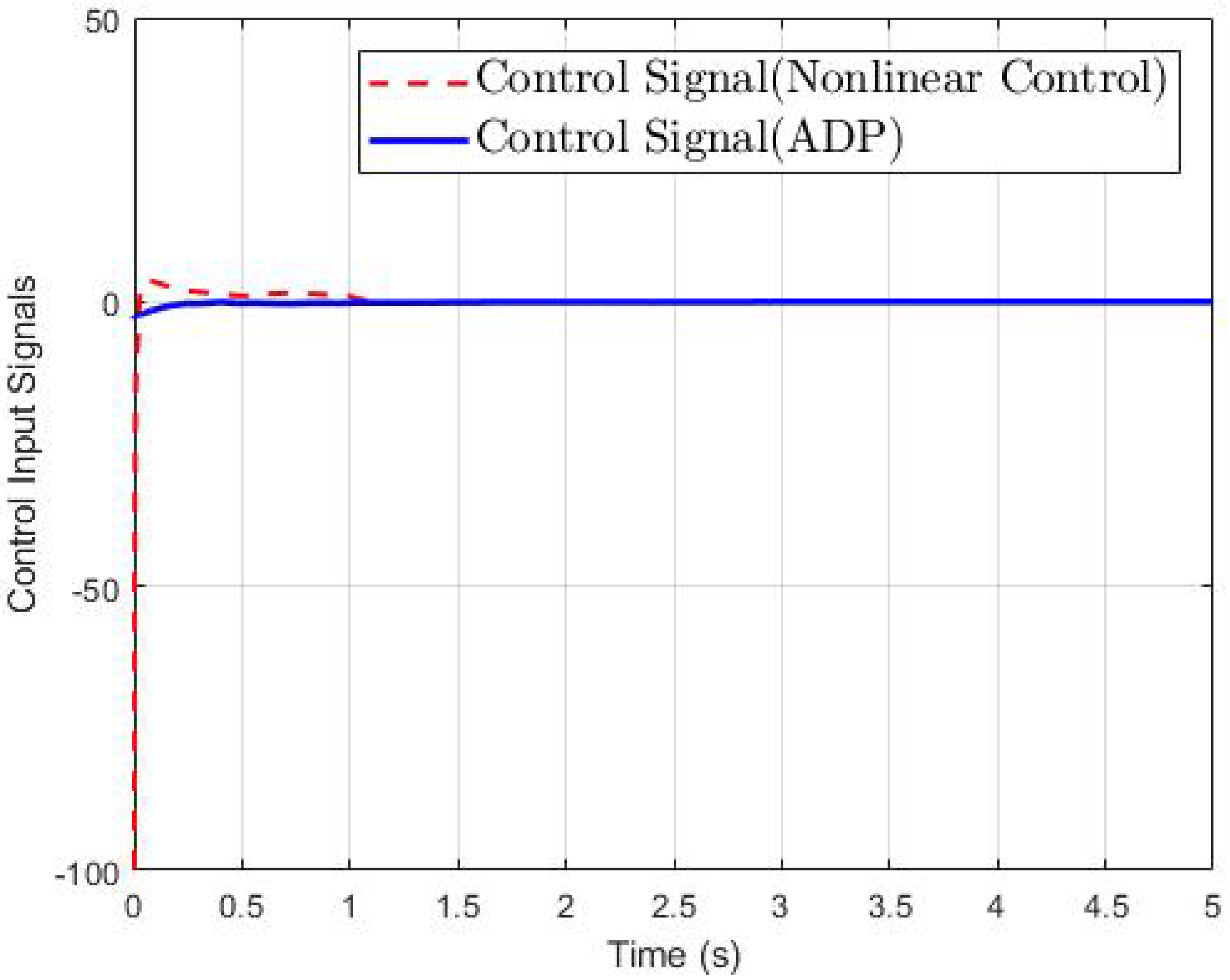
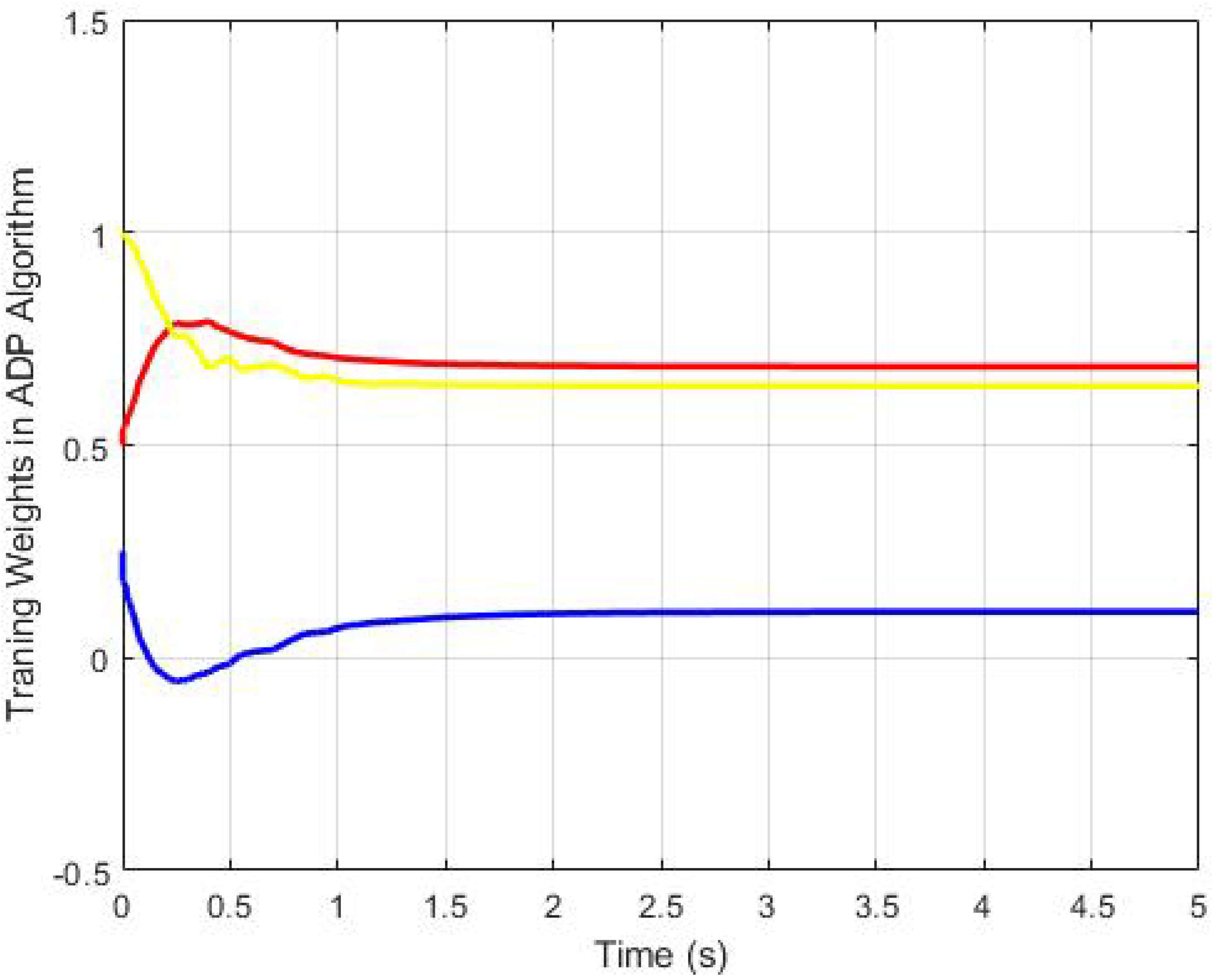
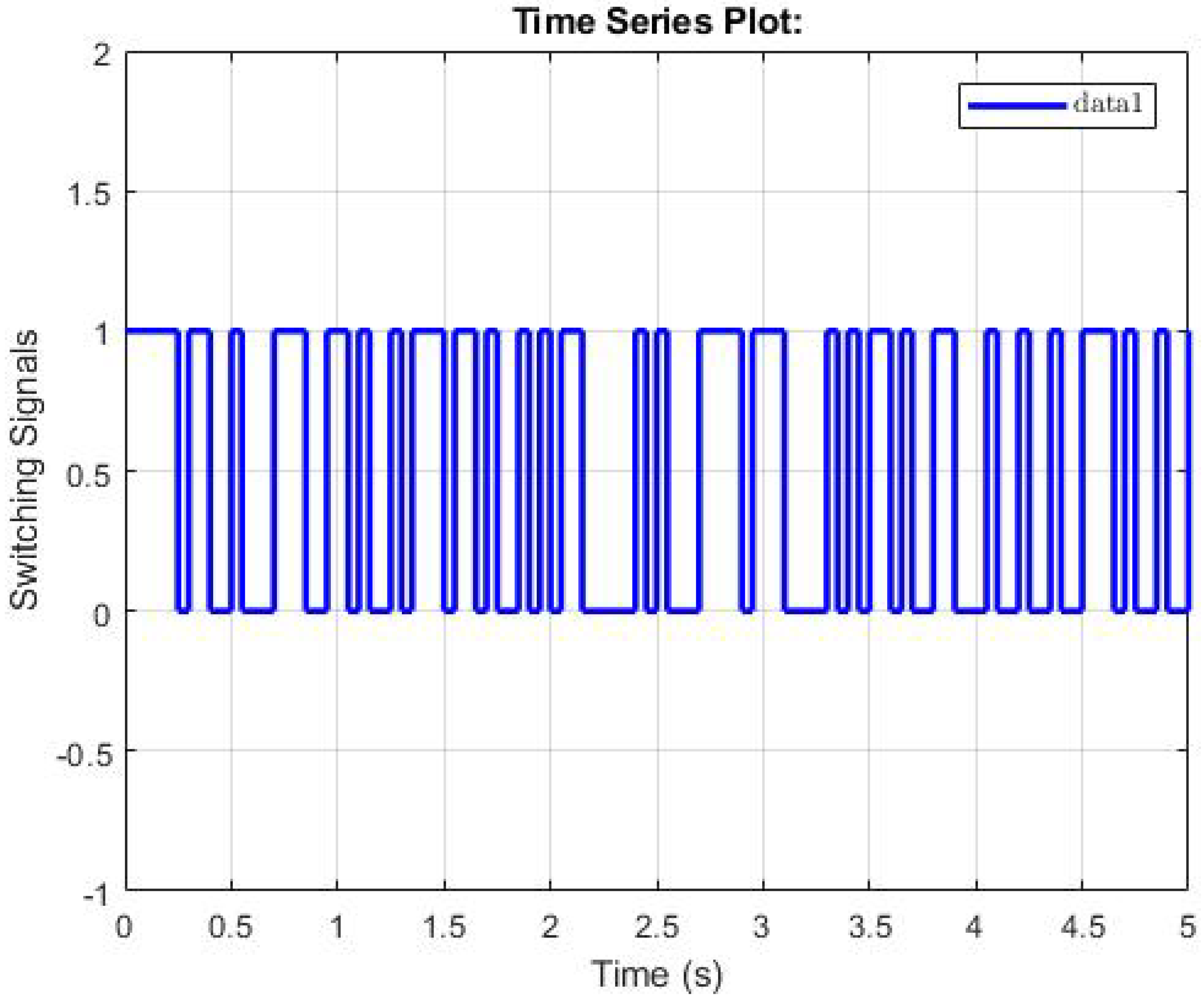
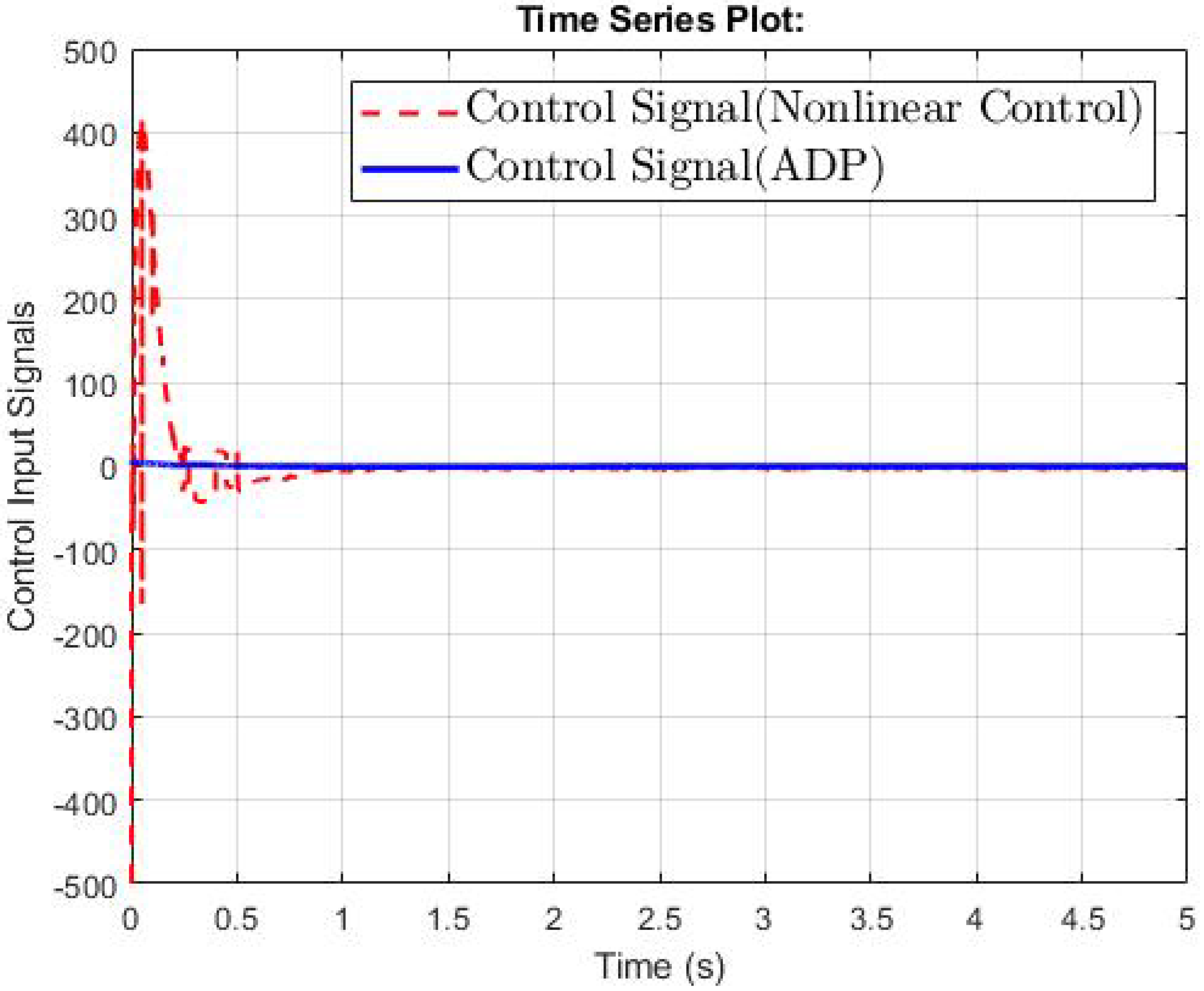
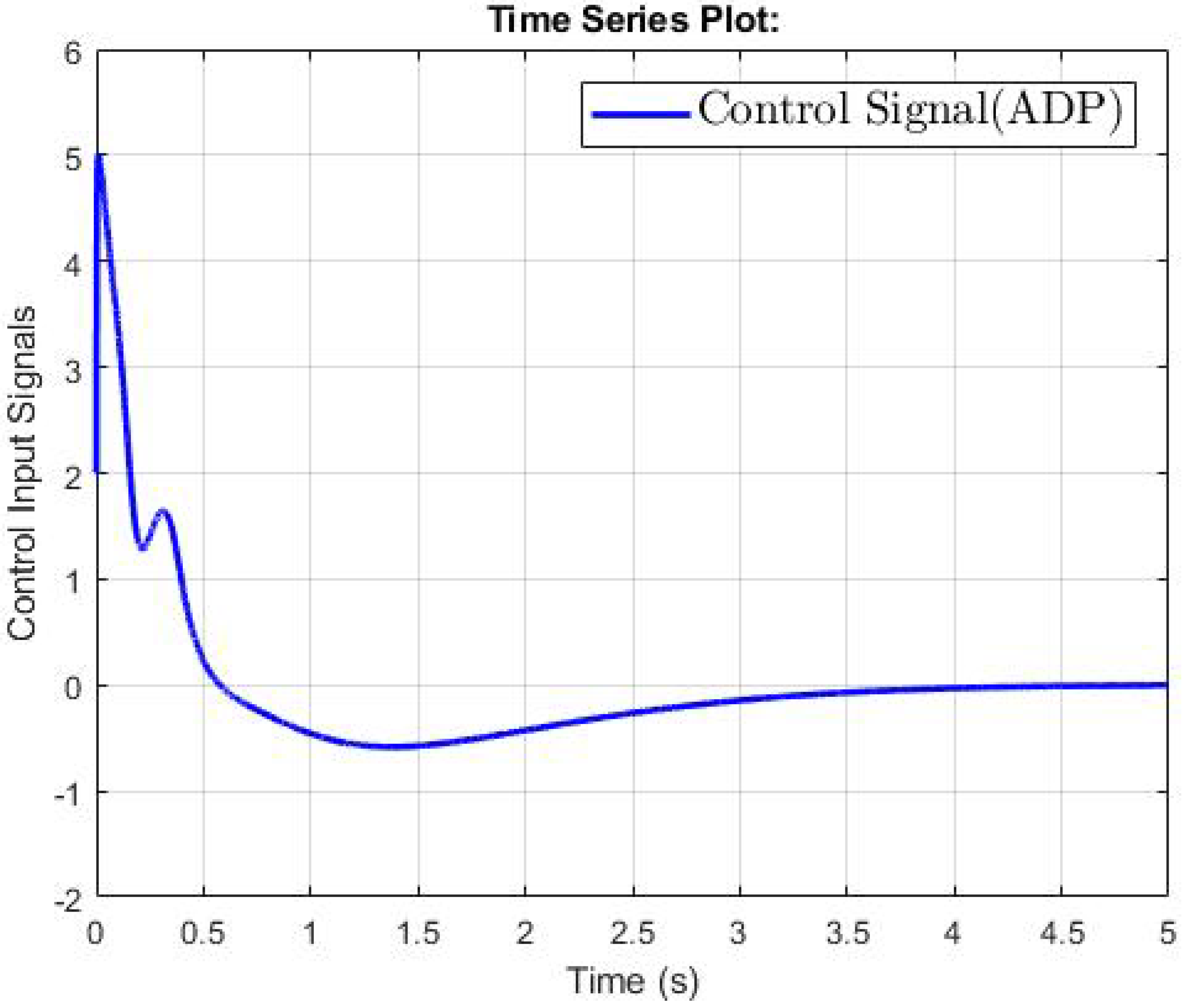
4.1. The Second-Order Switched Nonlinear Systems
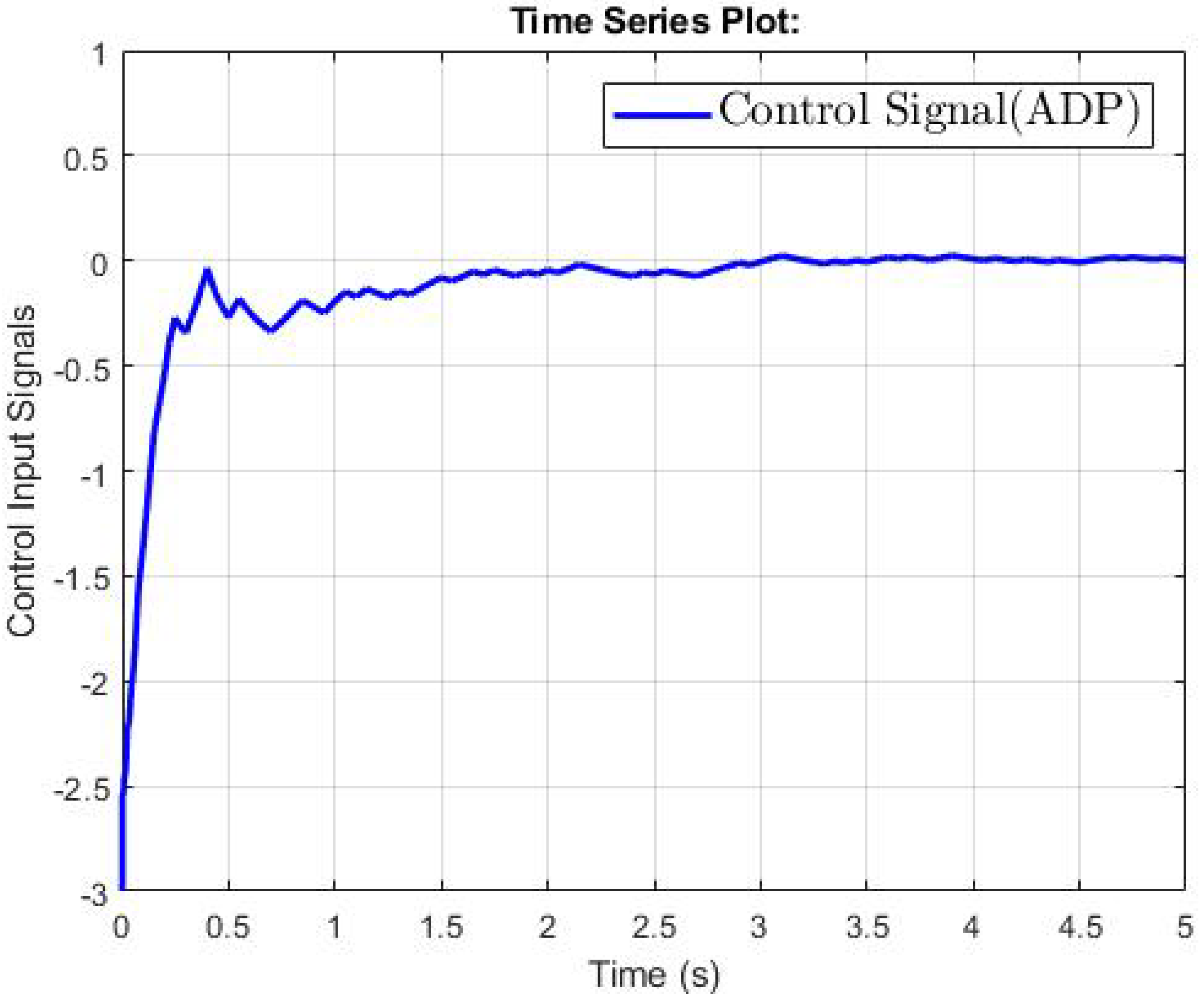
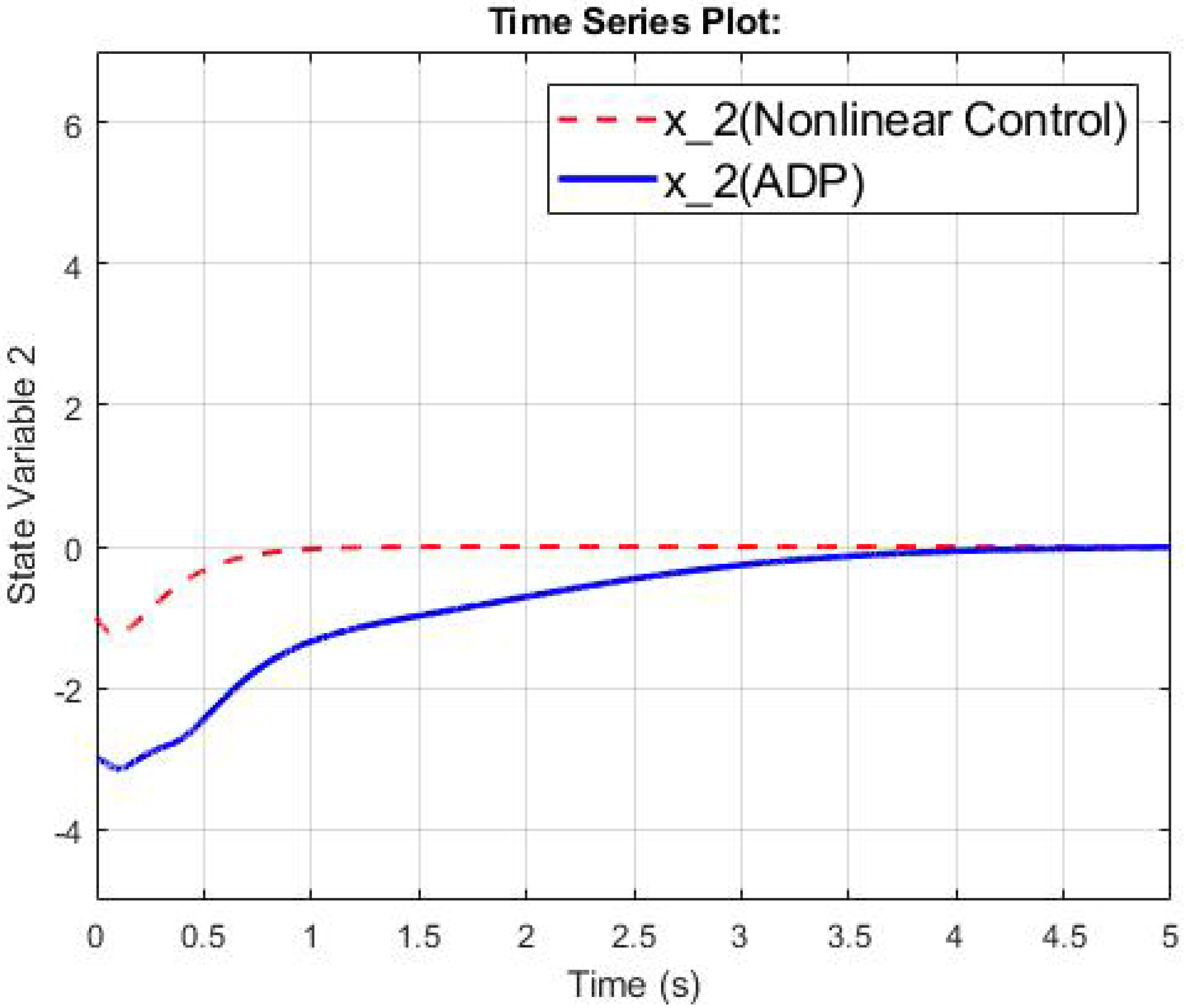
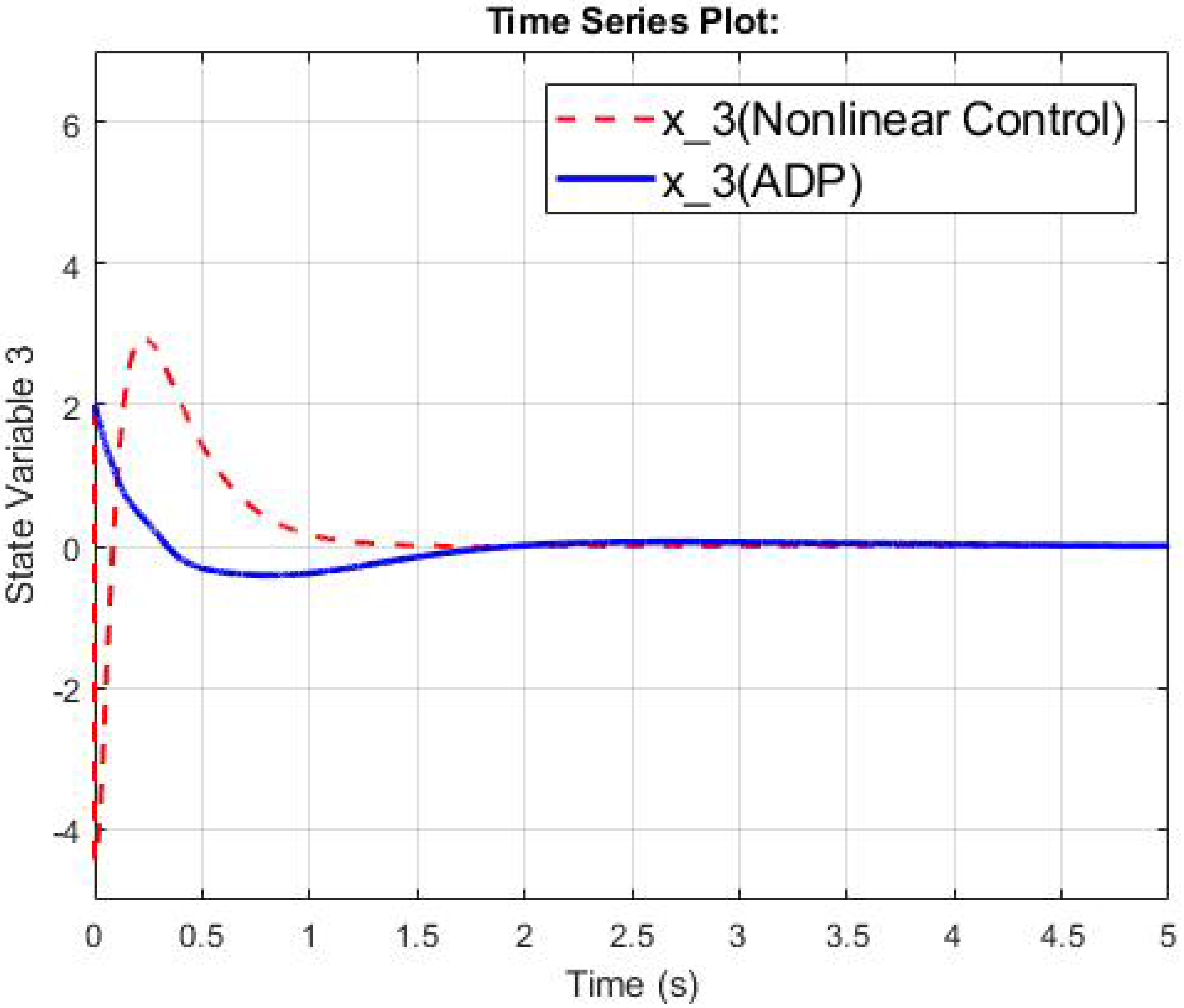
4.2. The Third-Order Switched Nonlinear Systems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ARL | Adaptive Reinforcement Learning |
| ADP | Adaptive Dynamic Programming |
| UUB | Uniformly Ultimately Bounded |
| NNs | Neural Networks |
| HJB | Hamilton–Jacobi–Bellman |
References
- Loschi, H.; Smolenski, R.; Lezynski, P.; Nascimento, D.; Demidova, G. Aggregated Conducted Electromagnetic Interference Generated by DC/DC Converters with Deterministic and Random Modulation. Energies 2020, 13, 3698. [Google Scholar] [CrossRef]
- Bakeer, A.; Chub, A.; Vinnikov, D. Step-Up Series Resonant DC–DC Converter with Bidirectional-Switch- Based Boost Rectifier for Wide Input Voltage Range Photovoltaic Applications. Energies 2020, 13, 3747. [Google Scholar] [CrossRef]
- Premkumar, M.; Subramaniam, U.; Haes Alhelou, H.; Siano, P. Design and Development of Non-Isolated Modified SEPIC DC-DC Converter Topology for High-Step-Up Applications: Investigation and Hardware Implementation. Energies 2020, 13, 3960. [Google Scholar] [CrossRef]
- Korkh, O.; Blinov, A.; Vinnikov, D.; Chub, A. Review of Isolated Matrix Inverters: Topologies, Modulation Methods and Applications. Energies 2020, 13, 2394. [Google Scholar] [CrossRef]
- Chen, B.-Y.; Shangguan, X.-C.; Jin, L.; Li, D.-Y. An Improved Stability Criterion for Load Frequency Control of Power Systems with Time-Varying Delays. Energies 2020, 13, 2101. [Google Scholar] [CrossRef]
- Zhang, L.; Xiang, W. Mode-identifying time estimation and switching-delay tolerant control for switched systems: An elementary time unit approach. Automatica 2016, 64, 174–181. [Google Scholar] [CrossRef]
- Yuan, S.; Zhang, L.; De Schutter, B.; Baldi, S. A novel Lyapunov function for a non-weighted L2 gain of asynchronously switched linear systems. Automatica 2018, 87, 310–317. [Google Scholar] [CrossRef]
- Xiang, W.; Lam, J.; Li, P. On stability and H∞ control of switched systems with random switching signals. Automatica 2018, 95, 419–425. [Google Scholar] [CrossRef]
- Lin, J.; Zhao, X.; Xiao, M.; Shen, J. Stabilization of discrete-time switched singular systems with state, output and switching delays. J. Frankl. Inst. 2019, 356, 2060–2089. [Google Scholar] [CrossRef]
- Briat, C. Convex conditions for robust stabilization of uncertain switched systems with guaranteed minimum and mode-dependent dwell-time. Syst. Control. Lett. 2015, 78, 63–72. [Google Scholar] [CrossRef]
- Lian, J.; Li, C. Event-triggered control for a class of switched uncertain nonlinear systems. Syst. Control. Lett. 2020, 135, 104592. [Google Scholar] [CrossRef]
- Vu, T.A.; Nam, D.P.; Huong, P.T.V. Analysis and control design of transformerless high gain, high efficient buck-boost DC-DC converters. In Proceedings of the 2016 IEEE International Conference on Sustainable Energy Technologies (ICSET), Hanoi, Vietnam, 14–16 November 2016; pp. 72–77. [Google Scholar]
- Nam, D.P.; Thang, B.M.; Thanh, N.T. Adaptive Tracking Control for a Boost DC–DC Converter: A Switched Systems Approach. In Proceedings of the 2018 4th International Conference on Green Technology and Sustainable Development (GTSD), Ho Chi Minh City, Vietnam, 23–24 November 2018; pp. 702–705. [Google Scholar]
- Thanh, N.T.; Sam, P.N.; Nam, D.P. An Adaptive Backstepping Control for Switched Systems in presence of Control Input Constraint. In Proceedings of the 2019 International Conference on System Science and Engineering (ICSSE), Quang Binh, Vietnam, 19–21 July 2019; pp. 196–200. [Google Scholar]
- Chiang, M.-L.; Fu, L.-C. Adaptive stabilization of a class of uncertain switched nonlinear systems with backstepping control. Automatica 2014, 50, 2128–2135. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Vrabie, D.; Lewis, F.L. Online adaptive algorithm for optimal control with integral reinforcement learning. Int. J. Robust Nonlinear Control. 2014, 24, 2686–2710. [Google Scholar] [CrossRef]
- Bai, W.; Zhou, Q.; Li, T.; Li, H. Adaptive reinforcement learning neural network control for uncertain nonlinear system with input saturation. IEEE Trans. Cybern. 2019, 50, 3433–3443. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Xu, H. Adaptive optimal dynamic surface control of strict-feedback nonlinear systems with output constraints. J. Frankl. Inst. 2020, 30, 2059–2078. [Google Scholar] [CrossRef]
- Lv, Y.; Na, J.; Yang, Q.; Wu, X.; Guo, Y. Online adaptive optimal control for continuous-time nonlinear systems with completely unknown dynamics. Int. J. Control 2016, 89, 99–112. [Google Scholar] [CrossRef]
- Chen, C.; Modares, H.; Xie, K.; Lewis, F.L.; Wan, Y.; Xie, S. Reinforcement learning-based adaptive optimal exponential tracking control of linear systems with unknown dynamics. IEEE Trans. Autom. Control 2019, 64, 4423–4438. [Google Scholar] [CrossRef]
- Yang, X.; Wei, Q. Adaptive Critic Learning for Constrained Optimal Event-Triggered Control with Discounted Cost. IEEE Trans. Neural Netw. Learn. Syst. 2020. [Google Scholar] [CrossRef]
- Wen, G.; Ge, S.S.; Chen, C.L.P.; Tu, F.; Wang, S. Adaptive tracking control of surface vessel using optimized backstepping technique. IEEE Trans. Cybern. 2018, 49, 3420–3431. [Google Scholar] [CrossRef]
- Wang, D.; Mu, C. Adaptive-critic-based robust trajectory tracking of uncertain dynamics and its application to a spring–mass–damper system. IEEE Trans. Ind. Electron. 2017, 65, 654–663. [Google Scholar] [CrossRef]
- Li, S.; Ding, L.; Gao, H.; Liu, Y.-J.; Huang, L.; Deng, Z. ADP-based online tracking control of partially uncertain time-delayed nonlinear system and application to wheeled mobile robots. IEEE Trans. Cybern. 2019, 50, 3182–3194. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.L.P.; Ge, S.S.; Yang, H.; Liu, X. Optimized adaptive nonlinear tracking control using actor–critic reinforcement learning strategy. IEEE Trans. Ind. Inform. 2019, 15, 4969–4977. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Ferraz, H. Model-free event-triggered control algorithm for continuous-time linear systems with optimal performance. Automatica 2018, 87, 412–420. [Google Scholar] [CrossRef]
- Gao, W.; Jiang, Y.; Jiang, Z.-P.; Chai, T. Output-feedback adaptive optimal control of interconnected systems based on robust adaptive dynamic programming. Automatica 2016, 72, 37–45. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y.; Gao, Z.; Sun, C. ADP-based robust tracking control for a class of nonlinear systems with unmatched uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Huang, Y. Optimal guaranteed cost control of uncertain non-linear systems using adaptive dynamic programming with concurrent learning. IET Control Theory Appl. 2018, 12, 1025–1035. [Google Scholar] [CrossRef]
- Tang, D.; Chen, L.; Tian, Z.F.; Hu, E. Modified value-function-approximation for synchronous policy iteration with single-critic configuration for nonlinear optimal control. Int. J. Control 2019, 1–13. [Google Scholar] [CrossRef]
- Fan, B.; Yang, Q.; Tang, X.; Sun, Y. Robust ADP design for continuous-time nonlinear systems with output constraints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2127–2138. [Google Scholar] [CrossRef]
- Chun, T.Y.; Lee, J.Y.; Park, J.B.; Choi, Y.H. Adaptive dynamic programming for discrete-time linear quadratic regulation based on multirate generalised policy iteration. Int. J. Control 2018, 91, 1223–1240. [Google Scholar] [CrossRef]
- Mu, C.; Wang, D. Neural-network-based adaptive guaranteed cost control of nonlinear dynamical systems with matched uncertainties. Neurocomputing 2017, 245, 46–54. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dao, P.N.; Nguyen, H.Q.; Ngo, M.-D.; Ahn, S.-J. On Stability of Perturbed Nonlinear Switched Systems with Adaptive Reinforcement Learning. Energies 2020, 13, 5069. https://doi.org/10.3390/en13195069
Dao PN, Nguyen HQ, Ngo M-D, Ahn S-J. On Stability of Perturbed Nonlinear Switched Systems with Adaptive Reinforcement Learning. Energies. 2020; 13(19):5069. https://doi.org/10.3390/en13195069
Chicago/Turabian StyleDao, Phuong Nam, Hong Quang Nguyen, Minh-Duc Ngo, and Seon-Ju Ahn. 2020. "On Stability of Perturbed Nonlinear Switched Systems with Adaptive Reinforcement Learning" Energies 13, no. 19: 5069. https://doi.org/10.3390/en13195069
APA StyleDao, P. N., Nguyen, H. Q., Ngo, M.-D., & Ahn, S.-J. (2020). On Stability of Perturbed Nonlinear Switched Systems with Adaptive Reinforcement Learning. Energies, 13(19), 5069. https://doi.org/10.3390/en13195069






