Experimental Research into the Evolution of Permeability of Sandstone under Triaxial Compression
Abstract
:1. Introduction
2. Test Materials and Equipment
3. The Mechanical Characteristics of Failure of Sandstone under Hydro-Mechanical Coupling
3.1. Failure Morphology
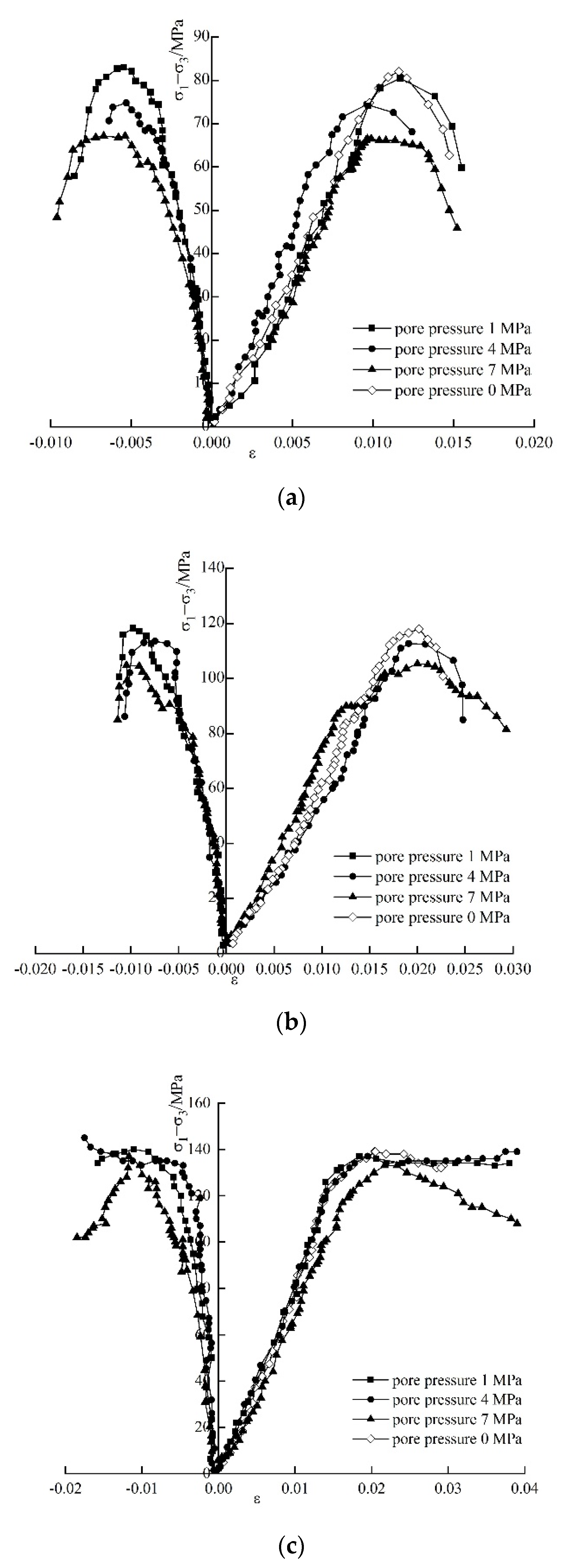
3.2. Stress–Strain Relationship
3.3. Relationships of Characteristic Stress with Confining Pressure and Seepage Pressure
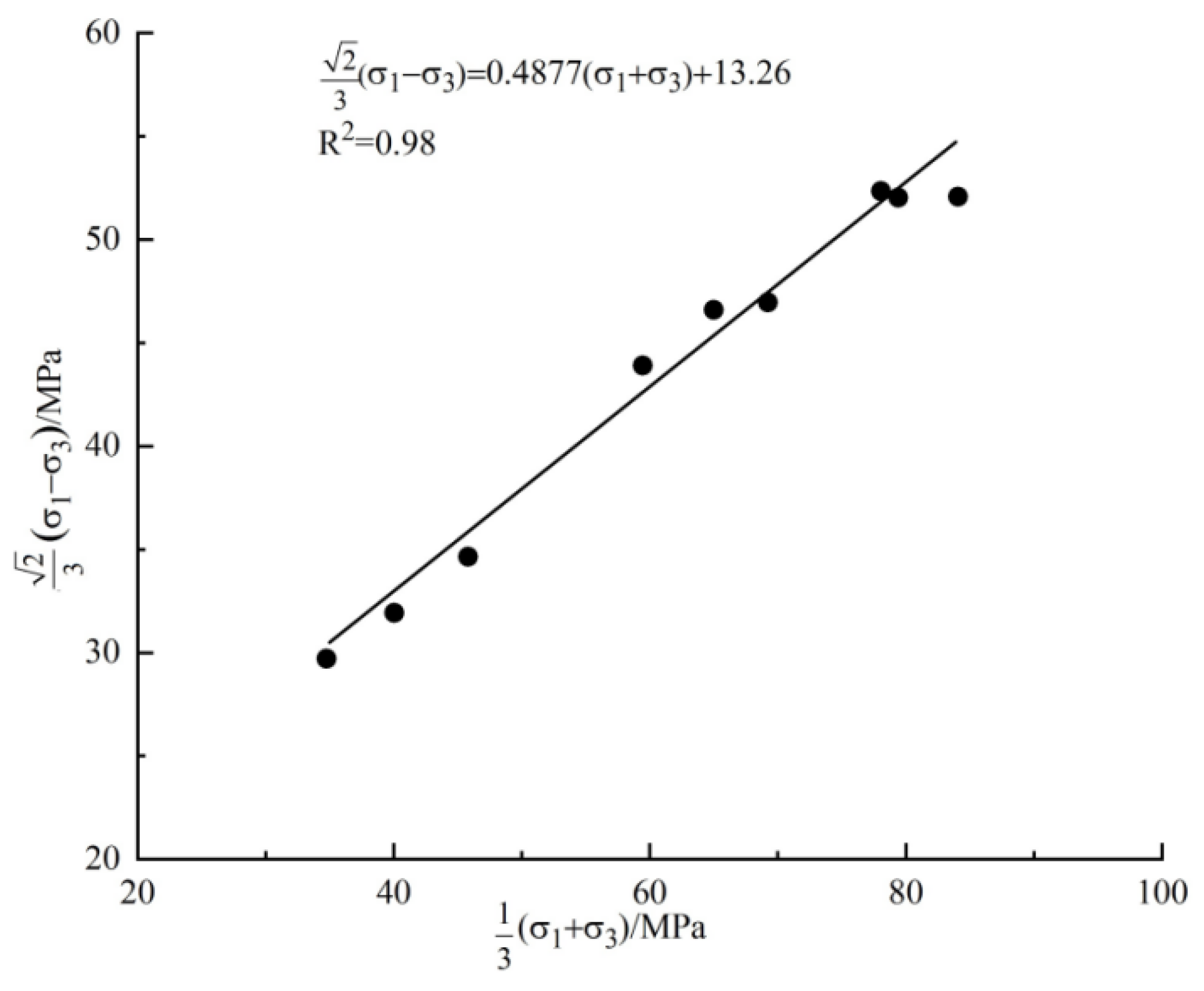
3.4. Failure Criterion
4. Evolution of Permeability of Sandstone under Darcy Flow
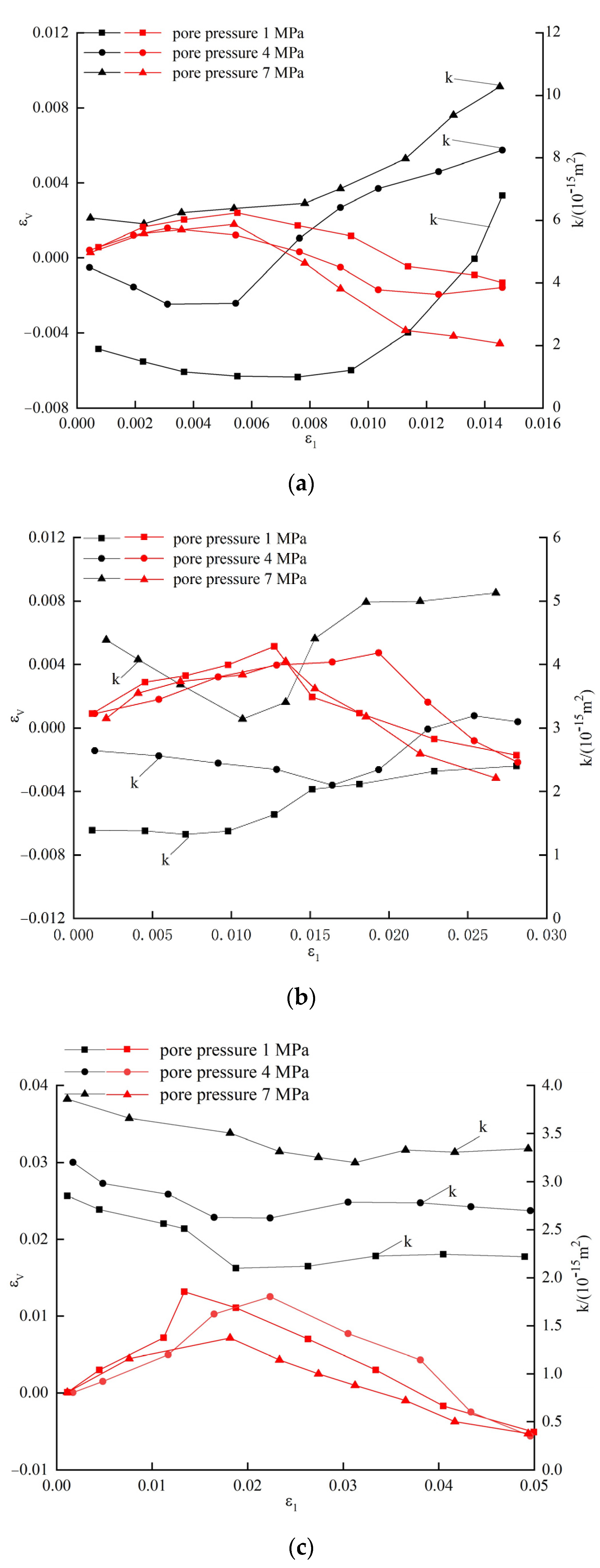
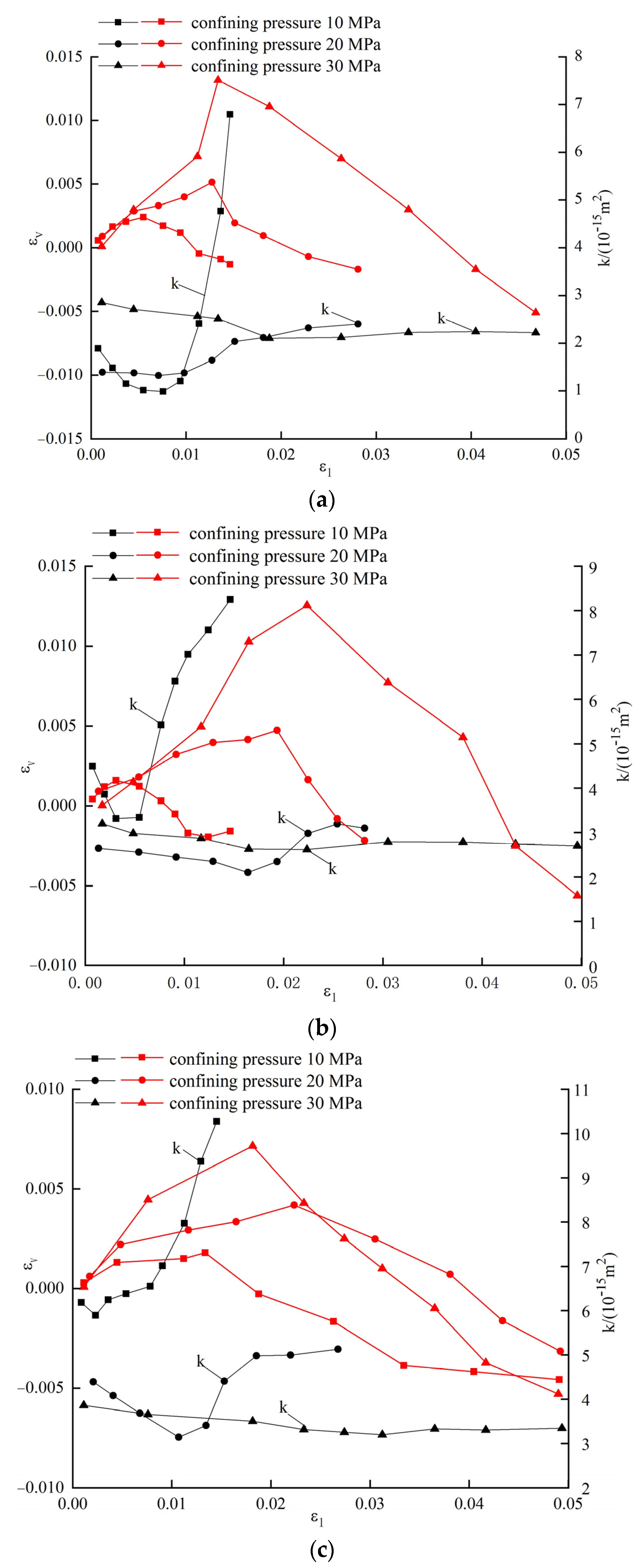
4.1. Relationship between Permeability and Axial Strain
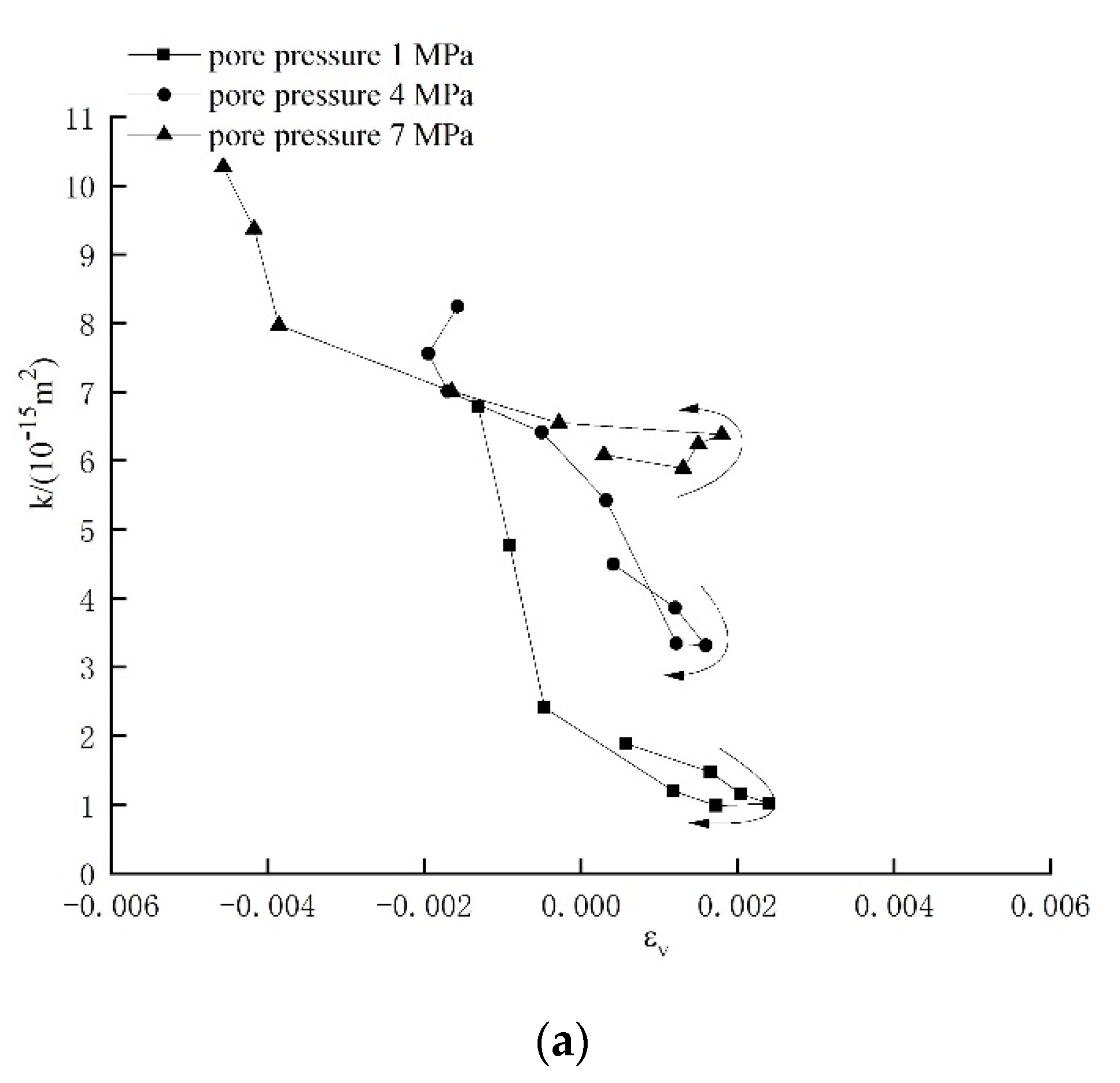
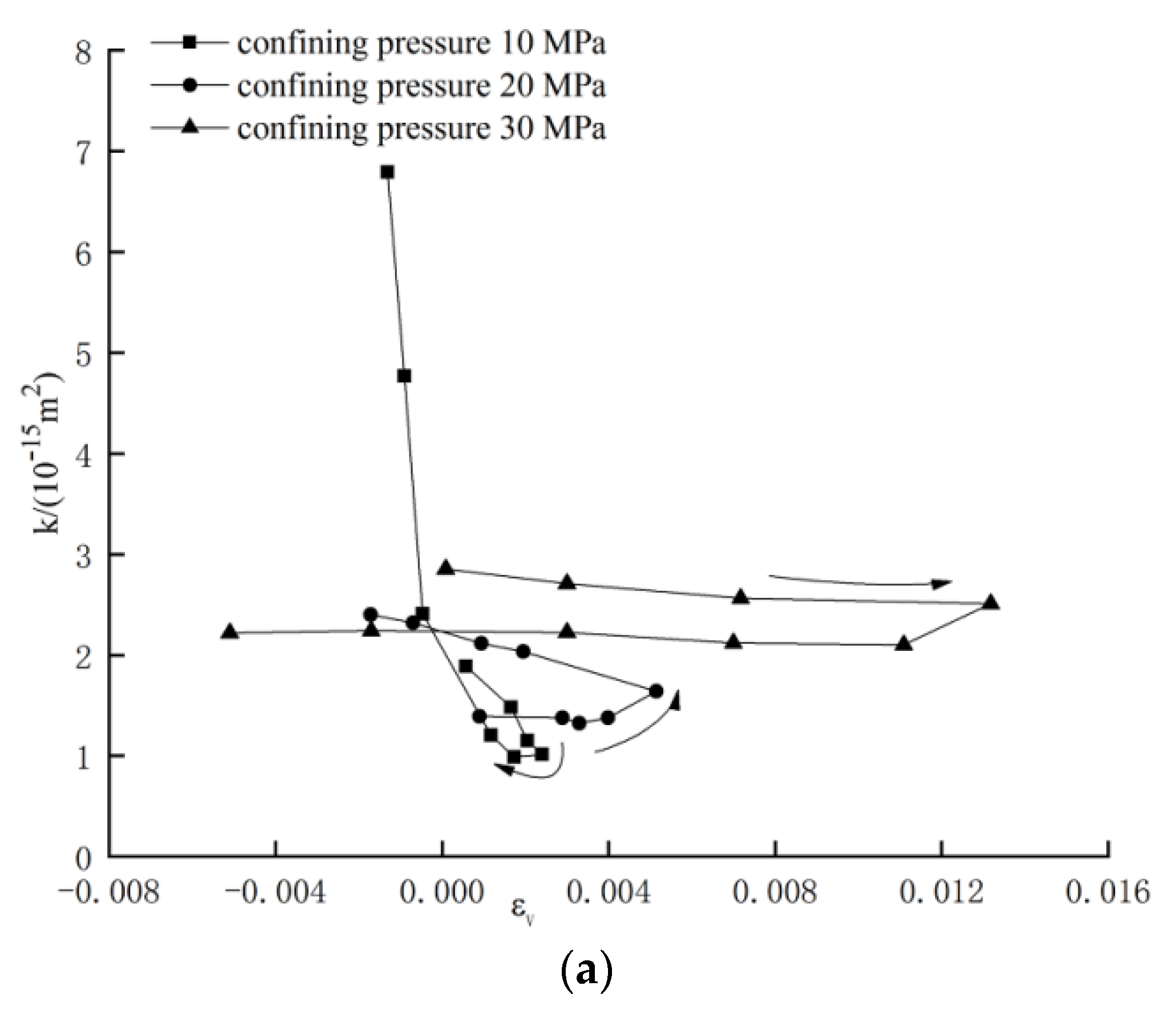
4.2. Relationship between Permeability and Volumetric Strain
5. Evolution of Permeability of Sandstone under Non-Darcy Flow
5.1. Calculation of Non-Darcy Seepage
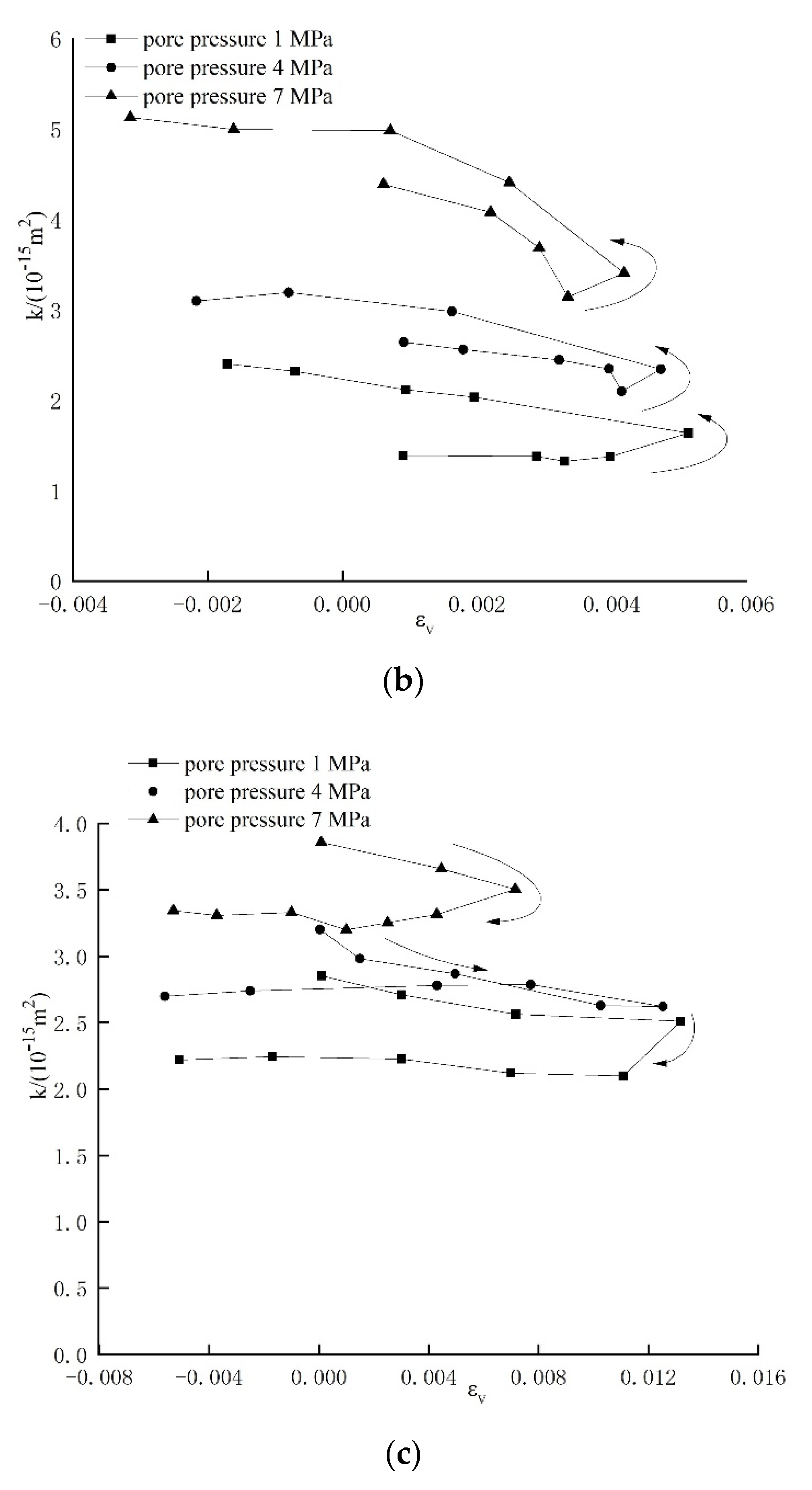
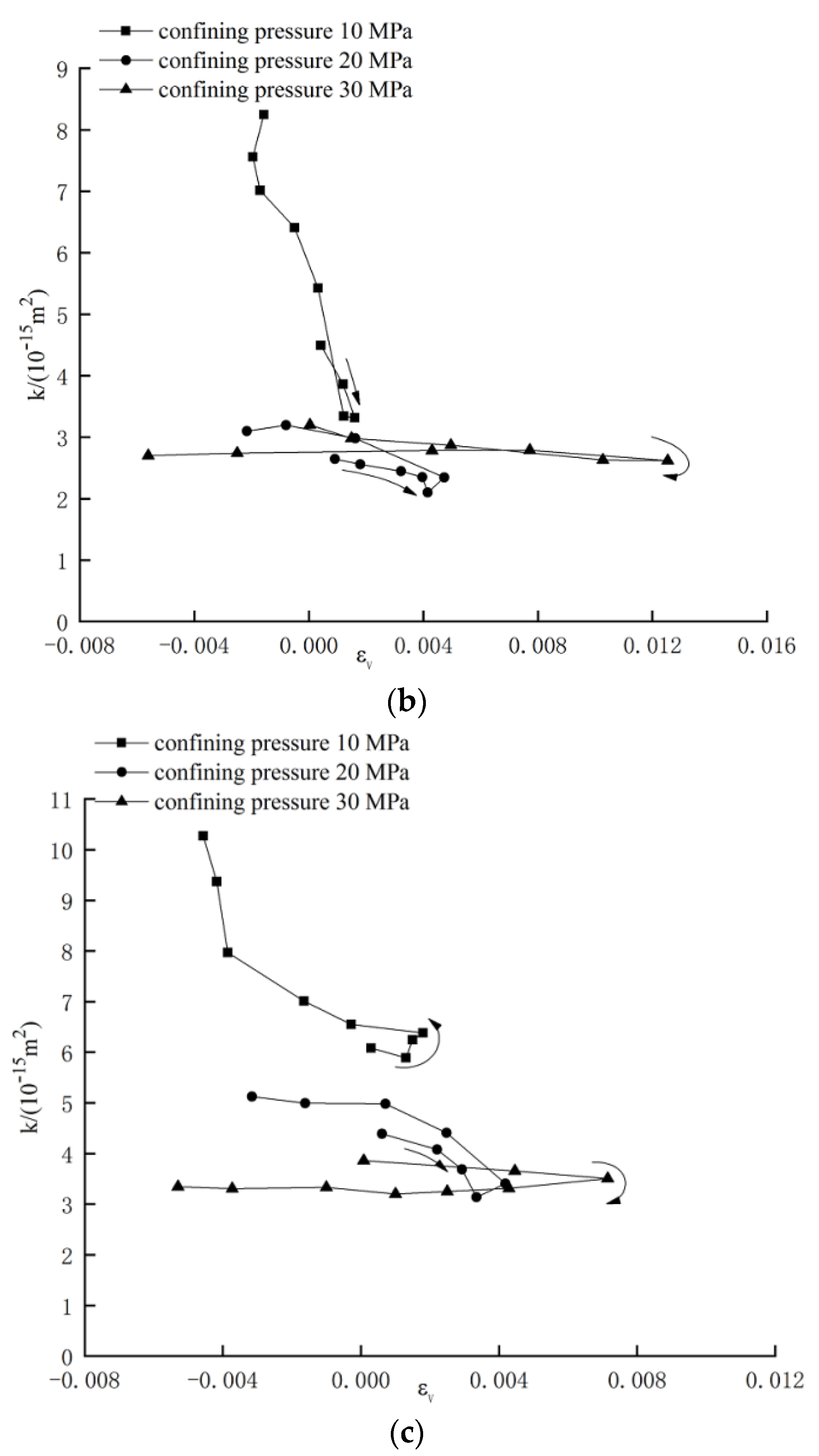
5.2. Changes in Permeability during Non-Darcy Seepage
6. Discussion
6.1. Explanation of Certain Behavioral Phenomena
6.2. Existing Problems
7. Conclusions
- The permeability first decreases and exhibits two distinct trends: a V-shaped increase and a S-shaped plateau in the non-linear stage. The greater the seepage pressure, the more obvious the V-shaped trend in permeability. With increasing confining pressure, the variation in the permeability gradually changes from V-shaped to S-shaped.
- Compared with the case at a high confining pressure, under low confining pressure, the increase in permeability appears earlier, and the permeability rises faster. Moreover, the decrease in permeability happens faster and the time at which it increases again is earlier. The confining pressure exerts a greater effect on the permeability than the seepage pressure.
- In comparison with the axial strain, volumetric strain better reflects any changes in permeability during compaction and dilation of the specimens. In the compaction stage, the permeability first decreases, then stabilizes with decreasing volumetric strain. Upon dilation of the specimen, the permeability increases rapidly with increasing volumetric strain.
- The crack initiation stress, dilation stress, and peak stress all increase with the effective confining pressure, while decreasing with increasing seepage pressure. Failure of sandstone specimens under hydro-mechanical coupling is governed by the Mogi–Coulomb strength criterion.
- Permeabilities calculated based on Darcy flow and non-Darcy flow vary within the same range, while the changes therein differ significantly in terms of process: under non-Darcy flow, dissipation of pore pressure gradient and changes in permeability are significantly non-linear.
Author Contributions
Funding
Conflicts of Interest
References
- Tsang, C.F.; Stephansson, O.; Jing, L.; Kautsky, F. Decovalex project: From 1992 to 2007. Environ. Geol. 2009, 57, 1221–1237. [Google Scholar] [CrossRef]
- Zhao, Y.S. Multi-field coupling theory of porous media and its engineering applications. Sci. Press 2010, 27, 171–230. [Google Scholar]
- Ferfera, F.M.R.; Sarda, J.P.; Bouteca, M.; Vincke, O. Experimental study of monophasic permeability changes under various stress paths. Int. J. Rock Mech. Min. Sci. 1997, 34, 1–12. [Google Scholar] [CrossRef]
- Wang, H.L.; Xu, W.Y.; Shao, J.F.; Skoczylas, F. The gas permeability properties of low permeabilit rock in the process of triaxial compression test. Mater. Lett. 2014, 116, 386–388. [Google Scholar] [CrossRef]
- Liu, L.; Xu, W.Y.; Wang, H.L.; Wang, W.; Wang, R.B. Permeability evolution of granite gneiss during triaxial creep tests. Rock Mech. Rock Eng. 2016, 49, 3455–3462. [Google Scholar] [CrossRef]
- Park, H.D.; Wang, J.A. Fluid permeability of sedimentary rocks in a complete stress-strain process. Eng. Geol. 2012, 63, 291–300. [Google Scholar]
- Otto, S.; Till, P.; Hartmut, K. Development of damage and permeability in deforming rock salt. Eng. Geol. 2001, 61, 163–180. [Google Scholar]
- Tzelepis, V.; Moutsopoulos, K.N.; Papaspyros, J.N.E.; Tsihrintzis, V.A. Experimental investigation of flow behavior in smooth and rough artificial fractures. J. Hydrol. 2015, 521, 108–118. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, H.; Tang, Z. Forchheimer flow to a well-considering time-dependent critical radius. Hydrol. Earth Syst. Sci. 2014, 18, 2437–2448. [Google Scholar] [CrossRef] [Green Version]
- Aulisa, E.; Ibragimov, A.; Toka, M. Geometric framework for modeling nonlinear flows inporous media and its applications in engineering. Nonlinear Anal. Real World Appl. 2010, 11, 1734–1751. [Google Scholar] [CrossRef]
- Yu, J.; Liu, G.Y.; Cai, Y.; Zhou, J.F. Time-dependent deformation mechanism for swelling soft-rock tunnels in coal mines and its mathematical deduction. Int. J. Geomech. 2020, 20, 04019186. [Google Scholar] [CrossRef]
- Tang, J.; Shao, J.F.; Xu, W.Y.; Zhou, C.B. Experimental investigation and micromechanical analysis of damage and permeability variation in brittle rocks. Int. J. Rock Mech. Min. Sci. 2010, 47, 703–713. [Google Scholar]
- Oda, M.; Takemura, T.; Aoki, T. Damage growth and permeability change in triaxial compression tests of Inada granite. Mech. Mater. 2002, 34, 313–331. [Google Scholar] [CrossRef]
- Mitchell, T.M.; Faulkner, D.R. Towards quantifying the matrix permeability of fault damage zones in low porosity rocks. Earth Planet. Sci. Lett. 2012, 339, 24–31. [Google Scholar] [CrossRef]
- Alkan, H. Percolation model for dilatancy-induced permeability of the excavation damaged zones in rock salt. Int. J. Rock Mech. Min. Sci. 2009, 46, 69–79. [Google Scholar] [CrossRef]
- Nara, Y.; Meredith, P.G.; Yoneda, T.; Kaneko, K. Influence of macro-fractures and microfracture on permeability and elastic wave velocities in basalt at elevated pressure. Tectonophysics 2011, 50, 52–59. [Google Scholar] [CrossRef] [Green Version]
- Pereira, J.M.; Arson, C. Retention and permeability properties of damaged porous rocks. Comput. Geotech. 2013, 48, 272–282. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.B.; Xie, S.Y.; Shao, J.F.; Conil, N. Multi-step triaxial compressive creep behaviour and induced gas permeability change of clay-rich rock. Géotechnique 2018, 68, 281–289. [Google Scholar] [CrossRef]
- Li, S.P.; Li, Y.S.; Wu, Z.Y. The permeability-strain equations relating to complete stress-strain path of the rock. Chin. J. Geotech. Eng. 1995, 17, 13–19. [Google Scholar]
- Pradip Kumar, G.N.; Venkataraman, P. Non-Darcy converging flow through coarse granular media. J. Inst. Eng. Civ. Eng. Div. 1995, 76, 6–11. [Google Scholar]
- Legrand, J. Revisited analysis of pressure drop in flow through crushed rocks. J. Hydraul. Eng. 2002, 128, 1027–1031. [Google Scholar] [CrossRef]
- Ohnson, J.; Brown, S.; Steckman, H. Fluid flow and mixing in rough-walled fracture intersections. J. Geophys. Res. Solid Earth 2006, 111, 1–16. [Google Scholar] [CrossRef]
- Qian, J.Z.; Zhan, H.B.; Luo, S.H.; Zhao, W. Experimental evidence of scale-dependent hydraulic conductivity for fully developed turbulent flow in a single fracture. J. Hydrol. 2007, 339, 206–215. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Nemcik, J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures. J. Hydrol. 2013, 47, 139–151. [Google Scholar] [CrossRef]
- Zou, L.C.; Jing, L.R.; Cvetkovic, V. Roughness decomposition and nonlinear fluid flow in a single rock fracture. Int. J. Rock Mech. Min. Sci. 2015, 75, 102–118. [Google Scholar] [CrossRef]
- Wen, Z.; Huang, G.; Zhan, H. An analytical solution for non-Darcian flow in a confined aquifer using the power law functione. Adv. Water Resour. 2008, 31, 44–55. [Google Scholar] [CrossRef]
- Wu, Y.S. Numerical Simulation of Single-phase and Multiphase Non-Darcy Flow in Porous and Fractured Reservoirs. Transp. Porous Media 2002, 49, 209–240. [Google Scholar] [CrossRef]
- Zhou, H.W.; Yang, S. Fractional derivative approach to non-Darcian flow in porous media. J. Hydrol. 2018, 566, 910–918. [Google Scholar] [CrossRef]
- Chen, Y.D.; Lian, H.J.; Liang, W.G.; Yang, J.F.; Nguyen, V.P.; Bordas, S.P.A. The influence of fracture geometry variation on non-Darcy flow in fractures under confining stresses. Int. J. Rock Mech. Min. Sci. 2019, 113, 59–71. [Google Scholar] [CrossRef]
- Qin, Y.P.; Luo, W.; Yang, X.B. Study on parameters quantification of Horkheimer equation and the critical point of Darcy transition to Non-Darcy flow. J. Southwest Jiao Tong Univ. 2018, 12, 1–8. [Google Scholar]
- Zeng, F.H.; Zhao, G. The optimal hydraulic fracture geometry under non-Darcy flow effects. J. Pet. Sci. Eng. 2010, 72, 143–157. [Google Scholar] [CrossRef]
- Yu, B.Y.; Chen, Z.Q.; Ding, Q.L.; Wang, L.Z. Non-Darcy flow seepage characteristics of saturated broken rocks under compression with lateral constraint. Int. J. Rock Mech. Min. Sci. 2016, 26, 1145–1151. [Google Scholar] [CrossRef]
- Jin, Y.; Li, H.; Chen, X.; Cai, Y.Y.Y.; Wu, N.; Mu, K. Triaxial experimental study of associated permeability-deformation of sandstone uner hydro-mechanical coupling. Chin. J. Rock Mech. Eng. 2013, 32, 1203–1213. [Google Scholar]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Zhang, L.M.; Cong, Y.; Meng, F.Z.; Guo, S. Energy evolution analysis and failure criteria for rock under different stress paths. Acta Geotech. 2020. [Google Scholar] [CrossRef]
- Mogi, K. Fracture and flow of rocks under high triaxial compression. J. Geophys. Res. 1971, 76, 1255–1269. [Google Scholar] [CrossRef]
- Zhang, L.M.; Gao, S.; Wang, Z.Q.; Ren, M. Analysis on deformation characteristics and energy dissipation of marble under different unloading rates. Teh. Vjesn. 2014, 21, 987–993. [Google Scholar]
- Sun, M.G.; Huang, X.W.; Li, T.Z.; Lei, G.Y.; Mao, X.B. Seepage properties of non-Darcy flow in complete failure process of limestone. Chin. J. Rock Mech. Eng. 2006, 25, 484–491. [Google Scholar]
- Qian, J.Z.; Wang, M.; Zhang, Y.; Zhao, W.D. Experimental study of the transition from non-Darcian to Darcy behavior for flow through a single fracture. J. Hydrodyn. 2015, 27, 679–688. [Google Scholar] [CrossRef]
- Quinn, P.M.; Cherry, J.A.; Parker, B.L. R Quantification of non-Darcian flow observed during packer testing in fractured sedimentary rock. Water Resour. Res. 2011, 47, 1–15. [Google Scholar] [CrossRef]







| Confining Pressure/MPa | Seepage Pressure/MPa | Initial Permeability/10−15 m2 | Peak Strength/MPa |
|---|---|---|---|
| 0 | - | - | 66.9 |
| 10 | - | 85.3 | |
| 20 | 0 | 120.2 | |
| 30 | 140.2 | ||
| 10 | 1 | 1.79 | 82.7 |
| 10 | 4 | 4.43 | 74.1 |
| 10 | 7 | 6.27 | 67.1 |
| 20 | 1 | 0.53 | 119.0 |
| 20 | 4 | 1.44 | 114.1 |
| 20 | 7 | 2.64 | 106.0 |
| 30 | 1 | 0.34 | 138.9 |
| 30 | 4 | 0.35 | 134.6 |
| 30 | 7 | 0.36 | 134.4 |
| Effective Confining Pressure/MPa | Crack Initiation Stress/MPa | Dilation Initiation Stress/MPa | Peak Stress/MPa |
|---|---|---|---|
| 3 | 46.1 | 53.6 | 67.1 |
| 6 | 52.2 | 64.3 | 74.1 |
| 9 | 52.4 | 70.4 | 82.7 |
| 13 | 80.1 | 95.8 | 106.0 |
| 16 | 81.2 | 96.5 | 114.1 |
| 19 | 78.2 | 96.0 | 119.0 |
| 23 | 94.5 | 115.7 | 134.4 |
| 26 | 92.2 | 121.0 | 134.6 |
| 29 | 90.5 | 121.4 | 138.9 |
| 10 | 55.8 | 72.3 | 85.3 |
| 20 | 79.1 | 98.0 | 120.2 |
| 30 | 95.1 | 121.5 | 140.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Jiang, S.; Yu, J. Experimental Research into the Evolution of Permeability of Sandstone under Triaxial Compression. Energies 2020, 13, 5065. https://doi.org/10.3390/en13195065
Zhang L, Jiang S, Yu J. Experimental Research into the Evolution of Permeability of Sandstone under Triaxial Compression. Energies. 2020; 13(19):5065. https://doi.org/10.3390/en13195065
Chicago/Turabian StyleZhang, Liming, Shengqun Jiang, and Jin Yu. 2020. "Experimental Research into the Evolution of Permeability of Sandstone under Triaxial Compression" Energies 13, no. 19: 5065. https://doi.org/10.3390/en13195065
APA StyleZhang, L., Jiang, S., & Yu, J. (2020). Experimental Research into the Evolution of Permeability of Sandstone under Triaxial Compression. Energies, 13(19), 5065. https://doi.org/10.3390/en13195065






