Investigation and Modeling of the Magnetic Nanoparticle Aggregation with a Two-Phase CFD Model
Abstract
1. Introduction
2. Micro-Domain Model
2.1. Magnetization
2.2. Forces Effecting the Particle
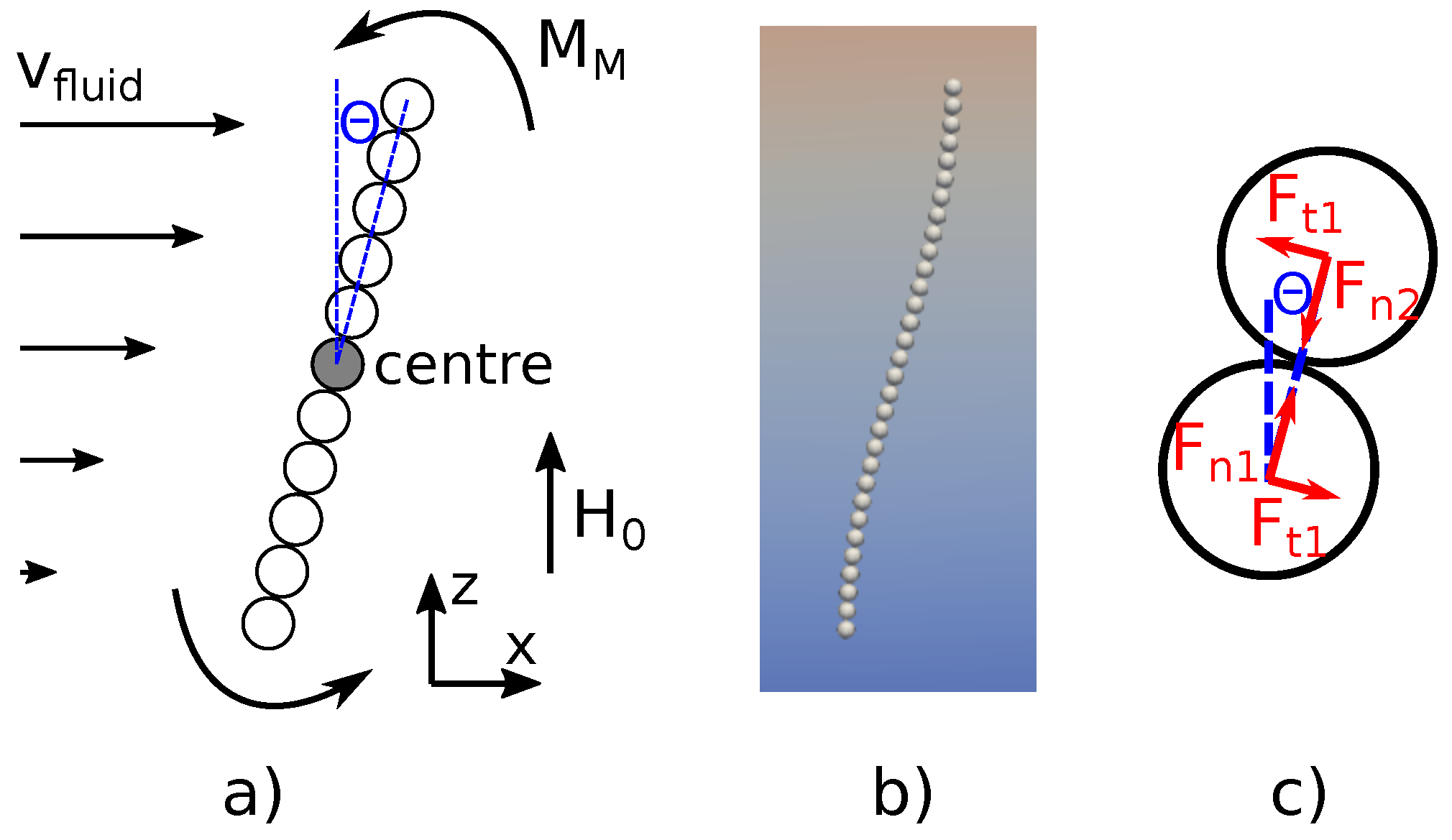
2.3. Chain Formulation
- The normal force between the particles is attractive until . This attractive force is the main reason for the chain formulation.
- The tangential force is 0 at , and it approximately linearly increases with the increasing at small angles.
3. The Two-Phase CFD Model
3.1. Governing Equations
3.2. Viscosity Model
3.3. Numerical Model
4. Experimental Setup
4.1. The Microfluidic Chip
4.2. Magnetic Nanoparticles
4.3. Measurement Setup
5. Experimental Results
5.1. Measurement of the MNP Aggregate in the Magnetic Field
5.2. Thermal Measurements
6. Numerical Results
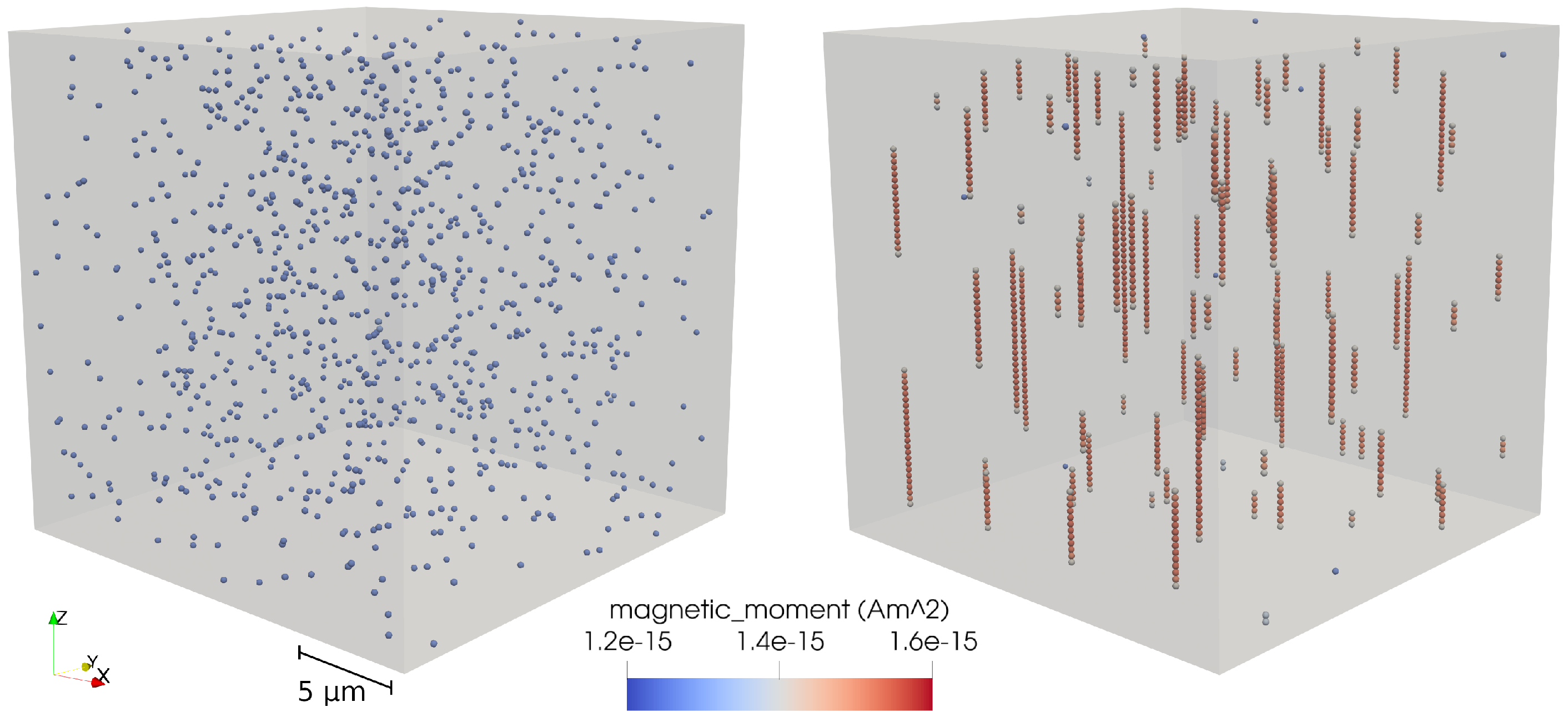
6.1. Modeling the Chain Length Distribution at Different Concentrations
6.2. Simulation Setup for the Aggregation in the Microchannel
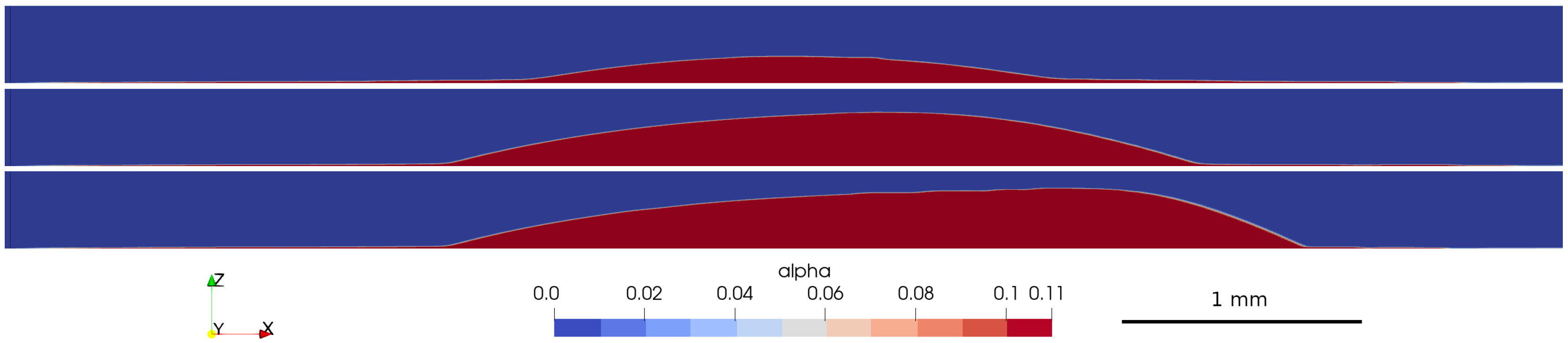
6.3. Results of Modeled Aggregation in the Microchannel
7. Comparison of the Experimental and Numerical Results
Further Work
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| General notation | scalar, vector |
| magnetic field [ ], [ ] | |
| magnetization [ ] | |
| magnetic moment of particle i [ ] | |
| p | pressure [ ] |
| Q | flow rate [ ] |
| velocity [ ] | |
| volume fraction | |
| strain rate [ ] | |
| dynamic viscosity [ ] | |
| density [ ] | |
| magnetic torque density [ ] | |
| magnetic susceptibility | |
| volumetric flux on a face [ ] | |
| CFD | computational fluid dynamics |
| MNP | magnetic nanoparticle |
References
- Fan, J.; Gao, Y. Nanoparticle-supported catalysts and catalytic reactions–a mini-review. J. Exp. Nanosci. 2006, 1, 457–475. [Google Scholar] [CrossRef]
- Ender, F.; Weiser, D.; Nagy, B.; Bencze, C.L.; Paizs, C.; Pálovics, P.; Poppe, L. Microfluidic multiple cell chip reactor filled with enzyme-coated magnetic nanoparticles—An efficient and flexible novel tool for enzyme catalyzed biotransformations. J. Flow Chem. 2016, 6, 43–52. [Google Scholar] [CrossRef]
- Weiser, D.; Bencze, L.C.; Bánóczi, G.; Ender, F.; Kiss, R.; Kókai, E.; Szilágyi, A.; Vértessy, B.G.; Farkas, Ö.; Paizs, C.; et al. Phenylalanine Ammonia-Lyase-Catalyzed Deamination of an Acyclic Amino Acid: Enzyme Mechanistic Studies Aided by a Novel Microreactor Filled with Magnetic Nanoparticles. ChemBioChem 2015, 16, 2283–2288. [Google Scholar] [CrossRef] [PubMed]
- Pálovics, P.; Ender, F.; Rencz, M. Towards the CFD model of flow rate dependent enzyme-substrate reactions in nanoparticle filled flow microreactors. Microelectron. Reliab. 2018, 85, 84–92. [Google Scholar] [CrossRef]
- Pálovics, P.; Ender, F.; Rencz, M. Geometric optimization of microreactor chambers to increase the homogeneity of the velocity field. J. Micromech. Microeng. 2018, 28, 064002. [Google Scholar] [CrossRef]
- Ahrberg, C.D.; Manz, A.; Chung, B.G. Polymerase chain reaction in microfluidic devices. Lab Chip 2016, 16, 3866–3884. [Google Scholar] [CrossRef] [PubMed]
- Sosnovik, D.E.; Nahrendorf, M.; Weissleder, R. Magnetic nanoparticles for MR imaging: Agents, techniques and cardiovascular applications. Basic Res. Cardiol. 2008, 103, 122–130. [Google Scholar] [CrossRef]
- Reddy, L.H.; Arias, J.L.; Nicolas, J.; Couvreur, P. Magnetic nanoparticles: Design and characterization, toxicity and biocompatibility, pharmaceutical and biomedical applications. Chem. Rev. 2012, 112, 5818–5878. [Google Scholar] [CrossRef]
- Das, P.; Colombo, M.; Prosperi, D. Recent advances in magnetic fluid hyperthermia for cancer therapy. Colloids Surf. B Biointerfaces 2019, 174, 42–55. [Google Scholar] [CrossRef]
- Gui, N.G.J.; Stanley, C.; Nguyen, N.T.; Rosengarten, G. Ferrofluids for heat transfer enhancement under an external magnetic field. Int. J. Heat Mass Transf. 2018, 123, 110–121. [Google Scholar]
- Goharkhah, M.; Salarian, A.; Ashjaee, M.; Shahabadi, M. Convective heat transfer characteristics of magnetite nanofluid under the influence of constant and alternating magnetic field. Powder Technol. 2015, 274, 258–267. [Google Scholar] [CrossRef]
- Lajvardi, M.; Moghimi-Rad, J.; Hadi, I.; Gavili, A.; Isfahani, T.D.; Zabihi, F.; Sabbaghzadeh, J. Experimental investigation for enhanced ferrofluid heat transfer under magnetic field effect. J. Magn. Magn. Mater. 2010, 322, 3508–3513. [Google Scholar] [CrossRef]
- Li, Q.; Xuan, Y. Experimental investigation on heat transfer characteristics of magnetic fluid flow around a fine wire under the influence of an external magnetic field. Exp. Therm. Fluid Sci. 2009, 33, 591–596. [Google Scholar] [CrossRef]
- Han, K.; Feng, Y.; Owen, D. Three-dimensional modelling and simulation of magnetorheological fluids. Int. J. Numer. Methods Eng. 2010, 84, 1273–1302. [Google Scholar] [CrossRef]
- Karvelas, E.; Lampropoulos, N.; Sarris, I.E. A numerical model for aggregations formation and magnetic driving of spherical particles based on OpenFOAM®. Comput. Methods Programs Biomed. 2017, 142, 21–30. [Google Scholar]
- Boutopoulos, I.D.; Lampropoulos, D.S.; Bourantas, G.C.; Miller, K.; Loukopoulos, V.C. Two-Phase Biofluid Flow Model for Magnetic Drug Targeting. Symmetry 2020, 12, 1083. [Google Scholar] [CrossRef]
- Ghaffari, A.; Hashemabadi, S.H.; Bazmi, M. CFD simulation of equilibrium shape and coalescence of ferrofluid droplets subjected to uniform magnetic field. Colloids Surfaces A Physicochem. Eng. Asp. 2015, 481, 186–198. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Guyon, E.; Hulin, J.P.; Petit, L.; Mitescu, C.D. Physical Hydrodynamics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Saliba, A.E.; Saias, L.; Psychari, E.; Minc, N.; Simon, D.; Bidard, F.C.; Mathiot, C.; Pierga, J.Y.; Fraisier, V.; Salamero, J.; et al. Microfluidic sorting and multimodal typing of cancer cells in self-assembled magnetic arrays. Proc. Natl. Acad. Sci. USA 2010, 107, 14524–14529. [Google Scholar]
- Bossis, G.; Volkova, O.; Lacis, S.; Meunier, A. Magnetorheology: Fluids, structures and rheology. In Ferrofluids; Springer: Berlin, Germany, 2002; pp. 202–230. [Google Scholar]
- Martin, J.E.; Anderson, R.A. Chain model of electrorheology. J. Chem. Phys. 1996, 104, 4814–4827. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, University of London, London, UK, 2002. [Google Scholar]
- Wen, C.Y. Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Berlin, Germany, 2002; Volume 3. [Google Scholar]
- Pimenta, F.; Alves, M. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J.Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Rajput, S.; Pittman, C.U., Jr.; Mohan, D. Magnetic magnetite (Fe3O4) nanoparticle synthesis and applications for lead (Pbr2+) and chromium (Cr6+) removal from water. J. Colloid Interface Sci. 2016, 468, 334–346. [Google Scholar] [CrossRef]
- Goya, G.; Berquo, T.; Fonseca, F.; Morales, M. Static and dynamic magnetic properties of spherical magnetite nanoparticles. J. Appl. Phys. 2003, 94, 3520–3528. [Google Scholar] [CrossRef]
- Daoush, W. Co-precipitation and magnetic properties of magnetite nanoparticles for potential biomedical applications. J. Nanomed. Res. 2017, 5, 1–6. [Google Scholar] [CrossRef]
- Thompson, R.; Oldfield, F. Magnetic properties of natural materials. In Environmental Magnetism; Springer: Berlin, Germany, 1986; pp. 21–38. [Google Scholar]
- Pimenta, F.; Alves, M. rheoTool. 2016. Available online: https://github.com/fppimenta/rheoTool (accessed on 21 May 2020).








| Q (mL h ) | Gap Size ( ) |
|---|---|
| 50 | 0–45 |
| 100 | 60 |
| 150 | 75 |
| 200 | 90 |
| 300 | 90–115 |
| Flow Rate | MNP Free Channel | MNP Filled Channel | ||||
|---|---|---|---|---|---|---|
| Q (mL h ) | ( ) | ( ) | (%) | ( ) | ( ) | (%) |
| 100 | 46.6 | 18.1 | 38.8 | 50.7 | 18.8 | 37.1 |
| 50 | 42.3 | 8 | 18.9 | 41.4 | 6.2 | 15.0 |
| 25 | 25.1 | 1.7 | 6.8 | 26.9 | 1.5 | 5.6 |
| 10 | 11.4 | 1.6 | 14.0 | 16.1 | 0 | 0 |
| (N m ) | |
|---|---|
| 2.00 | |
| 7.23 | |
| 16.79 |
| Flow Rate (mL h ) | Simulated Gap ( ) |
|---|---|
| 50 | 53 |
| 100 | 67 |
| 150 | 69 |
| 200 | 85 |
| 300 | 101 |
| Flow Rate (mL h ) | Measured Gap ( ) | Simulated Gap ( ) | Difference ( ) |
|---|---|---|---|
| 50 | 0–45 | 53 | 8–53 |
| 100 | 60 | 67 | 7 |
| 150 | 75 | 69 | 6 |
| 200 | 90 | 85 | 5 |
| 300 | 90–115 | 101 | 0–14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pálovics, P.; Németh, M.; Rencz, M. Investigation and Modeling of the Magnetic Nanoparticle Aggregation with a Two-Phase CFD Model. Energies 2020, 13, 4871. https://doi.org/10.3390/en13184871
Pálovics P, Németh M, Rencz M. Investigation and Modeling of the Magnetic Nanoparticle Aggregation with a Two-Phase CFD Model. Energies. 2020; 13(18):4871. https://doi.org/10.3390/en13184871
Chicago/Turabian StylePálovics, Péter, Márton Németh, and Márta Rencz. 2020. "Investigation and Modeling of the Magnetic Nanoparticle Aggregation with a Two-Phase CFD Model" Energies 13, no. 18: 4871. https://doi.org/10.3390/en13184871
APA StylePálovics, P., Németh, M., & Rencz, M. (2020). Investigation and Modeling of the Magnetic Nanoparticle Aggregation with a Two-Phase CFD Model. Energies, 13(18), 4871. https://doi.org/10.3390/en13184871





