A Coordinated Dispatching Model Considering Generation and Operation Reserve in Wind Power-Photovoltaic-Pumped Storage System
Abstract
1. Introduction
2. The Ultra-Short-Term Prediction Error Probability Distribution Model of the Wind and PV Output
2.1. The Non-Parametric Kernel Density Estimation Method
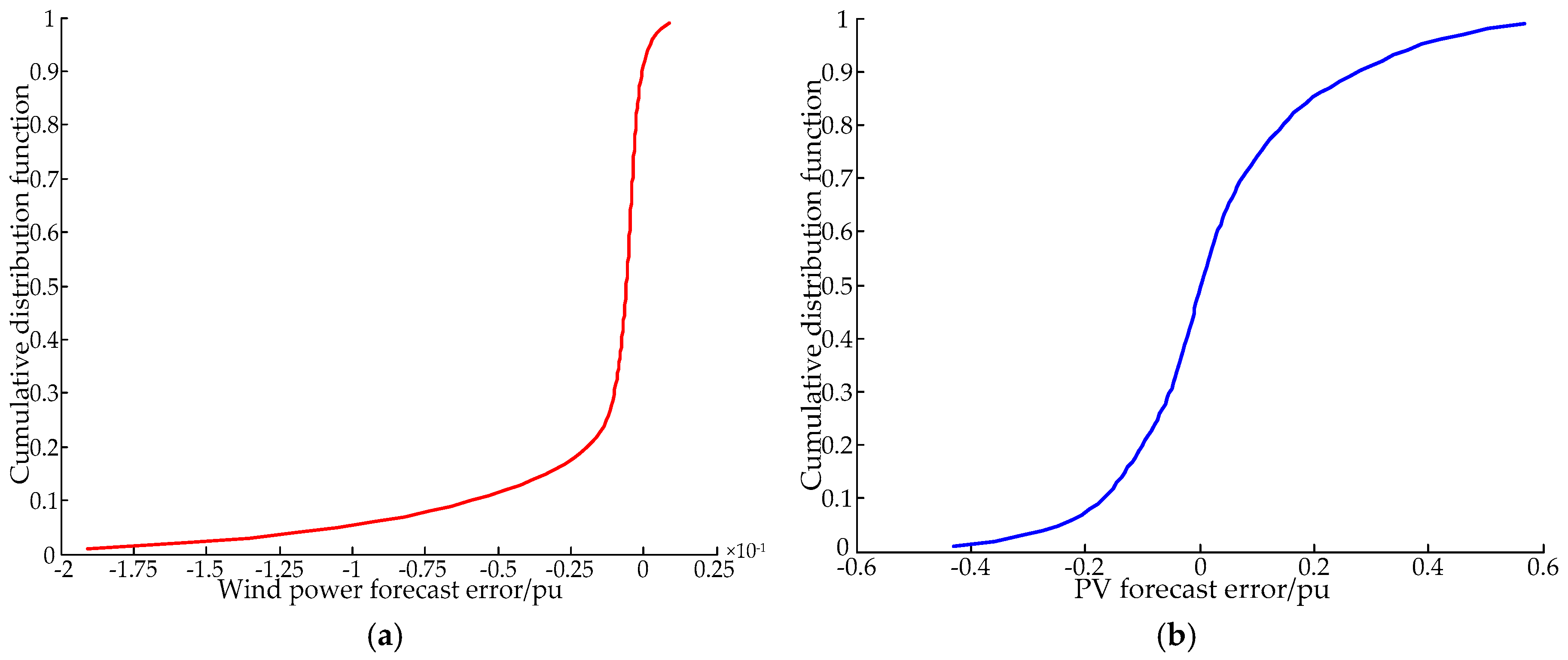
2.2. Prediction Error Probability Distribution of the Wind Power Output and PV Power Output
3. Uncertain Scenario Set Description
3.1. Scene Generation Based on Latin Hypercube Sampling
3.2. Scenario Reduction Based on Simultaneous Backward Reduction Method
4. Reserve Capacity Quantitative Model Based on the Reliability Index
4.1. The Expected Energy Not Supplied
4.2. Expected Wind Power and PV Curtailed
5. The Coordination and Optimization Model of Power Generation and Reserve
5.1. Objective Function
5.2. Constraints
5.2.1. Operation Constraints of Thermal Power Units
5.2.2. Operation Constraints of Gas Power Units
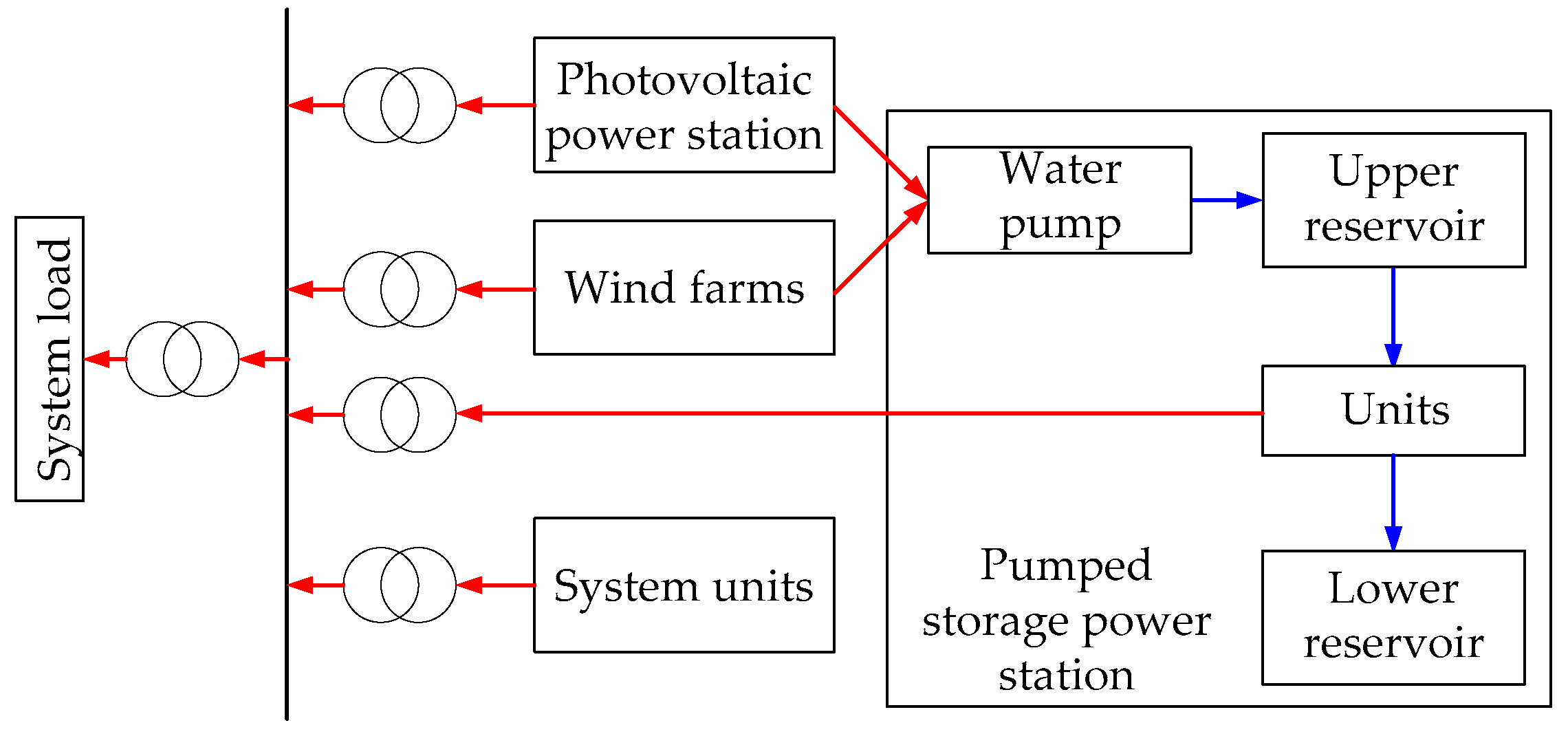
5.2.3. Constraints of Pumped Storage Power Station
5.2.4. System Constraints
5.3. Calculating Procedures
6. Case Study
6.1. Parameters of the Calculation Example
6.2. Scenario Generation and Reduction
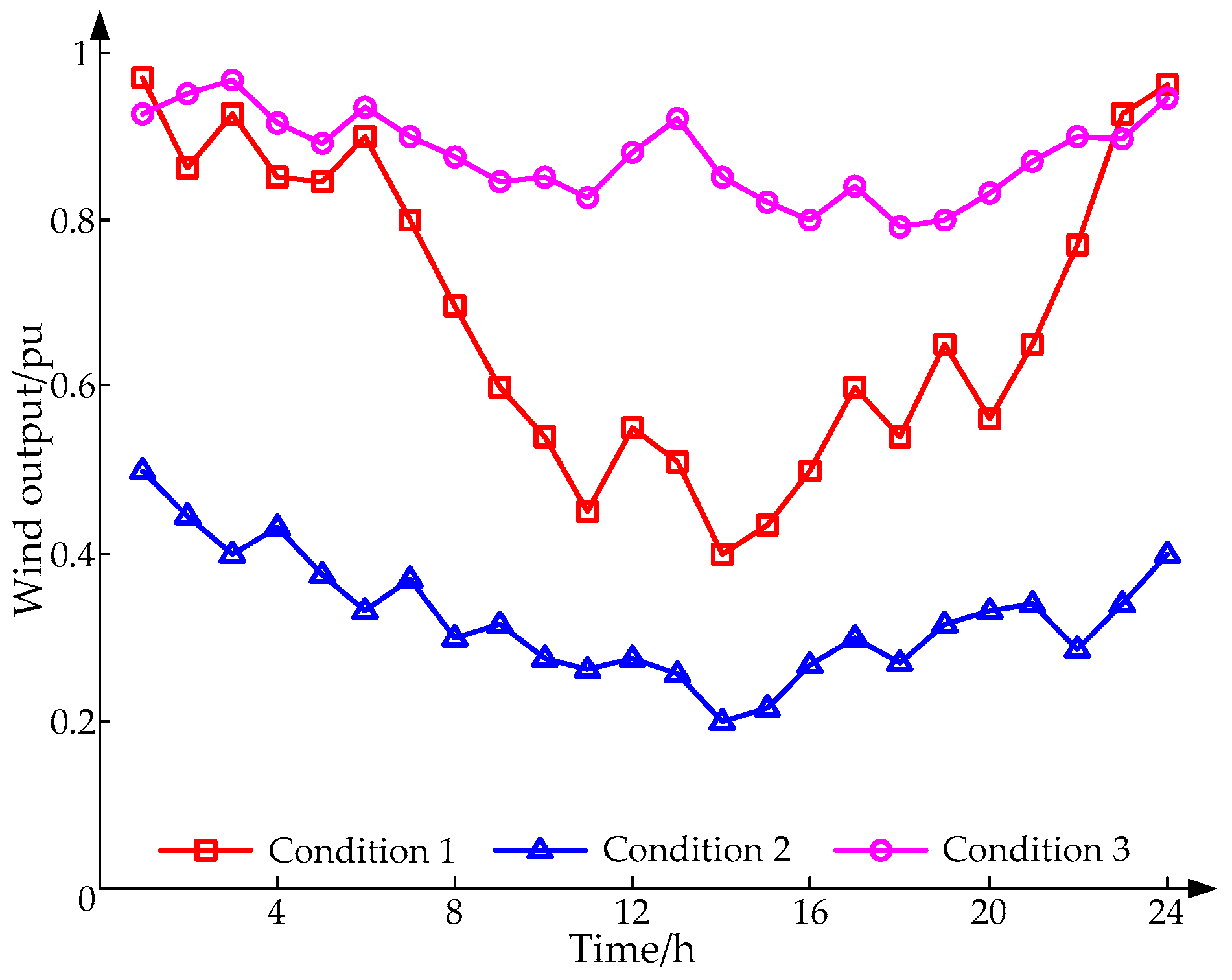
6.3. The Dispatching Test Results under Different Working Conditions
6.3.1. Ordinary Operating Conditions
6.3.2. The Working Conditions with Continuous Large Wind Power Output
6.3.3. The Working Conditions with Continuous Small Wind Power Output
7. Conclusions
- The non-parametric kernel density estimation method did not need to assume the distribution model of variables and had little limitation on the model. According to Figure 2, the modeling process of the non-parametric method was simple and was subject to little interference from external factors. Compared with the parametric method, the results obtained by the non-parametric method had a small error and was highly practical.
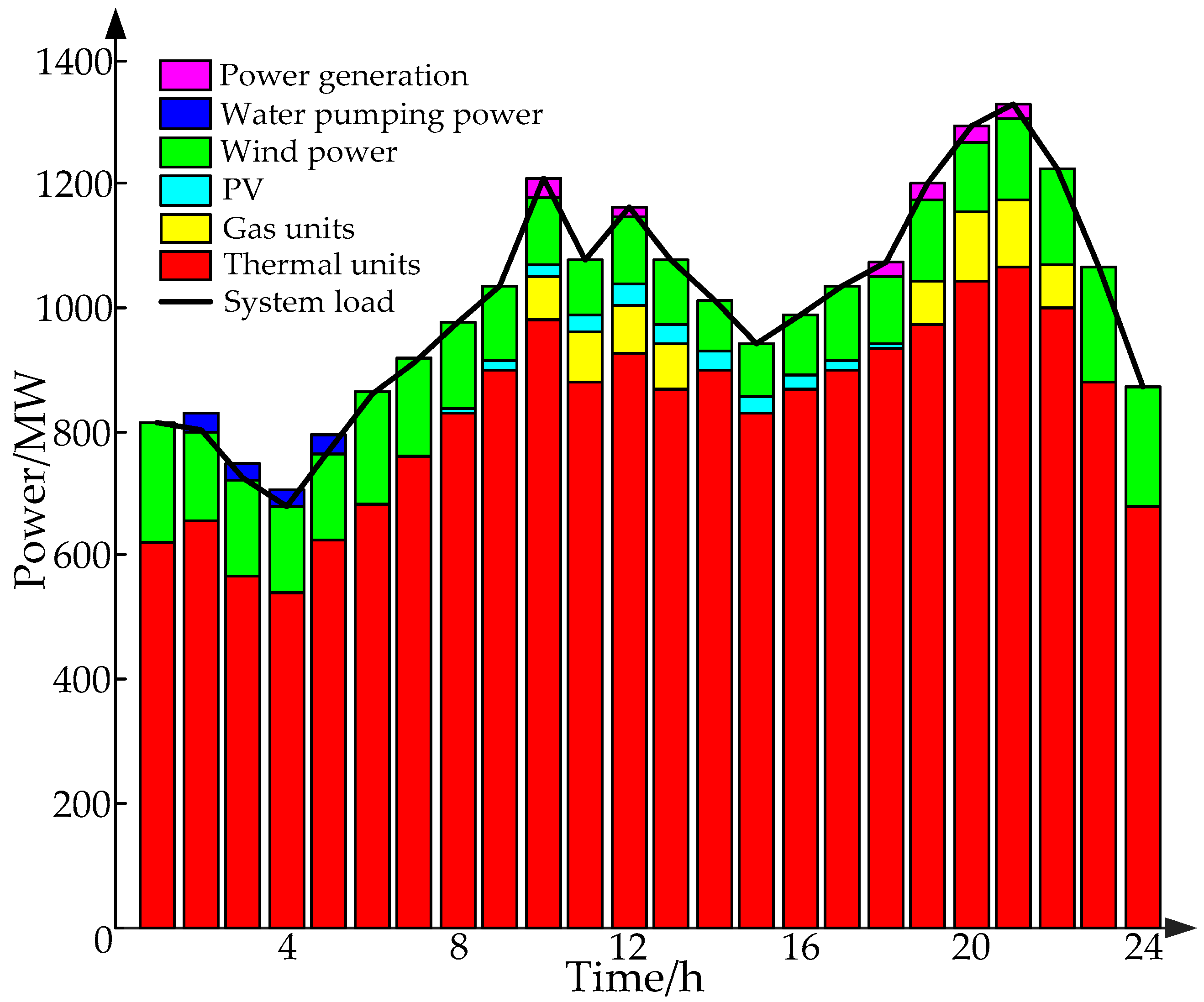
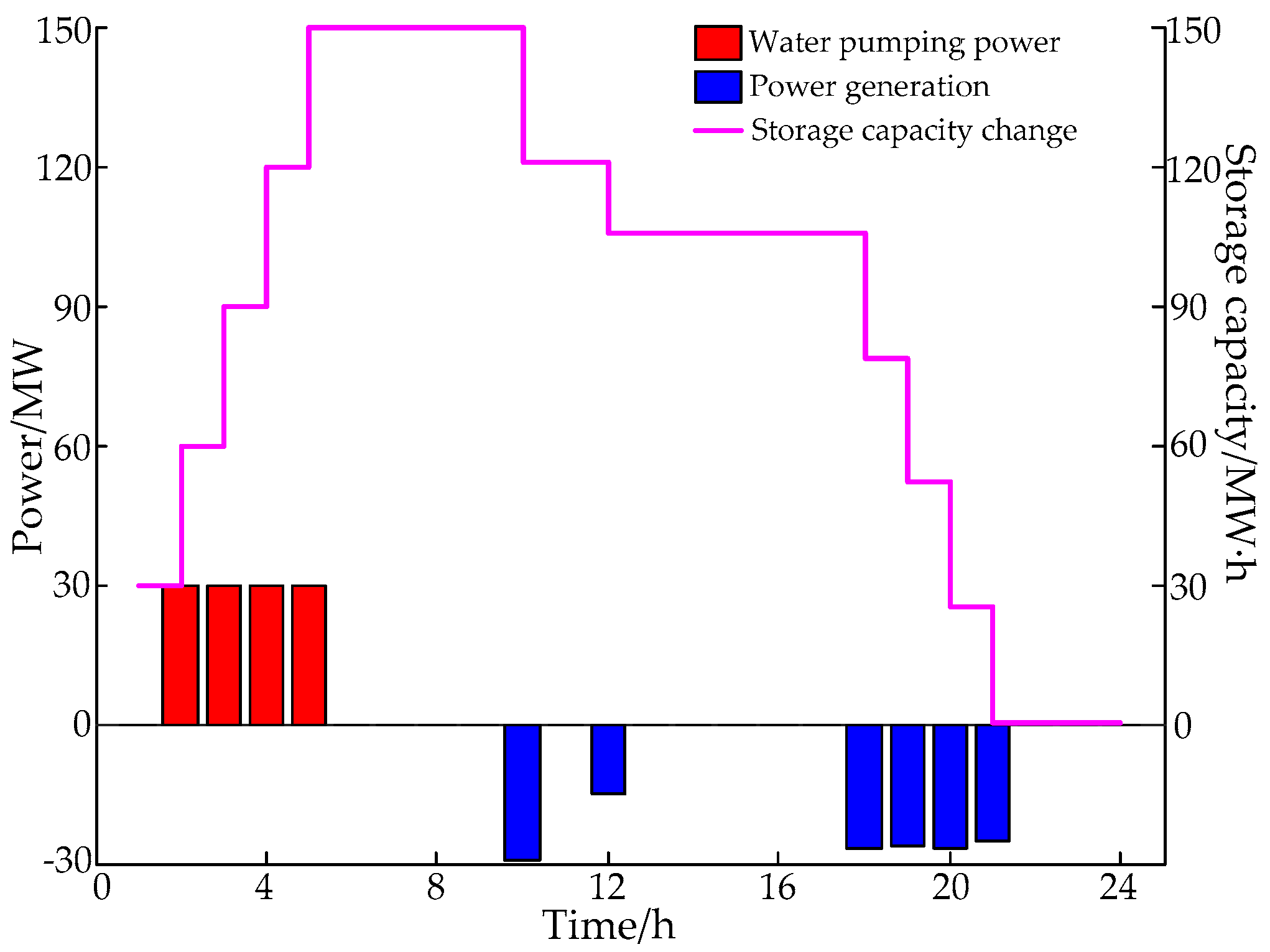
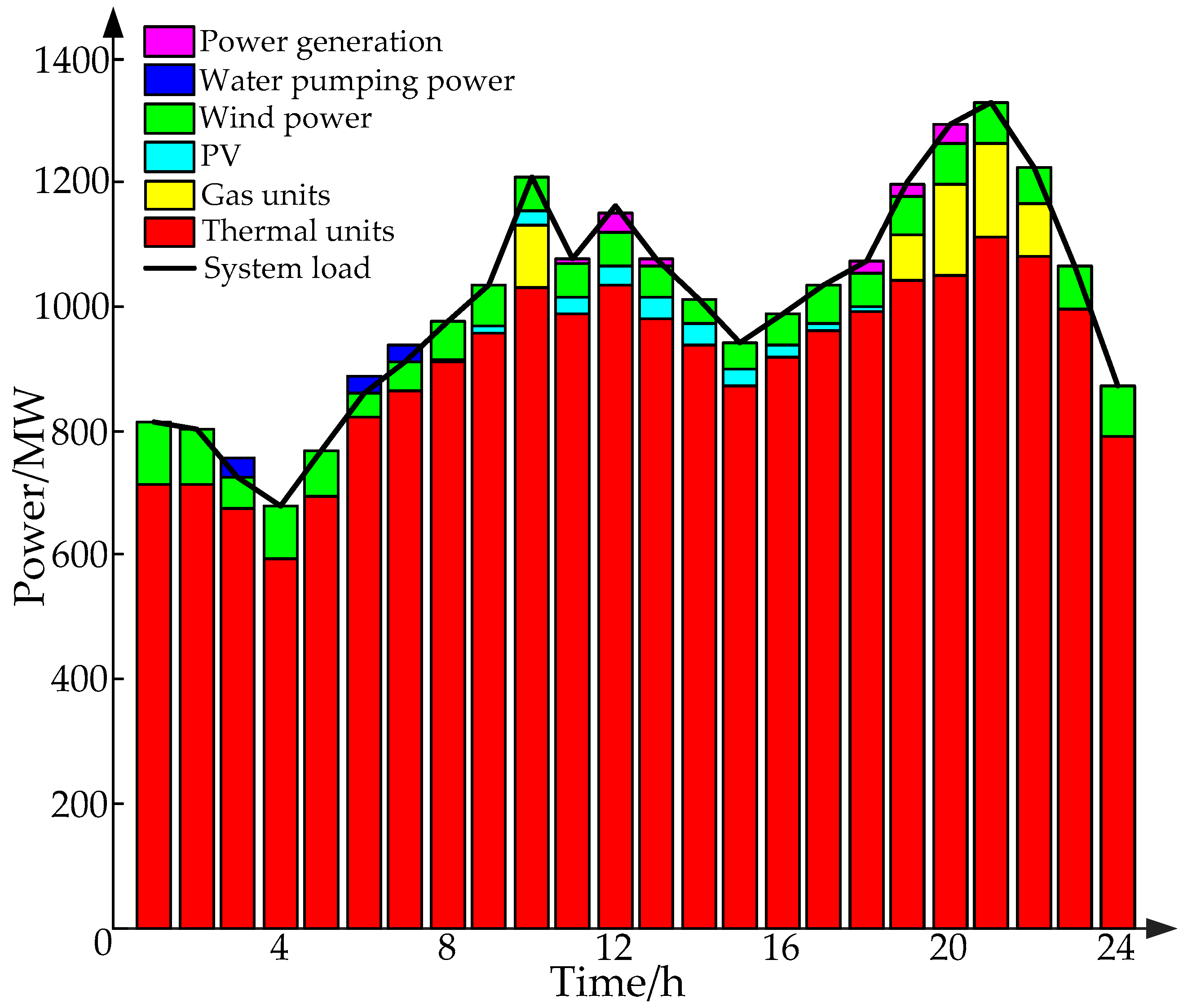
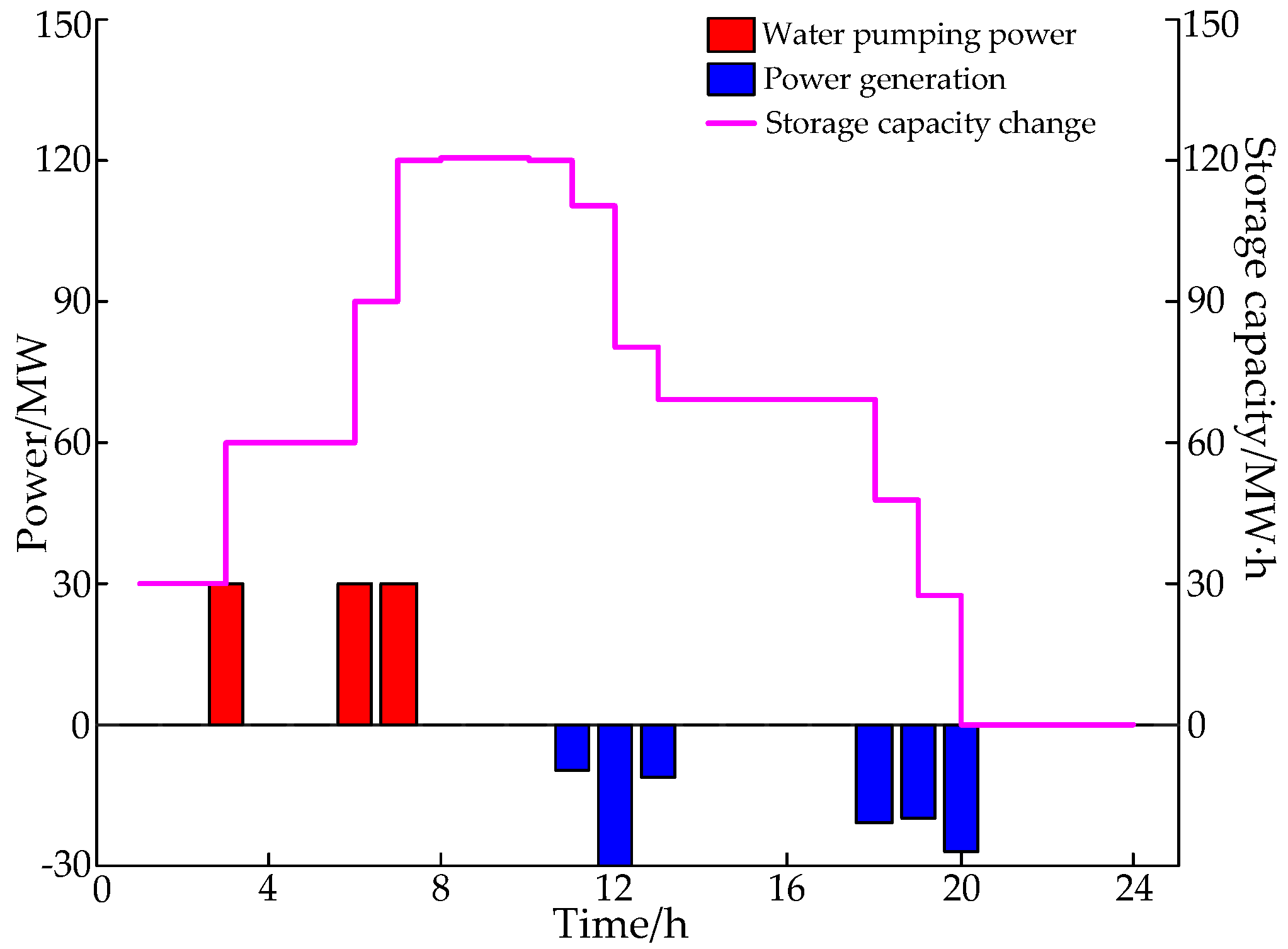
- According to Figure 9, Figure 12 and Figure 15, it can be seen that the PSPS achieved peak load cutting and valley load reduction, as well as reduced the peak-valley difference of load. The gas power unit had flexible adjustment ability and provided a large amount of reserve capacity. Therefore, globally, the number of gas power units and PSPSs were appropriately increased so that they can participate in power grid dispatching, which effectively relieved peak pressure of thermal power units and further reduced renewable energy waste and load cutting accidents.
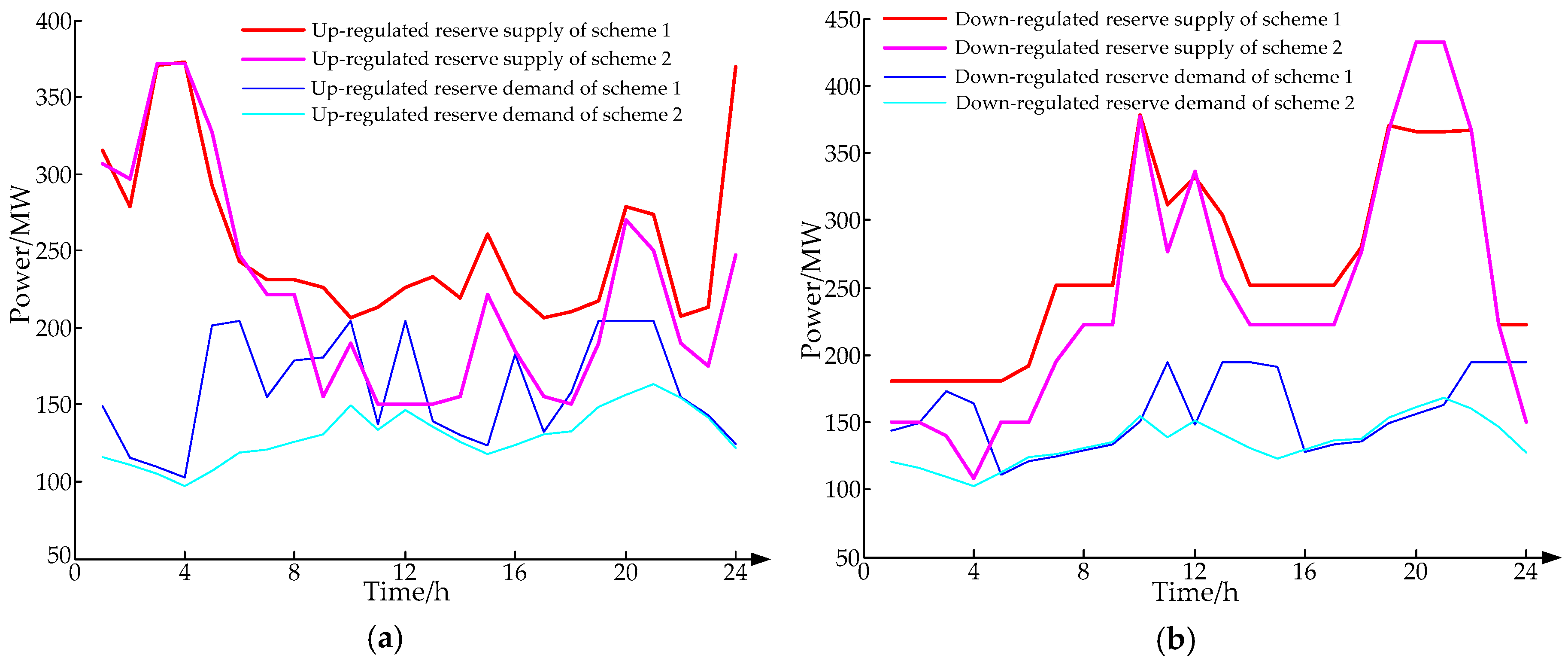
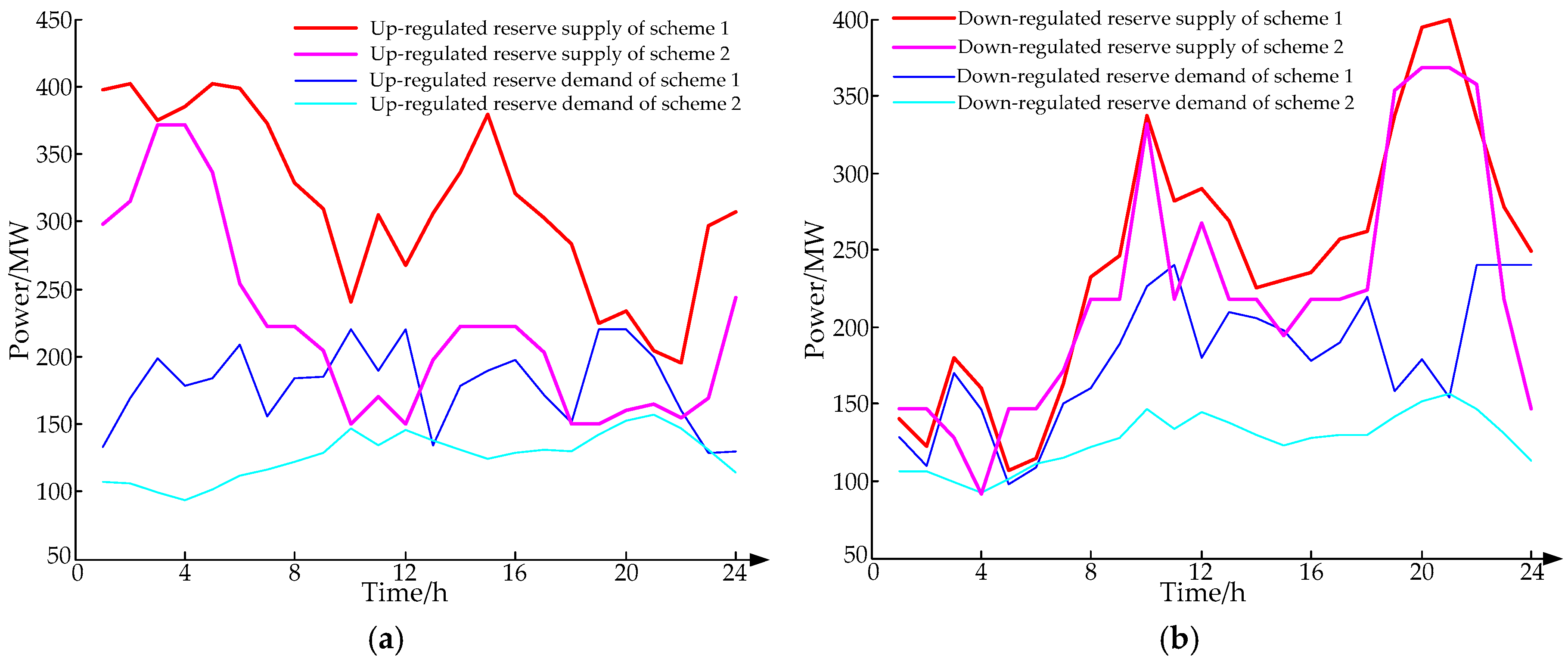
- Compared with the traditional deterministic alternative decision method, the method proposed in this paper effectively solved its blindness. By comparing Figure 11, Figure 14, and Figure 17, we can clearly find that the method proposed in this paper met the system power balance constraint and reserve capacity constraint in all scenarios, and the results of the reserve demand and supply were higher than those of the traditional deterministic reserve decision method. Therefore, there was no shortage of reserve in the operation process. The method proposed in this paper is of great practical value for active power dispatching of power systems with large-scale renewable energy sources.
- The correlation between WP output and PV output was not considered. WP output and PV output have certain complementarity, i.e., negative correlation. In the follow-up research, different Copula functions can be introduced to form the WP-PV joint probability distribution model according to the situation, which can better fit with the engineering practice.
- The actual power system parameters should be used for verification and more reference examples should be added, so that the analysis of the problem are more convincing and targeted.
- The coordinated scheduling problem proposed in this paper is an unusually complex mixed integer nonlinear programming problem. When the system size is large, it is very difficult to directly optimize and solve the problem. Therefore, it is urgent to seek an optimization algorithm to solve this problem.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| // | the second-order fitting coefficients of the operating cost of thermal power unit |
| // | the second-order fitting coefficients of the operating cost of gas power unit |
| operation cost of thermal power units at time under scenario (USD) | |
| operation cost of gas power units at time under scenario (USD) | |
| operation cost of PSPS at time under scenario (USD) | |
| total number of scenarios | |
| predicted value of load at time (MW) | |
| predicted output of WP at time (MW) | |
| predicted output of PV at time (MW) | |
| output of thermal power unit at time under scenario (MW) | |
| output of gas power unit at time under scenario (MW) | |
| generation power of the PSPS at time under scenario (MW) | |
| pumped storage power of the PSPS at time under scenario (MW) | |
| minimum output operating limits of thermal power unit (MW) | |
| maximum output operating limits of thermal power unit (MW) | |
| minimum output operating limits of gas power unit (MW) | |
| maximum output operating limits of gas power unit (MW) | |
| maximum generation power of PSPS (MW) | |
| maximum storage power of PSPS (MW) | |
| curtailed WP at time under scenario (MW) | |
| curtailed PV at time under scenario (MW) | |
| load shedding power at time under scenario (MW) | |
| power of line at time under scenario (MW) | |
| / | the limits of (MW) |
| up-regulated reserve capacity that can be provided by the system at time under scenario (MW) | |
| up-regulated reserve capacity that can be provided by thermal power unit at time under scenario (MW) | |
| up-regulated reserve capacity that can be provided by gas power unit at time under scenario (MW) | |
| up-regulated reserve capacity that can be provided by pumped storage unit at time under scenario (MW) | |
| down-regulated reserve capacity that can be provided by the system at time under scenario (MW) | |
| down-regulated reserve capacity that can be provided by thermal power unit at time under scenario (MW) | |
| down-regulated reserve capacity that can be provided by gas power unit at time under scenario (MW) | |
| down-regulated reserve capacity that can be provided by pumped storage unit at time under scenario (MW) | |
| maximum up-climb rates of thermal power unit (MW/min) | |
| maximum down-climb rates of thermal power unit (MW/min) | |
| maximum up-climb rates of gas power unit (MW/min) | |
| maximum down-climb rates of gas power unit (MW/min) | |
| / | the minimum running time/shut down time allowed by the gas power unit |
| start-stop status of gas power unit at time ; equal to 1 if gas power unit starts-up at time | |
| / | two working states of PSPS; is 1 for pumping state, is 1 for power generation state |
| storage capacity of PSPS at time under scenario (WM·h) | |
| minimum storage capacity of PSPS (WM·h) | |
| maximum storage capacity of PSPS (WM·h) | |
| probability of scenario | |
| prediction error of load at time at time under scenario (MW) | |
| WP output prediction error at time at time under scenario (MW) | |
| PV output prediction error at time at time under scenario (MW) | |
| penalties for unit curtailment of WP/PV/ load shedding (USD/MW) | |
| pumping efficiency of the PSPS | |
| / | coefficients of power generation cost and pumping cost of PSPS(USD/MW) |
| scheduling interval(h) |
Appendix A
| Pmax (MW) | Pmin (MW) | a ($/MWh2) | b ($/MWh) | c ($/h) | Ru (MW/min) | Rd (MW/min) | On ($) | Off ($) | T (h) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 455 | 150 | 0.00031 | 16.19 | 200 | 2.5 | 2.5 | 20,000 | 20,000 | 12 |
| 2 | 455 | 150 | 0.00031 | 17.26 | 200 | 2.5 | 2.5 | 20,000 | 20,000 | 12 |
| 3 | 300 | 70 | 0.00031 | 16.60 | 300 | 1.2 | 1.2 | 18,000 | 18,000 | 10 |
| 4 | 80 | 20 | 0.00025 | 16.50 | 400 | 1.2 | 1.2 | 15,000 | 15,000 | 8 |
| 5 | 60 | 15 | 0.00511 | 19.70 | 800 | 1.0 | 1.0 | 5000 | 5000 | 1 |
| 6 | 60 | 15 | 0.00712 | 22.26 | 800 | 1.0 | 1.0 | 5000 | 5000 | 2 |
| Full Name | Acronym |
|---|---|
| photovoltaic | PV |
| wind power | WP |
| pumped storage power station | PSPS |
| Latin Hypercube Sampling | LHS |
| Simultaneous Backward Reduction | SBR |
| expected energy not supplied | EENS |
| expected wind power and PV curtailed | EWPPC |
References
- Jamaly, M.; Bosch, J.L.; Kleissl, J.; Zheng, Y.H. Performance Analysis of Power Output of Photovoltaic Systems in San Diego County. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Xue, Y.S.; Lei, X.; Xue, F.; Yu, C.; Dong, C.Y.; Wen, F.S.; Jv, P. A review on impacts of wind power uncertainties on power systems. Proc. CSEE 2014, 34, 5029–5040. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, L.; Zhang, S.; Tang, D. Study on a novel co-operated heat and power system for improving energy efficiency and flexibility of cogeneration plants. Appl. Therm. Eng. 2019, 163, 1–13. [Google Scholar] [CrossRef]
- Gyalai-Korpos, M.; Zentkó, L.; Hegyfalvi, C.; Detzky, G.; Tildy, P.; Hegedűsné Baranyai, N.; Pintér, G.; Zsiborács, H. The Role of Electricity Balancing and Storage: Developing Input Parameters for the European Calculator for Concept Modeling. Sustainability 2020, 12, 811. [Google Scholar] [CrossRef]
- Liu, H.L.; Brown, T.; Andresen, G.B.; Schlachtberger, D.P.; Greiner, M. The role of hydro power, storage and transmission in the decarbonization of the Chinese power system. Appl. Energy 2019, 239, 1308–1321. [Google Scholar] [CrossRef]
- Xu, Y.M.; Lang, Y.S.; Wen, B.Y.; Yang, X.N. An Innovative Planning Method for the Optimal Capacity Allocation of a Hybrid Wind–PV–Pumped Storage Power System. Energies 2019, 12, 2809. [Google Scholar] [CrossRef]
- Wang, W.X.; Li, C.S.; Liao, X.; Qin, H. Study on unit commitment problem considering pumped storage and renewable energy via a novel binary artificial sheep algorithm. Appl. Energy 2017, 187, 612–626. [Google Scholar] [CrossRef]
- Fu, Y.W.; Dong, L.; Hu, W.; Wang, Y.T.; Zhang, J.T.; Wu, S.; Lu, Z.X. Research on joint optimal dispatching method for hybrid power system considering system security. Appl. Energy 2019, 238, 147–163. [Google Scholar] [CrossRef]
- Li, Y.H.; Chen, C.M.; Zhang, J.F. The optimal control strategy for integrated system of wind/photovoltaic/energy storage considering the frequency constraint. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 6355–6362. [Google Scholar] [CrossRef]
- Zhang, L.X.; Zhou, Y.T.; Flynn, D.; Mutale, J.; Mancarella, P. System-level operational and adequacy impact assessment of photovoltaic and distributed energy storage, with consideration of inertial constraints, dynamic reserve and interconnection flexibility. Energies 2017, 10, 989. [Google Scholar] [CrossRef]
- Marneris, I.G.; Biskas, P.N.; Bakirtzis, A.G. Stochastic and Deterministic Unit Commitment Considering Uncertainty and Variability Reserves for High Renewable Integration. Energies 2017, 10, 140. [Google Scholar] [CrossRef]
- Cheng, J.; Duan, D.; Cheng, X.; Yang, L.; Cui, S. Probabilistic Microgrid Energy Management with Interval Predictions. Energies 2020, 13, 3116. [Google Scholar] [CrossRef]
- Nag, S.; Lee, K.Y. Network and Reserve Constrained Economic Analysis of Conventional, Adjustable-Speed and Ternary Pumped-Storage Hydropower. Energies 2020, 13, 4140. [Google Scholar] [CrossRef]
- Vázquez Pombo, D.; Iov, F.; Stroe, D.-I. A Novel Control Architecture for Hybrid Power Plants to Provide Coordinated Frequency Reserves. Energies 2019, 12, 919. [Google Scholar] [CrossRef]
- Liu, T.; Ye, X.H.; Wu, G.Y.; Su, Z.D.; Zhong, W.Z.; Song, L.X.; Huang, Y.N. An Active Power Control Model of Wind Power Generating Unit Suitable for Medium- and Long-Term Dynamic Simulation of Power Grid. Power Syst. Technol. 2014, 38, 1210–1215. [Google Scholar] [CrossRef]
- Chen, J.H.; Wu, W.C.; Zhang, B.M.; Wang, B.; Guo, Q.L. A Spinning Reserve Allocation Method for Power Generation Dispatch Accommodating Large-Scale Wind Power Integration. Energies 2013, 6, 5357. [Google Scholar] [CrossRef]
- Zhou, M.; Li, Y.; Li, G.Y. A Day-ahead Power Generation-reserve Bi-level Decision-making Model for Power System Based on Probabilistic Production Simulation. Power Syst. Technol. 2019, 43, 1606–1613. [Google Scholar] [CrossRef]
- Yuan, B.; Zhou, M.; Li, G.Y.; Zong, J. A Coordinated Dispatching Model Considering Generation and Operating Reserve for Wind Power Integrated Power System Based on ELNSR. Power Syst. Technol. 2013, 37, 800–807. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, Y.; Sun, H.; Wei, Q.H. Dynamic Economic Dispatch in Wind Power Integrated System. Proc. CSEE 2009, 29, 13–18. [Google Scholar] [CrossRef]
- Ge, J.; Wang, F.; Zhang, L.Z. Spinning Reserve Model in the Wind Power Integrated Power System. Autom. Electr. Power Syst. 2010, 34, 32–36. [Google Scholar]
- Ortega-Vazquez, M.A.; Kirschen, D.S. Optimizing the Spinning Reserve Requirements Using a Cost/Benefit Analysis. IEEE Trans. Power Syst. 2007, 22, 24–33. [Google Scholar] [CrossRef]
- Morales, J.M.; Conejo, A.J.; Perez-Ruiz, J. Economic Valuation of Reserves in Power Systems with High Penetration of Wind Power. IEEE Trans. Power Syst. 2009, 24, 900–910. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Dominguez-Navarro, J.A.; Llombart, A. Statistical Analysis of Wind Power Forecast Error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Kaplani, E.; Kaplanis, S. A stochastic simulation model for reliable PV system sizing providing for solar radiation fluctuations. Appl. Energy 2012, 97, 970–981. [Google Scholar] [CrossRef]
- Sarkar, S.; Ajjarapu, V. MW Resource Assessment Model for a Hybrid Energy Conversion System with Wind and Solar Resources. IEEE Trans. Sustain. Energy 2011, 2, 383–391. [Google Scholar] [CrossRef]
- Zou, K.; Agalgaonkar, A.P.; Muttaqi, K.M.; Perera, S. Distribution System Planning With Incorporating DG Reactive Capability and System Uncertainties. IEEE Trans. Sustain. Energy 2012, 3, 112–123. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on Some Nonparametric Estimates of a Density Function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, Q.R.; Li, F.X. Probabilistic Model of Payment Cost Minimization Considering Wind Power and Its Uncertainty. IEEE Trans. Sustain. Energy 2013, 4, 716–724. [Google Scholar] [CrossRef]
- Wu, Y.K.; Su, P.E.; Wu, T.Y.; Hong, J.S. Probabilistic Wind-Power Forecasting Using Weather Ensemble Models. IEEE Trans. Ind. Appl. 2018, 54, 5609–5620. [Google Scholar] [CrossRef]
- Liao, G.D.; Ming, J.; Wei, B.Y.; Xiang, H.J.; Jiang, N.; Ai, P.; Dai, C.H.; Xie, X.T.; Li, M.J. Wind Power Prediction Errors Model and Algorithm Based on Non-parametric Kernel Density Estimation. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Changsha, China, 26–29 November 2015. [Google Scholar] [CrossRef]
- Zhou, J.G.; Jia, H.J.; Tian, Z.; Hu, L.L. Short-term wind speed forecasting based on non-parametric kernel density estimation. In Proceedings of the 2012 IEEE Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012. [Google Scholar] [CrossRef]
- Qin, Z.L.; Li, W.Y.; Xiong, X.F. Estimating wind speed probability distribution using kernel density method. Electr. Power Syst. Res. 2013, 81, 2139–2146. [Google Scholar] [CrossRef]
- Li, R.S.; Wu, B.X.; Li, X.W.; Zhou, F.Q.; Li, Y.B. Design of wind-solar and pumped-storage hybrid power supply system. In Proceedings of the 2010 3rd IEEE International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010. [Google Scholar] [CrossRef]
- Pan, W.X.; Fan, Y.W.; Zhu, L.; Gao, A. The Optimal Sizing for Pumped Storage System in Wind Farm. Trans. China Electrotech. Soc. 2008, 23, 120–124. [Google Scholar] [CrossRef]
- Zhao, Y.; Shen, Z.J.; Zhou, N.C.; Zhou, J.Q.; Xu, K.Y. Reliability assessment of bulk power systems utilizing sequential simulation and nonparametric kernel density estimation. Autom. Electr. Power Syst. 2008, 32, 14–19. [Google Scholar] [CrossRef]
- EirGrid System Performance Data [DB/OL]. Available online: http://www.eirgrid.com/operations/systemperformancedata/ (accessed on 12 December 2019).
- Zhao, S.Q.; Hu, L.N.; Tian, J.F.; Xu, Z.Y. Contract power decomposition model of multi-energy power system based on mid-long term wind power and photovoltaic electricity forecasting. Electr. Power Autom. Equip. 2019, 39, 13–19. [Google Scholar] [CrossRef]
- Ai, X.M.; Tayierjiang, B.; Yang, L.B.; Yang, J.H.; Fang, J.K.; Wen, J.Y. Optimizing the Spinning Reserve in Wind Power System Using Scenario Method. Power Syst. Technol. 2018, 42, 835–841. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, J.; Cheng, S. Probabilistic Load Flow Method Based on Nataf Transformation and Latin Hypercube Sampling. IEEE Trans. Sustain. Energy 2013, 4, 294–301. [Google Scholar] [CrossRef]
- Heitsch, H.; Römisch, W. Scenario reduction algorithms in stochastic programming. Comput. Optimization Appl. 2003, 24, 187–206. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Alinezhad, L.; Jadid, S. Optimum Simultaneous Clearing of Energy and Spinning Reserve Markets with High Penetration of Wind Power. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010. [Google Scholar] [CrossRef]
- Teng, X.B.; Wu, Z.; Huang, J.; He, J.; Liu, M.; Kang, C.Q. Model and Algorithm of Coal-Fired Unit Cyclic Operation Toward Low-Carbon Development. Power Syst. Technol. 2011, 35, 33–39. [Google Scholar] [CrossRef]








| WP Reduction Scenario | PV Reduction Scenario | |
|---|---|---|
| Scenario 1 | 0.616 | 0.342 |
| Scenario 2 | 0.176 | 0.340 |
| Scenario 3 | 0.208 | 0.318 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, D.; Xu, F.; Ge, W.; Huang, P.; Zhou, Y. A Coordinated Dispatching Model Considering Generation and Operation Reserve in Wind Power-Photovoltaic-Pumped Storage System. Energies 2020, 13, 4834. https://doi.org/10.3390/en13184834
Cui D, Xu F, Ge W, Huang P, Zhou Y. A Coordinated Dispatching Model Considering Generation and Operation Reserve in Wind Power-Photovoltaic-Pumped Storage System. Energies. 2020; 13(18):4834. https://doi.org/10.3390/en13184834
Chicago/Turabian StyleCui, Dai, Fei Xu, Weichun Ge, Pengxiang Huang, and Yunhai Zhou. 2020. "A Coordinated Dispatching Model Considering Generation and Operation Reserve in Wind Power-Photovoltaic-Pumped Storage System" Energies 13, no. 18: 4834. https://doi.org/10.3390/en13184834
APA StyleCui, D., Xu, F., Ge, W., Huang, P., & Zhou, Y. (2020). A Coordinated Dispatching Model Considering Generation and Operation Reserve in Wind Power-Photovoltaic-Pumped Storage System. Energies, 13(18), 4834. https://doi.org/10.3390/en13184834





