A Study on Axial Compression Performance of Concrete-Filled Steel-Tubular Shear Wall with a Multi-Cavity T-Shaped Cross-Section
Abstract
1. Introduction
2. Experimental Program
2.1. Specimen Design
2.2. Material Selection and Material Test
2.3. Loading System
3. Numbering Rules and Measuring Points for Specimens
4. Experimental Phenomena
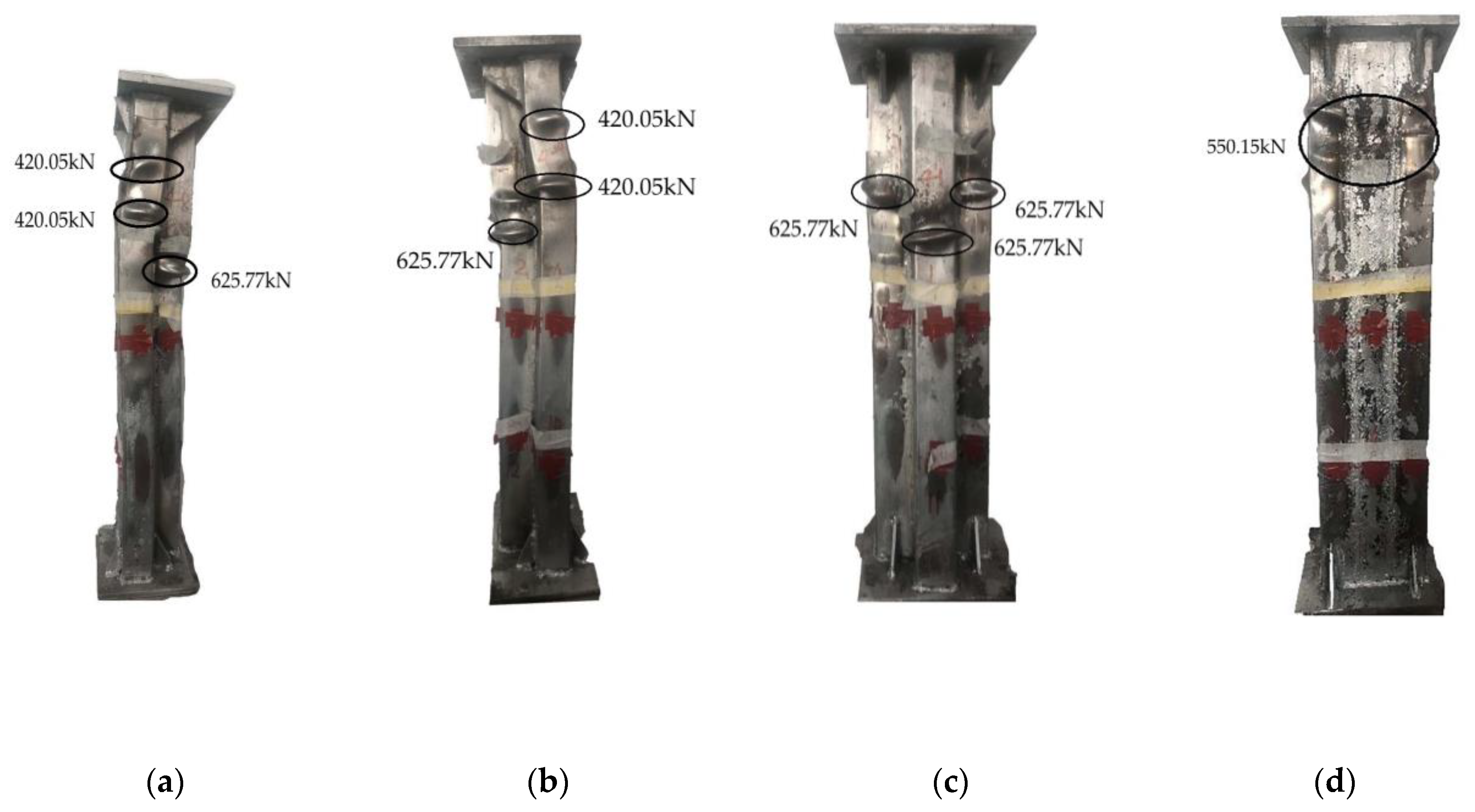
4.1. TA4-600 Shear Wall Test Phenomenon
4.2. TA5-600 Shear Wall Test Phenomenon
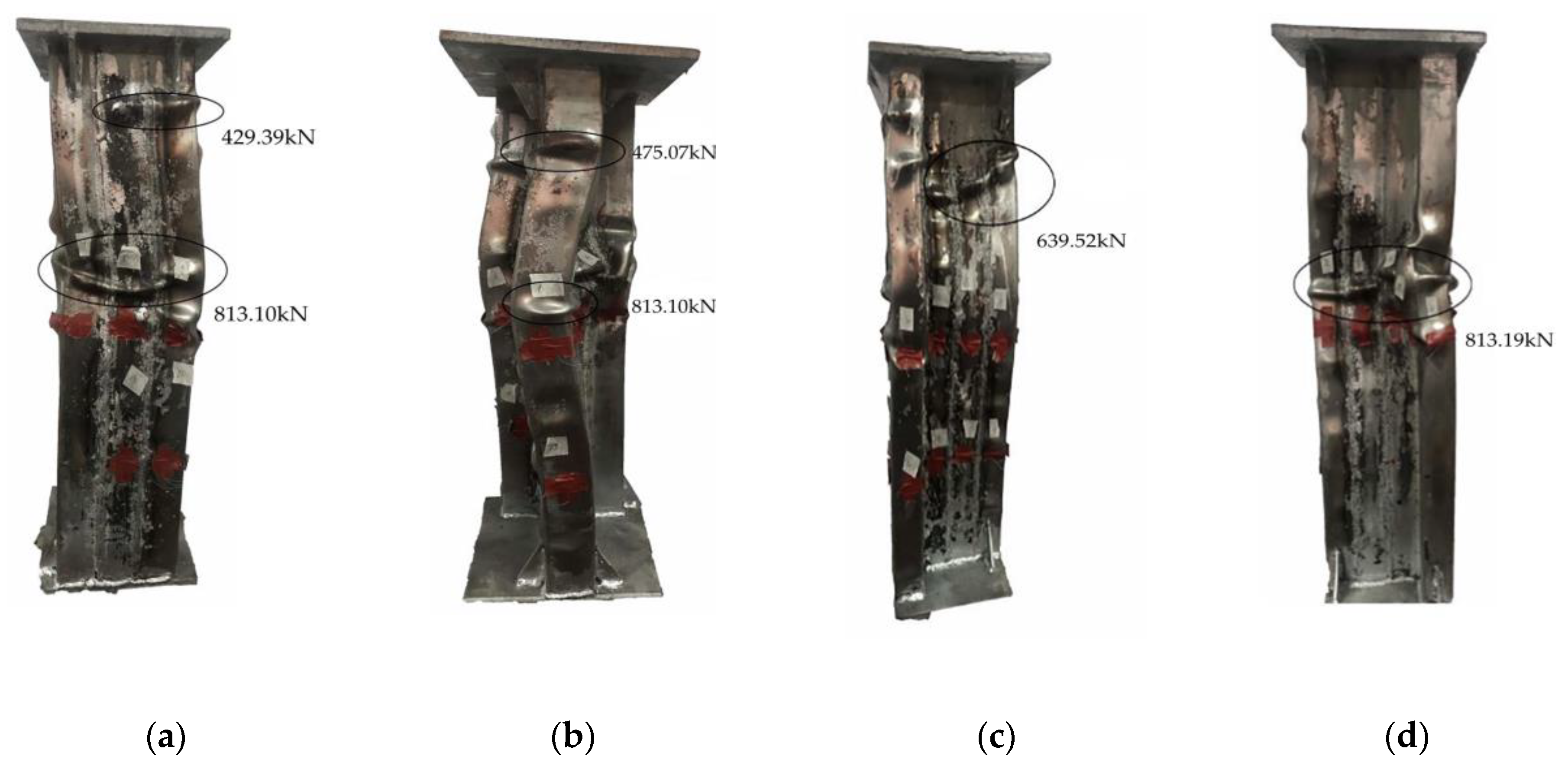
4.3. TA6-600 Shear Wall Test Phenomenon
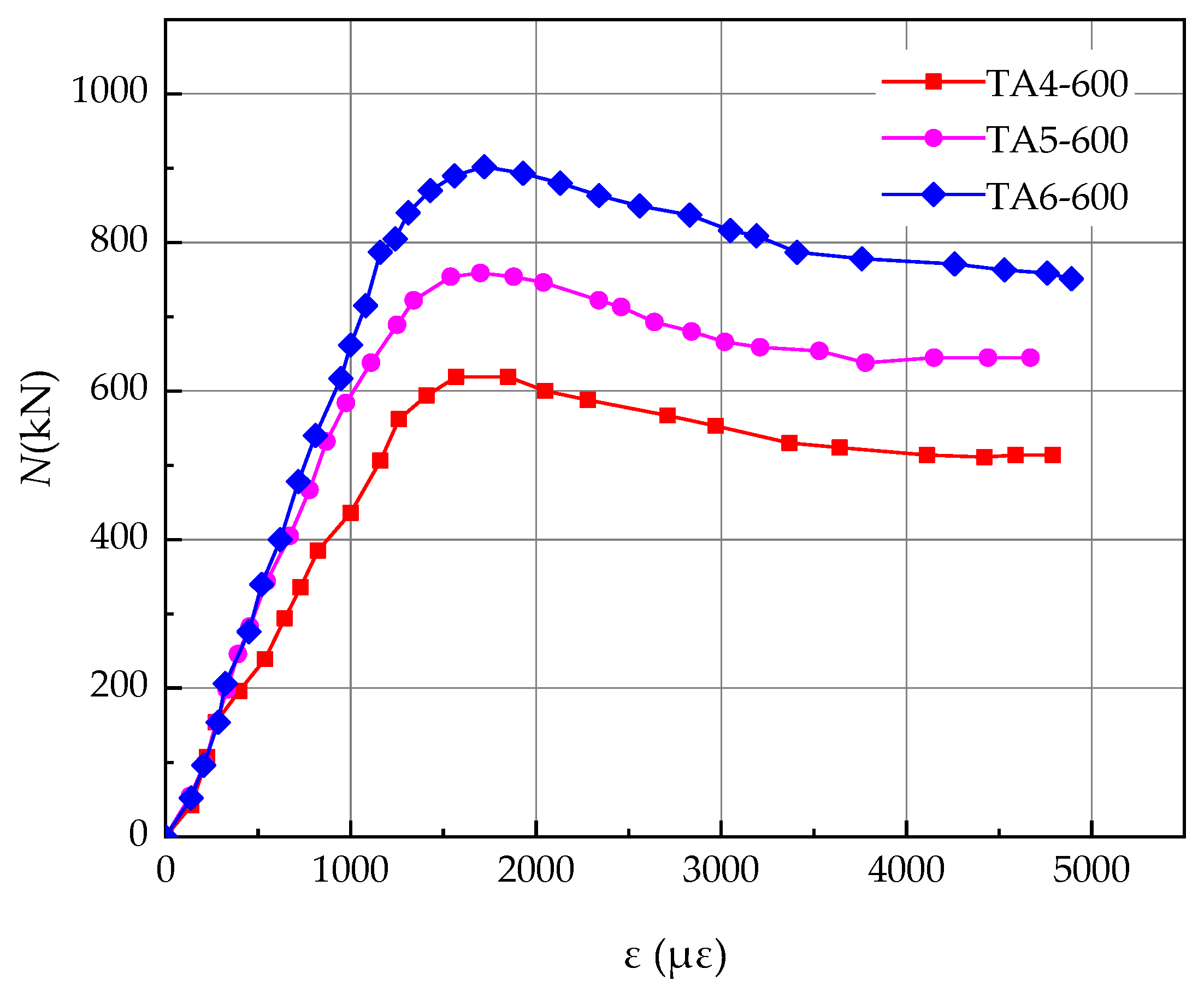
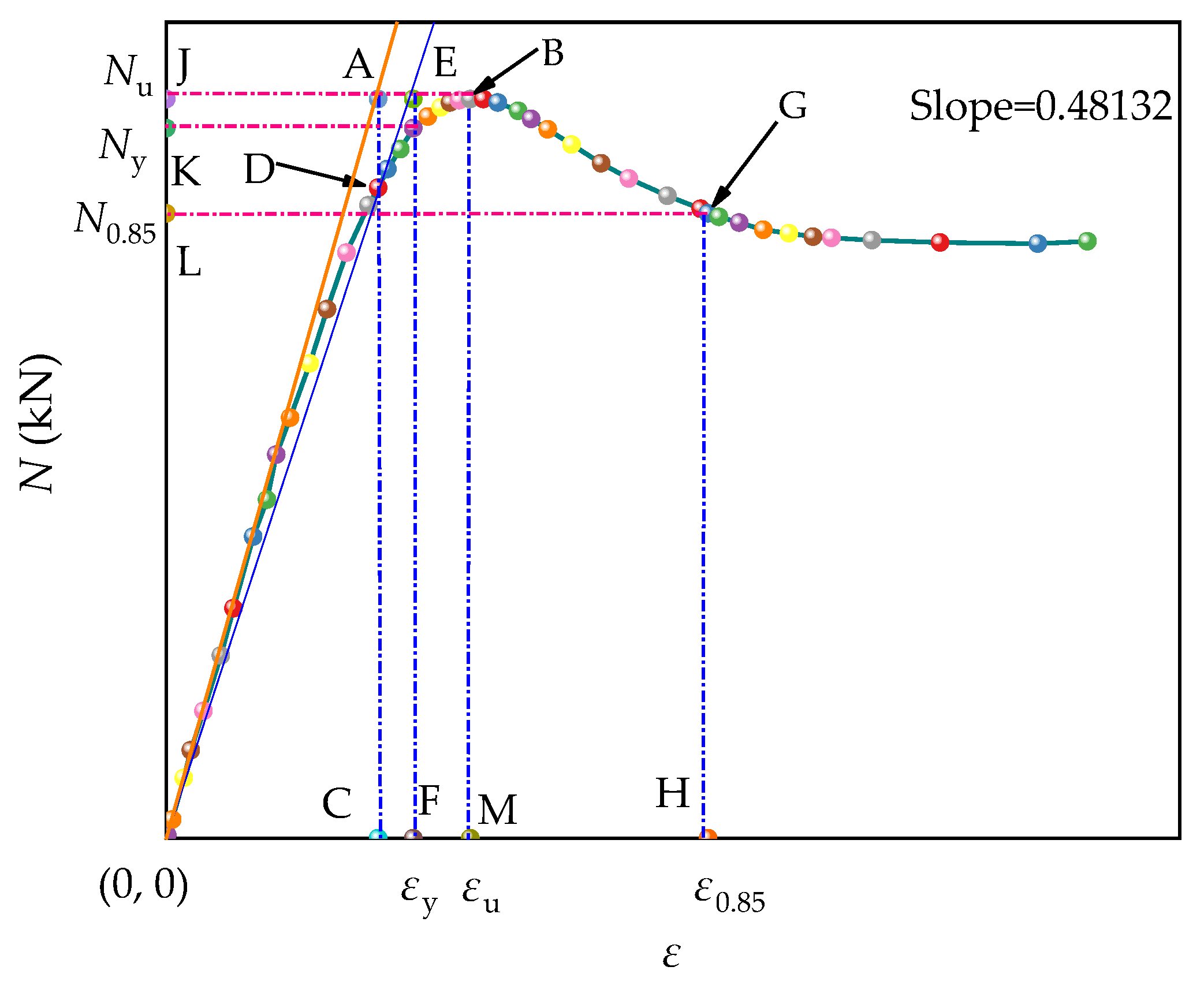
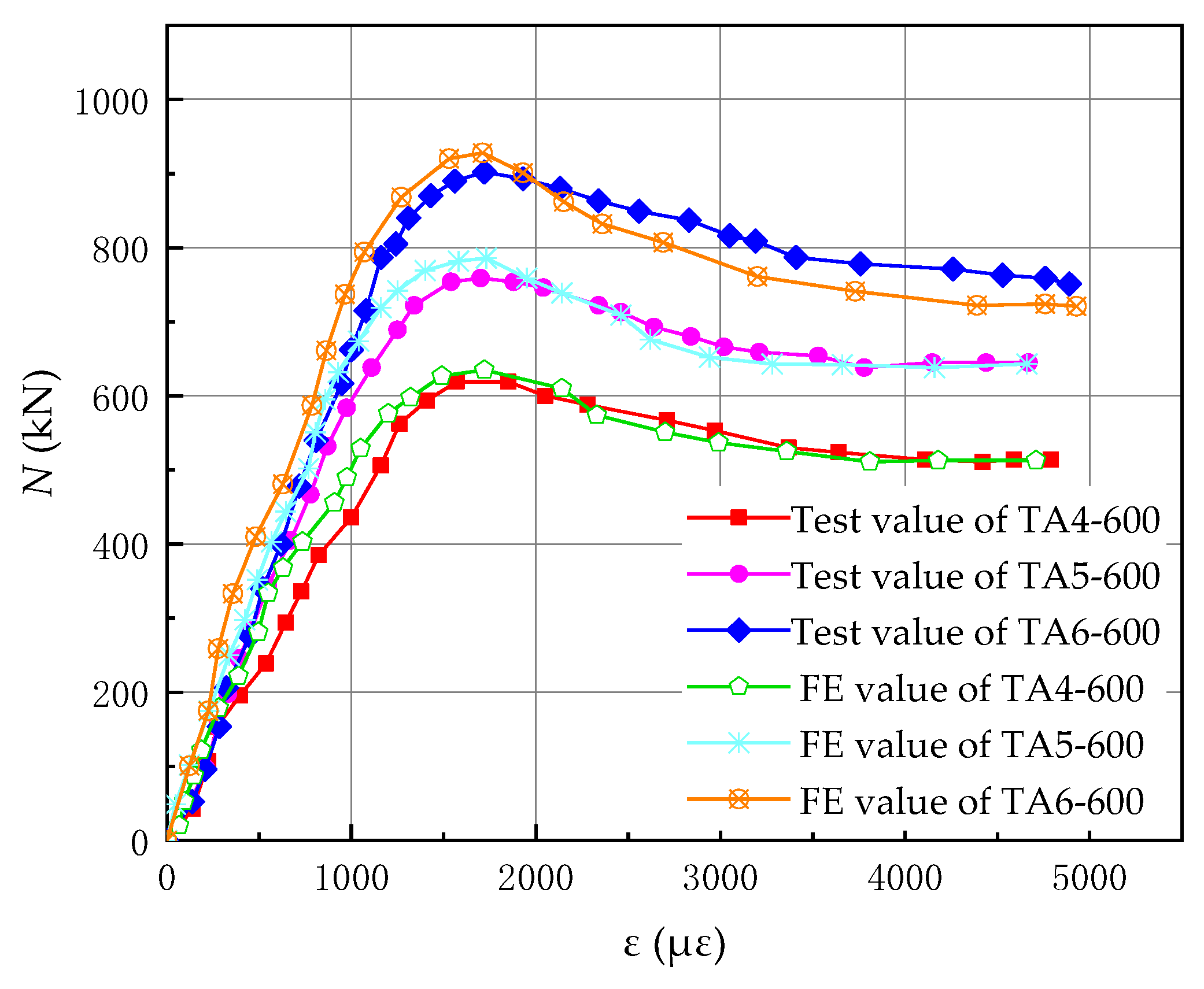
5. Axial Load–Strain Relationship Curve and Ductility Coefficient
| No. | Specimen Number | Ny (kN) | Nu (kN) | Ny/Nu | Ductility Coefficient |
|---|---|---|---|---|---|
| 1 | TA4-600 | 594.39 | 625.67 | 0.95 | 2.27 |
| 2 | TA5-600 | 738.22 | 768.98 | 0.96 | 2.15 |
| 3 | TA6-600 | 886.19 | 913.60 | 0.97 | 1.79 |
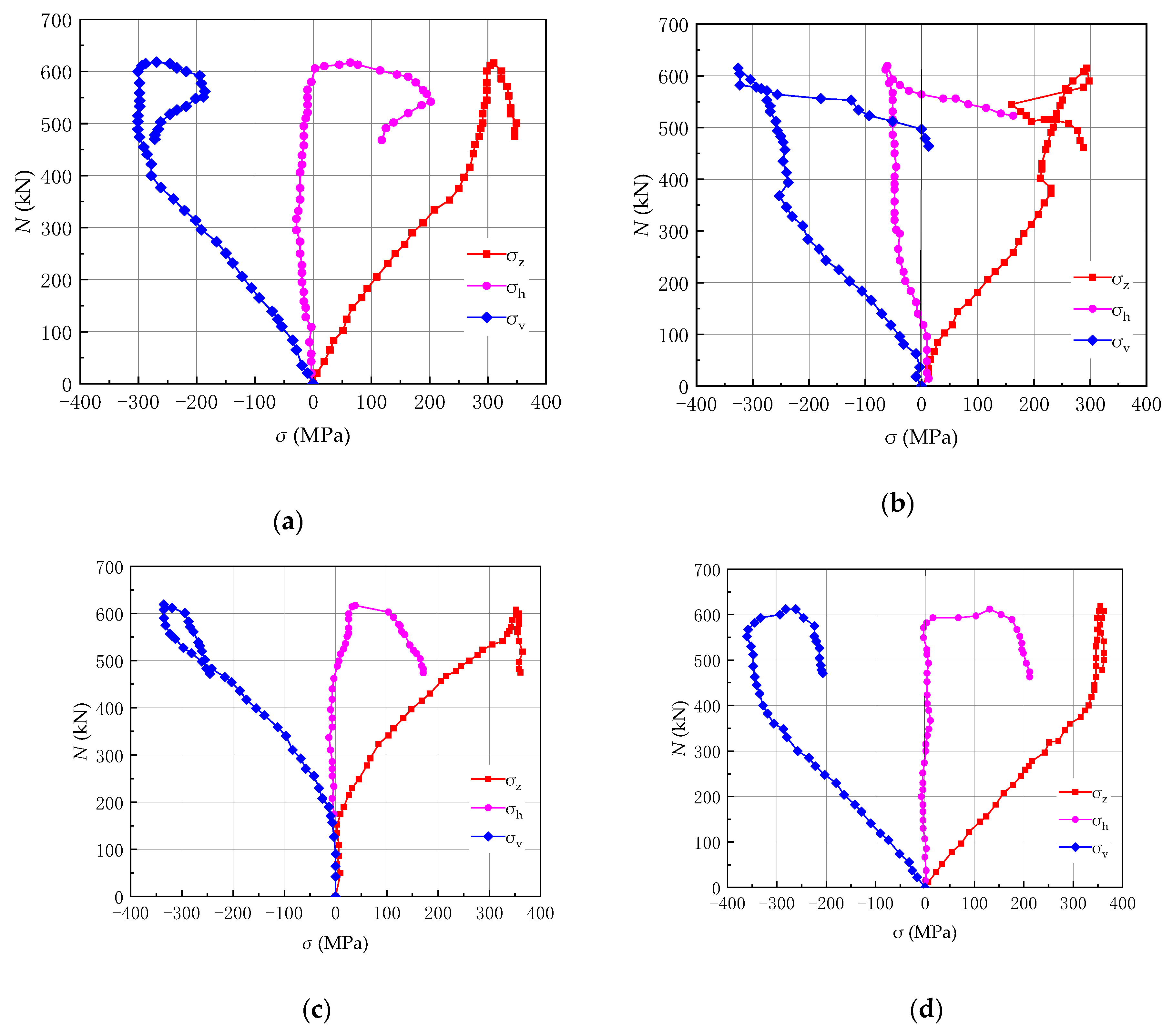
6. Load–Stress Relationship Curve
7. Establishment and Analysis of the Finite Element (FE) Model
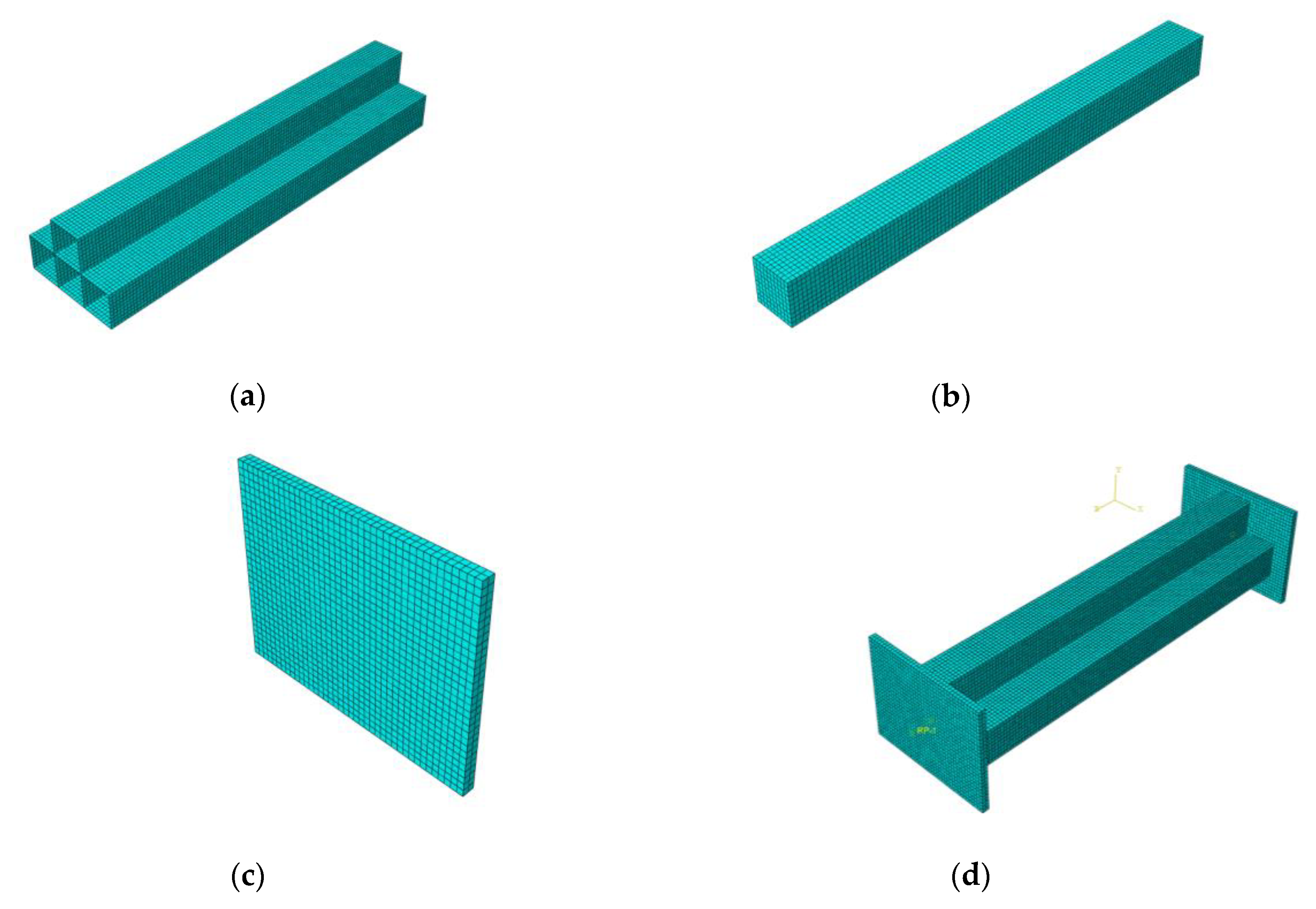
7.1. Establishment of Finite Element (FE) Model
7.2. Finite Element Results and Analysis
7.2.1. Axial Load–Strain Relationship Curve
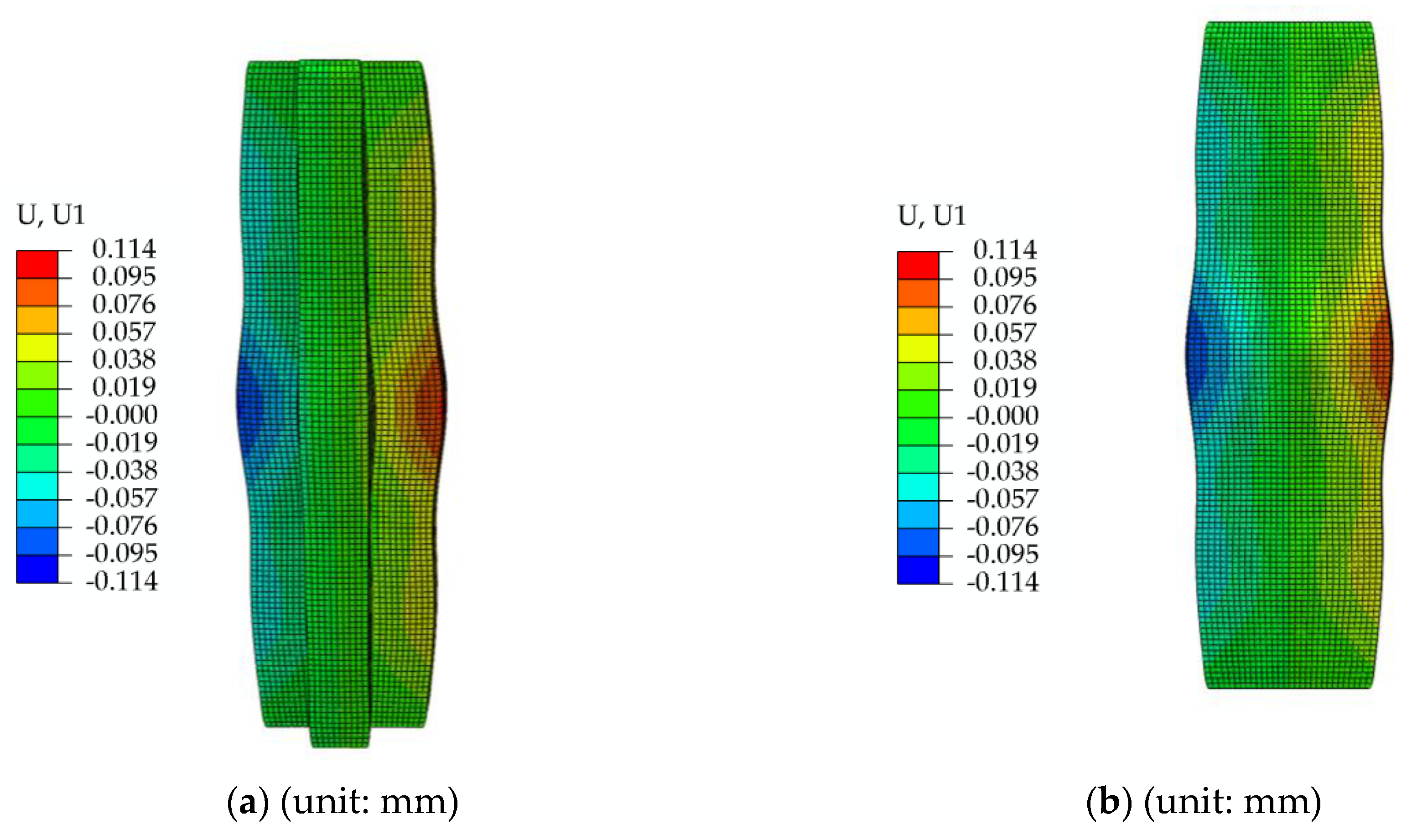
7.2.2. Final Deformation of the Specimen
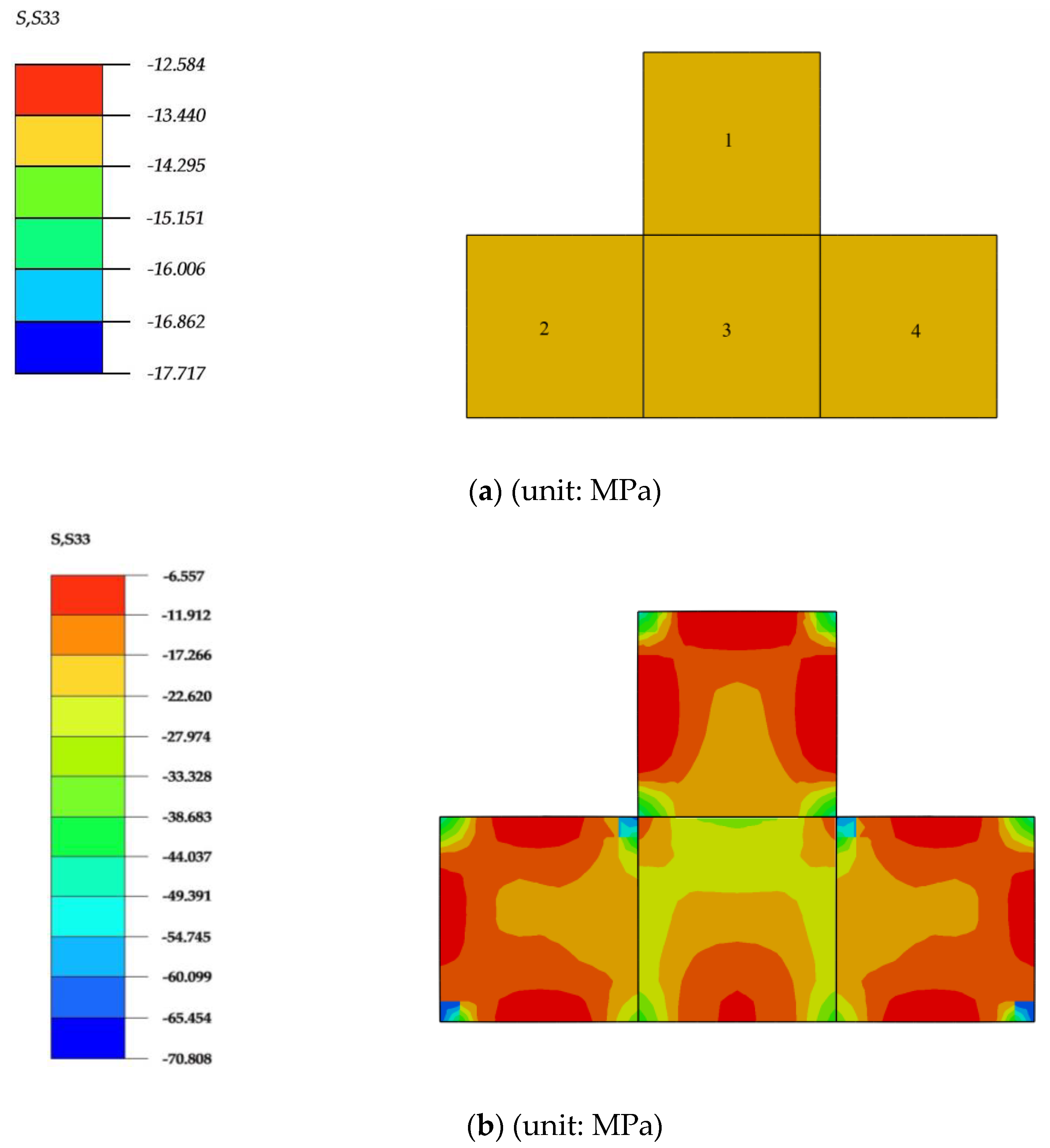
7.2.3. Steel Tube and Concrete Interaction
8. Bearing Capacity Equation Deduction
9. Conclusions
- It can be drawn from the test phenomenon that there is no obvious rule for the location of local buckling of steel tubes and local crushing of concrete. The failure mode of the T-shaped multi-cavity CFSTSW as mainly multi-wave buckling failure. All parts of the test specimen worked well together with good ductility.
- As the number of cavities increased, the axial compression bearing capacity of the T-shaped multi-cavity CFSTSW increased, but the ductility performance decreased accordingly.
- The three-dimensional finite element analysis results were in good agreement with the experimental results, indicating that the ABAQUS finite element model used in the article can simulate the axial compression performance of the multi-cavity CFSTSW well.
- A practical calculation equation for the bearing capacity of the T-shaped multi-cavity CFSTSW axial load column is proposed, which can provide a reference for the design of axial compression members of T-shaped multi-cavity CFSTSWs.
Author Contributions
Funding
Conflicts of Interest
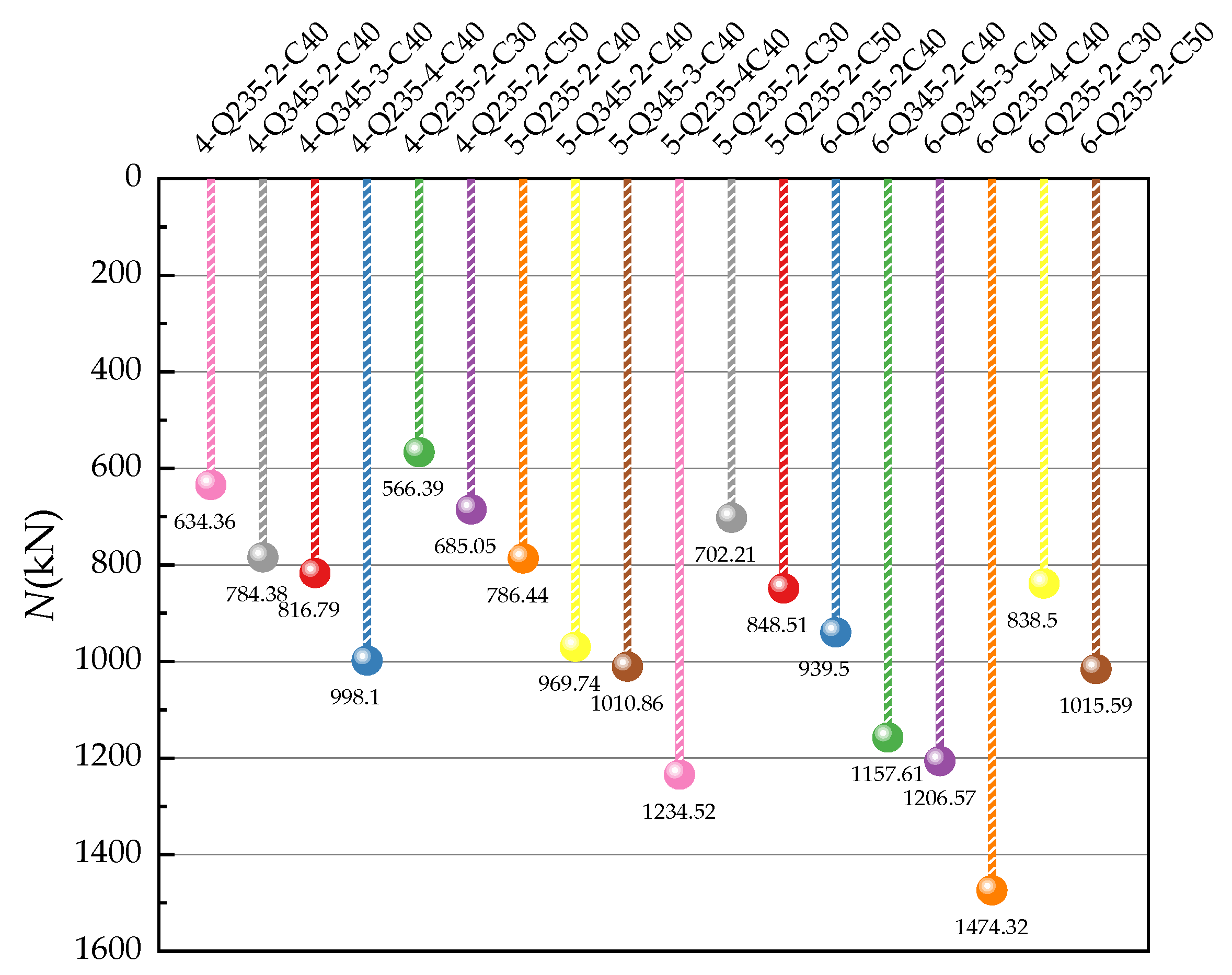
Appendix A
| No. | fc (MPa) | fs (MPa) | n | T (mm) | Nc (kN) | Ns (kN) | Difference Value (%) |
|---|---|---|---|---|---|---|---|
| TA4-600-1 | 38.17 | 235 | 4 | 2 | 644.34 | 634.37 | 1.548 |
| TA4-600-2 | 38.17 | 345 | 4 | 2 | 799.44 | 784.38 | 1.884 |
| TA4-600-3 | 38.17 | 235 | 4 | 3 | 810.02 | 816.79 | 0.836 |
| TA4-600-4 | 38.17 | 235 | 4 | 4 | 975.69 | 998.10 | 2.296 |
| TA4-600-5 | 30.80 | 235 | 4 | 2 | 583.91 | 566.39 | 3.000 |
| TA4-600-6 | 44.00 | 235 | 4 | 2 | 692.15 | 685.05 | 1.026 |
| TA5-600-1 | 38.17 | 235 | 5 | 2 | 802.49 | 786.44 | 2.000 |
| TA5-600-2 | 38.17 | 345 | 5 | 2 | 994.99 | 969.74 | 2.538 |
| TA5-600-3 | 38.17 | 235 | 5 | 3 | 1008.12 | 1010.86 | 0.272 |
| TA5-600-4 | 38.17 | 235 | 5 | 4 | 1213.74 | 1234.52 | 1.712 |
| TA5-600-5 | 30.80 | 235 | 5 | 2 | 726.95 | 702.21 | 3.403 |
| TA5-600-6 | 44.00 | 235 | 5 | 2 | 862.25 | 848.51 | 1.594 |
| TA5-600-1 | 38.17 | 235 | 6 | 2 | 960.64 | 939.50 | 2.201 |
| TA5-600-2 | 38.17 | 345 | 6 | 2 | 1190.54 | 1157.61 | 2.766 |
| TA5-600-3 | 38.17 | 235 | 6 | 3 | 1206.22 | 1206.57 | 0.029 |
| TA5-600-4 | 38.17 | 235 | 6 | 4 | 1451.79 | 1474.32 | 1.552 |
| TA5-600-5 | 30.80 | 235 | 6 | 2 | 869.99 | 838.50 | 3.620 |
| TA5-600-6 | 44.00 | 235 | 6 | 2 | 1032.35 | 1015.59 | 1.623 |
References
- Chiaia, B.; Kumpyak, O.; Placidi, L.; Maksimov, V. Experimental analysis and modeling of two-way reinforced concrete slabs over different kinds of yielding supports under short-term dynamic loading. Eng. Struct. 2015, 96, 88–99. [Google Scholar] [CrossRef]
- Han, L.-H.; An, Y.-F. Performance of concrete-encased CFST stub columns under axial compression. J. Constr. Steel Res. 2014, 93, 62–76. [Google Scholar] [CrossRef]
- Ding, F.-X.; Zhu, J.; Cheng, S. Comparative study of stirrup-confined circular concrete-filled steel tubular stub columns under axial loading. Thin-Walled Struct. 2018, 123, 294–304. [Google Scholar] [CrossRef]
- Portolés, J.M.; Romero, M.L.; Bonet, J.L. Experimental study of high strength concrete-filled circular tubular columns under eccentric loading. J. Constr. Steel Res. 2011, 67, 623–633. [Google Scholar] [CrossRef]
- Liu, D.; Zuo, J.; Wang, J.; Zhang, D.; Guo, S. Bending failure mechanism and strengthening of concrete-filled steel tubular support. Eng. Struct. 2019, 198. [Google Scholar] [CrossRef]
- Serras, D.N.; Skalomenos, K.A.; Hatzigeorgiou, G.D. Modeling of circular concrete-filled steel tubes subjected to cyclic lateral loading. Structures 2016, 8, 75–93. [Google Scholar] [CrossRef]
- Zhou, J.; Li, P.; Guo, N. Seismic performance assessment of a precast concrete-encased CFST composite wall with twin steel tube connections. Eng. Struct. 2020, 207. [Google Scholar] [CrossRef]
- Ding, F.-X.; Wang, W.-J.; Lu, D.-R. Study on the behavior of concrete-filled square double-skin steel tubular stub columns under axial loading. Structures 2020, 23, 665–676. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T. Behavior of square and rectangular ultra high-strength concrete-filled FRP tubes under axial compression. Compos. Part B Eng. 2013, 54, 97–111. [Google Scholar] [CrossRef]
- Qu, Q.-S.; Liu, Q.; Liao, W.-Z. Analysis on compression-bending behavior of concrete-filled rectangular steel column. J. Guangxi Univ. 2018, 43, 1149–1160. [Google Scholar]
- Wang, Y.-J.; Fan, Z.; Hou, C. Mechanical behavior of rectangular CFST columns under biaxial compression-bending-shearing loading condition. J. Build. Struct. 2019, 40, 257–263. [Google Scholar]
- Chen, Z.; Jing, C.; Xu, J. Seismic performance of recycled concrete-filled square steel tube columns. Earthq. Eng. Eng. Vib. 2017, 16, 119–130. [Google Scholar] [CrossRef]
- Xu, J.-J.; Chen, Z.-P.; Xue, J.-Y. Simulation of seismic behavior of square recycled aggregate concrete—Filled steel tubular columns. Constr. Build. Mater. 2017, 149, 553–566. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, C.; Lu, X. Experimental study of hysteretic behaviour for concrete-filled square thin-walled steel tubular columns. J. Constr. Steel Res. 2007, 63, 317–325. [Google Scholar] [CrossRef]
- Scerrato, D.; Giorgio, I.; Madeo, A.; Limam, A.; Darve, F. A simple non-linear model for internal friction in modified concrete. Int. J. Eng. Sci. 2014, 80, 136–152. [Google Scholar] [CrossRef][Green Version]
- Giorgio, I.; Scerrato, D. Multi-scale concrete model with rate-dependent internal friction. Eur. J. Environ. Civ. Eng. 2016, 21, 821–839. [Google Scholar] [CrossRef]
- Du, G.; Zhang, J.; Li, Y. Experimental study on hysteretic model for L-shaped concrete-filled steel tubular column subjected to cyclic loading. Thin-Walled Struct. 2019, 144. [Google Scholar] [CrossRef]
- Zuo, Z.-L.; Cai, J.; Yang, C. Axial load behavior of L-shaped CFT stub columns with binding bars. Eng. Struct. 2012, 37, 88–98. [Google Scholar] [CrossRef]
- Zuo, Z.-L.; Cai, J.; Chen, Q.-J. Performance of T-shaped CFST stub columns with binding bars under axial compression. Thin-Walled Struct. 2018, 129, 183–196. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Yang, Y. Resistance of special-shaped concrete-filled steel tube columns under compression and bending. J. Constr. Steel Res. 2020, 169. [Google Scholar] [CrossRef]
- Huang, H.; Cha, B.-J.; Yang, C. Mechanical behavior of T-shaped concrete-filled steel ribbed tubular short columns. J. Build. Struct. 2018, 39, 132–137. (In Chinese) [Google Scholar]
- Fu, X.-Y.; Wu, B.; Di, B. Research on T-shaped stiffener design for concrete-filled rectangular steel tube column. J. Build. Struct. 2017, 38, 49–54. [Google Scholar]
- Liu, J.; Yang, Y.; Song, H.; Wang, Y. Numerical analysis on seismic behaviors of T-shaped concrete-filled steel tubular columns with reinforcement stiffeners. Adv. Struct. Eng. 2017, 21, 1273–1287. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Fu, F.; Liu, J. Static behavior of T-shaped concrete-filled steel tubular columns subjected to concentric and eccentric compressive loads. Thin-Walled Struct. 2015, 95, 374–388. [Google Scholar] [CrossRef]
- Li, H.; Sun, H.; Tian, J.; Yang, Q.; Wan, Q. Mechanical and Ultrasonic Testing of Self-Compacting Concrete. Energies 2019, 12, 2187. [Google Scholar] [CrossRef]
- Li, H.; Sun, H.; Zhang, W.; Gou, H.; Yang, Q. Study on Mechanical Properties of Self-Compacting Concrete and Its Filled in-Line Multi-Cavity Steel Tube Bundle Shear Wall. Energies 2019, 12, 3466. [Google Scholar] [CrossRef]
- Golewski, G.L. Energy Savings Associated with the Use of Fly Ash and Nanoadditives in the Cement Composition. Energies 2020, 13, 2184. [Google Scholar] [CrossRef]
- Contrafatto, L.; Cuomo, M.; Greco, L. Meso-scale simulation of concrete multiaxial behaviour. Eur. J. Environ. Civ. Eng. 2016, 21, 896–911. [Google Scholar] [CrossRef]
- Zhong, S. The Concrete-Filled Steel Tubular Structures, 3rd ed.; Tsinghua University Press: Beijing, China, 2003; pp. 40–51. (In Chinese) [Google Scholar]
- Ding, F.-X.; Fu, L.; Gong, Y.-Z. Behavior of concrete-filled square steel tubular stub columns under axially compressive loading. J. Shenzhen Univ. 2014, 31, 583–592. (In Chinese) [Google Scholar] [CrossRef]
- Ding, F.-X.; Yu, Z.-W.; Yu, B. Elasto-plastic analysis of circular concrete-filled steel tube stub columns. J. Constr. Steel Res. 2011, 67, 1567–1577. [Google Scholar] [CrossRef]
- American Institute of Steel Construction ANSI/AISC 341-10. Seismic Provisions for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2010. [Google Scholar]
- Eurocode 4: Design of Composite Steel and Concrete Structures-Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004.
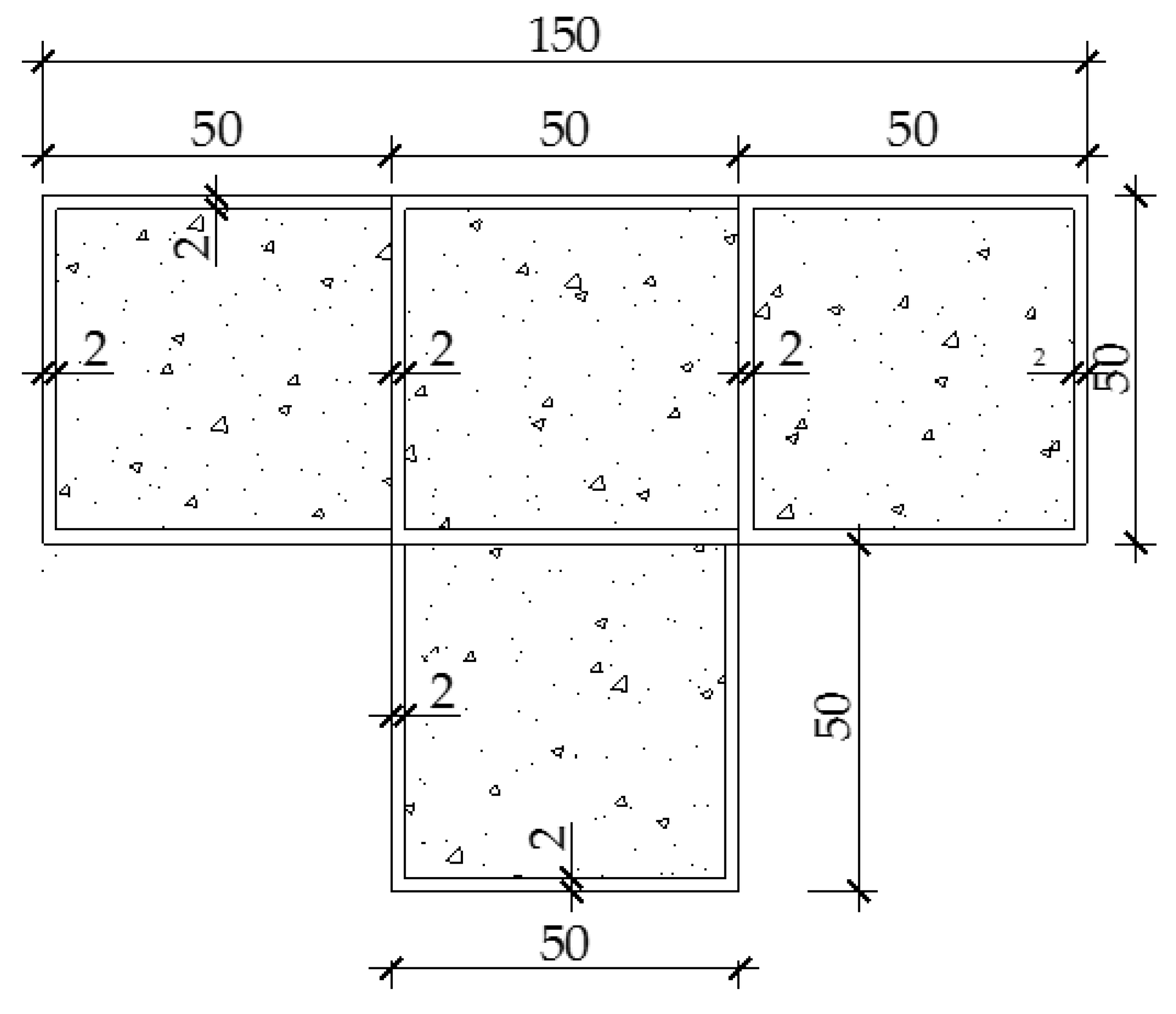
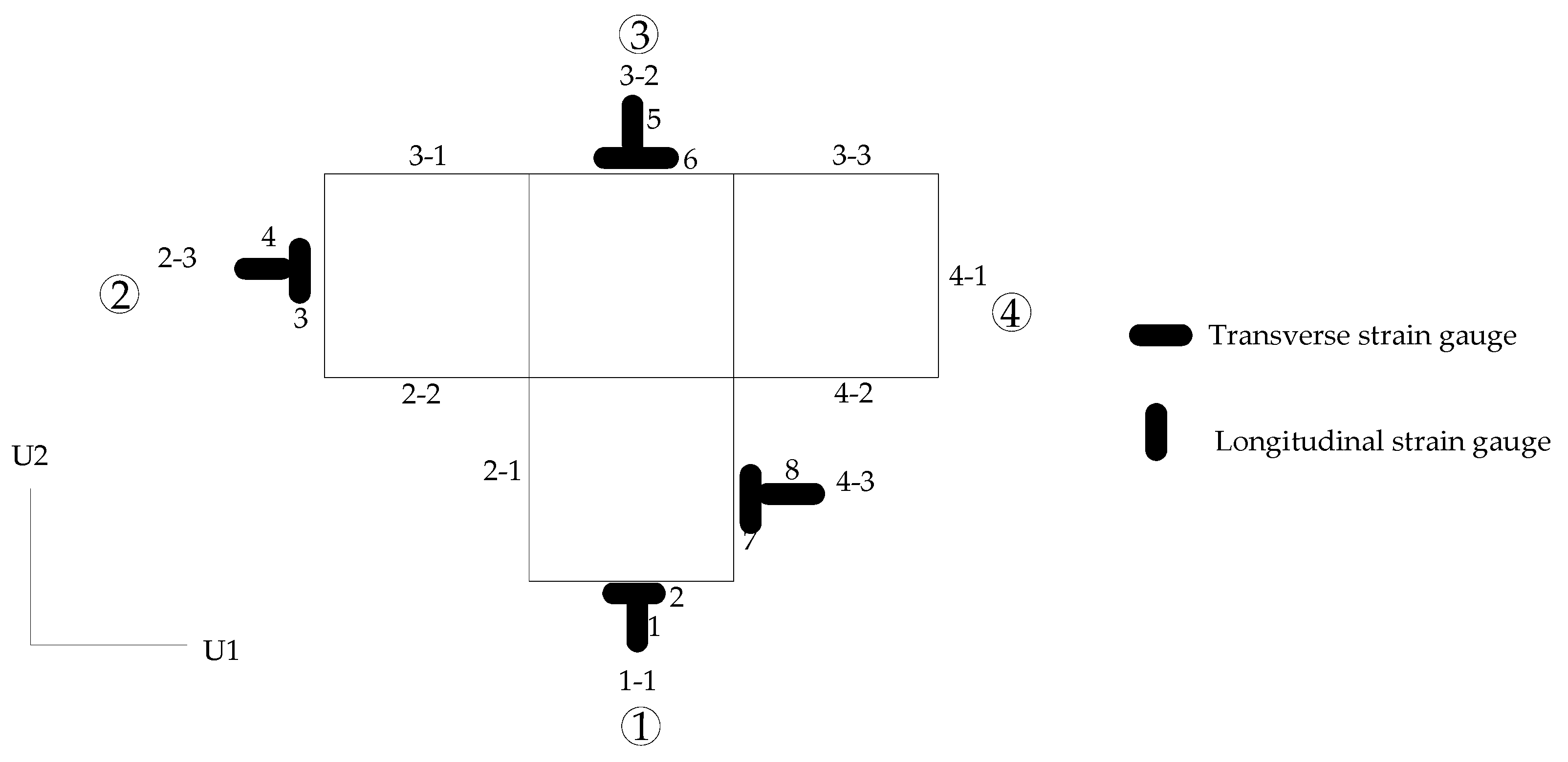



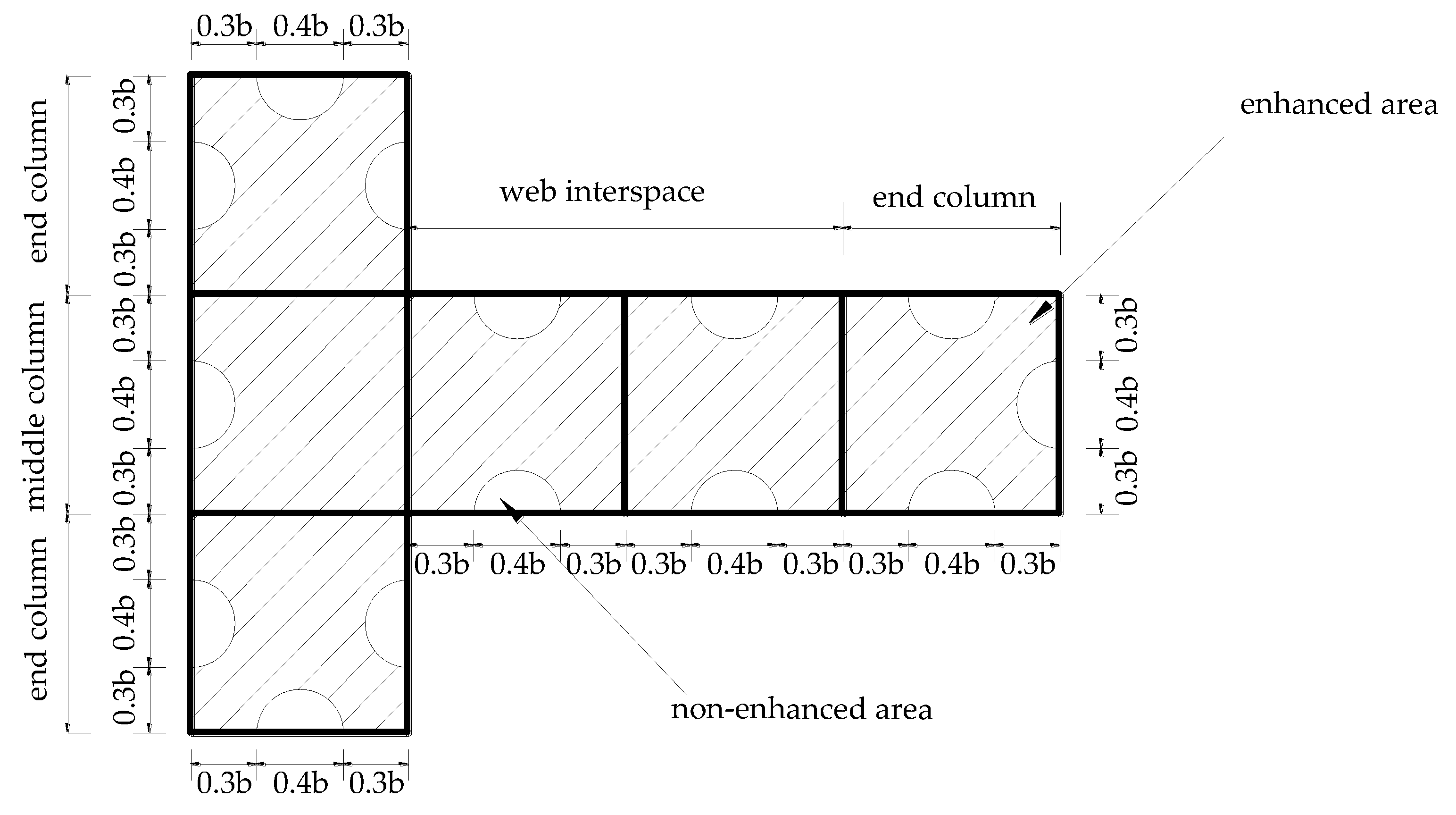
| No. | Specimen Number | Cavity Thickness | Nominal Thickness | Total Number of Cavities | Specimen Height | Nominal Steel Content (%) |
|---|---|---|---|---|---|---|
| tw (mm) | t (mm) | |||||
| 1 | TA4-600 | 50 | 2 | 4 | 600 | 13.40 |
| 2 | TA5-600 | 50 | 2 | 5 | 600 | 13.10 |
| 3 | TA6-600 | 50 | 2 | 6 | 600 | 13.04 |
| Loading Age | Concrete Strength | Elasticity Modulus | Poisson’s Ratio | |
|---|---|---|---|---|
| (Days) | fcu (MPa) | fc (MPa) | Ec (×105 MPa) | μc |
| 28 | 55.580 | 38.170 | 0.276 | 0.220 |
| Measured Thickness | Tensile Strength | Yield Strength | Elasticity Modulus | Poisson’s Ratio | Elongation |
|---|---|---|---|---|---|
| T (mm) | fu (MPa) | fy (MPa) | Es (×105 MPa) | μs | |
| 1.72 | 416.70 | 298.42 | 2.07 | 0.29 | 0.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Xu, Q.; Yan, P.; Yin, J.; Lou, P. A Study on Axial Compression Performance of Concrete-Filled Steel-Tubular Shear Wall with a Multi-Cavity T-Shaped Cross-Section. Energies 2020, 13, 4831. https://doi.org/10.3390/en13184831
Sun H, Xu Q, Yan P, Yin J, Lou P. A Study on Axial Compression Performance of Concrete-Filled Steel-Tubular Shear Wall with a Multi-Cavity T-Shaped Cross-Section. Energies. 2020; 13(18):4831. https://doi.org/10.3390/en13184831
Chicago/Turabian StyleSun, Hao, Qingyuan Xu, Pengfei Yan, Jianguang Yin, and Ping Lou. 2020. "A Study on Axial Compression Performance of Concrete-Filled Steel-Tubular Shear Wall with a Multi-Cavity T-Shaped Cross-Section" Energies 13, no. 18: 4831. https://doi.org/10.3390/en13184831
APA StyleSun, H., Xu, Q., Yan, P., Yin, J., & Lou, P. (2020). A Study on Axial Compression Performance of Concrete-Filled Steel-Tubular Shear Wall with a Multi-Cavity T-Shaped Cross-Section. Energies, 13(18), 4831. https://doi.org/10.3390/en13184831





