Two-Stage Fuzzy Logic Inference Algorithm for Maximizing the Quality of Performance under the Operational Constraints of Power Grid in Electric Vehicle Parking Lots
Abstract
1. Introduction
- The energy requirements of the EV owners are identified using realistic traveling distance patterns from the US national household travel survey (NHTS) and their G2V and V2G operations are formulated and solved through a TSFLIA.
- The first stage fuzzy inference system (FIS) is developed based on the real data obtained from the NHTS to compute the aggregated charging and discharging energies of EVs according to their next trip travelling distances. The second stage FIS utilizes the inputs from EVs and the power grid to determine an adequately accurate charging and discharging preferences for each of the connected EVs.
- The TSFLIA is developed with five sub-algorithms: (1) Manage_new_arrival, (2) First_stage_FLM (Fuzzy Logic Module), (3) Second_stage_FLM, (4) Manage_charge_discharge, and (5) Manage_departure. The registration of new arriving EVs, the departure of served EVs and the maintenance of PL occupancies are serviced by Manage_new_arrival and Manage_departure. The First_stage_FLM resolves the departure time from home and arrival time to PL to compute the SoC and required SoC of EVs according to their traveled and next trip distances and categorizes the operation of EVs in G2V, V2G and idle modes. The Second_stage_FLM account an accurate preference for each of the connected EVs by comprehensively solving the complexity of temporal based varying available power, required SoC for the next trip and EVs remaining parking duration. In each sampling period, the scheduled G2V and V2G operations of EVs are controlled according to their preference values through the sub-algorithm Manage_charge_discharge.
- The proposed TSFLIA is applied to three different PLs connected to the IEEE 34-node distribution system and the results are validated against the FLIA.
2. Related Work
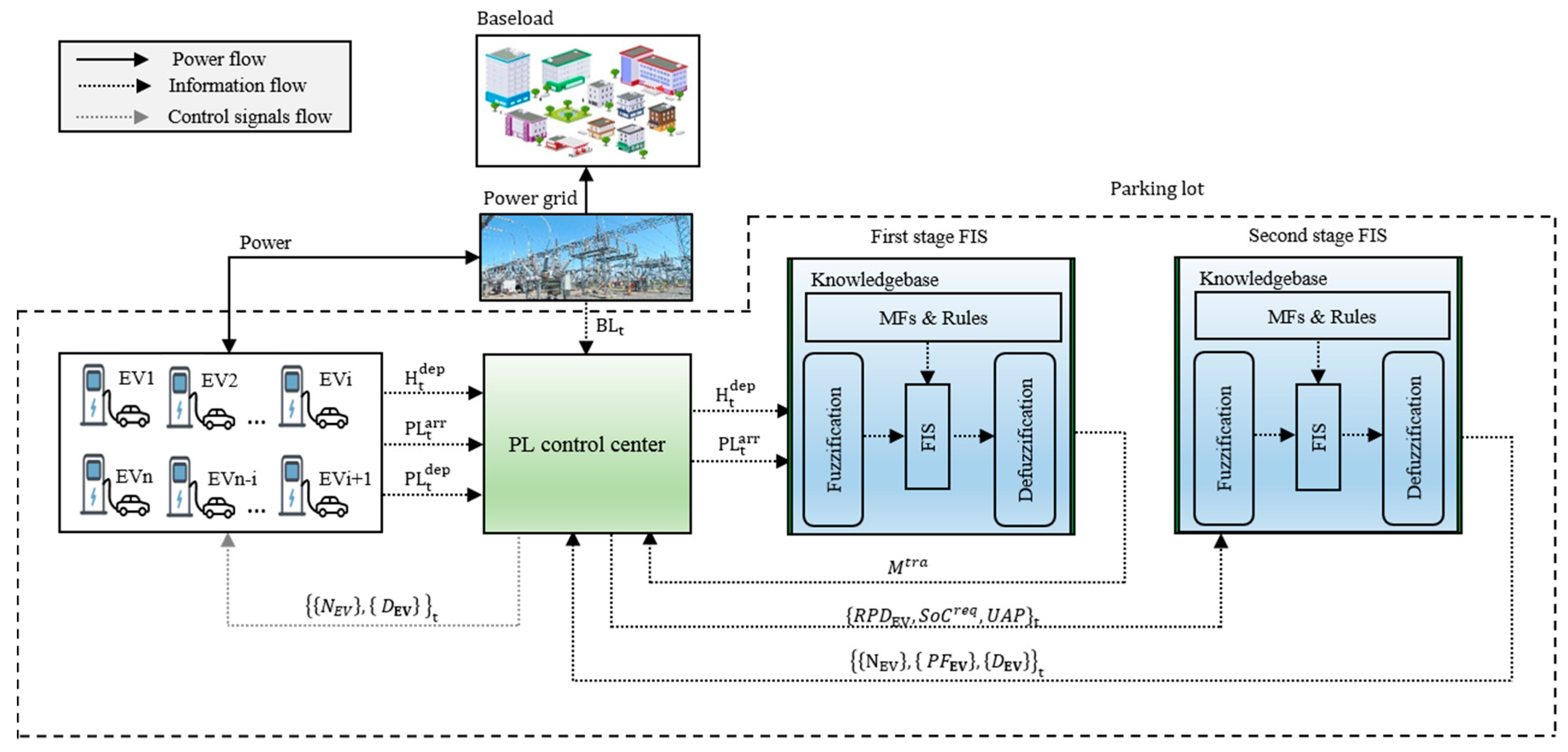
3. Proposed Two-Stage Fuzzy Logic Inference Algorithm
3.1. System Model of the Proposed TSFLIA
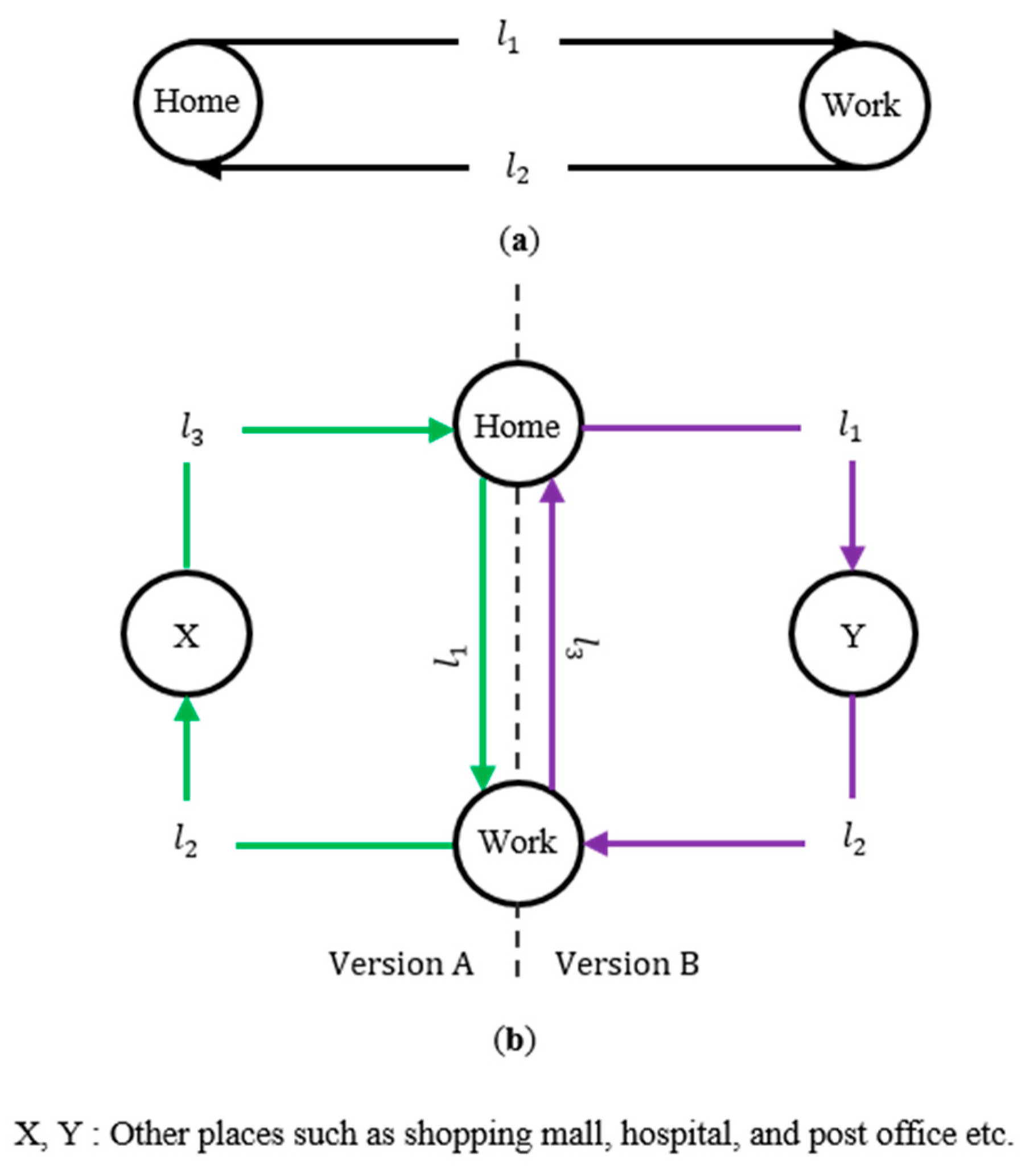
3.1.1. National Household Survey Data and the Probability based Functions
- (1)
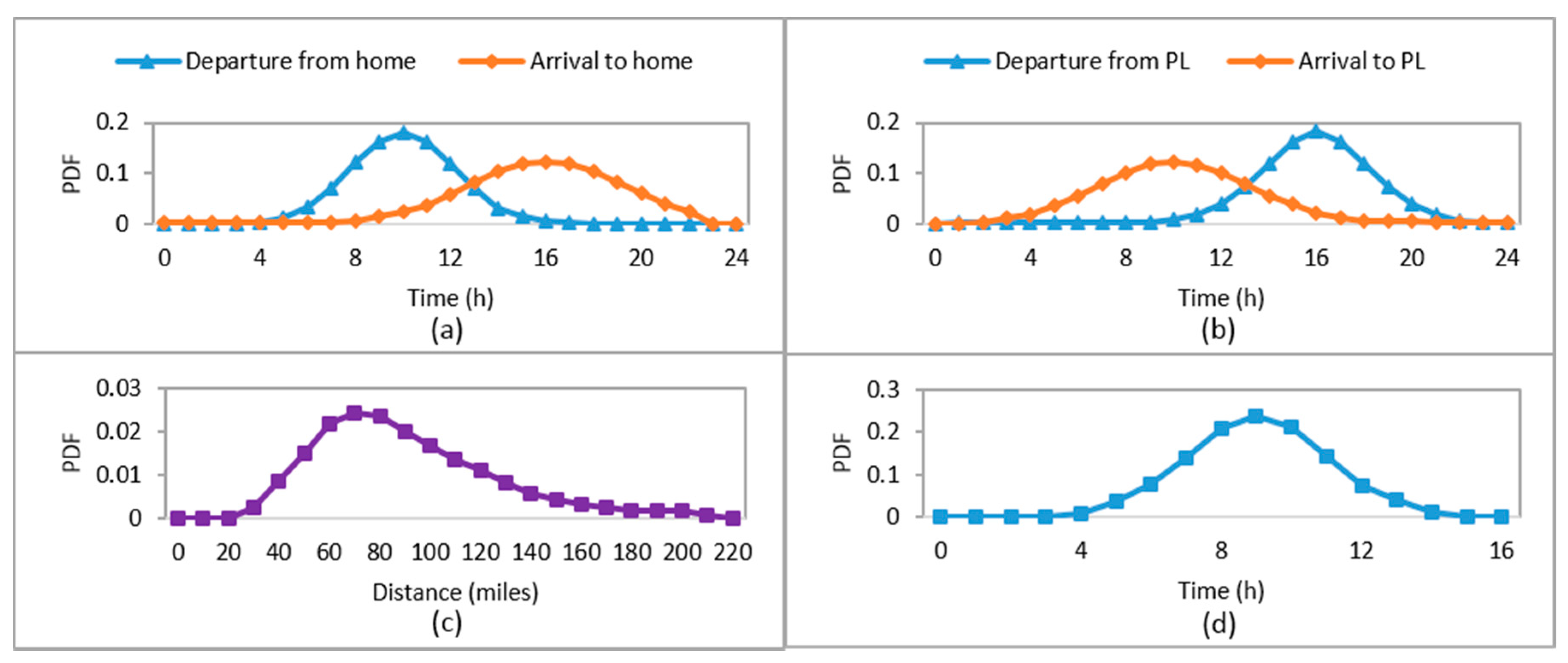
- Arrival and departure PDF: The arrival time (from home to PL) and departure time (from PL to home) of EVs are considered to follow a normal distribution function as given in Equation (1) and shown in Figure 3a, and Figure 3b, respectively [32]:where the mean for arrival and departure to/from home and PL are , , and , respectively. Similarly, the standard deviation for arrival and departure to/from home and PL are and , respectively. The mean and standard deviation values are obtained from the NHTS-2009 data based on [32].
- (2)
- (3)
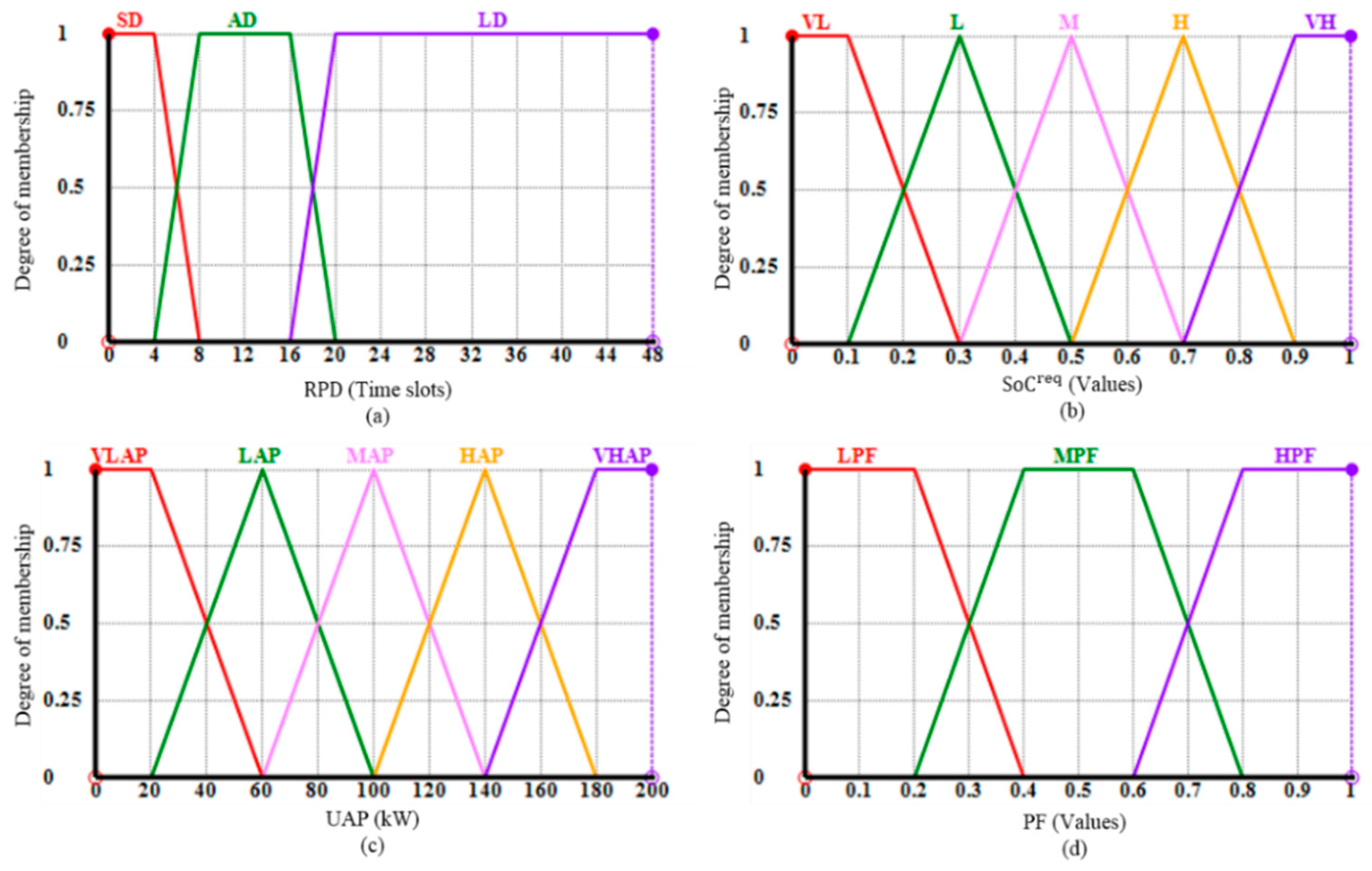
3.1.2. First Stage Fuzzy Logic Inference System
3.1.3. Problem Formulation and Objective Function
- G2V operation: The EVs are considered to perform the G2V if their required SoCs are greater than their corresponding initial SoCs.
- V2G operation: The EVs with required SoCs less than their initial SoCs are scheduled to participate in V2G operation.
- Idle (no-participation): The EVs are considered to remain idle if their required SoCs are equivalent to their initial SoCs.
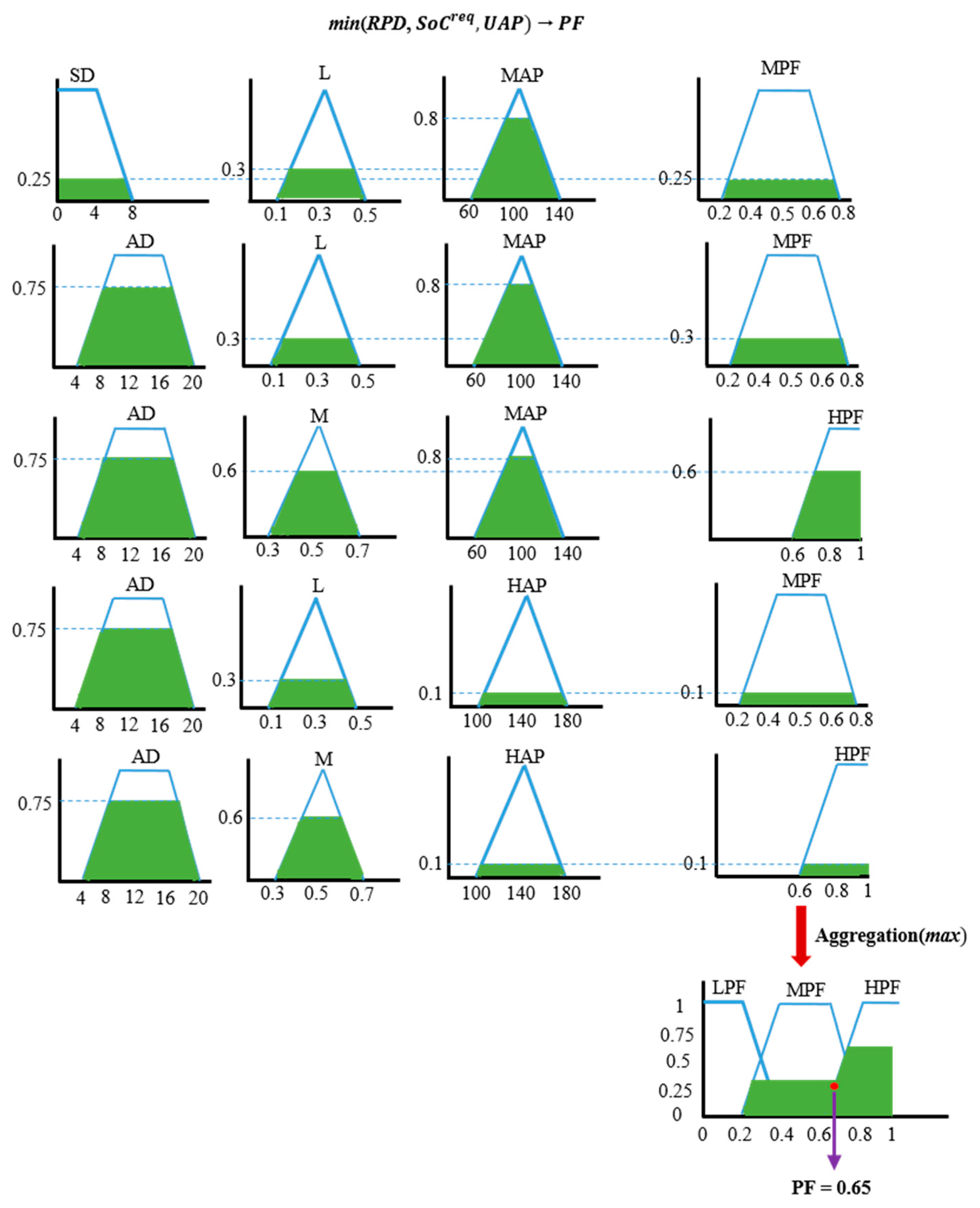
3.1.4. Second Stage Fuzzy Logic Inference System
3.1.5. Pseudocode of the Proposed TSFLIA
| Algorithm 1: | Two-Stage Fuzzy Logic Inference Main Algorithm |
 | |
| Algorithm 2 | Manage_new_arrivals (,) |
 | |
| Algorithm 3 | First_stage_FLM () |
| 1. | FIS.load(rules file) */ Load the fuzzy rule file from Table 1 */ |
| 2. | /* Evaluate through FIS and categorize the EVs into G2V, V2G, and idle using Equations (4)–(6) */ |
| 3. | or |
| 4. | or |
| 5. | If ( [j]) |
| 6. | |. /* Set flag for full charge and compute QoE according to Equation (27) */ |
| 7. | Else if ( [j]) |
| 8. | | /* Set flag for partial charge and compute QoE according to Equation (27) */ |
| 9. | Else if () |
| 10. | | /* Set flag for idle and compute QoE according to Equation (27) */ |
| 11. | Else if () |
| 12. | | /* Flag for discharge and compute QoE according to Equation (27) */ |
| 13. | End |
| 14. | Return updated and |
| Algorithm 4 | Second_stage_FLM) |
 | |
| Algorithm 5 | Manage_charge_discharge () |
 | |
| Algorithm 6 | Manage_departure (,,) |
| 1. | Check the departure time constraints defined by Equation (19) |
| 2. | If () |
| 3. | | + 1 |
| 4. | Else if () |
| 5. | | + 1 |
| 6. | End if |
| 7. | −1 /*Decrement list of EVs*/ |
| 8. | Return updated and |
4. Simulation Results and Discussion
4.1. Simulation Setting and Assumption
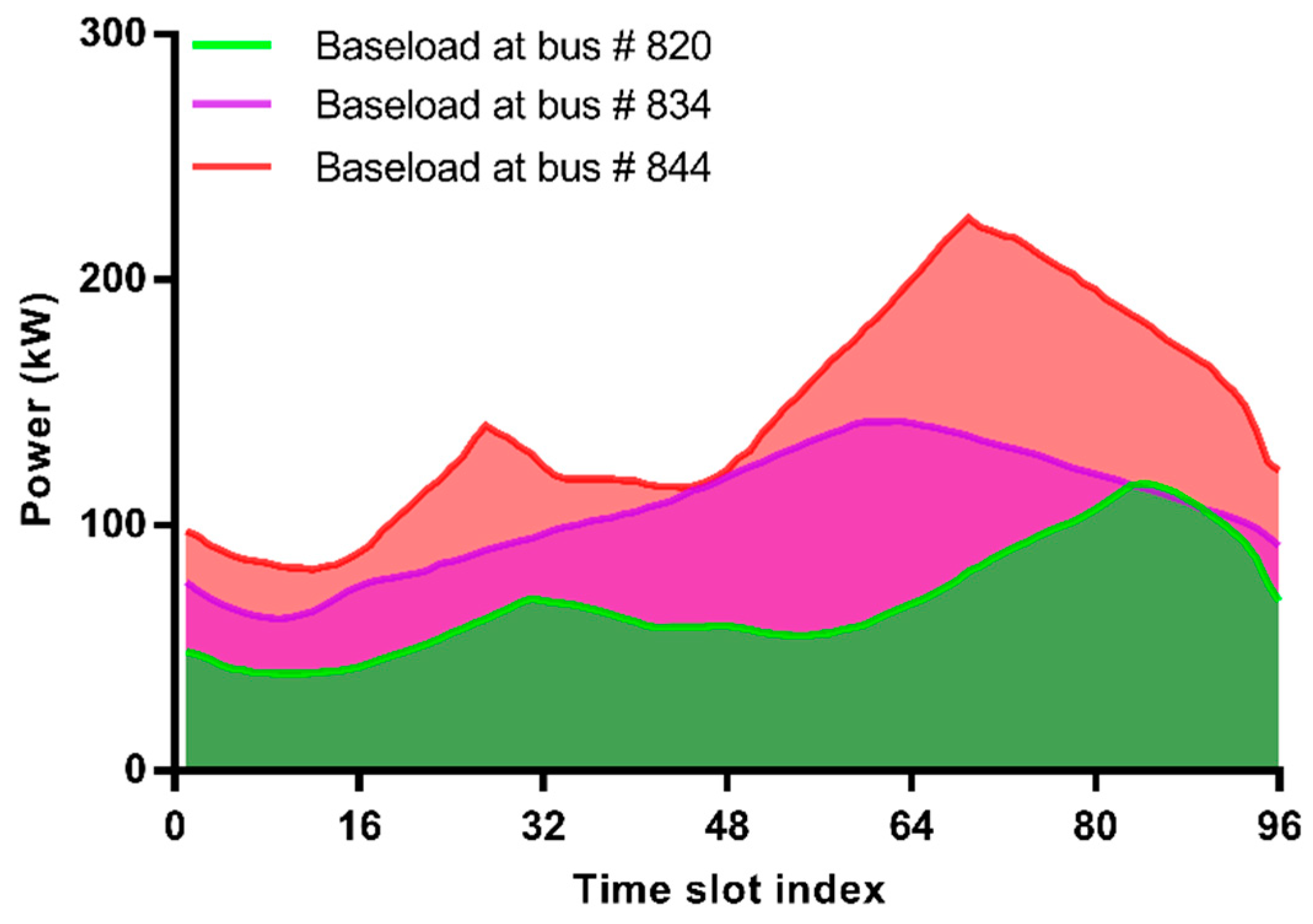
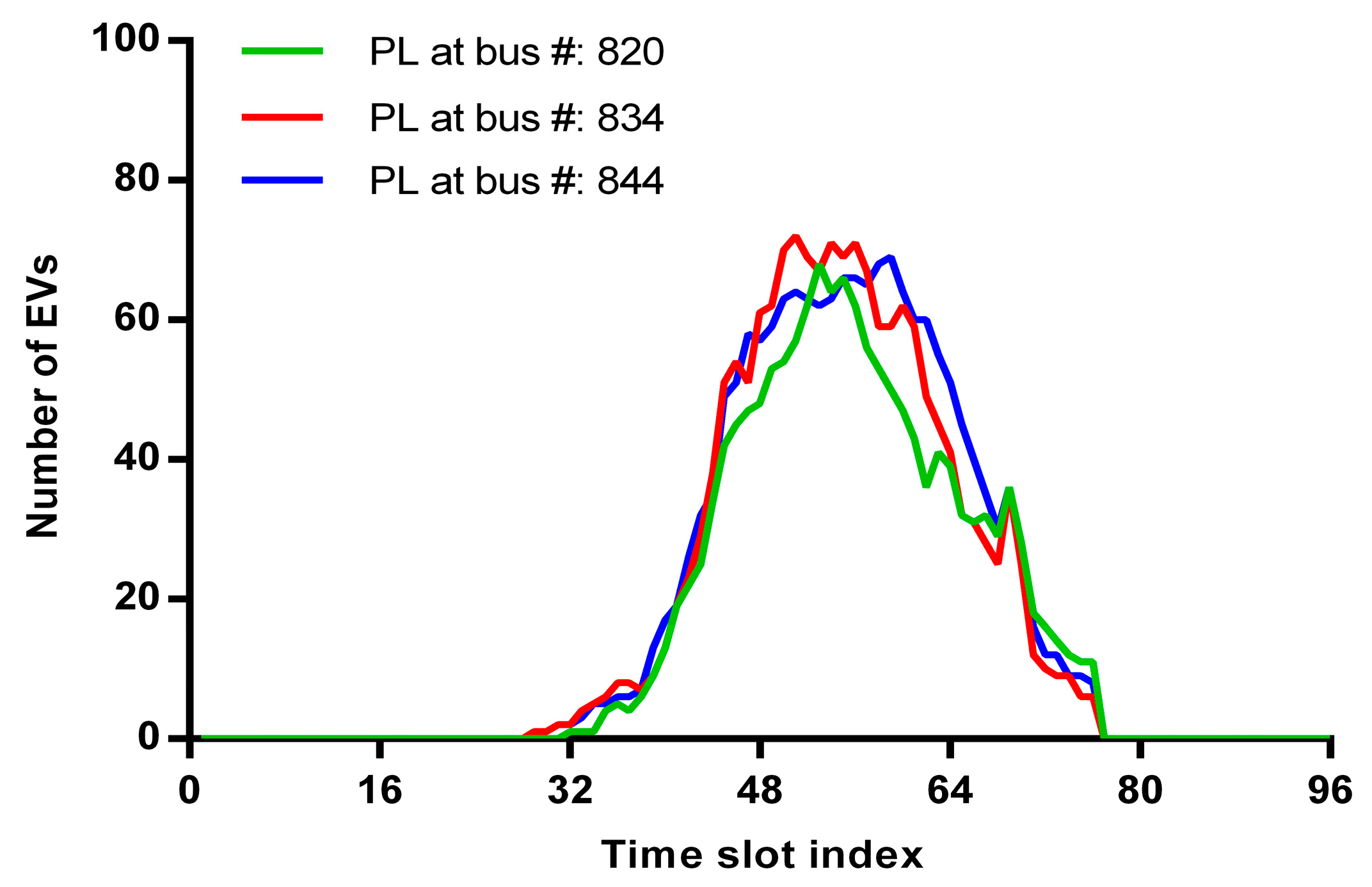
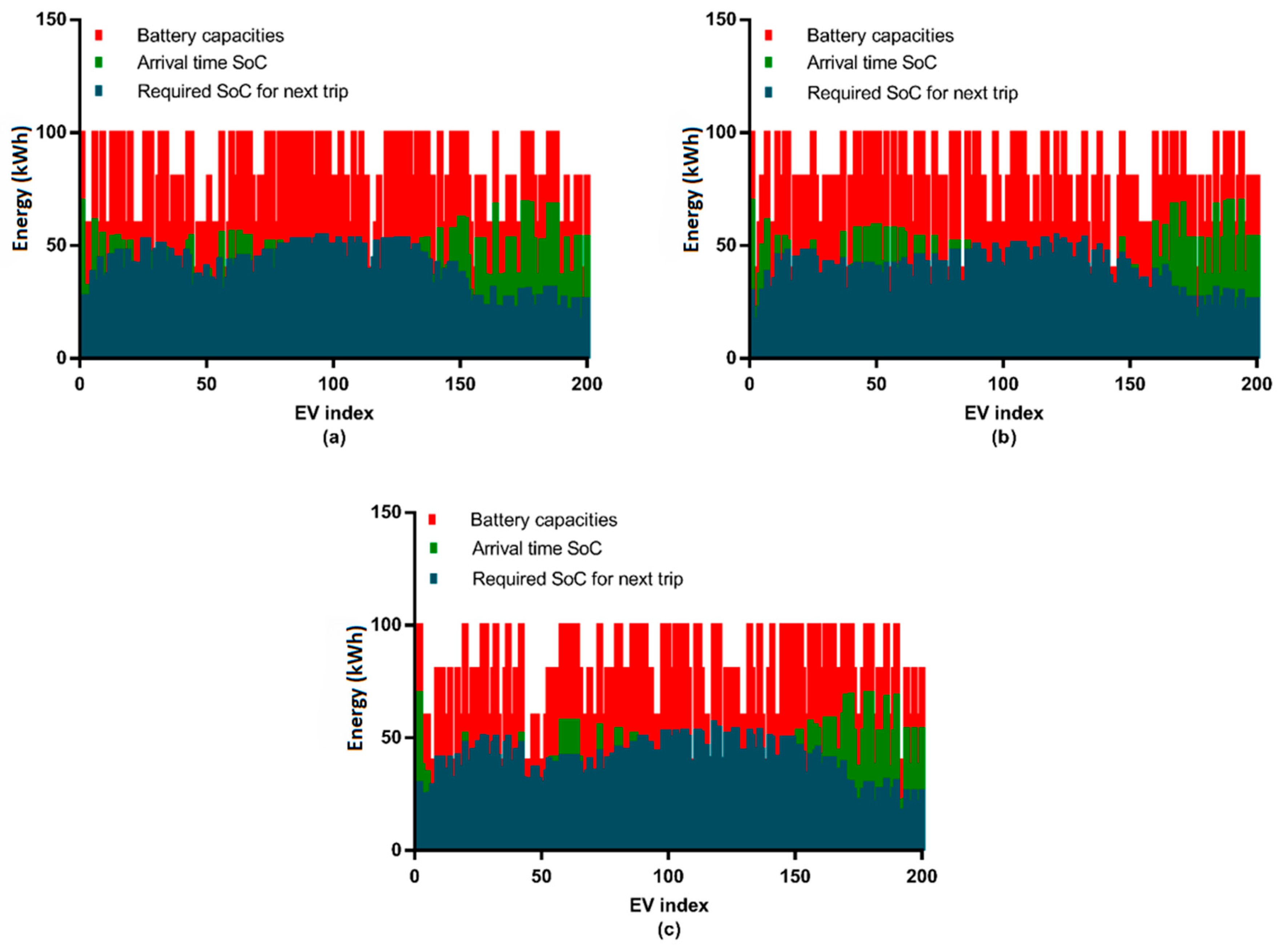
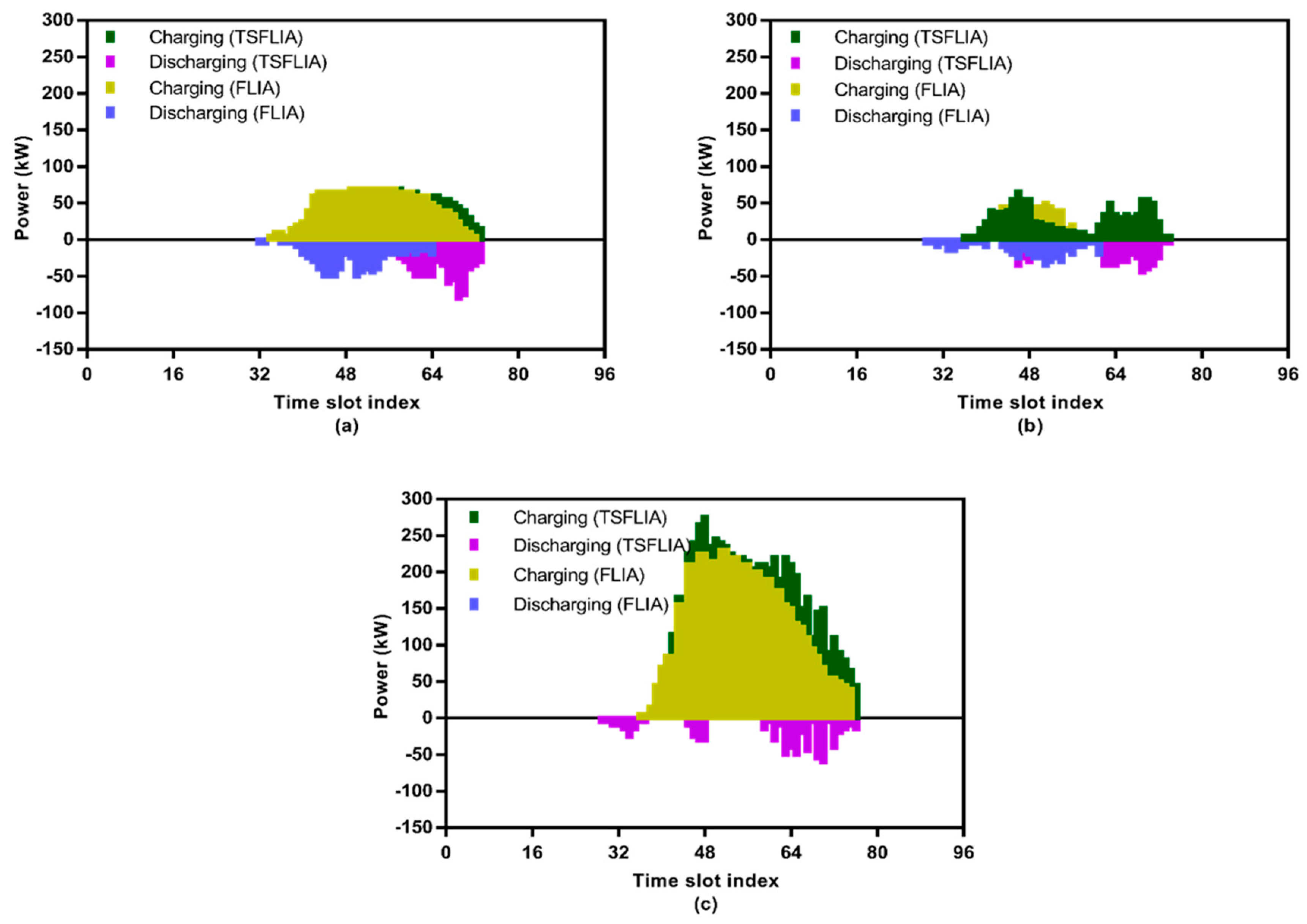
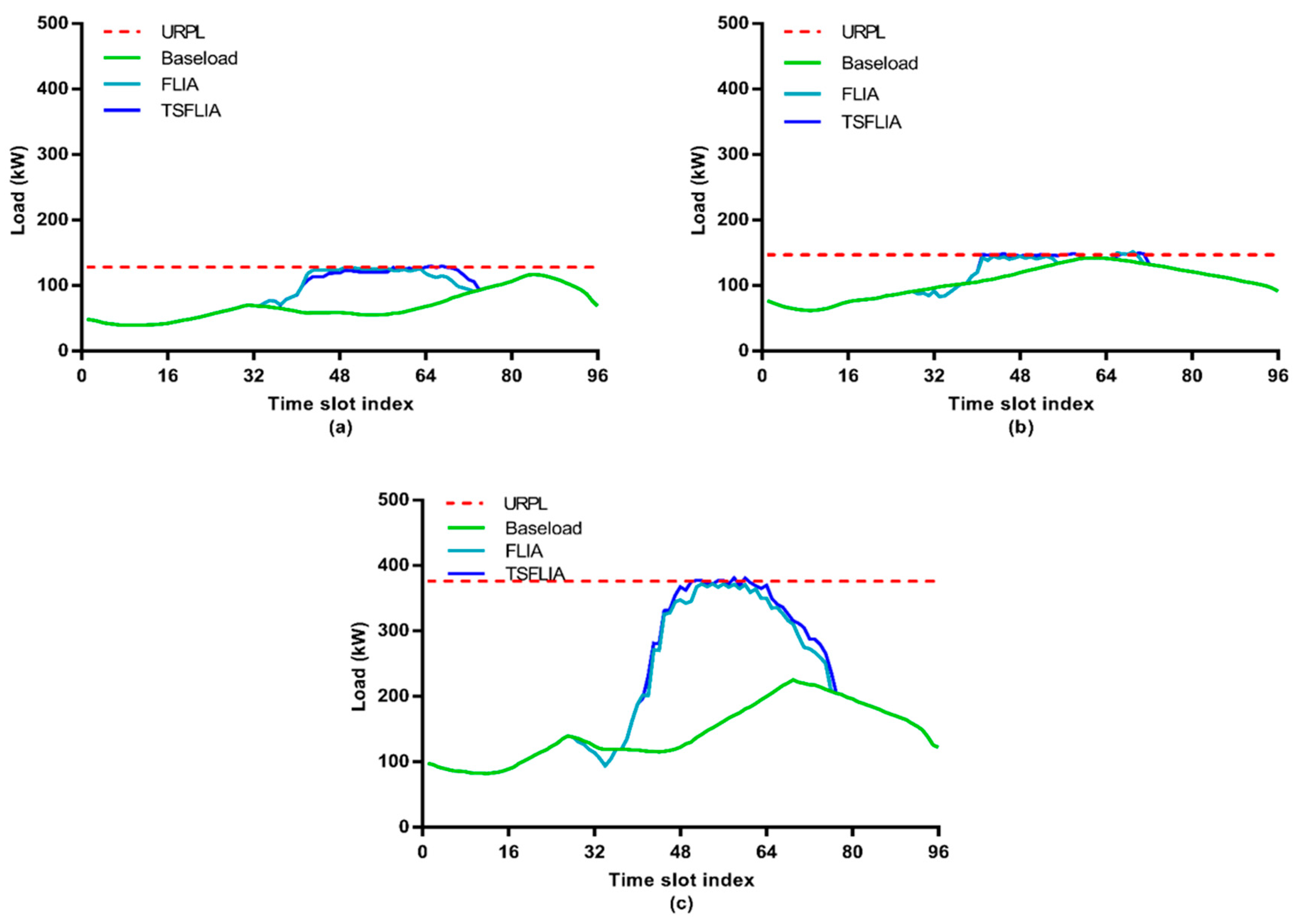
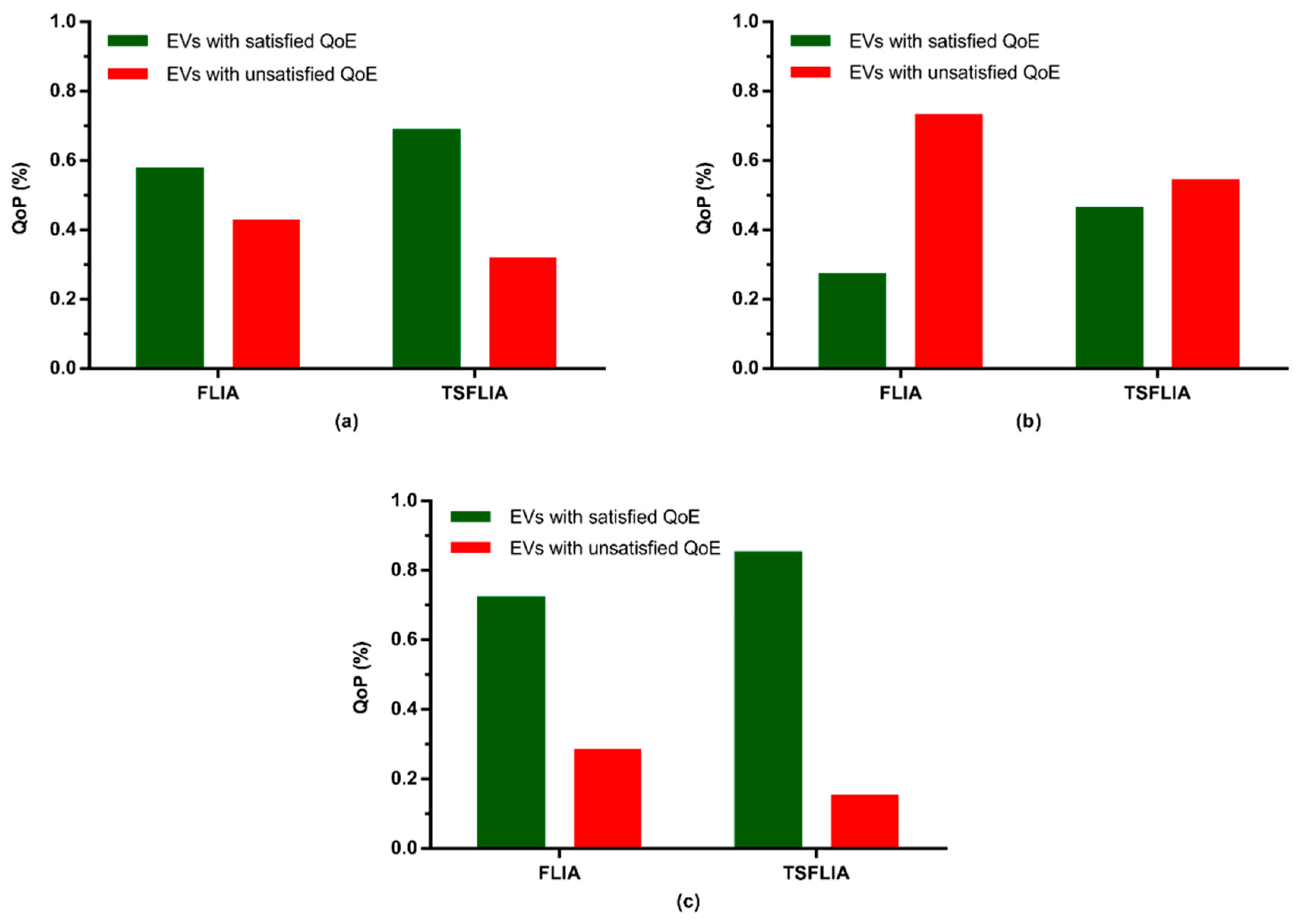
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nour, M.; Said, S.M.; Ali, A.; Farkas, C. Smart Charging of Electric Vehicles According to Electricity Price. In Proceedings of the Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 8–9 February 2020; pp. 432–437. [Google Scholar]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F. Minimization of load variance in power grids—Investigation on optimal vehicle-to-grid scheduling. Energies 2017, 10, 1880. [Google Scholar] [CrossRef]
- Neyestani, N.; Catalão, J.P. The value of reserve for plug-in electric vehicle parking lots. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Neyestani, N.; Damavandi, M.Y.; Shafie-Khah, M.; Bakirtzis, A.G.; Catalão, J.P. Plug-in electric vehicles parking lot equilibria with energy and reserve markets. IEEE Trans. Power Syst. 2016, 32, 2001–2016. [Google Scholar] [CrossRef]
- Moghaddam, Z.; Ahmad, I.; Habibi, D.; Phung, Q.V. Smart charging strategy for electric vehicle charging stations. IEEE Trans. Transp. Electrif. 2017, 4, 76–88. [Google Scholar] [CrossRef]
- Hariri, A.O.; El Hariri, M.; Youssef, T.; Mohammed, O.A. A bilateral decision support platform for public charging of connected electric vehicles. IEEE Trans. Veh. Technol. 2018, 68, 129–140. [Google Scholar] [CrossRef]
- An, J.; Wen, G.; Xu, W. Improved results on Fuzzy H∞ filter design for TS Fuzzy systems. Discret. Dyn. Nat. Soc. 2010, 2010, 1–21. [Google Scholar] [CrossRef]
- An, J.; Li, T.; Wen, G.; Li, R. New stability conditions for uncertain TS fuzzy systems with interval time-varying delay. Int. J. Control Autom. Syst. 2012, 10, 490–497. [Google Scholar] [CrossRef]
- Park, J.; Sim, Y.; Lee, G.; Cho, D.-H. A Fuzzy Logic Based Electric Vehicle Scheduling in Smart Charging Network. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–6. [Google Scholar]
- Hariri, A.O.; Esfahani, M.M.; Mohammed, O. A Cognitive Price-Based Approach for Real-Time Management of En-Route Electric Vehicles. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 15 June 2018; pp. 922–927. [Google Scholar]
- Sah, B.; Kumar, P.; Rayudu, R.; Bose, S.K.; Inala, K.P. Impact of Sampling in the Operation of Vehicle to Grid and its Mitigation. IEEE Trans. Ind. Inform. 2018, 15, 3923–3933. [Google Scholar] [CrossRef]
- Singh, M.; Kumar, P.; Kar, I. Implementation of vehicle to grid infrastructure using fuzzy logic controller. IEEE Trans. Smart Grid 2012, 3, 565–577. [Google Scholar] [CrossRef]
- Mehta, R.; Srinivasan, D.; Trivedi, A. Optimal Charging Scheduling of Plug-In Electric Vehicles for Maximizing Penetration within a Workplace Car Park. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–26 July 2016; pp. 3646–3653. [Google Scholar]
- Mirzaei, M.J.; Kazemi, A.; Homaee, O. A probabilistic approach to determine optimal capacity and location of electric vehicles parking lots in distribution networks. IEEE Trans. Ind. Inform. 2015, 12, 1963–1972. [Google Scholar] [CrossRef]
- Yao, L.; Damiran, Z.; Lim, W.H. A Fuzzy Logic Based Charging Scheme for Electric Vechicle Parking Station. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Akhavan-Rezai, E.; Shaaban, M.F.; El-Saadany, E.F.; Karray, F. Online Intelligent Demand Management of Plug-In Electric Vehicles in Future Smart Parking Lots. IEEE Syst. J. 2015, 10, 483–494. [Google Scholar] [CrossRef]
- Jiyao, A.; Tang, J.; Yu, Y. Fuzzy Multi-Objective Optimized with Efficient Energy and Time-Varying Price for EV Charging System. In Proceedings of the Proceedings on the International Conference on Artificial Intelligence (ICAI), Las Vegas, NV, USA, 12–15 July 2010; pp. 47–53. [Google Scholar]
- Mohamed, A.; Salehi, V.; Ma, T.; Mohammed, O. Real-time energy management algorithm for plug-in hybrid electric vehicle charging parks involving sustainable energy. IEEE Trans. Sustain. Energy 2013, 5, 577–586. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, M.A.; Lee, K.-B.; Kim, Y.-C. Fuzzy Logic Weight Based Charging Scheme for Optimal Distribution of Charging Power among Electric Vehicles in a Parking Lot. Energies 2020, 13, 3119. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, M.A.; Kim, Y.-C. Efficient Power Management Algorithm Based on Fuzzy Logic Inference for Electric Vehicles Parking Lot. IEEE Access 2019, 7, 65467–65485. [Google Scholar] [CrossRef]
- Vaidya, B.; Mouftah, H.T. Smart electric vehicle charging management for smart cities. IET Smart Cities 2020, 2, 4–13. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Fang, Z.; Wang, S.; Zhang, F.; Zhang, D. FairCharge: A data-driven fairness-aware charging recommendation system for large-scale electric taxi fleets. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 1–25. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S. Electric vehicle charging on residential distribution systems: Impacts and mitigations. IEEE Access 2015, 3, 1871–1893. [Google Scholar] [CrossRef]
- Kuran, M.Ş.; Viana, A.C.; Iannone, L.; Kofman, D.; Mermoud, G.; Vasseur, J.P. A smart parking lot management system for scheduling the recharging of electric vehicles. IEEE Trans. Smart Grid 2015, 6, 2942–2953. [Google Scholar] [CrossRef]
- Hussain, S.; Muhammad, F.; Kim, Y.-C. Communication Network Architecture Based on Logical Nodes for Electric Vehicles. In Proceedings of the 2017 International Symposium on Information Technology Convergence, Shijiazhuang, China, 19–21 October 2017; pp. 321–326. [Google Scholar]
- Nijhuis, M.; Gibescu, M.; Cobben, J. Valuation of measurement data for low voltage network expansion planning. Electr. Power Syst. Res. 2017, 151, 59–67. [Google Scholar] [CrossRef]
- National Household Travel Survey. Available online: http://nhts.ornl.gov (accessed on 1 January 2019).
- Tan, J.; Wang, L. Integration of plug-in hybrid electric vehicles into residential distribution grid based on two-layer intelligent optimization. IEEE Trans. Smart Grid 2014, 5, 1774–1784. [Google Scholar] [CrossRef]
- Mu, Y.; Wu, J.; Jenkins, N.; Jia, H.; Wang, C. A spatial–temporal model for grid impact analysis of plug-in electric vehicles. Appl. Energy 2014, 114, 456–465. [Google Scholar] [CrossRef]
- Rezaee, S.; Farjah, E.; Khorramdel, B. Probabilistic analysis of plug-in electric vehicles impact on electrical grid through homes and parking lots. IEEE Trans. Sustain. Energy 2013, 4, 1024–1033. [Google Scholar] [CrossRef]
- Stephens, T. An Agent-Based Model of Energy Demand and Emissions from Plug-In Hybrid Electric Vehicle Use. Master’s Thesis, University of Michigan, Ann Arbor, MI, USA, 31 August 2010. [Google Scholar]
- Preethi, A.A.; Nesamalar, J.J.D.; Suganya, S.; Raja, S.C. Economic Scheduling of Plug-In Hybrid Electric Vehicle Considering Various Travel Patterns. In Proceedings of the 2018 National Power Engineering Conference (NPEC), Madurai, India, 9–10 March 2018; pp. 1–7. [Google Scholar]
- Mendoza, C.C.; Quintero, A.M.; Santamaria, F. Estimation of electric energy required by electric vehicles based on travelled distances in a residential zone. Tecciencia 2016, 11, 17–24. [Google Scholar] [CrossRef]
- Du, J.; Li, F.; Li, J.; Wu, X.; Song, Z.; Zou, Y.; Ouyang, M. Evaluating the technological evolution of battery electric buses: China as a case. Energy 2019, 176, 309–319. [Google Scholar] [CrossRef]
- Ma, T.; Mohammed, O.A. Optimal charging of plug-in electric vehicles for a car-park infrastructure. IEEE Trans. Ind. Appl. 2014, 50, 2323–2330. [Google Scholar] [CrossRef]
- Andrenacci, N.; Genovese, A.; Ragona, R. Determination of the level of service and customer crowding for electric charging stations through fuzzy models and simulation techniques. Appl. Energy 2017, 208, 97–107. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, D. Fundamentals of Fuzzy Logic Control—Fuzzy Sets, Fuzzy Rules and Defuzzifications. In Advanced Fuzzy Logic Technologies in Industrial Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 17–36. [Google Scholar]
- Abdelsamad, S.F.; Morsi, W.G.; Sidhu, T.S. Probabilistic impact of transportation electrification on the loss-of-life of distribution transformers in the presence of rooftop solar photovoltaic. IEEE Trans. Sustain. Energy 2015, 6, 1565–1573. [Google Scholar] [CrossRef]
- Geiles, T.J.; Islam, S. Impact of PEV Charging and Rooftop PV Penetration on Distribution Transformer Life. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21—25 July 2013; pp. 1–5. [Google Scholar]
- Mehta, R.; Srinivasan, D.; Khambadkone, A.M.; Yang, J.; Trivedi, A. Smart charging strategies for optimal integration of plug-in electric vehicles within existing distribution system infrastructure. IEEE Trans. Smart Grid 2016, 9, 299–312. [Google Scholar] [CrossRef]
- Kong, P.-Y.; Karagiannidis, G.K. Charging schemes for plug-in hybrid electric vehicles in smart grid: A survey. IEEE Access 2016, 4, 6846–6875. [Google Scholar] [CrossRef]
- El-Bayeh, C.Z.; Mougharbel, I.; Saad, M.; Chandra, A.; Lefebvre, S.; Asber, D.; Lenoir, L. A Novel Approach for Sizing Electric Vehicles Parking Lot Located at Any Bus on a Network. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef]
- Shahidinejad, S.; Filizadeh, S.; Bibeau, E. Profile of charging load on the grid due to plug-in vehicles. IEEE Trans. Smart Grid 2011, 3, 135–141. [Google Scholar] [CrossRef]
- Shah, B.; Iqbal, F.; Abbas, A.; Kim, K.-I. Fuzzy logic-based guaranteed lifetime protocol for real-time wireless sensor networks. Sensors 2015, 15, 20373–20391. [Google Scholar] [CrossRef] [PubMed]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2009, 25, 371–380. [Google Scholar]
- Lu, S.; Samaan, N.; Diao, R.; Elizondo, M.; Jin, C.; Mayhorn, E.; Zhang, Y.; Kirkham, H. Centralized and decentralized control for demand response. In Proceedings of the ISGT 2011, Anaheim, CA, USA, 17–19 January 2011; pp. 1–8. [Google Scholar]
- Brodt-Giles, D. WREF 2012: OPENEI-An Open Energy Data and Information Exchange for International Audiences. Available online: https://www.osti.gov/biblio/1063035 (accessed on 1 January 2019).
- Mazidi, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Rastegar, M. Optimal Allocation of PHEV Parking Lots to Minimize Distribution System Losses. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Cingolani, P.; Alcalá-Fdez, J. jFuzzyLogic: A java library to design fuzzy logic controllers according to the standard for fuzzy control programming. Int. J. Comput. Intell. Syst. 2013, 6, 61–75. [Google Scholar] [CrossRef]
- Tamura, S.; Kikuchi, T. V2G Strategy for Frequency Regulation Based on Economic Evaluation Considering EV Battery Longevity. In Proceedings of the 2018 IEEE International Telecommunications Energy Conference (INTELEC), Turino, Italy, 7–11 October 2018; pp. 1–6. [Google Scholar]
- Wang, Q.; Jiang, B.; Li, B.; Yan, Y. A critical review of thermal management models and solutions of lithium-ion batteries for the development of pure electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Q.; Wang, G.; Lu, P.; Zhao, M.; Bao, W. A review on research status and key technologies of battery thermal management and its enhanced safety. Int. J. Energy Res. 2018, 42, 4008–4033. [Google Scholar] [CrossRef]
- Kongjeen, Y.; Bhumkittipich, K. Impact of plug-in electric vehicles integrated into power distribution system based on voltage-dependent power flow analysis. Energies 2018, 11, 1571. [Google Scholar] [CrossRef]
- Holtsmark, B.; Skonhoft, A. The Norwegian support and subsidy policy of electric cars. Should it be adopted by other countries? Environ. Sci. Policy 2014, 42, 160–168. [Google Scholar] [CrossRef]
- Miedema, G.; Infrastructure, E.C. Revolutionizing Fast Charging for Electric Vehicles. EV Charg. Infrastruct. 2012, 1–6. [Google Scholar]
- Shafiee, S.; Fotuhi-Firuzabad, M.; Rastegar, M. Investigating the impacts of plug-in hybrid electric vehicles on power distribution systems. IEEE Trans. Smart Grid 2013, 4, 1351–1360. [Google Scholar] [CrossRef]



| VEAPL | EAPL | NAPL | LAPL | VLAPL | ||
|---|---|---|---|---|---|---|
| VEDH | VSMT | SMT | NMT | LMT | VLMT | |
| EDH | VSMT | SMT | SMT | NMT | LMT | |
| NDH | VSMT | VSMT | SMT | NMT | NMT | |
| LDH | VLMT | VSMT | VSMT | SMT | SMT | |
| VLDH | VLMT | VLMT | VSMT | VSMT | VSMT | |
| UAP | ||||||
|---|---|---|---|---|---|---|
| VLAP | LAP | MAP | HAP | VHAP | ||
| VL | LPF | LPF | LPF | LPF | MPF | |
| L | LPF | LPF | MPF | MPF | MPF | |
| M | LPF | MPF | MPF | MPF | HPF | |
| H | MPF | APF | HPF | HPF | HPF | |
| VH | HPF | HPF | HPF | HPF | HPF | |
| UAP | ||||||
|---|---|---|---|---|---|---|
| VLAP | LAP | MAP | HAP | VHAP | ||
| VL | LPF | LPF | LPF | MPF | MPF | |
| L | LPF | LPF | MPF | MPF | MPF | |
| M | LPF | LPF | HPF | HPF | HPF | |
| H | MPF | HPF | HPF | HPF | HPF | |
| VH | MPF | HPF | HPF | HPF | HPF | |
| UAP | ||||||
|---|---|---|---|---|---|---|
| VLAP | LAP | MAP | HAP | VHAP | ||
| VL | LPF | LPF | LPF | LPF | MPF | |
| L | LPF | LPF | LPF | MPF | MPF | |
| M | LPF | LPF | MPF | MPF | MPF | |
| H | LPF | LPF | HPF | HPF | HPF | |
| VH | MPF | HPF | HPF | HPF | HPF | |
| Node # | Lumped Load (kW) | Residential Load (kW) | Number of Houses |
|---|---|---|---|
| 860 | 60 | 42 | 15 |
| 840 | 27 | 19 | 7 |
| 844 | 405 | 284 | 102 |
| 848 | 60 | 42 | 15 |
| 890 | 450 | 315 | 113 |
| 830 | 45 | 32 | 11 |
| Total | 1047 | 733 | 264 |
| From Bus # | To Bus # | Lumped Load (kW) | Assumed Residential Load (kW) | Number of Houses |
|---|---|---|---|---|
| 802 | 806 | 55 | 39 | 14 |
| 808 | 810 | 16 | 11 | 4 |
| 818 | 820 | 34 | 24 | 9 |
| 820 | 822 | 135 | 95 | 34 |
| 816 | 824 | 5 | 4 | 1 |
| 824 | 826 | 40 | 28 | 10 |
| 824 | 828 | 4 | 3 | 1 |
| 828 | 830 | 7 | 5 | 2 |
| 854 | 856 | 4 | 3 | 1 |
| 832 | 858 | 15 | 11 | 4 |
| 858 | 864 | 2 | 1 | 1 |
| 858 | 834 | 32 | 22 | 8 |
| 834 | 860 | 146 | 102 | 37 |
| 860 | 836 | 82 | 57 | 21 |
| 836 | 840 | 40 | 28 | 10 |
| 862 | 838 | 28 | 20 | 7 |
| 842 | 844 | 9 | 6 | 2 |
| 844 | 846 | 45 | 32 | 11 |
| 846 | 848 | 23 | 16 | 6 |
| Total | 722 | 505 | 182 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, S.; Lee, K.-B.; A. Ahmed, M.; Hayes, B.; Kim, Y.-C. Two-Stage Fuzzy Logic Inference Algorithm for Maximizing the Quality of Performance under the Operational Constraints of Power Grid in Electric Vehicle Parking Lots. Energies 2020, 13, 4634. https://doi.org/10.3390/en13184634
Hussain S, Lee K-B, A. Ahmed M, Hayes B, Kim Y-C. Two-Stage Fuzzy Logic Inference Algorithm for Maximizing the Quality of Performance under the Operational Constraints of Power Grid in Electric Vehicle Parking Lots. Energies. 2020; 13(18):4634. https://doi.org/10.3390/en13184634
Chicago/Turabian StyleHussain, Shahid, Ki-Beom Lee, Mohamed A. Ahmed, Barry Hayes, and Young-Chon Kim. 2020. "Two-Stage Fuzzy Logic Inference Algorithm for Maximizing the Quality of Performance under the Operational Constraints of Power Grid in Electric Vehicle Parking Lots" Energies 13, no. 18: 4634. https://doi.org/10.3390/en13184634
APA StyleHussain, S., Lee, K.-B., A. Ahmed, M., Hayes, B., & Kim, Y.-C. (2020). Two-Stage Fuzzy Logic Inference Algorithm for Maximizing the Quality of Performance under the Operational Constraints of Power Grid in Electric Vehicle Parking Lots. Energies, 13(18), 4634. https://doi.org/10.3390/en13184634








