Next Article in Journal
The Effect of SMiShing Attack on Security of Demand Response Programs
Next Article in Special Issue
Environmental Impacts of Integrated Photovoltaic Modules in Light Utility Electric Vehicles
Previous Article in Journal
Thermal Analysis of Dry-Type Air-Core Coils for the Optimization of Passive Filtering Systems
Previous Article in Special Issue
Sustainable E-Bike Charging Station That Enables AC, DC and Wireless Charging from Solar Energy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 13
Issue 17
10.3390/en13174541
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling

by
Asaad Mohammad
,
Ramon Zamora
and
Tek Tjing Lie
*
Department of Electrical and Electronic Engineering, Auckland University of Technology, Auckland 1010, New Zealand
*
Author to whom correspondence should be addressed.
Energies 2020, 13(17), 4541; https://doi.org/10.3390/en13174541
Submission received: 23 July 2020 / Revised: 25 August 2020 / Accepted: 31 August 2020 / Published: 2 September 2020
(This article belongs to the Special Issue PV Charging and Storage for Electric Vehicles)
Browse Figures
Versions Notes

Abstract

:
Electric vehicles (EVs) are one of a prominent solution for the sustainability issues needing dire attention like global warming, depleting fossil fuel reserves, and greenhouse gas (GHG) emissions. Conversely, EVs are shown to emit higher emissions (measured from source to tailpipe) for the fossil fuel-based countries, which necessitates renewable energy sources (RES) for maximizing EV benefits. EVs can also act as a storage system, to mitigate the challenges associated with RES and to provide the grid with ancillary services, such as voltage regulation, frequency regulation, spinning reserve, etc. For extracting maximum benefits from EVs and minimizing the associated impact on the distribution network, modelling optimal integration of EVs in the network is required. This paper focuses on reviewing the state-of-the-art literature on the modelling of grid-connected EV-PV (photovoltaics) system. Further, the paper evaluates the uncertainty modelling methods associated with various parameters related to the grid-connected EV-PV system. Finally, the review is concluded with a summary of potential research directions in this area. The paper presents an evaluation of different modelling components of grid-connected EV-PV system to facilitate readers in modelling such system for researching EV-PV integration in the distribution network.

Graphical Abstract

1. Introduction

The issues like global warming, depleting fossil fuel reserves, and greenhouse gas (GHG) emissions need dire attention for ensuring a sustainable future. Because the transportation sector is one of the largest contributors to the rising harmful emissions, the electrification of transportation is seen as a promising solution for this problem. Electric vehicle (EV) technology has existed for more than a century peaking commercially around 1900. However, due to the easy availability of fossil fuels, advancements in internal combustion (IC) technology, and simplicity in the use of IC engines, EVs were put on hold and limited to golf carts and delivery vehicles. Figure 1 shows the progression timeline of the EVs. The dependency on petroleum imports for transportation purposes is also reduced by electrification of transportation, thereby increasing energy security. However, the adoption rate of EVs remains slow owing to factors, such as high initial cost, battery degradation, inadequate charging infrastructure, range anxiety, etc. [1]. Various policies and incentives are made available by governments around the world to promote the uptake of EV and to prevent these barriers from realizing a complete shift to electrified transportation. As per the report “Global EV outlook” of the International Energy Agency, the total number of EVs are projected to reach 130 million by 2030 [2].
However, high penetration of EVs also poses distribution network quality issues, particularly network congestion, three-phase voltage imbalance and off-nominal frequency problems. The EVs are a mobile single-phase load so they can be randomly plugged in at any one of three phases within distribution networks, leading to a scenario that electrical components in one particular phase, such as power supply cable, overhead line or transformer may be heavily loaded while the rest of two phases are not. The unbalanced three-phase loading may lead to a series of negative impact on power quality issue: Transformer failures, equipment loss-of-life, relay misfunction, etc. Moreover, as EVs are highly spatial and temporally uncertain, handling EVs as additional loads while maintaining the reliability and security of the grid is difficult. The coincidence of timing between EV home charging and residential load peaks leads to additional system peaks. Moreover, multiple EV chargers in a neighbourhood can introduce significant harmonics, thereby reducing power quality [3]. Therefore, the integration of substantial EV penetration in the distribution networks is a significant area of interest in the research and engineering community, especially optimally controlling EV charging to minimise the impact of the above-described issues.
Another significant contributor to harmful emissions is the power industry, particularly fossil fuel-based power generation. Renewable energy sources (RES), such as wind and solar are increasingly adopted to mitigate the power industry emissions. The variable nature of RES which depends on the weather, time, location, etc. creates voltage stability and reliability issues for the power grid requiring integration of Energy Storage System (ESS). Also, there may not be sufficient demand requirement during the period of high RES generation, which leads to the under-utilisation of average generated capacity. Using ESS with RES can result in its effective utilisation as ESS can store energy when demand is low and supply back when demand is high. Apart from using ESS, application of demand-side management techniques like load shifting, time of use pricing, and demand bidding can also solve the aforementioned problems associated with RES although the impact of these techniques is limited compared to ESS [4,5].
Large-scale integration of RES requires an increased size (or capacity) of ESS. Hence, it leads to a significant capital requirement, especially due to the high per-unit cost of ESS. As we are already moving towards electric vehicles to combat GHG emissions and these EVs essentially run on the batteries, the EVs can also act as a dynamic natured ESS, due to the vehicle-to-grid (V2G) feature, in which EVs deliver energy stored in their batteries back to the grid [6]. Additionally, EVs spend a considerable amount of time (22 h) in parked conditions [7], so they can be suitably used as ESS without creating inconvenience (e.g., range anxiety issues) for users. However, battery degradation is still an issue which can be offset by giving incentives to users/aggregators to participate in V2G. As the battery capacity of each EV is minuscule compared to grid load requirements, an aggregation of EVs is generally required to provide the grid with the backup power. Apart from storing surplus energy generated by RES, EVs can also provide the grid with additional ancillary services, such as voltage regulation, frequency regulation, spinning reserve, etc. EVs can also participate in energy trading, to be a source of revenue for the aggregator/users to compensate for the battery degradation, due to participation in V2G. However, most of the energy markets around the world require a minimum capacity to participate, which would require an aggregator of a large number of EVs. To counteract this, more research is being done on transactive or peer-to-peer (P2P) trading mechanisms [8].
Moreover, the emission benefits of electrified transportation cannot be maximised if the source of EV charging is based on non-renewable sources. In fact, EVs are shown to emit higher emissions, measured from well to wheel, i.e., source to the tailpipe for the countries whose primary source of power generation is based on fossil fuels [9]. However, using RES to charge the EVs could result in reducing GHG emissions, as shown in Reference [10], where 50,000 EVs charged from a mix of wind and PV energy sources resulted in 400 Mtons less emissions per year.
Based on these factors, this paper presents a general framework for designing a grid-connected EV-PV system. Several papers have also reviewed the different aspects of the interaction of EV-PV system and distribution network in the literature. References [11,12,13,14] discuss charging EVs using PV generation with a focus on control architectures and algorithms, and economic framework. The impact of the charging infrastructure of EV on the grid in terms of power quality is reviewed in Reference [15]. An overview of EV modelling techniques is presented in References [16,17,18] with an emphasis on modelling methods for EV loads and charging stations.
These review papers study the limited aspects of the interaction of grid-connected EV with RES, particularly PV, focusing on the modelling of control methods or EV loads. Also, a detailed review of modelling the uncertainties present in the grid-connected EV-PV system is not present in the literature to the knowledge of the authors. Therefore, this paper presents a comprehensive review of all aspects of modelling a grid-connected EV-PV system viz., control architectures, charging algorithms, and uncertainty analysis. This paper aims to provide an evaluation of these aspects to enable the researchers to model a grid-connected EV-PV system for carrying out impact or implementation studies of EV integration into the distribution system. The grid is represented by a distribution network as EV and PV both are on the distribution side. Throughout the paper, EV-PV system is considered as a single entity (limited to the times when connected to the grid for charging or vehicle-to-grid), and the PV is considered as a complementary energy source to charge EVs other than the grid. Figure 2 shows the analytical framework of the modelling aspects of grid-connected EV-PV system.
The organisation of the paper is as follows: Section 2 provides an overview of the modes of EV integration with the grid. Section 3 discusses the control architectures of connecting EVs to the grid. Section 4 describes the state-of-the-art literature of smart charging algorithms of grid-connected EV-PV system. Section 5 reviews the uncertainty analysis methods for EV demand, PV generation, and load distribution. The suggestions for future research with concluding remarks are presented in Section 6.

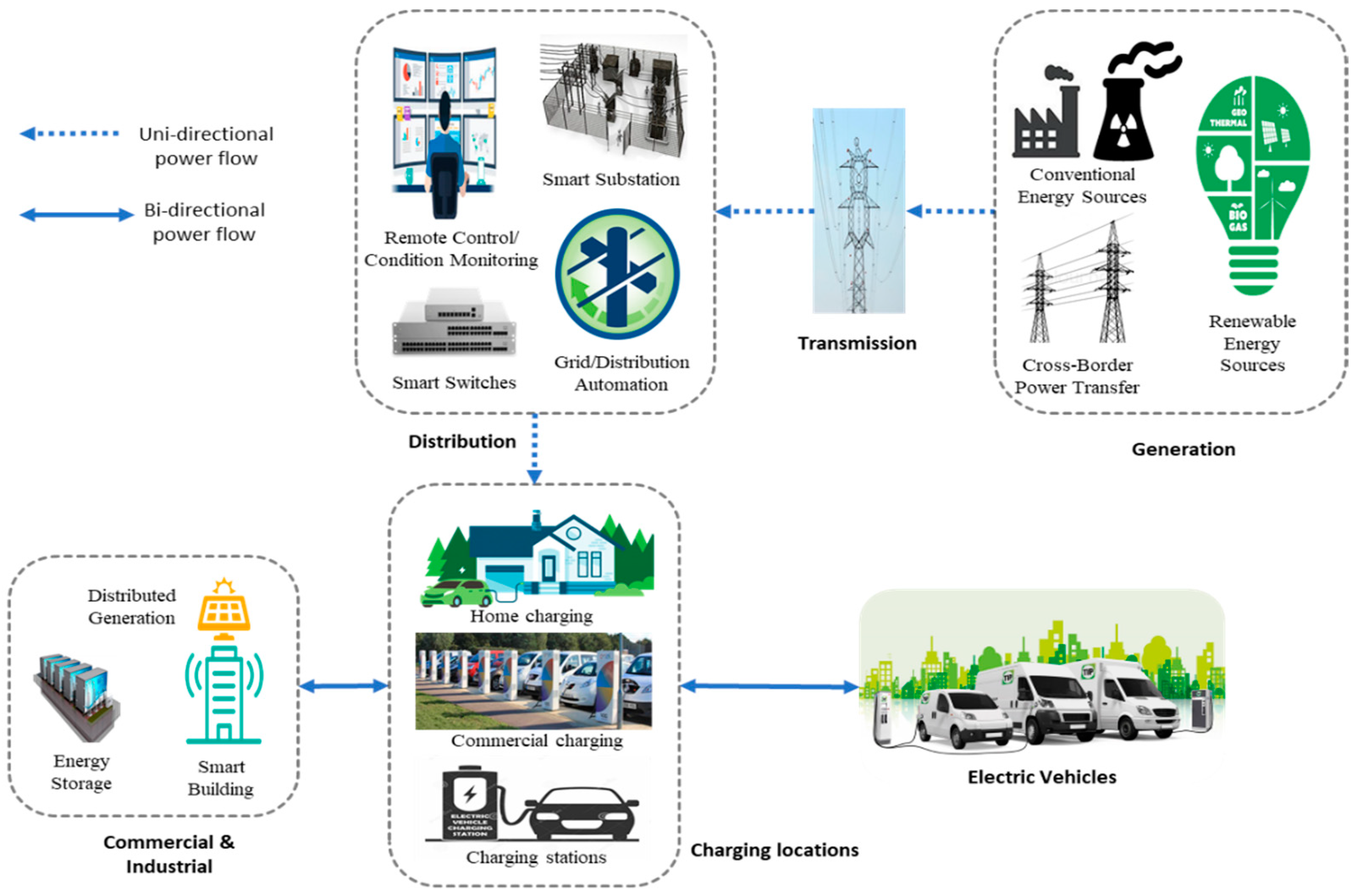
2. EV Interaction with the Distribution Network

Figure 3 shows a general representation of an EV connected to the electrical grid. The technology which allows the bidirectional flow of energy between EV and grid is known as vehicle-to-grid (V2G). It is achieved by the integration of Information and Communication Technologies (ICT) with the EV charging system. The modelling research of EV interaction with the distribution network has transitioned from unidirectional mode in the initial stage to bidirectional mode in the current stage [6,7].
With the increasing level of EV penetration, the associated technical issues, e.g., system imbalance, decreased stability, and power quality, as well as increased system cost, are becoming more prominent, due to additional energy and power demand. The unidirectional approach, i.e., G2V mode, has been extensively studied in the literature in the form of topics like smart charging [19], safety [20], and control features [21]. The focus of these studies is on minimizing the charging cost [22] or minimizing the impact on the distribution system [23,24].
However, in the bidirectional mode, EV is not only the load for the grid, but also a distributed generation and storage. The initial idea was to use EV battery to store energy and send it back to the grid in peak period, known as peak load shaving [6]. Reference [25] presents a review of peak shaving strategies using demand-side management, energy storage systems, and electric vehicles. Table 1 illustrates the characteristical differences between the unidirectional and bidirectional modes. As an individual EV has a small battery capacity, a major challenge is the synchronisation of a large number of EVs charging/discharging operation required for them to be an effective storage system. Also, the limited uptake of EV did not quite make this idea of using EV in the bidirectional mode mainstream. Research later indicated that the application of bidirectional V2G in the ancillary market: Spinning reserve and voltage control is much more important than peak load reduction. Spinning reserve is the extra generation that can be made readily available, and it is paid for the availability along with the time it is called for deployment (compared to peak load shaving), which makes deployment of EV in ancillary service provision very economically favourable. Moreover, in terms of frequency of deployment, the voltage regulation is needed more than 300 times per day compared to the need for peak load shaving, which is only a few hundred hours per year [26].
Initially, V2G involved only energy transfer from EVs to the distribution system. However, with the advancement in technology, two new energy transfer modes (V2H and V2V) are added. Therefore, the bi-directional energy transfer from EV can now be classified into:
  • Vehicle-to-grid (V2G): Energy transfer from EV to the distribution network.
  • Vehicle-to-home/building (V2H/V2B): Energy transfer from EV to home/building.
  • Vehicle-to-vehicle (V2V): Energy transfer from one EV to another EV.

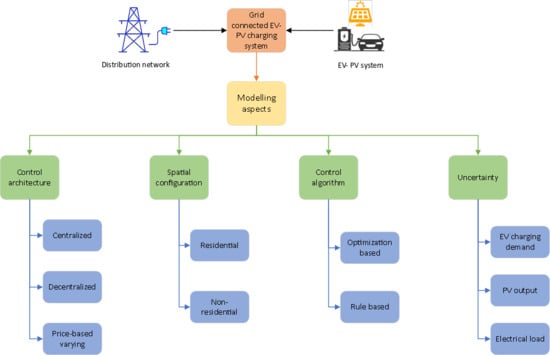
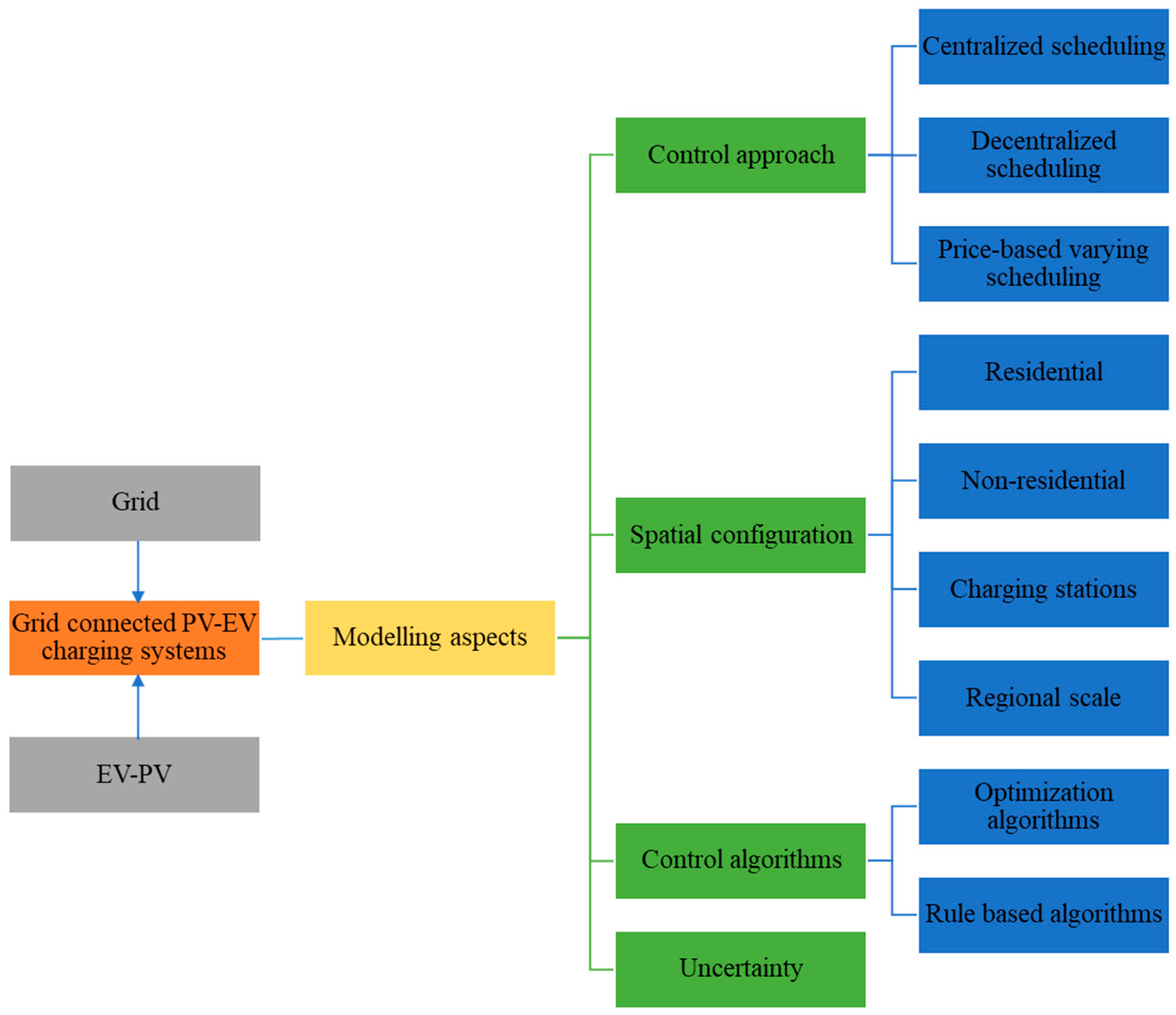
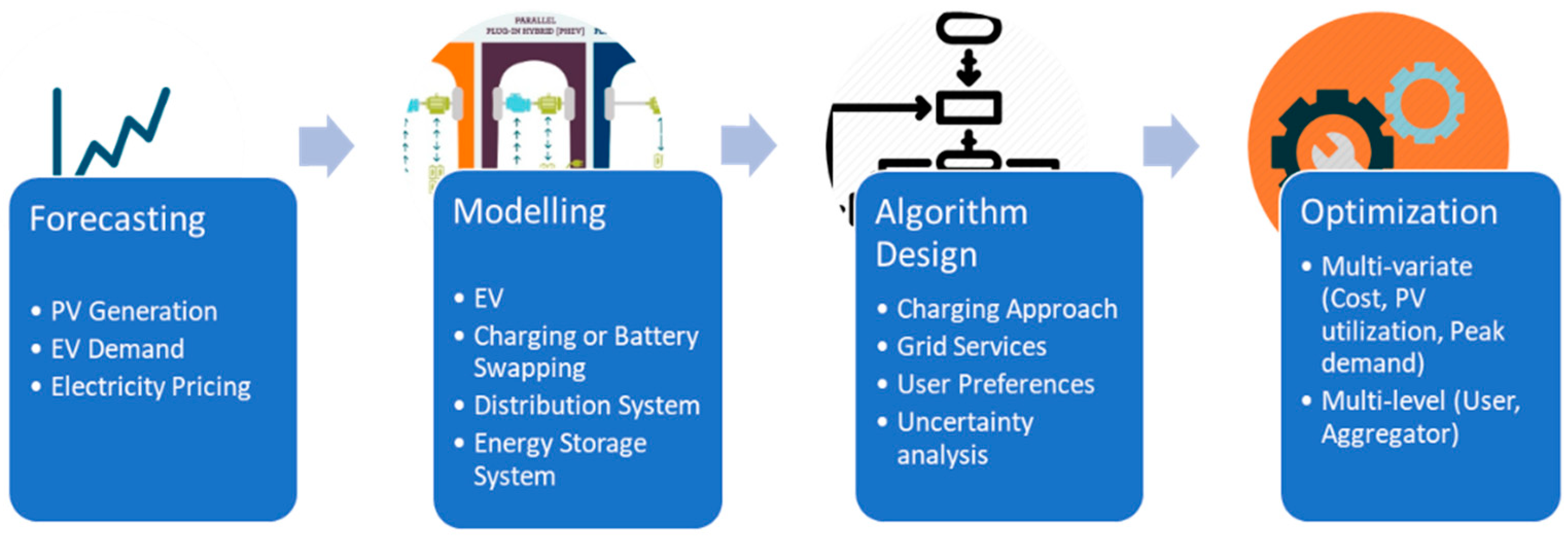
3. Modelling of Grid-Connected EV-PV System

The sustainability of EV depends on the source of charging. All forms of EVs, i.e., plug-in electric vehicle (PEV), hybrid electric vehicle (HEV), or plug-in hybrid electric vehicle (PHEV), have lower emissions if the energy supplied for charging is based on clean fuel, such as renewable sources. However, contrary to popular belief if the EVs are charged from fossil fuel or gas-based generation, the emissions are significant and not zero. The RES, i.e., PV, wind, tidal, geothermal, or hydro, are excellent options to power electric vehicles. Moreover, the following reasons make PV an admirable source to charge the EVs:
  • The cost of PV has been dropping continuously and is currently less than $1/Wp [32].
  • PV is highly accessible, i.e., PV modules are generally installed on the building rooftops and carparks, close to EV locations.
  • PV modules do not require maintenance and are also noise-free.
  • EVs can store the surplus generated solar energy, thereby eliminating the need for battery systems [33,34].
Figure 4 shows a general framework for designing a smart charging system for integrating EV-PV system into the grid. As the focus of this review paper is on modelling aspect of the grid-connected EV-PV system, this section will provide an overview of the modelling of control approaches with subsequent sections reviewing about charging models/algorithms and uncertainty.
The control architectures for grid-connected EVs (with or without PVs) can be categorised into the following three methodologies:
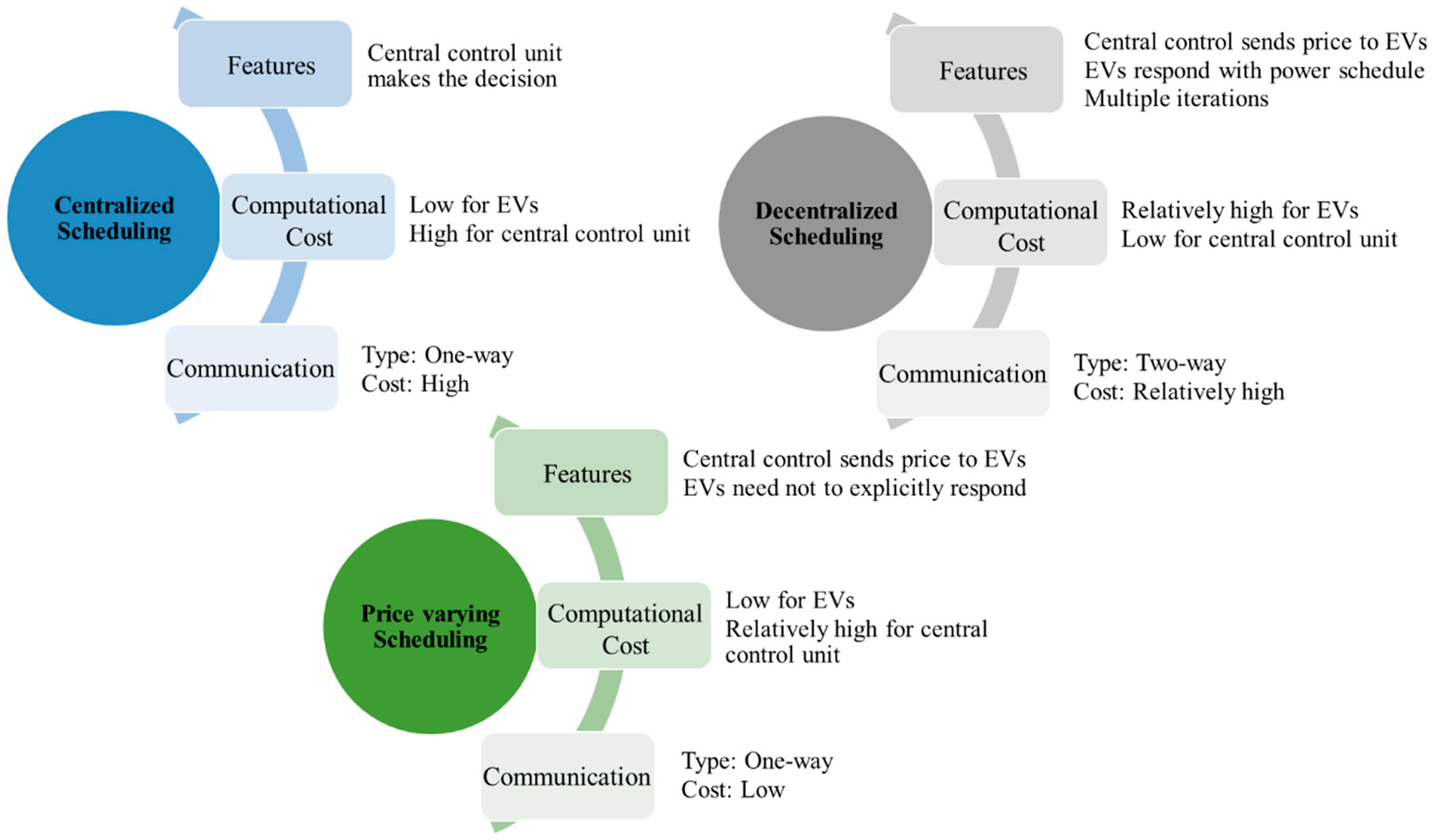
  • Centralised scheduling;
  • Decentralised scheduling;
  • Price-varying scheduling.
In centralised scheduling method, EV aggregator plays a crucial role in integrating EV with the grid. Initially, each EV sends the necessary charging related information to the aggregator. After which aggregator computes the optimal charging strategy and participates in the energy trading through bidding, which is verified by grid system operators. The general objective functions in centralised type scheduling are charging cost minimisation [35], line power loss minimisation [36], aggregator profit maximisation [37,38], voltage regulation [39] and frequency regulation [40]. Due to the aggregation of many EVs, this method is very good for providing backup power and ancillary services. However, in the centralised method, EV users have to relinquish the charging process control to centralised authority. Other drawbacks of this approach are high dependency on the control centre and large communication bandwidth.
In decentralised scheduling method, individual EVs are controlled directly instead of through a central control unit. Firstly, EV aggregator formulates a bidding strategy based on EV load demand data collected or forecasted in a given period. Then, the bids are submitted to the central grid operator and cleared in the energy market the same as in centralised scheduling. After the bids are approved, and an agreement is done with the grid operator, the aggregator broadcasts the charging prices to individual EV users. Based on the price and convenience, users decide whether to charge/discharge their EVs in a given period. The advantage of this type of scheduling is that the infrastructure is simple and of low cost. However, due to a random number of EVs guaranteed to be available at a given time, this method’s capability of the provision of backup power and ancillary services is low. Also, privacy and security issues are there. The general objective function in decentralised type scheduling is mainly charging cost minimisation [41,42,43]. Other objectives are RES integration [44], load profile levelling [45], voltage regulation [46] and frequency regulation [47].
The price-varying scheduling has the same structure as decentralised scheduling, however, the charging behaviours of EVs are directly affected by varying electricity pricing. Instead of two-way communication, i.e., price and power schedule information exchanged in decentralised scheduling, here the only price is communicated to EVs. Reference [48] discusses the feasibility of using time-of-use (TOU) based pricing for EV energy management. Reference [49] presents a socially optimal pricing system between EV aggregators and utility. Reference [50] introduces a smart EV energy management algorithm that takes dynamic factors, such as user participation and load variation into account.
Figure 5 presents an overview of the comparison between the scheduling strategies discussed above [51]. Even though the price-varying scheduling is overall less complex, it is less attractive for commercial entities to participate in V2G, due to the high cost of computation on their side. Hence, the focus of research is generally more on centralised and decentralised scheduling strategies.
The grid-connected EV-PV systems are designed based on spatial configuration requirements, i.e., for homes or office use etc. Generally, in the literature, four space-based levels are used: Residential (individual house), non-residential (commercial/workplaces), public charging stations and inter-territory region. Due to the large size of EV loads, which almost doubles the electricity consumption of a household, it is reasonable to provide another energy source (like PV) [52]. Nevertheless, it appears through the literature that while coupling EV with PV inside households can be beneficial, the benefits are bounded by the EV utilisation for mobility. Most of the EVs are usually away from home during the day, and therefore, cannot benefit from maximal PV generation. It is reasonable to assume that usually, EVs will be at non-residential places (commercial/workplaces) during this day period when peak PV generation happens. So, EVs will be either at residential or non-residential areas. Therefore, the focus of this paper is only on the modelling of residential and non-residential (commercial/workplace) EV-PV system. The PV based EV charging stations are not yet economically feasible, due to the marginal cost associated with PV generation and the cost of energy storage systems [53]. Reference [54] is one example of the limited literature available on standalone PV based EV charging stations.

4. EV Smart Charging Using PV and Grid

Multiple studies have explored the advantages of a PV based EV charging system. Reference [55] demonstrates the advantage of using PV to charge the EV and show that it allows for greater penetration of both PV and EV. EVs can also mitigate the negative effects of excess PV generation [56]. Reference [57] presents a case study of Columbus, USA, in which it is demonstrated that charging EV from the PV is more economical and produces less CO2 footprint than charging EV from the grid. A case study presented in Reference [58] compares charging of EVs through the modes: Only grid, only PV with battery storage and grid integrated PV and finds that the grid integrated PV performs better economically compared to the other two systems. In Reference [59], the authors discuss the application of PV energy and EV as an energy storage system to mitigate the peak loading in the grid. These studies demonstrate the advantages of PV based EV charging over grid EV charging. There is a vast amount of literature on different charging algorithms or achieving different economic, technical, or social objectives related to PV based EV charging. Table 2 provides a summary of key smart charging related works for the grid-connected EV-PV system. The optimisation model type depends on the problem formulation. Generally, the convex type problems (linear, mixed-integer, quadratic) can achieve optimal solutions with a low computational cost. For non-convex problems, meta-heuristic type optimisation methods (Genetic Algorithm, Particle Swarm Optimisation) are useful to achieve a near-optimal solution with a low computational burden. The rule-based algorithm or heuristic type optimisation methods can produce good enough solutions for random instantaneous events (e.g., plugging/unplugging of EVs, PV power variation) with little data and computational power requirements. The focus of the literature is generally on residential or office PV based EV charging system, not on commercial applications, due to less complexity in analysis and modular integration in the distribution system. Moreover, almost all the smart charging research focuses on the specific aspects of optimizing the EV integration into grid, e.g., slow/fast charging, market participation, ancillary services. For emulating the real-life implementation, a comprehensive system with multiple aspects is required. Reference [60,61] are some early stages work on a comprehensive system combining multiple aspects which are usually studied in isolation.
The stochastic behaviour of the PV generation is a major disadvantage for EV charging. The approach of a smart charging algorithm is to provide flexibility in EV charging to account for the uncertainty in PV generation. Reference [71] has shown that smart charging, along with the V2G technology, increases PV self-consumption and reduces peak demand. Reference [76] varies the EV charging power with time to match with the generated PV power and achieves the condition of maximum PV utilisation. Another way to counteract uncertainty is the sequential charging in which the total number of EVs charging at constant power is varied dynamically so that the net charging power follows the PV generation, as seen in Reference [77]. Reference [78] considers multiple cases to show the superiority of sequential charging over concurrent charging in terms of PV utilisation under stochastic conditions. However, due to no associated time constraints, it is not feasible for workplace charging.

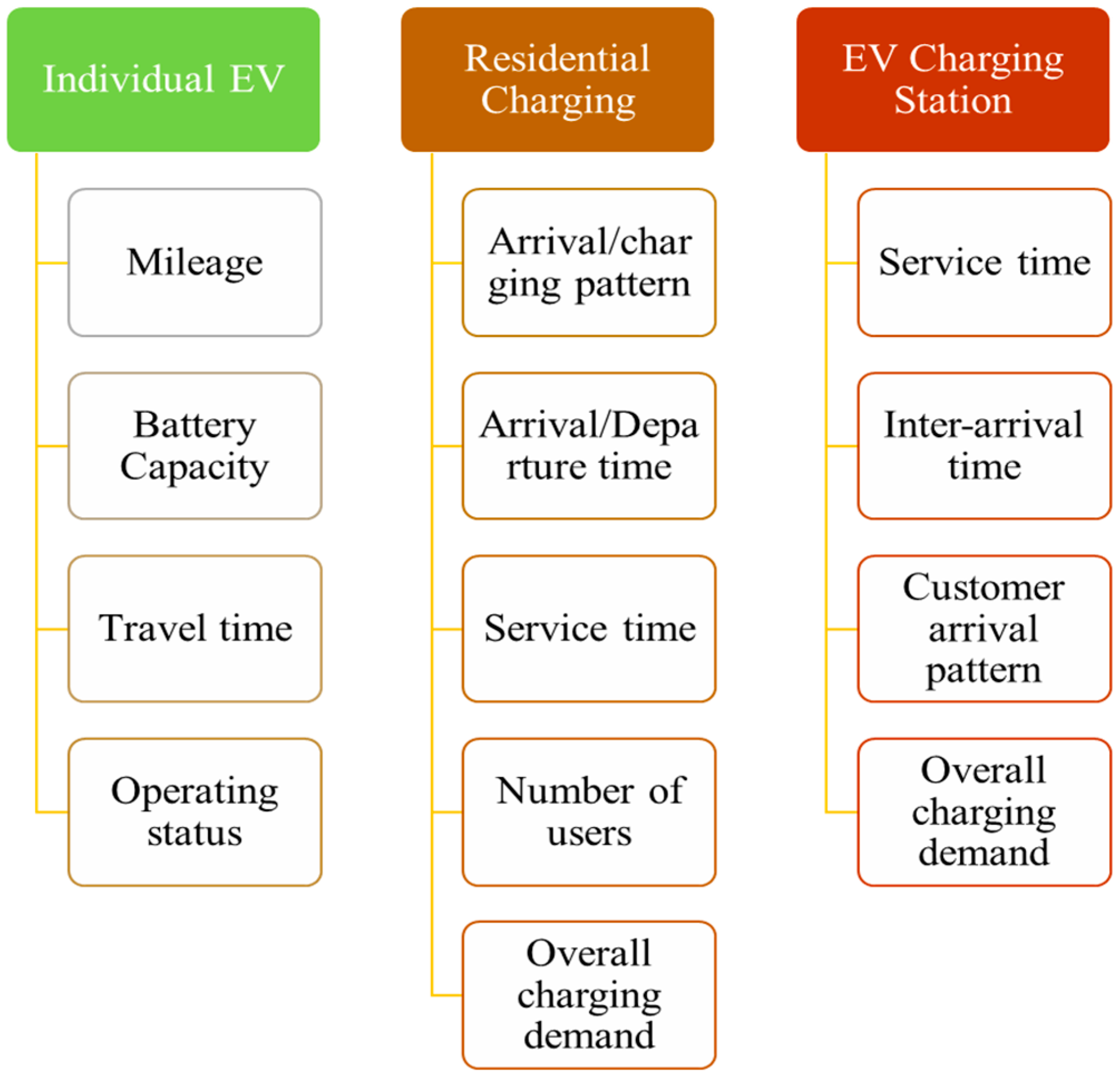
5. Uncertainty Modelling

This section reviews the methods for modelling the uncertainties present with the various input parameters for the EV-PV grid integrated system. Three input factors are of main interest: EV charging demand, PV generation, and Electrical load distribution. The tables in respective sections summarise the techniques used to model the uncertainties present. The remarks show the comparative analyses of these techniques in terms of system size, computational cost, and accuracy.

5.1. EV Charging Demand

The uncertainties in EV charging demand are due to multiple factors, e.g., user behaviour, charging infrastructure, and operational parameters. Table 3 presents an overview of various uncertainty methods for modelling EV load demand in terms of application and associated drawbacks. Generally, Monte Carlo and Probability distribution based modelling method is common practice in the literature. However, due to computational cost and accuracy issues associated with them, respectively, more advanced methods like Markov chain and Information gap decision theory are used for specific applications. A hybrid approach of combining methods is also used to minimise the associated drawbacks.
Figure 6 shows the various input parameters for the uncertainty modelling of EV load demand. The parameters related to time (e.g., arrival, departure, travel, service) and charging power demand required are common in all the three modes of charging: Individual, residential, and commercial, while others are specific to the application. The uncertainties in the parameters involving human factors, i.e., travel/arrival/departure time and pattern are difficult to describe accurately, and also the literature is quite scarce on the effect of human learning capability on EV charging demand. Reference [44] is an example of paucity of research on the practical effect of human factors on EV charging.

5.2. PV Generation

A PV module converts energy from the sun into electrical form depending upon the incident radiation on the module surface. This incident solar radiation is highly variable and depends on various geographical and metrological factors. The common variables used in uncertainty modelling of PV generation are solar irradiance, sky type index (clear, cloudy, sunny), module and air temperature, wind speed, and humidity. Table 4 shows a summary of commonly used uncertainty modelling methods for PV generation. The commonly practiced methods are Point estimation, Monte Carlo, Scenario based analysis, and statistical methods (Autoregressive Moving Average). These methods are less complex and work well with small system size. However, for bigger PV systems, Rolling Horizon approach and Kernal Density are more suitable. Generative Adversarial Network (GAN) is the latest uncertainty modelling method based on a machine learning approach.
References [103,104] describes the implementation details of various forecasting techniques for PV power generation. More details about uncertainty modelling for the RES systems can be found in References [105,106,107,108]. The literature of PV based uncertainty modelling is scarce as the cumulative effect of PV power on the system is small compared to other uncertain variables (load, EV demand).
The most common method to mitigate the PV uncertainty is using an external battery storage system, i.e., different from the EV batteries [109]. The excess PV generation, usually in the afternoon, is stored in the battery pack and used to charge the EVs when PV generation is inadequate. Reference [110] compares three different algorithms for finding the best operation characteristics for the battery storage and finds that using a sigmoid function-based discharging algorithm, while charging EVs during the night and storing PV excess is the best approach. However, these studies do not consider the optimal sizing of the external battery storage system as it is a quite expensive component. Apart from mitigating PV uncertainty, the external battery storage system also minimises the impact of EV demand uncertainty parameters constrained by time.

5.3. Electrical Load Demand

The consumption of electricity is highly spatially and temporally uncertain, varying between different load sources, seasons, and the time of day. The main factors for introducing uncertainty in load sources are user behaviours, climatic conditions, and electrical equipment variation [111]. Table 5 shows an overview of various common methods used for modelling uncertainty in electrical loads. Readers can refer to [105,108,111,112,113] for implementation details of these and other methods used to model uncertainties present in electrical load. The convolution and cumulant based techniques are traditional methods popular in the late nineties’ era. However, with the scaling of computational cost with system size, the point estimation became a more popular method. Monte Carlo and Scenario based analysis are also fairly common in the literature.

6. Conclusions and Future Research Suggestions

Electric vehicles and renewable energy-based generation are a promising solution to rising GHG emissions. Further, EVs can act as a dynamic energy storage system through the technology of V2G, thereby, facilitating RES integration in the smart grid. Also, well to wheel emissions from EVs depend upon the charging source. Therefore, RES based EV charging is desired for the overall reduction in emissions and getting the best of both technologies. Thus, this research area is quite popular and needs further exploration for worldwide implementation. This paper presents a state-of-the-art comprehensive review of the modelling of grid-connected EV-PV charging systems. A general framework of designing the grid-connected EV-PV system is described along with a focus on smart charging algorithms. The modelling techniques for associated uncertainties with the grid-connected EV-PV system, i.e., EV demand, electrical load, and PV generation are also intensely reviewed. The study reveals that although the research in this area is plentiful, few gaps need to be investigated. Some future research directions are suggested as following:
  • Smart charging algorithms
The EV charging models need to be more comprehensive in nature, i.e., multiple charging powers, charging station and battery-swapping station, and wholesale market trading and ancillary services provisions, in order to more accurately and realistically model the practical implementation. More studies with respect to finding the optimal trade-offs between computational burden and performance should be made.
  • P2P V2G power transfer
There is a need for more research on peer-to-peer or transactive type charging systems as this encourages all types (big, small, etc.) EV aggregators to trade energy with one another instead of only sizeable aggregator participating in central energy trading. Another advantage is that transactive trading can operate independently of direct influence from the grid so that the price signal from the central power station may not affect the performance of the transactive trading the way it influences the scheduling and trading of energy in existing systems.
  • Uncertainty analysis
The focus of future research should be on finding more realistic forecasting and uncertainty analysis techniques that optimally balance simplicity and performance. Also, more advancement is needed in the modelling of challenging variables like human behaviour, etc. Further, almost all the current research focuses on improving PV forecasting accuracy rather than addressing uncertainties associated with PV generation.
  • PV based EV charging stations
With PV based EV charging being a viable solution for emission issues, more research is needed on the commercial aspects, e.g., solar charging stations as current research focus more on residential EV-PV systems. The impact analysis and interaction with the distribution system needs to be studied in detail.
  • Price-varying scheduling
Because of easy implementation and effectiveness for managing charging load in peak/valley times, price-varying scheduling is very attractive to aggregators. Therefore, more research is required for charging models based on price response and price elasticity.

Author Contributions

Conceptualization, A.M. and R.Z.; methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, A.M.; writing—review and editing, visualization A.M., R.Z., and T.T.L.; supervision, project administration, R.Z. and T.T.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Asaad, M.; Shrivastava, P.; Alam, M.S.; Rafat, Y.; Pillai, R.K. Viability of xEVs in India: A public opinion survey. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2018; Volume 487, pp. 165–178. ISBN 9789811082481. [Google Scholar]
  2. Bunsen, T.; Cazzola, P.; Gorner, M.; Paoli, L.; Scheffer, S.; Schuitmaker, R.; Tattini, J.; Teter, J. Global EV Outlook 2018: Towards Cross-Modal Electrification; International Energy Agency: Paris, France, 2018. [Google Scholar]
  3. Monteiro, V.; Gonçalves, H.; Afonso, J.L. Impact of Electric Vehicles on power quality in a Smart Grid context. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar]
  4. Jordehi, A.R. Optimisation of demand response in electric power systems, a review. Renew. Sustain. Energy Rev. 2019, 103, 308–319. [Google Scholar] [CrossRef]
  5. Strbac, G. Demand side management: Benefits and challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
  6. Kempton, W.; Letendre, S.E. Electric vehicles as a new power source for electric utilities. Transp. Res. Part D Transp. Environ. 1997, 2, 157–175. [Google Scholar] [CrossRef]
  7. Paşaoğlu, G.; Fiorello, D.; Martino, A.; Zani, L.; Zubaryeva, A.; Thiel, C. Travel patterns and the potential use of electric cars—Results from a direct survey in six European countries. Technol. Forecast. Soc. Chang. 2014, 87, 51–59. [Google Scholar] [CrossRef]
  8. Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.K.; Poor, H.V.; Wood, K.L. Transforming energy networks via peer-to-peer energy trading: The Potential of game-theoretic approaches. IEEE Signal Process. Mag. 2018, 35, 90–111. [Google Scholar] [CrossRef] [Green Version]
  9. Woo, J.; Choi, H.; Ahn, J. Well-to-wheel analysis of greenhouse gas emissions for electric vehicles based on electricity generation mix: A global perspective. Transp. Res. Part D Transp. Environ. 2017, 51, 340–350. [Google Scholar] [CrossRef]
  10. Saber, A.Y.; Venayagamoorthy, G.K. Plug-in vehicles and renewable energy sources for cost and emission reductions. IEEE Trans. Ind. Electron. 2010, 58, 1229–1238. [Google Scholar] [CrossRef]
  11. Bhatti, A.R.; Salam, Z.; Aziz, M.J.A.; Yee, K.P.; Ashique, R. Electric vehicles charging using photovoltaic: Status and technological review. Renew. Sustain. Energy Rev. 2016, 54, 34–47. [Google Scholar] [CrossRef]
  12. Hoarau, Q.; Perez, Y. Interactions between electric mobility and photovoltaic generation: A review. Renew. Sustain. Energy Rev. 2018, 94, 510–522. [Google Scholar] [CrossRef] [Green Version]
  13. Shepero, M.; Munkhammar, J.; Widén, J.; Bishop, J.D.; Boström, T. Modeling of photovoltaic power generation and electric vehicles charging on city-scale: A review. Renew. Sustain. Energy Rev. 2018, 89, 61–71. [Google Scholar] [CrossRef] [Green Version]
  14. Fachrizal, R.; Shepero, M.; Van Der Meer, D.; Munkhammar, J.; Widén, J. Smart charging of electric vehicles considering photovoltaic power production and electricity consumption: A review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
  15. Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
  16. Ma, C.-T. System planning of grid-connected electric vehicle charging stations and key technologies: A review. Energies 2019, 12, 4201. [Google Scholar] [CrossRef] [Green Version]
  17. Ahmadian, A.; Mohammadi-Ivatloo, B.; Elkamel, A. A Review on plug-in electric vehicles: Introduction, Current status, and load modeling techniques. J. Mod. Power Syst. Clean Energy 2020, 8, 412–425. [Google Scholar] [CrossRef]
  18. Richardson, D.B. Electric vehicles and the electric grid: A review of modeling approaches, impacts, and renewable energy integration. Renew. Sustain. Energy Rev. 2013, 19, 247–254. [Google Scholar] [CrossRef]
  19. Su, J.; Lie, T.; Zamora, R. Modelling of large-scale electric vehicles charging demand: A New Zealand case study. Electr. Power Syst. Res. 2019, 167, 171–182. [Google Scholar] [CrossRef]
  20. Chung, C.-Y.; Youn, E.; Chynoweth, J.S.; Qiu, C.; Chu, C.-C.; Gadh, R. Safety design for smart Electric Vehicle charging with current and multiplexing control. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013; pp. 540–545. [Google Scholar]
  21. Zheng, Y.; Niu, S.; Shang, Y.; Shao, Z.; Jian, L. Integrating plug-in electric vehicles into power grids: A comprehensive review on power interaction mode, scheduling methodology and mathematical foundation. Renew. Sustain. Energy Rev. 2019, 112, 424–439. [Google Scholar] [CrossRef]
  22. He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
  23. Ahn, C.; Li, C.-T.; Peng, H. Optimal decentralized charging control algorithm for electrified vehicles connected to smart grid. J. Power Sources 2011, 196, 10369–10379. [Google Scholar] [CrossRef]
  24. Hu, J.; You, S.; Lind, M.; Østergaard, J. Coordinated charging of electric vehicles for congestion prevention in the distribution grid. IEEE Trans. Smart Grid 2013, 5, 703–711. [Google Scholar] [CrossRef] [Green Version]
  25. Uddin, M.; Romlie, M.; Abdullah, M.F.; Halim, S.A.; Abu Bakar, A.H.; Kwang, T.C. A review on peak load shaving strategies. Renew. Sustain. Energy Rev. 2018, 82, 3323–3332. [Google Scholar] [CrossRef]
  26. Letendre, S.E.; Kempton, W. The V2G concept: A new model for power? Public Util. Fortn. 2002, 140, 16–26. [Google Scholar]
  27. Guille, C.; Gross, G. A conceptual framework for the vehicle-to-grid (V2G) implementation. Energy Policy 2009, 37, 4379–4390. [Google Scholar] [CrossRef]
  28. Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y. Integration of electric vehicles in smart grid: A review on vehicle to grid technologies and optimization techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar] [CrossRef]
  29. Sortomme, E.; El-Sharkawi, M.A. Optimal charging strategies for unidirectional vehicle-to-grid. IEEE Trans. Smart Grid 2010, 2, 131–138. [Google Scholar] [CrossRef]
  30. Boynuegri, A.; Uzunoglu, M.; Erdinc, O.; Gokalp, E. A new perspective in grid connection of electric vehicles: Different operating modes for elimination of energy quality problems. Appl. Energy 2014, 132, 435–451. [Google Scholar] [CrossRef]
  31. Turker, H.; Hably, A.; Bacha, S. Housing peak shaving algorithm (HPSA) with plug-in hybrid electric vehicles (PHEVs): Vehicle-to-Home (V2H) and Vehicle-to-Grid (V2G) concepts. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 753–759. [Google Scholar]
  32. Feldman, D.; Barbose, G.; Margolis, R.; Wiser, R.; Darghouth, N.; Goodrich, A. Photovoltaic (PV) Pricing Trends: Historical, Recent, and Near-Term Projections; National Renewable Energy Laboratory: Golden, CO, USA, 2012.
  33. Goli, P.; Shireen, W. PV powered smart charging station for PHEVs. Renew. Energy 2014, 66, 280–287. [Google Scholar] [CrossRef]
  34. Carli, G.; Williamson, S.S. Technical considerations on power conversion for electric and plug-in hybrid electric vehicle battery charging in photovoltaic installations. IEEE Trans. Power Electron. 2013, 28, 5784–5792. [Google Scholar] [CrossRef]
  35. Van Der Meer, D.; Mouli, G.R.C.; Morales-Espana, G.; Elizondo, L.R.; Bauer, P. Erratum to energy management system with pv power forecast to optimally charge evs at the workplace. IEEE Trans. Ind. Inform. 2018, 14, 3298. [Google Scholar] [CrossRef]
  36. Oliveira, D.; De Souza, A.Z.; Delboni, L. Optimal plug-in hybrid electric vehicles recharge in distribution power systems. Electr. Power Syst. Res. 2013, 98, 77–85. [Google Scholar] [CrossRef]
  37. Ahmad, F.; Alam, M.S.; Shahidehpour, M. Profit maximization of microgrid aggregator under power market environment. IEEE Syst. J. 2019, 13, 3388–3399. [Google Scholar] [CrossRef]
  38. Sarker, M.R.; Dvorkin, Y.; Ortega-Vazquez, M. Optimal participation of an electric vehicle aggregator in day-ahead energy and reserve markets. IEEE Trans. Power Syst. 2015, 31, 3506–3515. [Google Scholar] [CrossRef]
  39. Reddy, K.R.; Meikandasivam, S. Load flattening and voltage regulation using plug-in electric vehicle’s storage capacity with vehicle prioritization using ANFIS. IEEE Trans. Sustain. Energy 2020, 11, 260–270. [Google Scholar] [CrossRef]
  40. Ko, K.S.; Han, S.; Sung, D.K. Performance-based settlement of frequency regulation for electric vehicle aggregators. IEEE Trans. Smart Grid 2018, 9, 866–875. [Google Scholar] [CrossRef]
  41. Zhou, K.; Cai, L. Randomized PHEV charging under distribution grid constraints. IEEE Trans. Smart Grid 2014, 5, 879–887. [Google Scholar] [CrossRef]
  42. Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized charging control of large populations of plug-in electric vehicles. IEEE Trans. Control. Syst. Technol. 2011, 21, 67–78. [Google Scholar] [CrossRef]
  43. Unda, I.G.; Papadopoulos, P.; Skarvelis-Kazakos, S.; Cipcigan, L.M.; Jenkins, N.; Zabala, E. Management of electric vehicle battery charging in distribution networks with multi-agent systems. Electr. Power Syst. Res. 2014, 110, 172–179. [Google Scholar] [CrossRef]
  44. Chaudhari, K.; Kandasamy, N.K.; Krishnan, A.; Ukil, A.; Gooi, H.B. Agent-based aggregated behavior modeling for electric vehicle charging load. IEEE Trans. Ind. Inform. 2018, 15, 856–868. [Google Scholar] [CrossRef]
  45. Liu, M.; Phanivong, P.K.; Shi, Y.; Callaway, D.S. Decentralized charging control of electric vehicles in residential distribution networks. IEEE Trans. Control. Syst. Technol. 2019, 27, 266–281. [Google Scholar] [CrossRef] [Green Version]
  46. Torreglosa, J.P.; García-Triviño, P.; Fernández-Ramírez, L.M.; Jurado, F. Decentralized energy management strategy based on predictive controllers for a medium voltage direct current photovoltaic electric vehicle charging station. Energy Convers. Manag. 2016, 108, 1–13. [Google Scholar] [CrossRef]
  47. Weckx, S.; D’Hulst, R.; Driesen, J. Primary and secondary frequency support by a multi-agent demand control system. IEEE Trans. Power Syst. 2014, 30, 1394–1404. [Google Scholar] [CrossRef]
  48. Paterakis, N.G.; Erdinc, O.; Bakirtzis, A.G.; Catalão, J.P. Optimal household appliances scheduling under day-ahead pricing and load-shaping demand response strategies. IEEE Trans. Ind. Inform. 2015, 11, 1509–1519. [Google Scholar] [CrossRef]
  49. Xi, X.; Sioshansi, R. Using price-based signals to control plug-in electric vehicle fleet charging. IEEE Trans. Smart Grid 2014, 5, 1451–1464. [Google Scholar] [CrossRef]
  50. Pan, J.; Jain, R.; Paul, S.; Vu, T.; Saifullah, A.; Sha, M. A internet of things framework for smart energy in buildings: Designs, prototype, and experiments. IEEE Internet Things J. 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]
  51. Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sustain. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef] [Green Version]
  52. Fischer, D.; Harbrecht, A.; Surmann, A.; McKenna, R. Electric vehicles’ impacts on residential electric local profiles—A stochastic modelling approach considering socio-economic, behavioural and spatial factors. Appl. Energy 2019, 644–658. [Google Scholar] [CrossRef]
  53. Nunes, P.; Figueiredo, R.; Brito, M.C. The use of parking lots to solar-charge electric vehicles. Renew. Sustain. Energy Rev. 2016, 66, 679–693. [Google Scholar] [CrossRef]
  54. Prakash, K.; Vaithilingam, C.A.; Rajendran, G.; Vaithilingam, C.A. Design and sizing of mobile solar photovoltaic power plant to support rapid charging for electric vehicles. Energies 2019, 12, 3579. [Google Scholar] [CrossRef] [Green Version]
  55. Denholm, P.; Kuss, M.; Margolis, R.M. Co-benefits of large scale plug-in hybrid electric vehicle and solar PV deployment. J. Power Sources 2013, 236, 350–356. [Google Scholar] [CrossRef]
  56. Nunes, P.; Farias, T.L.; Brito, M.C. Day charging electric vehicles with excess solar electricity for a sustainable energy system. Energy 2015, 80, 263–274. [Google Scholar] [CrossRef]
  57. Tulpule, P.; Marano, V.; Yurkovich, S.; Rizzoni, G. Economic and environmental impacts of a PV powered workplace parking garage charging station. Appl. Energy 2013, 108, 323–332. [Google Scholar] [CrossRef]
  58. Sarkar, J.; Bhattacharyya, S. Operating characteristics of transcritical CO2 heat pump for simultaneous water cooling and heating. Arch. Thermodyn. 2011, 33, 23–40. [Google Scholar] [CrossRef]
  59. Kempton, W.; Tomić, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
  60. Moghaddam, Z.; Ahmad, I.; Habibi, D.; Phung, Q.V.; Habibi, D. Smart charging strategy for electric vehicle charging stations. IEEE Trans. Transp. Electrif. 2018, 4, 76–88. [Google Scholar] [CrossRef]
  61. Mouli, G.R.C.; Kefayati, M.; Baldick, R.; Bauer, P. Integrated PV charging of EV fleet based on energy prices, V2G, and offer of reserves. IEEE Trans. Smart Grid 2017, 10, 1313–1325. [Google Scholar] [CrossRef]
  62. Ioakimidis, C.S.; Thomas, D.; Rycerski, P.; Genikomsakis, K.N. Peak shaving and valley filling of power consumption profile in non-residential buildings using an electric vehicle parking lot. Energy 2018, 148, 148–158. [Google Scholar] [CrossRef]
  63. Ivanova, A.; Fernandez, J.A.; Crawford, C.; Sui, P.-C. Coordinated charging of electric vehicles connected to a net-metered PV parking lot. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
  64. Mohamed, A.A.; Salehi, V.; Ma, T.; Mohammed, O.A. Real-time energy management algorithm for plug-in hybrid electric vehicle charging parks involving sustainable energy. IEEE Trans. Sustain. Energy 2014, 5, 577–586. [Google Scholar] [CrossRef]
  65. Liu, N.; Chen, Q.; Liu, J.; Lu, X.; Li, P.; Lei, J.; Zhang, J. A heuristic operation strategy for commercial building microgrids containing EVs and PV system. IEEE Trans. Ind. Electron. 2014, 62, 2560–2570. [Google Scholar] [CrossRef]
  66. Zhang, Y.; Cai, L. Dynamic charging scheduling for EV parking lots with photovoltaic power system. IEEE Access 2018, 6, 56995–57005. [Google Scholar] [CrossRef]
  67. Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. Effective utilization of available PEV battery capacity for mitigation of solar PV impact and grid support with integrated V2G functionality. IEEE Trans. Smart Grid 2015, 7, 1562–1571. [Google Scholar] [CrossRef] [Green Version]
  68. Wi, Y.-M.; Lee, J.-U.; Joo, S.-K. Electric vehicle charging method for smart homes/buildings with a photovoltaic system. IEEE Trans. Consum. Electron. 2013, 59, 323–328. [Google Scholar] [CrossRef]
  69. Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef] [Green Version]
  70. Eldeeb, H.H.; Faddel, S.; Mohammed, O.A. Multi-objective optimization technique for the operation of grid tied PV powered EV charging station. Electr. Power Syst. Res. 2018, 164, 201–211. [Google Scholar] [CrossRef]
  71. Van Der Kam, M.; Van Sark, W. Smart charging of electric vehicles with photovoltaic power and vehicle-to-grid technology in a microgrid; a case study. Appl. Energy 2015, 152, 20–30. [Google Scholar] [CrossRef] [Green Version]
  72. Bhatti, A.R.; Salam, Z. A rule-based energy management scheme for uninterrupted electric vehicles charging at constant price using photovoltaic-grid system. Renew. Energy 2018, 125, 384–400. [Google Scholar] [CrossRef]
  73. Barone, G.; Buonomano, A.; Calise, F.; Forzano, C.; Palombo, A. Building to vehicle to building concept toward a novel zero energy paradigm: Modelling and case studies. Renew. Sustain. Energy Rev. 2019, 101, 625–648. [Google Scholar] [CrossRef]
  74. Ghotge, R.; Snow, Y.; Farahani, S.; Lukszo, Z.; Van Wijk, A.J. Optimized scheduling of EV charging in solar parking lots for local peak reduction under eV demand uncertainty. Energies 2020, 13, 1275. [Google Scholar] [CrossRef] [Green Version]
  75. Fachrizal, R.; Munkhammar, J. Improved photovoltaic self-consumption in residential buildings with distributed and centralized smart charging of electric vehicles. Energies 2020, 13, 1153. [Google Scholar] [CrossRef] [Green Version]
  76. Nunes, P.; Farias, T.L.; Brito, M.C. Enabling solar electricity with electric vehicles smart charging. Energy 2015, 87, 10–20. [Google Scholar] [CrossRef]
  77. Kadar, P.; Varga, A. PhotoVoltaic EV charge station. In Proceedings of the 2013 IEEE 11th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovenia, 31 January–2 February 2013; pp. 57–60. [Google Scholar]
  78. Brenna, M.; Dolara, A.; Foiadelli, F.; Leva, S.; Longo, M. Urban scale photovoltaic charging stations for electric vehicles. IEEE Trans. Sustain. Energy 2014, 5, 1234–1241. [Google Scholar] [CrossRef]
  79. Leou, R.-C.; Su, C.-L.; Lu, C.-N. Stochastic analyses of electric vehicle charging impacts on distribution network. IEEE Trans. Power Syst. 2013, 29, 1055–1063. [Google Scholar] [CrossRef]
  80. Khodayar, M.E.; Wu, L.; Shahidehpour, M. Hourly Coordination of electric vehicle operation and volatile wind power generation in SCUC. IEEE Trans. Smart Grid 2012, 3, 1271–1279. [Google Scholar] [CrossRef]
  81. Liu, Z.; Wen, F.; Ledwich, G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties. IEEE Trans. Power Deliv. 2011, 26, 2541–2551. [Google Scholar] [CrossRef]
  82. Soares, J.; Borges, N.; Ghazvini, M.A.F.; Vale, Z.; Oliveira, P.M. Scenario generation for electric vehicles’ uncertain behavior in a smart city environment. Energy 2016, 111, 664–675. [Google Scholar] [CrossRef] [Green Version]
  83. Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
  84. Soroudi, A.; Ehsan, M. A possibilistic–probabilistic tool for evaluating the impact of stochastic renewable and controllable power generation on energy losses in distribution networks—A case study. Renew. Sustain. Energy Rev. 2011, 15, 794–800. [Google Scholar] [CrossRef] [Green Version]
  85. Ahmad, F.; Alam, M.S.; Shariff, S.M.; Krishnamurthy, M. A Cost-efficient approach to ev charging station integrated community microgrid: A case study of Indian power market. IEEE Trans. Transp. Electrif. 2019, 5, 200–214. [Google Scholar] [CrossRef]
  86. Shepero, M.; Munkhammar, J. Spatial Markov chain model for electric vehicle charging in cities using geographical information system (GIS) data. Appl. Energy 2018, 231, 1089–1099. [Google Scholar] [CrossRef]
  87. Gupta, N. Gauss-quadrature-based probabilistic load flow method with voltage-dependent loads including WTGS, PV, and EV charging uncertainties. IEEE Trans. Ind. Appl. 2018, 54, 6485–6497. [Google Scholar] [CrossRef]
  88. Zhou, B.; Yang, X.; Yang, D.; Yang, Z.; Littler, T.; Li, H. Probabilistic load flow algorithm of distribution networks with distributed generators and electric vehicles integration. Energies 2019, 12, 4234. [Google Scholar] [CrossRef] [Green Version]
  89. Baringo, L.; Amaro, R.S. A stochastic robust optimization approach for the bidding strategy of an electric vehicle aggregator. Electr. Power Syst. Res. 2017, 146, 362–370. [Google Scholar] [CrossRef] [Green Version]
  90. Sarker, M.R.; Pandžić, H.; Ortega-Vazquez, M. Optimal Operation and services scheduling for an electric vehicle battery swapping station. IEEE Trans. Power Syst. 2014, 30, 901–910. [Google Scholar] [CrossRef]
  91. Zhao, J.; Wan, C.; Xu, Z.; Wang, J. Risk-based day-ahead scheduling of electric vehicle aggregator using information gap decision theory. IEEE Trans. Smart Grid 2015, 8, 1609–1618. [Google Scholar] [CrossRef]
  92. Soroudi, A.; Keane, A. Risk averse energy hub management considering plug-in electric vehicles using information gap decision theory. In Power Systems; Springer: Singapore, 2015; Volume 89, pp. 107–127. [Google Scholar]
  93. Aien, M.; Fotuhi-Firuzabad, M.; Rashidinejad, M. Probabilistic optimal power flow in correlated hybrid WindPhotovoltaic power systems. IEEE Trans. Smart Grid 2014, 5, 130–138. [Google Scholar] [CrossRef]
  94. Al-Dahidi, S.; Ayadi, O.; Alrbai, M.; Adeeb, J. Ensemble approach of optimized artificial neural networks for solar photovoltaic power prediction. IEEE Access 2019, 7, 81741–81758. [Google Scholar] [CrossRef]
  95. Zhao, Q.; Wang, P.; Goel, L.; Ding, Y. Evaluation of nodal reliability risk in a deregulated power system with photovoltaic power penetration. IET Gener. Transm. Distrib. 2013, 8, 421–430. [Google Scholar] [CrossRef]
  96. Zhao, J.; Wang, W.; Sheng, C. Industrial prediction intervals with data Uncertainty. In Information Fusion and Data Science; Springer: Cham, Switzerland, 2018; pp. 159–222. [Google Scholar]
  97. Wu, X.; Wang, X.; Qu, C. A hierarchical framework for generation scheduling of microgrids. IEEE Trans. Power Deliv. 2014, 29, 2448–2457. [Google Scholar] [CrossRef]
  98. Ehsan, A.; Yang, Q. Coordinated investment planning of distributed multi-type stochastic generation and battery storage in active distribution networks. IEEE Trans. Sustain. Energy 2019, 10, 1813–1822. [Google Scholar] [CrossRef]
  99. Wang, R.; Wang, P.; Xiao, G. A robust optimization approach for energy generation scheduling in microgrids. Energy Convers. Manag. 2015, 106, 597–607. [Google Scholar] [CrossRef]
  100. Sun, Y.; Huang, P.; Huang, G. A multi-criteria system design optimization for net zero energy buildings under uncertainties. Energy Build. 2015, 97, 196–204. [Google Scholar] [CrossRef]
  101. Koraki, D.; Strunz, K. Wind and solar power integration in electricity markets and distribution networks through service-centric virtual power plants. IEEE Trans. Power Syst. 2017, 33, 473–485. [Google Scholar] [CrossRef]
  102. Chen, Y.; Wang, Y.; Kirschen, D.S.; Zhang, B. Model-free renewable scenario generation using generative adversarial networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef] [Green Version]
  103. Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
  104. Das, U.K.; Soon, T.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
  105. Ramadhani, U.H.; Shepero, M.; Munkhammar, J.; Widén, J.; Etherden, N. Review of probabilistic load flow approaches for power distribution systems with photovoltaic generation and electric vehicle charging. Int. J. Electr. Power Energy Syst. 2020, 120, 106003. [Google Scholar] [CrossRef]
  106. Zakaria, A.; Ismail, F.B.; Lipu, M.S.H.; Hannan, M. Uncertainty models for stochastic optimization in renewable energy applications. Renew. Energy 2020, 145, 1543–1571. [Google Scholar] [CrossRef]
  107. Ehsan, A.; Yang, Q. State-of-the-art techniques for modelling of uncertainties in active distribution network planning: A review. Appl. Energy 2019, 239, 1509–1523. [Google Scholar] [CrossRef]
  108. Kumar, K.P.; Saravanan, B. Recent techniques to model uncertainties in power generation from renewable energy sources and loads in microgrids—A review. Renew. Sustain. Energy Rev. 2017, 71, 348–358. [Google Scholar] [CrossRef]
  109. Kawamura, N.; Muta, M. Development of solar charging system for plug-in hybrid electric vehicles and electric vehicles. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–5. [Google Scholar]
  110. Castello, C.C.; LaClair, T.J.; Curt Maxey, L. Control strategies for electric vehicle (EV) charging using renewables and local storage. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–7. [Google Scholar]
  111. Prusty, B.R.; Jena, D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach. Renew. Sustain. Energy Rev. 2017, 69, 1286–1302. [Google Scholar] [CrossRef]
  112. Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
  113. Jordehi, A.R. How to deal with uncertainties in electric power systems? A review. Renew. Sustain. Energy Rev. 2018, 96, 145–155. [Google Scholar] [CrossRef]
  114. Verbič, G.; Canizares, C.A. Probabilistic optimal power flow in electricity markets based on a two-point estimate method. IEEE Trans. Power Syst. 2006, 21, 1883–1893. [Google Scholar] [CrossRef]
  115. Morales, J.; Perez-Ruiz, J. Point estimate schemes to solve the probabilistic power flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
  116. Alaee, S.; Hooshmand, R.-A.; Hemmati, R. Stochastic transmission expansion planning incorporating reliability solved using SFLA meta-heuristic optimization technique. CSEE J. Power Energy Syst. 2016, 2, 79–86. [Google Scholar] [CrossRef]
  117. Cai, D.; Shi, D.; Chen, J. Probabilistic load flow with correlated input random variables using uniform design sampling. Int. J. Electr. Power Energy Syst. 2014, 63, 105–112. [Google Scholar] [CrossRef]
  118. Soares, J.; Ghazvini, M.A.F.; Vale, Z.; Oliveira, P.M. A multi-objective model for the day-ahead energy resource scheduling of a smart grid with high penetration of sensitive loads. Appl. Energy 2016, 162, 1074–1088. [Google Scholar] [CrossRef]
  119. Talari, S.; Haghifam, M.-R.; Yazdaninejad, M. Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads. IET Gener. Transm. Distrib. 2015, 9, 1498–1509. [Google Scholar] [CrossRef]
  120. El Motaleb, A.M.A.; Bekdache, S.K.; Alvarado-Barrios, L. Optimal sizing for a hybrid power system with wind/energy storage based in stochastic environment. Renew. Sustain. Energy Rev. 2016, 59, 1149–1158. [Google Scholar] [CrossRef]
  121. Allan, R.; Da Silva, A.; Burchett, R. Evaluation methods and accuracy in probabilistic load flow solutions. IEEE Trans. Power Appar. Syst. 1981, 2539–2546. [Google Scholar] [CrossRef]
  122. Schwippe, J.; Krause, O.; Rehtanz, C. Probabilistic load flow calculation based on an enhanced convolution technique. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
  123. Munkhammar, J.; Rydén, J.; Widén, J. Characterizing probability density distributions for household electricity load profiles from high-resolution electricity use data. Appl. Energy 2014, 135, 382–390. [Google Scholar] [CrossRef]
  124. Li, G.; Zhang, X.-P. Comparison between two probabilistic load flow methods for reliability assessment. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar]
Energies 13 04541 g001 550
Figure 1. The evolution of electric vehicles (EVs).
Figure 1. The evolution of electric vehicles (EVs).
Energies 13 04541 g001
Energies 13 04541 g002 550
Figure 2. An analytical framework for grid-connected EV-PV (photovoltaics) interaction.
Figure 2. An analytical framework for grid-connected EV-PV (photovoltaics) interaction.
Energies 13 04541 g002
Energies 13 04541 g003 550
Figure 3. EV integration with the electrical grid.
Figure 3. EV integration with the electrical grid.
Energies 13 04541 g003
Energies 13 04541 g004 550
Figure 4. A general outline for modelling a grid-connected EV-PV charging system.
Figure 4. A general outline for modelling a grid-connected EV-PV charging system.
Energies 13 04541 g004
Energies 13 04541 g005 550
Figure 5. An overview of scheduling strategies in V2G mode [51].
Figure 5. An overview of scheduling strategies in V2G mode [51].
Energies 13 04541 g005
Energies 13 04541 g006 550
Figure 6. EV load demand parameters used for uncertainty modelling.
Figure 6. EV load demand parameters used for uncertainty modelling.
Energies 13 04541 g006
Table
Table 1. Modes of Interaction between EV and grid.
Table 1. Modes of Interaction between EV and grid.
FeaturesUnidirectionalBidirectional
Power flowGrid-to-vehicle (G2V)G2V and vehicle-to-grid (V2G)
InfrastructureCommunicationCommunication, bidirectional charger
CostLowHigh
ComplexityLowHigh
ServicesLoad profile management, Frequency regulation [27]Backup power support, frequency regulation, voltage regulation, active power support [28]
AdvantagesOverloading prevention, load levelling, profit maximisation, emission minimisation [29]Overloading prevention, profit maximisation, emission minimisation, renewable energy sources (RES) integration, voltage profile improvement, harmonic filtering [30], load levelling, power loss reduction [31]
DisadvantagesLimited servicesBattery degradation, high complexity, and cost, social barriers
Table
Table 2. Summary of literature related to smart charging of grid-connected EV-PV system.
Table 2. Summary of literature related to smart charging of grid-connected EV-PV system.
ReferencesObjectivesOptimisation ModelSoftware/ImplementationKey Findings
[62]Peak shaving and valley fillingLinear programmingMATLABThe effectiveness of the proposed algorithm is dependent on a high number of available parking spots.
[35]Maximizing profit and PV utilisationMixed Integer Linear programmingGAMSDue to battery degradation cost, V2G is not economically feasible unless high PV production is present
[63]Minimizing system costMixed Integer Linear programmingCPLEXSmart charging can result in saving of operational cost for charging and PV usage for the parking lot owner
[64]Minimizing charging costFuzzy logicMATLABThe algorithm is not optimisation based so targets several objectives: Reduction in charging cost and system losses, improvement in voltage profile.
[65]Maximizing PV utilisationMetaheuristicMATLABThe proposed heuristic algorithm achieves desired objectives with low computational cost and without forecasting of uncertain variables.
[66]Maximizing EV aggregator benefitsHybrid MPC-The proposed algorithm achieves near-optimal solution of EV charge scheduling problem with better efficiency than standard MPC
[67]Maximizing PV utilisation and reducing EV charging impactLinear programmingCase study: New South Wales distribution systemThe proposed strategy controls the charging/discharging profile of EVs to match with the shape of the PV output to achieve desired objectives.
[68]Minimizing charging costMixed Integer Linear programmingCase study: KoreaThe proposed algorithm does not consider selling excess power and demonstrates charging cost savings compared to uncoordinated charging
[61]Minimizing system costMixed Integer Linear programmingMicrosoft Solver FoundationA comprehensive system to achieve one optimal charging profile will result in a larger net benefit compared to individual applications.
[69]Minimizing charging costConvex programmingMATLABESS can significantly reduce charging cost and bi-directional V2H is cheaper than H2V
[70]Maximizing profit and ESS lifeNon-linear programmingGAMSConsidering only revenue maximisation will result in an adverse effect on ESS life
[71]Maximizing PV utilisationLinear programmingCase study: LomboXnetProposed algorithm increases PV self-consumption and reduces peak demand by half
[72]Minimizing charging costRule-based algorithmMATLABRule-based charging is superior to conventional charging for less charging cost and reduced grid loading
[73]Maximizing PV utilisationRule-based algorithmMATLABV2B can be an effective strategy if initial capital costs and electricity price are fitting
[74]Minimizing peak demandMPCMATLABEV scheduling can reduce both the magnitude and frequency of peak loading
[75]Peak shaving and valley fillingQuadratic programmingMATLABNet load variation was lower in case of low PV power-sharing and vice-versa
V2H, vehicle-to-home; H2V, home-to-vehicle; V2B, vehicle-to-building; MPC, model predictive control.
Table
Table 3. Overview of uncertainty modelling methods for EV load demand.
Table 3. Overview of uncertainty modelling methods for EV load demand.
MethodRemarksReferences
Scenario reduction
  • Simple and less computationally intensive
  • Approximate uncertainty modelling, accuracy depends on the amount of historical data available
[79,80]
Monte Carlo simulation
  • High accuracy, but also computationally intensive
  • Accuracy depends on the amount of historical data available
[19,81]
Fuzzy logic
  • Historical data not required
  • Accuracy depends on rule settings which are based on researcher experience
[82,83]
Hybrid Monte Carlo-fuzzy
  • High accuracy, but also computationally intensive
  • Can model both temporal and spatial uncertainty
[84]
Artificial Neural Network
  • Accuracy depends on input dataset quality
  • Considers the correlation between forecasted and observed data
[37,85]
Markov chain
  • Very high accuracy with moderate computational cost
  • Performance depends on input data dimension
[86]
Probability distribution fitting
  • Very simple, but also less accurate
[87,88]
Robust optimisation
  • Low computationally intensive however difficult to employ with non-linear problems
  • Not flexible, i.e., give a single solution which might be infeasible
[89,90]
Information gap decision theory
  • Useful for dealing with severe uncertainties
  • Complex implementation
[91,92]
Table
Table 4. Overview of common uncertainty modelling methods for PV.
Table 4. Overview of common uncertainty modelling methods for PV.
MethodRemarksReferences
Point estimation
  • Computationally intensive with more input variables
[93]
Bootstrap
  • Simple and low computational cost
  • High accuracy
[94]
Monte Carlo simulation
  • High accuracy, but also computationally intensive
[95]
Mean-Variance estimation
  • Based on the assumption that uncertainty is normally distributed
  • Simple, but less accurate for practical cases
[96]
Two stage scheduling
  • Upper level deals with global adjustment and lower with local adjustment
  • Simple, flexible and accurate
[97]
Scenario based analysis
  • Very commonly used method with a high degree of accuracy
  • Accuracy depends upon the scenario generation technique
[98]
Kernel Density estimation
  • Needs to analyse a large amount of historical data
[99]
Autoregressive Moving Average
  • Accuracy depends on historical time-series dataset
  • Needs a lot of historical data and analysis
[35]
Probability distribution fitting
  • Very simple, but also less accurate
[100]
Rolling Horizon approach
  • Effective for large scale system with moderate computational cost
[101]
Generative Adversarial network
  • Very new and highly accurate scenario based method
[102]
Table
Table 5. Overview of common uncertainty modelling methods for electrical load demand.
Table 5. Overview of common uncertainty modelling methods for electrical load demand.
MethodRemarksReferences
Point estimation
  • Does not require complete knowledge about the system, but computationally intensive with more input variables
  • Two-point is the simplest and three-point is most efficient
[114,115]
Monte Carlo simulation
  • High accuracy, but also computationally intensive
  • Different sampling techniques reduce the computational burden
[116,117]
Fuzzy logic
  • Less computationally intensive and robust in nature
  • Vital parameters are decided by the researcher based on experience
[118]
Scenario based analysis
  • Very commonly used method with a high degree of accuracy
  • Accuracy depends upon the scenario generation technique
[119]
Autoregressive Moving Average
  • Accuracy depends on historical time-series dataset
  • Needs a lot of historical data and analysis
[85,120]
Convolution based
  • Traditional analytical method with low computation efficiency
  • Applicable to linear systems with independent inputs
[121,122]
Probability distribution fitting
  • Very simple, but also less accurate
[88,123]
Cumulant based
  • Traditional analytical method with high computation efficiency
  • Accuracy decreases with higher order systems
[124]

Share and Cite

MDPI and ACS Style

Mohammad, A.; Zamora, R.; Lie, T.T. Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies 2020, 13, 4541. https://doi.org/10.3390/en13174541

AMA Style

Mohammad A, Zamora R, Lie TT. Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies. 2020; 13(17):4541. https://doi.org/10.3390/en13174541

Chicago/Turabian Style

Mohammad, Asaad, Ramon Zamora, and Tek Tjing Lie. 2020. "Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling" Energies 13, no. 17: 4541. https://doi.org/10.3390/en13174541

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop