Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling
Abstract
1. Introduction
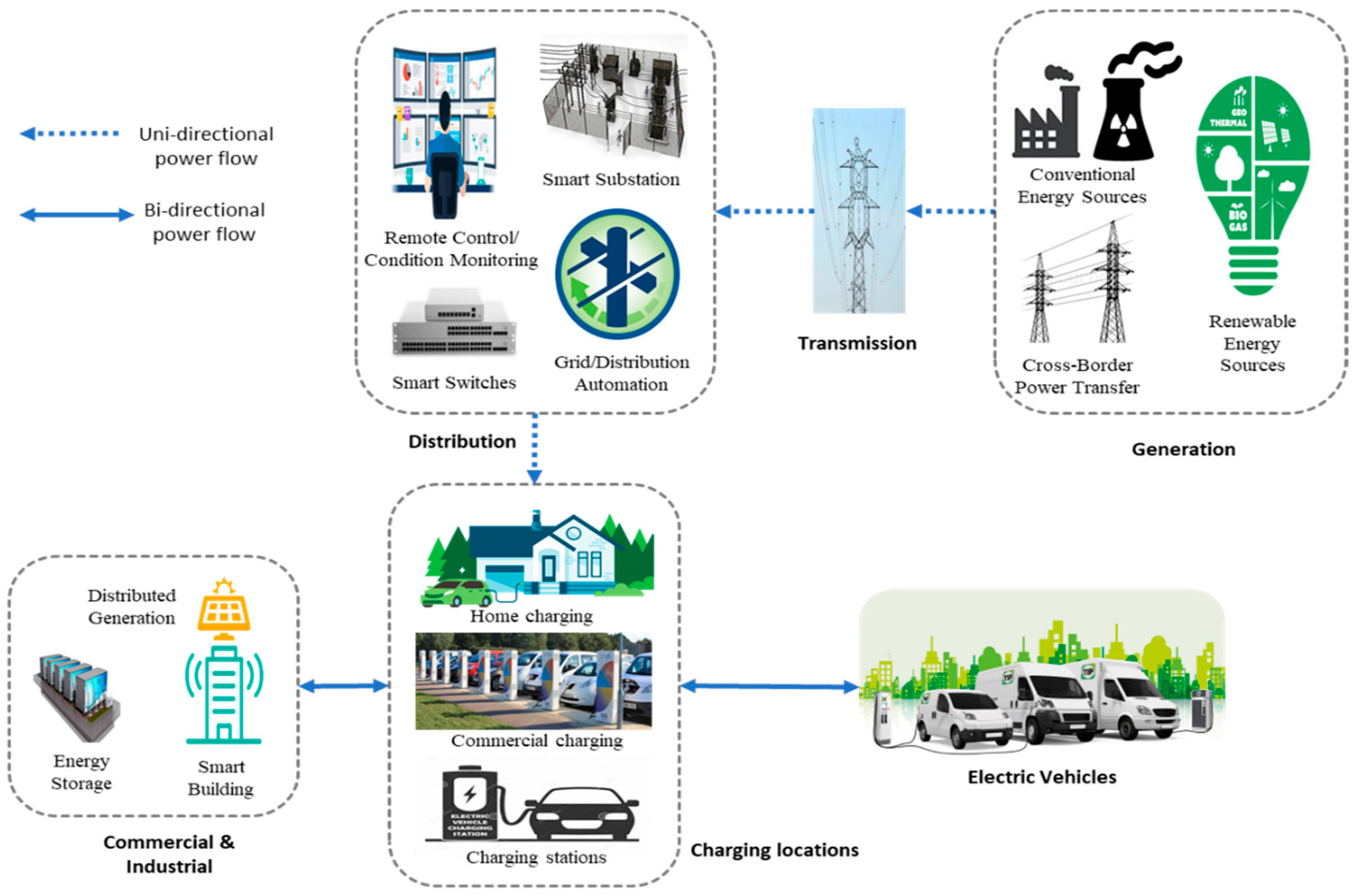
2. EV Interaction with the Distribution Network
- Vehicle-to-grid (V2G): Energy transfer from EV to the distribution network.
- Vehicle-to-home/building (V2H/V2B): Energy transfer from EV to home/building.
- Vehicle-to-vehicle (V2V): Energy transfer from one EV to another EV.
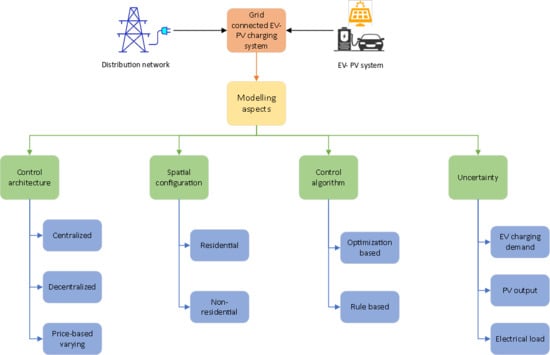
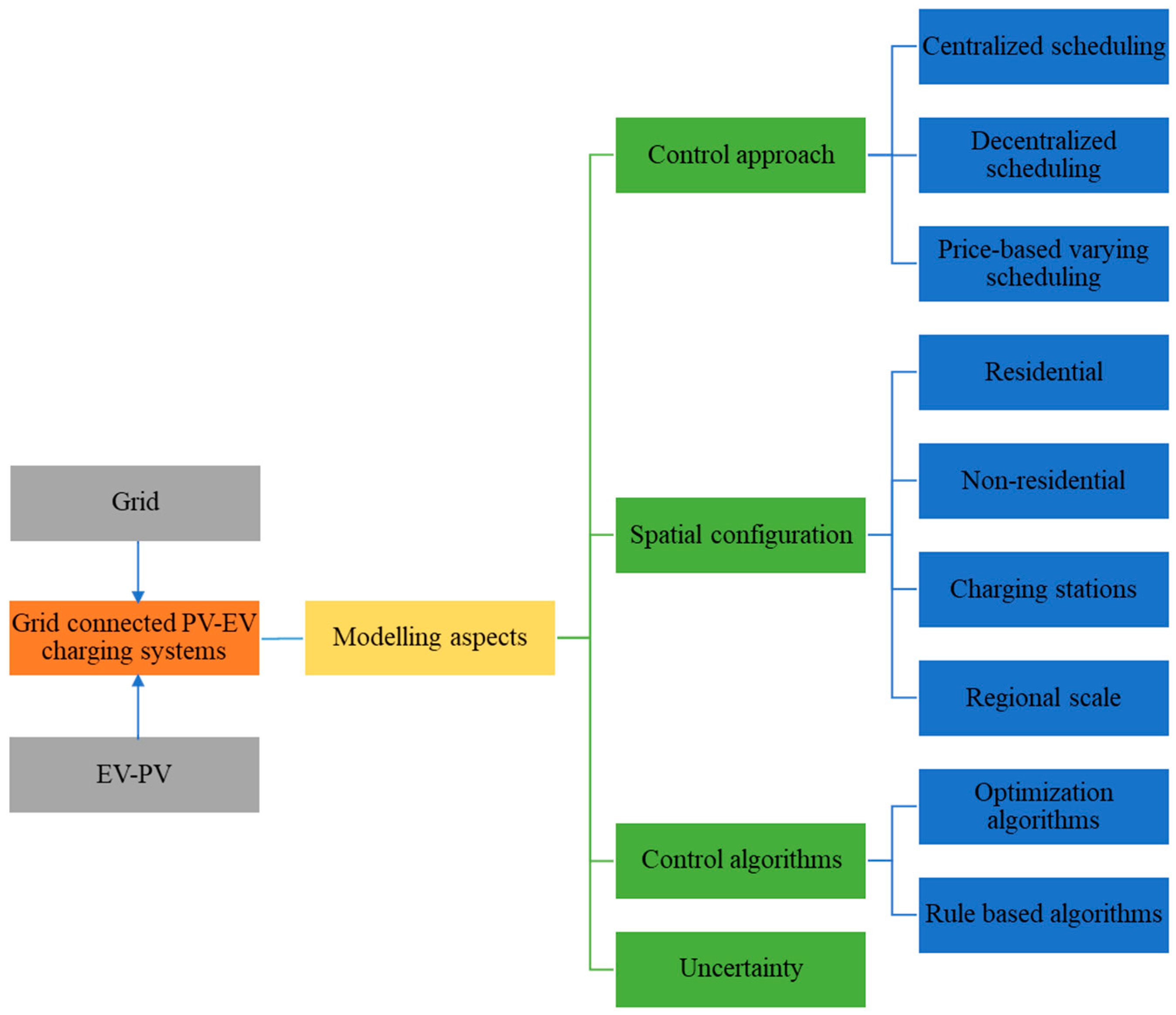
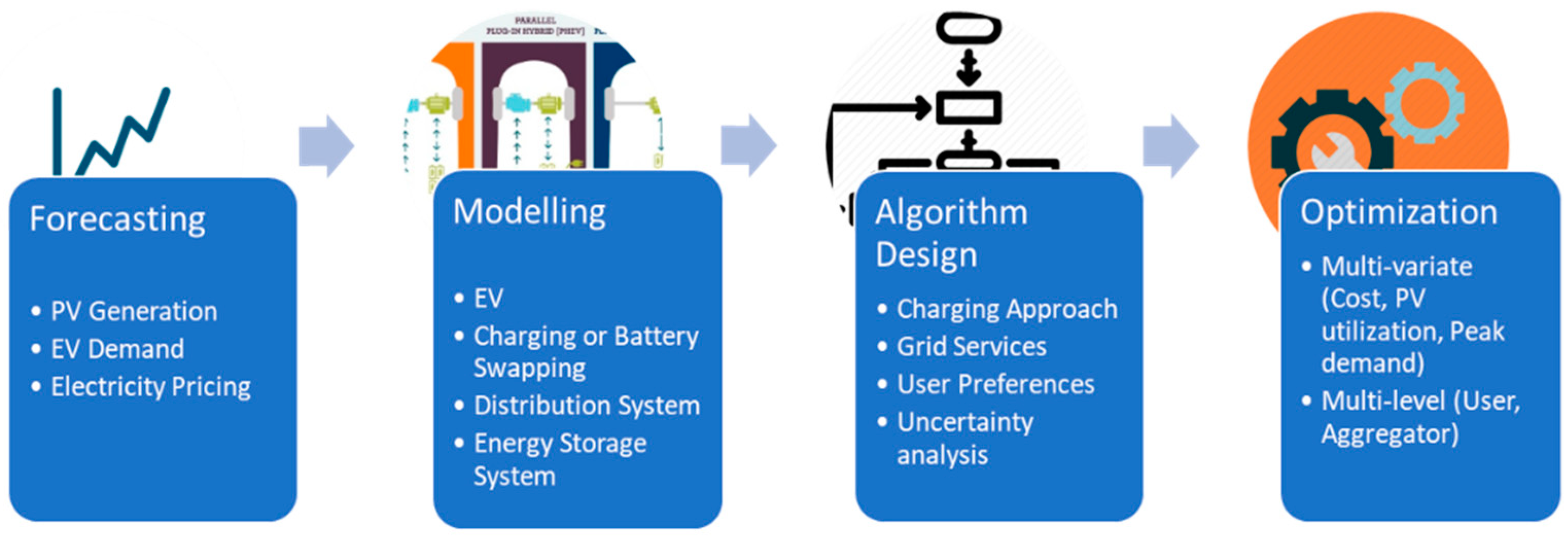
3. Modelling of Grid-Connected EV-PV System
- The cost of PV has been dropping continuously and is currently less than $1/Wp [32].
- PV is highly accessible, i.e., PV modules are generally installed on the building rooftops and carparks, close to EV locations.
- PV modules do not require maintenance and are also noise-free.
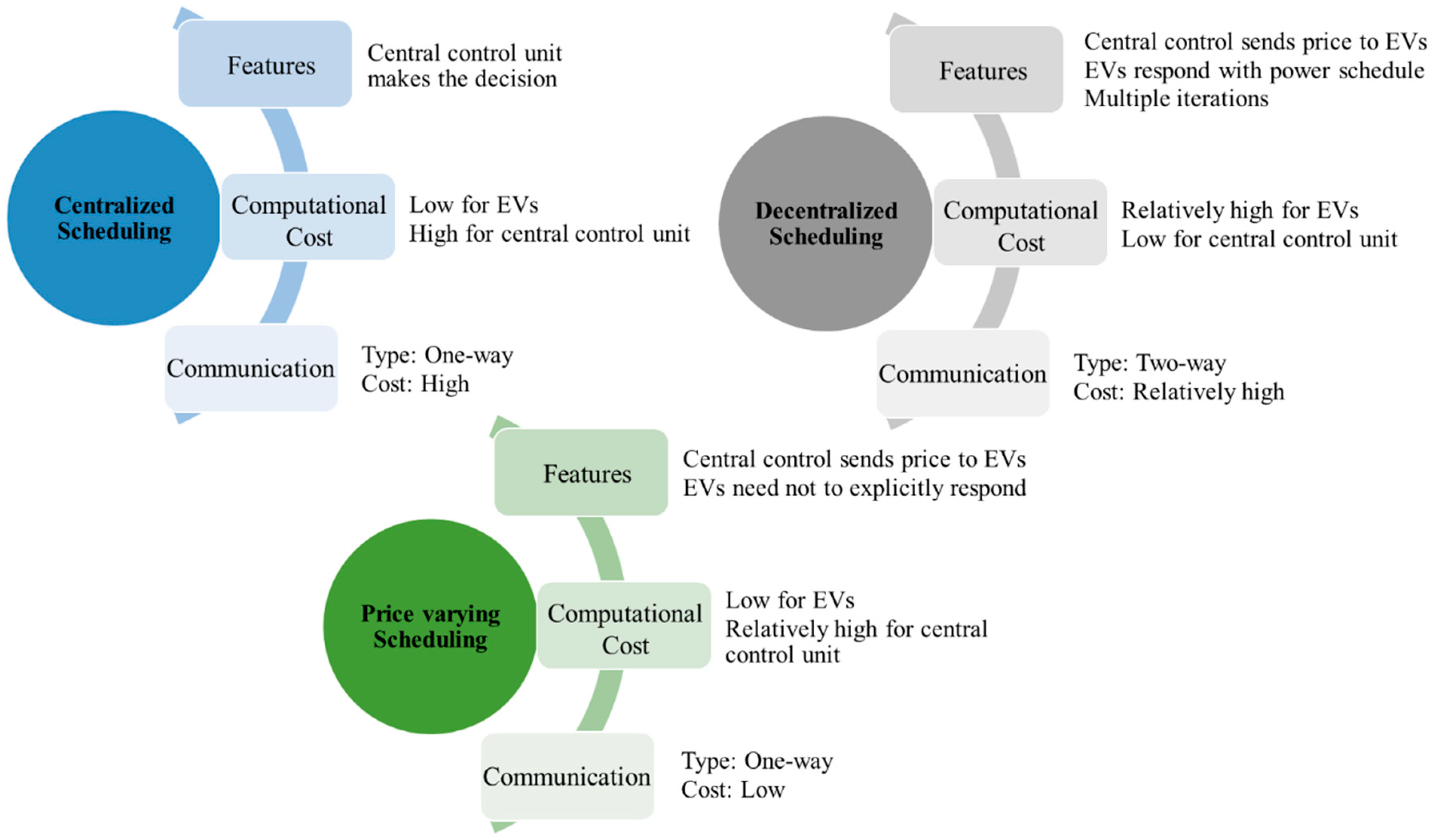
- Centralised scheduling;
- Decentralised scheduling;
- Price-varying scheduling.
4. EV Smart Charging Using PV and Grid
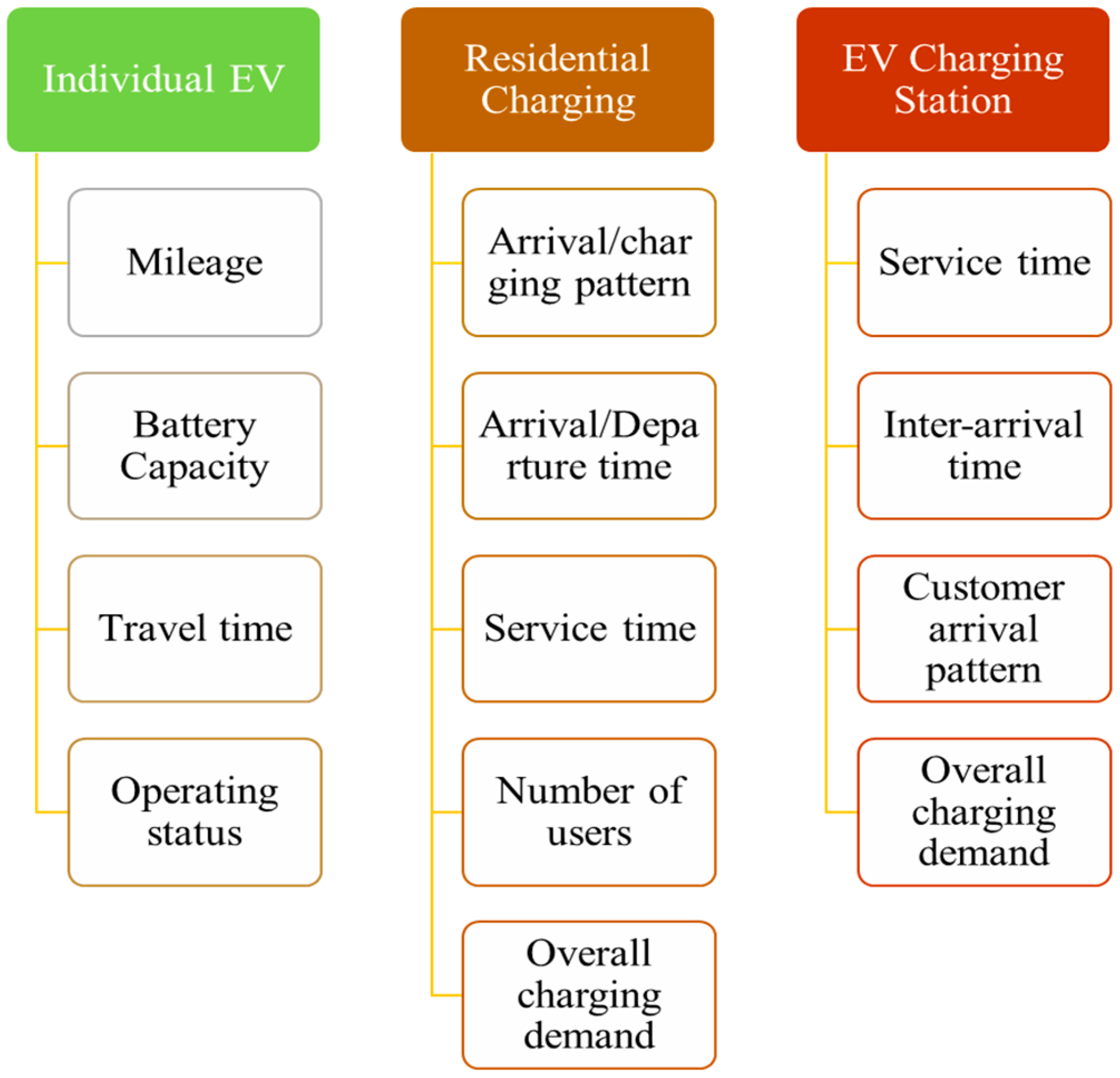
5. Uncertainty Modelling
5.1. EV Charging Demand
5.2. PV Generation
5.3. Electrical Load Demand
6. Conclusions and Future Research Suggestions
- Smart charging algorithms
- P2P V2G power transfer
- Uncertainty analysis
- PV based EV charging stations
- Price-varying scheduling
Author Contributions
Funding
Conflicts of Interest
References
- Asaad, M.; Shrivastava, P.; Alam, M.S.; Rafat, Y.; Pillai, R.K. Viability of xEVs in India: A public opinion survey. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2018; Volume 487, pp. 165–178. ISBN 9789811082481. [Google Scholar]
- Bunsen, T.; Cazzola, P.; Gorner, M.; Paoli, L.; Scheffer, S.; Schuitmaker, R.; Tattini, J.; Teter, J. Global EV Outlook 2018: Towards Cross-Modal Electrification; International Energy Agency: Paris, France, 2018. [Google Scholar]
- Monteiro, V.; Gonçalves, H.; Afonso, J.L. Impact of Electric Vehicles on power quality in a Smart Grid context. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar]
- Jordehi, A.R. Optimisation of demand response in electric power systems, a review. Renew. Sustain. Energy Rev. 2019, 103, 308–319. [Google Scholar] [CrossRef]
- Strbac, G. Demand side management: Benefits and challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
- Kempton, W.; Letendre, S.E. Electric vehicles as a new power source for electric utilities. Transp. Res. Part D Transp. Environ. 1997, 2, 157–175. [Google Scholar] [CrossRef]
- Paşaoğlu, G.; Fiorello, D.; Martino, A.; Zani, L.; Zubaryeva, A.; Thiel, C. Travel patterns and the potential use of electric cars—Results from a direct survey in six European countries. Technol. Forecast. Soc. Chang. 2014, 87, 51–59. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.K.; Poor, H.V.; Wood, K.L. Transforming energy networks via peer-to-peer energy trading: The Potential of game-theoretic approaches. IEEE Signal Process. Mag. 2018, 35, 90–111. [Google Scholar] [CrossRef]
- Woo, J.; Choi, H.; Ahn, J. Well-to-wheel analysis of greenhouse gas emissions for electric vehicles based on electricity generation mix: A global perspective. Transp. Res. Part D Transp. Environ. 2017, 51, 340–350. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Plug-in vehicles and renewable energy sources for cost and emission reductions. IEEE Trans. Ind. Electron. 2010, 58, 1229–1238. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z.; Aziz, M.J.A.; Yee, K.P.; Ashique, R. Electric vehicles charging using photovoltaic: Status and technological review. Renew. Sustain. Energy Rev. 2016, 54, 34–47. [Google Scholar] [CrossRef]
- Hoarau, Q.; Perez, Y. Interactions between electric mobility and photovoltaic generation: A review. Renew. Sustain. Energy Rev. 2018, 94, 510–522. [Google Scholar] [CrossRef]
- Shepero, M.; Munkhammar, J.; Widén, J.; Bishop, J.D.; Boström, T. Modeling of photovoltaic power generation and electric vehicles charging on city-scale: A review. Renew. Sustain. Energy Rev. 2018, 89, 61–71. [Google Scholar] [CrossRef]
- Fachrizal, R.; Shepero, M.; Van Der Meer, D.; Munkhammar, J.; Widén, J. Smart charging of electric vehicles considering photovoltaic power production and electricity consumption: A review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Ma, C.-T. System planning of grid-connected electric vehicle charging stations and key technologies: A review. Energies 2019, 12, 4201. [Google Scholar] [CrossRef]
- Ahmadian, A.; Mohammadi-Ivatloo, B.; Elkamel, A. A Review on plug-in electric vehicles: Introduction, Current status, and load modeling techniques. J. Mod. Power Syst. Clean Energy 2020, 8, 412–425. [Google Scholar] [CrossRef]
- Richardson, D.B. Electric vehicles and the electric grid: A review of modeling approaches, impacts, and renewable energy integration. Renew. Sustain. Energy Rev. 2013, 19, 247–254. [Google Scholar] [CrossRef]
- Su, J.; Lie, T.; Zamora, R. Modelling of large-scale electric vehicles charging demand: A New Zealand case study. Electr. Power Syst. Res. 2019, 167, 171–182. [Google Scholar] [CrossRef]
- Chung, C.-Y.; Youn, E.; Chynoweth, J.S.; Qiu, C.; Chu, C.-C.; Gadh, R. Safety design for smart Electric Vehicle charging with current and multiplexing control. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013; pp. 540–545. [Google Scholar]
- Zheng, Y.; Niu, S.; Shang, Y.; Shao, Z.; Jian, L. Integrating plug-in electric vehicles into power grids: A comprehensive review on power interaction mode, scheduling methodology and mathematical foundation. Renew. Sustain. Energy Rev. 2019, 112, 424–439. [Google Scholar] [CrossRef]
- He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Ahn, C.; Li, C.-T.; Peng, H. Optimal decentralized charging control algorithm for electrified vehicles connected to smart grid. J. Power Sources 2011, 196, 10369–10379. [Google Scholar] [CrossRef]
- Hu, J.; You, S.; Lind, M.; Østergaard, J. Coordinated charging of electric vehicles for congestion prevention in the distribution grid. IEEE Trans. Smart Grid 2013, 5, 703–711. [Google Scholar] [CrossRef]
- Uddin, M.; Romlie, M.; Abdullah, M.F.; Halim, S.A.; Abu Bakar, A.H.; Kwang, T.C. A review on peak load shaving strategies. Renew. Sustain. Energy Rev. 2018, 82, 3323–3332. [Google Scholar] [CrossRef]
- Letendre, S.E.; Kempton, W. The V2G concept: A new model for power? Public Util. Fortn. 2002, 140, 16–26. [Google Scholar]
- Guille, C.; Gross, G. A conceptual framework for the vehicle-to-grid (V2G) implementation. Energy Policy 2009, 37, 4379–4390. [Google Scholar] [CrossRef]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y. Integration of electric vehicles in smart grid: A review on vehicle to grid technologies and optimization techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal charging strategies for unidirectional vehicle-to-grid. IEEE Trans. Smart Grid 2010, 2, 131–138. [Google Scholar] [CrossRef]
- Boynuegri, A.; Uzunoglu, M.; Erdinc, O.; Gokalp, E. A new perspective in grid connection of electric vehicles: Different operating modes for elimination of energy quality problems. Appl. Energy 2014, 132, 435–451. [Google Scholar] [CrossRef]
- Turker, H.; Hably, A.; Bacha, S. Housing peak shaving algorithm (HPSA) with plug-in hybrid electric vehicles (PHEVs): Vehicle-to-Home (V2H) and Vehicle-to-Grid (V2G) concepts. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 753–759. [Google Scholar]
- Feldman, D.; Barbose, G.; Margolis, R.; Wiser, R.; Darghouth, N.; Goodrich, A. Photovoltaic (PV) Pricing Trends: Historical, Recent, and Near-Term Projections; National Renewable Energy Laboratory: Golden, CO, USA, 2012.
- Goli, P.; Shireen, W. PV powered smart charging station for PHEVs. Renew. Energy 2014, 66, 280–287. [Google Scholar] [CrossRef]
- Carli, G.; Williamson, S.S. Technical considerations on power conversion for electric and plug-in hybrid electric vehicle battery charging in photovoltaic installations. IEEE Trans. Power Electron. 2013, 28, 5784–5792. [Google Scholar] [CrossRef]
- Van Der Meer, D.; Mouli, G.R.C.; Morales-Espana, G.; Elizondo, L.R.; Bauer, P. Erratum to energy management system with pv power forecast to optimally charge evs at the workplace. IEEE Trans. Ind. Inform. 2018, 14, 3298. [Google Scholar] [CrossRef]
- Oliveira, D.; De Souza, A.Z.; Delboni, L. Optimal plug-in hybrid electric vehicles recharge in distribution power systems. Electr. Power Syst. Res. 2013, 98, 77–85. [Google Scholar] [CrossRef]
- Ahmad, F.; Alam, M.S.; Shahidehpour, M. Profit maximization of microgrid aggregator under power market environment. IEEE Syst. J. 2019, 13, 3388–3399. [Google Scholar] [CrossRef]
- Sarker, M.R.; Dvorkin, Y.; Ortega-Vazquez, M. Optimal participation of an electric vehicle aggregator in day-ahead energy and reserve markets. IEEE Trans. Power Syst. 2015, 31, 3506–3515. [Google Scholar] [CrossRef]
- Reddy, K.R.; Meikandasivam, S. Load flattening and voltage regulation using plug-in electric vehicle’s storage capacity with vehicle prioritization using ANFIS. IEEE Trans. Sustain. Energy 2020, 11, 260–270. [Google Scholar] [CrossRef]
- Ko, K.S.; Han, S.; Sung, D.K. Performance-based settlement of frequency regulation for electric vehicle aggregators. IEEE Trans. Smart Grid 2018, 9, 866–875. [Google Scholar] [CrossRef]
- Zhou, K.; Cai, L. Randomized PHEV charging under distribution grid constraints. IEEE Trans. Smart Grid 2014, 5, 879–887. [Google Scholar] [CrossRef]
- Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized charging control of large populations of plug-in electric vehicles. IEEE Trans. Control. Syst. Technol. 2011, 21, 67–78. [Google Scholar] [CrossRef]
- Unda, I.G.; Papadopoulos, P.; Skarvelis-Kazakos, S.; Cipcigan, L.M.; Jenkins, N.; Zabala, E. Management of electric vehicle battery charging in distribution networks with multi-agent systems. Electr. Power Syst. Res. 2014, 110, 172–179. [Google Scholar] [CrossRef]
- Chaudhari, K.; Kandasamy, N.K.; Krishnan, A.; Ukil, A.; Gooi, H.B. Agent-based aggregated behavior modeling for electric vehicle charging load. IEEE Trans. Ind. Inform. 2018, 15, 856–868. [Google Scholar] [CrossRef]
- Liu, M.; Phanivong, P.K.; Shi, Y.; Callaway, D.S. Decentralized charging control of electric vehicles in residential distribution networks. IEEE Trans. Control. Syst. Technol. 2019, 27, 266–281. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; García-Triviño, P.; Fernández-Ramírez, L.M.; Jurado, F. Decentralized energy management strategy based on predictive controllers for a medium voltage direct current photovoltaic electric vehicle charging station. Energy Convers. Manag. 2016, 108, 1–13. [Google Scholar] [CrossRef]
- Weckx, S.; D’Hulst, R.; Driesen, J. Primary and secondary frequency support by a multi-agent demand control system. IEEE Trans. Power Syst. 2014, 30, 1394–1404. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinc, O.; Bakirtzis, A.G.; Catalão, J.P. Optimal household appliances scheduling under day-ahead pricing and load-shaping demand response strategies. IEEE Trans. Ind. Inform. 2015, 11, 1509–1519. [Google Scholar] [CrossRef]
- Xi, X.; Sioshansi, R. Using price-based signals to control plug-in electric vehicle fleet charging. IEEE Trans. Smart Grid 2014, 5, 1451–1464. [Google Scholar] [CrossRef]
- Pan, J.; Jain, R.; Paul, S.; Vu, T.; Saifullah, A.; Sha, M. A internet of things framework for smart energy in buildings: Designs, prototype, and experiments. IEEE Internet Things J. 2015, 2, 1. [Google Scholar] [CrossRef]
- Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sustain. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef]
- Fischer, D.; Harbrecht, A.; Surmann, A.; McKenna, R. Electric vehicles’ impacts on residential electric local profiles—A stochastic modelling approach considering socio-economic, behavioural and spatial factors. Appl. Energy 2019, 644–658. [Google Scholar] [CrossRef]
- Nunes, P.; Figueiredo, R.; Brito, M.C. The use of parking lots to solar-charge electric vehicles. Renew. Sustain. Energy Rev. 2016, 66, 679–693. [Google Scholar] [CrossRef]
- Prakash, K.; Vaithilingam, C.A.; Rajendran, G.; Vaithilingam, C.A. Design and sizing of mobile solar photovoltaic power plant to support rapid charging for electric vehicles. Energies 2019, 12, 3579. [Google Scholar] [CrossRef]
- Denholm, P.; Kuss, M.; Margolis, R.M. Co-benefits of large scale plug-in hybrid electric vehicle and solar PV deployment. J. Power Sources 2013, 236, 350–356. [Google Scholar] [CrossRef]
- Nunes, P.; Farias, T.L.; Brito, M.C. Day charging electric vehicles with excess solar electricity for a sustainable energy system. Energy 2015, 80, 263–274. [Google Scholar] [CrossRef]
- Tulpule, P.; Marano, V.; Yurkovich, S.; Rizzoni, G. Economic and environmental impacts of a PV powered workplace parking garage charging station. Appl. Energy 2013, 108, 323–332. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. Operating characteristics of transcritical CO2 heat pump for simultaneous water cooling and heating. Arch. Thermodyn. 2011, 33, 23–40. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Moghaddam, Z.; Ahmad, I.; Habibi, D.; Phung, Q.V.; Habibi, D. Smart charging strategy for electric vehicle charging stations. IEEE Trans. Transp. Electrif. 2018, 4, 76–88. [Google Scholar] [CrossRef]
- Mouli, G.R.C.; Kefayati, M.; Baldick, R.; Bauer, P. Integrated PV charging of EV fleet based on energy prices, V2G, and offer of reserves. IEEE Trans. Smart Grid 2017, 10, 1313–1325. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Thomas, D.; Rycerski, P.; Genikomsakis, K.N. Peak shaving and valley filling of power consumption profile in non-residential buildings using an electric vehicle parking lot. Energy 2018, 148, 148–158. [Google Scholar] [CrossRef]
- Ivanova, A.; Fernandez, J.A.; Crawford, C.; Sui, P.-C. Coordinated charging of electric vehicles connected to a net-metered PV parking lot. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Mohamed, A.A.; Salehi, V.; Ma, T.; Mohammed, O.A. Real-time energy management algorithm for plug-in hybrid electric vehicle charging parks involving sustainable energy. IEEE Trans. Sustain. Energy 2014, 5, 577–586. [Google Scholar] [CrossRef]
- Liu, N.; Chen, Q.; Liu, J.; Lu, X.; Li, P.; Lei, J.; Zhang, J. A heuristic operation strategy for commercial building microgrids containing EVs and PV system. IEEE Trans. Ind. Electron. 2014, 62, 2560–2570. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, L. Dynamic charging scheduling for EV parking lots with photovoltaic power system. IEEE Access 2018, 6, 56995–57005. [Google Scholar] [CrossRef]
- Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. Effective utilization of available PEV battery capacity for mitigation of solar PV impact and grid support with integrated V2G functionality. IEEE Trans. Smart Grid 2015, 7, 1562–1571. [Google Scholar] [CrossRef]
- Wi, Y.-M.; Lee, J.-U.; Joo, S.-K. Electric vehicle charging method for smart homes/buildings with a photovoltaic system. IEEE Trans. Consum. Electron. 2013, 59, 323–328. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef]
- Eldeeb, H.H.; Faddel, S.; Mohammed, O.A. Multi-objective optimization technique for the operation of grid tied PV powered EV charging station. Electr. Power Syst. Res. 2018, 164, 201–211. [Google Scholar] [CrossRef]
- Van Der Kam, M.; Van Sark, W. Smart charging of electric vehicles with photovoltaic power and vehicle-to-grid technology in a microgrid; a case study. Appl. Energy 2015, 152, 20–30. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z. A rule-based energy management scheme for uninterrupted electric vehicles charging at constant price using photovoltaic-grid system. Renew. Energy 2018, 125, 384–400. [Google Scholar] [CrossRef]
- Barone, G.; Buonomano, A.; Calise, F.; Forzano, C.; Palombo, A. Building to vehicle to building concept toward a novel zero energy paradigm: Modelling and case studies. Renew. Sustain. Energy Rev. 2019, 101, 625–648. [Google Scholar] [CrossRef]
- Ghotge, R.; Snow, Y.; Farahani, S.; Lukszo, Z.; Van Wijk, A.J. Optimized scheduling of EV charging in solar parking lots for local peak reduction under eV demand uncertainty. Energies 2020, 13, 1275. [Google Scholar] [CrossRef]
- Fachrizal, R.; Munkhammar, J. Improved photovoltaic self-consumption in residential buildings with distributed and centralized smart charging of electric vehicles. Energies 2020, 13, 1153. [Google Scholar] [CrossRef]
- Nunes, P.; Farias, T.L.; Brito, M.C. Enabling solar electricity with electric vehicles smart charging. Energy 2015, 87, 10–20. [Google Scholar] [CrossRef]
- Kadar, P.; Varga, A. PhotoVoltaic EV charge station. In Proceedings of the 2013 IEEE 11th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovenia, 31 January–2 February 2013; pp. 57–60. [Google Scholar]
- Brenna, M.; Dolara, A.; Foiadelli, F.; Leva, S.; Longo, M. Urban scale photovoltaic charging stations for electric vehicles. IEEE Trans. Sustain. Energy 2014, 5, 1234–1241. [Google Scholar] [CrossRef]
- Leou, R.-C.; Su, C.-L.; Lu, C.-N. Stochastic analyses of electric vehicle charging impacts on distribution network. IEEE Trans. Power Syst. 2013, 29, 1055–1063. [Google Scholar] [CrossRef]
- Khodayar, M.E.; Wu, L.; Shahidehpour, M. Hourly Coordination of electric vehicle operation and volatile wind power generation in SCUC. IEEE Trans. Smart Grid 2012, 3, 1271–1279. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties. IEEE Trans. Power Deliv. 2011, 26, 2541–2551. [Google Scholar] [CrossRef]
- Soares, J.; Borges, N.; Ghazvini, M.A.F.; Vale, Z.; Oliveira, P.M. Scenario generation for electric vehicles’ uncertain behavior in a smart city environment. Energy 2016, 111, 664–675. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Soroudi, A.; Ehsan, M. A possibilistic–probabilistic tool for evaluating the impact of stochastic renewable and controllable power generation on energy losses in distribution networks—A case study. Renew. Sustain. Energy Rev. 2011, 15, 794–800. [Google Scholar] [CrossRef]
- Ahmad, F.; Alam, M.S.; Shariff, S.M.; Krishnamurthy, M. A Cost-efficient approach to ev charging station integrated community microgrid: A case study of Indian power market. IEEE Trans. Transp. Electrif. 2019, 5, 200–214. [Google Scholar] [CrossRef]
- Shepero, M.; Munkhammar, J. Spatial Markov chain model for electric vehicle charging in cities using geographical information system (GIS) data. Appl. Energy 2018, 231, 1089–1099. [Google Scholar] [CrossRef]
- Gupta, N. Gauss-quadrature-based probabilistic load flow method with voltage-dependent loads including WTGS, PV, and EV charging uncertainties. IEEE Trans. Ind. Appl. 2018, 54, 6485–6497. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, X.; Yang, D.; Yang, Z.; Littler, T.; Li, H. Probabilistic load flow algorithm of distribution networks with distributed generators and electric vehicles integration. Energies 2019, 12, 4234. [Google Scholar] [CrossRef]
- Baringo, L.; Amaro, R.S. A stochastic robust optimization approach for the bidding strategy of an electric vehicle aggregator. Electr. Power Syst. Res. 2017, 146, 362–370. [Google Scholar] [CrossRef]
- Sarker, M.R.; Pandžić, H.; Ortega-Vazquez, M. Optimal Operation and services scheduling for an electric vehicle battery swapping station. IEEE Trans. Power Syst. 2014, 30, 901–910. [Google Scholar] [CrossRef]
- Zhao, J.; Wan, C.; Xu, Z.; Wang, J. Risk-based day-ahead scheduling of electric vehicle aggregator using information gap decision theory. IEEE Trans. Smart Grid 2015, 8, 1609–1618. [Google Scholar] [CrossRef]
- Soroudi, A.; Keane, A. Risk averse energy hub management considering plug-in electric vehicles using information gap decision theory. In Power Systems; Springer: Singapore, 2015; Volume 89, pp. 107–127. [Google Scholar]
- Aien, M.; Fotuhi-Firuzabad, M.; Rashidinejad, M. Probabilistic optimal power flow in correlated hybrid WindPhotovoltaic power systems. IEEE Trans. Smart Grid 2014, 5, 130–138. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Alrbai, M.; Adeeb, J. Ensemble approach of optimized artificial neural networks for solar photovoltaic power prediction. IEEE Access 2019, 7, 81741–81758. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, P.; Goel, L.; Ding, Y. Evaluation of nodal reliability risk in a deregulated power system with photovoltaic power penetration. IET Gener. Transm. Distrib. 2013, 8, 421–430. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Sheng, C. Industrial prediction intervals with data Uncertainty. In Information Fusion and Data Science; Springer: Cham, Switzerland, 2018; pp. 159–222. [Google Scholar]
- Wu, X.; Wang, X.; Qu, C. A hierarchical framework for generation scheduling of microgrids. IEEE Trans. Power Deliv. 2014, 29, 2448–2457. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Coordinated investment planning of distributed multi-type stochastic generation and battery storage in active distribution networks. IEEE Trans. Sustain. Energy 2019, 10, 1813–1822. [Google Scholar] [CrossRef]
- Wang, R.; Wang, P.; Xiao, G. A robust optimization approach for energy generation scheduling in microgrids. Energy Convers. Manag. 2015, 106, 597–607. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, P.; Huang, G. A multi-criteria system design optimization for net zero energy buildings under uncertainties. Energy Build. 2015, 97, 196–204. [Google Scholar] [CrossRef]
- Koraki, D.; Strunz, K. Wind and solar power integration in electricity markets and distribution networks through service-centric virtual power plants. IEEE Trans. Power Syst. 2017, 33, 473–485. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Kirschen, D.S.; Zhang, B. Model-free renewable scenario generation using generative adversarial networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Das, U.K.; Soon, T.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Ramadhani, U.H.; Shepero, M.; Munkhammar, J.; Widén, J.; Etherden, N. Review of probabilistic load flow approaches for power distribution systems with photovoltaic generation and electric vehicle charging. Int. J. Electr. Power Energy Syst. 2020, 120, 106003. [Google Scholar] [CrossRef]
- Zakaria, A.; Ismail, F.B.; Lipu, M.S.H.; Hannan, M. Uncertainty models for stochastic optimization in renewable energy applications. Renew. Energy 2020, 145, 1543–1571. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. State-of-the-art techniques for modelling of uncertainties in active distribution network planning: A review. Appl. Energy 2019, 239, 1509–1523. [Google Scholar] [CrossRef]
- Kumar, K.P.; Saravanan, B. Recent techniques to model uncertainties in power generation from renewable energy sources and loads in microgrids—A review. Renew. Sustain. Energy Rev. 2017, 71, 348–358. [Google Scholar] [CrossRef]
- Kawamura, N.; Muta, M. Development of solar charging system for plug-in hybrid electric vehicles and electric vehicles. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–5. [Google Scholar]
- Castello, C.C.; LaClair, T.J.; Curt Maxey, L. Control strategies for electric vehicle (EV) charging using renewables and local storage. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–7. [Google Scholar]
- Prusty, B.R.; Jena, D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach. Renew. Sustain. Energy Rev. 2017, 69, 1286–1302. [Google Scholar] [CrossRef]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Jordehi, A.R. How to deal with uncertainties in electric power systems? A review. Renew. Sustain. Energy Rev. 2018, 96, 145–155. [Google Scholar] [CrossRef]
- Verbič, G.; Canizares, C.A. Probabilistic optimal power flow in electricity markets based on a two-point estimate method. IEEE Trans. Power Syst. 2006, 21, 1883–1893. [Google Scholar] [CrossRef]
- Morales, J.; Perez-Ruiz, J. Point estimate schemes to solve the probabilistic power flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Alaee, S.; Hooshmand, R.-A.; Hemmati, R. Stochastic transmission expansion planning incorporating reliability solved using SFLA meta-heuristic optimization technique. CSEE J. Power Energy Syst. 2016, 2, 79–86. [Google Scholar] [CrossRef]
- Cai, D.; Shi, D.; Chen, J. Probabilistic load flow with correlated input random variables using uniform design sampling. Int. J. Electr. Power Energy Syst. 2014, 63, 105–112. [Google Scholar] [CrossRef]
- Soares, J.; Ghazvini, M.A.F.; Vale, Z.; Oliveira, P.M. A multi-objective model for the day-ahead energy resource scheduling of a smart grid with high penetration of sensitive loads. Appl. Energy 2016, 162, 1074–1088. [Google Scholar] [CrossRef]
- Talari, S.; Haghifam, M.-R.; Yazdaninejad, M. Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads. IET Gener. Transm. Distrib. 2015, 9, 1498–1509. [Google Scholar] [CrossRef]
- El Motaleb, A.M.A.; Bekdache, S.K.; Alvarado-Barrios, L. Optimal sizing for a hybrid power system with wind/energy storage based in stochastic environment. Renew. Sustain. Energy Rev. 2016, 59, 1149–1158. [Google Scholar] [CrossRef]
- Allan, R.; Da Silva, A.; Burchett, R. Evaluation methods and accuracy in probabilistic load flow solutions. IEEE Trans. Power Appar. Syst. 1981, 2539–2546. [Google Scholar] [CrossRef]
- Schwippe, J.; Krause, O.; Rehtanz, C. Probabilistic load flow calculation based on an enhanced convolution technique. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
- Munkhammar, J.; Rydén, J.; Widén, J. Characterizing probability density distributions for household electricity load profiles from high-resolution electricity use data. Appl. Energy 2014, 135, 382–390. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.-P. Comparison between two probabilistic load flow methods for reliability assessment. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar]
| Features | Unidirectional | Bidirectional |
|---|---|---|
| Power flow | Grid-to-vehicle (G2V) | G2V and vehicle-to-grid (V2G) |
| Infrastructure | Communication | Communication, bidirectional charger |
| Cost | Low | High |
| Complexity | Low | High |
| Services | Load profile management, Frequency regulation [27] | Backup power support, frequency regulation, voltage regulation, active power support [28] |
| Advantages | Overloading prevention, load levelling, profit maximisation, emission minimisation [29] | Overloading prevention, profit maximisation, emission minimisation, renewable energy sources (RES) integration, voltage profile improvement, harmonic filtering [30], load levelling, power loss reduction [31] |
| Disadvantages | Limited services | Battery degradation, high complexity, and cost, social barriers |
| References | Objectives | Optimisation Model | Software/Implementation | Key Findings |
|---|---|---|---|---|
| [62] | Peak shaving and valley filling | Linear programming | MATLAB | The effectiveness of the proposed algorithm is dependent on a high number of available parking spots. |
| [35] | Maximizing profit and PV utilisation | Mixed Integer Linear programming | GAMS | Due to battery degradation cost, V2G is not economically feasible unless high PV production is present |
| [63] | Minimizing system cost | Mixed Integer Linear programming | CPLEX | Smart charging can result in saving of operational cost for charging and PV usage for the parking lot owner |
| [64] | Minimizing charging cost | Fuzzy logic | MATLAB | The algorithm is not optimisation based so targets several objectives: Reduction in charging cost and system losses, improvement in voltage profile. |
| [65] | Maximizing PV utilisation | Metaheuristic | MATLAB | The proposed heuristic algorithm achieves desired objectives with low computational cost and without forecasting of uncertain variables. |
| [66] | Maximizing EV aggregator benefits | Hybrid MPC | - | The proposed algorithm achieves near-optimal solution of EV charge scheduling problem with better efficiency than standard MPC |
| [67] | Maximizing PV utilisation and reducing EV charging impact | Linear programming | Case study: New South Wales distribution system | The proposed strategy controls the charging/discharging profile of EVs to match with the shape of the PV output to achieve desired objectives. |
| [68] | Minimizing charging cost | Mixed Integer Linear programming | Case study: Korea | The proposed algorithm does not consider selling excess power and demonstrates charging cost savings compared to uncoordinated charging |
| [61] | Minimizing system cost | Mixed Integer Linear programming | Microsoft Solver Foundation | A comprehensive system to achieve one optimal charging profile will result in a larger net benefit compared to individual applications. |
| [69] | Minimizing charging cost | Convex programming | MATLAB | ESS can significantly reduce charging cost and bi-directional V2H is cheaper than H2V |
| [70] | Maximizing profit and ESS life | Non-linear programming | GAMS | Considering only revenue maximisation will result in an adverse effect on ESS life |
| [71] | Maximizing PV utilisation | Linear programming | Case study: LomboXnet | Proposed algorithm increases PV self-consumption and reduces peak demand by half |
| [72] | Minimizing charging cost | Rule-based algorithm | MATLAB | Rule-based charging is superior to conventional charging for less charging cost and reduced grid loading |
| [73] | Maximizing PV utilisation | Rule-based algorithm | MATLAB | V2B can be an effective strategy if initial capital costs and electricity price are fitting |
| [74] | Minimizing peak demand | MPC | MATLAB | EV scheduling can reduce both the magnitude and frequency of peak loading |
| [75] | Peak shaving and valley filling | Quadratic programming | MATLAB | Net load variation was lower in case of low PV power-sharing and vice-versa |
| Method | Remarks | References |
|---|---|---|
| Scenario reduction |
| [79,80] |
| Monte Carlo simulation |
| [19,81] |
| Fuzzy logic |
| [82,83] |
| Hybrid Monte Carlo-fuzzy |
| [84] |
| Artificial Neural Network |
| [37,85] |
| Markov chain |
| [86] |
| Probability distribution fitting |
| [87,88] |
| Robust optimisation |
| [89,90] |
| Information gap decision theory |
| [91,92] |
| Method | Remarks | References |
|---|---|---|
| Point estimation |
| [93] |
| Bootstrap |
| [94] |
| Monte Carlo simulation |
| [95] |
| Mean-Variance estimation |
| [96] |
| Two stage scheduling |
| [97] |
| Scenario based analysis |
| [98] |
| Kernel Density estimation |
| [99] |
| Autoregressive Moving Average |
| [35] |
| Probability distribution fitting |
| [100] |
| Rolling Horizon approach |
| [101] |
| Generative Adversarial network |
| [102] |
| Method | Remarks | References |
|---|---|---|
| Point estimation |
| [114,115] |
| Monte Carlo simulation |
| [116,117] |
| Fuzzy logic |
| [118] |
| Scenario based analysis |
| [119] |
| Autoregressive Moving Average |
| [85,120] |
| Convolution based |
| [121,122] |
| Probability distribution fitting |
| [88,123] |
| Cumulant based |
| [124] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad, A.; Zamora, R.; Lie, T.T. Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies 2020, 13, 4541. https://doi.org/10.3390/en13174541
Mohammad A, Zamora R, Lie TT. Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies. 2020; 13(17):4541. https://doi.org/10.3390/en13174541
Chicago/Turabian StyleMohammad, Asaad, Ramon Zamora, and Tek Tjing Lie. 2020. "Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling" Energies 13, no. 17: 4541. https://doi.org/10.3390/en13174541
APA StyleMohammad, A., Zamora, R., & Lie, T. T. (2020). Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies, 13(17), 4541. https://doi.org/10.3390/en13174541