Intraday Electricity Pricing of Night Contracts
Abstract
1. Introduction
2. Stylized Facts
2.1. Data
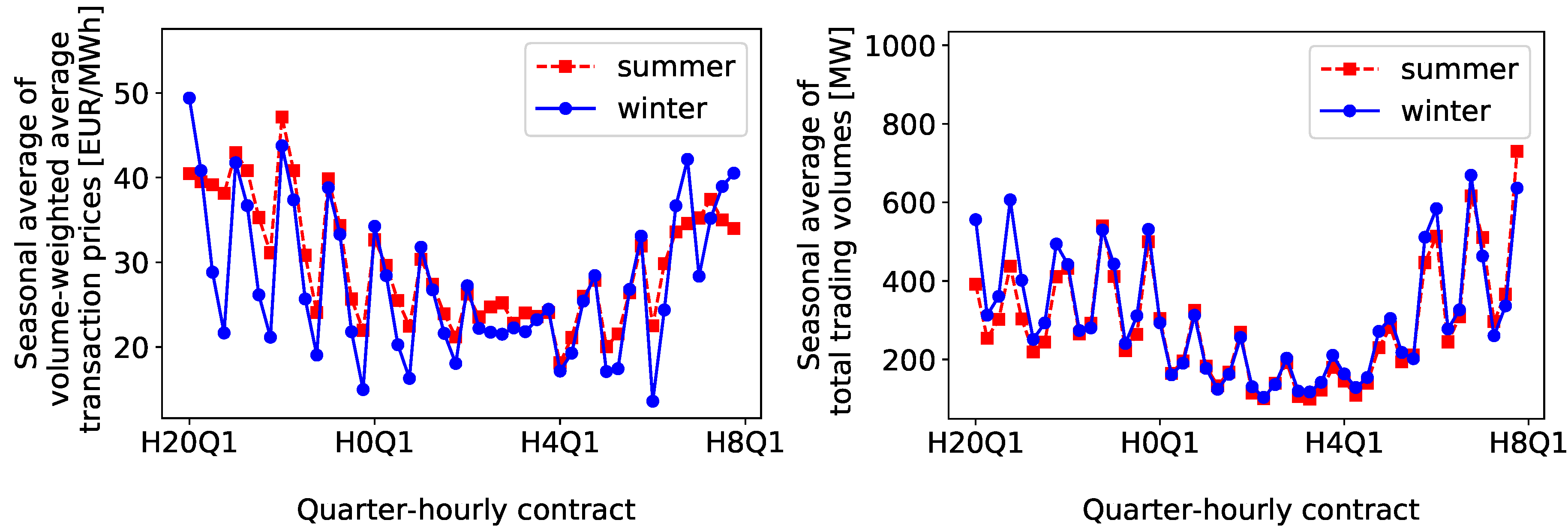
2.2. Hourly Seasonality
3. Methodology
3.1. Econometric Model
- make a scatter plot of intraday auction prices versus expected demands ;
- fit the empirical merit-order-curve function to the price–demand data;
- compute the derivative of the fitted merit-order-curve function; and,
- substitute empirical demands to obtain merit-order-curve slopes .
3.2. Threshold Regression
4. Estimation Results
4.1. Threshold Regression
4.2. Linear Regression
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- BMWi. Energiedaten und -szenarien: Gesamtausgabe der Energiedaten—Datensammlung des BMWi. 2020. Available online: https://www.bmwi.de/Redaktion/EN/Artikel/Energy/energy-data.html (accessed on 16 July 2020).
- EPEX SPOT SE. Press Release: EPEX SPOT SE Accomplishes a Year of European Power Market Integration—Trading Volumes Rise Significantly in 2010. 2011. Available online: https://www.epexspot.com/sites/default/files/download_center_files/2011-01-12_EPEX_ANNUAL%20PR_EN-D-FR.pdf (accessed on 16 July 2020).
- EPEX SPOT SE. Press Release: EPEX SPOT Annual Market Review 2019 – New Trading Record on EPEX SPOT in 2019. 2020. Available online: https://www.epexspot.com/sites/default/files/download_center_files/200113_EPEX%20SPOT_2019_Annual%20Press%20Release_.pdf (accessed on 16 July 2020).
- International Energy Agency. Germany 2020 Energy Policy Review. 2020. Available online: https://www.bmwi.de/Redaktion/DE/Downloads/G/germany-2020-energy-policy-review.pdf?__blob=publicationFile&v=4 (accessed on 16 July 2020).
- Kiesel, R.; Paraschiv, F. Econometric analysis of 15-min intraday electricity prices. Energy Econ. 2017, 64, 77–90. [Google Scholar] [CrossRef]
- Kremer, M.; Kiesel, R.; Paraschiv, F. An econometric model for intraday electricity trading. Philos. Trans. R. Soc. A 2020, forthcoming. [Google Scholar]
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. J. Commod. Mark. 2019, 100107. [Google Scholar] [CrossRef]
- Hagemann, S. Price determinants in the German intraday market for electricity: An empirical analysis. J. Energy Mark. 2015, 8, 21–45. [Google Scholar] [CrossRef]
- Pape, C.; Hagemann, S.; Weber, C. Are fundamentals enough? Explaining price variations in the German day-ahead and intraday power market. Energy Econ. 2016, 54, 376–387. [Google Scholar] [CrossRef]
- Ziel, F. Modeling the impact of wind and solar power forecasting errors on intraday electricity prices. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017. [Google Scholar] [CrossRef]
- Gürtler, M.; Paulsen, T. The effect of wind and solar power forecasts on day-ahead and intraday electricity prices in Germany. Energy Econ. 2018, 75, 150–162. [Google Scholar] [CrossRef]
- Goodarzi, S.; Perera, H.N.; Bunn, D. The impact of renewable energy forecast errors on imbalance volumes and electricity spot prices. Energy Policy 2019, 134, 110827. [Google Scholar] [CrossRef]
- Kulakov, S.; Ziel, F. The Impact of Renewable Energy Forecasts on Intraday Electricity Prices. 2019. Available online: https://arxiv.org/abs/1903.09641 (accessed on 16 July 2020).
- Garnier, E.; Madlener, R. Balancing forecast errors in continuous-trade intraday markets. Energy Syst. 2015, 6, 361–388. [Google Scholar] [CrossRef]
- Aïd, R.; Gruet, P.; Pham, H. An optimal trading problem in intraday electricity markets. Math. Financ. Econ. 2015, 10, 49–85. [Google Scholar] [CrossRef]
- Glas, S.; Kiesel, R.; Kolkmann, S.; Kremer, M.; von Luckner, N.G.; Ostmeier, L.; Urban, K.; Weber, C. Intraday renewable electricity trading: Advanced modeling and optimal control. In Progress in Industrial Mathematics at ECMI 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 469–475. [Google Scholar] [CrossRef]
- Glas, S.; Kiesel, R.; Kolkmann, S.; Kremer, M.; Graf von Luckner, N.; Ostmeier, L.; Urban, K.; Weber, C. Intraday renewable electricity trading: Advanced modeling and numerical optimal control. J. Math. Ind. 2020, 10, 1–17. [Google Scholar] [CrossRef]
- Uniejewski, B.; Marcjasz, G.; Weron, R. Understanding intraday electricity markets: Variable selection and very short-term price forecasting using LASSO. Int. J. Forecast. 2019, 35, 1533–1547. [Google Scholar] [CrossRef]
- Janke, T.; Steinke, F. Forecasting the price distribution of continuous intraday electricity trading. Energies 2019, 12, 4262. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Estimation and simulation of the transaction arrival process in intraday electricity markets. Energies 2019, 12, 4518. [Google Scholar] [CrossRef]
- Graf von Luckner, N.; Kiesel, R. Modeling Market Order Arrivals on the Intraday Market for Electricity Deliveries in Germany with the Hawkes Process. 2020. Available online: https://ssrn.com/abstract=3526795 (accessed on 16 July 2020).
- Kramer, A.; Kiesel, R. Exogenous Factors for Order Arrivals on the Intraday Electricity Market. 2020. Available online: https://ssrn.com/abstract=3540991 (accessed on 16 July 2020).
- Märkle-Huß, J.; Feuerriegel, S.; Neumann, D. Contract durations in the electricity market: Causal impact of 15 min trading on the EPEX SPOT market. Energy Econ. 2018, 69, 367–378. [Google Scholar] [CrossRef]
- Knaut, A.; Paschmann, M. Short-Term Price Volatility in Commodity Markets Explained—Evidence from the Power Sector. 2016. Available online: https://www.researchgate.net/publication/303973354_Short-term_Price_Volatility_in_Commodity_Markets_Explained_-Evidence_from_the_Power_Sector (accessed on 16 July 2020).
- Ciarreta, A.; Muniain, P.; Zarraga, A. Modeling and forecasting realized volatility in German–Austrian continuous intraday electricity prices. J. Forecast. 2017, 36, 680–690. [Google Scholar] [CrossRef]
- Kath, C.; Ziel, F. The value of forecasts: Quantifying the economic gains of accurate quarter-hourly electricity price forecasts. Energy Econ. 2018, 76, 411–423. [Google Scholar] [CrossRef]
- EPEX SPOT SE. Press Release: EPEX SPOT and ECC Successfully Reduce Lead Time on All Intraday Markets. 2015. Available online: https://www.epexspot.com/sites/default/files/download_center_files/2015-07-16_EPEX%20SPOT_Lead%20time%20reduction.pdf (accessed on 16 January 2020).
- EPEX SPOT SE. Press Release: Exchange Council Approves the Introduction of 15-min Contracts on the Belgian and Dutch Market – Trading until Delivery to Be Launched on the German Market on 14 June 2017. 2017. Available online: https://www.epexspot.com/sites/default/files/download_center_files/170612_EPEX%20SPOT_Exchange%20Council.pdf (accessed on 16 January 2020).
- Li, W.; Paraschiv, F. Modelling the Evolution of Wind and Solar Power Infeed Forecasts. 2020. Available online: https://ssrn.com/abstract=3600775 (accessed on 16 July 2020).
- European Energy Exchange AG. EPEX SPOT DE/AT 15-min Continuous Intraday Market Transaction Data. 2016. Available online: https://www.eex.com (accessed on 16 July 2016).
- European Energy Exchange AG. EPEX SPOT DE 15-min Intraday Auction Market Data. 2016. Available online: https://www.eex.com (accessed on 16 July 2016).
- EWE TRADING GmbH. Intradaily Updated Forecast Data of Wind and Solar Power Generation. 2016. Available online: https://www.ewe.com (accessed on 16 July 2016).
- European Network of Transmission System Operators for Electricity Transparency Platform. Day-Ahead Total Load Forecast Data. 2016. Available online: https://transparency.entsoe.eu (accessed on 16 July 2016).
- European Energy Exchange AG Transparency Platform. Available Generation Capacity Data. 2016. Available online: https://www.eex-transparency.com (accessed on 16 July 2016).
- Balardy, C. An Empirical Analysis of the Bid–Ask Spread in the German Power Continuous Market. 2018. Available online: http://www.ceem-dauphine.org/assets/wp/pdf/0918-CEEM_Working_Paper_35_Clara_BALARDY.pdf (accessed on 31 March 2020).
- Kremer, M.; Benth, F.E.; Felten, B.; Kiesel, R. Volatility and liquidity on high-frequency electricity futures markets: Empirical analysis and stochastic modeling. Int. J. Theor. Appl. Financ. 2020, 23, 2050027. [Google Scholar] [CrossRef]
- Hansen, B.E. Sample splitting and threshold estimation. Econometrica 2000, 68, 575–603. [Google Scholar] [CrossRef]
- Kremer, M. thrreg: Threshold Regression Model. 2020. R package version 0.1.1. Available online: https://github.com/mlkremer/thrreg (accessed on 28 July 2020).
| Variable [Unit] (Granularity) | Description | Source |
|---|---|---|
| Transaction price[EUR/MWh] (1-min.) | Transaction price of 15-min. contracts traded on the German continuous intraday power market at EPEX SPOT SE | European Energy Exchange AG [30] |
| Trading volume [MW] (1-min) | Trading volume of 15-min. contracts traded on the German continuous intraday power market at EPEX SPOT SE | European Energy Exchange AG [30] |
| Auction price [EUR/MWh] (quarter-hourly) | Market clearing price of 15-min. contracts traded in the German 15-min. intraday auction at EPEX SPOT SE (published: daily after 3:10 PM) | European Energy Exchange AG [31] |
| Wind power forecast [GW] (quarter-hourly) | Intradaily updated forecast of wind power generation for each quarter-hour on the delivery day in Germany | EWE TRADING GmbH [32] |
| Expected demandl [GW] (quarter-hourly) | Day-ahead total load forecast for each quarter-hour on the delivery day in Germany (published: daily at 10 AM) | European Network of Transmission System Operators for Electricity Transparency Platform [33] |
| Expected conventional capacityc [GW] (daily) | Expected daily average of available generation capacity of conventional power plants on the delivery day in Germany (published: daily at 10 AM) | European Energy Exchange AG Transparency Platform [34] |
| H1Q1 | H1Q2 | ||||
|---|---|---|---|---|---|
| Variable | Estimate | Std Error | Variable | Estimate | Std Error |
| Const | 0.160 | (0.808) | Const | −0.263 | (0.890) |
| −0.378 | (2.508) | 2.251 | (3.204) | ||
| −0.393 | (0.024) | −0.406 | (0.028) | ||
| −0.201 | (0.020) | −0.196 | (0.022) | ||
| −0.098 | (0.014) | −0.079 | (0.022) | ||
| 0.022 | (0.012) | 0.014 | (0.010) | ||
| 0.014 | (0.005) | 0.124 | (0.023) | ||
| 0.157 | (0.032) | 0.119 | (0.017) | ||
| 0.033 | (0.016) | 0.011 | (0.013) | ||
| 0.020 | (0.016) | 0.003 | (0.017) | ||
| −0.054 | (0.007) | −0.050 | (0.013) | ||
| −0.059 | (0.261) | −1.073 | (0.373) | ||
| −2.085 | (0.246) | −1.177 | (0.250) | ||
| c | 0.000 | (0.021) | c | −0.009 | (0.021) |
| 0.071 | (0.032) | 0.002 | (0.040) | ||
| #Obs | 6649 | #Obs | 6421 | ||
| 0.224 | 0.203 | ||||
| H1Q3 | H1Q4 | ||||
| Variable | Estimate | Std Error | Variable | Estimate | Std Error |
| Const | −5.207 | (4.508) | Const | −2.601 | (1.632) |
| 39.743 | (45.309) | 10.180 | (11.879) | ||
| −0.358 | (0.025) | −0.608 | (0.084) | ||
| −0.177 | (0.018) | −0.351 | (0.086) | ||
| −0.101 | (0.013) | −0.157 | (0.045) | ||
| 0.023 | (0.014) | 0.047 | (0.021) | ||
| 0.078 | (0.020) | 0.170 | (0.024) | ||
| 0.223 | (0.021) | 0.169 | (0.094) | ||
| 0.033 | (0.018) | 0.041 | (0.027) | ||
| 0.016 | (0.012) | 0.027 | (0.016) | ||
| 0.030 | (0.010) | 0.011 | (0.013) | ||
| −1.032 | (0.492) | −1.291 | (0.435) | ||
| −1.090 | (0.229) | −0.621 | (0.270) | ||
| c | 0.006 | (0.024) | c | 0.004 | (0.029) |
| −0.078 | (0.040) | −0.180 | (0.061) | ||
| #Obs | 7075 | #Obs | 7914 | ||
| 0.207 | 0.290 | ||||
| H3Q1 | H3Q2 | ||||
| Variable | Estimate | Std Error | Variable | Estimate | Std Error |
| Const | −1.352 | (0.881) | Const | 0.865 | (0.810) |
| −3.468 | (4.834) | −2.496 | (1.742) | ||
| −0.399 | (0.020) | −0.365 | (0.024) | ||
| −0.214 | (0.017) | −0.190 | (0.019) | ||
| −0.076 | (0.015) | −0.102 | (0.016) | ||
| 0.039 | (0.018) | 0.017 | (0.014) | ||
| 0.014 | (0.016) | 0.119 | (0.017) | ||
| 0.140 | (0.020) | 0.139 | (0.024) | ||
| 0.037 | (0.017) | 0.069 | (0.017) | ||
| 0.029 | (0.009) | 0.011 | (0.015) | ||
| 0.024 | (0.010) | 0.037 | (0.011) | ||
| −1.012 | (0.360) | −0.702 | (0.283) | ||
| −1.669 | (0.275) | −1.289 | (0.181) | ||
| c | 0.031 | (0.023) | c | 0.009 | (0.020) |
| 0.038 | (0.036) | −0.050 | (0.033) | ||
| #Obs | 6357 | #Obs | 6309 | ||
| 0.208 | 0.191 | ||||
| H3Q3 | H3Q4 | ||||
| Variable | Estimate | Std Error | Variable | Estimate | Std Error |
| Const | −0.227 | (1.475) | Const | −1.199 | (0.913) |
| 4.497 | (8.890) | −1.381 | (2.122) | ||
| −0.428 | (0.027) | −0.370 | (0.021) | ||
| −0.174 | (0.016) | −0.166 | (0.018) | ||
| −0.053 | (0.021) | −0.057 | (0.013) | ||
| 0.053 | (0.015) | 0.023 | (0.014) | ||
| 0.072 | (0.017) | 0.183 | (0.015) | ||
| 0.210 | (0.020) | 0.049 | (0.016) | ||
| 0.075 | (0.028) | 0.035 | (0.016) | ||
| 0.005 | (0.011) | 0.021 | (0.011) | ||
| 0.015 | (0.010) | −0.010 | (0.008) | ||
| −0.711 | (0.242) | −0.809 | (0.280) | ||
| −1.063 | (0.167) | −0.981 | (0.223) | ||
| c | −0.015 | (0.020) | c | 0.030 | (0.024) |
| −0.042 | (0.030) | −0.027 | (0.033) | ||
| #Obs | 6610 | #Obs | 7337 | ||
| 0.219 | 0.174 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kremer, M.; Kiesel, R.; Paraschiv, F. Intraday Electricity Pricing of Night Contracts. Energies 2020, 13, 4501. https://doi.org/10.3390/en13174501
Kremer M, Kiesel R, Paraschiv F. Intraday Electricity Pricing of Night Contracts. Energies. 2020; 13(17):4501. https://doi.org/10.3390/en13174501
Chicago/Turabian StyleKremer, Marcel, Rüdiger Kiesel, and Florentina Paraschiv. 2020. "Intraday Electricity Pricing of Night Contracts" Energies 13, no. 17: 4501. https://doi.org/10.3390/en13174501
APA StyleKremer, M., Kiesel, R., & Paraschiv, F. (2020). Intraday Electricity Pricing of Night Contracts. Energies, 13(17), 4501. https://doi.org/10.3390/en13174501






