Condition Maintenance Decision of Wind Turbine Gearbox Based on Stochastic Differential Equation
Abstract
:1. Introduction
2. Gearbox State Transition Modeling
- , is a measurable function defined on .
- There is a constant K, let:
3. The Determination of the State Characteristic Value of the Gear Box
3.1. Selection of Modeling Indicators
- Oil temperature (OT): the oil temperature of the gearbox reflects the operation of the gearbox air cooler, lubrication system, and relief valve. If these parts are functioning abnormally, then the gearbox temperature will rise sharply.
- Shaft temperature (ST): the increase in the gearbox shaft temperature means that the frictional force increases, which may be caused by gear wear, abnormal denature or bite, or aging and deterioration of lubricating oil.
- Amplitude: the rapid increase in gearbox amplitude may be caused by problems with rotors, shafts, gears, and bearings.
3.2. Weights of Modeling Indicators
4. Model Construction and Parameter Solution
4.1. Failure Rate Model
4.1.1. Weibull Distribution Model
4.1.2. State Influence Rate Model
4.1.3. Gearbox Failure Rate Model
4.1.4. Solving Model Parameters
4.2. State Volatility Model
5. Example Analysis
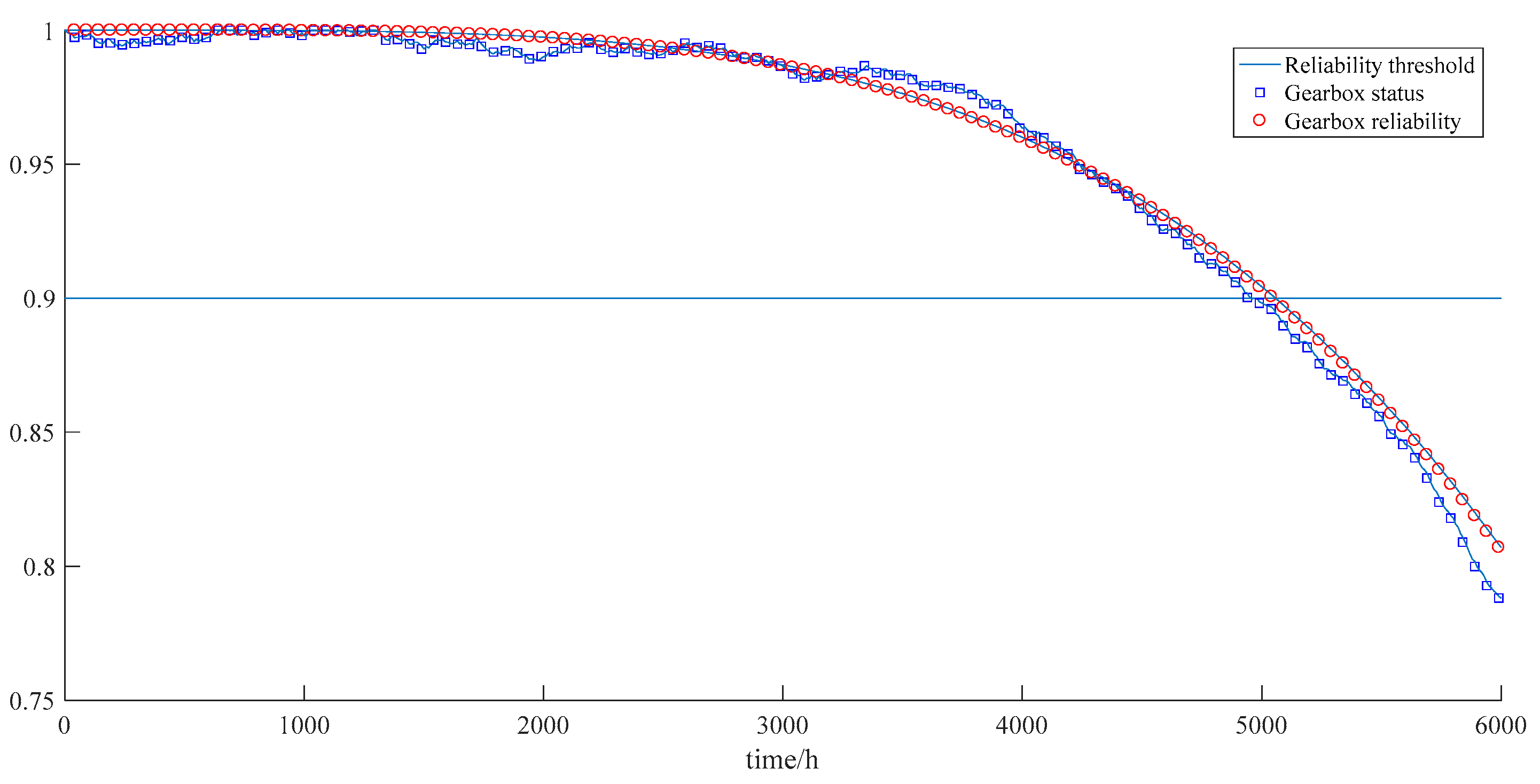
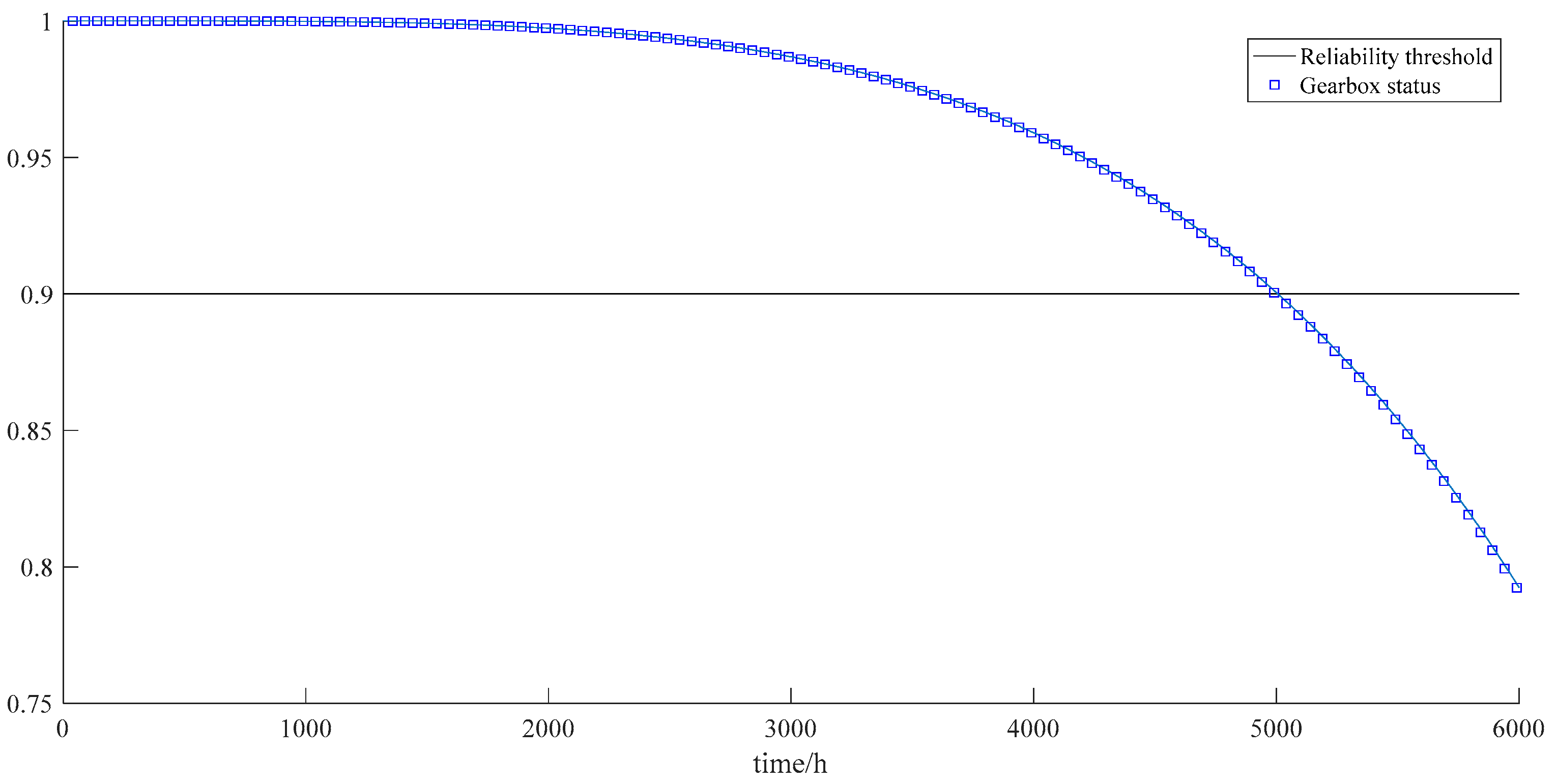
5.1. Weibull Polynomial Approximation Stochastic Model
- The state and reliability of the gearbox both decrease with the increase in time, thereby indicating that in the actual operation process, the gearbox is more prone to failure and the rate of failure increases at an accelerated rate as the operating time increases.
- The state of the gearbox is not a smooth curve that changes with time because the state is affected by random disturbances from outside and fluctuates, but the overall trend is downward.
- During the first 1500 h of the operation of the gearbox, the state and reliability of the equipment did not change significantly. This finding shows that the maintenance interval for the equipment should not be too small; otherwise, the equipment will be prone to excessive maintenance.
- When the reliability of the gearbox reaches the threshold of 0.9, the running time is about 5000 h, which is closer to the failure time of the gearbox at 4937 h, indicating that the model has a certain accuracy.
5.2. Ordinary Differential Equation Model
5.3. Gamma Distribution Model Application
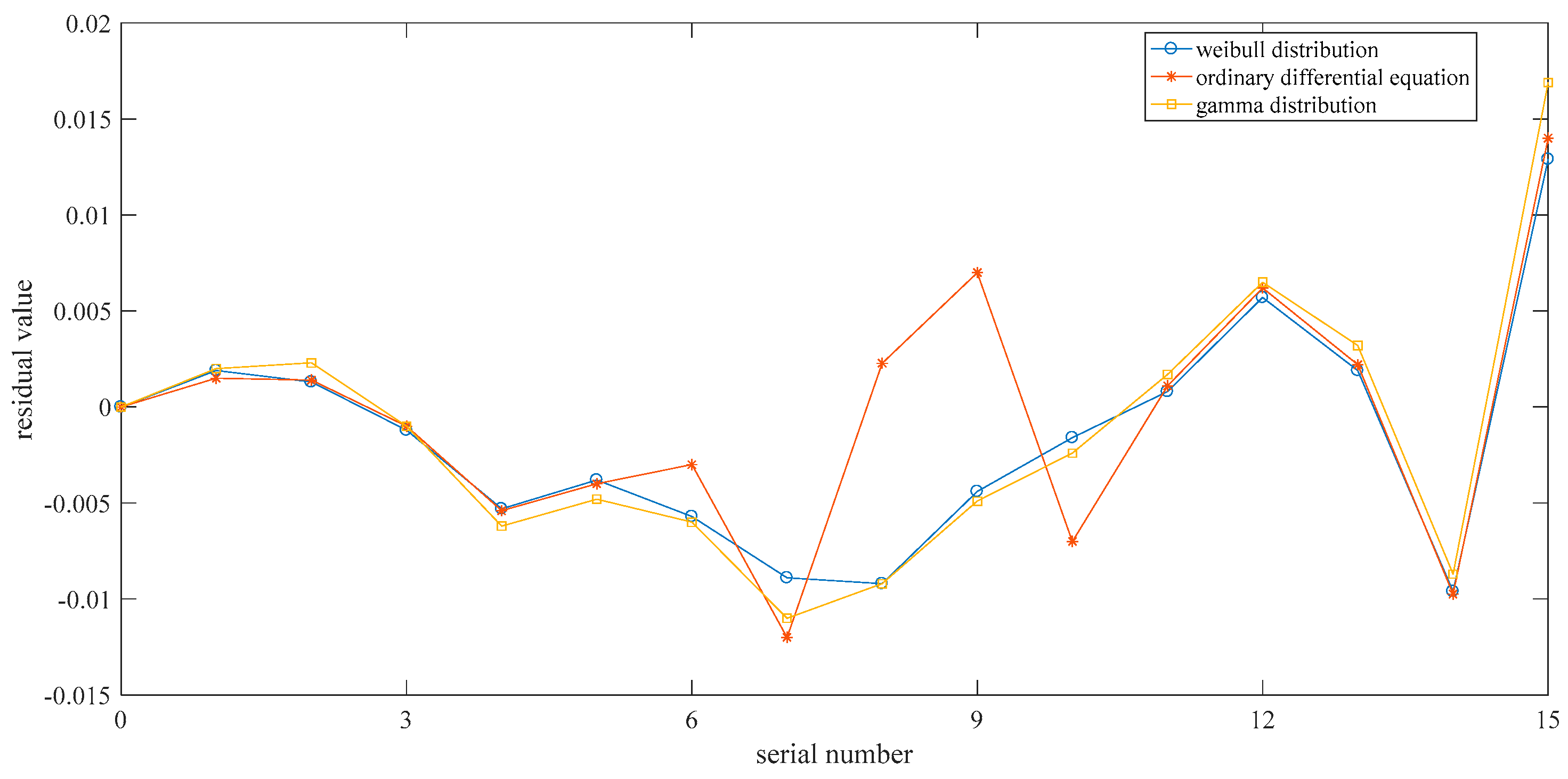
- The gearbox state transition model constructed by ordinary differential equations has a large abrupt change in the state residual value, thereby indicating that the model cannot track and simulate the state change of the gearbox in a sudden situation. Compared with the stochastic differential equation, the mean value of the residual is larger, indicating that the stochastic differential equation can more accurately reflect the state of the device and has higher applicability and accuracy.
- When adopts the Gamma distribution, the predicted value of the state of the gear box differs greatly from the true value and is greater than the residual value in the Weibull proportional hazard model. This finding further demonstrates the correctness of using the Weibull model in the construction of the gearbox state model.
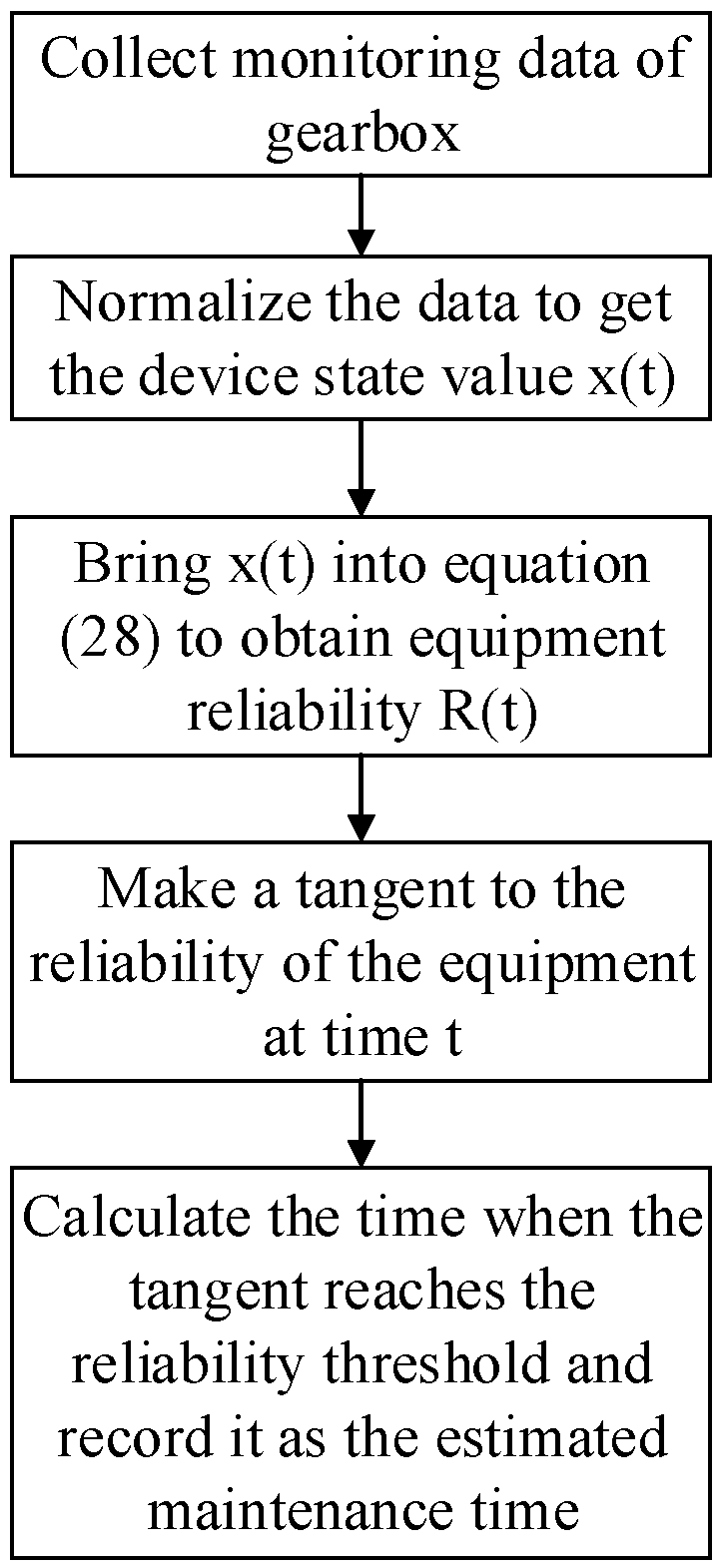
5.4. Example Verification Analysis
6. Results
Author Contributions
Funding
Conflicts of Interest
References
- Hang, J.; Zhang, J.Z.; Cheng, M. An overview of condition monitoring and fault diagnostic for wind energy conversion system. Trans. China Electrotech. Soc. 2013, 28, 261–271. [Google Scholar]
- Wu, L.Y.; Zhou, Z.Y.; Han, X. Talking about the early failure form of wind power gearbox. Heilongjiang Sci. Technol. Inf. 2011, 13, 4. [Google Scholar]
- Pang, M.T.; Guo, J.M.; Zhang, Y.H. An optimization method for the calculation of hard-time maintenance interval. Sichuan Ordnance J. 2013, 34, 39–40. [Google Scholar]
- Wang, X.Y.; Cao, L.R.; Liu, Y. Analysis and research on repair interval of equipment. Qual. Reliab. 2019, 4, 26–29. [Google Scholar]
- Guo, P.; David, I.; Yang, X.Y. Wind turbine gearbox temperature trend state monitoring and analysis method. Chin. J. Electr. Eng. 2011, 31, 129–136. [Google Scholar]
- Zhang, Y.Z.; Zhang, X.H.; Zeng, J.C. Optimal decision of condition-based maintenance strategy for leased equipment. Syst. Eng. Theory Pract. 2019, 39, 1732–1743. [Google Scholar]
- Cheng, Z.H.; Zhang, J.G. Application of based maintenance technology and its computer aided analysis system. Power Syst. Technol. 2003, 27, 16–24. [Google Scholar]
- Long, Q.; Liu, Y.Q.; Yang, Y.P. Applications of condition monitoring and fault diagnosis to wind turbines. Mod. Electr. Power 2008, 25, 55–59. [Google Scholar]
- Zhu, W. Wind Turbines Operation State Monitoring and Analysis; North China Electric Power University: Beijing, China, 2012. [Google Scholar]
- Hameed, Z.; Hong, Y.S.; Cho, Y.M. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Anders, G.J.; Endrenyi, J.; Ford, G.L. A probabilistic model for evaluating the remaining life of evaluating the remaining life of electrical insulation in rotating machines. IEEE Trans. Energy Convers. 1999, 5, 761–767. [Google Scholar] [CrossRef]
- Kang, Y.Q. Control Strategy Study on Preventive Maintenance of Repairable Complex Power Equipment Based on Condition Monitoring; Lanzhou Jiaotong University: Lanzhou, China, 2015. [Google Scholar]
- Zhu, T.W.; Ma, H.M.; Qin, Y. Condition maintenance decision of wind turbine gear box based on proportional hazard model. Electr. Power Sci. Eng. 2016, 32, 32–35. [Google Scholar]
- Chen, M.F.; Wang, Y.H. Introduction to Random Processes, 1st ed.; Higher Education Press: Beijing, China, 2007; pp. 145–147. [Google Scholar]
- Zhang, S.X.; Liu, Y.L.; Chen, J.X. Multi-attribute fuzzy decision-making method of test interval based on weibull proportional hazards model. J. Acad. Armored Force Eng. 2012, 26, 20–23. [Google Scholar]
- Liu, L.J.; Fu, Y.; Ma, S.W. Maintenance strategy for offshore wind turbine based on condition monitoring and prediction. Power Syst. Technol. 2015, 39, 3292–3297. [Google Scholar]
- Xiang, W.J. Research on Signal Analysis Methods and System for Fault Sources of Gearbox; Zhejiang University: Hangzhou, China, 2007. [Google Scholar]
- Gao, P. The Research on Preventive Maintenance Decision of Complex Equipment based on Reliability Analysis; Tsinghua University: Beijing, China, 2008. [Google Scholar]
- Wang, R.S. Functional Analysis and Optimization Theory, 1st ed.; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2003; pp. 66–68. [Google Scholar]
- Lu, X. Fundamentals of Mathematical Statistics, 1st ed.; China Statistics Press: Beijing, China, 1998; pp. 101–103. [Google Scholar]
- Chen, C. Reasearch on Shape Estimation for the Two-Parameter Gamma Distribution; Shandong University of Technology: Zibo, China, 2015. [Google Scholar]
| Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Fault time/h | 4937 | 4532 | 5167 | 5233 | 4825 |
| Number | Operation Hours/h | OT/°C | ST/°C | Amplitude/mm |
|---|---|---|---|---|
| 1 | 75 | 24.2 | 27.1 | 0.353 |
| 2 | 150 | 24.3 | 27.2 | 0.357 |
| 3 | 228 | 24.6 | 27.5 | 0.348 |
| 4 | 309 | 25.2 | 27.8 | 0.363 |
| 5 | 375 | 25.8 | 28.2 | 0.372 |
| 6 | 500 | 26.1 | 28.4 | 0.471 |
| 7 | 757 | 26.7 | 29.1 | 0.593 |
| 8 | 906 | 27.1 | 30.3 | 0.746 |
| 9 | 1014 | 27.4 | 30.5 | 0.783 |
| 10 | 1130 | 27.6 | 30.5 | 1.075 |
| 11 | 1630 | 32.1 | 38.9 | 1.521 |
| 12 | 2365 | 36.3 | 43.2 | 1.637 |
| 13 | 3128 | 40.2 | 52.4 | 2.135 |
| 14 | 3931 | 46.7 | 61.6 | 4.348 |
| 15 | 4763 | 61.2 | 77.3 | 6.153 |
| Operation Hours/h | OT/°C | ST/°C | Amplitude/mm | EMI/h | MD |
|---|---|---|---|---|---|
| 1178 | 25.1 | 27.9 | 0.675 | 5849 | continue to monitor |
| 1866 | 26.9 | 29.1 | 0.778 | 4983 | continue to monitor |
| 2495 | 28.2 | 30.6 | 0.846 | 4137 | continue to monitor |
| 2948 | 31.1 | 33.4 | 1.087 | 3496 | continue to monitor |
| 3306 | 32.4 | 37.5 | 1.343 | 2897 | continue to monitor |
| 3707 | 33.9 | 39.1 | 1.668 | 2092 | continue to monitor |
| 4016 | 36.3 | 42.2 | 2.065 | 1496 | continue to monitor |
| 4238 | 39.4 | 44.6 | 2.498 | 874 | continue to monitor |
| 4493 | 42.8 | 48.7 | 3.079 | 419 | continue to monitor |
| 4622 | 45.4 | 54.9 | 3.997 | 197 | service |
| 4788 | malfunction | malfunction | malfunction |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Wang, D.; Duan, X. Condition Maintenance Decision of Wind Turbine Gearbox Based on Stochastic Differential Equation. Energies 2020, 13, 4480. https://doi.org/10.3390/en13174480
Su H, Wang D, Duan X. Condition Maintenance Decision of Wind Turbine Gearbox Based on Stochastic Differential Equation. Energies. 2020; 13(17):4480. https://doi.org/10.3390/en13174480
Chicago/Turabian StyleSu, Hongsheng, Dantong Wang, and Xuping Duan. 2020. "Condition Maintenance Decision of Wind Turbine Gearbox Based on Stochastic Differential Equation" Energies 13, no. 17: 4480. https://doi.org/10.3390/en13174480
APA StyleSu, H., Wang, D., & Duan, X. (2020). Condition Maintenance Decision of Wind Turbine Gearbox Based on Stochastic Differential Equation. Energies, 13(17), 4480. https://doi.org/10.3390/en13174480





