Abstract
Maintenance decision analysis is necessary to ensure the safe and stable operation of wind turbine equipment. To address gearboxes with a high failure rate in wind turbines, this paper establishes a new stochastic differential equation model of gearbox state transition to maximize the utilization of gearboxes. This model divides the state of the gearbox into two parts: internal degradation and external random interference. Weibull distribution and polynomial approximation were used to construct the internal degradation model of the gearbox. The external random interference is simulated by Brownian motion. On the basis of the analysis of monitoring data, the parameters of the gearbox state model were solved using the Newton–Raphson iterative method and entropy method. The state change of the gearbox was simulated in MATLAB, and the residual value between the predicted state and the real state was calculated. Compared with the state transformation model constructed by the traditional ordinary differential equation and the gamma distribution, the Weibull polynomial approximation stochastic model can better reflect the state of the device. With reliability set as the decision goal, the maintenance time of the gearbox is predicted, and the validity of the model is verified through case analysis.
1. Introduction
In the context of the global energy crisis, wind energy has been attracting increasing attention as a clean and pollution-free renewable energy source, and the installed capacity of wind power has increased significantly. With the increase in the stock of operational equipment, the wind power operation and maintenance market has ushered in development opportunities and space, thereby becoming an important factor that affects the development of the wind power industry. With the high price of wind turbines, the harsh working environment, the remote location, and the high height of equipment, maintenance work is very inconvenient. When a shutdown failure occurs, the wind farm must pay an expensive fee for repairs. Therefore, because the gearbox is one of the components with the highest failure rate in wind turbines, reliability analysis and the optimization of maintenance strategies are necessary [1,2].
Preventive maintenance is aimed at preventing the occurrence of failures. Through the inspection and monitoring of equipment, failure symptoms are discovered, and various maintenance activities are carried out before failures occur to maintain the prescribed functional status. This approach is an effective way to ensure that the equipment is in good condition. Nowadays, two main types of preventive maintenance are used. The first is time-based maintenance, which can ensure that the unit meets the desired performance requirements after implementation, equipment maintenance is conducted at fixed time intervals, and sufficient maintenance resources are arranged at corresponding time points [3,4,5]. The second is condition-based maintenance (CBM). This maintenance strategy can determine the abnormality of the device and predict the development trend of the unit status by monitoring and diagnosing the equipment status, and make a maintenance plan in advance, thereby improving equipment utilization and overcoming many defects of traditional fault repair and active maintenance [6,7,8]. Therefore, the CBM is receiving growing attention.
In CBM, according to the different ways of condition detection, it can be divided into continuous monitoring state maintenance and discrete detection state maintenance. Continuous state monitoring means that it can continuously return to the real-time operating status of the system through wireless communication technology after a one-time installation. Zhu [9] uses a multivariate state estimation technique to estimate the bearing temperature of the wind turbine gearbox, and judges whether the gearbox operates normally through the real-time change trend of the residual error between the estimated value and the actual value of the bearing temperature. Hameed [10] uses back propagation neural network to model and predict the state of the gearbox and generator, as well as a multi-agent method to comprehensively analyze the diagnosis results of different components and gives the overall operating state of the unit. The one-time installation cost of continuous monitoring is high, and the requirements for data acquisition and signal processing are high. It is suitable for nuclear power plants, aviation components and other systems with high safety requirements. Discrete detection needs to carry specific detection equipment at a specific interval to detect the key components of the system. The cost of single detection is high, and the probability of system failure is high between two successive detections. Anders [11] considers two types of random failures and aging failures in the system, with maintenance including minor repair and replacement. The unit state is represented by a state probability vector, and the adjacent state probability vectors were linked together by one-step transition probability. A method for determining the maintenance time by using Markov chain theory to estimate the remaining life of the system is proposed. Kang [12] takes the continuous degradation state as the independent variable and the continuous detection interval as the dependent variable, and derives the functional relationship between the state and the detection interval based on the established ordinary differential equation describing the state transition of the system. Zhu [13] uses a proportional hazard model to reflect the relationship between gearbox status and failure rate and take reliability as the maintenance goal to predict the maintenance interval of the gearbox. It can be seen that the state of the equipment plays an important role in finding the best detection time. However, when constructing the state transition model of the equipment, most of the studies did not consider the impact and interference of random factors such as daily inspection, maintenance, and repair on the system process behavior, which cannot accurately estimate the state of the equipment. It is worth noting that when the state of the device is different, the same disturbance will affect the state of the device to different degrees.
For equipment maintenance, constructing a state transition model of the equipment is very important. The judgment of equipment status has a direct effect on the selection of maintenance strategy. In light of the aforementioned problems, this study took a wind turbine gearbox as the research object paper, and the stochastic differential equation model of the gearbox state transition was established. Compared with the traditional ordinary differential equation, this model considers that the equipment failure rate is affected by the equipment state in addition to the time. At the same time, it takes into account the influence of the external random disturbance on the equipment state and integrates the relationship between the equipment failure rate and external random interference. This model can more accurately predict the state of the equipment, thereby more accurately predicting the inspection moment.
The remainder of this paper is organized as follows. Section 2 constructs the state transition model of the gearbox. Section 3 introduces the constituent indicators and weight distribution of the gearbox state. Section 4 introduces the construction method and parameter-solving method of the failure rate model and the state volatility model in the state transition model. Section 5 verifies that this model is more accurate through comparison and analysis with traditional differential equations, and then with reliability taken as the decision goal, the best maintenance time of the gearbox is predicted, and validates the effectiveness of the model through an example analysis.
2. Gearbox State Transition Modeling
The change of the gearbox state is formed by the combination of the decline of the gearbox itself and external factors. The decline of the gearbox itself is represented by the failure rate, and the received external interference is random.
Definition 1.
x(t) represents the state of the gearbox at time t. x(t) = 1 means that the device is in a brand-new state at t, and x(t) = 0 means that the device is in a completely damaged state at t.
Definition 2.
The failure rate of the gearbox is related to the state of the equipment and the operating time of the equipment. The strength of the random disturbance received by the gearbox on the equipment state is related to the state of the equipment.
Hypothesis 1 (H1).
The gearbox repair process is completed in an instant, and each repair means that the equipment enters a new life cycle. The change of x(t) represents the state change process of the gearbox in one life cycle.
Hypothesis 2 (H2).
The random disturbance of the gearbox at all times is independent and stable.
Hypothesis 3 (H3).
The expected value of the random disturbance of the gearbox is zero.
The state transition model of the gearbox is constructed as follows:
In (1), the first term on the right side of the equation is the decline of the gearbox itself and is the failure rate of the gearbox, the second term represents the random disturbance received by the gearbox, is the random disturbance coefficient, which is called the equipment state fluctuation rate, and B(t) is the Brownian motion, which satisfies the Hypotheses 2 and 3.
- , is a measurable function defined on .
- There is a constant K, let:
In (2), both and are the solutions of (1), (2) proves the uniqueness of the solution of (1), and (3) proves the existence of the solution of (1). If 1 and 2 are both satisfied, then Equation (1) has a unique solution x(t), and x(t) is continuous with respect to t [14].
3. The Determination of the State Characteristic Value of the Gear Box
3.1. Selection of Modeling Indicators
In the condition-monitoring system of wind turbines, the commonly used condition monitoring parameters are wind direction, wind speed, tower torque and bending moment, oil temperature, shaft temperature, and main bearing vibration [15,16,17]. In establishing the gearbox state transformation model, the following variables that are closely related to the gearbox state are selected to form the observation indicators:
- Oil temperature (OT): the oil temperature of the gearbox reflects the operation of the gearbox air cooler, lubrication system, and relief valve. If these parts are functioning abnormally, then the gearbox temperature will rise sharply.
- Shaft temperature (ST): the increase in the gearbox shaft temperature means that the frictional force increases, which may be caused by gear wear, abnormal denature or bite, or aging and deterioration of lubricating oil.
- Amplitude: the rapid increase in gearbox amplitude may be caused by problems with rotors, shafts, gears, and bearings.
3.2. Weights of Modeling Indicators
The oil temperature, shaft temperature, and amplitude are closely related to the state of the gearbox. Therefore, when a state change model is being built, the degree of influence of the three observation indicators on the state needs to be clarified, that is, these indicators must be weighted. In this paper, the entropy method is used to weight the observed indicators.
Construct the data matrix:
In (4), is the value of the jth observation index at the ith moment (j = 1, 2, 3).
The measurement units of the various observation indicators are not uniform, which is why they must be normalized before the overall state of the device is calculated. In this paper, a large x(t) corresponds to a good device state. The data must be translated to avoid the meaningless logarithm of the entropy value. The specific methods are as follows:
Calculate the weight of the jth observation indicator at the ith moment in the indicator:
Calculate the entropy value of the jth feature observation indicator:
where k is related to the number of samples n, generally let k = −1/ln n.
For the ith moment, a great difference in the value corresponds to a great effect on the program evaluation and a small entropy value. Therefore, the difference coefficient of the jth index is calculated as , a large index corresponds to its increased importance.
The weight of each observation indicator is:
The weight set constructed to reflect the relative importance of each observation indicator is:
4. Model Construction and Parameter Solution
4.1. Failure Rate Model
The failure rate of the gearbox is affected by two factors. The first is time. The probability of gearbox failure inevitably increases with the increase in use time. The second is the state of the gearbox. When the running time is t, if the condition of the No. 1 gearbox is better than that of the No. 2 gearbox, then the failure rate of the No. 1 gearbox at time t should be less than that of the No. 2 gearbox. Therefore, the failure rate of the gearbox is abstracted into two parts: one is the basic failure rate under the influence of time without any external interference, and the other is the increase or decrease in the basic failure rate due to the state of the gearbox.
4.1.1. Weibull Distribution Model
Among the many life distribution models (such as Weibull distribution, exponential distribution, and Gamma distribution), Weibull distribution is one of the most widely used distributions for life data analysis. This is mainly because the Weibull distribution can fit a variety of sample data in reality by adjusting its shape parameters, scale parameters, and position parameters. Particularly, the variety of shape parameters in the distribution can describe various situations such as the decline, stability, and rise of sample data [18].
In view of the characteristics of the Weibull distribution, the basic failure rate of the gearbox is selected as the Weibull distribution:
In (10), is the shape parameter and is the scale parameter.
4.1.2. State Influence Rate Model
g(x(t)), which is the effect of the gearbox state on the failure rate, is a continuous function, and its domain [0, 1]. According to Weierstrass’ first approximation theorem [19], the following can be considered:
infinitely approaching g(x(t)).
For the polynomial function p(x(t)), no matter what value x(t) takes, there is a variable constant k, which makes q(x(t)) approximate to p(x(t)), so it can be considered that q(x(t)) approximates g(x(t)):
When x(t) = 0, the device is in a completely damaged state and has no effect on the device failure rate. At this time, g(0) = 1, so . Therefore:
q(x(t)) approximates the Taylor expansion of from Equation (13), Therefore, let:
In (14), represents the parameter of the influence of the equipment state on the failure rate function, also known as regression coefficients.
4.1.3. Gearbox Failure Rate Model
The gearbox failure rate is a continuous function, so it can be approximated by polynomials. is the basic failure rate, thus, g(x(t)) is a function that affects the basic failure rate based on the state of the gearbox, and its Taylor expansion is a polynomial. Therefore, the failure rate model of the gearbox is constructed as follows:
4.1.4. Solving Model Parameters
According to the gearbox failure rate model, the reliability function of this model is:
According to the fault density function , construct the likelihood function as
In (17), n is the number of data, is the detection value of the data at time .
Take the logarithm of both sides of Equation (17) and simplify it, and get the log-likelihood function as
The Newton–Raphson iterative method [20] is used to solve the parameter estimation of the failure rate model. First, according to Equation (18), the partial derivatives of are obtained:
Let:
Partial derivation of in Equation (22), let:
The iterative formula for the parameters constructed by the Newton–Raphson method:
When k = 0, the parameter estimates can be obtained according to the iterative formula after selecting the initial values of .
4.2. State Volatility Model
The interference received by the device is random and is unrelated to the running time, but its impact on the state of the device, which is called the state fluctuation rate, is related to the state of the device at the time. Therefore, the state fluctuation rate is recorded, and the following method is used to find the value of the parameter k.
In the (0, T) period, the step size is , and . In the time period of , the change of state value is recorded as , there is:
which is:
When Δt→0, the failure rate of the gearbox can be regarded as a fixed value , substitute it into (26), it can be obtained that:
Average the (27), it can be obtained that:
5. Example Analysis
5.1. Weibull Polynomial Approximation Stochastic Model
The establishment of a gearbox state transformation model based on the Weibull proportional hazard model requires the state monitoring data and fault data of the wind turbine gearbox. In this paper, the actual operating data of a wind farm were selected for simulation analysis. Table 1 lists the life data of five gearboxes, and Table 2 lists part of the state monitoring data of gearbox 1.

Table 1.
Partial failure data of the gearbox.

Table 2.
Partial state monitoring data of the gearbox.
According to the monitoring data in Table 2, the three entropy vectors were weighted by the entropy method. After calculation, the weights are:
W = (0.33, 0.325, 0.345)
According to the condition monitoring data of the gearbox, through the model parameter-solving method of Section 4.1.1, the parameters in the Weibull proportional risk model are programmed on the MATLAB to be:
The failure rate function of the gearbox is:
According to the condition monitoring data of the gearbox, through the model parameter-solving method of Section 4.1.1, the available equipment state fluctuation rate parameter is calculated to be 0.00127.
Therefore, the state transition model of the gearbox is:
The reliability function of the gearbox is:
The reliability requirement of the gearbox in trouble-free operation is 0.9. Therefore, the gearbox is repaired at a reliability threshold of 0.9. When the reliability of the gearbox is less than 0.9, the equipment will be repaired.
The state transformation model and reliability model of the gearbox were simulated in MATLAB. The change in the state and reliability of the gearbox with time is shown in Figure 1.
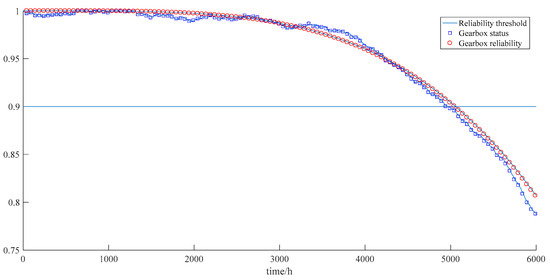
Figure 1.
Gear box state and reliability transform diagram.
Through the research and analysis shown in Figure 1, the following conclusions can be obtained:
- The state and reliability of the gearbox both decrease with the increase in time, thereby indicating that in the actual operation process, the gearbox is more prone to failure and the rate of failure increases at an accelerated rate as the operating time increases.
- The state of the gearbox is not a smooth curve that changes with time because the state is affected by random disturbances from outside and fluctuates, but the overall trend is downward.
- During the first 1500 h of the operation of the gearbox, the state and reliability of the equipment did not change significantly. This finding shows that the maintenance interval for the equipment should not be too small; otherwise, the equipment will be prone to excessive maintenance.
- When the reliability of the gearbox reaches the threshold of 0.9, the running time is about 5000 h, which is closer to the failure time of the gearbox at 4937 h, indicating that the model has a certain accuracy.
5.2. Ordinary Differential Equation Model
At present, most studies use the ordinary differential equation model when constructing the gearbox state transition model. For the example of Section 5.1, is selected as the Weibull proportional hazard model, and the state transformation model of the gearbox constructed with the ordinary differential equations is:
The maximum likelihood estimation method [21] can be used to solve the Equation (32), , then, the gearbox state transition model is:
According to Equation (33), the state transformation of the gearbox is shown in Figure 2.
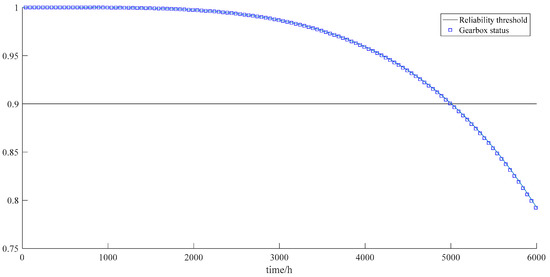
Figure 2.
Gear box state transform diagram.
It can be seen from Figure 2 that the state curve of the gearbox under this equation is a smooth curve, which cannot reflect the sudden change of state when a sudden situation occurs. However, for the stochastic differential equation model, x(t) can approximate any value at time t due to the independent incremental nature of Brownian motion.
5.3. Gamma Distribution Model Application
The life distribution model has exponential distribution, Gamma distribution, and normal distribution in addition to the Weibull distribution. If the life distribution of the gearbox is assumed to conform to the Gamma distribution, then the probability density of x(t) is:
In Equation (34), is the scale parameter, is the shape parameter, and is the Gamma function.
The failure rate is:
and .
The maximum likelihood estimation method can be used to solve the parameter of Gamma distribution, , then:
Bring (36) into (15), and re-simulate the state transformation model and reliability model of the gearbox. The residual values of the predicted state and the actual state when the models belong to Weibull distribution, ordinary differential equation, and gamma distribution are shown in Figure 3.
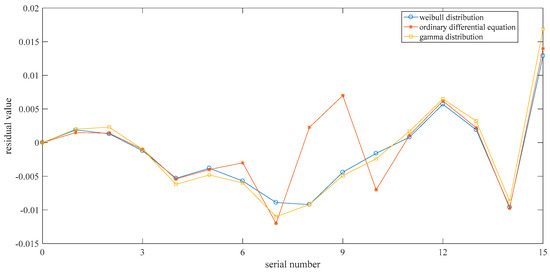
Figure 3.
Residual value between the actual state and the expected state of the gearbox.
After calculation, the average residuals in the three maintenance models are 0.0046, 0.0051, 0.0055. In combination with Figure 3, the following conclusions can be drawn:
- The gearbox state transition model constructed by ordinary differential equations has a large abrupt change in the state residual value, thereby indicating that the model cannot track and simulate the state change of the gearbox in a sudden situation. Compared with the stochastic differential equation, the mean value of the residual is larger, indicating that the stochastic differential equation can more accurately reflect the state of the device and has higher applicability and accuracy.
- When adopts the Gamma distribution, the predicted value of the state of the gear box differs greatly from the true value and is greater than the residual value in the Weibull proportional hazard model. This finding further demonstrates the correctness of using the Weibull model in the construction of the gearbox state model.
5.4. Example Verification Analysis
Another gearbox of the same model was selected as the verification sample, and the estimated maintenance interval and maintenance decision were calculated at each monitoring time on the basis of its condition monitoring data. Compared with the actual operation maintenance decision, the finding proves the accuracy and reliability of the model. The calculation method of estimated maintenance time is shown in Figure 4:
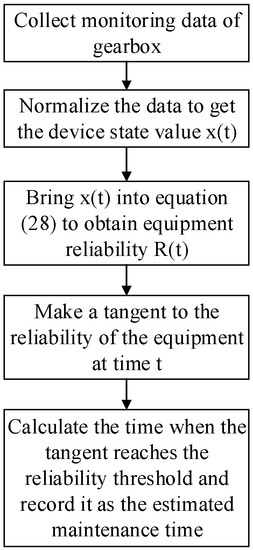
Figure 4.
Calculation method of the estimated maintenance time.
The estimated maintenance time of the equipment can be obtained by subtracting the estimated maintenance time from the state monitoring time. After calculation, the estimated maintenance interval (EMI) and maintenance decision (MD) at each monitoring time were obtained and are shown in Table 3.

Table 3.
Estimated maintenance interval and maintenance decision.
The above table shows that the maintenance time interval predicted by the gearbox reliability model continues to decrease with the increase in use time. When the running time reaches 4622 h, the gearbox is expected to reach the maintenance threshold after 197 h. Thus, repair is recommended. In actual operation, the gearbox fails after 166 h. The reliability model can then be deemed to be very accurate, and the life of the gearbox can be utilized to the maximum extent under the premise of satisfying the reliability.
6. Results
To address the problem of wind turbine gearbox failure, this paper builds a stochastic differential equation model of gearbox state transition, which can accurately predict the equipment state and maintenance time. In the model, the Weibull model and polynomial approximation were used to construct the failure rate function of the equipment, and Brownian motion was used to simulate the external random disturbance, which integrates the relationship between the equipment’s own degradation and external interference. At the same time, the accuracy of the model were verified by comparing with the ordinary differential model and the gamma distribution model. In the case analysis, the validity of the model was verified by predicting the maintenance time. Hence the state transition model constructed by stochastic differential equations is more accurate and effective. Clearly, the application of this model has a positive effect on the development of CBM.
Author Contributions
H.S. proposed the main idea of this study. D.W. established a gearbox state transition model based on Weibull polynomial approximation stochastic equations and simulated it in MATLAB. D.W. and X.D. conducted the comparative study and analysis. H.S., D.W. and X.D. actively contributed to writing this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (61867003), and the the 2020 Gansu Provincial College Innovation Fund Program (2020A-044).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hang, J.; Zhang, J.Z.; Cheng, M. An overview of condition monitoring and fault diagnostic for wind energy conversion system. Trans. China Electrotech. Soc. 2013, 28, 261–271. [Google Scholar]
- Wu, L.Y.; Zhou, Z.Y.; Han, X. Talking about the early failure form of wind power gearbox. Heilongjiang Sci. Technol. Inf. 2011, 13, 4. [Google Scholar]
- Pang, M.T.; Guo, J.M.; Zhang, Y.H. An optimization method for the calculation of hard-time maintenance interval. Sichuan Ordnance J. 2013, 34, 39–40. [Google Scholar]
- Wang, X.Y.; Cao, L.R.; Liu, Y. Analysis and research on repair interval of equipment. Qual. Reliab. 2019, 4, 26–29. [Google Scholar]
- Guo, P.; David, I.; Yang, X.Y. Wind turbine gearbox temperature trend state monitoring and analysis method. Chin. J. Electr. Eng. 2011, 31, 129–136. [Google Scholar]
- Zhang, Y.Z.; Zhang, X.H.; Zeng, J.C. Optimal decision of condition-based maintenance strategy for leased equipment. Syst. Eng. Theory Pract. 2019, 39, 1732–1743. [Google Scholar]
- Cheng, Z.H.; Zhang, J.G. Application of based maintenance technology and its computer aided analysis system. Power Syst. Technol. 2003, 27, 16–24. [Google Scholar]
- Long, Q.; Liu, Y.Q.; Yang, Y.P. Applications of condition monitoring and fault diagnosis to wind turbines. Mod. Electr. Power 2008, 25, 55–59. [Google Scholar]
- Zhu, W. Wind Turbines Operation State Monitoring and Analysis; North China Electric Power University: Beijing, China, 2012. [Google Scholar]
- Hameed, Z.; Hong, Y.S.; Cho, Y.M. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Anders, G.J.; Endrenyi, J.; Ford, G.L. A probabilistic model for evaluating the remaining life of evaluating the remaining life of electrical insulation in rotating machines. IEEE Trans. Energy Convers. 1999, 5, 761–767. [Google Scholar] [CrossRef]
- Kang, Y.Q. Control Strategy Study on Preventive Maintenance of Repairable Complex Power Equipment Based on Condition Monitoring; Lanzhou Jiaotong University: Lanzhou, China, 2015. [Google Scholar]
- Zhu, T.W.; Ma, H.M.; Qin, Y. Condition maintenance decision of wind turbine gear box based on proportional hazard model. Electr. Power Sci. Eng. 2016, 32, 32–35. [Google Scholar]
- Chen, M.F.; Wang, Y.H. Introduction to Random Processes, 1st ed.; Higher Education Press: Beijing, China, 2007; pp. 145–147. [Google Scholar]
- Zhang, S.X.; Liu, Y.L.; Chen, J.X. Multi-attribute fuzzy decision-making method of test interval based on weibull proportional hazards model. J. Acad. Armored Force Eng. 2012, 26, 20–23. [Google Scholar]
- Liu, L.J.; Fu, Y.; Ma, S.W. Maintenance strategy for offshore wind turbine based on condition monitoring and prediction. Power Syst. Technol. 2015, 39, 3292–3297. [Google Scholar]
- Xiang, W.J. Research on Signal Analysis Methods and System for Fault Sources of Gearbox; Zhejiang University: Hangzhou, China, 2007. [Google Scholar]
- Gao, P. The Research on Preventive Maintenance Decision of Complex Equipment based on Reliability Analysis; Tsinghua University: Beijing, China, 2008. [Google Scholar]
- Wang, R.S. Functional Analysis and Optimization Theory, 1st ed.; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2003; pp. 66–68. [Google Scholar]
- Lu, X. Fundamentals of Mathematical Statistics, 1st ed.; China Statistics Press: Beijing, China, 1998; pp. 101–103. [Google Scholar]
- Chen, C. Reasearch on Shape Estimation for the Two-Parameter Gamma Distribution; Shandong University of Technology: Zibo, China, 2015. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).