Abstract
In this paper, the feasibility study to develop strain-based seismic design criteria applicable for the components of nuclear power plants are carried out as an alternative rule to the current stress-based criteria. To do this, two acceptance criteria are investigated through the detailed example of an application for the surge line nozzles in a nuclear steam supply system, which are known as one of the seismic fragile components in nuclear power plants. These strain-based seismic design criteria are primarily to prevent two types of failure modes, such as a ductile fracture and a cyclic fatigue-induced damage due to continuous large amplitude cyclic loads during seismic event. Through the example problem, the required procedures are described step-by-step with calculations of an accumulated plastic strain, triaxiality factor by the elasto-plastic seismic analysis using the finite element method. For a precise inelastic seismic analysis, the Chaboche kinematic and Voce isotropic hardening material parameters are identified by the test data and used for an inelastic material model. The results by the strain-based criteria are compared with those by the ASME (American Society of Mechanical Engineers) stress-based design criteria for a service level D limits. From the study, it is expected that the strain-based seismic design method investigated in this paper will be beneficial for the nuclear components, especially when the design basis earthquakes are large enough to cause severe plastic strains at a critical location.
1. Introduction
Since the Fukushima accident, the importance of earthquake design for beyond-design-basis earthquakes in nuclear power plants has been greatly emphasized. In the meantime, there is public demand requiring a higher level of the seismic design loads to assure the ultimate safety of nuclear power plants against strong earthquakes. These requirements place a great burden on the currently used elastic stress based seismic design approach. In fact, if a large earthquake occurs in a nuclear power plant’s structure, system, and components constructed with ductile materials, it will inevitably cause plastic deformation before failure. In this case, it is reasonable to use the strain-based design rather than stress-based design in the seismic design.
The ASME nuclear codes and standards provide a strain-based design criteria applicable to energy-limited events, such as drop impact, specifically for construction of high-level nuclear waste storage and transport containers [1,2]. The ASME Boiler and Pressure Vessel Codes Section III Mandatory Appendix XXVII, Paragraph XXVII-3340 provides the strain criteria for components, but says “This paragraph is under development. If strain criteria are provided in referencing design rules, they may be applied.” [3]. Recently, as an alternative to this rule, ASME has approved a new code case prescribing strain-based design criteria based on the elasto-plastic finite element analysis applicable for Class 1, 2, and 3 nuclear piping [4]. There are also efforts to develop the related Code Case of the nuclear piping systems by using the inelastic seismic analysis and strain-based design criteria [5]. These efforts are all related with application only for the piping systems.
The strain criteria newly implemented in the ASME Code Case is based on the cyclic fatigue-inducing damage as the seismic failure mode. Moreover, a strong earthquake is deeply related with low cycle fatigue-induced damage. In particular, when we use artificial seismic time histories generated from the design response spectrum at the floor where the components are installed, it is required that each excitation waveform should be generated, to result in (at least) ten maximum peak stress cycles [6], which may primarily invoke a fatigue-induced potential damage. Therefore, the strain-based ASME code case is expected to be very useful for the evaluation of a seismic design, in case the design-basis-earthquake invokes a large plastic strain in the nuclear piping systems. However, the scope of this rule is confined to be used for piping only, so that it needs to be extended to components, because the most critical location of the seismic fragile parts is the nozzle safe-end, which is classified as a part of the components.
At very low-reversing dynamic loads, it has been studied that the failure mode is almost the same as a ductile fracture [7]. Therefore, as a predictable seismic failure mode, the ductile fracture needs to be considered when the earthquake levels are very high and contain relatively low cycle frequency contents.
In this paper, strain-based seismic design criteria applicable for nuclear components, as alternative rules to the current stress-based criteria are studied, and the application procedures are investigated through the exampled application for the surge line nozzles in a nuclear steam supply system, which are known as one of the seismic fragile components in nuclear power plants. Through the example problem, the required procedures are investigated step-by-step with calculations of an accurate accumulated plastic strain, triaxiality factor (TF), and so on, by using the elasto-plastic seismic analysis with the finite element method.
The results of the strain-based criteria are compared with those of the ASME stress-based design criteria for service level D limits, to see the benefit of the strain-based seismic design method investigated in this paper.
2. Strain-Based Acceptance Criteria
This paper focus on strain-based acceptance criteria for a seismic structural integrity evaluation of component nozzles subjected to a Safe Shutdown Earthquake (SSE) load for which Level D Service Limits are specified. The strain-based acceptance criteria establishes plastic strain limits that maintain pressure boundary integrity in component nozzles subjected to SSE loads combined with other sustained loads, such as internal pressure and dead weight.
To assure the structural integrity against a SSE load, two acceptance criteria are proposed to prevent a ductile fracture failure and a fatigue-induced failure. These criteria need to be satisfied simultaneously.
2.1. Acceptance Criteria-1: Ductile Fracture Failure
When metal components experience very high plastic strain cyclic loading, the ductile fracture failure mechanism takes place as part of the very low cycle fatigue failure [7]. In this high plastic strain condition, material ductility dominantly depends on the stress triaxiality described in Section 2.3.
To prevent a ductile fracture failure during the SSE load, the acceptance criteria-1 is conservatively considered to require that the maximum product of the equivalent plastic strain and the associated TF value (at any time and at any location of the components) should be as follows [2]:
where:
In the above Equation (1), the εu is a true uniform strain limit or the true strain just prior to the onset of necking in a uniaxial tensile test at the coincident average through-wall temperature of the base or weld material. The εf is a true strain at fracture in a uniaxial tensile test at the coincident average through-wall temperature of the base or weld material. The total equivalent plastic strain, in Equation (2) is a sum of the maximum plastic strain due to the seismic anchor motion (SAM) and an accumulated equivalent plastic strain during time t.
2.2. Acceptance Criteria-2: Fatigue-Induced Failure
When the seismic failure in metal components is dominated by the fatigue mechanism due to continuous reversing dynamic cycles of seismic impact loads, the fatigue damage may be initiated on any location of surface in the form of small surface cracks. To prevent the seismic fatigue-induced damage failure mode, this paper extents the strain-based acceptance criteria of ASME Code Case [4] (currently applicable to only the piping system) to component nozzles by the modified expression with the maximum total equivalent plastic strain and the associated averaged TF value at any nozzle location as follows:
where:
εeq = total equivalent strain;
= equivalent elastic strain for sustained loads;
= equivalent elastic strain for SAM;
= equivalent elastic strain for seismic inertia load;
εa = the allowable true strain amplitude as defined in Equation (7);
t1 = initiation time of an equivalent plastic strain occurrence;
E = Young’s modulus obtained from Figure I-9.1 or I-9.2 of ASME Section III Mandatory Appendix I as applicable [8];
Ky = Ea/E, where Ea is Young’s modulus used in numerical analysis;
Sa(N) = allowable stress amplitude Sa for N cycles of load and can be obtained from Figure I-9.1 or I-9.2 of ASME Section III Appendix I [8];
N = number of cycles invoking significant accumulations of an equivalent plastic strain; N shall not be less than 10;
a = 2.3 for Sa values from ASME Section III Appendices, Mandatory Appendix I, Figure I-9.1 [4];
a = 1.5 for Sa values from ASME Section III Appendices, Mandatory Appendix I, Figure I-9.2 [4].
In Equations (1) and (3), the left side items are called as the seismic demand (SD) value, which will be calculated by the elasto-plastic seismic time history analysis. As shown in Equation (3), the triaxiality factors, which are in conditions of a plastic strain and larger than 1.0, are only considered in calculating the averaged value. Actually, it has been known that the material damage is accelerated under multi-axial stress and plastic strain conditions. However, it is not clear in dynamic conditions such as earthquakes, which are the reversing dynamic loads. The ASME Boiler and Pressure Vessel Codes Section III Appendix FF [2] allows either the peak TF value at a location (time independent) or the instantaneous TF value at a location for the strain-based acceptance criteria for energy-limited events, such as the impact loads. However, when the seismic demand value required to prevent fatigue-induced failure is determined by the product of the maximum peak TF value at a location (time independent) and the maximum , it may result in excessively conservative seismic evaluation, and may lose the benefit of the strain-based criteria, which employs a high-cost elasto-plastic seismic time history analysis.
Total equivalent strain, is sum of the elastic and the plastic equivalent strain at a critical location to be evaluated, as shown in Equation (4). The elastic equivalent strain is the sum of the maximum equivalent elastic strain by normal sustained loads, SAM, and seismic inertia response as shown in Equation (5). Especially for the elastic equivalent strain by the seismic inertia response, the maximum value throughout the time history response should be considered when the isotropic hardening material model is used for numerical analysis because the maximum yield value changes due to the cyclic hardening behavior of metal during seismic event. As shown in Equation (6), the total equivalent plastic strain is the sum of the equivalent plastic strain by the SAM and the accumulated equivalent plastic strain up to time t.
2.3. Triaxiality Factor
The stress triaxiality factor is based on the principal stresses, and is the sum of three principal stresses (first stress invariant) divided by the effective (von Mises) stress at a location as follows:
In calculating the seismic demand values based on the strain, the equivalent plastic strain correctly calculates the strain condition on the von Mises yield surface in the absence of damage (crack initiation or flaw propagation). However, real materials experience damage under plastic deformation, which is accelerated when multi-axial tensile stress conditions exist [9]. To consider this effect, the concept of a stress TF is adapted as shown in Equation (8). This concept has been proposed and widely discussed by many researchers [9,10,11].
Many theories and formulations have been proposed to account for material damage under multi-axial stress and plastic strain conditions. However, the chosen methodology employed in these criteria, as discussed in EPRI (Electric Power Research Institute) Report NP-1921 [9], uses the TF in a simple formulation.
To calculate the seismic demand values from Equation (1) and (3), the determination of the TF values to be multiplied by the equivalent strain is an important issue in actual seismic time history response when combined with sustained loads and seismic anchor motion.
As fundamental requirements, the strain-based acceptance criteria should be implemented using strains calculated from an analytical model with suitable convergence and sensitivity studies that demonstrate the accurate capability of the model. For calculations of the accurate seismic-induced accumulated equivalent plastic strains at a nozzle, including the safe-end, the elasto-plastic seismic time history analysis should be performed with a coupled analytical model, including both the nozzle and the connected piping systems, because the seismic inertia response of the piping systems will dominantly invoke the strain response at a nozzle.
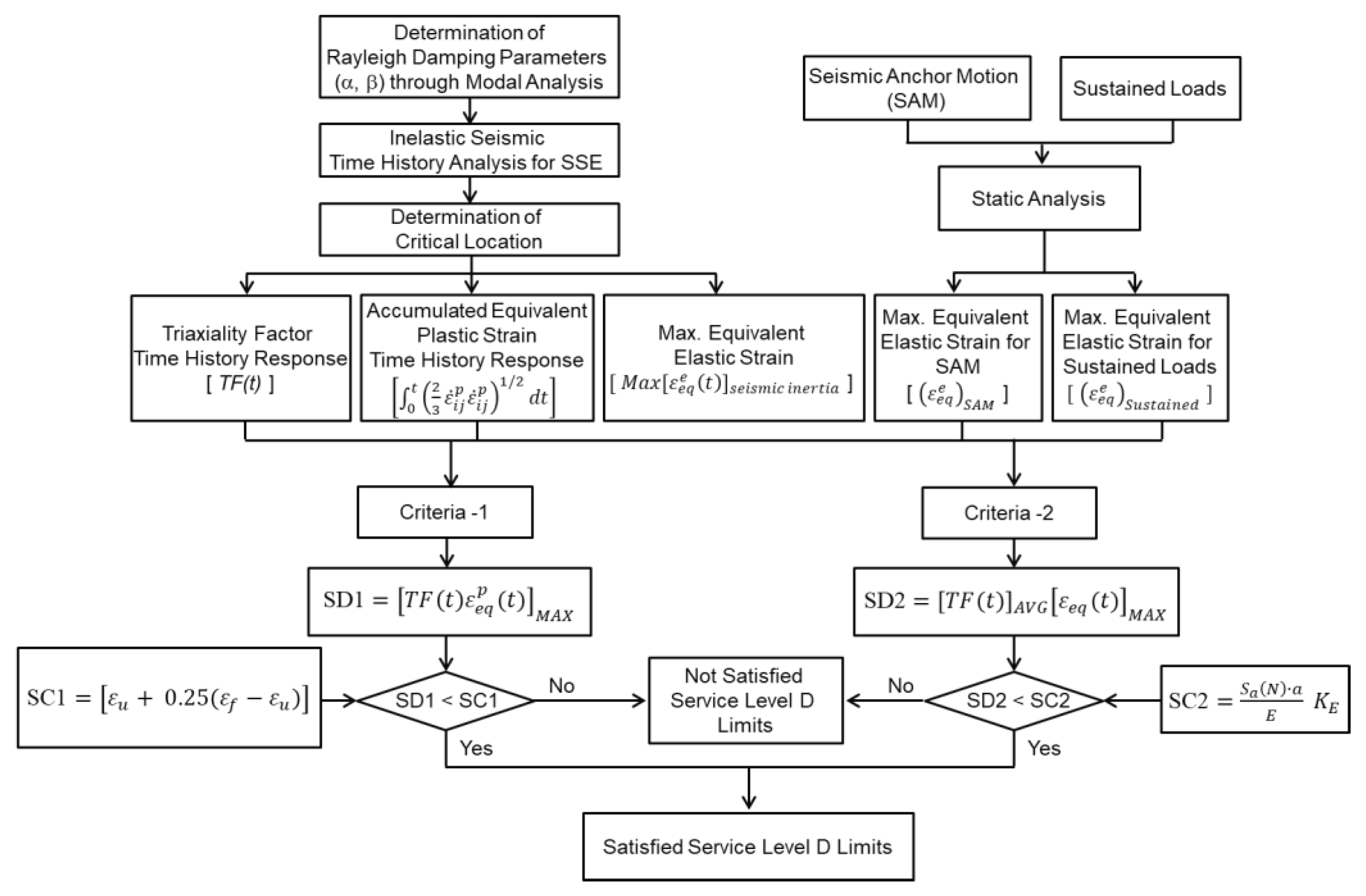
Figure 1 presents the proposed overall procedures of the strain-based seismic design by inelastic seismic analysis applicable for components of NPPs (Nuclear Power Plants).
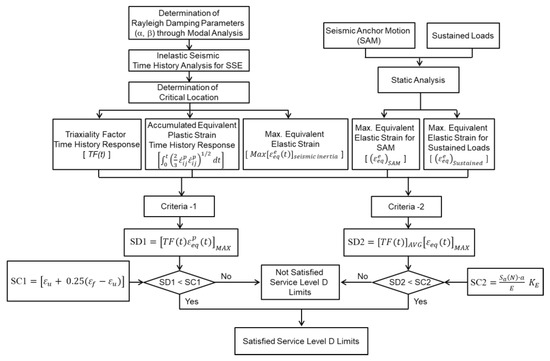
Figure 1.
Proposed procedures for strain-based seismic design.
3. Examples of Application
3.1. Description of Example Problem
An example of an application used in this study is focused on the pressure retaining nozzles, which are categorized as one of the seismic fragile components in the nuclear steam supply system. Because the seismic responses on the nozzles are dominantly due to piping seismic behavior, they are required to use a coupled seismic analysis model, including both nozzles and their connected piping. In this study, the surge nozzles (i.e., pressurizer surge nozzle and hot leg surge nozzle) connected to the surge line piping are investigated as an example.
The used damping value is 4% for the piping system as required by the United States Regulatory Commission, Regulatory Guides 1.61 [12] for Safe Shutdown Earthquake (SSE). For the modeling of damping, the proportional damping (Rayleigh damping) is used [13]. As well known, the selection of the frequency range in the Rayleigh damping can significantly affect inelastic seismic response calculations. In this study, the first frequency is defined as the first modal frequency and the second frequency is conservatively defined to be 50 Hz, which can cover the dominant seismic spectrum frequency.
The internal pressure of 15.5 MPa is applied as a sustained normal load. The deflection due to dead weight of piping is neglected because the used hangers are all constant spring hangers, which compensate the dead weight of piping. The commercial computer program ANSYS ver.15 [14] was used.
3.1.1. Coupled Finite Element Model and Boundary Conditions
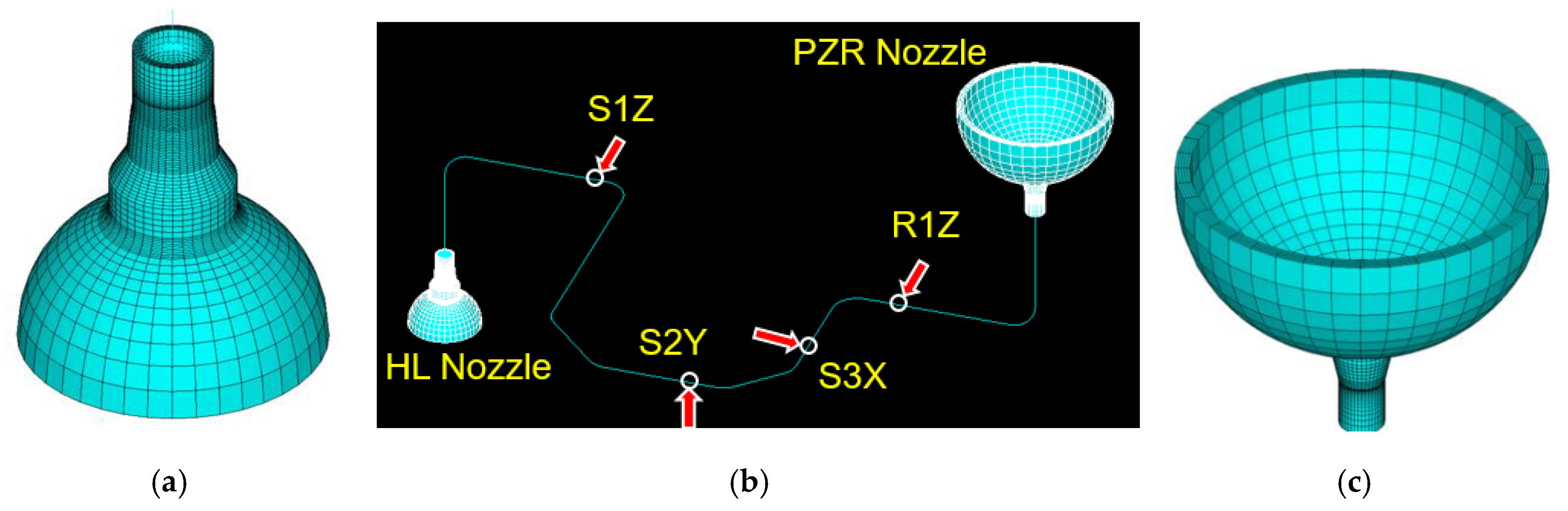
Figure 2 presents a coupled finite element model used in this study. This model consists of a surge line piping and two nozzles, which are: a pressurizer surge nozzle at the top end and a hot leg surge nozzle at the bottom end of a surge line pipe. The surge line pipe has the outer diameter of 330 mm and the thickness of 33 mm. The curvatures of all elbows is 457 mm. The slope of a run pipe in a horizontal plane is neglected in this study. As shown in Figure 2 are three snubbers (S1Z, S2Y, S3X), and one sway-strut (R1Z) in the surge line piping system. They are assumed to be a rigid support and excitation points for the seismic analysis. Moreover, it is assumed that the seismic inputs are also applied at the end of the nozzles with the same effects through the pressurizer skirt support and the hot leg piping.
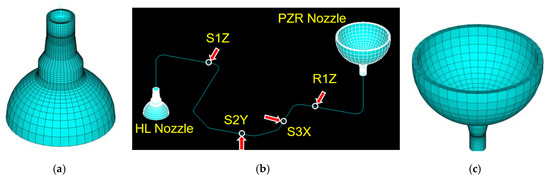
Figure 2.
Used coupled finite element seismic analysis model: (a) zoomed hot leg nozzle; (b) coupled model; (c) zoomed pressurizer surge nozzle.
To reduce the numerical computing time, the surge line piping is modeled using three dimensional pipe elements of PIPE289 for the straight section and of ELBOW290 for the elbow section. The nozzles are modeled using three dimensional solid element of SOLID185, which has eight nodes with three degree of freedom at each node. In nozzle modeling, the nozzle part connected to the component is extended enough to minimize the end effects with an equivalent curvature as shown in Figure 2. The connection between the pipe element and solid element is modeled using the multipoint constraint element of MPC184 having the rigid beam option in ANSYS.
The finite element models for the nozzle are generated with fully solid mapped mesh, and it is confirmed that the mesh size is enough to assure the stabilized seismic response by the sensitivity study, especially at critical locations.
3.1.2. Material Properties
The materials used for the surge line piping and the nozzle are Type 316 stainless steel and the low alloy steel of SA508 Grade 3 Class 1 respectively. Table 1 presents the physical and mechanical properties at 316 °C used in this paper.

Table 1.
Physical properties used for analysis (at 316 °C).
3.1.3. Inelastic Material Models
The used inelastic material models are the Chaboche three-decomposed kinematic hardening model combined with the Voce isotropic hardening model [15], which are available in ANSYS. The constitutive equation for revolution of back stress tensor , in the Chaboche model can be expressed as follows:
where Ck and γk (k = 1–3) are material constants and is an accumulated plastic strain expressed as follows:
The constitutive equation for revolution of drag stress, in the Voce isotropic hardening model can be expressed as follows:
where b and Q are material constants.
To assure the inelastic seismic analysis, the material parameters required in the above equations are identified by the test data. The summaries of inelastic material parameters used in this paper are presented in Table 2.

Table 2.
Parameters for inelastic material models.
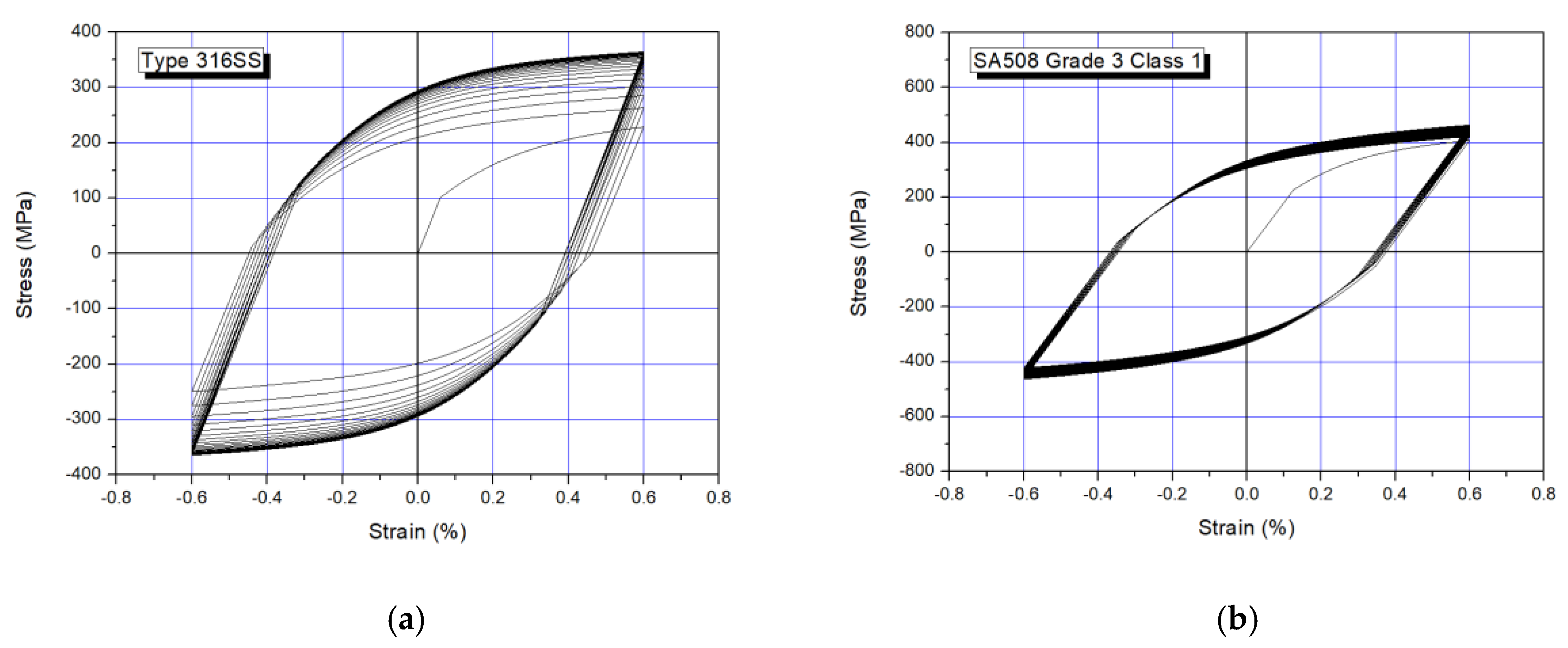
Figure 3 shows the hysteretic behavior simulated by the strain-controlled for both material constitutive equations of Equations (7)–(9). As shown in the figure, Type 316 SS reveals significant isotropic hardening behavior whereas the SA508 Grade 3 Class 1 steel stabilizes quickly after a few cycles without the change of yield surface.
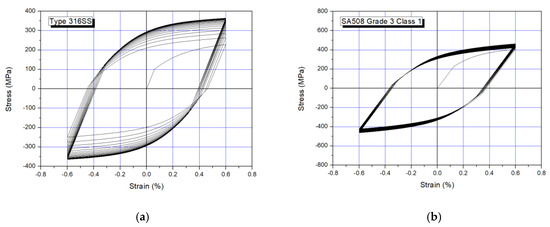
Figure 3.
Simulation results of cyclic behavior: (a) Type 316 SS; (b) SA 508 Grade 3 Cl 1.
3.1.4. Seismic Input Motions
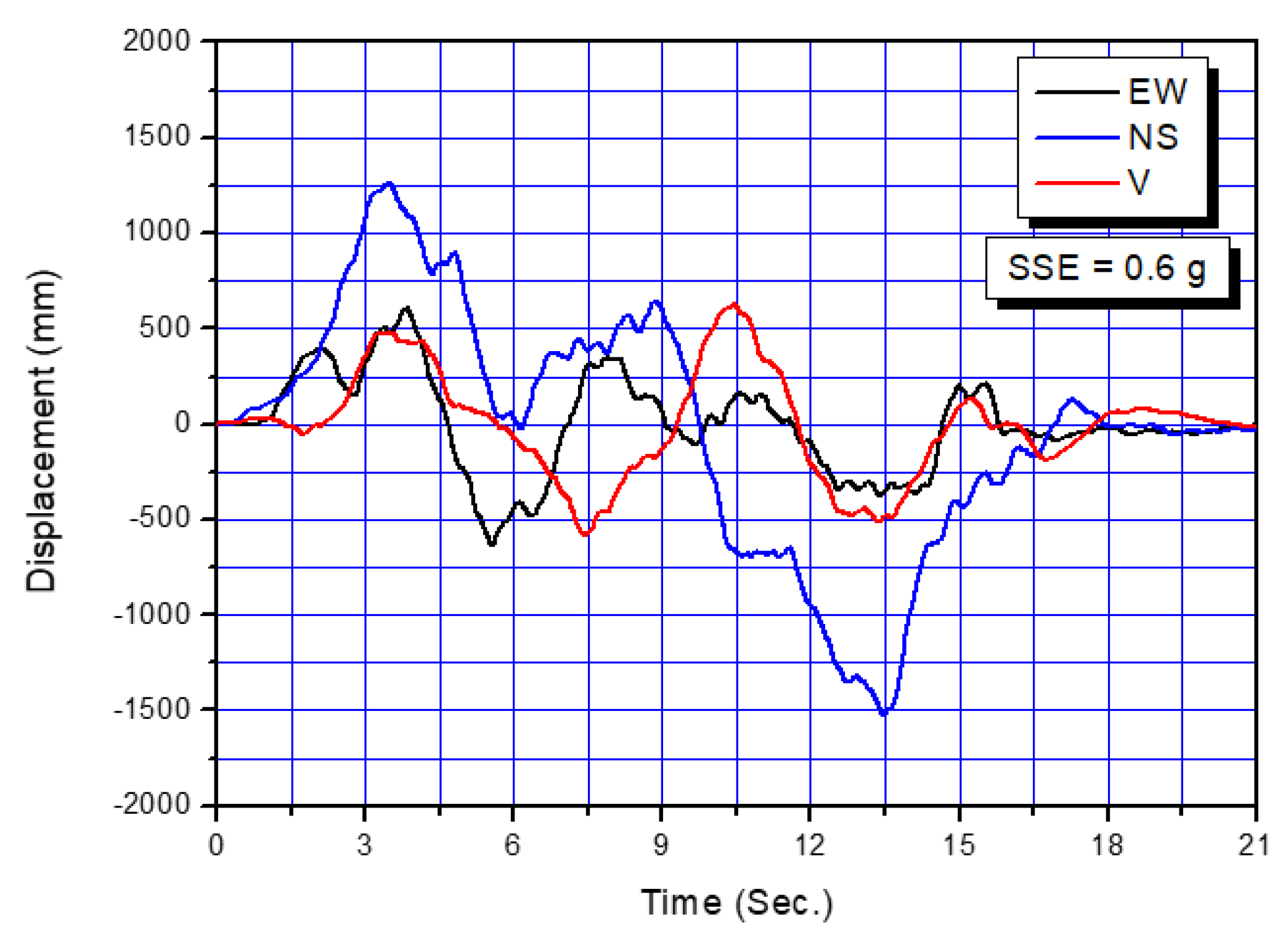
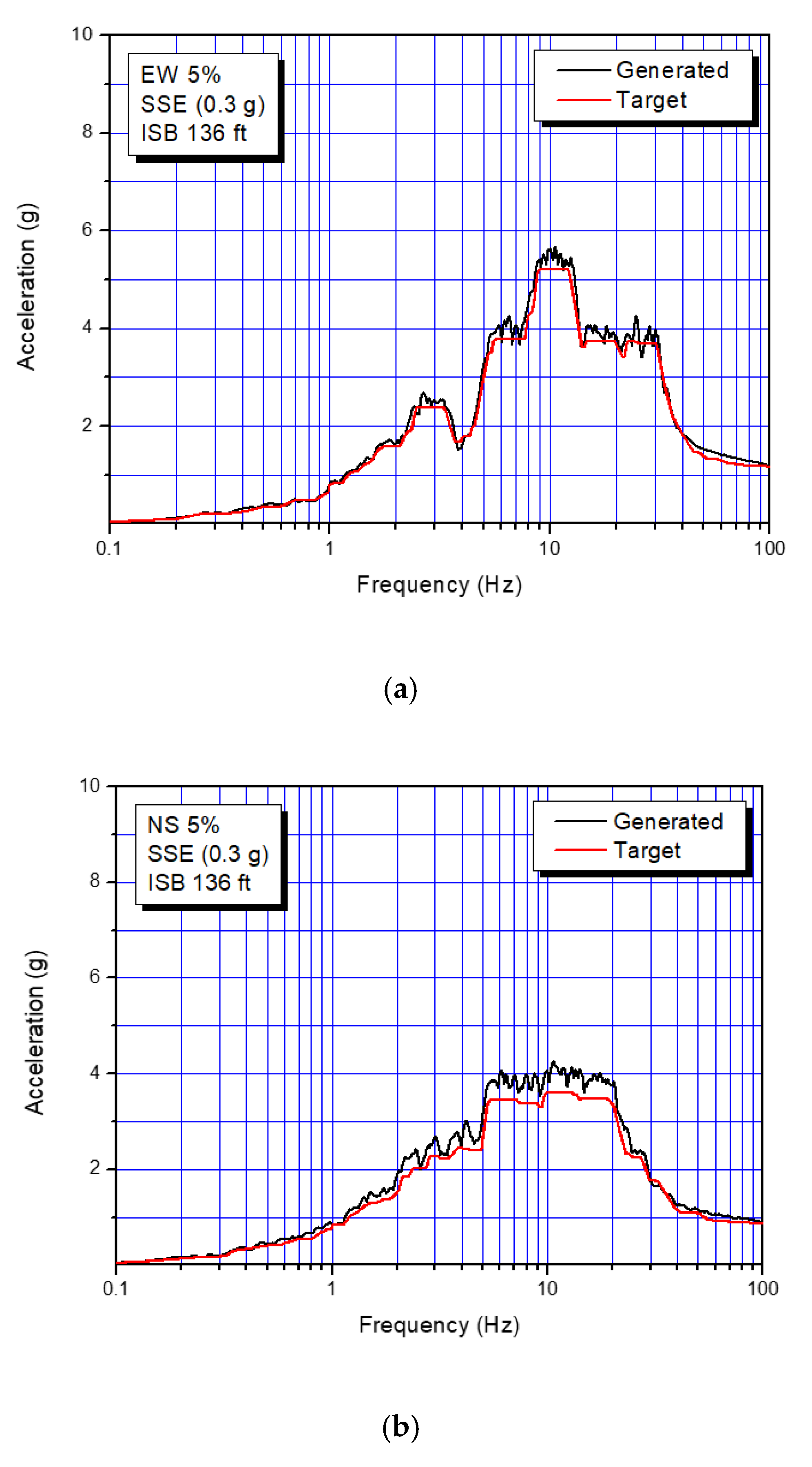
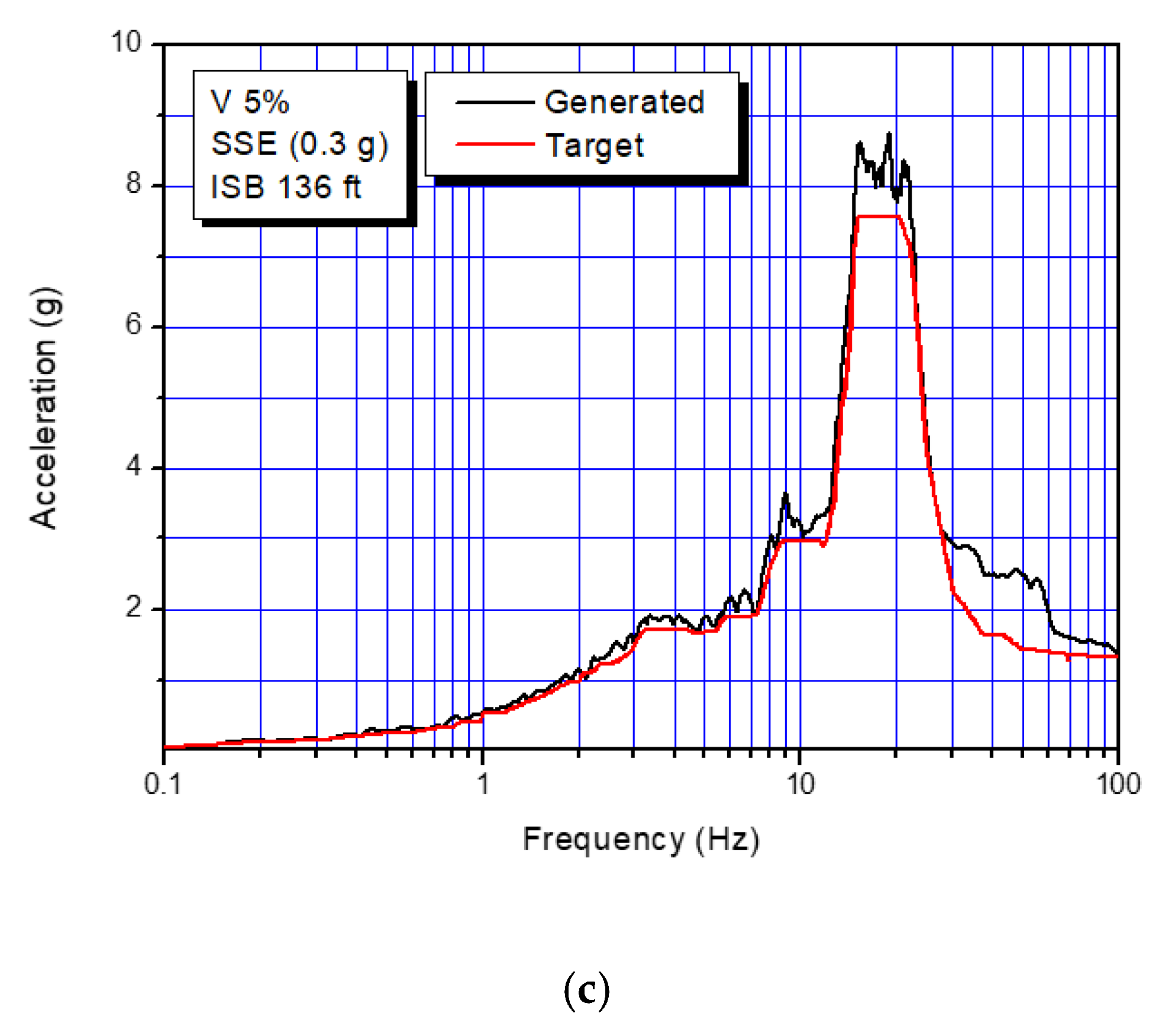
In this study, two times of 0.3 g, Safe Shutdown Earthquake (SSE) is considered as a design seismic load in order to investigate the feasibility of the strain-based seismic design criteria. The seismic displacement input motions used in this study are presented in Figure 4 for each direction (two horizontal and one vertical). These artificial seismic time history motions are obtained from the enveloped design floor response spectra from all design response spectrum for each support location, and are simultaneously applied to all support locations for seismic analysis. Figure 5 presents the enveloped design response spectra at an elevation of the surge line. As shown in the figure, it is confirmed that the generated response spectra from the artificial time histories (ATH) used in analysis can envelop the target design response spectra with sufficient margin.
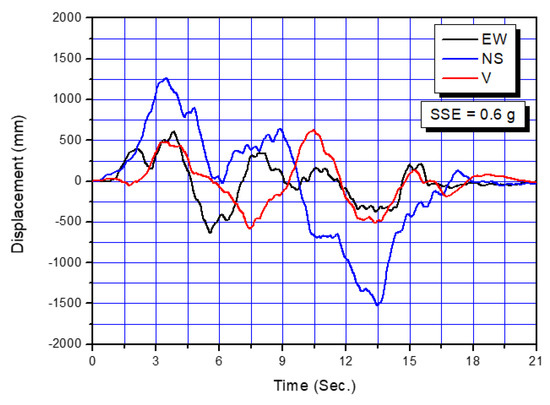
Figure 4.
Displacement seismic input motions in case of Safe Shutdown Earthquake (SSE) = 0.6 g.
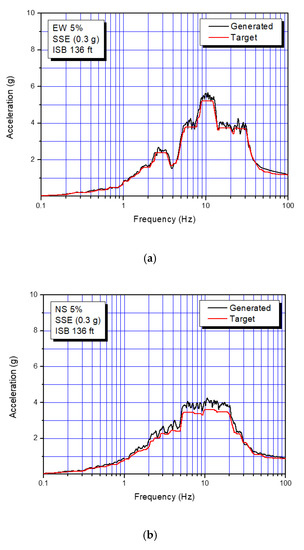
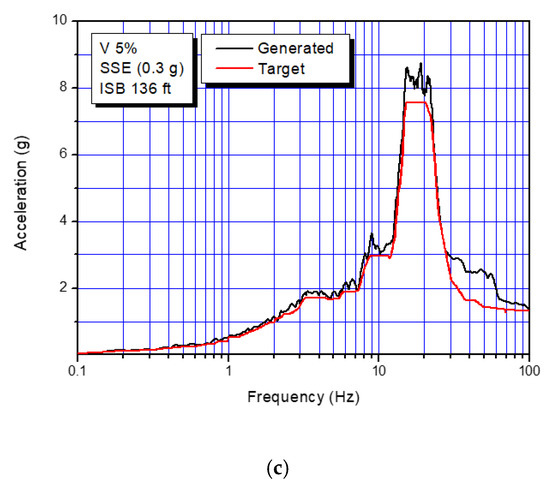
Figure 5.
Design response spectra of target and generated from artificial time histories (ATH) for each direction: (a) EW (East-West); (b) NS (North-South); (c) V (vertical).
The time interval used for the seismic time history analysis is 0.005 s, corresponding to a sampling frequency of 200 Hz, i.e., Nyquist cut-off frequency of 100 Hz. Three directional input motions of Figure 4 are simultaneously applied to all supports and nozzles shown in Figure 2 for seismic inertia response analysis.
In consideration of the seismic anchor motions for multi-supports, which are used for an equivalent static seismic analysis, the anchor motions at the snubbers and sway strut are assumed to be in-phase motion due to the common floor level. Table 3 presents the displacements for seismic anchor motions at hot leg, snubbers, and sway-strut, and pressurizer (PZR) support. For an equivalent static seismic analysis, the most severe combinations of the seismic anchor motions in Table 3 are used in order to result in a conservative seismic response.

Table 3.
Displacements for seismic anchor motions used in analysis.
3.1.5. Modal Analysis and Damping
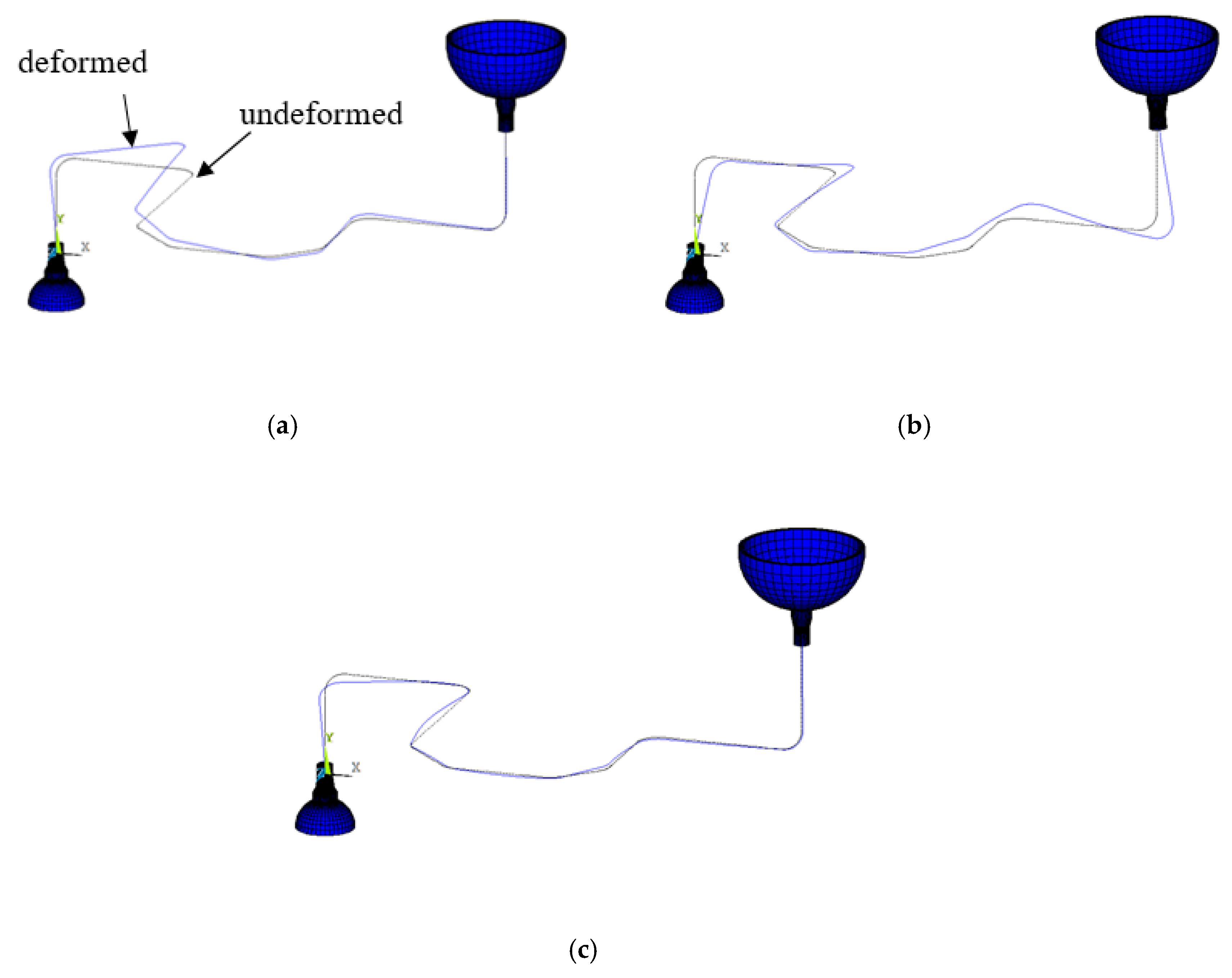
Table 4 presents the results of modal analysis. As shown in table, the first modal frequency is 7.77 Hz in dominantly vertical direction (V). For horizontal directions, the dominant modal frequencies are 20.37 Hz for the EW direction and 48.02 Hz for the NS direction. Figure 6 shows the representative mode shapes corresponding to these modal frequencies.

Table 4.
Summaries of modal analysis.

Figure 6.
Representative mode shapes: (a) 1st mode (7.77 Hz, EW); (b) 5th mode (20.34 Hz); (c) 10th mode (48.02 Hz, NS).
Actually, critical seismic fragile parts will be component nozzles in the piping system and their seismic responses are basically affected by the dynamic response characteristics of the piping system. Therefore, determination of the controlling analysis parameter, such as damping model is very important in the seismic response analysis, especially component nozzle analysis. In this paper, the proportional damping (Rayleigh damping) model is used for the seismic response analysis. In this damping model a damping matrix [C] is formed by a linear combination of the mass [M] and stiffness matrix [K] as follows [13]:
In Equation (12), α and β are proportional damping coefficients are given by:
where f1, f2 and ξ indicate the minimum, maximum frequency, and a critical damping ratio respectively. From the expression of Equation (13), the Rayleigh damping can be expressed with function of frequencies as follows:
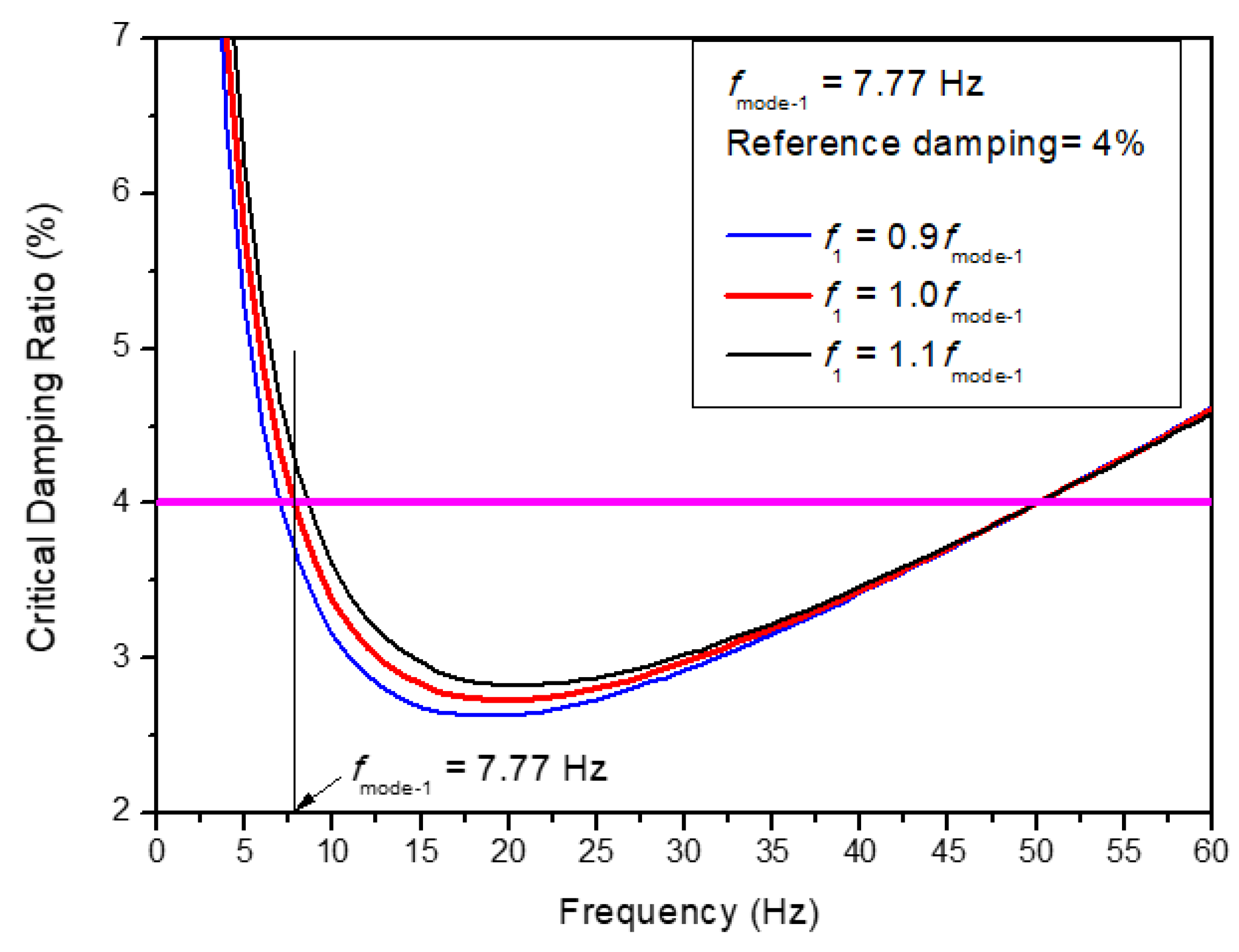
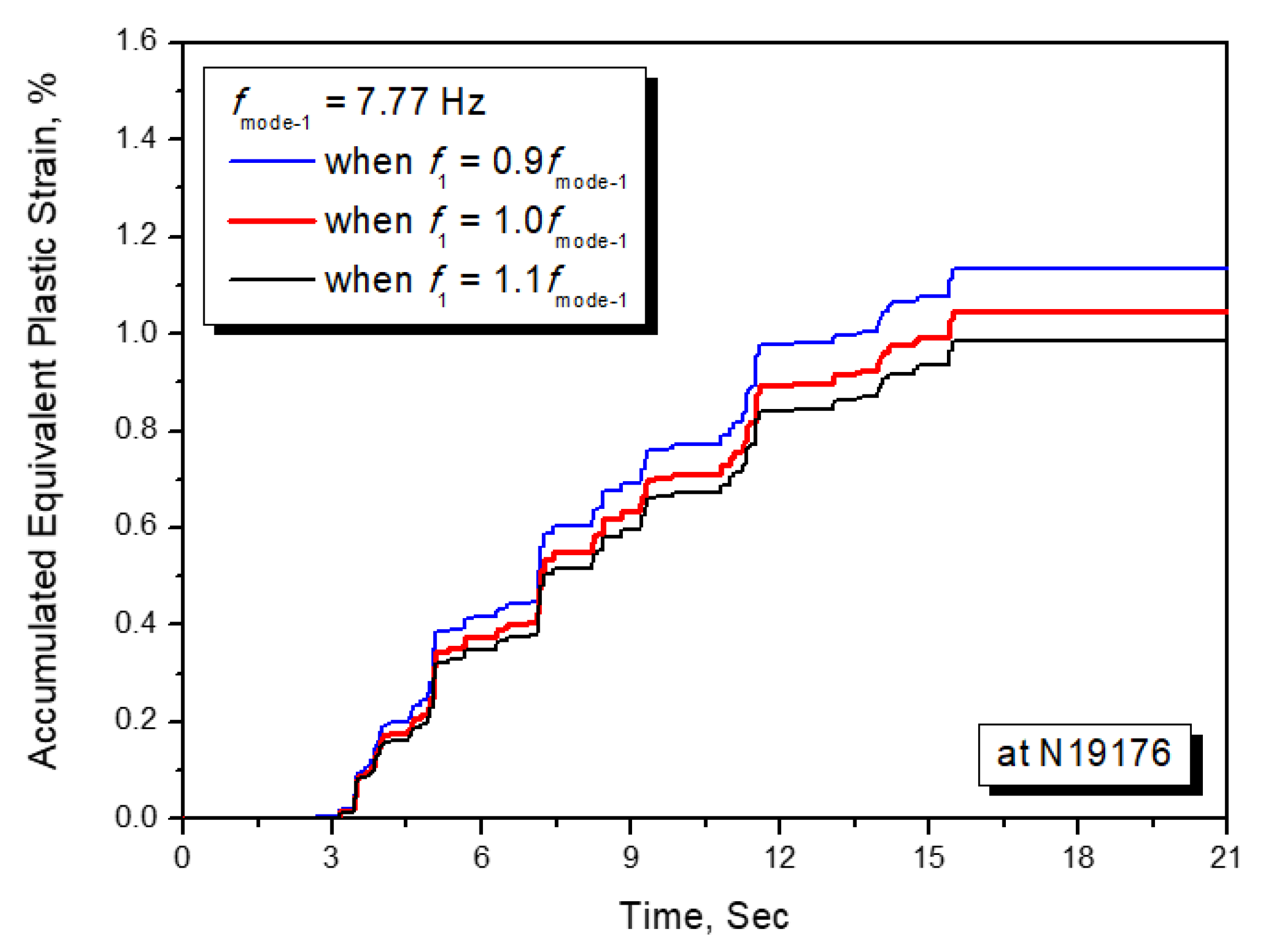
Figure 7 presents the sensitivity of the frequency parameters of f1 and f2 on the Rayleigh damping for 4% critical damping ratio used in this paper with f2 = 50 Hz. As shown in the figure, when the minimum frequency, f1 is used to be 10% less than the first modal frequency of fmode-1 = 7.77 Hz, the damping value will be underestimated to be 3.7%, and when the minimum frequency is 10% larger than the first modal frequency, then the damping will be overestimated to be 4.3%. This damping uncertainty is investigated on the calculation of the accumulated equivalent plastic strain in Section 3.2.2.
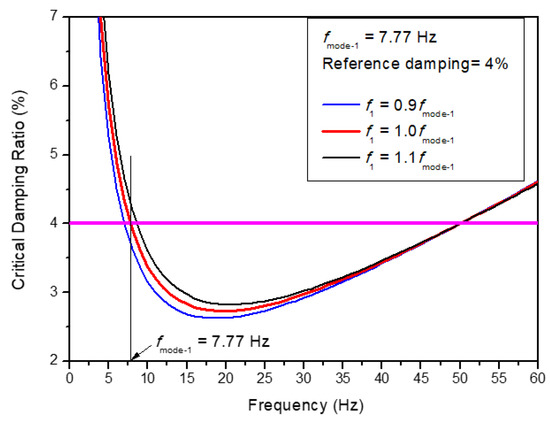
Figure 7.
Sensitivity of the minimum frequency, f1 on the Rayleigh damping.
3.2. Strain-Based Acceptance Criteria-1
3.2.1. Critical Location for Evaluation
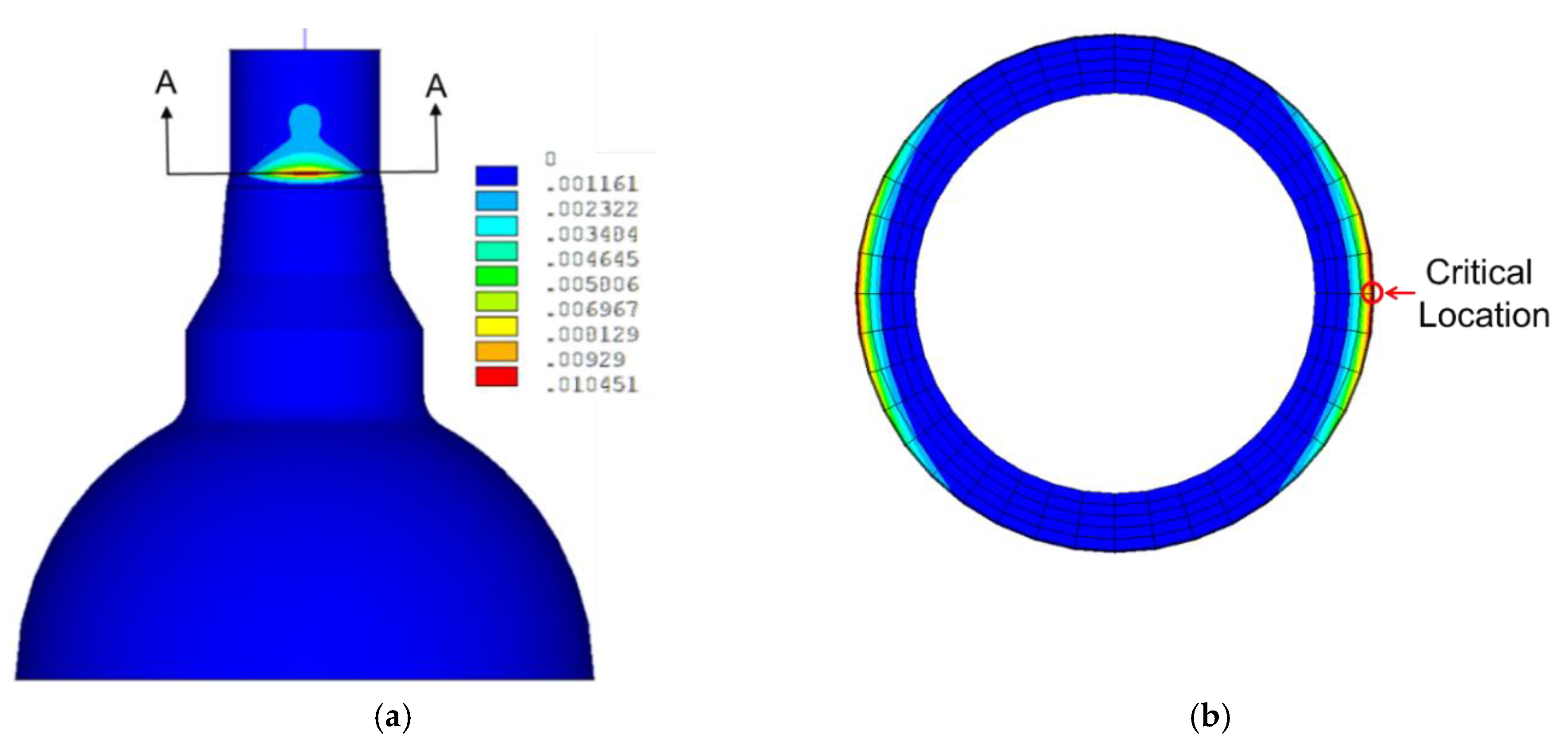
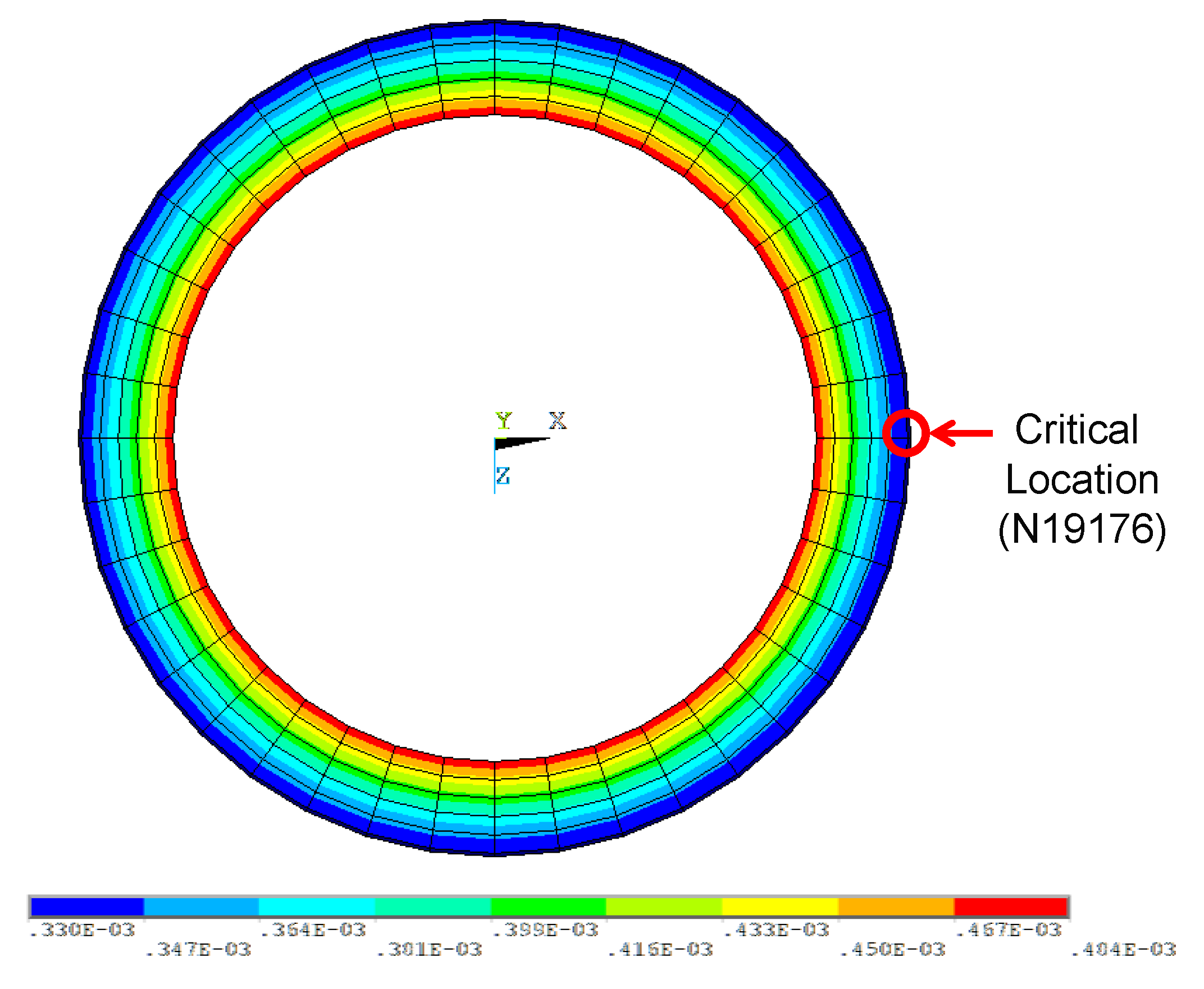
Figure 8 reveals the contour of the accumulated equivalent plastic strain at the end time of the seismic input motion. From the figure, we can define that the safe-end part of the hot leg surge nozzle is a critical location, which represents the maximum value of the accumulated equivalent plastic strain. In this study, the node number 19176, which is located on outer surface shown in Figure 8b, is selected as the most seismic fragile location to be evaluated by the strain-based seismic criteria.
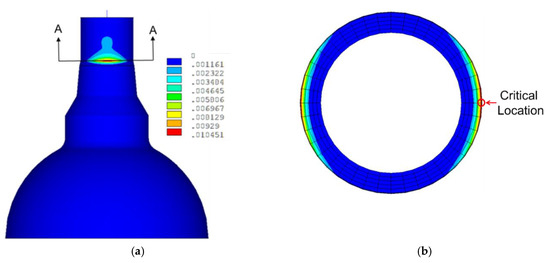
Figure 8.
Contour plots of an accumulated equivalent plastic strain at end of time: (a) at hot leg surge nozzle; (b) sectional contour (A-A).
3.2.2. Accumulated Equivalent Plastic Strain
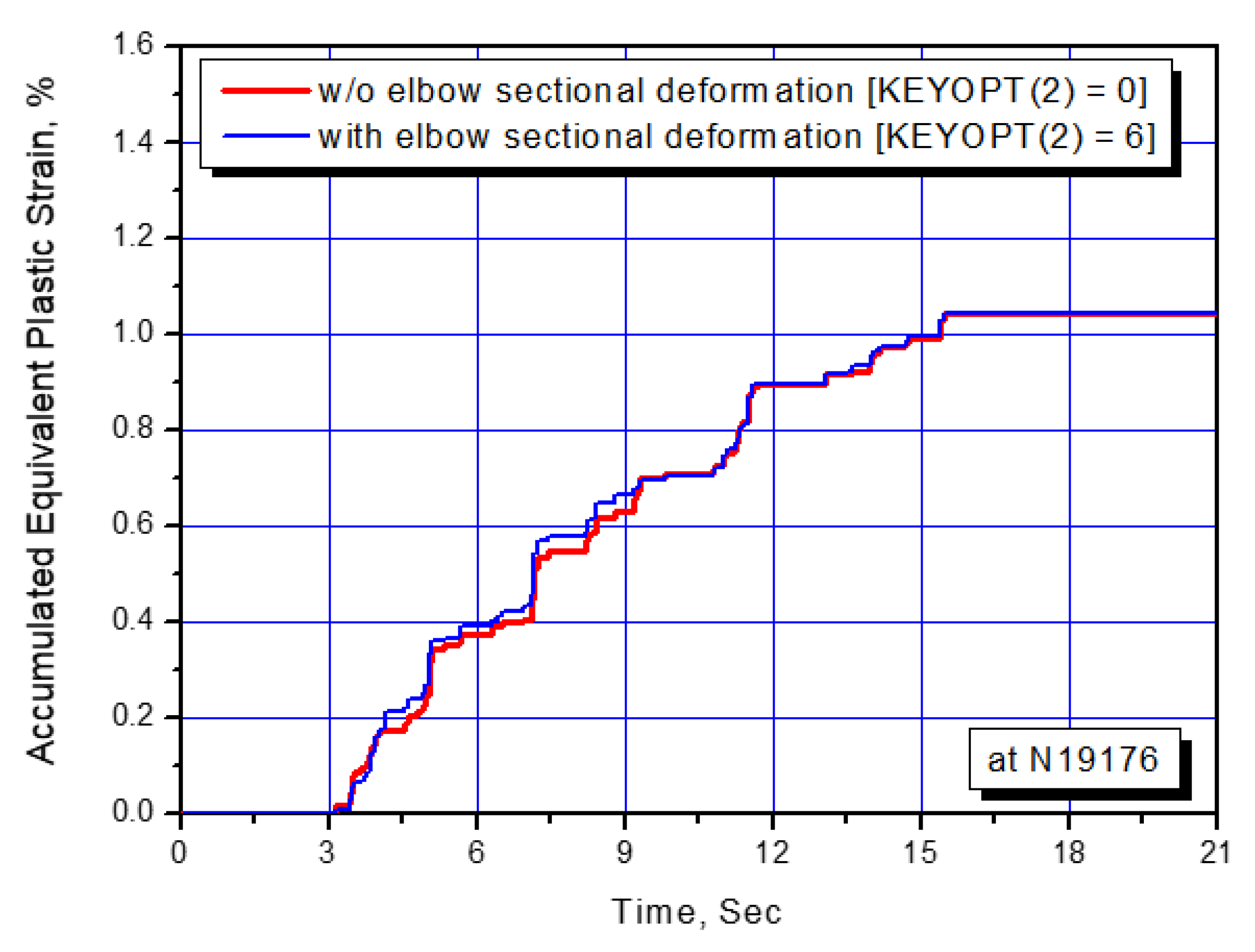
Figure 9 presents the time history responses of the accumulated equivalent plastic strain at the critical location. Even though the pipe thickness of 33 mm used in this example is thick, the sensitivity of the cross-sectional deformation including radial expansion, ovalization, and warping at elbow is investigated, but it is found that the sectional flexibility consideration (KEYOPT (2) = 6 option in ANSYS) at elbow is negligible for the accumulated equivalent plastic strain response as shown in Figure 9.
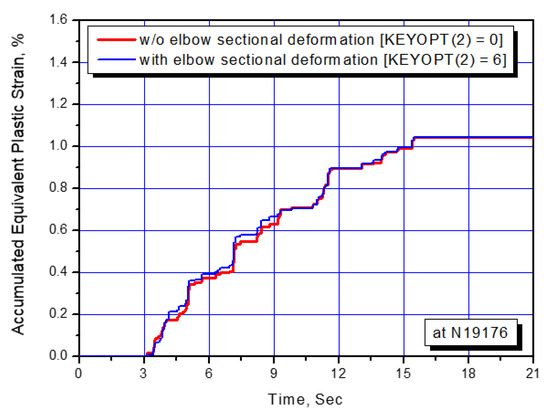
Figure 9.
Accumulated equivalent plastic strain response at critical location.
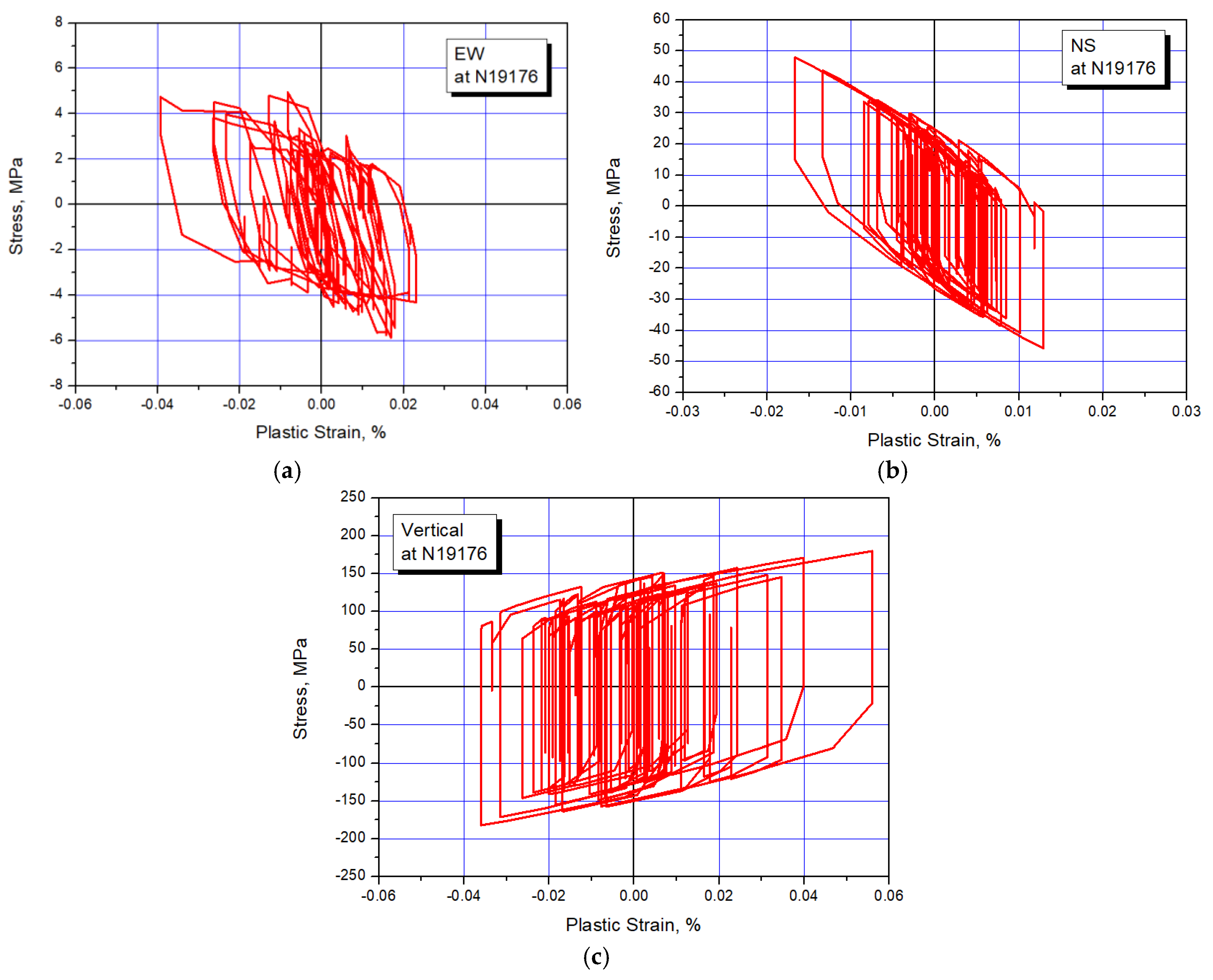
Figure 10 presents the hysteretic stress-plastic strain behavior at the critical location. As shown in the figure, we can see that the used Type 316 stainless steel significantly reveals both kinematic hardening and isotropic hardening, and the maximum elastic strain is changing when an isotropic hardening behavior occurs.
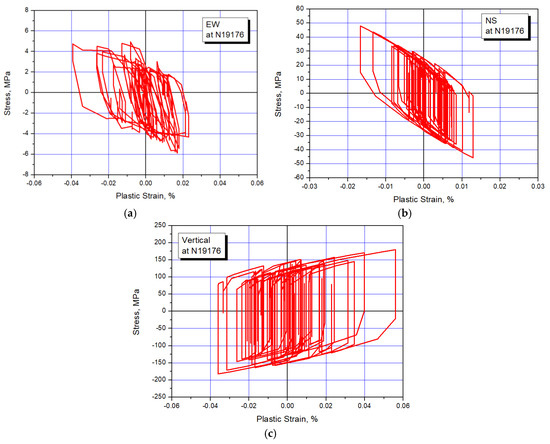
Figure 10.
Cyclic stress-plastic strain response at critical location: (a) EW; (b) NS; (c) vertical.
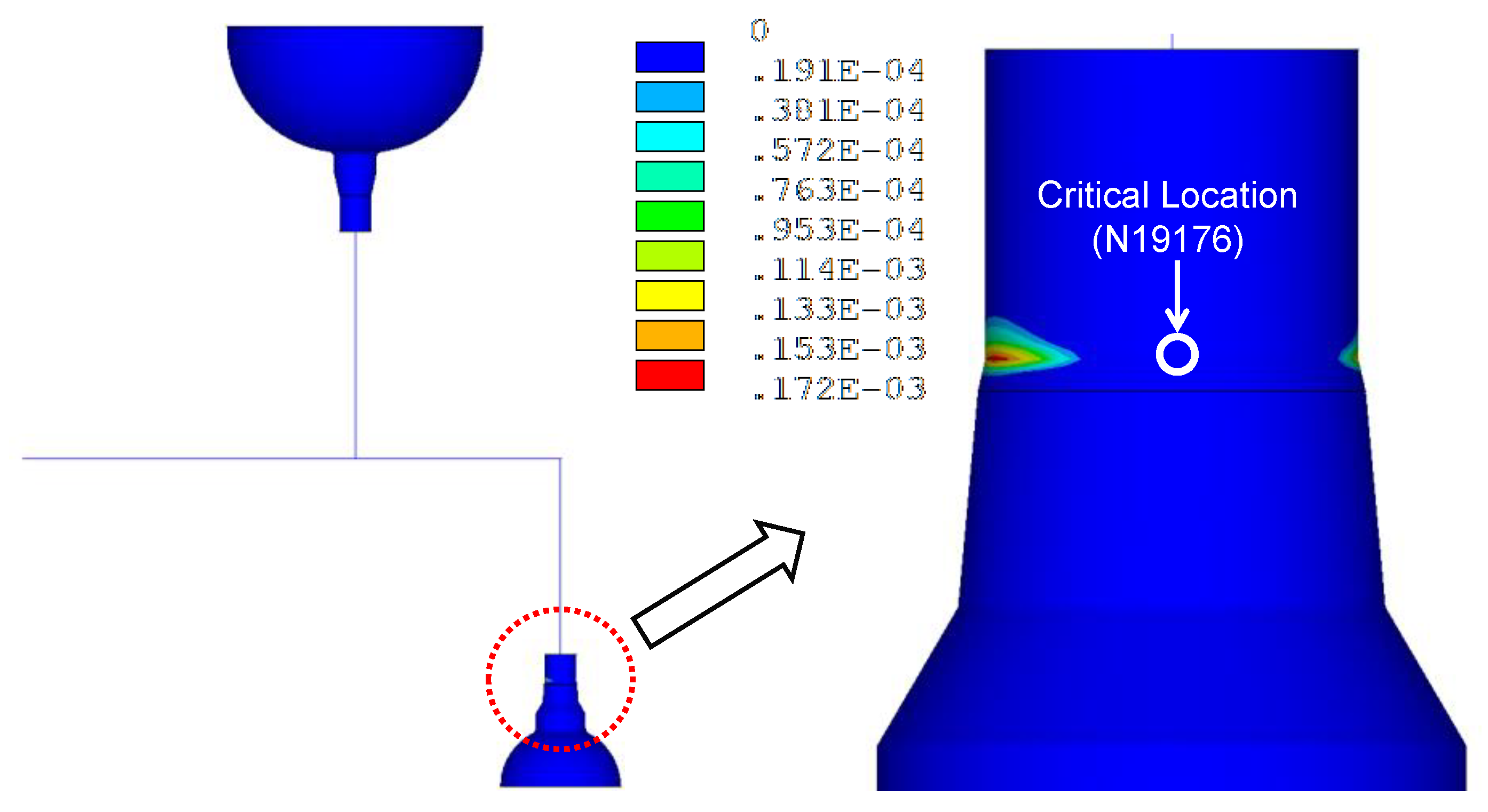
Figure 11 presents the distribution of an equivalent plastic strain due to the seismic anchor motion. As shown in the figure, the maximum equivalent plastic strain is 0.0172% at the hot leg surge nozzle, but the location is not coincident with the critical location. The plastic deformation does not occur at a critical location as shown in the figure. Therefore, there is no additional plastic strain due to the SAM in calculation of the seismic demand at the critical location.
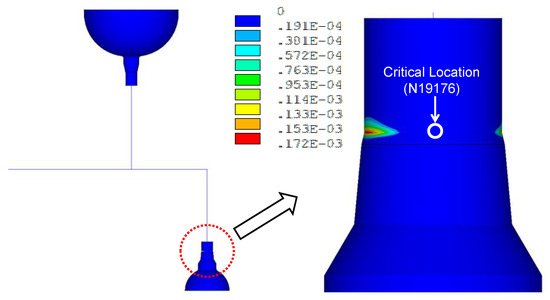
Figure 11.
Equivalent plastic strain contour for seismic anchor motion.
To investigate the sensitivity of the Rayleigh damping parameter of f1 in Equation (13) on the calculation of an accumulated equivalent plastic strain, the inelastic seismic analyses are carried out with ±10% variations of f1 with a reference frequency of fmode-1 = 7.77 Hz. Figure 12 presents the results of the accumulated equivalent plastic strain time history responses for three cases. As shown in the figure, the calculated maximum accumulated equivalent plastic strains vary from 0.986% to 1.133% according to the variation of the Rayleigh damping parameter, f1. This implies that the Rayleigh damping parameter, f1 should be taken less than the dominant first modal frequency for a conservatism of a seismic design.
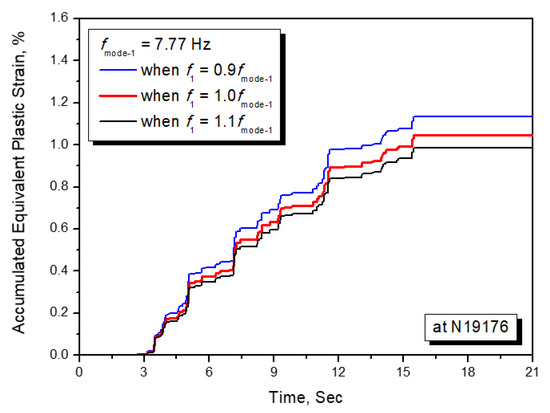
Figure 12.
Accumulated equivalent plastic strain response at critical location.
3.2.3. Triaxiality Factor
The TF does not indicate that plastic straining is occurring. It merely indicates the associated stress state. Therefore, only the TF calculated while plastic straining is occurring is applicable in the strain-based acceptance criteria. When plastic straining has stopped, the TF simply indicates the elastic stress state. The strain-based acceptance criteria indicates that a minimum TF of 1.0 (positive value) must be used. Using a minimum factor of 1.0 conservatively ignores the potential strengthening/damage inhibiting effects of compressive stresses [1].
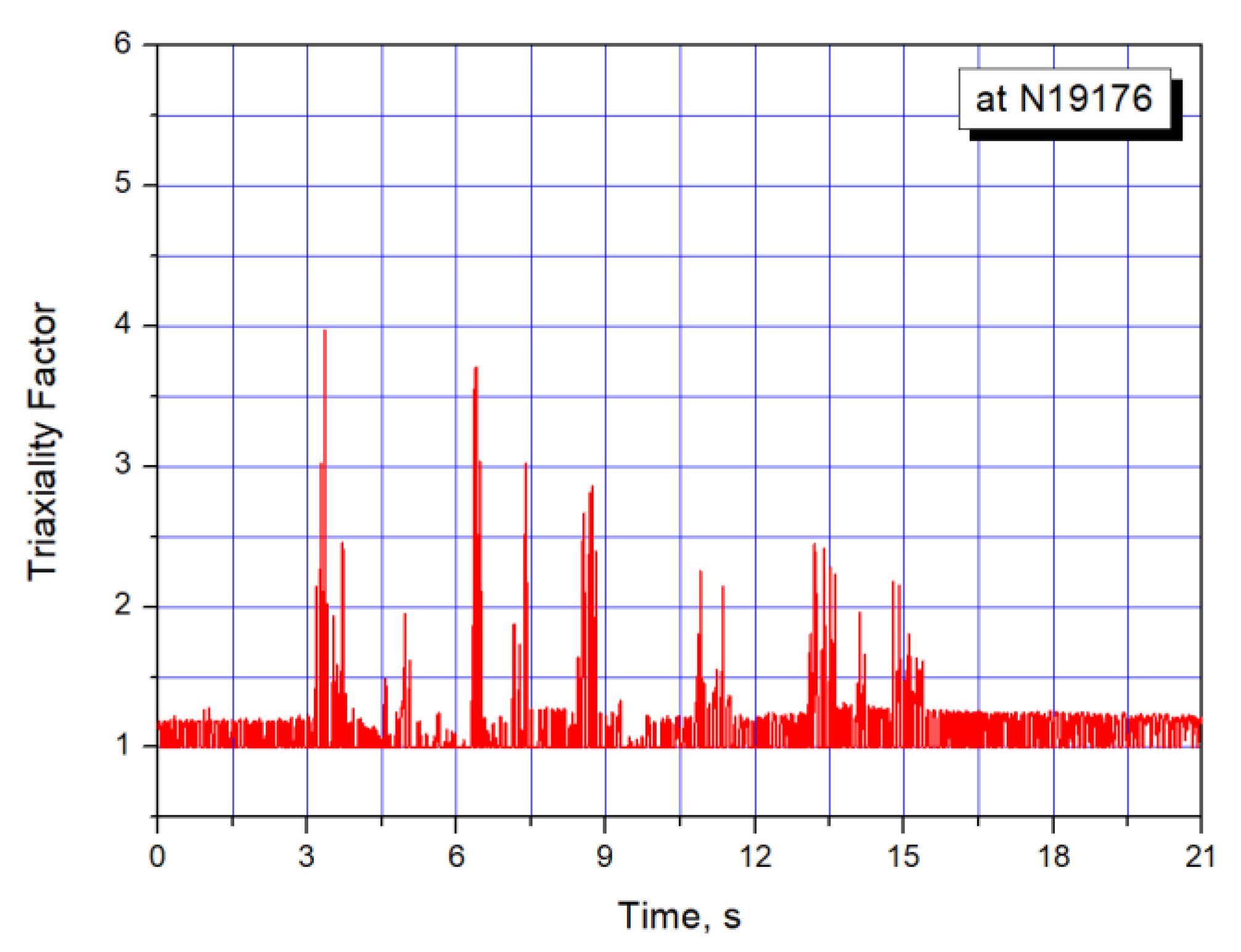
Figure 13 presents the instantaneous TF calculated at each time step during the seismic event. The TF value less than 1.0 is set to 1.0.
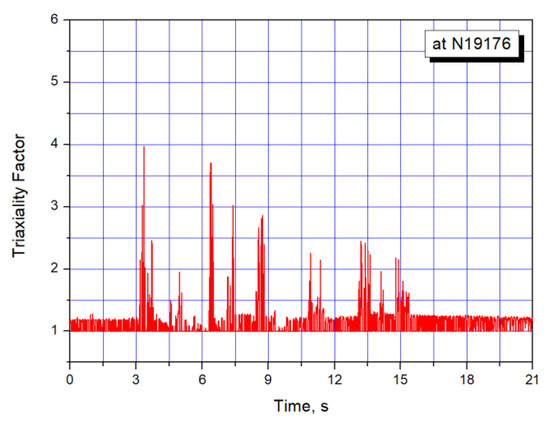
Figure 13.
Triaxiality factor time history response at a critical location.
As shown in Figure 13, the peak TF values occur at several time points when the plastic strains are significantly accumulated. Note that the TF of 1.0 represents uniaxial tension, a factor of 2.0 represents biaxial tension, and greater than 2.0 indicates a triaxial tension state.
3.2.4. Results of Seismic Design Evaluation
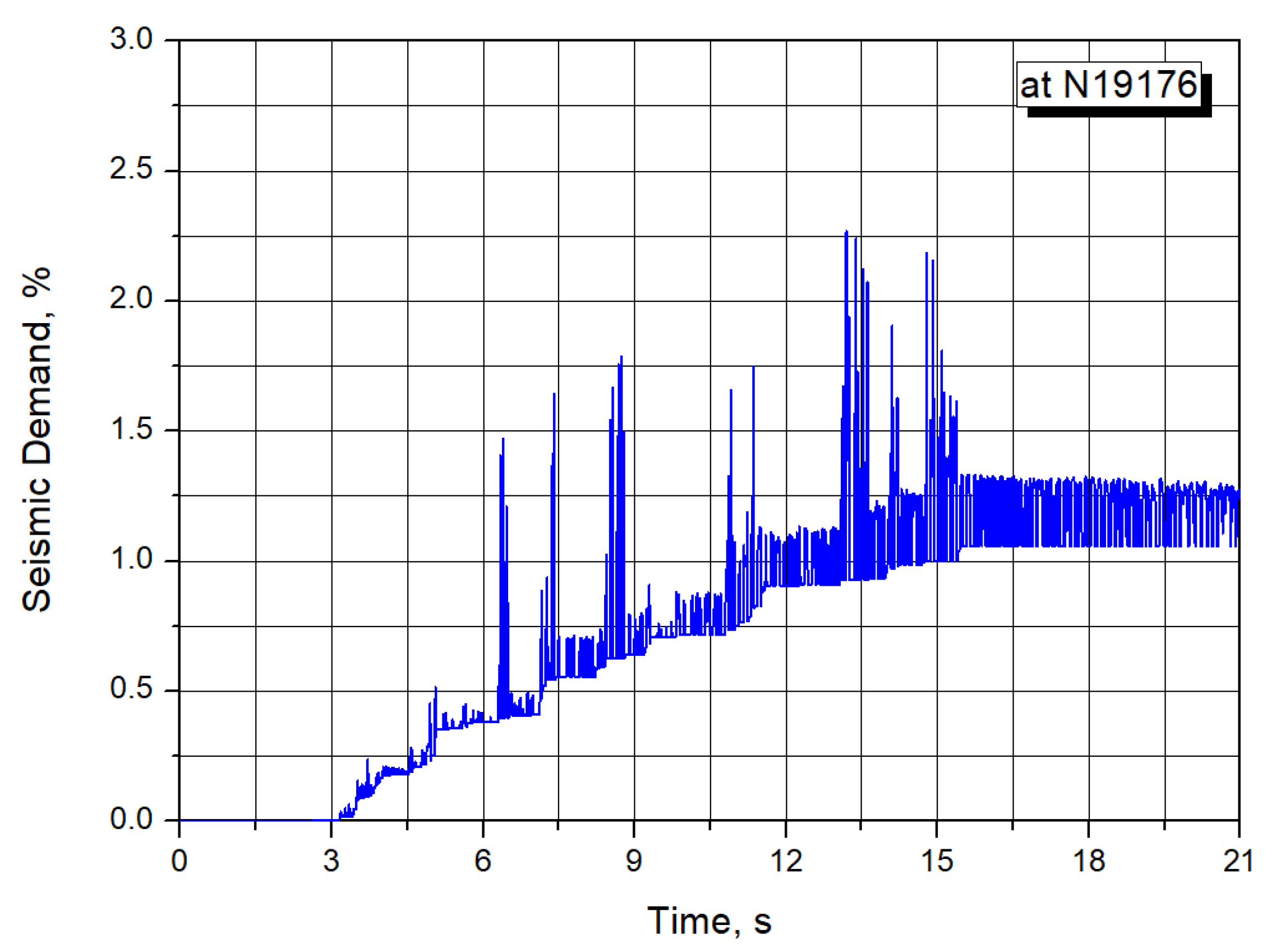
Figure 14 presents the calculated seismic demand time history using Equation (1) at the critical location. As shown in the figure, the maximum SD value is 2.268% at time, t = 13.2 s calculated as follows:
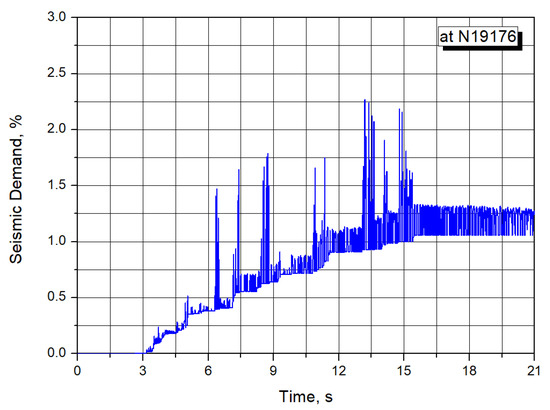
Figure 14.
Calculated seismic demand response for criteria-1 at a critical location.
For an acceptance criteria in Equation (1), the true uniform elongation, εu and the total elongation, εf for Type 316 SS are conservatively assumed to be 30% and 40% at 316 °C, respectively [1,16]. Then, the exampled nozzle satisfies the acceptance criteria-1 for a ductile rupture failure as follows:
3.3. Strain-Based Acceptance Criteria-2
3.3.1. Maximum Total Equivalent Strain
For an acceptance criteria-2, the maximum total strain including elastic and plastic is required at the critical location defined in Section 3.2.1. The accumulated equivalent plastic strain response is shown in Figure 12 and the equivalent elastic strains by internal pressure, SAM and seismic inertia load should be included.
Figure 15 presents the contour plot of an equivalent elastic strain due to an internal pressure (15.5 MPa) for the cross section of the critical location. The maximum value at the critical location is 0.0332%.
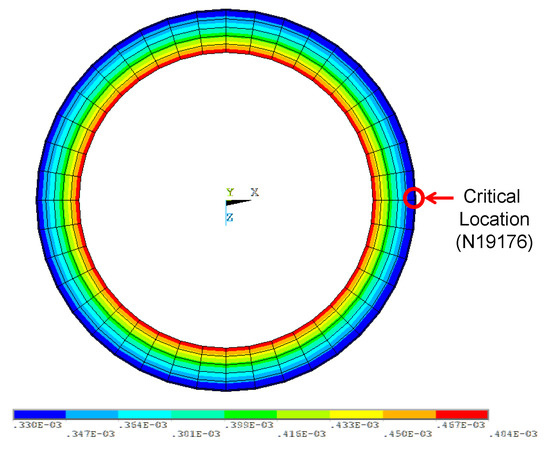
Figure 15.
Sectional contour plot of an equivalent elastic strain for internal pressure.
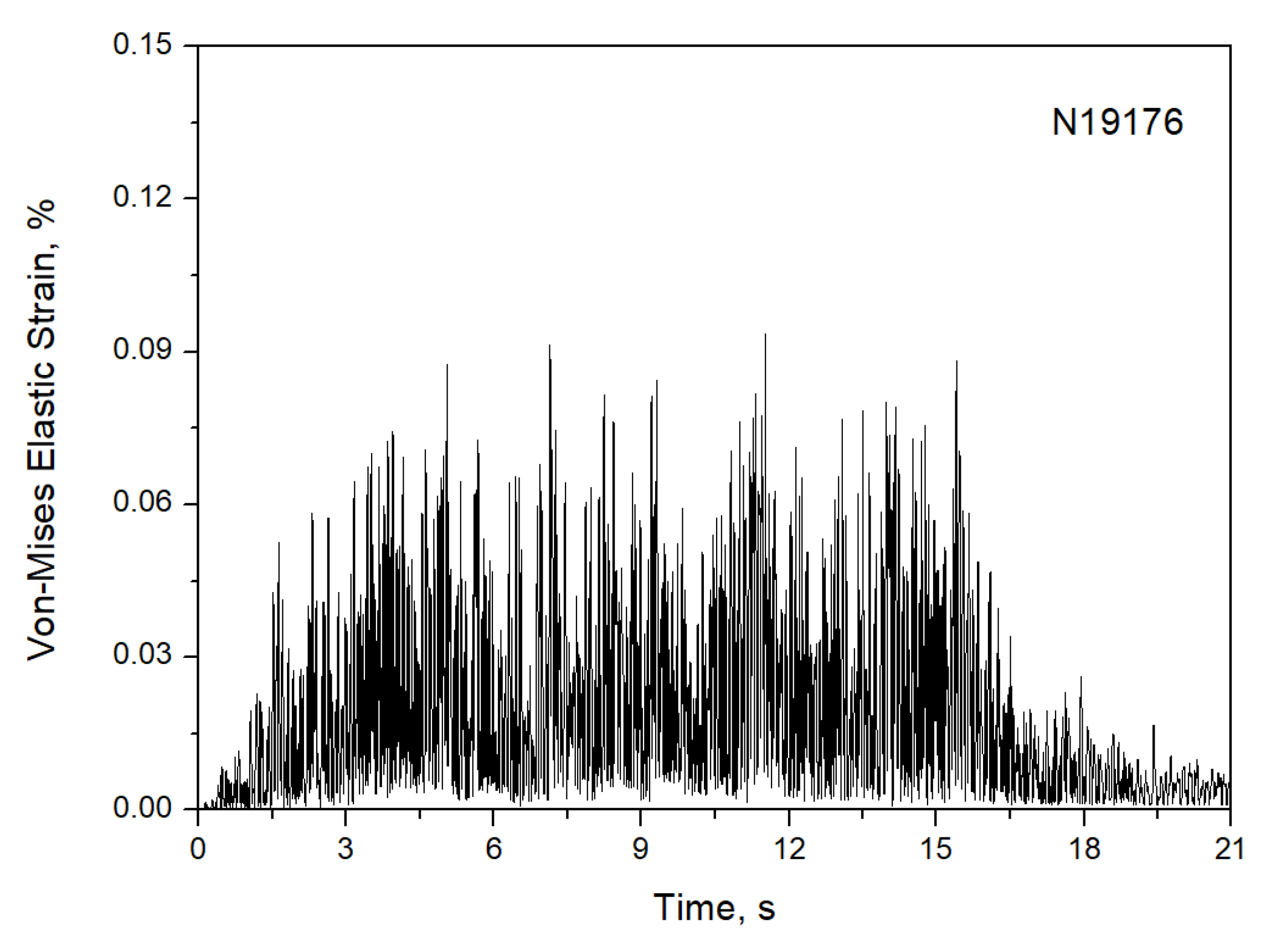
The dead weight is one of the normal sustained loads but it is not considered in this evaluation because the constant spring hangers, which maintain balance of an equal pipe weight during the seismic event, are used for the surge line. The equivalent elastic strain due to the seismic anchor motion is calculated to be 0.0365% at the critical location. Figure 16 presents the equivalent elastic strain time history response at the critical location for the seismic inertia loads. As shown in the figure, the maximum equivalent elastic strain value is 0.0938% at time 11.52 s, where the initial yield strain is 0.057% when calculated with an elastic modulus and the yield stress (σo) in Table 1 and Table 2, respectively.
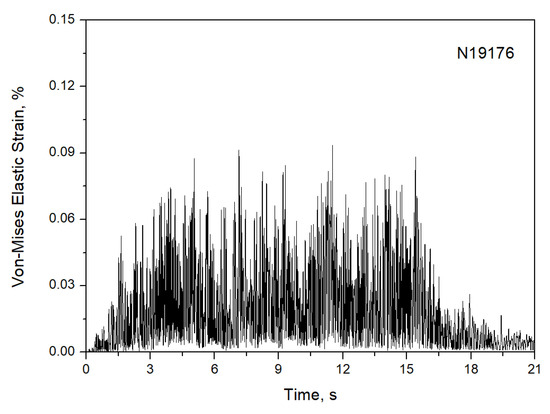
Figure 16.
von Mises elastic strain response for seismic inertia load at a critical location.
Therefore, numerically combined maximum total equivalent elastic strain, is 0.164% at the critical location as follows:
In the above, the elastic strain by the dead weight is assumed to be neglected because the surge line piping is supported by the constant hangers, which can accommodate dead weight without reaction force during the seismic event.
3.3.2. Average TF Value
The average TF value is 1.26, which is calculated from Figure 13 by using Equation (6) with an initiation time point of an equivalent plastic strain, t1 = 2.625 s. As shown in the TF time history response, the maximum peak TF value is 3.97 at time, t = 3.345 s, which is about 3.2 times of an averaged value. In acceptance criteria of Equation (3), the TF value is equivalent to directly lowering the allowable strain limit value of εa in design fatigue curves. Therefore, the average TF value proposed in this paper is reasonable when considering the role of the TF in fatigue-induced failure by earthquakes. This approach gives a simple evaluation method rather than the strain cycle counting method for fatigue, but requires a validation by experiments.
3.3.3. Results of Seismic Design Evaluation
The seismic demand value for the acceptance criteria-2 is 1.541% calculated as follows:
The allowable strain limits, εa is determined as follows:
In the above calculations, the factor of Ky is determined as follows:
where E is Young’s modulus obtained from Figure I-9.2M of ASME Section III Appendix I and Ea is Young’s modulus value used in numerical analysis. When we use the N = 10 and N = 20 as a lower and upper bound of cycles, the allowable strain limits become 2.977% and 4.153%, respectively. As defined above, N is proposed not to be less than 10 and to be a number causing significant accumulation of plastic strain during the seismic event. Even when we conservatively select N = 10 as a lower bound value in design point of view, we can confirm that the surge line nozzles selected as seismic fragile component in this paper satisfy the strain-based design criteria for 0.6 g SSE level as follows:
Table 5 presents the summaries of the exampled strain-based seismic evaluations performed in this paper. As shown in the table, the seismic integrity of the exampled nozzles can be assured against the ductile rupture failure with enough design margin by the Criteria-1. The Criteria-2, which is against for the fatigue-induced failure, gives less design margin and governs the seismic failure mode for nozzles.

Table 5.
Summaries of exampled strain-based seismic evaluations (SD: Seismic Demand).
3.4. Comparison With Stress-Based Criteria
In this paper, two stress-based criteria complied with the ASME BPV III Appendix XXVII are considered as follows [3]:
For elastic analysis (XXVII-3200):
For plastic analysis (XXVII-3300):
In the above, Pm, Pb and PSI are the general primary membrane stress intensity, primary bending stress intensity, and the maximum stress intensity value, respectively. Among them, Pm and Pb should be calculated through the entire wall thickness and PSI should be calculated at any location. The values of Sm, Su, and Sy indicate the allowable stress intensity, the ultimate tensile strength, and the yield strength respectively.
For the elastic seismic analysis, the time history seismic analysis without inelastic material models is carried out with the same input motions of Figure 4. In this result, the critical location is found to be the same as that of the inelastic seismic analysis.
Table 6 presents the summary results of the stress-based seismic evaluations for the exampled component nozzles in this paper.

Table 6.
Summaries of exampled stress-based seismic evaluations.
4. Conclusions
In this paper, feasibility studies on the strain-based seismic design criteria are carried out, in case significant plastic strain is expected in a component seismic design of NPP. Two strain-based acceptance criteria are investigated through the actual exampled application for the surge line nozzles in a nuclear steam supply system, which are known as one of seismic fragile components. In applying the strain-based seismic criteria, it is found that one of the important steps is to calculate an accurate accumulated plastic strain and triaxiality factors by the elasto-plastic seismic analysis. The determination of appropriate allowable strain limit values from the true stress-strain tensile curves and the design fatigue curves are also important steps in this approach.
From the feasibility studies carried out for component nozzles, we found some important issues for an actual application of the strain-based criteria as follows:
- appropriate coupled finite element model, both with piping and nozzles, to be able to assure the stabilized seismic response at critical location;
- inelastic material constitutive equations to be able to consider the kinematic hardening and isotopic hardening behavior;
- determination of frequency range for Rayleigh damping;
- validation of the TF effects on ductile failure and fatigue-induced failure;
- determination of true uniform and fracture strain limits by quasi-static tensile tests;
- determination of the number of cycles, N, for an allowable strain limit value from design fatigue curve
The approach and general procedures investigated in this paper are expected to be used for a seismic design of the safety-related nuclear components where the seismic design levels are high enough to invoke plastic strain at critical locations.
Author Contributions
Conceptualization, G.-H.K., J.-S.K., and Y.-J.K.; methodology, G.-H.K. and J.-S.K.; validation, G.-H.K. and Y.-J.K.; formal analysis, G.-H.K.; investigation, J.-S.K. and Y.-J.K.; writing—original draft preparation, G.-H.K.; writing—review and editing, J.-S.K. and Y.-J.K.; funding acquisition, G.-H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Ministry of Trade, Industry and Energy through KETEP (Korea Institute of Energy Technology Evaluation Planning). (No. 20181510102380).
Acknowledgments
This study was supported by the Ministry of Trade, Industry and Energy through KETEP (Korea Institute of Energy Technology Evaluation Planning). (No. 20181510102380).
Conflicts of Interest
The authors declare no conflict of interest.
References
- ASME BPVC Section III Appendices. Nonmandatory Appendix EE: Strain-Based Acceptance Criteria Definitions and Background Information; ASME: New York, NY, USA, 2019. [Google Scholar]
- ASME BPVC Section III Appendices. Nonmandatory Appendix FF: Strain-Based Acceptance Criteria for Energy-Limited Events; ASME: New York, NY, USA, 2019. [Google Scholar]
- ASME BPVC Section III Appendices. Mandatory Appendix XXVII: Design by Analysis for Service Level D; ASME: New York, NY, USA, 2019. [Google Scholar]
- Alternative Rules for Level D Service Limits of Class 1, 2, and 3 Piping Systems, Section III, Division 1; ASME Code Case (Record No. 13-1438); ASME: New York, NY, USA.
- Masaki, M.; Akihiro, O.; Tomoyoshi, W.; Izumi, N.; Tadahiro, S.; Masaki, S. Seismic qualification of piping systems by detailed inelastic response analysis: Part 1—A code case for piping seismic evaluation based on detailed inelastic response analyses. In Proceedings of the ASME 2017 PVP Conference, Waikoloa, HI, USA, 16–20 July 2017; Volume 8. [Google Scholar]
- IEEE Std 344-1987. IEEE Recommended Practice for Seismic Qualification of Class 1E Equipment for Nuclear Power Generating Stations; IEEE, Inc.: Piscataway, NJ, USA, 1987. [Google Scholar]
- Algarni, M.; Bai, Y.; Zwawi, M.; Ghazali, S. Damage Evaluation Due to Extremely Low-Cycle Fatigue for Inconel 718 Alloy. Metals 2019, 9, 1109. [Google Scholar] [CrossRef]
- ASME BPVC Section III Appendices. Mandatory Appendix I: Design Fatigue Curve; ASME: New York, NY, USA, 2019. [Google Scholar]
- Cooper, W.E. Rational for a Standard on the Requalification of Nuclear Class 1 Pressure-Boundary Components; NP-1921, Research Project 1756-1; Electric Power Research Institute: Washington, DC, USA, 1981. [Google Scholar]
- Davis, E.A.; Connelly, F.M. Stress Distribution and Plastic Deformation in Rotating Cylinders of Strain-Hardening Material. J. Appl. Mech. 1959, 26, 25–30. [Google Scholar]
- Design and Development Guide for NNSA Type B Packages; National Nuclear Security Administration, SG-100 Rev. 2, Appendix M: Washington, DC, USA, 2005.
- Damping Values for Seismic Design of Nuclear Power Plants; Regulatory Guide 1.61; US NRC: North Bethesda, MD, USA, 2007.
- Seismic Analysis of Safety-Related Nuclear Structures; ASCE/SEI Standard 4-16; ASCE: Reston, VA, USA, 2017.
- ANSYS Mechanical APDL Release 15.0; ANSYS, Inc.: Canonsburg, PA, USA, 2013.
- Koo, G.H.; Kwon, J.H. Development of Inelastic Material Parameters for Modified 9Cr-1Mo Steel Applicable to the Plastic and Viscoplastic Constitutive Equations. Int. J. PVP 2011, 88, 26–33. [Google Scholar]
- Zhang, X.; Xu, C.; Wang, L.; Chen, Y. iRadMat: A Thermo-Mechanical Testing System for In Situ High-Energy X-ray Characterization of Raioactive Specimens. Rev. Sci. Instrum. 2017, 88, 015111. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).