A Theoretical Model of Residual Magnetic Field around a Pre-Magnetized Casing String

Abstract

In the field of petroleum drilling engineering, passive magnetic ranging technology is generally used for specialized drilling operations such as connecting relief wells, preventing wellbore collisions, guiding parallel horizontal wells, etc. Although pre-magnetized casing strings have been used to improve the detection distance and accuracy, the theoretical mechanism is not well understood. Based on the equivalent current model of a permanent magnet, a theoretical magnetic field model around the pre-magnetized casing string was established by using the vector potential method and vector superposition principle and validated by the COMSOL Multiphysics software. Our results show that connecting pre-magnetized individual casings with homogeneous magnetic poles can enlarge the magnetic induction intensity around the total casing string. Furthermore, the magnitude close to the casing coupling is significantly larger than that close to the middle of the individual casing. Connecting pre-magnetized individual casings with heterogeneous magnetic poles results in a low magnetic induction intensity around the total casing string. In order to improve the detection distance and accuracy of the magnetic ranging, the pre-magnetized individual casings should be connected with homogeneous magnetic poles. The results of this study can provide guidelines for the development of passive magnetic ranging technology.

1. Introduction

In the field of oil-drilling engineering, magnetic ranging technology is used in special drilling operations, such as connecting relief wells [1,2,3], preventing wellbore collisions [4,5,6], guiding parallel horizontal wells or U-shape well [7,8], etc. Existing magnetic ranging methods can be classified into active method and passive method. For the first method, the relative position of the adjacent casing string is determined by applying an electromagnetic excitation signal in one well and detecting it in another well by additional magnetic instrument. Since excitation signals are applied artificially, this method has some advantages such as high detection accuracy and large detection distance. However, this method mainly adopts the dual-well operation mode described above and its application conditions are greatly limited if the adjacent well has been put into production or is suffering a wild blowout [3,4,5,6,7,8]. For the second method, the accept instrument is located in the drilling well by detecting the magnetic field characteristics of the adjacent casing string and no additional instrument need put into the adjacent well. This is to say, this method adopts the single-well operation mode and has great potential to be used widely. However, the self-induced magnetic field intensity of the adjacent casing string itself is relatively small and exhibits more uncertainties. Hence, this method is still restricted by relatively low detection accuracy and small detection distance [1,2,9,10].

In view of the limitations above, an improved passive magnetic ranging method with pre-magnetized casing string has been introduced [11,12,13,14,15]. Before the current well is drilled, the individual casing strings are pre-magnetized on the ground and then run into the adjacent drilled well as and when required. When the current well is being drilled, the magnetic field characteristics of adjacent casing string is measured in current well by using a Magnetometer. Then, the relative position of the adjacent casing string is derived. Since no additional excitation signal is required in the adjacent well, single-well operation mode can provide high efficiency. In addition, because the magnetic field of the adjacent casing string is due to the remanence produced by the pre-magnetization, and its intensity and distribution characteristics are known in advance, the detection accuracy is relatively high, and the detection distance is relatively large. For example, the maximum detection distance has been enlarged beyond 20 m by the Scientific Drilling Company [9,10,11,13,14,15].

Although the pre-magnetized casing string is currently used to improve the passive magnetic ranging technology, the theoretical studies have not been discussed intensively yet. In order to develop the passive magnetic ranging technology independently, a robust theoretical magnetic field model around the pre-magnetized casing string is to be established by the modern electromagnetic theory and validated by COMSOL Multiphysics software in this article.

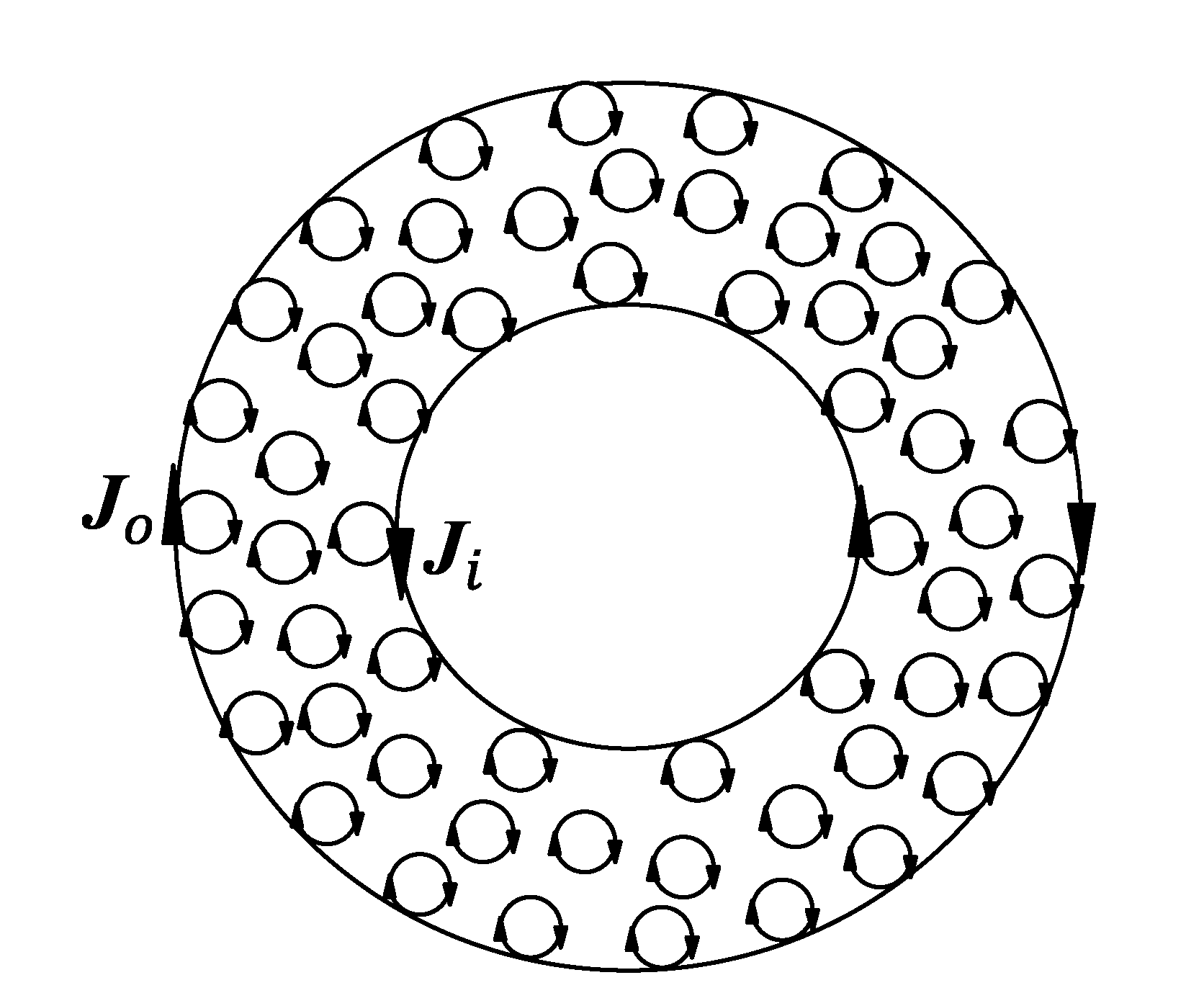
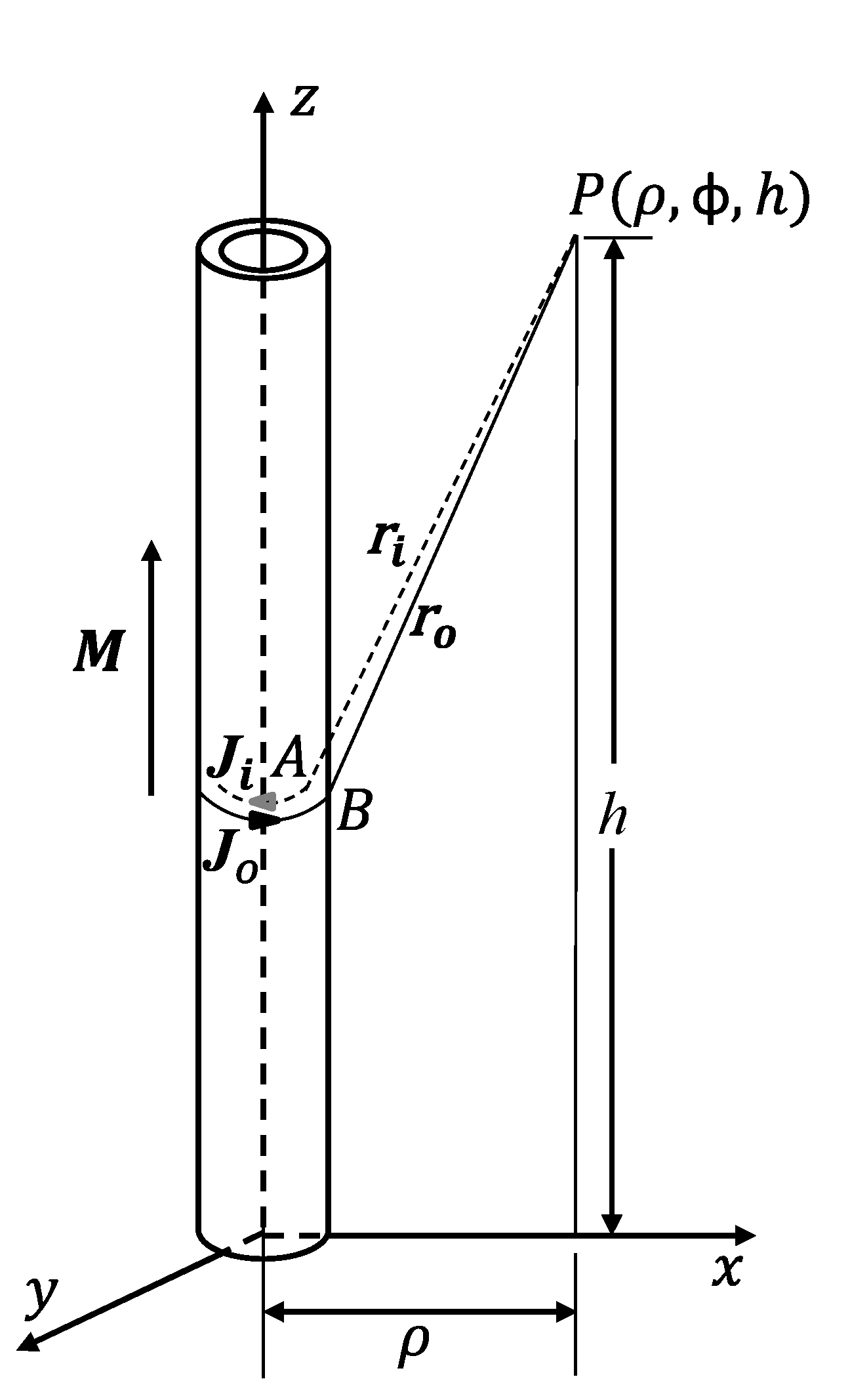
2. Magnetic Field Model of Pre-Magnetized Individual Casing

The petroleum drilling casing string is formed by connecting individual casings (high-quality seamless steel tube, about 12 m each) with specialized casing couplings. A pre-magnetized individual casing can be considered as a hollow cylindrical permanent magnet; its external magnetic field distribution can be calculated by using the equivalent current model of the permanent magnet.

As per the modern electromagnetic theory, there are no magnetic charges inside a permanent magnet. The magnetic phenomenon just originates from the molecular current. When the magnetic medium is not magnetized, all molecule magnetic moments are organized in a random manner and countered each other. As a result, no macroscopic magnetism phenomenon is observed. If the magnetic medium is uniformly magnetized, all molecule magnetic moments are directionally aligned, and a macroscopic magnetism phenomenon is observed. The pre-magnetized individual casing can be considered as a uniformly magnetized hollow permanent magnet [16].

As shown in Figure 1, all annular molecular currents of the pre-magnetized individual casing are equivalent to the annular surface currents with inner and outer surface current density $J_i$ and $J_o$, respectively. The calculation methods to determine the external magnetic field distribution of a permanent magnet mainly include the scalar and vector magnetic potential methods [17]. According to Maxwell equations, the scalar and vector magnetic potentials are introduced, and the corresponding differential equations are derived for numeric solution. Although the scalar and vector magnetic potential methods have the same function, only the latter method matches to the equivalent current method. In this study, the external magnetic field distribution around the pre-magnetized individual casing is derived by using the vector magnetic potential method, based on the equivalent current method [18,19].

As shown in Figure 2, the external magnetic field model of the pre-magnetized individual casing is established. Here, the coordinate origin O is located at the bottom center of the individual casing; the total length is set as L; the inner and outer radii are set as $R_i$ and $R_o$, respectively. The vector magnetization intensity is set as $M$ and upward. The corresponding equivalent currents on the inner and outer walls are set as $J_i$ and $J_o$, respectively. The upper and lower ends denote N and S poles, respectively. $\mathrm{A}\left(R_i,\phi ,z\right)$ and $\mathrm{B}\left(R_o,\phi ,z\right)$ denote an arbitrary source point on the inner and outer walls, respectively. $\mathrm{P}\left(\rho ,\varphi ,h\right)$ denotes an arbitrary field point outside the casing string. The vector distances from source points A and B to the field point P are set as $r_i$ and $r_o$, respectively. According to the equivalent current model, the vector magnetic potential $A_m$ at field point P is given by:

$$A_m\left(\mathrm{P}\right)=\frac{\mu }{4\pi }{{\displaystyle \oint }}_V\frac{M\times r}{r^3}dV=\frac{\mu }{4\pi }{{\displaystyle \oint }}_V\frac{\nabla \times M}{r}dV+\frac{\mu }{4\pi }{{\displaystyle \oint }}_S\frac{M\times n}{r}dS$$

(1)

where, $\mu$ denotes the relative magnetic conductivity of the formation around the casing string; r denotes the vector distance from the source point to the field point; S denotes the magnet surface; $n$ denotes the normal vector of the magnet surface and $\nabla$ denotes the divergence operation.

Volume current density is given by:

$$J_v=\nabla \times M$$

(2)

Surface current density is expressed as:

$$J_s=M\times n$$

(3)

When the individual casing is uniformly magnetized along its axial direction, the magnetization intensity $M$ is a constant vector. From Equations (2) and (3), it can be seen that in this case the volume current density $J_v$ = 0, the magnitude of surface current density $J_s$ is equal to that of the magnetization intensity $M$. Its direction is perpendicular to the magnetization intensity $M$ and the unit normal n. In other words, there is no volume current density and only the annular surface currents are present on its inner and outer surfaces. Hence, Equation (1) can be simplified as:

$$A_m\left(\mathrm{P}\right)=\frac{\mu }{4\pi }{{\displaystyle \oint }}_S\frac{J_s}{r}dS=\frac{\mu }{4\pi }{{\displaystyle \oint }}_{S_i}\frac{J_i}{r_i}d{S}_i+\frac{\mu }{4\pi }{{\displaystyle \oint }}_{S_o}\frac{J_o}{r_o}d{S}_o$$

(4)

where, $S_i$ and $S_o$ denote the inner and outer surfaces, respectively.

The magnetic induction intensity B at the field point P is given by:

$$B\left(\mathrm{P}\right)=\nabla \times A_m=\frac{\mu }{4\pi }{{\displaystyle \oint }}_S\nabla \times \frac{J_s}{r}dS=\frac{\mu }{4\pi }{{\displaystyle \oint }}_{S_i}\frac{J_i\times r_i}{r_i{}^3}d{S}_i+\frac{\mu }{4\pi }{{\displaystyle \oint }}_{S_o}\frac{J_o\times r_o}{r_o{}^3}d{S}_o$$

(5)

The equivalent surface current densities $J_i$ and $J_o$ on inner and outer walls are given by:

$$\{\begin{array}{c}{J}_{\mathrm{i}}=M\sin \phi i-M\cos \phi j+0k\\ J_o=-M\sin \phi i+M\cos \phi j+0k\end{array}$$

(6)

where, i, j and k denote unit vectors along x-axis, y-axis and z-axis, respectively.

The vector distances $r_i$ and $r_o$ from points A, B to point P are expressed as:

$$\{\begin{array}{c}{r}_i=\left(\rho \cos \varphi -R_i\cos \phi \right)i+\left(\rho \sin \varphi -R_i\sin \phi \right)j+\left(h-z\right)k\\ r_o=\left(\rho \cos \varphi -R_o\cos \phi \right)i+\left(\rho \sin \varphi -R_o\sin \phi \right)j+\left(h-z\right)k\end{array}$$

(7)

When Equations (6) and (7) are combined with Equation (5), the magnetic induction intensity components $B_x$, $B_y$ and $B_z$ at the field point P are obtained as:

$$B_x=\frac{\mu }{4\pi }{{\displaystyle \int }}_0^L{{\displaystyle \int }}_0^{2\pi }\left\{\frac{-M{R}_i\cos \mathsf{\phi }\left(h-z\right)}{{\left[{\rho }^2+R_i{}^2-2\rho R_i\cos \left(\varphi -\phi \right)+{\left(h-z\right)}^2\right]}^{3/2}}+\frac{M{R}_o\cos \mathsf{\phi }\left(h-z\right)}{{\left[{\rho }^2+R_o{}^2-2\rho R_o\cos \left(\varphi -\phi \right)+{\left(h-z\right)}^2\right]}^{3/2}}\right\}\mathrm{d}\phi \mathrm{d}z$$

(8)

$$B_y=\frac{\mu }{4\pi }{{\displaystyle \int }}_0^L{{\displaystyle \int }}_0^{2\pi }\left\{\frac{-M{R}_i\sin \phi \left(h-z\right)}{{\left[{\rho }^2+R_i{}^2-2\rho R_i\cos \left(\varphi -\phi \right)+{\left(h-z\right)}^2\right]}^{3/2}}+\frac{M{R}_o\sin \phi \left(h-z\right)}{{\left[{\rho }^2+R_o{}^2-2\rho R_o\cos \left(\varphi -\phi \right)+{\left(h-z\right)}^2\right]}^{3/2}}\right\}\mathrm{d}\phi \mathrm{d}z$$

(9)

$$B_z=\frac{\mu }{4\pi }{{\displaystyle \int }}_0^L{{\displaystyle \int }}_0^{2\pi }\left\{\frac{M{R}_i\left[\rho \cos \left(\varphi -\phi \right)-R_i\right]}{{\left[{\rho }^2+R_i{}^2-2\rho R_i\cos \left(\varphi -\phi \right)+{\left(h-z\right)}^2\right]}^{3/2}}+\frac{M{R}_o\left[-\rho \cos \left(\varphi -\phi \right)+R_o\right]}{{\left[{\rho }^2+R_o{}^2-2\rho R_o\cos \left(\varphi -\phi \right)+{\left(h-z\right)}^2\right]}^{3/2}}\right\}\mathrm{d}\phi \mathrm{d}z$$

(10)

For columnar permanent magnets, it is still difficult to directly solve Equations (8)–(10) by using analytical methods, hence numeric integration methods are employed [20,21,22]. In this study, the above models are solved by using MATLAB software.

3. Magnetic Field Model of Axially Magnetized Casing String with Couplings

The petroleum drilling casing string is connected by individual casings (about 12 m each) with specialized casing couplings. There are two connection modes for the two pre-magnetized individual casings: the homogeneous pole connection mode (N–N connection or S–S connection) and the heterogeneous pole connection mode (N–S connection or S–N connection). If the magnetic pole connection mode is different, the external magnetic field distribution is also different.

3.1. Under the Homogeneous Magnetic Pole Connection Mode

As shown in Figure 3, when the pre-magnetized individual casings are connected by homogeneous magnetic poles, the N–N and the S–S connections appear alternately, and the magnetic field distribution patterns of two adjacent individual casings are similar—except that the magnetic field is in the opposite direction.

As shown in Figure 3b, a theoretical model of the magnetic field around the axially magnetized casing string is established by taking the N–N connection mode as an example. In this case, the coordinate origin O is located at the center of the nearest casing coupling to the field point P, and the z-axis is along the axis of the casing string and pointed upward. The magnetic induction strengths at field point P generated by the individual casings above the reference casing coupling are set as $B_{+1}$, $B_{+2}$, $B_{+3}$, …… e. The others below the reference casing coupling are set as $B_{-1},B_{-2}$, $B_{-3}$ …… Compared to the long body of an individual casing, the effect of the casing coupling itself could be ignored [13]. The total magnetic field induction intensity at field point P is given by:

$$B\left(\mathrm{P}\right)={\displaystyle \sum }_{i=1}^m{B}_{+i}+{\displaystyle \sum }_{j=1}^n{B}_{-j}$$

(11)

where, m and n denote the numbers of individual casings above and below the nearest casing coupling to the field point P, respectively.

Considering the individual casing has large length (mainly 12 m each) and length/diameter ratio (mainly 20–100), it is sufficient to take four individual casings and three casing couplings nearby the field point P into account, for which m = n = 2. Considering the reference casing coupling is in the N–N connection mode, and the other two adjacent casing couplings are in the S–S connect mode. The scalar magnetization intensity of each individual casing is set as M and then the vector magnetization intensities of four individual casings are $M$, $-M$, $M$ and $-M$ from top to bottom, respectively. Substituting Equation (5) into Equation (11), the following expression is obtained:

$$\begin{array}{cc}\hfill B\left(\mathrm{P}\right)=\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{i,+1}}& \frac{J_i\times r_i}{{r_i}^3}d{S}_{i,+1}+\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{o,+1}}\frac{J_o\times r_o}{{r_o}^3}d{S}_{o,+1}+\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{i,-1}}\frac{J_i\times r_i}{{r_i}^3}d{S}_{i,-1}\hfill \\ & +\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{o,-1}}\frac{J_o\times r_o}{{r_o}^3}d{S}_{o,-1}+\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{i,+2}}\frac{J_i\times r_i}{{r_i}^3}d{S}_{i,+2}\hfill \\ & +\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{o,+2}}\frac{J_o\times r_o}{{r_o}^3}d{S}_{o,+2}+\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{i,-2}}\frac{J_i\times r_i}{{r_i}^3}d{S}_{i,-2}\hfill \\ & +\frac{u}{4\pi }{{\displaystyle \oint }}_{S_{o,-2}}\frac{J_o\times r_o}{{r_o}^3}d{S}_{o,-2}\hfill \end{array}$$

(12)

In Equation (12), the capital S with double subscripts represents the inner or outer surface of an individual casing above or below the reference casing coupling. For the double subscripts, i and o refer to the inner and outer surfaces, respectively; “+” and “−” represent above or below the reference casing coupling, respectively; 1 and 2 indicate the number of an individual casing, respectively.

The expression of the magnetic induction intensity around the pre-magnetized casing string can be obtained by substituting Equations (8)–(10) into Equation (12).

3.2. Under the Heterogeneous Magnetic Pole Connection Mode

When the heterogeneous pole connection mode is adopted, the magnetic field distribution patterns of N–S or S–N connection are similar, with the magnetic field directions being opposite to each other. Taking the N–S connection mode as an example, the magnetization intensity of each individual casing has the same orientation. According to the derivation process mentioned above, the equation of the magnetic induction intensity can be directly obtained and omitted here.

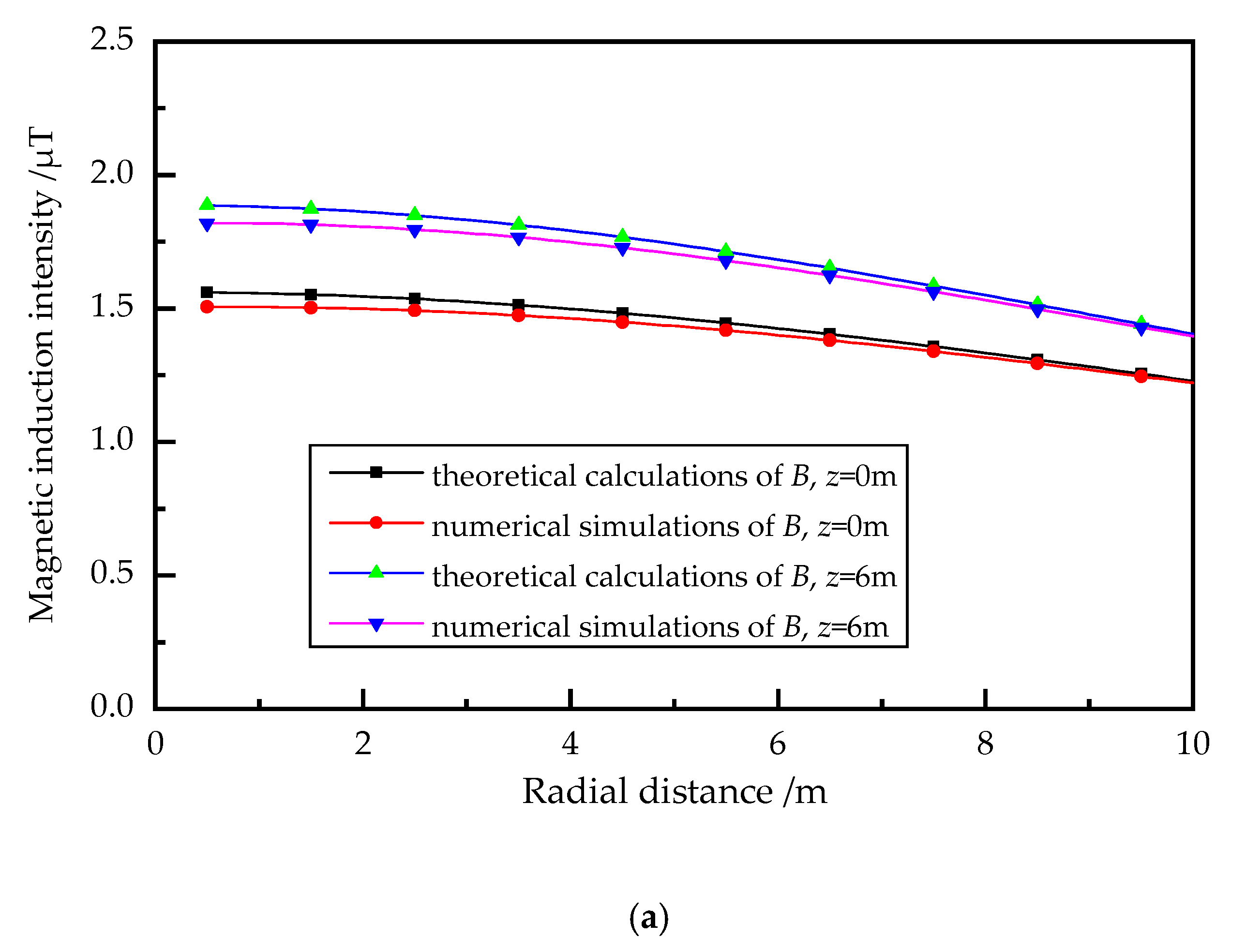
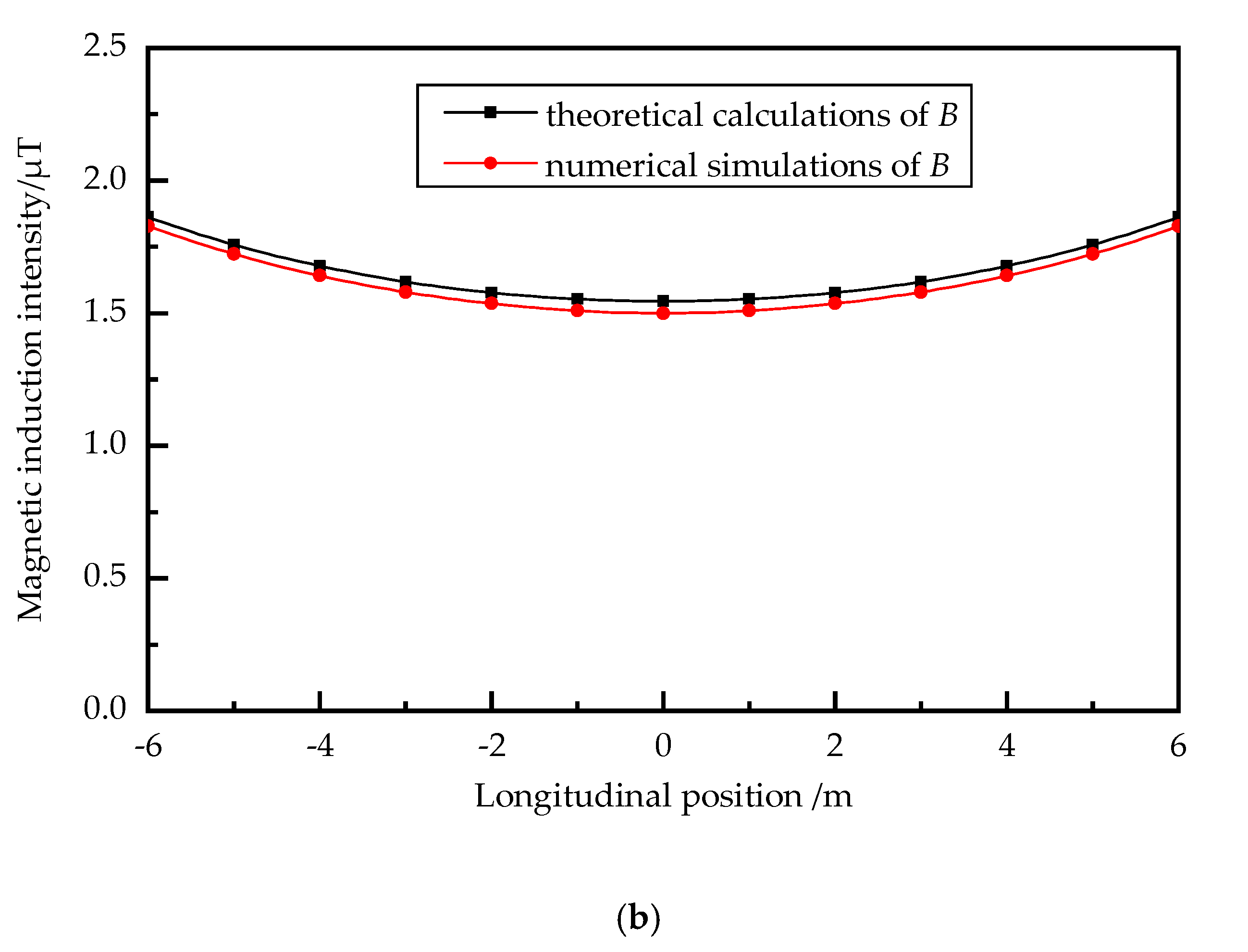
4. Model Validation and Analysis

According to technical specifications, the outer and inner diameters, the length of the individual casing are set as 177.8 mm, 150.4 mm and 12 m, respectively. Earlier studies have showed that the magnetic intensity at the end of the pre-magnetized individual casing could exceed 3000 μWb [15]. Based on this magnetization effect, the remanence intensity of each pre-magnetized individual casing is set as 0.8 T in this study. The numeric solution of Equation (12) is evaluated by using MATLAB software and numeric simulations are carried out by using the COMSOL Multiphysics package, to validate the established magnetic field distribution model above.

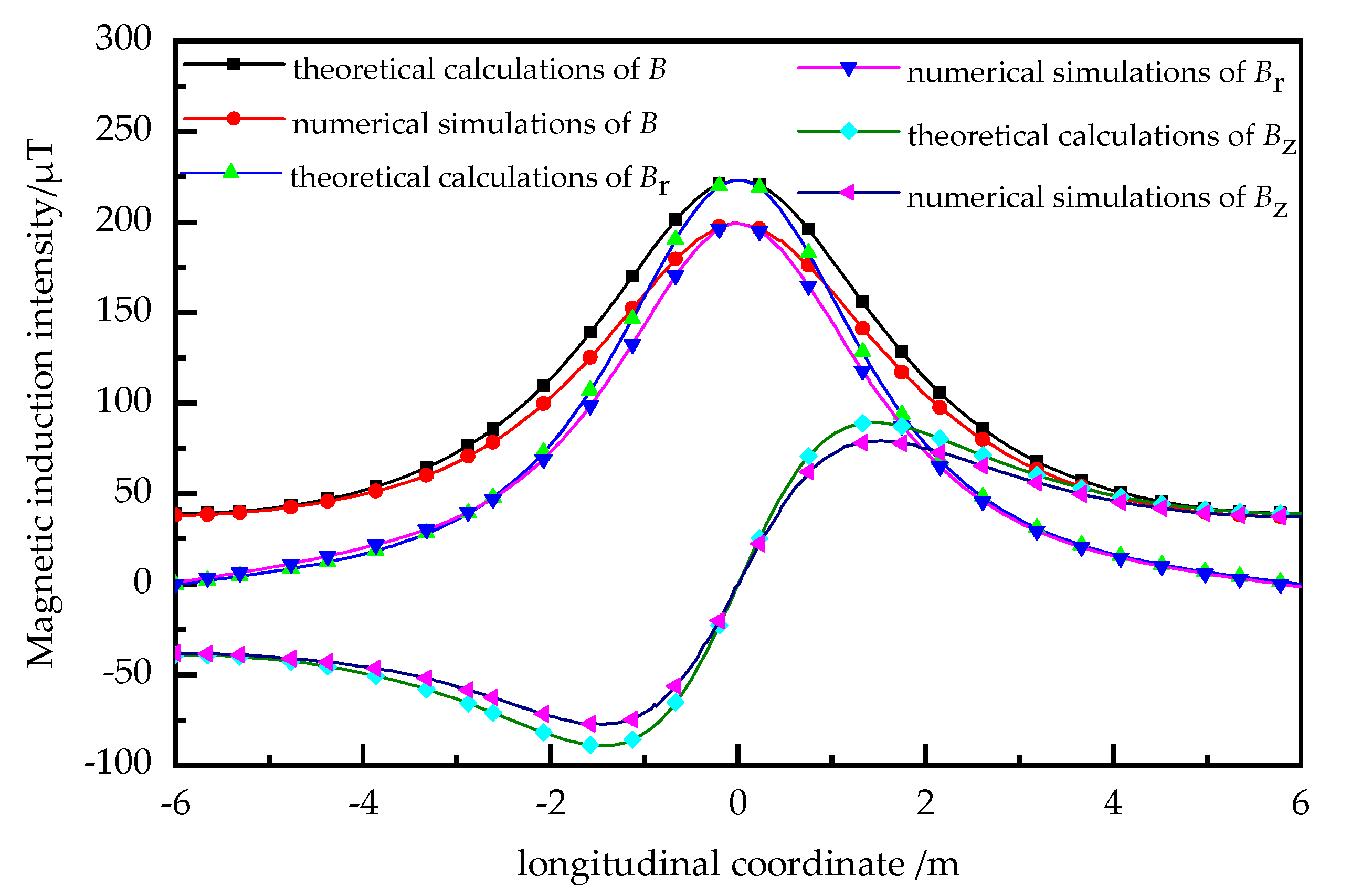
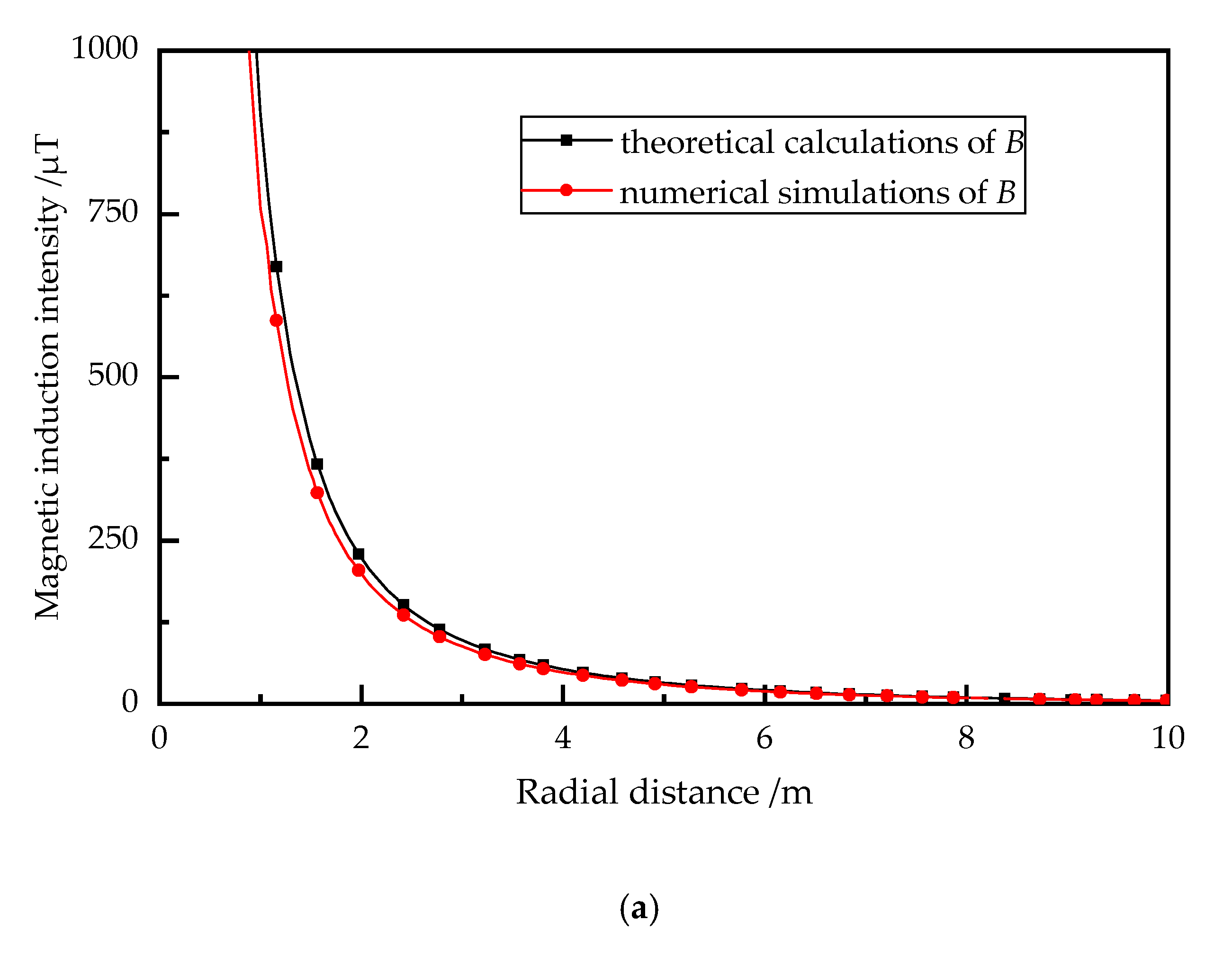
4.1. Under the Homogeneous Magnetic Pole Connection Mode

To validate the analytical magnetic field model, some test lines were selected, and then the magnetic induction intensity and its components were calculated as follows:

First, select a profile passing through the axis of the casing string and then select a longitudinal test line with the same radial distance ρ = 2 m and longitudinal coordinate z = −6 m–+6 m. Second, select two cross-sections with the longitudinal coordinates z = 0 (at the center of the reference casing coupling) and z = 6 m (at the middle of the reference individual casing) and then select a radial test line on each cross-section. Finally, the magnetic induction intensities along three test lines are calculated by using Equation (12) and COMSOL Multiphysics software and shown in Figure 4 and Figure 5.

Comparative analyses between theoretical calculations and numeric simulations have showed that the average error of the total magnetic induction intensity $B$ and its components is 6.85% in Figure 4, 8.58% in Figure 5a and 6.68% in Figure 5b, respectively, indicating that the magnetic field distribution model established above is quite accurate. In addition, the magnetic field distribution pattern of the casing string under this condition is consistent with the relevant experimental results [23], which further validate the proposed theoretical model.

From Figure 4, it is also evident that magnetic induction intensity $B$ is numerically distributed symmetrically above and below the casing coupling, and its magnitude close to the casing coupling is significantly greater than that close to the middle of the individual casing. The radial component $B_r$ is 0 in the middle of the individual casing and has the maximum value in the middle of the casing coupling. The longitudinal component $B_z$ is 0 in the middle of the casing coupling, and its positive and negative extreme maximum values are located above and below near the casing coupling, respectively. From Figure 5, it can also be seen that the magnetic induction intensity decreases rapidly with the radial distance of the field point. Its magnitude and influence distance close to the casing coupling are greater than those close to the middle of the individual casing.

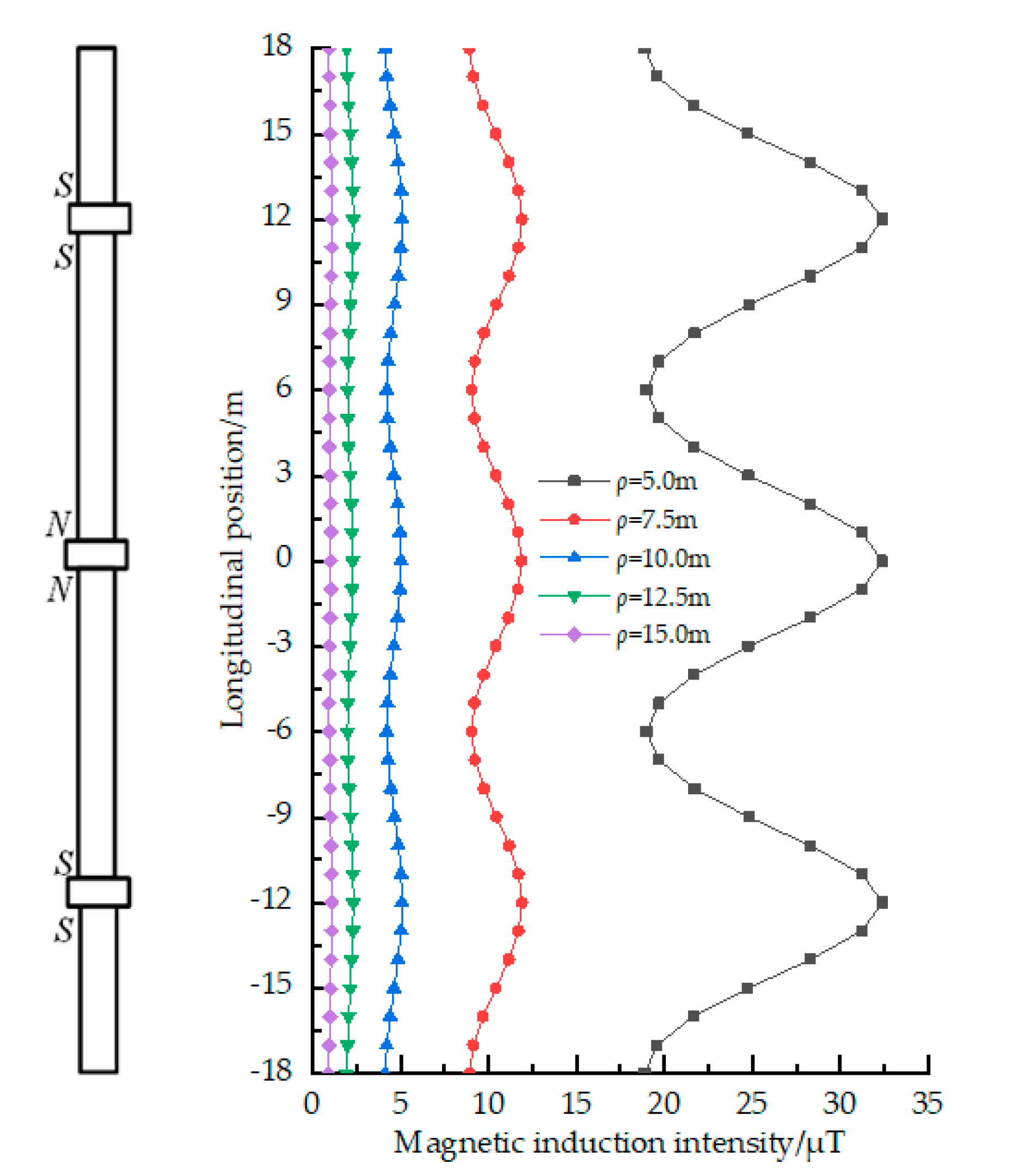
4.2. Under the Heterogeneous Magnetic Pole Connection Mode

Under N–S connection condition, the magnetic induction intensities along the same three test lines described above are calculated and shown in Figure 6. It can be seen that all the theoretical calculations and numeric simulations results are also in reasonable agreement. The magnetic induction intensity close to the casing coupling is similar to that close to the middle of the casing, and all magnitudes are much smaller than those under the homogeneous magnetic pole connection mode. This observation can be explained by the fact that the magnetic fields generated by the N and S poles have cancelled each other. The pre-magnetized casing string with couplings under the heterogeneous pole connection mode can be equivalent to an integral casing string without couplings.

4.3. Comparisons between Tow Magnetic Pole Connection Modes

Comparing all calculation results in Section 4.1 and Section 4.2, it can be seen that under the homogeneous pole connection mode, the magnetic induction intensity around the pre-magnetized casing string and its influencing range are enlarged, especially close to the casing coupling; under heterogeneous pole connection mode, they are not enlarged. Clearly, the homogeneous pole connection mode should be adopted to improve the detection distance and accuracy [24].

Illustrated by a pre-magnetized casing string with three couplings under the homogeneous pole connection mode, the magnetic induction intensities along five longitudinal test lines are calculated by Equation (12) and shown in Figure 7. It can be seen that if the longitudinal test line is close to the casing string, the magnetic induction intensity is larger and fluctuates visibly and periodically within one individual casing. If the field point is further from the casing string, the magnetic induction intensity decreases rapidly and does not visibly fluctuate. For the longitudinal test line at the radial distance ρ = 15 m, the magnetic induction intensity is approximate 1 μT. It means that the maximum detectable distance for most directional drilling instruments can reach to 15 m or so. In fact, the maximum detection distance was enlarged beyond 20 m by the Scientific Drilling Company [9,10,11,13,14,15].

5. Conclusions

In this study, a mathematical model of magnetic field distribution around a pre-magnetized casing string is established and validated. Some instructive conclusions and understandings are obtained for the development of passive magnetic ranging technology.

(1)

The theoretical magnetic field model around the pre-magnetized casing string established and validated in this article can provide foundations to the passive magnetic ranging technology;

(2)

When the pre-magnetized individual casings are connected by homogeneous magnetic poles, the magnetic induction intensity around the casing string is enhanced and its magnitude near to the casing coupling is larger than that near to the middle of the individual casing;

(3)

When the pre-magnetized individual casings are connected with heterogeneous magnetic poles, the magnetic induction intensity around the casing string is relatively smaller and has smaller differences along the whole casing string;

(4)

The pre-magnetized casing string should adopt the homogeneous magnetic pole connection mode to improve the detection distance and accuracy.