Optimal Design of Combined Two-Tank Latent and Metal Hydrides-Based Thermochemical Heat Storage Systems for High-Temperature Waste Heat Recovery
Abstract
1. Introduction
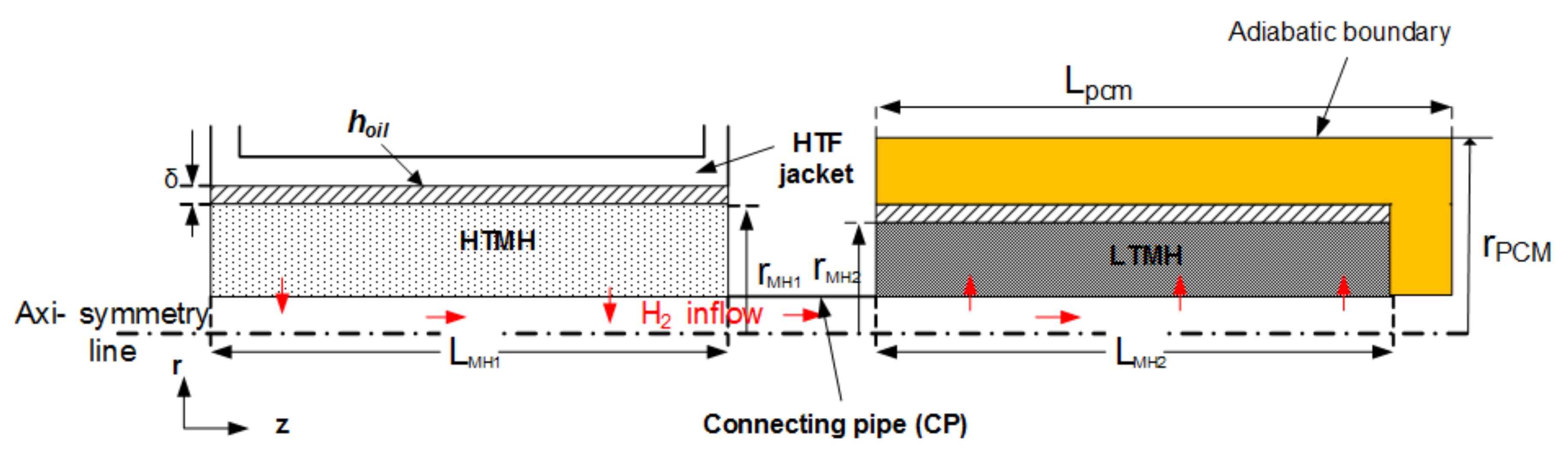
2. Mathematical Model
2.1. Governing Equations
- The thermo-physical properties of hydride are independent of temperature and concentration.
- The thermal equilibrium between the gas and solid is established.
- The radiative heat transfer is neglected.
- The hysteresis in the equilibrium pressure is negligible for any material under study.
- The thermo-physical properties (density, solid–liquid specific heat, thermal conductivity.) of the phase change materials are assumed constant.
- The latent heat of phase change is temperature-independent.
- The natural convection is disregarded since the system is laid horizontally. Therefore, gravity effect on the PCM is neglected.
- The PCMs experience negligible or small (<5%) volume expansion. As a result, the density of PCM is constant in liquid and solid phase [33].
- Energy balance
2.2. Performance Indexes of the Heat Storage System
- The volumetric energy storage density during the heat discharging:With , where VT is the total volume of the heat storage components accounting for the MH beds and the PCM jacket, td is the heat discharging time,
- The specific power during the heat-discharging step:where mHTMH is the weight of the high temperature metal hydride.
- The energy storage efficiency, which is the ratio between the useful heat output to the heat input:
2.3. Optimization Procedure
3. Results and Discussion
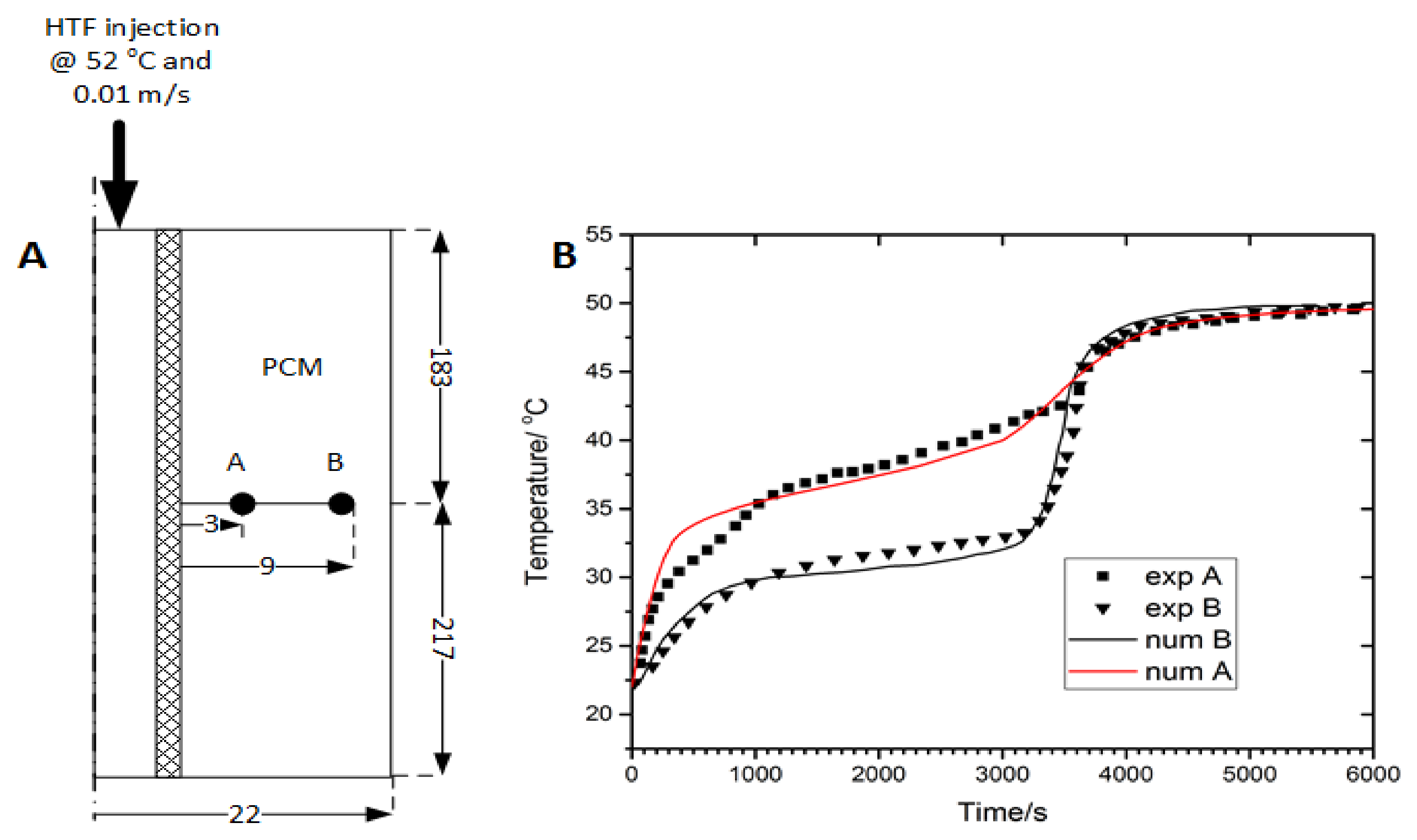
3.1. Model Validation
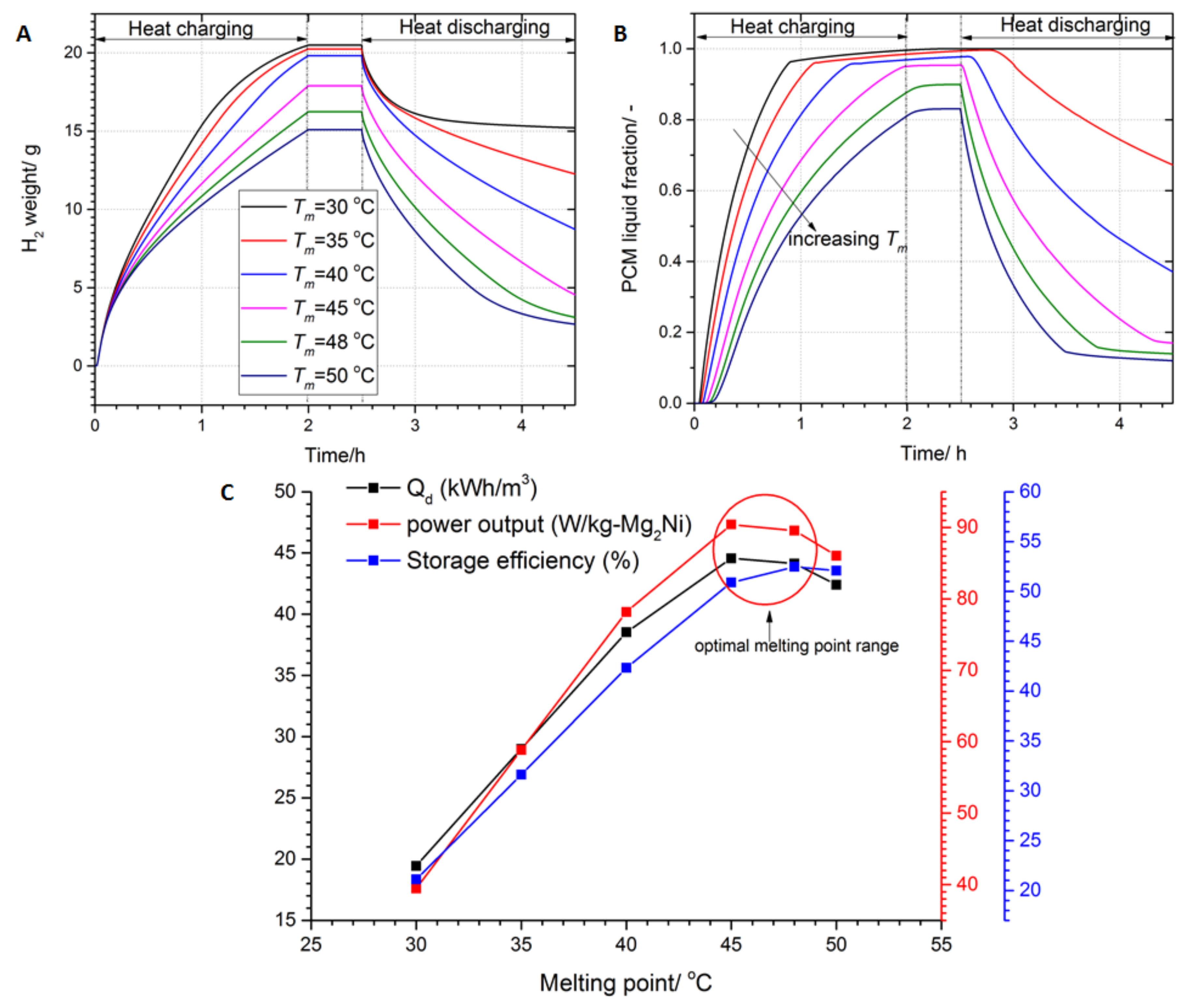
3.2. Effect of the PCM Melting Point on the Performance of the Storage System
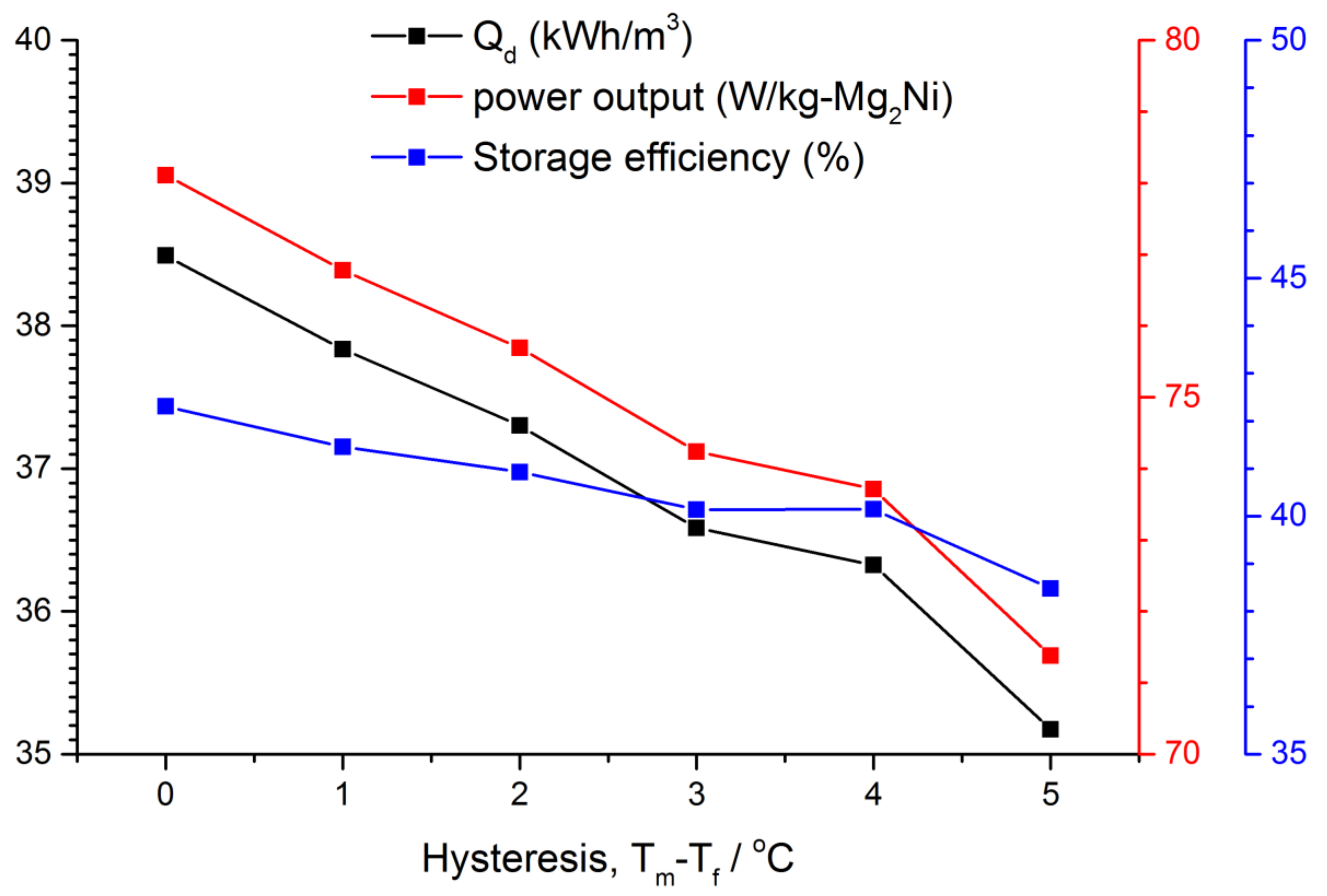
3.3. Effect of the PCM Hysteresis on the Performance Indexes
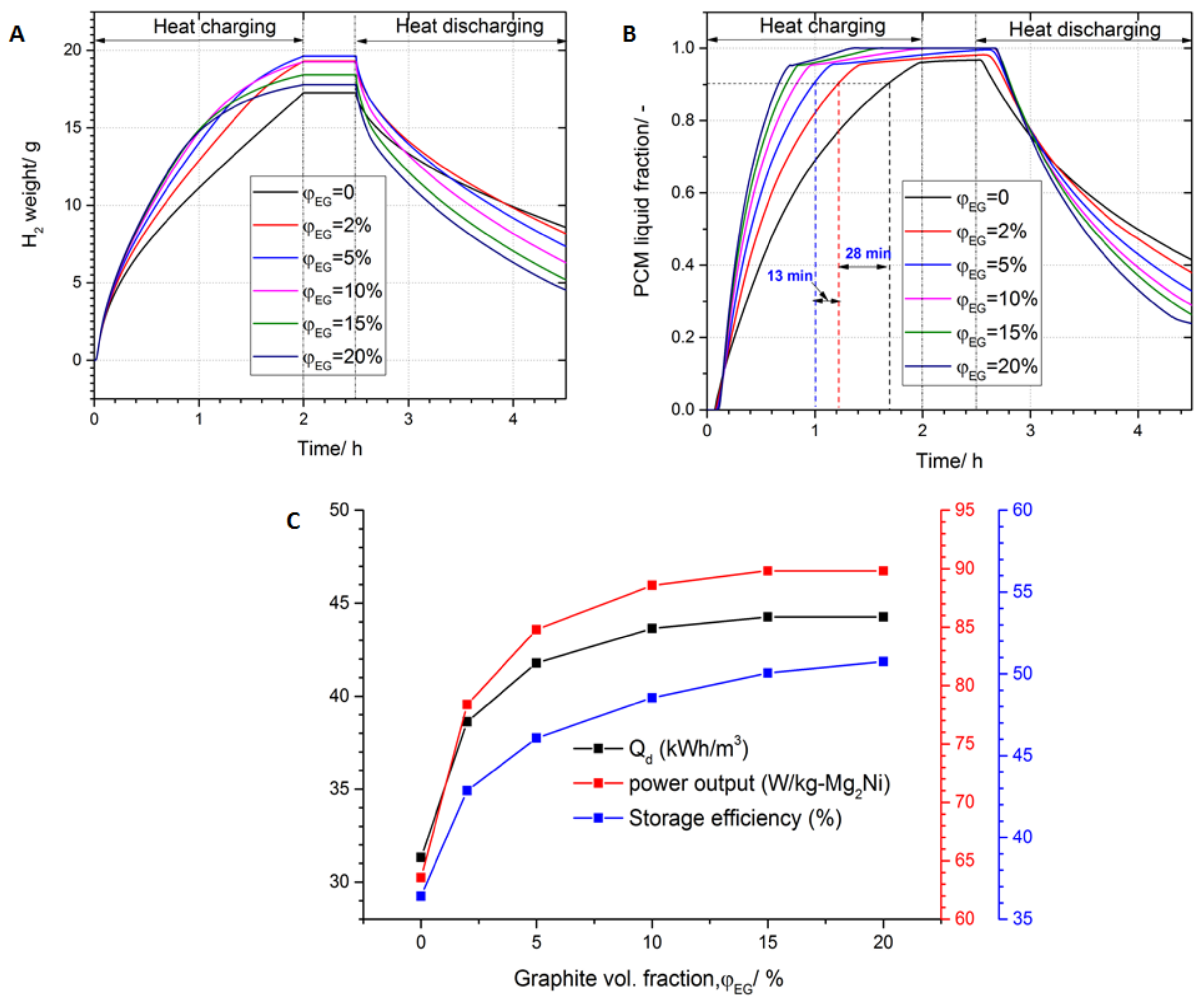
3.4. Effect of Thermal Conductivity Enhancement on the System Performance
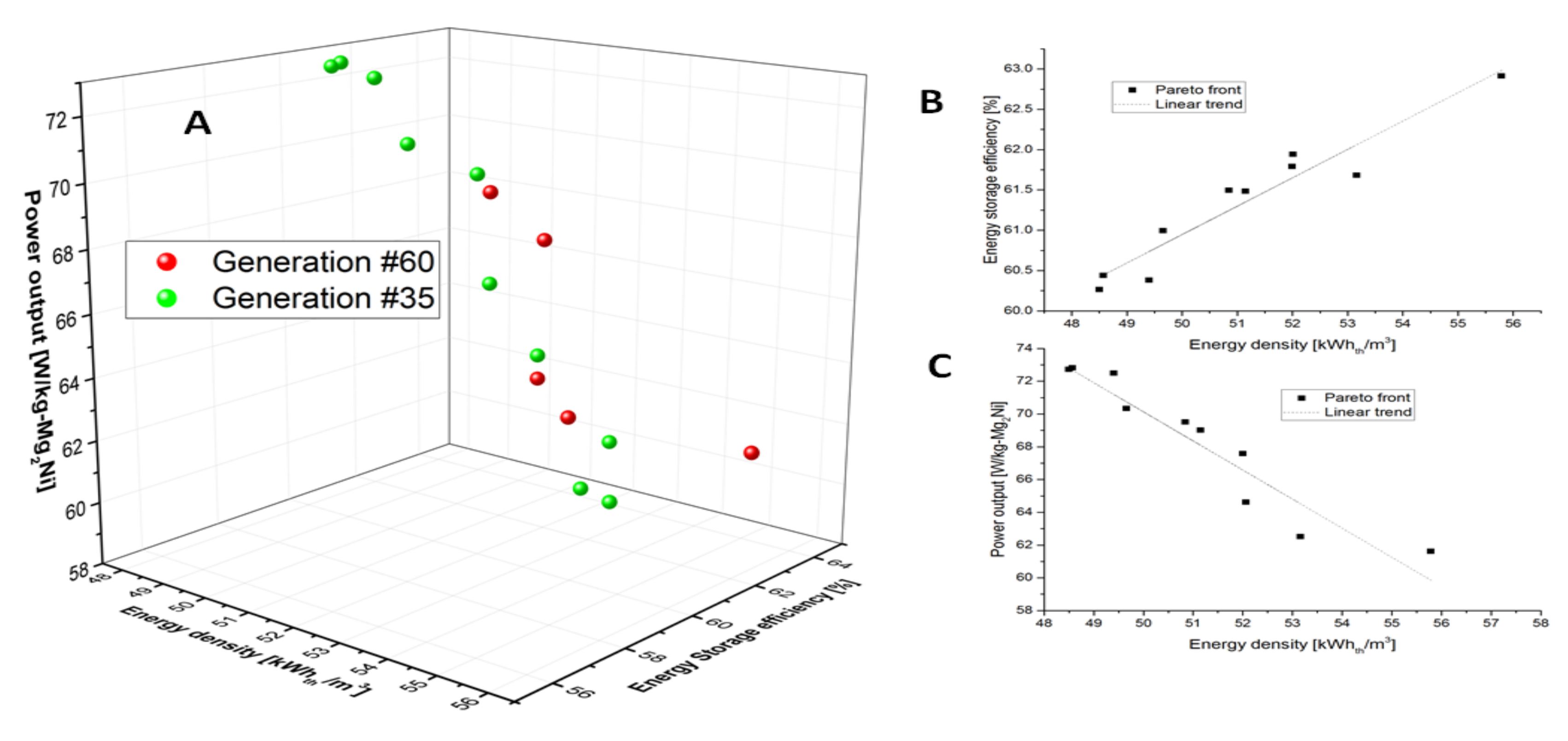
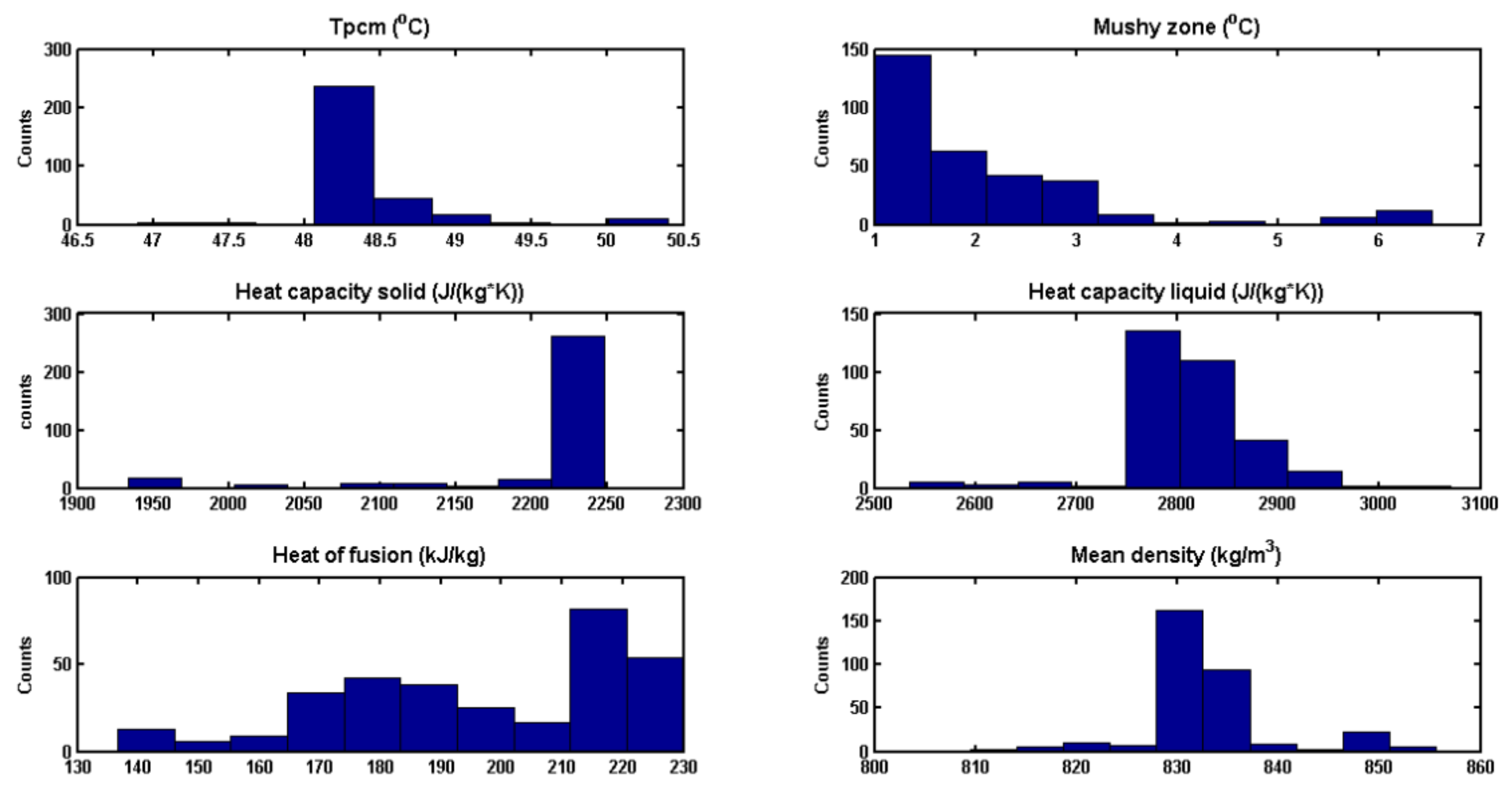
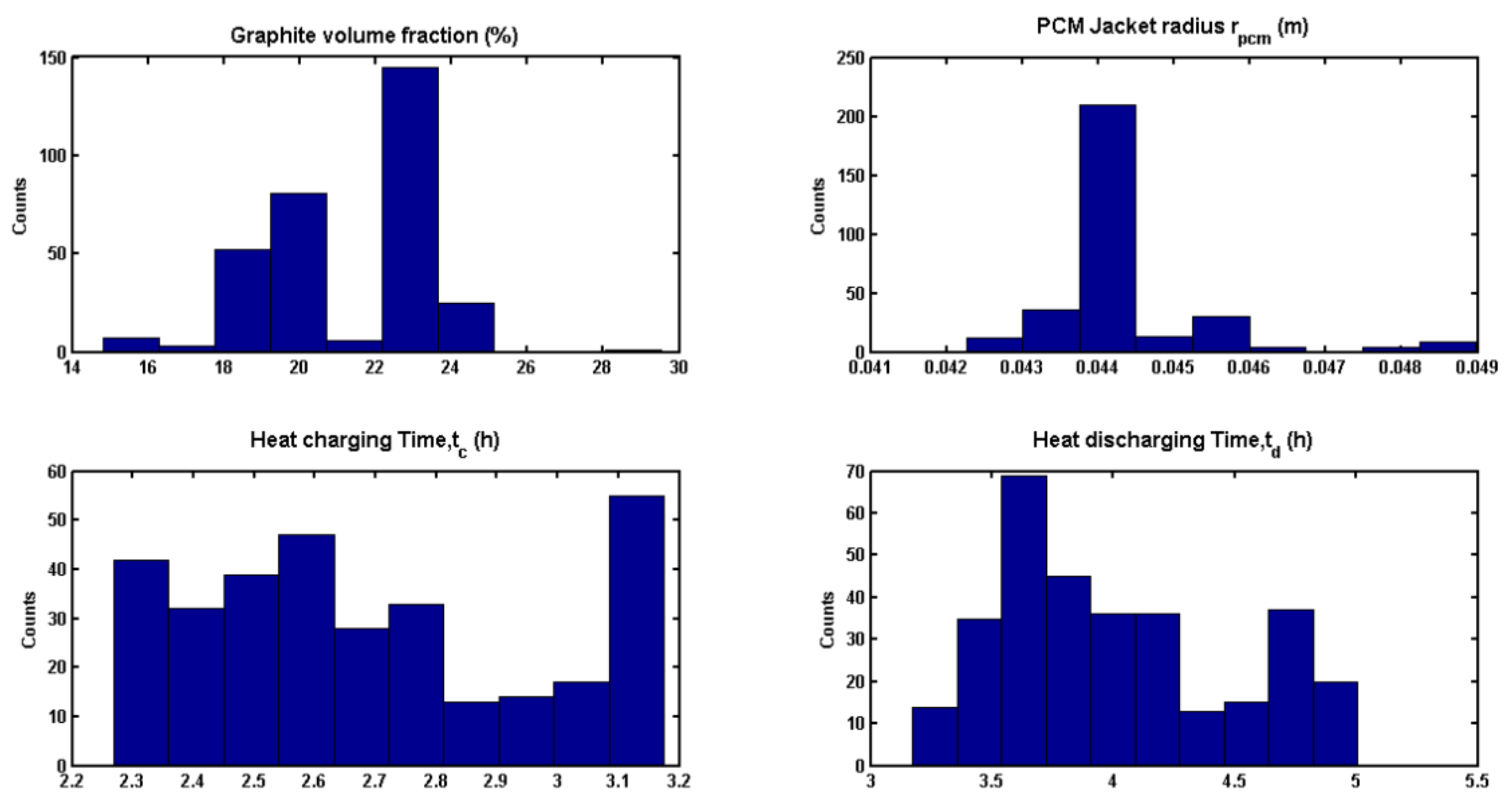
3.5. Optimization Results
4. Conclusions
- The melting point of the PCM should be located in the range defined by the maximum/minimum operating temperatures of the LTMH bed. However, the energy density and power output increase with the increases in melting point up to 45–48 °C then fall thereafter. This is because, at that melting point, the thermodynamic driving force of the reaction between beds is the same during heat charging and discharging processes.
- For a given melting point, the decrease in freezing point by 1–5 °C adversely impacts the heat discharging performance by a maximum of 8%.
- The PCM thermal conductivity enhancement with the addition of different proportions (2, 5, 10, 15 and 20%) of graphite shows a significant improvement (As high as 23%) compared to the case of plain PCM. Moreover, a graphite fraction of 10% was considered as an optimum value, since beyond that, no significant performance improvement was observed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Surface area/m2 | Greek symbols | |
| Cp | Specific heat capacity/J kg−1 K−1 | A | Reacted fraction |
| E | Activation energy/J mol−1 | Δ | Fin thickness/m |
| h | Convective heat transfer coefficient/W m−2 K−1 | Ε | Porosity, Effectiveness/- |
| HTF | Heat transfer fluid | H | Thermal Efficiency/- |
| HTMH | High temperature metal hydride | Φ | Volume fraction/- |
| ΔH | Reaction heat/J mol−1 H2 | Λ | Thermal conductivity/W m−1K−1 |
| k | Reaction rate constant/s−1 | µ | Dynamic viscosity, Pa s |
| K | Permeability/m2 | ρ | Density/kg m−3 |
| L | Reactor length/m | Subscripts | |
| LTMH | Low temperature metal hydride | a | Absorption |
| M | Molecular weight/g mol−1 | c | charging |
| p | Pressure/bar | d | Desorption/discharging |
| PCM | Phase change material | eq | Equilibrium |
| Q | Thermal energy/kWhth | eff | Effective |
| r | Radius, Radial coordinate/m | f | Fluid, PCM freezing |
| Rg | Universal gas constant/J mol−1 K−1 | g | Hydrogen gas |
| ΔS | Entropy change/J mol−1 K−1 | i | inlet |
| t | Time/s | H | Hydrogen |
| ΔT | Temperature range of phase transition/K | MH | Metal hydride |
| V | Volume/m3, hydrogen velocity/m s−1 | wall | Reactor wall |
| wt | Hydrogen weight fraction/% | ||
References
- Miró, L.; Gasia, J.; Cabeza, L.F. Thermal energy storage (TES) for industrial waste heat (IWH) recovery: A review. Appl. Energy 2016, 179, 284–301. [Google Scholar] [CrossRef]
- Singh, D.V.; Pedersen, E. A review of waste heat recovery technologies for maritime apiplications. Energy Convers. Manag. 2016, 111, 315–328. [Google Scholar] [CrossRef]
- Bademlioglu, A.H.; Canbolat, A.S.; Yamankaradeniz, N.; Kaynakli, O. Investigation of parameters affecting organic rankine cycle efficiency by using Taguchi and ANOVA methods. Appl. Therm. Eng. 2018, 145, 221–228. [Google Scholar] [CrossRef]
- Varga, Z.; Palotai, B. Comparison of low temperature waste heat recovery methods. Energy 2017, 137, 1286–1292. [Google Scholar] [CrossRef]
- Yamankaradeniz, N.; Bademlioglu, A.H.; Kaynakli, O. Performance assessments of an organic Rankine cycle with internal heat exchanger based on exergetic approach. J. Energy Resour. Technol. 2018, 140, 102001–102008. [Google Scholar] [CrossRef]
- Wang, T.; Luan, W.; Wang, W.; Tu, S.T. Waste heat recovery through plate heat exchanger based thermoelectric generator system. Appl. Energy 2014, 136, 860–865. [Google Scholar] [CrossRef]
- Yu, X.; Li, Z.; Lu, Y.; Huang, R.; Roskilly, A.P. Investigation of organic Rankine cycle integrated with double latent thermal energy storage for engine waste heat recovery. Energy 2019, 170, 1098–1112. [Google Scholar] [CrossRef]
- Magro, F.D.; Jimenez-Arreola, M.; Romagnoli, A. Improving energy recovery efficiency by retrofitting a PCM-based technology to an ORC system operating under thermal power fluctuations. Appl. Energy 2017, 208, 972–985. [Google Scholar] [CrossRef]
- Gopal, K.N.; Subbarao, R.; Pandiyarajan, V.; Velraj, R. Thermodynamic analysis of a diesel engine integrated with a PCM based energy storage system. Int. J. Thermodyn. 2010, 13, 15–21. [Google Scholar]
- Wang, W.; Guo, S.; Li, H.; Yan, J.; Zhao, J.; Li, X.; Ding, J. Experimental study on the direct/indirect contact energy storage container in mobilized thermal energy system (M-TES). Appl. Energy 2014, 119, 181–189. [Google Scholar] [CrossRef]
- Guo, S.P.; Zhao, J.; Wang, W.L.; Yan, J.Y.; Jin, G.; Wang, X.T. Techno-economic assessment of mobilized thermal energy storage for distributed users: A case study in China. Appl. Energy 2017, 194, 481–486. [Google Scholar] [CrossRef]
- Guo, S.; Liu, Q.; Zhao, J.; Jin, G.; Wu, W.; Yan, J.; Li, H.; Jin, H. Mobilized thermal energy storage: Materials, containers and economic evaluation. Energy Convers. Manag. 2018, 177, 315–329. [Google Scholar] [CrossRef]
- Yan, T.; Wang, R.Z.; Li, T.X.; Wang, L.W.; Fred, I.T. A review of promising candidate reactions for chemical heat storage. Renew. Sustain. Energy Rev. 2015, 43, 13–31. [Google Scholar] [CrossRef]
- Jarimi, H.; Aydin, D.; Yanan, Z.; Ozankaya, G.; Chen, X.; Riffat, S. Review on the recent progress of thermochemical materials and processes for solar thermal energy storage and industrial waste heat recovery. Int. J. Low-Carbon Technol. 2019, 14, 44–69. [Google Scholar] [CrossRef]
- Yu, N.; Wang, R.Z.; Wang, L.W. Sorption thermal storage for solar energy. Prog. Energy Combust. Sci. 2013, 39, 489–514. [Google Scholar] [CrossRef]
- Li, T.X.; Xu, J.X.; Yan, T.; Wang, R.Z. Development of sorption thermal battery for low-grade waste heat recovery and combined cold and heat energy storage. Energy 2016, 107, 347–359. [Google Scholar] [CrossRef]
- Li, T.X.; Wu, S.; Yan, T.; Wang, R.Z.; Zhu, J. Experimental investigation on a dual-mode thermochemical sorption energy storage system. Energy 2017, 140, 383–394. [Google Scholar] [CrossRef]
- Gao, P.; Wang, L.W.; Wang, R.Z.; Zhang, X.F.; Li, D.P.; Liang, Z.W.; Cai, A.F. Experimental investigation of a MnCl2/CaCl2-NH3 two-stage solid sorption freezing system for a refrigerated truck. Energy 2016, 103, 16–26. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, L.W.; Wang, R.Z.; Zhu, F.Q.; Lu, Y.J.; Roskilly, A.P. Experimental investigation on an innovative resorption system for energy storage and upgrade. Energy Convers. Manag. 2017, 138, 651–658. [Google Scholar] [CrossRef]
- Sharma, R.; Anil Kumar, E. Study of ammoniated salts based thermochemical energy storage system with heat up-gradation: A thermodynamic approach. Energy 2017, 141, 1705–1716. [Google Scholar] [CrossRef]
- Mugnier, D.; Goetz, V. Energy storage comparison of sorption systems for cooling and refrigeration. Sol. Energy 2001, 71, 47–55. [Google Scholar] [CrossRef]
- Weber, R.; Dorer, V. Long-term heat storage with NaOH. Vacuum 2008, 82, 708–716. [Google Scholar] [CrossRef]
- Fopah-Lele, A.; Rohde, C.; Neumann, K.; Tietjen, T.; Rönnebeck, T.; N’Tsoukpoe, K.E.; Osteerland, T.; Opel, O.; Ruck, W.K.L. Lab-scale experiment of a closed thermochemical heat storage system including honeycomb heat exchanger. Energy 2016, 114, 225–238. [Google Scholar] [CrossRef]
- N’Tsoukpoe, K.E.; Schmidt, T.; Rammelberg, H.U.; Watts, B.A.; Ruck, W.K.L. A systematic multi-step screening of numerous salt hydrates for low temperature thermochemical energy storage. Appl. Energy 2014, 124, 1–16. [Google Scholar] [CrossRef]
- Clark, R.J.; Mehrabadi, A.; Farid, M. State of the art on salt hydrate thermochemical energy storage systems for use in building applications. J. Energy Storage 2020, 27, 101145. [Google Scholar] [CrossRef]
- Fernandez, A.G.; Fullana, M.; Calabrese, L.; Palomba, V.; Frazzica, A.; Cabeza, L.F. Corrosion assessment of promising hydrated salts as sorption materials for thermal energy storage systems. Renew. Energy 2020, 150, 428–434. [Google Scholar] [CrossRef]
- Bogdanovic, B.; Ritter, A.; Splietho, B. A process steam generator based on the high temperature magnesium hydride/magnesium heat storage system. Int. J. Hydrogen Energy 1995, 20, 811–822. [Google Scholar] [CrossRef]
- Reiser, A.; Bogdanovic, B.; Schlichte, K. The application of Mg-based metal hydrides as heat energy storage systems. Int. J. Hydrogen Energy 2000, 25, 425–430. [Google Scholar] [CrossRef]
- Nyallang, S.N.; Lototskyy, M.; Tolj, I. Selection of metal hydrides-based thermal energy storage: Energy storage efficiency and density targets. Int. J. Hydrogen Energy 2018, 43, 22568–22583. [Google Scholar]
- Sheppard, D.A.; Paskevicius, M.; Humphries, T.D.; Felderhoff, M.; Capurso, G.; Bellosta von Colbe, J.; Dornheim, M.; Klassen, T.; Ward, P.A.; Teprovich, J.A.; et al. Metal hydrides for concentrating solar thermal power energy storage. Appl. Phys. A 2016, 122, 395. [Google Scholar] [CrossRef]
- Nyamsi, N.S.; Tolj, I.; Lototskyy, M. Metal hydride beds-phase change materials: Dual mode thermal energy storage for medium-high temperature industrial waste heat recovery. Energies 2019, 12, 3949. [Google Scholar] [CrossRef]
- Mellouli, S.; Abhilash, E.; Askri, F.; Nasrallah, S.B. Integration of thermal energy storage unit in a metal hydride hydrogen storage tank. Appl. Therm. Eng. 2016, 102, 1185–1196. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Afrouzi, H.H.; Moshfegh, A.; Farhadi, M. Absorption and desorption of hydrogen in long metal hydride tank equipped with phase change material jacket. Int. J. Hydrogen Energy 2016, 41, 9595–9610. [Google Scholar] [CrossRef]
- Lizana, J.; Chacartegui, R.; Barrios-Padura, A.; Valverde, J.M. Advances in thermal energy storage materials and their applications towards zero energy buildings: A critical review. Appl. Energy 2017, 203, 219–239. [Google Scholar] [CrossRef]
- Warzoha, R.J.; Weigand, R.M.; Fleischer, A.S. Temperature-dependent thermal properties of a paraffin phase change material embedded with herringbone style graphite nanofibers. Appl. Energy 2015, 137, 716–725. [Google Scholar] [CrossRef]
- Yang, X.; Wei, P.; Cui, X.; Jin, L.; He, Y.L. Thermal response of annuli filled with metal foam for thermal energy storage: An experimental study. Appl. Energy 2019, 250, 1457–1467. [Google Scholar] [CrossRef]
- Ling, Z.; Chen, J.; Xu, T.; Fang, X.; Gao, X.; Zhang, Z. Thermal conductivity of an organic phase change material/expanded graphite composite across phase change temperature range and a novel thermal conductivity model. Energy Convers. Manag. 2015, 102, 202–208. [Google Scholar] [CrossRef]
- Siyabi, I.A.; Khanna, S.; Mallick, T.; Sundaram, S. An experimental and numerical study on the effect of inclination angle of phase change materials thermal energy storage system. J. Energy Storage 2019, 23, 57–68. [Google Scholar] [CrossRef]
- Chung, C.A.; Lin, C.S. Prediction of hydrogen desorption performance of Mg2Ni hydride reactors. Int. J. Hydrogen Energy 2009, 34, 9409–9423. [Google Scholar] [CrossRef]
- Merlin, K.; Soto, J.; Delaunay, D.; Traonvouez, L. Industrial waste heat recovery using an enhanced conductivity latent heat thermal energy storage. Appl. Energy 2016, 183, 491–503. [Google Scholar] [CrossRef]
- Longeon, M.; Soupart, A.; Fourmigué, J.F.; Bruch, A.; Marty, P. Experimental and numerical study of annular PCM storage in the presence of natural convection. Appl. Energy 2013, 112, 175–184. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S. A fast and elitist multiobjective genetic algorithm: NSGA-II. Evolutionary Computation. IEEE Trans. 2002, 6, 182–197. [Google Scholar]
- Sarı, A.; Karaipekli, A. Thermal conductivity and latent heat thermal energy storage characteristics of paraffin/expanded graphite composite as phase change material. Appl. Therm. Eng. 2007, 27, 1271–1277. [Google Scholar] [CrossRef]
- Ji, H.; Sellan, D.P.; Pettes, M.T.; Kong, X.; Ji, J.; Shi, L.; Ruoff, R.S. Enhanced thermal conductivity of phase change materials with ultrathin-graphite foams for thermal energy storage. Energy Environ. Sci. 2014, 7, 1185–1192. [Google Scholar] [CrossRef]
- Hajabdollahi, Z.; Hajabdollahi, H.; Kim, K.C. Heat transfer enhancement and optimization of a tube fitted with twisted tape in a fin-and-tube heat exchanger. J. Therm. Anal. Calorim. 2020, 140, 1015–1027. [Google Scholar] [CrossRef]
- Arora, R.; Kaushik, S.C.; Kumar, R.; Arora, R. Soft computing based multi-objective optimization of Brayton cycle power plant with isothermal heat addition using evolutionary algorithm and decision making. Appl. Soft Comput. 2016, 46, 267–283. [Google Scholar] [CrossRef]
| Mg2Ni | LaNi5 | SS316L | Graphite | |
|---|---|---|---|---|
| Heat of reaction/kJ/mol | 64.5 | 30 | - | - |
| Entropy change/J/mol/K | 122.5 | 108 | - | - |
| Activation energy, abs-des/kJ/mol | 52.20/63.46 | 21.17/16.47 | - | - |
| Rate constant, abs-des/s−1 | 175/5452.2 | 59.18/9.57 | - | |
| Density/kg/m3 | 3200 | 8400 | 7990 | 2200 |
| Specific heat/J/kg/K | 697 | 419 | 500 | 710 |
| H2 capacity/wt.% | 3.6 | 1.3 | - | - |
| Effective thermal conductivity/W/mK | 1 | 1 | 16.2 | 25 |
| Bed thickness/m | 0.015 | 0.015 | 0.002 | - |
| Reactor volume/m3 | 4.948 × 10−4 | 4.948 × 10−4 | - | - |
| Overall heat transfer coefficient hoil/W/m2/K | 500 | - | - | - |
| Rubitherm PCM (RT35) | Range | |
|---|---|---|
| Melting point range Tm/°C | 35 | 30–55 |
| Hysteresis behavior Tm-Tf/°C | 0 | 0,1,2,3,4,5 |
| Mushy zone ΔTtr/°C | 1 | 1–20 |
| Density: solid-liquid/kg m−3 | 880 | 760–2000 |
| Effective thermal conductivity/W m−1 K−1 | 1 | - |
| Specific heat, Cp/J kg−1 K−1 | 2000 | 1800–3000 |
| Latent heat of fusion, ∆Hpcm/kJ kg−1 | 165 | 110–230 |
| Volumetric energy density/MJ m−3 | 145 | - |
| PCM jacket radius/m | 0.04 | 0.035–0.07 |
| PCM jacket length Lpcm/m | 0.52 | - |
| Graphite fraction, /% | - | 0–30 |
| Melting Point Tm (°C) | Peq,LTMH(Tm)(bar) | Heat Charging Process | Heat Discharging Process | ||
|---|---|---|---|---|---|
| Thermodynamic Driving Force: | Maximum H2 Exchanged (g) | Thermodynamic Driving Force: | Maximum H2 Exchanged (g) | ||
| 30 | 2.95 | 3.2 | 20.49 | 0.927 | 5.27 |
| 35 | 3.58 | 2.63 | 20.25 | 1.12 | 7.97 |
| 40 | 4.31 | 2.19 | 19.82 | 1.35 | 11.08 |
| 45 | 5.17 | 1.82 | 17.90 | 1.62 | 13.35 |
| 48 | 5.74 | 1.64 | 16.24 | 1.80 | 13.14 |
| 50 | 6.16 | 1.53 | 15.09 | 1.93 | 12.41 |
| Design Parameters | Baseline Design (RT35) | Optimized Design |
|---|---|---|
| Melting point Tm (°C) | 35 | 48.25 |
| Mushy zone ΔT (°C) | 1 | 1.15 |
| Heat capacity Cps(J/kg/K) | 2000 | 2200 |
| Heat capacity Cpl(J/kg/K) | 2000 | 2700 |
| Latent heat ΔH(kJ/kg) | 165 | 220 |
| Density, ρpcm(kg/m3) | 880 | 840 |
| Graphite fraction, (vol.%) | 0 | 23 |
| Thermal conductivity using Equation (22) (W/mK) | 0.2 | 5.9 |
| Heat charging time, tc (h) | 2 | 2.66 |
| Heat discharging time, td (h) | 2 | 3.60 |
| Performance indexes | ||
| Power density (W/kg-Mg2Ni) | 30.8 | 67.48 |
| Energy density (kWhth/m3) | 15.17 | 50.16 |
| Energy storage efficiency (%) | 19.69 | 61.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyamsi, S.N.; Lototskyy, M.; Tolj, I. Optimal Design of Combined Two-Tank Latent and Metal Hydrides-Based Thermochemical Heat Storage Systems for High-Temperature Waste Heat Recovery. Energies 2020, 13, 4216. https://doi.org/10.3390/en13164216
Nyamsi SN, Lototskyy M, Tolj I. Optimal Design of Combined Two-Tank Latent and Metal Hydrides-Based Thermochemical Heat Storage Systems for High-Temperature Waste Heat Recovery. Energies. 2020; 13(16):4216. https://doi.org/10.3390/en13164216
Chicago/Turabian StyleNyamsi, Serge Nyallang, Mykhaylo Lototskyy, and Ivan Tolj. 2020. "Optimal Design of Combined Two-Tank Latent and Metal Hydrides-Based Thermochemical Heat Storage Systems for High-Temperature Waste Heat Recovery" Energies 13, no. 16: 4216. https://doi.org/10.3390/en13164216
APA StyleNyamsi, S. N., Lototskyy, M., & Tolj, I. (2020). Optimal Design of Combined Two-Tank Latent and Metal Hydrides-Based Thermochemical Heat Storage Systems for High-Temperature Waste Heat Recovery. Energies, 13(16), 4216. https://doi.org/10.3390/en13164216







