Air Temperature Forecasting Using Machine Learning Techniques: A Review
Abstract
1. Introduction
2. Overview of Machine Learning Based Strategies and Forecast Performance Factors
- Supervised Learning, which has information of the predicted outputs to label the training set and is used for the model training.
- Unsupervised Learning, which does not have information about the desired output to label the training data. Consequently, the learning algorithm must find patterns to cluster the input data.
- Semi-supervised Learning, which uses labeled and unlabeled data in the training process.
- Reinforcement Learning, which uses the maximization of a scalar reward or reinforcement signal to perform the learning process, being positive or negative based on the system goal. Positive ones are known as “rewards” while negative ones are known as “punishments”.
2.1. Artificial Neural Networks
- Tangent Hyperbolic Function: ,
- Sigmoid Function: ,
- Rectified Linear Unit (ReLU) Function: max,
- Gaussian Function: ,
- Linear Function: ,
2.2. Support Vector Machines
- A Linear kernel: ,
- A Polynomial kernel: ,
- A Radial kernel: ,
- A Sigmoid kernel: ,
2.3. Evaluation Measures
- Mean Absolute Error (MAE): This measure is an error statistic that averages the distances between the estimated and the observed data for N samples:
- Median Absolute Error (MdAE): This measure is defined as the median of the absolute differences for any N pairs of forecasts and measurements:
- Mean Square Error (MSE): This measure is defined as the average squared difference between the predicted and the observed temperature data, for N samples:
- Root Mean Square Error (RMSE): This measure is the standard deviation of the difference between the estimation and the true observed data (See Equation (10)). This measure is more sensitive to big prediction errors:
- Mean Absolute Percentage Error (MAPE): This measure offers a proportionate nature of error with respect to the input data. It is defined as:
- Root Mean Square Percentage Error (RMSPE) RMSPE is calculated according to:
- Relative Mean Absolute Error (RMAE): This measure is computed as:where and are calculated by using Equation (7) for the forecasting model and the reference model, respectively.
- Relative Root Mean Square Error (RRMSE): This measure is calculated in a similar way to the RMAE, but in this case using the error defined in Equation (10):
2.4. Input Features, Time Horizon, and Spatial Scale
- The model is based on other meteorological or geographical variables (e.g., solar radiation, rain, relative humidity measurements, among others).
- The model only takes into account the historically observed data of temperature as system input.
- The model takes a combination of both temperature values and other parameters, to perform the prediction.
3. Long-Term Global Temperature Forecasting
4. Regional Temperature Forecasting
4.1. Hourly Temperature Forecasting
4.2. Daily Temperature Forecasting
4.3. Monthly Temperature Forecasting
5. Discussion and Research Gaps Identification
- Most of the research presented in this review is focused on the local analysis of the air temperature. However, there is not an extensive study about the anomalies prediction of temperature at a global level by means of these ML-based approaches. Taking into account the robust data currently available in diverse web sites, different ML-strategies and input features could be used to accurately predict temperature anomalies at the global level.
- Research reported at the regional level has not deeply analyzed the dependency of the temperature values of the surrounding area in the temperature estimation. A study oriented to analyze the impact of using temperature values of surrounding stations as inputs, based on the distance each other, could be of particular interest.
- A large number of the works described in this review do not include a time horizon analysis. The lack of these results makes it difficult to have a better idea of the accuracy of the method proposed. Likewise, a set of evaluation measures must be calculated in order to facilitate the comparison with other methods which may use the same data-set.
- Taking into account that accuracy results strongly depend on the data-set analyzed, a comprehensive study of the influence of the data-set size for training and testing should be done to offer a more fair comparison between strategies.
- A comparative analysis with all the available ANN-based techniques (MLPNN, RBFNN, ERNN, GRNN, JPSN, RCNN, and SDAE) and SVM variations (LS-SVM, PSVM, WT+SVM) should be carried out in order to determine the best strategy and algorithms to forecast air temperature for different time horizon. In this sense, as well as it is developed in other areas, a competition using a complete standard data-set could help in this objective.
- The effect analysis of each variable, such as maximum, minimum, and average temperature, precipitation, pressure, Mean Sea Level, Wind Speed and Direction, Relative Humidity, Sunshine, Evaporation, Daylight, Time (Hour, day or Month), Solar Radiation, geographical variables (latitude, longitude, and altitude), cloudiness, and CO2 emissions, used in the prediction is required to be taken into account to increase the temperature prediction accuracy.
- A further study about the feature selection, based on their relevance, should be performed. Different strategies, such as Automatic Relevance Determination, closely-related sparse Bayesian learning, or Niching genetic algorithm have not been taken into account.
- Recently, Deep Learning strategies have shown a great performance for classification tasks [97]. However, a few studies have proven, with promising results, that prediction could be accurately done by means of these techniques. More further analysis should be developed in this area.
- For the evaluation of RNN, the size of the time series required to accurately predict a single value of temperature should be studied. Likewise, a comprehensive study about the structure of the recurrent unit should be included.
- In-depth analysis using statistical significance tests is required in order to assess the forecasting model’s performance in terms of its ability to generate both unbiased and accurate forecasts. In these cases, the respective accuracy is evaluated by using both error magnitude and directional change error criteria.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AANN | Abductive Artificial Neural Network |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| AR | Auto-Regressive |
| DT | Daily Temperature |
| EN | Elastic Net |
| ENSO | El Niño Southern Oscillation |
| ERNN | Elman Recurrent Neural Network |
| GLOT | Global Land-Ocean Temperature |
| GSVM | Generalized Support Vector Machine |
| GT | Global Temperature |
| HFM | Hopfield model |
| HT | Hourly Temperature |
| JPSN | Jordan Pi-Sigma Network |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LS-SVM | Least Squares-Support Vector Machine |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MdAE | Median Absolute Error |
| ML | Machine Learning |
| MLPNN | MultiLayer Perceptron Neural Network |
| MSE | Mean Squared Error |
| PNN | Probabilistic Neural Network |
| PSO | Particle Swarm Optimization |
| RBFNN | Radial Basis Functions Neural Network |
| RCNN | Recurrent Convolutional Neural Network |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| SDAE | Stacked Denoising Auto-Encoders |
| SI | Solar Irradiance |
| SOD | Stratospheric Optical Depth |
| SOFM | Self-Organizing Feature Map |
| SVM | Support Vector Machine |
| WNN | Wavelet Neural Network |
References
- Tol, R.S. Estimates of the damage costs of climate change. Part 1: Benchmark estimates. Environ. Resour. Econ. 2002, 21, 47–73. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014. [Google Scholar]
- Abdel-Aal, R. Hourly temperature forecasting using abductive networks. Eng. Appl. Artif. Intell. 2004, 17, 543–556. [Google Scholar] [CrossRef]
- Li, S.; Goel, L.; Wang, P. An ensemble approach for short-term load forecasting by extreme learning machine. Appl. Energy 2016, 170, 22–29. [Google Scholar] [CrossRef]
- Ruano, A.E.; Crispim, E.M.; Conceiçao, E.Z.; Lúcio, M.M.J. Prediction of building’s temperature using neural networks models. Energy Build. 2006, 38, 682–694. [Google Scholar] [CrossRef]
- García, M.A.; Balenzategui, J. Estimation of photovoltaic module yearly temperature and performance based on nominal operation cell temperature calculations. Renew. Energy 2004, 29, 1997–2010. [Google Scholar] [CrossRef]
- Dombaycı, Ö.A.; Gölcü, M. Daily means ambient temperature prediction using artificial neural network method: A case study of Turkey. Renew. Energy 2009, 34, 1158–1161. [Google Scholar] [CrossRef]
- Camia, A.; Bovio, G.; Aguado, I.; Stach, N. Meteorological fire danger indices and remote sensing. In Remote Sensing of Large Wildfires; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–59. [Google Scholar] [CrossRef]
- Ben-Nakhi, A.E.; Mahmoud, M.A. Cooling load prediction for buildings using general regression neural networks. Energy Convers. Manag. 2004, 45, 2127–2141. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Santamouris, M.; Tsangrassoulis, A. On the energy consumption in residential buildings. Energy Build. 2002, 34, 727–736. [Google Scholar] [CrossRef]
- Smith, D.M.; Cusack, S.; Colman, A.W.; Folland, C.K.; Harris, G.R.; Murphy, J.M. Improved surface temperature prediction for the coming decade from a global climate model. Science 2007, 317, 796–799. [Google Scholar] [CrossRef]
- World Meteorological Organization. 2019. Available online: https://public.wmo.int/en/our-mandate/what-we-do (accessed on 1 February 2019).
- Penland, C.; Magorian, T. Prediction of Nino 3 sea surface temperatures using linear inverse modeling. J. Clim. 1993, 6, 1067–1076. [Google Scholar] [CrossRef]
- Penland, C.; Matrosova, L. Prediction of tropical Atlantic sea surface temperatures using linear inverse modeling. J. Clim. 1998, 11, 483–496. [Google Scholar] [CrossRef]
- Johnson, S.D.; Battisti, D.S.; Sarachik, E. Empirically derived Markov models and prediction of tropical Pacific sea surface temperature anomalies. J. Clim. 2000, 13, 3–17. [Google Scholar] [CrossRef]
- Newman, M. An empirical benchmark for decadal forecasts of global surface temperature anomalies. J. Clim. 2013, 26, 5260–5269. [Google Scholar] [CrossRef]
- Figura, S.; Livingstone, D.M.; Kipfer, R. Forecasting groundwater temperature with linear regression models using historical data. Groundwater 2015, 53, 943–954. [Google Scholar] [CrossRef]
- Bartos, I.; Jánosi, I. Nonlinear correlations of daily temperature records over land. Nonlinear Process. Geophys. 2006, 13, 571–576. [Google Scholar] [CrossRef]
- Bonsal, B.; Zhang, X.; Vincent, L.; Hogg, W. Characteristics of Daily and Extreme Temperatures over Canada. J. Clim. 2001, 14, 1959–1976. [Google Scholar] [CrossRef]
- Miyano, T.; Girosi, F. Forecasting Global Temperature Variations by Neural Networks; Technical Report; Massachusetts Institute of Technology, Cambridge Artificial Intelligence Laboratory: Cambridge, MA, USA, 1994. [Google Scholar]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Combining neural networks and ARIMA models for hourly temperature forecast. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, IJCNN 2000, Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000. [Google Scholar]
- Tasadduq, I.; Rehman, S.; Bubshait, K. Application of neural networks for the prediction of hourly mean surface temperatures in Saudi Arabia. Renew. Energy 2002, 25, 545–554. [Google Scholar] [CrossRef]
- Lanza, P.A.G.; Cosme, J.M.Z. A short-term temperature forecaster based on a novel radial basis functions neural network. Int. J. Neural Syst. 2001, 11, 71–77. [Google Scholar] [CrossRef]
- Maqsood, I.; Khan, M.R.; Abraham, A. An ensemble of neural networks for weather forecasting. Neural Comput. Appl. 2004, 13, 112–122. [Google Scholar] [CrossRef]
- Smith, B.A.; McClendon, R.W.; Hoogenboom, G. Improving air temperature prediction with artificial neural networks. Int. J. Comput. Intell. 2006, 3, 179–186. [Google Scholar]
- Smith, B.A.; Hoogenboom, G.; McClendon, R.W. Artificial neural networks for automated year-round temperature prediction. Comput. Electron. Agric. 2009, 68, 52–61. [Google Scholar] [CrossRef]
- Jallal, M.A.; Chabaa, S.; El Yassini, A.; Zeroual, A.; Ibnyaich, S. Air temperature forecasting using artificial neural networks with delayed exogenous input. In Proceedings of the 2019 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS), Fez, Morocco, 3–4 April 2019. [Google Scholar]
- Pal, N.R.; Pal, S.; Das, J.; Majumdar, K. SOFM-MLP: A hybrid neural network for atmospheric temperature prediction. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 2783–2791. [Google Scholar] [CrossRef]
- Maqsood, I.; Abraham, A. Weather analysis using ensemble of connectionist learning paradigms. Appl. Soft Comput. 2007, 7, 995–1004. [Google Scholar] [CrossRef]
- Ustaoglu, B.; Cigizoglu, H.K.; Karaca, M. Forecast of daily mean, maximum and minimum temperature time series by three artificial neural network methods. Meteorol. Appl. 2008, 15, 431–445. [Google Scholar] [CrossRef]
- Hayati, M.; Mohebi, Z. Application of artificial neural networks for temperature forecasting. World Acad. Sci. Eng. Technol. 2007, 28, 275–279. [Google Scholar]
- Abhishek, K.; Singh, M.; Ghosh, S.; Anand, A. Weather Forecasting Model using Artificial Neural Network. Procedia Technol. 2012, 4, 311–318. [Google Scholar] [CrossRef]
- Chevalier, R.F.; Hoogenboom, G.; McClendon, R.W.; Paz, J.A. Support vector regression with reduced training sets for air temperature prediction: A comparison with artificial neural networks. Neural Comput. Appl. 2010, 20, 151–159. [Google Scholar] [CrossRef]
- Ortiz-García, E.; Salcedo-Sanz, S.; Casanova-Mateo, C.; Paniagua-Tineo, A.; Portilla-Figueras, J. Accurate local very short-term temperature prediction based on synoptic situation Support Vector Regression banks. Atmos. Res. 2012, 107, 1–8. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Benghanem, M. Least squares support vector machine for short-term prediction of meteorological time series. Theor. Appl. Climatol. 2013, 111, 297–307. [Google Scholar] [CrossRef]
- Mori, H.; Kanaoka, D. Application of support vector regression to temperature forecasting for short-term load forecasting. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, Florida, USA, 12–17 August 2017. [Google Scholar]
- Radhika, Y.; Shashi, M. Atmospheric Temperature Prediction using Support Vector Machines. Int. J. Comput. Theory Eng. 2009, 55–58. [Google Scholar] [CrossRef]
- Paniagua-Tineo, A.; Salcedo-Sanz, S.; Casanova-Mateo, C.; Ortiz-García, E.; Cony, M.; Hernández-Martín, E. Prediction of daily maximum temperature using a support vector regression algorithm. Renew. Energy 2011, 36, 3054–3060. [Google Scholar] [CrossRef]
- Abubakar, A.; Chiroma, H.; Zeki, A.; Uddin, M. Utilising key climate element variability for the prediction of future climate change using a support vector machine model. Int. J. Glob. Warm. 2016, 9, 129–151. [Google Scholar] [CrossRef]
- Hewage, P.; Trovati, M.; Pereira, E.; Behera, A. Deep learning-based effective fine-grained weather forecasting model. Pattern Anal. Appl. 2020, 1–24. [Google Scholar] [CrossRef]
- Roesch, I.; Günther, T. Visualization of Neural Network Predictions for Weather Forecasting. Comput. Graph. Forum 2018, 38, 209–220. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Duveiller, G.; Fasbender, D.; Meroni, M. Revisiting the concept of a symmetric index of agreement for continuous datasets. Sci. Rep. 2016, 6, 19401. [Google Scholar]
- Kalogirou, S.A. Artificial neural networks in renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks; Prentice Hall: New York, NY, USA, 1994; Volume 2. [Google Scholar]
- Haykin, S.S.; Haykin, S.S.; Haykin, S.S.; Elektroingenieur, K.; Haykin, S.S. Neural Networks and Learning Machines; Pearson Education: Bengaluru, India, 2009; Volume 3. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Gunn, S.R. Support vector machines for classification and regression. In ISIS Technical Report; University of Southampton: Southampton, UK, 1998; Volume 14, pp. 5–16. [Google Scholar]
- Mellit, A. Artificial Intelligence technique for modelling and forecasting of solar radiation data: A review. Int. J. Artif. Intell. Soft Comput. 2008, 1, 52–76. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Argiriou, A. Use of neural networks for tropospheric ozone time series approximation and forecasting— A review. Atmos. Chem. Phys. Discuss. 2007, 7, 5739–5767. [Google Scholar] [CrossRef]
- Wang, W.; Xu, Z.; Weizhen Lu, J. Three improved neural network models for air quality forecasting. Eng. Comput. 2003, 20, 192–210. [Google Scholar] [CrossRef]
- Ko, C.N.; Lee, C.M. Short-term load forecasting using SVR (support vector regression)-based radial basis function neural network with dual extended Kalman filter. Energy 2013, 49, 413–422. [Google Scholar] [CrossRef]
- Topcu, I.B.; Sarıdemir, M. Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 41, 305–311. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Shcherbakov, M.; Brebels, A. Outliers and anomalies detection based on neural networks forecast procedure. In Proceedings of the 31st Annual International Symposium on Forecasting, ISF, Prague, Czech Republic, 26–29 June 2011. [Google Scholar]
- Armstrong, J.; Collopy, F. Error measures for generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef]
- Banhatti, A.G.; Deka, P.C. Effects of Data Pre-processing on the Prediction Accuracy of Artificial Neural Network Model in Hydrological Time Series. In Urban Hydrology, Watershed Management and Socio-Economic Aspects; Springer International Publishing: Cham, Switzerland, 2016; pp. 265–275. [Google Scholar] [CrossRef]
- Chen, C.; Twycross, J.; Garibaldi, J.M. A new accuracy measure based on bounded relative error for time series forecasting. PLoS ONE 2017, 12, e0174202. [Google Scholar] [CrossRef]
- Shcherbakov, M.V.; Brebels, A.; Shcherbakova, N.L.; Tyukov, A.P.; Janovsky, T.A.; Kamaev, V.A. A survey of forecast error measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar]
- Solomon, S.; Qin, D.; Manning, M.; Averyt, K.; Marquis, M. Climate Change 2007—The Physical Science Basis: Working Group I Contribution to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, MA, USA, 2007; Volume 4. [Google Scholar]
- Lee, T.C.; Zwiers, F.W.; Zhang, X.; Tsao, M. Evidence of decadal climate prediction skill resulting from changes in anthropogenic forcing. J. Clim. 2006, 19, 5305–5318. [Google Scholar] [CrossRef][Green Version]
- Stott, P.A.; Kettleborough, J.A. Origins and estimates of uncertainty in predictions of twenty-first century temperature rise. Nature 2002, 416, 723. [Google Scholar] [CrossRef]
- Knutti, R.; Stocker, T.; Joos, F.; Plattner, G.K. Probabilistic climate change projections using neural networks. Clim. Dyn. 2003, 21, 257–272. [Google Scholar] [CrossRef]
- Pasini, A.; Lorè, M.; Ameli, F. Neural network modelling for the analysis of forcings/temperatures relationships at different scales in the climate system. Ecol. Model. 2006, 191, 58–67. [Google Scholar] [CrossRef]
- Pasini, A.; Pelino, V.; Potestà, S. A neural network model for visibility nowcasting from surface observations: Results and sensitivity to physical input variables. J. Geophys. Res. Atmos. 2001, 106, 14951–14959. [Google Scholar] [CrossRef]
- Fildes, R.; Kourentzes, N. Validation and forecasting accuracy in models of climate change. Int. J. Forecast. 2011, 27, 968–995. [Google Scholar] [CrossRef]
- Hassani, H.; Silva, E.S.; Gupta, R.; Das, S. Predicting global temperature anomaly: A definitive investigation using an ensemble of twelve competing forecasting models. Phys. A Stat. Mech. Its Appl. 2018, 509, 121–139. [Google Scholar] [CrossRef]
- Jones, P.; Wigley, T.; Wright, P. Global temperature variations between 1861 and 1984. Nature 1986, 322, 430–434. [Google Scholar] [CrossRef]
- Jones, P.; New, M.; Parker, D.E.; Martin, S.; Rigor, I.G. Surface air temperature and its changes over the past 150 years. Rev. Geophys. 1999, 37, 173–199. [Google Scholar] [CrossRef]
- University of East Anglia. Climatic Research Unit. 2019. Available online: http://www.cru.uea.ac.uk/ (accessed on 1 March 2019).
- GesDisc. Solar Irradiance Anomalies. 2019. Available online: http://www.soda-pro.com/ (accessed on 1 March 2019).
- GISS. Stratospheric Aerosol Optical Thickness. 2019. Available online: https://data.giss.nasa.gov/modelforce/strataer/ (accessed on 1 March 2019).
- NCEI. Ocean Carbon Data System (OCADS). 2019. Available online: https://www.nodc.noaa.gov/ocads/ (accessed on 1 March 2019).
- NASA. GISS Surface Temperature Analysis (GISTEMP v3). 2019. Available online: https://data.giss.nasa.gov/gistemp/index_v3.html (accessed on 1 March 2019).
- Xuejie, G.; Zongci, Z.; Yihui, D.; Ronghui, H.; Giorgi, F. Climate change due to greenhouse effects in China as simulated by a regional climate model. Adv. Atmos. Sci. 2001, 18, 1224–1230. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A practical guide to support vector classification. 2003. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 1 March 2019).
- Hossain, M.; Rekabdar, B.; Louis, S.J.; Dascalu, S. Forecasting the weather of Nevada: A deep learning approach. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015. [Google Scholar] [CrossRef]
- Pardo, A.; Meneu, V.; Valor, E. Temperature and seasonality influences on Spanish electricity load. Energy Econ. 2002, 24, 55–70. [Google Scholar] [CrossRef]
- Samani, Z. Estimating solar radiation and evapotranspiration using minimum climatological data. J. Irrig. Drain. Eng. 2000, 126, 265–267. [Google Scholar] [CrossRef]
- Afzali, M.; Afzali, A.; Zahedi, G. The Potential of Artificial Neural Network Technique in Daily and Monthly Ambient Air Temperature Prediction. Int. J. Environ. Sci. Dev. 2012, 3, 33–38. [Google Scholar] [CrossRef][Green Version]
- Husaini, N.A.; Ghazali, R.; Nawi, N.M.; Ismail, L.H. Jordan Pi-Sigma Neural Network for Temperature Prediction. In Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 547–558. [Google Scholar] [CrossRef]
- Rastogi, A.; Srivastava, A.; Srivastava, V.; Pandey, A. Pattern analysis approach for prediction using Wavelet Neural Networks. In Proceedings of the 2011 Seventh International Conference on Natural Computation, Shanghai, China, 26–28 July 2011. [Google Scholar] [CrossRef]
- Sharma, A.; Agarwal, S. Temperature Prediction using Wavelet Neural Network. Res. J. Inf. Technol. 2012, 4, 22–30. [Google Scholar] [CrossRef][Green Version]
- Wang, G.; Qiu, Y.F.; Li, H.X. Temperature Forecast Based on SVM Optimized by PSO Algorithm. In Proceedings of the 2010 International Conference on Intelligent Computing and Cognitive Informatics, Kuala Lumpur, Malaysia, 22–23 June 2010. [Google Scholar] [CrossRef]
- Karevan, Z.; Mehrkanoon, S.; Suykens, J.A. Black-box modeling for temperature prediction in weather forecasting. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J.A.K. Spatio-temporal feature selection for black-box weather forecasting. In Proceedings of the 24th European Symposium on Artificial Neural Networks, ESANN 2016, Bruges, Belgium, 27–29 April 2016. [Google Scholar]
- Ashrafi, K.; Shafiepour, M.; Ghasemi, L.; Araabi, B. Prediction of climate change induced temperature rise in regional scale using neural network. Int. J. Environ. Res. 2012, 6, 677–688. [Google Scholar]
- Bilgili, M.; Sahin, B. Prediction of Long-term Monthly Temperature and Rainfall in Turkey. Energy Sources Part A Recover. Util. Environ. Eff. 2009, 32, 60–71. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. Prediction of long-term monthly air temperature using geographical inputs. Int. J. Climatol. 2013, 34, 179–186. [Google Scholar] [CrossRef]
- De, S.; Debnath, A. Artificial neural network based prediction of maximum and minimum temperature in the summer monsoon months over India. Appl. Phys. Res. 2009, 1, 37. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, S.; Li, L. Prediction of Temperature Time Series Based on Wavelet Transform and Support Vector Machine. J. Comput. 2012, 7. [Google Scholar] [CrossRef][Green Version]
- Salcedo-Sanz, S.; Deo, R.C.; Carro-Calvo, L.; Saavedra-Moreno, B. Monthly prediction of air temperature in Australia and New Zealand with machine learning algorithms. Theor. Appl. Climatol. 2015, 125, 13–25. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Univariate Time Series Forecasting of Temperature and Precipitation with a Focus on Machine Learning Algorithms: A Multiple-Case Study from Greece. Water Resour. Manag. 2018, 32, 5207–5239. [Google Scholar] [CrossRef]
- Gamboa, J.C.B. Deep learning for time-series analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
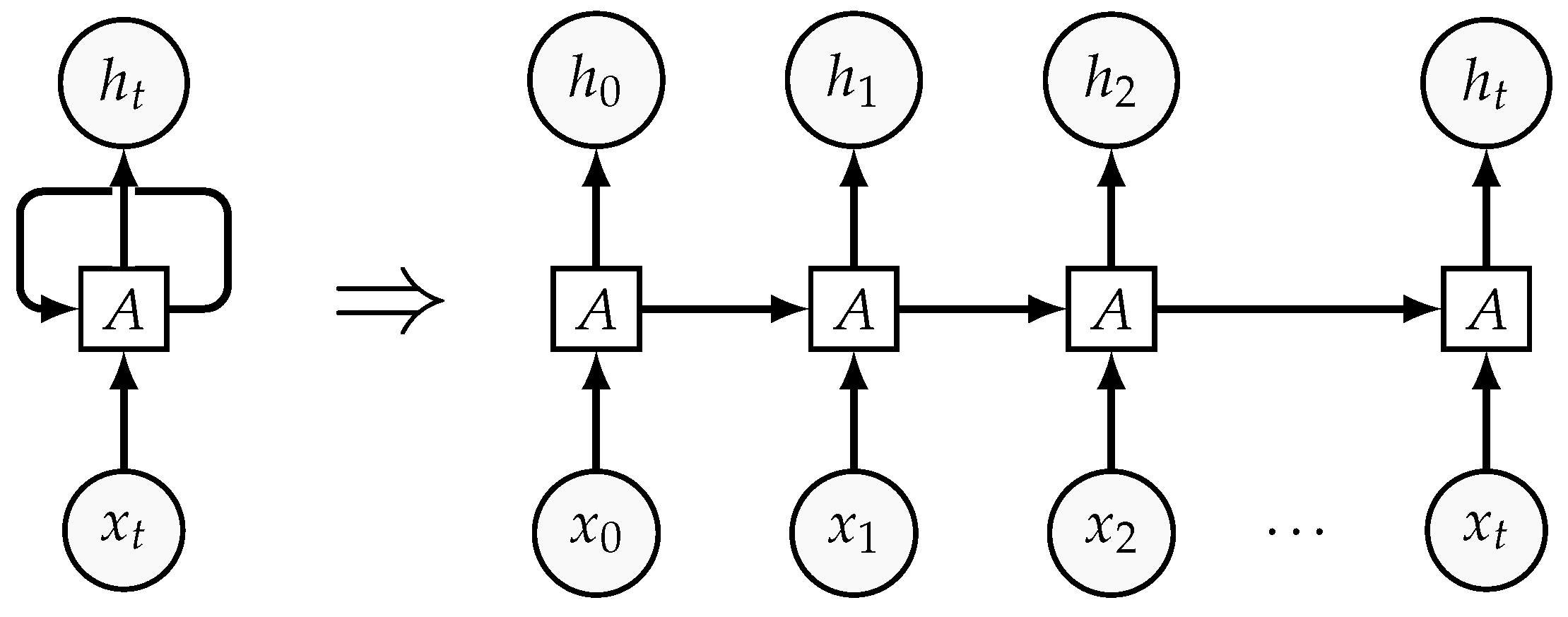
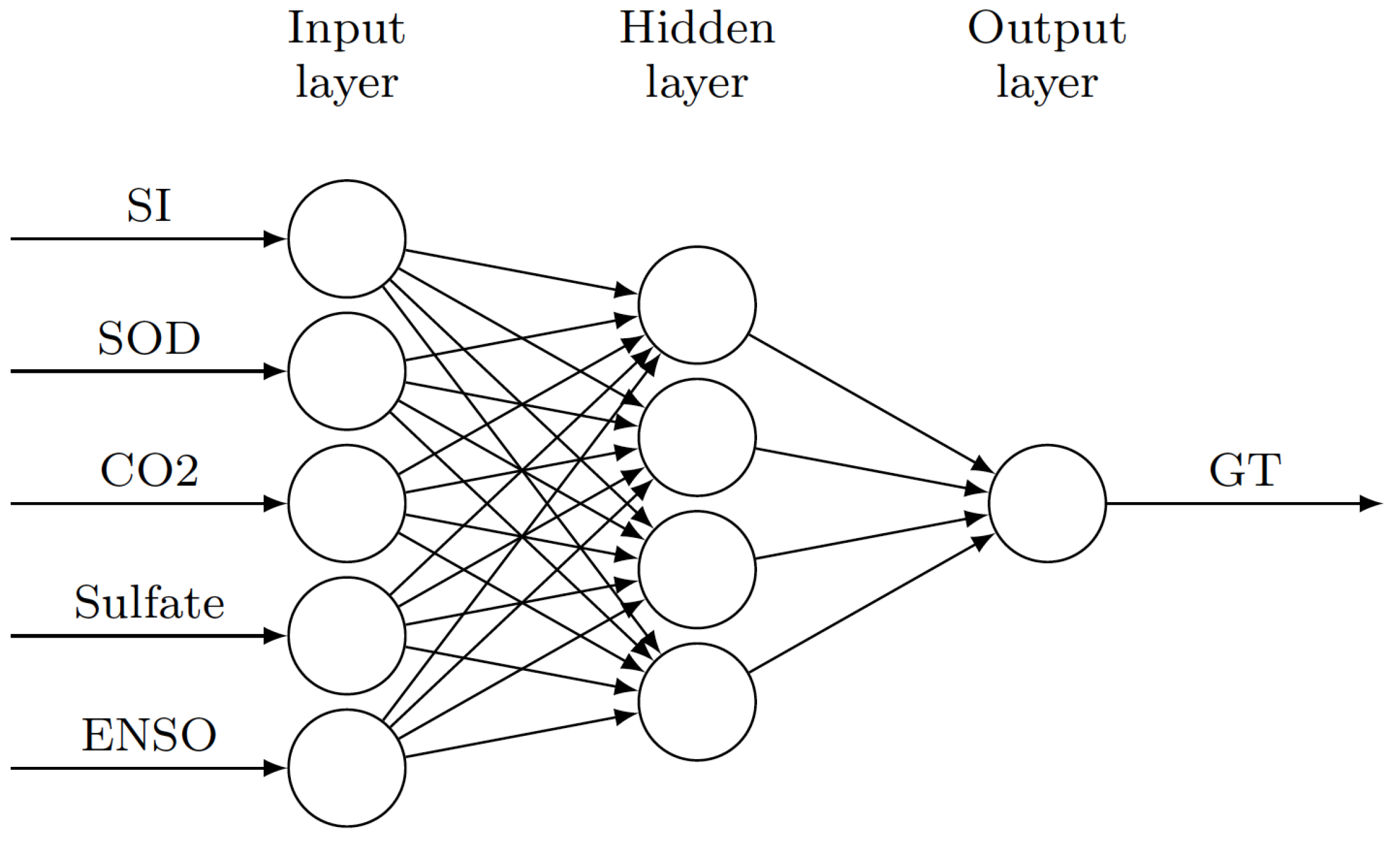
| Reference | Input | Dataset | Hidden Neurons | Training Algorithm | Activation Function | Evaluation Criteria/Time Horizon |
|---|---|---|---|---|---|---|
| [20] | GT | [71] | 4 | Generalized Delta Rule | Sigmoid | 1-step RMSE = 0.12 °C |
| [66] | Surface Warming, Global Ocean Heat Uptake | [72] [73] | 10 | Levenberg-Marquardt | Sigmoid-Linear | MSE ≈ 0.5 °K |
| [67] | SI-SOD CO2-Sulfate ENSO | [73], [74], [75], [76] | 4.5 | Widrow-Hoff Rule | Normalized Sigmoid | R = 0.877 |
| [69] | GT-CO | [77] | 11.8 | Levenberg-Marquardt | Tanh | 1-4-step MAEs(MdAEs) = 0.088 (0.70) °C 10-step MAEs(MdAEs) = 0.078 (0.053) °C 20-step MAEs(MdAEs) = 0.078 (0.053) °C |
| [39] | Rain, Pressure Wind Speed, GT, Relative Humidity | [77] | 11 | Levenberg-Marquardt | Sigmoid-Linear | 1-step MSE(RMSE) = 0.0891(1.6571) °C |
| [70] | GT-CO2 | [77] | 1 | rprop+ | Sigmoid | 1-step RRMSE = 0.67 °C |
| Reference | Input | Region | ML Algorithm | Configuration | Evaluation Criteria/Time Horizon |
|---|---|---|---|---|---|
| [21] | HT | Brazil | ARMA+MLPNN | Hidden nodes = 10, Algorithm = Levenberg–Marquardt, Activation Function = Tanh-Linear | 1-step MAPE = 2.66% |
| [22] | T, | Saudi Arabia | MLPNN | Hidden nodes = 4, Algorithm = Batch learning | 1-step MPD = 3.16%, 4.17%, 2.83% |
| [23] | coded h, T | Texas | RBFNN | RBF = Multi-quadratic, Model Selection = Bayesian Size (hyperrectangles, RBF centres) = 10 | 1-step MAE = 0.4466 °C |
| [3] | (), Tmax, Tmin, ETmax, ETmin ( | Seattle | AANN | Models range from (single element-single layer) to (Five-input, two-element, two-layer) Complexity Penalty Multiplier = 1 | Next,-h MAE (MAPE) = 1.68 F (3.49%) Next,-d MAE (MAPE) = 1.05 F (2.14%) |
| [24] | HT, Wind Speed and Relative Humidity | Canada | MLPNN+RBFN +ERNN+HFM | (MLPNN, ERNN): Hidden nodes = 45 Algorithm = one-step secant Activation Function: Tanh, sigmoid (RBFN): 2 hidden layers, 180 nodes Activation Function: Gaussian | 24-step Winter MAE = 0.0783 °C 24-step Summer MAE = 0.1127 °C 24-step Spring MAE = 0.0912 °C 24-step Fall MAE = 0.2958 °C |
| [25] | Up to prior 24 h: HT, Wind Speed Rain,Relative Humidity Solar Radiation (10 k–400 k) | Georgia | Ward MLPNN | Hidden Layer = 3 parallel slabs Hidden nodes: (2–75) nodes per slab Activation Function = Gaussian, Tanh, Sigmoid | 1-step MAE = 0.53 C 4-step MAE = 1.34 C 8-step MAE = 2.01 C 12-step MAE = 2.33 C |
| [33] | Radial-basis function kernel = 0.05, , = 0.0104 | 1-step MAE = 0.514 C 4-step MAE = 1.329 C 8-step MAE = 1.964 C 12-step MAE = 2.303 C | |||
| [26] | Up to prior 24 h: HT,Wind Speed Rain, Relative Humidity Solar Radiation (1.25 million) | Ward MLPNN | Hidden Layer = 3 parallel slabs Hidden nodes: 120 nodes per slab Activation Function = Tanh | 1-step MAE = 0.516 C 4-step MAE = 1.187 C 8-step MAE = 1.623 C 12-step MAE = 1.873 C | |
| [33] | SVM | Radial-basis function kernel = 0.05, , = 0.0104 | 1-step MAE = 0.513 C 4-step MAE = 1.203 C 8-step MAE = 1.664 C 12-step MAE = 1.922 C | ||
| [27] | Global Solar Radiation | Morocco | AR + MLPNN | 2 hidden layers (5 and 8 neurons) Activation function = tanh | 1-step MSE = 0.272 C |
| [34] | Relative humidity, Precipitation Pressure, Global Radiation HT, Wind Speed and Direction | Spain | SVM Banks | 4 SVMs for: zonal, mixed, meridional, transition Gaussian Function Kernels | 1-step RMSE = 0.61 C 2-step RMSE = 0.94 C 4-step RMSE = 1.21 C 6-step RMSE = 1.34 C |
| [35] | Saudi Arabia | LS-SVM | Radial-basis function kernel Optimal combination (C,) for a MSE = 0.0001 | 1-step MAPE = 1.20% | |
| MLPNN | Hidden layers = 2, Hidden Nodes = 24, 19 | 1-step MAPE = 2.36% | |||
| RBFNN | Hidden layers = 1, Hidden Nodes = 22 | 1-step MAPE = 1.98% | |||
| RNN | Hidden layers = 1, Hidden Nodes = 17 | 1-step MAPE = 1.62% | |||
| PNN | Hidden layers = 3, Hidden Nodes = 4, 3, 2 | 1-step MAPE = 1.58% | |||
| [80] | Previous 24 h values of HT, barometric pressure, humidity and wind speed | Nevada | SDAE | Hidden Layers = 3, Hidden nodes = 384 Learning Rate = 0.0005, Noise = 0.25 | 1-step RMSE = 1.38% |
| MLPNN | Hidden Layers = 3, Hidden nodes = 384 Learning Rate = 0.1 | 1-step RMSE = 4.19% | |||
| [40] | Surface temperature and pressure, wind, rain, humidity snow, and soil temperature | Simulated Data | LSTM | 5 layers, activation functions: linear, tanh Learning Rate = 0.01, Adam Optimizer | 1-step MSE = 0.002041361K |
| CRNN | 5 layers (Filter size: 32, 64, 128, 256,512) Learning Rate = 0.01, Adam Optimizer | 1-step MSE = 0.001738656K |
| Ref. | Input | Region | Algorithm | Configuration | Evaluation Criteria/Time Horizon |
|---|---|---|---|---|---|
| SOFM+MLPNN | Hidden layer = 1, Hidden Nodes = 10 | Error (Max DT) ≤ 2 °C in 88.6% cases | |||
| For 3 previous days: 2 measures | Activation Function= Sigmoid | Error (Min DT) ≤ 2 °C in 87.3% cases | |||
| [28] | of mean sea level and vapor | Calcutta | MLPNN | Hidden layer = 1, Hidden Nodes = 15 | Error (Max DT) ≤ 2 °C in 83.8% cases |
| pressures, and relative humidity, | Activation Function= Sigmoid | Error (Min DT) ≤ 2 °C in 85.2% cases | |||
| Max DT, Min DT, Rainfall | RBFNN | Size (RBF centres) = 50 | Error (Max DT) ≤ 2 °C in 80.65% cases | ||
| Error (Min DT) ≤ 2 °C in 81.66% cases | |||||
| MLPNN | Hidden layer = 1, Hidden Nodes = 45 | MAPE = 6.05% RMSE = 0.6664 °C | |||
| Levenberg–Marquardt Algorithm | MAE = 0.5561 °C | ||||
| ERNN | Hidden layer = 1, Hidden Nodes = 45 | MAPE = 5.52% RMSE = 0.5945 °C | |||
| [29] | Average DT, Wind Speed and | Canada | Levenberg–Marquardt Algorithm | MAE = 0.5058 °C | |
| Relative Humidity | RBFNN | Hidden = 2, RBF Nodes = 180 | MAPE = 2.49% RMSE = 0.2765 °C | ||
| Gaussian Activation Function | MAE = 0.2278 °C | ||||
| Ensemble | Arithmetic mean and weighted | MAPE = 2.14% RMSE = 0.2416 °C | |||
| average of all the results | MAE = 0.1978 °C | ||||
| MLPNN | Levenberg–Marquardt Algorithm | Mean RMSE (Tmean) = 1.7767 °C | |||
| Daily mean, maximum | Hidden Layers = 1, Hidden Nodes = 5 | Mean RMSE (Tmin,Tmax) = 2.21, 2.86 °C | |||
| [30] | and minimum temperature | Turkey | RBFNN | RBF Nodes = 5–13 | Mean RMSE (Tmean) = 1.79 °C |
| Spread parameter = 0.99 | Mean RMSE (Tmin,Tmax) = 2.20, 2.75 °C | ||||
| GRNN | Spread Parameter = 0.05 | Mean RMSE (Tmean) = 1.817 °C | |||
| Mean RMSE (Tmin,Tmax) = 2.24, 2.87 °C | |||||
| Daily Gust Wind, mean, minimum and maximum DT, | Hidden layer = 1, Hidden Nodes = 6 | ||||
| [31] | precipitation, mean humidity, mean pressure, | Iran | MLPNN | Scaled Conjugate Gradient | MAE ≈ 1.7 °C |
| sunshine, radiation and evaporation | Activation Function (Hidden/Output) = Tanh-Sig /Pure Linear | ||||
| Month of the year, day of the month | Hidden layer = 1, Hidden Nodes = 6, Levenberg–Marquardt | RMSE (train) = 1.85240 °C | |||
| [7] | and Mean DT of the previous day | Turkey | MLPNN | Algorithm, Activation Function = Tanh-Sig | RMSE (test) = 1.96550 °C |
| [32] | Previous 365 DT | Toronto | MLPNN | Hidden layer (nodes) = 5 (10–16), Levenberg–Marquardt | MSE = 0.201 °C |
| Algorithm, Activation Function = Tanh-Sig | |||||
| ERNN | Hidden Layers = 1, Hidden Nodes = 15 | MSE (Max DT) = 0.008 °C | |||
| Previous Mean, Maximum and | Levenberg-Marqardt Algorithm | MAE (Max DT) = 0.064 °C | |||
| [83] | Minimum DT | Iran | MLPNN | Activation Function (hidden) = Tanh-Sig | MSE (Max DT) = 0.008 °C |
| Activation Function (output) = Pure Linear | MAE (Max DT) = 0.067 °C | ||||
| [84] | Mean DT | Malaysia | JPSN | Hidden Nodes = 2–5, Gradient Descent Algorithm | MSE, MAE = 0.006462, 0.063458 °C |
| MLPNN | Activation Function (Hidden/Output) = Sigmoid/Pure Linear | MSE, MAE = 0.006549, 0.063646 °C | |||
| [85] | Previous DT | Window Size = 3, Hidden Layers = 2 | MAE = 0.7–0.9 °C | ||
| [86] | Previous DT and cloud Density | Taipei | WNN | Feed Forward Back Propagation, Learning Rate = 0.01 | MAE = 0.25–0.62 °C |
| Maximum, minimum and average DT, Average and | SVM | Mahalanobis Kernel, , | MAPE = 2.6% | ||
| [36] | Minimum Daily Humidity, Maximum Daily Wind Speed, | Tokyo | MLPNN | Hidden layer = 1, Hidden Nodes = 12, Learning Rate = 0.2 | MAPE = 3.4% |
| Daily Wind Direction and Daylight, Daily Isolation | RBFNN | RBF Nodes = 12, Learning Rate = 0.05 | MAPE = 2.7% | ||
| [37] | 5 previous values of DT | Cambridge | SVM | Radial Basis Function, Grid Search for optimal | MSE = 7.15 |
| MLPNN | Hidden layer = 1, Hidden Nodes = 2*num_inputs+1 | MSE = 8.07 | |||
| Maximum, minimum DT, global radiation, | 10 stations in Europe | SVM | Gaussian Kernel | RMSE (Norway) = 1.5483 °C | |
| [38] | precipitation, sea level pressure, relative humidity, | Grid Search for optimal | |||
| synoptic situation and monthly cycle | MLPNN | Levenberg–Marquardt algorithm, Sigmoid Activation Function | RMSE (Norway) = 1.5711 °C | ||
| [87] | Previous Minimum DT | Beijing | PSVM | Gaussian Kernel, 12.2658, 5.5987, 100 | MSE = 1.1026 °C |
| SVM | Gaussian Kernel, 9.2568, | MSE = 1.3058 °C | |||
| K-M+EN | 1-step MAE(MaxT) = 1.07, (MinT) = 1.15 °C | ||||
| [88] | +LS-SVM | 6-step MAE(MaxT) = 1.73, (MinT) = 1.50 °C | |||
| Minimum and maximum DT, | LS-SVM | Radial Function Base Kernel | 1-step MAE(MaxT) = 1.35, (MinT) = 1.38 °C | ||
| precipitation, humidity, wind | Brussels | Parameter Tuning: Cross-Validation | 6-step MAE(MaxT) = 2.03, (MinT) = 2.34 °C | ||
| speed and sea level pressure | ST-LASSO | Penalization | 1-step MAE(MaxT)=2.11, (MinT)=1.33 °C | ||
| +LS-SVM | 3-step MAE(MaxT) = 2.44, (MinT) = 2.01 °C | ||||
| [89] | LS-SVM | Radial Function Base Kernel | 1-step MAE(MaxT) = 2.21, (MinT) = 1.38 °C | ||
| Parameter Tuning: Cross-Validation | 3-step MAE(MaxT) = 2.40, (MinT) = 2.02 °C | ||||
| [41] | Temperature, Wind and Surface Pressure | Zurich | RCNN | 8 Convolutional Filters () + | MAE = 0.88 °K |
| Max Pooling () + 2 LSTM RNN |
| Ref. | Input | Output | Region | Algorithm | Configuration | Evaluation Criteria/Time Horizon |
|---|---|---|---|---|---|---|
| Hidden Layer = 1, Hidden Nodes = 32 | ||||||
| [91] | Turkey | MLPNN | Levenberg–Marquardt algorithm | 1-step MAE = 0.508 °C | ||
| Latitud, Longitude, | Monthly | Activation Function (Hidden) = Log-Sig | ||||
| Altitude, Month | Temperature | Hidden Layers = 1, Hidden Nodes = 15 | Station with Min RMSE = 1.53 °C | |||
| [92] | Iran | MLPNN | Levenberg-Marqardt Algorithm | Station with Min MAE = 1.27 °C | ||
| Activation Function = Tanh-Sig | ||||||
| January to May | Max and Min | Hidden Layer = 1, Hidden Nodes = 2 | June MAE(Tmin, Tmax) = 0.0154, 0.0197 °C | |||
| [93] | maximum and minimum | Monthly | India | MLPNN | Steepest Descent algorithm | July MAE (Tmin, Tmax) = 0.0107, 0.0162 °C |
| temperature | Temperature | Learning rate = 0.9 | Aug MAE (Tmin, Tmax) = 0.01013, 0.0099 °C | |||
| For 1, 6, 12 and 24 months before: | BP- | Not Specified | MSE (Testing) = 0.0196 °C | |||
| Mean temperature, dew point | MLPNN | |||||
| [90] | temperature, relative humidity, | Monthly | Iran | GA- | Not Specified | MSE (Testing) = 0.0224 °C |
| wind speed, solar radiation, | Temperature | MLPNN | ||||
| cloudiness, rainfall, station level | PSO- | Not Specified | MSE (Testing) = 0.0228 °C | |||
| pressure and green house gases | MLPNN | |||||
| Monthly | ERNN | Hidden Layers = 1, Hidden Nodes = 15 | 1-step MSE (Tmin, Tmax) = 0.081, 0.060 °C | |||
| Previous Mean, Maximum and | Mean, | Levenberg-Marqardt Algorithm | 1-step MAE (Tmin, Tmax) = 0.228, 0.193 °C | |||
| [83] | Minimum Temperature | Max, and | Iran | MLPNN | Activation Function (hidden) = Tanh-Sig | 1-step MSE (Tmin, Tmax) = 0.083, 0.064 °C |
| Min Temperature | Activation Function (output) = Linear | 1-step MAE (Tmin, Tmax) = 0.223, 0.201 °C | ||||
| WT+ | 10–20, 0.1–0.5 | Min. MSE = 0.0937 °C | ||||
| SVM | 0.05–0.55, Radial basis Kernel | |||||
| [94] | Mean Monthly Temperature | Monthly | Tangshan | 10–20, 0.1–0.5 | Min. MSE = 0.5451 °C | |
| Temperature | SVM | σ 0.05–0.55, Radial basis Kernel | ||||
| Not Specified | Min. MSE = 1.0076 °C | |||||
| MLPNN | ||||||
| SVM | Gaussian Kernel | Mean MAE = 1.0073 °C | ||||
| Monthly | Australia | Grid Search for optimal | ||||
| [95] | Mean Monthly Temperature | Temperature | and New | MLPNN | Levenberg– Marquardt algorithm | 1-step Mean MAE = 1.0662 °C |
| Zealand | Activation Function = Logistic | |||||
| SVM | Gaussian Kernel | 1-step Mean RMSE = 1.31 °C | ||||
| Monthly | and | |||||
| [96] | Mean Monthly Temperature | Temperature | Greece | MLPNN | Hidden Layers = 1, Hidden Nodes = 5 | Mean RMSE = 1.7 °C |
| Activation Function = Logistic |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cifuentes, J.; Marulanda, G.; Bello, A.; Reneses, J. Air Temperature Forecasting Using Machine Learning Techniques: A Review. Energies 2020, 13, 4215. https://doi.org/10.3390/en13164215
Cifuentes J, Marulanda G, Bello A, Reneses J. Air Temperature Forecasting Using Machine Learning Techniques: A Review. Energies. 2020; 13(16):4215. https://doi.org/10.3390/en13164215
Chicago/Turabian StyleCifuentes, Jenny, Geovanny Marulanda, Antonio Bello, and Javier Reneses. 2020. "Air Temperature Forecasting Using Machine Learning Techniques: A Review" Energies 13, no. 16: 4215. https://doi.org/10.3390/en13164215
APA StyleCifuentes, J., Marulanda, G., Bello, A., & Reneses, J. (2020). Air Temperature Forecasting Using Machine Learning Techniques: A Review. Energies, 13(16), 4215. https://doi.org/10.3390/en13164215







