The Value of PV Power Forecast and the Paradox of the “Single Pricing” Scheme: The Italian Case Study
Abstract
1. Introduction
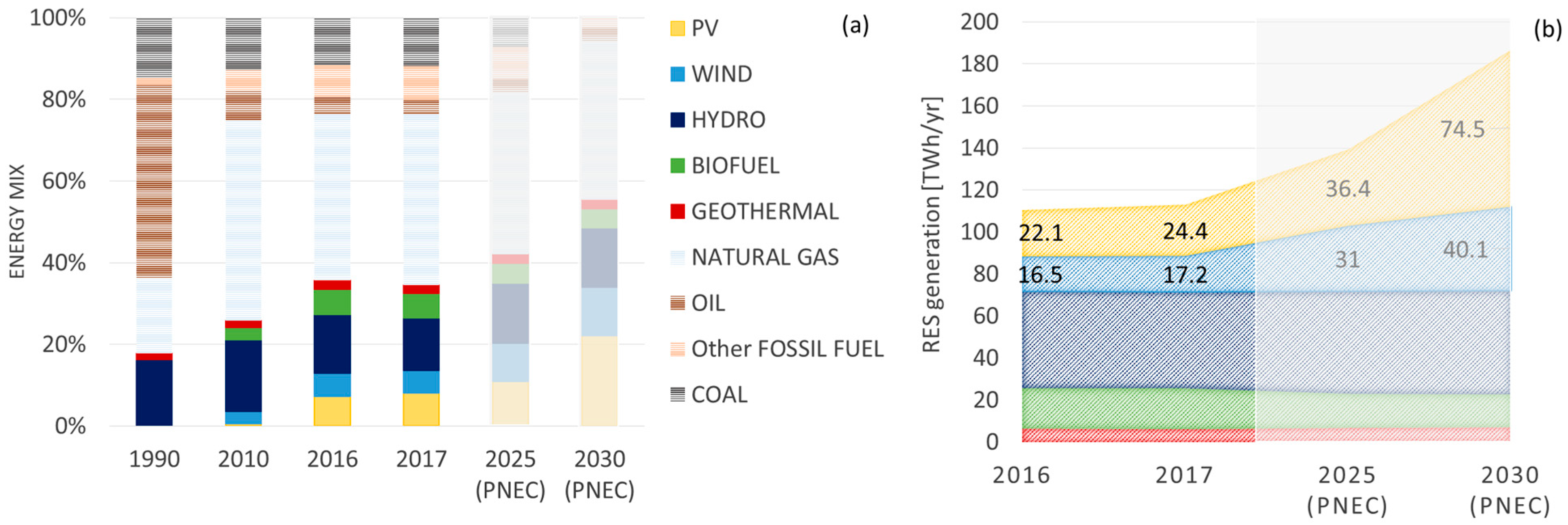
- The objective of the PNIEC by 2030 will inevitably require an increase in the capacity of utility scale PV plants with respect to the distributed one and in fact, we now have tenders to cover this part although at the moment only wind projects are presented to problems in getting building permits for PV plants.
- To predict the day-ahead supply and reserves, Terna needs to forecast the whole Italian PV generation. The forecast model is strongly based on the large plant generation scheduling: “Terna receives the forecast from several external suppliers, subject to a pre-qualification process and continuous performance monitoring, who make their own forecasts … Before the execution of each sub-stage of the planning phase, the individual forecasts are then processed, together with the final photovoltaic production … by a statistical algorithm of “meta-forecasting”, which provides the best combination of the different forecasts, in order to minimize the overall forecast error” [7].
- In Section 2, we report the novelty of work with respect to the existing literature
- In Section 3, we summarize the main features of the Italian energy market and of the solar imbalance regulation framework
- In Section 4, we present the satellite and numerical weather prediction data employed to estimate and forecast the generation of utility scale PV plants all over Italy
- In Section 5, we describe the methodology used to carry out our study
- In Section 6, we report the main accuracy and economic metrics used to assess the forecast performance and its related imbalance economic value for large solar producers/traders
- In Section 7, we discuss the results emerging from our investigation. We show the forecast accuracy of the photovoltaic generation of utility scale solar plants on 1325 locations in Italy and we compute the imbalance values of their forecasts. These values are compared with those obtained with a baseline forecast to evaluate the economic advantage of the forecast accuracy improvements
- In Section 8, we suggest a possible market regulation revision
- In Section 9, conclusions are reported
2. Existing Literature and Novelty of the Work
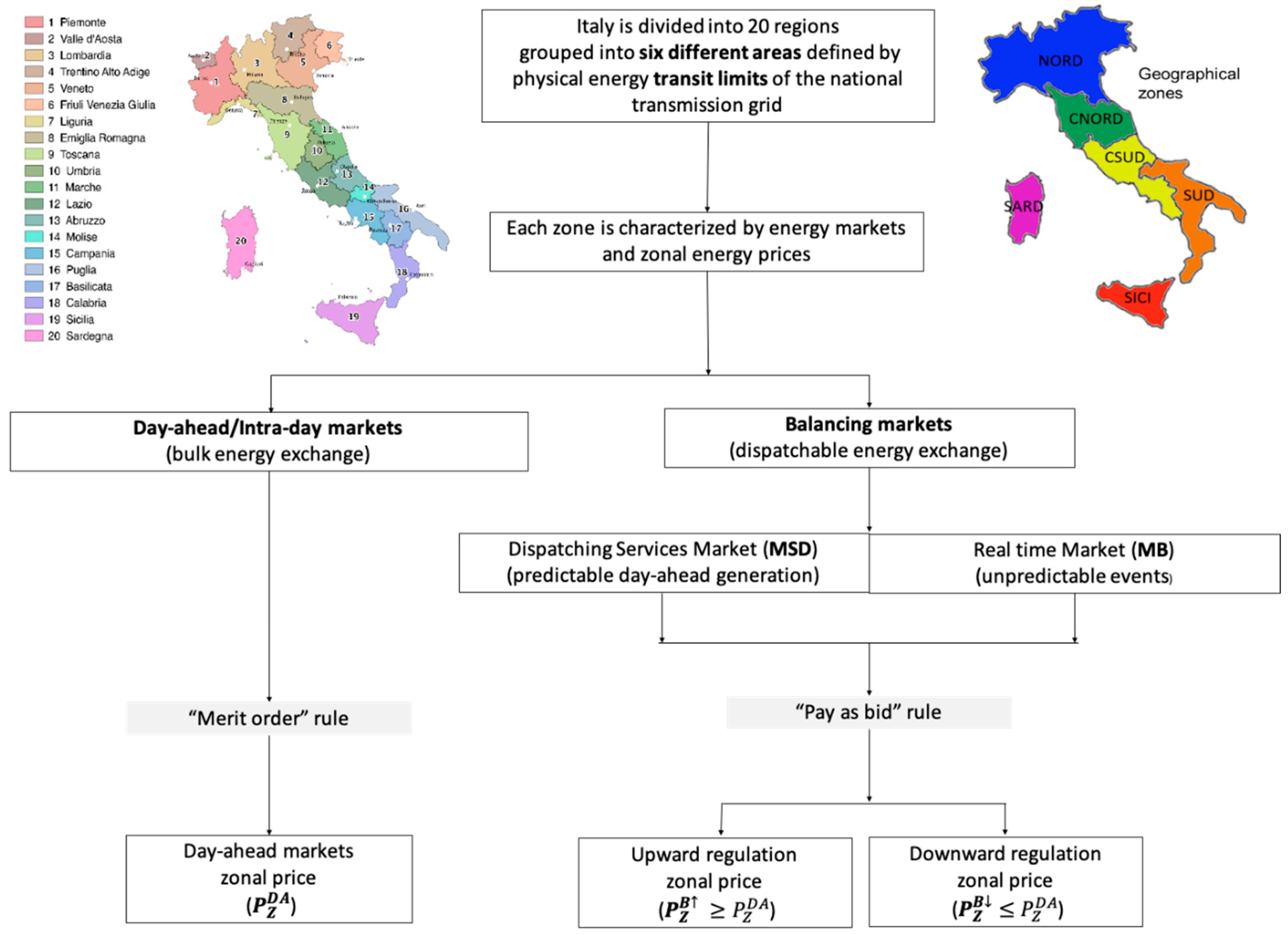
3. Spot Market Structure and Imbalance Regulatory Framework for Production Units in Italy
3.1. Spot Market Structure
- The DAM is the place of negotiation for the bulk supply/purchase electricity bids for each hour of the delivery day. All electrical operators can participate in the DAM. The bids are accepted by the Italian Energy Services Manager (GME) according to the “Merit Order” rule that will define the energy price, i.e., the equilibrium price between supply/purchase bids. If accepted, the energy of the supply bid is remunerated at the zonal price (P_Z^DAM) while the energy of the purchased bid at the single national price (PUN). The PUN is the average zonal price weighted over the relative amount of exchanged energy. Accepted bids determine the preliminary scheduling for the energy supply and withdrawal of each grid connection point for the day of delivery. The zonal prices depend on the transit capacity limits between the market zones according to the Italian TSO (Terna) requirement [24].
- The IDM is the place of negotiation for the supply/purchase electricity exchange for each hour of the current day, with the purpose of adjusting the injection/withdrawal scheduling defined by the DAM.
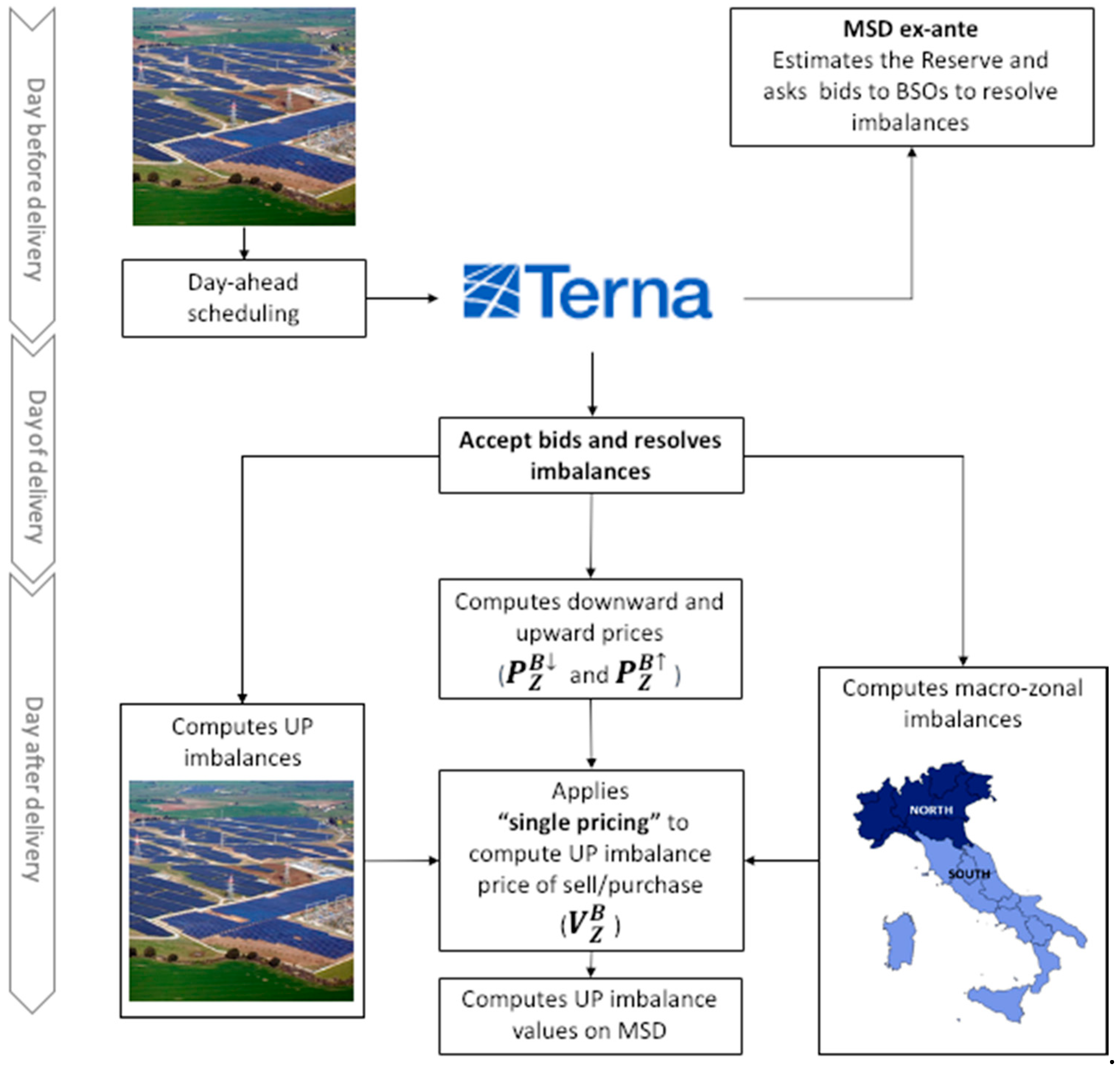
- The BEM is the place for the negotiation of bids for the supply/purchase of dispatching services, used by Terna for the resolution of intra-zonal congestions, for the supply of the reserves and for the balancing in real time between demand/supply. The BEM is divided into two: the market of the dispatching service (MSD ex-ante) and the real time balancing market (MB). On the MSD ex-ante, Terna defines the reserves margin and acquires/sells the energy needed to compensate the day-ahead imbalance and to resolve congestions. On MB, Terna acquires/sells in real time (by sending dispatching orders) and the energy is needed to correct the imbalance due to unpredictable events or errors in the reserve estimation
3.2. Production Unit Imbalance and Economic Valorization on MSD
- If the signs of the imbalance are the same, the day-ahead generation scheduling errors of the “relevant” solar farm contribute to an increase in the imbalance of the macro-zone. In this case, the imbalance value will be negative, i.e., a cost for the producer.
- If the imbalance signs are different, the scheduling errors contribute to reduce the macro-zone imbalance and the imbalance value will be positive, i.e., a revenue for the producer.
4. Satellite and Numerical Weather Prediction Data
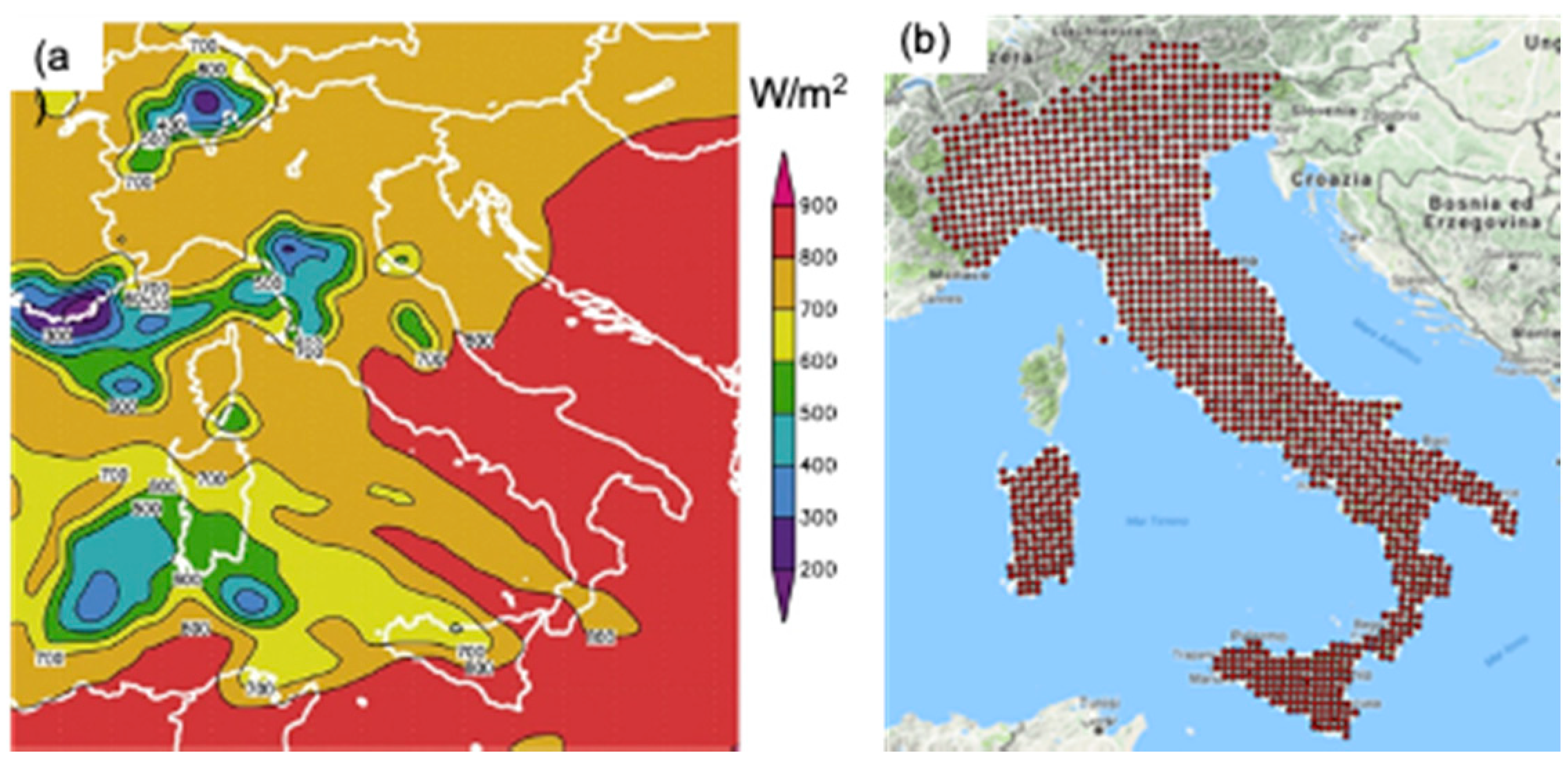
4.1. Satellite Derived Data
4.2. Numerical Weather Prediction Forecast Data
- The initial contour data for model initialization comes from the GFS model output with a spatial resolution of 12 km × 12 km (Figure 6)
- Radiation scheme: “Rapid Radiative Transfer Model”
- Forecast horizon: 24 h/temporal output resolution: 1 h/spatial resolution 12 km × 12 km covering all the country (1325 points)
- Each of the 1325 daily hindcasts time series covered the period 2014–2017
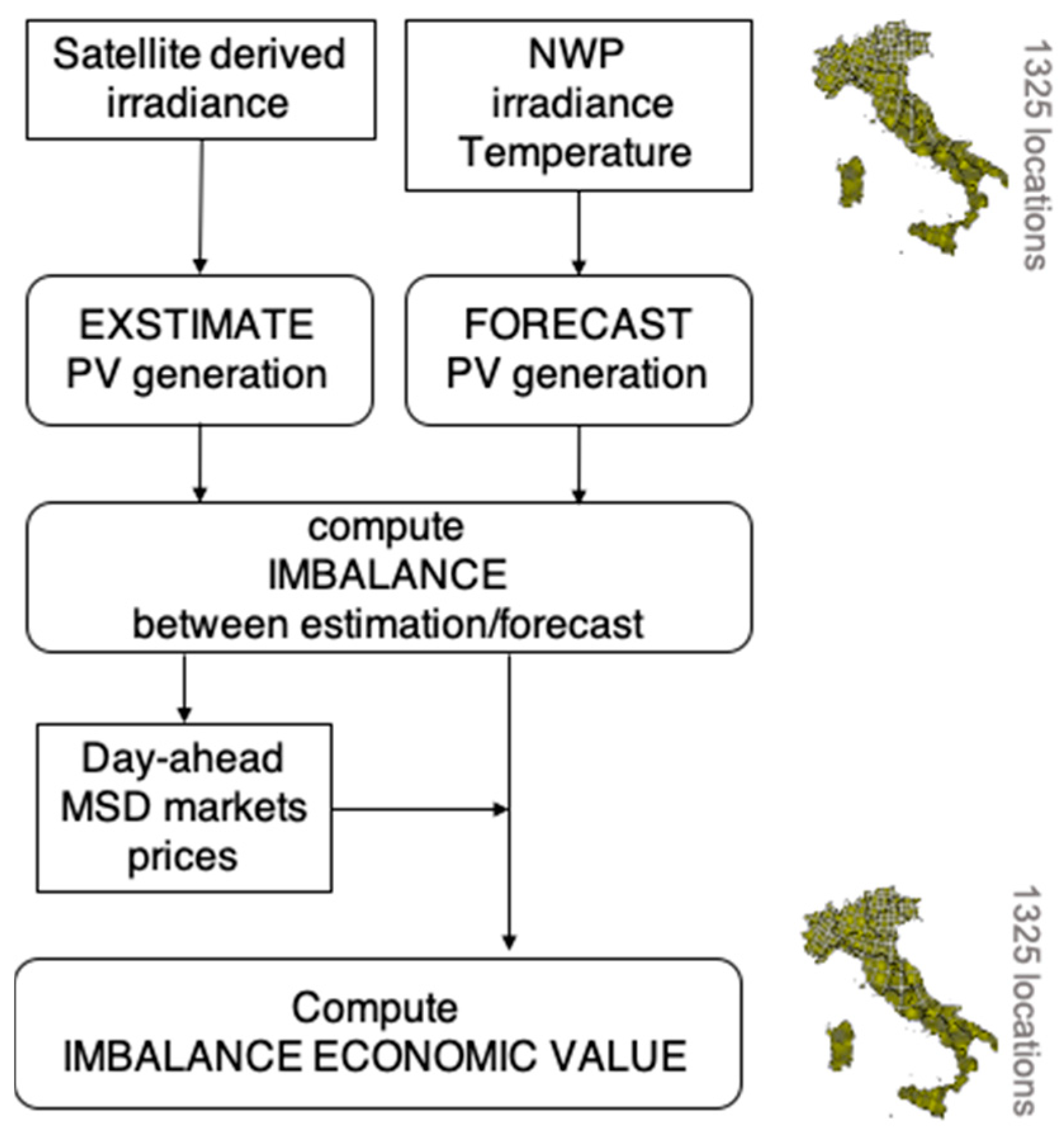
5. Materials and Methods
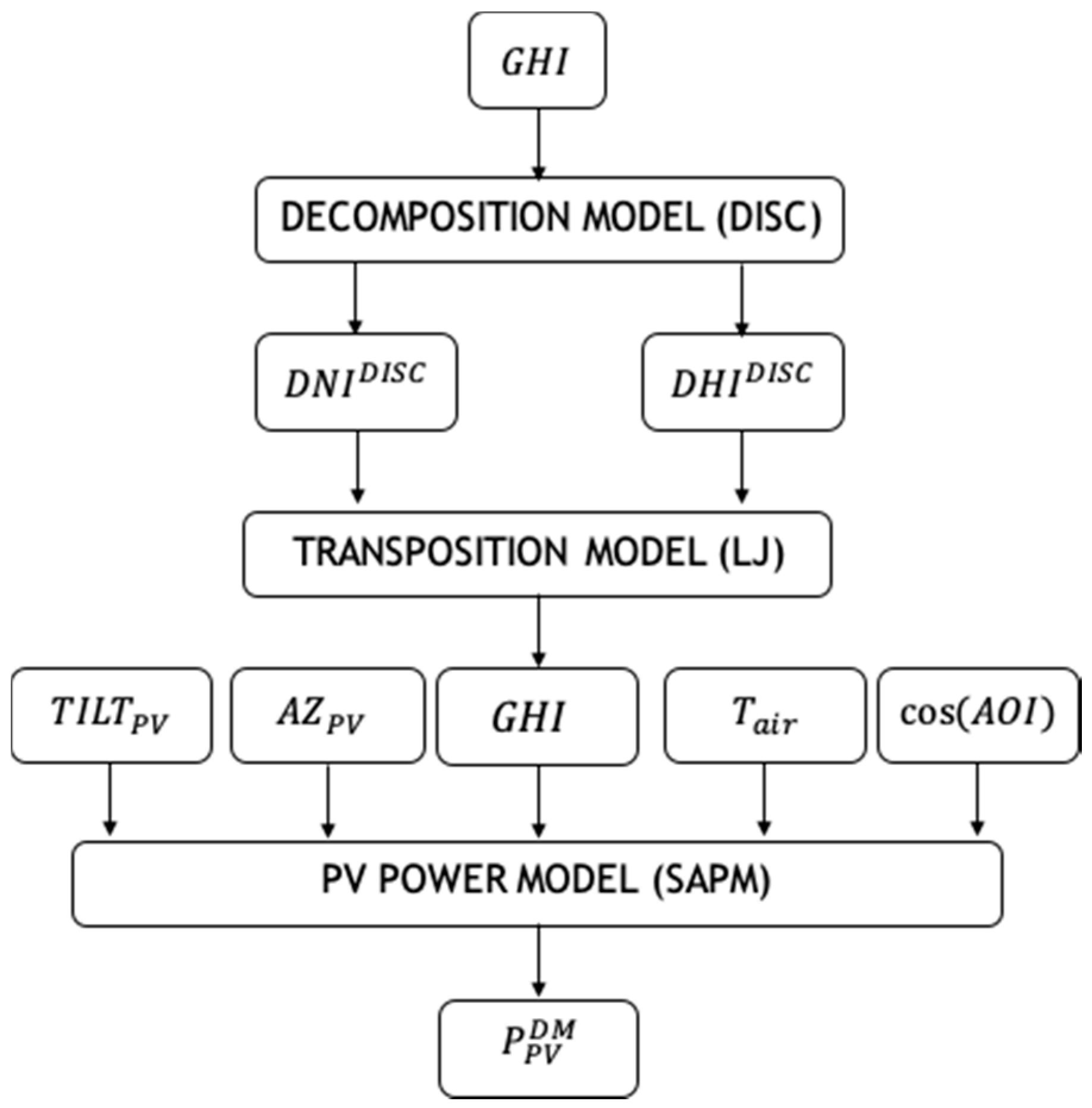
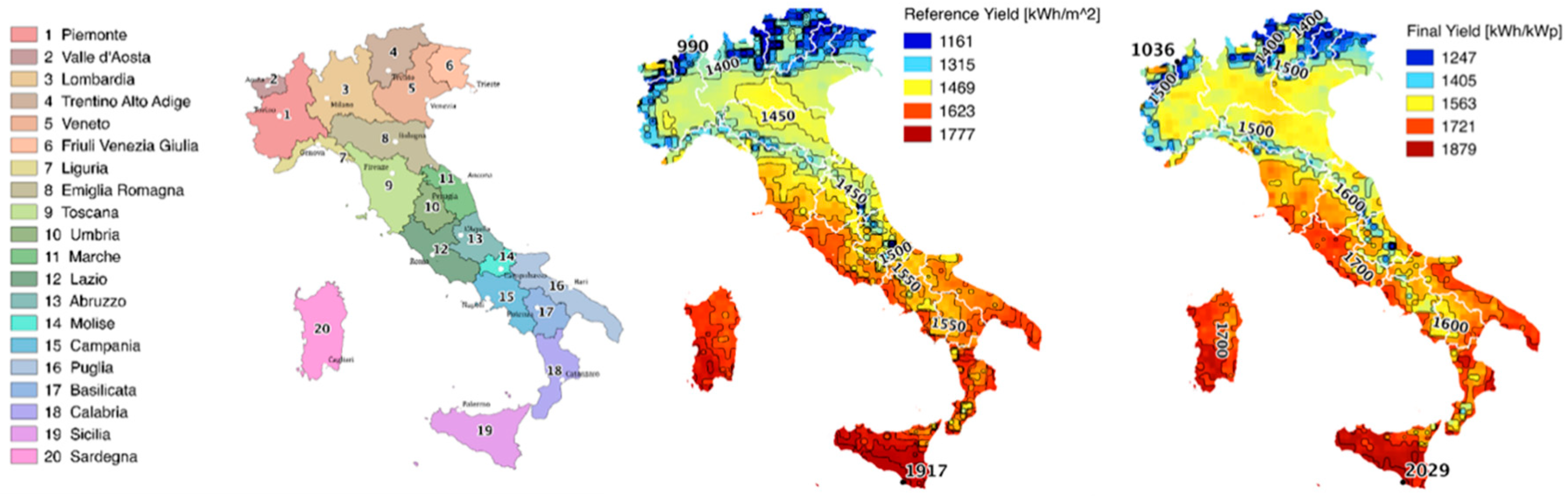
- We mapped the satellite and the NWP irradiance into the generation of nominal PV plants placed on an optimal plane of array (30° tilted and south oriented) by a deterministic PV power method described in Section 4.1. The nominal PV production was simulated for each of the 1325 grid points covering Italy using four years of hourly data: 2014–2017 (see Figure 6b). The PV geometry was chosen taking into account that the “relevant” solar farms (PV systems with a capacity ≥10 MWp) are all optimally tilted and oriented.
- We computed the energy imbalance between the current satellite derived PV generation and the day-ahead scheduled production for each point.
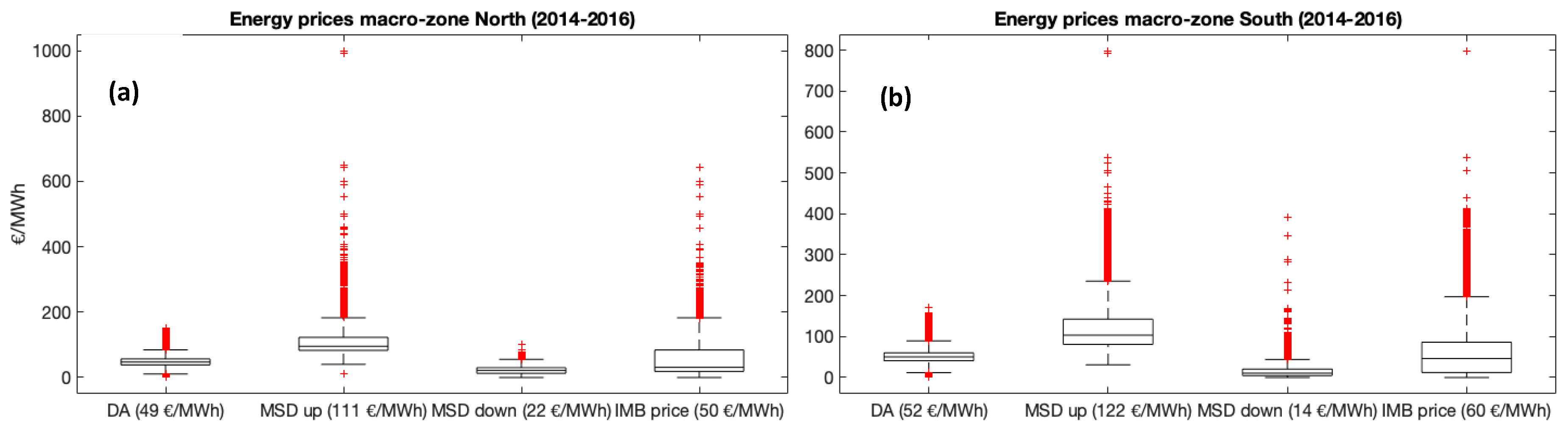
- We evaluated the PV forecast economic value for each single “relevant” solar producer, by the DA and MSD ex-ante energy prices and the macro-zone imbalance signs related to the years 2014–2016. These energy price data were archived by Terna Spa, and are of public domain and downloadable from the TSO website [30].
6. Metrics to Evaluate the Accuracy and Economic Imbalance Value
7. Results
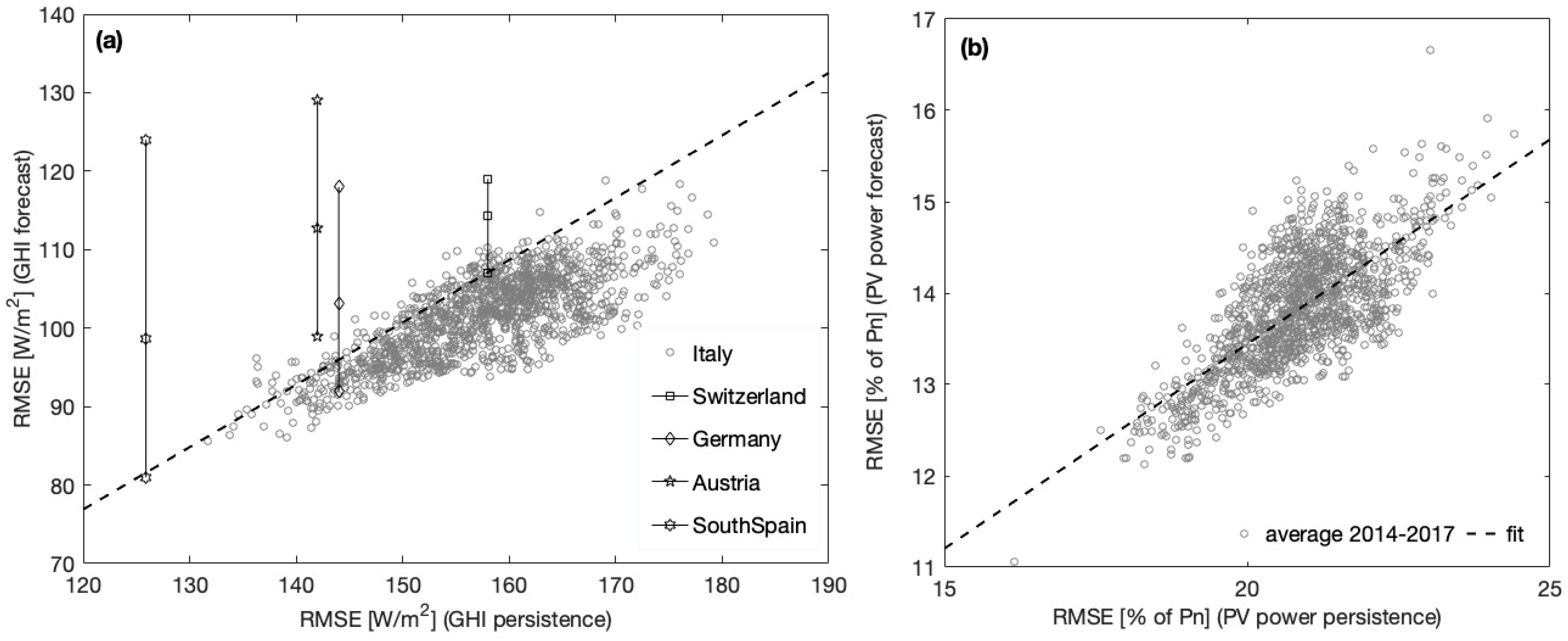
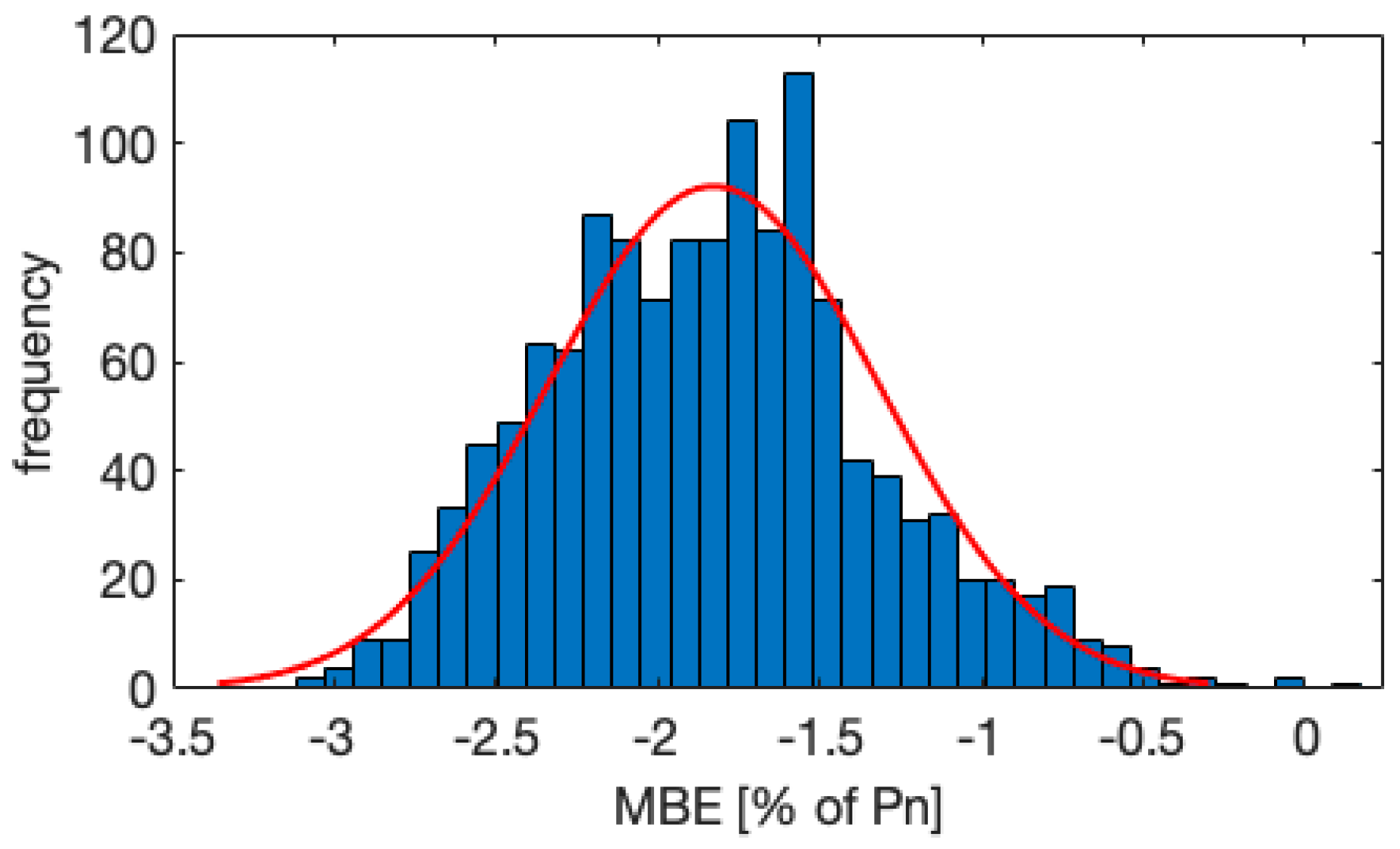
7.1. Forecast Results
7.2. Benchmarking the Economic Value of the Imbalance of “Relevant” PV Plants
8. Proposed Revision to the Dispatching Market Regulatory Framework
9. Conclusions
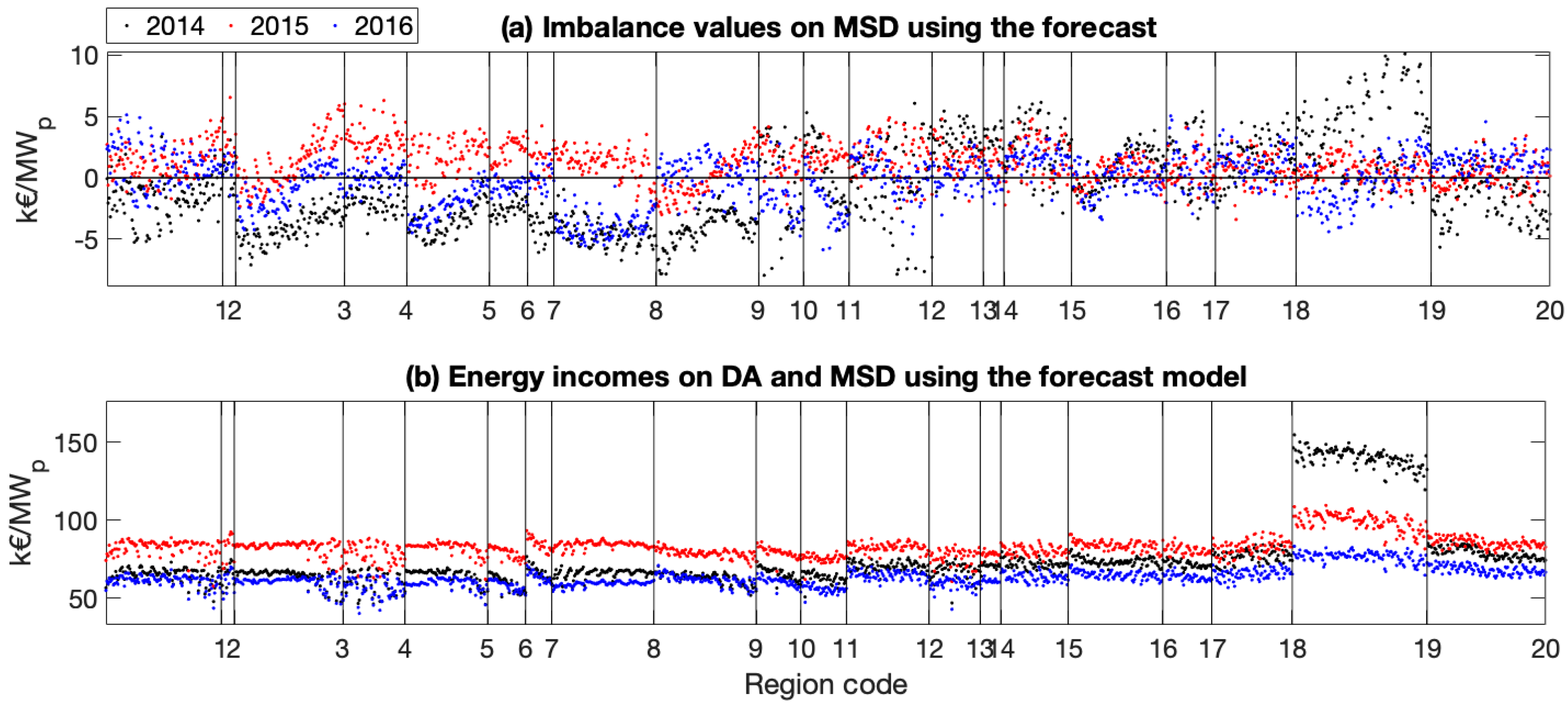
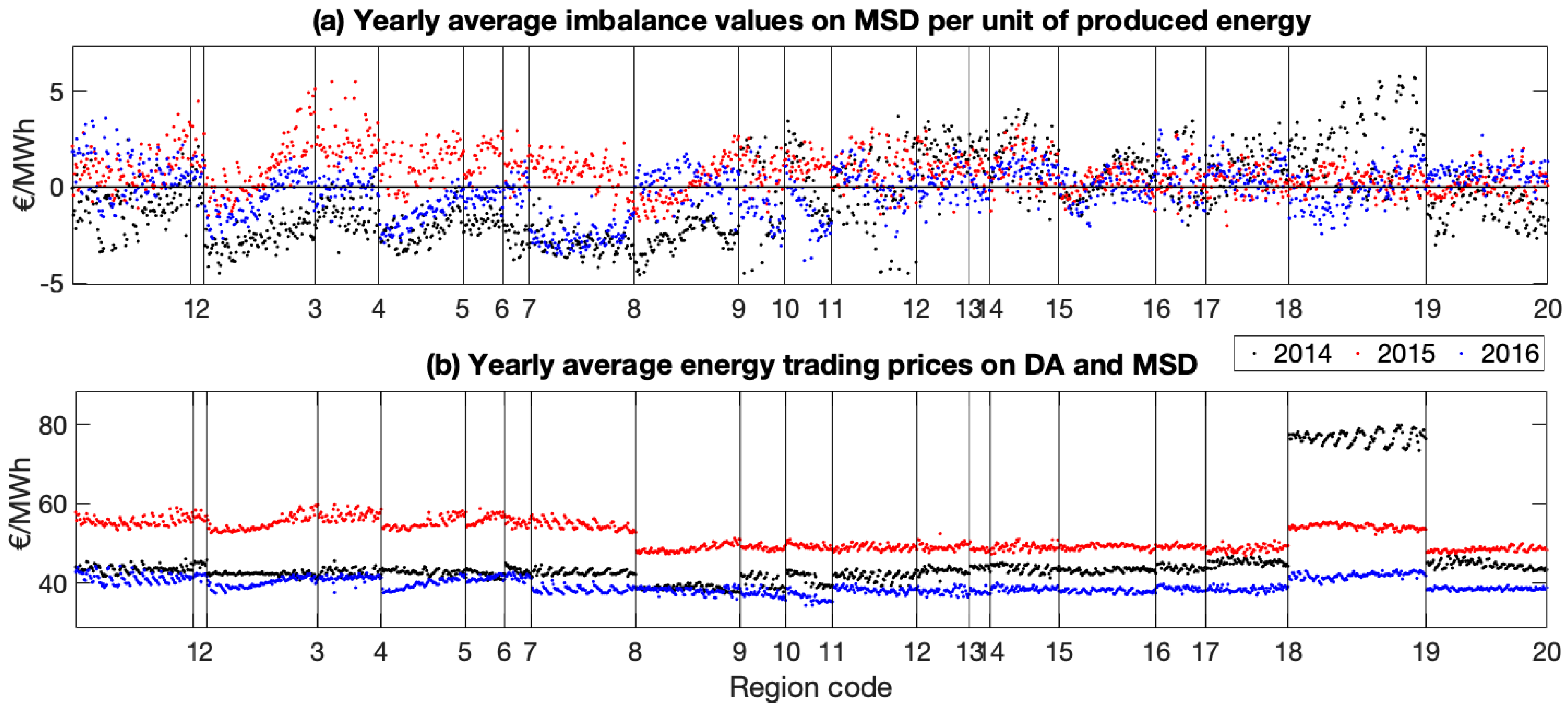
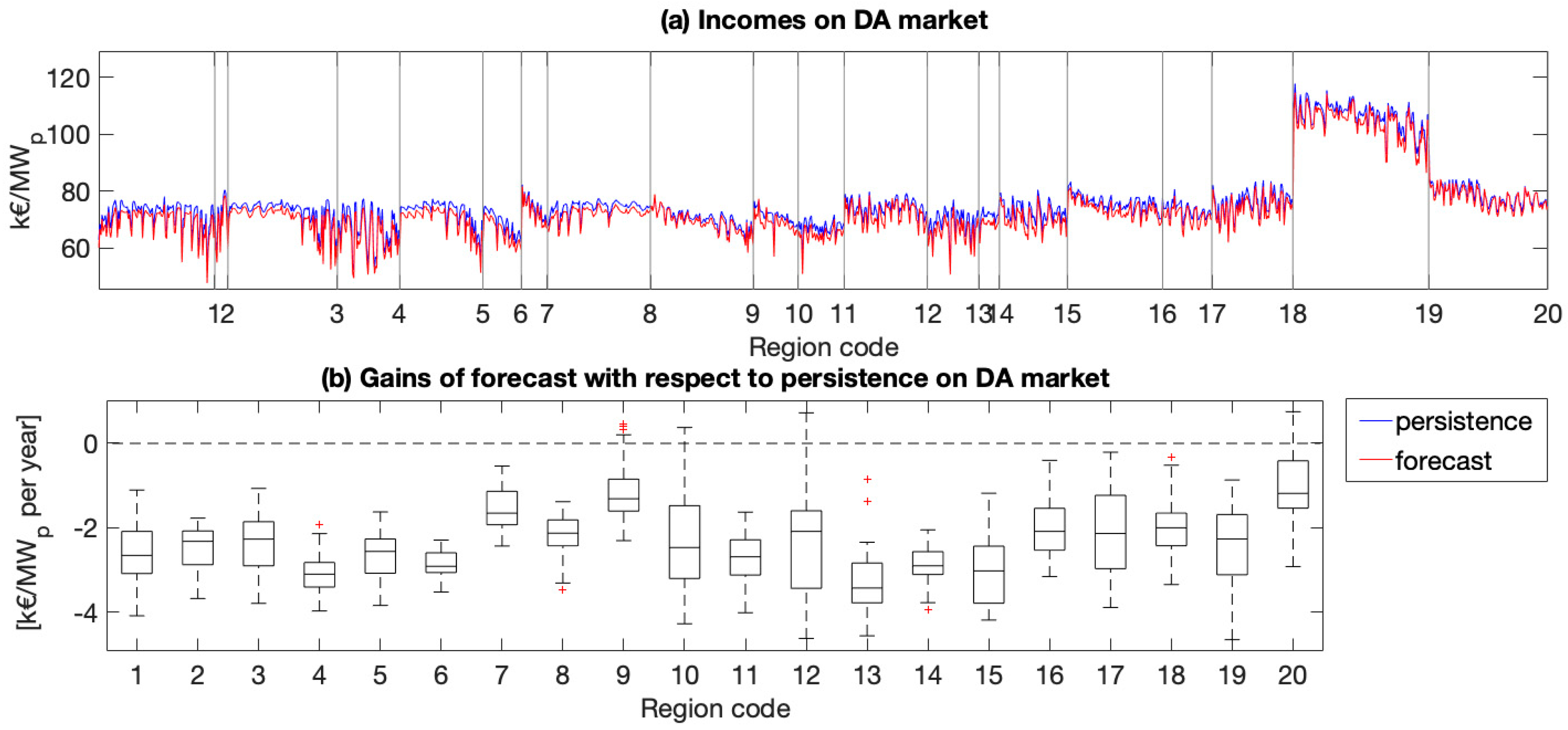
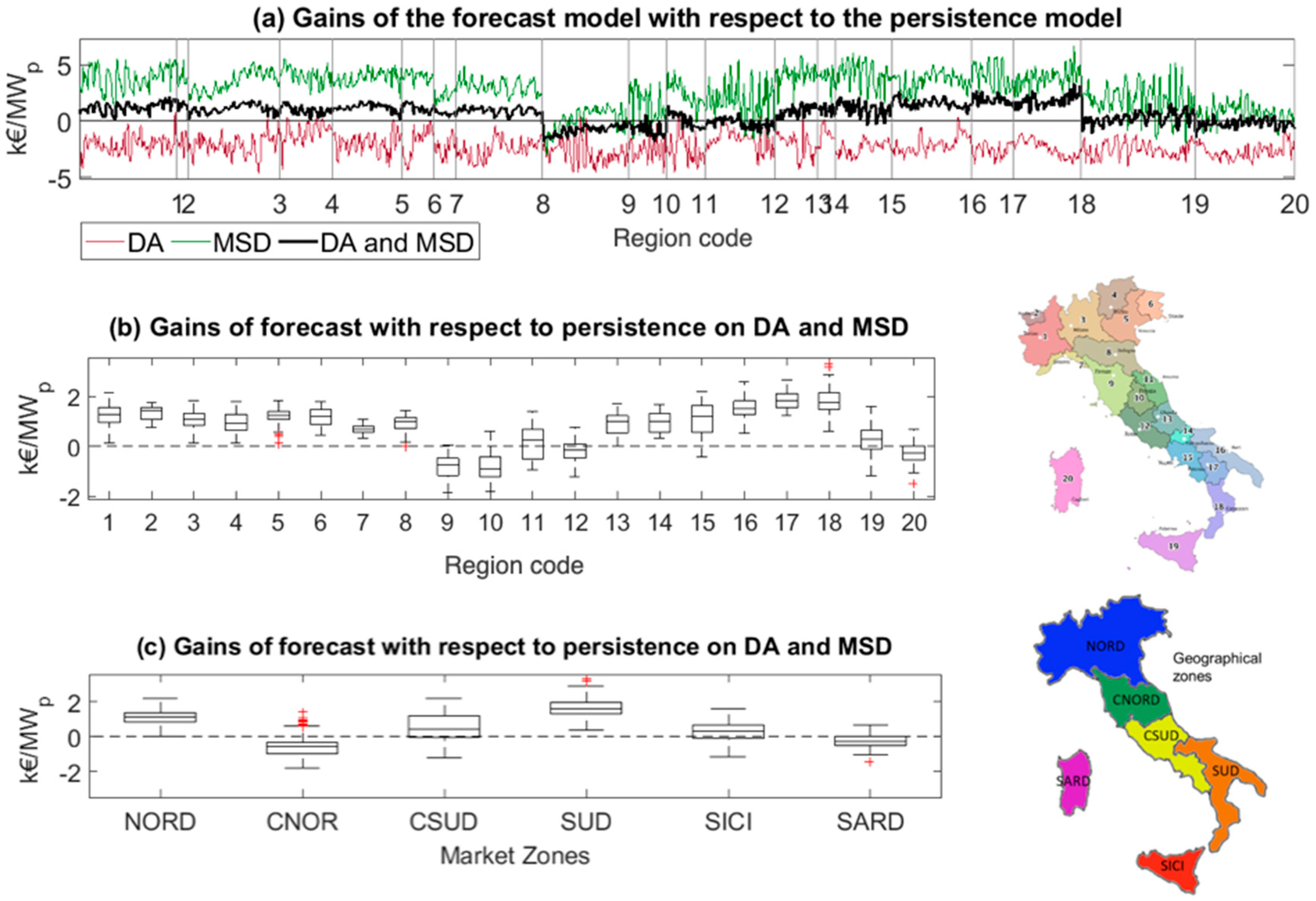
- The net imbalance absolute values (that ranges from −5 to 5 kEUR/MWp per year) are very small if compared with the total energy incomes on the DA and MSD markets (that ranges from 50 to 150 kEUR/MWp per year) hence, with the current market rules, the imbalances have a small impact on the total energy revenues of the PV producers/traders.
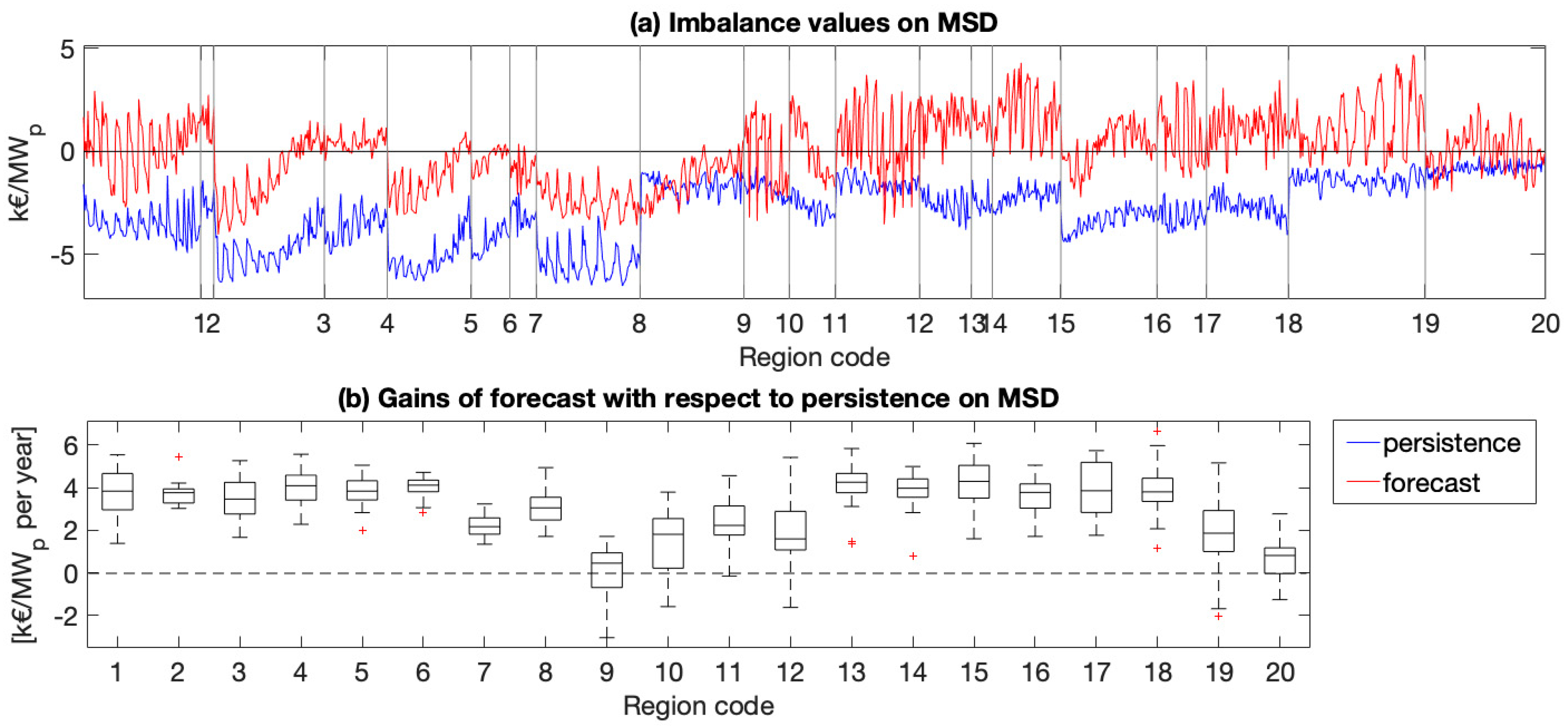
- The net imbalance values that should be always negative (economic losses for producers) in some locations can be also positive (economic revenues). Hence, a poorly predicted PV generation could even lead to higher profits than an “ideal” perfectly predictable generation (that will not produce a solar-induced imbalance).
- Not only is the benefit of using a more accurate forecast with respect to a simple persistence very small, but in some regions persistence predictions produce even higher revenues. Therefore, in these regions, there is no economic need to improve the forecast accuracy reducing the solar imbalance volumes.
- For energy producer/traders, it is much more important, in order to maximize revenues, to predict the right macro-zonal imbalance sign and then deliver to Terna a suitable under/over PV generation forecast than provide Terna with the most accurate power prediction.
- Therefore, we demonstrated that, in Italy, the current market regulation framework is in complete disagreement with the physical need of reducing imbalances and hence it requires a significant revision to allow a higher PV penetration.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ministry of Environment. SEN (Strategia Energetica Nazionale); Ministry of Environment: Rome, Italy, 2017.
- Proposta dI Piano Nazionale Integrato per l’Energia e il Clima. Available online: https://www.mise.gov.it/images/stories/documenti/Proposta_di_Piano_Nazionale_Integrato_per_Energia_e_il_Clima_Italiano.pdf (accessed on 1 December 2019).
- Sandbag, D.; Agora Energiewende. The European Power Sector in 2018. Up-to-Date Analysis on the Electricity Transition; Agora Energiewende: Berlin, Germany, 2019. [Google Scholar]
- IEA. Trends 2018 in Photovoltaic Applications. 2018. Available online: http://www.iea-pvps.org/fileadmin/dam/intranet/task1/IEA_PVPS_Trends_2018_in_Photovoltaic_Applications.pdf (accessed on 1 August 2020).
- ISPRA. Fattori di Emissione di Gas Serra e Altri Gas Nel Settore Elettrico 280/2018; ISPRA: Rome, Italy, 2018.
- Terna Spa. Il Mercato per il Servizi di Dispacciamento (Seminario RSE). 17 October 2016. Available online: www.rse-web.it/commons/layout/partUploaderView.jsp?CM=FILEVIEW&FILE_TO_UPLOAD=WF_3323_Terna+-+SEMINARIO+RSE_MSD_20161017.pdf%2B%2B%2Bapplications%5Cwebwork%5Csite_rse%5Clocal%5Cdocument%2F003323.Terna+-+SEMINARIO+RSE_MSD_20161017.pdf&TREATASATTACH=yes (accessed on 1 August 2020).
- Terna Spa. Methodologia di Previsione della Domanda Elettrica e della Previsione da Fonti Rinnovabili ai Fini della Dase di Programmazione di MSD; Terna Spa: Rome, Italy, 2016. [Google Scholar]
- Zhang, J.; Hodge, B.; Lu, S.; Hamann, H.; Lehman, B. Baseline and target values for regional and point PV power forecasts: Toward improved solar forecasting. Sol. Energy 2015, 122, 804–819. [Google Scholar] [CrossRef]
- Martinez-Anido, C.B.; Botor, B.; Florita, A.; Draxl, C.; Lu, S.; Hamann, H.; Hodge, B. The value of day-ahead solar power forecasting improvement. Sol. Energy 2016, 129, 192–203. [Google Scholar] [CrossRef]
- Wu, J.; Botterud, A.; Mills, A.; Zhou, Z.; Hodge, B.; Heaney, M. Integrating solar PV (photovoltaics) in utility system operations: Analytical framework and Arizona case study. Energy 2015, 85, 1–9. [Google Scholar] [CrossRef]
- Joos, M.S. Short-term integration costs of variable renewable energy: Wind curtailment and balancing in Britain and Germany. Renew. Sustain. Energy Rev. 2018, 86, 45–65. [Google Scholar] [CrossRef]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Photovoltaic generation forecast for power transmission scheduling: A real case study. Sol. Energy 2018, 174, 976–990. [Google Scholar] [CrossRef]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Residual load probabilistic forecast for reserve assessment: A real case study. Renew. Energy 2020, 149, 508–522. [Google Scholar] [CrossRef]
- Pierro, M.; Perez, R.; Perez, M.; Moser, D.; Cornaro, C. Italian protocol for massive solar integration: Imbalance mitigation strategies. Renew. Energy 2020, 153, 725–739. [Google Scholar] [CrossRef]
- Perez, R.; Perez, M.; Pierro, M.; Kivalov, S.; Schlemmer, J.; Dise, J.; Keelin, P.; Grammatico, M.; Swierc, A.; Ferreira, J.; et al. Operationally perfect solar power forecasts: A scalable strategy to lowest-cost firm solar power generation. In Proceedings of the 46th IEEE PV Specialists Conference, Chicago, IL, USA, 16–21 June 2019. [Google Scholar]
- Perez, M.; Perez, R.; Rábago, K.; Putnam, M. Overbuilding & curtailment: The cost-effective enablers of firm PV generation. Sol. Energy 2019, 180, 412–422. [Google Scholar]
- Gari da Silva Fonseca, J., Jr.; Nishitsuji, Y.; Udagawa, Y.; Oozeki, T. Improving regional PV power curtailment with better day-ahead PV forecasts: An evaluation of 3 forecasts. In Proceedings of the IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC), Waikola, HI, USA, 10–15 June 2018. [Google Scholar]
- Kaur, A.; Nonnenmacher, L.; Pedro, H.; Coimbra, C. Benefits of solar forecasting for energy imbalance markets. Renew. Energy 2016, 86, 819–830. [Google Scholar] [CrossRef]
- De Giorgi, M.; Congedo, P.; Malvoni, M.; Laforgia, D. Error analysis of hybrid photovoltaic power forecasting models: A case study of mediterranean climate. Energy Convers. Manag. 2015, 100, 117–130. [Google Scholar] [CrossRef]
- Bignucolo, F.; Raciti, A.; Rossi, B.; Zingales, A. Management of renewable generation plants: Imbalance costs and local storage systems. In Proceedings of the AEIT Annual Conference, Palermo, Italy, 3–5 October 2013. [Google Scholar]
- Antonanzas, J.; Pozo-Vázquez, D.; Fernandez-Jimenez, L.; Martinez-De-Pison, F.J. The value of day-ahead forecasting for photovoltaics in the Spanish electricity market. Sol. Energy 2017, 158, 140–146. [Google Scholar] [CrossRef]
- Ibagon, C.N.; Oliveri, V.; Delfanti, M. Analysis of European RES Imbalance Charge: THE impact on PV and Wind Plants. 2014. Available online: https://www.politesi.polimi.it/bitstream/10589/86586/3/2013_12_Ibagon.pdf (accessed on 1 August 2020).
- Terna Spa (92/2019). 2019. Available online: https://www.terna.it/it/sistema-elettrico/mercato-elettrico/zome-mercato (accessed on 1 August 2020).
- GME. 2019. Available online: http://www.mercatoelettrico.org/it/Mercati/MercatoElettrico/MPE.aspx (accessed on 1 August 2020).
- Terna Spa. Piano di Sviluppo 2019; Terna Spa: Rome, Italy, 2019. [Google Scholar]
- Clo’, S.; Fumagalli, E. The effect of price regulation on energy imbalances: A Difference in differences design. Energy Econ. 2019, 81, 754–764. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D. A Description of the Advanced Research WRF Version 3. NCAR Tech; Note NCAR/TN-4751STR; Technical Report NCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Houghton, J. The Physics of Atmospheres, 3rd ed.; Cambridge University Press: Cambridge, UK, 2002; p. 340. [Google Scholar]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Model output statistics cascade to improve day ahead solar irradiance forecast. Sol. Energy J. 2015, 117, 99–113. [Google Scholar] [CrossRef]
- Terna Spa. Available online: https://www.terna.it (accessed on 1 August 2020).
- Ineichen, P.; Perez, R.; Seal, R.; Zalenka, A. Dynamic global-to-direct irradiance conversion models. ASHRAE Trans. 1992, 98, 354–369. [Google Scholar]
- Perez, R.; Seals, R.; Zelenka, A.; Ineichen, P. Climatic evaluation of models that predict hourly direct irradiance from hourly global irradiance: Prospects for performance improvements. Sol. Energy 1990, 44, 99–108. [Google Scholar] [CrossRef]
- Marion, B. A model for deriving the direct normal and diffuse horizontal irradiance from the global tilted irradiance. Sol. Energy 2015, 122, 1037–1046. [Google Scholar] [CrossRef]
- Liu, B.; Jordan, R.C. Daily insolation on surfaces tilted towards equator. ASHRAE 1961, 10, 526–541. [Google Scholar]
- Maxwell, A.L. A Quasi-Physical Model for Converting Hourly Global Horizontal to Direct Normal Insolation; Technical Report SERI/TR-215-3087; Solar Energy Research Institute: Golden, CO, USA, 1987. [Google Scholar]
- King, D.; Kratochvil, J.; Boyson, W. Photovoltaic Array Performance Model; Sandia National Laboratories: Albuquerque, NM, USA, 2004. [Google Scholar]
- Pierro, M.; Bucci, F.; Cornaro, C. Full characterization of photovoltaic modules in real operating conditions: Theoretical model, measurement method and results. In Progress in Photovoltaics; Wiley Online Library: Hoboken, NJ, USA, 2015; Volume 23, pp. 443–461. [Google Scholar]
- Pierro, M.; Bucci, F.; Cornaro, C. Impact of light soaking and thermal annealing on amorphous silicon thin film performance. In Progress in Photovoltaics; Wiley Online Library: Hoboken, NJ, USA, 2015; Volume 23, pp. 1581–1596. [Google Scholar]
- Lorenz, E.; Remund, J.; Muller, S.C.; Traunmull, W.; Steinmaurer, G.; Pozo, D.; Ruiz-Arias, J.; Fanego, V.L.; Ramirez, L.; Romeo, M.G. Benchmarking of different approaches to forecast solar irradiance. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–25 September 2009. [Google Scholar]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hekmer, K., Jr.; Rene, D.; Hoff, T.E. Validation of short and medium term operational solar radiation forecasts in the US. Sol. Energy 2010, 84, 2161–2172. [Google Scholar] [CrossRef]
- Perez, R.; Schlemmer, J.; Kankiewicz, A.; Dise, J.; Tadese, A.; Hoff, T. Detecting calibration drift at ground truth stations a demonstration of satellite irradiance models’ accuracy. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017. [Google Scholar]
- Yang, D.; Perez, R. Can we gauge forecasts using satellite-derived solar irradiance? J. Renew. Sustain. Energy 2019, 11, 023704. [Google Scholar] [CrossRef]
- André, M.; Perez, R.; Soubdhan, T.; Schlemmer, J.; Calif, R.; Monjoly, S. Preliminary assessment of two spatio-temporal forecasting technics for hourly satellite-derived irradiance in a complex meteorological context. Sol. Energy 2019, 177, 703–712. [Google Scholar] [CrossRef]
- Palmer, D.; Koubli, E.; Cole, I.; Betts, T.; Gottschalg, R. Satellite or ground-based measurements for production of site specific T hourly irradiance data: Which is most accurate and where? Sol. Energy 2018, 165, 240–255. [Google Scholar] [CrossRef]
- Lorenz, E. PV Production Forecast of Balance Zones in Germany; PVPS Task 14 & SHC Task 46; IEA: Paris, France, 2015.
- Pelland, S.; Galanis, G.; Kallos, G. Solar and photovoltaic forecasting through post-processing of the Global Environmental Multiscale numerical weather prediction model. Prog. Photovolt Res. Appl. 2013, 21, 284–296. [Google Scholar] [CrossRef]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production part I: Deterministic forecast of hourly production. Sol. Energy 2014, 115, 792–803. [Google Scholar] [CrossRef]
- Antonanzas, J.; Perpinan-Lamigueiro, O.; Urraca, R.; Antonanzas-Torresa, F. Influence of electricity market structures on deterministic solar forecasting verification. Sol. Energy 2020, in press. [Google Scholar] [CrossRef]
- Pierro, M.; Defelice, M.; Bucci, F.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Multi-model ensemble for day ahead prediction of photovoltaic power generation. Sol. Energy 2016, 134, 132–146. [Google Scholar] [CrossRef]
- Pierro, M.; Perez, R.; Perez, M.; Moser, D.; Cornaro, C. Italian protocol for massive solar integration: From solar imbalance mitigation to 24/365 solar power generation. Renew. Energy 2020. under peer review. [Google Scholar]




 | Sign of the Imbalance of Relevant Production Unit (Market Zone Z) | |||
| Over generation with respect the day-ahead scheduling) | Under generation with respect the day-ahead scheduling) | |||
| (+) | (−) | |||
| Sign of Macro-zonal Imbalance | Over generation | (+) | UP sells to TSO their imbalance at minimum MSD price | UP purchases from TSO their imbalance at minimum MSD price |
| min {, }. | min {, }. | |||
| Negative imbalance value (cost) | Positive imbalance value (revenue) | |||
| Under generation | (−) | UP sells to TSO their imbalance at maximum MSD price | UP purchases from TSO their imbalance at maximum MSD price | |
| max {, } | max {, } | |||
| Positive imbalance value (revenue) | Negative imbalance value (cost) | |||
| Name | Acronym and Formulae |
|---|---|
| Forecast error [W/m2 or MW-% of peak power] | |
| Root mean square error [W/m2 or MW-% of peak power] | |
| Skill score [%] | |
| Current and scheduled PV generation [MW/MWp] | , |
| UP Imbalance [MW or % of peak power] | |
| UP absolute energy imbalance [MWh/year per MWp] | |
| UP net imbalance value [kEUR/year] | |
| UP energy income on DA [kEUR/year] | |
| UP imbalance value on MSD [kEUR/year] | |
| UP total energy income [kEUR/year] | |
| UP energy income on DA with perfect scheduling (no imbalance) [kEUR/year] |
| Day-Ahead Forecast | |||
|---|---|---|---|
| Work | Country | RMSE [% of Pn] | Skill Score [%] |
| Current work | Italy (benchmark) | in the range 11%–16.7% | in the range 25.7%–39.7% |
| Lorenz et al. [45]. | Germany (average single site forecast accuracy) | 12.8% | - |
| Pelland et al. [46] | Canada (forecast of three Canadian PV plants generation) | in the range 6.38%–9.17% | in the range 36.7%–64% |
| Zamo et al. [47] | France (different single site PV power forecast methods) | - | in the range 29.4%–47% |
| Antonanzas et al. [48] | Spain (different single site PV power forecast methods) | in the range 22.54%–28% | in the range 14.5%–31.4% |
| Pierro et al. [49] | Italy (different single site PV power forecast methods) | in the range 11.1%–12.8% | in the range 34%%–42.5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pierro, M.; Moser, D.; Perez, R.; Cornaro, C. The Value of PV Power Forecast and the Paradox of the “Single Pricing” Scheme: The Italian Case Study. Energies 2020, 13, 3945. https://doi.org/10.3390/en13153945
Pierro M, Moser D, Perez R, Cornaro C. The Value of PV Power Forecast and the Paradox of the “Single Pricing” Scheme: The Italian Case Study. Energies. 2020; 13(15):3945. https://doi.org/10.3390/en13153945
Chicago/Turabian StylePierro, Marco, David Moser, Richard Perez, and Cristina Cornaro. 2020. "The Value of PV Power Forecast and the Paradox of the “Single Pricing” Scheme: The Italian Case Study" Energies 13, no. 15: 3945. https://doi.org/10.3390/en13153945
APA StylePierro, M., Moser, D., Perez, R., & Cornaro, C. (2020). The Value of PV Power Forecast and the Paradox of the “Single Pricing” Scheme: The Italian Case Study. Energies, 13(15), 3945. https://doi.org/10.3390/en13153945






