1. Introduction
Wind energy is one of the most popular renewable energy sources; over the last decades, wind turbines have been extensively developed [
1]. In the wind industry, single rotor 3-bladed Horizontal Axis Wind Turbines (HAWT) are, most often, in operation. This type of a wind turbine is also commonly studied. However, different types have been proposed, designed, and tested. Vertical Axis Wind Turbines (VAWT), due to their capability to operate independently from wind direction, have gained some industry interest. Another possible solution is the Magnus effect-based wind turbine, which uses rotating cylinders acting as blades. Power coefficient can be potentially increased with a Counter-Rotating Wind Turbine (CRWT). A Counter-Rotating Wind Turbine is a turbine with two counter-rotating rotors. However, this type of a wind turbine is not yet operating on a commercial scale and still needs development and studies.
Even with well-designed rotor blades in HAWT, due to the physical limitations, a large part of wind energy is not being captured. In the case of Single Rotor Wind Turbine (SRWT), energy extraction efficiency is limited to 59.3%, following classical Betz’s theory [
2]. In a real-world operation, the turbine’s efficiency reaches 40–50% [
3]. In CRWT, the second rotor is added and placed in the first rotor wake in order to extract the part of energy that is left in the wind. Newman showed in [
4,
5] that for an ideal turbine with two rotors, such as CRWT, energy extraction efficiency can be increased to 64%. In the case of an infinite number of rotors—that number goes to 66.7%. Schönball [
6] is one of the first to describe a mechanism, which is composed of two counter-rotating rotors. In the generator, a rotor is driven by one wind turbine rotor, while commonly stationary stator is driven by another one. Due to the counter rotation of two rotors, the relative speed between them may be doubled and, thus, the efficiency may be correspondingly increased when comparing with a conventional, single-rotor generator. McCombs [
7] developed a wind turbine equipped with two sets of blades that are connected to the generator’s rotor and stator directly.
When considering the design of a CRWT, there are few configurations possible. Placement of the rotors, the distance between each other, as well as its diameters can vary. When both rotors are placed at the upwind side of a tower (as for example in [
8]), there is commonly small axial distance between them. Otherwise, bending torque caused by unevenly distributed hub weight would significantly stress tower construction. When rotors are placed at upwind and downwind sides and weight is distributed evenly, axial distance can be much larger. This, however, may result in a massive hub construction. In [
9], authors proposed and investigated a turbine in such a configuration. CRWT can consist of rotors with different diameters, as one proposed for example in [
10]. In that study, a smaller rotor is located at the downwind of the large one’s side.
There are generally two approaches for designing an electrical generator for CRWT. Shafts from both rotors can be coupled by a differential mechanism. The output is then attached to a single conventional generator. Such a design was presented for example in [
9,
11,
12]. Aiming to extend the use of counter-rotating rotors wind generators to medium- and large-scale applications, the latest paper [
13] introduces and analyzes a new high-performance solution. The authors proposed a system that integrates two counter-rotating rotors, planetary speed increaser with one degree of freedom and four inputs and outputs, and an electric generator with counter-rotating windings. The proposed solution has compact design, increased power output (which makes it suitable for medium and large-scale wind turbines), and allows electric generator to operate in more efficient manner.
However, mechanical gearing introduces complexity and may increase the turbine’s weight, maintenance, and spare parts costs for the system [
14]. The second approach is to attach rotors shafts directly to separate, counter-rotating armatures. Due to higher relative rotational speed, the overall size of a generator and volume of magnetic materials used can be reduced. Studies on a separated generator have been conducted (e.g., [
15,
16]), as well as on a complete CRWT system with such an electrical machine (see [
17,
18]).
The CRWT concept is being studied both experimentally and numerically. Experimental investigations include tests in wind tunnels, see e.g., [
17] or [
19]. There were several field test reports as well. Study results of a 6 kW CRWT carried out over a period of 4 months have been presented in [
20]. Operational field tests of a small CRWT have been described in [
8]. Numerical investigations are mainly performed with use of the Computational Fluids Dynamics (CFD). Some simpler methods have been developed and used with examples presented in [
21,
22]. Those methods, however, do not take into account all the complexity of a flow around CRWT wind turbine, especially the influence of turbulent structures created behind the first rotor. Therefore, despite a costly computation, CFD is often chosen before CRWT experimental investigation.
Different techniques, accurately differentiated in [
23], are considered when simulating wind turbines with CFD. Rotor’s geometry can be recreated on a numerical grid. This approach, however, requires an extremely dense mesh in boundary layers. Moreover, compressibility effects can occur at the tip of the blade. This would result in additional terms in solving equations (nevertheless some authors used direct rotor representation for CRWT simulation, see for example [
24]). Therefore, several simplified methods have been proposed containing Actuator Disk Model (ADM) [
25] or Actuator Surface Model (ASM) [
26]. In the present study, Actuator Line Model (ALM) introduced in [
27] has been used. This technique allows to represent a single blade of a wind turbine and to simulate its influence at the flow at a relatively low computational cost.
A number of studies, with one of such methods, have been performed investigating SRWT performance. Results of these studies verified its viability (see for example [
14,
15,
16] or [
17]). Moreover, trials with CRWT have been previously conducted, with such extensive ones as CRWT wind farm simulation [
18]. To predict the annual energy gain Shen et al. in [
19] used ALM for different turbine’s configurations. In that study, rotors were accurately counter-rotating for all studied configurations. A more extensive parametric study has been presented in [
20]. However, in that study, authors utilized Actuator Disc Model. That approach does not take into account an influence of a single blade. Thus, it does not produce blade tip vortices. Additionally, authors performed simulations in steady state and used averaged turbulence model. Averaging leads to neglecting of rotors dynamic interactions. Turbine diameter was also much larger, resulting in completely different operational conditions.
The goal of this study is to find the optimal configuration and operational point for proposed CRWT. For that reason, a parametric CFD study has been performed with ALM method employed to model CRWT. Tip speed ratio (TSR) of each rotor and distance between them have been chosen as the parameters. The following chapters of this article present the basics of the numerical calculation method, the design of rotor for simulations, as well as the model simulation setup and its verification. The main substantive results of the parametric study and their analysis are contained in
Section 4.
2. Numerical Method
Airflow around the wind turbine can be described by the Navier–Stokes equations. Solution for these highly nonlinear, differential equations can be approximated numerically with Computational Fluid Dynamics (CFD) techniques. In general, flow can be described as follows:
where
u is the fluid velocity vector,
p stands for fluid pressure,
ρ represents fluid density,
is the kinematic viscosity.
is described as Laplacian operator and
is external forces vector. When flow is turbulent, it is extremely costly to find a direct numerical solution (DNS) for the studied case. Therefore, several simplifying methods for a turbulence modeling have been proposed. For steady state cases, turbulence can be averaged over time and space. This approach is known as Reynolds-averaged Navier–Stokes (RANS) and is utilized with appropriate turbulence models applied. However, in present research dynamic interference between the turbine’s blades is to be studied. Therefore, Large Eddy Scale (LES) has been incorporated for a turbulence modeling. In this approach, smaller turbulent structures are modeled using sub-grid scale models. Only those that were not filtered out are solved numerically. This kind of fluid flow equations filtering converts Equations (1) and (2) to form:
where
is the sub-grid scale viscosity. In the present study, it is modelled with the standard Smagorinsky model [
28].
stands for filtered velocity vector,
represents filtered pressure.
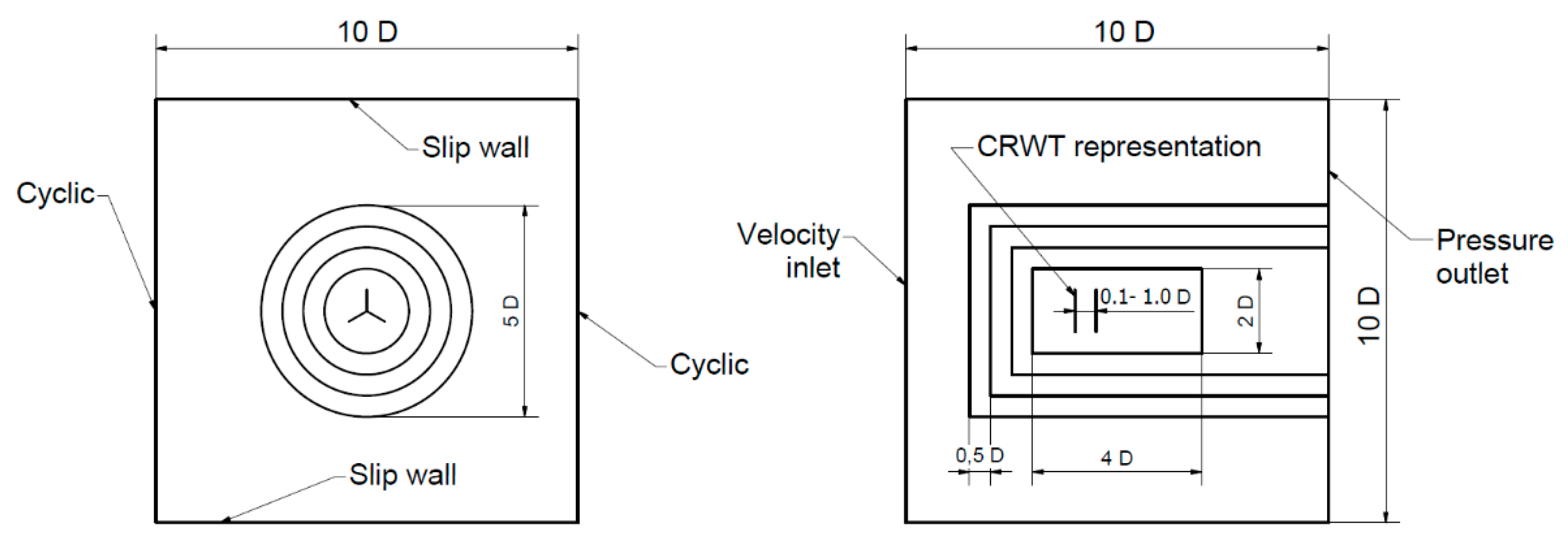
Wind turbine representation has to be put into the computational domain in order to investigate performance and to analyze the turbine’s wake. It can be done in several manners. One can transpose blades geometry onto the numerical grid. However, to simulate flow in the boundary layers, the mesh close to the blade’s surface has to be extremely dense, thus increasing computational expense. Moreover, since modern blades have complex shape with profile that changes as a function of span, keeping grid structured can be difficult as well. Actuator models introduced into the domain are much simpler alternatives. Such models predict the rotor thrust and torque without fully resolving the rotor and blade geometry. In this study, the Actuator Line Model (ALM) has been used. Along with the capability to represent separated blades and thus to investigate dynamic interactions between rotors’ blades, its computational cost is also relatively low. Moreover, this approach does not require any modification of the computational grid but a fully structured one can be utilized which is easier to create and refine.
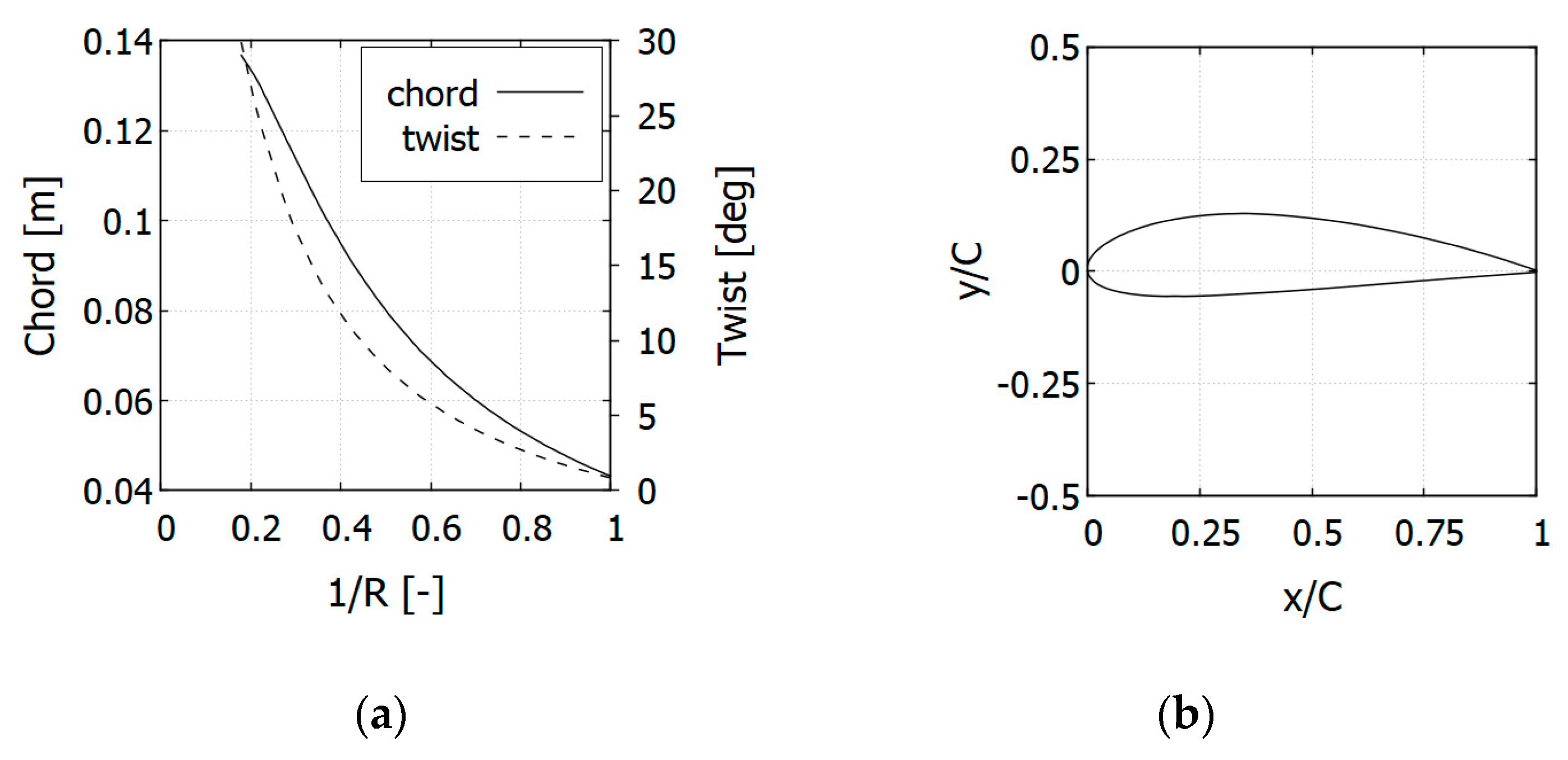
In the Actuator Line Model, each rotor blade is represented by a set of discrete segments distributed evenly along the blade’s span. Body force is applied to a fluid flow at the center of each segment. Drag
and lift
can be calculated based on the segment’s location and width
, as well as airfoil chord
and twist, local wind speed
and tabulated lift
and drag
coefficients values at the determined angle of attack
. Drag and lift forces are given by the following equations:
Applied body force is equal and opposite in direction to the vector sum of lift and drag forces. The Gaussian function is used to project it in on surrounding finite elements:
where
is calculated force,
stands for Gaussian projection width and
is distance from the center of an actuator segment.
For the accurate power prediction, proper selection of the ALM model’s parameters is crucial. The most important is the projection width
, which determines force distribution in an actuator point proximity. If a too high value is selected, the force is projected far beyond the actual blade swept area. On the other hand, a too low value results in discontinuous force distribution. Often, a set of trials is required to determine the proper value, but the general rule is to use
, where
is finite element edge size. Lower values may introduce numerical instabilities into the solver. Another important factor is the simulation time step, which should be small enough to not let virtual blade move more than one finite element at a time. It ensures smooth application of a body force as well. Time step is correlated with a grid resolution. The denser mesh the better but limit has to be set to ensure reasonable calculation time. A sufficient number of actuation points should be used to ensure the continuous distribution of force. It is good practice to have actuator points in twice the number of finite elements along the blade span. Best practices and guidelines for simulation with ALM have been presented, e.g., in [
29].
4. CRWT Parametric Study
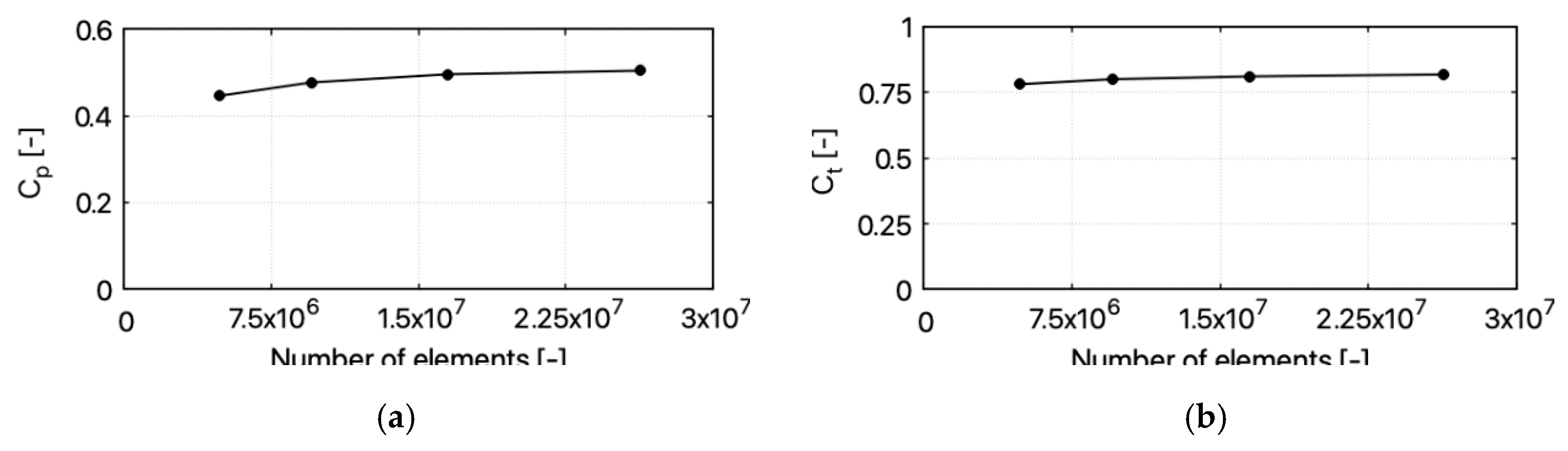
With a numerical setup verified, a parametric study for CRWT has been performed. The amount of energy extracted from a stream of air is expected to significantly increase when a second rotor is added. The second rotor model has been placed in a computational domain and different configurations and operational points have been studied. The chosen parameters were the distance between rotors and the TSR of each rotor (for both rotors TSR was calculated in relation to wind velocity at domain input). Rotors were separated by distances 0.1 D, 0.25 D, 0.5 D, 0.75 D, and 1 D. In each configuration, TSR of front and rear rotor were changing in a range from 2 to 8 with step equal to 1; thus, 49 simulations were performed for every distance giving 245 simulations in total. Average calculations time of a single simulation was about 7 h. Even though simulations were paralleled on 768 cores each, it took over 1700 computational hour in total to conduct this parametric study. Cluster where simulation have been carried out is based on Intel
® Xeon
® Processor E5 v3 @ 2, 3 GHz. In the previous papers [
32,
33], authors presented partial simulations results obtained with proposed approach while in the present one full parametric study results are described.
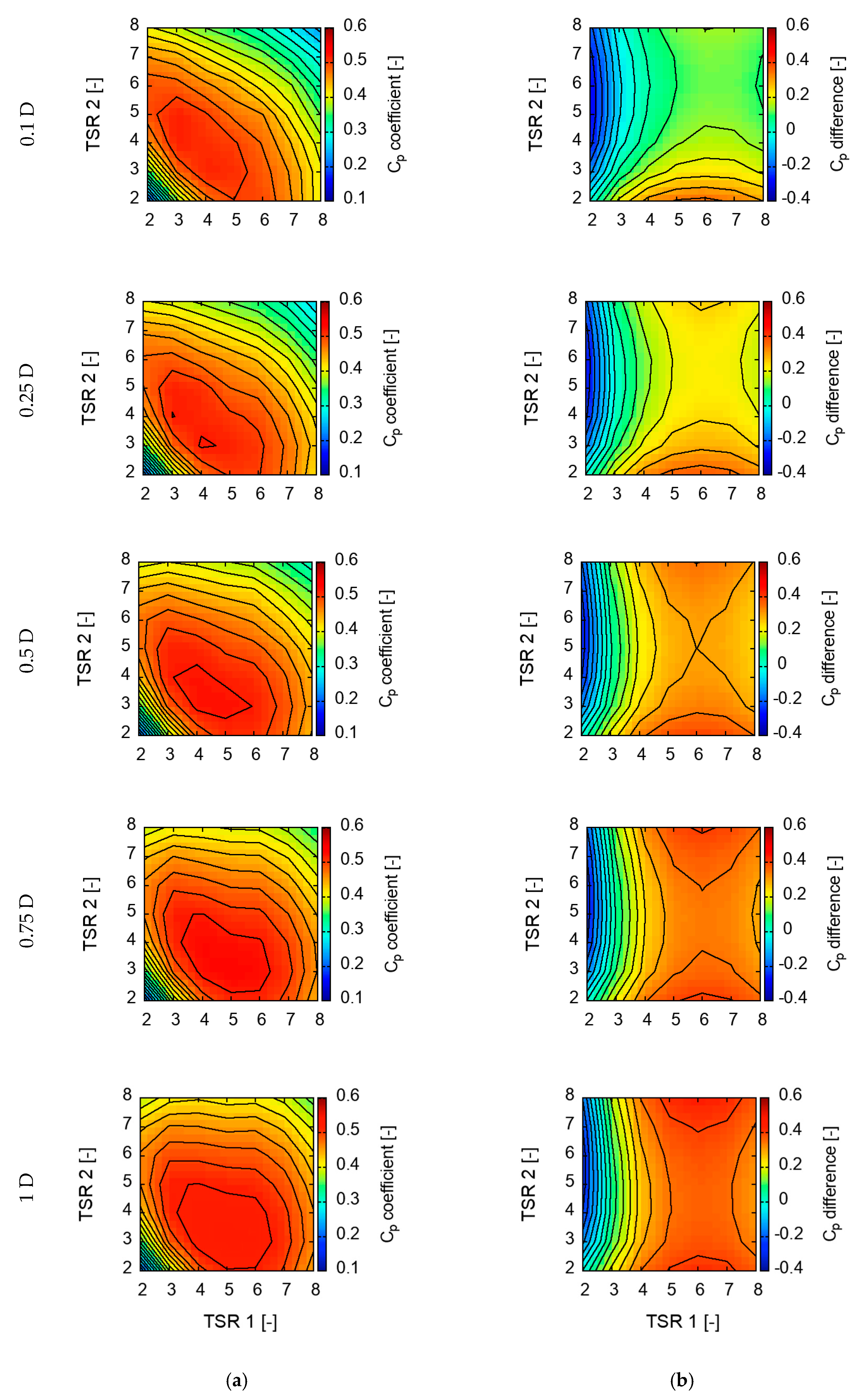
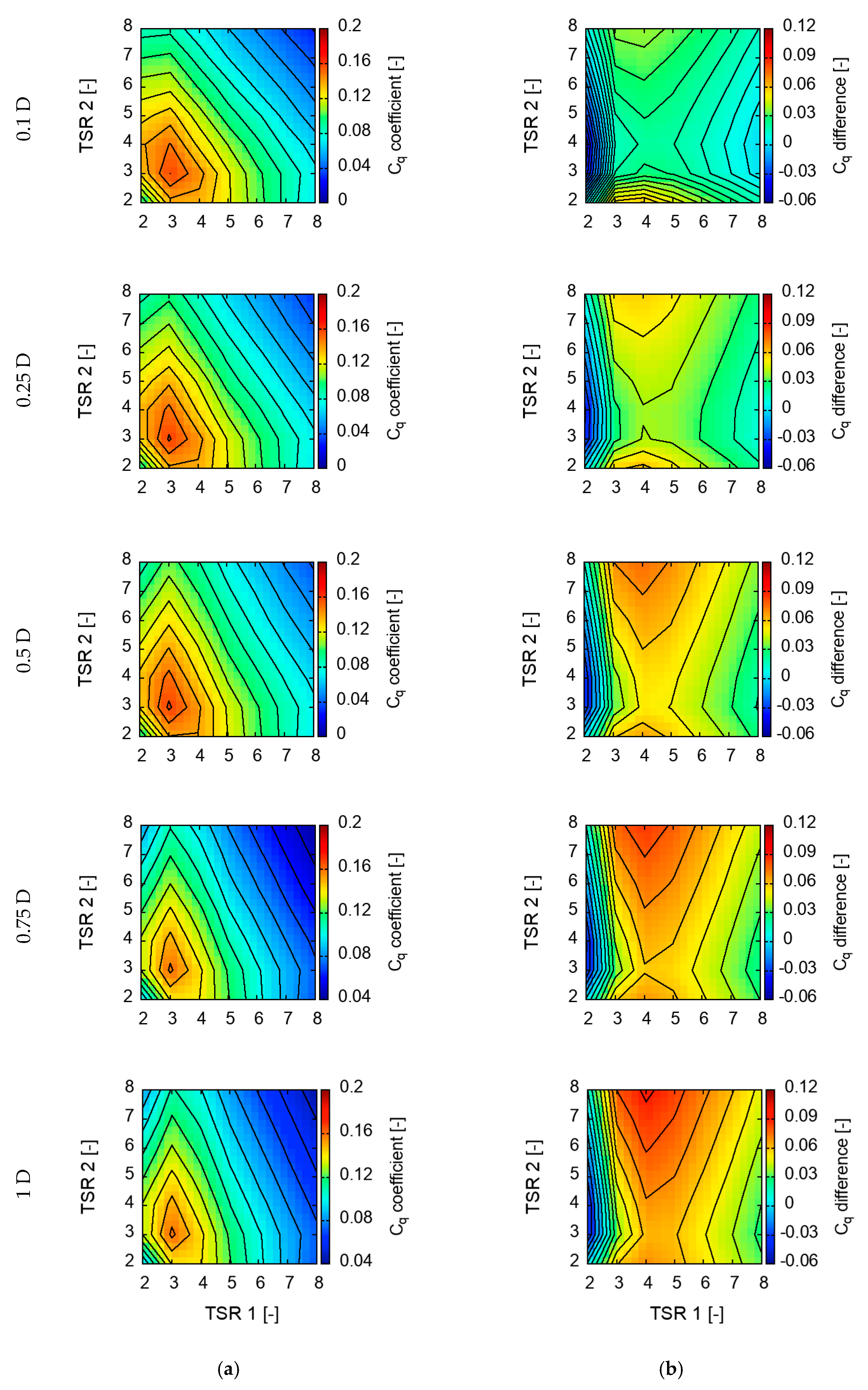
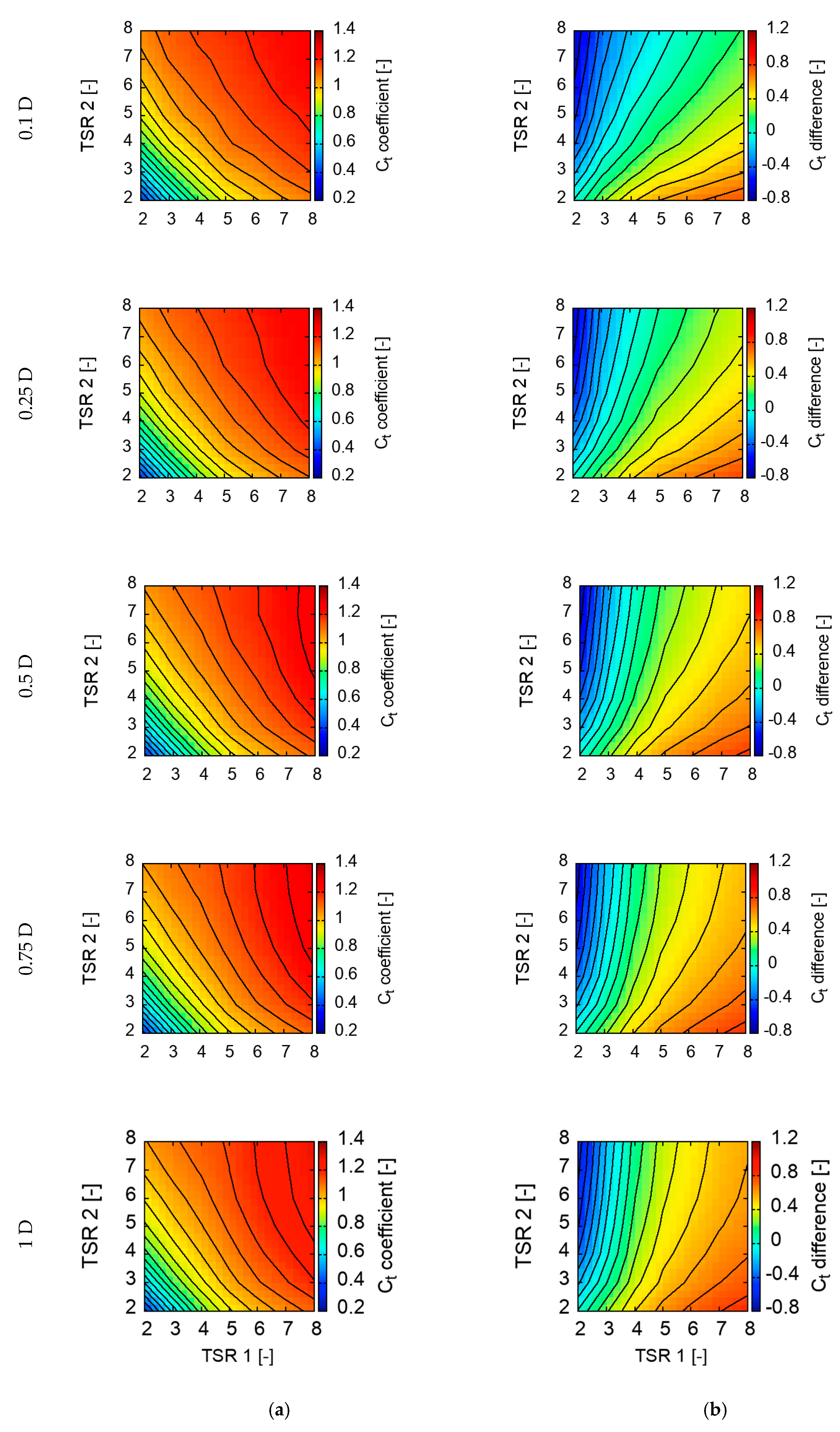
Results of simulations were collected and presented in the form of maps. Calculated power, torque, and thrust coefficients were plotted in a function of front and rear rotors’ TSR. Additionally, the differences between those values for both rotors were plotted as well. Value maps are presented in
Figure 6,
Figure 7 and
Figure 8. Results analysis helped to find the best configuration and operational point for CRWT. Thanks to the utilization of a transient solver, interactions between rotors could be observed and analyzed. Obtained fields contours were discussed as well. In the following sections, the term “configuration” relates to the distance between rotors, while the term “operational point” relates to the values of TSR for the front (TSR
1) and rear (TSR
2) rotor in a certain configuration.
4.1. CRWT Performance
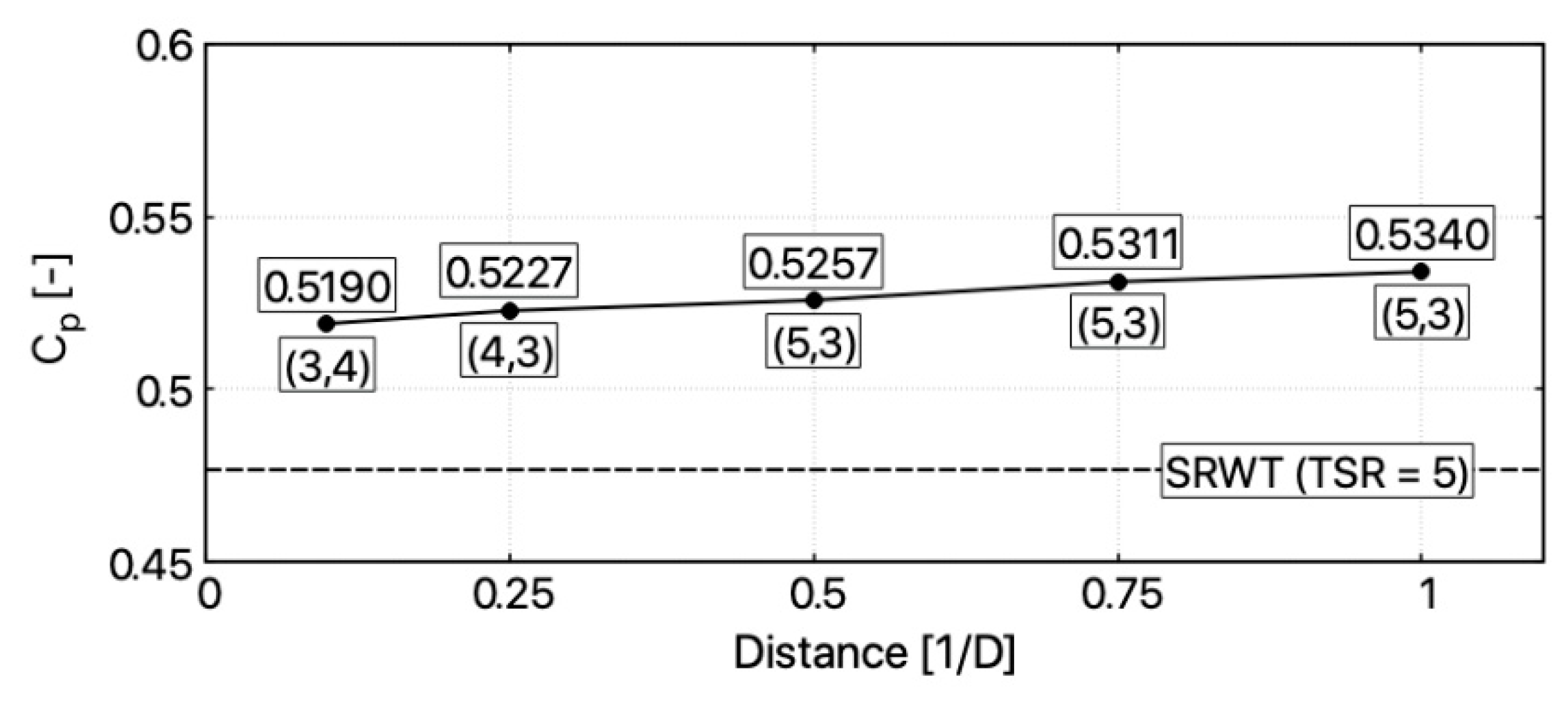
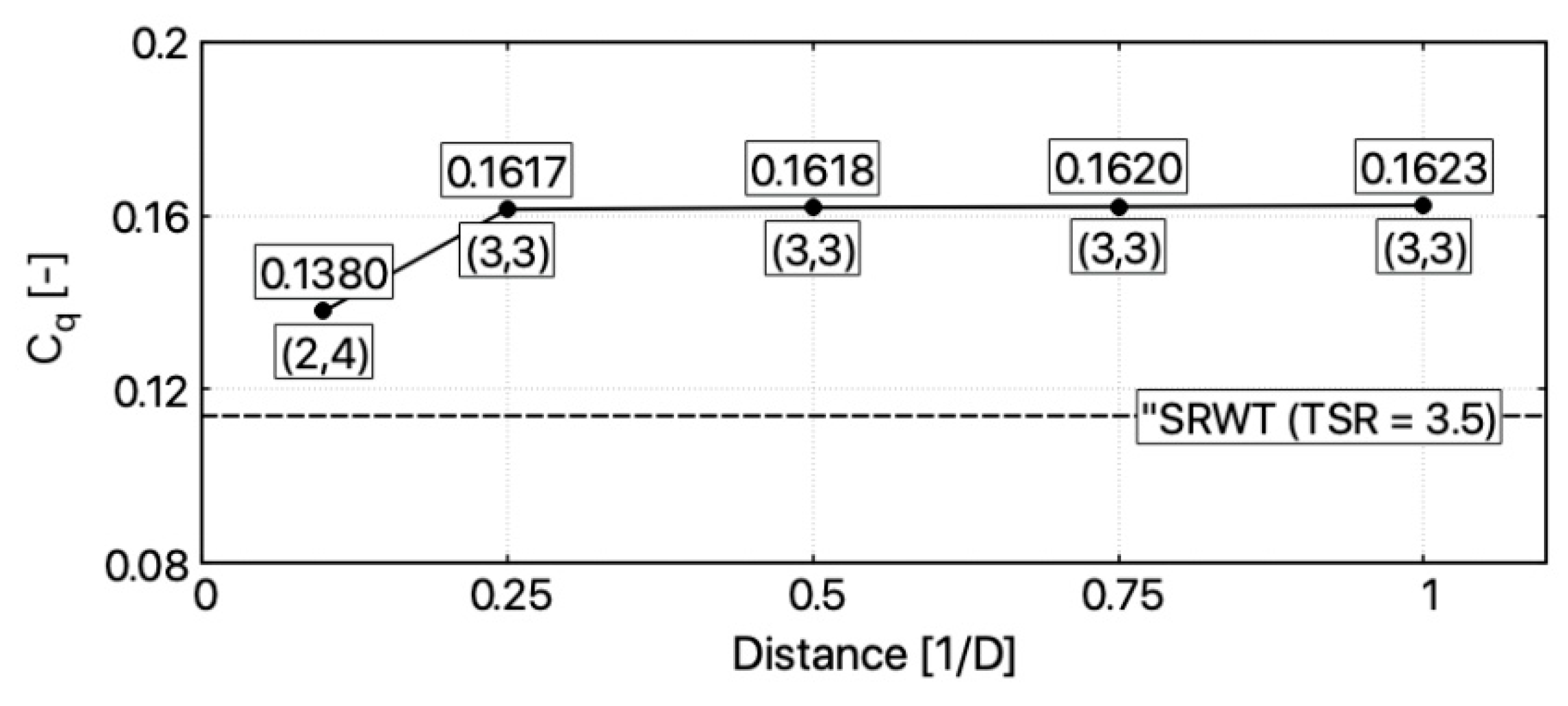
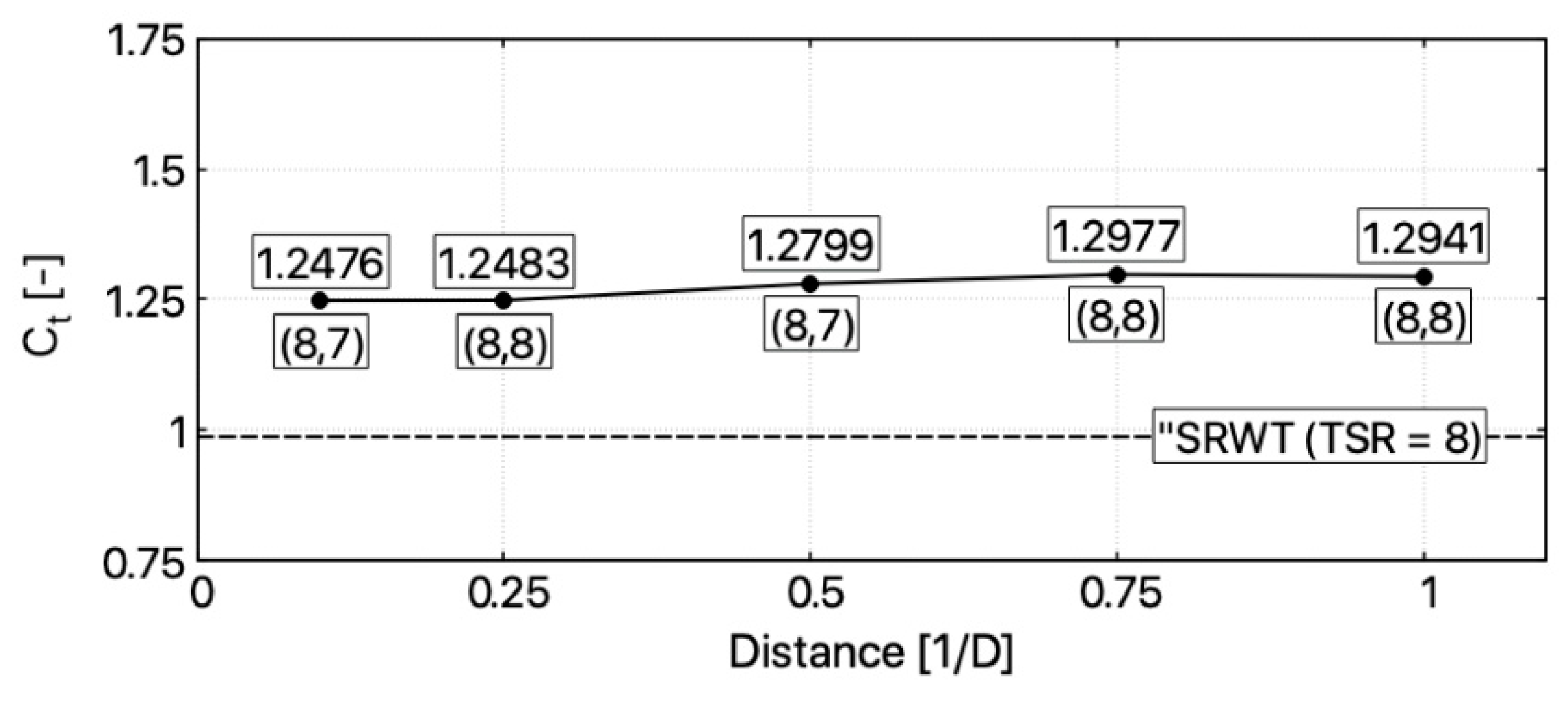
The optimal values of power, torque, and thrust coefficients for each studied configuration are presented in
Figure 9,
Figure 10 and
Figure 11. Rotors’ TSR at these operational points are marked as well. The following are the main results analyses findings:
for all the studied distances separating CRWT’s rotors, there is an optimal operational point where power coefficient Cp is higher than for SRWT operating with designed TSR = 5;
optimal power coefficient tends to grow with a distance between rotors;
highest power coefficient was observed in the configuration where rotors were separated by distance 1 D, the front rotor was operating with TSR = 5 and rear one with TSR = 3. In this configuration increase in Cp value, in comparison to SRWT, is significant and equals to 12.02%. The lowest increase in Cp was obtained in configuration 0.1 D (8.87%). TSR in optimal operational point for this configuration was equal to 3 and 4 for the front and rear rotor, respectively;
for all the studied configuration points, only for distance 0.1 D is the optimal operational obtained when TSR of the rear rotor is higher than for the front one. In other configurations, Cp optimum occurs when the front rotor rotates faster. In the best configuration (distance 1 D, TSR1 = 5, TSR2 = 3) the rear rotor rotates 40% slower. However, due to the counter-rotation, the relative rotational speed at the generator shaft increases by 60% in comparison to SRTW;
most of the power is generated by the front rotor as it can be clearly observed in maps presenting differences in rotor performance;
for all the configurations, the 0.1 D increase in torque coefficient C
q is similar and observed when rotors are exactly counter-rotating with TSR
1 = TSR
2 = 3. Torque at the generator shaft is higher by about 40% than the torque generated by SRWT in optimal point (for torque coefficient optimal TSR is always lower than for power coefficient for which the turbine is designed. As seen in
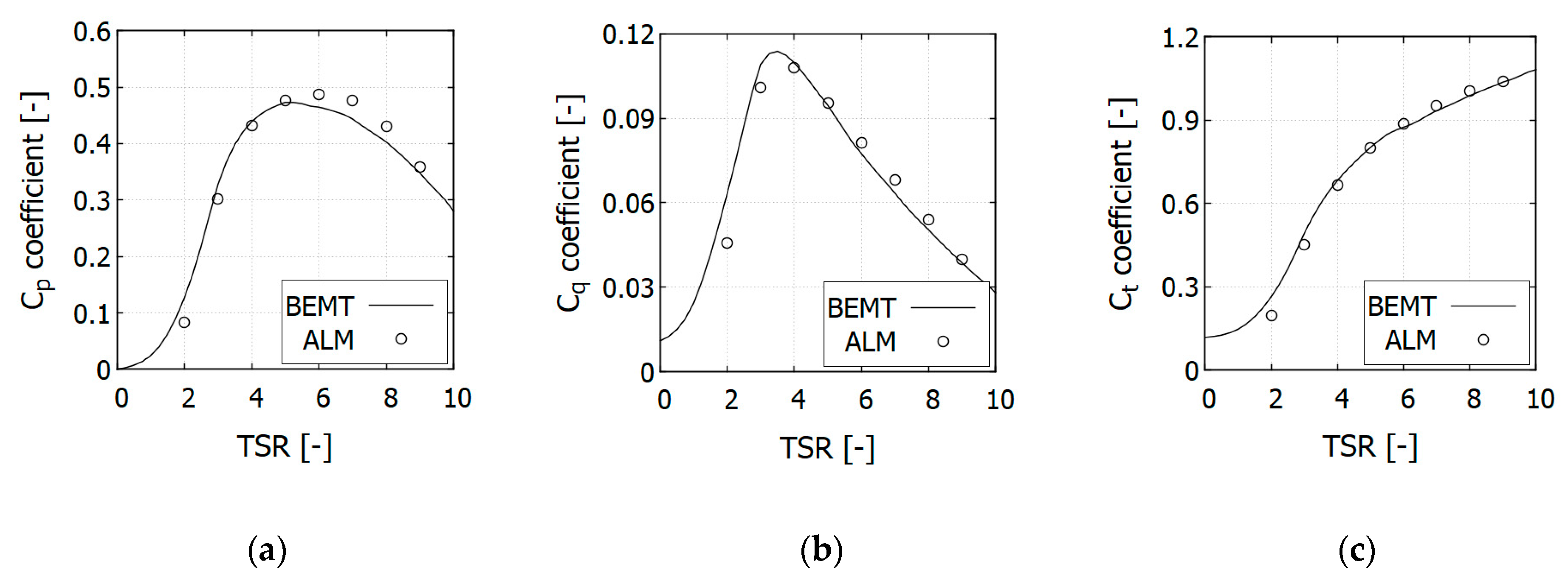
Figure 3, the highest SRWT torque is obtained with TSR ~ 3.5);
as expected, thrust is much higher than in the case of SRWT. Maximum value of thrust coefficient for each configuration is similar. It is observed when both rotors operate close to TSR = 8. A substantial increase in thrust results in a much more expanded wake, as seen in Figure 13.
4.2. Rotors Interaction and Wake Analysis
The selected CFD solver is a transient one therefore it was possible to analyze the dynamic interactions between the front and rear rotor. Moreover, with the ALM approach applied for rotor modeling, it is also possible to observe an influence of a single rotor’s blade on a fluid flow. SOWFA software comes with build functions for calculating torque and power at the turbine’s shaft. It is done by integrating over forces generated at each actuator point.
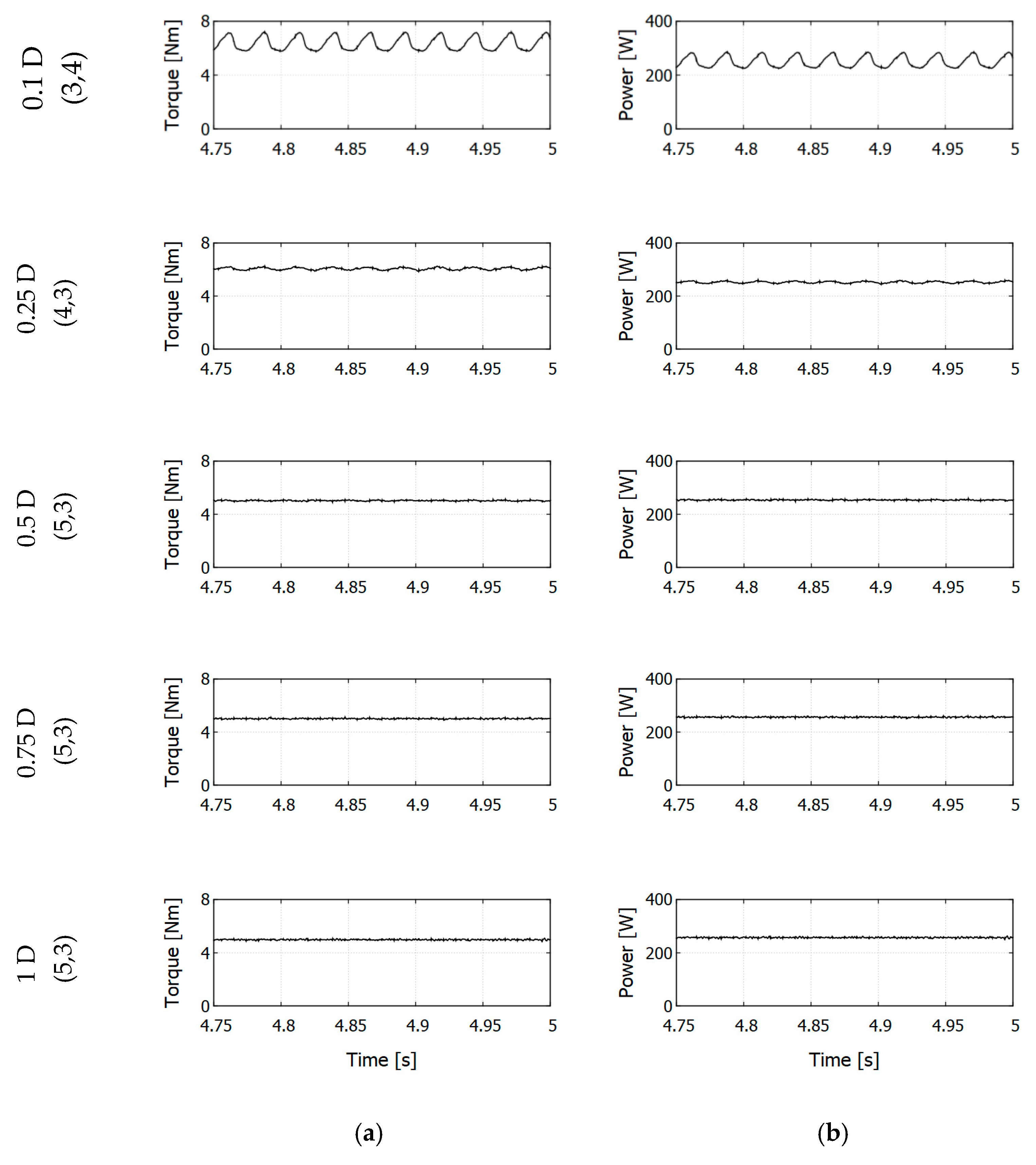
In
Figure 12, the generated total torque (left-hand side) and power (right-hand side) have been plotted. For each configuration, optimal operational points have been presented in terms of C
p. The plot from a simulation last quarter of a second is shown (from 4.75 s to 5 s). State of the model in that period is considered to be very stable and steady. The selected period represents slightly more than 2 revolutions for rotor operating with TSR = 5.
High fluctuations in a torque are clearly visible for configuration 0.1 D. Maximums correspond to blades from separate rotors passing each other. Frequency of the fluctuations relates to an operational point, which is to the rotational speed of the rotors. Variations can be also observed for configuration 0.25 D; however, their amplitude is much lower. With the separation between rotors equal and higher than 0.5 D, fluctuations become unnoticeable. In terms of standard deviation, fluctuations in torque and power for cases 0.1 D and 0.25 D have a magnitude of ~8% and ~1.5% of average values, respectively. For configurations 0.5 D, 0.75 D, and 1 D deviation does not exceed 1% of the average value. Therefore, it can be stated that interactions in these configurations are negligible.
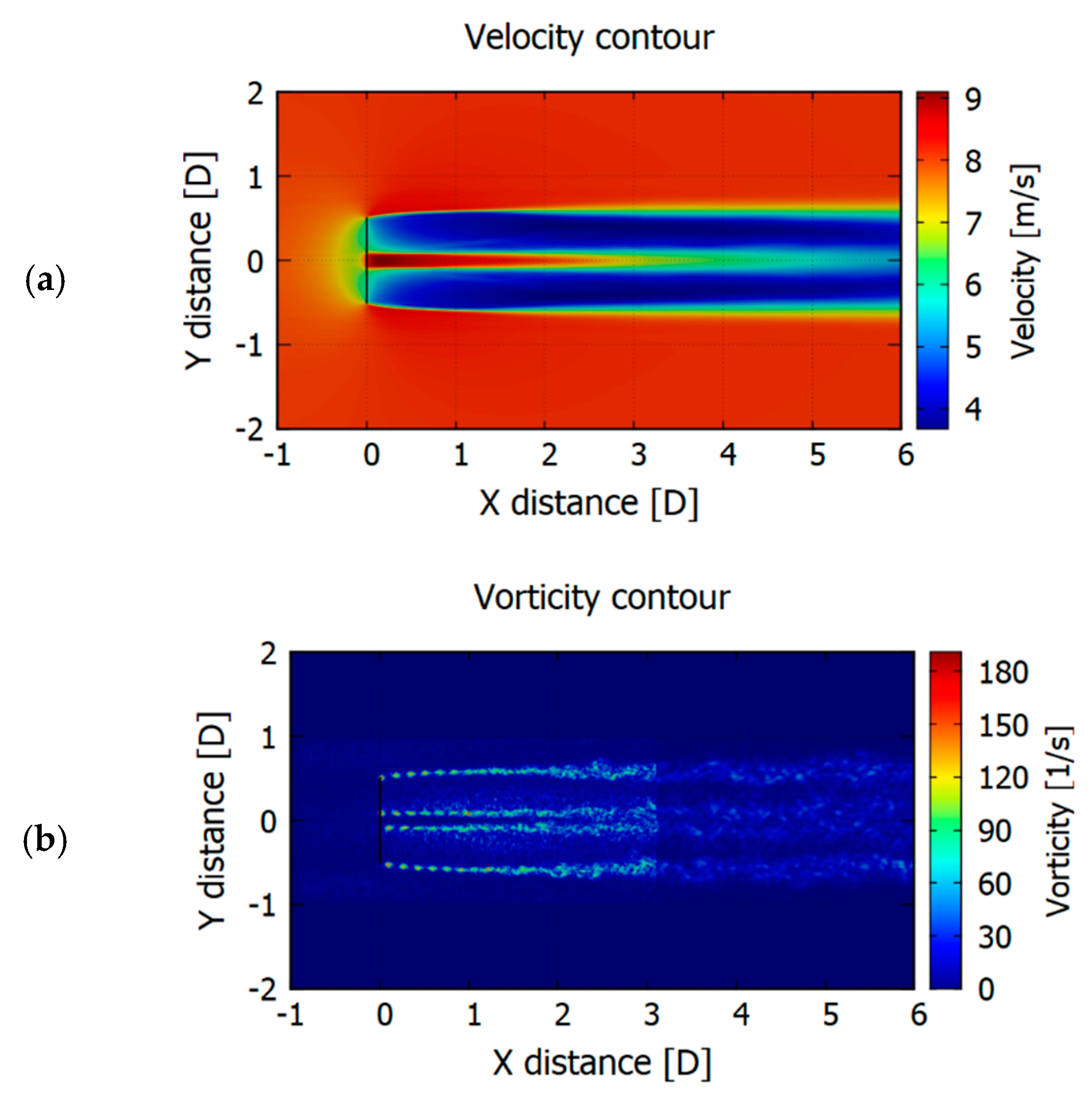
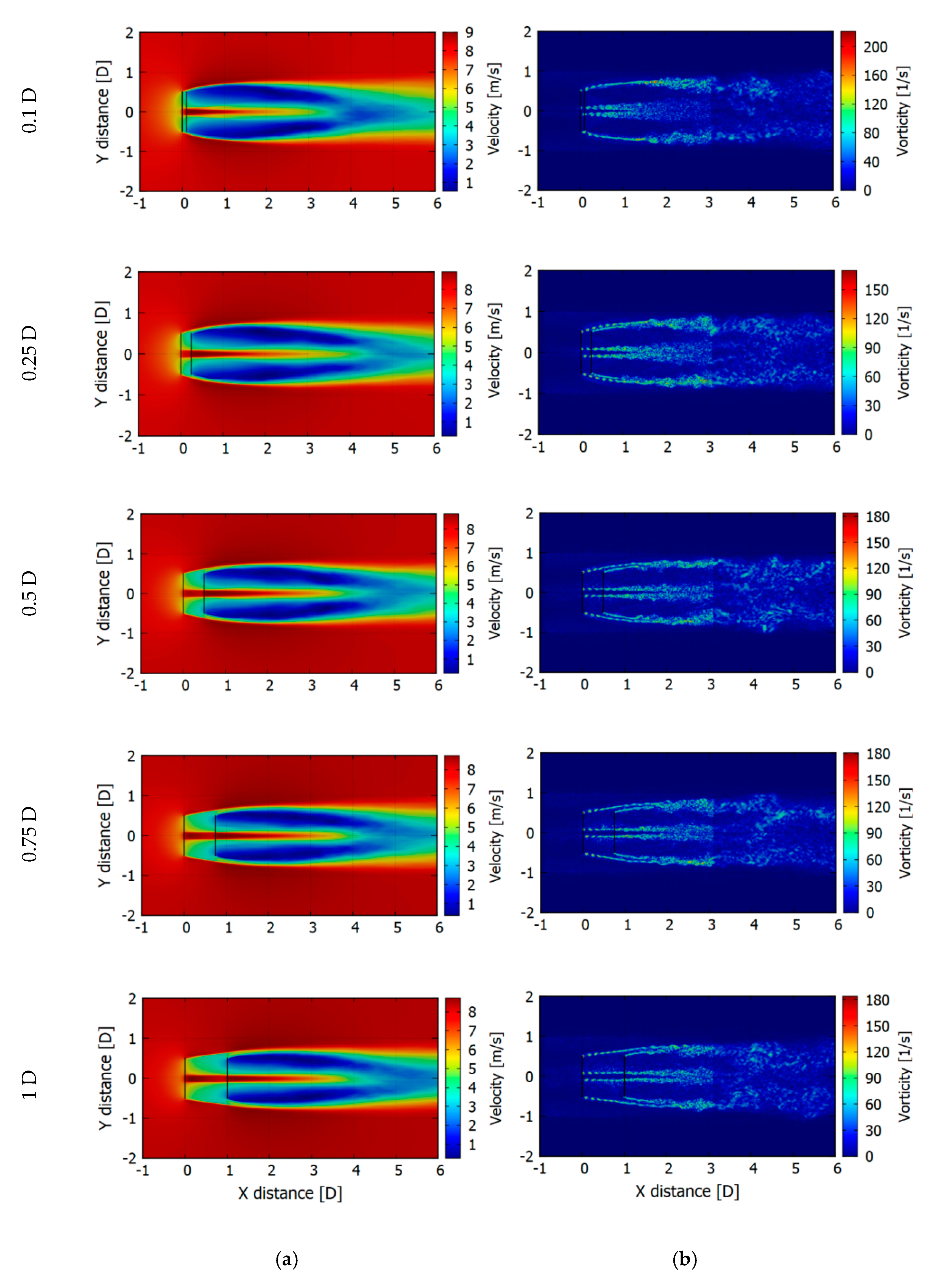
In
Figure 13, contours for mean wind speed (averaged from 3 s to 5 s) and vorticity are presented. For comparison, the same operational point for each configuration is plotted. Rotors are exactly counter-rotating with TSR = 5. High thrust, and thus largely expanded wake can be clearly noticed. A large reduction in a wind velocity is observed right behind the rear rotor. The aerodynamic wake seems to be similar for all the cases, with a tendency to be more coherent with rotors separation rising. Wake loses its stability around 2 D behind the second rotor. Unphysical transition in the vorticity at distance 3 D behind first rotor is visible. It is related to an end of the finest grid region. Even if it can be considered as a near wake region, it should not affect a power performance or its effect would be negligible.
However, a more comprehensive study is required in order to precisely characterize CRWT wake. A denser mesh should be applied in all the region of near wake and the domain ought to be extended for the far wake region as well. In this study, due to the extensive parameters range, the wake region was outside of the research scope. In the present setup, no hub, nor tower representations, were included into a computational domain. Tower would cause an additional fluctuation in power generation, while hub could affect velocity field behind a first rotor.
5. Conclusions
In this paper, the parametrical CFD study on a small counter-rotating wind turbine (CRWT) performance has been carried out. Influence of the axial distance and tip speed ratio of each rotor have been chosen as the studied parameters. In all the configurations, rotors counter-rotated with variable rotational speed ranging from 2 to 8. Investigated axial distance range stretches from 0.1 D to 1 D. Calculated CRWT Cp coefficient in optimal points was higher for all studied axial distances in comparison to reference SRWT. Power gain extended from 8.87% to 12.02%. The optimal case was 1 D. Power gain has a tendency to grow together with the increase of an axial distance. As expected, values for thrust coefficient were much higher than for the SRWT. Value of Ct was ranging from 1.2476 to 1.2941. In all the cases, wake behind a second rotor was similar. In comparison to a single rotor case, it has expanded much more and has lost its stability faster. When dynamic interaction between rotors are taken into considering, large fluctuations in torque and power are observed for distance 0.1 D. The magnitude of fluctuations reaches 8% of the average value in the case of a torque. Together with an increase of axial distance, fluctuations tend to decrease. It can be stated that they disappear starting from distance 0.5 D. The fluctuation in torque and power plots were induced by rotors’ blades passing each other.
Based on the conducted study’s results, the following conclusions can be established. For CRWT configurations, when rotors are separated by the distance from 0.1 D to 0.5 D, significant increase in power is observed. However, for cases 0.1 D and 0.25 D, large dynamic interactions in torque and power values would lead to extreme fatigue loads on the turbine’s construction. Furthermore, it would cause an uneven power generation. Obtained results showed that the distance between CRWT’s rotors ought to be contained in the range between 0.5 D to 1 D. Noticeable power gain is observed for configurations in that range. It reaches a maximum of 12% for 1 D case. Additionally, no significant dynamic interactions are noticed. Therefore, it can be stated that a CRWT with both rotors at the same side of the tower are not preferable, because distance in a range 0.5 D–1 D is not appropriate for this type of a construction. CRWT with rotors at upwind and downwind side seems to be more rational. However, the wind turbine’s hub would become oversized if rotor distance would be more than 1 D, even though power gain has a tendency to grow further beyond that distance. As study results showed, when one considers CRWT prototyping, it should be designed in following fashion: turbine rotors should be located at different sides of the tower and distance between them should be contained in the range 0.5 D–1 D.
Used in this study, Actuator Line Model (ALM) turns out to be computationally cost-effective. Moreover, it has the ability to reveal dynamic interactions between rotors. When considering future study areas, these should include a detailed investigation of near and far CRWT wakes. Tower and hub influence could also be investigated. The simulation model seems to have fulfilled its role and further physical research is needed. Performed simulation tests require confirmation through laboratory tests in an aerodynamic chamber. Therefore, the low power physical CRWT model has been prepared with the ability not only to change the distance between the rotors, but also to test the turbine performance at different blade numbers.
Summing up the results of the simulation tests, it can be stated that when constructing a CRWT turbine, rotors should be placed at a distance of at least 0.5 D or more. The power increase of around 10% compared to a single rotor turbine can then expected, together with increased shaft relative rotational speed. Placing a second rotor closer than 0.5 D guarantees a significant increase in power (approximately 8–10%); however, in such configurations, dynamic interactions between the rotors can occur. Interactions result in fluctuations in torque and power, which will lead to vibrations of the turbine structure and fatigue loads. Uneven power production in the turbine generator can be observed as well. Dynamic interactions between rotor blades above distance of 0.5 D are negligible. Additional economic analysis is necessary to investigate that obtained increase in power can justify a cost of adding a second rotor.