Transient Pressure Analysis of a Multiple Fractured Well in a Stress-Sensitive Coal Seam Gas Reservoir
Abstract
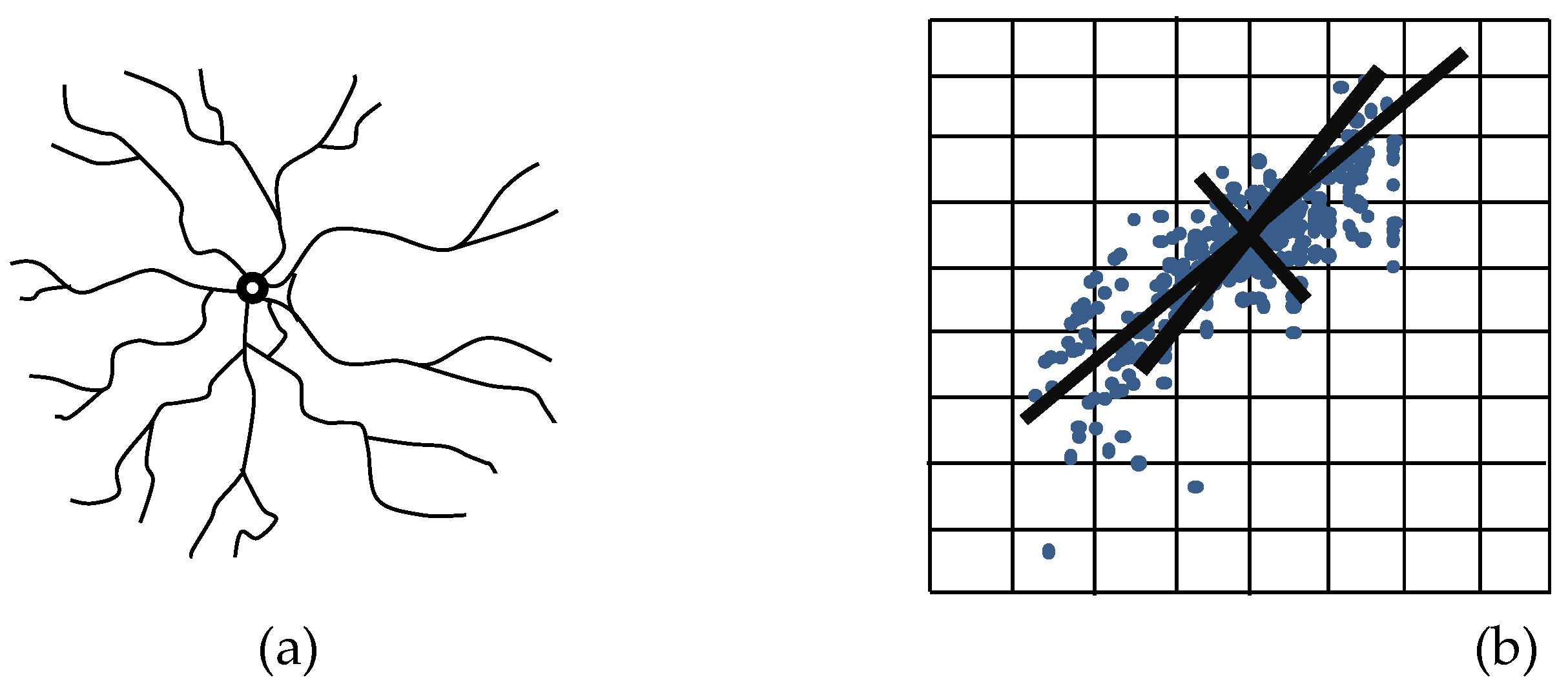
1. Introduction
2. Model Description
- (1)
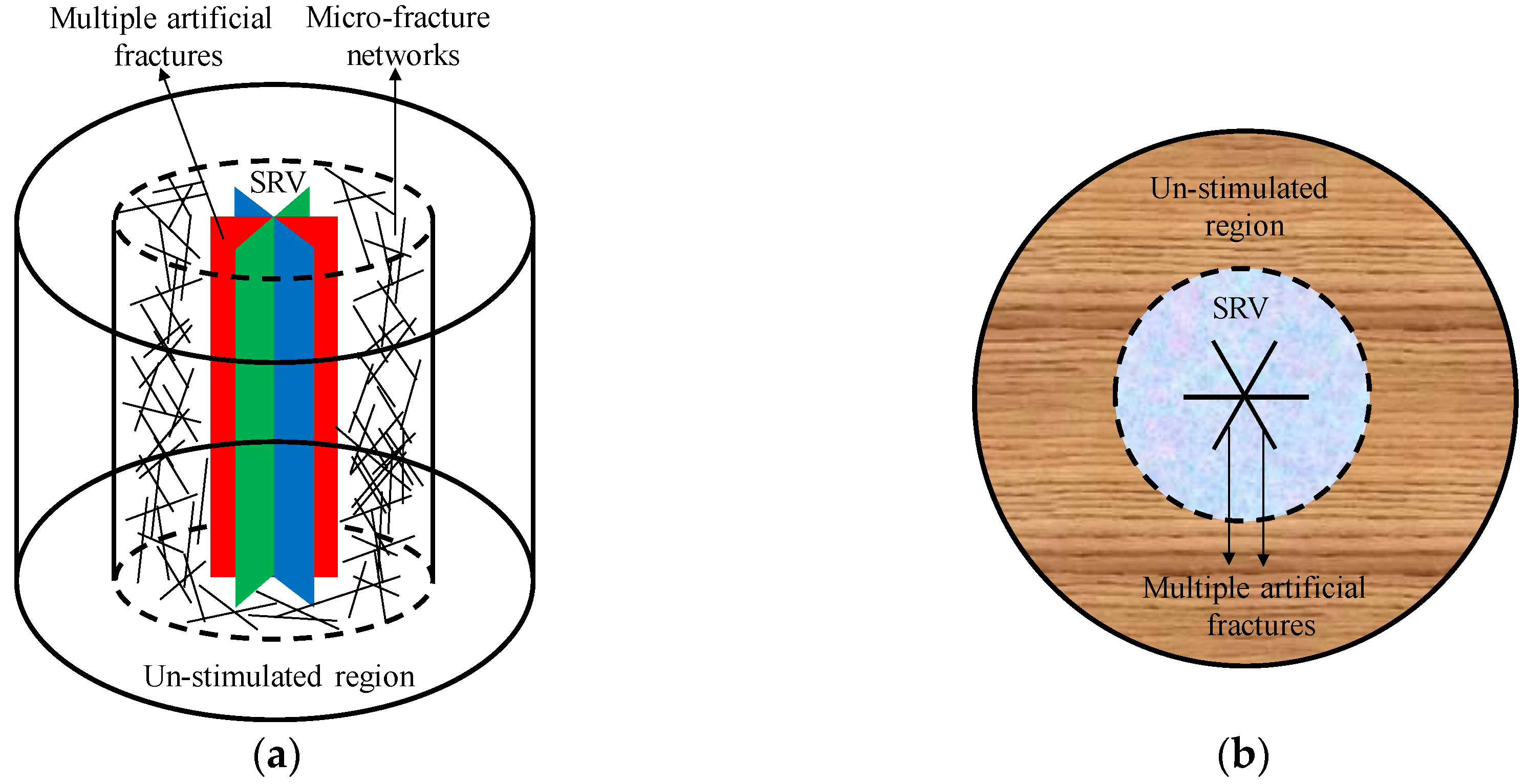
- The CBM reservoir can be radially divided into two regions, region 1 and region 2. Region 1, the inner region, includes the micro-fracture network. Whereas region 2 represents the un-stimulated region.
- (2)
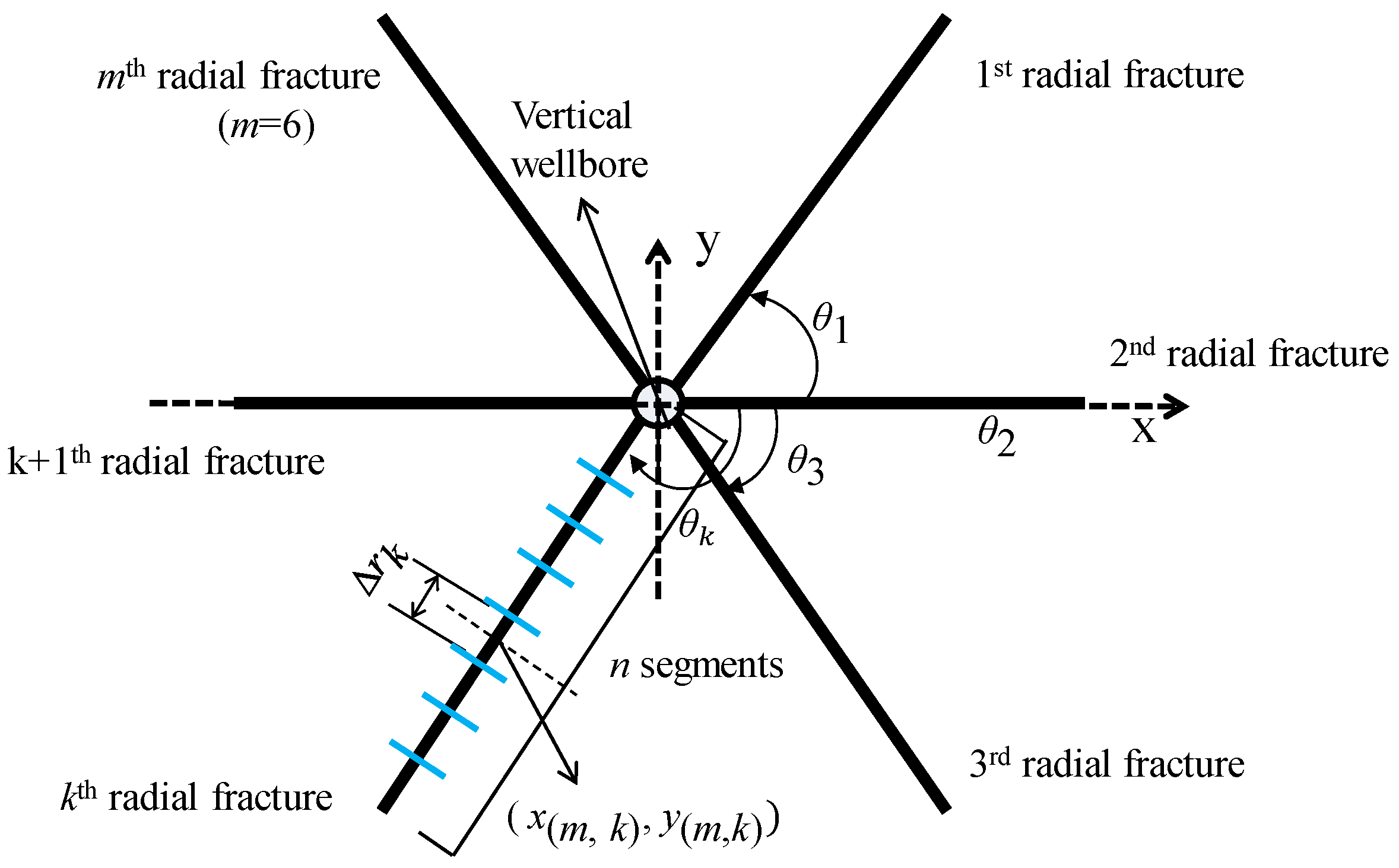
- Due to the influences of stimulation treatment, a multiple radial fractures model is adopted to veritably describe the dynamic flow process of CBM.
- (3)
- Infinite-conductivity artificial fractures are considered.
- (4)
- The constant production rate of MFVW is defined as qsc, however, the production rates at different locations of a certain fracture are unique.
- (5)
- The permeability of the micro-fracture network in SRV is considered stress-sensitive.
- (6)
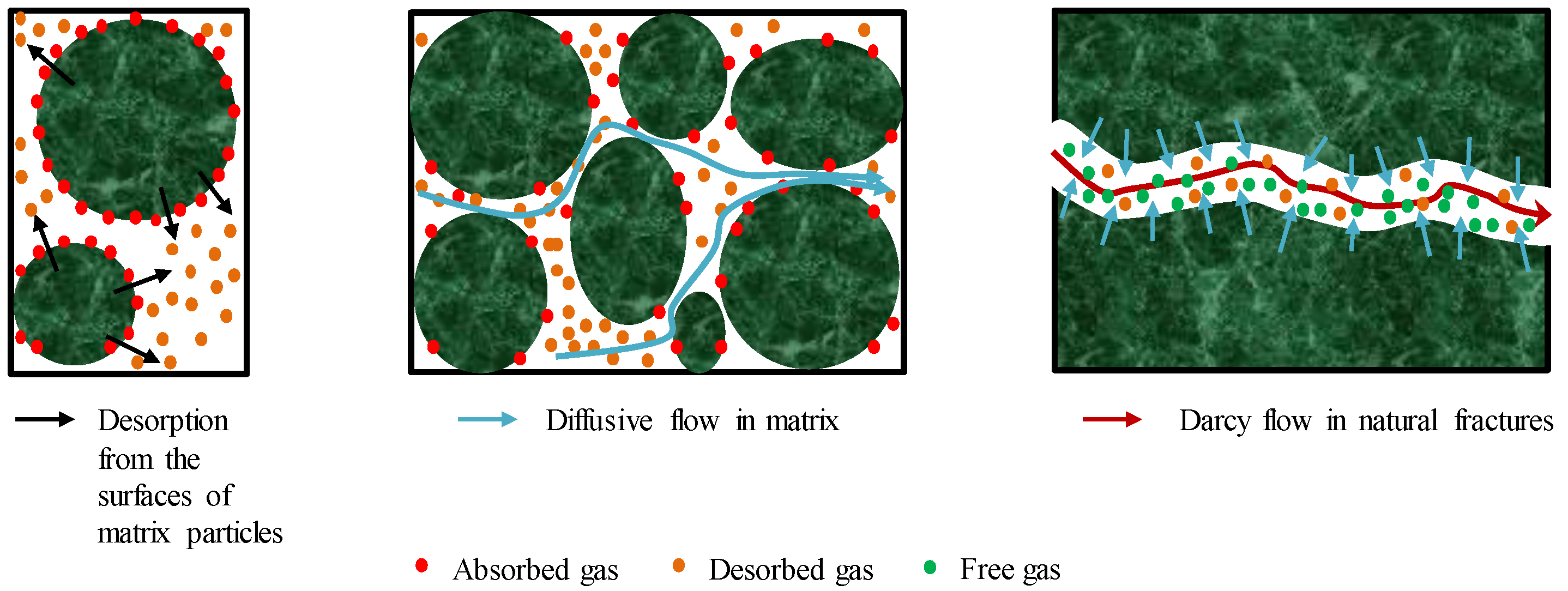
- The pseudo-steady state gas diffusion and unsteady state gas diffusion from matrix to fracture network both are considered in this model.
- (7)
- The outer boundary is infinite and the bottom boundary and top boundary are both impermeable.
- (8)
- Ignoring capillary pressure and gravity.
3. Mathematical Model
3.1. Continuous Line-Source Solution
3.2. Mathematical Model of MFVW
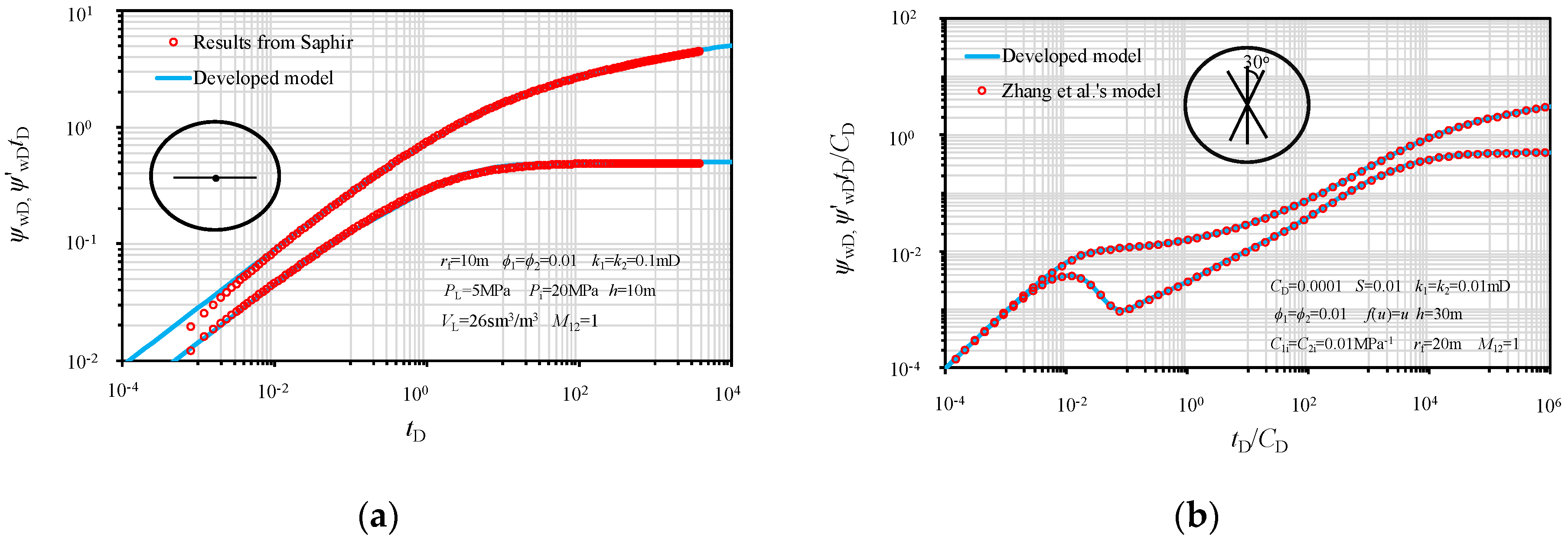
4. Model Validation
5. Results and Discussion
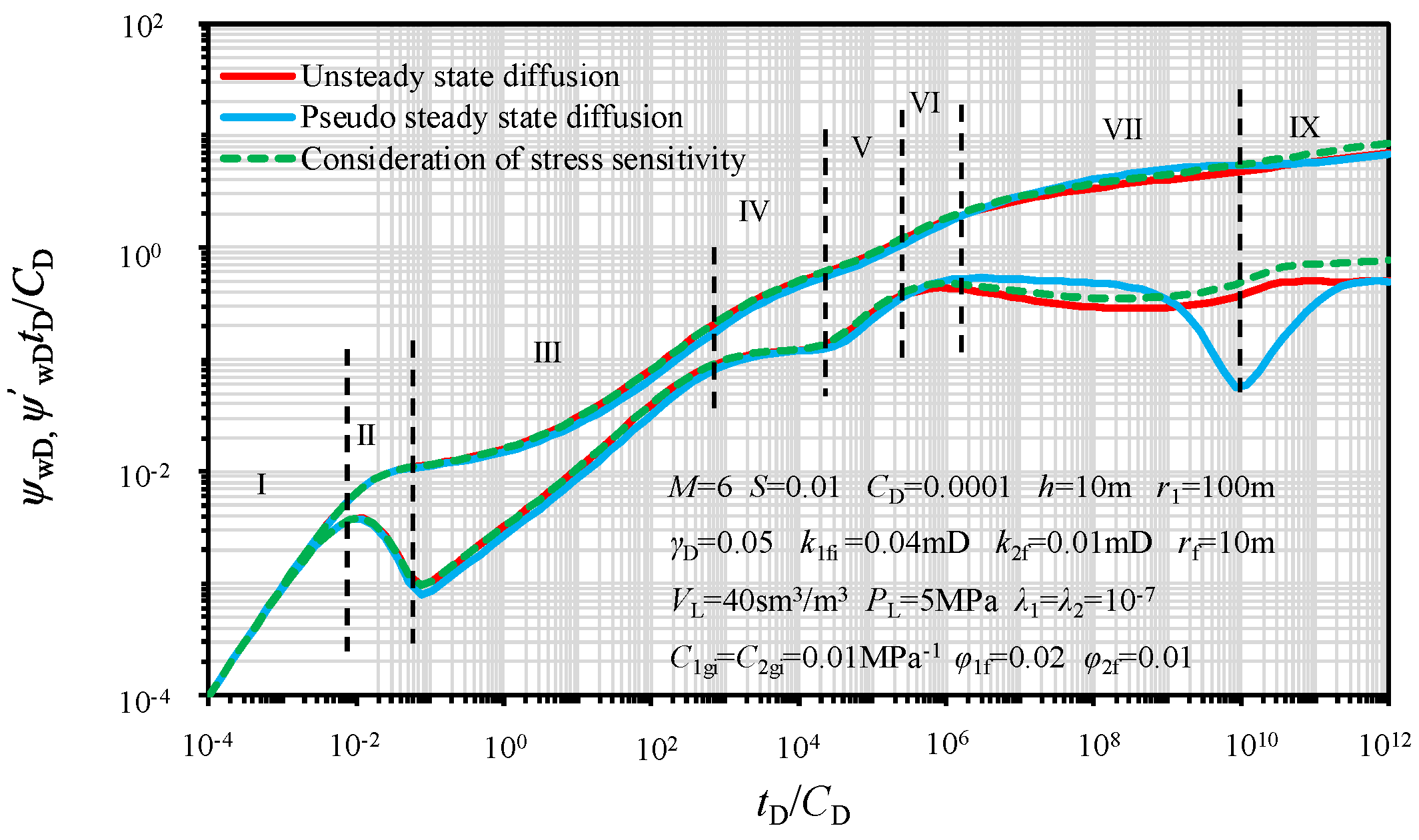
5.1. Type Curves for the Proposed Model
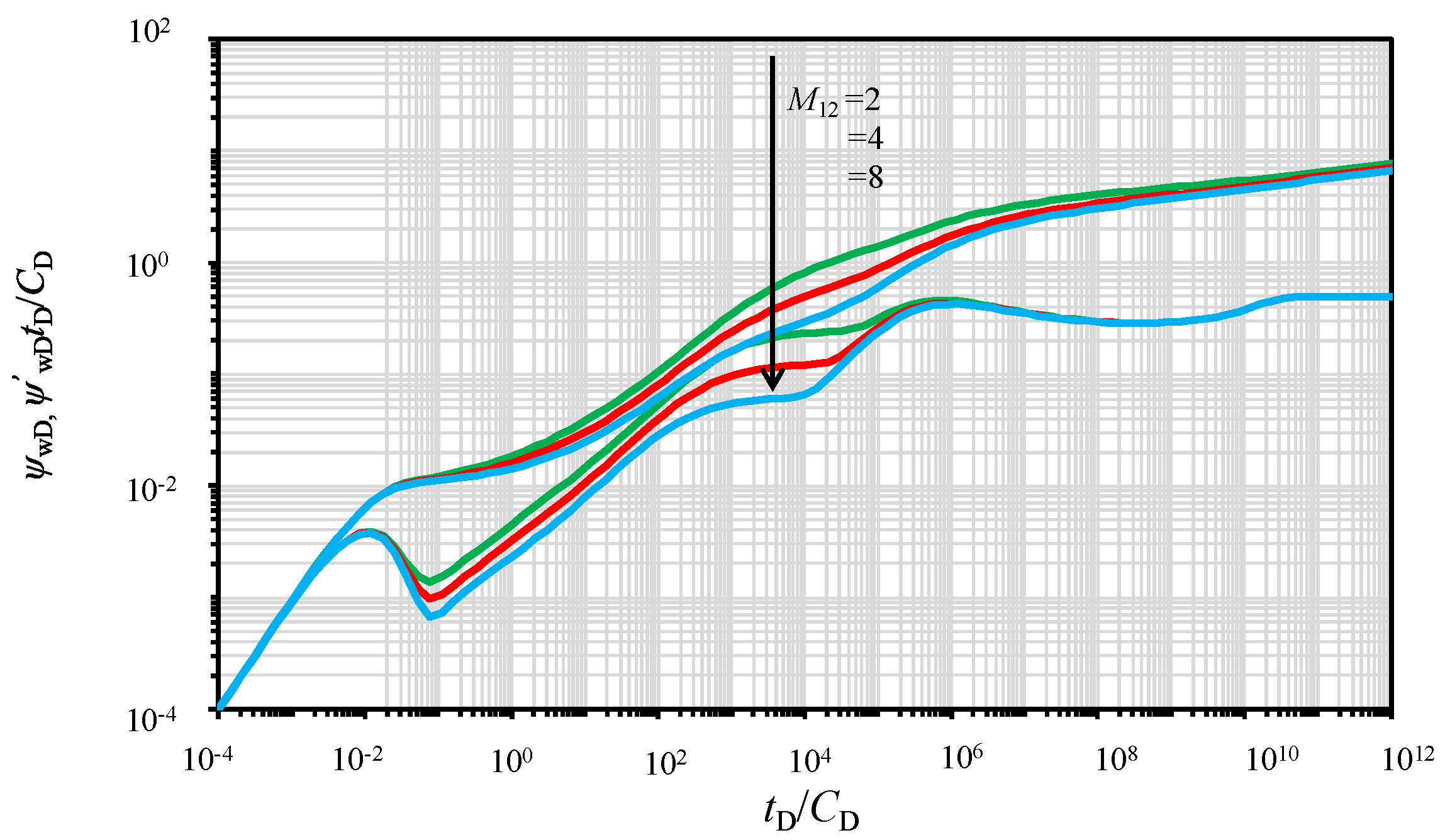
5.2. Effect of the Ratio of Permeability in the Inner Region on that in the Outer Region
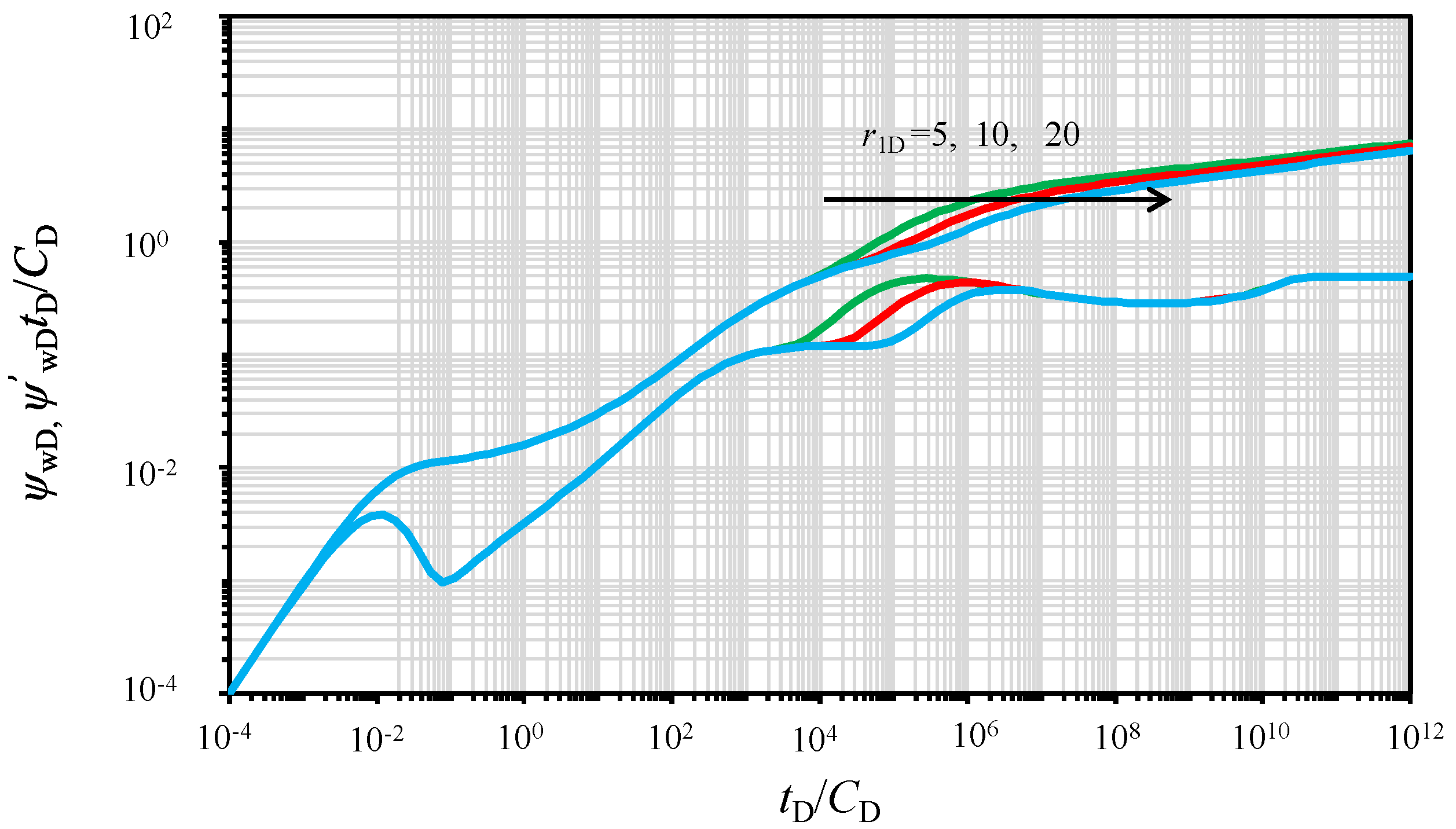
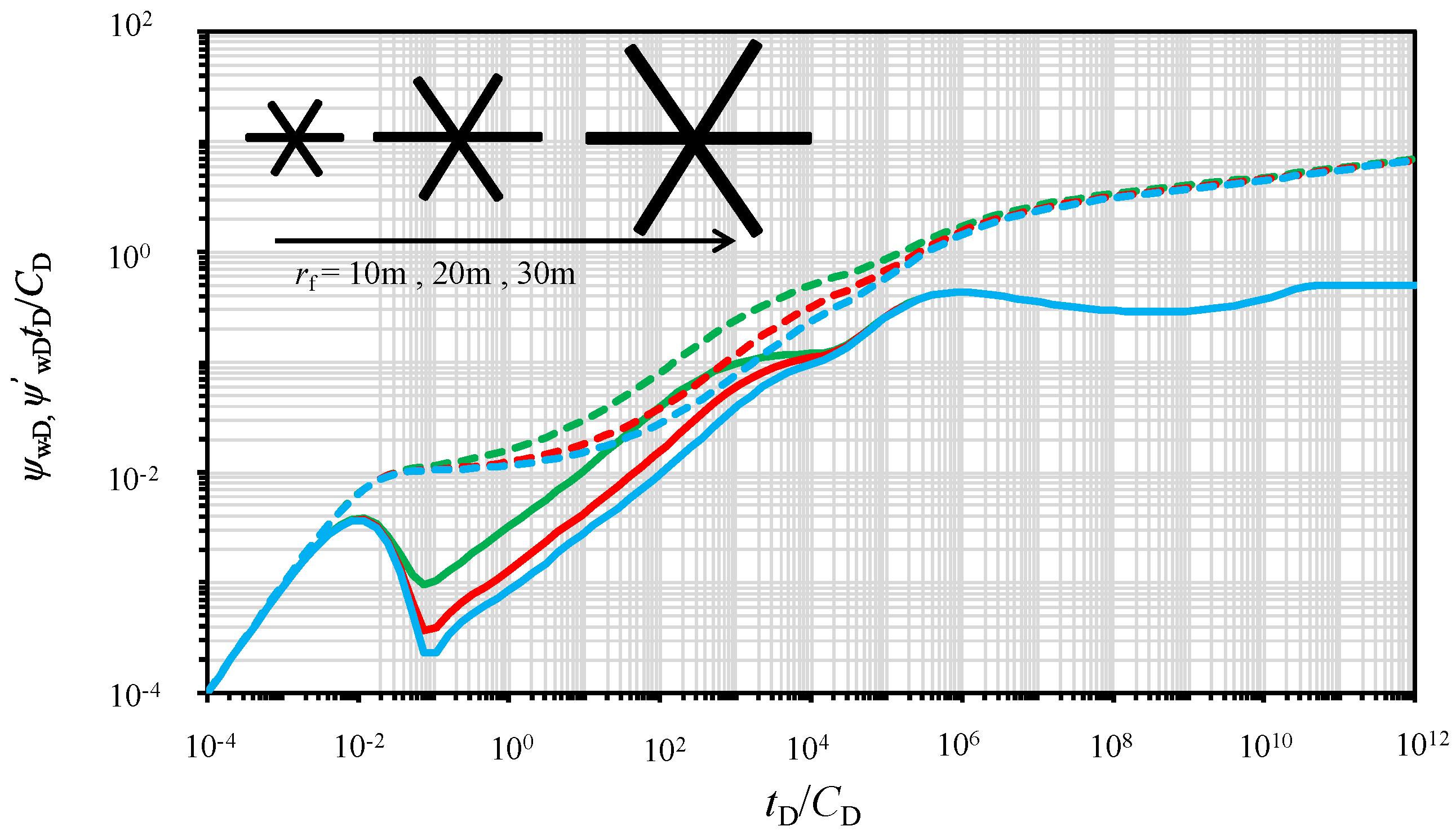
5.3. Effect of the Radius of SRV Region
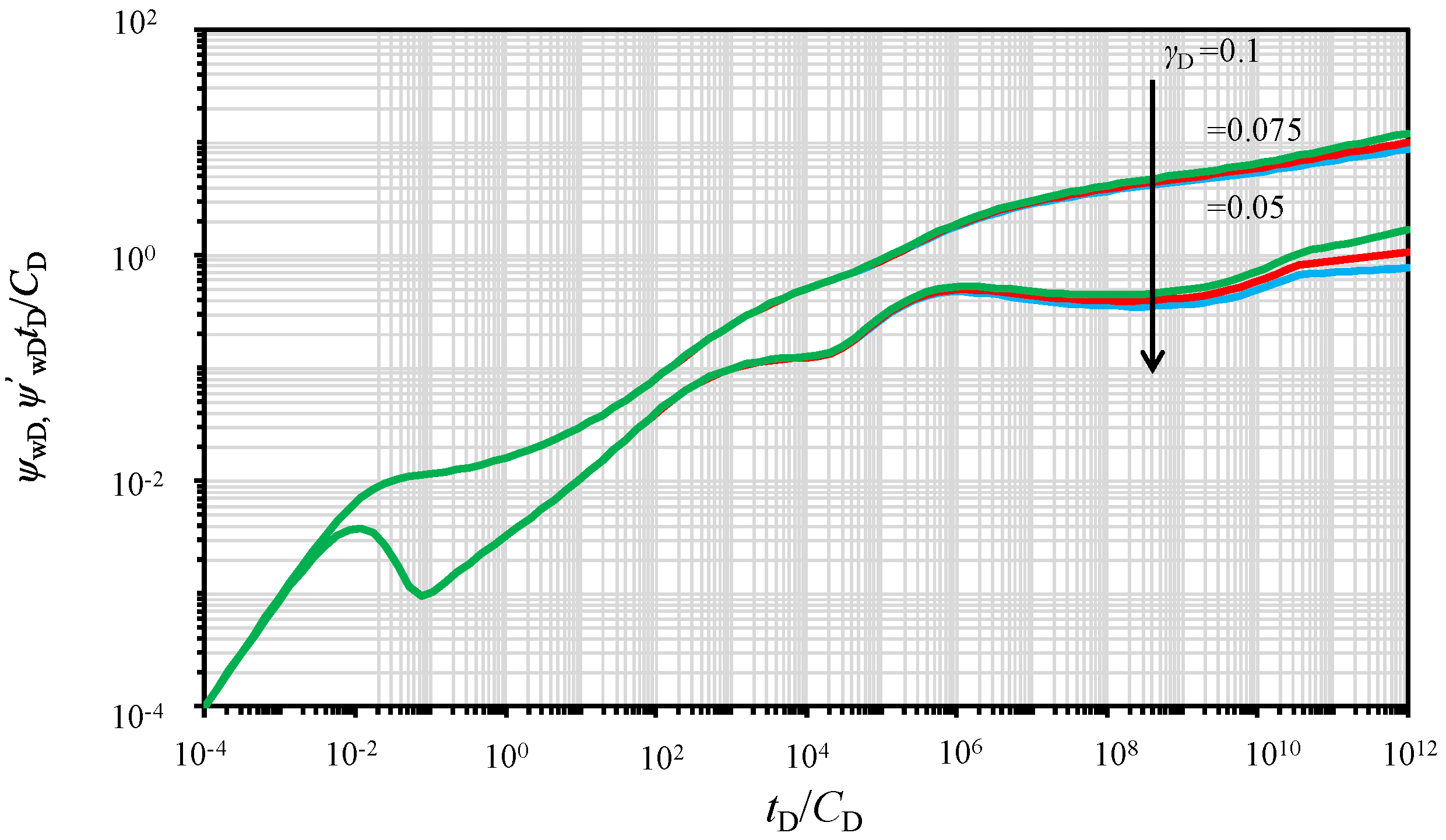
5.4. Effect of Permeability Modulus
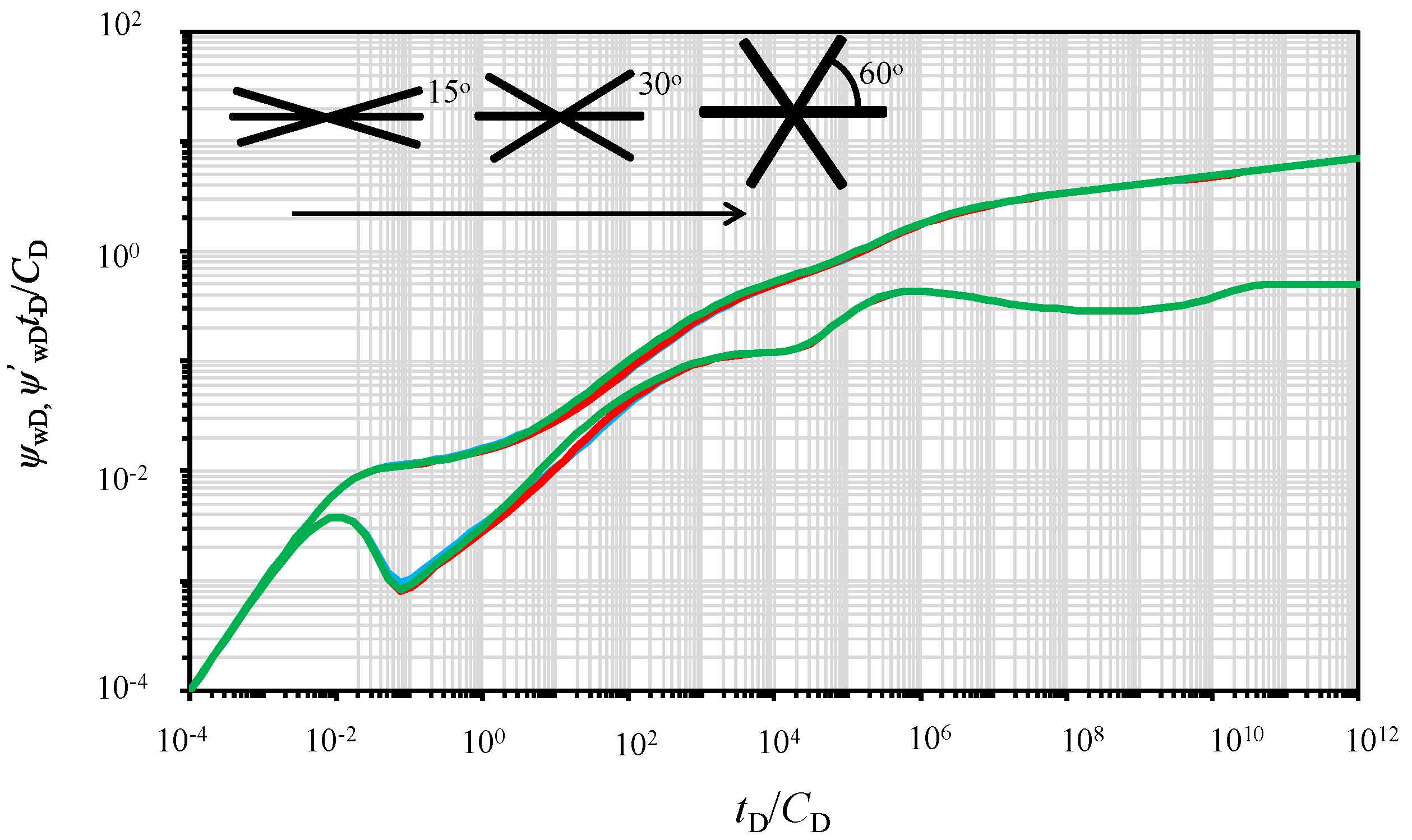
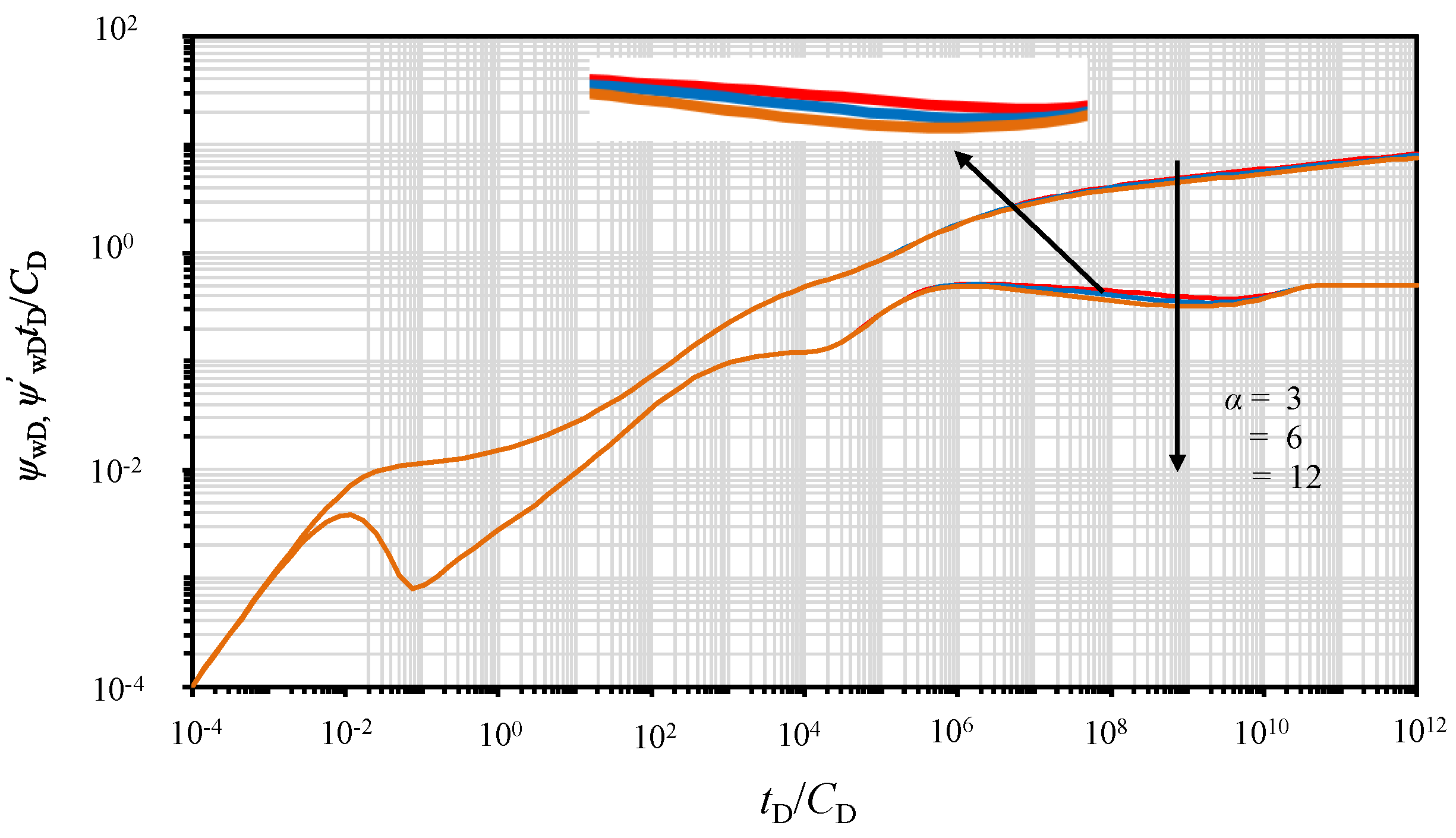
5.5. Effect of Radial Fracture Angle Symmetry
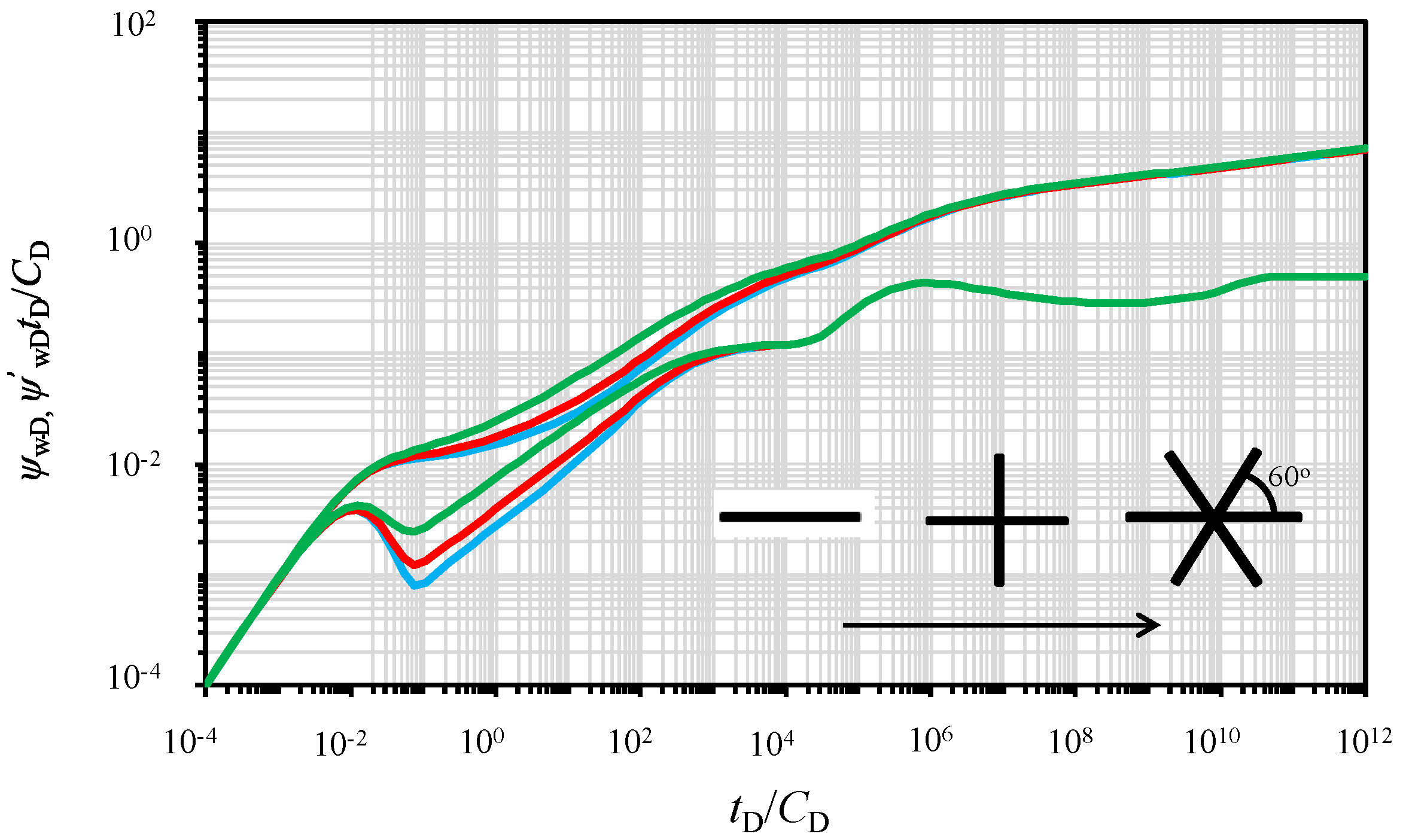
5.6. Effect of the Number of Fracture Wings
5.7. Effect of the Length of Hydraulic Fracture Wings
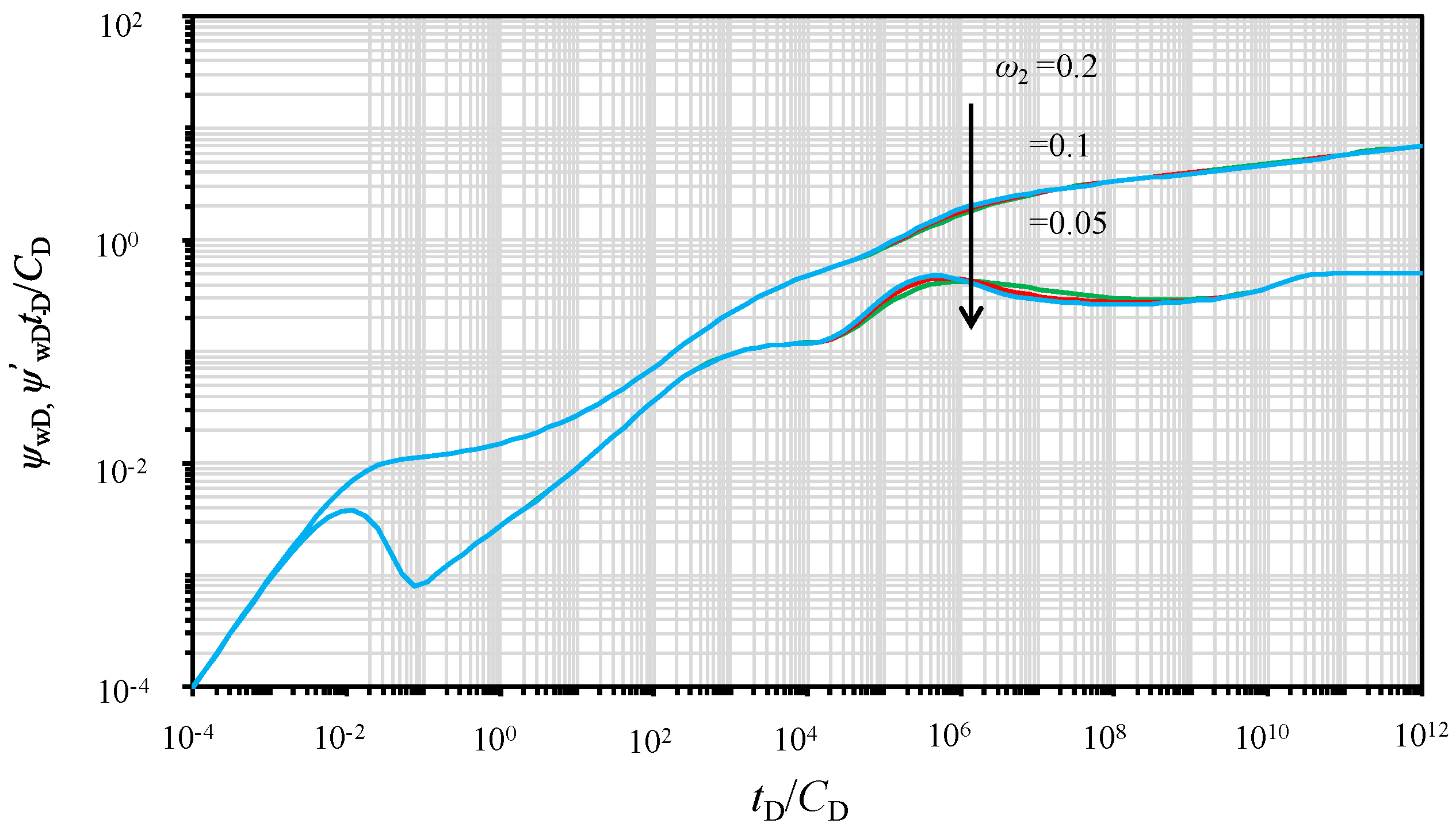
5.8. Effect of the Storativity Ratio of the Outer Region
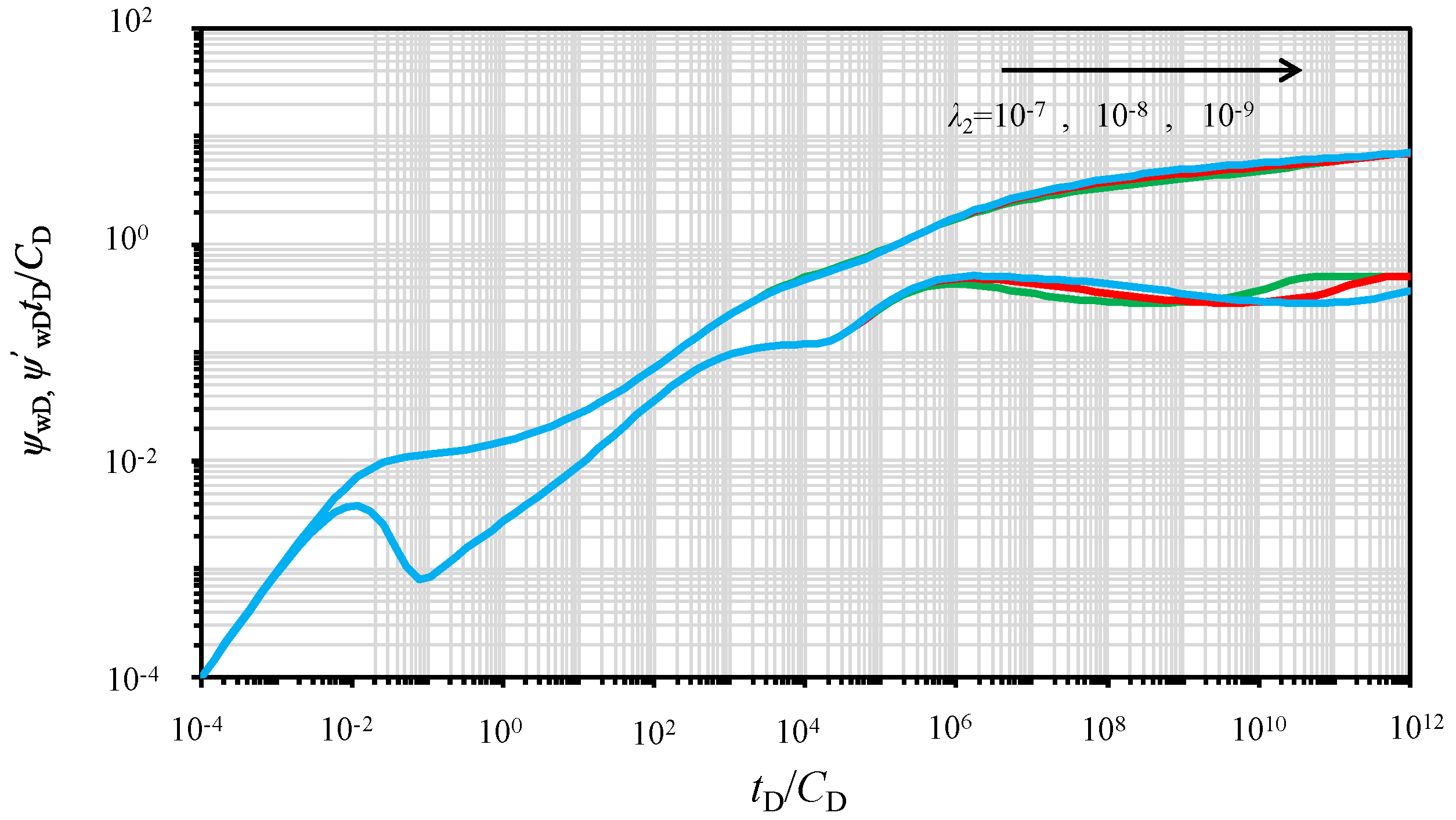
5.9. Effect of the Inter-Porosity Flow Parameter
5.10. Effect of the Adsorption–Desorption Constant
6. Conclusions
- (1)
- The linear flow between adjacent radial fracture wings, the radial flow in the SRV, and the radial flow in the outer region are the three main flow regimes for the proposed model in CBM reservoirs.
- (2)
- The impact of stress sensitivity on the PPR/PPD is obvious. The existence of stress sensitivity in the micro-fracture network results in larger pressure depletion in later flow regimes.
- (3)
- The SRV, which includes the micro-fracture network and radial fracture wings, is able to reduce the pressure depletion. As the size of the SRV becomes smaller, the transition flow regime from pseudo-radial flow in the SRV to radial flow in the outer region occurs earlier.
- (4)
- The properties and distribution of multiple radial fracture wings affect the PPR/PPD in CBM reservoirs drastically. An increase in the number of radial fracture wings leads to a decrease in the pressure depletion when producing. The well model with an un-uniform fracture wing distribution requires more energy consumption compared to that with a uniform fracture wing distribution when producing at the same rate.
- (5)
- The storativity ratio and the inter-porosity flow parameter of the outer region, two parameters in a double-porosity system, mainly affect the diffusion flow regime, where the storativity ratio of the outer region represents the capacity of gas supply for the matrix and the inter-porosity flow parameter denotes the diffusion occurrence time. In addition, the adsorption–desorption constant characterizes the amount of adsorbed gas in the matrix.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | wellbore storage coefficient: m3/Pa |
| Cg | gas compressibility, Pa−1 |
| h | formation thickness, m |
| k | permeability, m2 |
| L | reference length, m |
| Lf | length of hydraulic fracture, m |
| M | number of hydraulic fracture wings |
| P | pressure, Pa |
| q | production rate, m3/s |
| strength of continuous line source, m3/s | |
| r | radial distance, m |
| r1 | radius of inner region, m |
| S | skin factor |
| t | times, s |
| T | temperature, K |
| u | Laplace transform variable |
| x,y | spatial coordinates, m |
| Z | Z-factor |
| V | gas concentration in matrix |
| inter-porosity flow coefficient | |
| storativity ratio | |
| viscosity, Pa·s | |
| porosity | |
| pseudo pressure, , Pa/s |
Superscripts
| — | variables in the Laplace domain |
Subscripts
| D | dimensionless |
| f | natural fracture |
| m | matrix |
| 1 | SRV region |
| 2 | un-stimulated region |
| 1m | matrix system in the SRV region |
| 2m | matrix system in the un-stimulated region |
| 1f | natural fracture system in the SRV region |
| 2fi | natural fracture system in the un-stimulated region at initial condition |
| gi | gas at initial condition |
| i | initial condition |
| sc | standard condition |
| w | wellbore |
Appendix A. Dimensionless Variables Definition
Appendix B. Continuous Line-Source Function under Pseudo-Steady State Diffusion in Composite CBM Reservoir
Appendix C. Continuous Line-Source Function under Unsteady State Diffusion in Composite CBM Reservoir
References
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. SPE J. 1953, 3. [Google Scholar] [CrossRef]
- Kou, Z.; Dejam, M. Dispersion due to combined pressure-driven and electro-osmotic flows in a channel surrounded by a permeable porous medium. Phys. Fluids 2019, 31, 056603. [Google Scholar] [CrossRef]
- Wang, H. Performance of multiple fractured horizontal wells in shale gas reservoirs with consideration of multiple mechanisms. J. Hydrol. 2014, 510, 299–312. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; Zhang, L. Transient pressure behavior for a horizontal well with multiple finite-conductivity fractures in tight reservoirs. J. Geophys. Eng. 2016, 12, 638–656. [Google Scholar] [CrossRef]
- Wang, H.; Guo, J.; Zhang, L. A semi-analytical model for multilateral horizontal wells in low-permeability naturally fractured reservoirs. J. Pet. Sci. Eng. 2017, 20, 564–578. [Google Scholar] [CrossRef]
- Shovkun, I.; Espinoza, D.N. Coupled fluid flow-geomechanics simulation in stress-sensitive coal and shale reservoirs: Impact of desorption-induced stresses, shear failure, and fines migration. Fuel 2017, 195, 260–272. [Google Scholar] [CrossRef]
- Pedrosa, O.A., Jr. Pressure transient response in stress-sensitive formations. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. SPE 15115. [Google Scholar]
- Zhang, M.; Ambastha, A. New insights in pressure-transient analysis for stress-sensitive reservoirs. In Proceedings of the SPE annual technical conference and exhibition, New Orleans, LA, USA, 25–28 September 1994. [Google Scholar]
- Chen, Z.; Liao, X.; Zhao, X.; Dou, X.; Zhu, L. A Semi-Analytical Mathematical Model for Transient Pressure Behavior of Multiple Fractured Vertical Well in Coal Reservoirs Incorporating with Diffusion, Adsorption, and Stress-Sensitivity. J. Nat. Gas Sci. Eng. 2015, 29, 570–582. [Google Scholar] [CrossRef]
- Wei, M.; Duan, Y.; Dong, M.; Fang, Q.; Dejam, M. Transient production decline behavior analysis for a multi-fractured horizontal well with discrete fracture network in shale gas reservoirs. J. Porous Media 2019, 22, 343–361. [Google Scholar] [CrossRef]
- Wei, M.; Duan, Y.; Dong, M.; Fang, Q. Blasingame decline type curves with material balance pseudo-time modified for multi-fractured horizontal wells in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2016, 31, 340–350. [Google Scholar] [CrossRef]
- Yuan, Y.; Yan, W.; Chen, F.; Li, J.; Xiao, Q.; Huang, X. Numerical simulation for shale gas flow in complex fracture system of fractured horizontal well. Int. J. Nonlinear Sci. Num. Simul. 2018, 19, 367–377. [Google Scholar] [CrossRef]
- King, G.R.; Ertekin, T.; Schwerer, F.C. Numerical Simulation of the Transient Behaviour of Coal-Seam Degasification Wells. SPE Form. Eval. 1986, 1, 165–183. [Google Scholar] [CrossRef]
- Anbarci, K.; Ertekin, T. A Comprehensive Study of Pressure Transient Analysis with Sorption Phenomena for Single-Phase Gas Flow in Coal Seams. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990. [Google Scholar]
- Anbarci, K.; Ertekin, T. Pressure Transient Behavior of Fractured Wells in Coalbed Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar]
- Engler, T.W.; Rajtar, J.M. Pressure Transient Testing of Horizontal Wells in Coalbed Reservoirs. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 18–21 May 1992. [Google Scholar]
- Clarkson, C.R.; Jordan, C.L.; Ilk, D.; Blasingame, T.A. Production Data Analysis of Fractured and Horizontal CBM Wells. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 23–25 September 2009. [Google Scholar]
- Nie, R.; Meng, Y.; Guo, J.; Jia, Y. Modeling transient flow behavior of a horizontal well in a coal seam. Int. J. Coal. Geo. 2012, 92, 54–68. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Feng, G.; Zhang, B.; Kang, B. Performance Analysis of Fractured Wells with Stimulated Reservoir Volume in Coal Seam Gas Reservoirs. Oil Gas Sci. Technol. 2016, 71, 8. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, Z.; Wang, H.; Zhao, Y.; Dejam, M.; Guo, J.; Du, J. Performance Analysis for A Model of A Multi-Wing Hydraulically Fractured Vertical Well in A Coalbed Methane Gas Reservoir. J. Pet. Sci. Eng. 2018, 166, 104–120. [Google Scholar] [CrossRef]
- Kou, Z.H.; Dejam, M. A mathematical model for a hydraulically fractured well in a coal seam reservoir by considering desorption, viscous flow, and diffusion. Proceedings of 71st Annual Meeting of the APS Division of Fluid Dynamics, Atlanta, GA, USA., 18–20 November 2018. [Google Scholar]
- Luo, W.J.; Tang, C.F. Pressure-transient analysis of multi-wing fractures connected to a vertical wellbore. SPE J. 2014, 20, 360–367. [Google Scholar] [CrossRef]
- Germanovich, L.N.; Ring, L.M.; Astakhov, D.K.; Shlyapobersky, J.; Mayerhofer, M.J. Hydraulic Fracture with Multiple Segments II. Modeling. Int. J. Rock Mech. Min. Sci. 1997, 34, e1–e15. [Google Scholar] [CrossRef]
- Craig, D.P.; Blasingame, T.A. Constant-Rate Drawdown Solutions Derived for Multiple Arbitrarily Oriented Uniform-Flux, Infinite-Conductivity, or Finite-Conductivity Fractures in an Infinite-slab Reservoir. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 15–17 May 2006. [Google Scholar]
- Choo, Y.K.; Wu, C.H. Transient Pressure Behavior of Multiple-Fractured Gas Wells. In Proceedings of the SPE/DOE Low Permeability Reservoirs Symposium, Denver, CO, USA, 18–19 May 1987. [Google Scholar]
- Tiab, D. Analysis of Pressure Derivative Data of Hydraulically Fractured Wells by the Tiab’s Direct Synthesis Technique. J. Pet. Sci. Eng. 2005, 49, 1–21. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, X.; Guo, B. Mathematical Modeling of Fluid Flow to Unconventional Oil Wells with Radial Fractures and Its Testing with Field Data. ASME J. Energy Resour. Technol. 2019, 141, 070702. [Google Scholar] [CrossRef]
- He, L.; Mei, H.Y.; Hu, X.R.; Dejam, M.; Kou, Z.H.; Zhang, M.L. Advanced flowing material balance to determine original gas-in-place of shale gas considering adsorption hysteresis. SPE Reser. Eval. Eng. 2019, 22, 1282–1292. [Google Scholar] [CrossRef]
- Chen, Z.M.; Liao, X.W.; Zhao, X.L.; Dou, X.J.; Zhu, L.T. Performance of horizontal wells with fracture networks in shale gas formation. J. Pet. Sci. Eng. 2015, 133, 646–664. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; Zhang, L. Transient Pressure and Production Dynamics of Multi-stage Fractured Horizontal Wells in Shale Gas Reservoirs with Stimulated Reservoir Volume. J. Nat. Gas Sci. Eng. 2016, 35, 425–443. [Google Scholar] [CrossRef]
- Kucuk, F.; Ayestaran, L. Analysis of Simultaneously Measured Pressure and Sandface Flow Rate in Transient Well Testing. J. Pet. Technol. 1985, 37, 323–334. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J.; Raghavan, R. Applied Pressure Analysis for Fractured Wells. J. Pet. Technol. 1975, 27, 887–892. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.D. Type Curves Analysis for Asymmetrically Fractured Wells. ASME J. Energy Resour. Technol. 2013, 136, 023101. [Google Scholar] [CrossRef]
- Lu, T.; Liu, S.; Li, Z. A new approach to model shale gas production behavior by considering coupled multiple flow mechanisms for multiple fractured horizontal well. Fuel 2019, 237, 283–297. [Google Scholar] [CrossRef]
- Yuan, B.; Su, Y.; Moghanloo, R.; Rui, Z.; Wang, W.; Shang, Y. A New Analytical Multi-Linear Solution for Gas Flow toward Fractured Horizontal Wells with Different Fracture Intensity. J. Nat. Gas Sci. Eng. 2015, 23, 227–238. [Google Scholar] [CrossRef]
- Cai, J.; Wei, W.; Hu, X.; Liu, R.; Wang, J. Fractal Characterization of Dynamic Fracture Network Extension in Porous Media. Fractals 2017, 25, 1750023. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, Z.; Wang, H. Transient Pressure Analysis of a Multiple Fractured Well in a Stress-Sensitive Coal Seam Gas Reservoir. Energies 2020, 13, 3849. https://doi.org/10.3390/en13153849
Kou Z, Wang H. Transient Pressure Analysis of a Multiple Fractured Well in a Stress-Sensitive Coal Seam Gas Reservoir. Energies. 2020; 13(15):3849. https://doi.org/10.3390/en13153849
Chicago/Turabian StyleKou, Zuhao, and Haitao Wang. 2020. "Transient Pressure Analysis of a Multiple Fractured Well in a Stress-Sensitive Coal Seam Gas Reservoir" Energies 13, no. 15: 3849. https://doi.org/10.3390/en13153849
APA StyleKou, Z., & Wang, H. (2020). Transient Pressure Analysis of a Multiple Fractured Well in a Stress-Sensitive Coal Seam Gas Reservoir. Energies, 13(15), 3849. https://doi.org/10.3390/en13153849




