Uncertainty Quantification of the Effects of Blade Damage on the Actual Energy Production of Modern Wind Turbines
Abstract
1. Introduction
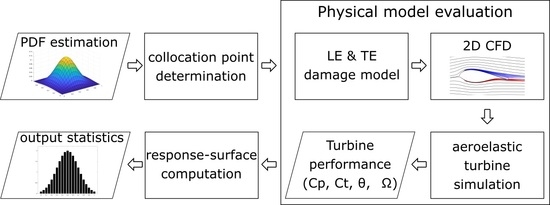
2. Materials and Methods
2.1. Stochastic Approach
2.2. Probability Density Functions
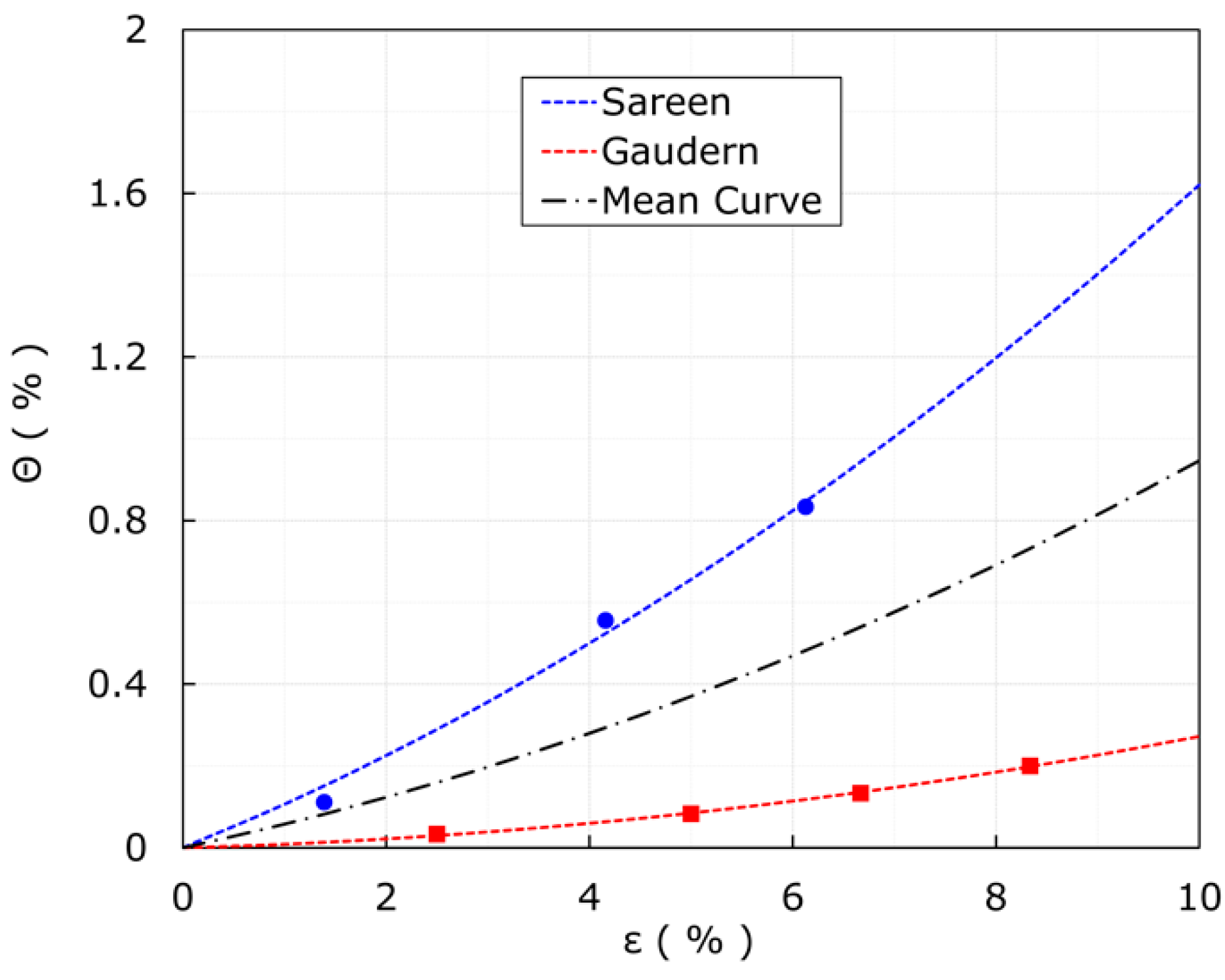
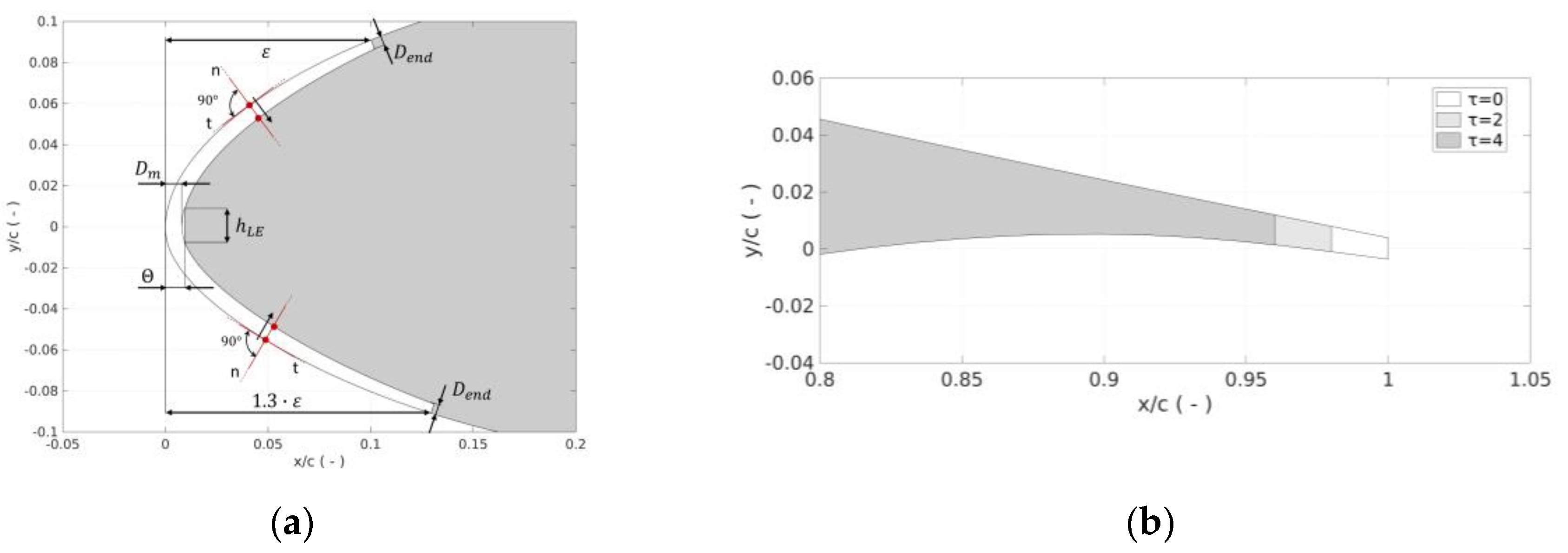
2.3. Blade-Damage Model
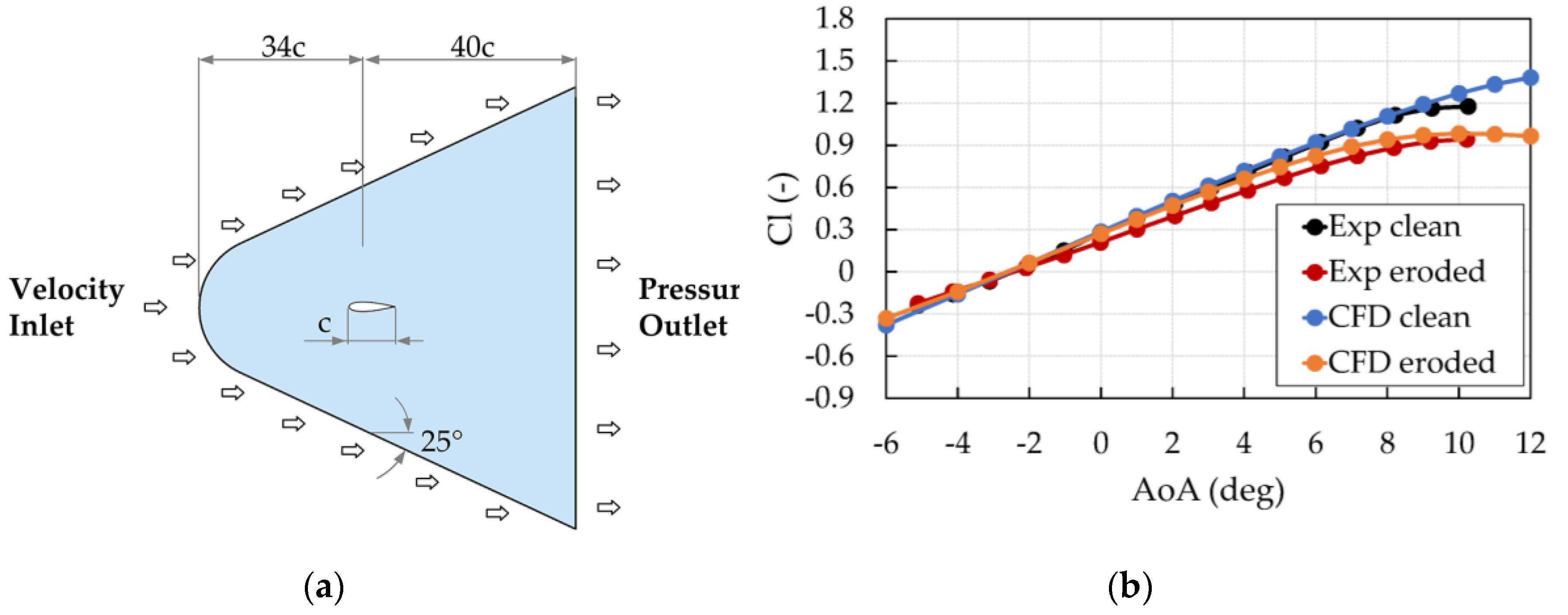
2.4. CFD Setup
2.5. Aeroelastic Setup
2.6. General DLC Setup
3. Results
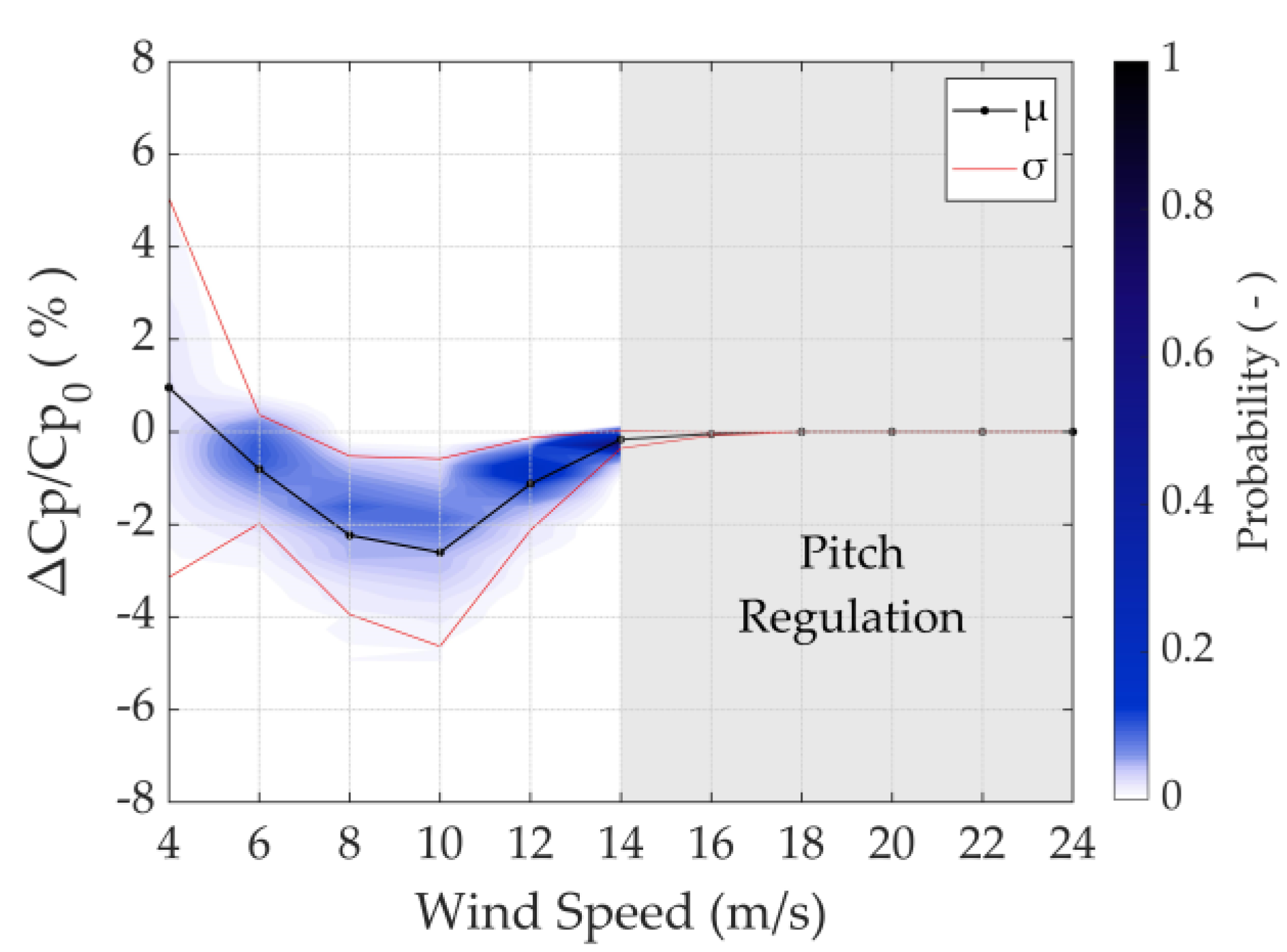
3.1. Aerodynamic Performance
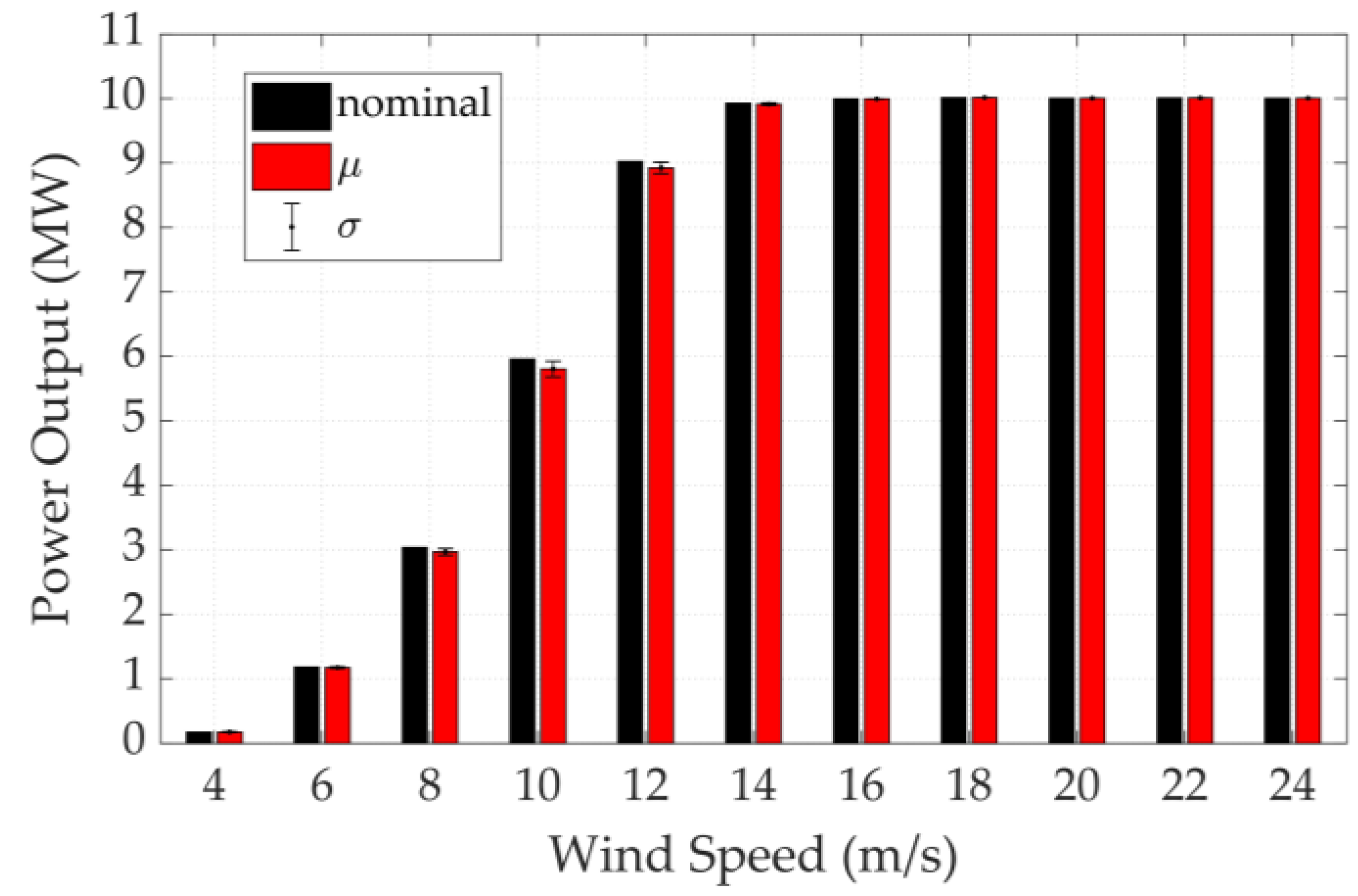
3.2. Annual Energy Production (AEP)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| AEP | Annual energy production, kWh |
| aPC | Arbitrary polynomial chaos |
| BEM | Blade element momentum |
| CFD | Computational fluid dynamics |
| DLC | Design load case |
| DRC | Delft research controller |
| IEC | International electrotechnical commission |
| LE | Leading edge |
| PC | Polynomial chaos |
| PCM | Probabilistic collocation point |
| Probability desity function | |
| RANS | Reynolds averaged navier stokes |
| SST | Shear stress transport |
| TE | Trailing edge |
| Latin Letters | |
| AoA | Angle of attack, deg. |
| c | Blade chord, m |
| ci | Expansion coefficients |
| Cd | Drag coefficient |
| Cl | Lift coefficient |
| CP | Turbine power coefficient |
| Dend | Delamination depth at the end of damaged area, m |
| FT | Thrust force, N/m |
| Fϑ | Tangential force, N/m |
| h | Leading edge flattened area height, m |
| P(i) | Orthogonal polynomials |
| RM | Polinomial expansion remainder |
| Y | Specific output of interest |
| Greek Letters | |
| α, β | Beta function’s shape parameters |
| γ | Collocation point |
| ε | Leading edge erosion factor |
| Θ | Leading edge erosion depth |
| μ | Momentum |
| ξ | Generic aleatory variable |
| σ | Standard deviation |
| τ | Trailing edge damage factor |
| ω | Weighting term |
References
- Rempel, L. Rotor Blade Leading Edge Erosion-Real Life Experiences. Wind Syst. Mag. 2012, 11, 22–24. [Google Scholar]
- Røndgaard, F.-K. February 23, Ersen-; Europe, 2018 Structural Failure Denmark UK WindAction|Siemens Sets Billions: Ørsted must Repair Hundreds of Turbines. Available online: http://www.windaction.org/posts/47883-siemens-sets-billions-orsted-must-repair-hundreds-of-turbines#.XfzepkdKiUl (accessed on 20 December 2019).
- Régis, D. Why Inspect Wind Turbine Blades? How to Avoind Major Wind Turbine Blade Damage and Cost. Sustainable Energy Consulting and Software (3E). 2014. Available online: https://www.3e.eu/wp-content/uploads/2014/06/3E_Why-Wind-Turbine-Blade-Inspections_20140507_final.pdf (accessed on 10 July 2020).
- Wood, K. Blade Repair: Closing the Maintenance Gap. Available online: https://www.compositesworld.com/articles/blade-repair-closing-the-maintenance-gap (accessed on 9 June 2020).
- Sareen, A.; Sapre, C.A.; Selig, M.S. Effects of leading edge erosion on wind turbine blade performance: Effects of leading edge erosion. Wind Energ. 2014, 17, 1531–1542. [Google Scholar] [CrossRef]
- Han, W.; Kim, J.; Kim, B. Effects of contamination and erosion at the leading edge of blade tip airfoils on the annual energy production of wind turbines. Renew. Energy 2018, 115, 817–823. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060, 947422; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Castorrini, A.; Corsini, A.; Rispoli, F.; Venturini, P.; Takizawa, K.; Tezduyar, T.E. Computational analysis of performance deterioration of a wind turbine blade strip subjected to environmental erosion. Comput Mech. 2019, 64, 1133–1153. [Google Scholar] [CrossRef]
- Herring, R.; Dyer, K.; Martin, F.; Ward, C. The increasing importance of leading edge erosion and a review of existing protection solutions. Renew. Sustain. Energy Rev. 2019, 115, 109382. [Google Scholar] [CrossRef]
- Papi, F.; Cappugi, L.; Bianchini, A.; Perez-Becker, S. Numerical Modeling of the Effects of Leading-Edge Erosion and Trailing-Edge Damage on Wind Turbine Loads and Performance; ASME TurboExpo: London, UK, 2020. [Google Scholar]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Natarajan, A.; Hansen, M. Description of the DTU 10 MW Reference Wind Turbine; DTU Wind Energy: Copenhagen, Denmark, 2013. [Google Scholar]
- OpenFAST. Available online: https://github.com/OpenFAST (accessed on 31 October 2019).
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Iaccarino, G. Quantification of Uncertainty in Flow Simulations Using Probabilistic Methods; VKI Lecturers Series; von Karman Institute: Rhode-St-Genèse, Belgium, 2009. [Google Scholar]
- Carnevale, M.; Montomoli, F.; D’Ammaro, A.; Salvadori, S.; Martelli, F. Uncertainty Quantification: A Stochastic Method for Heat Transfer Prediction Using LES. J. Turbomach 2013, 135, 1–8. [Google Scholar] [CrossRef]
- Ahlfeld, R.; Montomoli, F.; Carnevale, M.; Salvadori, S. Autonomous Uncertainty Quantification for Discontinuous Models Using Multivariate Padé Approximations. J. Turbomach 2018, 140. [Google Scholar] [CrossRef]
- Tatang, M.A.; Pan, W.; Prinn, R.G.; McRae, G.J. An efficient method for parametric uncertainty analysis of numerical geophysical models. J. Geophys. Res. Atmos. 1997, 102, 21925–21932. [Google Scholar] [CrossRef]
- Carnevale, M.; D’Ammaro, A.; Montomoli, F.; Salvadori, S. Film Cooling and Shock Interaction: An Uncertainty Quantification Analysis with Transonic Flows; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2014. [Google Scholar]
- Salvadori, S.; Carnevale, M.; Fanciulli, A.; Montomoli, F. Uncertainty Quantification of Non-Dimensional Parameters for a Film Cooling Configuration in Supersonic Conditions. Fluids 2019, 4, 155. [Google Scholar] [CrossRef]
- Bortolotti, P.; Canet, H.; Bottasso, C.L.; Loganathan, J. Performance of non-intrusive uncertainty quantification in the aeroservoelastic simulation of wind turbines. Wind Energy Sci. 2019, 4, 397–406. [Google Scholar] [CrossRef]
- Gaudern, N. A practical study of the aerodynamic impact of wind turbine blade leading edge erosion. J. Phys. Conf. Ser. 2014, 524, 012031. [Google Scholar] [CrossRef]
- Schramm, M.; Rahimi, H.; Stoevesandt, B.; Tangager, K. The Influence of Eroded Blades on Wind Turbine Performance Using Numerical Simulations. Energies 2017, 10, 1420. [Google Scholar] [CrossRef]
- Cavazzini, A.; Minisci, E.; Campobasso, M.S. Machine Learning-Aided Assessment of Wind Turbine Energy Losses due to Blade Leading Edge Damage.; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2019; IOWTC2019-7578. [Google Scholar]
- Fiore, G.; Selig, M.S. Simulation of Damage Progression on Wind Turbine Blades Subject to Particle Erosion. In Proceedings of the 54th AIAA Aerospace Sciences Meeting; American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Viterna, L.A.; Janetzke, D.C. Theoretical and Experimental Power from Large Horizontal-Axis Wind Turbines; National Aeronautics and Space Administration: Cleveland, OH, USA, 1982.
- Adams, T.; Grant, C.; Watson, H. A Simple Algorithm to Relate Measured Surface Roughness to Equivalent Sand-grain Roughness. IJMEM 2012, 1, 66–71. [Google Scholar] [CrossRef]
- Wind Energy: Handbook; Burton, T., Ed.; J. Wiley: Chichester, UK; New York, NY, USA, 2001; ISBN 978-0-471-48997-9. [Google Scholar]
- Mulders, S.; van Wingerden, J. Delft Research Controller: An open-source and community-driven wind turbine baseline controller. J. Phys. Conf. Ser. 2018, 1037, 032009. [Google Scholar] [CrossRef]
- Borg, M. LIFES50+ Deliverable D1.2: Wind Turbine Models for the Design; DTU Wind Energy: Risø, Denmark, 2015; p. 29. [Google Scholar]
- International Electrotechnical Commission. Wind Turbines-Part1: Design Requirements; Technical Standard IEC61400-1:2005; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012, 13, N14. [Google Scholar] [CrossRef]
- Nandi, T.N.; Herrig, A.; Brasseur, J.G. Non-steady wind turbine response to daytime atmospheric turbulence. Phil. Trans. R. Soc. A 2017, 375, 20160103. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, D.; Laustsen, S.; Stege, J. Wind turbine blade coating leading edge rain erosion model: Development and validation. Wind Energy 2018, 21, 942–951. [Google Scholar] [CrossRef]
- Fiore, G.; Selig, M.S. Simulation of Damage for Wind Turbine Blades Due to Airborne Particles. Wind Eng. 2015, 39, 399–418. [Google Scholar] [CrossRef]
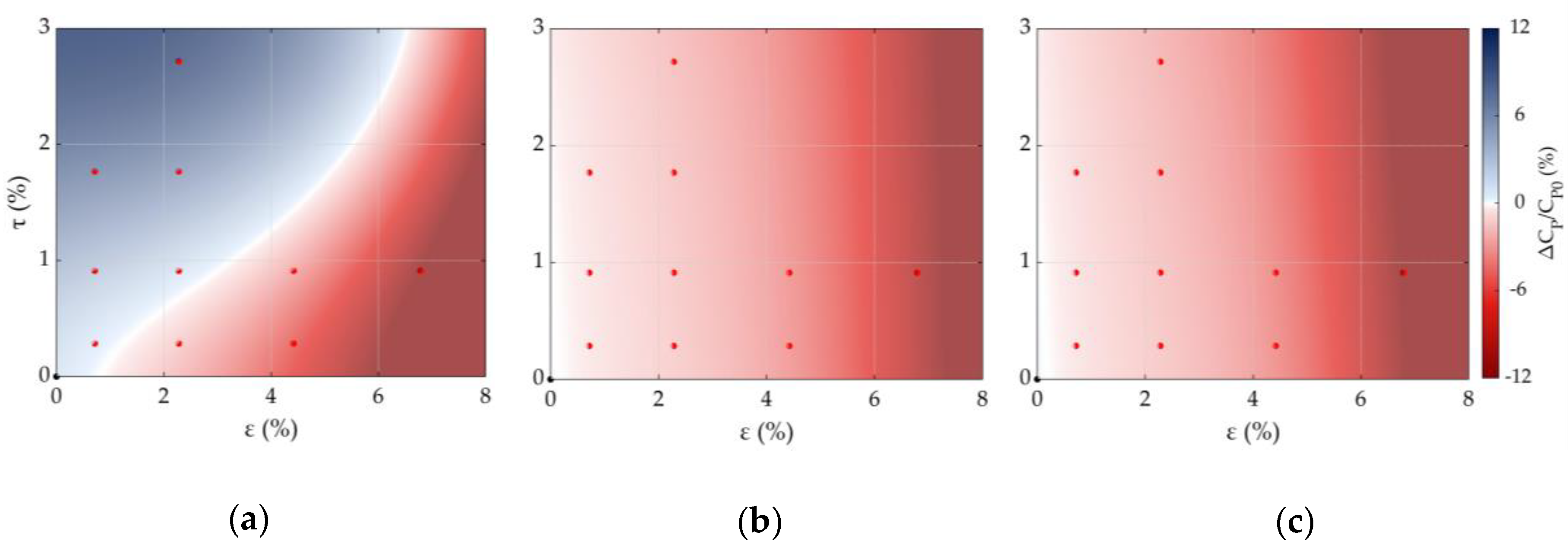
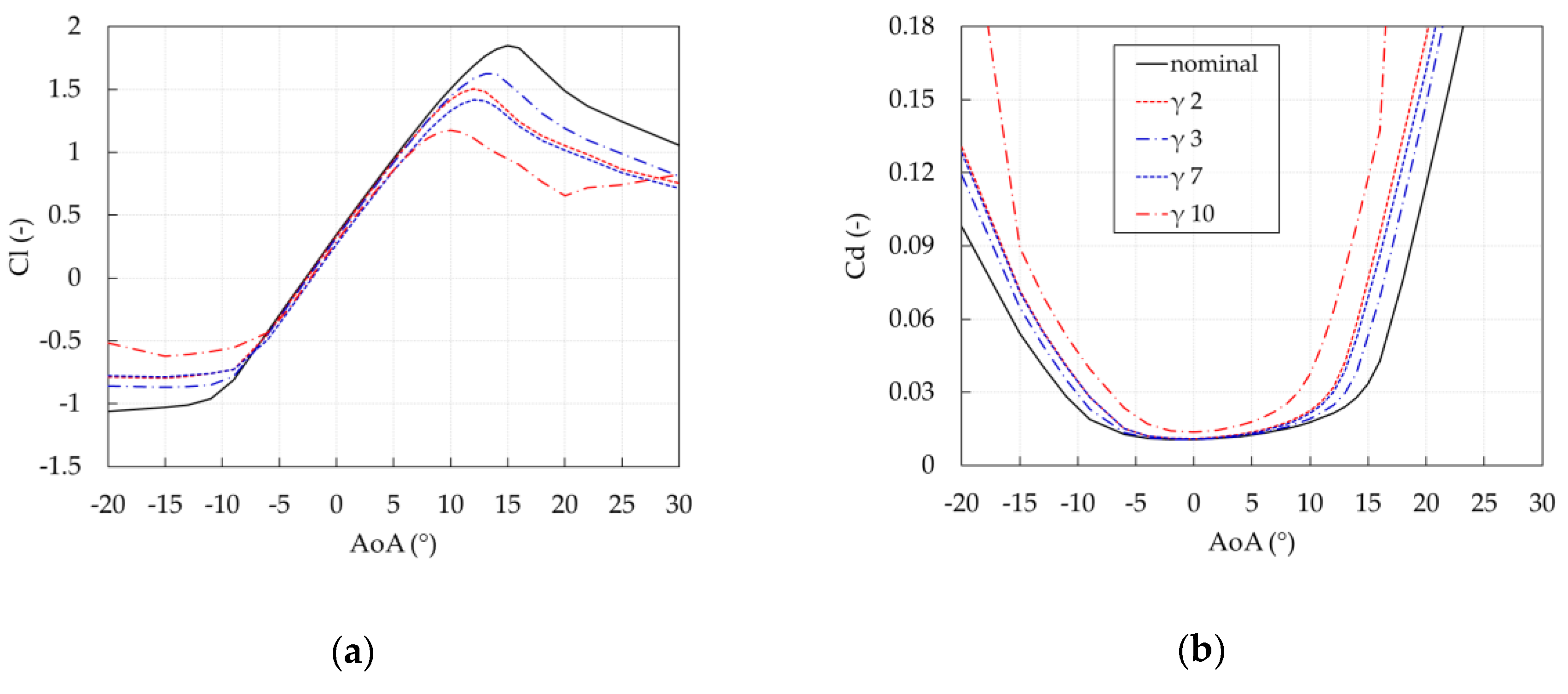
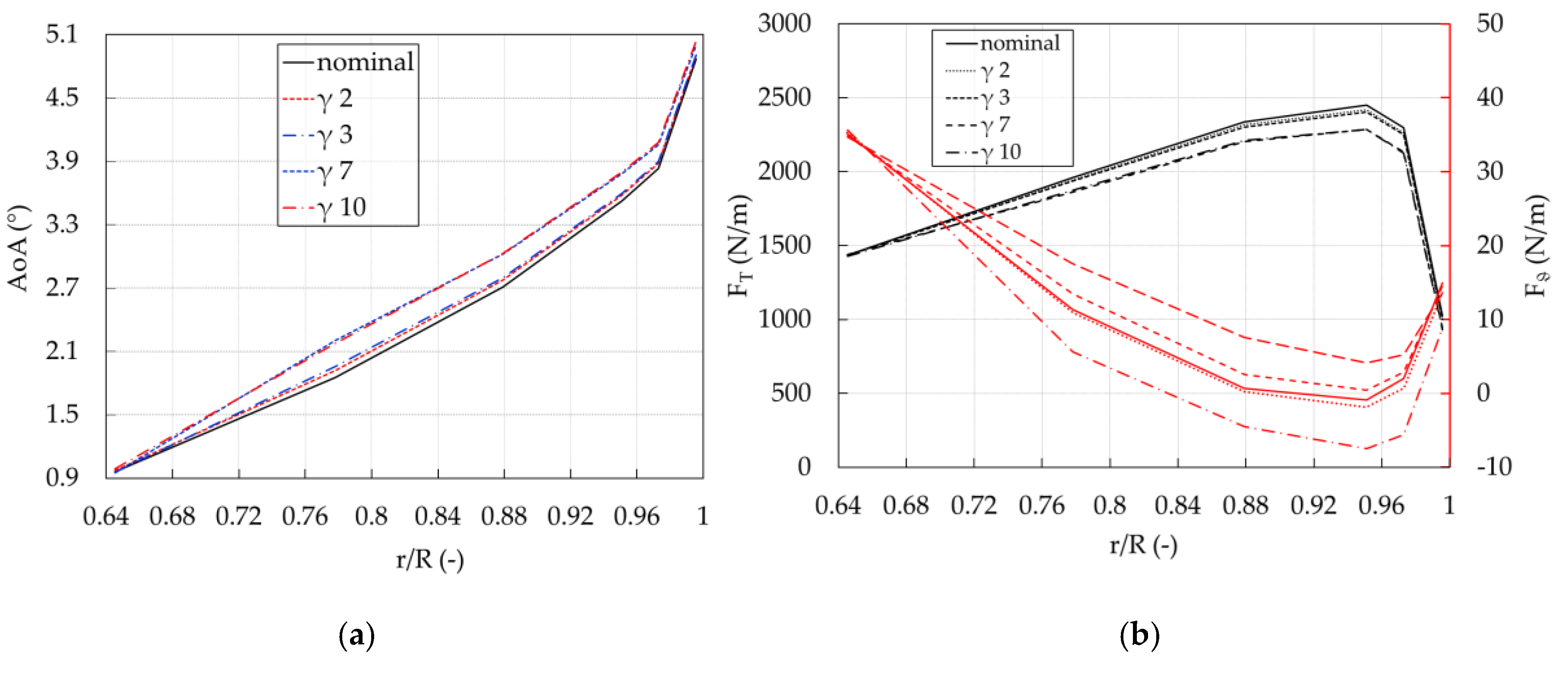
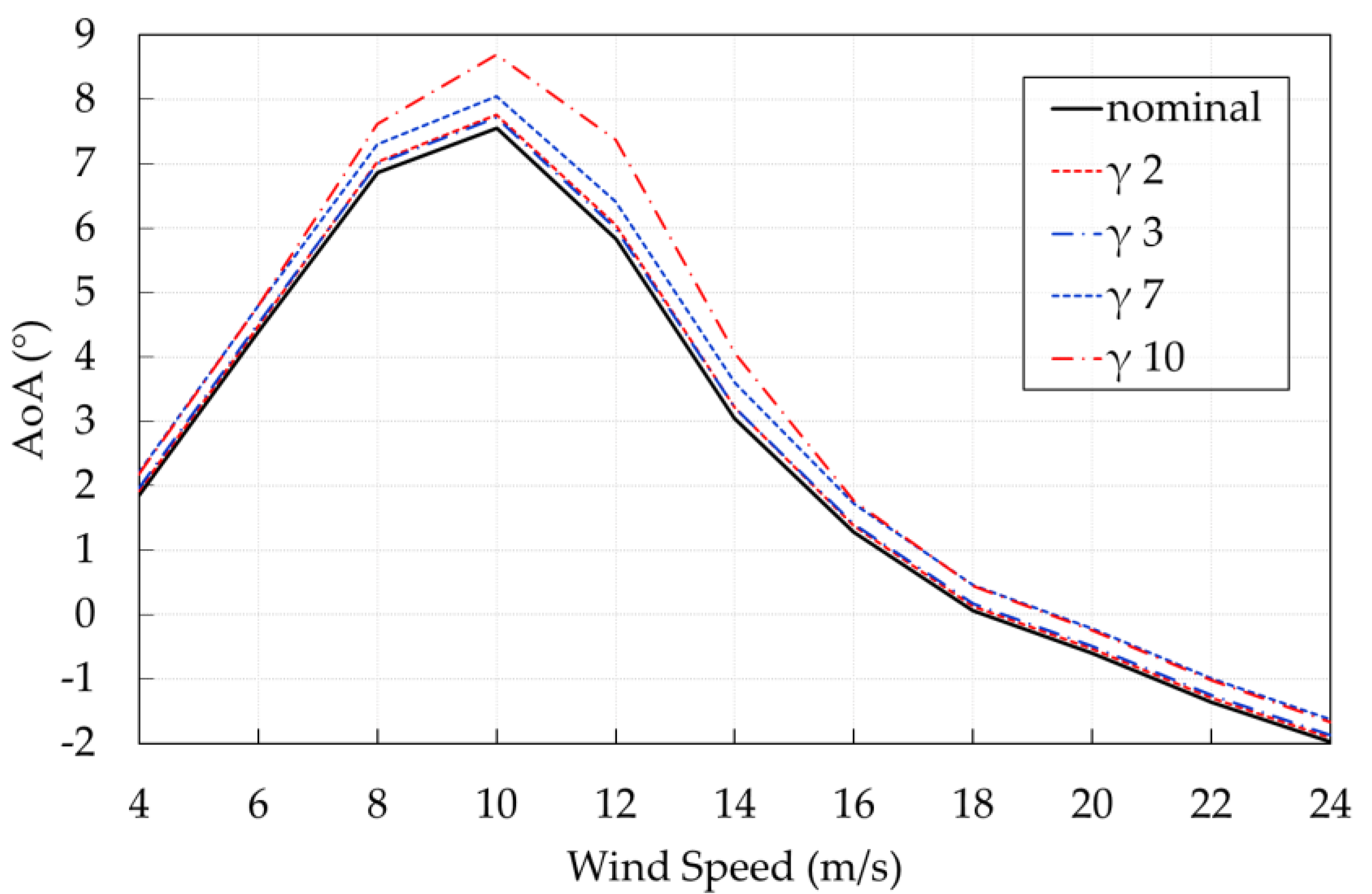
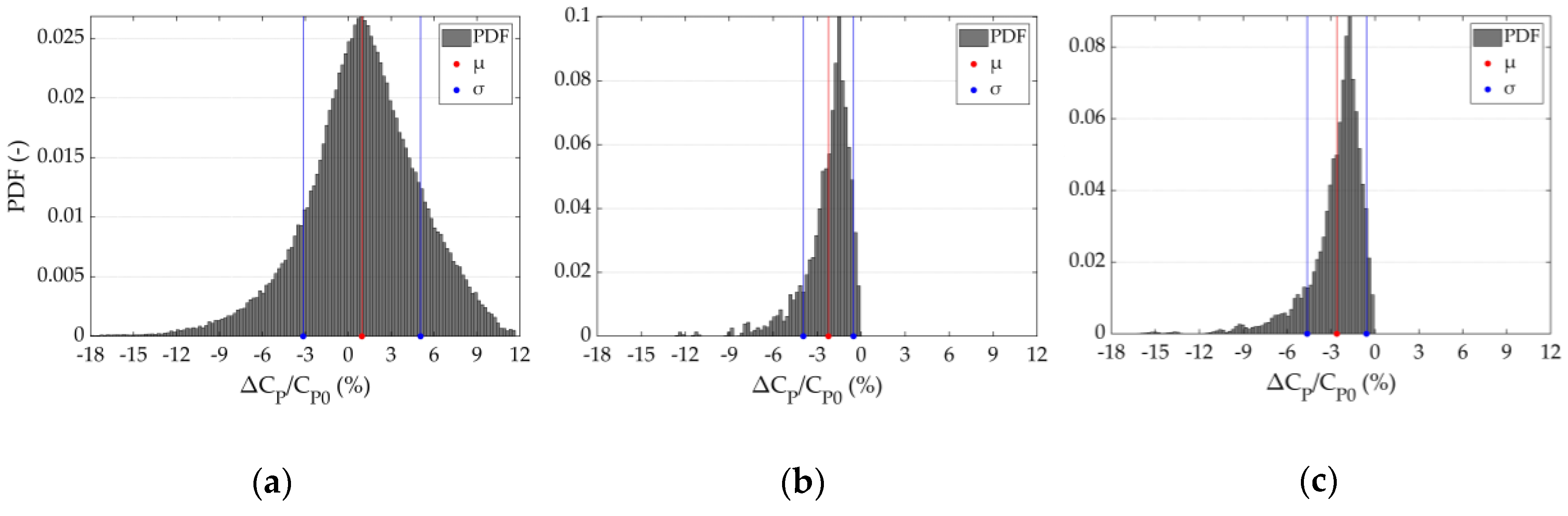
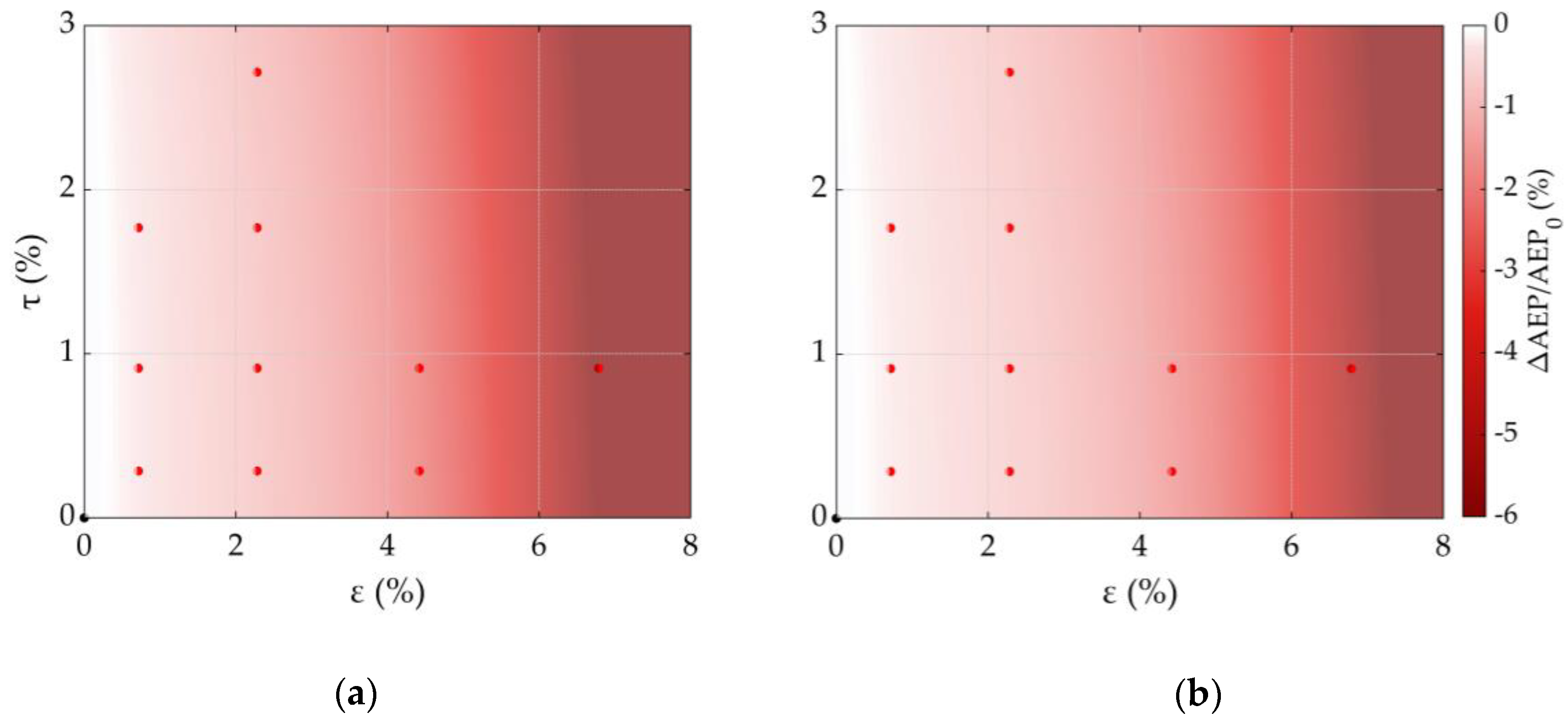
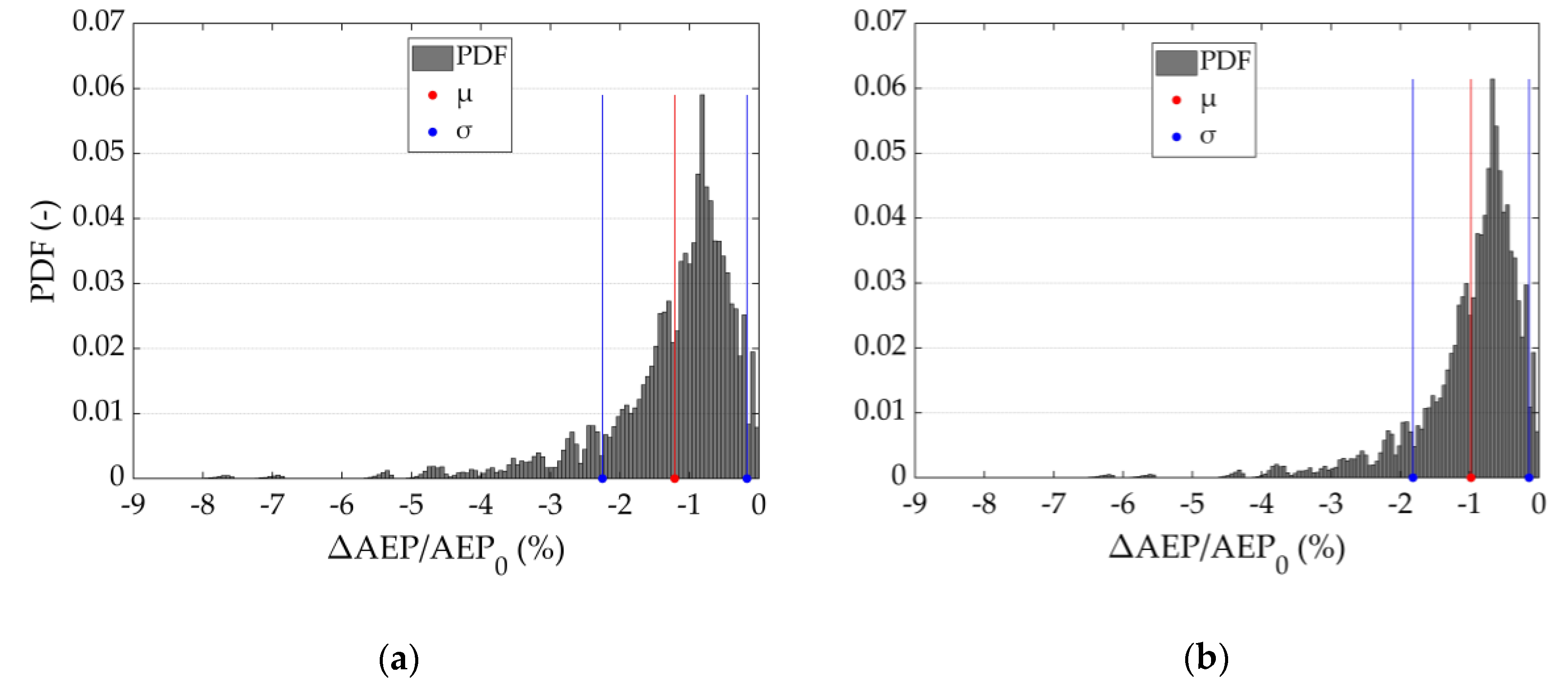
| Parameter | α | β | Support | |
|---|---|---|---|---|
| ε | Beta | 2.0 | 6.0 | 0–10 (%) |
| τ | Beta | 2.0 | 6.0 | 0–4 (%) |
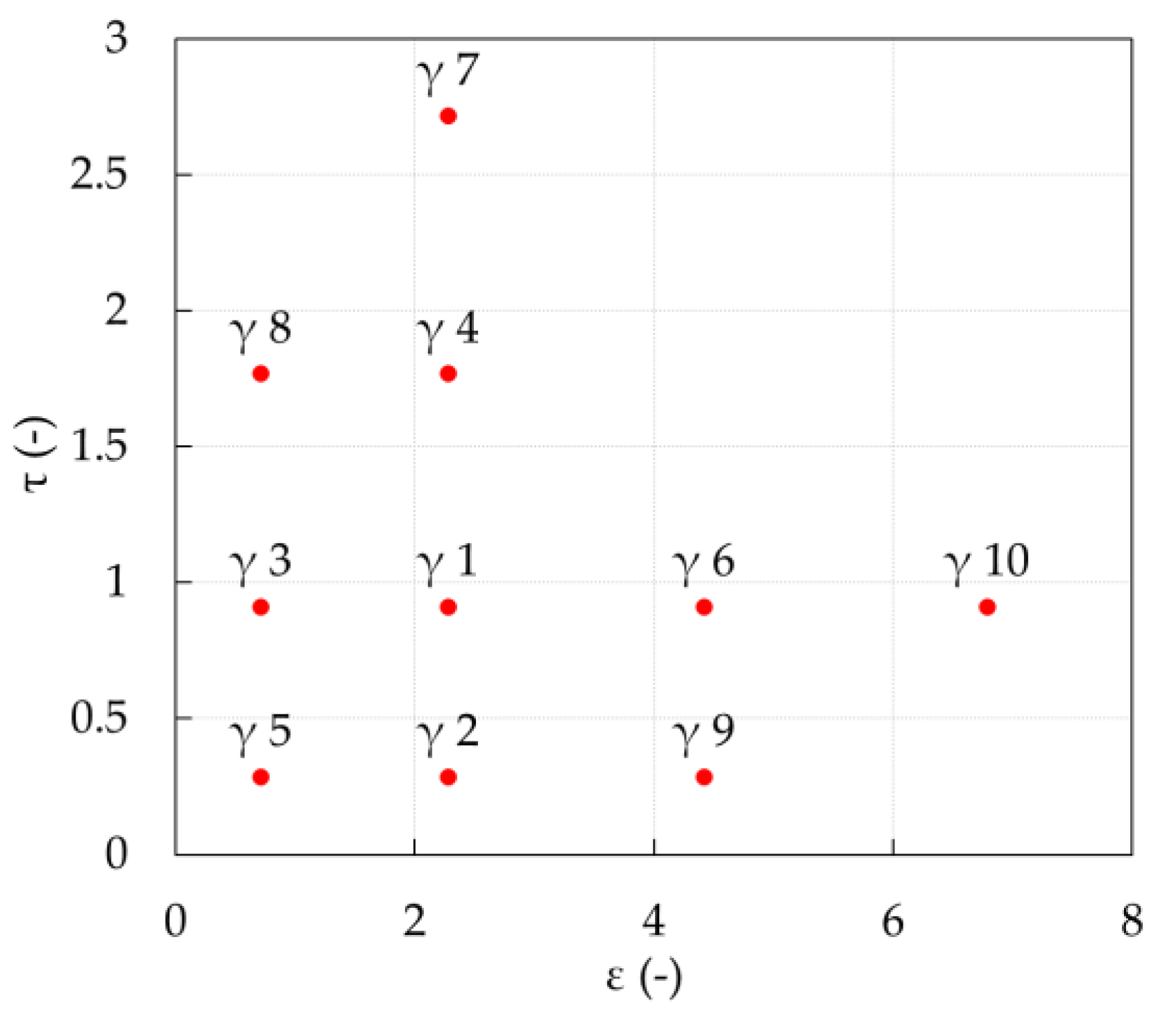
| γ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| ε | 2.2792 | 2.2792 | 0.7134 | 2.2792 | 0.7134 | 4.4189 | 2.2792 | 0.7134 | 4.4189 | 6.7884 |
| τ | 0.9118 | 0.2854 | 0.9118 | 1.7677 | 0.2854 | 0.9118 | 2.7157 | 1.7677 | 0.2854 | 0.9118 |
| ε | τ | ΔAEP/AEP0 (%) |
|---|---|---|
| 0 | 0 | 0.00 |
| 0 | 3 | 0.00 |
| 4 | 0 | −1.87 |
| 4 | 3 | −2.24 |
| 8 | 0 | −9.69 |
| 8 | 3 | −10.51 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papi, F.; Cappugi, L.; Salvadori, S.; Carnevale, M.; Bianchini, A. Uncertainty Quantification of the Effects of Blade Damage on the Actual Energy Production of Modern Wind Turbines. Energies 2020, 13, 3785. https://doi.org/10.3390/en13153785
Papi F, Cappugi L, Salvadori S, Carnevale M, Bianchini A. Uncertainty Quantification of the Effects of Blade Damage on the Actual Energy Production of Modern Wind Turbines. Energies. 2020; 13(15):3785. https://doi.org/10.3390/en13153785
Chicago/Turabian StylePapi, Francesco, Lorenzo Cappugi, Simone Salvadori, Mauro Carnevale, and Alessandro Bianchini. 2020. "Uncertainty Quantification of the Effects of Blade Damage on the Actual Energy Production of Modern Wind Turbines" Energies 13, no. 15: 3785. https://doi.org/10.3390/en13153785
APA StylePapi, F., Cappugi, L., Salvadori, S., Carnevale, M., & Bianchini, A. (2020). Uncertainty Quantification of the Effects of Blade Damage on the Actual Energy Production of Modern Wind Turbines. Energies, 13(15), 3785. https://doi.org/10.3390/en13153785