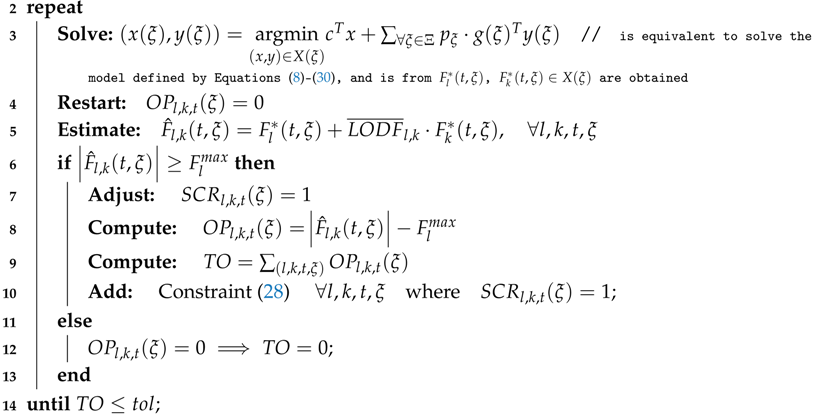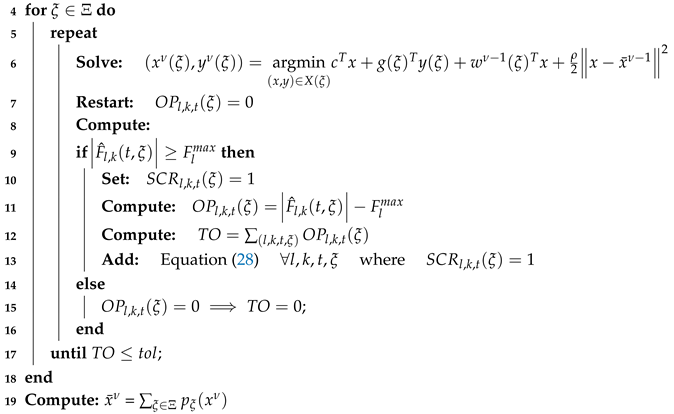1. Introduction
The security constrained unit commitment (SCUC) problem is the optimization model that schedules a set of power generation units to meet an expected energy demand over a typical time horizon of 24 h while meeting several system constraints (e.g., operational limits of the generation units and transmission limits) under normal operating conditions and also under
contingencies. The SCUC problem is widely used in day ahead and real time markets to obtain an economically, reliably, and safely operation of the power system [
1]. The SCUC is a complex mixed integer programming (MIP) problem since it belongs to the class of NP-hard problems [
2]. This feature has challenged researchers to approach the complexity of the SCUC problem in different ways when dealing with large-scale power systems. Examples of these solution approaches include Lagrangian relaxation (LR) and Benders decomposition (BD) techniques, which have been implemented to solve the SCUC model in efficient computing times [
3,
4,
5,
6,
7]. Dealing with
security constraints posses a challenge when solving the SCUC problem. Therefore, several authors have proposed different alternatives to tackle them. In [
8], the authors defined necessary and sufficient conditions to identify and eliminate inactive
security constraints. Similarly, H. Wu et al. [
9] presented analytical feasibility conditions to define only the subset of security constraints of the SCUC problem feasible region. Likewise, in [
10], the authors mathematically ruled out unnecessary security constraints using again necessary and sufficient conditions. However, the application of these methods could be limited for large-scale practical problems, and therefore decomposition techniques such as BD should be required in a complementary manner [
9,
10]. On the other hand, some authors have addressed this challenge without relying to decomposition techniques or any of the previously mentioned methods. This is the case of Capitanescu et al. [
11] who developed a preventive security-constrained optimal power flow (PSCOPF) defining two constraint filtering techniques under the concepts of dominated and non-dominated constraints. Including only the latter in the PSCOPF model accelerates its solution time.
Currently, a key factor to reduce the computing times when solving the SCUC problem is the use of linear sensitivity factors (LSFs) to model the power grid. The Power Transfer Distribution Factor (PTDF) and the Line Outage Distribution Factor (LODF) estimate power flows changes under power injection variations in buses and line outages (i.e.,
contingencies), respectively [
12]. Nonetheless, Eslami et al. [
13] proposed a new method for reducing SCUC variables and constraints under a conventional formulation of the power grid for post-contingency constraints. Several iterative methodologies based on LSFs have been developed to increase the computational efficiency of SCUC models for large-scale power systems. In [
2], the authors added only binding
security constraints to the SCUC problem using the Gurobi deferred constraints function (i.e., lazy constraints). Similarly, Marín-Cano et al. [
14] proposed the implementation of user cuts to improve the computational performance of the SCUC and presented indices that provide expansion signals for the transmission network. Xavier et al. [
15] added effective security constraints based on the concept of priority queue, adding at most only one
security constraint per line. All these methodologies aim to generate iteratively the feasible region of the SCUC problem reducing effectively the computation times needed to solve this problem. However, it is noteworthy that none of the aforementioned methodologies has been applied in the analysis of the safe operation of electrical systems under uncertainty [
16].
Recently, the evolution of power systems has imposed major challenges in the solution of the SCUC due to the uncertainty caused by the integration of large amounts of intermittent renewable resources. One way to address these challenges is through the SSCUC problem [
17]. In [
18], the authors evaluated security through a multi-stage stochastic programming model where random system disturbances (generation unit and transmission line failures) are modeled through scenario trees. To solve the SSCUC, they decomposed the problem using LR. The authors of [
19] used BD to solve a SSCUC considering the intermittency and volatility of wind generation through scenarios. Two different procedures to tackle the SSCUC are compared in [
17]. The first one is based on scenarios, whereas the second one is based on optimization intervals. The SSCUC model presented in [
20] considers wind power production scenarios and non-spinning reserves. The authors relied on chance-constrained programming to solve this variant of the SSCUC. Similarly, the authors of [
21] studied an
security and chance-constrained unit commitment (SCCUC) model. They formulated this SCCUC problem as a mixed-integer second-order cone program with two types of reserves to consider wind fluctuations and single component outages (i.e., generators or transmission lines outages). In [
22], the authors relied on BD to solve a SSCUC model considering different types of pumped-storage hydropower plants. Finally, Park et al. [
23] modeled a SSCUC using two-stage stochastic programming, considering dynamic line rating to improve the use of transmission lines during
conditions.
The above references highlight the importance of the SSCUC models as a way to hedge against uncertainty in the safe operation of power systems. However, it should be pointed out that high computational speed is of great importance for operators at the moment of real-time decision-making, since the mathematical models for UC under uncertainty are computationally much more complex than their deterministic counterparts [
24]. To the best of our knowledge, there are few studies that address the computational complexity of the SSCUC problem and focus on solving the problem quickly and effectively. Among them, Wang and Fu [
1] proposed a fully parallel stochastic SCUC approach to obtain efficient and fast solutions in large-scale electrical systems and N. Yang et al. [
25] proposed a method that aims to improve the efficiency of the SSCUC problem under constrained ordinal optimization (COO). This approach has two advantages: The first one is a recognition of discrete variables to reduce the solution space of the approximate COO rough model. The second one is the inclusion of a strategy to reduce non-effective security constraints, as presented in [
26], which in turn is based on the analytical conditions proposed in [
8].
Following the authors of [
1,
25], in this work, we propose a novel and easy-to-implement strategy to efficiently solve a SSCUC problem under the uncertainty of large penetration of intermittent energy sources. This strategy has the following features: (i) it uses sensitivity linear factors to compute power flows to reduce the number of variables and constraints when compared to conventional network modeling; (ii) it considers user cuts to dynamically add active
security constraints, as proposed in [
14]; and (iii) it uses the PHA decomposition algorithm to relax the SSCUC model. As shown in [
27], the PHA is able to achieve high-quality solutions for stochastic optimization in large-scale power systems. As an additional result from the proposed strategy, we define several indices that allow identifying the most critical and vulnerable lines in terms of the overloads they cause or suffer under single contingencies. Such information is useful to the system planner for short-term transmission expansion analyses.
The rest of the paper is organized as follows.
Section 2 introduces some preliminary background on stochastic optimization and presents the SSCUC model studied in this paper.
Section 3 presents the elements of the solution strategy proposed in the paper as well as the general framework that embeds
security cuts into the progressive hedging algorithm.
Section 4 includes the results of the evaluation of the proposed strategy in the IEEE RTS-96 test system.
Section 5, introduces and exemplifies transmission expansion indices calculated with the results of the proposed strategy. Finally,
Section 6 concludes the paper and provides additional research extensions.
4. Results
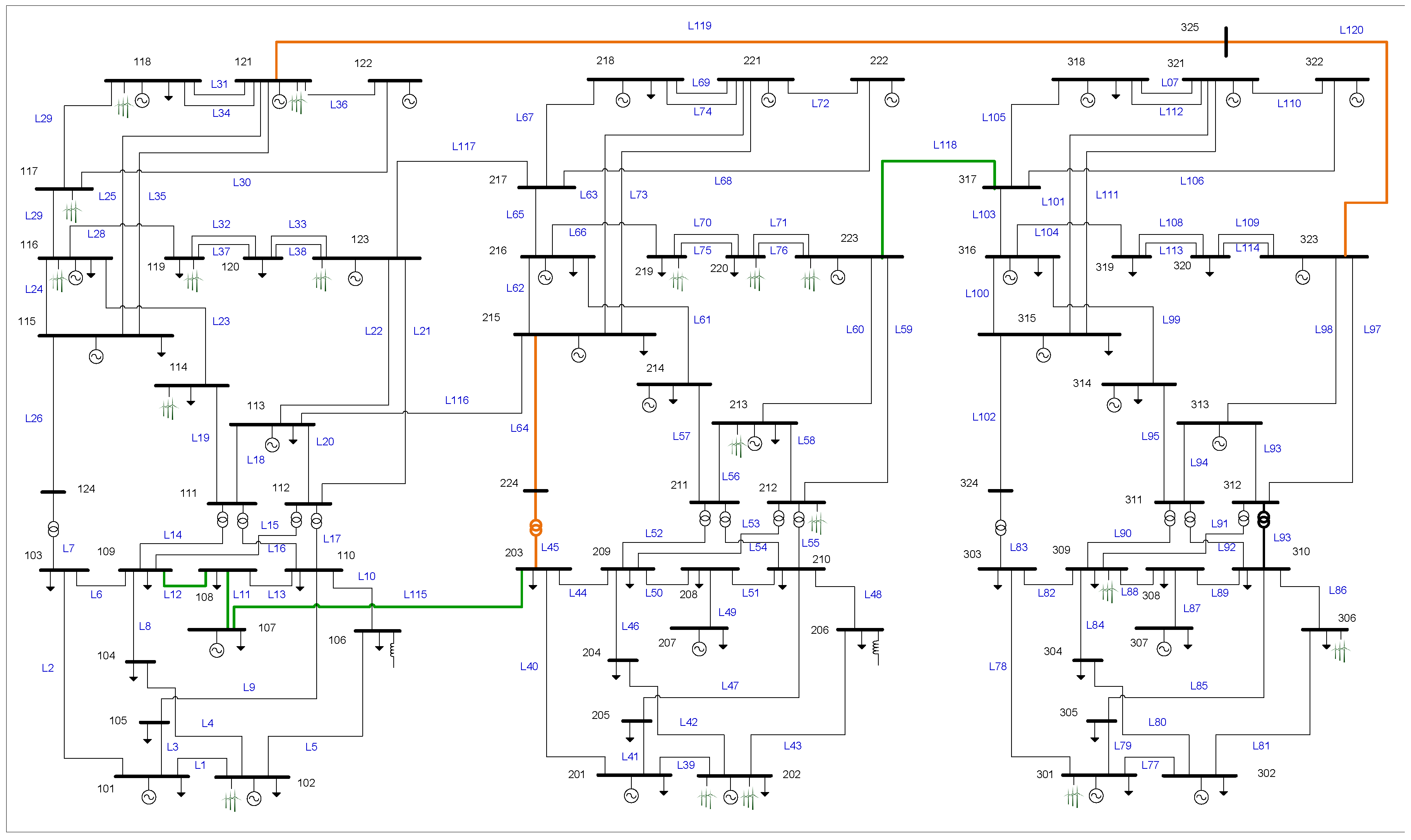
The test system used to evaluate the proposed strategy is the IEEE RTS-96 (see
Figure 1) used previously whose information is fully available in [
30]. This system is made up of 73 buses, 120 transmission lines, 96 thermal generators, and 19 wind farms (with an installed capacity of 6900 MW and located at buses 102, 114, 116, 118, 121, 119, 123, 202, 212, 213, 219, 220, 223, 301, 306 and 309. There are 51 loads with a maximum demand of 7539 MW and an average demand of 6258 MW. A time horizon of 24 h is considered. The SSCUC problem for this system considers 10 scenarios each with a given probability representing different generation outputs of the wind farms throughout the 24 h of the day. A detailed description of the scenarios under consideration, as well as the Excel sheets containing all input data, can be consulted in [
30].
The proposed computational strategy was tested on two computers: an Intel Xeon E5 @ 2.40GHz server with 44 cores and 256 GB of RAM memory (hereafter, server) and an Intel Core i7 @ 3.4GHz desktop computer with 8 cores and 8 GB of RAM memory (hereafter, desktop). The proposed approach was implemented using the commercial algebraic modeling system GAMS version 24.8.5, with CPLEX V12.6.1 as optimization engine.
4.1. Parameters Setting for the PHA
One of the first parameters to be adjusted is the penalty factor
. Values of
based on energy production costs of the hedging variable are suggested as a good option to foster the convergence of the PHA [
36]. Additionally, we selected two of the updating strategies cited in
Section 3.2.1:
is the strategy proposed by Watson and Woodruff [
27], whereas
is the one proposed by Ordoudis et al. [
36].
Another important factor is the selection of the hedging variable. Some authors have carried out experiments to study which is the best hedging variable within the Stochastic UC problem [
35,
36]. Under different adjustment strategies of
, Ordoudis et al. [
36] showed that the best-performing hedging variable is the on/off status variable, rather than the start and stop down variable. Accordingly, in our computational experiments, we used as hedging variable the on/off state variable (
).
Finally, to guarantee convergence and feasible PHA solutions in the different tests of the proposed computational strategy, we set parameters
and
in the context of the so-called
rounding technique. It is advisable to assign 0 to
to guarantee whole availability of generation units to have a higher chance of reaching feasibility as mentioned in [
35,
36]. On the other hand,
must be set for every problem. In this case, an initial value of
is set and small variations over this value are performed. As illustrated in [
36], small increments of
can provide high quality solutions in short PHA running times. Therefore, in our experiments, we set
to zero, and the values of
were set heuristically. Beginning at a given (relatively high value) of
, we ran PHA reducing the value of
iteratively in steps of
until reaching a good trade-off between solution quality and running time. In this case, we stopped the search at
. Below this value, PHA presented convergence problems. The results presented in this section (on the
server) were obtained with this value. It is noteworthy that the value of
was set to a different value (
) for the experiments performed on the
desktop.
4.2. Formulations
To validate the performance of the strategy proposed in this work, we carried out a comparative analyses between the following three formulations:
Formulation A: Extensive Formulation of the SSCUC without the cut-adding method.
Formulation B: Extensive Formulation of the SSCUC with the cut-adding method.
Formulation C: This formulation corresponds to the computational strategy proposed in this work. That is, the SSCUC formulation with the
cut-adding method embedded within PHA. Additionally, we compared two methods for adjusting
in this formulation (
and
), as defined in
Section 3.2.1.
As a benchmark, we first solved the EF of the SSCUC problem (
Formulation A). This gives some key metrics to compare the performance of the other formulations: the optimality gap and the objective function of the optimal solution of the problem (i.e., the best relaxed solution). As stopping criterion, the minimum relative optimality gap defined in GAMS was set to 1% for all tested formulations. The optimality gap was calculated as the difference between the solution of a formulation and the best relaxed solution, divided by the best relaxed solution.
Table 1 presents the values of the objective function, the computing time, and the optimality gap of
Formulation A, obtained with the
server.
4.3. Analysis and Comparison of Results
Ten scenarios were used to consider the uncertainty associated to wind production within the IEEE-RTS-96 test case, which were taken from Pandzic et al. [
30].
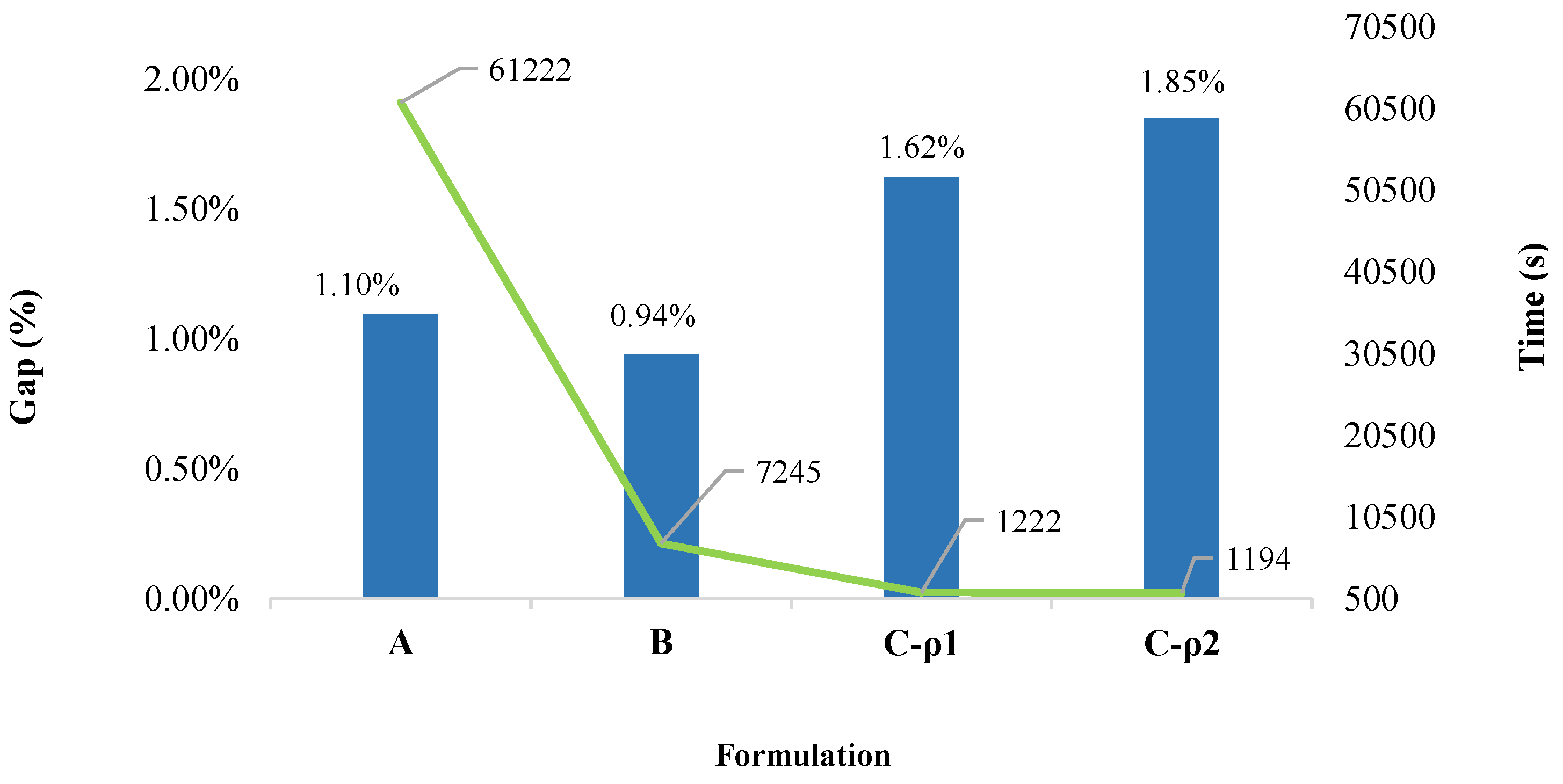
Figure 2 compares the gap (%) (blue bars) and running time (s) (green line), taken to solve the SSCUC model for each formulation on the
server. As shown by Ordoudis et al. [
36], PHA is a promising algorithm with great potential to efficiently address the stochastic unit commitment problem in large-scale power systems as the number of scenarios increases.
Figure 2 shows that Formulation A takes a (large) computing time of
s (approximately 17 h) to reach an optimality gap of
% with an objective function of
MUS
$. Meanwhile, the performance of Formulation B is notably better; it took only 7245 s (approximately 2 h) to find a solution with an optimality gap of
% (which corresponds to an objective function of
MUS
$). This is
times faster with respect to the running time of Formulation A for a solution of even better quality. This first result illustrates that the inclusion of the
cut-adding method proposed by Marín-Cano et al. [
14] generates a more compact SSCUC model. Additionally, considering explicitly single contingencies for all 118 lines generates 3.3 million
security constraints (in Formulation A). By contrast, the
cut-adding method of Formulation C generated only 0.116 million binding security constraints defining the feasible region of the SSCUC problem. As a result, the cut-adding method embedded in PHA reduces the size of the model (of Formulation A) by 99.6% (by ignoring unnecessary security constraints within this model). As a consequence, the comparison of Formulations A and C (with
and
) shows that the latter formulation achieves results of comparable quality in much faster running times. Even though the solutions reached by Formulation C have slightly greater optimality gaps (compared to the other formulations), it reaches acceptable sub-optimal solutions (with a gap of 1.62% for Formulation C-
and 1.85% for Formulation C-
) in roughly 1200 s (approximately 20 min). Remarkably, Formulation C (with
or
) is on average 50 times faster than Formulation A, and it is six times faster than Formulation B.
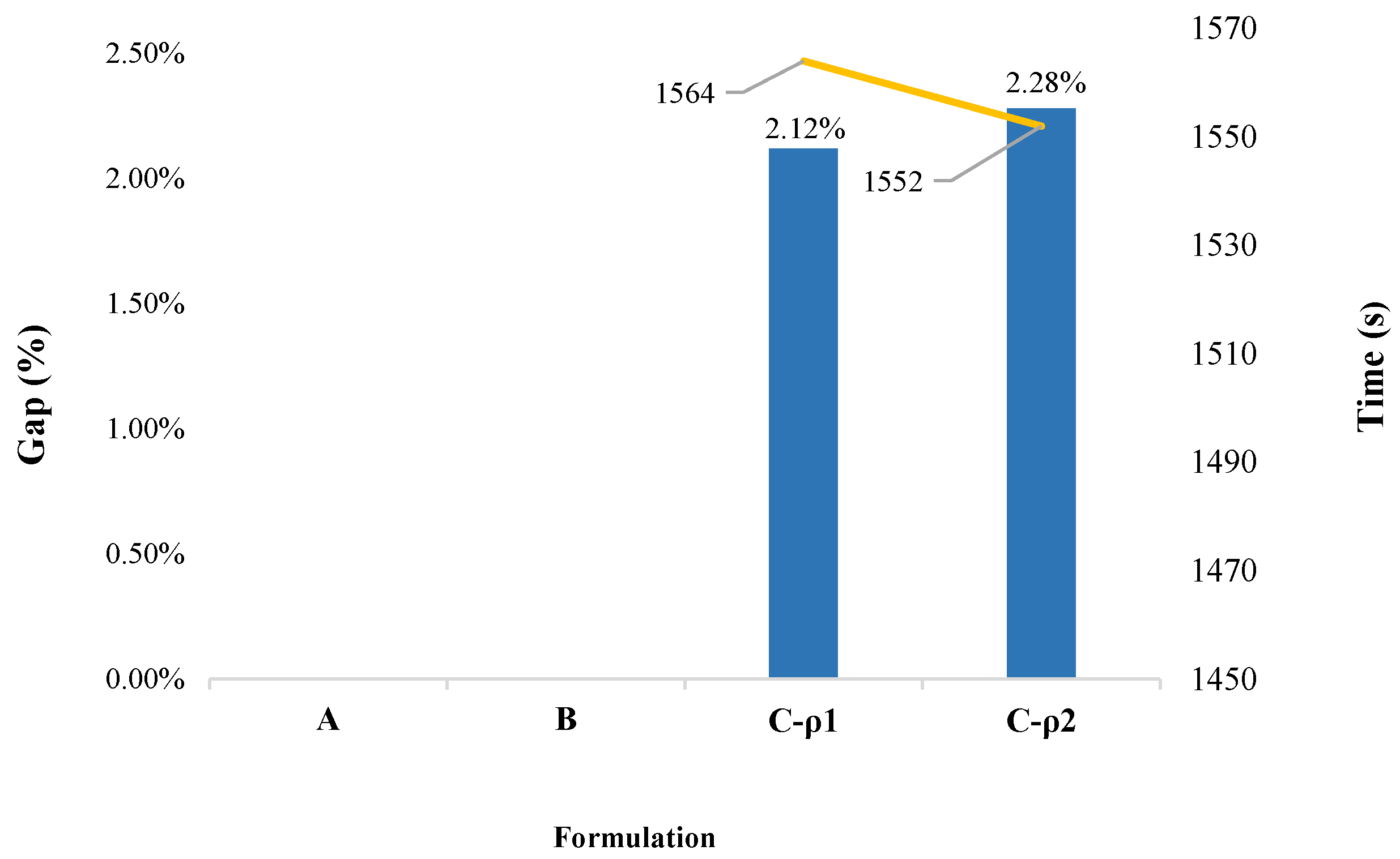
Figure 3 presents the performance of the proposed method in the test performed in the
desktop, where blue bars are the optimality gap and yellow line is the running time taken by each formulation. This figure depicts clearly the value of the solution strategy presented in this paper. First, for Formulations A and B, no results were obtained, because a (standard) desktop computer does not have the computational resources required by these formulations. On the other hand, Formulation C (in both variants of the penalty factor update
and
) obtained solutions with optimality gaps of around 2%. For example, Formulation C-
managed to obtain a gap of 2.12% (with a solution of 1.1223 MUS
$) in a running time of 1564 s (26.1 min), whereas Formulation C-
reached a gap of
% in 1552 s (
min). Notably, the results of both variants of Formulation C on the
server (see
Figure 2) and on the
desktop computers (see
Figure 3) are comparable in terms of both solution quality and running time. This, once again, shows the contribution of our novel strategy when it comes to obtaining high-quality solutions in short times, even when using computing resources of limited capacity.
On the other hand, Formulation C was unable to get solutions with gaps below 1% on the
server (see
Figure 2), as well as to get gaps below 2%, on the
desktop computer (see
Figure 3). This behavior is due to the fact that the
SSCUC problem is an MIP problem with high dimensionality and PHA is a method that guarantees convergence and optimality only for convex problems. Therefore, some authors (e.g., Guo et al. [
41]) have proposed integrating PHA with dual decomposition to have exact solutions for stochastic mixed-integer programming problems. However, Formulation C offers a good trade-off between the degree of suboptimality of the solution and the elapsed running time. The choice of the penalty factor updating strategies (Formulation C-
or Formulation C-
) offers an additional control parameter, since the better is the quality of the solution (with Formulation C-
) the longer is the running time. As a reference, detailed results of the experiments presented in this section are given in
Appendix B.
5. Expansion Transmission Indices
In addition to establishing the safe operation of the system, an added value of the
outage addition method proposed by Marín-Cano et al. [
14] is the identification of the most severe line faults and vulnerable lines under contingency analysis. This additional information serves as indicative signals of needed expansion of the transmission system. These indices are computed considering the number of overloads and most severe outage of the network in scenario
(i.e.,
.
The most severe line failures are those whose contingency generates the greatest amount of overloads on other lines
l. Index
estimates the expected value of the number of lines
l affected by contingency
k, and it is obtained by rounding the weighted sum of the parameter
over the sets of time periods
t, contingencies
l and scenarios
. Briefly,
indicates which line contingencies are the most severe, generating the greatest number of overloads on other lines.
As an example,
Figure 4 shows the most severe line faults that cause the greatest overload impact on the system, according to parameter
. Outages of lines L119, L120, L118 and L64 (highlighted in orange in
Figure 1) would generate, respectively, 176, 176, 81 and 60 thermal overloads in the transmission lines that remain in operation on the system.
Index
, estimates the expected value of the number of times that line
l is overloaded when the contingency analysis is performed. This index show how vulnerable a line is when other lines are out of service. That is,
indicates the number of overloads that a line experiences when transmission contingencies are produced in the system. This parameter is calculated by rounding the weighted sum of
over the sets of time periods
t, contingencies
k and scenarios
.
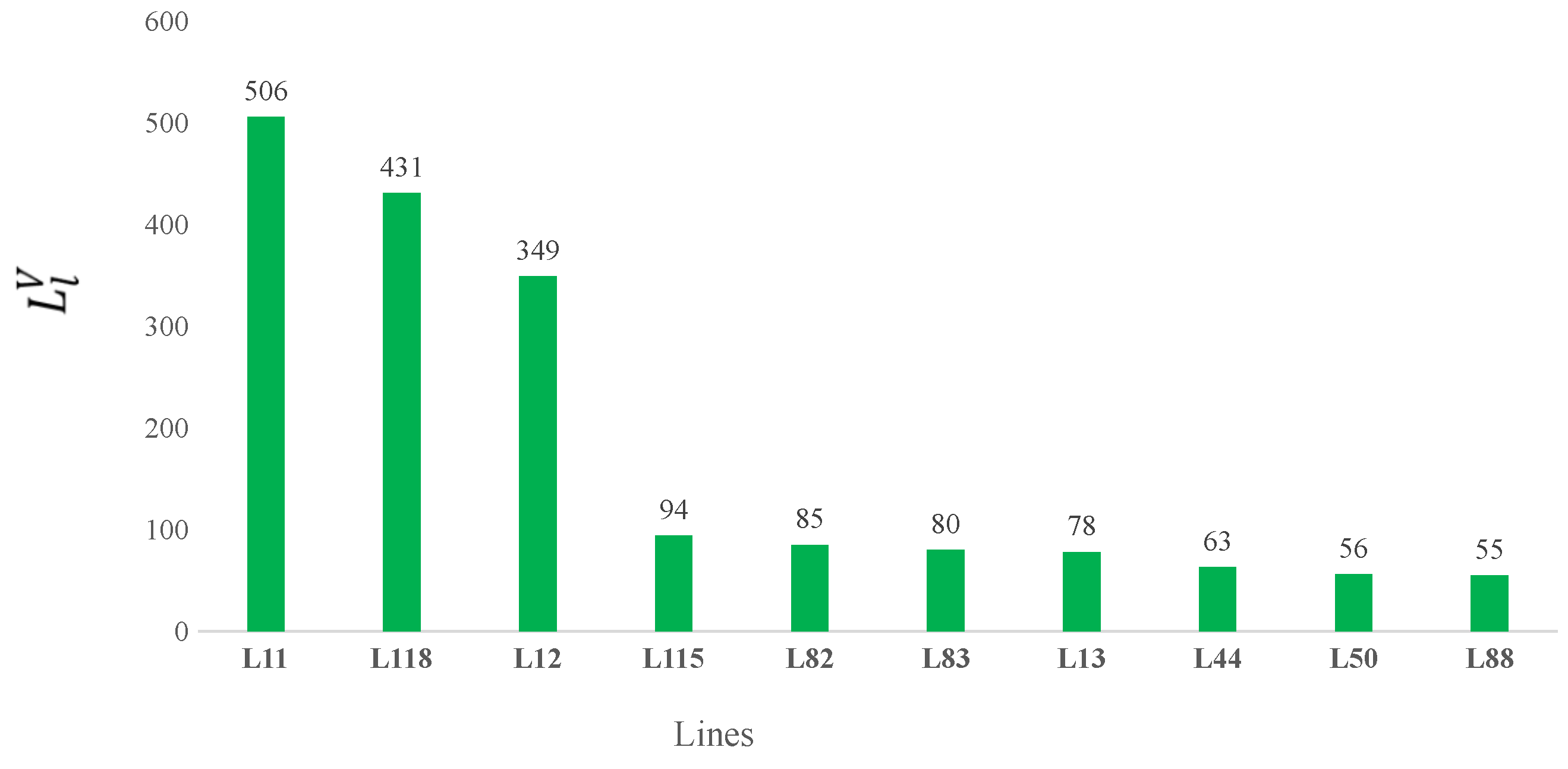
Figure 5 shows the most vulnerable lines of the IEEE-RTS-96 test system based on Index
. In this system, the lines with the highest number of overloads for different
contingencies are L11, L118, L12 and L115 (highlighted in green in
Figure 1), with 506, 349, 94 and 431 expected overloads over the time horizon and all scenarios, respectively.
Finally, the results of these indices suggest which lines to prioritize for the reinforcement of the transmission network through parallel circuits on some of the lines with the highest values of and . This could guide short-term transmission expansion analyses aimed at reducing the risks of post-contingency overloads on other elements of the network. That, in turn, increases the security, reliability and operating margins of the power system to deal with an increasing demand in the short and medium terms.
6. Conclusions
This work presented a novel strategy to efficiently solve the Stochastic Security Constrained Unit Commitment (SSCUC) problem (coined as Formulation C through the paper). It combines Linear Sensitivity Factors (LSF), an efficient cut-adding method and the progressive hedging algorithm (PHA). The use of the cut-adding method reduces drastically (by 99%) the size of the problem by only including active security constraints in the model. Embedding (for the first time) this method into the PHA provides an effective and efficient solution approach, which is able to obtain solution of comparable quality but is 50 times faster than the extensive formulation (EF) of the SSCUC problem (Formulation A through the paper). Computational experiments also showed that the proposed solution strategy is stable to the choice of the updating procedure of the penalty factor, a key parameter for the successful convergence of the PHA. Additionally, the fine tuning of parameters and depends on the problem characteristics (i.e., power system topology) and the need for high quality solutions of the SSCUC problem in short running times. The setting of these values allow the exploration of the trade-off between running time and solution quality. This characteristic of the proposed approach is valuable and can be exploited by the system operator when very short running times are needed.
Similarly, computational experiments on a (rather standard) desktop computer showed its value when it comes to obtain high quality solutions of the SSCUC problem with limited computational resources (where the EF or even the cut-adding method without PHA are not implementable). Additionally, as a side result of the proposed solution strategy, it is possible to identify the most affected (overloaded) lines before contingencies, as well as the most critical contingencies in the system. This is possible thanks to the values of two indices calculated with the information of the cuts added during the execution of the PHA iterative process. These two indices provide valuable information for decision-making during short- to medium-term transmission system expansion studies.
Although the PHA technique is more stable than other step-wise decomposition algorithms such as Benders decomposition, it is advisable to test the performance of the security constraint addition method with this type of technique. This suggest the integration of PHA and a promising decomposition method for Stochastic Mixed-Integer Programming: (i.e., Fenchel decomposition based on PHA), which has not yet been reported on the analysis of stochastic models for the operation of electrical power systems. Likewise, to further reduce the running time of the proposed approach, parallel versions of the solution strategy could be tested.
Finally, the method proposed in the paper can be extended to take into account other sources of uncertainty such as photovoltaic generation and demand, as well as batteries to hedge against them. For this, new constraints must be taken into account, such as the charging and discharging of batteries during the time horizon and the expected generation of the photovoltaic plants, among others.