General Formula for SHE Problem Solution

Abstract

This paper considers cascaded H-bridges multilevel inverters with $2^n$ dc sources, n integer, $n>0$ and proposes a new general formula to compute those $2^n$ switching angles capable of eliminating $n+1$ harmonics and their respective multiples from the output voltage waveform. The proposed procedure uses only scalar products and avoids linear systems, therefore it has a low computational cost. Computed angles do not depend on modulation index, moreover, voltage sources vary linearly. A mathematical proof is given to validate the formula. Three-phase implementations eliminate or mitigate a significant amount of low order harmonics, thus resulting in very low total harmonic distortion. The proposed formula has been experimentally validated using a single-phase nine-level cascaded H-bridge inverter prototype, resulting in a Total Harmonic Distortion (THD) of 5.59%; the first not-mitigated harmonic is the 17th.

1. Introduction

Due to their low Total Harmonic Distortion (THD), low electromagnetic interference, and high efficiency, the use of multilevel inverters (MLI) is expanding in many applications [1,2,3]. Cascaded H-bridge (CHB) topology, in particular, is receiving more attention than neutral point clamped (NPC) and flying capacitor (FC) topologies because it offers modularity and better overall operations [4,5,6].

Operations at fundamental frequency greatly improve efficiency, therefore they are preferred at high power. The main approaches for selection of switching angles at a modulation of low frequency are: (i) THD minimization and (ii) Selective Harmonics Elimination (SHE) [7,8]. The first one can be achieved using either frequency or time domain algorithms. SHE consists in elimination of a number of harmonics imposing their magnitudes to zero, depending on degrees of freedom and consequently on applied switching frequency [9].

SHE Pulse Width Modulation (SHE-PWM) strategies have been introduced to improve dynamic performances in conventional SHE, thus resulting in the advantages of both techniques. In order to further improve THD, Selective Harmonic Mitigation Pulse Width Modulation (SHM-PWM) has been introduced, obtaining a high number of reduced harmonics capable of bounding harmonics content within grid standards allowing the connection of the power converter with the public grid [10].

The SHE and SHM problems are based on the solution of nonlinear transcendental equations or inequalities [11,12]. In this regard, stochastic optimization techniques have been presented in the literature, such as genetic algorithms (GA) [13], bee algorithms (BA) [14], cuckoo search algorithms (CSA) [15] and particle swarm optimization (PSO) [16,17,18].

In [19], a modified version of the fish swarm optimization algorithm has been examined for computing optimum switching angles required to control the switched-diode dual source single switch MLI. Suitability and superiority of the derived algorithm have been established by comparison with traditional SHE techniques. Analytical methods have been proposed for five level inverters in [20] and for multilevel inverters in [21], which are based on a novel pulse amplitude modulation (PAM) strategy. In [22], a method was introduced as a substitute for the Newton–Raphson method and similar iteration methods that can perform a real-time calculation of switching angles in seven level inverters.

In [23], CHB l-level inverters, $l=2s+1$, with $s=2^n$, n integer, $n>0$ have been considered and a linear system $2^n\times 2^n$ has been proposed to find switching angles. In this paper, the same topologies are considered and a simple mathematical formula consisting of s scalar products by two vectors returning s switching angles is proposed, which require lower computational cost than that obtained by the procedure in [23]. These angles allow to eliminate $n+1$ harmonics and their respective multiple from the output voltage waveform and do not depend on modulation index m. Typical applications of the proposed method are uninterruptible power supplies (UPS), high voltage dc (HVDC) and aircrafts.

Section 2 describes the mathematical formula for computation of the switching angles, the related procedure, its mathematical proof and computational cost. Section 3 presents simulation results and comparisons with the procedure in [21]. Section 4 reports and discusses experimental validation. Section 5 draws some conclusions and remarks.

2. Mathematical Formulation

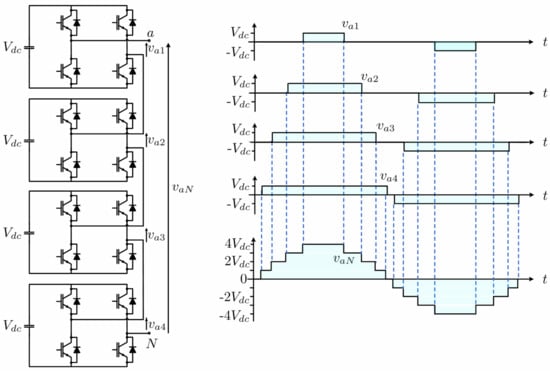
2.1. Mathematical Model

The proposed SHE strategy computes $s=2^n$ switching angles that eliminate $n+1$ harmonics and their multiple from the output voltage of an l-level CHB inverter with s dc sources, $n=1,2,3,\dots$ and $l=2s+1$. Each H-bridge is fed by a dc voltage source in which the amplitude is $V_1=V_2=\dots =V_s=V$ and, in per unit (p.u.): $V^{*}=\frac{V}{V_{dc}}$ being $V_{dc}$ the rated voltage. Figure 1 shows a three-phase CHB l-level inverter.

Considering the phase A output voltage $v_{AN}$, its Fourier decomposition is

$$v_{AN}\left(\omega t\right)=\sum _{k=1,3,5,...}^{\infty }{H}_{k}sin\left(k\omega t\right)$$

(1)

where $H_k=\frac{4}{\pi k}\left({\sum }_{i=1}^s{V}^{*}cos\left(k{\alpha }_i\right)\right)$ is the kth harmonic. The following SHE system is considered

$$cos\left(k{\alpha }_1\right)+cos\left(k{\alpha }_2\right)+\cdots +cos\left(k{\alpha }_s\right)=0,k=r_1,r_2,\dots ,r_{n+1}$$

(2)

where $r_i,i=1,2,\dots ,n+1$ are the $n+1$ harmonics to delete, which can be arbitrarily chosen; for single-phase configurations $r_1=3,$ $r_2=5$ and so on; instead, for three-phase configurations, the third and multiple are automatically zero and $r_1=5,$$r_2=7$ and so on.

The switching angles ${\alpha }_1$$,\dots ,{\alpha }_s$ are the unknowns of the problem that have to satisfy the following conditions

$$\begin{array}{cc}0<{\alpha }_k<\frac{\pi }{2},k=1,2,3,\dots ,& s\end{array}$$

(3)

$V^{*}$ is assumed linearly depending on modulation index $m=\frac{\pi H_1}{4·s}$, where $H_1$ is the fundamental harmonic amplitude of output voltage

$$V^{*}=Cm$$

(4)

with C positive coefficient, computed as

$$C=\genfrac{}{}{.05ex}{}{s}{cos\left({\alpha }_1\right)+cos\left({\alpha }_2\right)+...cos\left({\alpha }_s\right)}$$

(5)

In the next subparagraph, a theorem will be introduced to obtain Formula (7), equivalent to Formula (10), which returns the switching angles that do not depend on the modulation index. Due to this, both the amplitude of the fundamental harmonic and the dc voltage source linearly depend on m. Given a value to m, the following quantities are calculated, in this order: (1) switching angles, (2) parameter C, (3) dc voltage source $V^{*}=Cm$, (4) $H_1=\frac{4sm}{\pi }=\frac{4s{V}^{*}}{\pi C}$. Figure 2 and Figure 3 show the behaviors of switching angles, dc voltage source and fundamental harmonic, as a function of m, for single-phase five-level and three-phase nine-level configurations, respectively.

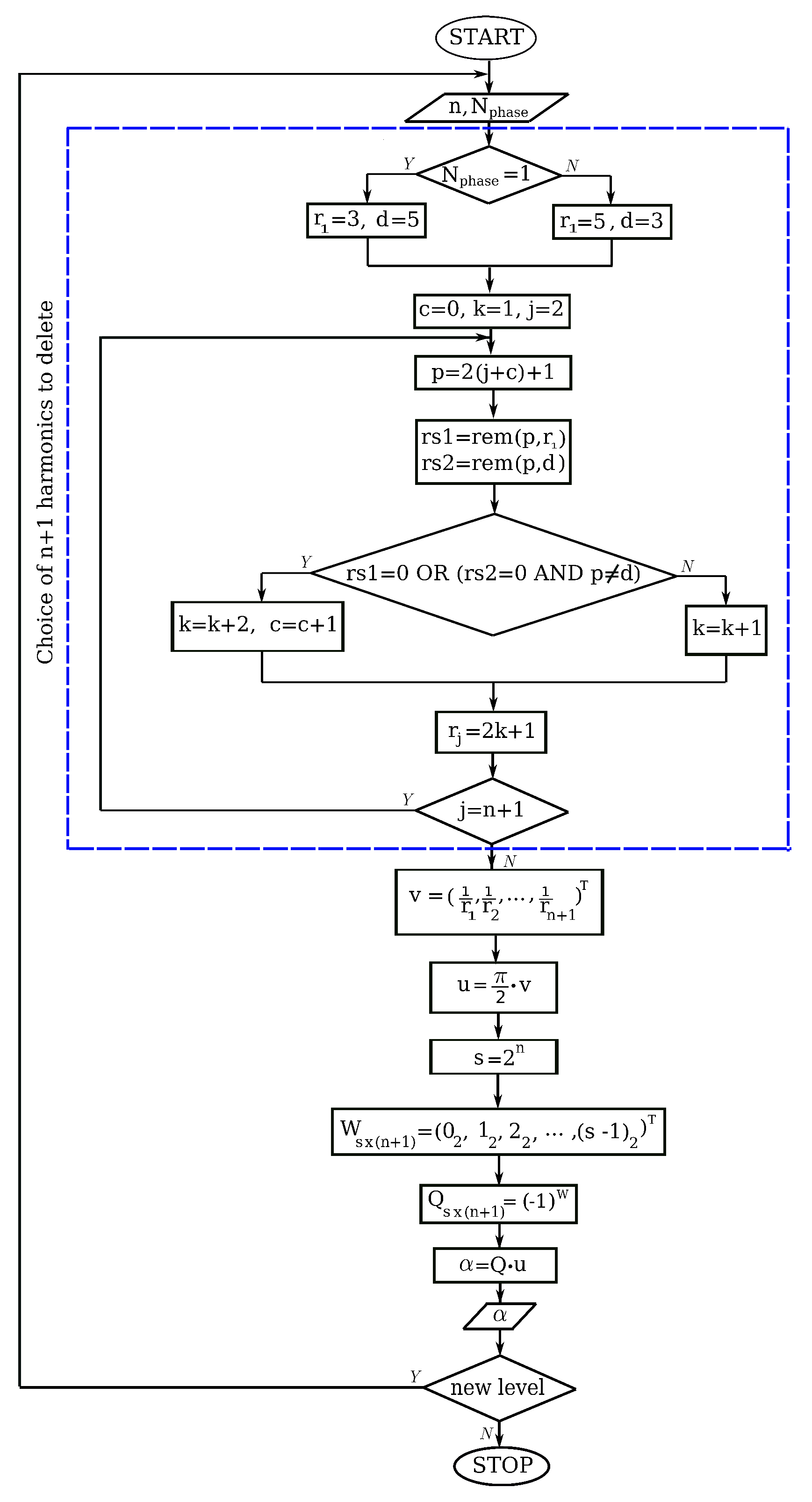
2.2. Fast Algorithm to Obtain the General Formula

The proposed algorithm computes $s=2^n$, $n>0$ switching angles through s scalar products between vectors of size $n+1$. To achieve the goal, the following theorem is introduced.

Theorem 1.

Let $s=2^n$ with n integer, $n>0$; the system

$$cos\left(k{\alpha }_1\right)+cos\left(k{\alpha }_2\right)+\cdots +cos\left(k{\alpha }_s\right)=0,k=r_1,r_2,\dots ,r_{n+1}$$

(6)

is considered in the unknowns${\alpha }_i$, $i=1,\dots ,s$ with $r_j$ odd integer number, $j=1,\dots ,n+1$, $r_j\ge 3$.

Then a solution of (6) is

$$\alpha =\frac{\pi }{2}{\left(\sum _{j=1}^{n+1}{\left(-1\right)}^{w_{1j}}\frac{1}{r_j},\sum _{j=1}^{n+1}{\left(-1\right)}^{w_{2j}}\frac{1}{r_j},\cdots ,\sum _{j=1}^{n+1}{\left(-1\right)}^{w_{sj}}\frac{1}{r_j}\right)}^T$$

(7)

where$w_{ij},i=1,\dots ,s,j=1,\dots ,n+1$are the elements of the matrix$W_{s\times \left(n+1\right)}$in which theith row represents the integer number$i-1$in a binary base with$n+1$digits.

This solution satisfies also

$$cos\left(k{\alpha }_1\right)+cos\left(k{\alpha }_2\right)+\cdots +cos\left(k{\alpha }_s\right)=0,k=q{r}_1,q{r}_2,\dots ,q{r}_{n+1},q>1,\mathrm{odd}\mathrm{number}$$

(8)

Proof. 

In [23], the system (6) has been transformed in the following $s\times s$ linear system in the unknown $\alpha ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s\right)}^T$ that satisfies (6) and (8)

$$A\alpha =b$$

(9)

For instance, if $n=4$, the system matrix $A_{16\times 16}$ was

$$A_{2^4\times 2^4}=\left(\begin{array}{cccccccc}{S}_1& O& O& O& O& O& O& O\\ O& S_1& O& O& O& O& O& O\\ O& O& S_1& O& O& O& O& O\\ O& O& O& S_1& O& O& O& O\\ O& O& O& O& S_1& O& O& O\\ O& O& O& O& O& S_1& O& O\\ O& O& O& O& O& O& S_1& O\\ O& O& O& O& O& O& O& S_1\\ S_2& S_2& O& O& O& O& O& O\\ O& O& S_2& S_2& O& O& O& O\\ O& O& O& O& S_2& S_2& O& O\\ O& O& O& O& O& O& S_2& S_2\\ S_2& -S_2& S_2& -S_2& O& O& O& O\\ O& O& O& O& S_2& -S_2& S_2& -S_2\\ S_2& -S_2& -S_2& S_2& S_2& -S_2& -S_2& S_2\\ S_2& -S_2& -S_2& S_2& -S_2& S_2& S_2& -S_2\end{array}\right)$$

where $S_1=[$1 1], $S_2=[$1 −1], $O=[$0 0]. The vector b in (9) was

$$b_{2^4\times 1}={\left(\underset{2^{4-1}}{\underbrace{\frac{\pi }{r_1},\cdots ,\frac{\pi }{r_1}}}\underset{2^{4-2}}{\underbrace{,\frac{2\pi }{r_2},\cdots ,\frac{2\pi }{r_2}}},\underset{2^{4-3}}{\underbrace{\frac{2^2\pi }{r_3},\cdots ,\frac{2^2\pi }{r_3}},}\underset{2^0}{\underbrace{\frac{2^{4-1}\pi }{r_4}}},\underset{2^0}{\underbrace{\frac{2^{4-1}\pi }{r_{4+1}}}}\right)}^T$$

The switching angles in [23] have been obtained by solving (9)) through LU factorization of A. For this proof, introducing the matrix $G_{2^n\times 2^n}$ that, for the considered example ($n=4$), is defined as

$$G_{2^4\times 2^4}=\left(\begin{array}{cccccccc}\frac{1}{2}{S}_1& O& O& O& O& O& O& O\\ O& \frac{1}{2}{S}_1& O& O& O& O& O& O\\ O& O& \frac{1}{2}{S}_1& O& O& O& O& O\\ O& O& O& \frac{1}{2}{S}_1& O& O& O& O\\ O& O& O& O& \frac{1}{2}{S}_1& O& O& O\\ O& O& O& O& O& \frac{1}{2}{S}_1& O& O\\ O& O& O& O& O& O& \frac{1}{2}{S}_1& O\\ O& O& O& O& O& O& O& \frac{1}{2}{S}_1\\ \frac{1}{2^2}{S}_2& \frac{1}{2^2}{S}_2& O& O& O& O& O& O\\ O& O& \frac{1}{2^2}{S}_2& \frac{1}{2^2}{S}_2& O& O& O& O\\ O& O& O& O& \frac{1}{2^2}{S}_2& \frac{1}{2^2}{S}_2& O& O\\ O& O& O& O& O& O& \frac{1}{2^2}{S}_2& \frac{1}{2^2}{S}_2\\ \frac{1}{2^3}{S}_2& -\frac{1}{2^3}{S}_2& \frac{1}{2^3}{S}_2& -\frac{1}{2^3}{S}_2& O& O& O& O\\ O& O& O& O& \frac{1}{2^3}{S}_2& -\frac{1}{2^3}{S}_2& \frac{1}{2^3}{S}_2& -\frac{1}{2^3}{S}_2\\ \frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& \frac{1}{2^4}{S}_2& \frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& \frac{1}{2^4}{S}_2\\ \frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& \frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2& \frac{1}{2^4}{S}_2& \frac{1}{2^4}{S}_2& -\frac{1}{2^4}{S}_2\end{array}\right)$$

It is easy to verify that $G^{T}A=I$, where I is the identity matrix; therefore $G^T=A^{-1}$ and the solution $\alpha =G_{s\times s}^T{b}_{s\times 1}$ presents a very easy systematic frame equal to the scalar product $Q_{s\times \left(n+1\right)}{u}_{\left(n+1\right)\times 1}$

$$\alpha =Q_{s\times \left(n+1\right)}{u}_{\left(n+1\right)\times 1}$$

(10)

where the vector $u=\frac{\pi }{2}{\left(\frac{1}{r_1},\frac{1}{r_2},\cdots ,\frac{1}{r_{n+1}}\right)}^T$ and the matrix Q is

$$Q={\left(-1\right)}^W=\left(\begin{array}{cccc}{\left(-1\right)}^{w_{11}}& {\left(-1\right)}^{w_{12}}& \cdots & {\left(-1\right)}^{w_{1,n+1}}\\ {\left(-1\right)}^{w_{21}}& {\left(-1\right)}^{w_{22}}& \cdots & {\left(-1\right)}^{w_{2,n+1}}\\ ⋮& ⋮& \cdots & ⋮\\ ⋮& ⋮& \cdots & ⋮\\ ⋮& ⋮& \cdots & ⋮\\ {\left(-1\right)}^{w_{s1}}& {\left(-1\right)}^{w_{s2}}& \cdots & {\left(-1\right)}^{w_{s,n+1}}\end{array}\right).$$

The exponents $w_{ij},i=1,\dots ,s,j=1,\dots ,n+1$ are the elements of the matrix $W_{s\times \left(n+1\right)}$ in which the ith row represents the integer number $i-1$ in the binary base with $n+1$ digits. Therefore, the solution of (6) and (8) is

$$\alpha =\frac{\pi }{2}{\left(\sum _{j=1}^{n+1}{\left(-1\right)}^{w_{1j}}\frac{1}{r_j},\sum _{j=1}^{n+1}{\left(-1\right)}^{w_{2j}}\frac{1}{r_j},\cdots ,\sum _{j=1}^{n+1}{\left(-1\right)}^{w_{sj}}\frac{1}{r_j}\right)}^T$$

□

The flow chart of the proposed strategy is shown in Figure 4.

The first part of the flow chart, bounded by a dashed line, represents the preliminary algorithm that, based on single or three-phase system, chooses the first $n+1$ harmonics to be deleted. In particular, given the number of phases $N_{phase}$, the algorithm considers the order of the first harmonic to be deleted, equal to $r_1=3$ if $N_{phase}=1$ or $r_1=5$ if $N_{phase}\ne 1$ (three-phase) and for successive harmonics it jumps the multiple of 3 and 5, because they will be eliminated by the proposed method (see (8)). The harmonics multiple of 7, 11 and greater have not been considered because they referred to very high level inverters; in fact, for example, the odd multiples of 7 are 21, 35, 49 and so on, but as 21 is multiple of 3 and 35 is multiple of 5, they have already been skipped, and 49 is the first multiple after $r_1=3,r_2=5,r_3=7,r_4=11,r_5=13,r_6=17,r_7=19,r_8=23,r_9=29,r_{10}=31,r_{11}=37,r_{12}=41,r_{13}=43,r_{14}=47$ that is related to $l=2·2^{14}+1$ for single-phase configuration and $l=2·2^{13}+1$ for three-phase configuration.

In the flow chart, the function $rem$ is used to detect the order of multiple harmonics; in fact $rem(x,y)$ returns the division rest between x and y. Of course if $rem(x,y)=0$ then x is multiple of y. The generic row of matrix W, denoted with $nu{m}_2$, represents the number $num$ in binary base with $n+1$ digits. The generic element of the matrix ${\left(-1\right)}^W$ is ${\left(-1\right)}^{w_{ij}}$, $i=1,2,\dots ,2^n$, $j=1,2,\dots ,n+1$.

2.3. Computational Complexity

The procedure in [23] solves the $2^n\times 2^n$ system (9)) by LU factorization and by solution of two triangular systems, therefore it has computational complexity $T_{sys}$

$$T_{sys}=O\left(\frac{2^{3n}}{3}\right)+O\left(2^{2n}\right)$$

(11)

that becomes very high when n grows.

Thee proposed procedure multiplies a matrix of elements $\pm 1$ of size $2^n\times \left(n+1\right)$ by a vector of length $n+1$, therefore it has computational complexity $T_{sc}$

$$T_{sc}=O\left(n{2}^n\right)$$

(12)

that is very low with respect to (11).

3. Results

Simulation results have been obtained considering both single and three-phase l-level CHB inverters with $l=5,9,17,33$ connected to an RL load, characterized by $R=48.80\Omega$ and $L=0.94$ mH with $V^{*}=1$ per unit (p. u.) and switching frequency equal to 50 Hz. Total harmonic distortion, defined by the following formula, is computed to estimate the quality of output voltage waveforms.

$$\mathrm{THD}=\frac{\sqrt{{\sum }_{k=3,5\dots }^{301}{H}_k^2}}{H_1}$$

(13)

For grid connection applications, the CIGRE WG 36–05 and the EN 50160 grid codes [24,25] impose, for each harmonic amplitude $H_n$, the admissible levels $l_n\%=H_n/H_1\%$. These harmonic levels, given in percentage to the fundamental, are shown in

Table 1. Grid codes EN 50160 and CIGRE WG 36-05.

	Odd	Harmonics		Even	Harmonics
Not multiple	of 3	Multiple	of 3
n	$l_n$ (%)	n	$l_n$ (%)	n	$l_n$ (%)
5	6	3	5	2	2
7	5	9	1.5	4	1
11	3.5	15	0.5	6....10	0.5
13	3	21	0.5	>10	0.2
17	2	>21	0.2
19	1.5
23	1.5
25	1.5
>25	0.2+32.5/n

.

In the following, the matrices W, Q, the vector u and the solution $\alpha$ are given for the considered configurations.

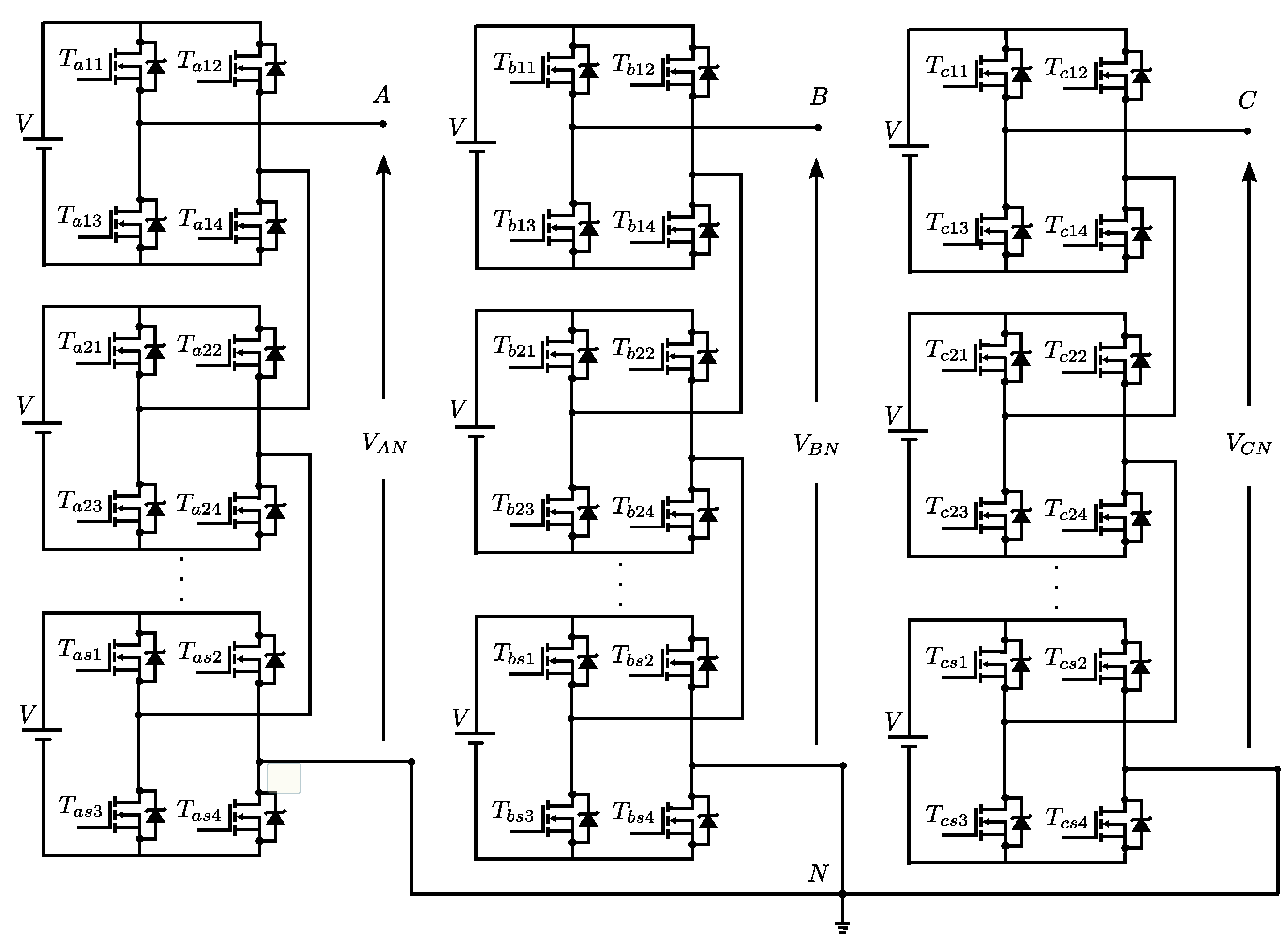
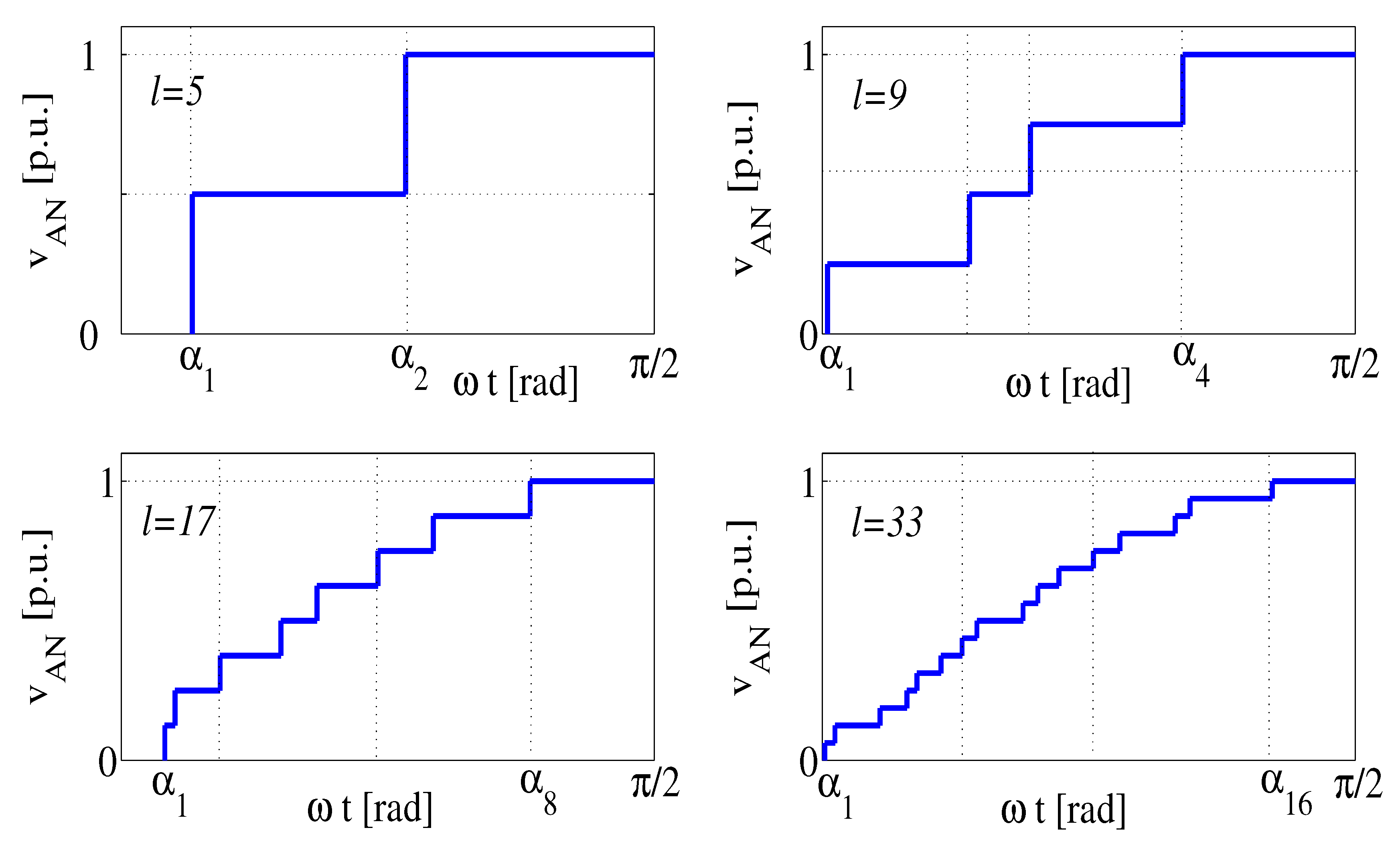
3.1. CHB 5-Level Inverter ($n=1$)

$W_{2\times 2}=\left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right)$, $Q_{2\times 2}=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$, Single-phase ($r_1=3$, $r_2=5$): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}\\ \frac{1}{5}\end{array}\right)$ and $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}+\frac{1}{5}\\ \frac{1}{3}-\frac{1}{5}\end{array}\right)$, Three-phase ($r_1=5$, $r_2=7$): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}\\ \frac{1}{7}\end{array}\right)$ and $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}+\frac{1}{7}\\ \frac{1}{5}-\frac{1}{7}\end{array}\right)$.

Figure 5 shows the harmonic analysis that is the harmonics amplitude $H_n$ with respect to the fundamental $H_1$, for single-phase and three-phase configurations. It is possible to observe that the first not eliminated harmonic is the 7th for single-phase configuration and the 11th for the three-phase one.

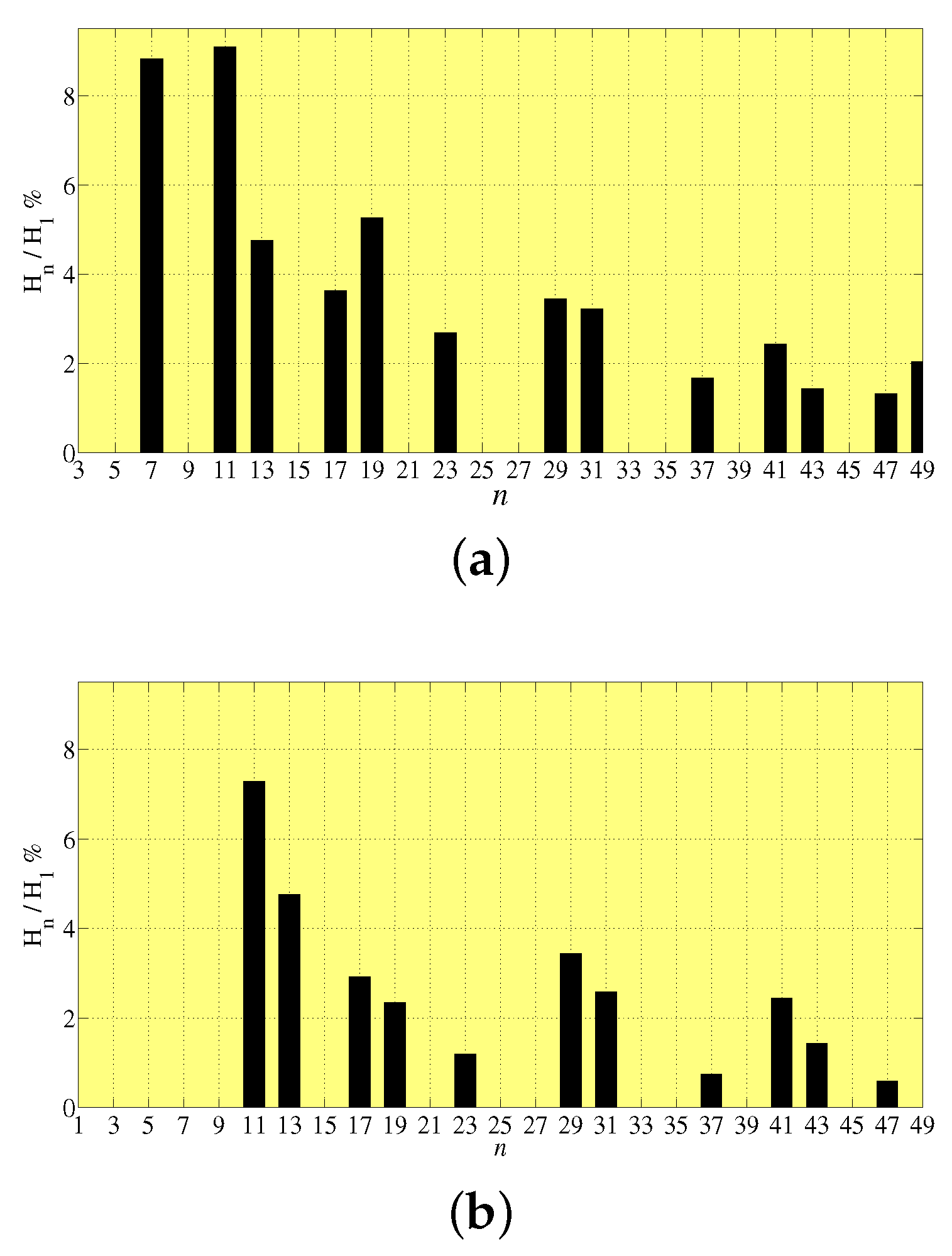
3.2. CHB 9-Level Inverter ($n=2$)

$W_{4\times 3}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 1& 0\\ 0& 1& 1\end{array}\right)$, $Q_{4\times 3}=\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& -1\\ 1& -1& 1\\ 1& -1& -1\end{array}\right)$, Single-phase ($r_1=3$, $r_2=5$, $r_3=7$): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}\\ \frac{1}{5}\\ \frac{1}{7}\end{array}\right)$ and $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}+\frac{1}{5}+\frac{1}{7}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}\end{array}\right)$, Three-phase ($r_1=5$, $r_2=7$, $r_3=11$): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}\\ \frac{1}{7}\\ \frac{1}{11}\end{array}\right)$ and $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}+\frac{1}{7}+\frac{1}{11}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}\end{array}\right)$.

The harmonic spectrum of single-phase nine-level inverter is not shown because, from the computed results, it is observed that it coincides with that of three-phase five-level configuration in Figure 5b. Figure 6 shows the harmonic analysis of the three-phase configuration, highlighting that the first five harmonics are eliminated, the 13th is mitigated according to code requirements (see Table 1) and the 15th is deleted [24,25].

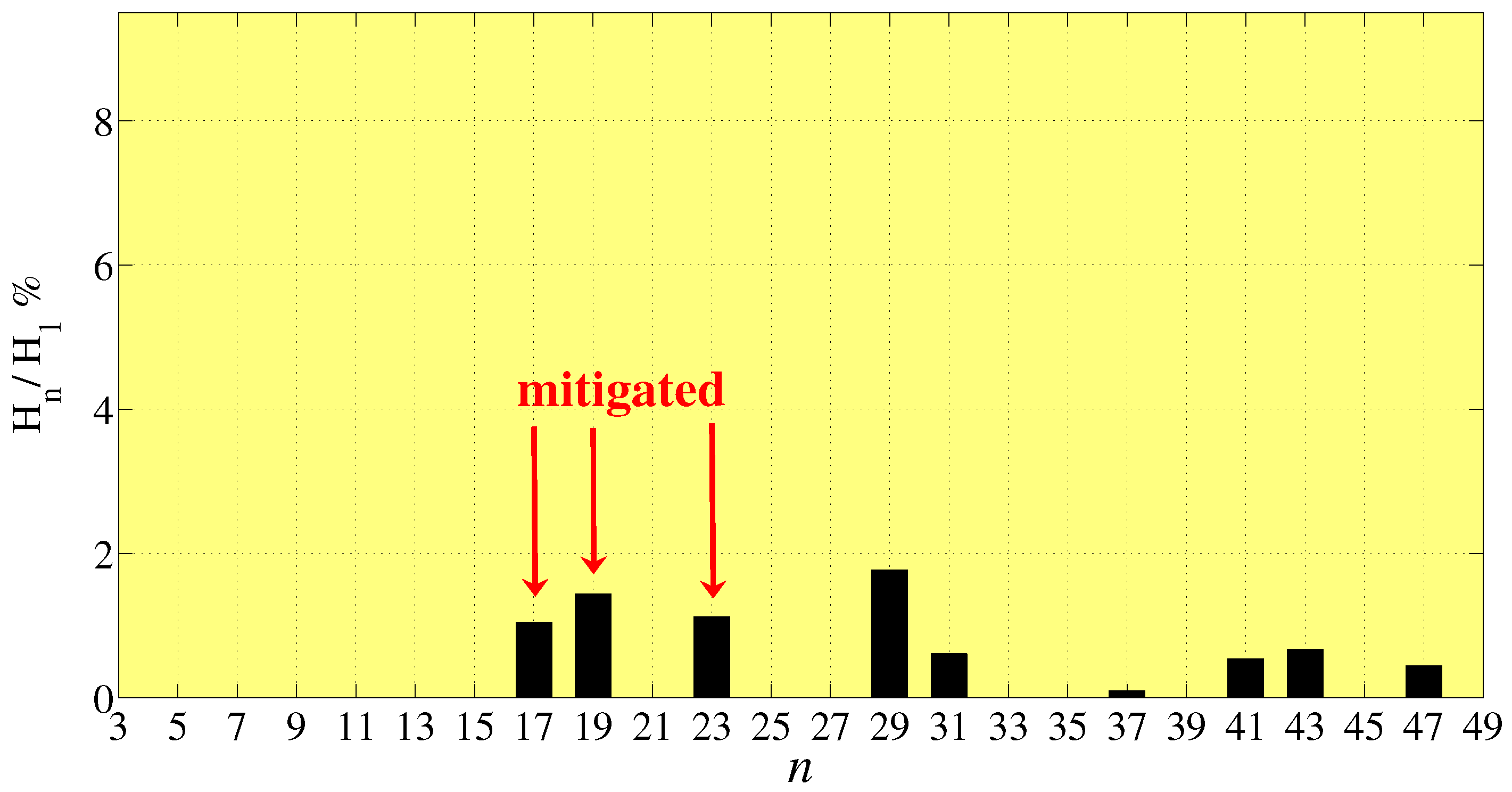
3.3. CHB 17-Level Inverter ($n=3$)

$W_{8\times 4}=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 0& 1& 1\\ 0& 1& 0& 0\\ 0& 1& 0& 1\\ 0& 1& 1& 0\\ 0& 1& 1& 1\end{array}\right)$, $Q_{8\times 4}=\left(\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& 1& -1\\ 1& 1& -1& 1\\ 1& 1& -1& -1\\ 1& -1& 1& 1\\ 1& -1& 1& -1\\ 1& -1& -1& 1\\ 1& -1& -1& -1\end{array}\right)$, Single-phase ($r_1=3$, $r_2=5$, $r_3=7$, $r_4=11$ ): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}\\ \frac{1}{5}\\ \frac{1}{7}\\ \frac{1}{11}\end{array}\right)$, $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}\\ \frac{1}{3}+\frac{1}{5}+\frac{1}{7}-\frac{1}{11}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}-\frac{1}{11}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}+\frac{1}{11}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}+\frac{1}{11}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}-\frac{1}{11}\end{array}\right)$, Three-phase ($r_1=5$, $r_2=7$, $r_3=11$, $r_4=13$ ): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}\\ \frac{1}{7}\\ \frac{1}{11}\\ \frac{1}{13}\end{array}\right)$, $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}\\ \frac{1}{5}+\frac{1}{7}+\frac{1}{11}-\frac{1}{13}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}-\frac{1}{13}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}+\frac{1}{13}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}-\frac{1}{13}\end{array}\right)$.

The obtained results show that the harmonic spectrum of a single-phase 17-level inverter is the same of the three-phase nine-level configuration in Figure 6, and for this reason, this graph is not shown here. Figure 7 shows the harmonic analysis for three phase configuration; the first not mitigated harmonic is the 29th, the previous ones are zero except the 17th, 19th and 23rd, which are mitigated [24,25].

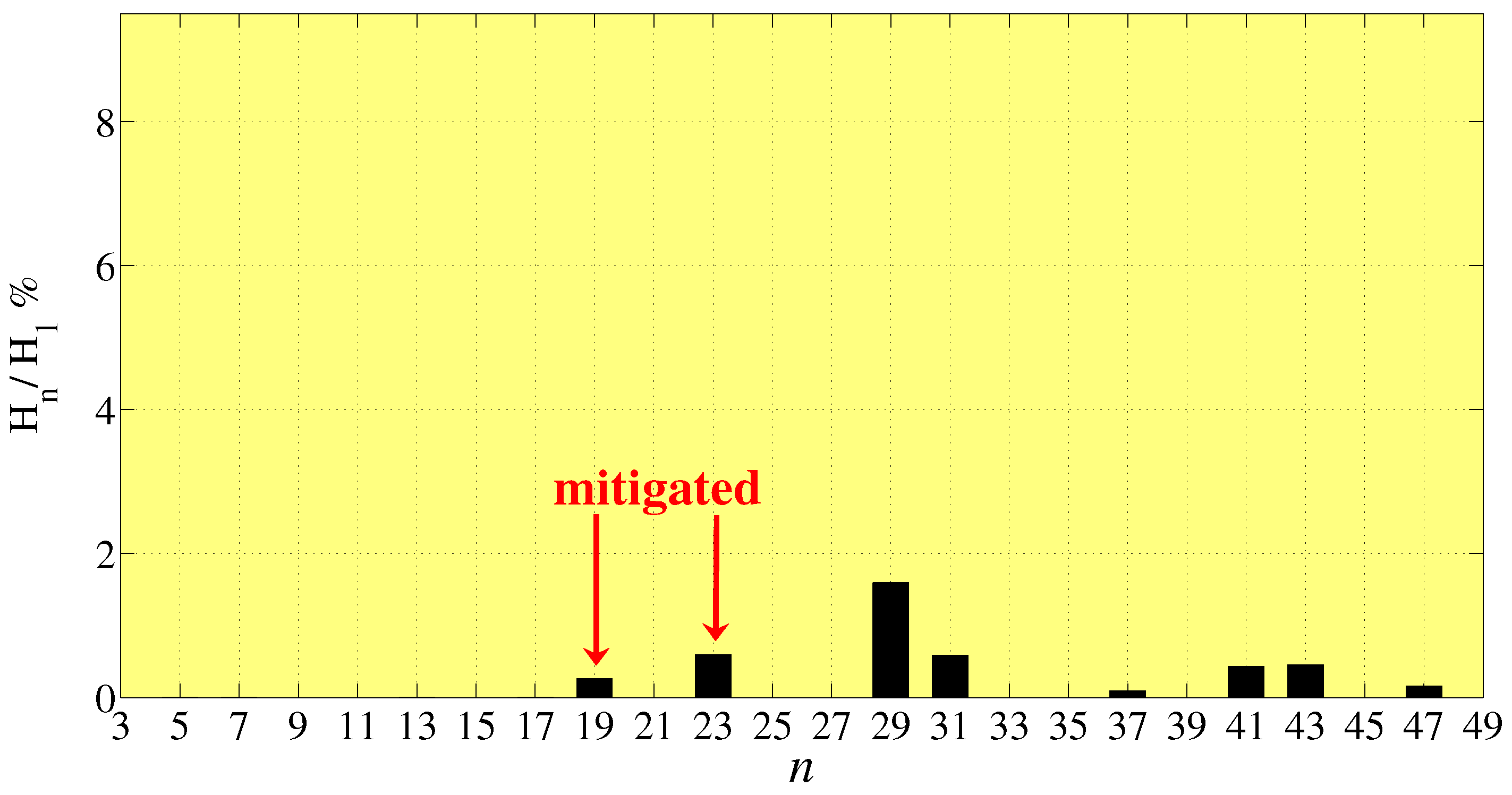
3.4. CHB 33-Level Inverter ($n=4$)

$W_{16\times 5}=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 1\\ 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 1\\ 0& 0& 1& 1& 0\\ 0& 0& 1& 1& 1\\ 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 1\\ 0& 1& 0& 1& 0\\ 0& 1& 0& 1& 1\\ 0& 1& 1& 0& 0\\ 0& 1& 1& 0& 1\\ 0& 1& 1& 1& 0\\ 0& 1& 1& 1& 1\end{array}\right)$, $Q_{16\times 5}=\left(\begin{array}{ccccc}1& 1& 1& 1& 1\\ 1& 1& 1& 1& -1\\ 1& 1& 1& -1& 1\\ 1& 1& 1& -1& -1\\ 1& 1& -1& 1& 1\\ 1& 1& -1& 1& -1\\ 1& 1& -1& -1& 1\\ 1& 1& -1& -1& -1\\ 1& -1& 1& 1& 1\\ 1& -1& 1& 1& -1\\ 1& -1& 1& -1& 1\\ 1& -1& 1& -1& -1\\ 1& -1& -1& 1& 1\\ 1& -1& -1& 1& -1\\ 1& -1& -1& -1& 1\\ 1& -1& -1& -1& -1\end{array}\right)$, Single-phase ($r_1=3$, $r_2=5$, $r_3=7$, $r_4=11$, $r_4=13$): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}\\ \frac{1}{5}\\ \frac{1}{7}\\ \frac{1}{11}\\ \frac{1}{13}\end{array}\right)$ and $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}+\frac{1}{7}-\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}+\frac{1}{5}-\frac{1}{7}-\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}+\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}+\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\\ \frac{1}{3}-\frac{1}{5}-\frac{1}{7}-\frac{1}{11}-\frac{1}{13}\end{array}\right)$, Three-phase ($r_1=5$, $r_2=7$, $r_3=11$, $r_4=13$, $r_4=17$ ): $u=\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}\\ \frac{1}{7}\\ \frac{1}{11}\\ \frac{1}{13}\\ \frac{1}{17}\end{array}\right)$ and $\alpha =\frac{\pi }{2}\left(\begin{array}{c}\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}+\frac{1}{11}-\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}+\frac{1}{11}-\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}-\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}+\frac{1}{7}-\frac{1}{11}-\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}+\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}+\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}+\frac{1}{13}-\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}-\frac{1}{13}+\frac{1}{17}\\ \frac{1}{5}-\frac{1}{7}-\frac{1}{11}-\frac{1}{13}-\frac{1}{17}\end{array}\right).$

Also in this case, it is observed that the harmonic spectrum of a single-phase 33-level inverter is the same as a three-phase 17-level inverter in Figure 7. Figure 8 shows the harmonic analysis that highlights that in three-phase configuration, the first not-mitigated harmonic is the 29th, the previous are eliminated except the 19th and 23rd, which are mitigated [24,25].

Table 2. Parameter C and THD%.

Level l	Parameter C	THD%	THD% [21]	THD%	THD% [21]
		Single-Phase	Single-Phase	Three-Phase	Three-Phase
5	1.214	17.30	18.14	11.53	12.80
9	1.245	11.53	9.92	5.59	9.92
17	1.258	5.59	5.15	3.47	3.74
33	1.267	3.47	2.56	2.34	2.56

shows the parameter C values and the obtained THD%. In the same table, the THD% values achieved by the pulse active width modulation in [21] are indicated. It can be observed that for three-phase configurations the proposed technique returns lower THD than the procedure in [21], this is more evident for nine-level inverters. As observed before, the same harmonic spectrum and THD% are obtained for three-phase configuration of level $2\times 2^n+1$ and single-phase configuration of level $2·2^{n+1}+1$.

Figure 9 shows the output voltages, in p.u., for 5-level, 9-level, 17-level and 33-level inverters, highlighting, for the last case, the very good quality of the waveform.

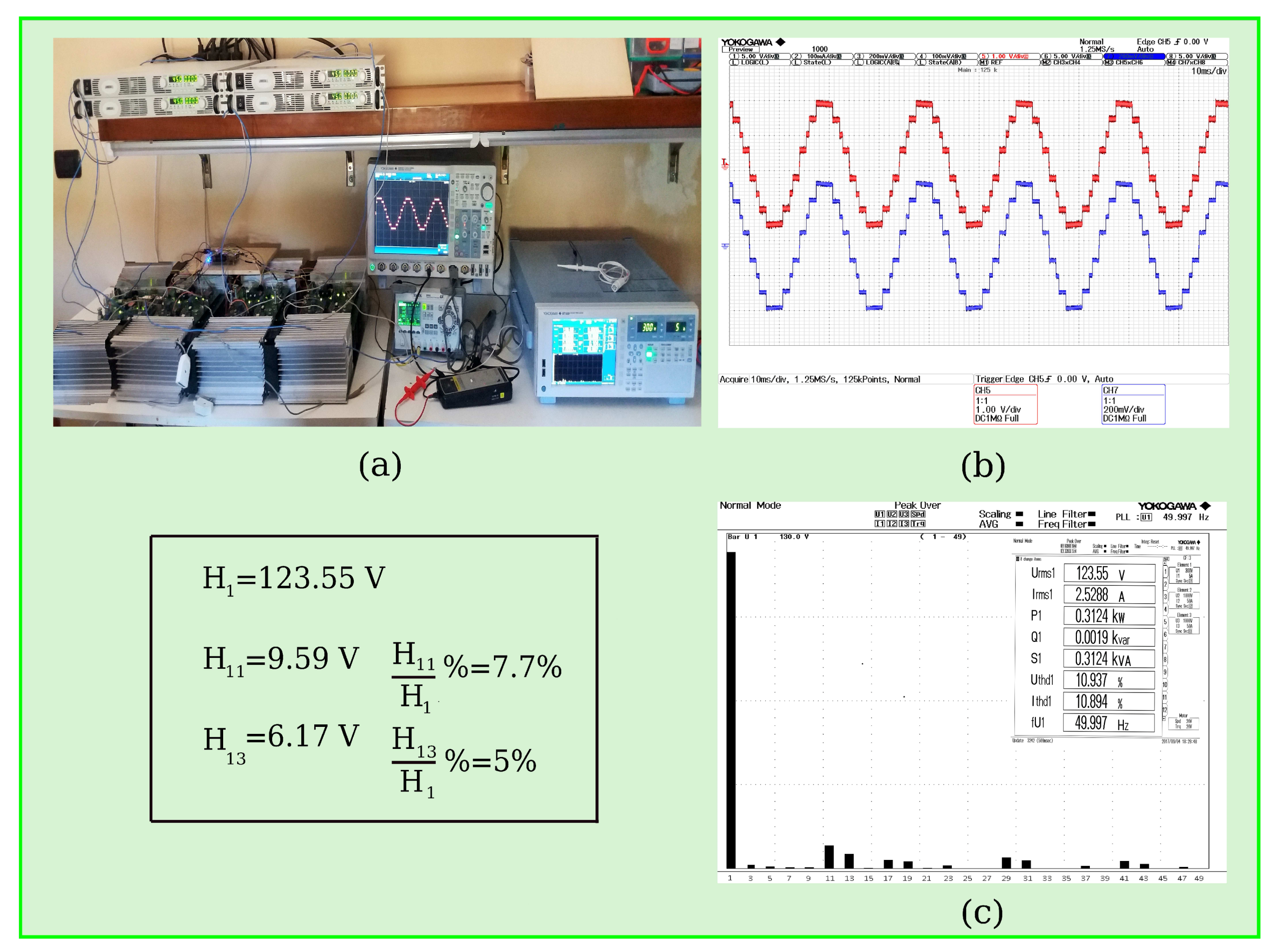
4. Experimental Results

In order to validate the proposed procedure, an experimental prototype of a single-phase CHB nine-level inverter is built. It is shown in Figure 10a. The voltage dc source is equal to 45 V and the connected load has $R=48.80\Omega$ and $L=0.94mH$. Figure 10b shows the output voltage and current waveforms and Figure 10c the harmonic analysis of the output voltage [26,27]. Considering until the 49th harmonic, the THD%, measured is equal to $10.94\%$, which is very close to the corresponding computed value that is $10.89\%$.

5. Conclusions and Remarks

In this paper, a new general formula, valid for cascaded multilevel inverters having s dc sources and a number of levels $l=2s+1$ with $s=2^n$$n=1,2,3,...$, has been proposed to compute s switching angles that eliminate $n+1$ harmonics and their respective multiple from output voltage waveform. The formula has been demonstrated by a mathematical proof. Some examples have been discussed. Very low THD% have been obtained; for the thirty-three level topology, the obtained THD%$=3.47\%$ for single-phase configuration and $2.34\%$ for the three-phase one. A very efficient configuration is the nine-level three-phase CHB inverter that has returned THD%$=5.59\%$ lower than the value obtained by applying the procedure in [21], which is $9.92\%$. In order to validate the proposed procedure, a prototype of a nine-level inverter has been built and experimental results have been carried out in terms of a harmonic spectrum and THD%. Experimental analysis has shown the accuracy of the proposed procedure.

The features of the proposed procedure can be summarized as follows:

• The formulation is very easy, in fact the switching angles vector is obtained through a very simple rule as highlighted by the examples; directly, these rules could allow obtaining the manual solution without any computation;
• The computational cost of the procedure is low;
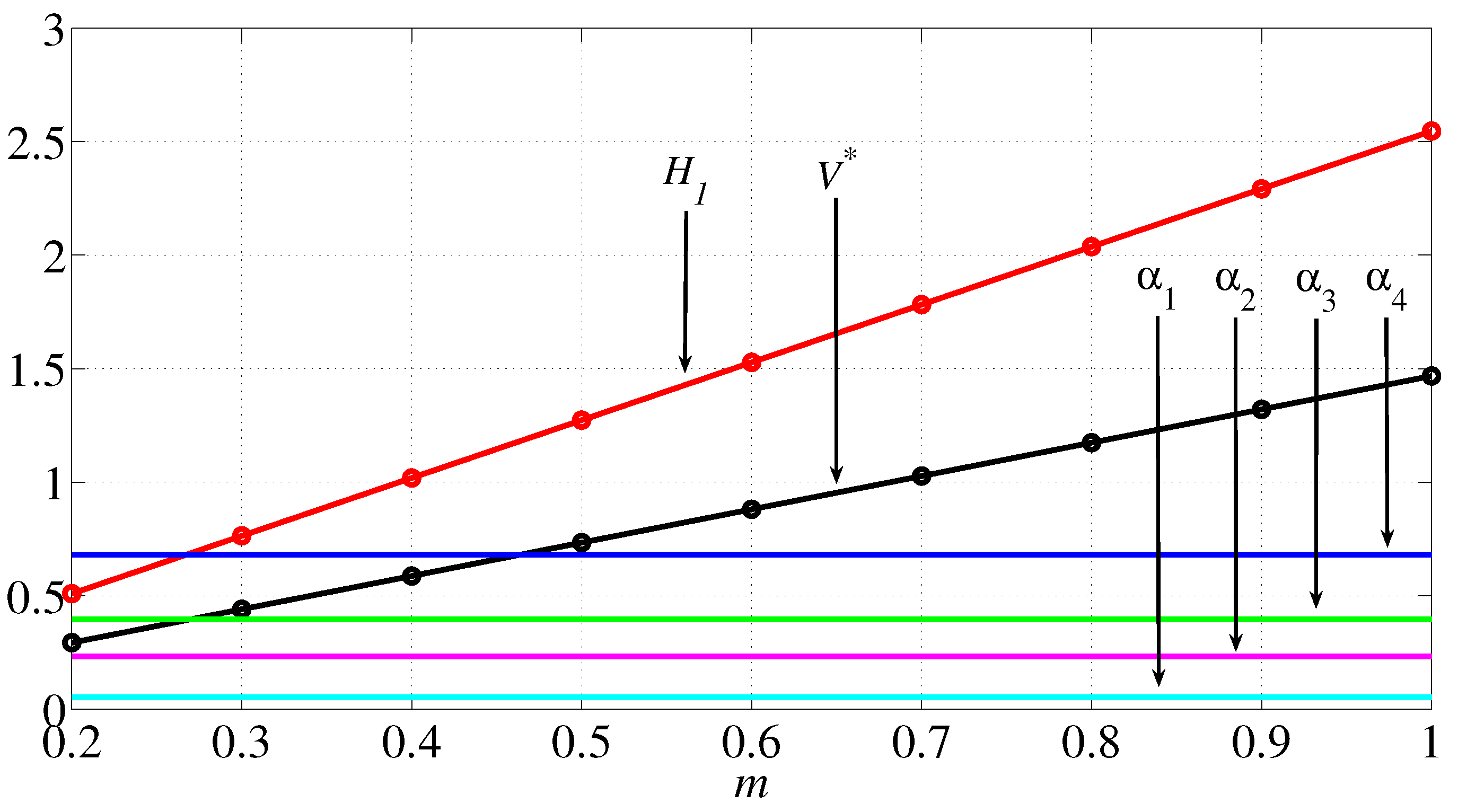
• For three-phase configurations and in particular for a nine-level inverter, a great number of low order harmonics are eliminated and/or mitigated, returning a very low THD. The first not mitigated harmonic is the 17th, allowing a light and cheap filter;
• Three-phase configuration of level $2·2^n+1$ presents the same harmonic spectrum of a single-phase configuration of level $2·2^{n+1}+1$;
• Switching angles and THD do not depend on the modulation index.