Metamodeling for Uncertainty Quantification of a Flood Wave Model for Concrete Dam Breaks
Abstract
1. Introduction
2. Methodology
2.1. Uncertainty Quantification Framework
2.2. Step A. Computational Model
2.3. Step B. Quantification of Sources of Uncertainties
2.3.1. Identification of The Sources of Uncertainties
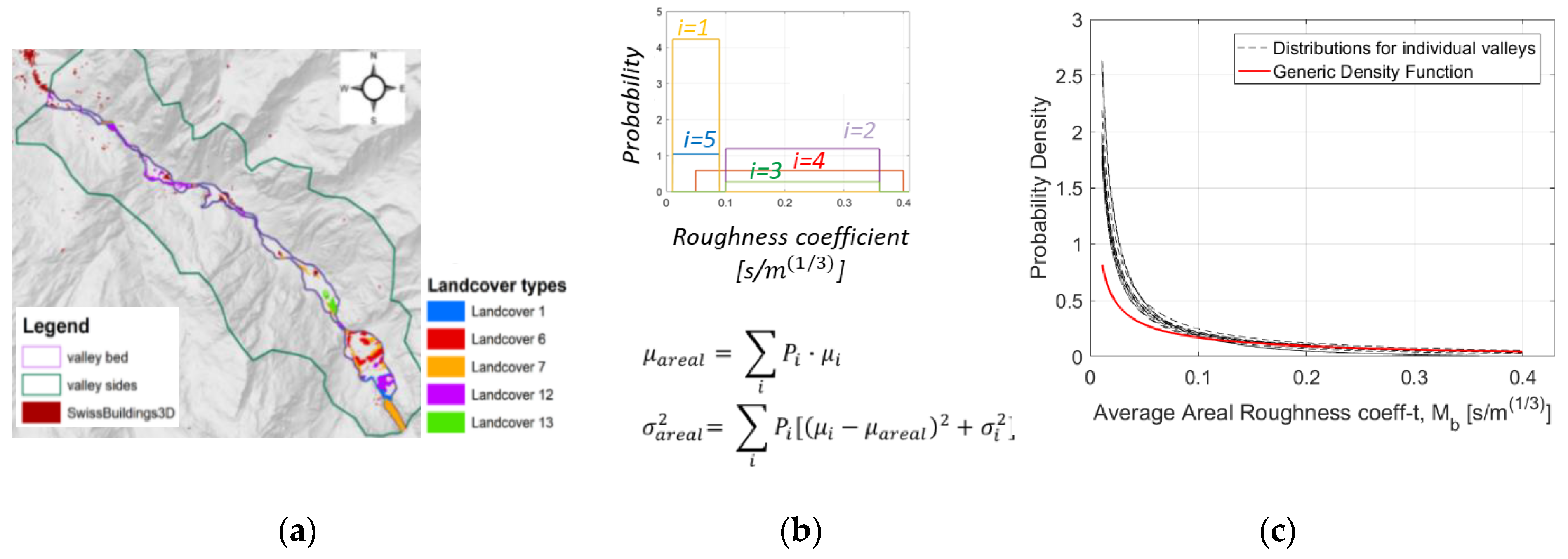
2.3.2. Modeling the Sources of Uncertainties
2.4. Step C. Uncertainty Propagation
2.5. Step D. Global Sensitivity Analysis
3. Results and Discussion
3.1. Step A: Computational Model
3.1.1. Required Model Input
3.1.2. Required Model Response
3.2. Step B. Modeling the Sources of Uncertainties
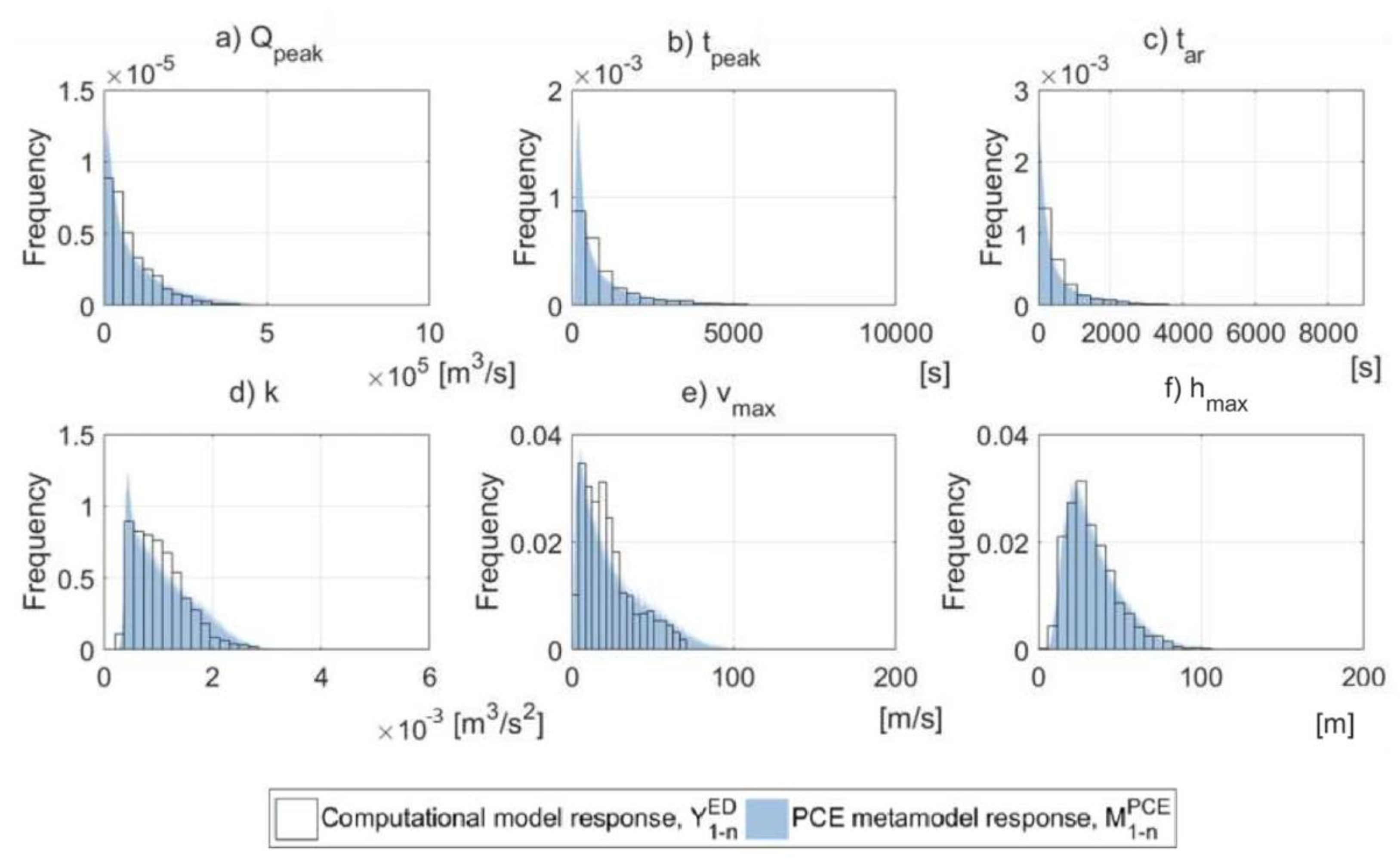
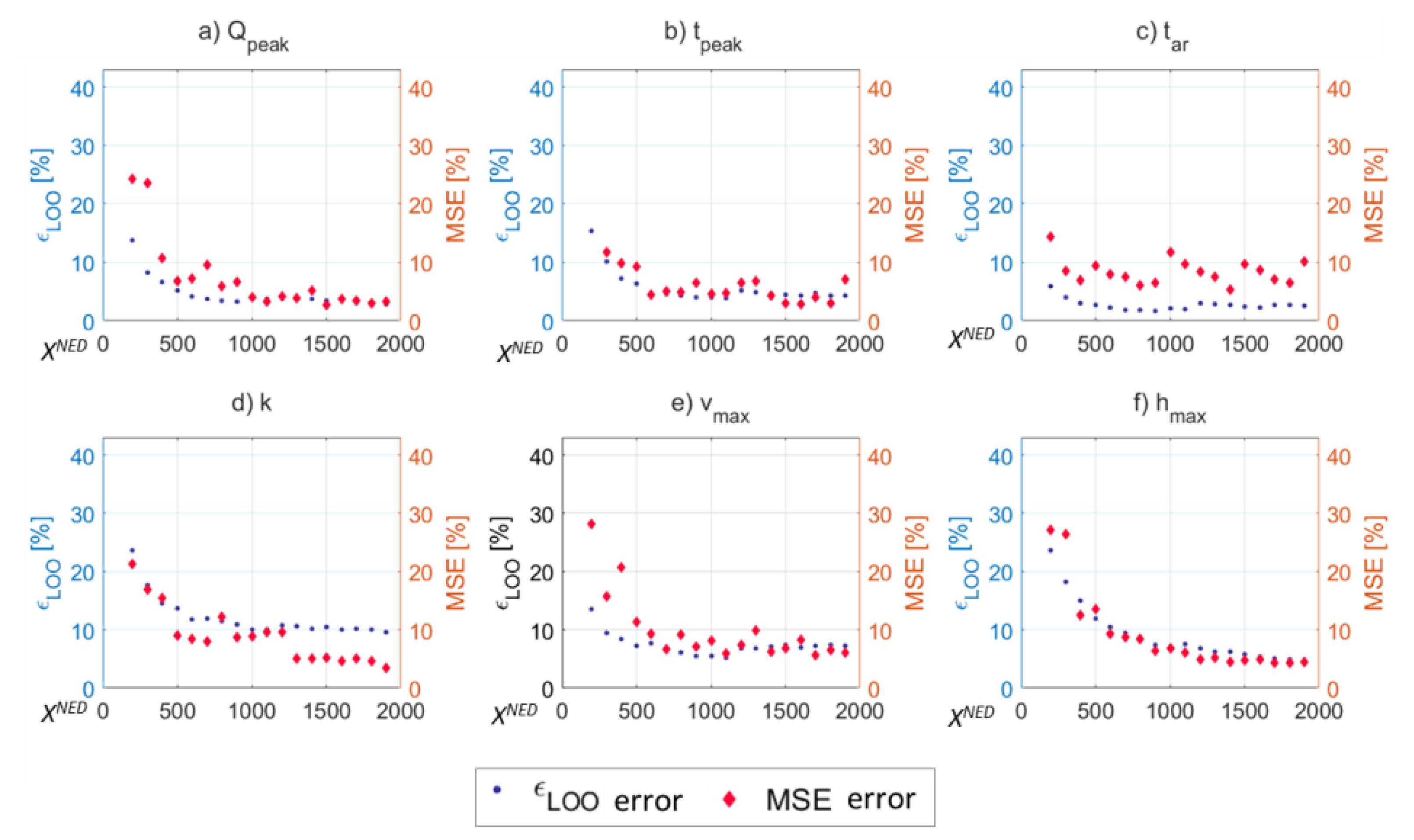
3.3. Step C. Uncertainty Propagation
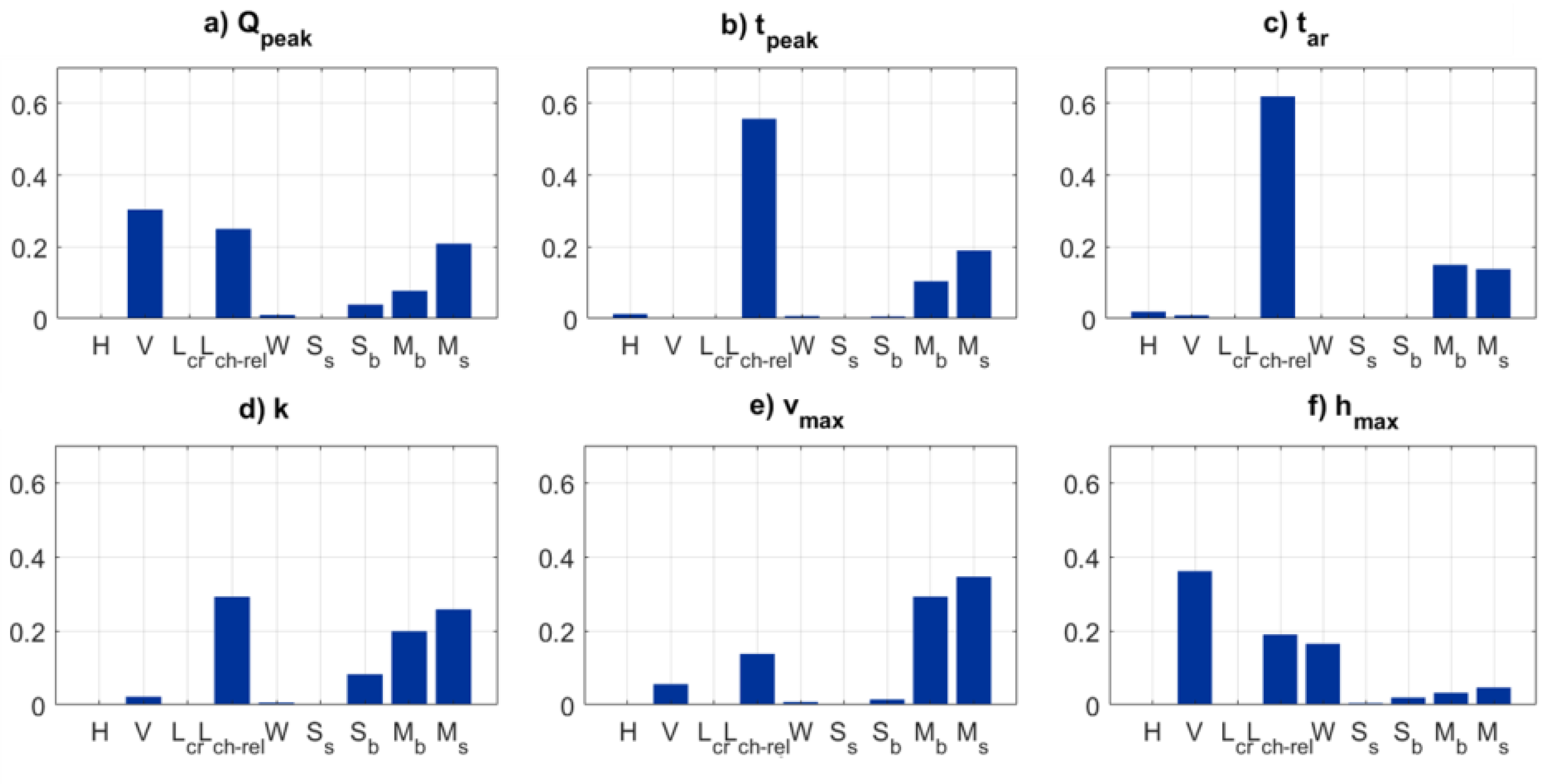
3.4. Step D. Global Sensitivity Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Physical Parameters of the Model | ||
| = | maximum water depth at the last cross section at the end of the channel; | |
| H | = | dam height; |
| k | = | recession constant; |
| Lcr | = | length of the dam crest; |
| Lch-rel | = | channel length relative to the dam height; |
| = | roughness coefficient of the channel sides; | |
| = | roughness coefficient of the channel bed; | |
| = | discharge at time zero; | |
| = | peak discharge; | |
| = | discharge at time t corresponding to the total run time; | |
| = | slope of the channel bed; | |
| = | side slopes; | |
| = | time to the peak discharge; | |
| = | time to the flood arrival; | |
| = | time between and given for the outflow hydrograph; | |
| = | maximum water velocity at the cross section of the channel end; | |
| V | = | reservoir volume; and |
| W | = | channel width; |
| Marginal Distributions | ||
| = | lower boundary of a Uniform function; | |
| = | lower boundary of the support for a four-parameter Beta function; | |
| = | upper boundary of a Uniform function; | |
| = | upper boundary of the support for a four-parameter Beta function; | |
| = | Beta function; | |
| = | support of a random continuous variable X, ; | |
| = | expected value; | |
| = | Probability density function (PDF) of a continuous variable X; | |
| = | entropy of a variable X with PDF ; | |
| = | Interval for the support of a random continuous variable X; | |
| = | Uniform function; | |
| = | first shape parameter of a Beta function; | |
| = | second shape parameter of a Beta function; | |
| = | mean value; | |
| = | standard deviation; and | |
| = | first derivative of Euler’s gamma | |
| Saint-Venant Equations | ||
| A | = | wetter cross section; |
| g | = | gravitational acceleration; |
| = | friction slope; | |
| = | time; | |
| Q | = | discharge; |
| = | gradient of the water surface elevation; and | |
| = | distance between cross sections | |
| Uncertainty Propagation and Sensitivity Analysis | ||
| = | partial variance calculated as ; | |
| = | total variance calculated as a sum ; | |
| = | Probability density function (PDF) of X; | |
| = | evaluation of the computational model; | |
| = | PCE metamodel response built on the experimental design ; | |
| = | PCE metamodel response built on the experimental design ; | |
| M | = | dimensions of the computational model; |
| N | = | number of sampling points in the experimental design; |
| = | rank-equivalent; | |
| = | support of the parameter X; | |
| = | first-order Sobol’ index of the input parameter ; | |
| = | one value realization; | |
| = | random vector; | |
| = | probability density function of ; | |
| = | joint distribution of ; | |
| = | sample set (collection of realizations); | |
| = | model experimental design (model input parameters); | |
| = | model experimental design (model output parameters); | |
| = | model experimental design excluding ; | |
| = | coefficient for the actual term of the sum for the PCE; | |
| = | degree of the underlying polynomials (); | |
| = | leave-one-out cross-validation error; | |
| = | mean value of the computational model; | |
| = | Spearman coefficient between two input parameters (ith and jth); | |
| = | multivariate polynomials. i.e., the product of the underlying orthonormal polynomials; and | |
| = | Orthonormal polynomials | |
References
- Lafitte, R. Classes of risk for dams. Hydropower Dams 1996, 6, 59–66. [Google Scholar]
- Molinaro, P. Dam break analysis: A state of the art. In Computational Water Resources; Bensar, D., Brebbia, C.A., Ovazar, D., Eds.; CMP: Boston, MA, USA, 1991. [Google Scholar]
- Betamio de Almeida, A.; Bento Franco, A. Modeling of dam break flows. In Computer Modeling of Free Surface and Pressurized Flows; Chaudhry, M.H., Mays, L.W., Eds.; NATO ASI Series: Heidelberg, Germany, 1993; pp. 343–375. [Google Scholar]
- ICOLD. Dictionary. International Commission on Large Dams. Available online: http://www.icold-cigb.net/GB/Dictionary/dictionary.asp (accessed on 3 May 2016).
- SwissCOD. Dams in Switzerland. Available online: http://www.swissdams.ch/index.php/en/swiss-dams/dams-in-switzerland (accessed on 5 May 2018).
- Zhang, L.; Peng, M.; Chang, D.; Xu, Y. Dam Failure Mechanisms and Risk Assessment; Jon Wiley and Sons, Inc.: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Pearce, F. Dams and Floods; WWF: Gland, Switzerland, 2001. [Google Scholar]
- Froehlich, D.C. Peak Outflow from Breached Embankment Dam. J. Water Resour. Plan. Manag. 1995, 121. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modeling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational dam-break hydraulics over erodible sediment bed. J. Hydraul. Eng. 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Zagonjolli, M. Dam Break Modeling, Risk Assessment and Uncertainty Analysis for Flood Mitigation. Ph.D. Thesis, Delft University of Technology and of the Academic Board of the UNESCO-IHE Institute for Water Education, Delft, The Netherlands, 2007. [Google Scholar]
- Hartford, D.; Baecher, G. Risk and Uncertainty in Dam Safety; Thomas Telford Publishing: London, UK, 2004. [Google Scholar]
- Peter, S.J.; Siviglia, A.; Nagel, J.; Marelli, S.; Boes, R.M.; Vetsch, D.; Sudret, B. Development of probabilistic dam breach model using Bayesian inference. Water Resour. Res. 2018, 54, 4376–4400. [Google Scholar] [CrossRef]
- Romanowicz, R.; Beven, K. Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resour. Res. 2003, 39, SWC41–SWC412. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Aronica, G.; Beven, K. Bayesian updating of flood inundation likelihoods conditioned on flood extent data. Hydrol. Process. 2004, 18, 3347–3370. [Google Scholar] [CrossRef]
- Konakli, K.; Mylonas, C.; Marelli, S.; Sudret, B. UQLab User Manual—Canonical Low-Rank Approximations; Report UQLab-V1.1-108; Chair of Risk, Safety & Uncertainty Quantification, ETH Zürich: Zurich, Switzerland, 2018. [Google Scholar]
- Yazdi, J.; Salehi Neyshabouri, S.A.A. Adaptive surrogate modeling for optimization of flood control detention dams. Environ. Model. Softw. 2014, 61, 106–120. [Google Scholar] [CrossRef]
- Dwelle, M.C.; Kim, J.; Sargsyan, K.; Ivanov, V.Y. Streamflow, stomata, and soil pits: Sources of inference for complex models with fast, robusr uncertainty quantification. Adv. Water Resour. 2019, 125, 13–31. [Google Scholar] [CrossRef]
- Ginsbourger, D.; Rosspopoff, B.; Pirot, G.; Durrande, N.; Renard, P. Distance-based kriging relying on proxy simulations for inverse conditioning. Adv. Water Resour. 2013, 52, 275–291. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G. The Wiener-Askey polynomial chaos for stochastic equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B. Combining Polynomial Chaos Expansions and Kriging; RSUQ-2014-001; Chair of Risk, Safety and Uncertainty Quantification, IBK, D-BAUG, ETH Zurich: Zurich, Switzerland, 2014. [Google Scholar]
- Behzadian, K.; Kapelan, Z.; Savic, D.; Ardeshir, A. Stochastic sampling design using a multi-objective genetic algorithm and adaptive neural networks. Environ. Model. Softw. 2009, 24, 530–541. [Google Scholar] [CrossRef]
- Linde, N.; Ginsbourger, D.; Irving, J.; Nobile, F.; Doucet, A. On uncertainty quantification in hydrogeology and hydrogeophysics. Adv. Water Resour. 2017, 110, 166–181. [Google Scholar] [CrossRef]
- Le Gratiet, L.; Marelli, S.; Sudret, B. Metamodel-Based Sensitivity Analysis: Polynomial Chaos Expansions and Gaussian Processes. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer: Cham, Switzerland, 2017; pp. 1289–1325. [Google Scholar] [CrossRef]
- Norton, J. An introduction to sensitivity assessment of simulation models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Leskens, J.G.; Brugnach, M.; Hoekstra, A.Y.; Schuurmans, W. Why are decisions in flood disaster management so poorly supported by information from flood models? Environ. Model. Softw. 2014, 53, 53–61. [Google Scholar] [CrossRef]
- Sudret, B. Uncertainty Propagation and Sensitivity Analysis in Mechanical Models: Contributions to Structural Reliability and Stochastic Spectral Methods; Habilitation a diriger des Recherches, Universit’e Blaise Pascal: Clermont-Ferrand, France, 2007. [Google Scholar]
- De Rocquigny, E.; Devictor, N.; Tarantola, S. Uncertainty in Industrial Practice—A Guide to Quantitative Uncertainty Management; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Toro, E.T. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin, Germany, 1999. [Google Scholar] [CrossRef]
- Soares Frazão, S.; Lories, D.; Taminiau, S.; Zech, Y. Dam-break flow in a channel with a sudden enlargement. In Proceedings of the 30th IAHR Congress, Thessaloniki, Greece, 1 August 2003; pp. 221–228. [Google Scholar]
- Brunner, G.W. HEC-RES River Analysis System—User’s Manual Version 5.0. US Army Corps of Engineers; Institute for Water Resources, Hydrologic Engineering Center (HEC): Davis, CA, USA, 2016; p. 962. [Google Scholar]
- DHI. MIKE 11-A Modeling System for Rivers and Channels—User Guide; DHI: Copenhagen, Denmark, 2003; p. 430. [Google Scholar]
- Pilotti, M.; Maranzoni, A.; Milanesi, L.; Tomirotti, M.; Valerio, G. Dam-break Modeling in Apline Valleys. J. Mt. Sci. 2014, 11, 1429–1441. [Google Scholar] [CrossRef]
- Cunge, J.A.; Holly, F.M.; Verwey, A. Practical Aspects of Computational River Hydraulics; Pitman Advanced Pub.: Boston, MA, USA, 1980. [Google Scholar]
- Vetsch, D.F.; Siviglia, A.; Caponi, F.; Ehrbar, D.; Facchini, M.; Gerke, E.; Kammerer, S.; Koch, A.; Peter, S.; Vonwiller, L.; et al. BASEMENT Version 2.7; ETH Zurich: Zurich, Switzerland, 2017. [Google Scholar]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley: New York, NY, USA, 2001. [Google Scholar]
- McCann, M.W.J.; Paxson, G. Uncertainty in dam Failure Consequence Estimates. In Proceedings of the FLOODrisk2016-3rd European Conference on Flood Risk Management, Lyon, France, 17–21 October 2016. [Google Scholar]
- Baecher, G.B. Uncertainty in dam safety risk analysis. GEORISK 2016, 10, 92–108. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.J.; Neal, J.; Schumann, G.; Hall, J.; Bates, P. Flood Risk and Uncertainty. In Risk and Uncertainty Assessment for Natural Hazards; Cambridge University Press: Cambridge, UK, 2011; pp. 190–233. [Google Scholar]
- Bales, J.D.; Wagner, C.R. Sources of uncertainty in flood inundation maps. Flood Risk Manag. 2009, 2, 139–147. [Google Scholar] [CrossRef]
- Beven, K. Facets of uncertainty: Epistemic uncertainty, nonstationarity, likelihood, hypothesis testing, and communication. Hydrol. Sci. J. 2016, 61, 1652–1665. [Google Scholar] [CrossRef]
- Zellnerr, A.; Highfiled, R. Calculation of Maximum Entropy Distributions and Approximation of Marginal Posterior Distributions. J. Econom. 1988, 37, 195–209. [Google Scholar] [CrossRef]
- Faber, M.H.; Kübler, O.; Köhler, J. Tutorial for the JCSS Code Calibration Program CodeCal 03; ETH Zürich: Zürich, Switzerland, 2003. [Google Scholar]
- Matz, A.W. Maximum Likelihood Parameter Estimation for the Quartic Exponential Distribution. Technometrics 1978, 20, 475–484. [Google Scholar] [CrossRef]
- Bhat, H.S.; Kumar, N. On the Derivation of the Bayesian Information Criterion; School of Natural Sciences, University of California: Berkeley, CA, USA, 2010. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nelsen, R. An Introduction to Copulas, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Arbenz, P. Bayesian Copulae Distributions, with Application to Operational Risk Management—Some Comments. Methodol. Comput. Appl. Probab. 2013, 15, 105–108. [Google Scholar] [CrossRef]
- Ghanem, R.; Spanos, P. Stochastic Finite Elements—A Spectral Aprroach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Lebrun, R.; Dutfoy, A. Do Rosenblatt and Nataf isoprobabilistic transformations really differ? Prob. Eng. Mech. 2009, 24, 577–584. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 2, 239–245. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R.; Ishwaran, H.; Knight, K.; Loubes, J.-M.; Massart, P.; Madigan, D.; Ridgeway, G.; et al. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on Least Angle Regression. J.Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in Matlab 257 Vulnerability, Uncertainty, and Risk. In Proceedings of the 2nd Int. Conf. on Vulnerability, Risk Analysis and Management (ICVRAM2014), Liverpool, UK, 13–16 July 2014; pp. 2554–2563. [Google Scholar]
- Marelli, S.; Sudret, B. UQLab User Manual—Polynomial Chaos Expansions. Techincal Report; Chair of Risk, Safety & Uncertainty Quantification, ETH Zürich: Zürich, Switzerland, 2017. [Google Scholar]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Galetti, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; WILEY: New York, NY, USA, 2008. [Google Scholar]
- Zhang, X.-Y.; Trame, M.N.; Lesko, L.J.; Schmidt, S. Sobol Sensitivity Analysis: A Tool to Guide the Development and Evaluation of systems Pharmacology Models. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef]
- Sobol, I. Sensitivity estimates for nonlinear mathematical models. Math. Comput. Model. 1993, 1, 407–414. [Google Scholar]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A Review on Global Sensitivity Analysis Methods. In Uncertainty Management in Simulation-Optimization of Complex Systems; Springer: Boston, MA, USA, 2015; Volume 59, pp. 101–122. [Google Scholar] [CrossRef]
- Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An analysis of the influence of riparian vegetation on the propagation of flood waves. Environ. Model. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Swisstopo. SwissALTI3D; Swiss Federal Office of Topography: Wabern, Switzerland, 2016.
- Rosgen, D.L. Applied River Morphology; CO: Wildland Hydrology: Pagosa Springs, CA, USA, 1996. [Google Scholar]
- Rosgen, D.; Rosgen, B.; Collins, S.; Nankervis, J.; Wright, K.; Appendix, B. Stream Classification & Valley Types. In Waldo Canyon Fire Watershed Assessment; Wildland Hydrology: Pagosa Springs, CA, USA, 2013. [Google Scholar]
- BBC. Intermediate Geography Rivers. Hydrographs. Available online: https://www.bbc.co.uk/scotland/education/int/geog/rivers/hydrographs/index.shtml (accessed on 13 April 2018).
- Sharma, D. Chapter 5: Hydrograph Analysis. Available online: https://www.slideshare.net/DeeneshSharma/ch5-hydrograph-analysis (accessed on 1 November 2017).
- SFSO. Ständige und Nichtständige Wohnbevölkerung nach Institutionellen Gliederungen, Geburtsort und Staatsangehörigkeit (in German), (STAT-TAB); Swiss Federal Statistical Office: Neuchatel, Switzerland, 2017.
- Swisstopo. SwissTLM3D. Available online: https://www.swisstopo.admin.ch/en/knowledge-facts/topographic-landscape-model.html (accessed on 6 November 2018).
- McCuen, R.H. Hydrologic Analysis and Design; Prentice-Hall: New Jersey, NJ, USA, 1998. [Google Scholar]
- Kalyanapu, A.J.; Burian, S.J.; McPherson, T.N. Effect of land use-based surface roughness on hydrologic model output. J. Spat. Hydrol. 2009, 9, 51–71. [Google Scholar]
- NLCD. National Land Cover Database 2006; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2006.
- Lehner, B.; Liermann, C.R.; Revenga, C.; Voeroesmarty, C.; Fekete, B.; Crouzet, P.; Doell, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. GRanD. Global Reservoir and Dam Database. Version 1.1; Global Water System Project (GWSP): Bonn, Germany. Available online: https://doi.org/10.7927/H4N877QK (accessed on 1 March 2018).
- Torre, E.; Marelli, S.; Embrechts, P.; Sudret, B. Data-driven polynomial chaos expansion for machine learning regression. J. Comput. Phys. 2019, 388, 601–623. [Google Scholar] [CrossRef]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2013. [Google Scholar]
- Schöbi, R.; Marelli, S.; Sudret, B. UQLab User Manual—PC-Kriging; Report UQLab-V1.1-109; Chair of Risk, Safety & Uncertainty Quantification, ETH Zürich: Zürich, Switzerland, 2018. [Google Scholar]
- Froehlich, D.C. Embankment Dam Breach Parameters and Their Uncertainties. J.Hydraul. Eng. 2008, 13, 1708–1721. [Google Scholar] [CrossRef]
- Borgonovo, E.; Castaings, W.; Tarantola, S. Model emulation and moment-independent sensitivity analysis: An application to environmental modeling. Environ. Model. Softw. 2012, 34, 105–115. [Google Scholar] [CrossRef]
- Kucherenko, S.; Tarantola, S.; Annoni, P. Estimation of global sensitivity indices for models with dependent variables. Comput. Phys. Commun. 2012, 183, 937–946. [Google Scholar] [CrossRef]
- Caniou, Y. Global Sensitivity Analysis for Nested and Multiscale Modeling. Ph.D Thesis, Blaise Pascal University-Clermont II, Clermont-Ferrand, France, 2012. [Google Scholar]

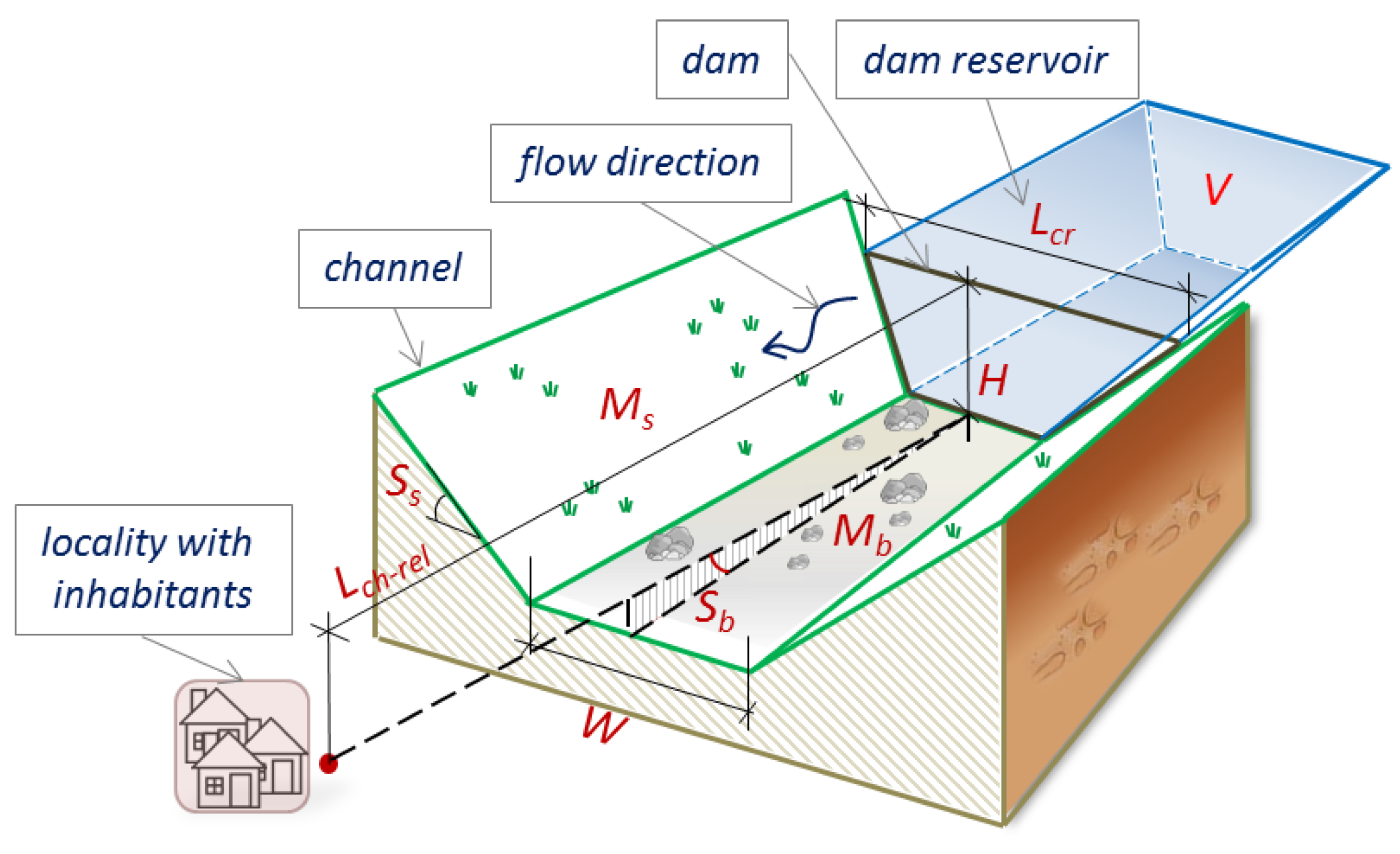

| Parameter | Name | Unit | Definition |
|---|---|---|---|
| Physical characteristics of the dam and reservoir | |||
| H | Dam height | (m) | Dam height |
| V | Reservoir volume | (m3) | Volume of the water in the reservoir formed by the dam |
| Length of the dam crest | (m) | Length of the crest of the dam | |
| Physical characteristics of the channel | |||
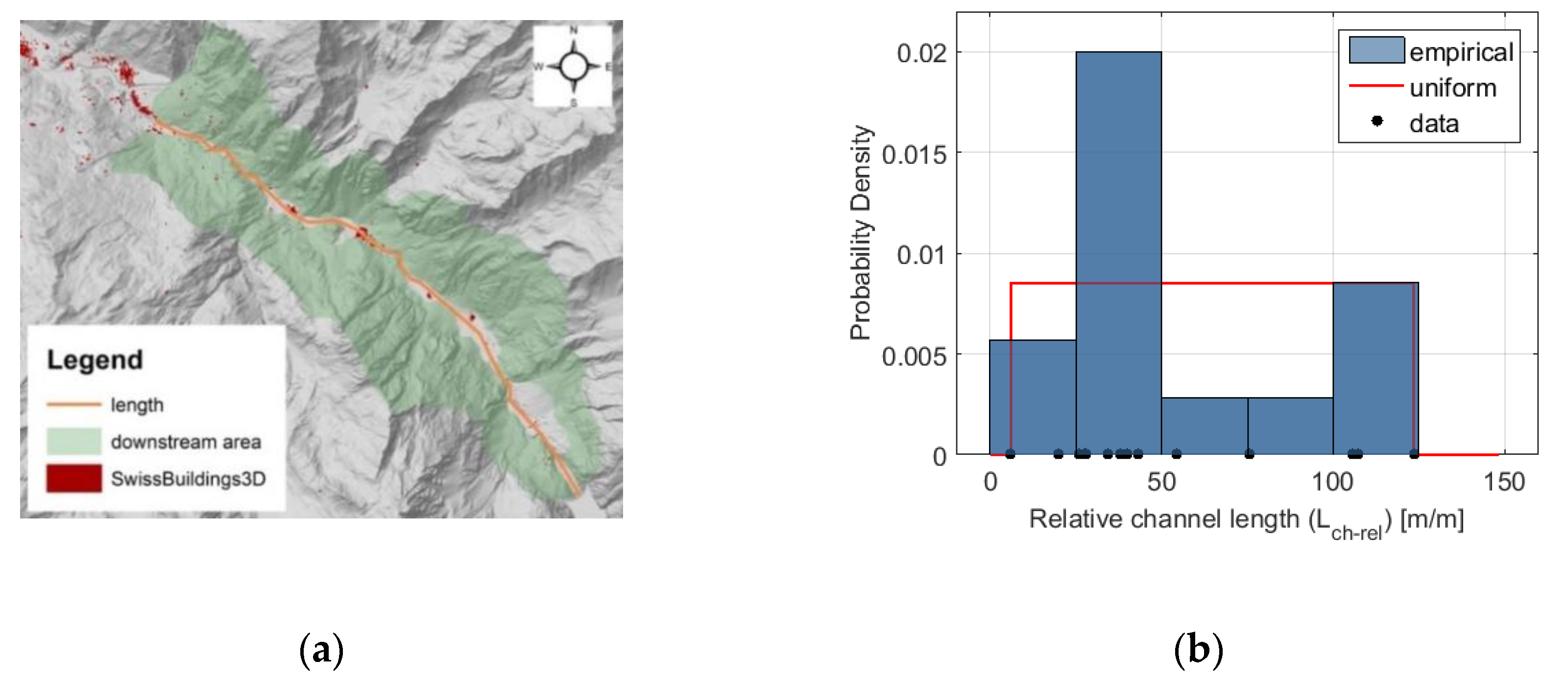
| Relative channel length | (m/m) | Length of the channel between the dam and the location, where the flow quantities are defined; expressed as relative to the height of the dam | |
| W | Channel width | (m) | Width of the channel bed. |
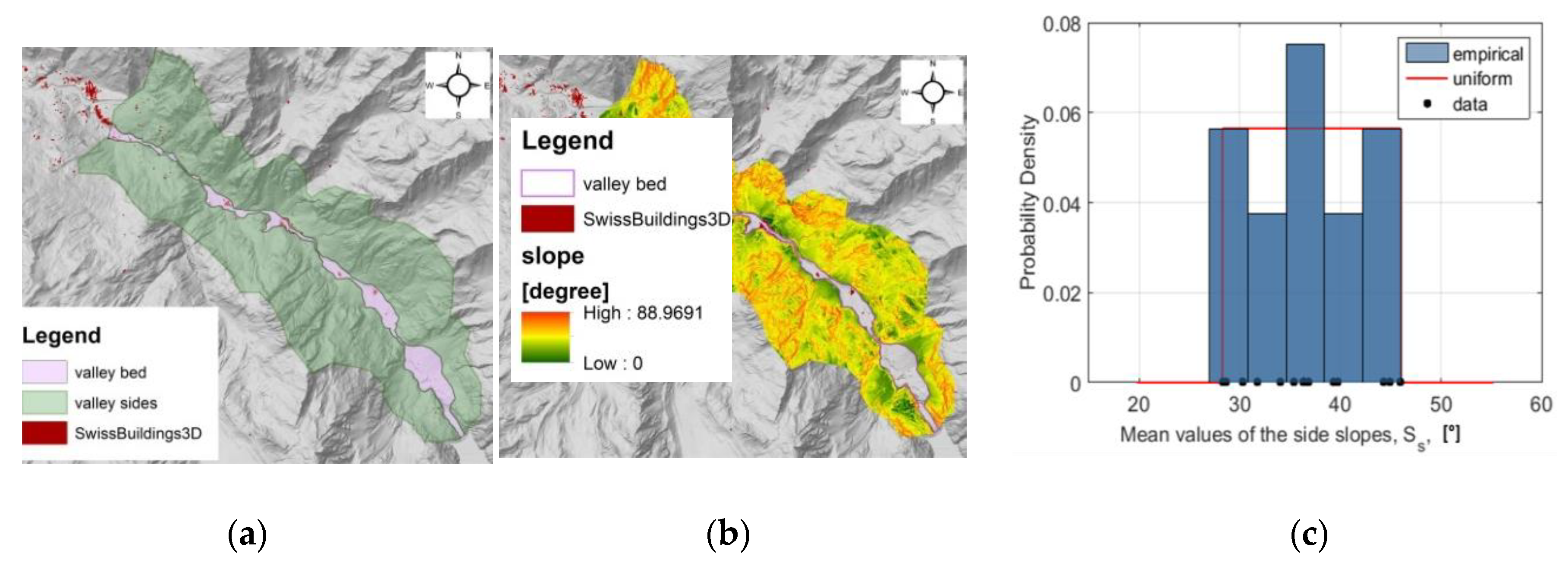
| Slopes of channel sides | (°) | Slopes of the sides of the channel cross section. A trapezoidal cross section is assumed. | |
| Slopes of channel bed | (m/m) | Average slope of the channel bed. | |
| Characteristics of the environment | |||
| Roughness coefficient of the channel sides | (s/m1/3) | Roughness coefficient of the channel side slopes. It is given as a Manning roughness coefficient. | |
| Roughness coefficient of the channel bed | (s/m1/3) | Roughness coefficient of the channel bed. It is given as a Manning roughness coefficient. | |
| Valley Type Based on Rosgen [66] & Rosgen, Rosgen, Collins, Nankervis and Wright [67] | Dam-downstream Valleys in Switzerland Simplified Geometry | ||
|---|---|---|---|
| Class 1: Channel with a triangular cross section | |||
Moderately steep, gentle-sloping side-slopes (often in colluvial valleys)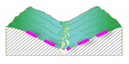 | Steep, confined, V-notched canyons, rejuvenated side-slopes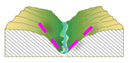 | Zevreila dam | Channel with a triangular cross section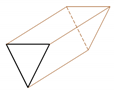 |
| Class 2: Channel with a trapezoidal cross section | |||
Moderately steep, U-shaped glacial-through valleys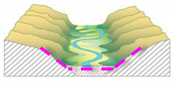 | Santa Maria dam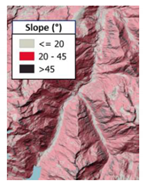 | Moiry dam | Channel with a trapezoidal cross section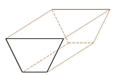 |
| Class 3: Other topographies | |||
Joint-, bedrock-controlled valleys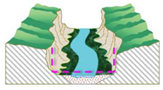 | Gigerwald dam | Channel with a rectangular cross section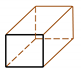 | |
| Feature | Definition | Visualization |
|---|---|---|
| Peak discharge, , (m3/s) | Maximum outflow reached during the flood event | 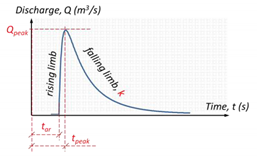 |
| Time-to-peak discharge, , (s) | Time interval between the start of the computational time and the peak discharge | |
| Time-to-flood arrival, , (s) | Time interval between the start of the computational time and the time of the first non-zero discharge value. Knowing , , and the rising limb of the hydrograph can be built, i.e., the curve reflecting the increase of the discharge. | |
| Recession constant, , (m3/s2) | The recession limb begins at time to peak and continues while the value of discharge decreases. This limb is characterized by a recession constant, k, of the line between the peak discharge and a discharge at time t after the peak discharge. | |
| Distribution | Density Function | Parameters | Entropy |
|---|---|---|---|
| Beta | , for x defined on the support [0,1] or (0,1) | Where is the Beta function, is a first shape parameter and is a second shape parameter. A Beta distribution is an alternative for bounded parameters with non-uniform distributions. | , where is the first derivative of Euler’s gamma |
| for y with a support [, ] or (, ): Therefore, | |||
| Uniform | Where is a lower boundary and is an upper boundary. A Uniform distribution is applied when little is known about the parameter (e.g., distance, loads). | ||
| Landcover Type (SwissTLM3D) | Number | Name According to US National Land Cover Dataset (NLCD) | Manning’s Coefficients (s/m1/3) |
|---|---|---|---|
| Rock | 1 | barren land | 0.011–0.09 |
| Shrubbery forest | 6 | shrub/scrub | 0.05–0.4 |
| Soil, earth | 7 | barren land | 0.011–0.09 |
| Wetlands | 11 | woody/emergent herbaceous wetlands | 0.086–0.14/0.045–0.3 |
| Forest | 12 | deciduous forest/evergreen forest | 0.1–0.36/0.1–0.32 |
| Forest (open) | 13 | deciduous forest/evergreen forest | 0.1–0.36/0.1–0.32 |
| Para-Meter | Unit | Distribution | Hyper Parameters | Truncation | Mean and Variance |
|---|---|---|---|---|---|
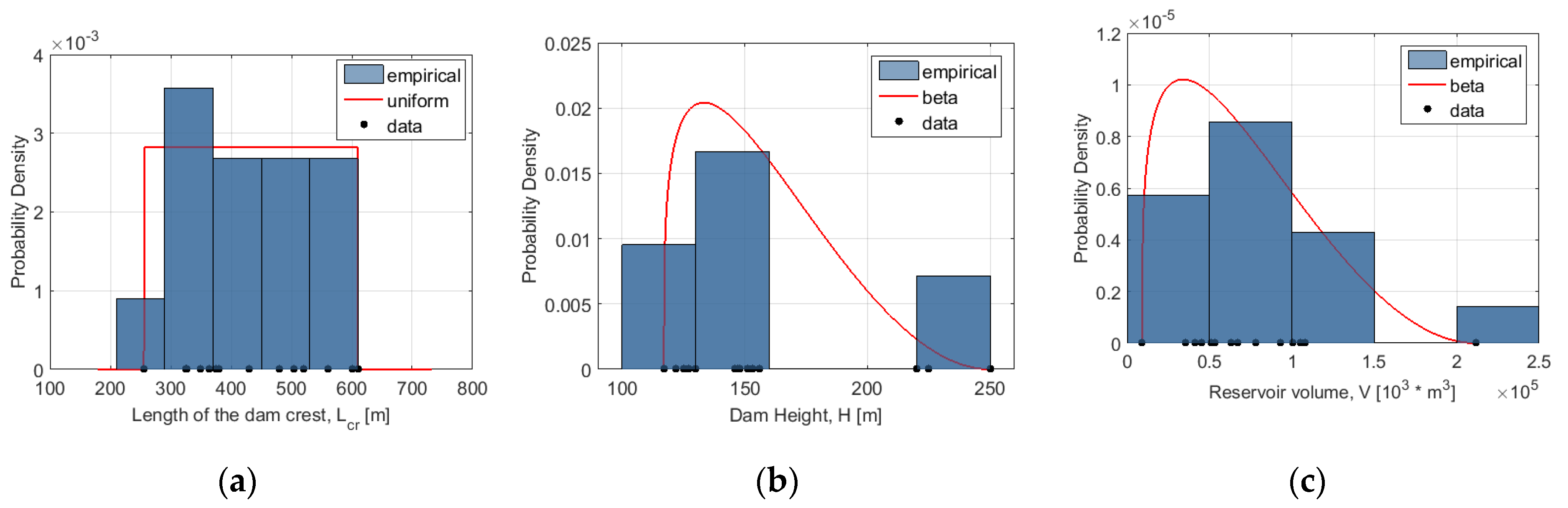
| H | (m) | - | 159.9, 26.6 | ||
| V | (m3) | - | 69,890, 40,460 | ||
| (m) | - | 433, 102.19 | |||
| (m/m) | - | 64.75, 33.98 | |||
| (m) | - | 82.33, 46.96 | |||
| (°) | - | 37.13, 5.11 | |||
| (m/m) | [0.03, 0.23] | 0.090, 0.047 | |||
| (s/m1/3) | [0.01, 0.4] | 0.14, 0.19 | |||
| (s/m1/3) | [0.01, 0.4] | 0.17, 0.12 |
| Parameter | H | V | W | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | 1 | 0.574 | 0.218 | −0.512 | 0.082 | 0.213 | −0.020 | −0.007 | 0.125 |
| V | 1 | 0.574 | −0.253 | 0.298 | 0.112 | −0.156 | 0.046 | −0.108 | |
| 1 | −0.336 | 0.280 | −0.138 | 0.143 | 0.196 | −0.380 | |||
| 1 | 0.417 | −0.341 | −0.385 | 0.354 | 0.165 | ||||
| W | 1 | −0.179 | −0.347 | 0.378 | 0.223 | ||||
| 1 | 0.196 | −0.442 | −0.380 | ||||||
| 1 | −0.073 | −0.521 | |||||||
| 1 | 0.292 | ||||||||
| 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalinina, A.; Spada, M.; Vetsch, D.F.; Marelli, S.; Whealton, C.; Burgherr, P.; Sudret, B. Metamodeling for Uncertainty Quantification of a Flood Wave Model for Concrete Dam Breaks. Energies 2020, 13, 3685. https://doi.org/10.3390/en13143685
Kalinina A, Spada M, Vetsch DF, Marelli S, Whealton C, Burgherr P, Sudret B. Metamodeling for Uncertainty Quantification of a Flood Wave Model for Concrete Dam Breaks. Energies. 2020; 13(14):3685. https://doi.org/10.3390/en13143685
Chicago/Turabian StyleKalinina, Anna, Matteo Spada, David F. Vetsch, Stefano Marelli, Calvin Whealton, Peter Burgherr, and Bruno Sudret. 2020. "Metamodeling for Uncertainty Quantification of a Flood Wave Model for Concrete Dam Breaks" Energies 13, no. 14: 3685. https://doi.org/10.3390/en13143685
APA StyleKalinina, A., Spada, M., Vetsch, D. F., Marelli, S., Whealton, C., Burgherr, P., & Sudret, B. (2020). Metamodeling for Uncertainty Quantification of a Flood Wave Model for Concrete Dam Breaks. Energies, 13(14), 3685. https://doi.org/10.3390/en13143685







