Risk-Based Planning of Diagnostic Testing of Turbines Operating with Increased Flexibility †
Abstract
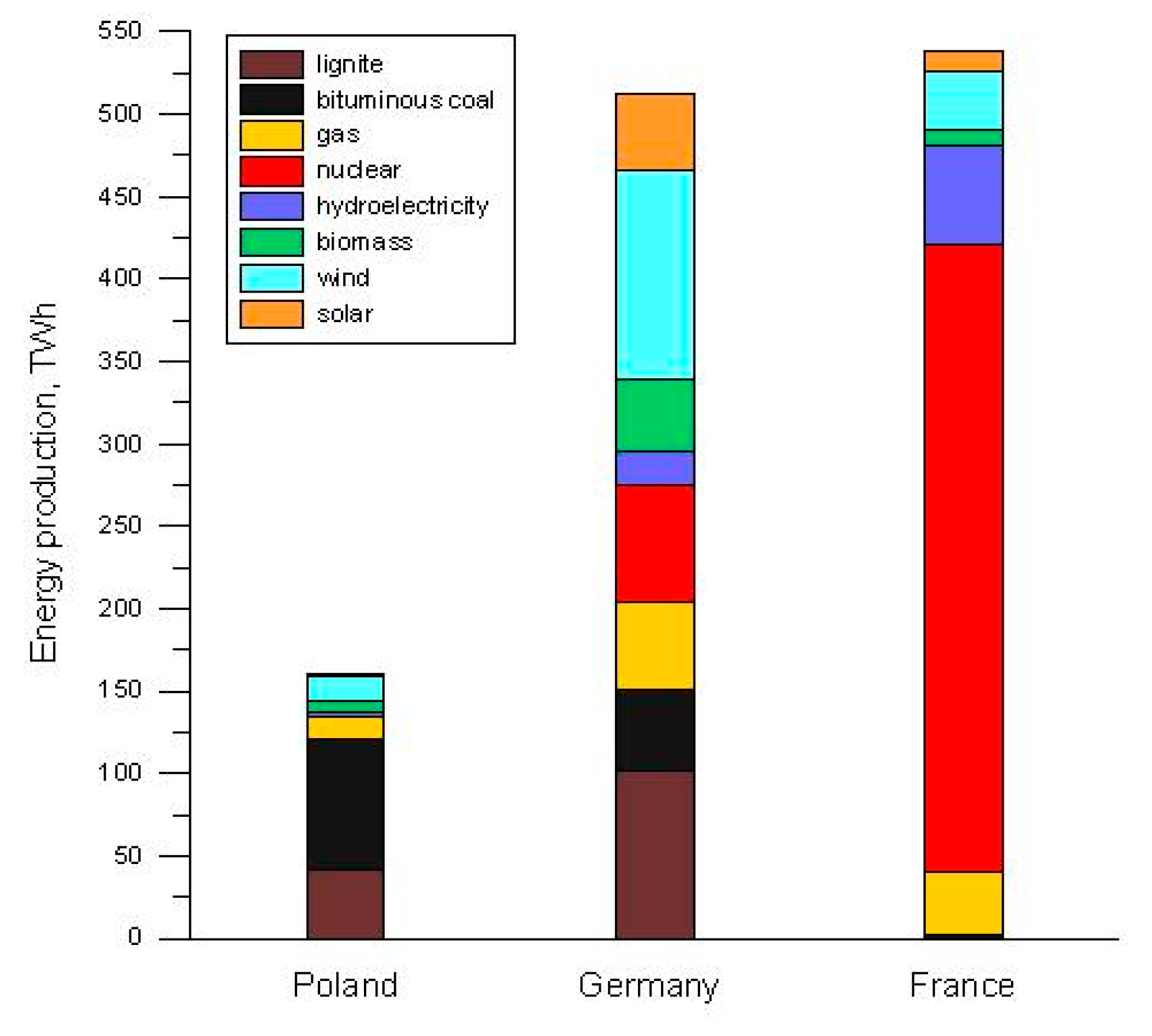
:1. Introduction
2. Planning for Testing Based on the Avoided Risk Criterion
- avoided risk value—;
- outlays made to reduce risk—;
- other risk value—.
- —cash flows related to costs of repairs, diagnostic testing or replacement in year t;
- —probability of failure in the period prior to diagnostic testing, repairs or replacement;
- —probability of failure in the period after diagnostic testing, repairs or replacement;
- —discount rate;
- —year index;
- —total planned service life (years);
- —year in which the element is tested, repaired or replaced.
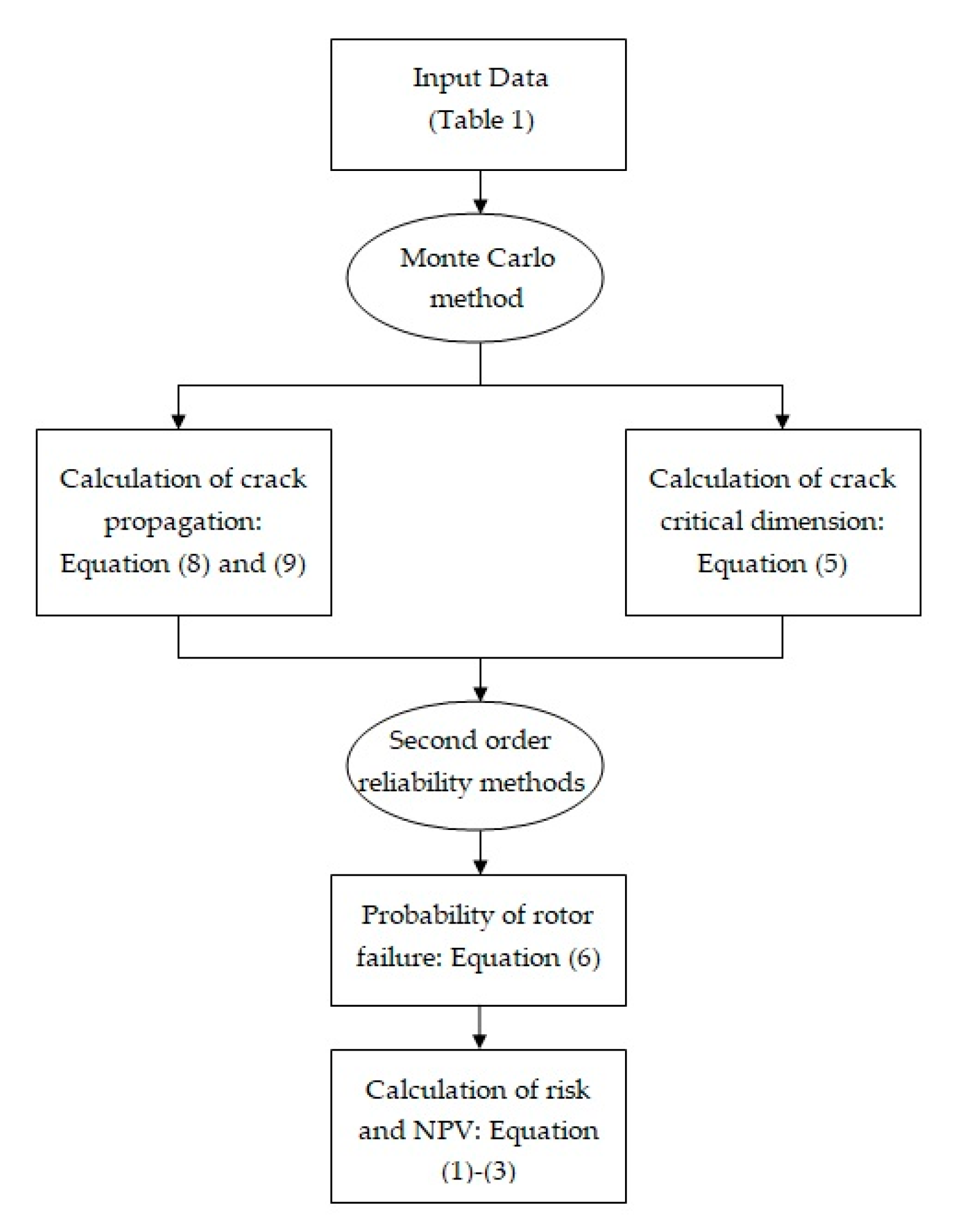
- defining hazardous scenarios, selecting the most hazardous scenario;
- working out a model of the development of wear processes, determining the failure criterion;
- calculating the change in the element failure probability;
- optimizing the times of maintenance activities that ensure maximization of the NPV index.
3. Turbine Rotor Failure Scenario
3.1. Rotor Failure Criterion
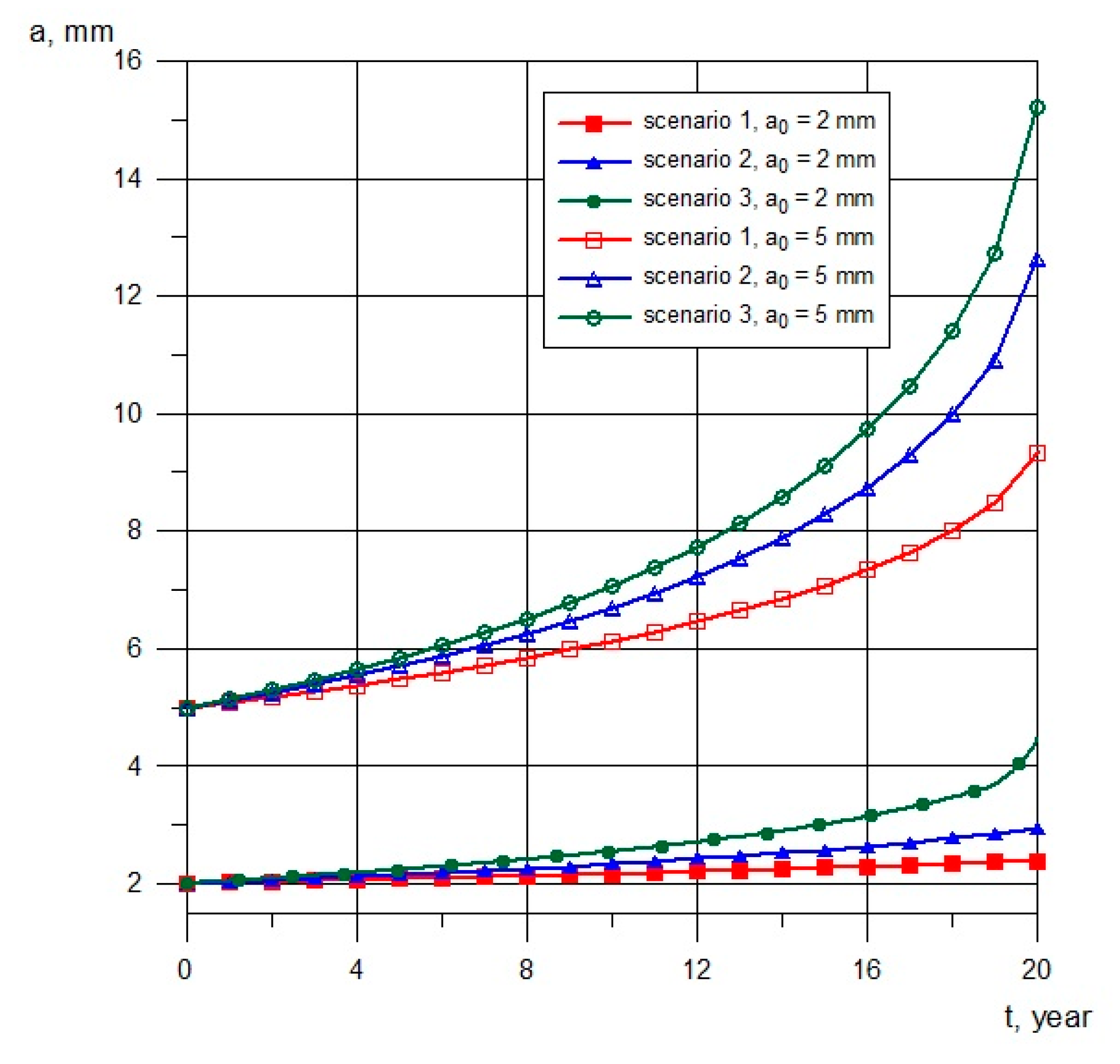
3.2. Crack Propagation in the Turbine Rotor
4. Optimization of Diagnostic Testing Intervals
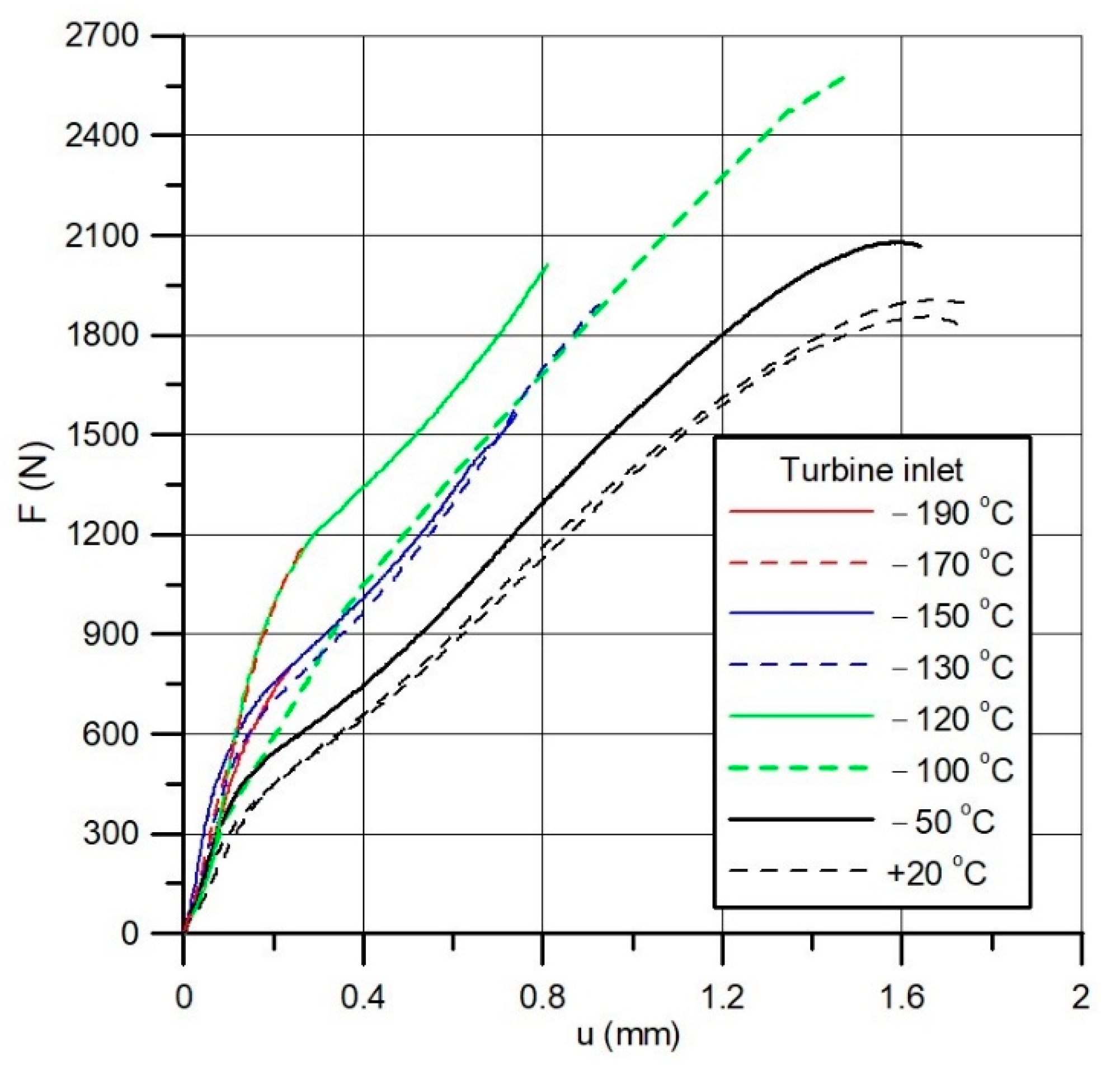
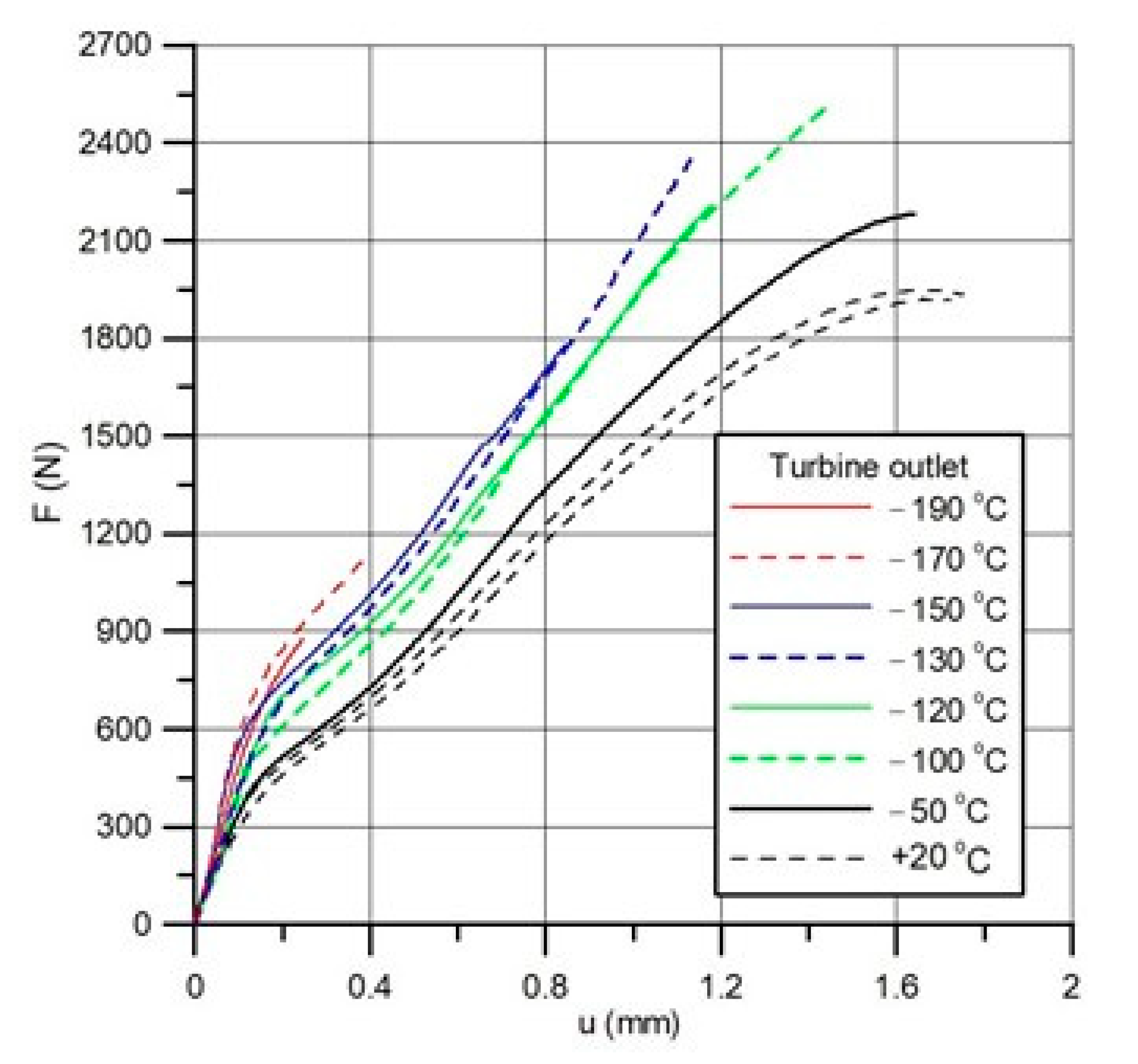
4.1. SPT-Based Estimation of the Decrease in Rotor Steel Toughness
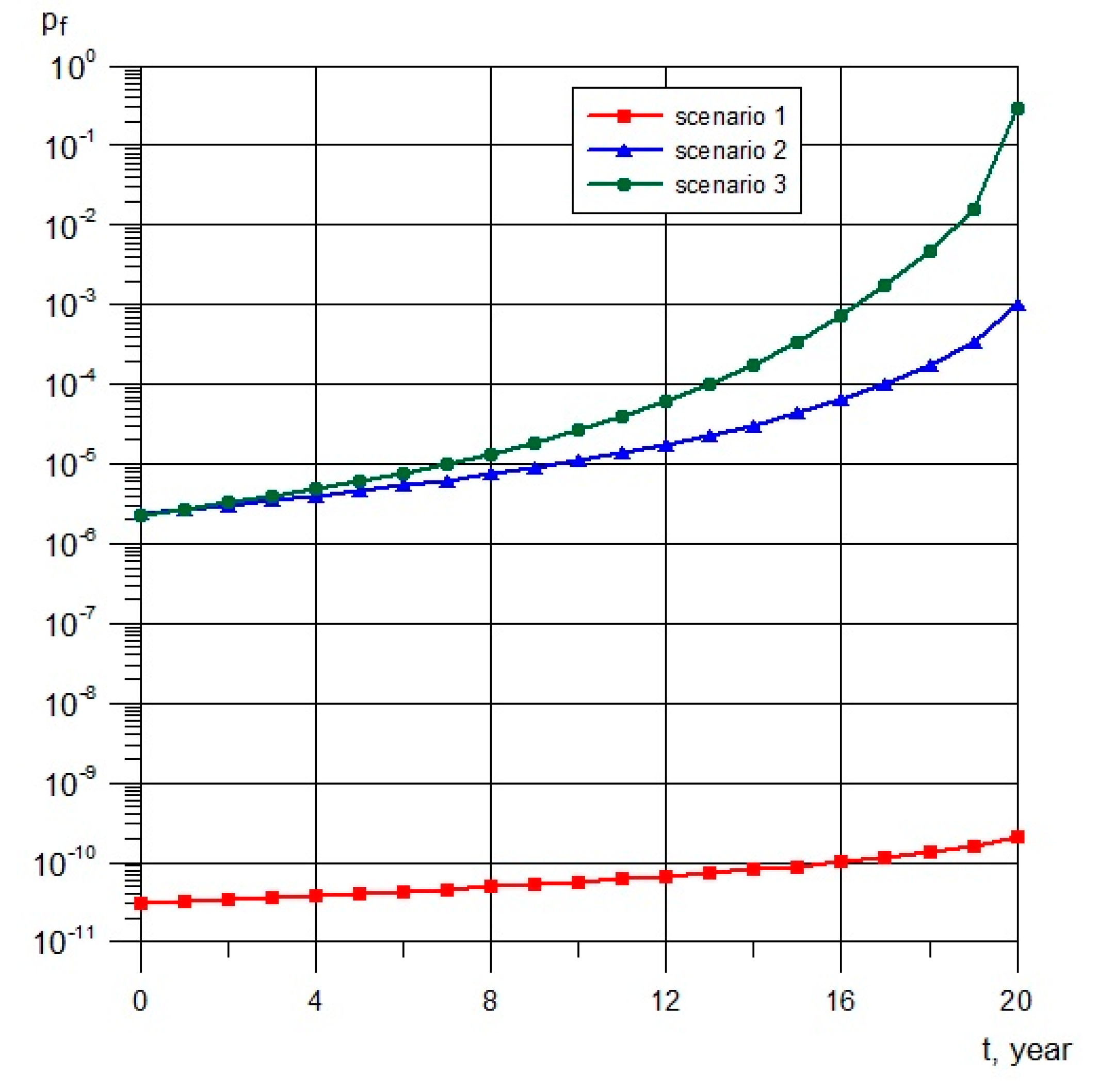
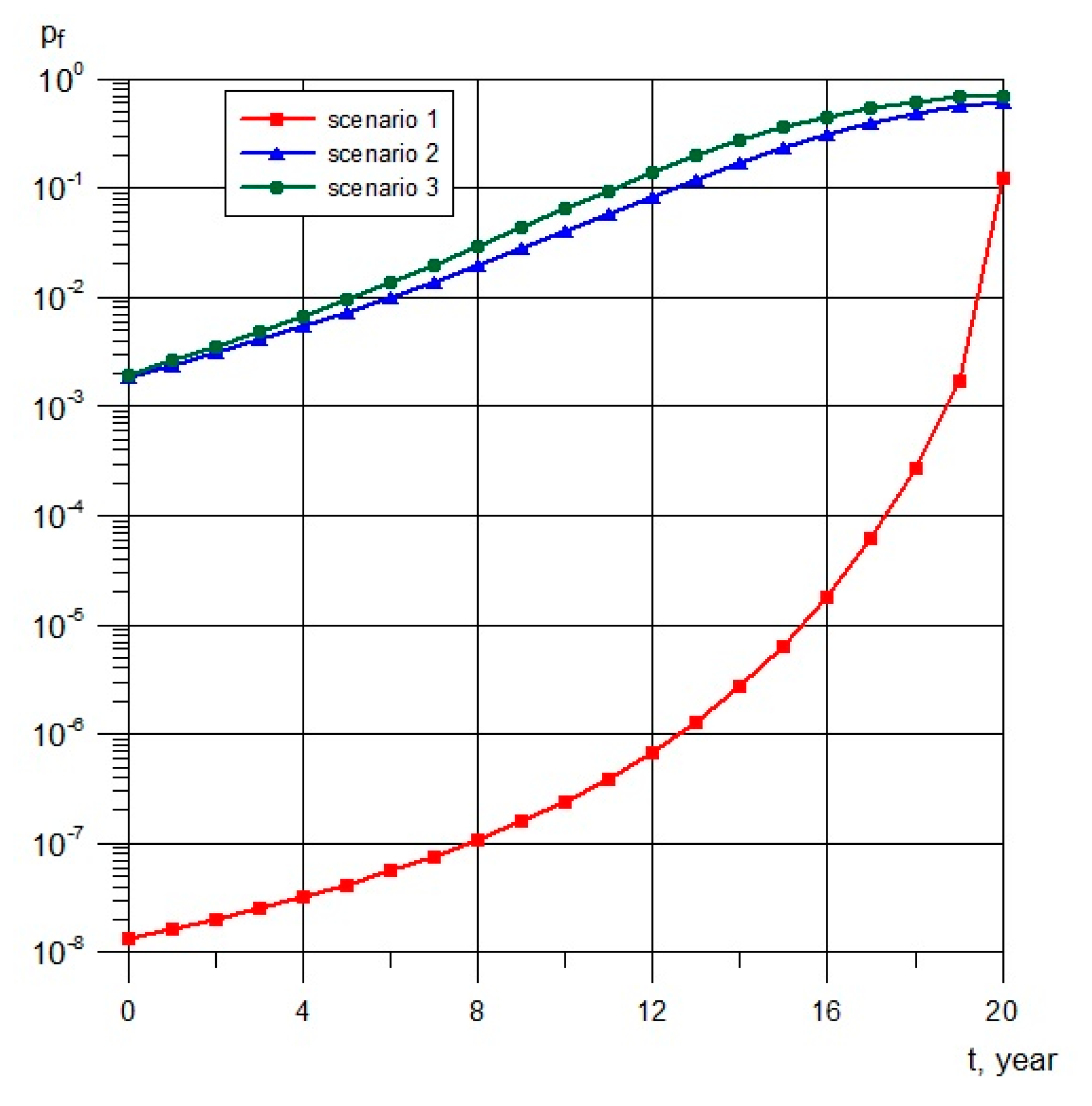
4.2. Probability of the Turbine Rotor Failure
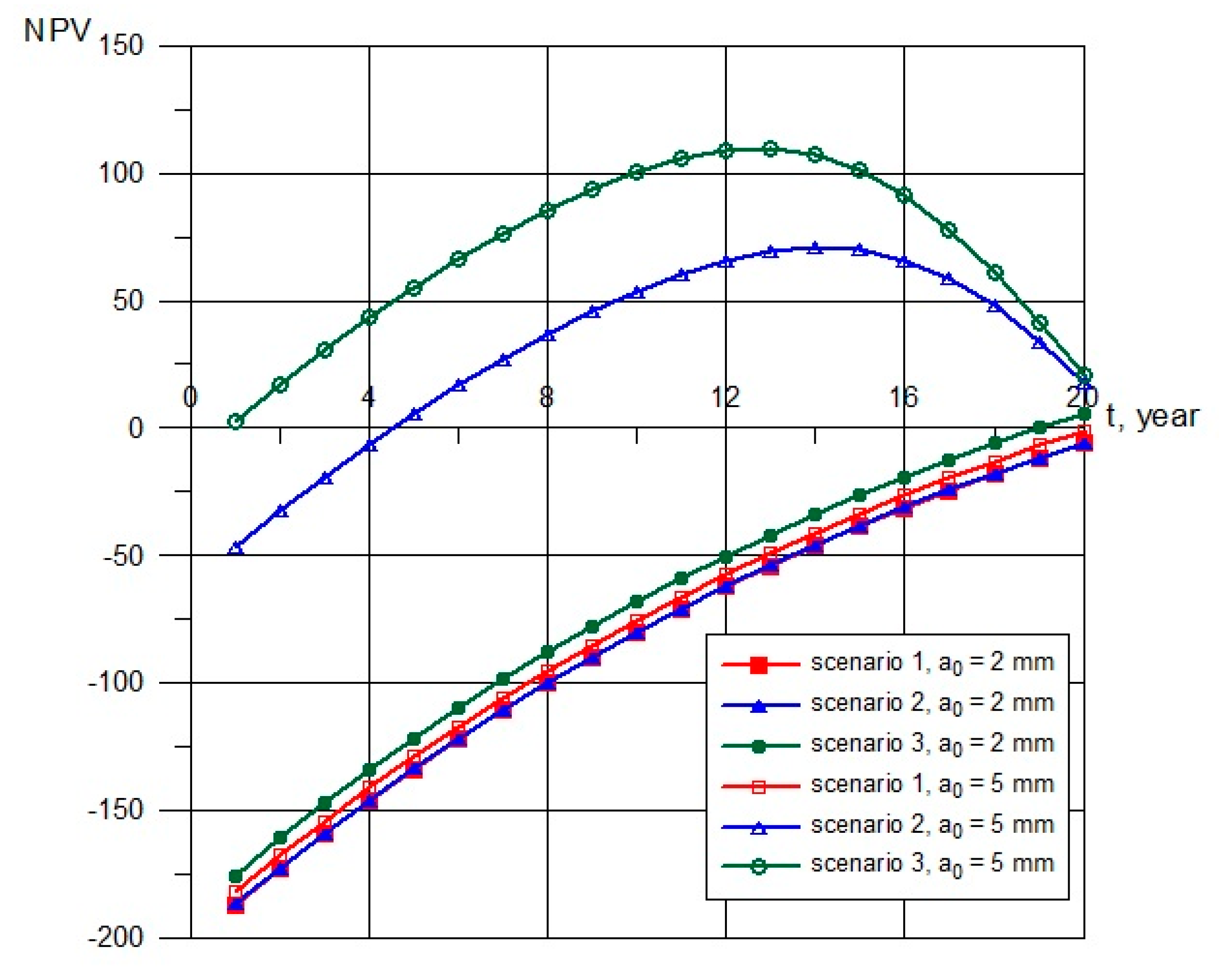
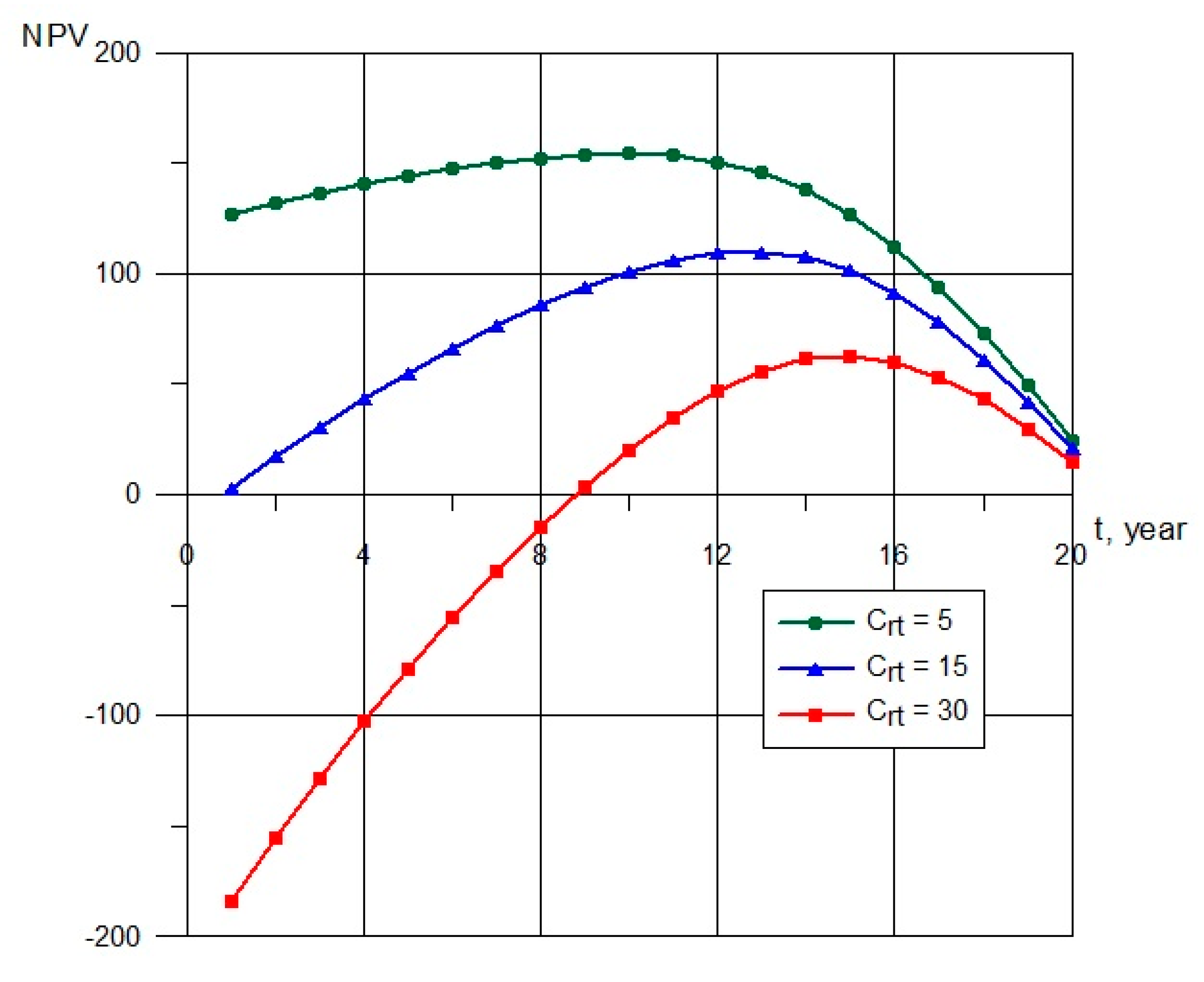
4.3. Optimization of Diagnostic Testing Intervals
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Forum energii. Available online: https://www.forum-energii.eu/pl/dane-o-energetyce/za-rok-2019 (accessed on 17 June 2020).
- Monthly Electricity Generation in Germany in 2020. Fraunhofer ISE. Available online: https://www.energy-charts.de/energy.htm (accessed on 17 June 2020).
- Bilan électrique de la France: que Retenir de 2019? Connaissance des Energies. Available online: https://www.connaissancedesenergies.org/la-production-delectricite-en-france-metropolitaine-tous-les-chiffres-cles-de-2019-200212-0 (accessed on 17 June 2020).
- Rusin, A.; Wojaczek, A. Trends of changes in the power generation system structure and their impact on the system reliability. Energy 2015, 92, 128–134. [Google Scholar] [CrossRef]
- Markewitz, P.; Robinius, M.; IStolten, D. The Future of Fossil Fired Power Plants in Germany—A Lifetime Analysis. Energies 2018, 11, 1616. [Google Scholar] [CrossRef] [Green Version]
- Łukowicz, H.; Rusin, A. The impact of the control method of cyclic operation on the power unit efficiency and life. Energy 2018, 150, 565–574. [Google Scholar] [CrossRef]
- Stoppato, A.; Mirandola, A.; Meneghetti, G.; Lo Casto, E. On the operation strategy of steam power plants working at variable load: Technical and economic issues. Energy 2012, 37, 228–236. [Google Scholar] [CrossRef]
- Keatley, P.; Shibli, A.; Hewitt, N.J. Estimating power plant start costs in cyclic operation. Appl. Energy 2013, 111, 550–557. [Google Scholar]
- Rusin, A. Technical risk involved in long-term operation of steam turbines. Reliab. Eng. Syst. Saf. 2007, 92, 1242–1249. [Google Scholar] [CrossRef]
- Rusin, A. Assessment of operational risk of steam turbine valves. Int. J. Press. Vessel. Pip. 2004, 81, 373–379. [Google Scholar] [CrossRef]
- Jovanovic, A. Overview of RIMAP project and its deliverables in the area of power plants. Int. J. Press. Vessel. Pip. 2004, 81, 815–824. [Google Scholar] [CrossRef]
- Gräber, U. Advanced maintenance strategies for power plant operators—Introducing inter-plant life cycle management. Int. J. Press. Vessel. Pip. 2004, 81, 861–865. [Google Scholar] [CrossRef]
- Ji, D.; Sun, J.; Sun, Q.; Guo, H.-C.; Ren, J. Optimization of start-up scheduling and life assessment for a steam turbine. Energy 2018, 160, 160–170. [Google Scholar]
- Price, J. The economics of repeated tube thickness surveys. Int. J. Press. Vessel. Pip. 2002, 79, 555–559. [Google Scholar] [CrossRef]
- Nowak, G.; Rusin, A.; Łukowicz, H.; Tomala, M. Improving the power unit operation flexibility by the turbine start-up optimization. Energy 2020, 198, 117303. [Google Scholar] [CrossRef]
- Melani, A.H.A.; Murad, C.A.; Netto, A.C.; Souza, G.F.M.; Nabeta, S.I. Criticality-based maintenance of a coal-fired power plant. Energy 2018, 147, 767–781. [Google Scholar] [CrossRef]
- Ciarapica, F.E.; Giacchetta, G. Managing the condition-based maintenance of a combined-cycle power plant: An approach using soft computing techniques. J. Loss Prev. Process Ind. 2006, 19, 316–325. [Google Scholar] [CrossRef]
- Dachyar, M.; Nurcahyo, R.; Tohir, Y. Maintenance strategy selection for steam power plant in range of capacity 300-625 MW. ARPN J. Eng. Appl. Sci. 2018, 13, 2571–2580. [Google Scholar]
- Yang, Y.; Sorensen, J.D. Cost-optimal maintenance planning of defects on wind turbine blades. Energies 2019, 12, 998. [Google Scholar] [CrossRef] [Green Version]
- Damnjanovic, I.; Røed, W. Risk management in operations of petrochemical plants: Can better planning prevent major accidents and save money at the same time? J. Loss Prev. Process Ind. 2016, 44, 223–231. [Google Scholar] [CrossRef]
- Hameed, A.; Khan, F. A framework to estimate the risk-based shutdown interval for a processing plant. J. Loss Prev. Process Ind. 2014, 32, 18–29. [Google Scholar] [CrossRef]
- Bertolini, M.; Bevilacqua, M.; Ciarapica, F.E.; Giacchetta, G. Development of Risk-Based Inspection and Maintenance Procedures for an Oil Refinery. J. Loss Prev. Process Ind. 2009, 22, 244–253. [Google Scholar] [CrossRef]
- Krishnasamy, L.; Khan, F.; Haddara, M. Development of a risk-based maintenance (RBM) strategy for a power-generating plant. J. Loss Prev. Process Ind. 2005, 18, 69–81. [Google Scholar] [CrossRef]
- Orme, G.J.; Venturini, M. Property risk assessment for power plants: Methodology, validation and application. Energy 2011, 36, 3189–3203. [Google Scholar] [CrossRef]
- Carazas, F.G.; Souza, G.F.M. Risk-based decision making method for maintenance policy selection of thermal power plant equipment. Energy 2010, 35, 964–975. [Google Scholar] [CrossRef]
- Noori, S.A.; Price, J.W.H. A risk approach to the management of boiler tube thinning. Nucl. Eng. Des. 2006, 236, 405–414. [Google Scholar] [CrossRef]
- Shayesteh, E.; Yu, J.; Hilber, P. Maintenance optimization of power systems with renewable energy sources integrated. Energy 2018, 149, 577–586. [Google Scholar] [CrossRef]
- Ozcan, E.; Yumusak, R.; Eren, T. Risk based maintenance in the hydroelectric power plants. Energies 2019, 12, 1502. [Google Scholar] [CrossRef] [Green Version]
- ARC Advisory Group. Available online: https://www.arcweb.com/blog/iiot-expands-maintenance-maturity-model (accessed on 28 June 2020).
- Learning Center. Information for Building Effective Maintenance Programs. Available online: https://www.onupkeep.com/learning/maintenance-types/reactive-maintenance (accessed on 28 June 2020).
- Juneja, R.; Wadhwa, H. Study on Turbine Maintenance: Overhauling, Emergency shutdown, Fault trading. Int. J. Mech. Eng. 2016, 3. [Google Scholar] [CrossRef] [Green Version]
- Learning Center. Information for Building Effective Maintenance Programs. Available online: https://www.onupkeep.com/learning/maintenance-types/routine-maintenance (accessed on 28 June 2020).
- Condition-Based Maintenance: A Complete Guide. Reliable Plant. Available online: https://www.reliableplant.com/condition-based-maintenance-31823 (accessed on 28 June 2020).
- Road to Reliability. Available online: https://www.roadtoreliability.com/types-of-maintenance (accessed on 28 June 2020).
- Assets Insights. Available online: https://assetinsights.net/Glossary/G_Time_Based_Maintenance.html (accessed on 28 June 2020).
- Latcovich, J.; Astrom, T.; Frankhuizen, P.; Hamberg, H.; Keller, S. Maintenance and Overhaul of Steam Turbines. In Proceeding of the International Association of Engineering Insurers 38th Annual Conference, Moscow, Russia, 19–21 September 2005. [Google Scholar]
- Rusin, A.; Bieniek, M. Maintenance planning of power plant elements based on avoided risk value. Energy 2017, 134, 672–680. [Google Scholar] [CrossRef]
- Marais, K.B.; Saleh, J.H. Beyond its cost, the value of maintenance: An analytical framework for capturing its net present value. Reliab. Eng. Syst. Saf. 2009, 94, 644–657. [Google Scholar] [CrossRef]
- British Electricity International. Turbines Generators and Associated Plant; Pergamon: Oxford, UK, 1991. [Google Scholar]
- Altstadt, E.; Houska, M.; Simonovski, I.; Bruchhausen, M.; Holmström, S.; Lacelle, R. On the estimation of ultimate tensile stress from small punch testing. Int. J. Mech. Sci. 2018, 136, 85–93. [Google Scholar] [CrossRef]
- Altstadt, E.; Ge, H.E.; Kuksenko, V.; Serrano, M.; Houska, M.; Lasan, M.; Bruchhausen, M.; Lapetite, J.M.; Dai, Y. Critical evaluation of the small punch test as a screening procedure for mechanical properties. J. Nucl. Mater. 2016, 472, 186–195. [Google Scholar] [CrossRef]
- Ortiz-Mariscal, A.; Saucedo-Munoz, M.L.; Komazaki, S. Application of small punch creep testing for evaluation of creep properties of as-received and artificially aged 5Cr-0.5 Mo steel. Mater. Sci. Eng. 2018, A709, 322–329. [Google Scholar] [CrossRef]
- Kumar, K.; Madhusoodanan, K.; Singh, R.N. Miniature test techniques for life management of operating equipment. Nucl. Eng. Des. 2017, 323, 345–358. [Google Scholar] [CrossRef]
- Moreno, M.F. Application of small punch testing on the mechanical and microstructural characterizations of P91 steel at room temperature. Int. J. Press. Vessel. Pip. 2016, 142–143, 1–9. [Google Scholar] [CrossRef]
- Rasche, S.; Kuna, M. Improved small punch testing and parameter identification of ductile to brittle materials. Int. J. Press. Vessel. Pip. 2015, 125, 23–34. [Google Scholar] [CrossRef]
- Rodríguez, C.; Fernández, M.; Cabezas, J.G.; Garciá, T.E.; Belzunce, F.J. The use of the small punch test to solve practical engineering problems. Theor. Appl. Fract. Mech. 2016, 86, 109–116. [Google Scholar] [CrossRef]
- Rusin, A.; Wojaczek, A.; Tomala, M. Analysis and management of operating risk created by turbine operation under flexible regimes. E3S Web Conf. 2019, 137, 01026. [Google Scholar] [CrossRef]
- NESSUS 8.30; Southwest Research Institute: San Antonio, TX, USA, 2010.

| Maintenance Type | Description |
|---|---|
| Reactive | It is the most popular type of maintenance, commonly used for noncritical assets with low failure probability. It relies on repairing elements only after breakdown or poor performance [29,30]. |
| Preventive | This type of maintenance is based on preventing failure through periodic inspection, diagnosis and observation. It is used for assets with a predictable failure frequency connected with wear processes. Its main purpose is to extend the lifetime of elements [29,31]. |
| Predictive | This is a prediction-based maintenance type using algorithms and machine learning to provide the most reliable condition monitoring and failure alerting. For this method, it is necessary to carry out appropriate measurements [18,29]. |
| Routine | It is strongly connected with time-based maintenance that relies on regular inspections and servicing. Actions lead to decrease of breakdown possibility owing to continuous care of the technical condition [14,32]. |
| Prescriptive | It is the method complementary to the predictive one in which the diagnosis process and repair guidance is provided. It is also focused on failure impact and the action priority [29]. |
| Opportunistic | In this method, downtime of the plant caused by element failure is the opportunity to take care of other areas, even when the breakdown is not found [31]. |
| Condition-Based (CBM) | CBM requires real-time monitoring of a specific parameter to detect failure symptoms. Early detection of irregularities allows prevention from serious breakdown or reduction of the undesirable effects. This method requires data collection, effective results interpretation, decision making and intervention. In CBM, the most frequently used techniques are vibration analysis, infrared thermography, ultrasonic analysis and oil analysis [29,33]. |
| Time-Based (TBM) | It is one of the most basic maintenance types. Element repair or replacement takes place at a specific interval without condition assessment. The method is popular for objects in which failure is cyclic and appears in fixed time. It is also used when diagnosis tests or measurements are not economically justified. The TBM is based on routine tasks often implemented by contracted services [34,35]. |
| Cost-Optimal | This is the type of maintenance in which the main purpose is to minimize costs while ensuring the appropriate technical condition for assets. The main parameters that are taken into consideration during optimization process are cost of downtime due to a breakdown, cost of corrective maintenance (repair/replacement), cost of preventive maintenance, acceptable degree of degradation and inspection time [19]. |
| Criticality-Based | In criticality-based maintenance, the most important aspects are the critical elements of the power plant. Main activities should focus on assets that have the largest effect on performance in the case of a breakdown [16]. |
| Risk-Based (RBM) | RBM is the maintenance type which places the greatest emphasis on protecting assets with the greatest failure risk (failure probability times consequences). These assets are subjected to more frequent conservation and inspection. RBM is a preventive method of maintenance that allows for the reduction of costs and scope of activities [34,36]. |
| Reliability Centered (RCM) | In the RCM method, three issues are taken into consideration: genesis of failure, its consequences and purpose of present prevention effort. The aim is to ensure high reliability of the system. It helps to find elements whose failure threaten further operation of the plant and which are not included in other maintenance types [18]. |
| Failure Finding (FFM) | The aim of FFM is to find the hidden problems in elements which are not in constant use before the breakdown occurs. The searching process for latent failure is based on fixed time intervals or risk calculation [34] |
| Input Data | Mean Value | Standard Deviation |
|---|---|---|
| 200 MPa | 10 MPa | |
| 250 MPa | 12.5 MPa | |
| 300 MPa | 15 MPa | |
| 2 × 10−12 | 1 × 10−13 | |
| 3.4537 | 0.173 | |
| 65 MPa | 3.25 MPa | |
| 3 × 10−14 | 1.5 × 10−15 | |
| 5.6572 | 0.283 | |
| 1.98 | 0.086 | |
| 2–5 mm | 0.5 mm | |
| 100 MPa | 5 MPa |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomala, M.; Rusin, A.; Wojaczek, A. Risk-Based Planning of Diagnostic Testing of Turbines Operating with Increased Flexibility. Energies 2020, 13, 3464. https://doi.org/10.3390/en13133464
Tomala M, Rusin A, Wojaczek A. Risk-Based Planning of Diagnostic Testing of Turbines Operating with Increased Flexibility. Energies. 2020; 13(13):3464. https://doi.org/10.3390/en13133464
Chicago/Turabian StyleTomala, Martyna, Andrzej Rusin, and Adam Wojaczek. 2020. "Risk-Based Planning of Diagnostic Testing of Turbines Operating with Increased Flexibility" Energies 13, no. 13: 3464. https://doi.org/10.3390/en13133464
APA StyleTomala, M., Rusin, A., & Wojaczek, A. (2020). Risk-Based Planning of Diagnostic Testing of Turbines Operating with Increased Flexibility. Energies, 13(13), 3464. https://doi.org/10.3390/en13133464





