Hydrodynamic Effects of Tidal-Stream Power Extraction for Varying Turbine Operating Conditions
Abstract
1. Introduction
- Influence of the turbine’s wake induction factor in the thrust and power coefficients calculation.
- Flow rate effect due to power extraction for increasing values of the blockage ratio.
- Evaluation of plausible ranges of the turbine’s wake induction factor and blockage ratio values and their effect on the local hydrodynamics through the examination of the elevation and velocity profiles.
- Assessment of the tidal-stream potential energy resource considering optimal conditions of turbine performance.
2. Modelling Approach
2.1. Hydrodynamic Models
2.1.1. Gradually Varying Flows
2.1.2. Rapidly Varying Flows
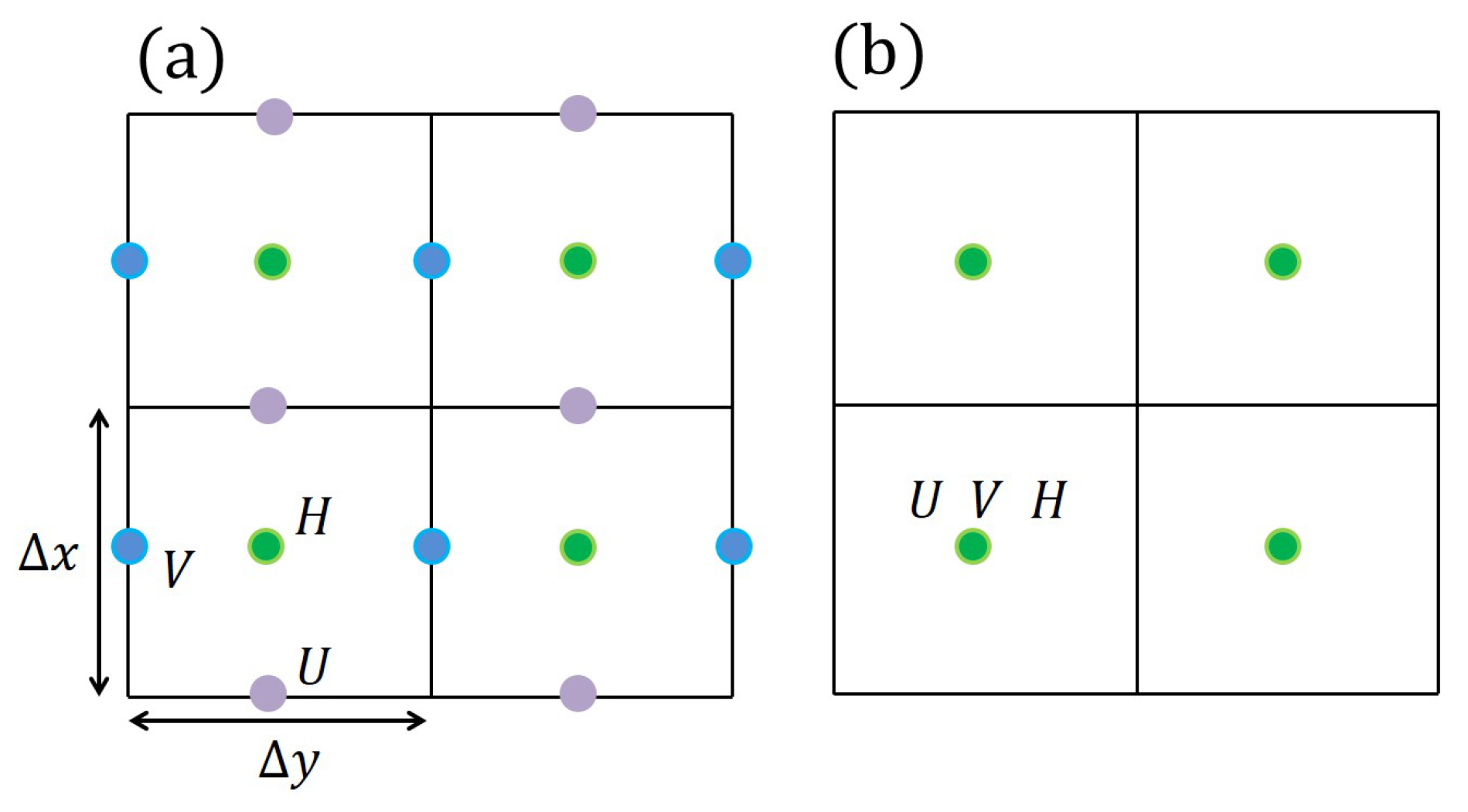
2.1.3. Grid Structures
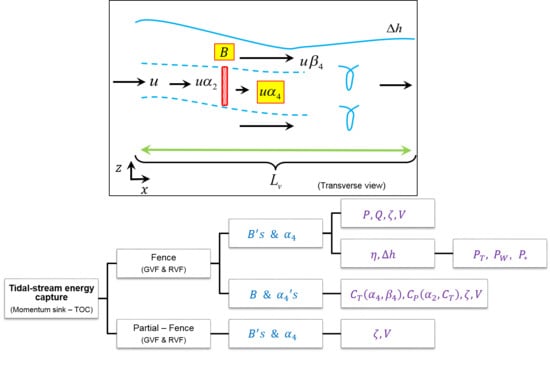
2.2. Turbine-Array Representation
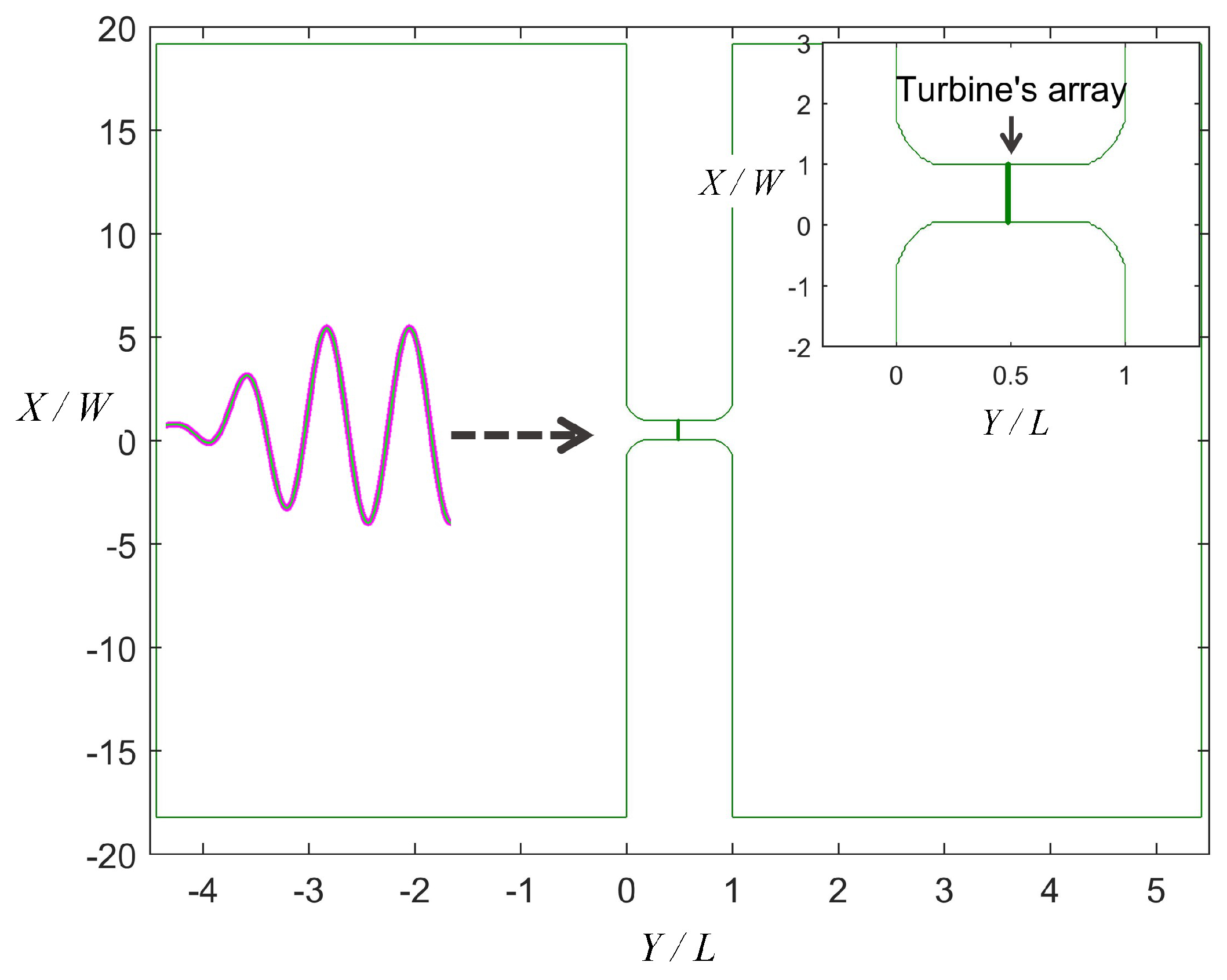
2.3. Domain and Array Configuration
3. Hydrodynamic Effects of Power Extraction
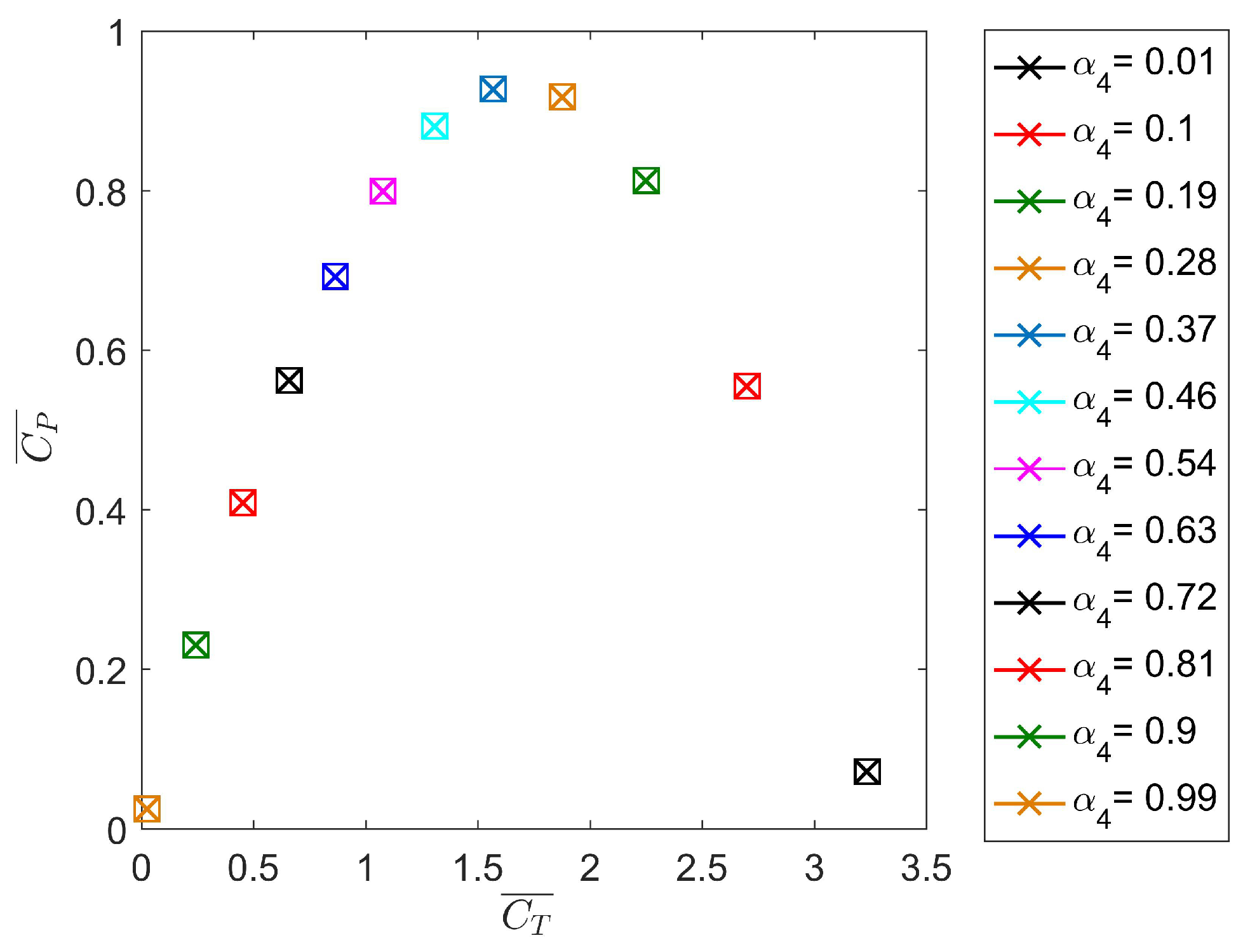
3.1. Wake-Induction Factor
3.2. Power Extraction and Flow Rate Affectation
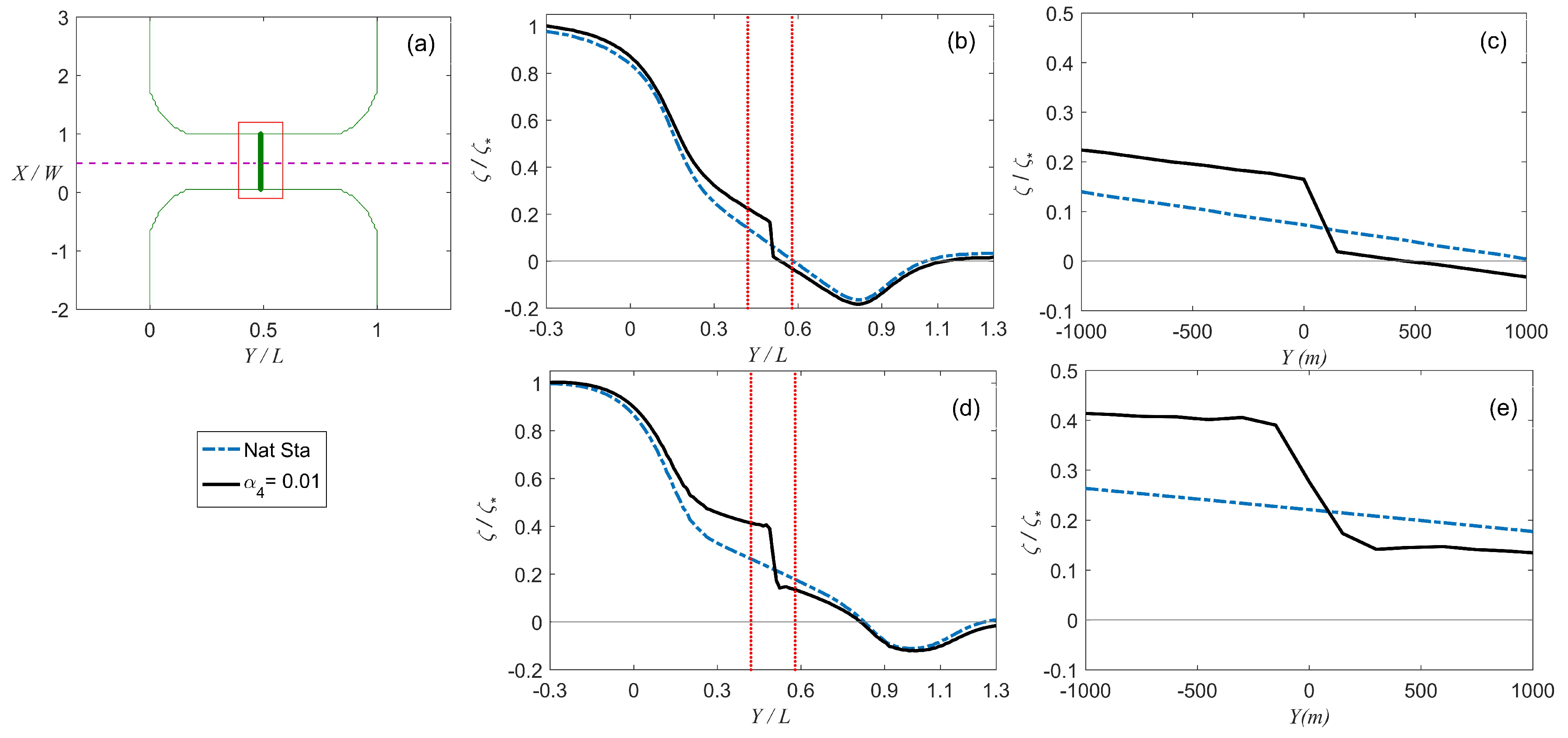
3.3. Wake-Induction Factor Influence on the Tidal-Stream
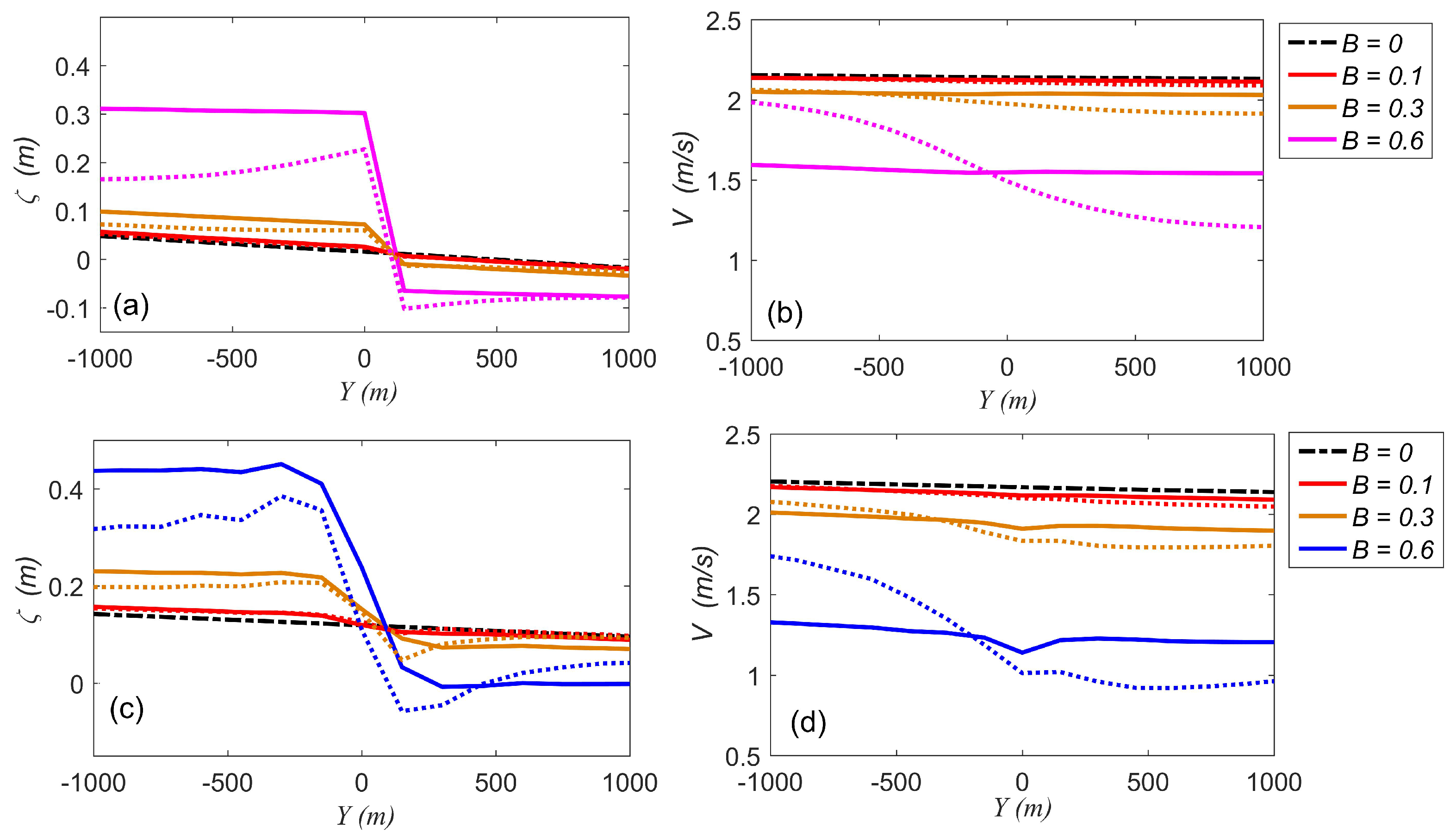
3.4. Array Configuration and Blockage Ratio Influence on the Tidal-Stream
4. Energy Resource Assessment
4.1. Relative Head Drop and Turbine Efficiency
4.2. Power Metrics
5. Discussion and Conclusions
- The turbine’s operating conditions played an important role in determining the available power for electrical energy generation.
- The maximisation of power extraction for electrical generation required the use of the optimum turbine-wake induction factor and an adequate blockage ratio, so that the power loss due to the turbine’s wake mixing was reduced.
- Situations where limiting values of the turbine’s operating conditions are used should be avoided, as they led to negligible power available.
- –
- A low wake induction factor was related to high thrust forces, characterised by low porosity turbines. These conditions produced (i) high downstream turbine-wake mixing and, consequently, a high power loss, (ii) strong velocity reduction, and (iii) significant head drop.
- –
- A high wake induction factor indicated low thrust forces, produced by high porosity turbines. This limit indicated (i) less flow disturbance, (ii) small velocity reduction, and (iii) negligible head drop.
- –
- Large blockage ratios also produced high thrust forces, which reduced the flow rate, intensified the magnitudes of flow bypassing the turbines, and enhanced turbine-wake mixing dissipation, reducing the amount of power extracted by the turbines.
- An accurate evaluation of the turbine’s operating conditions’ effect on local hydrodynamics was provided by an RVF solver. Particularly satisfactory results were obtained for a partial-fence.
- For scenarios where power was extracted uniformly across a channel (fence configuration), the GVF solver was a computationally economical tool to assess the resource; however, prudence should be taken as the solver underestimated the velocity reduction produced by power extraction.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Houlsby, G.; Vogel, C. The power available to tidal turbines in an open channel flow. Proc. Inst. Civ. Eng. Energy 2017, 170, 12–21. [Google Scholar] [CrossRef]
- Draper, S. Tidal Stream Energy Extraction in Coastal Basins. Ph.D. Thesis, St Catherine’s College, University of Oxford, Oxford, UK, 2011. [Google Scholar]
- Johnson, B.; Francis, J.; Howe, J.; Whitty, J. Computational Actuator Disc Models for Wind and Tidal Applications. J. Renew. Energy 2014, 2014, 172461. [Google Scholar] [CrossRef]
- Bryden, I.G.; Grinsted, T.; Melville, G.T. Assessing the potential of a simple tidal channel to deliver useful energy. Appl. Ocean Res. 2004, 26, 198–204. [Google Scholar] [CrossRef]
- Bryden, I.G.; Couch, S.J. How much energy can be extracted from moving water with a free surface: A question of importance in the field of tidal current energy? Renew. Energy 2007, 32, 1961–1966. [Google Scholar] [CrossRef]
- Blanchfield, J.; Garrett, C.; Wild, P.; Rowe, A. The extractable power from a channel linking a bay to the open ocean. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 289–297. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. The power potential of tidal currents in channels. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2563–2572. [Google Scholar] [CrossRef]
- Serhadlioglu, S. Tidal Stream Resource Assessment of the Anglesey Skerries and the Bristol Channel. Ph.D. Thesis, University of Oxford, Oxford, UK, 2014. [Google Scholar]
- Nash, S.; Phoenix, A. A review of the current understanding of the hydro-environmental impacts of energy removal by tidal turbines. Renew. Sustain. Energy Rev. 2017, 80, 648–662. [Google Scholar] [CrossRef]
- Sutherland, G.; Foreman, M.; Garrett, C. Tidal current energy assessment for Johnstone Strait, Vancouver Island. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 147–157. [Google Scholar] [CrossRef]
- Karsten, R.H.; McMillan, J.M.; Lickley, M.J.; Haynes, R.D. Assessment of tidal current energy in the Minas Passage, Bay of Fundy. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 493–507. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.; Bockelmann-Evans, B. Far-field modelling of the hydro-environmental impact of tidal stream turbines. Renew. Energy 2012, 38, 107–116. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.A. Assessment of array shape of tidal stream turbines on hydro-environmental impacts and power output. Renew. Energy 2012, 44, 318–327. [Google Scholar] [CrossRef]
- Hartnett, M.; Nash, S.; Olbert, A.; O’Brien, N. Modelling of Hydro-Environmental Impacts from the Installation of Tidal Stream Devices in the Shannon Estuary; Technical Report; Department of Civil Engineering, National University of Ireland: Galway, Ireland, 2012. [Google Scholar]
- Fallon, D.; Hartnett, M.; Olbert, A.; Nash, S. The effects of array configuration on the hydro-environmental impacts of tidal turbines. Renew. Energy 2014, 64, 10–25. [Google Scholar] [CrossRef]
- Nash, S.; O’Brien, N.; Olbert, A.; Hartnett, M. Modelling the far field hydro-environmental impacts of tidal farms—A focus on tidal regime, inter-tidal zones and flushing. Comput. Geosci. 2014, 71, 20–27. [Google Scholar] [CrossRef]
- O’Brien, N. Development of Computationally Efficient Nested Hydrodynamic Models. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 2013. [Google Scholar]
- Nash, S.; Olbert, A.; Hartnett, M. Towards a Low-Cost Modelling System for Optimising the Layout of Tidal Turbine Arrays. Energies 2015, 8, 13521–13539. [Google Scholar] [CrossRef]
- Phoenix, A. Development of a Tidal Flow Model for Optimisation of Tidal Turbine Arrays. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 2017. [Google Scholar]
- Coppinger, D. Development of a Nested 3D Hydrodynamic Model for Tidal Turbine Impact Assessment. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 2016. [Google Scholar]
- Sun, X.; Chick, J.P.; Bryden, I.G. Laboratory-scale simulation of energy extraction from tidal currents. Renew. Energy 2008, 33, 1267–1274. [Google Scholar] [CrossRef]
- Neill, S.; Jordan, J.R.; Couch, S.J. Impact of tidal energy converter (TEC) arrays on the dynamics of headland sand banks. Renew. Energy 2012, 37, 387–397. [Google Scholar] [CrossRef]
- Plew, D.; Stevens, C. Numerical modelling of the effect of turbines on currents in a tidal channel—Tory Channel, New Zealand. Renew. Energy 2013, 57, 269–282. [Google Scholar] [CrossRef]
- Ramos, V.; Carballo, R.; Álvarez, M.; Sánchez, M.; Iglesias, G. Assessment of the impacts of tidal stream energy through high-resolution numerical modeling. Energy 2013, 61, 541–554. [Google Scholar] [CrossRef]
- Sheng, J.; Thompson, K.; Greenberg, D.; Hill, P. Assessing the Far Field Effects of Tidal Power Extraction on the Bay of Fundy, Gulf of Maine and Scotian Shelf—Final Report; Department of Oceanography, Dalhousie University: Halifax, NS, Canada, 2012. [Google Scholar]
- Whelan, J.I.; Graham, J.M.R.; Peiró, J. A free-surface and blockage correction for tidal turbines. J. Fluid Mech. 2009, 624, 281. [Google Scholar] [CrossRef]
- Draper, S.; Houlsby, G.T.; Oldfield, M.L.G.; Borthwick, A.G.L. Modelling tidal energy extraction in a depth-averaged coastal domain. IET Renew. Power Gener. 2010, 4, 545. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Draper, S.; Oldfield, M.L.G. Application of Linear Momentum Actuator Disc Theory to Open Channel Flow; Technical Report OUEL2296/08; Oxford University Engineering Laboratory UK: Oxford, UK, 2008. [Google Scholar]
- Adcock, T.A.A.; Draper, S.; Houlsby, G.T.; Borthwick, A.G.L.; Serhadlioglu, S. The available power from tidal stream turbines in the Pentland Firth. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130072. [Google Scholar] [CrossRef]
- Draper, S.; Adcock, T.A.A.; Borthwick, A.G.L.; Houlsby, G.T. Estimate of the tidal stream power resource of the Pentland Firth. Renew. Energy 2014, 63, 650–657. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Draper, S. Power extraction from tidal channels—Multiple tidal constituents, compound tides and overtides. Renew. Energy 2014, 63, 797–806. [Google Scholar] [CrossRef]
- Serhadlıoğlu, S.; Adcock, T.A.A.; Houlsby, G.T.; Draper, S.; Borthwick, A.G.L. Tidal stream energy resource assessment of the Anglesey Skerries. Int. J. Mar. Energy 2013, 3–4, e98–e111. [Google Scholar] [CrossRef]
- Flores Mateos, L.; Hartnett, M. Incorporation of a Non-constant Thrust Force Coefficient to Assess Tidal-stream Energy. Energies 2019, 12, 4151. [Google Scholar] [CrossRef]
- Shyue, K.M. An Efficient Shock-Capturing Algorithm for Compressible Multicomponent Problems. J. Comput. Phys. 1998, 142, 208–242. [Google Scholar] [CrossRef]
- Falconer, R. Temperature distributions in tidal flow field. J. Environ. Eng. 1984, 110, 1099–1116. [Google Scholar] [CrossRef]
- Sparks, T.D.; Bockelmann-Evans, B.N.; Falconer, R.A. Laboratory Validation of an Integrated Surface Water–Groundwater Model. J. Water Resour. Prot. 2013, 05, 377–394. [Google Scholar] [CrossRef]
- Gao, G.; Falconer, R.; Lin, B. Numerical modelling of sedimente-bacteria interaction processes in surface waters. Water Res. 2011, 45, 10. [Google Scholar] [CrossRef]
- Kadiri, M.; Ahmadian, R.; Bockelmann-Evans, B.; Rauen, W.; Falconer, R. A review of the potential water quality impacts of tidal renewable energy systems. Renew. Sustain. Energy Rev. 2012, 16, 329–341. [Google Scholar] [CrossRef]
- Kadiri, M.; Ahmadian, R.; Bockelmann-Evans, B.; Kay, D.; Falconer, R. Impact of Different Marine Renewable Energy Scheme Operating Modes on the Eutrophication Potential of the Severn Estuary. In Proceedings of the 35th IAHR World Congress, Chengdu, China, 8–13 September 2013; pp. 1554–1559. [Google Scholar]
- Sparks, T.D.; Bockelmann-Evans, B.N.; Falconer, R.A. Development and Analytical Verification of an Integrated 2-D Surface Water–Groundwater Model. Water Resour. Manag. 2013, 27, 2989–3004. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.; Wicks, J. Benchmarking of flood inundation extent using various dynamically linked one- and two-dimensional approaches. Flood Risk Manag. 2015, 11, S314–S328. [Google Scholar] [CrossRef]
- Kvočka, D.; Falconer, R.A.; Bray, M. Appropriate model use for predicting elevations and inundation extent for extreme flood events. Nat. Hazards 2015, 79, 1791–1808. [Google Scholar] [CrossRef]
- Liang, D.; Falconer, R.A.; Lin, B. Comparison between TVD-MacCormack and ADI-type solvers of the shallow water equations. Adv. Water Resour. 2006, 29, 1833–1845. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. Simulation of rapidly varying flow using an efficient TVD–MacCormack scheme. Int. J. Numer. Methods Fluids 2007, 53, 811–826. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. A boundary-fitted numerical model for flood routing with shock-capturing capability. J. Hydrol. 2007, 332, 477–486. [Google Scholar] [CrossRef]
- Liang, D.; Wang, X.; Falconer, R.A.; Bockelmann-Evans, B.N. Solving the depth-integrated solute transport equation with a TVD-MacCormack scheme. Environ. Model. Softw. 2010, 25, 1619–1629. [Google Scholar] [CrossRef]
- Hunter, N.M.; Villanueva, I.; Pender, G.; Lin, B.; Mason, D.C.; Falconer, R.A.; Neelz, S.; Crossley, A.J.; Bates, P.D.; Liang, D.; et al. Benchmarking 2D hydraulic models for urban flooding. Proc. ICE Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Neelz, S.; Pender, G. Desktop Review of 2D Hydraulic Modelling Packages; Technical Report SC080035; Department for Environment Food and Rural Affairs: Bristol, UK, 2006.
- Falconer, R.A. An Introduction to Nearly-horizontal flows. In Coastal, Estuarial and Harbour Engineers’ Reference Book; Abbott, M.B., Price, W.A., Eds.; Chapman and Hall: London, UK, 1993; Chapter 2. [Google Scholar]
- Draper, S.; Borthwick, A.G.; Houlsby, G.T. Energy potential of a tidal fence deployed near a coastal headland. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 20120176. [Google Scholar] [CrossRef]
- Adcock, T.A.; Draper, S.; Nishino, T. Tidal power generation—A review of hydrodynamic modelling. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 755–771. [Google Scholar] [CrossRef]
- Nishino, T.; Willden, R.H.J. Effects of 3-D channel blockage and turbulent wake mixing on the limit of power extraction by tidal turbines. Int. J. Heat Fluid Flow 2012, 37, 123–135. [Google Scholar] [CrossRef]
- Perez-Ortiz, A.; Borthwick, A.; McNaughton, J.; Avdis, A. Characterization of the Tidal Resource in Rathlin Sound. Renew. Energy 2017. [Google Scholar] [CrossRef]
- Flores Mateos, L.; Hartnett, M. Depth average tidal resource assessment considering an open channel flow. In Advances in Renewable Energies Offshore: Proceedings of the 3rd International Conference on Renewable Energies Offshore (RENEW); Soares Guedes, C., Ed.; Taylor & Francis Group: Abingdon, UK, 2018; p. 10. [Google Scholar]
- Flores Mateos, L.M.; Hartnett, M. Tidal-stream power assessment—A novel modelling approach. Energy Rep. 2020, 6, 108–113. [Google Scholar] [CrossRef]
- Falconer, R.; Lin, B. DIVAST Model Reference Manual; Report; Cardiff University: Cardiff, UK, 2001. [Google Scholar]
- Stelling, G.S.; Wiersman, A.K.; Willemse, J.B.T.M. Practical aspects of accurate tidal computations. J. Hydraul. Eng. 1986, 112, 802–816. [Google Scholar] [CrossRef]
- Ming, H.T.; Chu, C.R. Two-dimensional shallow water flows simulation using TVD-MacCormack Scheme. J. Hydraul. Res. 2000, 38, 123–131. [Google Scholar] [CrossRef]
- Rogers, B.D.; Borthwick, A.G.L.; Taylor, P.H. Mathematical balancing of flux gradient and source terms prior to using Roe’s approximate Riemann solver. J. Comput. Phys. 2003, 192, 422–451. [Google Scholar] [CrossRef]
- Flores Mateos, L. Tidal Stream Energy Assessment with and without a Shock Capture Scheme—Incorporating a Non-Constant Thrust Force Coefficient. Ph.D. Thesis, NUI Galway, Galway, Ireland, 2019. [Google Scholar]
- Kvocka, D. DIVAST-TVD User Manual; Technical Report; Hydro-Environmental Research Centre School of Engineering Cardiff University: Cardiff, UK, 2015. [Google Scholar]
- Whittaker, P. Modelling the Hydrodynamic Drag Force of Flexible RiparianWoodland. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2014. [Google Scholar]
- Kvočka, D. Modelling Elevations, Inundation Extent and Hazard Risk for Extreme Flood Events. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2017. [Google Scholar]
- Arakawa, A.; Lamb, V. Computational design of the basic dynamical processes of the UCLA general circulation model. Methods Comput. Phys. 1977, 17, 173–265. [Google Scholar]
- Nash, S. Development of an Efficient Dynamically-Nested Model for Tidal Hydraulics and Solute Transport. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 2010. [Google Scholar]
- Bellos, V.; Tsakiris, G. Grid coarsening and uncertainty in 2D hydrodynamic modelling. In Sustainable Hydraulics in the Era of Global Change; Erpicum, S., Dewals, B., Archambeau, P., Pirotton, M., Eds.; Taylor & Francis Group: London, UK, 2016; pp. 714–720. [Google Scholar] [CrossRef]
- Takafumi, N.; Willden, R.H. The Efficiency Of Tidal Fences: A Brief Review And Further Discussion On the Effect of Wake Mixing. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; p. 10. [Google Scholar]
- Vogel, C.; Willden, R.; Houlsby, G. A correction for depth-averaged simulations of tidal turbine arrays. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Perez-Campos, E.; Nishino, T. Numerical Validation of the Two-Scale Actuator Disc Theory for Marine Turbine Arrays. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; p. 8. [Google Scholar]
- Blunden, L.S.; Bahaj, A.S. Tidal energy resource assessment for tidal stream generators. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 221, 137–146. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. Limits to tidal current power. Renew. Energy 2008, 33, 2485–2490. [Google Scholar] [CrossRef]
- Nishino, T.; Willden, R.H.J. The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 2012, 708, 596–606. [Google Scholar] [CrossRef]
- Bonar, P.A.J.; Bryden, I.G.; Borthwick, A.G.L. Social and ecological impacts of marine energy development. Renew. Sustain. Energy Rev. 2015, 47, 486–495. [Google Scholar] [CrossRef]





| Model | Configuration | Scenario | B | (s) | |
|---|---|---|---|---|---|
| ADI | Fence | 1 | 12 | ||
| 2 | B = 0.2 | 0 1 | 12 | ||
| Partial-Fence | 3 | 12 | |||
| TVD | Fence | 4 | 1.5 | ||
| 5 | B = 0.2 | 0 1 | 1.5 | ||
| Partial-Fence | 6 | 1.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores Mateos, L.; Hartnett, M. Hydrodynamic Effects of Tidal-Stream Power Extraction for Varying Turbine Operating Conditions. Energies 2020, 13, 3240. https://doi.org/10.3390/en13123240
Flores Mateos L, Hartnett M. Hydrodynamic Effects of Tidal-Stream Power Extraction for Varying Turbine Operating Conditions. Energies. 2020; 13(12):3240. https://doi.org/10.3390/en13123240
Chicago/Turabian StyleFlores Mateos, Lilia, and Michael Hartnett. 2020. "Hydrodynamic Effects of Tidal-Stream Power Extraction for Varying Turbine Operating Conditions" Energies 13, no. 12: 3240. https://doi.org/10.3390/en13123240
APA StyleFlores Mateos, L., & Hartnett, M. (2020). Hydrodynamic Effects of Tidal-Stream Power Extraction for Varying Turbine Operating Conditions. Energies, 13(12), 3240. https://doi.org/10.3390/en13123240