Spatial Differences in Carbon Intensity in Polish Households
Abstract
1. Introduction
2. Literature Review
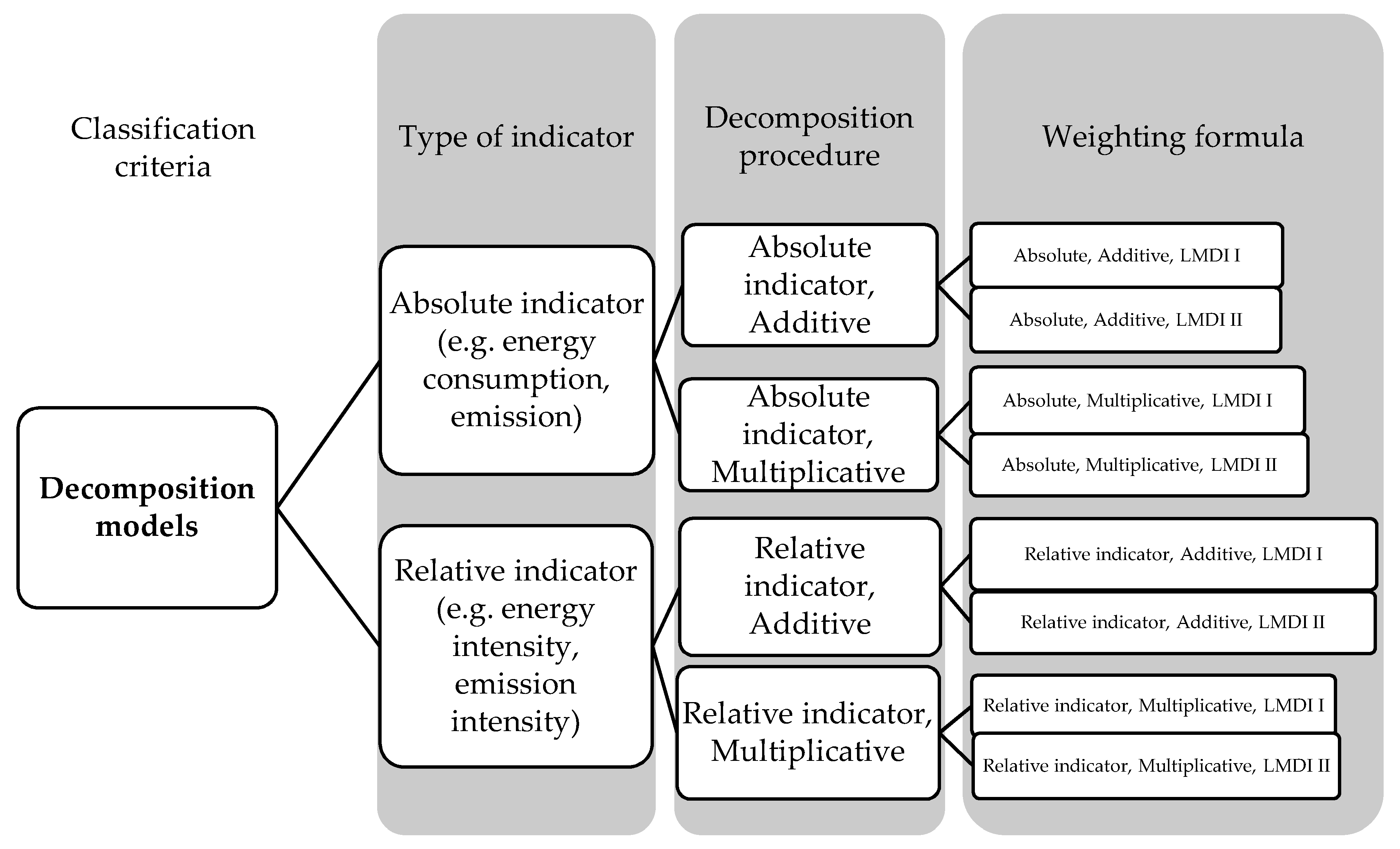
2.1. Logarithmic Mean Divisia Index Methodology
- Completeness—a residual equals zero; while most of techniques using arithmetic mean weights leave a residual in the calculations, the LMDI uses a logarithmic mean weight and allows perfect decomposition;
- Factor-reversal and time-reversal—the order of factors and direction of comparison over time do not affect the results;
- Zero value robustness—in case of LMDI, zeroes in the data set are replaced with a small positive number.
2.2. Research Outcomes
3. Materials and Methods
3.1. Socio-Economic Characteristics of Regions
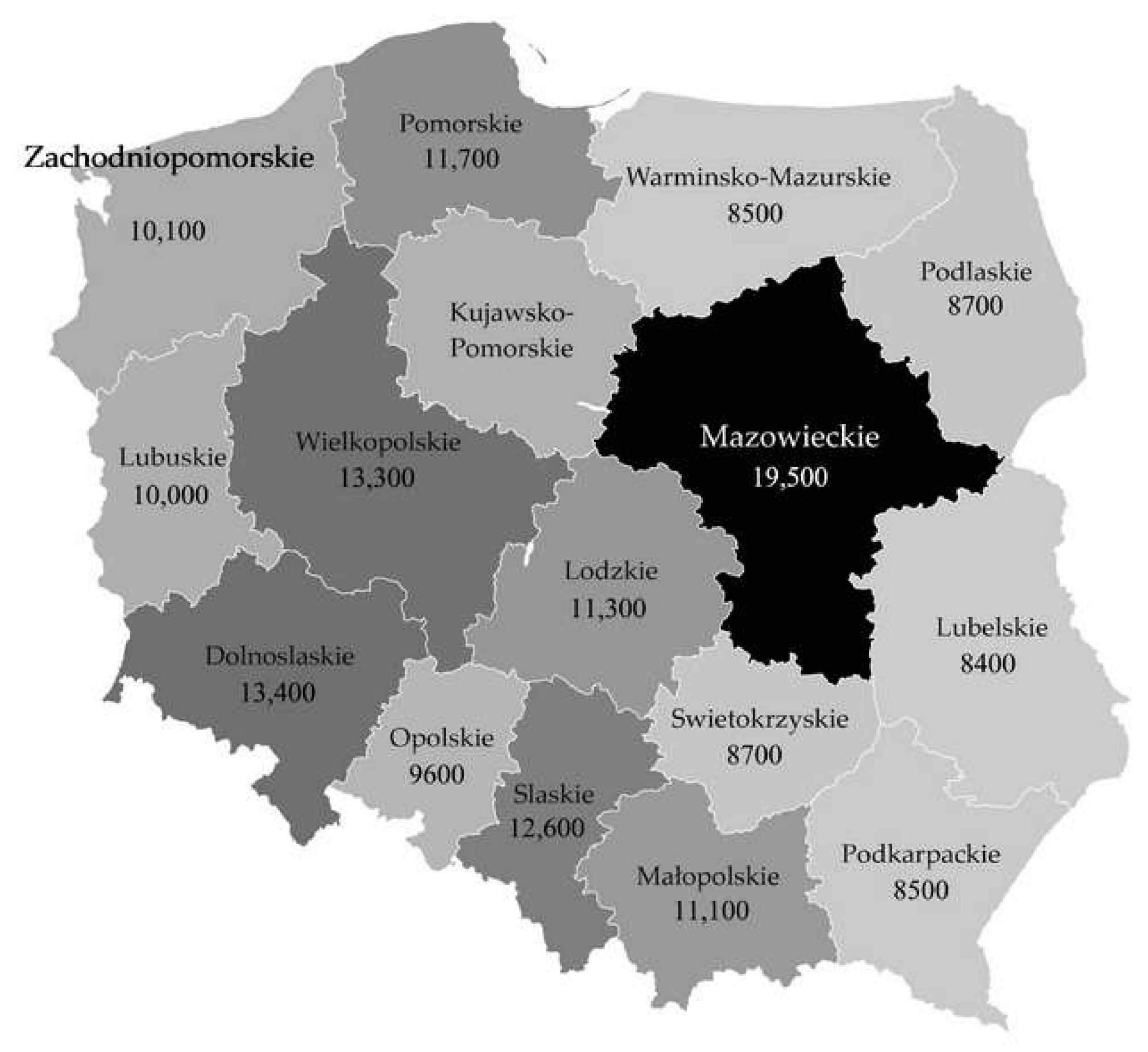
- Difference between the central region and the remaining regions (Mazowieckie with Warsaw, the capital of Poland evidently dominates in terms of GDP per capita, as shown in Figure 2);
- Geographical axis: North East–South West (less developed regions except for Mazowieckie are in the north-east and most developed regions are in the west and south-west),
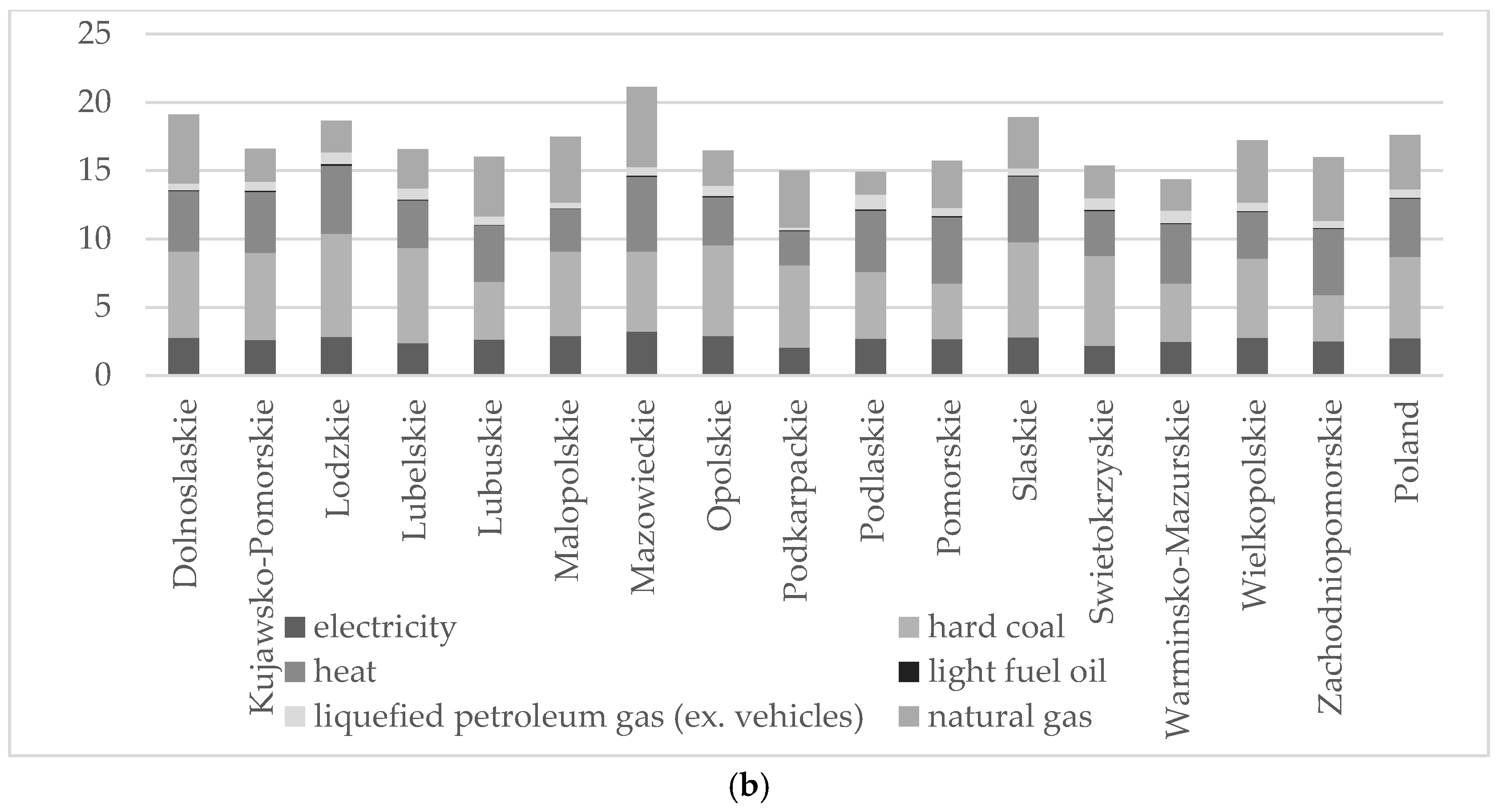
- Concentration of industry, including energy industry in some regions (Table 1).
3.2. Index Decomposition Analysis Methodology
4. Results
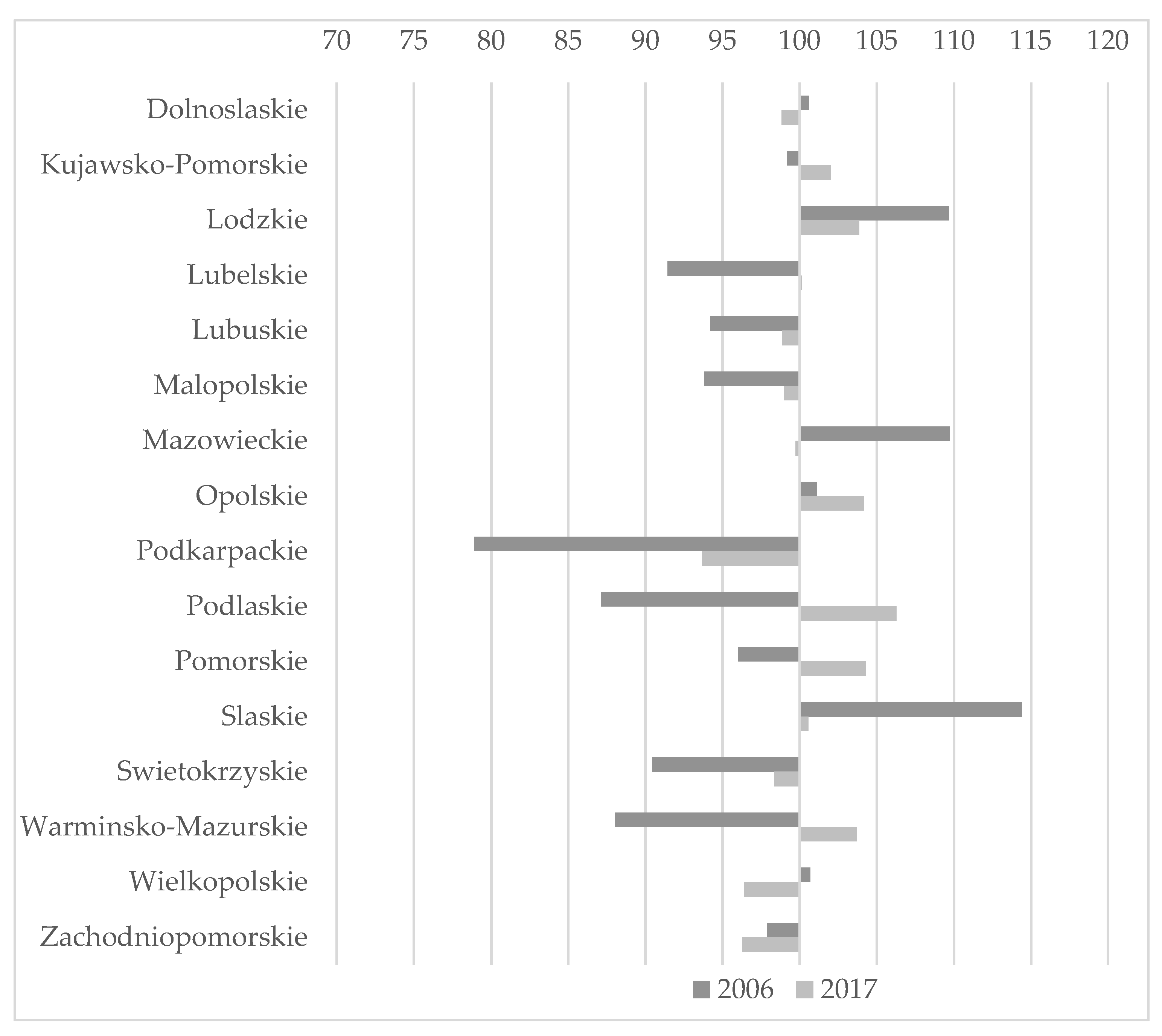
4.1. Decomposition of Differences in Total GHG Emission per Capita
4.2. Decomposition of Differences in CO2 Emission per Capita in Households
5. Discussion
Funding
Conflicts of Interest
References
- A Policy Framework for Climate and Energy in the Period from 2020 to 2030. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of Regions, COM/2014/015 Final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52014DC0015 (accessed on 24 May 2020).
- EU Cohesion Policy 2014–2020, Targeting Investments on Key Growth Priorities. Available online: https://ec.europa.eu/regional_policy/sources/docgener/informat/2014/fiche_low_carbon_en.pdf (accessed on 30 August 2019).
- Proposal for a Regulation of the European Parliament and of the Council on the European Regional Development Fund and on the Cohesion Fund, COM/2018/372 Final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2018%3A372%3AFIN (accessed on 24 May 2020).
- Proposal for a Regulation of the European Parliament and of the Council establishing the Just Transition Fund, COM/2020/22 Final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52020PC0022 (accessed on 24 May 2020).
- Updated Draft Energy Policy of Poland until 2040. Available online: https://www.gov.pl/web/aktywa-panstwowe/zaktualizowany-projekt-polityki-energetycznej-polski-do-2040-r (accessed on 24 May 2020).
- Resolution of the Council of Ministers of 16 July 2019 on the State Environmental Policy 2030 (Uchwała nr 67 Rady Ministrów z dnia 16 lipca 2019 r. w Sprawie Przyjęcia “Polityki Ekologicznej Państwa 2030—Strategii Rozwoju w Obszarze środowiska i Gospodarki Wodnej). Available online: http://prawo.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WMP20190000794 (accessed on 24 May 2020).
- National Strategy for Regional Development (Krajowa Strategia Rozwoju Regionalnego). 2019. Available online: https://www.gov.pl/attachment/38c54257-5b35-4b2d-b379-c897a31c85e7 (accessed on 25 May 2020).
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-89560-6. [Google Scholar]
- Ang, B.W.; Liu, N. Energy decomposition analysis: IEA model versus other methods. Energy Policy 2007, 35, 1426–1432. [Google Scholar] [CrossRef]
- Ang, B.W.; Goh, T. Index decomposition analysis for comparing emission scenarios: Applications and challenges. Energy Econ. 2019, 83, 74–87. [Google Scholar] [CrossRef]
- Su, B.; Ang, B.W. Structural decomposition analysis applied to energy and emissions: Some methodological developments. Energy Econ. 2012, 34, 177–188. [Google Scholar] [CrossRef]
- Hoekstra, R.; van den Bergh, J.C.J.M. Comparing structural decomposition analysis and index. Energy Econ. 2003, 25, 39–64. [Google Scholar] [CrossRef]
- Sun, J.W. Changes in energy consumption and energy intensity: A complete decomposition model. Energy Econ. 1998, 20, 85–100. [Google Scholar] [CrossRef]
- Ang, B.W. LMDI decomposition approach: A guide for implementation. Energy Policy 2015, 86, 233–238. [Google Scholar] [CrossRef]
- Ang, B.W. Decomposition analysis for policymaking in energy: Which is the preferred method? Energy Policy 2004, 32, 1131–1139. [Google Scholar] [CrossRef]
- Soytaş, U.; Sarı, R. Routledge Handbook of Energy Economics; Routledge: Abington, UK, 2019; ISBN 978-1-315-45963-9. [Google Scholar]
- Choi, K.-H.; Ang, B.W. Attribution of changes in Divisia real energy intensity index—An extension to index decomposition analysis. Energy Econ. 2012, 34, 171–176. [Google Scholar] [CrossRef]
- Su, B.; Ang, B.W. Multi-region comparisons of emission performance: The structural decomposition analysis approach. Ecol. Indic. 2016, 67, 78–87. [Google Scholar] [CrossRef]
- Ang, B.W.; Xu, X.Y.; Su, B. Multi-country comparisons of energy performance: The index decomposition analysis approach. Energy Econ. 2015, 47, 68–76. [Google Scholar] [CrossRef]
- Song, C.; Zhao, T.; Wang, J. Spatial-temporal analysis of China’s regional carbon intensity based on ST-IDA from 2000 to 2015. J. Clean. Prod. 2019, 238, 117874. [Google Scholar] [CrossRef]
- Zhang, W.; Li, K.; Zhou, D.; Zhang, W.; Gao, H. Decomposition of intensity of energy-related CO2 emission in Chinese provinces using the LMDI method. Energy Policy 2016, 92, 369–381. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, Y.; Yu, Y. Spatial decomposition analysis of water intensity in China. Socioecon. Plann. Sci. 2020, 69, 100680. [Google Scholar] [CrossRef]
- Huang, J.; Du, D.; Tao, Q. An analysis of technological factors and energy intensity in China. Energy Policy 2017, 109, 1–9. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Y.; Li, Y. The spillovers of foreign direct investment and the convergence of energy intensity. J. Clean. Prod. 2019, 206, 611–621. [Google Scholar] [CrossRef]
- Yan, H. Provincial energy intensity in China: The role of urbanization. Energy Policy 2015, 86, 635–650. [Google Scholar] [CrossRef]
- Aldieri, L.; Kotsemir, M.; Paolo Vinci, C. Environmental innovations and productivity: Empirical evidence from Russian regions. Resour. Policy 2019, in press. [Google Scholar] [CrossRef]
- Bossanyi, E. UK primary energy consumption and the changing structure of final demand. Energy Policy 1979, 7, 253–258. [Google Scholar] [CrossRef]
- Ang, B.W.; Zhang, F.Q. A survey of index decomposition analysis in energy and environmental studies. Energy 2000, 25, 1149–1176. [Google Scholar] [CrossRef]
- Xu, X.Y.; Ang, B.W. Index decomposition analysis applied to CO2 emission studies. Ecol. Econ. 2013, 93, 313–329. [Google Scholar] [CrossRef]
- Ang, B.W.; Zhang, F.Q. Inter-regional comparisons of energy-related CO2 emissions using the decomposition technique. Energy 1999, 24, 297–305. [Google Scholar] [CrossRef]
- Kim, K.; Kim, Y. International comparison of industrial CO2 emission trends and the energy efficiency paradox utilizing production-based decomposition. Energy Econ. 2012, 34, 1724–1741. [Google Scholar] [CrossRef]
- Fernández González, P.; Landajo, M.; Presno, M.J. Multilevel LMDI decomposition of changes in aggregate energy consumption. A cross country analysis in the EU-27. Energy Policy 2014, 68, 576–584. [Google Scholar] [CrossRef]
- Liu, N.; Ma, Z.; Kang, J. A regional analysis of carbon intensities of electricity generation in China. Energy Econ. 2017, 67, 268–277. [Google Scholar] [CrossRef]
- Hang, Y.; Wang, Q.; Wang, Y.; Su, B.; Zhou, D. Industrial SO2 emissions treatment in China: A temporal-spatial whole process decomposition analysis. J. Environ. Manag. 2019, 243, 419–434. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, H.; Wu, F.; Chiu, Y.; Zhang, C. The Driving Effect of Spatial Differences of Water Intensity in China. Nat. Resour. Res. 2019, 1–14. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, H.; Zhang, C.; Zhang, W. Driving effects of spatial differences of water consumption based on LMDI model construction and data description. Clust. Comput. 2019, 22, 6315–6334. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G.; Dong, Y.; Cheng, Y.; Shang, P. The Scale, Structure and Influencing Factors of Total Carbon Emissions from Households in 30 Provinces of China—Based on the Extended STIRPAT Model. Energies 2018, 11, 1125. [Google Scholar] [CrossRef]
- Shi, Y.; Han, B.; Han, L.; Wei, Z. Uncovering the national and regional household carbon emissions in China using temporal and spatial decomposition analysis models. J. Clean. Prod. 2019, 232, 966–979. [Google Scholar] [CrossRef]
- Zhang, P.; Duan, M.; Yin, G. The Periodic Characteristics of China’s Economic Carbon Intensity Change and the Impacts of Economic Transformation. Energies 2018, 11, 961. [Google Scholar] [CrossRef]
- Lin, J.; Liu, Y.; Hu, Y.; Cui, S.; Zhao, S. Factor decomposition of Chinese GHG emission intensity based on the Logarithmic Mean Divisia Index method. Carbon Manag. 2014, 5, 579–586. [Google Scholar] [CrossRef]
- Xu, X.; Tan, Y.; Chen, S.; Yang, G.; Su, W. Urban Household Carbon Emission and Contributing Factors in the Yangtze River Delta, China. PLoS ONE 2015, 10, e0121604. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Baiocchi, G.; Creutzig, F. CO2 Emissions from Direct Energy Use of Urban Households in India. Environ. Sci. Technol. 2015, 49, 11312–11320. [Google Scholar] [CrossRef] [PubMed]
- Hargreaves, K.; Preston, I.; White, V.; Thumim, J. The distribution of household CO2 emissions in Great Britain. JRF Programme Pap. Clim. Chang. Soc. Justice Updat. Version Suppl. Proj. Pap. 2013, 1, 1998–2004. [Google Scholar]
- Andrés, L.; Padilla, E. Energy intensity in road freight transport of heavy goods vehicles in Spain. Energy Policy 2015, 85, 309–321. [Google Scholar] [CrossRef]
- Fernández González, P.; Landajo, M.; Presno, M.J. The Divisia real energy intensity indices: Evolution and attribution of percent changes in 20 European countries from 1995 to 2010. Energy 2013, 58, 340–349. [Google Scholar] [CrossRef]
- Fernández González, P. Exploring energy efficiency in several European countries. An attribution analysis of the Divisia structural change index. Appl. Energy 2015, 137, 364–374. [Google Scholar] [CrossRef]
- Fernández González, P.; Presno, M.J.; Landajo, M. Regional and sectoral attribution to percentage changes in the European Divisia carbonization index. Renew. Sustain. Energy Rev. 2015, 52, 1437–1452. [Google Scholar] [CrossRef]
- Fernández González, P.; Landajo, M.; Presno, M.J. The Driving Forces of Change in Environmental Indicators; Lecture Notes in Energy; Springer International Publishing: Cham, Switzerland, 2014; Volume 25, ISBN 978-3-319-07505-1. [Google Scholar]
- Barrett, J.; Wiedmann, T.; Minx, J. Understanding Changes in UK CO2 Emissions 1992–2004: A Structural Decomposition Analysis; Report to the UK Department for Environment, Food and Rural Affairs; Stockholm Environment Institute and Durham Business School, 2009; Available online: https://www.sei.org/mediamanager/documents/Publications/SEI-ResearchReport-Minx-UnderstandingChangesInUKCO2Emissions-1992-2004-AStructuralDecompositionApproach-2009.pdf (accessed on 25 February 2020).
- Hammond, G.P.; Norman, J.B. Decomposition analysis of energy-related carbon emissions from UK manufacturing. Energy 2012, 41, 220–227. [Google Scholar] [CrossRef]
- Seibel, S. Decomposition Analysis of Carbon Dioxide-Emission Changes in Germany—Conceptual Framework and Empirical Results (PDF); Office for Official Publications of the European Communities: Luxembourg, 2003. [Google Scholar]
- Jensen, P.R.; Olsen, T. Analysis of Changes in Air Emissions in Denmark; Statistics Denmark: Copenhagen, Denmark, 2003. [Google Scholar]
- van Megen, B.; Bürer, M.; Patel, M.K. Comparing electricity consumption trends: A multilevel index decomposition analysis of the Genevan and Swiss economy. Energy Econ. 2019, 83, 1–25. [Google Scholar] [CrossRef]
- Ivanova, D.; Vita, G.; Steen-Olsen, K.; Stadler, K.; Melo, P.C.; Wood, R.; Hertwich, E.G. Mapping the carbon footprint of EU regions. Environ. Res. Lett. 2017, 12, 54013. [Google Scholar] [CrossRef]
- Gozdek, A.; Szaruga, E. Analiza dekompozycyjna wzrostu emisji gazów cieplarnianych z transportu samochodowego na przykładzie Polski i Rumunii. Zesz. Naukowe. Probl. Transp. Logist. Uniw. Szczec. 2015, 29, 371–383. [Google Scholar] [CrossRef]
- Iskrzycki, K.; Suwała, W.; Kaszyński, P. Dekompozycja redukcji emisji dwutlenku siarki w polskich elektrowniach, 1995–2008. Polityka Energ. 2011, 14, 107–125. [Google Scholar]
- Suwała, W. Perspektywy technologii węglowych w energetyce w warunkach ograniczenia emisji dwutlenku węgla/Prospects of coal based power in the carbon emissions limiting system. Polityka Energ. 2008, 11, 489–497. [Google Scholar]
- Statistics Poland—Local Data Bank. Available online: https://bdl.stat.gov.pl/BDL/dane/podgrup/temat (accessed on 7 March 2020).
- Wartości Opałowe (WO) i Wskaźniki Emisji CO2 (WE) w roku 2017 do Raportowania w Ramach Systemu Handlu Uprawnieniami do Emisji za rok 2020 (Calorific Values and Emission Factors in 2017 for Reporting within the Emissions Trading Scheme in 2020); Krajowy Ośrodek Bilansowania i Zarządzania Emisjami/The National Centre for Emissions Management: Warsaw, Poland, 2019; Available online: https://www.kobize.pl/uploads/materialy/download/WO_i_WE_do_monitorowania-ETS-2020.pdf (accessed on 10 February 2020).
- Wskaźniki Emisyjności CO2, SO2, NOx, CO i pyłu Całkowitego dla Energii Elektrycznej na Podstawie Informacji Zawartych w Krajowej bazie o Emisjach Gazów Cieplarnianych i Innych Substancji za 2017 rok (Emission Factors for CO2, SO2, NOx, CO and Dust for Electricity, According to National Base on Emissions of Greenhouse Gases, 2017); Krajowy Ośrodek Bilansowania i Zarządzania Emisjami/The National Centre for Emissions Management: Warsaw, Poland, 2018; Available online: https://www.kobize.pl/uploads/materialy/materialy_do_pobrania/wskazniki_emisyjnosci/Wskazniki_emisyjnosci_grudzien_2019.pdf (accessed on 10 February 2020).
- Energetyka Cieplna w Liczbach 2018 (Heat Sector in Numbers 2018, Document in Polish); Urząd Regulacji Energetyki/Energy Regulatory Office: Warsaw, Poland, 2018. Available online: https://www.ure.gov.pl/download/9/10380/Energetykacieplnawliczbach-2018.pdf (accessed on 11 February 2020).
- Environment, Energy, and Economy: Strategies for Sustainability; Kaya, Y., Yokobori, K., Eds.; United Nations University Press: Tokyo, Japan, 1997. [Google Scholar]
- Ang, B.W.; Choi, K.-H. Decomposition of Aggregate Energy and Gas Emission Intensities for Industry: A Refined Divisia Index Method. Energy J. 1997, 18, 59–73. [Google Scholar] [CrossRef]
- Choi, K.-H.; Ang, B.W. Decomposition of aggregate energy intensity changes in two measures: Ratio and difference. Energy Econ. 2003, 25, 615–624. [Google Scholar] [CrossRef]
- Ottelin, J.; Heinonen, J.; Nässén, J.; Junnila, S. Household carbon footprint patterns by the degree of urbanisation in Europe. Environ. Res. Lett. 2019, 14, 114016. [Google Scholar] [CrossRef]
- Druckman, A.; Jackson, T. The carbon footprint of UK households 1990–2004: A socio-economically disaggregated, quasi-multi-regional input–output model. Ecol. Econ. 2009, 68, 2066–2077. [Google Scholar] [CrossRef]
- Zhang, H.; Lahr, M.L.; Bi, J. Challenges of green consumption in China: A household energy use perspective. Econ. Syst. Res. 2016, 28, 183–201. [Google Scholar] [CrossRef]
- Wang, C.; Guo, Y.; Shao, S.; Fan, M.; Chen, S. Regional carbon imbalance within China: An application of the Kaya-Zenga index. J. Environ. Manag. 2020, 262, 110378. [Google Scholar] [CrossRef]
- Jones, C.; Kammen, D.M. Spatial Distribution of U.S. Household Carbon Footprints Reveals Suburbanization Undermines Greenhouse Gas Benefits of Urban Population Density. Environ. Sci. Technol. 2014, 48, 895–902. [Google Scholar] [CrossRef] [PubMed]

| Region | Population [Thousands] | Population Density [Person/km2] | GDP per Inhabitant [% of National Average] | Sold Production of Industry [% of Total Production] | Electricity Production [% of Total Production] | Share of Renewable Energy Sources [% of Electricity Production] |
|---|---|---|---|---|---|---|
| Poland | 38,433.6 | 123 | 100.0 | 100.0 | 100.0 | 14.2 |
| Dolnoslaskie | 2902.5 | 146 | 109.8 | 8.7 | 38.4 | 1.2 |
| Kujawsko-Pomorskie | 2082.9 | 116 | 80.3 | 4.2 | 4.2 | 51.4 |
| Lubelskie | 2126.3 | 85 | 68.9 | 2.7 | 1.3 | 23.5 |
| Lubuskie | 1016.8 | 73 | 82.0 | 2.5 | 1.9 | 21 |
| Lodzkie | 2476.3 | 136 | 92.6 | 5.8 | 22.6 | 4.3 |
| Malopolskie | 3391.4 | 223 | 91.0 | 6.9 | 3.7 | 8.4 |
| Mazowieckie | 5384.6 | 151 | 159.8 | 19.1 | 14.6 | 6.6 |
| Opolskie | 990.1 | 105 | 78.7 | 2.0 | 5.0 | 5.5 |
| Podkarpackie | 2129.1 | 119 | 69.7 | 3.4 | 1.5 | 25.7 |
| Podlaskie | 1184.5 | 59 | 71.3 | 2.0 | 0.7 | 54.7 |
| Pomorskie | 2324.3 | 127 | 95.9 | 6.5 | 2.7 | 53.1 |
| Slaskie | 4548.2 | 369 | 103.3 | 16.7 | 16.3 | 3.2 |
| Swietokrzyskie | 1247.7 | 107 | 71.3 | 2.0 | 6.0 | 20.4 |
| Warminsko-Mazurskie | 1433.9 | 59 | 69.7 | 2.4 | 0.8 | 87.2 |
| Wielkopolskie | 3489.2 | 117 | 109.0 | 12.3 | 7.2 | 14.7 |
| Zachodnio-pomorskie | 1705.5 | 75 | 82.8 | 2.9 | 5.5 | 47.8 |
| Region | GDP per Capita [PLN/person] | GDP Emission Intensity [t CO2 eq /mln PLN] | Emission per Capita [t CO2 eq /person/year] | Emission per Capita [%, Poland = 100%] |
|---|---|---|---|---|
| Poland-mean | 40,125 | 268.3 | 10.8 | 100.0 |
| Dolnoslaskie | 40,928 | 202.4 | 8.3 | 76.9 |
| Kujawsko-Pomorskie | 32,098 | 272.6 | 8.7 | 81.3 |
| Lodzkie | 37,372 | 587.5 | 22.0 | 203.9 |
| Lubelskie | 26,935 | 322.9 | 8.7 | 80.8 |
| Lubuskie | 33,715 | 250.3 | 8.4 | 78.4 |
| Malopolskie | 34,665 | 239.0 | 8.3 | 77.0 |
| Mazowieckie | 66,172 | 162.1 | 10.7 | 99.6 |
| Opolskie | 29,238 | 672.9 | 19.7 | 182.8 |
| Podkarpackie | 28,617 | 171.3 | 4.9 | 45.5 |
| Podlaskie | 26,865 | 315.0 | 8.5 | 78.6 |
| Pomorskie | 38,897 | 182.6 | 7.1 | 66.0 |
| Slaskie | 46,911 | 334.1 | 15.7 | 145.6 |
| Swietokrzyskie | 28,391 | 534.8 | 15.2 | 141.0 |
| Warminsko-Mazurskie | 26,784 | 241.2 | 6.5 | 60.0 |
| Wielkopolskie | 41,187 | 228.8 | 9.4 | 87.5 |
| Zachodnio-pomorskie | 32,735 | 275.7 | 9.0 | 83.8 |
| Fuel | Calorific Value | Emissivity Factor | ||||
|---|---|---|---|---|---|---|
| 2006 | 2017 | Unit | 2006 | 2017 | Unit | |
| electricity | 3.6 | 3.6 | MJ/kWh | 825.4 | 814.0 | kgCO2/MWh |
| heat | 1.0 * | 1.0 * | MJ/MJ | 110.4 | 99.50 | kgCO2/GJ |
| hard coal | 26.3 | 22.4 | MJ/kg | 2.47 | 2.12 | kgCO2/kg |
| light fuel oil | 43.0 | 43.0 | MJ/kg | 3.19 | 3.19 | kgCO2/kg |
| liquefied petroleum gas (ex. vehicles) | 47.3 | 47.3 | MJ/kg | 2.95 | 2.98 | kgCO2/kg |
| natural gas | 1.0 * | 1.0 * | MJ/MJ | 55.82 | 55.41 | kgCO2/GJ |
| Region | Emission per Capita [t] | Energy Emissivity [kg/GJ] | GDI per Capita [PLN2006] | Energy Intensity of GDI [MJ/PLN2006] | ||||
|---|---|---|---|---|---|---|---|---|
| 2006 | 2017 | 2006 | 2017 | 2006 | 2017 | 2006 | 2017 | |
| Dolnoslaskie | 1.97 | 1.98 | 106.48 | 103.65 | 18,090 | 32,075 | 1.02 | 0.74 |
| Kujawsko-Pomorskie | 1.94 | 1.82 | 109.93 | 109.70 | 16,669 | 27,749 | 1.06 | 0.74 |
| Lodzkie | 2.15 | 2.04 | 111.90 | 109.47 | 18,538 | 31,465 | 1.04 | 0.74 |
| Lubelskie | 1.79 | 1.76 | 107.89 | 106.25 | 14,911 | 26,626 | 1.11 | 0.77 |
| Lubuskie | 1.85 | 1.69 | 106.51 | 105.71 | 17,015 | 27,608 | 1.02 | 0.72 |
| Malopolskie | 1.84 | 1.85 | 106.66 | 105.73 | 16,739 | 29,034 | 1.03 | 0.75 |
| Mazowieckie | 2.15 | 2.20 | 107.47 | 104.10 | 20,836 | 37,128 | 0.96 | 0.71 |
| Opolskie | 1.98 | 1.83 | 112.24 | 111.12 | 15,608 | 27,417 | 1.13 | 0.75 |
| Podkarpackie | 1.55 | 1.53 | 100.94 | 102.10 | 14,156 | 24,416 | 1.08 | 0.77 |
| Podlaskie | 1.71 | 1.69 | 114.51 | 113.33 | 15,038 | 25,667 | 0.99 | 0.72 |
| Pomorskie | 1.88 | 1.71 | 112.34 | 108.69 | 17,322 | 29,909 | 0.97 | 0.65 |
| Slaskie | 2.24 | 2.02 | 108.36 | 106.59 | 19,681 | 33,848 | 1.05 | 0.70 |
| Swietokrzyskie | 1.77 | 1.64 | 106.00 | 106.62 | 16,060 | 26,964 | 1.04 | 0.71 |
| Warminsko-Mazurskie | 1.72 | 1.59 | 111.73 | 110.64 | 15,877 | 26,720 | 0.97 | 0.67 |
| Wielkopolskie | 1.97 | 1.81 | 103.88 | 105.31 | 18,777 | 32,334 | 1.01 | 0.66 |
| Zachodnio-pomorskie | 1.92 | 1.67 | 103.74 | 104.26 | 18,065 | 29,748 | 1.02 | 0.67 |
| Poland | 1.96 | 1.87 | 107.75 | 106.28 | 17,769 | 30,711 | 1.02 | 0.71 |
| Region | GDP per Capita | GDP Emission Intensity | Emission per Capita—Total Difference from the Average | Type of Cluster |
|---|---|---|---|---|
| Dolnoslaskie | 1.7 | −24.8 | −23.1 | H-L |
| Kujawsko-Pomorskie | −20.2 | 1.4 | −18.7 | L-H |
| Lubelskie | −35.9 | 16.7 | −19.2 | L-H |
| Lubuskie | −15.4 | −6.2 | −21.6 | L-L |
| Lodzkie | −10.4 | 114.3 | 103.9 | L-H |
| Malopolskie | −12.9 | −10.2 | −23.0 | L-L |
| Mazowieckie | 49.9 | -50.3 | -0.4 | H-L |
| Opolskie | −43.4 | 126.2 | 82.8 | L-H |
| Podkarpackie | −23.4 | −31.1 | −54.5 | L-L |
| Podlaskie | −35.7 | 14.3 | −21.4 | L-H |
| Pomorskie | −2.5 | −31.5 | −34.0 | L-L |
| Slaskie | 19.0 | 26.6 | 45.6 | H-H |
| Swietokrzyskie | −41.3 | 82.3 | 41.0 | L-H |
| Warminsko-Mazurskie | −31.7 | −8.3 | −40.0 | L-L |
| Wielkopolskie | 2.4 | −14.9 | −12.5 | H-L |
| Zachodniopomorskie | −18.7 | 2.5 | −16.2 | L-H |
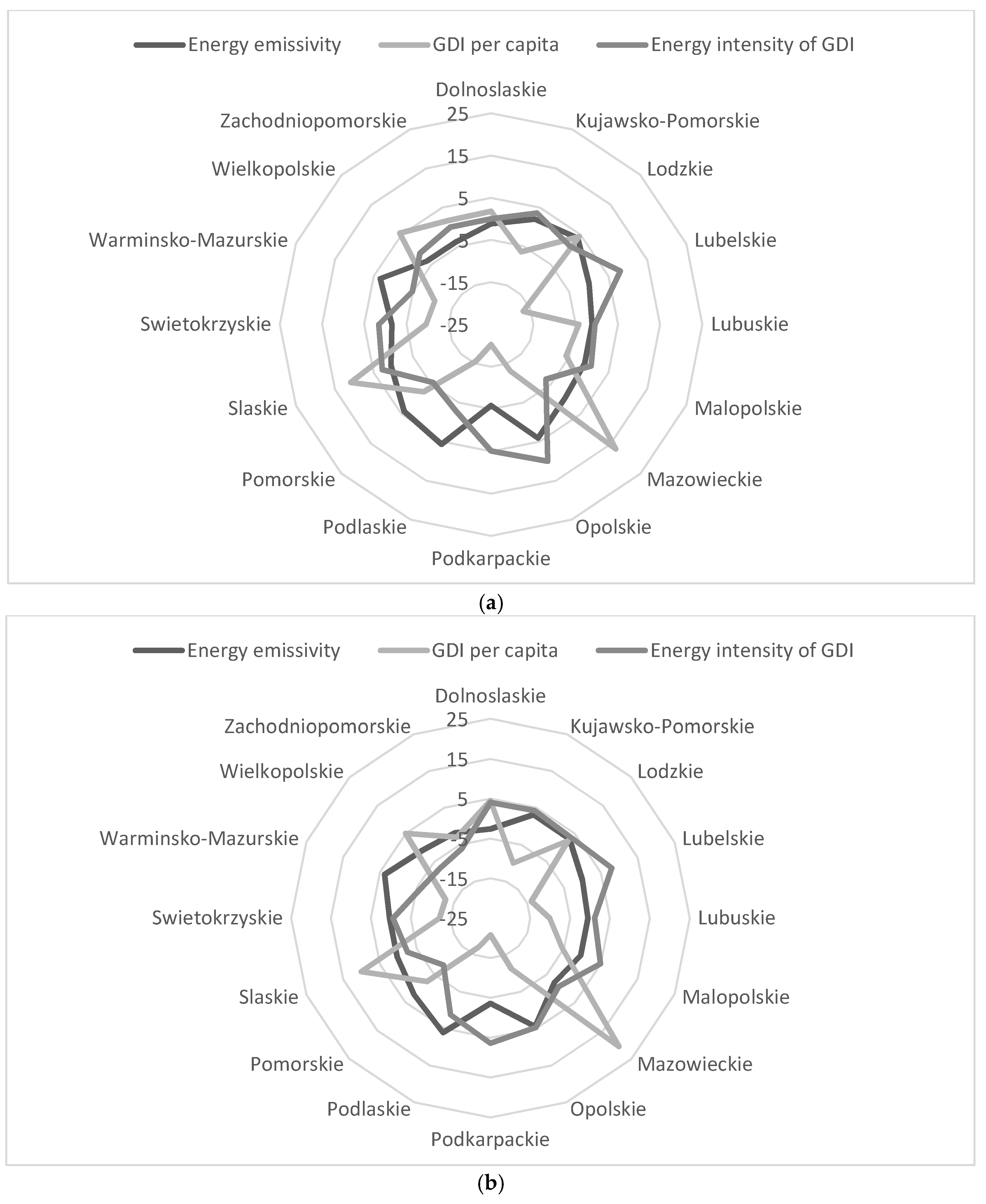
| Region | Energy Emissivity | GDI per Capita | Energy Intensity of GDI | Total Difference in Emission per Capita |
|---|---|---|---|---|
| Dolnoslaskie | −1.19 | 1.80 | 0.01 | 0.62 |
| Kujawsko-Pomorskie | 2.00 | −6.36 | 3.54 | −0.82 |
| Lubelskie | 3.96 | 4.44 | 1.27 | 9.67 |
| Lubuskie | 0.12 | −16.77 | 8.09 | −8.56 |
| Lodzkie | −1.13 | −4.21 | −0.44 | −5.78 |
| Malopolskie | −0.98 | −5.79 | 0.59 | −6.17 |
| Mazowieckie | −0.27 | 16.69 | −6.68 | 9.74 |
| Opolskie | 4.10 | −13.04 | 10.05 | 1.11 |
| Podkarpackie | −5.81 | −20.24 | 4.98 | −21.08 |
| Podlaskie | 5.68 | −15.59 | −2.98 | −12.89 |
| Pomorskie | 4.09 | −2.50 | −5.61 | −4.01 |
| Slaskie | 0.61 | 10.94 | 2.85 | 14.39 |
| Swietokrzyskie | −1.56 | −9.62 | 1.61 | −9.57 |
| Warminsko-Mazurskie | 3.41 | −10.57 | −4.80 | −11.97 |
| Wielkopolskie | −3.67 | 5.54 | −1.18 | 0.68 |
| Zachodniopomorskie | −3.75 | 1.63 | −0.01 | −2.12 |
| Region | Energy Emissivity | GDI per Capita | Energy Intensity of GDI | Total Difference in Emission per Capita |
|---|---|---|---|---|
| Dolnoslaskie | −2.58 | 4.47 | 4.03 | 5.93 |
| Kujawsko-Pomorskie | 3.13 | −10.01 | 4.22 | −2.66 |
| Lubelskie | 3.10 | 2.54 | 3.64 | 9.28 |
| Lubuskie | −0.02 | −13.85 | 7.97 | −5.91 |
| Lodzkie | −0.51 | −10.14 | 1.19 | −9.45 |
| Malopolskie | −0.51 | −5.58 | 4.87 | −1.22 |
| Mazowieckie | −2.24 | 20.60 | −0.78 | 17.57 |
| Opolskie | 4.41 | −11.23 | 4.70 | −2.11 |
| Podkarpackie | −3.63 | −20.80 | 6.43 | −18.01 |
| Podlaskie | 6.11 | −17.05 | 1.22 | −9.72 |
| Pomorskie | 2.15 | −2.53 | −8.31 | −8.69 |
| Slaskie | 0.31 | 10.10 | −2.53 | 7.89 |
| Swietokrzyskie | 0.30 | −12.18 | −0.59 | −12.47 |
| Warminsko-Mazurskie | 3.71 | −12.85 | −5.90 | −15.03 |
| Wielkopolskie | −0.90 | 5.07 | −7.24 | −3.07 |
| Zachodniopomorskie | −1.81 | −3.01 | −6.16 | −10.97 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorczuk-Pietraszko, E. Spatial Differences in Carbon Intensity in Polish Households. Energies 2020, 13, 3108. https://doi.org/10.3390/en13123108
Sidorczuk-Pietraszko E. Spatial Differences in Carbon Intensity in Polish Households. Energies. 2020; 13(12):3108. https://doi.org/10.3390/en13123108
Chicago/Turabian StyleSidorczuk-Pietraszko, Edyta. 2020. "Spatial Differences in Carbon Intensity in Polish Households" Energies 13, no. 12: 3108. https://doi.org/10.3390/en13123108
APA StyleSidorczuk-Pietraszko, E. (2020). Spatial Differences in Carbon Intensity in Polish Households. Energies, 13(12), 3108. https://doi.org/10.3390/en13123108





