1. Introduction
Multi-objective optimization techniques have commonly been used in the context of resource allocation problems. These problems can be modeled as agent systems [
1,
2], with agents that express rational behavior, but where objectives between agents may be conflicting and evaluation function outcomes are incomparable. Often, such problems are modeled in a way where the immediate outcome of the optimization is a Pareto set of viable solutions [
3,
4]. In cases with conflicting objectives among agents, the Pareto set contains multiple solutions that represent different trade-offs in conflicts over resources between objectives. The goal then is to select the best trade-off for the particular domain in which the optimization is applied.
Selecting the best trade-off solution from a Pareto set is a problem on its own. In multi-objective optimization, each objective has an individual objective function, which means that the cost values returned by these objective functions are not necessarily directly comparable. Even in cases where the cost values are comparable, selecting a best trade-off is not possible without a metric to determine which solution is best [
5]. To this end, the concept of social welfare [
6] has been used to rank solutions in Pareto sets depending on their social properties [
5]. The authors in [
7,
8] used such a notion of social welfare to achieve a fair compromise direction when exploring the negotiation space and obtain a solution that can be considered fair. Another notion of social fairness proposed by [
9] is to find a solution from a Pareto set, which ensures that total utility is fairly divided among negotiating agents. The authors in [
10] used multi-objective optimization to achieve a fair balance in requirement fulfillment for users of hand-held communication devices. Here, the authors minimized the standard deviation in the number of fulfilled requirements per customer to achieve a notion of fairness in the final solution. Other approaches have focused on the wellbeing of the society as a whole, where they consider only the combined utility. The authors in [
11] used a genetic algorithm on a climate control optimization problem to create a set of Pareto-optimal solutions. They then applied a utilitarian social metric to select a final solution from the generated Pareto set. The authors in [
12] maximized social welfare in terms of the Nash product on scores given by agents to distributions of indivisible goods in order to select the best distribution.
The authors in [
5] found that the state-of-the-art in many cases considered derivable and quasi-concave utility functions, thus failing to consider cases with non-linear utility functions. Further approaches in the state-of-the-art often apply a social welfare criterion during agent negotiation and use these criteria on agent utility values that are not normalized. This means that while the approaches do offer a metric to compare and rank solutions, they assume homogenous utility functions with comparable values. Finally, the work in [
5] found that work on comparing the performance of different social welfare metrics was limited in existing literature. To this end, the work in [
5] made an effort to compare and evaluate different notions of social welfare on a common problem to get an indication of their properties. Here, Umair et al. introduced the concept of a relative importance graph and post-optimization normalization of objective function values to ensure compatibility between heterogeneous objectives while avoiding the use of weighted functions that do not translate to application domains. This also addresses another challenge in applying multi-objective optimization to a particular problem: the practical application of multi-objective optimization often associates objectives with an implied order of importance. As an example, consider a case where a multi-objective algorithm is to optimize the control of actuators in a building. While minimizing energy consumption is certainly an objective, it is often more important to maintain the comfort of the individuals in the building. This implies a certain order between objectives, where a certain preference exists from the perspective of the building owner/operator. Such a preference has often been modeled using a weighted sum method [
4,
13] where a set of weights or a preference function is defined, in order to select a solution from the Pareto set, which has some desired characteristics. However, using this approach is non-trivial: while the concept of weights is easy to understand, determining weights for a particular problem instance is a challenge on its own.
This paper provides a complete revision of and an extension to the work of [
5]. This paper contains the following contributions in this regard:
A formal definition and a posteriori normalization method used to normalize cost value vectors in the presented social welfare metrics.
An overview of social welfare metrics and the uses identified in the literature in table form.
A revised version of the social welfare metric definitions, the concepts of relative importance, the relative importance graph, and social welfare ordering, as well as a revised presentation of experimental results.
An extended discussion of the implication of social welfare metrics and the use of relative importance in multi-objective optimization by generalizing on the results of the experiments made with commercial greenhouse growers.
The rest of the paper is organized as follows. We start in
Section 2 by introducing an a posteriori normalization method used to make social welfare metrics applicable to problems with heterogeneous objective functions. We then introduce 10 social welfare metrics along with their mathematical definition in
Section 3. In
Section 4, we present the concepts of relative importance and social welfare ordering, and then, in
Section 5, we present the case and formulate it as a multi-objective optimization problem. We also introduce the optimization framework that we utilize along with its configuration. In
Section 6, we present the results of the experiments, and in
Section 7 and
Section 8, we discuss the experimental results and conclude the paper.
2. A Posteriori Normalization
This paper considers the problem of selecting a final solution, , from the Pareto set generated by a multi-objective optimization algorithm. Each solution C contains values for each of the variables being optimized and is associated with a cost value vector, , with n elements, where n is the total number of objectives in the optimization. Element then constitutes the cost values for objective i. The cost value vector is used to determine if solution C belongs to the Pareto set using the Pareto criterion. The Pareto criterion states that a solution C is said to dominate a solution if it is at least as good for all objectives and better for at least one objective. A solution belongs to the Pareto set if it is not dominated by any other solution in the set.
The objective functions may be heterogeneous, meaning that the costs of objective
i and objective
may not be directly comparable. This does not constitute a problem towards determining Pareto optimality, but it does pose a problem when selecting a final solution from the Pareto set. Here, the use of the weighted sum method [
13] can in theory normalize and prioritize cost values returned by heterogeneous objective functions. The trade-off is the inherent drawbacks of using weights in a combined objective function, as these are non-trivial to determine, are only stable within a known range, and do not map to any properties in the problem domain. Another approach is to perform an a priori normalization where each objective function is made to return a value in the range of 0–1. Obviously, this normalizes the values yielded by the objective functions, but it is only possible to do if the entire non-normalized range, over which the objective function spans, is known a priori, before the optimization. That is, we must know the best possible values for the variables over which we optimize for each objective before we begin optimizing.
To cope with these challenges, Umair et al. [
5] suggested an a posteriori-based normalization. As the objective functions may operate on different scales, a normalized cost value vector
with elements containing the normalized cost values for solution
C is created for each solution
C. Here, each element
is normalized on a 0–1 scale defined by the minimum and maximum value for objective
i from any
[
14] for a given instance of
. Thus, the minimum and maximum values could vary between optimization instances, yielding a dynamic normalization mechanism that always takes into account the current solution space. The method is formally defined in Equation (
1).
3. Social Welfare Metrics
One approach to rank solutions in the Pareto set
is to translate the cost value vector into a scalar to compare the magnitude of the scalar between different solutions. To this end, Umair et al. [
5] applied social welfare metrics.
In the context of resource allocation, the purpose of social welfare metrics is to allocate resources in a way that maximizes the social welfare among society members. When resource allocation is performed by means of multi-objective optimization, objectives constitute individuals, and all objectives in a given optimization form the society. The goal is to find values for the optimization variables that represent a desired resource allocation according to the applied social welfare metric.
The work of Umair et al. [
5] surveyed the literature to identify different social welfare metrics and categorize them based on their behavior on a specific resource allocation problem with energy distribution among commercial greenhouse growers.
Table 1 presents the information in aggregated form along with sources in the literature where these methods have found application. From
Table 1, it can be noticed that each social welfare metric has a type associated with it. In total, three types of social welfare metrics were identified by Umair et al. [
5]. These include the inequality based metrics, the fairness based metrics (presented as equality based metrics by Umair et al), and the overall utility based metrics. The social welfare types and the individual metrics are formally defined in the context of multi-objective optimization in the following subsections. We assumed that costs are normalized according to the a posteriori normalization method described in
Section 2. This means that each solution
C is associated with an a posteriori normalized cost for each objective
.
3.1. Inequality Based Metrics
Inequality based metrics comprise metrics that favor the best off individual with the purpose of securing at least one objective in the society to be as good off as possible. This could happen at the expense of all other individuals in the society.
Elitist Social Welfare
The elitist social welfare metric strives to ensure that one individual is favored to the extent possible. The elitist social welfare metric is defined in Equation (
2).
Equation (
2) shows how the elitist social welfare metric ranks solutions based on the normalized cost of the best off objective. Hence, this metric prefers solution
C over solution
if and only if
, where
represents the reordering of the normalized cost value vector
in ascending order.
3.2. Fairness Based Metrics
Fairness based metrics are social welfare metrics that include a notion of fairness. Fairness in the context of optimization social welfare is ensuring, to the extent possible, fair adherence to the goals of all objectives in the optimization. That is, all objectives should be considered equal when selecting a final solution.
3.2.1. Egalitarian Social Welfare
The egalitarian social welfare metric defines fairness as ensuring that the worst off objective is as good off as possible. The egalitarian social welfare metric is defined in Equation (
3).
This means that the egalitarian social welfare metric prefers a solution C over solution if and only if where contains the values of the normalized cost vector rearranged in descending order.
The egalitarian social welfare metric has a weakness in that it only takes into account the normalized cost of the worst off objective while defining the ordering of solutions. Consider three normalized cost value vectors (1,1,0), (1,1,1), and (1,0,0) for solutions , , and , respectively. Each of the vectors is comprised of normalized cost values in decreasing order. The highest cost value in all the cost value vectors is one. In this case, the egalitarian social welfare metric fails to distinguish between solutions that have the same highest (worst) cost and assigns the same order to all three solutions, irrespective of the fact that is better objectively than and .
3.2.2. Lexi-Min Ordering
The lexi-min ordering social welfare metric prefers a solution C over solution if and only if an integer exists such that the following two conditions are satisfied:
Here again, is the normalized cost vector arranged in descending order.
This means that the lexi-min ordering social welfare metric addresses the weakness of the egalitarian social welfare metric by considering the next worst off cost value in compared solutions until their values no longer coincide. The lexi-min ordering social welfare metric will successfully distinguish among three solutions used in the example of the egalitarian social welfare metric and assign different rank to them, , and , respectively.
While the lexi-min ordering social welfare metric offers an improvement over the egalitarian social welfare metric, it deviates from the other social welfare metrics in that it offers no collective cost value. Rather, it presents a method for direct comparison between solutions.
3.2.3. Approximated Fairness
The approximated fairness social welfare metric [
9] has adopted the concept of simple fair division, explained in social choice and game theory [
19], in order to implement the concept of fairness. The metric is defined in Equation (
4).
Equation (
4) shows how the approximated fairness social welfare metric ranks solutions based on the sum of the squared difference between the individual, normalized cost values of the objectives, and the average normalized cost value across all objectives. This means that the approximated fairness social welfare metric prefers a solution
C over solution
if and only if
.
3.2.4. Fairness Analysis
The concept behind the fairness analysis social welfare metric is very much similar to the concept behind the approximated fairness social welfare metric. This metric is used to balance the requirement fulfillment between customers of Motorola Company for hand-held communication devices [
10]. The aim is to minimize the standard deviation of the number of fulfilled requirements for each customer in order to treat customers on a fair basis. The fairness analysis social welfare metric is defined in Equation (
5).
Equation (
5) shows that the fairness analysis social welfare metric ranks solutions based on the standard deviation of the normalized cost value of each objective in order to achieve fairness. Hence, the fairness analysis social welfare metric prefers a solution
C over solution
if and only if
.
3.2.5. Quantitative Fairness
The quantitative fairness social welfare metric is based on Jain’s index or fairness index [
17], which is shown in Equation (
6), where
X is a particular resource allocation across
n individuals and
is the resource allocated to individual
.
According to Jain’s index, the allocation of resources is fair and ideal when the index is equal to one. We can translate this into the quantitative fairness social welfare metric based on cost values by substituting the individual resource allocations with individual cost values and substituting the result from one to reflect minimization as defined in Equation (
7). In this case, the metric value is equal to zero when all objectives have the same normalized cost value.
r is a constant with arbitrary value added to each cost value to avoid division by zero.
In Equation (
7), a positive integer
r is added to the normalized cost value of each objective to avoid cases with division by zero. The quantitative fairness social welfare metric prefers a solution
C over solution
if and only if
.
3.2.6. Entropy
The authors in [
18] introduced entropy as a fairness metric. This metric considers the proportion,
, of resource
X allocated to individual
in a population of
n individuals. The entropy,
H, of the distribution of
X can be calculated as shown in Equation (
8).
Here, the entropy will be larger the more fair an allocation is. In Equation (
9), the entropy metric is expressed as a social welfare metric defined in terms of normalized cost values, where
is an arbitrary, large number
and
r is a constant added to avoid division by zero.
The entropy social welfare metric prefers a solution C over a solution if and only if .
3.3. Overall Utility Based Metrics
Overall utility based metrics again do not consider fairness among objectives, but rather strive to get the best overall utility from a final solution. Here, no guarantees are made towards any single objective, and one objective could be much worse than any other objective with the selected solution. However, the solution is guaranteed to yield the highest overall utility across the society.
3.3.1. Utilitarian Social Welfare
The utilitarian social welfare metric is one of the most simple notions of social welfare, which ranks solutions based on the sum of individual normalized cost values of objectives. The metrics are defined in Equation (
10).
From Equation (
10), we see that the utilitarian social welfare metric prefers a solution
C over solution
if and only if
.
3.3.2. Nash Product
The Nash product social welfare metric combines the features of the utilitarian and the egalitarian social welfare metrics. This notion of social welfare seeks to achieve the best combined cost value across the society of objectives while working to reduced inequality among objectives. Its definition is found in Equation (
11).
The Nash product social welfare metric ranks solutions based on the product of individual normalized cost values of objectives. Hence, the Nash product social welfare metric prefers a solution C over a solution if and only if .
The Nash product metric maximizes society wellbeing by minimizing the combined product of the normalized cost values in a particular solution. Adherence to fairness comes from the fact that the contribution from high normalized cost values contributes proportionally The Nash product social welfare metric is meaningful for cost value vectors without zero value elements. If zero elements are present, only the zero element considered as the Nash product will yield zero regardless of the other values. To account for this fact, we modified the Nash product social welfare metric according to Equation (
11), where we added the same non-zero value to all vector elements. This way, we never end up in a zero product situation.
3.3.3. Median Rank Dictators
The median rank dictators [
15] social welfare metric ranks solutions based on their median cost value as shown in Equation (
13). Here,
is the
cost value in
, which is the normalized cost value vector rearranged in descending order. Here,
r is calculated as
, when the number of individuals
n is even and
when the number of individuals
n is odd.
The median rank dictator social welfare metric prefers a solution C over a solution if and only if .
4. Relative Importance and Social Welfare Ordering
While social welfare metrics do offer a way of prioritizing solutions in a Pareto set, they pose a limitation. The social welfare metrics are not able to rank objectives according to importance. To this end, Umair et al. [
5] introduced the notion of relative importance and the Relative Importance Graph (RIG). By combining social welfare metrics and relative importance, we get a social welfare ordering method. Both relative importance and social welfare ordering are explained below.
4.1. Relative Importance and the Relative Importance Graph
The relative importance between objectives and can be expressed through the integer values −1, 1, and 0. Here, a value of −1 means that objective is relatively more important than . Likewise, a value of 1 reflects that objective is relatively less important than . Finally, a value of zero reflects that objective and objective are equally important. Under this assumption we define an abstraction, relation, which allows us to specify the relative importance of an objective towards another objective. When all possible relation instances have been created, a list of sorted objectives can be created by adding all objectives that are not part of a relation in which they are relatively less important than any other objective to the top of the list. This (or these in case of multiple) objective(s) are then followed by the objectives that are only relatively less important than the objectives already added to the list. This continues until all objectives have been added to the list.
An RIG can be constructed as a directed graph,
, based on the list of sorted objectives. Here,
is a set of nodes where each node
comprises an objective or a group of objectives that are equally important, and
is a set of edges that contains edges between all nodes
N, where
represents a direction between node
and node
based on the relative importance of objectives residing in nodes
and
. The graph is constructed by creating a root node containing the first objective
from the sorted list of objectives. The next objective in the sorted list,
, is then added to the RIG through comparison with objective
: If
is relatively equally important to objective
, then it is added to the same node as shown in
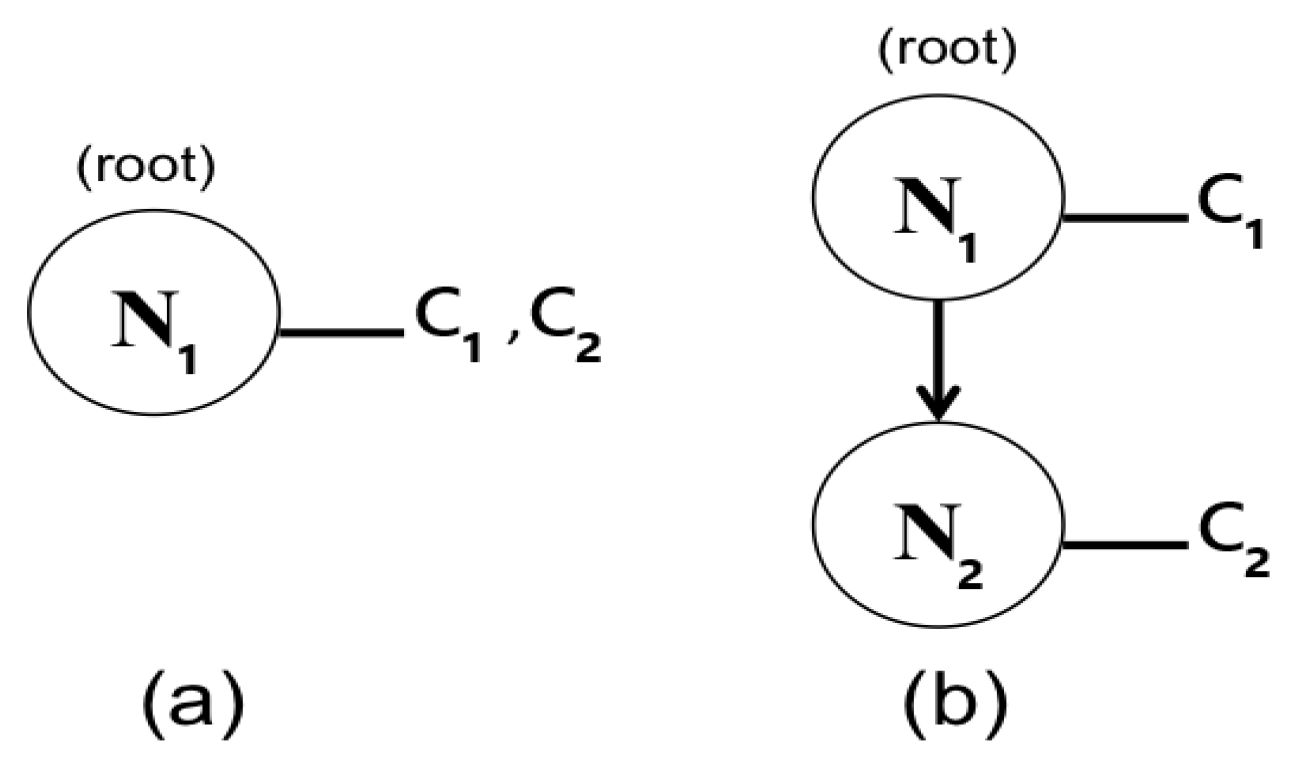
Figure 1a. If objective
is relatively less important than objective
, then it is added to a new empty node
as illustrated in
Figure 1b. In this case, a directed edge is created from node
to node
to represent the hierarchy between the objectives contained in the nodes. This process is repeated until all nodes in the sorted list have been added to the RIG, at which point, the RIG constitutes a graph in which nodes (and consequently objectives) can be traversed in order of relative importance. While this creates an absolute hierarchy of objectives, this voids the task of assigning an absolute importance to the individual objectives.
4.2. Social Welfare Ordering
The social welfare ordering is constructed by assigning a social welfare metric to each node in the RIG. This then applies that specific notion of social welfare to the group of objectives within that node, which enables selecting a final solution from the Pareto set through a simple algorithm, which will start by visiting node in the RIG and apply the social welfare criterion associated with that particular node to the part of the normalized cost vector that contains costs from objectives in node . This will yield a subset of one or more solutions that are equal (in terms of the value returned by the applied social welfare metric) from the perspective of objectives in node . If this subset contains only one solution, the algorithm will terminate and return the solution. Otherwise, the algorithm will continue to traverse the RIG until (a) a subset containing exactly one solution is found or (b) the entire RIG has been traversed. In the latter case, the algorithm will return an arbitrary solution from the final subset, as every solution in this subset is considered equally good from the perspective of every objective in the optimization instance. The pseudo code for the social welfare ordering algorithm can be found in Algorithm 1. The concept of social welfare ordering ensures that higher ranking objectives are prioritized over lower ranking ones during the selection of the final solution. Further, the application of a social welfare metric to each node in the RIG ensures that any conflicts are resolved based on the social welfare metric applied to the particular node level.
| Algorithm 1 Pseudo code of the social welfare ordering algorithm. |
1: ← ▹ initially contains the entire Pareto set. 2: 3: while do 4: 5: ← 6: 7: ← 8: 9: end while 10: 11: ←
|
5. Experimental Setup
To test the influence of the social welfare ordering and different social welfare metrics, we considered a set of experiments built around a case with commercial greenhouse growers. The case and the associated formal problem definition are described in this section along with the optimization framework and its associated configuration used to solve the problem.
5.1. Case
In northern countries, Commercial Greenhouse Growers (CGGs) are heavy consumers of energy used to power supplementary lighting, which is needed to facilitate plant growth [
14]. We considered a case in which a Resource Domain (RD) was responsible for allocating energy to three CGGs. In this scenario, the task of the RD was to ensure that energy allocation never exceeded system-wide energy limits while adhering to the best of its ability to the energy needs of the CGGs. CGGs use energy for supplemental light to increase plant yield. However, light is not provided to the plants arbitrarily [
20]. Long-day photo-periodic plants require long, uninterrupted periods of light to bloom. Here, supplemental light is often used to extend the natural day length. Short-day plants on the other hand require shorter days and are sensitive to long, uninterrupted periods of darkness. Here, supplemental light is used only when natural daylight is scarce, and only for a limited period of time. Day-neutral plants are insensitive to the length of the day or night and will always be able to utilize the provided supplemental light. To simplify the complexity of the optimization problem, we assumed that the CGGs had only two consumption levels, namely on, at which stage it would consume 1 MW of electricity, or off, where consumption would be 0 MW. However, each CGG can be on or off independent of the other CGGs. This type of problem translates to any domain in which energy allocation is necessary to run a facility.
The case was modeled as a multi-objective multi-variable optimization problem with 7 objectives and 3 variable vectors in total. We optimized to find a 24 h energy allocation schedule for each of the three CGGs.
We used 3 variable vectors to represent the hourly planned electricity allocation for each of the CGGs. To represent 24 h, we set
. Here, each element could take on a value of either 0 or 1 (MW). Their definition is found in Equation (
14).
The 7 objectives in the optimization problem include 1 system-wide energy constraint objective and 6 objectives that map to the 3 CGGs, 2 objectives for each CGG.
Equation (
15) formulates the objective function for the system-wide energy limit objective. It considers the combined energy allocation for each of the CGGs and compares it to its preference vector
by summarizing the absolute distance between elements of the combined allocation vector and the preference vector.
Each of the CGGs has 2 objectives representing it. One objective is focused on the amount of energy allocated and the time at which it is allocated for the CGG, whereas the other objective is concerned only with the total amount of energy allocated to the CGG, disregarding the time at which it is allocated. This may seem redundant, but in the context of this optimization problem, this means that shifting energy is perceived as better for the consumers than shedding or removing the energy, in cases where insufficient energy is available in one or more time slots.
Equations (
16) and (
17) show the definitions for the objective that is concerned with the allocated amount and time of allocation and the objective that is concerned only with the combined allocation across the entire schedule for
. Equations (
18)–(
21) are similar objective definitions for
and
.
The combined optimization problem is defined in Equation (
22).
5.2. Optimization Framework
The multi-objective optimization problem described in
Section 5.1 was solved using Controleum [
21,
22]. Controleum is an object-oriented genetic algorithm framework. Controleum is one framework to employ a Pareto set to store outcomes. The Pareto set is used to store populations of solutions between evolutions, and once optimization has terminated, a final solution is drafted from the resulting Pareto set. To this end, Controleum uses objective priority and a non-normalized utilitarian social welfare to select a final solution from the Pareto frontier.
Controleum uses the concern abstraction to represent objectives and the issue abstraction to represent optimization variables as vectors. An optimization context in Controleum is defined by N concerns that negotiate over M issues. Each concern , defines an evaluation function that takes into account values of each of the issues, , , which are part of the objective function. Further, the evaluation function takes into account a concern-specific preference vector, which describes a target that the concern is aiming for. An issue, defines a number of vector elements t, as well as the range from which these elements can draw values. In the context of Controleum, a solution, C, is a set of values for each of the M issues defined. The solution is defined as , where is the value for issue in solution C.
The initiation of the algorithm and the optimization process itself was explained in depth in [
5], in which Controleum was also extended by (1) introducing the notion of the relative importance of objectives to determine their ordering, (2) utilizing normalized costs of objectives in the selection of a final outcome, and (3) implementing the notions of social welfare presented in
Section 3. This enables the configuration of Controleum to use a specific social welfare ordering by deciding on a social welfare metric and by assigning relative importance to objectives.
5.2.1. Issue Configuration
The variable vectors described in
Section 5.1 were translated to three corresponding issues,
, in Controleum. Each issue was configured with
to cover 24 1 h slots. This meant that each solution comprised 3 vectors, each with 24 values of either 0 or 1. This constituted a complete allocation for each of the CGGs presented as part of the case.
5.2.2. Concern Configuration
Each of the objectives described in
Section 5.1 was translated 1:1 to concerns. This meant that we had 7 concerns in Controleum representing the 7 objectives in the optimization problem. These 7 concerns were distributed across 3 types of concerns; we had 1 system-wide energy concern (
), 3 CGG resource concerns (
), which consider the amount of energy allocated and the time at which it is allocated for each of the CGGs, and finally, 3 CGG resource sum concerns (
) that consider the total amount of energy allocated and disregard the temporal dimension. Algorithms 2–4 show a pseudo code representation of each of these types of concerns.
| Algorithm 2 Pseudo code representation of the evaluation method in the system-wide energy concern. |
Precondition:n is the number of hours being allocated. 1: Precondition: is the system-wide energy limit vector with n elements. 2: 3: function EVALUATE(solution) 4: 5: 6: 7: while do 8: 9: 10: 11: end while 12: 13: 14: 15: return 16: 17: end function
|
| Algorithm 3 Pseudo code representation of evaluation method of the CGG resource concern (). |
Precondition:n is the number of hours being allocated, and x is a CGG ID from 1-3. 1: Precondition: is the demand for energy in CGG x. 2: 3: function EVALUATE(solution) 4: 5: 6: 7: 8: 9: return 10: 11: end function
|
| Algorithm 4 Pseudo code representation of evaluation method of the CGG resource sum concern (). |
Precondition: n is the number of hours being allocated, and x is a CGG ID from 1–3. 1: Precondition: is the demand for energy in CGG x.
2: 3: function EVALUATE(solution) 4: 5: 6: 7: 8: 9: for do ▹ Sum all elements in both vectors 10: 11: 12: 13: 14: 15: end for 16: 17: ▹ Absolutes sum difference 18: 19: return 20: 21: end function
|
The variable
denotes the system-wide energy constraint. As seen from the pseudo code in Algorithm 2, the absolute differences between elements in this vector and the sum of elements in the allocations for each of the CGGs are considered. This means that the system will not tolerate allocations above or below the system-wide energy constraint. We ran two sets of experiments where we varied the value of
. In one case, the value of the
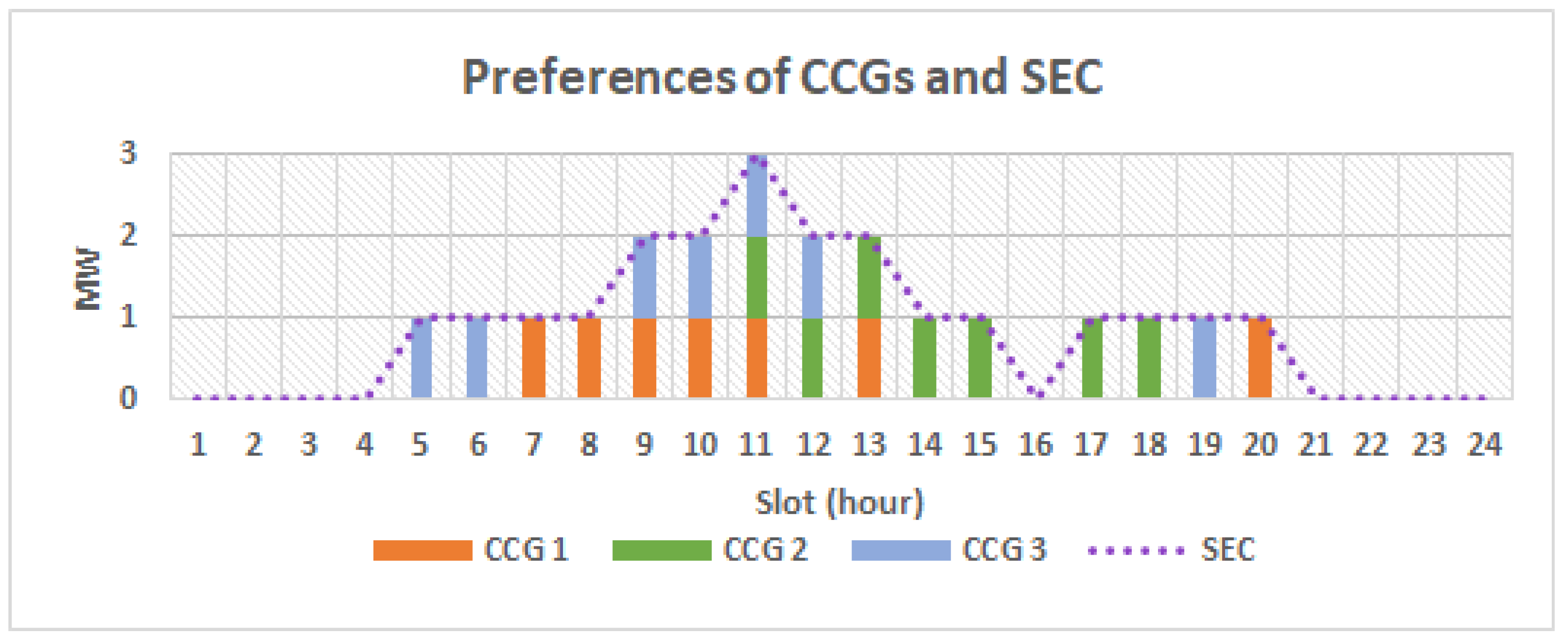
vector was equal to the sum of elements in each of the demand vectors of the CGGs. This is illustrated in
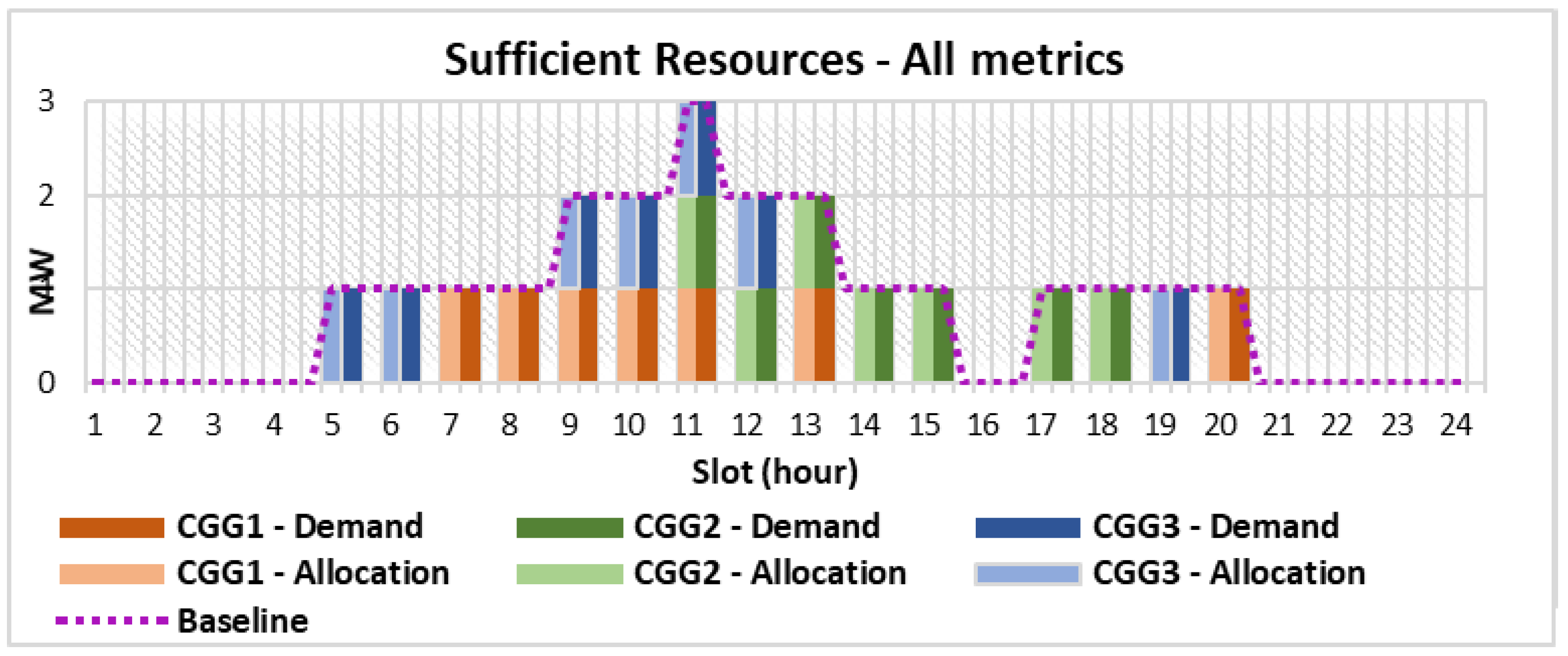
Figure 2, where the columns are the demands presented by each of the CGGs and the dotted line is a plot of
. This translates into a resource allocation problem where sufficient resources are available and where the problem is one of allocating these resources to each of the CGGs in a way where every CGGs gets what it demands.
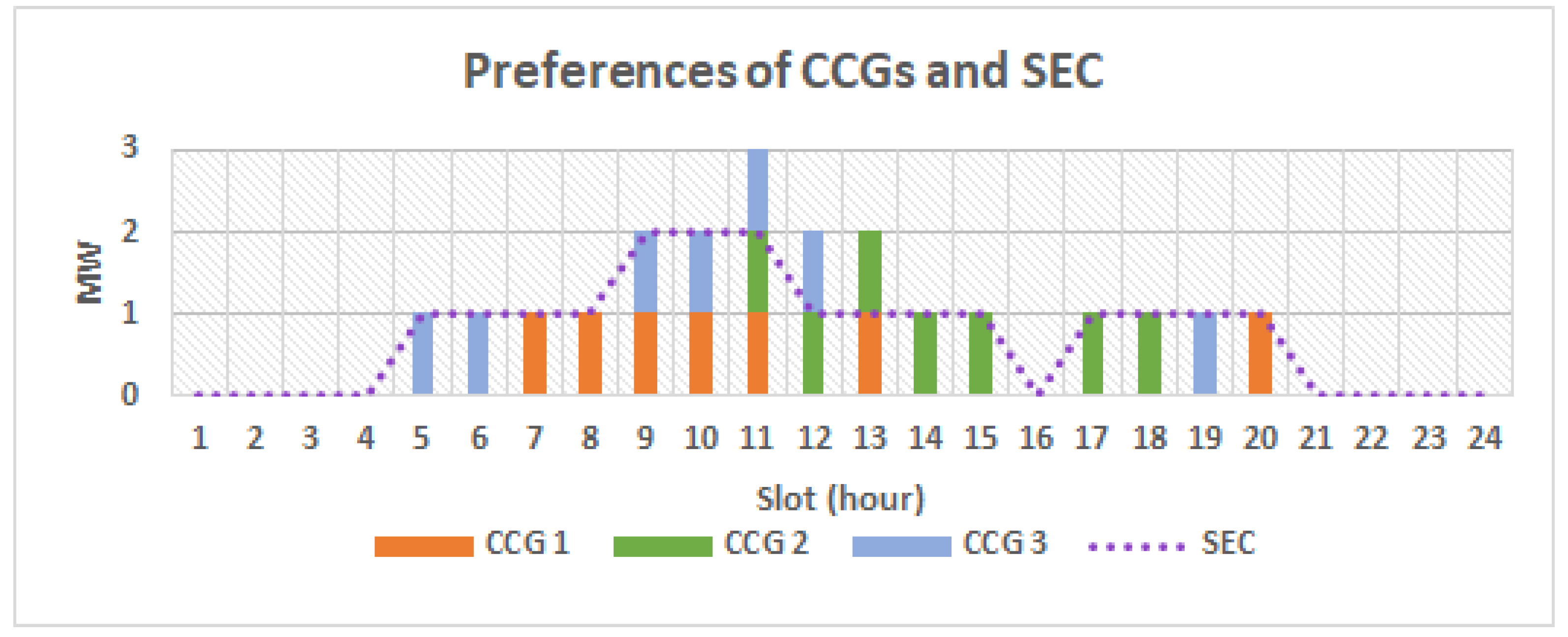
In the other case, we introduced a constraint on the amount of resources available to the system, by altering
as shown in
Figure 3. Here, we see that
did not match the need for energy in Slots 11, 12, and 13. In a resource allocation context, the task of the system in this case was to gracefully degrade. Here, the definition of graceful degradation depended on the resource allocation strategy: some systems would like to see the consequences distributed across as many entities as possible. Here, a strategy that distributed resources across entities in a fair manner was needed. In other cases, the number of entities affected by the system state should be reduced. Here, the resource allocation strategy should ensure that the least possible entities were influenced, at the expense of fewer entities, which would be influenced more severely.
5.3. Social Welfare Ordering
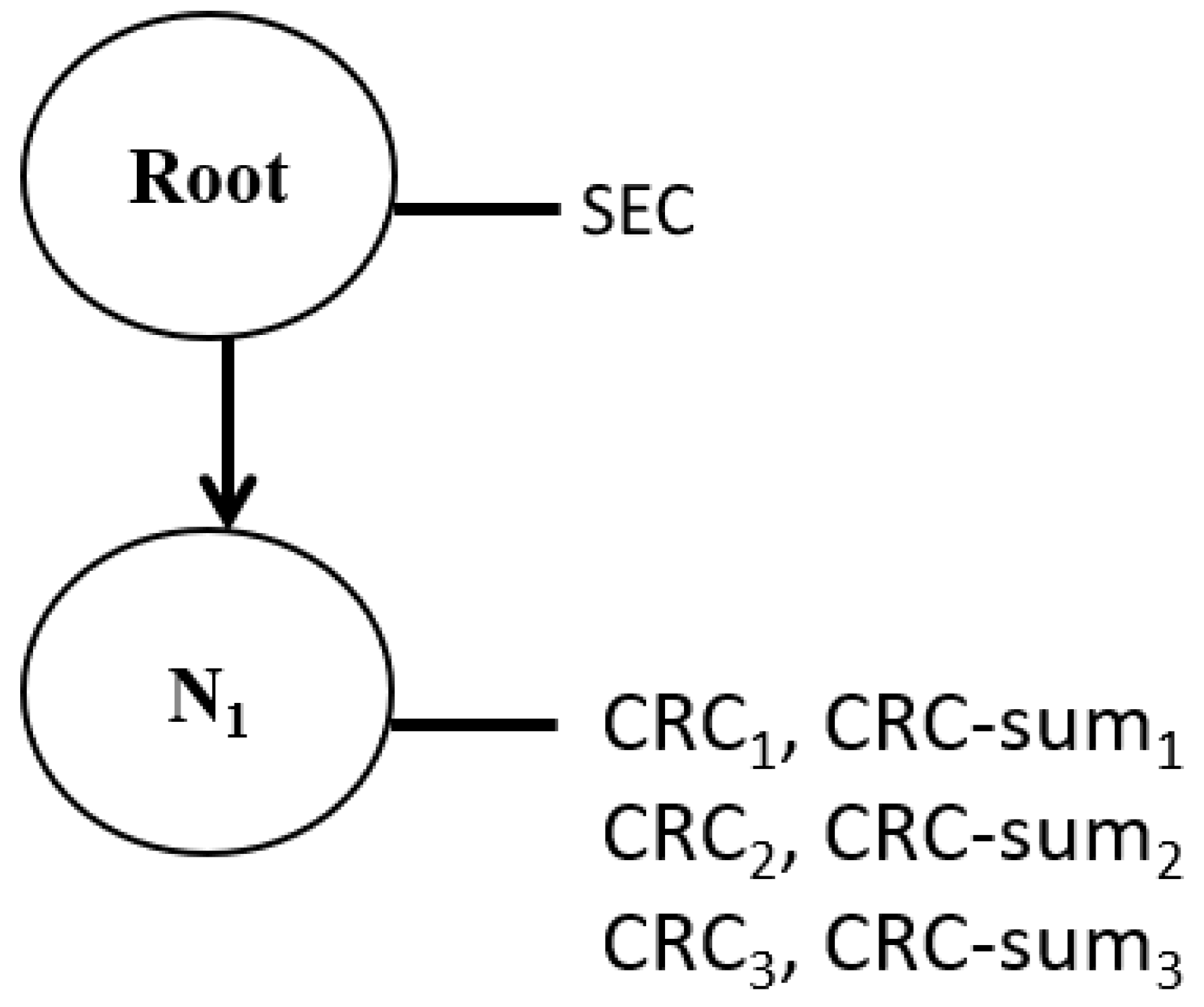
The goal of the system as presented in the case of this section was to adhere to system energy limits while allocating energy to each of the CGGs to the best of its ability under this constraint. Thus, the SEC was more important than the six CGG concerns in terms of relative importance. As the case did not describe any priority between each of the CGGs, the remaining six concerns were relatively equally important. The resulting relative importance graph is shown in
Figure 4, where the SEC is placed in the node immediately above the CRCand the CRC-sum concerns. This configuration had several properties. First, the SEC was always prioritized over any of the CRC concerns, meaning that solutions that were ideal for the SEC were selected from the Pareto set first. The 10 social welfare metrics described in
Section 3 were then applied to node
in separate experiments to apply different methods for selecting a final solution from the Pareto set. This enabled us to analyze the impact of each of the social welfare metrics on the resulting resource allocation strategy in a society of 3 identical production entities.
6. Experiments
Based on the experimental setup described in
Section 5, two sets of experiments were conducted. The experiments were conducted in [
5]. Here, we present the results, and in
Section 7, we extrapolate the results to resource allocation strategies. The two sets of experiments describe two scenarios that are well known within resource allocation, namely one with sufficient resources and one with insufficient resources. From the experiments, we observed how different notions of social welfare (described in
Section 3) translated to resource allocation strategies and how this manifested as system consequences with respect to graceful degradation in the horticulture domain. Each set of experiments was executed 20 times to induce resilience towards the potential random behavior sparked by the use of an evolutionary algorithm.
6.1. Sufficient Resources
This experiment was conducted for each of the social welfare metrics described in
Section 3. However, here, the social welfare metric did not influence the outcome, which is displayed in the graph of
Figure 5 for all 10 metrics. We see the demand profile of each of the CGGs as stronger colored bars and allocations as weaker colored bars. When a weaker and a stronger colored bar of same color is placed in a time slot, this means that allocation and demand matched. We see from the figure that allocation matched demand in the case of sufficient resources irrespective of the employed resource allocation strategy.
6.2. Insufficient Resources
In these experiments, insufficient resources, in terms of available electricity power, were made available in Slots 11, 12 and 13. We conducted one series of experiments for each of the 10 metrics described in
Section 3. From the experiments, we notice that the resulting resource allocation strategy depended on the type of social welfare metric rather than the social welfare metric itself: similar types of social welfare metrics yielded the same results. Thus,
Figure 6,
Figure 7 and
Figure 8 show the results for the inequality based, the 6 fairness based, and the 3 overall utility based social welfare metrics, respectively. As a result, we present the results for each type of social welfare metric in the subsections below.
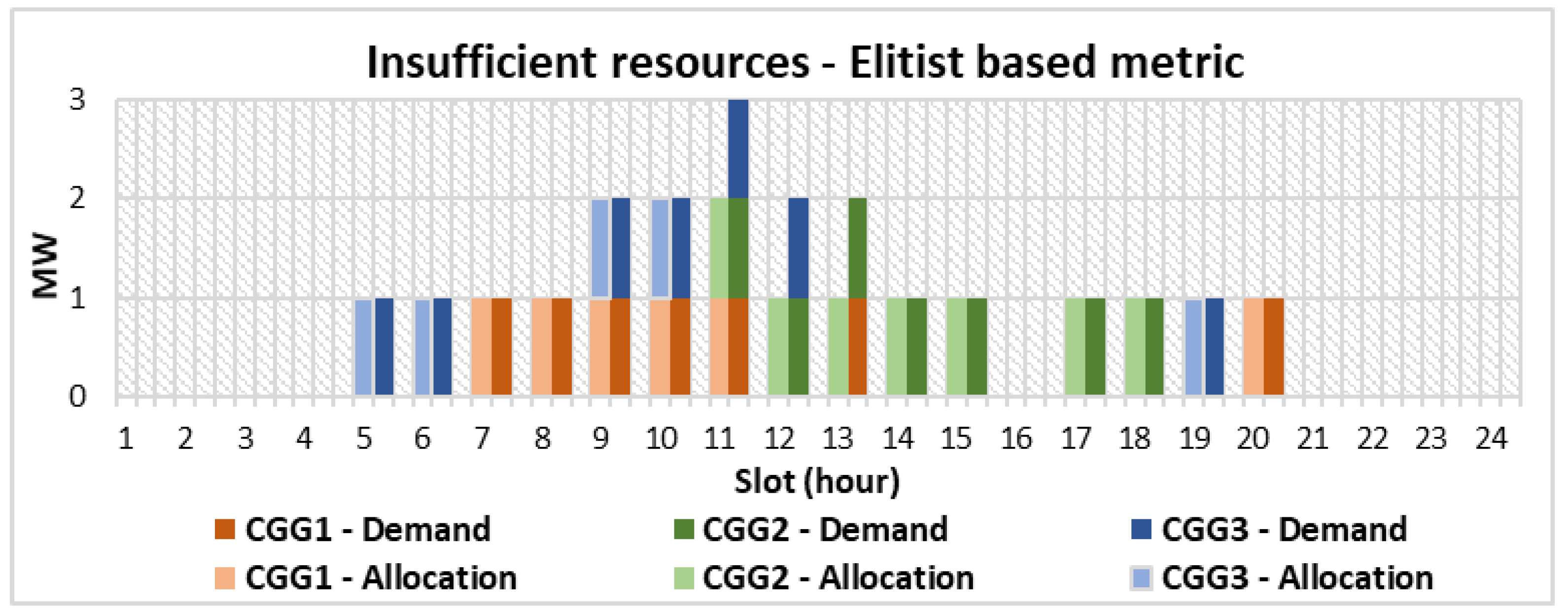
6.2.1. Results: Inequality Based Metrics
With an inequality based metric, we expected that one entity is best off, and indeed, we observed that
was allocated sufficient energy to match its demand at the expense of
and
, which were compromised of 1 and 2 MWh, respectively, as seen from
Figure 6.
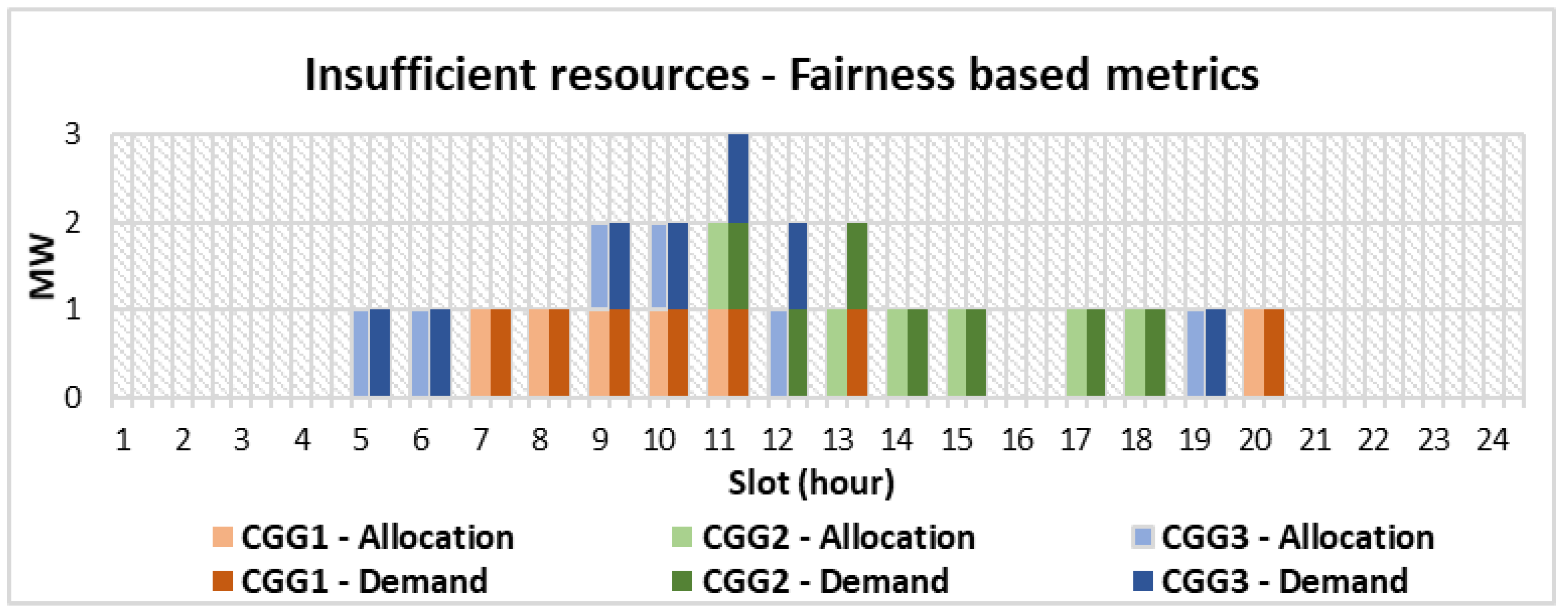
6.2.2. Results: Fairness Based Metrics
With fairness based metrics, we would expect that the negative impact of insufficient resources was equally distributed across all entities. From
Figure 7, we see that each of the entities lacked one 1 MWh of electricity allocation to meet their demand. As the entities in our model valued energy equally in all of their demand hours, this meant that this result fell within our expectations.
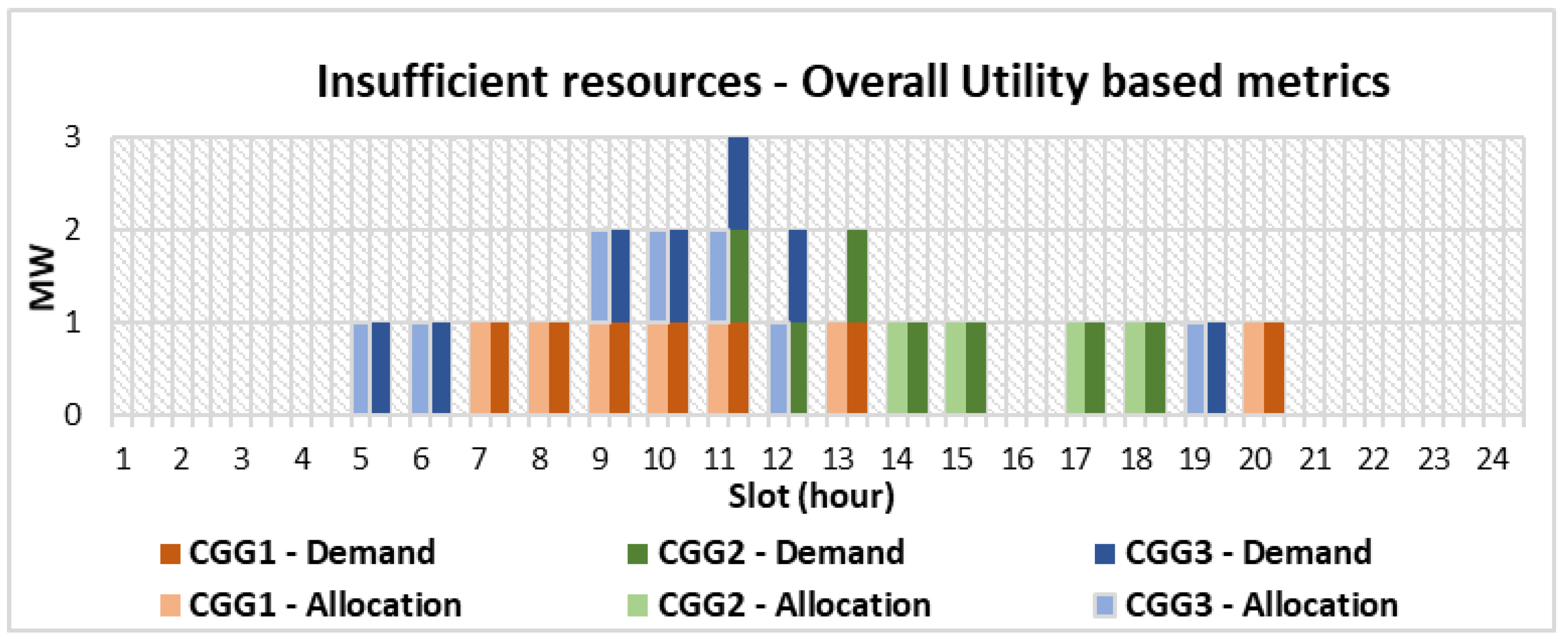
6.2.3. Results: Overall Utility Based Metrics
The results of applying either of the overall utility based metrics are seen in
Figure 8. Here, we see that a single entity (
) carried the entire consequence of having insufficient resources available in the system, leaving the two other entities unaffected.
6.3. Summary
The experiments are summarized in
Table 2 where we disregard the temporal dimension. The baseline demand of each CGG was 7 MWh, with the first set of experiments allocating this amount to each CGG entity regardless of the social welfare metric. The remaining three experiments showed how different types of social welfare metrics performed different tradeoffs between the entities.
7. Discussion
The experiments presented in this paper and by Umair et al. [
5] showed that the choice of social welfare metric was arbitrary in cases with sufficient resources. In the case with insufficient resources, the type of social welfare metric had an impact on the resource allocation strategy, while we observed no variance between social welfare metrics of a similar type. However, the variance between social welfare metric types manifested itself in vastly different resource allocation strategies and resulting domain consequences.
In the experiment with insufficient resources, we observed that one CGG was better off than the two others when using the inequality based social welfare metric. Here, two entities shared the consequences of the resource insufficiency. In the context of resource allocation, this type of resource allocation strategy could be employed to ensure sufficient allocation of resources to mission-critical processes, which requires an exact match of its demand to run without interruptions. This then happens at the expense of the non-mission critical processes, which are compromised, although in our case, one more than the other. In a grower domain, this resource allocation strategy could be relevant in the production of long-day photoperiodic plants, such as Rudbeckia and California poppy, which are sensitive to the duration of day-night. This strategy ensures that at least one of the CGGs gets the required amount of light, thereby preserving the production yield in that entity.
With the fairness based social welfare metrics, we saw that consequences were evenly distributed across all CGGs, with all entities compromising on their operation to an extent. This sort of resource allocation strategy could appeal to cases where processes can be interrupted without severe consequences and where no process should compromise more than any other. With long-day photo-periodic plants, this would be an inefficient strategy, as plants in all entities could be destroyed during such an event. However, for short-day plants like chrysanthemum, Christmas cactus, and poinsettia, such a strategy would not have any severe impact on production, as these plants would be able to compromise between the entities to reach their relatively sparse requirements for day light [
23].
Finally, with the overall utility based social welfare metrics, the consequences of the resource insufficiency are carried entirely by a single entity. This type of resource allocation strategy seems immediately appealing in that two entities are in fact entirely unaffected by the lack of resources. However, the mathematical properties of these metrics do nothing to guarantee this. Rather, the target is to maximize the overall utility of the society regardless of the consequences. This could be ideal for plant productions with day-neutral plants, which do not require any specific day length, such as rose and tomatoes. Here, the overall yield is more important than the wellbeing of any one entity.
The experiments presented in this paper and in Umair et al. [
5] failed to shed light on the variance between metrics of similar types. While this implies that these metrics are interchangeable, we believe that this maps back to the specific problem instance employed throughout the experiments. The problem presented a fixed constraint on resources, which, when combined with the nature of the objective functions, meant that no entity would ever attempt to shift its consumption to another time slot as it would have an adverse effect on the overall system state (and not be Pareto optimal). We believe that experiments where the RD suggests the CGGs to shift their consumption, by increasing allocation in alternative time slots, could help to shed light on inter-type differences between metrics.
8. Conclusions
This paper discussed the properties and impact of different notions of social welfare on a resource allocation problem solved through multi-objective optimization that generated a Pareto based solution set.
We presented 10 different notions of social welfare and categorized them based on their perceived behavior. To show their properties in the context of resource allocation, we considered a case with three commercial greenhouse growers with independent energy demands in a setting with a resource domain responsible for allocating energy to each of these entities. We formulated this as a multi-objective optimization problem and solved the problem with Controleum [
21,
22], a multi-objective optimization framework.
We carried out two sets of experiments: one set with sufficient resources and one set with insufficient resources. An experiment was conducted for each metric in each of the sets of experiments. Each experiment was repeated 20 times to mitigate the potential impact of randomness due to the nature of the genetic algorithm employed by Controleum. The results showed that different notions of social welfare led to different resource allocation strategies. These then translated to different impacts in the grower domain. This in turn meant that the choice of social welfare metric was not arbitrary and depended on the behavior that was expected of the system as a whole.
Author Contributions
Conceptualization, A.U., B.N.J., A.C. and Y.D.; methodology, A.C. and A.U.; software, A.C. and A.U.; validation, A.C., A.U. and B.N.J.; formal analysis, A.U. and A.C.; investigation, A.U. and A.C.; resources, B.N.J.; data curation, A.U.; writing–original draft preparation, A.C.; writing–review and editing, Y.D., B.N.J., A.U.; visualization, A.U. and A.C.; supervision, B.N.J. and Y.D.; project administration: B.N.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hosseini, H. Dynamic Multiagent Resource Allocation: Integrating Auctions and MDPs for Real-Time Decisions. In Proceedings of the Seventeenth AAAI/SIGART Doctoral Consortium, ON, Canada, 22–23 June 2012. [Google Scholar]
- Briola, D.; Mascardi, V. Multi Agent Resource Allocation: A Comparison of Five Negotiation Protocols. In Proceedings of the 12th Workshop on Objects and Agents (WOA 2011), Rende (CS), Italy, 4–6 July 2011; pp. 95–104. [Google Scholar]
- Clausen, A.; Umair, A.; Demazeau, Y.; Jørgensen, B.N. Agent-Based Integration of Complex and Heterogeneous Distributed Energy Resources in Virtual Power Plants. In Advances in Practical Applications of Cyber-Physical Multi-Agent Systems: The PAAMS Collection; PAAMS 2017; Lecture Notes in Computer Science; Demazeau, Y., Davidsson, P., Bajo, J., Vale, Z., Eds.; Springer: Cham, Switzerland, 2017; Volume 10349, pp. 43–55. [Google Scholar]
- Chaharsooghi, S.K.; Kermani, A.H.M. An effective ant colony optimization algorithm (ACO) for multi-objective resource allocation problem (MORAP). Appl. Math. Comput. 2008, 200, 167–177. [Google Scholar] [CrossRef]
- Umair, A.; Clausen, A.; Demazeau, Y.; Jørgensen, B.N. Impact of Social Welfare Methods on Multi-objective Resource Allocation in Energy Systems. In Proceedings of the 8th International Conference on Smart Cities and Green ICT Systems-Volume 1: SMARTGREENS, Heraklion, Greece, 3–5 May 2019; pp. 179–186. [Google Scholar] [CrossRef]
- Feldman, A.M.; Serrano, R. Welfare Economics and Social Choice Theory; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Li, M.; Vo, Q.B.; Kowalczyk, R. Searching for fair joint gains in agent-based negotiation. Proceedings of The 8th International Conference on Autonomous Agents and Multiagent Systems-Volume 2, Budapest, Hungary, 10–15 May 2009; pp. 1049–1056. [Google Scholar]
- Heiskanen, P.; Ehtamo, H.; Hämäläinen, R.P. Constraint proposal method for computing Pareto solutions in multi-party negotiations. Eur. J. Op. Res. 2001, 133, 44–61. [Google Scholar] [CrossRef]
- Fujita, K.; Ito, T.; Klein, M. A secure and fair protocol that addresses weaknesses of the Nash bargaining solution in nonlinear negotiation. Group Decis. Negotiat. 2012, 21, 29–47. [Google Scholar] [CrossRef][Green Version]
- Finkelstein, A.; Harman, M.; Mansouri, S.A.; Ren, J.; Zhang, Y. A search based approach to fairness analysis in requirement assignments to aid negotiation, mediation and decision making. Requir. Eng. 2009, 14, 231–245. [Google Scholar] [CrossRef]
- Sørensen, J.C.; Jørgensen, B.N. An extensible component-based multi-objective evolutionary algorithm framework. In Proceedings of the 6th International Conference on Software and Computer Applications, Bangkok, Thailand, 26–28 February 2017; pp. 191–197. [Google Scholar]
- Darmann, A.; Schauer, J. Maximizing Nash product social welfare in allocating indivisible goods. Eur. J. Op. Res. 2015, 247, 548–559. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Umair, A. An Agent Based Approach to Coordination of Resource Allocation and Process Performance. Ph.D. Thesis, University of Southern Denmark, Odense, Denmark, 2018. [Google Scholar]
- Chevaleyre, Y.; Dunne, P.E.; Endriss, U.; Lang, J.; Lemaitre, M.; Maudet, N.; Padget, J.; Phelps, S.; Rodriguez-Aguilar, J.A.; Sousa, P. Issues in multiagent resource allocation. Informatica 2006. Available online: https://staff.fnwi.uva.nl/u.endriss/MARA/mara-survey.pdf (accessed on 5 June 2020).
- Nguyen, N.T.; Nguyen, T.T.; Roos, M.; Rothe, J. Computational complexity and approximability of social welfare optimization in multiagent resource allocation. Auton. Agents Multi-Agent Syst. 2014, 28, 256–289. [Google Scholar] [CrossRef]
- Huaizhou, S.; Prasad, R.V.; Onur, E.; Niemegeers, I. Fairness in wireless networks: Issues, measures and challenges. IEEE Commun. Surv. Tutor. 2014, 16, 5–24. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mobile Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Robertson, J.; Webb, W. Cake-Cutting Algorithms: Be Fair if You Can; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Clausen, A.; Maersk-Moeller, H.; Soerensen, J.C.; Joergensen, B.; Kjaer, K.; Ottosen, C. Integrating commercial greenhouses in the smart grid with demand response based control of supplemental lighting. In Proceedings of the 2015 International Conference on Industrial Technology and Management Science, Tianjin, China, 27–28 March 2015. [Google Scholar]
- Sørensen, J.C.; Jørgensen, B.N.; Klein, M.; Demazeau, Y. An agent-based extensible climate control system for sustainable greenhouse production. In Agents in Principle, Agents in Practice; PRIMA 2011; Lecture Notes in Computer Science; Kinny, D., Hsu, J.Y., Governatori, G., Ghose, A.K., Eds.; Springer: Heidelberg, Berlin, 2011; Volume 7047, pp. 218–233. [Google Scholar]
- Clausen, A.; Demazeau, Y.; Jørgensen, B.N. An agent-based framework for aggregation of manageable distributed energy resources. In Highlights of Practical Applications of Heterogeneous Multi-Agent Systems; The PAAMS Collection; PAAMS 2014; Communications in Computer and Information Science; Corchado, J.M., Ed.; Springer: Cham, Switzerland, 2014; Volume 430, pp. 214–225. [Google Scholar]
- Kumpf, J. Lighting Systems. 2019. Available online: https://courses.cit.cornell.edu/hort494/greenhouse/lighting/lightlft.html (accessed on 4 January 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).