Development of a Transient Model of a Lightweight, Portable and Flexible Air-Based PV-T Module for UAV Shelter Hangars
Abstract
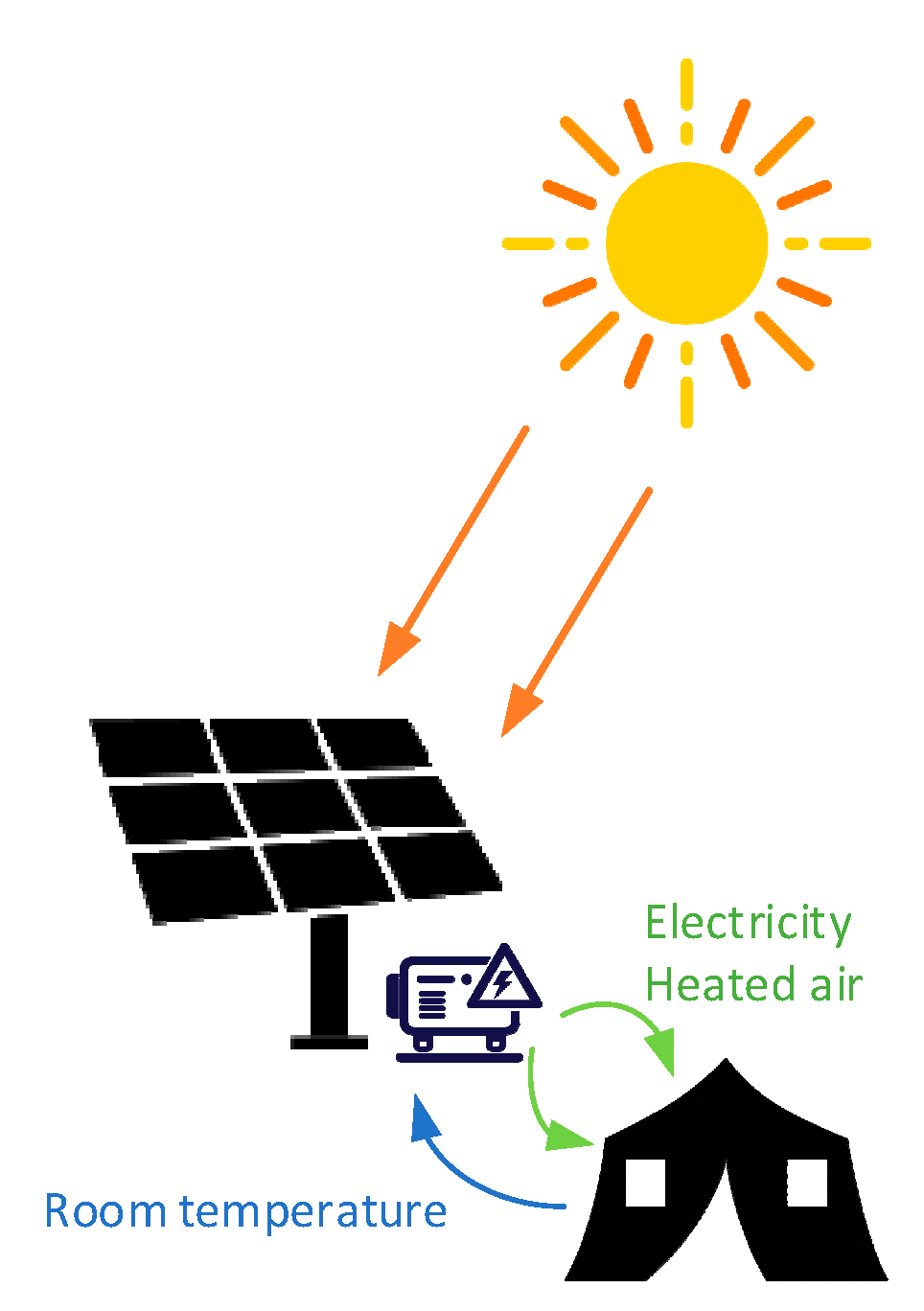
1. Introduction
2. Materials and Methods
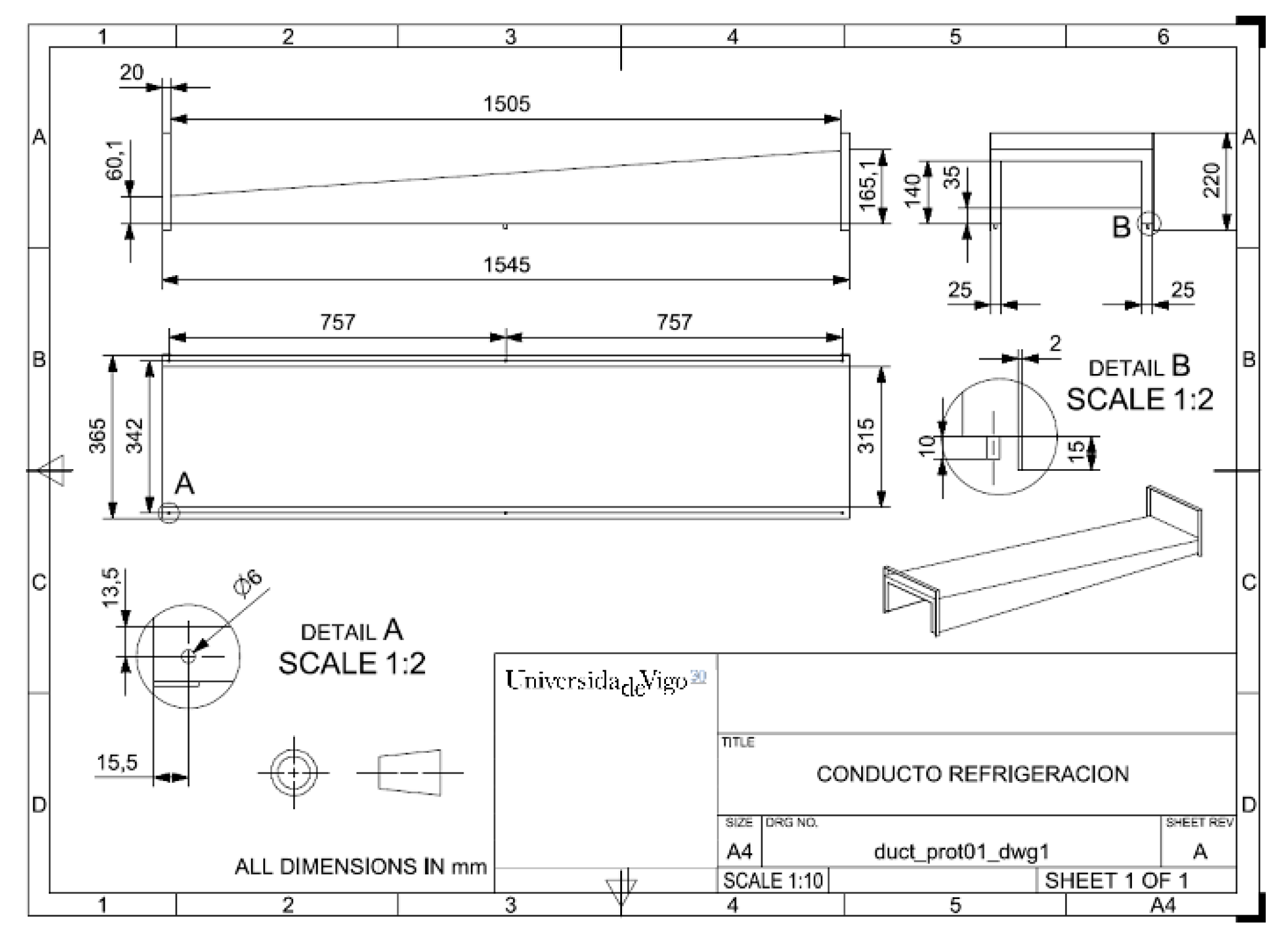
2.1. Experimental Setup
2.2. Thermal Model
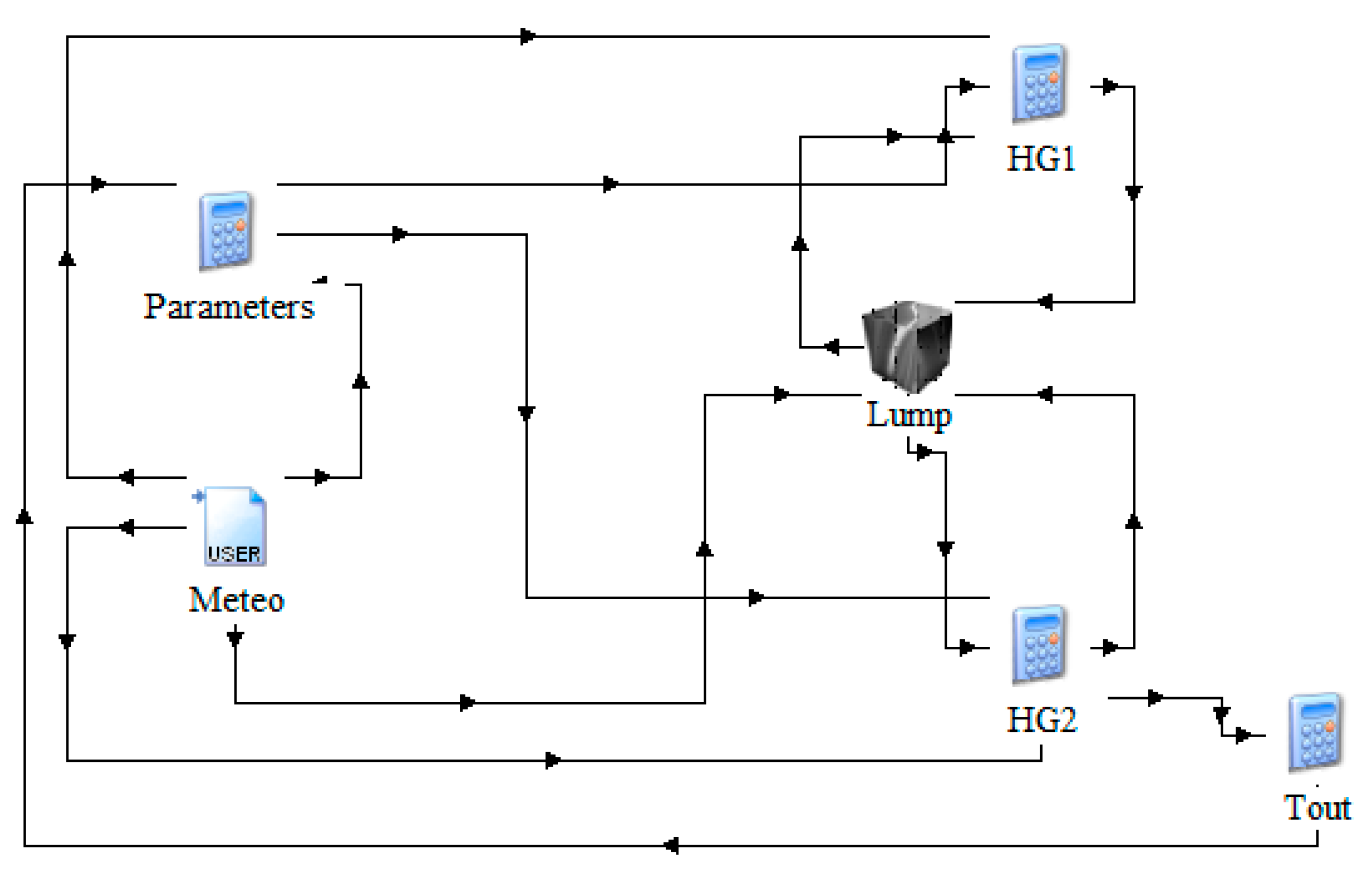
2.3. TRNSYS Simulation
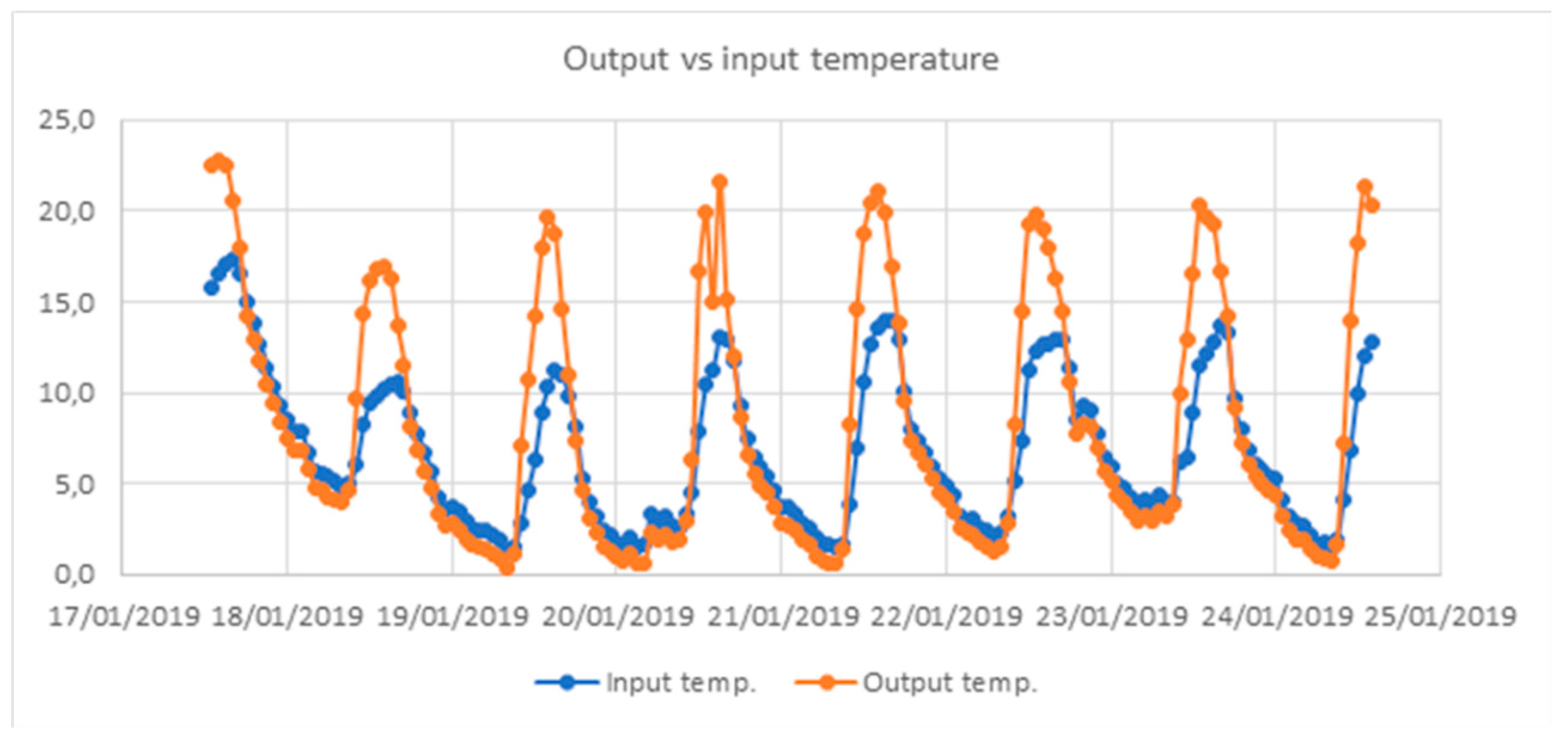
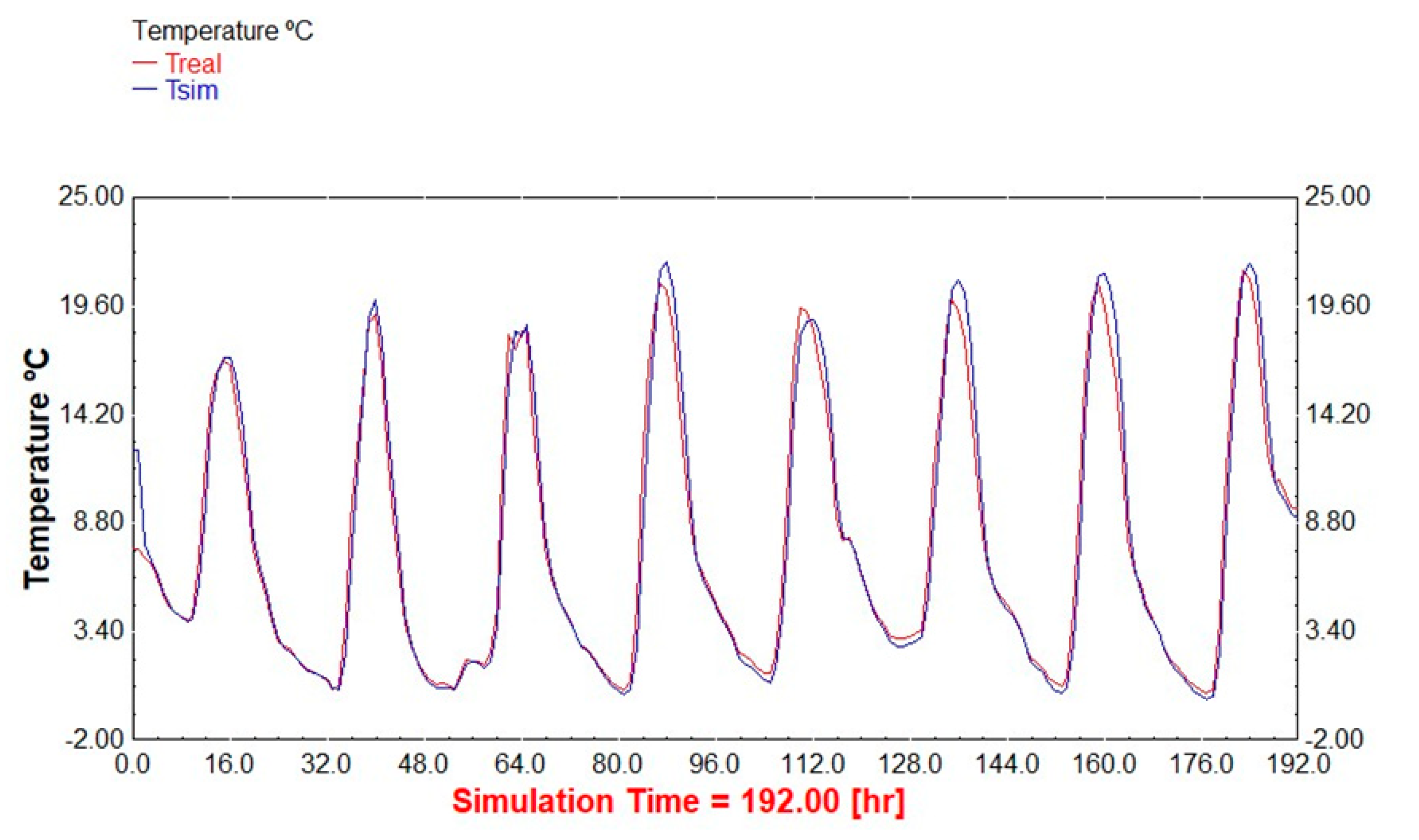
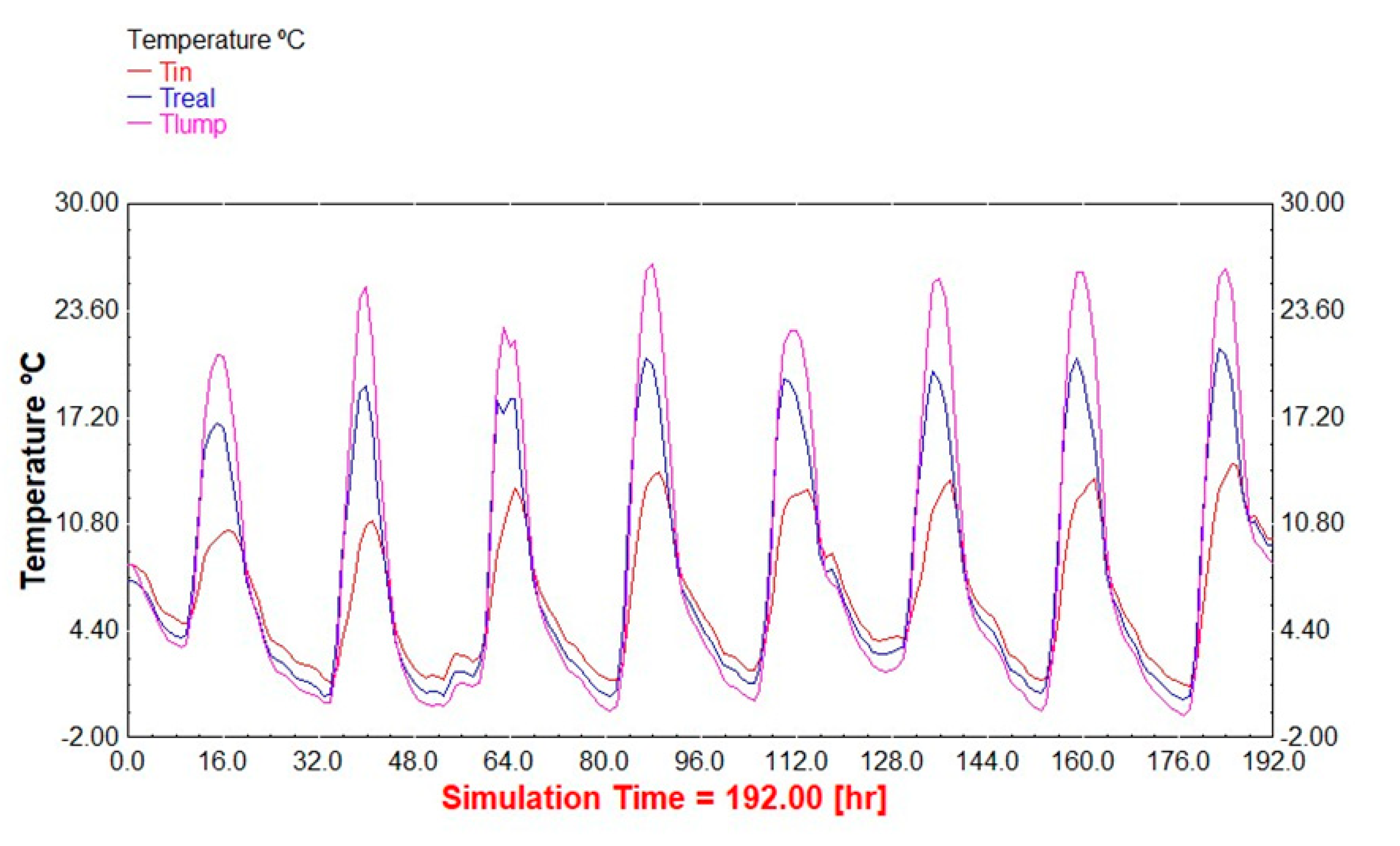
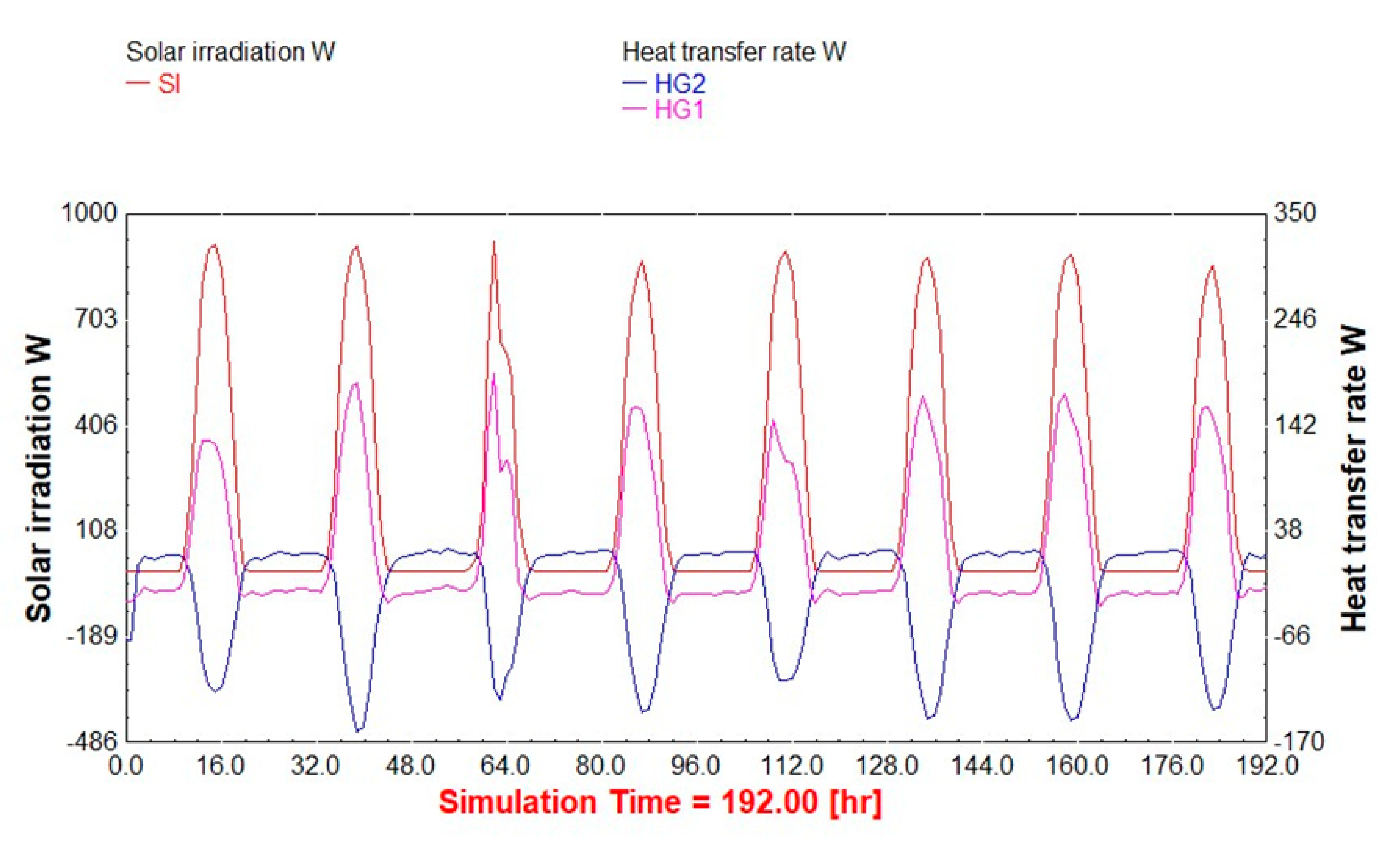
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| solar absorptivity [-] | |
| panel emissivity [-] | |
| σ | Stefan-Boltzmann’s constant [] |
| panel area [m2] | |
| air flow specific heat [ | |
| h | convection heat transfer [] |
| G | irradiation [W/m2] = mass air flow in cooling duct [kg/s] |
| Tamb | ambient temperature [K] |
| Tl | lump mass temperature [K] |
| Tma | average temperature of air fluid [K] |
| Tout | system’s output temperature [°C] |
| Ts | temperature of surface in touch with air fluid [K] |
| Tsky | temperature in the surroundings of the system [K] |
| Vw | wind speed [m/s] = system’s convection losses [W/m2] |
| heat speed transfer [W] |
References
- Chow, T.T. A review on photovoltaic/thermal hybrid solar technology. Appl. Energy 2010, 87, 365–379. [Google Scholar] [CrossRef]
- Hasan, M.A.; Sumathy, K. Photovoltaic thermal module concepts and their performance analysis: A review. Renew. Sustain. Energy Rev. 2010, 14, 1845–1859. [Google Scholar] [CrossRef]
- Kumar, R.; Rosen, M.A. A critical review of photovoltaic thermal solar collectors for air heating. Appl. Energy 2011, 88, 3603–3614. [Google Scholar] [CrossRef]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Daghigh, R.; Ruslan, M.H.; Sopian, K. Advances in liquid based photovoltaic/thermal (PV/T) collectors. Renew. Sustain. Energy Rev. 2011, 15, 4156–4170. [Google Scholar] [CrossRef]
- Ibrahim, A.; Othman, M.Y.; Ruslan, M.H.; Mat, S.; Sopian, K. Recent advances in flat plate photovoltaic/thermal (PV/T) solar collectors. Renew. Sustain. Energy Rev. 2011, 15, 352–365. [Google Scholar] [CrossRef]
- Tyagi, V.V.; Kaushik, S.C.; Tyagi, S.K. Advancement in solar photovoltaic/thermal (PV/T) hybrid collector technology. Renew. Sustain. Energy Rev. 2012, 16, 1383–1398. [Google Scholar] [CrossRef]
- Kamthania, D.; Tiwari, G.N. Photovoltaic thermal air collectors: A review. J. Renew. Sustain. Energy 2014, 6, 062701. [Google Scholar] [CrossRef]
- Hamid, S.A.; Othman, M.Y.; Sopian, K.; Zaidi, S.H. An overview of photovoltaic thermal combination (PV/T combi) technology. Renew. Sustain. Energy Rev. 2014, 38, 212–222. [Google Scholar] [CrossRef]
- Michael, J.J.; Iniyan, S.; Goic, R. Flat plate solar photovoltaic-thermal (PV/T) systems: A reference guide. Renew. Sustain. Energy Rev. 2015, 51, 62–88. [Google Scholar] [CrossRef]
- Bhargava, A.K.; Garg, H.P.; Agarwal, R.K. Study of a hybrid solar system solar air heater combined with solar cells. Energy Convers. Manag. 1991, 31, 471–479. [Google Scholar] [CrossRef]
- Sopian, K.; Yigit, K.S.; Liu, H.T.; Kakac, S.; Veziroglu, T.N. Performance analysis of photovoltaic thermal air heaters. Energy Convers. Manag. 1996, 37, 1657–1670. [Google Scholar] [CrossRef]
- Othman, M.Y.H.; Yatim, B.; Sopian, K.; Bakar, M.N.A. Performance analysis of a double-pass photovoltaic/thermal (PV/T) solar collector with CPC and fins. Renew. Energy 2005, 30, 2005–2017. [Google Scholar] [CrossRef]
- Tiwari, A.; Sodha, M.S. Parametric study of various configurations of hybrid PV/thermal air collector: Experimental validation of theoretical model. Sol. Energy Mater. Sol. Cell 2007, 91, 17–28. [Google Scholar] [CrossRef]
- Tonui, J.K.; Tripanagnostopoulos, Y. Air-cooled PV/T solar collectors with low cost performance improvements. Sol. Energy 2007, 81, 498–511. [Google Scholar] [CrossRef]
- Tonui, J.K.; Tripanagnostopoulos, Y. Performance improvement of PV/T solar collectors with natural air flow operation. Sol. Energy 2008, 82, 1–12. [Google Scholar] [CrossRef]
- Katekar, V.P.; Deshmukh, S.S. A review on research trends in solar still designs for domestic and industrial applications. J. Clean. Prod. 2020, 120544. [Google Scholar] [CrossRef]
- Pang, W.; Cui, Y.; Zhang, Q.; Wilson, G.J.; Yan, H. A comparative analysis on performances of flat plate photovoltaic/thermal collectors in view of operating media, structural designs, and climate conditions. Renew. Sustain. Energy Rev. 2020, 119, 109599. [Google Scholar] [CrossRef]
- Jia, Y.; Alva, G.; Fang, G. Development and applications of photovoltaic–thermal systems: A review. Renew. Sustain. Energy Rev. 2019, 102, 249–265. [Google Scholar] [CrossRef]
- Yazdanifard, F.; Ameri, M. Exergetic advancement of photovoltaic/thermal systems (PV/T): A review. Renew. Sustain. Energy Rev. 2018, 97, 529–553. [Google Scholar] [CrossRef]
- Sultan, S.M.; Efzan, M.E. Review on recent Photovoltaic/Thermal (PV/T) technology advances and applications. Sol. Energy 2018, 173, 939–954. [Google Scholar] [CrossRef]
- Chauhan, A.; Tyagi, V.V.; Anand, S. Futuristic approach for thermal management in solar PV/thermal systems with possible applications. Energy Convers. Manag. 2018, 163, 314–354. [Google Scholar] [CrossRef]
- Solanki, S.C.; Dubey, S.; Tiwari, A. Indoor simulation and testing of photovoltaic thermal (PV/T) air collectors. Appl. Energy 2009, 86, 2421–2428. [Google Scholar] [CrossRef]
- Joshi, A.S.; Tiwari, A.; Tiwari, G.N.; Dincer, I.; Reddy, B.V. Performance evaluation of a hybrid photovoltaic thermal (PV/T) (glass-to-glass) system. Int. J. Therm. Sci. 2009, 48, 154–164. [Google Scholar] [CrossRef]
- Sarhaddi, F.; Farahat, S.; Ajam, H.; Behzadmehr, A.M.I.N.; Adeli, M.M. An improved thermal and electrical model for a solar photovoltaic thermal (PV/T) air collector. Appl. Energy 2010, 87, 2328–2339. [Google Scholar] [CrossRef]
- Shahsavar, A.; Ameri, M. Experimental investigation and modeling of a direct coupled PV/T air collector. Sol. Energy 2010, 84, 1938–1958. [Google Scholar] [CrossRef]
- Kumar, R.; Rosen, M.A. Performance evaluation of a double pass PV/T solar air heater with and without fins. Appl. Therm. Eng. 2011, 31, 1402–1410. [Google Scholar] [CrossRef]
- Kamthania, D.; Nayak, S.; Tiwari, G.N. Performance evaluation of a hybrid photovoltaic thermal double pass facade for space heating. Energy Build. 2011, 43, 2274–2281. [Google Scholar] [CrossRef]
- Daghigh, R.; Khaledian, Y. Design and fabrication of a bi-fluid type photovoltaic-thermal collector. Energy 2017, 135, 112–127. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Liu, J.M.; Umar, M.L.; Lan, W.L.; Huang, C.Y.; Syu, S.S. The photovoltaic-thermal system parameter optimization design and practical verification. Energy Convers. Manag. 2019, 180, 358–371. [Google Scholar] [CrossRef]
- Thiers, S.; Aoun, B.; Peuportier, B. Experimental characterization, modeling and simulation of a wood pellet micro-combined heat and power unit used as a heat source for a residential building. Energy Build. 2010, 42, 896–903. [Google Scholar] [CrossRef]
- Lombardi, K.; Ugursal, V.I.; Beausoleil-Morrison, I. Proposed improvements to a model for characterizing the electrical and thermal energy performance of Stirling engine micro-cogeneration devices based upon experimental observations. Appl. Energy 2010, 87, 3271–3282. [Google Scholar] [CrossRef]
- Magri, G.; di Perna, C.; Serenelli, G. Analysis of electric and thermal seasonal performances of a residential microchip unit. Appl. Therm. Eng. 2012, 36, 193–201. [Google Scholar] [CrossRef]
- Ulloa, C.; Porteiro, J.; Eguía, P.; Pousada-Carballo, J.M. Application model for a stirling engine micro-generation system in caravans in different european locations. Energies 2013, 6, 717–732. [Google Scholar] [CrossRef]
- Ulloa, C.; Míguez, J.L.; Porteiro, J.; Eguía, P.; Cacabelos, A. Development of a Transient Model of a Stirling-Based CHP System. Energies 2013, 6, 3115–3133. [Google Scholar] [CrossRef]
- Keynejad, F.; Manzie, C. Cold start modeling of spark ignition engines. Control Eng. Pract. 2011, 19, 912–925. [Google Scholar] [CrossRef]
- Hasan, A.; Vuolle, M.; Sirén, K. Minimisation of life cost of a detached house using combined simulation and optimization. Build. Environ. 2008, 43, 2022–2034. [Google Scholar] [CrossRef]
- Yan, F.; Wang, J. Pressure-based transient intake manifold temperature reconstruction in Diesel engines. Control Eng. Pract. 2012, 20, 531–538. [Google Scholar] [CrossRef]
- Wang, X.; Chua, H.T. Two bed silica gel-water adsorption chillers: An effectual lumped parameter model. Int. J. Refrig. 2007, 30, 1417–1426. [Google Scholar] [CrossRef]
- HDT. HDT Global. 2017. Available online: https://www.hdtglobal.com/ (accessed on 1 February 2019).
- Ulloa, C.; Nuñez, J.M.; Lin, C.; Rey, G. AHP-based design method of a lightweight, portable and flexible air-based PV-T module for UAV shelter hangars. Renew. Energy 2018, 123, 767–780. [Google Scholar] [CrossRef]
- Petru, L.; Mazen, G. PWM control of a DC motor used to drive a conveyor belt. Procedia Eng. 2015, 100, 299–304. [Google Scholar] [CrossRef]
- Salamone, F.; Belussi, L.; Danza, L.; Ghellere, M.; Meroni, I. An open source low cost wireless control system for a forced circulation solar plant. Sensors 2015, 15, 27990–28004. [Google Scholar] [CrossRef]
- Avallone, E.; Cunha, D.G.; Padilha, A.; Scalon, V.L. Electronic multiplex system using the Arduino platform to control and record the data of the temperatures profiles in heat storage tank for solar collector. Int. J. Energy Environ. Eng. 2016, 7, 391–398. [Google Scholar] [CrossRef]
- Claros-Marfil, L.J.; Padial, J.F.; Lauret, B. A new and inexpensive open source data acquisition and controller for solar research: Application to a water-flow glazing. Renew. Energy 2016, 92, 450–461. [Google Scholar] [CrossRef]
- Swinbank, W. Long-wave radiation from clear skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Nusselt, W.; Jürges, W. Die Kühlung einer Ebenen Wand Durch einen Luftstrom (The Cooling of a Plane Wall by an Air Flow). In Gesundheits Ingenieur; 52. Heft, 45. Jahrgang; Umwelttechnik (Munchen); DIV: Munchen, Germany, 30 December 1922; pp. 641–642. [Google Scholar]









| Parameter | Number of Sensors | Sensor | Range | I/O Type | Power Supply |
|---|---|---|---|---|---|
| Temperature | 2 | DS18B20 Thermometer | −55–125 °C | Digital (One-Wire) | 5 VDC |
| Flow rate | 1 | Bosch HFM 5 Air-mass meter | 8–370 kg/h | Analog (0–5 V) | 8–17 VDC |
| Solar irradiation | 1 | Kipp & Zonen SMP10 Pyranometer | 0–1600 W/m2 | Analog (4–20 mA) | 5–30 VDC |
| Simulation Step (h) | |||
|---|---|---|---|
| 16 | 17.1 | 10.3 | 6.7 |
| 34 | 19.9 | 10.8 | 9.2 |
| 62 | 18.4 | 10.8 | 7.6 |
| 87 | 21.9 | 13.7 | 8.1 |
| 111 | 18.9 | 12.7 | 6.3 |
| 135 | 20.9 | 12.4 | 8.4 |
| 159 | 21.2 | 12.7 | 8.5 |
| 183 | 21.7 | 13.7 | 7.0 |
| Period | |||
|---|---|---|---|
| Simulation time ( | 7.7 | 6.6 | 1.2 |
| Heating time ( | 14.9 | 10.0 | 4.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orgeira-Crespo, P.; Ulloa, C.; Núñez, J.M.; Pérez, J.A. Development of a Transient Model of a Lightweight, Portable and Flexible Air-Based PV-T Module for UAV Shelter Hangars. Energies 2020, 13, 2889. https://doi.org/10.3390/en13112889
Orgeira-Crespo P, Ulloa C, Núñez JM, Pérez JA. Development of a Transient Model of a Lightweight, Portable and Flexible Air-Based PV-T Module for UAV Shelter Hangars. Energies. 2020; 13(11):2889. https://doi.org/10.3390/en13112889
Chicago/Turabian StyleOrgeira-Crespo, Pedro, Carlos Ulloa, José M. Núñez, and José A. Pérez. 2020. "Development of a Transient Model of a Lightweight, Portable and Flexible Air-Based PV-T Module for UAV Shelter Hangars" Energies 13, no. 11: 2889. https://doi.org/10.3390/en13112889
APA StyleOrgeira-Crespo, P., Ulloa, C., Núñez, J. M., & Pérez, J. A. (2020). Development of a Transient Model of a Lightweight, Portable and Flexible Air-Based PV-T Module for UAV Shelter Hangars. Energies, 13(11), 2889. https://doi.org/10.3390/en13112889






