Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles
Abstract
1. Introduction
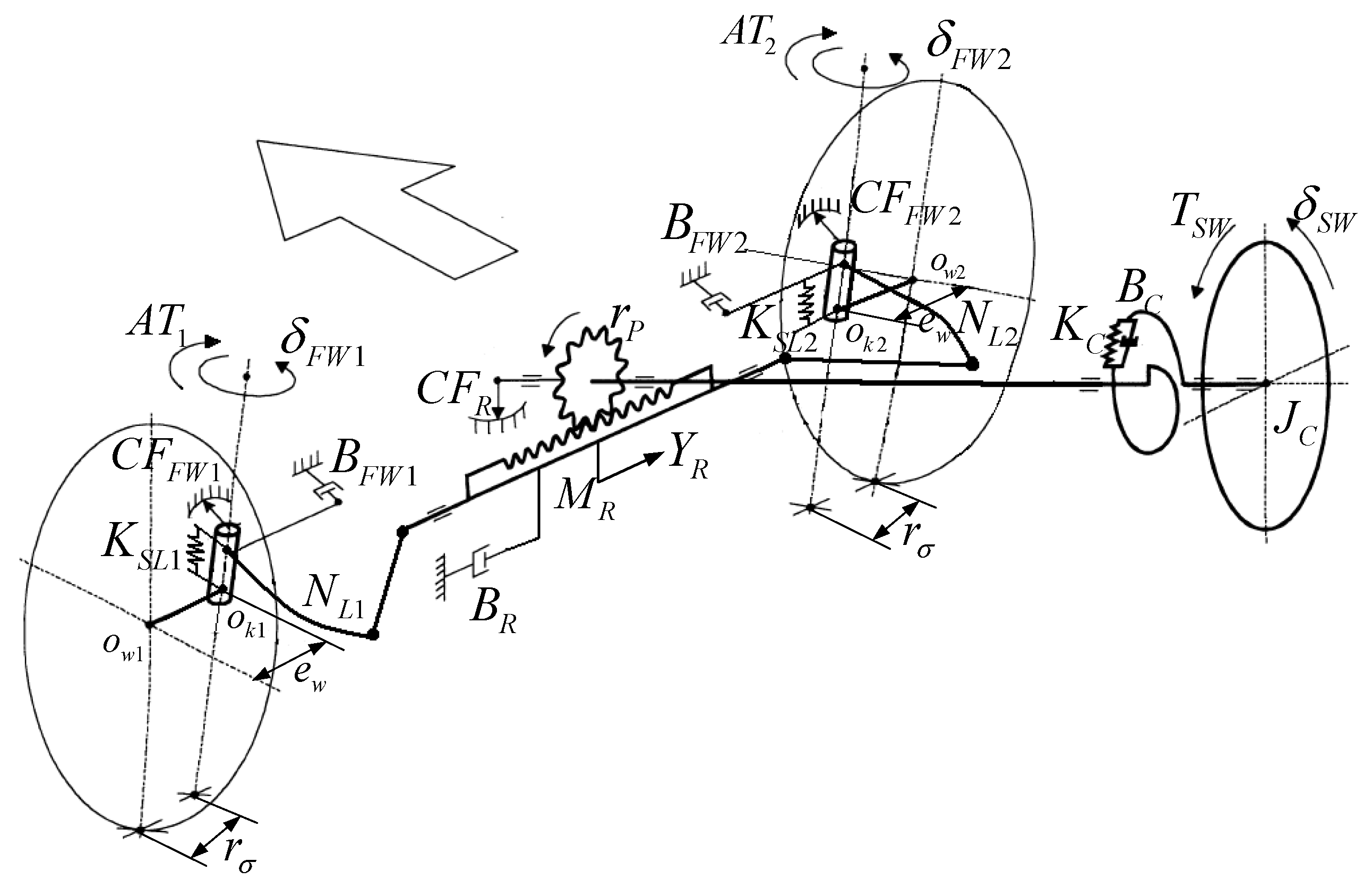
2. Independent-Wheel-Drive Electric Vehicle Dynamic Model
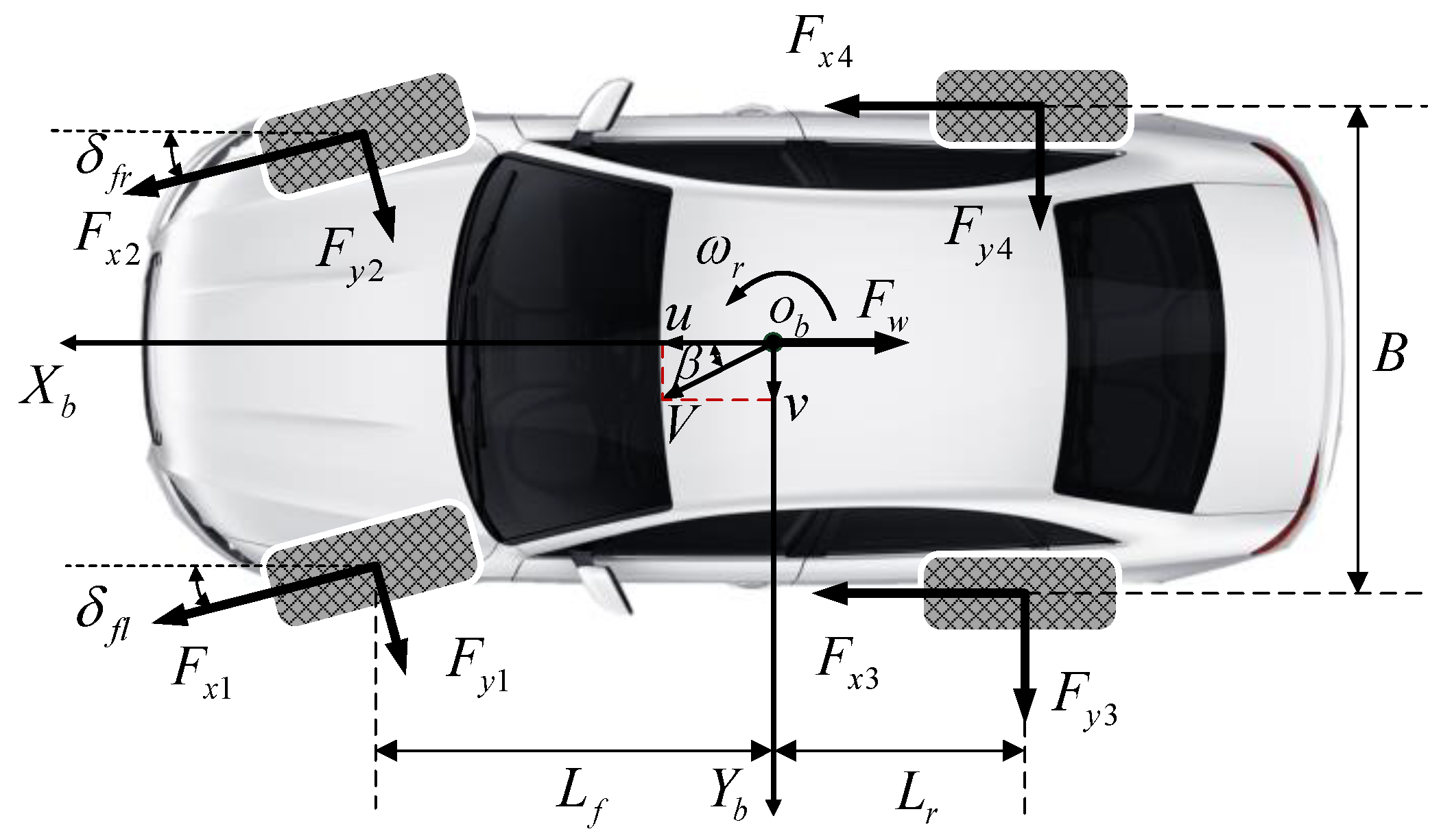
2.1. Vehicle Body Dynamic Model
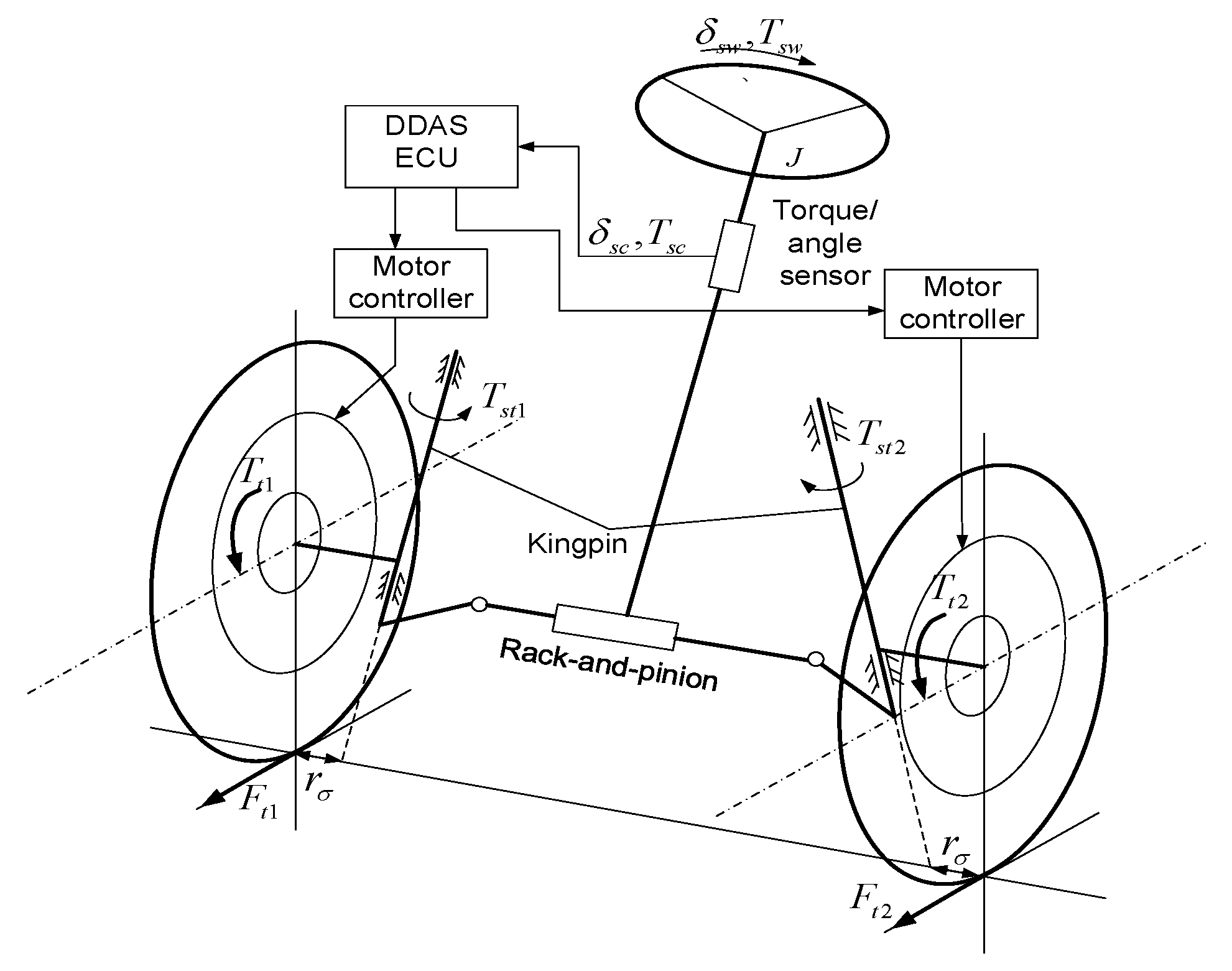
2.2. Four-DoF Mechanical Steering System Sub-Model
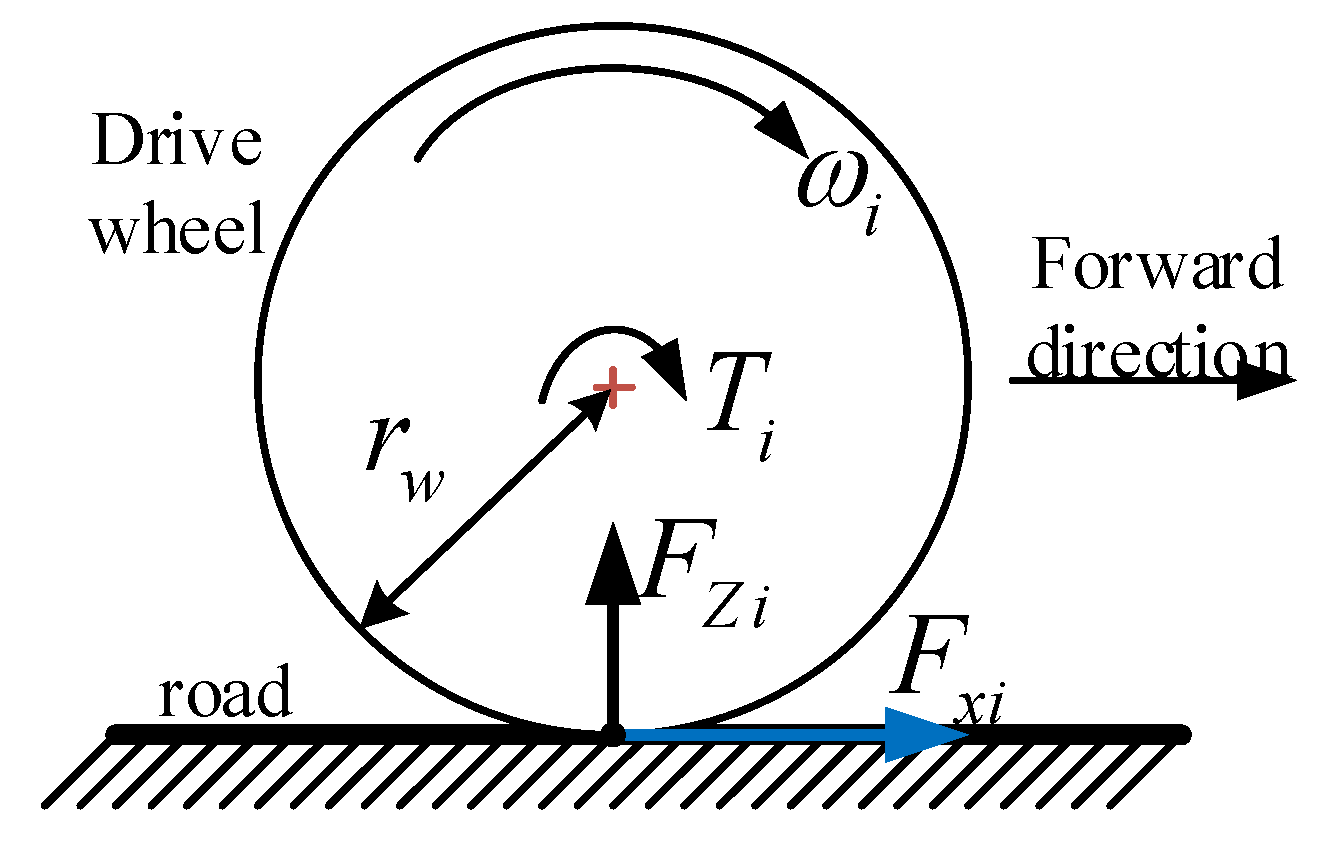
2.3. Wheel Rotation Dynamic Sub-Model
2.4. Tire Sub-Model
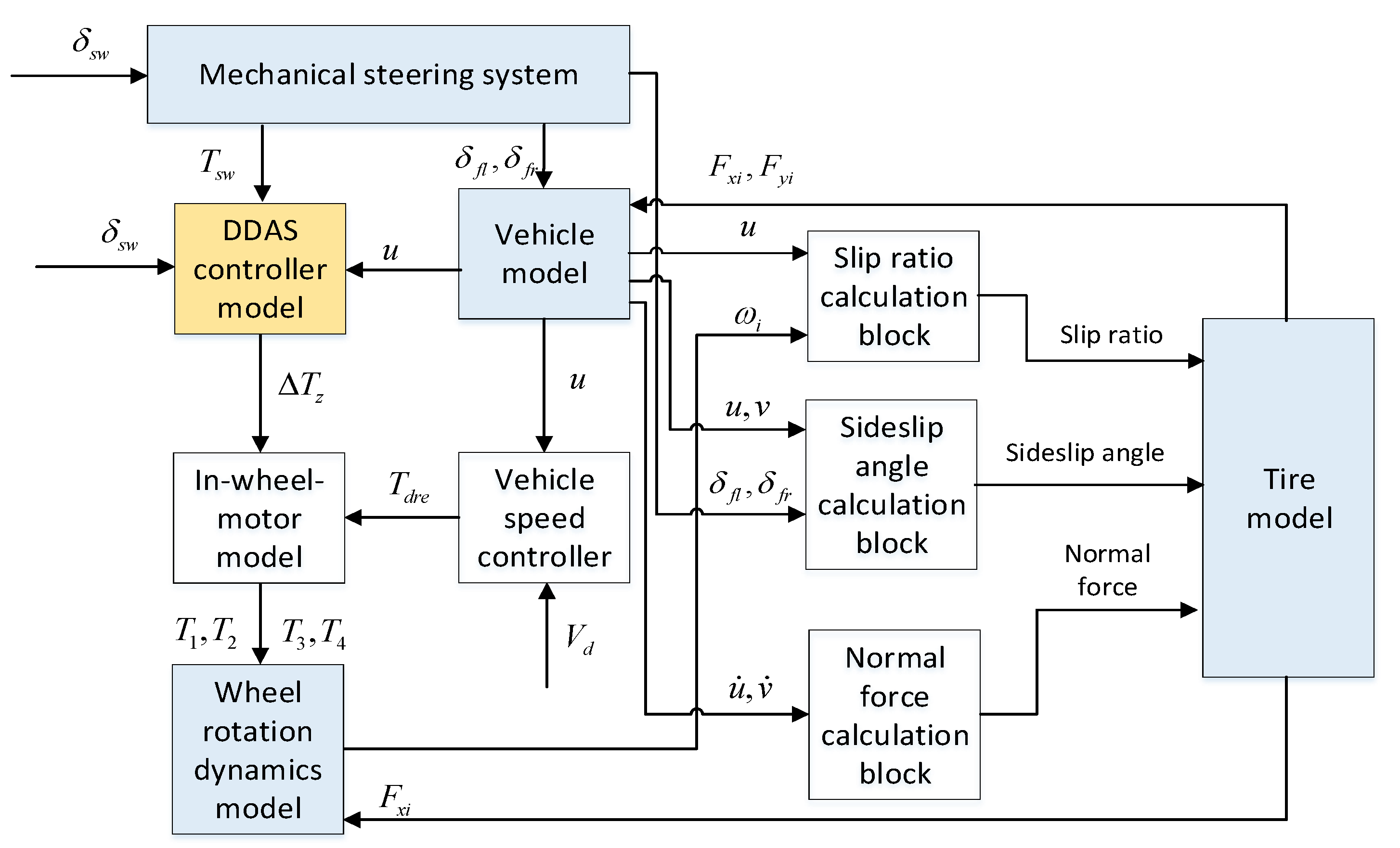
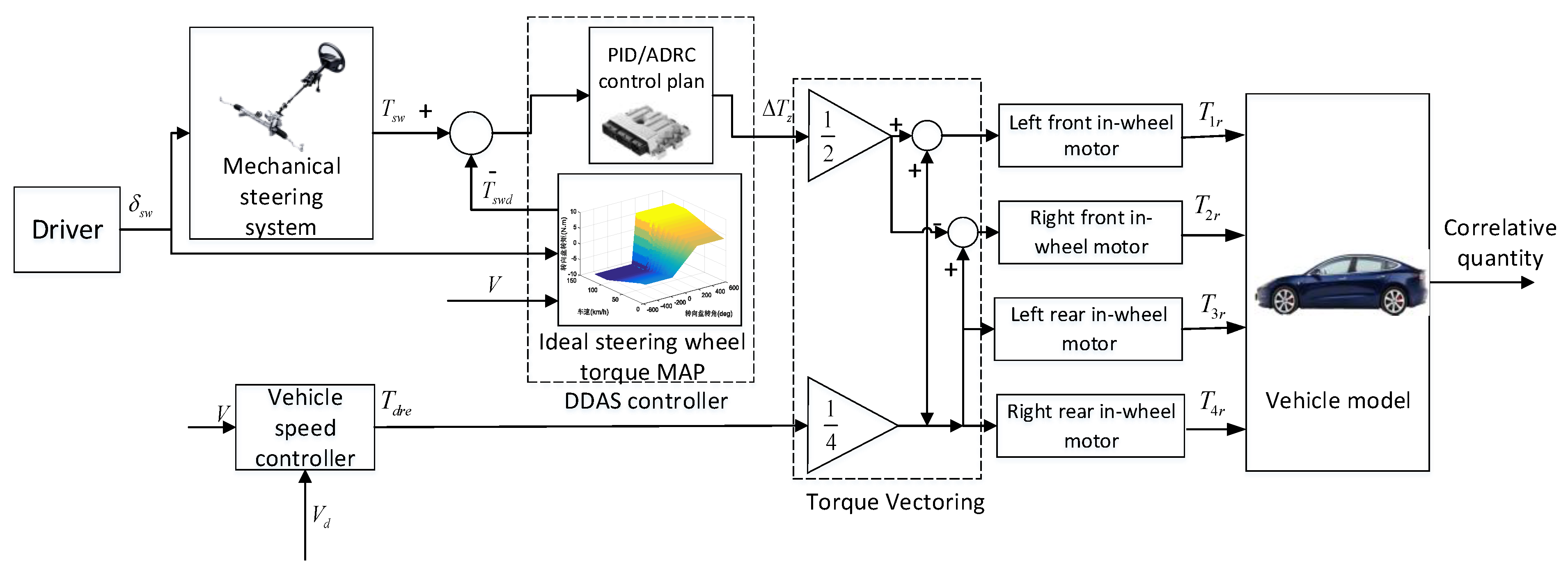
3. Design of DDAS Controller
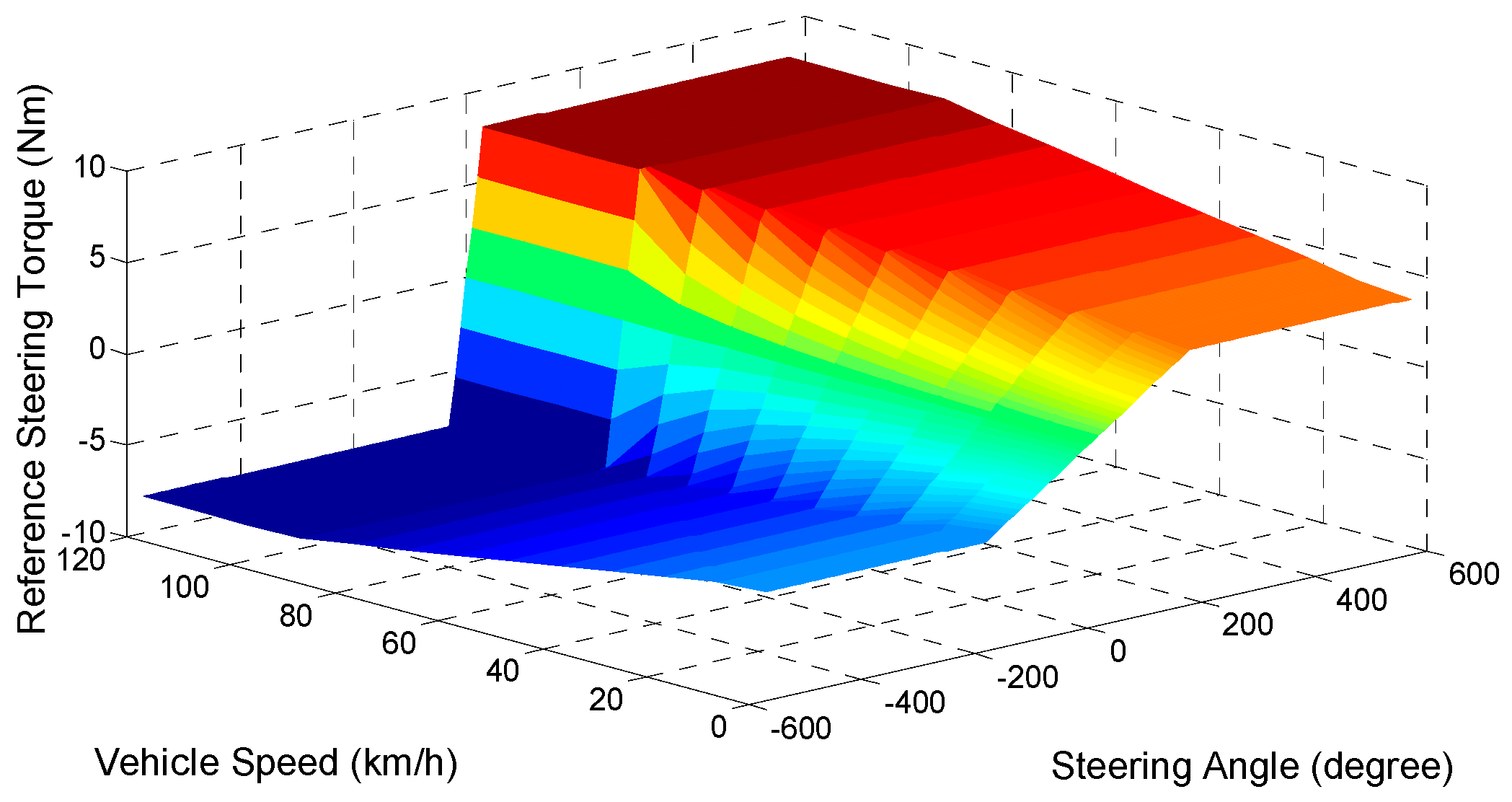
3.1. Steering-Wheel-Torque Direct Control Strategy
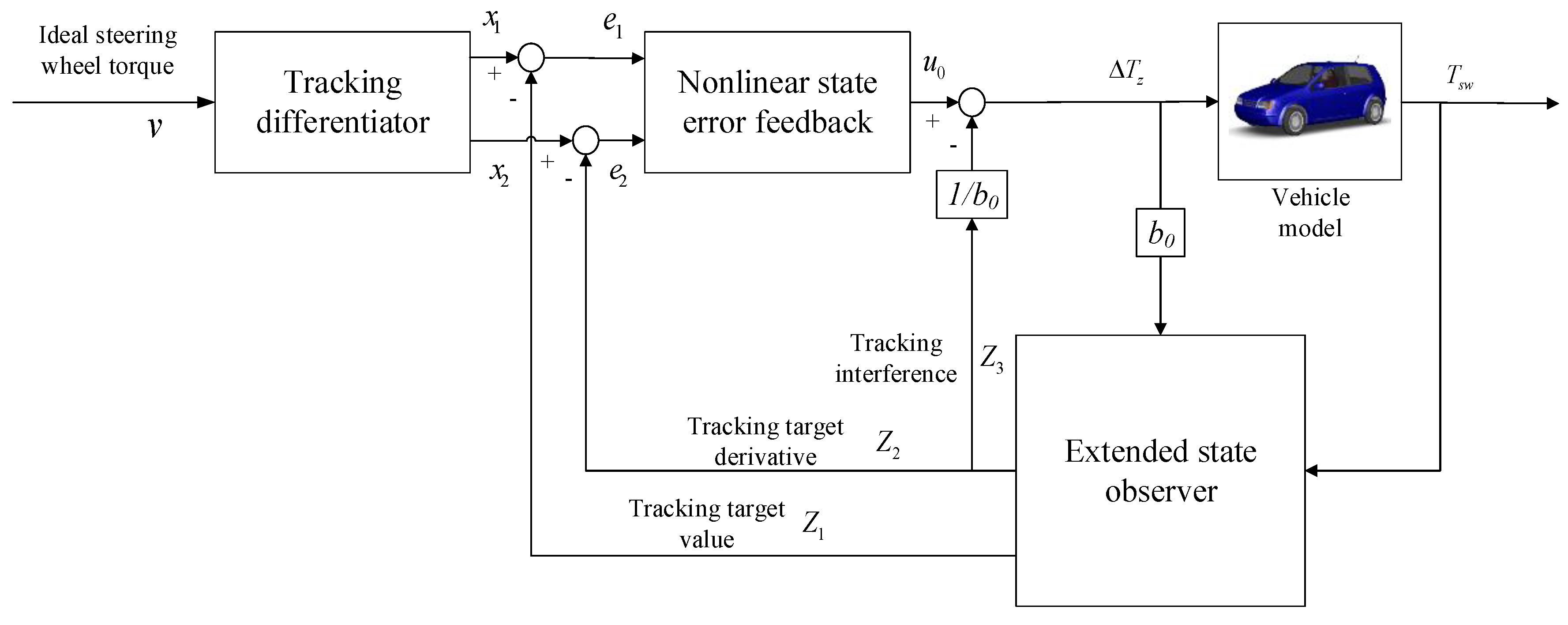
3.2. Design of the ADRC Controller of DDAS System
4. Controller Parameter Optimization Based on Simulated Annealing Algorithm
5. Simulation Analysis
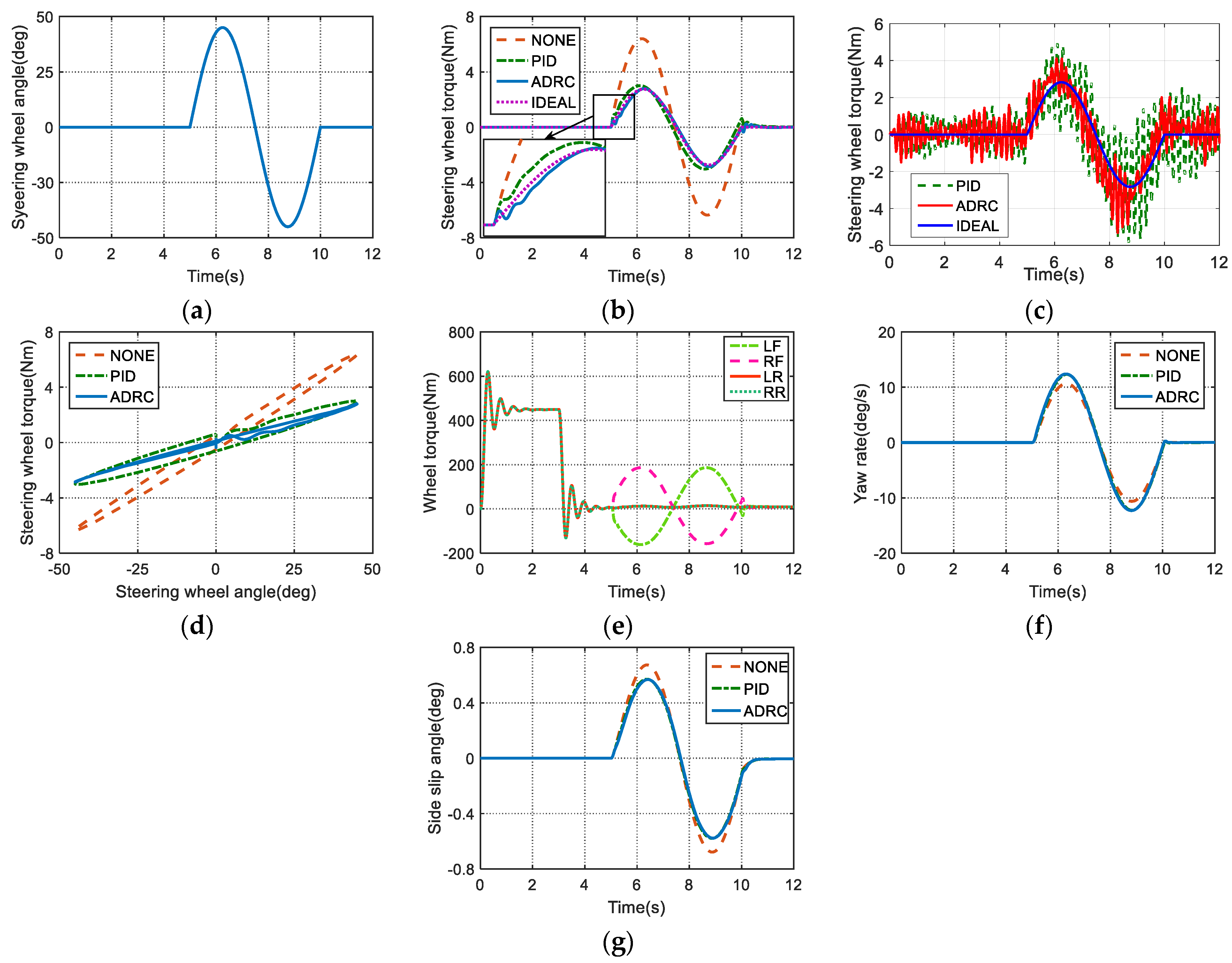
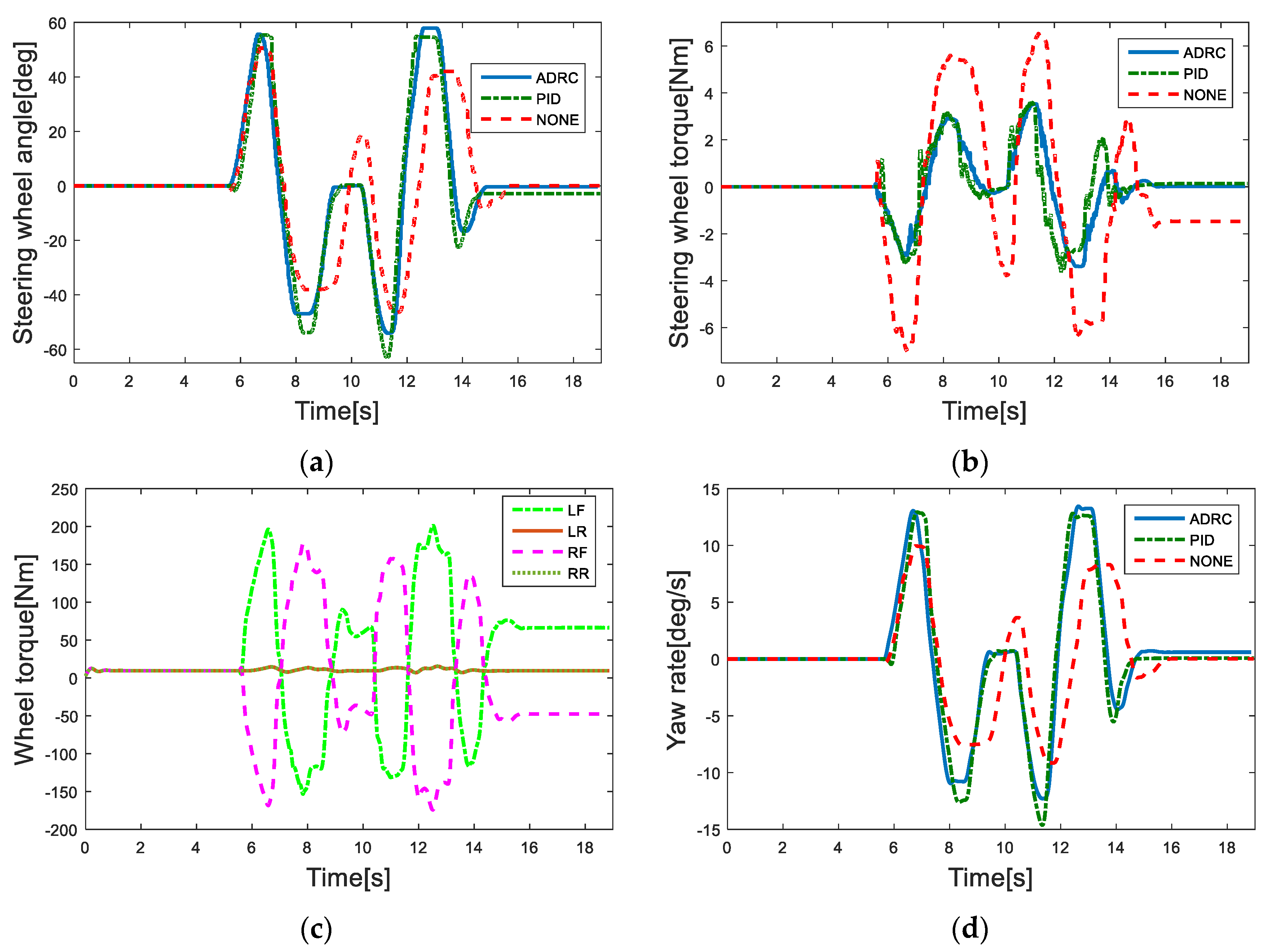
5.1. Sinusoidal Steering Wheel Angle Input Simulation
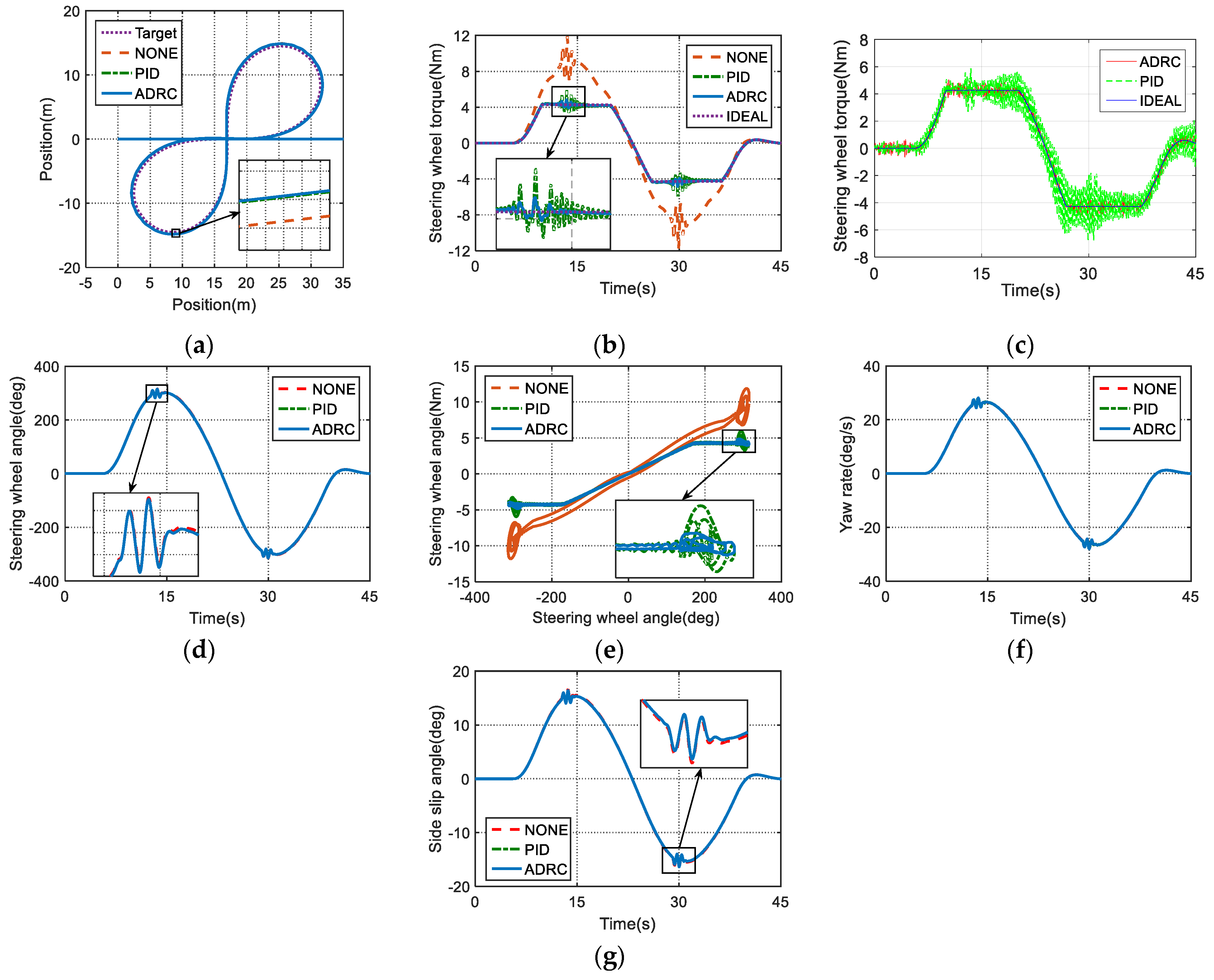
5.2. Closed-Loop Lemniscate Simulation
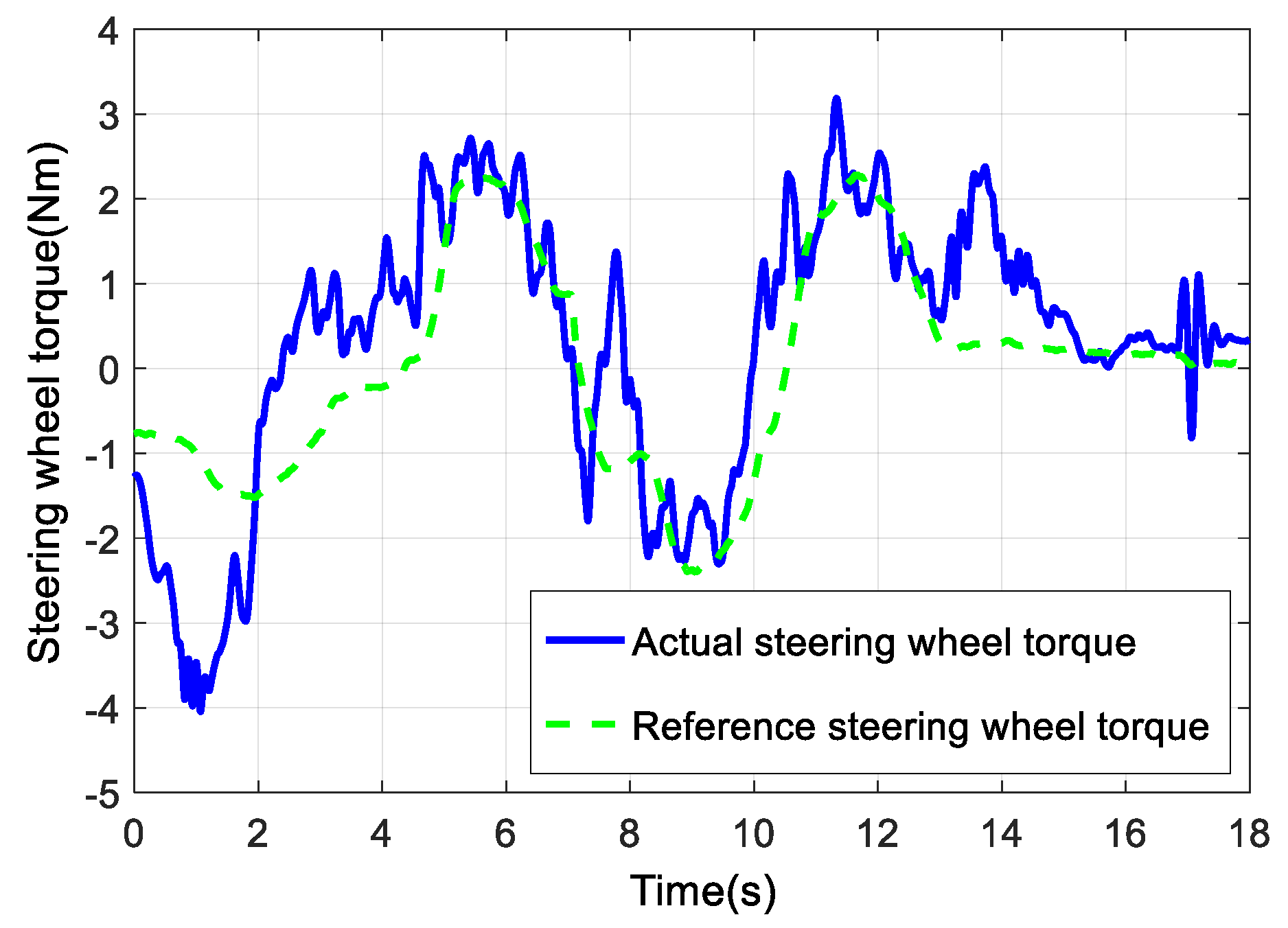
6. Hardware-in-the-Loop Experimental Validation
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| scrub radius | |
| tire rolling radius | |
| transmission ratio of the rack translation to the knuckle arm angular displacement | |
| moment of inertia of the wheel about its central axis | |
| the longitudinal and lateral forces of the left front wheel, the right front wheel, the left rear wheel, and the right rear wheel respectively | |
| the mass of the whole vehicle | |
| the longitudinal speed of the body centroid | |
| the longitudinal speed of the body centroid | |
| the yaw rate of the vehicle body | |
| the inertia of the body around the Z axis | |
| the air resistance coefficient | |
| the air density | |
| the frontal area | |
| steering angles of the left front wheel and the right front wheel | |
| the distance from the body centroid to the front axle | |
| the distance from the body centroid to the rear axle | |
| the wheelbase | |
| the steering wheel torque | |
| the damping of the steering column | |
| equivalent inertia of steering wheel and column | |
| steering wheel angle | |
| the mass of the rack | |
| the damping of the rack | |
| the displacement of the rack | |
| the radius of the pinion | |
| the forward transmitting efficiency of the steering gear | |
| the backward transmitting efficiency of the steering gear | |
| the torsional stiffness of the torsion bar | |
| the coulomb friction of the gear and rack | |
| the inertia of the road wheel round their kingpin | |
| the damping of kingpin | |
| the coulomb friction caused by the steerable wheels rotating the kingpin | |
| the total torque from the kingpins of the left front wheel and the right front wheels | |
| the steering angle of front wheels | |
| the torsional stiffness of the kingpin of the front wheels | |
| the alignment torque generated by the lateral force of the tire | |
| the alignment torque generated by the longitudinal force of the tire | |
| the component of the tire self-alignment torque about the kingpin | |
| the alignment torque generated by the normal force of the front axle | |
| the self-alignment torque of the tire | |
| the normal force of the wheels | |
| the kingpin caster angle | |
| the kingpin inclination angle | |
| the angular velocity of the wheels | |
| the driving torque of the wheels | |
| the target electromagnetic torque | |
| the motor characteristic parameter | |
| the target steering wheel torque | |
| the front wheels torque difference | |
| the total demand driving torque determined by the longitudinal driver model | |
| the target speed | |
| the proportional coefficient of the PID controller | |
| the integral coefficient of the PID controller | |
| the differential coefficient of the PID controller | |
| the speed factor | |
| the tracking step | |
| the control parameters | |
| the error term | |
| the length of the linear segment | |
| the nonlinear factor in the fal function | |
| the steering wheel torque error term | |
| the steering wheel torque change rate error term | |
| the nonlinear combination coefficients | |
| the control output of the nonlinear state error feedback | |
| the minimum curvature radius |
References
- Wang, J.; Wang, Q.; Jin, L.; Song, C. Independent wheel torque control of 4WD electric vehicle for differential drive assisted steering. Mechatronics 2011, 21, 63–76. [Google Scholar] [CrossRef]
- Zhao, W.Z.; Zhang, H. Coupling Control Strategy of Force and Displacement for Electric Differential Power Steering System of Electric Vehicle with Motorized Wheels. IEEE Trans. Veh. Technol. 2018, 10, 8118–8128. [Google Scholar] [CrossRef]
- Hu, C.; Qin, Y.C.; Cao, H.T. Lane keeping of autonomous vehicles based on differential steering with adaptive multivariable super-twisting control. Mech. Syst. Signal Process. 2019, 125, 330–346. [Google Scholar] [CrossRef]
- Kuslits, M.; Bestle, D. Modelling and control of a new differential steering concept. Veh. Syst. Dyn. 2019, 57, 520–542. [Google Scholar] [CrossRef]
- Peng, B.; Li, J.Q.; Sun, F.C. Research on Differential Steering Control Strategy of Distributed Electric Drive Vehicle. In Proceedings of the International Conference on Civil Engineering, Mechanics and Materials Science, Bangkok, Thailand, 17–19 May 2019. [Google Scholar]
- Wang, J.; Luo, Z.; Wang, Y.; Yang, B.; Assadian, F. Coordination control of differential drive assist steering and vehicle stability control for four-wheel-independent-drive EV. IEEE Trans. Veh. Technol. 2018, 67, 11453–11467. [Google Scholar] [CrossRef]
- Römer, J.; Kautzmann, P.; Frey, M.; Gauterin, F. Reducing Energy Demand Using Wheel-Individual Electric Drives to Substitute EPS-Systems. Energies 2018, 11, 247. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Wang, Q.; Assadian, F.; Fu, B. Simulation investigation of tractive energy conservation for a cornering rear-wheel-independent-drive electric vehicle through torque vectoring. Sci. China Technol. Sci. 2018, 61, 257–272. [Google Scholar] [CrossRef]
- Han, J. Auto Disturbances Rejection Control Technique; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Esmailzadeh, E.; Vossoughi, G.R.; Goodarzi, A. Dynamic modeling and analysis of a four motorized wheels electric vehicle. Veh. Syst. Dyn. 2001, 35, 163–194. [Google Scholar] [CrossRef]
- Pang, D.Y.; Jang, B.C.; Lee, S.C. Steering Wheel Torque Control of Electric Power Steering by PD-Control; ICCAS: Kintex, Korea, 2005. [Google Scholar]
- Badawy, A.; Zuraski, J.; Bolourchi, F.; Chandy, A. Modeling and Analysis of an Electric Power Steering System; International Congress and Exposition: Detroit, MI, USA, 1999. [Google Scholar]
- Salaani, M.K.; Heydinger, G.J.; Grygier, P.A. Closed Loop Steering System Model for the National Advanced Driving Simulator; 2004 SAE World Congress: Detroit, MI, USA, 2004. [Google Scholar]
- Guo, K. Vehicle Handling Dynamics; Jilin Science Press: Changchun, China, 1991. [Google Scholar]
- Jin, L.Q.; Song, C.X.; Peng, Y.H. Theory for Optimization Design of Steer Wheel Alignment Based on Returnability and Handiness. Trans. Chin. Soc. Agric. Mach. 2006, 37, 20–23. [Google Scholar]
- Wang, Q.; Wang, J.; Yan, L. Differential assisted steering applied on electric vehicle with electric motored wheels. J. Jilin Univ. (Eng. Technol. Ed.) 2009, 39, 1–6. [Google Scholar]
- Bakker, E.; Nyborg, L.; Pacejka, H.B. Tyre Modeling for Use in Vehicle Dynamics Studies; Society of Automotive Engineers: Warrendale, PA, USA, 1987. [Google Scholar]
- Shen, R.; Lin, Y.; Tai, X. Research on Modeling and Compensation Control Strategy of Electric Power Steering System. Trans. Chin. Soc. Agric. Mach. 2007, 38, 5–9. [Google Scholar]
- Bertollini, G.P.; Hogan, R.M. Applying Driving Simulation to Quantify Steering Effort Preference as a Function of Vehicle Speed; International Congress and Exposition: Detroit, MI, USA, 1999. [Google Scholar]
- Green, P.; Gillespie, T.; Reifeis, S. Subjective Evaluation of Steering Effort Levels; The University of Michigan Transportation Research Institute: Ann Arbor, MI, USA, 1984. [Google Scholar]
- Toffin, D.; Reymond, G.; Kemeny, A.; Droulez, J. Role of steering wheel feedback on driver performance: Driving simulator and modeling analysis. Veh. Syst. Dyn. 2007, 45, 375–388. [Google Scholar] [CrossRef]
- Shen, R.; Lin, Y.; Tai, X. Steering torque direct control strategy for vehicle electric power steering system. J. Jilin Univ. (Eng. Technol. Ed.) 2007, 37, 504–508. [Google Scholar]
- Ahi, B.; Haeri, M. Linear Active Disturbance Rejection Control from the Practical Aspects. IEEE/ASME Trans. Mechatron. 2018, 23, 2909–2919. [Google Scholar] [CrossRef]
- Han, J. Auto Disturbances Rejection Control Technique. Front. Sci. 2007, 1, 24–31. [Google Scholar]
- Zheng, Q.; Dong, L.; Lee, D.H. Active Disturbance Rejection Control for MEMS Gyroscopes. IEEE Trans. Control Syst. Technol. 2009, 17, 1432–1438. [Google Scholar] [CrossRef]
- Wang, K. Research on Active Disturbance Rejection Control of Full Vehicle Active Suspension Based on Adaptive Genetic Algorithm; Jilin University: Changchun, China, 2017. [Google Scholar]
- Zhao, J. Optimization Technology and MATLAB Optimization Toolbox; Mechanical Industry Press: Beijing, China, 2011. [Google Scholar]
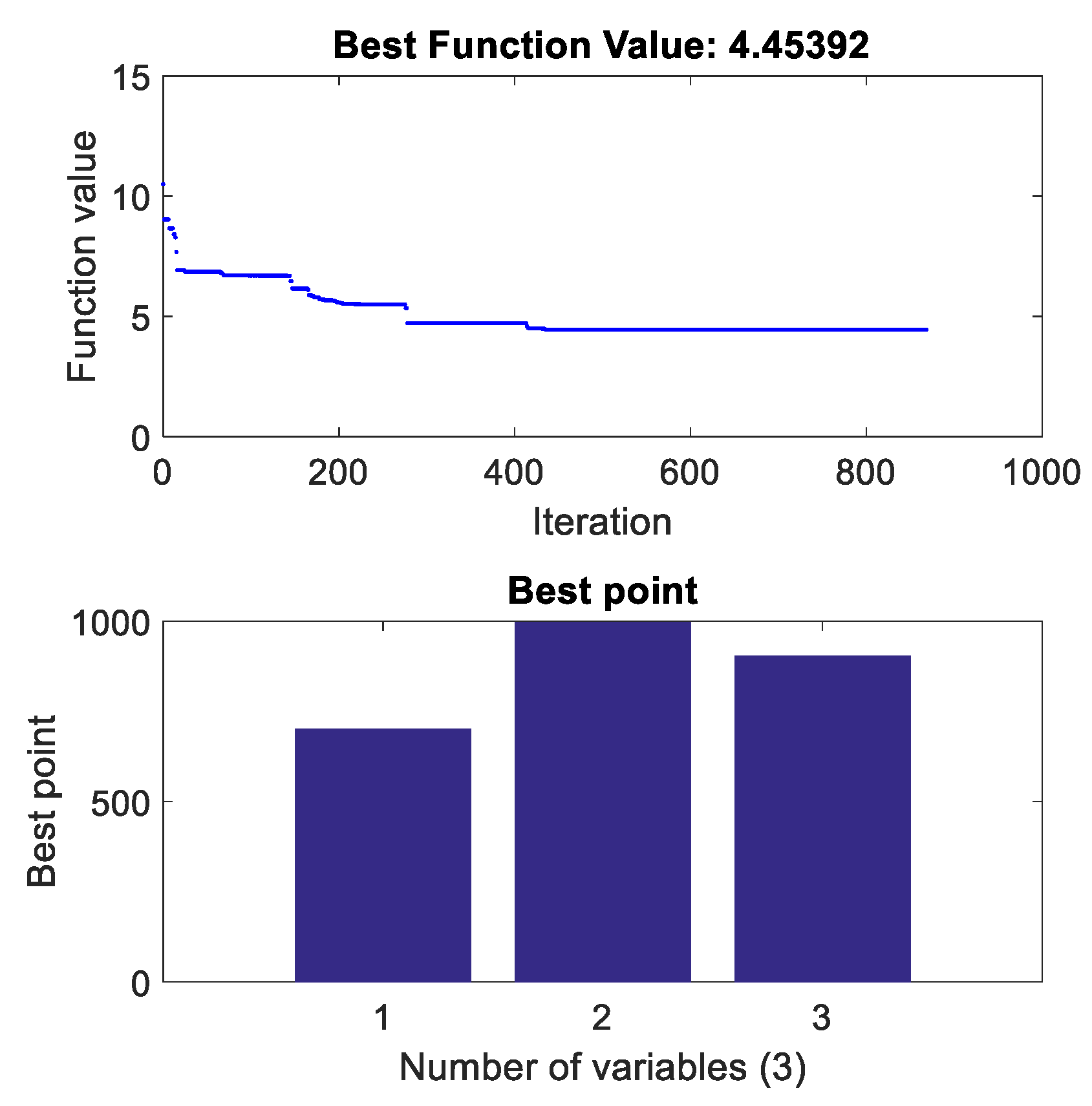

| Parameters | ||||||
|---|---|---|---|---|---|---|
| Initial value | 450 | 600 | 1000 | −350 | 30 | 1 |
| Optimal value | 700.955 | 997.714 | 903.922 | −425.893 | 0.372 | 2.801 |
| Performance | Uncontrolled | PID | ADRC |
|---|---|---|---|
| (Nm) | 1.674 | 0.2795 | 0.0867 |
| Performance | Uncontrolled | PID | ADRC |
|---|---|---|---|
| (Nm) | 2.176 | 0.2106 | 0.07809 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, X.; Luo, Z.; Assadian, F. Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles. Energies 2020, 13, 2647. https://doi.org/10.3390/en13102647
Wang J, Wang X, Luo Z, Assadian F. Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles. Energies. 2020; 13(10):2647. https://doi.org/10.3390/en13102647
Chicago/Turabian StyleWang, Junnian, Xiandong Wang, Zheng Luo, and Francis Assadian. 2020. "Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles" Energies 13, no. 10: 2647. https://doi.org/10.3390/en13102647
APA StyleWang, J., Wang, X., Luo, Z., & Assadian, F. (2020). Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles. Energies, 13(10), 2647. https://doi.org/10.3390/en13102647







