Analysis of Internal Overvoltages in Transformer Windings during Transients in Electrical Networks
Abstract
1. Introduction
- (1)
- A proposition of a transformer winding model, which can be implemented in EMTP-type software, for the analysis of overvoltages at selected points inside the winding during the transient state in an electrical network;
- (2)
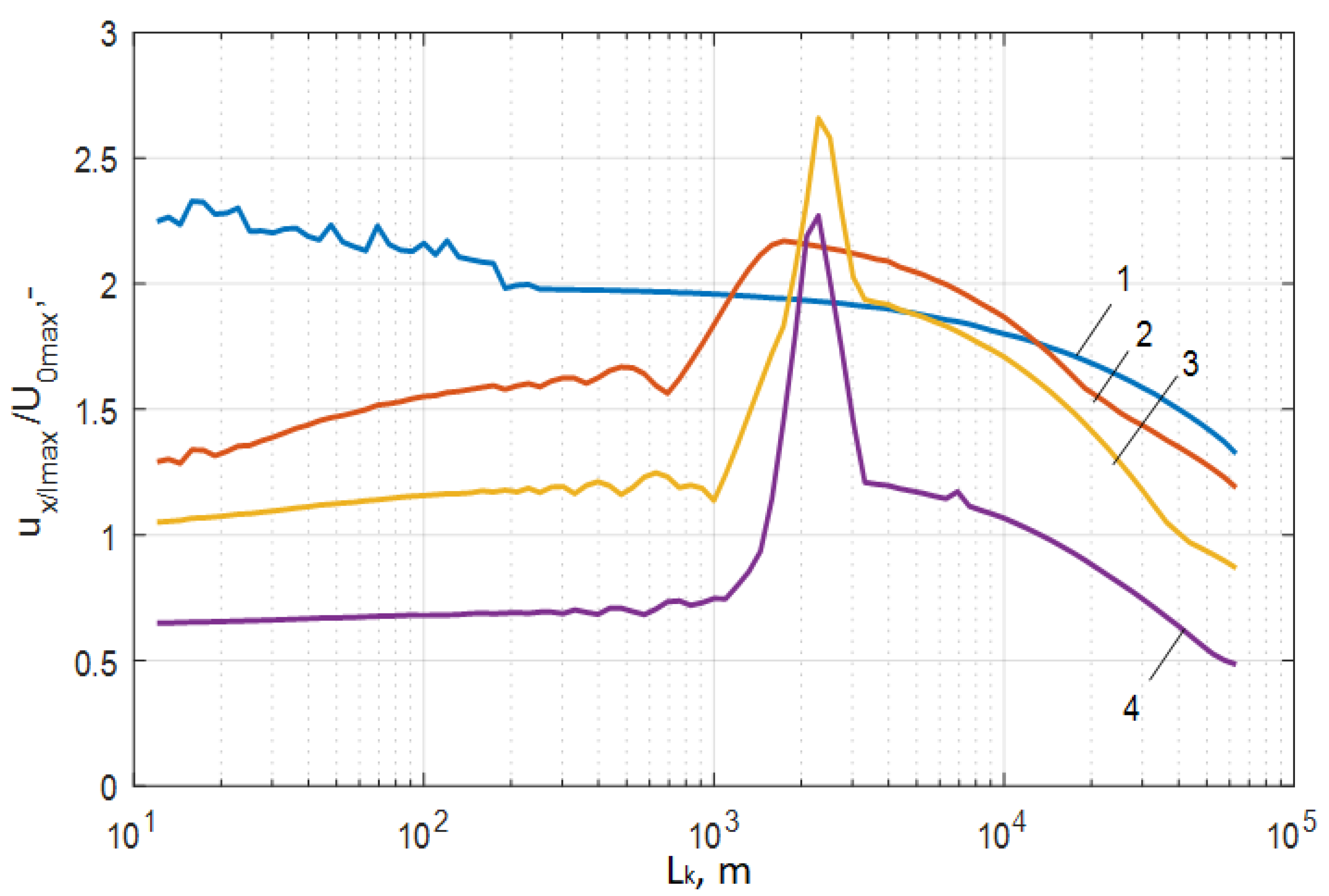
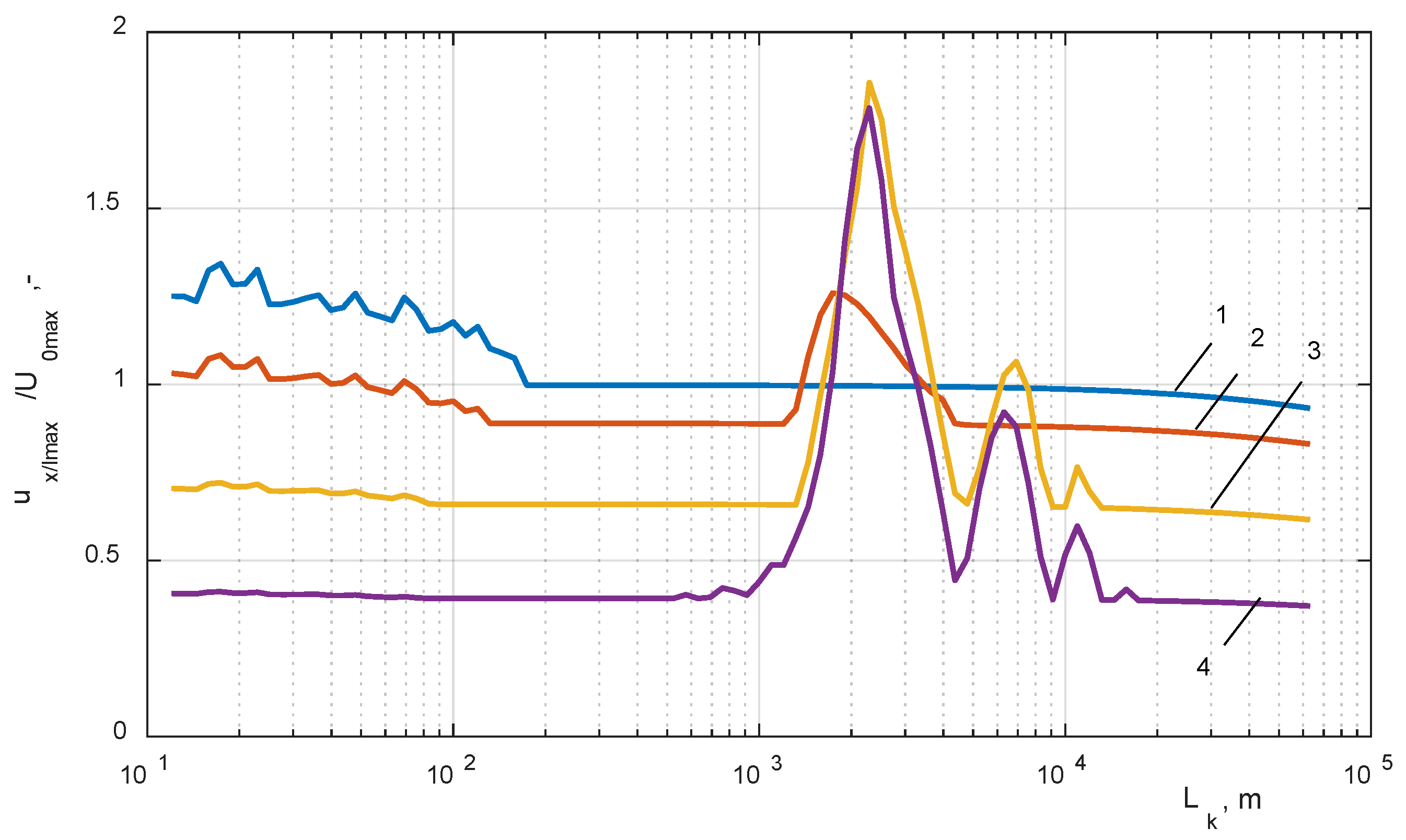
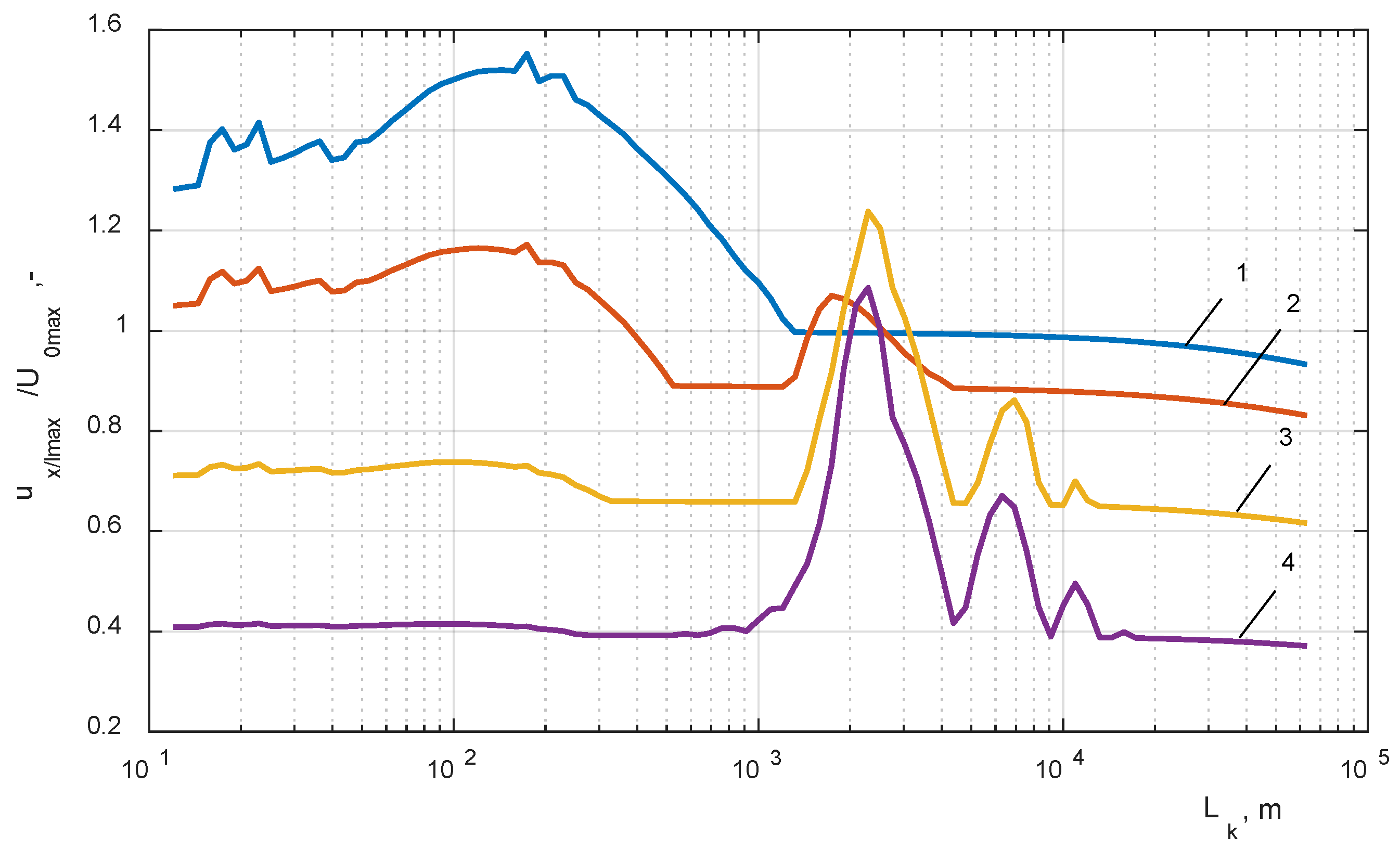
- A definition of a critical cable length in the setup with a circuit breaker in which the highest internal overvoltage level is observed; these kinds of overvoltages are related to the resonance phenomena;
- (3)
- A presentation of the impact of ground fault resistance on the mechanism of overvoltage distribution inside the winding.
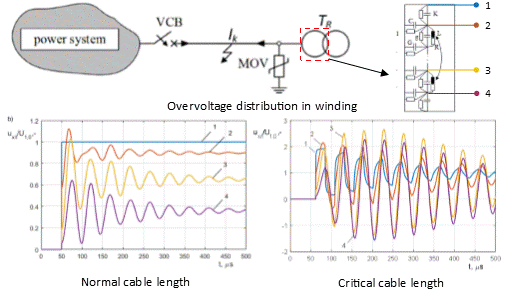
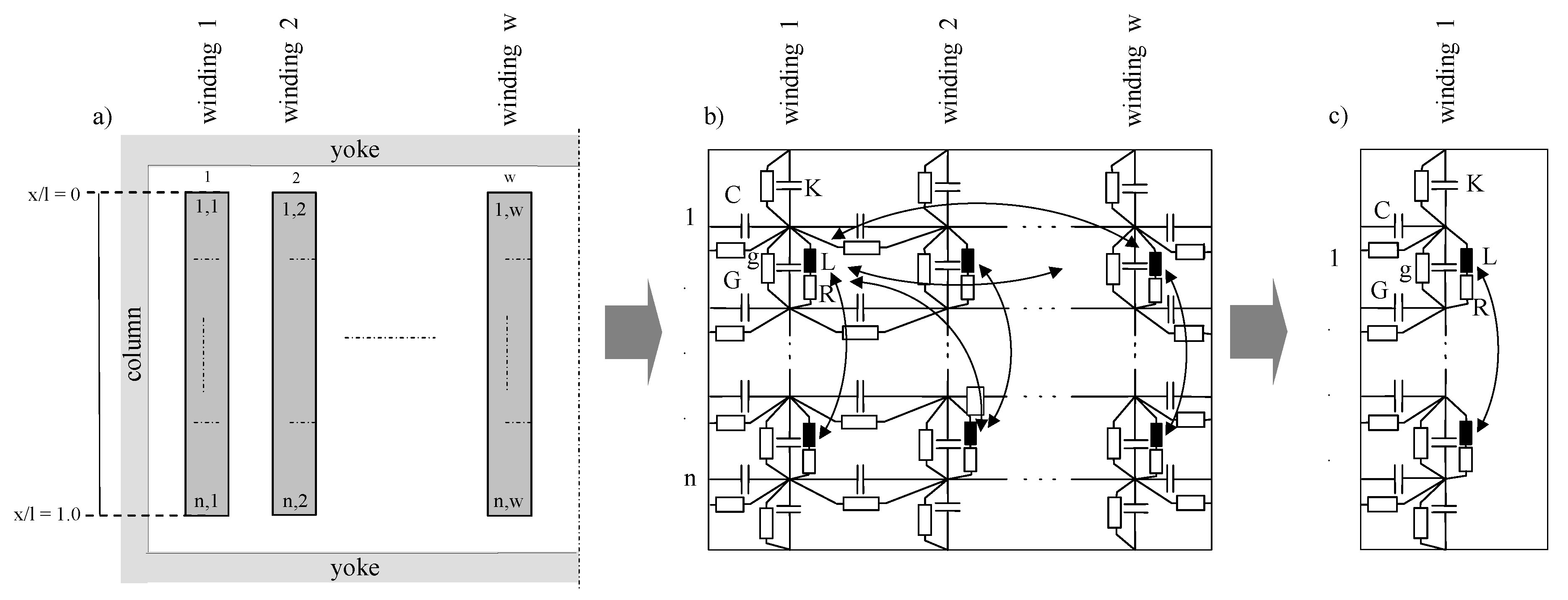
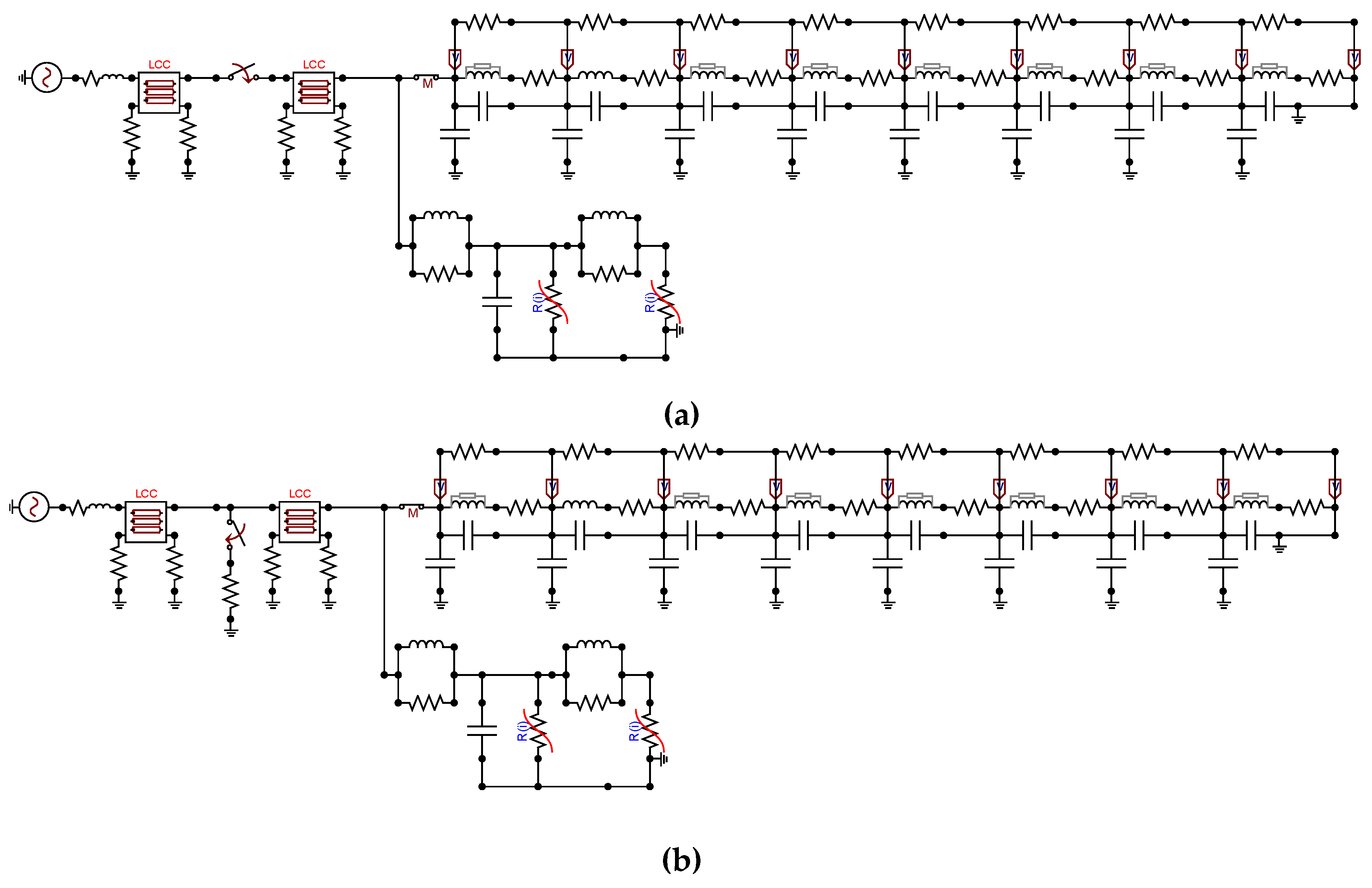
2. The Model System with a Cable Line and Distribution Transformer
- (1)
- energization of the distribution transformer connected with line Lk with variable length;
- (2)
- single-phase earth fault in the cable line Lk with different distances from the transformer and different values of the short circuit resistance.
3. The Simulation of Winding Internal Overvoltages
3.1. Simulation Models of a Power Transformer and Power Apparatus
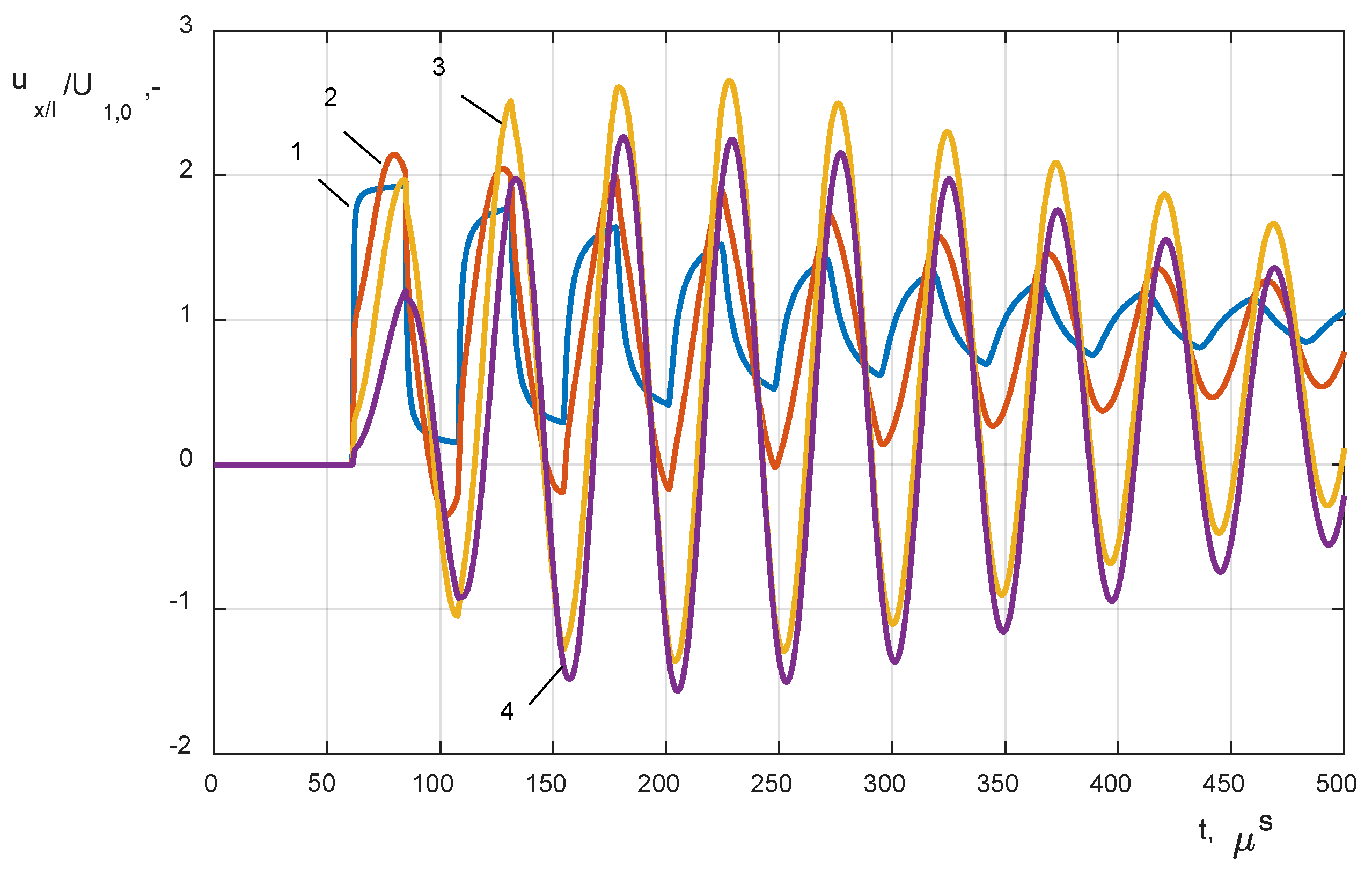
3.2. The Simulation of Winding Internal Overvoltages During a Switching Operation and Ground Faults
- (1)
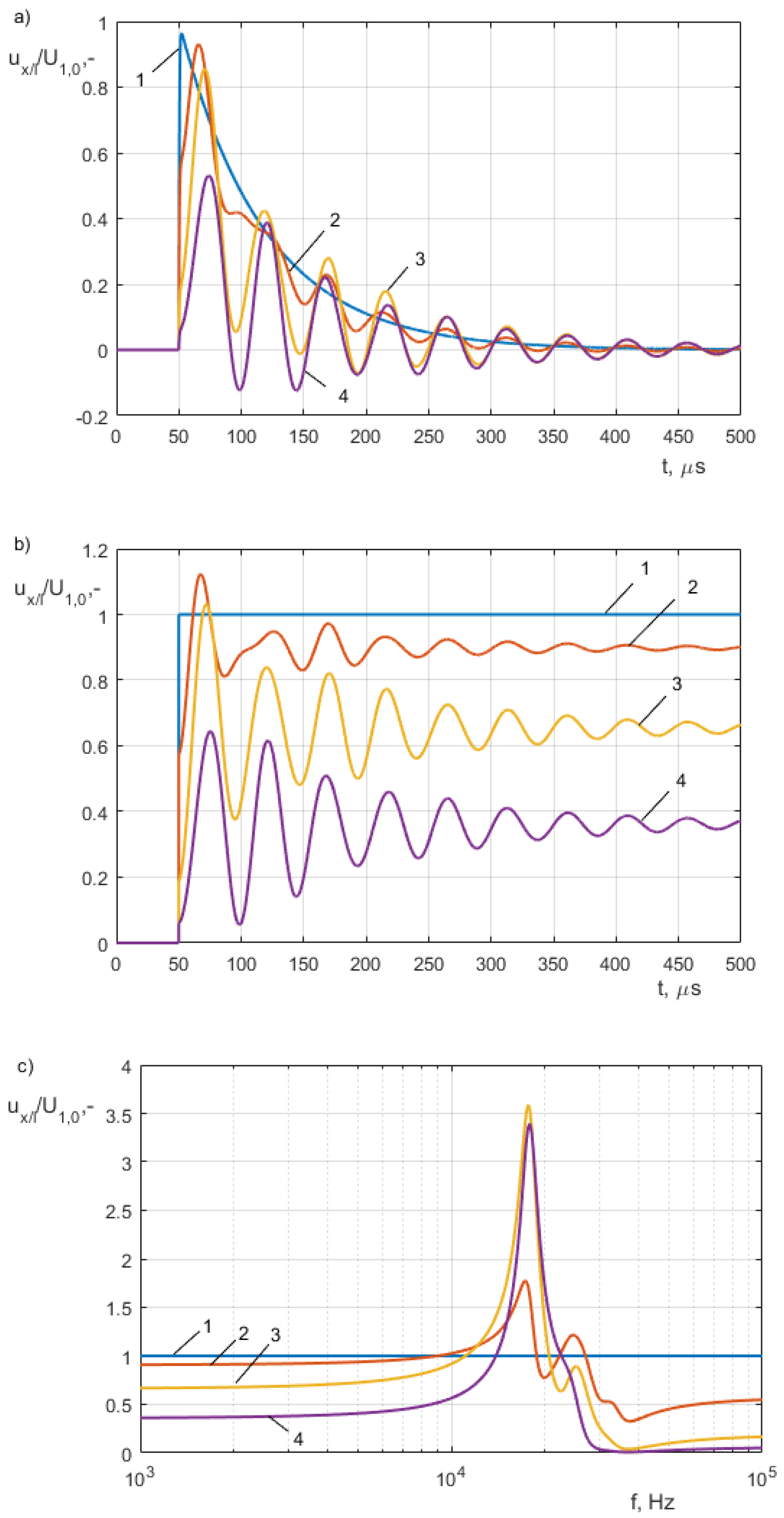
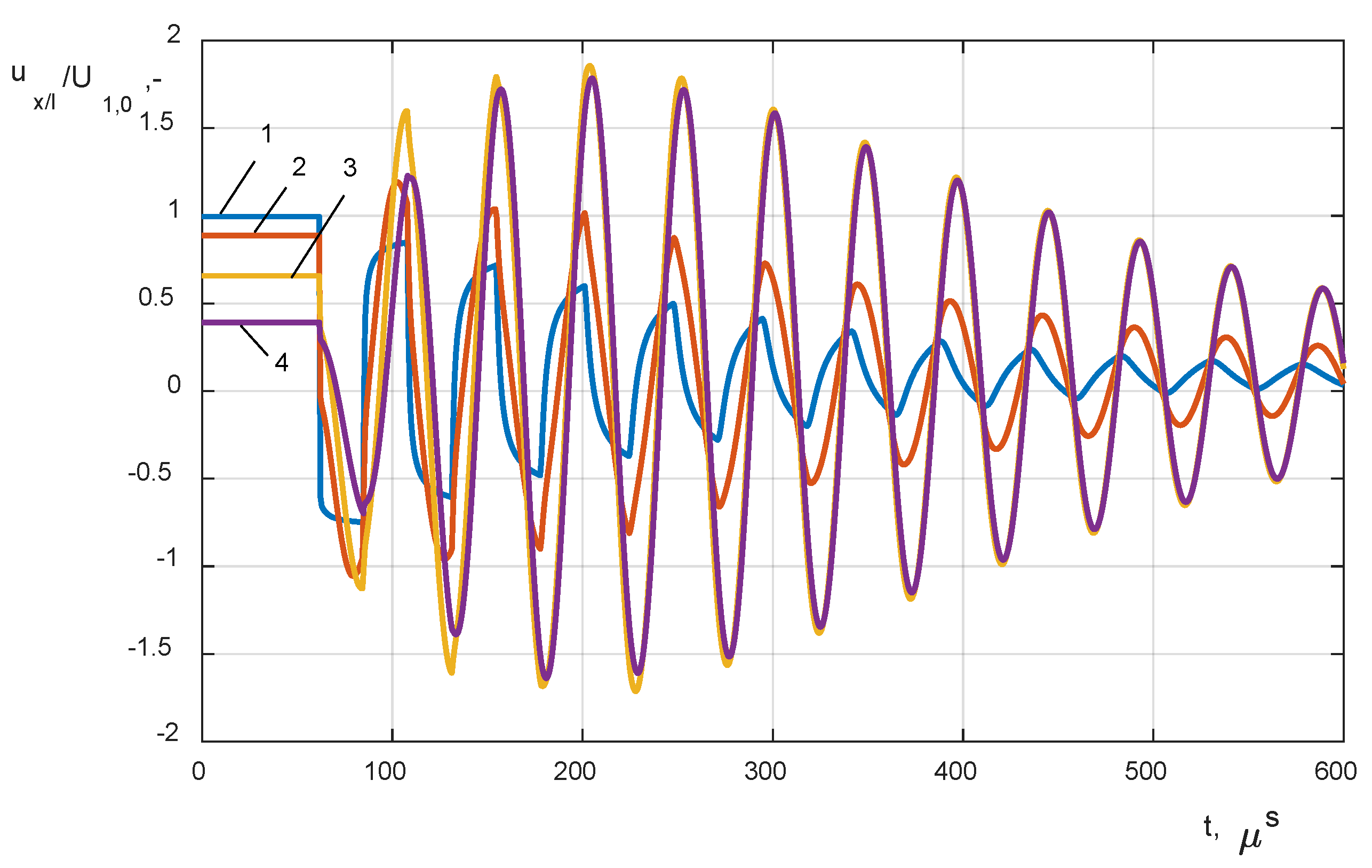
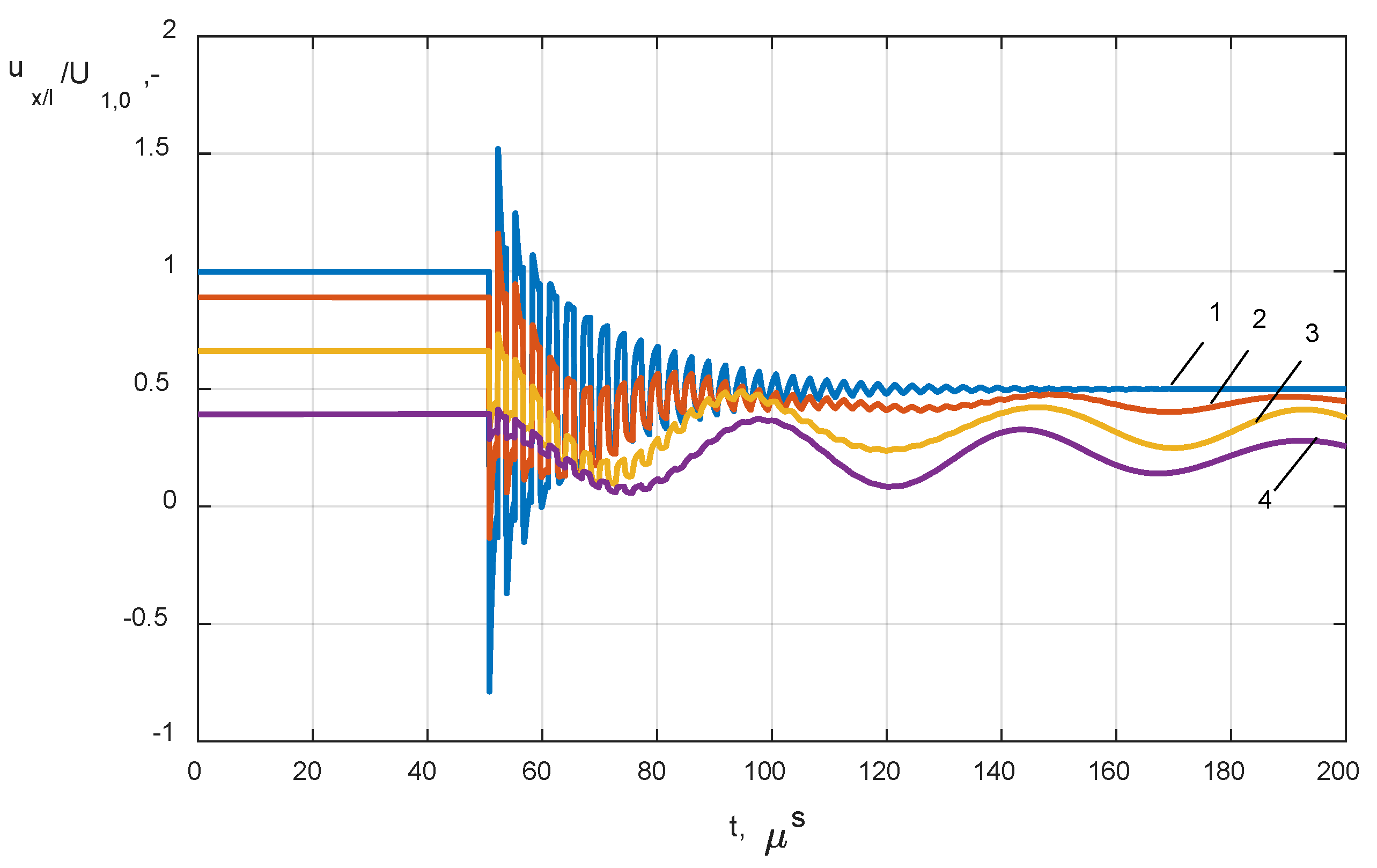
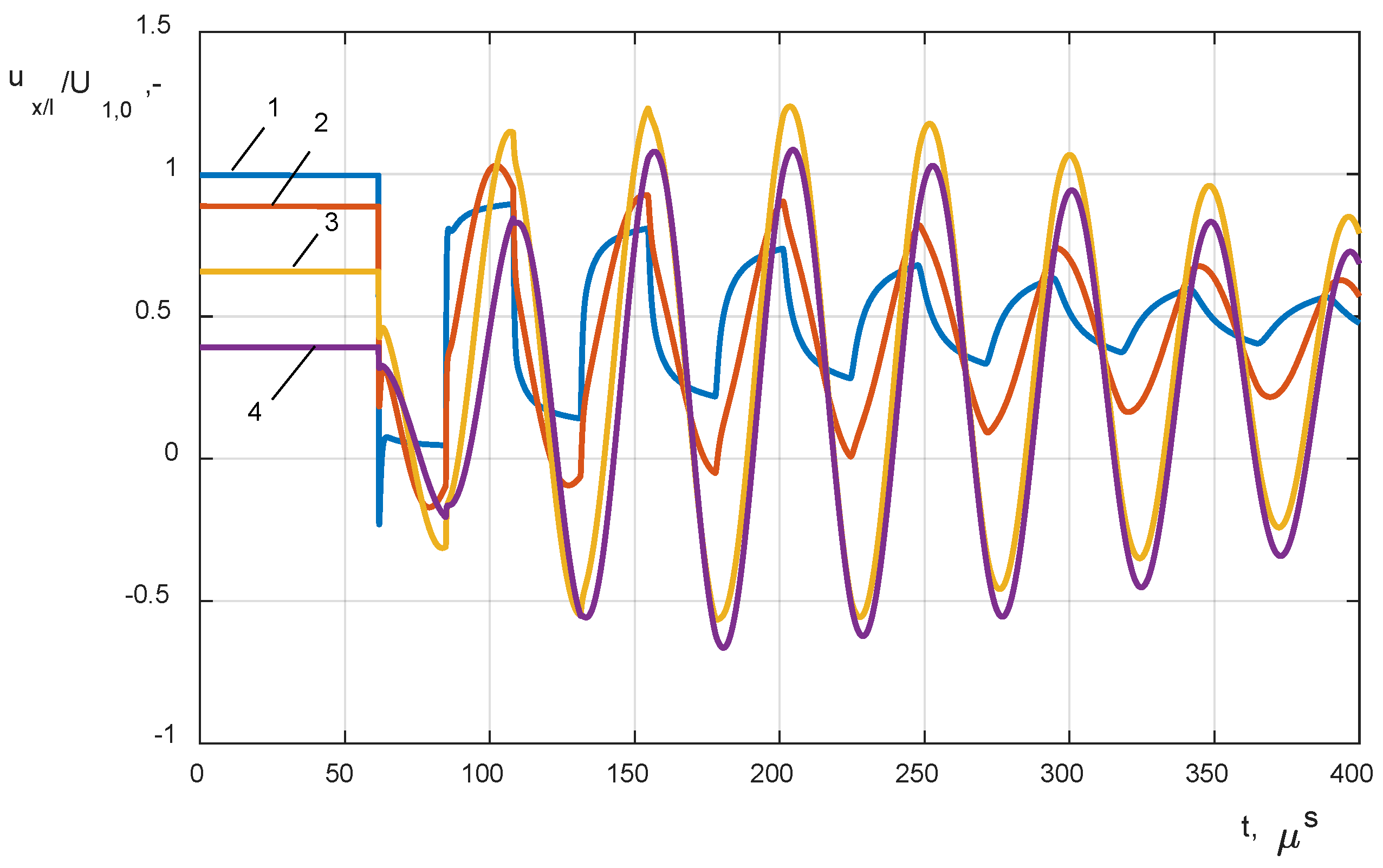
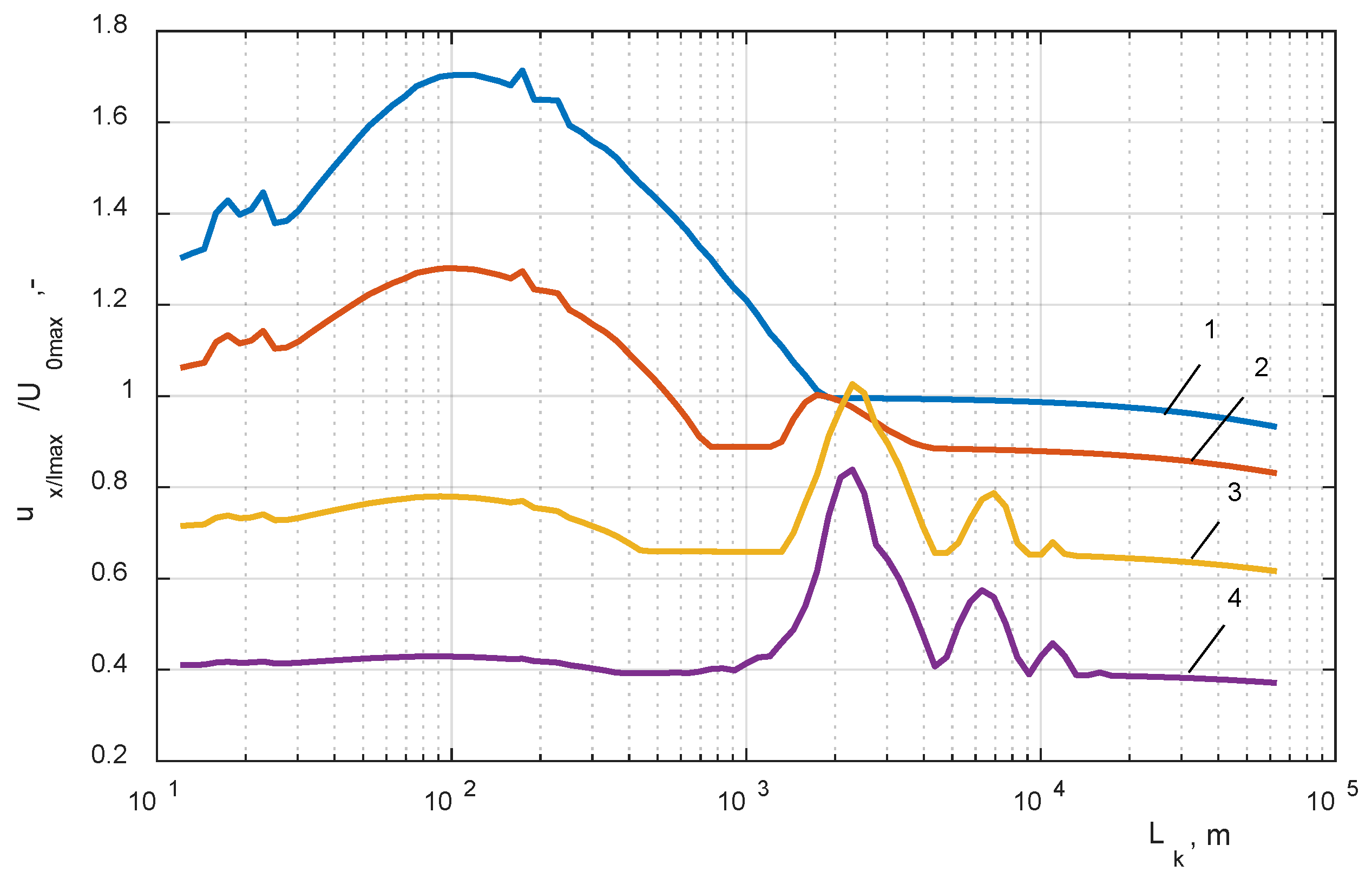
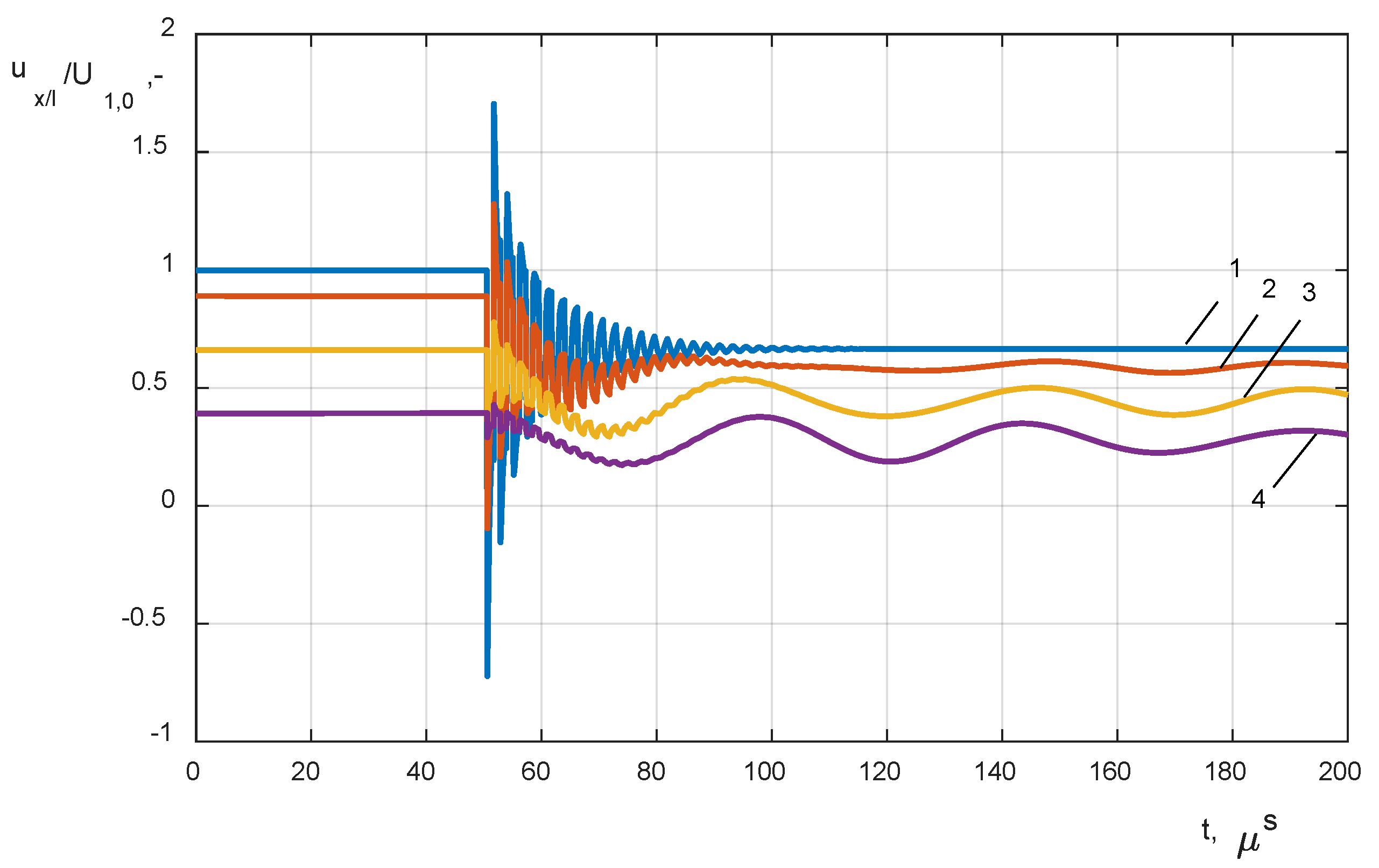
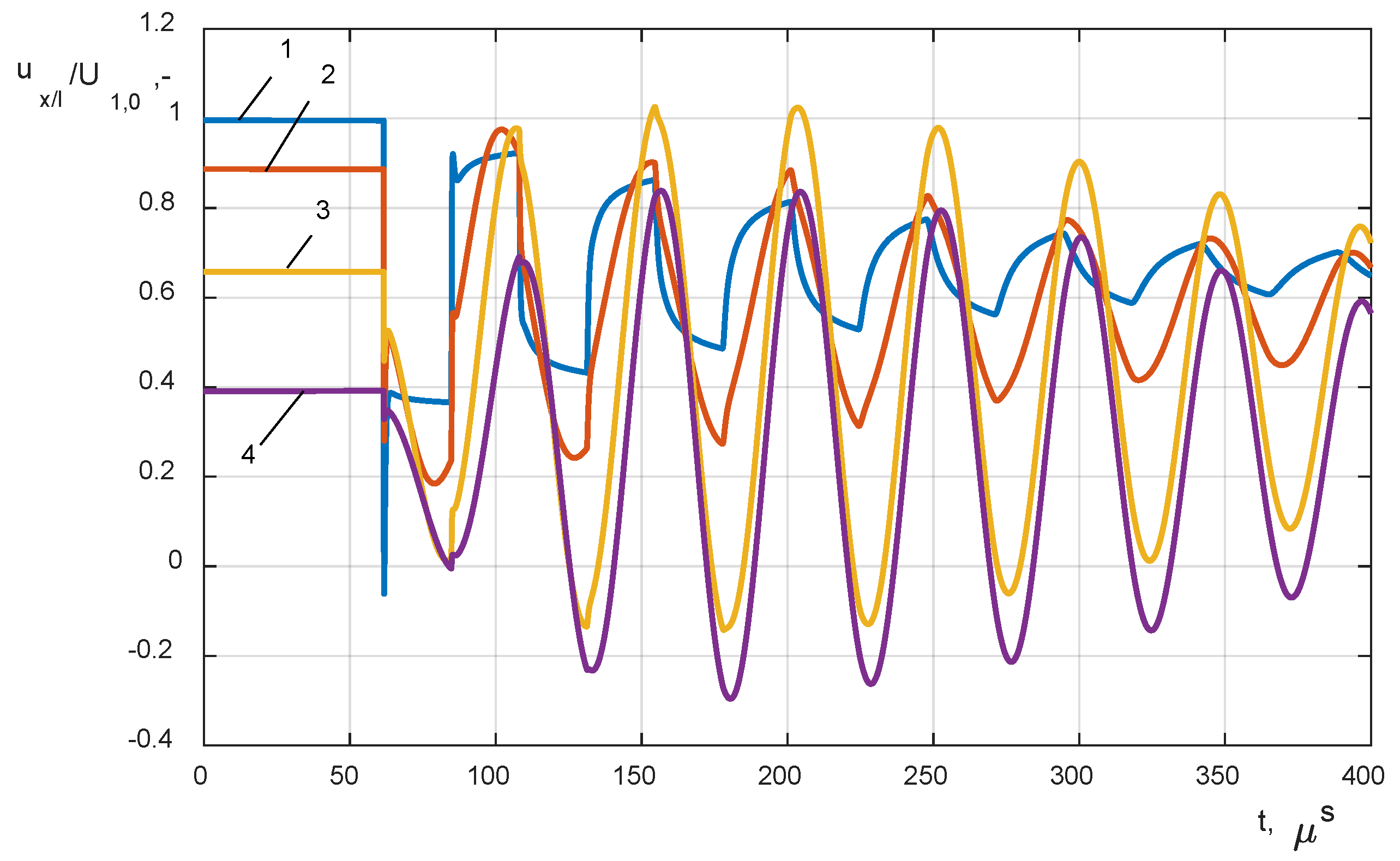
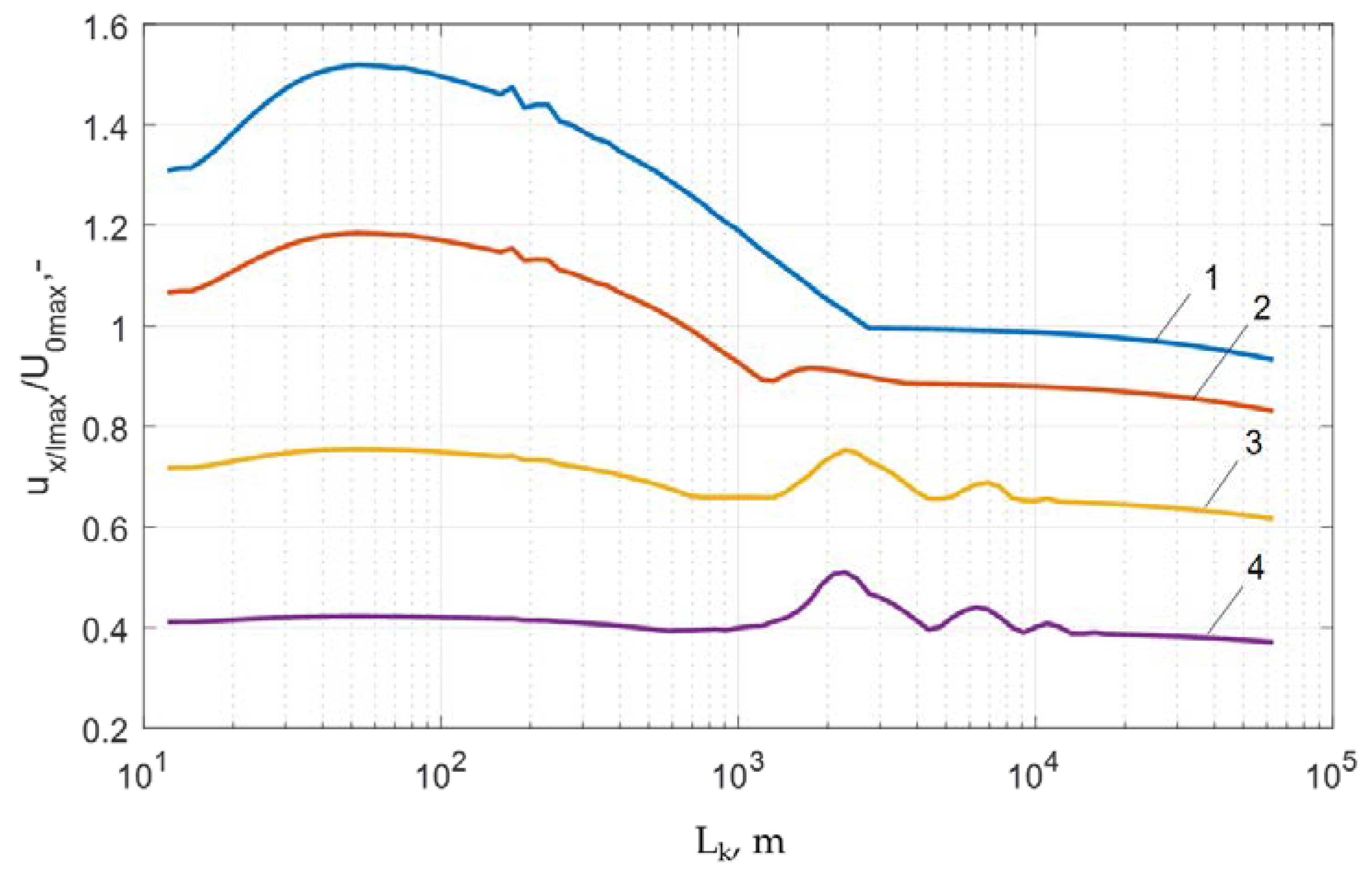
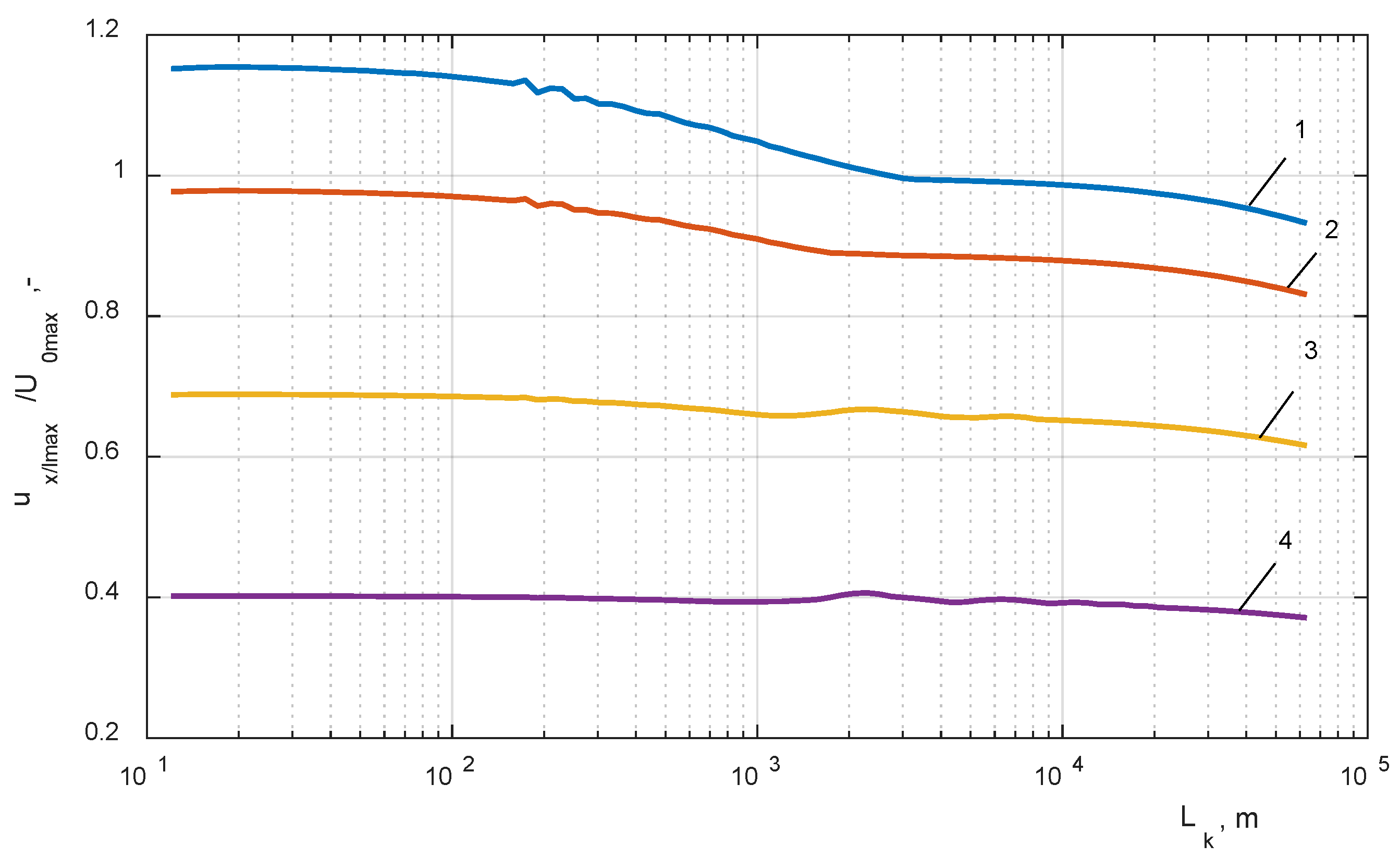
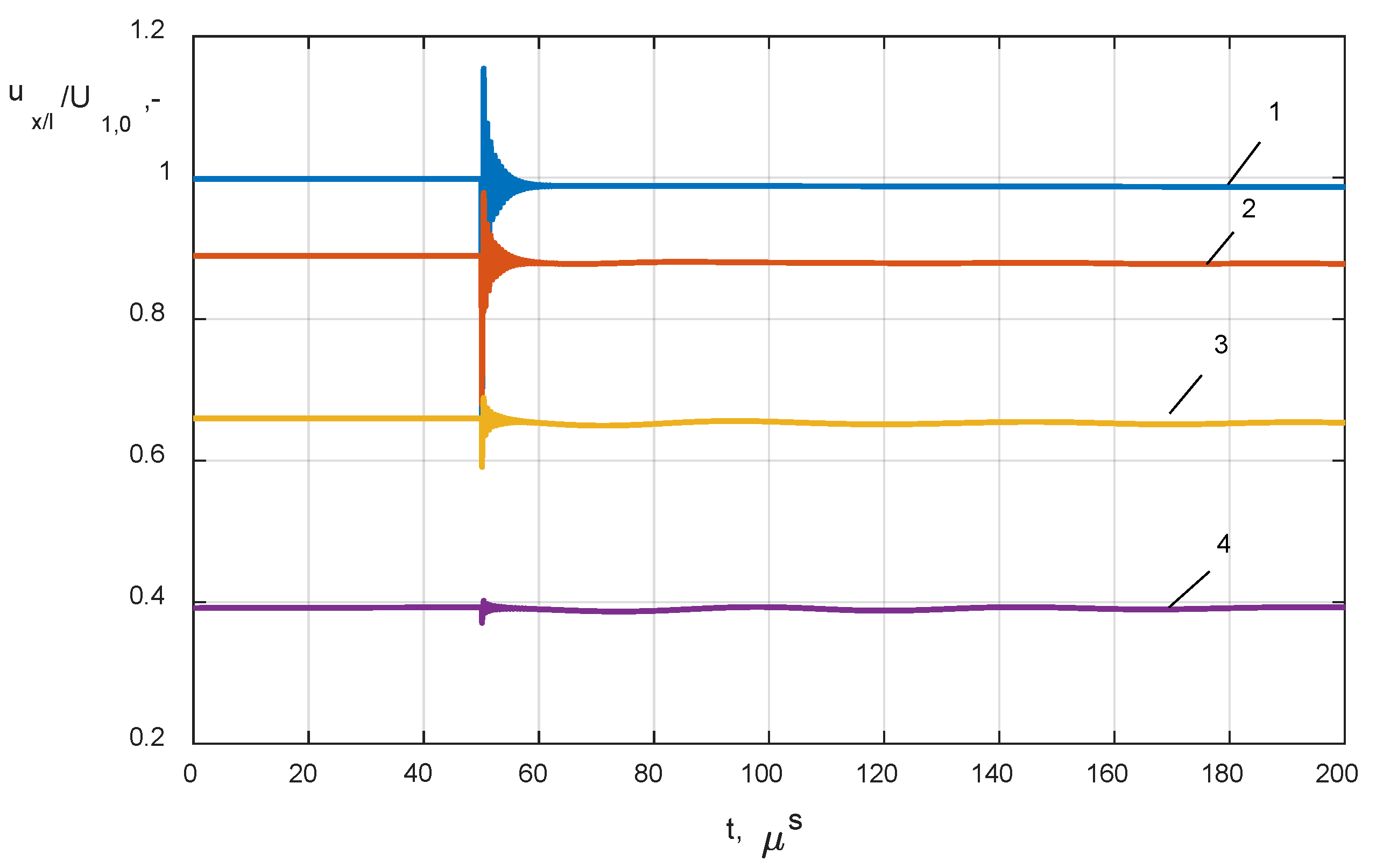
- closing the circuit breaker VCB connected to the cable line Lk and the HF transformer winding model, the variable length of the cable was changed in a range of 10 m to 60 km (Figure 5a);
- (2)
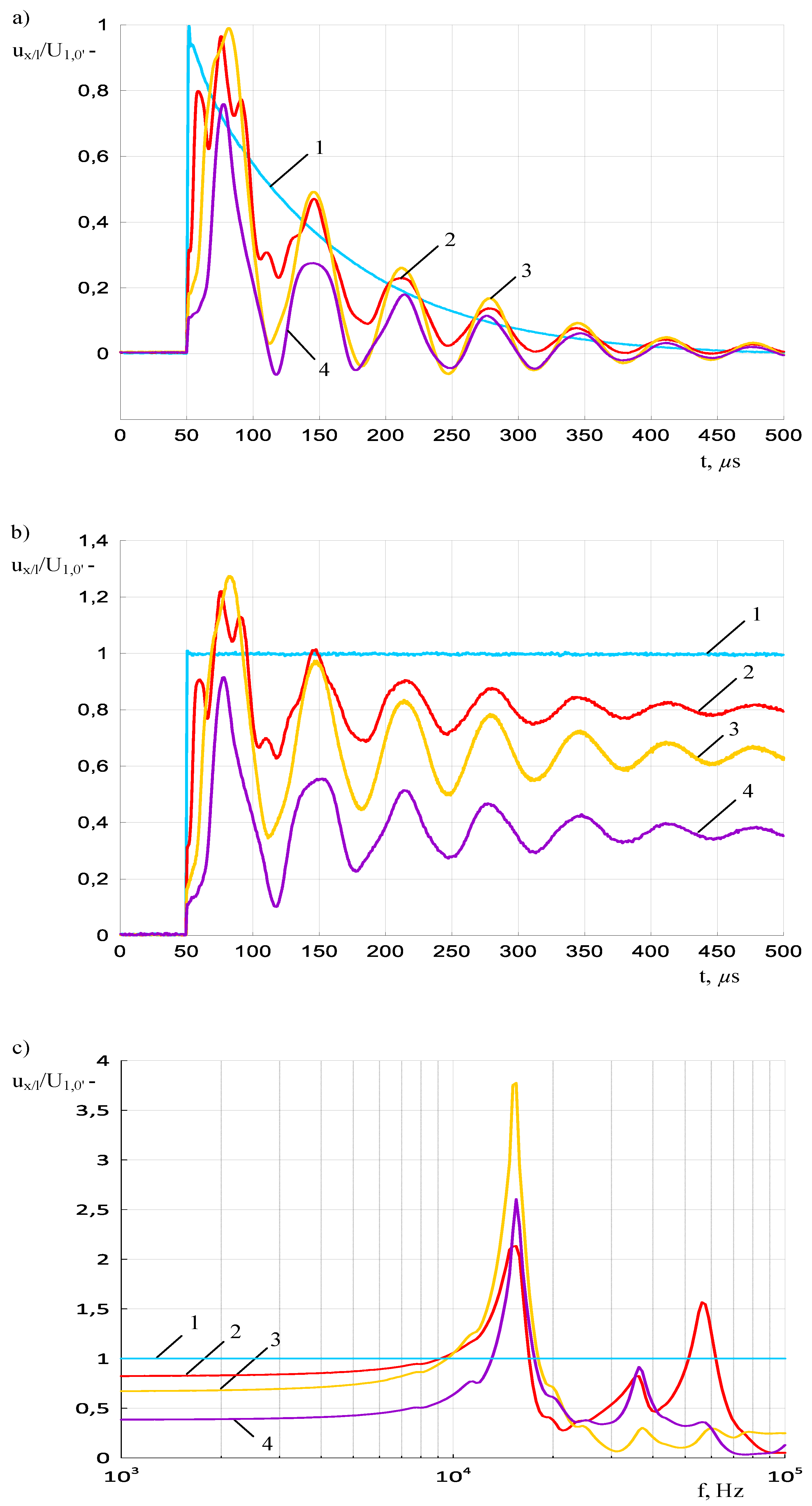
- analysis of the impact of a single-phase line to a ground fault with distance changing from 10 m to 60 km from the transformer terminals (Figure 5b);
- (3)
- analysis of the impact of short circuit resistance during a ground fault on the level and mechanism of internal overvoltage distribution; the analysis covered low and high ohmic faults, Rf = {0.01 Ω, 1 Ω, 2 Ω, 10 Ω, 100 Ω}.
4. Discussion
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Tenbohlen, S.; Jagers, J.; Vahidi, F. Results of a standardized survey about the reliability of power transformers. In Proceedings of the the 20th International Symposium on High Voltage Engineering, Buenos Aires, Argentina, 27 August–1 September 2017. [Google Scholar]
- Gustavsen, B.; Brede, A.P.; Tande, J.O. Multivariate analysis of transformer resonant overvoltages in power stations. IEEE Trans. Power Deliv. 2011, 26, 2563–2572. [Google Scholar] [CrossRef]
- Gustavsen, B. Study of transformer resonant overvoltages caused by cable-transformer high-frequency interaction. IEEE Trans. Power Deliv. 2010, 25, 770–779. [Google Scholar] [CrossRef]
- Rocha, A.C.O. Electrical Transient Interaction between Transformers and the Power System; CIGRÉ Session: Paris, France, 2008; p. C4-106; pp. 1–4. [Google Scholar]
- Florkowski, M.; Furgał, J.; Kuniewski, M. Propagation of overvoltages in distribution transformers with silicon steel and amorphous cores. IET Gener. Trans. Distrib. 2015, 9, 2736–2742. [Google Scholar] [CrossRef]
- Hori, M.; Nishioka, M.; Ikeda, Y.; Naguchi, K.; Kajimura, K.; Motoyama, H.; Kawamura, H. Internal winding filure due to resonance overvoltages in distribution transformer caused by winter lightning. IEEE Trans. Power Deliv. 2006, 21, 1600–1606. [Google Scholar] [CrossRef]
- Florkowski, M.; Furgał, J.; Kuniewski, M. Propagation of Overvoltages in the Form of Impulse, Chopped and Oscillating Waveforms in Transformer Windings—Time and Frequency Domain Approach. Energies 2020, 13, 304. [Google Scholar] [CrossRef]
- Van der Sluis, L. Transients in Power Systems; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2001; ISBN 0-471-48639-6. [Google Scholar]
- Debnath, A.D.; Chakrabarti, A. A Study on the Impact of Low-Amplitude Oscillatory Switching Transients on Grid Connected EHV Transformer Windings in a Longitudinal Power Supply System. IEEE Trans. Power Deliv. 2009, 24, 679–686. [Google Scholar]
- Christodoulou, C.A.; Vita, V.; Ekonomou, L. Studies for the more effective protection of MV/LV substations against lightning overvoltages. Int. J. Circuits Electron. 2017, 2, 11–15. [Google Scholar]
- Christodoulou, C.A.; Vita, V.; Ekonomou, L. Lightning performance of an air insulated high voltage substation. In Proceedings of the 21st International Symposium on High Voltage Engineering (ISH 2019), Budapest, Hungary, 26–30 August 2019. [Google Scholar] [CrossRef]
- Joint Working Group A2/C4.39-CIGRE. Electrical Transient Interaction between Transformers and the Power System (Part 1-Expertise, Part 2: Case Studies); CIGRE: Paris, France, 2014; ISBN 978-2-85873272-2. [Google Scholar]
- Larin, V.S.; Matveev, D.A.; Zhuikov, A.V. Approach to Analysis of Resonance Phenomena and Overvoltages due to Interaction between Power Transformer and External Network; CIGRE SC A2 & C4 Joint Colloquium: Zurich, Switzerland, 2013; pp. 1–8. [Google Scholar]
- Furgał, J.; Kuniewski, M.; Pająk, P. Propagation of switching overvoltages in transformer windings. In Przegląd Elektrotechniczny; Publisher Sigma-NOT: Warsaw, Poland, 2018; pp. 61–64. ISBN 0033-2097. [Google Scholar] [CrossRef]
- Hoogendorp, G.; Popov, M.; Van der Sluis, L. The Influence of a Cable on the Voltage Distribution in Transformer Windings. In Proceedings of the International Conference on Power System Transients-IPST2011, Delft, The Netherlands, 14–17 June 2011; pp. 1–6. [Google Scholar]
- Zhou, Z.; Guo, Y.; Jiang, X.; Liu, G.; Tang, W.; Deng, H.; Li, X.; Zheng, M. Study on Transient Overvoltage of Offshore Wind Farm Considering Different Electrical Characteristics of Vacuum Circuit Breaker. J. Mar. Sci. Eng. 2019, 7, 415. [Google Scholar] [CrossRef]
- Liu, G.; Guo, Y.; Xin, Y.; You, L.; Jiang, X.; Zheng, M.; Tang, W. Analysis of Switching Transients during Energization in Large Offshore Wind Farms. Energies 2018, 11, 470. [Google Scholar] [CrossRef]
- Soloot, A.H.; Høidalen, H.K.; Gustavsen, B. Influence of the winding design of wind turbine transformers for resonant overvoltage vulnerability. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1250–1257. [Google Scholar] [CrossRef]
- McBride, J.; Lopez-Fernandez, X.M.; Alvarez-Mariño, C. Integration of TDSF Analysis into TECAM Transformer on Line Monitoring System. In Proceedings of the 2019 6th International Advanced Research Workshop on Transformers (ARWtr), Cordoba, Spain, 7–9 October 2019. [Google Scholar]
- Theocharis, A.; Popov, M.; Terzija, V. Computation of internal voltage distribution in transformer windings by utilizing a voltage distribution factor. Electr. Power Syst. Res. 2016, 138, 11–17. [Google Scholar] [CrossRef][Green Version]
- Luna López, Z.; Gómez, P.; Espino-Cortés, F.P.; Pena-Rivero, R. Modeling of Transformer Windings for Fast Transient Studies: Experimental Validation and Performance Comparison. IEEE Trans. Power Deliv. 2017, 32, 1852–1860. [Google Scholar] [CrossRef]
- Heller, B.; Veverka, A. Surge Phenomena in Electrical Machines; Czechoslovak Academy of Sciences: Prague, Czech Republic, 1968. [Google Scholar]
- Trkulja, B.; Drandić, A.; Milardić, V.; Župan, T.; Žiger, I.; Filipović-Grčić, D. Lightning impulse voltage distribution over voltage transformer windings—Simulation and measurement. Electr. Power Syst. Res. 2017, 147, 185–191. [Google Scholar] [CrossRef]
- Župan, T.; Trkulja, B.; Štih, Ž. Power transformer winding model for lightning impulse testing. Procedia Eng. 2017, 202, 297–304. [Google Scholar] [CrossRef]
- Dommel, H.W. Electromagnetic Transients Program Reference Manual; (EMTP Theory Book); Prepared for BPA: Portland, OR, USA, 1986. [Google Scholar]
- Selection Guide for ABB HV Surge Arresters. Zinc Oxide Surge Arrester. Publ SESWG/A 2300 E, Techn. Inform. ABB. 2017. Available online: www.abb.pl (accessed on 2 February 2020).
- Surge Arrester POLIM-D. Data Sheet. Available online: www.abb.pl (accessed on 2 February 2020).
- Wilcox, D.J.; Conlon, M.; Hurley, W.G. Calculation of self and mutual impedances for coils in ferromagnetic cores. IEE Proc. 1988, 135 Pt A, 470–476. [Google Scholar] [CrossRef]
- Rezaei-Zare, A. Enhanced Transformer Model for Low- and Mid-Frequency Transients—Part I: Model Development. IEEE Trans. Power Deliv. 2015, 30, 307–315. [Google Scholar] [CrossRef]
- Tahir, M.; Tenbohlen, S.A. Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model. Energies 2020, 13, 105. [Google Scholar] [CrossRef]
- Gunawardana, M.; Fattal, F.; Kordi, B. Very Fast Transient Analysis of Transformer Winding Using Axial Multiconductor Transmission Line Theory and Finite Element Method. IEEE Trans. Power Deliv. 2019, 34, 1948–1956. [Google Scholar] [CrossRef]
- Aghmasheh, R.; Rashtchi, V.; Rahimpour, E. Gray Box Modeling of Power Transformer Windings for Transient Studies. IEEE Trans. Power Deliv. 2017, 32, 2350–2359. [Google Scholar] [CrossRef]
- Su, C.Q. Electromagnetic Transients in Transformer and Rotating Machine Windings; IGI Global: Hershey, PA, USA, 2012. [Google Scholar]
- Degeneff, R.C.A. General Method for Determining Resonances in Transformer Winding. IEEE Trans. Power Appar. Syst. 1977, 96, 423–430. [Google Scholar] [CrossRef]
- Florkowski, M.; Furgał, J. Experimental and Theoretical Determination of Transfer Function of Transformer Windings. Arch. Electr. Eng. 2003, 52, 137–152. [Google Scholar]
- Rahimpour, E.; Christian, J.; Feser, K.; Mohseni, H. Modellierung der Transformatorwicklung zur Berechnung der Übertragungsfunktion für die Diagnose von Transformatoren. Elektrie 2000, 54, 18–31. [Google Scholar]
- Massarini, A.; Kazimierczuk, M.K.; Grandi, G. Lumped Parameter Model for Single- and Multiple-Layer Inductors. In Proceedings of the Power Electronics Specialists Conference, Baveno, Italy, 23–27 June 1996; pp. 295–301. [Google Scholar]
- Mombello, E.E.; Ratta, G.; Rivera, J.F. Study of Internal Stresses in Transformer Windings Due to Lightning Transient Phenomena. Electr. Power Syst. Res. 1991, 21, 161–172. [Google Scholar] [CrossRef]
- De Leon, F.; Semlyen, A. Detailed Modelling of Eddy Current Effects for Transformer Transients. IEEE Trans. Power Deliv. 1994, 9, 1143–1150. [Google Scholar] [CrossRef]
- IEEE W G 3.4.11. Modelling of metal oxide surge arresters. Trans. Power Deliv. 1992, 7, 302–309. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| Apparent power Sn, kVA | 20 | |
| Primary side voltage UnHV, kV | 15 | |
| Secondary side voltage UnLV, kV | 0.4 | |
| number of phases | 3 | |
| Short circuit voltage Uz, % | 4.2 | |
| No-load losses ∆PFe, kW | 0.114 | |
| Load losses ∆PCu, kW | 0.525 | |
| Magnetizing current I0, % | 2.8 | |
| type of coils | uc* | rc ** |
| number of turns in the coil, - | 810 | 650 |
| number of coils, - | 4 | 4 |
| height of the winding l, mm | 280 | 250 |
| internal diameter do, mm | 157 | 157 |
| external diameter di, mm | 205 | 205 |
| width of the coil h, mm | 25 | 25 |
| Cross Section | Insulation Thickness | Screen Thickness | Outer Diameter | R |
|---|---|---|---|---|
| mm2 | mm | mm | mm | Ω km−1 |
| 95 | 4.5 | 2.5 | 31.6 | 0.193 |
| Rated Voltage | Residual Voltage Ures at Specified Impulse Current | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ur | Uc | 1/2.5 µs | 8/20 µs | 30/60 µs | |||||||
| 5 kA | 10 kA | 1 kA | 2.5 kA | 5 kA | 10 kA | 20 kA | 125 A | 250 A | 500 A | ||
| kV | |||||||||||
| 15 | 12 | 43.3 | 47.9 | 34.9 | 37.0 | 39.1 | 42.0 | 47.7 | 31.1 | 32.2 | 33.2 |
| Case | Switching | Ground Fault | ||||
|---|---|---|---|---|---|---|
| Rf = 0.01 Ω | Rf = 1 Ω | Rf = 2 Ω | Rf = 10 Ω | Rf = 100 Ω | ||
| Critical cable length, lcrit | 2291 m | 2291 m | 144 m (2291 m) | 109 m (2291 m) | 52.5 m | 22.9 m |
| 1 − x/l = 0 | 1.93 | 1 | 1.52 | 1.71 | 1.52 | 1.15 |
| 2 − x/l = 0.18 | 2.15 | 1.26 | 1.16 | 1.28 | 1.19 | 0.978 |
| 3 − x/l = 0.33 | 2.66 | 1.86 | (1.23) | (0.78) | 0.75 | 0.69 |
| 4 − x/l = 0.62 | 2.27 | 1.78 | (1.09) | (0.43) | 0.51 | 0.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Furgał, J.; Kuniewski, M.; Pająk, P. Analysis of Internal Overvoltages in Transformer Windings during Transients in Electrical Networks. Energies 2020, 13, 2644. https://doi.org/10.3390/en13102644
Furgał J, Kuniewski M, Pająk P. Analysis of Internal Overvoltages in Transformer Windings during Transients in Electrical Networks. Energies. 2020; 13(10):2644. https://doi.org/10.3390/en13102644
Chicago/Turabian StyleFurgał, Jakub, Maciej Kuniewski, and Piotr Pająk. 2020. "Analysis of Internal Overvoltages in Transformer Windings during Transients in Electrical Networks" Energies 13, no. 10: 2644. https://doi.org/10.3390/en13102644
APA StyleFurgał, J., Kuniewski, M., & Pająk, P. (2020). Analysis of Internal Overvoltages in Transformer Windings during Transients in Electrical Networks. Energies, 13(10), 2644. https://doi.org/10.3390/en13102644