A Comparative Study of Optimal Energy Management Strategies for Energy Storage with Stochastic Loads

1. Introduction

In order to reduce gas emissions in seaports and increase energy saving, ports are dramatically moving towards electrify rubber tyre gantry (RTG) cranes which will increase the electricity load on the ports’ network. To manage the increased peak demand, port operators are required to reinforce the electrical network. Traditional reinforcement solutions are effective but commercially expensive because they focus on upgrading existing infrastructure such as cables and transformers [1,2]. Reducing the peak demand on the port network would help to minimise the electrical infrastructure reinforcement costs and greenhouse gas emissions at the electricity supplier side. Electrified cranes represent the largest demand at the port and provide the biggest opportunity for peak demand reduction and energy saving [1,3].

The electric demand of an RTG crane is nonsmooth and stochastic [3] compared to other aggregated low voltage demands such as domestic customers or medium voltage loads. Therefore, smarter solutions are required in order to reduce the peak demand, decrease electricity costs and increase energy efficiency. One practical technology is an energy storage system (ESS), which are becoming increasingly important tools for generating an energy efficient network model and to help reduce gas emissions and environmental concerns. Generally, the main application for an ESS in a low voltage (LV) network is to minimise the electrical energy cost and decrease the need for upgrading the network by shifting energy consumption from peak to valley periods [4]. Typically, the energy storage devices are designed and controlled dependent on the main target of the energy storage such as peak demand reduction or cost saving. Therefore, it is important to explore and investigate how an ESS controlling can improve energy efficiency or economic performance of the storage device in LV network applications and RTG crane networks. This section will introduce the main literature for energy control algorithms for storage devices with stochastic loads [3]. The energy storage controllers for an LV network and RTG crane applications are commonly split into two main research areas in the literature:

• Conventional or traditional controllers such as set-point controller and proportional integral (PI): this type of storage controllers is limited to a specific target or reference value. These controllers generate control decisions based on a determined target or reference value such as current, energy level and voltage. The reference value is determined based on an a priori network data together with domain-expert knowledge. Due to the simplicity of these conventional controllers, they have been widely used in RTG crane systems with storage devices for reducing gas emissions and peak demand [5,6,7,8]. Furthermore, the set-point controller is also used as a standard benchmark control system for an ESS in LV applications [9] and RTG cranes [2]. However, these controllers are principally limited for controlling volatile and nonsmooth demands, solving complex energy problems and targeting the energy savings and peak reduction over long periods of time such as an entire day. In addition, the set-point and PI controllers are sensitive to the set-point and use no knowledge of the potential future demand.
• Optimal controllers: this energy control category can be further divided into optimal controllers that use, or do not use, forecast of the demand. Both controllers in this category work to find the optimal (the best) ESS operation plan based on the parameters and limitations of the electrical network and storage device [10,11]. However, the optimal controllers are more complex, with higher computational costs, compared to the conventional controllers [11,12]. While many papers have discussed and investigated optimal energy control strategies for LV demands such as residential customers, there is limited literature on using these strategies for reducing peak demand or energy costs for RTG crane networks. In 2017, Pena-Bello et al., presented an optimisation operation algorithm for a battery storage system for grid-connected housing with a PV system [13]. The model in [13] assumed a perfect forecast for the residential load and PV generation, which is unrealistic in practice. The research does not consider the impact of forecast error or the variability of the PV generation on the operational model and results. The literature [13,14,15] has shown that accurate forecasts are important to optimise the control of an ESS. The literature has introduced the optimal control of ESS with load forecasts as a key feature for improving the peak reduction and the cost savings. However, it has widely focused on developing different planning, operation schedules based on full future knowledge to increase the energy savings by assuming a perfect forecast for the residential load and PV generation [13], which is unrealistic in practice and assumes that the charged energy was fixed and equal to a specific magnitude in [16].

Throughout the literature, optimal controllers that use forecasts can be classified into two main groups: First, consider optimal controller which assume a complete future knowledge of the demand (perfect forecast). These controllers employ a perfect forecast without taking into account the prediction errors or the uncertainty in the demand over the forecast horizon. Many planning operation schedules for the ESS in an LV network based on perfect forecast rules has been developed in the literature in order to reduce peak demand and energy cost savings. For example, an optimal energy controller for a diesel RTG crane was developed by Hellendoorn et al. [16] by assuming a perfect knowledge of the diesel fuel consumption and fuel costs to increase energy saving and reduce costs. Similar to Hellendoorn et al., Alonso et al. created optimal controllers for charging electric vehicles based on the assumption that the ESS charging time and the initial and final state of charge are known to minimise the peak demand in LV networks. In general, the literature shows that perfect and accurate forecast demand models are an important component for optimising the energy storage operation [10]. However, having perfect load forecast profiles is not practical in practice, especially for applications with highly volatile behaviours such as RTG cranes and LV demand where the demand uncertainty is a core feature of the data.

Secondly, there are optimal energy control models based on load forecasting. These controllers aim to find the optimal ESS operation plan by using actual forecast models. The load forecast models estimate future demand profile which are not perfectly accurate, forecasting errors can therefore have a significant impact on the energy storage performance and results [10]. The volatile demand behaviour on LV network applications increases the challenge of accurately predicting the LV demand. In general, forecast error and uncertainty have a significant impact on optimal ESS control algorithms. Uncertainty and forecast error impacts on an optimal controller such as model predictive controller (MPC) solutions have been discussed in the literature [17,18,19]. The research, in [20], formulated a hybrid renewable energy system with battery energy storage in a family residential home, using an optimal energy operation strategy based on an MPC algorithm to minimise the energy costs and meet the electricity demand. Due to the high level of uncertainty regarding weather conditions that effect the renewable sources output, Wang et al. [20] used real time hourly weather forecast data to reduce the impact of uncertainty. Forecast errors in the prediction demand model used in an optimal energy controller are discussed in [21]. Holjevac et al. presented a microgrid system including electricity demand and energy storage that operated to meet consumer needs and minimise costs by using a receding horizon controller. The work of Holjevac et al. [21] showed that the efficiency of the energy operation model depends on demand and generation prediction output, and daily correction of the MPC controller schedule. The corrective schedule aimed to update the initial operation points, this helped to reduce the impact of the forecast errors by updating the demand and control model data at successive time steps. However, the receding horizon controller was designed to minimise the energy costs only based on the energy and balancing prices and did not investigate the peak demand reduction for the households in the network. Receding horizon controllers, such as MPCs and stochastic model predictive controllers (SMPCs), have often been effectively used within stochastic load applications such as LV peak demand reduction [22,23,24], and they use rolling forecasts to improve the energy storage performance without assuming perfect knowledge of future demand. In general, receding horizon controllers are an ideal candidate for reducing the impact of forecast errors and increasing energy storage device efficacy [25,26] since they are continually updated with the most recent data. To the best of the author’s knowledge, there has been limited literature on using predictive controllers such as MPCs and SMPCs for electrified RTG crane system to reduce peak demand or increase energy efficiency. The energy saving and peak demand reduction for networks of electrified RTGs have been presented only in the previous work of the authors who developed on-line receding horizon controllers (MPC and SMPC) in [10] and [11], based on a rolling forecast model. An artificial neural network (ANN) forecast model was designed to provide the MPC controller [9] the future demand profile. However, the MPC controller did not consider the uncertainty in the RTG crane demand or the forecast profile [11]. The RTG crane demand analysis in [3] showed that crane demands have a much higher degree of uncertainty compared to other low voltage applications due to the lack of any strong patterns, trends or seasonalities. Such volatile demand behaviour in the crane can affect the MPC controller performance. Therefore, Alasali et al. [11] investigated the benefits of generating different future demand scenarios to estimate the demand uncertainty and hence improve the storage control performance using an SMPC model [11].

Challenges in creating an accurate crane demand profile increase the difficulties of developing an optimal predictive controller compared to say, medium voltage (MV) or LV demand applications [3,12]. It also requires further and deeper analysis to investigates the stability and robustness of the proposed controllers on larger data sets, which has been limited in the literature. This work aims to fill this gap by developing and comparing different predictive optimal controllers for a network of electrified RTG cranes equipped with an ESS. The main applications of the storage controllers presented here are to minimise both the energy cost and peak demand. This paper presents the following key novel contributions.

• Firstly, we develop three predictive optimal controllers (MPC, SMPC and optimal controller with fixed forecast) for an ESS within an RTG crane network and compare the corresponding ESS performance. The comparison in this paper investigates the stability and robustness of the proposed controllers by using different forecast models and data sets to test the proposed ESS controllers. This evaluation is significant to understand the impact of forecast errors on the ESS control algorithms and due to the limited literature on developing predictive control algorithms for stochastic load, such as RTG crane demand.
• Secondly, unlike the limited literature [10,11], which do not investigate the complexity and computational cost of the predictive control model, this paper analyses the ESS performance by taking into consideration the main characteristics of the proposed optimal energy controllers. The analysis in this paper aims to introduce an initial assessment of the complexity for a practical implementation of the proposed optimal control systems.

The remainder of this work is organised as follows: the RTG crane and ESS model’s topology is introduced in Section 2. The electrified RTG crane demand analysis is presented in Section 3. In Section 4, the predictive optimal controllers are presented. Then, Section 5 discusses and presents the simulation results and analysis. The last section presents the summary of this work and conclusions.

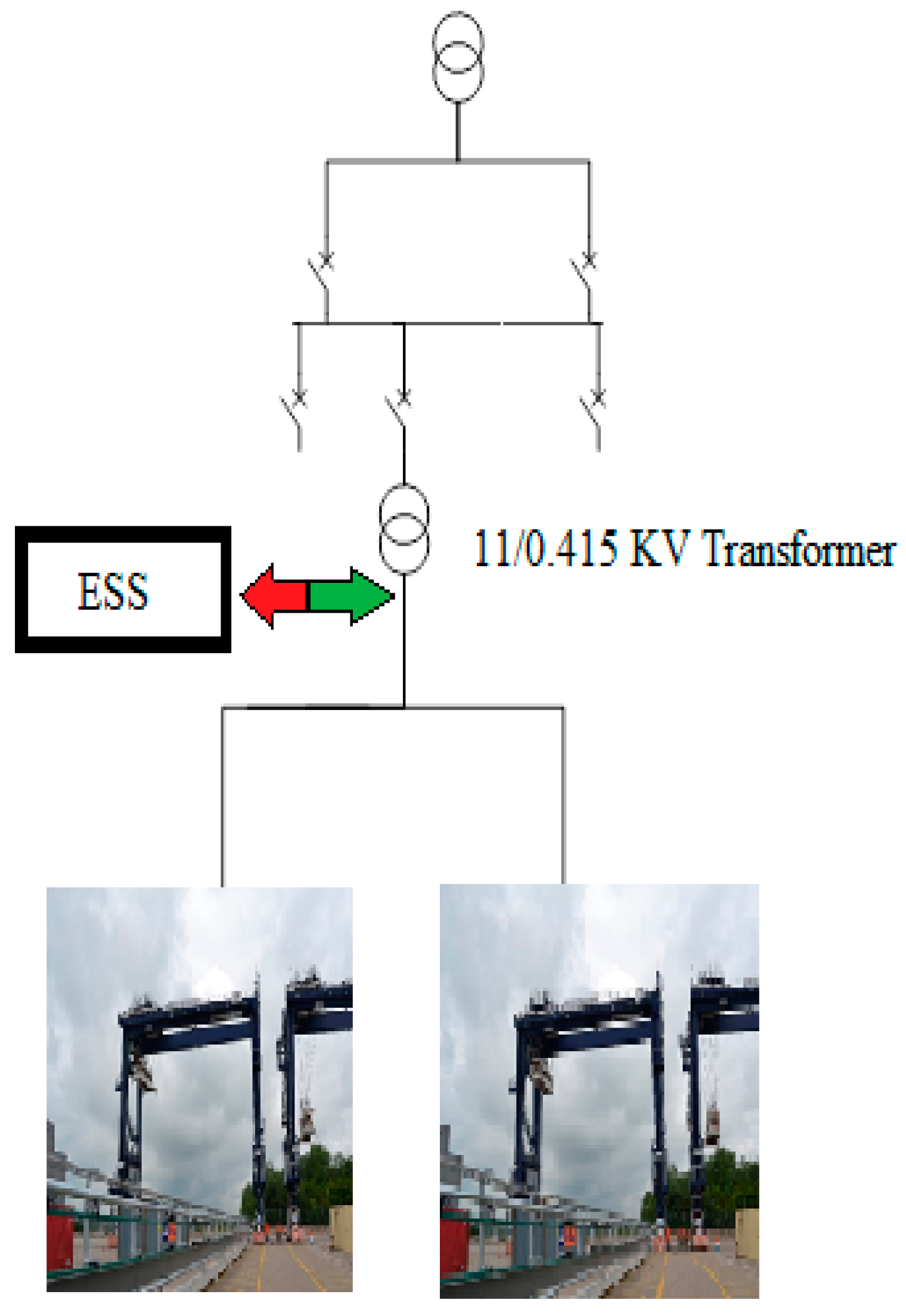
2. RTG Cranes and ESS Models Topology

This section presents the topology of the network of two electrified RTG cranes equipped with ESS used in the study. Connected to a real network in the Port of Felixstowe (PoF), the electrified RTG cranes are connected to the low voltage side of an 11 kV/0.415 kV rated retrofitted substation. In order to support peak demand reductions, the ESS is located on the 0.415 kV side. Figure 1 shows the RTGs in the PoF. Both cranes were manufactured and retrofitted by Shanghai Zhenhua Heavy Industries (ZPMC, Shanghai, China) [11,12] in order to be powered by the 0.415 kV distribution network through a conductor bar. The conductor bar length is 217 m and it was manufactured by Vahle (Kamen, Germany). In sea port terminals, container ships wait in the berths for the quay crane to load/unload the containers onto lorries. Then, the cargo is transferred by yard truck from the quayside to the yard, where the port stores the containers until transferring them to the cargo owner, using the yard crane [1,2]. The RTG cranes at the Port of Felixstowe have mainly three main types of motors to drive the crane and move containers as follows [4,5,6]:

• Four gantry motors to move the crane around the site.
• Hoist motor to raise container weights of up to 40 tones.
• Two trolley motors to move the hoisting unit across the span of the crane.

The LV network at the port aims to provide enough power to allow different RTG crane moves and tasks. Generally, the highest percentage of energy (65%) consumed by the RTG comes from the hoist motor from lifting the containers rather than the gantry and trolley motors [1,2,3,4,6]. In this article, unlike in the literature, two electrified RTG cranes in the LV network are connected to a central storage device, [2,4,5,6,7,8] which focuses on energy saving for a single RTG model. Figure 1 shows the single line diagram together with an actual electrical RTG cranes connected at the Port of Felixstowe, UK [10]. This connection shows that two RTGs are fed from the same step-down transformer. The storage device location in Figure 1 is motivated by the literature [9] that used a central storage device in a LV substation (close to transformer) for residential customers. Generally, the step-down transformer location at a port is close to the electrical RTGs which helps the ESS give extra support to the substation, reduce the power, energy losses and thermal issues in this zone. The aggregated demand for the cranes is matched by the power source and the ESS, as illustrated in Figure 1. In this section, the half hourly electrified RTG crane energy data over Q days for the complete historical data set is described by

$$\mathrm{P}={\left(\mathrm{P}\left(1\right),\dots ,\mathrm{P}\left(48\mathrm{Q}\right)\right)}^{\mathrm{T}}\in {ℝ}^{48\mathrm{Q}},$$

(1)

The LV network (step-down transformer), as seen in Figure 1, feeds all the required demand consumption to operate the RTGs and the changes in the storage device energy. The research objective of this study is to minimise the peak demand and the electricity bill for the RTG crane network by generating an optimal operation plan for an ESS over a 24-h period. Equation (2) describes the RTG cranes demand including the ESS.

$$\mathrm{D}\left(\mathrm{t}\right)=\left({\displaystyle \sum }_{\mathrm{i}=1}^{C=2}{\mathrm{P}}^{\mathrm{i}}\left(\Delta \mathrm{t}\right)\right)+\Delta \mathrm{E}\left(\mathrm{t}\right),$$

(2)

where $\mathrm{D}\left(\mathrm{t}\right)$ is the total substation demand supplied at half hour t, ${\displaystyle \sum }_{\mathrm{i}=1}^{C=2}{\mathrm{P}}^{\mathrm{i}}\left(\Delta \mathrm{t}\right)$ is the aggregation load of two electrified cranes (C = 2), and $\Delta \mathrm{E}\left(\mathrm{t}\right)$ is the charged or discharged energy in the storage device at each half hour t of the day of interest, t = 1, 2,…, 48, i.e., $(\Delta {\mathrm{E}}_{ }={\left(\Delta \mathrm{E}\left(1\right),\dots ,\Delta \mathrm{E}\left(\mathrm{t}\right)\right)}^{\mathrm{T}}\in ℝ)$.

In this paper, the optimal controller aims to determine the ∆E(t) value over the following day in order to maximize the reduction of the peak demand and electricity bill. The values of the storage device constraints and operation are typically given in terms of the average power flow,$\mathrm{P}$ in kW, and the stored energy in the ESS is therefore $\mathrm{P}\Delta \mathrm{t}$ in kWh during a period of time,$\Delta \mathrm{t},$ (hours or half hours). However, in this paper, the storage device controller aims to determine an optimal value of the increase or decrease of the stored energy, $\Delta \mathrm{E}$, [9,10]. The value of $\Delta \mathrm{E}\left(\mathrm{t}\right)$ can reflect a positive or negative change which describe the increase (charging mode) or decrease (discharging mode) respectively in the energy in the storage device [18,26]. Furthermore, the $\mathrm{SoC}\left(\mathrm{t}\right)$ describes the stored energy (State of Charge) at the end of each time step t and is given by Equation (3).

$$\mathrm{SoC}\left(\mathrm{t}\right)=\mathrm{SoC}\left(\mathrm{t}-1\right)+ɳ\Delta \mathrm{E}\left(\mathrm{t}\right).$$

(3)

The energy storage model considers the efficiency [8,9,10] by adding a variable, $ɳ$ $\in \left[0, 1\right]$, to the change in stored energy, ∆E(t), as described in Equation (3). When $\Delta \mathrm{E}$ < 0, the ESS efficiency is set to $\frac{1}{ɳ }$ and when $\Delta \mathrm{E}$ is ≥ 0, the ESS efficiency is $ɳ$. Furthermore, the storage device is subject to operation constraints, as described in Equations (4) and (5). The ${\mathrm{SoC}}^{\min }$ and ${\mathrm{SoC}}^{\max }$ represent the upper and lower limit of the energy stored in the ESS, respectively. The $\Delta {\mathrm{E}}^{\min }$ and $\Delta {\mathrm{E}}^{\max }$ is the minimum and maximum step change in energy, respectively [10,26], in other words, a limit on the speed of charging and discharging the ESS.

$$\begin{array}{c}{\mathrm{SoC}}^{\min }\le \mathrm{SoC}\left(\mathrm{t}\right) \le { \mathrm{SoC}}^{\max }\\ \Delta {\mathrm{E}}^{\min }\le \Delta \mathrm{E}\left(\mathrm{t}\right)\le \Delta {\mathrm{E}}^{\max }\end{array}\},\forall \mathrm{t}.\begin{array}{}\mathrm{(4)}\mathrm{(5)}\end{array}$$

3. The Electrified RTG Crane Demand

The previous section introduced the problem of high peak demand and energy costs on the LV network system, in particular on ports with electrified RTG cranes. Load forecasting was highlighted as one potential solution for supporting the network by facilitating a more optimal control of the energy storage system. To develop an accurate forecast model for LV applications, it is significant to understand the electrical demand behaviour and investigate the correlation between the demand and any exogenous variables. Due to the lack of understanding of the ports and the RTG crane energy demand behaviour, this section will analyse the demand characteristics of RTG cranes and explore the relationship between crane electrical demand and different exogenous variables. The detailed background and key findings in this section will be useful to develop and determine the most appropriate parameters for an accurate forecast model. To the author’s knowledge, there are no current studies which specifically investigate the characteristics of electrified RTG crane demand for forecasting or ESS control applications.

The RTG crane demand analysis in this section will be focused on finding patterns or cycles in crane demand based on the following:

• Overview of the electrified RTG crane demand;
• Time series analysis.

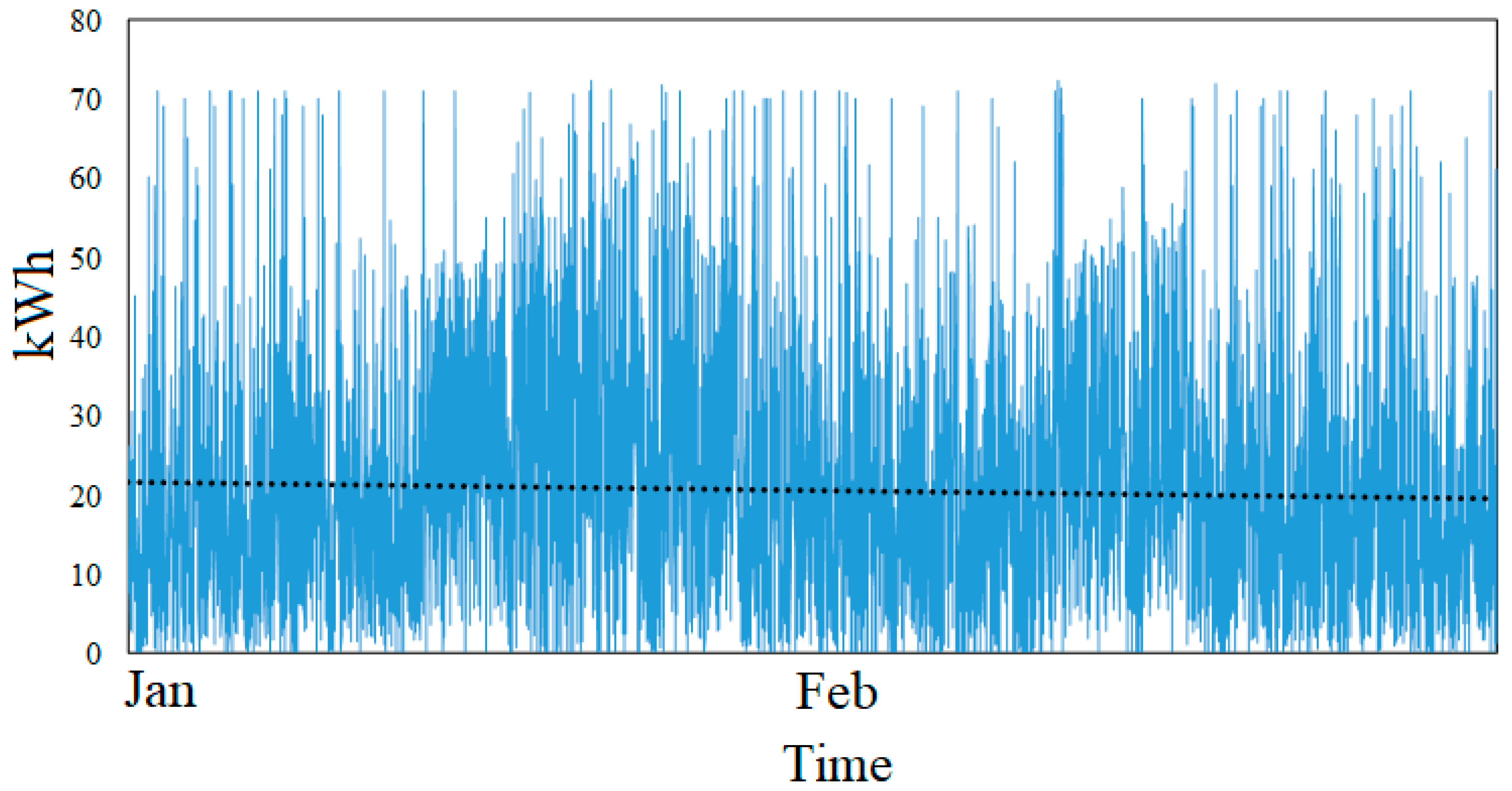
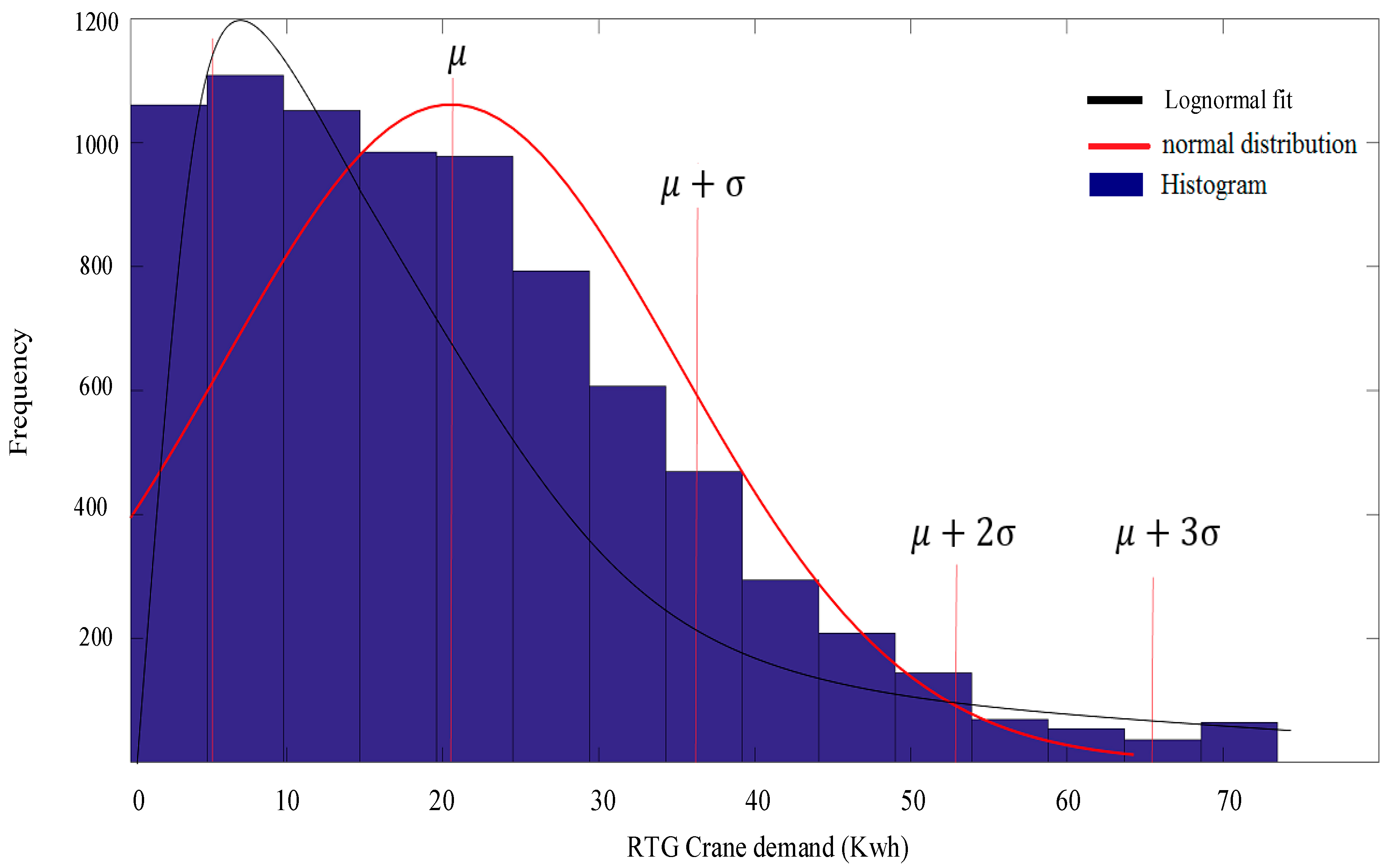
3.1. Overview of the Electrified RTG Crane Demand

In this paper, smart meters data was collected for two RTGs over a period of three months (from 1st of March to 30th of May 2018) at the Port of Felixstowe in the UK. The RTGs collected data on half hourly demand, number of cranes moves and the overall container weight. Typically, seaports have standard energy meters based on half hourly resolution for billing purposes since high-resolution substation monitoring systems are expensive, and for this reason, for the data and prediction model, we consider half hourly resolution data. The RTGs data represent the crane behaviour during several typical operational days. In order to present and investigate the RTG demand behaviour, the half hourly demand is plotted in Figure 2 for the first two months of the data set. This plot aims to highlight potential longer-term seasonal (daily or weekly) patterns. In addition, in order to examine any linear long-term trend in the RTG data, a line of best fit is also included in Figure 2 described by Equation (6) below,

$$\widehat{\mathrm{P}}\left(\mathrm{t}\right)= \mathrm{a}+\mathrm{b} \mathrm{t},$$

(6)

where $\widehat{\mathrm{P}}\in {ℝ}^{\mathrm{T}}$ is the RTG demand, T is the total length of analysed data and t is a half hour time step over the data set period. The coefficients $\mathrm{a},\mathrm{b}\in ℝ$ are found via least squares estimation and found to be $\mathrm{a}=21.1$ and $\mathrm{b}$ = −0.0003.

To measure and present how well the crane data fit with the regression line, R-squared (${\mathrm{R}}^2$) statistics were used in this section. The plotted trend line in Figure 2 show that the average demand (21.1 kWh) exhibits a significantly little linear trend and is quite flat from the start to the end of the data. The linear fit gives an ${\mathrm{R}}^2$ value of 0.017. In other words, the linear model only explains 1.7% of the RTG crane load variability. Therefore, the linear model is an insufficient tool for explaining the majority of the RTG demand behaviour. However, clearly it is difficult to extrapolate to the full year, but the results are expected to be similar as crane operation is continuous throughout the year. As seen in Figure 2, the crane is relatively volatile without strong seasonalities or patterns from month-to-month or week to week, which is in contrast with typical residential or LV level demand. Furthermore, Figure 3 presents an alternative representation of the distribution of RTG demand at the Port of Felixstowe. The half hourly RTG crane demand values are distributed between 0 kWh and 73 kWh, which gives a wide range of possible crane demand values and illustrates the uncertainty in the crane demand. In Figure 3, the mean value of the crane demand, μ, is 21.1 kWh and the standard deviation, $\mathsf{\sigma }$, is 14.85 kWh. It is observed that a high number of instances are clustered between 0 kWh to 15 kWh and not around the μ value, leading to further emphasis that the normal distribution is not able to accurately describe the distribution of the crane data. Furthermore, the lognormal gives a better fit compared to the normal distribution but still does not completely explain the data. The histogram distribution has a long tail compared to that expressed by a normal distribution, better describing the large values of demand which are more likely to occur. The high number of occurrences for the low demand, as presented in Figure 3, is mainly related to the large amount of low activity at the port including maintenance periods. In general, due to the nonsmooth behaviour of the RTGs load and the lack of seasonal behaviour in the time series and motivated by the literature [3,11], the gap in the time series or the longer time series is expected to have a negligible effect on the data analysis and forecast results. The irregular crane behaviour is likely due to the effect of the decisions of the crane operator individual and random distribution of containers within the site. In ports, work activity depends on the occurrence of shipments which do not have obvious or standard seasonal patterns. For example, a port may have two or three ships berthed at the same time and this would require increased crane activity.

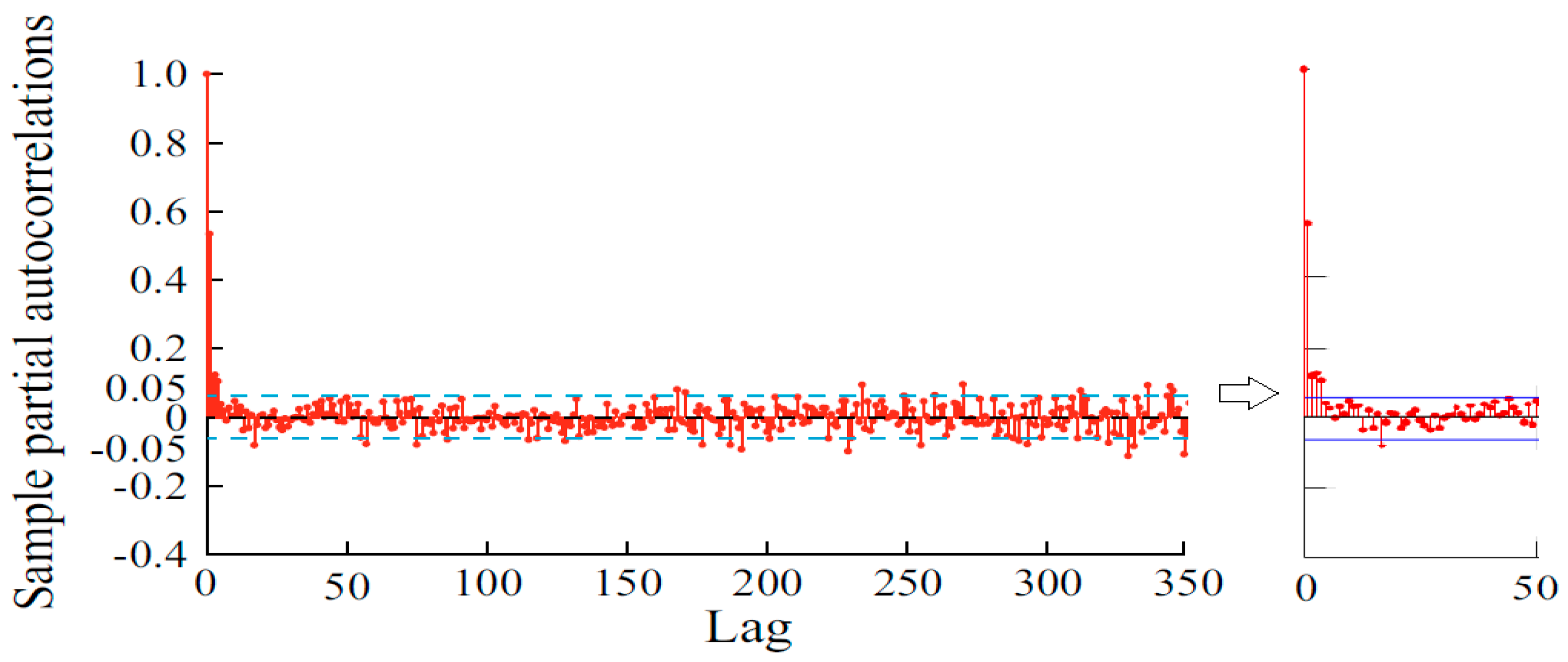
3.2. Time Series Analysis

The previous RTG demand analysis shows no obvious seasonality over the time period considered, however more subtle seasonalities can be found by considering the partial autocorrelation function (PACF). This is shown in in Figure 4 for 350-time lags (just over one week) [3]. The PACF calculation and plot can help to find intraday patterns or correlations [3]. The PACF can be defined as follows:

$$\mathrm{PACF} \left(\mathrm{i}\right)=\mathrm{corr} \left(\left(\mathrm{P}\left(\mathrm{t}\right), \mathrm{P}\left(\mathrm{t}-\mathrm{i}\right)| \mathrm{P}\left(\mathrm{t}-1\right),\dots , \mathrm{P}\left(\mathrm{t}-\mathrm{i}-1\right)\right)\right).$$

(7)

The PACF plot in Figure 4 shows only small values after lag number 4 and the distribution of the PACF plot does not show any clear patterns or seasonalities compared to other more typical LV demands, which often show significant lags at 48 (daily) for half hourly data, and further multiples. Similar to PACF, there are other tools and techniques to investigate the different periodicities in data—the most common being the Fourier transform [3].

Overall, the data for the RTGs shows random and volatile behaviour without clear half hourly or daily seasonalities. Hence, they are not useful features to include in a forecast model. The nonsmooth behaviour of RTG crane demand is mainly due to the effects of human and work environmental behaviour factors during the crane and port operation time [3,11]. The activity inside ports mainly depends on the relatively random occurrence and movement of shipments [27,28]. For example, a port may have many ships berthed at the same time and this requires increased crane activity. The terms “volatile” or “stochastic” have been defined as variables that change rapidly with low regularity These terms are used throughout the paper to qualitatively define and describe RTG crane demand. This paper aims to show how the forecast error affects the performance of the optimal controllers. As discussed in the literature, energy storage controllers for LV network applications have typically been developed with full knowledge of future demand [29,30] or using forecast models with relatively small errors of around 10% [26,29]. Therefore, in this paper, accurate and inaccurate forecast models have been used to feed the optimal energy controllers and evaluate the impact of forecast errors on the performance of the ESS. The two forecast models in this paper are as follows:

• Accurate forecasts: the half hourly demand for the next 48-time steps are generated by using the most accurate forecast model with the mean absolute percentage error (MAPE) forecast errors between 8% and 24%, as presented in [3]. This forecast model estimates the number of RTG moves, while assuming the container gross weight is known in advance.
• Inaccurate forecasts: the load forecast profile is generated by using an inaccurate forecast model with forecast errors between 21% and 39% [3]. This forecast model does not require any of the external variables data such as number of cranes moves or container weight [3].

In this section, the collected data from the RTGs network are divided into training data set (two months of demand data) and testing data (one month of data). The Mean Absolute Percentage Error (MAPE), as described in Equation (8), is used to evaluate the forecast models.

$$\mathrm{MAPE} =\frac{100}{\mathrm{N}}{\displaystyle \sum }_{\mathrm{t} =1}^{\mathrm{N}}\left|\frac{{\mathrm{P}}_{\mathrm{i}}-{\widehat{\mathrm{P}}}_{\mathrm{i}}}{{\mathrm{P}}_{\mathrm{i}}}\right|$$

(8)

where ${\mathrm{P}}_{\mathrm{i}}$ is the RTGs network demand at the time step i; $\widehat{\mathrm{P}}$ is the forecasted demand at the time step i; N is the number of observations.

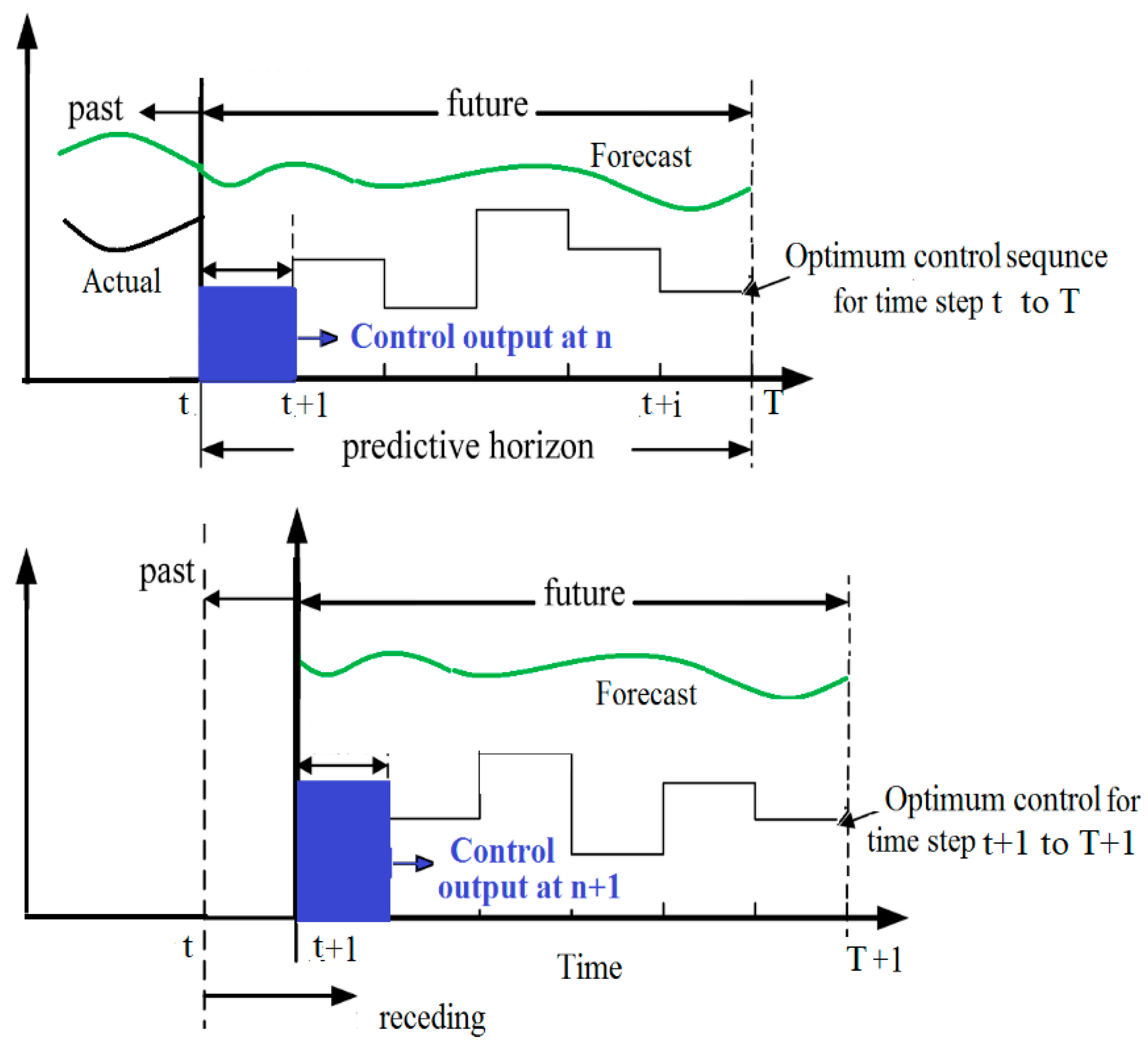
4. Optimal Energy Controllers for RTG Crane Network

The optimal controllers can be designed for multiple objectives compared to standard PI controllers or set-point algorithms. In this article, three optimisation controllers are presented to control the ESS as follow:

1

Optimal energy controller with a fixed load forecast profile: a 24 h-ahead RTG crane demand forecast and electricity price data are fed into the optimal control system. The control model will be updated once every 24 h. As discussed previously, the RTG crane demand profile is volatile and nonsmooth; therefore, developing an optimal controller for an RTG crane network is difficult and challenging [3,10].

2

Model Predictive Controller: the MPC aims to minimise the peak demand and electricity cost by finding the optimal ESS output and using a rolling forecast model to predict the RTG cranes demand. In this control model, the rolling forecasting minimises the impact of forecast error within the day on the ESS performance compared to the previous model with fixed load forecasts. However, in realistic scenarios, the RTG crane demand profile includes a high level of uncertainty. For example, the crane electrical demand is quite variable even when the RTG is lifting the same container gross weight [3,11], and this is mainly due to the human behavioural element (crane operator) during the lifting mode. The container gross weight and numbers of crane moves is used in [3] as input variables for the RTG demand forecast model.

3

Stochastic Model Predictive Controller: the SMPC is designed to handle the diverse and high level of uncertainty of the RTGs demand and the rolling forecast error. The SMPC aims to solve the RTG crane energy optimisation problem under the uncertainty conditions for the forecast demand. In this paper, the future crane demand is modelled as a stochastic variable by generating several future profiles, which is in contrast to the single-point forecast profile used in the MPC model [11].

4.1. Optimal Energy Controller with a Fixed Load Forecast Profile

The objective of the optimal controller is to minimise peak demand and energy costs for an RTG crane network, by finding an optimal charging regime, as described by Equation (9). The peak demand of the port substation is represented through $\max {\left({\displaystyle \sum }_{\mathrm{i}=1}^{C=2}{\widehat{\mathrm{P}}}^{\mathrm{i}}\left(\Delta \mathrm{t}\right)+\Delta \mathrm{E}\left(\mathrm{t}\right)\right)}^2$. The cost function in Equation (9) is optimised by generating a control signal to the ESS that aims to minimise the peak demand over the daily prediction horizon period subject to the ESS and RTG models described in Equations (10) to (12). The quadratic indices in Equation (9) are widely used in the literature and are the most common indices within energy and smart grid applications. Where it has a unique minimum, it penalises the larger deviation heavily in comparison to smaller deviation control. Generally, the optimal energy controllers are designed using a cost function that penalises deviation of a given reference point trajectory. The MATLAB MPC tool and optimisation solver has been used to minimise the cost function.

$$\underset{\Delta \mathrm{E}}{ \arg \min }{\displaystyle \sum }_{\mathrm{t}=1}^{\mathrm{T}}\max {\left({\displaystyle \sum }_{\mathrm{i}=1}^{C=2}{\widehat{\mathrm{P}}}^{\mathrm{i}}\left(\Delta \mathrm{t}\right)+\Delta \mathrm{E}\left(\mathrm{t}\right)\right)}^2,$$

(9)

where $\Delta \mathrm{E}\left(\mathrm{n}\right)$ is the change in the ESS energy, ${\displaystyle \sum }_{\mathrm{i}=1}^{C=2}{\widehat{\mathrm{P}}}^{\mathrm{i}}\left(\Delta \mathrm{t}\right)$ is a fixed RTG crane network demand forecast profile for day ahead, t is the current time step and T is the number of half the hour time steps in one day (T = 48) [9,11].

In this paper, the electrical energy cost saving is equal to the amount of shifted demand from high to low electricity price tariffs multiplied by the difference between the high and low electricity tariff. The high energy tariff (${\mathrm{Cost}}_{\mathrm{day}}$) in PoF is between 7:00 a.m. and midnight (${\mathrm{t}}_{\mathrm{set}}=14$), and the lower energy tariff is during the rest of the day period (${\mathrm{Cost}}_{\mathrm{night}})$ [10,11].

$$\mathrm{Cost}\left(\mathrm{t}\right)=\{\begin{array}{c}{\mathrm{Cost}}_{\mathrm{day}} \forall \mathrm{t}\ge {\mathrm{t} }_{\mathrm{set} } \\ {\mathrm{Cost}}_{\mathrm{night}} \forall \mathrm{t}<{\mathrm{t} }_{\mathrm{set}}\end{array},$$

(10)

In this paper, the reduction in the energy cost of the network of cranes is achieved by finding the optimal operation of the ESS that minimises the peak demand under the following constraints:

$$\mathrm{SoC}\left({\mathrm{t} }_{\mathrm{set}}\right)={\mathrm{SoC}}^{\max }$$

(11)

$$\mathrm{SoC}\left(\mathrm{T}\right)={\mathrm{SoC}}^{\min }$$

(12)

Under the constraints described in Equations (11) and (12), the aim is to fully charge the ESS during the low tariff period and fully discharge it during the high tariff period in order to achieve the maximum energy cost saving based on the electricity price term, Cost(t), as described in Equation (9). The optimal controller as a real-time controller is computationally expensive and the above control procedure helps to achieve the maximum cost saving and reduce the computational cost by simplifying the cost function. However, this procedure could affect the peak reduction term in order to satisfy the cost constraints. The optimal controller with a fixed load forecast in this section uses the peak shaving technique to achieve the minimum peak demand and electricity bill by finding the optimal charge and discharge schedule for the ESS which minimises the cost function in Equation (9). The storage device operation schedule is determined by solving Equation (9) under constraint Equations (11) and (12).

4.2. Model Predictive Controller

For an MPC controller, the model uses a rolling forecast model for the time period between t (current time step) and t + k, where k is the prediction horizon step and $\mathrm{t}+\mathrm{k}\le \mathrm{T}$ and T is the end of the day period T = 48, as illustrated in Figure 5. The rolling forecast model is designed to predict the load for one day ahead with half hourly updating procedure. The MPC controller uses the rolling forecast data to feed and update the MPC plan for each time step and regenerates a new future demand profile. The planned control moves, ∆E, are calculated from minimising a cost function as presented in Equation (9). The quadratic cost function has been widely used in the literature, as it is easy to solve and has useful theoretical properties. Generally, the MPC controller is designed using a cost function that penalises deviation of a given reference point trajectory. The MPC controller then recalculates and update the optimal control decisions for the rest of the day by solving Equation (9) in order to optimize the ESS actions on the RTG crane network. The previous steps are continuously repeated at every time step t + 1 throughout the day by using the updated forecast profile t + 1 + i and the ESS and crane system variables to compute the optima control signal. This control process is mainly referred to as the receding horizon controller [25,26], as illustrated in Algorithm 1. The current literature on LV network applications and microgrids [26] is increasingly investigating the benefits of treating the volatile demand as a stochastic element and developing a stochastic control in order to increase the efficiency performance of the ESS on the distribution network. In the next section the MPC method will be updated to consider a stochastic model predictive controller.

Algorithm 1: Basic concept of MPC for RTGs network with storage device.

Determine the control horizon, prediction horizon and the time step. Determine the objective function and constraints for RTGs network with ESS model. Initialise: the RTGs network, storage device and forecast. For t = 1 to T, do Solve optimal Equation (8) to find the optimal operation for the RTGs network with ESS, subject to the following constraints: The RTGs crane network Equation (2). Storage device model Equations (3) to (5). Electrical cost saving Equations (10) to (12). For (t = 1), the controller model computes the optimal solution based on the crane forecast profile and initial data. Find the optimal signal for (t + 1) and apply the control to the crane and ESS model. Update the crane demand forecast model for time step (t + 1) to T by regenerating the forecast profile with the new model information and observation. Set t = t + 1, An optimal control policy solution is achieved for the RTGs network with an ESS for the specific day. Repeat all steps for the next day.

4.3. Stochastic Model Predictive Controller

The high uncertainty in the RTG crane network and ESS applications have a significant impact on the performance of the energy controller. SMPC technique is a special subset of MPC algorithms that evaluate the objective function (Equation (9)) under uncertainty conditions. In this paper, generating a range of potential scenarios estimates the uncertainty in the optimisation problem by modelling some of the possible future scenarios. The future RTG crane demand for a day ahead, $\widehat{\mathrm{P}}$, is probabilistically modelled by generating M possible future demand profiles called ensembles (in this case, the forecast is generated using Monte Carlo realisations as inputs to an autoregressive integrated moving average with an explanatory variable (ARIMAX) model) [11,12]. The half hourly future RTG cranes demand of a day for ensemble m, where $m\in \left\{1,\dots ,\mathrm{M}\right\}$ can be written as

$${\widehat{\mathrm{P}}}^{\mathrm{M}}={\left({\widehat{\mathrm{P}}}^m\left(1\right),\dots ,{\widehat{\mathrm{P}}}^m\left(48\right)\right)}^{\mathrm{T}}\in {ℝ}^{48}$$

(13)

The SMPC controller aims to create an optimal charge and discharge operation schedule for the storage device (ESS control policy) to minimise the peak demand over the M ensembles for the future periods t, …, T by finding the empirical mean for the cost function [10]. In SMPC, a dynamic programming model is used to achieve the minimum value of the cost function by controlling decisions at each discrete time point. This is represented in Equation (14), where J is the cost function from Equation (9).

$$\Delta {\mathrm{E}}^{*}\left(\mathrm{t},\mathrm{t}+1,\dots ,\mathrm{T}\right)=\underset{\Delta \mathrm{E}\left(\mathrm{t}:\mathrm{T}\right)}{\arg \min }\frac{1}{\mathrm{M}}{\displaystyle \sum }_{\mathrm{m} =1}^{\mathrm{M}}\mathrm{J}\left({\widehat{\mathrm{P}}}^m,\Delta \mathrm{E}\right).$$

(14)

The dynamic programming model solves the RTG crane demand problem by first minimising the cost function at the end of the day from N = 48 and then working backward to the t-th time step. The cost function is updated as follow based on the dynamic programming model and the empirical mean tool as follows:

$${\mathrm{J}}^{*}{}_{\left(\mathrm{t}\right)}=\frac{1}{\mathrm{M}}{\displaystyle \sum }_{\mathrm{m} =1}^{\mathrm{M}}\max \left\{{\left({\widehat{\mathrm{P}}}^{\mathrm{m}} \left(\mathrm{t}\right)+\Delta \mathrm{E}\left(\mathrm{t}\right)\right)}^2 \right\}+{\mathrm{J}}^{*}{}_{\left(\mathrm{t}+1\right).}$$

(15)

In Equations (16), we find the ESS control decision, $\Delta \mathrm{E}$, that minimise the cost function over all paths in the search space from $\mathrm{t}$ to $\mathrm{t}+1$. The main goal of using the proposed SMPC model is the control decision for the storage device at each time step that minimise the RTG crane demand over all ensembles. The chosen ESS control policy is specified as: ${\mathsf{\pi }}^{*}\left(\mathrm{t}\right)={\left(\Delta {\mathrm{E}}^{*}\left(\mathrm{t}\right),\Delta {\mathrm{E}}^{*}\left(\mathrm{t}+1\right), \dots ,\Delta {\mathrm{E}}^{*}\left(48\right)\right)}^{\mathrm{T}}.$ The SMPC controller is computationally expensive compared to other methods, such as the set-point controller. Section 5.2 will investigate the complexity and computational cost of the different controllers.

5. Results and Discussion

The previous section presented optimal energy management systems for controlling an ESS in an RTG crane network. This section introduces a comparison analysis of these energy storage control strategies. The comparison aims to investigate and present the stability and robustness of the energy storage controllers by considering a specific RTG data set as presented in the previous section. This analysis is divided in two main categories:

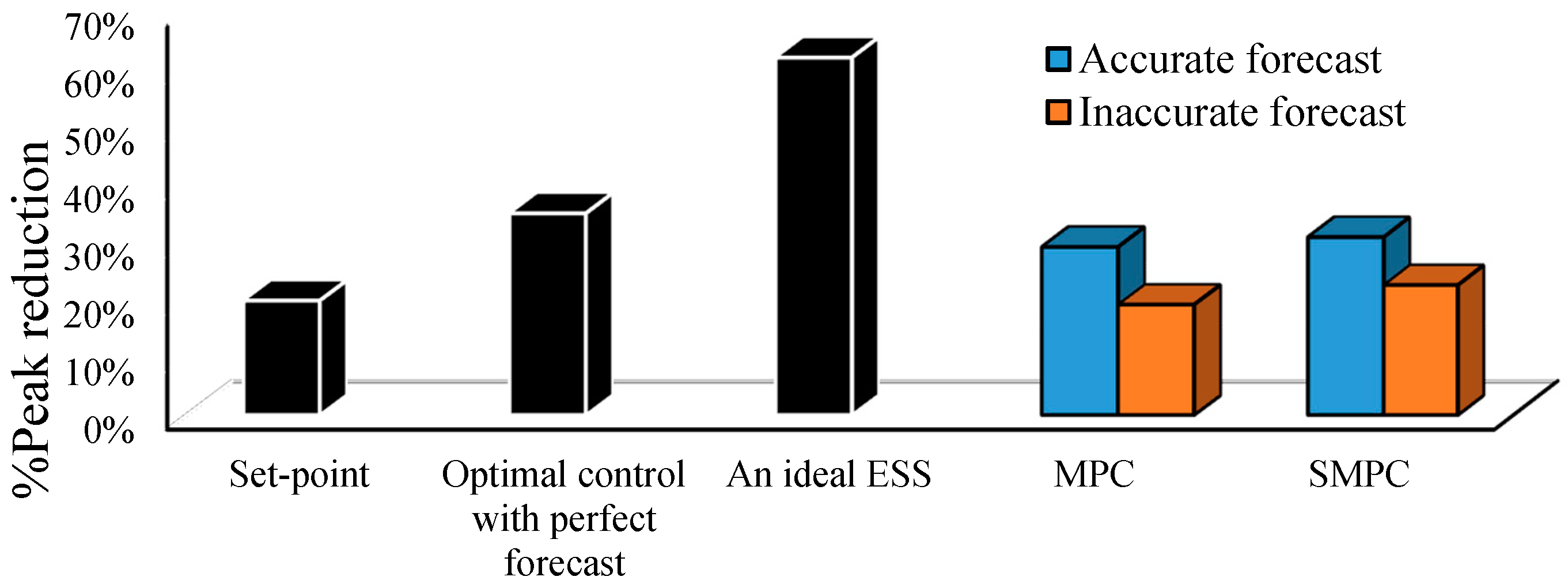
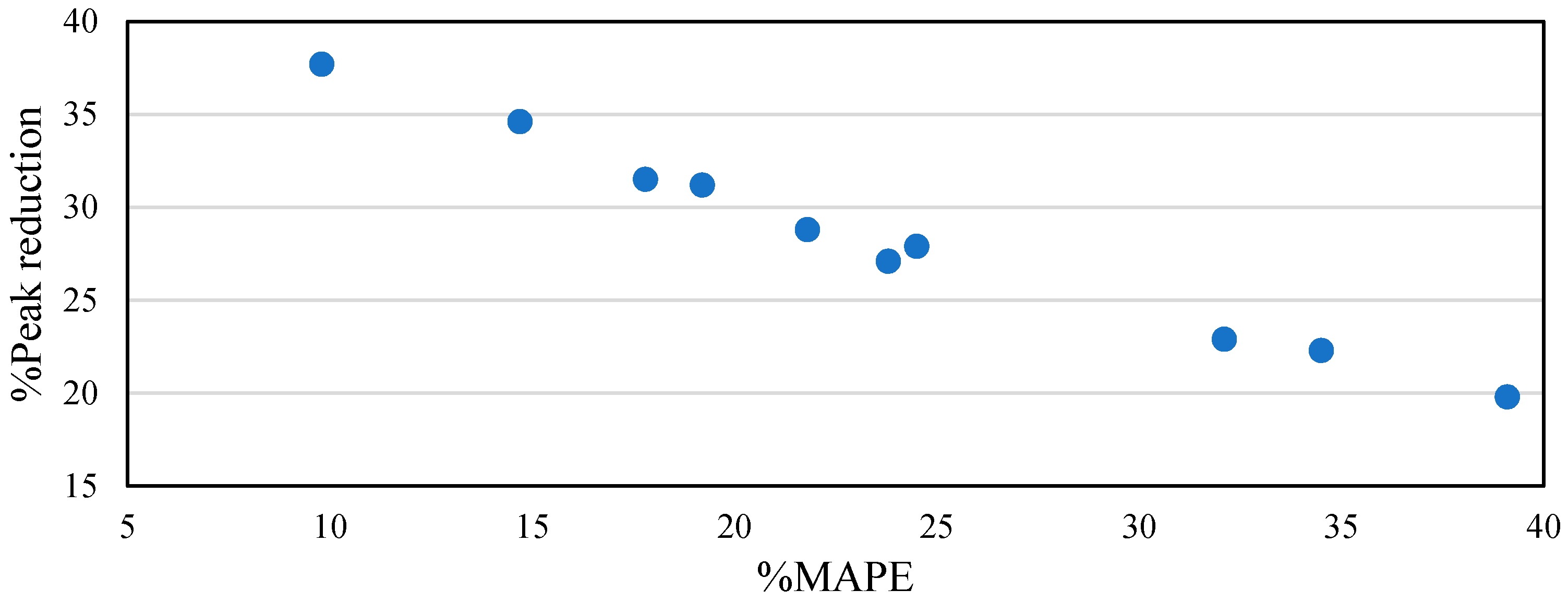
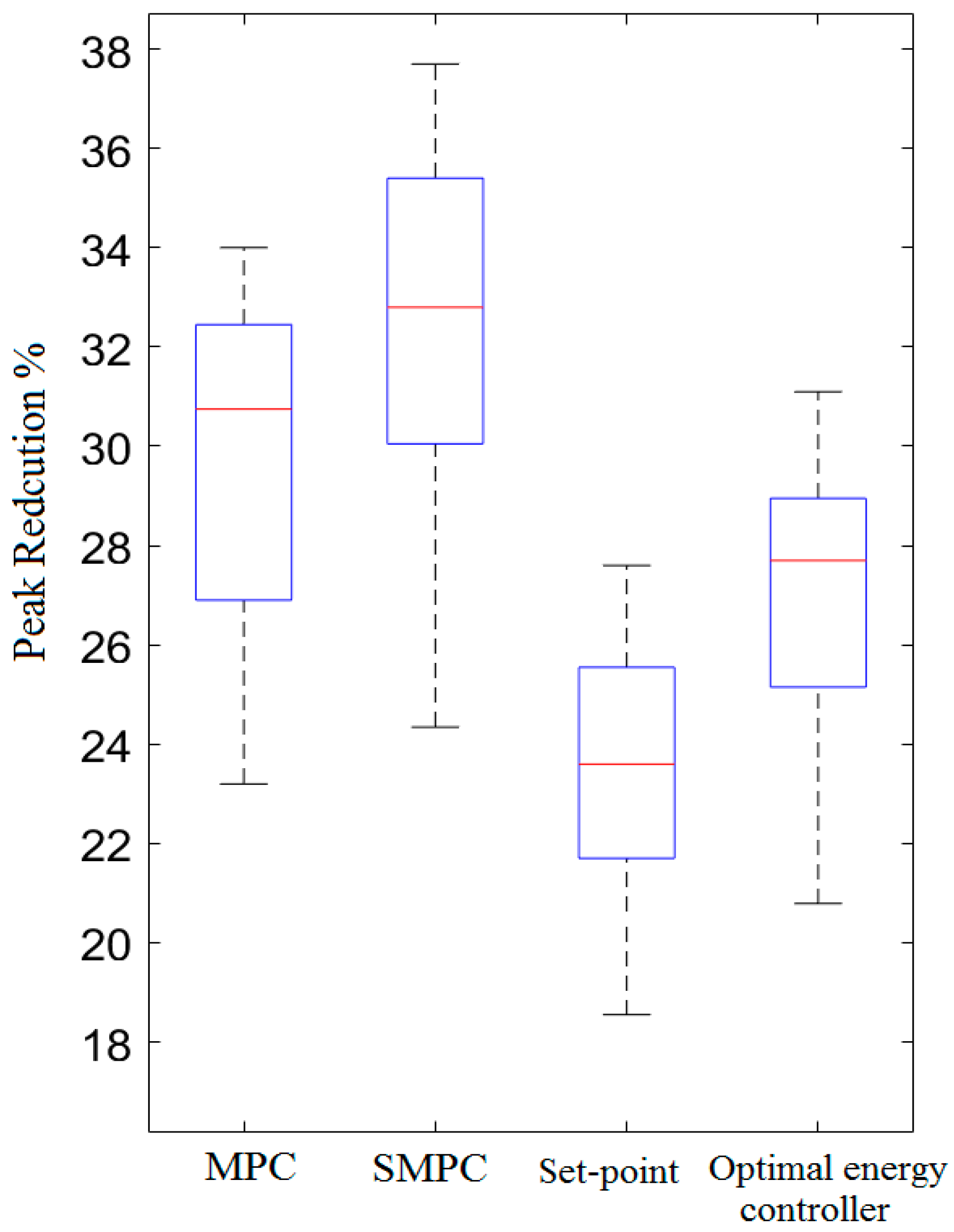
• Optimality for peak demand reduction and cost saving: the following section compares and evaluates the potential peak reduction and cost saving results for the predictive controllers (SMPC and MPC) with different levels of forecast accuracy, the set-point controller and the optimal energy controller model with perfect forecast profiles. In order to evaluate the predictive controllers, two future demand profiles from accurate and inaccurate forecast models have been used. This evaluation is significant in understanding the impact of forecast errors on the ESS control algorithms.
• Complexity and computational cost: Section 5.2 presents indicators regarding the complexity of a practical implementation of the predictive optimal controllers.

5.1. Analysis of Energy Storage Control Strategies

In order to determine the appropriate optimal control decisions sequence for the ESS, the predictive optimal controllers (MPC and SMPC) require a rolling forecast model.

Table 1. The average peak demand reduction and the mean absolute percentage error (MAPE) forecast errors for the model predictive controller (MPC) and the stochastic model predictive controller (SMPC).

ESS Control Model	Accurate Forecast Model	MAPE	Peak Reduction%	Inaccurate Forecast Model	MAPE	Peak Reduction%
MPC	ANN (Model B)	14.2%	30.2%	ANN (Model A)	28.3%	20.2%
SMPC	ARIMAX (Model C)	17.2%	32.6%	ARIMA (Model D)	30.1%	24.2%

presents two forecast models (accurate and inaccurate models) that have been used to implement the predictive optimal controllers’ which were developed in [11,12]. The parameters of the energy storage system and energy costs are described in [11,12] and have been used in this paper to operate the storage device on the RTGs network. This section aims to show how the forecast error affects the performance of the optimal controllers. As discussed in the literature, energy storage controllers for LV network applications have typically been developed with full knowledge of future demand [29,30] or using forecast models with relatively small errors of around 10% [26,29]. Therefore, in this section, accurate and inaccurate forecast models have been used to feed the optimal energy controllers and evaluate the impact of forecast errors on the performance of the ESS, as presented in Section 3. In Table 1, the MAPE decreased to 14.2% for the Artificial Neural Network (ANN) model (Model B) from 28.3% for Model (A) and to 17.2% for model (C) from 30.1% for the ARIMA model (Model D).

The results for the MPC and SMPC controllers are shown in Table 1. Figure 6 shows that the SMPC outperforms all controllers except the optimal controller which has full future knowledge, and thus ignores the volatile and uncertain nature of the RTG demand. The predictive controllers (MPC and SMPC) with receding horizon procedure and the rolling forecast model improve the energy storage performance considerably compared to a set-point controller when an accurate forecast is used. As presented in Figure 6 for the data given, the SMPC with accurate forecast improves the energy storage performance by increasing the peak demand reduction compared to using an inaccurate forecast. Furthermore, the SMPC controller achieved a 32.6% peak demand reduction compared to 30.2% for MPC, 23.9% for set-point and 36.1% for the optimal controller with a perfect load forecast. An ideal energy storage model has also been suggested as a benchmarking model where the ESS has infinite capacity and no charging or discharging limitations. This ideal model basically generates a flat demand profile, reached a highest possible peak reduction of 64.8%.

The predictive optimal controller results, shown in Figure 6 and Table 1, demonstrate that the accurate forecast profile is essential in order to maximise the ESS performance by increasing the peak demand reduction via optimal energy controllers. For illustration, the percentage of peak reduction increased to 30.2% from 20.2% for the MPC and to 32.6% from 24.2% for the SMPC, when using accurate versus inaccurate forecasts respectively. However, the stochastic algorithms allow the SMPC controller using an inaccurate forecast profile to outperform the MPC and set-point control algorithms. The SMPC generate an ESS operation plan based on a number of future RTG demand scenarios, which aims to reflect and minimises the impact of the high RTG demand volatility.

Figure 7 presents the relationship between the forecast accuracy and potential peak demand reduction for a predictive optimal controller (SMPC). The results in Figure 7 and Table 1 show that more accurate forecast models are directly related to greater peak demand reductions. The forecast error is a significant factor for potential energy cost saving and peak demand reduction in optimal energy controllers, and a high ESS performance is more likely when utilizing a more accurate forecast estimate [29]. However, Figure 7 shows that accurate forecast estimates do not always guarantee relatively high energy savings or peak reduction. This could be due to the forecast errors in some days of the experiment being concentrated at the peak period rather than distributed over the day. MAPE focuses on the mean value of the error and therefore root-mean squared errors may be preferable in this application.

The cost function used in the optimal energy control models aim to reduce the electricity costs and create substantial peak reduction in the RTGs network using the electrical tariff term and peak shifting strategy.

Table 2. The percentage of annual electric energy cost saving to the annual electricity energy bill.

Controller		Percentage of Cost Saving
	No Forecast/Perfect Forecast	Accurate	Inaccurate
Set-point	5.47	-	-
Optimal controller with perfect forecast	8.01	-	-
MPC	-	7.26%	5.88%
SMPC	-	7.98%	6.96%

presents the annual cost saving in the Port of Felixstowe, UK for the proposed control strategies based on the data collected from the port. However, clearly it is difficult to extrapolate to the full year, but the results are expected to be similar as crane operation is continuous throughout the year, as discussed in Section 3. The SMPC achieves annual cost savings of around 7.9% when utilising accurate forecasts, this cost saving is near the maximum possible energy cost savings of 8.01%. Similar to the peak demand reduction results, the optimal controller with accurate forecasts improves the ESS performance by increasing the cost savings with an improvement of 19% on average compared to the control models with inaccurate forecasts. For example, the percentage of annual cost saving decreased to 5.88% from 7.26% for the MPC and to 6.69% from 7.98% for the SMPC, when using inaccurate versus accurate forecasts respectively. Furthermore, the peak demand reduction on the RTGs network infrastructure introduces extra economic and technical benefits. As presented in Figure 6, all predictive optimal controllers utilizing an accurate forecast model outperform the standard set-point controller. In RTGs networks, the set-point controller usually depletes the stored energy quickly at insignificant earlier peaks. However, RTG demand is highly stochastic and thus the peak demands are randomly distributed over the 24 h a day. On the other hand, the resulting improvement for optimal controllers is due to the high energy costs at peak demand periods (during the latter half of the day). Furthermore, the rolling forecast model in MPC and SMPC controllers help to increase the peak reduction even more and increase the robustness of the controllers by better reacting to the most recent demand changes.

Results and Discussion for Optimal ESS Controllers

The results for the predictive controllers (MPC and SMPC) based on the accurate forecast models, set-point, and an optimal controller with fixed demand forecast are presented in Figure 8. Each box plot in Figure 8 presents the distribution of daily peak reductions for RTGs network with ESS. The box plot of the SMPC controller shows that the stochastic model outperforms all other energy controllers with a median peak reduction of around 33%. As seen in Figure 8, the set-point controller peak reduction box plot overlaps with other optimal controllers, and this is related to the high forecast error that affects the ESS performance for the optimal controller. However, optimal controllers using accurate forecast models show a better performance compared to the standard set-point controller. In receding horizon controllers with rolling load forecast models, the ESS performance is further increased over the full day time compared to the set-point controller or the optimal model with a fixed daily load forecast.

5.2. Complexity and Computational Cost

The MPC and SMPC algorithms with rolling forecast model allow use of the updated information of the forecast and RTGs network models data for each time step to generate the operation plan for the ESS. The rolling forecast models allow one to update to the control process as new information becomes available and thus reduce the impact of the forecast error and volatile behaviour of RTG demand on the ESS performance. The results of the receding horizon controllers showed decreased energy costs and increased peak reduction, compared to the standard set-point controller. However, for MPC and SMPC, the larger the control horizon size the higher the complexity and computational cost, but this also increases the possibility of reducing the daily peak demands as it encapsulates those which occur later in the horizon window. Small horizon windows reduce the computational cost but will decrease the possibility of reducing the maximum daily peak.

Furthermore, the MPC and SMPC controller must calculate the optimal operation plan every updated time step for the ESS by using the new available observations. Therefore, the SMPC and MPC has an additional cost compared to the set-point and fixed optimal controllers. In addition, the MPC and SMPC controllers require more technical skills and training processes to implement compared to set-point control, which is wildly used and tested in port energy saving applications.

SMPC and the Computational Effort

The performance of the SMPC must be considered in relation to the computational effort of the controller. The computational effort (total time duration) of the control simulation can be significant when the controller is developed and designed for a daily cycle where the optimisation process needs to be calculated at every time step. In the SMPC, the total computational cost relies on the number of RTG demand forecast scenarios, as shown in

Table 3. The computational effort for SMPC.

Number of Forecast Demand Scenarios	Average Simulation Duration (s)	Maximum Simulation Duration (s)
5	11	25
10	21	33
15	36	49

. More ensembles generally mean more possible scenarios are modelled, and hence the controller is more likely to be optimised. In daily optimisation with half hourly time step updating, each computational step for the model needs to be finished in approximately less than 30 sec, which for 48-time step will sum up to 25 min, Equation (16) [30].

$${\mathrm{t}}_{\mathrm{tot}}={ \mathrm{N} \mathrm{t}}_{\mathrm{s}}+{\mathrm{t}}_{\mathrm{d}},$$

(16)

where ${\mathrm{t}}_{\mathrm{tot}}$ is the total duration of time for the simulation, ${\mathrm{t}}_{\mathrm{s}}$ is the time for each step, N the number of the time steps during the day (N = 48) and ${\mathrm{t}}_{\mathrm{d}}$ is the time duration for data cycling (${\mathrm{t}}_{\mathrm{d}}=$ 2 min).

The SMPC model with 5 and 10 demand future scenarios is finished within the required time duration frame ($\le$25 min). The average of the total time duration is 10.8 and 18.8 min for the SMPC model with 5 and 10 demand future scenarios options, respectively. There are a few simulations that exceed the time limit (30 s) for the 10 demand future scenarios case with maximum time (33 s). However, the sum up of time for this case was 28.4 min which is still within the half hour time. The SMPC with the option of 15 demand future scenarios exceed the total duration limit and requires on average 30.8 min. Therefore, the number of demand future scenarios chosen was 10 for the SMPC model in Section 4.3, where the model simulated within the time frame and included the highest possible number of future demand scenarios. The model was run on PC Windows 8.1 with Intel(R) i5-4590 @ 3.3GHz processer with 8 GB RAM. However, a faster computer will reduce the computational time and improve the practicality of implementing the model. In addition, a higher data resolution such as minute of seconds will introduce more computational cost in the forecast model and the SMPC controller due to the large window size for peak reduction and cost saving over a day.

6. Conclusions

In this paper, the ESS performance analysis and comparison of different optimal energy control strategies have been presented and discussed. Different RTG demand forecast scenarios were used to evaluate the stability and robustness of the proposed optimal controllers. Energy cost savings and peak demand reduction were calculated to present the performance of each control strategy. The MPC and SMPC controllers showed operational improvements over the standard set-point control algorithm. This improvement relies on the forecast model’s accuracy, which is a significant factor in increasing the potential peak reduction in optimal controllers, and generally, more accurate forecasts are more likely increase peak reduction. Furthermore, each of the proposed control strategies has a number of advantages and drawbacks which were also discussed.

The performance of the energy storage system has been compared based on the specification and characteristics of different proposed control strategies. The set-point controller was too sensitive to the reference value compared to other control methods which were sensitive to the cost function and accuracy of the forecast profile. Overall, the SMPC outperforms other controllers and shows the best performance in terms of energy costs and peak reduction. The SMPC controller option was thus shown to be a potentially economically viable solution for peak demand reduction with much better performance compared to all other methods considered for the data given.