A Cost-Effective and Transferable Methodology for Rooftop PV Potential Assessment in Developing Countries
Abstract
1. Introduction
2. Literature Review of Potential Assessments for Rooftop PV
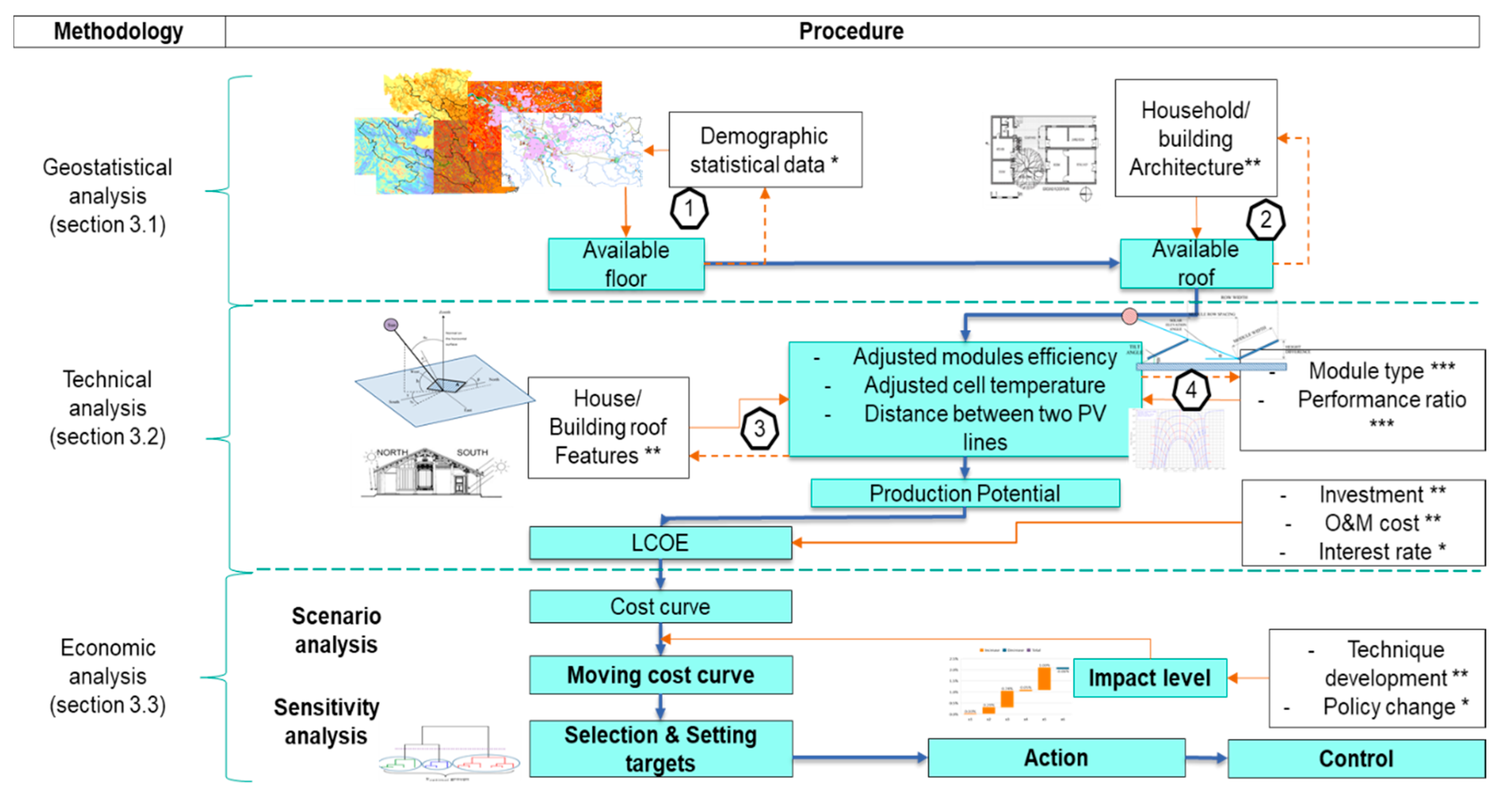
3. Methodology for Rooftop PV Potential Assessment
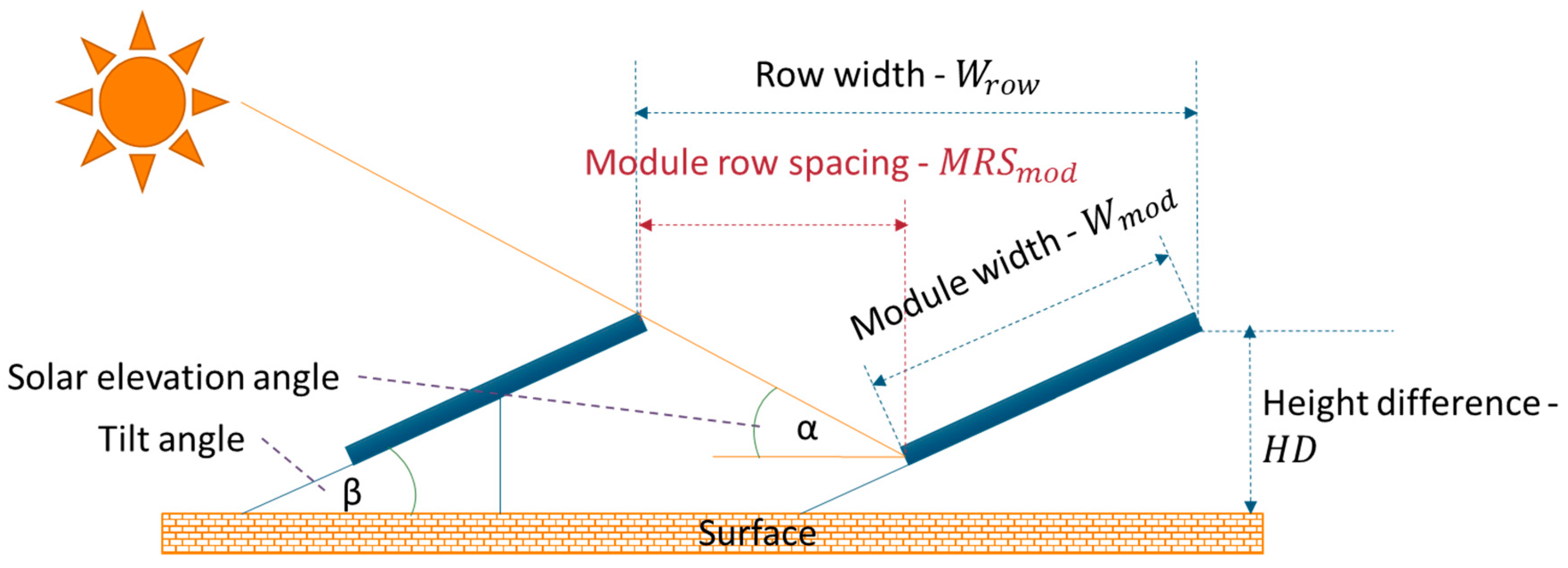
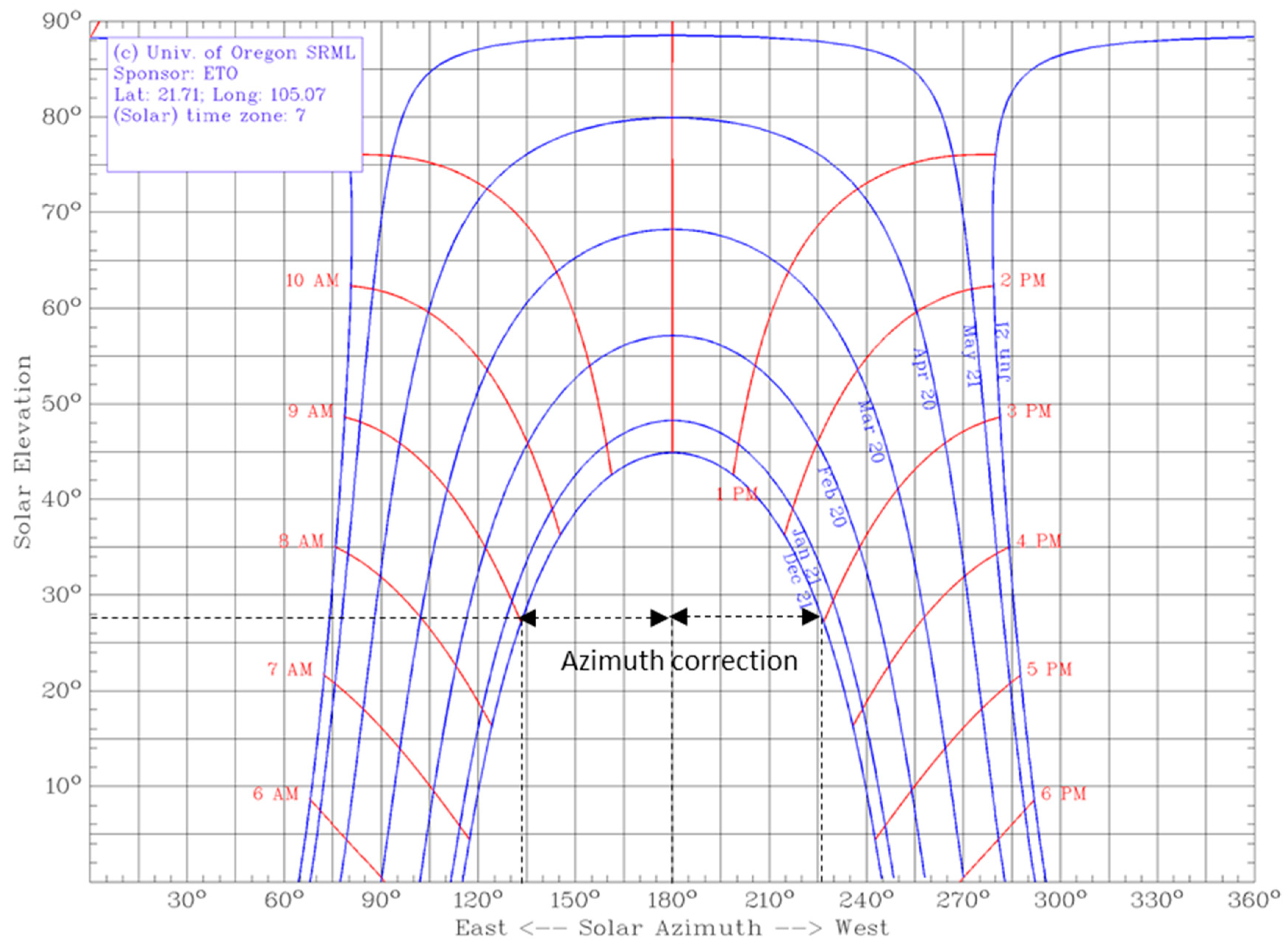
3.1. Geographical Potential
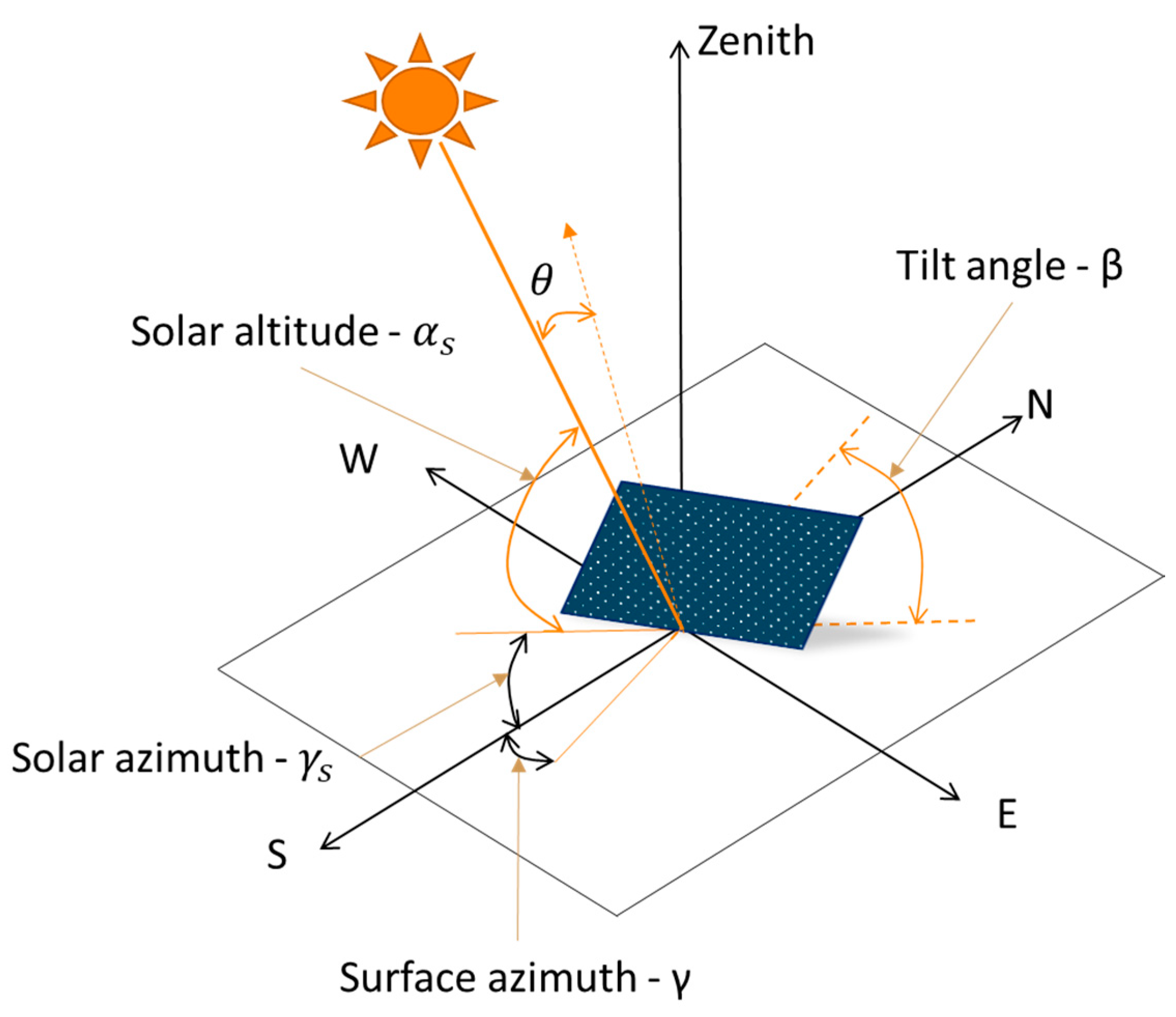
3.2. Technical Potential
3.3. Levelized Cost of Electricity (LCOE)
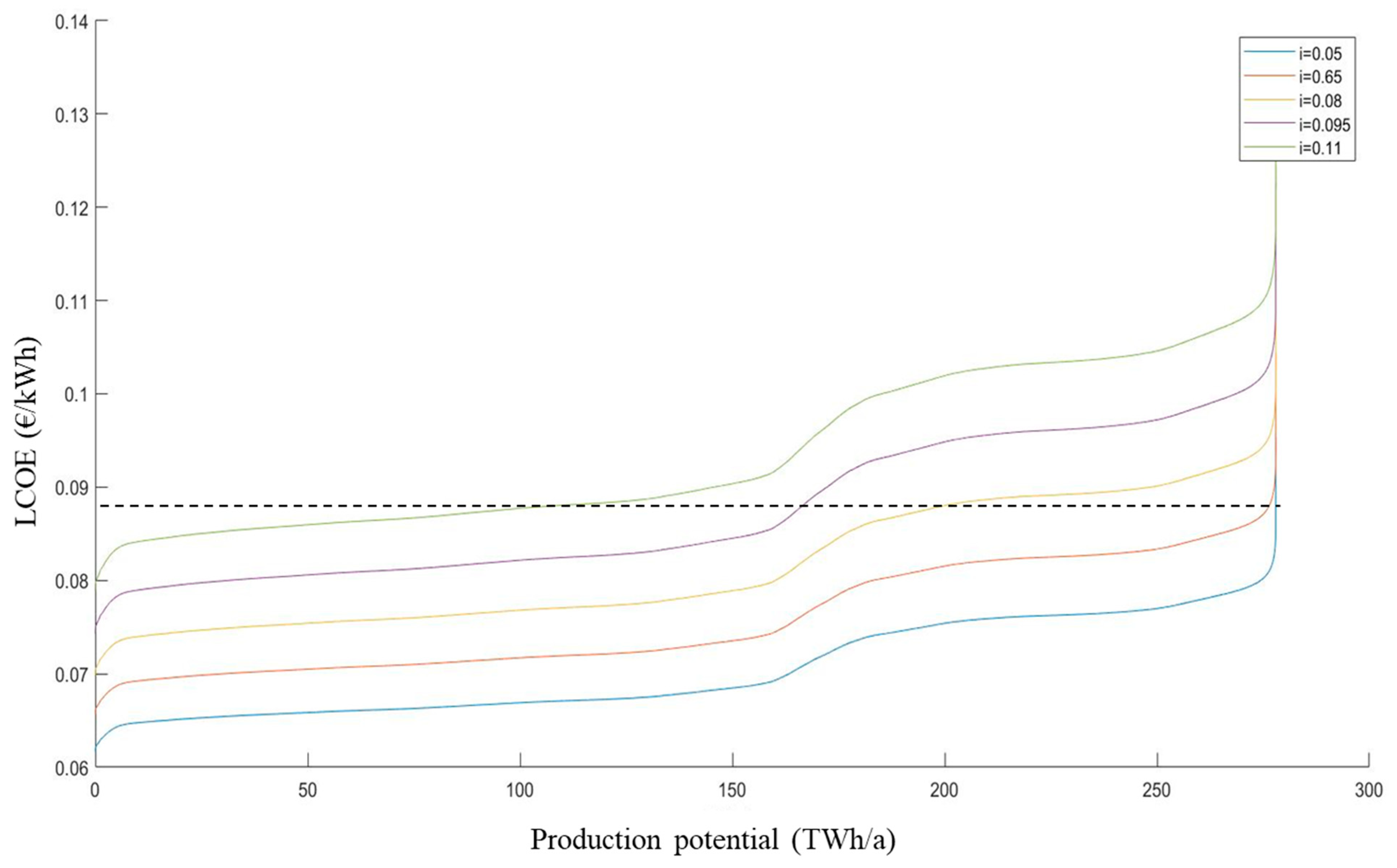
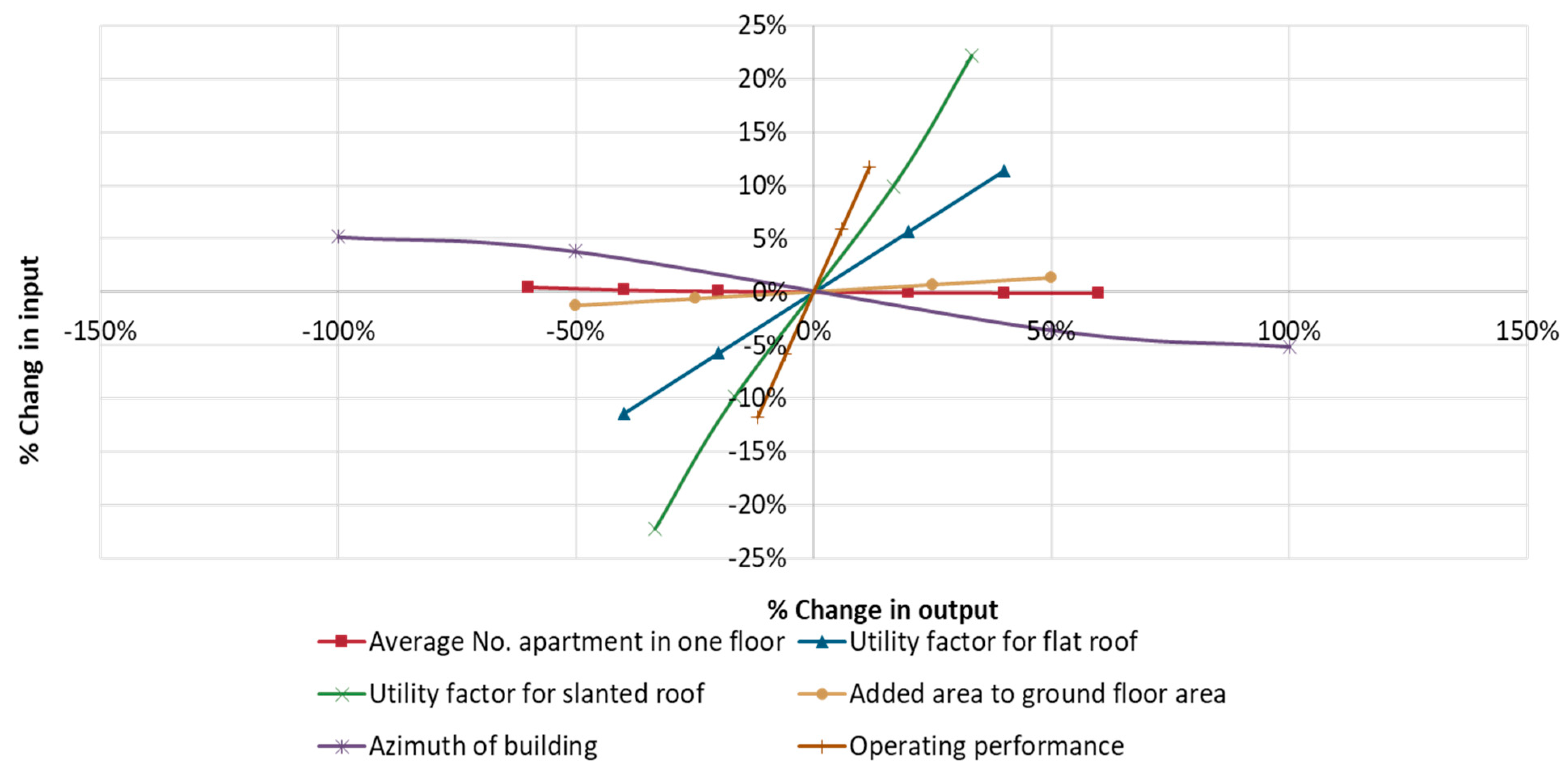
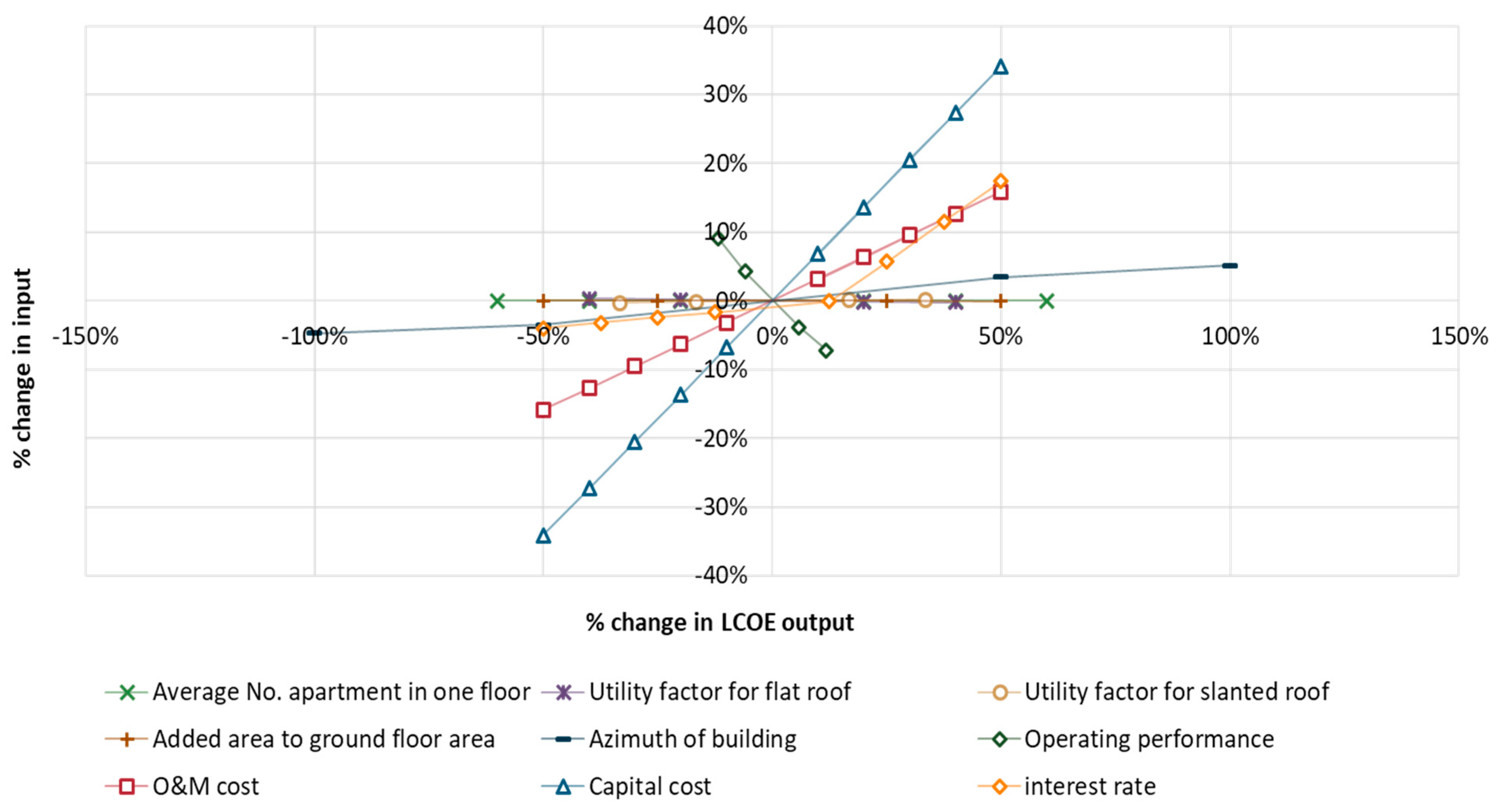
3.4. Sensitivity Analysis
4. Case Study and Results
4.1. Data and Assumptions
4.2. Results of the Potential Analysis
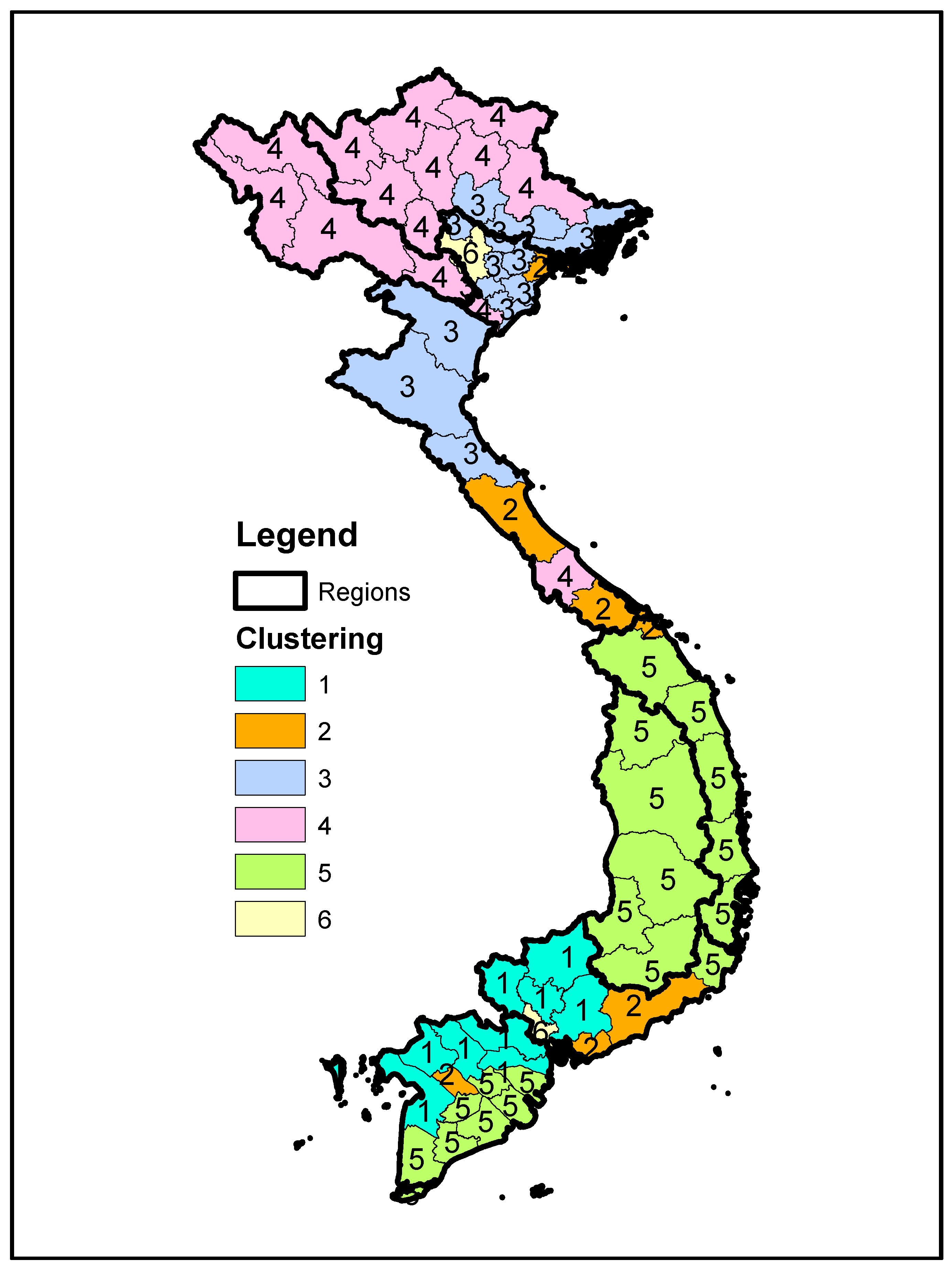
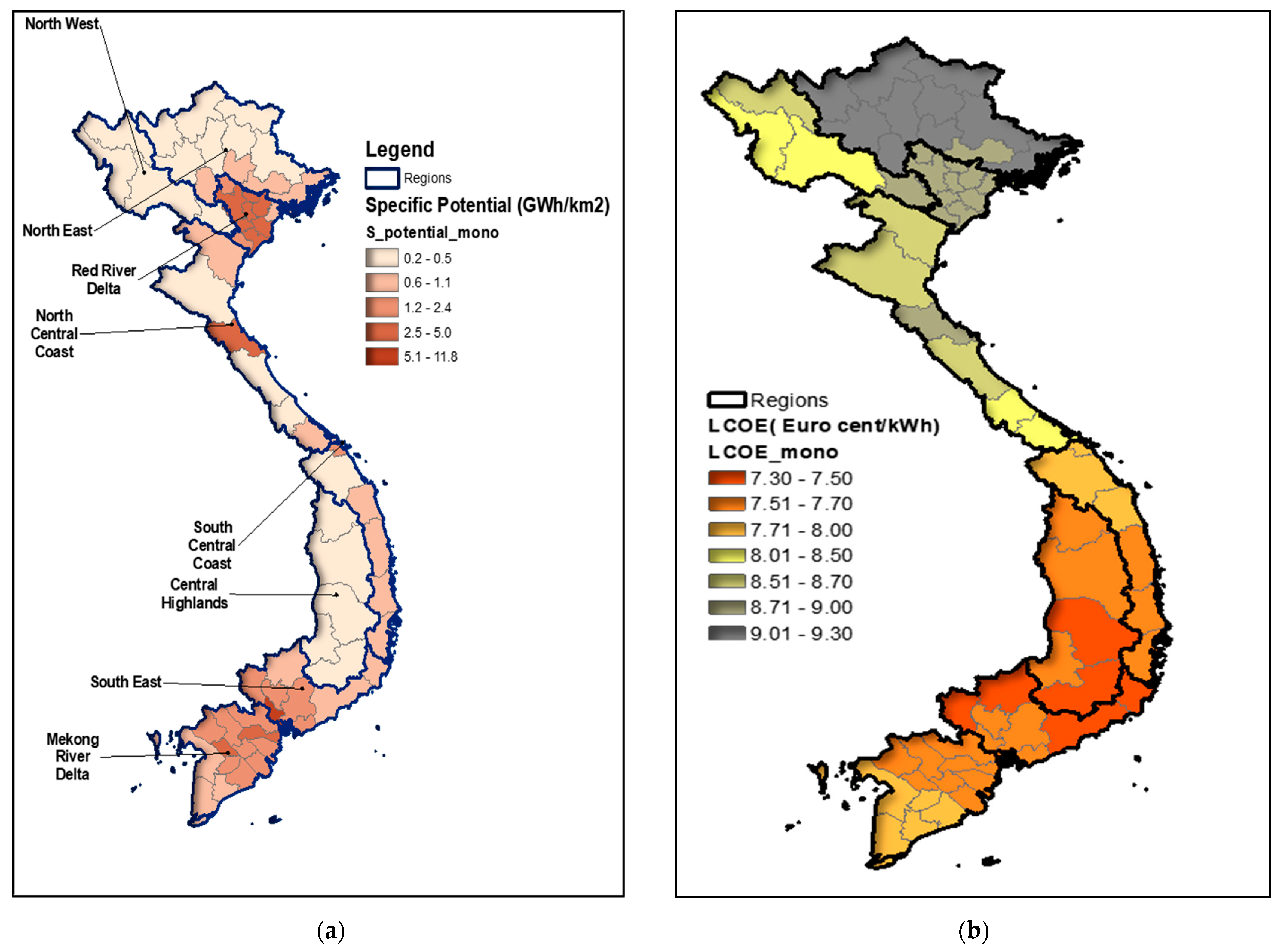
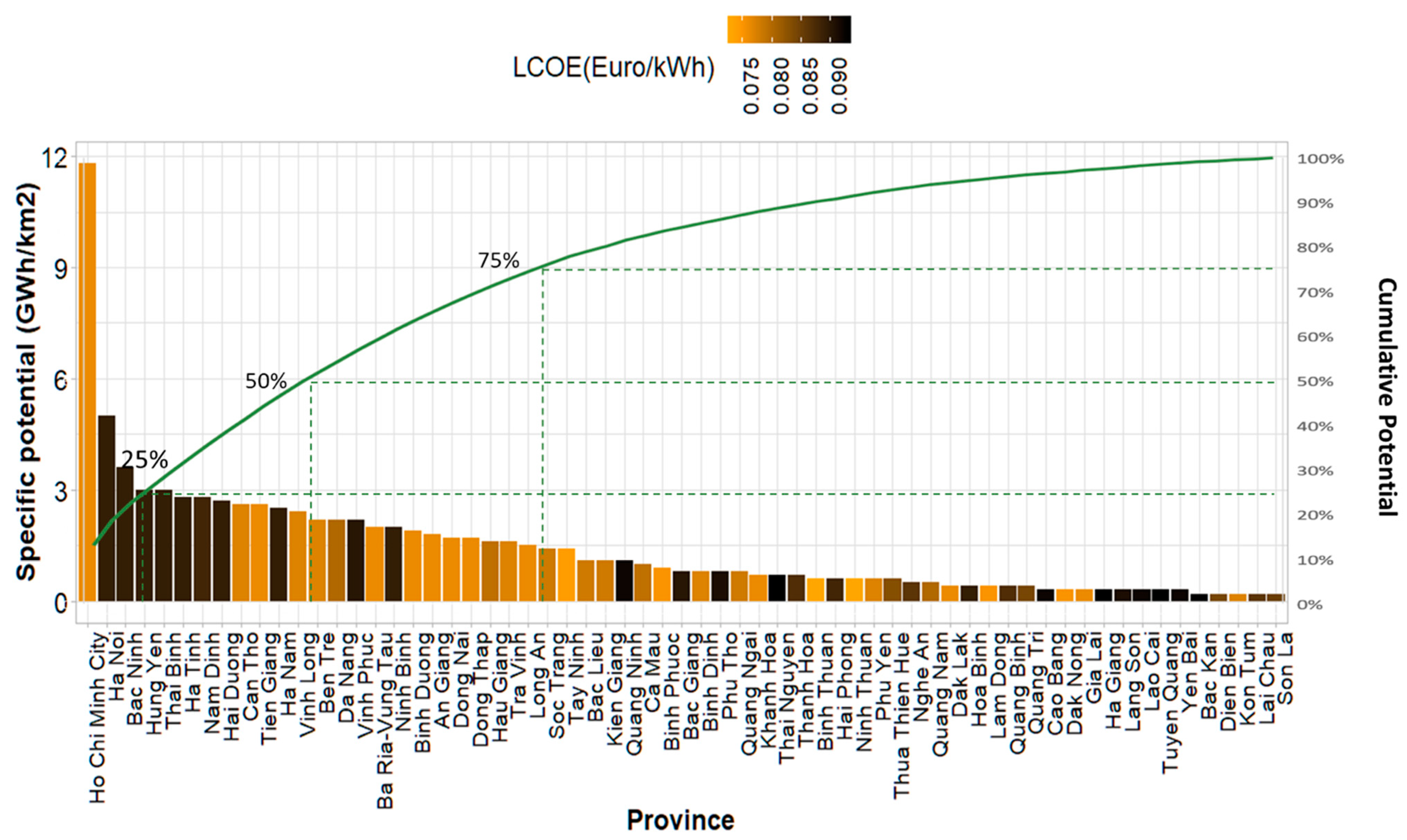
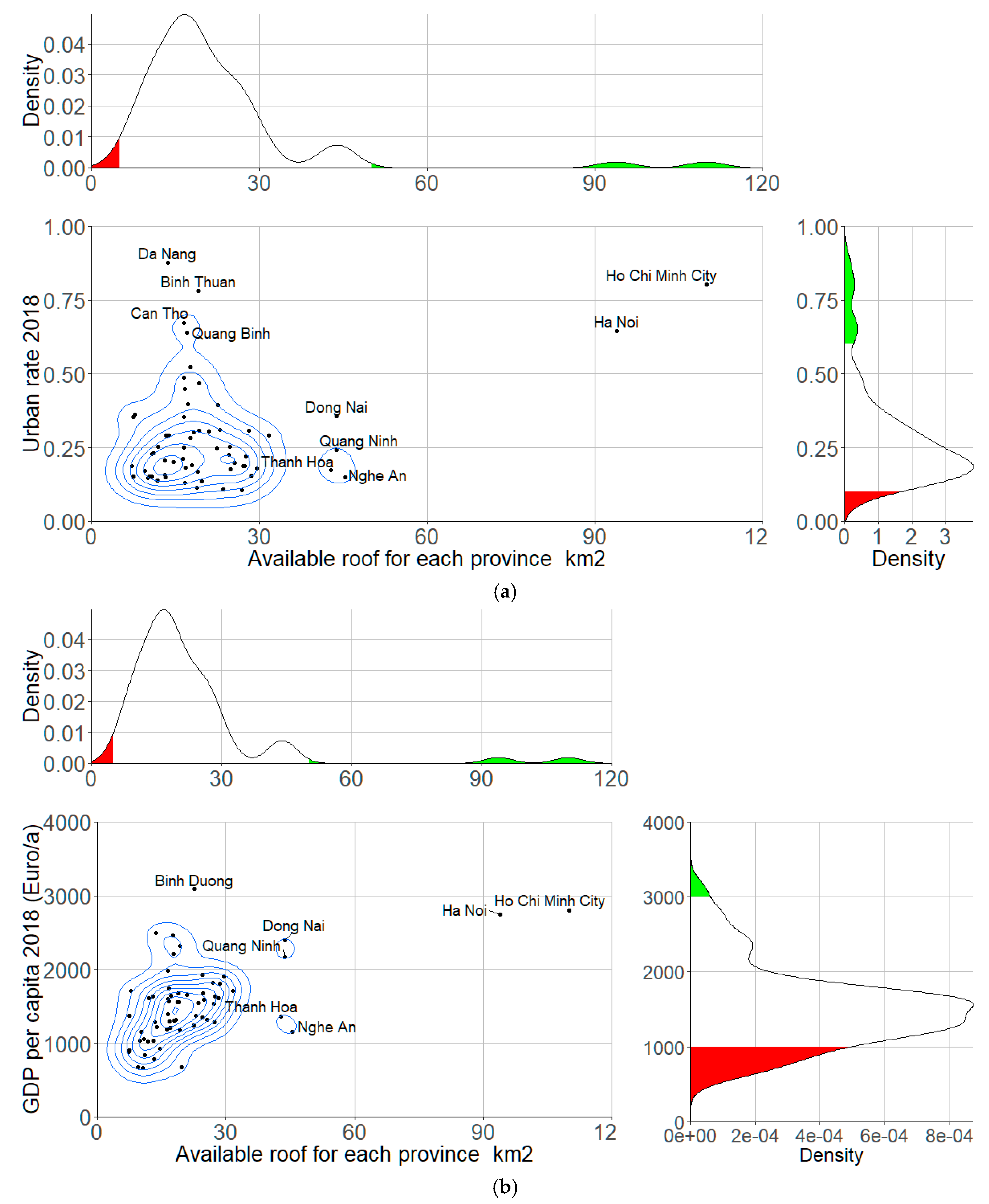
4.2.1. Spatial Potential Distribution of Rooftop PV
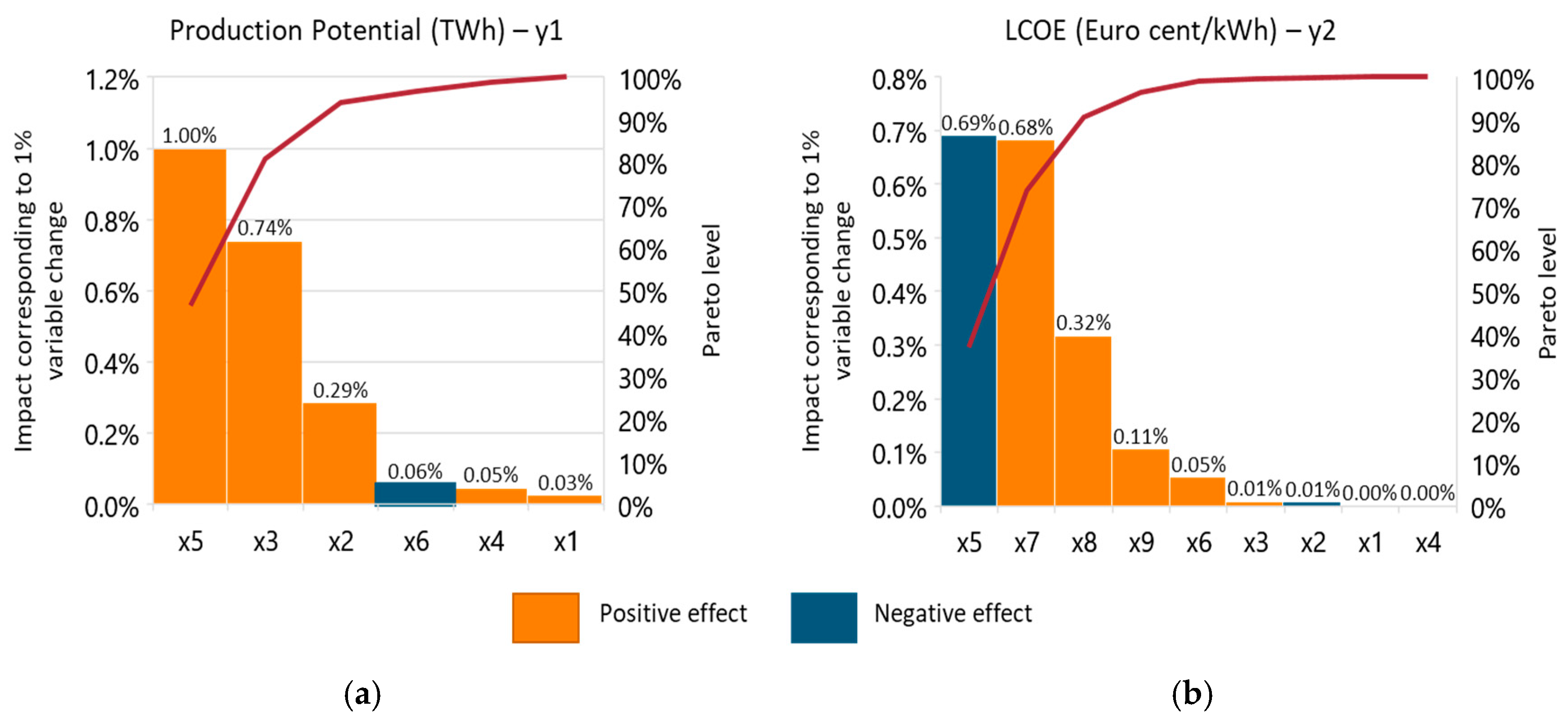
4.2.2. Sensitivity Analyses
| x1 | Area added to a ground floor area | x6 | Azimuth of building | |
| x2 | Utilization factor for flat roof | x7 | Capital cost | |
| x3 | Utilization factor for slanted roof | x8 | O&M cost | |
| x4 | Average number of apartments on one floor | x9 | Discount rate | |
| x5 | Performance ratio |
5. Deriving Policy Implications from the Potential Assessment Results
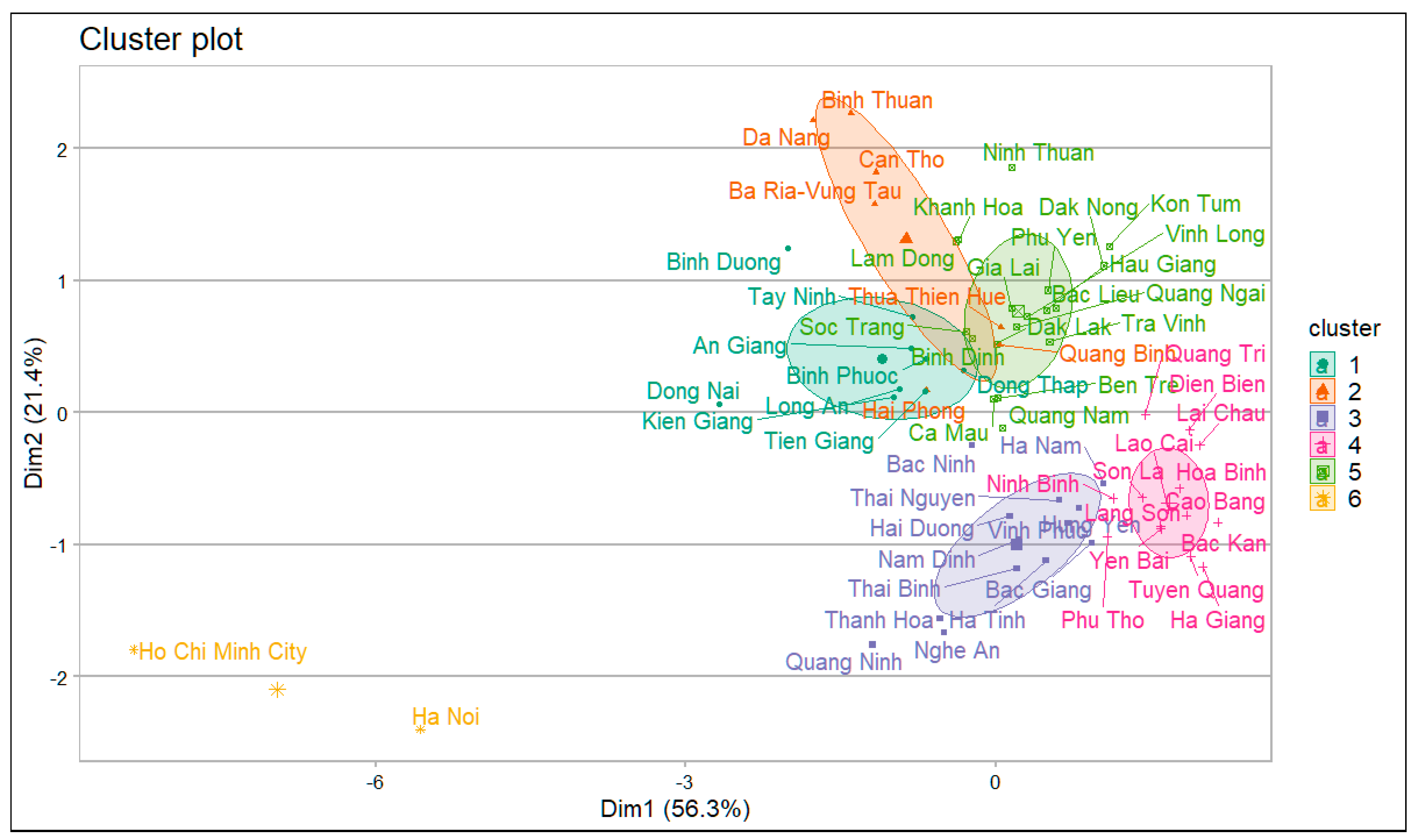
5.1. Defining Target Groups
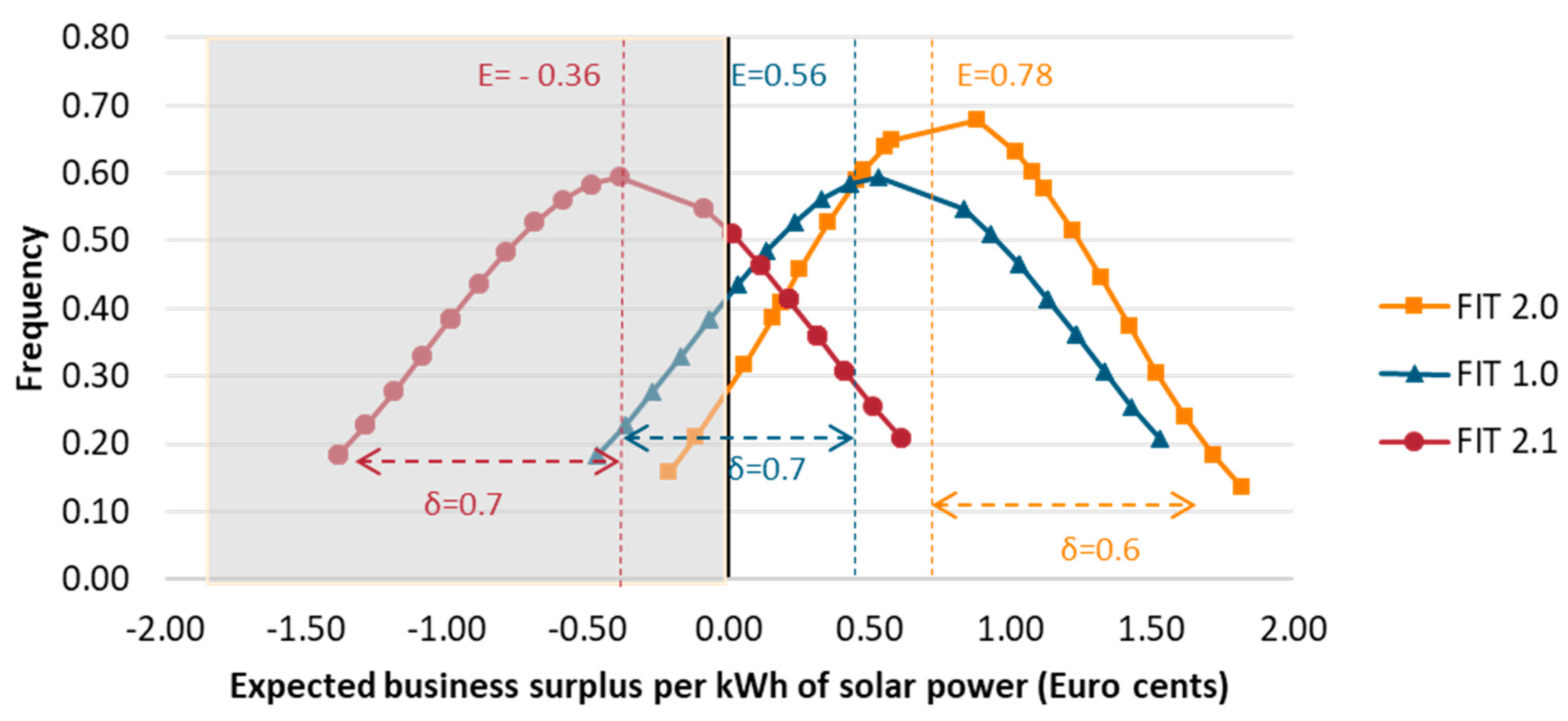
5.2. Assessing the Market Attractiveness and FIT
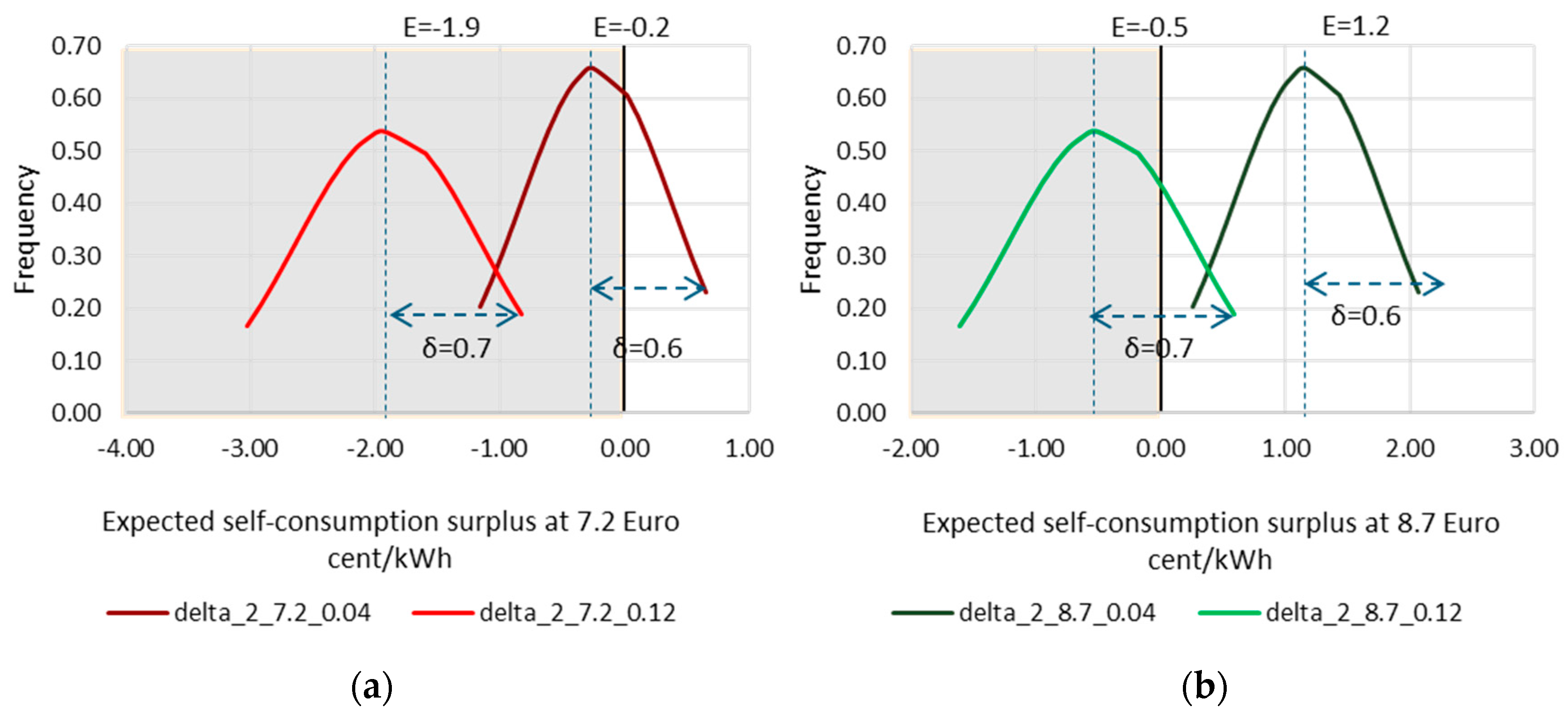
5.3. The Role of Grid Tariffs and PV Module Costs in Self-Sufficiency Developments
5.4. Critical Discussion
6. Conclusions and Policy Implications
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| PV | Photovoltaics |
| LIDAR | Light detection and ranging |
| HVAC | Heating, Ventilation and Air Conditioning |
| STC | Standard test conditions |
| AM | Air mass |
| NOCT | Nominal operating cell temperature |
| CT | Constant value |
| HD | Height difference |
| MRS | Module row spacing |
| PR | Performance ratio |
| LCOE | Levelized Cost of Electricity |
| GDP | Gross domestic product |
| Dim | Dimension |
| FIT | Feed-in tariff |
| MOIT | Vietnamese Ministry of Industry and Trade |
| EVN | Vietnam Electricity Enterprise |
| CAPEX | Capital expenditure |
| OPEX | Operational and maintenance expenditure |
Appendix A
| Customer Group | Rate (VND/kWh) | Rate (Euro cents/kWh) | |
|---|---|---|---|
| 1 | Retail price for household electricity | ||
| Rate 1: For 0–50 kWh | 1678 | 6.33 | |
| Rate 2: For 51–100 kWh | 1734 | 6.54 | |
| Rate 3: For 101–200 kWh | 2014 | 7.60 | |
| Rate 4: For 201–300 kWh | 2536 | 9.57 | |
| Rate 5: For 301–400 kWh | 2834 | 10.69 | |
| Rate 6: For 401 kWh onwards | 2927 | 11.05 | |
| 2 | Retail price for household electricity via prepaid card meter | 2461 | 9.29 |
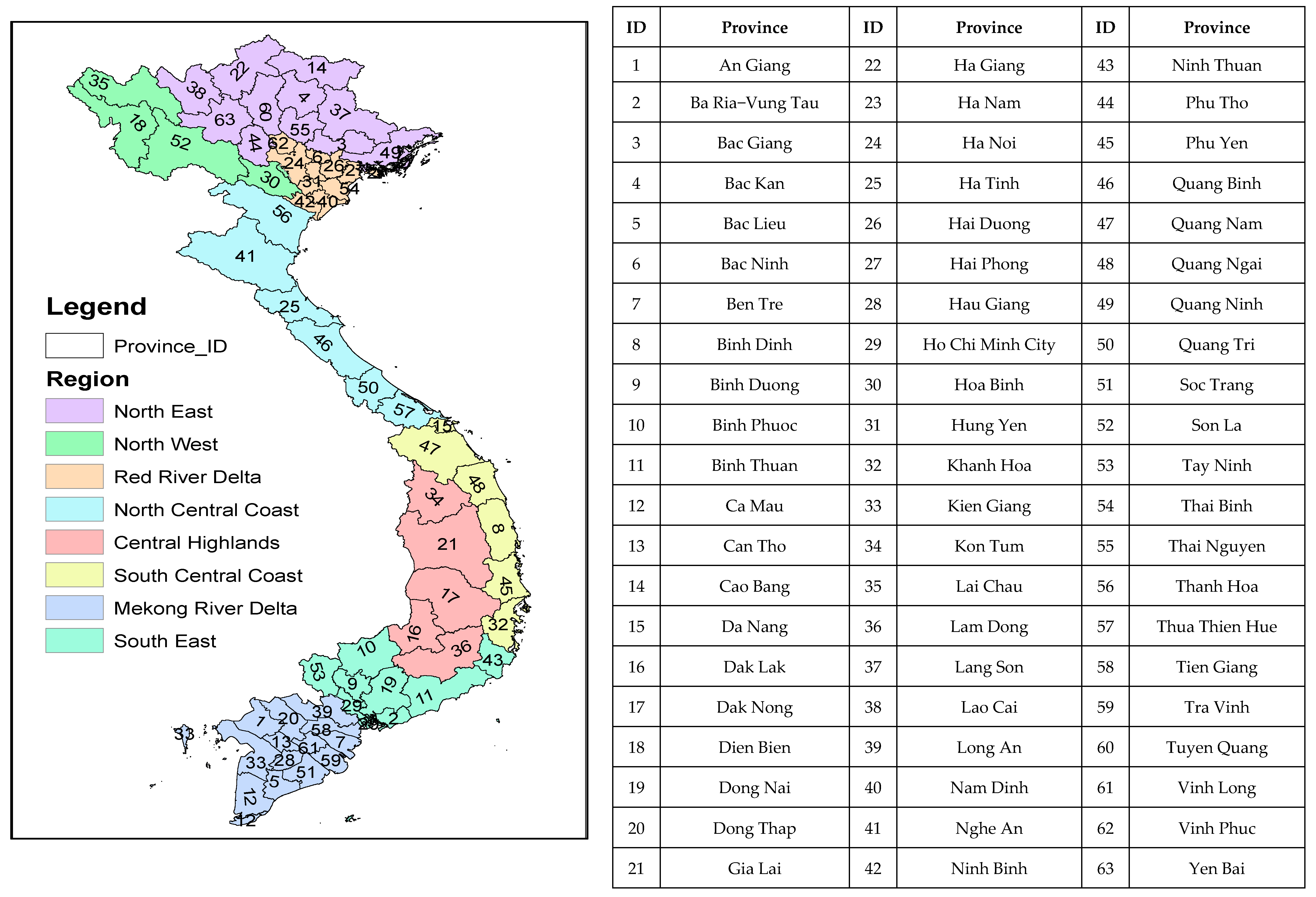
| ID | Province | Region | Total Area (km2) | Household Area (km2) | % of Household Area | Population | Urban Rate 2018 (%) | Gdp/a/person 2018 (Euro/a) |
|---|---|---|---|---|---|---|---|---|
| 1 | An Giang | Mekong river delta | 3536 | 135 | 3.8% | 2164.2 | 30.8% | 1612.1 |
| 2 | Ba Ria-Vung Tau | Southeast | 1979 | 71 | 3.6% | 1112.9 | 52.4% | 2210.3 |
| 3 | Bac Giang | Northern midlands | 3895 | 185 | 4.7% | 897.0 | 11.5% | 1562.3 |
| 4 | Bac Kan | Northern midlands | 4860 | 26 | 0.5% | 327.9 | 18.8% | 880.8 |
| 5 | Bac Lieu | Mekong river delta | 2668 | 49 | 1.8% | 1691.8 | 29.1% | 1222.2 |
| 6 | Bac Ninh | Red river delta | 822 | 104 | 12.7% | 1247.5 | 28.3% | 2466.1 |
| 7 | Ben Tre | Mekong river delta | 2395 | 81 | 3.4% | 1268.2 | 10.8% | 1543.7 |
| 8 | Binh Dinh | South central coast | 6066 | 94 | 1.5% | 2163.6 | 31.0% | 1369.4 |
| 9 | Binh Duong | Southeast | 2696 | 136 | 5.0% | 1534.8 | 39.4% | 3089.7 |
| 10 | Binh Phuoc | Southeast | 6878 | 65 | 0.9% | 979.6 | 22.0% | 1632.0 |
| 11 | Binh Thuan | South central coast | 7946 | 89 | 1.1% | 1239.2 | 78.2% | 1560.0 |
| 12 | Ca Mau | Mekong river delta | 5221 | 65 | 1.2% | 1229.6 | 22.7% | 1352.2 |
| 13 | Can Tho | Mekong river delta | 1439 | 82 | 5.7% | 540.4 | 67.3% | 1979.3 |
| 14 | Cao Bang | Northern midlands | 6701 | 56 | 0.8% | 1282.3 | 23.2% | 840.5 |
| 15 | Da Nang | South central coast | 1286 | 75 | 5.8% | 1080.7 | 87.8% | 2493.3 |
| 16 | Dak Lak | Central highlands | 13030 | 150 | 1.2% | 1919.2 | 24.7% | 1244.4 |
| 17 | Dak Nong | Central highlands | 6513 | 55 | 0.8% | 645.4 | 15.3% | 1372.1 |
| 18 | Dien Bien | Northern Mountains | 9542 | 50 | 0.5% | 3086.1 | 15.1% | 668.8 |
| 19 | Dong Nai | Southeast | 5863 | 177 | 3.0% | 1693.3 | 35.6% | 2400.0 |
| 20 | Dong Thap | Mekong river delta | 3383 | 146 | 4.3% | 576.7 | 17.8% | 1584.9 |
| 21 | Gia Lai | Central highlands | 15511 | 183 | 1.2% | 1458.5 | 30.9% | 1171.0 |
| 22 | Ha Giang | Northern midlands | 7929 | 71 | 0.9% | 846.5 | 15.1% | 781.1 |
| 23 | Ha Nam | Red river delta | 859 | 63 | 7.3% | 808.2 | 15.9% | 1633.8 |
| 24 | Ha Noi | Red river delta | 3360 | 407 | 12.1% | 7520.7 | 64.6% | 2741.4 |
| 25 | Ha Tinh | North central coast | 5990 | 121 | 2.0% | 1277.5 | 18.7% | 1287.8 |
| 26 | Hai Duong | Red river delta | 1666 | 167 | 10.0% | 1807.5 | 25.3% | 1672.3 |
| 27 | Hai Phong | Red river delta | 1561 | 145 | 9.3% | 2013.8 | 46.8% | 2316.7 |
| 28 | Hau Giang | Southeast | 1622 | 45 | 2.8% | 776.7 | 25.4% | 1606.6 |
| 29 | Ho Chi Minh City | Mekong river delta | 2062 | 282 | 13.7% | 8598.7 | 80.5% | 2797.1 |
| 30 | Hoa Binh | Northern Mountains | 4591 | 140 | 3.0% | 846.1 | 14.8% | 1039.2 |
| 31 | Hung Yen | Red river delta | 929 | 96 | 10.3% | 3558.2 | 13.0% | 1740.2 |
| 32 | Khanh Hoa | South central coast | 5139 | 67 | 1.3% | 1188.9 | 45.0% | 1564.5 |
| 33 | Kien Giang | Mekong river delta | 6348 | 137 | 2.2% | 1232.4 | 29.2% | 1711.2 |
| 34 | Kon Tum | Central highlands | 9675 | 84 | 0.9% | 1810.5 | 35.5% | 908.8 |
| 35 | Lai Chau | Northern Mountains | 9069 | 29 | 0.3% | 535.0 | 17.3% | 676.1 |
| 36 | Lam Dong | Central highlands | 9780 | 125 | 1.3% | 790.5 | 39.8% | 1648.8 |
| 37 | Lang Son | Northern midlands | 8310 | 81 | 1.0% | 1312.9 | 20.3% | 926.9 |
| 38 | Lao Cai | Northern Mountains | 6366 | 52 | 0.8% | 456.3 | 22.9% | 1052.4 |
| 39 | Long An | Mekong river delta | 4496 | 266 | 5.9% | 705.6 | 18.0% | 1908.7 |
| 40 | Nam Dinh | Red river delta | 1669 | 112 | 6.7% | 1503.1 | 18.7% | 1532.4 |
| 41 | Nghe An | North central coast | 16482 | 256 | 1.6% | 1854.4 | 15.1% | 1151.5 |
| 42 | Ninh Binh | Red river delta | 1385 | 68 | 4.9% | 3157.1 | 21.1% | 1191.4 |
| 43 | Ninh Thuan | South central coast | 3354 | 49 | 1.5% | 973.3 | 36.2% | 1710.8 |
| 44 | Phu Tho | Northern midlands | 3535 | 106 | 3.0% | 611.8 | 19.1% | 1309.6 |
| 45 | Phu Yen | South central coast | 5022 | 54 | 1.1% | 1404.2 | 29.1% | 1284.7 |
| 46 | Quang Binh | North central coast | 7999 | 63 | 0.8% | 909.5 | 63.9% | 1207.2 |
| 47 | Quang Nam | South central coast | 10574 | 204 | 1.9% | 887.6 | 19.8% | 1315.9 |
| 48 | Quang Ngai | South central coast | 5157 | 116 | 2.2% | 1501.1 | 30.3% | 1313.2 |
| 49 | Quang Ninh | Northern midlands | 6179 | 82 | 1.3% | 1272.8 | 24.3% | 2163.2 |
| 50 | Quang Tri | North central coast | 4623 | 43 | 0.9% | 1266.5 | 15.2% | 1151.5 |
| 51 | Soc Trang | Mekong river delta | 3314 | 57 | 1.7% | 630.6 | 30.6% | 1654.2 |
| 52 | Son La | Northern Mountains | 14124 | 86 | 0.6% | 1315.9 | 13.7% | 671.5 |
| 53 | Tay Ninh | Southeast | 4042 | 92 | 2.3% | 1242.7 | 22.6% | 1928.2 |
| 54 | Thai Binh | Red river delta | 1588 | 136 | 8.6% | 1133.4 | 10.5% | 1818.1 |
| 55 | Thai Nguyen | Northern midlands | 3526 | 123 | 3.5% | 1793.2 | 35.3% | 1606.2 |
| 56 | Thanh Hoa | North central coast | 11116 | 552 | 5.0% | 1268.3 | 17.3% | 1365.3 |
| 57 | Thua Thien Hue | North central coast | 4901 | 95 | 1.9% | 1163.6 | 48.9% | 1396.5 |
| 58 | Tien Giang | Mekong river delta | 2512 | 100 | 4.0% | 1762.3 | 15.5% | 1804.1 |
| 59 | Tra Vinh | Mekong river delta | 2356 | 49 | 2.1% | 1049.8 | 18.3% | 1299.2 |
| 60 | Tuyen Quang | Northern midlands | 5868 | 61 | 1.0% | 780.1 | 13.9% | 1024.3 |
| 61 | Vinh Long | Mekong river delta | 1524 | 60 | 3.9% | 1051.8 | 25.0% | 1398.8 |
| 62 | Vinh Phuc | Red river delta | 1237 | 79 | 6.4% | 1092.4 | 17.0% | 1675.0 |
| 63 | Yen Bai | Northern Mountains | 6887 | 54 | 0.8% | 815.6 | 20.7% | 1037.0 |
| ID | Province | Available Roof (km2) | LCOE Mono (Euro cents/ kWh) | LCOE Poly (Euro cents/ kWh) | Production Potentials Mono (TWh/a) | Production Potentials Poly (TWh/a) | Installable Potentials Mono (GWP) | Installable Potentials Poly (GWP) | Specific Potential Mono (GWh/ km2) | Specific Potential Poly (GWh/ km2) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | An Giang | 28.2 | 7.6 | 7.2 | 6.3 | 6 | 4.6 | 4.4 | 1.8 | 1.7 |
| 2 | Ba Ria-Vung Tau | 17.7 | 7.6 | 7.2 | 4 | 3.8 | 2.9 | 2.7 | 2 | 1.9 |
| 3 | Bac Giang | 18.8 | 9 | 8.5 | 3.1 | 2.9 | 3 | 2.8 | 0.8 | 0.8 |
| 4 | Bac Kan | 7.2 | 9.3 | 8.7 | 1.1 | 1.1 | 1.2 | 1.1 | 0.2 | 0.2 |
| 5 | Bac Lieu | 13.8 | 7.8 | 7.4 | 3 | 2.8 | 2.3 | 2.1 | 1.1 | 1.1 |
| 6 | Bac Ninh | 17.6 | 8.9 | 8.4 | 2.9 | 2.8 | 2.8 | 2.7 | 3.6 | 3.4 |
| 7 | Ben Tre | 23.5 | 7.7 | 7.2 | 5.3 | 5 | 3.9 | 3.6 | 2.2 | 2.1 |
| 8 | Binh Dinh | 23 | 7.7 | 7.3 | 5.1 | 4.8 | 3.8 | 3.6 | 0.8 | 0.8 |
| 9 | Binh Duong | 22.6 | 7.6 | 7.2 | 5.2 | 4.9 | 3.7 | 3.5 | 1.9 | 1.8 |
| 10 | Binh Phuoc | 27.5 | 7.5 | 7.1 | 6.4 | 6 | 4.5 | 4.2 | 0.9 | 0.9 |
| 11 | Binh Thuan | 19.1 | 7.3 | 6.9 | 4.6 | 4.4 | 3.1 | 2.9 | 0.6 | 0.6 |
| 12 | Ca Mau | 24.5 | 7.9 | 7.5 | 5.2 | 4.9 | 4 | 3.8 | 1 | 0.9 |
| 13 | Can Tho | 16.5 | 7.7 | 7.3 | 3.6 | 3.4 | 2.7 | 2.6 | 2.6 | 2.4 |
| 14 | Cao Bang | 11 | 9.2 | 8.7 | 1.7 | 1.6 | 1.7 | 1.7 | 0.3 | 0.2 |
| 15 | Da Nang | 13.7 | 8 | 7.6 | 2.8 | 2.7 | 2.2 | 2.1 | 2.2 | 2.1 |
| 16 | Dak Lak | 22.4 | 7.6 | 7.2 | 5.1 | 4.8 | 3.6 | 3.4 | 0.4 | 0.4 |
| 17 | Dak Nong | 7.5 | 7.5 | 7.1 | 1.7 | 1.6 | 1.2 | 1.1 | 0.3 | 0.2 |
| 18 | Dien Bien | 10.7 | 8.4 | 7.9 | 1.9 | 1.8 | 1.7 | 1.6 | 0.2 | 0.2 |
| 19 | Dong Nai | 43.8 | 7.6 | 7.2 | 9.9 | 9.4 | 7.1 | 6.8 | 1.7 | 1.6 |
| 20 | Dong Thap | 24.9 | 7.6 | 7.2 | 5.7 | 5.3 | 4.1 | 3.8 | 1.7 | 1.6 |
| 21 | Gia Lai | 19.3 | 7.6 | 7.2 | 4.3 | 4.1 | 3.1 | 2.9 | 0.3 | 0.3 |
| 22 | Ha Giang | 13.2 | 9.3 | 8.7 | 2 | 1.9 | 2.1 | 2 | 0.3 | 0.2 |
| 23 | Ha Nam | 13 | 8.9 | 8.4 | 2.2 | 2.1 | 2.1 | 2 | 2.5 | 2.4 |
| 24 | Ha Noi | 93.9 | 8.9 | 8.4 | 15.6 | 14.8 | 15.1 | 14.3 | 5 | 4.7 |
| 25 | Ha Tinh | 27.4 | 8.9 | 8.4 | 4.6 | 4.3 | 4.4 | 4.2 | 2.8 | 2.6 |
| 26 | Hai Duong | 24.7 | 8.9 | 8.3 | 4.2 | 3.9 | 4 | 3.8 | 2.7 | 2.6 |
| 27 | Hai Phong | 19.2 | 8.8 | 8.3 | 3.4 | 3.2 | 3.2 | 3 | 0.6 | 0.5 |
| 28 | Hau Giang | 11.9 | 7.9 | 7.4 | 2.5 | 2.4 | 2 | 1.8 | 1.6 | 1.5 |
| 29 | Ho Chi Minh City | 110 | 7.6 | 7.2 | 24.8 | 23.4 | 18 | 17 | 11.8 | 11.2 |
| 30 | Hoa Binh | 10 | 8.9 | 8.4 | 1.7 | 1.6 | 1.6 | 1.5 | 0.4 | 0.3 |
| 31 | Hung Yen | 16.6 | 8.9 | 8.4 | 2.8 | 2.6 | 2.7 | 2.5 | 3 | 2.9 |
| 32 | Khanh Hoa | 16.7 | 7.6 | 7.2 | 3.8 | 3.6 | 2.7 | 2.6 | 0.7 | 0.7 |
| 33 | Kien Giang | 31.7 | 7.8 | 7.4 | 6.8 | 6.5 | 5.2 | 4.9 | 1.1 | 1 |
| 34 | Kon Tum | 7.5 | 7.7 | 7.3 | 1.6 | 1.5 | 1.2 | 1.1 | 0.2 | 0.2 |
| 35 | Lai Chau | 9.5 | 8.6 | 8.1 | 1.6 | 1.6 | 1.5 | 1.4 | 0.2 | 0.2 |
| 36 | Lam Dong | 17.2 | 7.5 | 7.1 | 3.9 | 3.7 | 2.8 | 2.6 | 0.4 | 0.4 |
| 37 | Lang Son | 14.6 | 9.1 | 8.6 | 2.3 | 2.2 | 2.3 | 2.2 | 0.3 | 0.3 |
| 38 | Lao Cai | 10.8 | 9.2 | 8.7 | 1.7 | 1.6 | 1.7 | 1.6 | 0.3 | 0.3 |
| 39 | Long An | 29.6 | 7.6 | 7.2 | 6.8 | 6.4 | 4.8 | 4.6 | 1.5 | 1.4 |
| 40 | Nam Dinh | 27.1 | 8.8 | 8.3 | 4.7 | 4.4 | 4.4 | 4.1 | 2.8 | 2.7 |
| 41 | Nghe An | 45.4 | 8.6 | 8.1 | 8.1 | 7.7 | 7.4 | 7 | 0.5 | 0.5 |
| 42 | Ninh Binh | 16.3 | 8.9 | 8.3 | 2.8 | 2.6 | 2.6 | 2.5 | 2 | 1.9 |
| 43 | Ninh Thuan | 7.8 | 7.3 | 6.9 | 1.9 | 1.8 | 1.3 | 1.2 | 0.6 | 0.5 |
| 44 | Phu Tho | 17.9 | 9.1 | 8.6 | 2.9 | 2.7 | 2.9 | 2.7 | 0.8 | 0.8 |
| 45 | Phu Yen | 13.4 | 7.7 | 7.3 | 3 | 2.8 | 2.2 | 2.1 | 0.6 | 0.6 |
| 46 | Quang Binh | 17.1 | 8.7 | 8.2 | 3 | 2.9 | 2.8 | 2.7 | 0.4 | 0.4 |
| 47 | Quang Nam | 25.6 | 8 | 7.6 | 5.3 | 5 | 4.2 | 4 | 0.5 | 0.5 |
| 48 | Quang Ngai | 18.3 | 7.8 | 7.4 | 3.9 | 3.7 | 3 | 2.8 | 0.8 | 0.7 |
| 49 | Quang Ninh | 43.8 | 9.2 | 8.6 | 7 | 6.6 | 7 | 6.6 | 1.1 | 1.1 |
| 50 | Quang Tri | 10.3 | 8.4 | 7.9 | 1.9 | 1.8 | 1.7 | 1.6 | 0.4 | 0.4 |
| 51 | Soc Trang | 20.9 | 7.8 | 7.4 | 4.5 | 4.3 | 3.4 | 3.2 | 1.4 | 1.3 |
| 52 | Son La | 19.7 | 8.5 | 8 | 3.5 | 3.3 | 3.1 | 3 | 0.2 | 0.2 |
| 53 | Tay Ninh | 24.5 | 7.4 | 7.1 | 5.8 | 5.4 | 4 | 3.8 | 1.4 | 1.3 |
| 54 | Thai Binh | 26.9 | 8.9 | 8.3 | 4.6 | 4.3 | 4.3 | 4.1 | 3 | 2.8 |
| 55 | Thai Nguyen | 16.5 | 9.3 | 8.7 | 2.6 | 2.4 | 2.7 | 2.5 | 0.7 | 0.7 |
| 56 | Thanh Hoa | 42.8 | 8.7 | 8.2 | 7.5 | 7.1 | 6.9 | 6.6 | 0.7 | 0.6 |
| 57 | Thua Thien Hue | 16.5 | 8.3 | 7.8 | 3.2 | 3 | 2.7 | 2.5 | 0.6 | 0.6 |
| 58 | Tien Giang | 28.6 | 7.6 | 7.2 | 6.4 | 6.1 | 4.7 | 4.4 | 2.6 | 2.4 |
| 59 | Tra Vinh | 16.8 | 7.7 | 7.3 | 3.7 | 3.5 | 2.7 | 2.6 | 1.6 | 1.5 |
| 60 | Tuyen Quang | 11.7 | 9.3 | 8.7 | 1.8 | 1.7 | 1.9 | 1.8 | 0.3 | 0.3 |
| 61 | Vinh Long | 16.5 | 7.7 | 7.3 | 3.6 | 3.4 | 2.7 | 2.6 | 2.4 | 2.3 |
| 62 | Vinh Phuc | 18.9 | 9 | 8.5 | 3.1 | 2.9 | 3 | 2.9 | 2.2 | 2.1 |
| 63 | Yen Bai | 13.1 | 9.2 | 8.7 | 2.1 | 1.9 | 2.1 | 2 | 0.3 | 0.3 |
| ID | Province | Available Roof (km2) | LCOE Mono (Euro cents/kWh) | Production Potentials Mono (TWh/a) | Urban Rate 2018 (%) | gdp/a/Person 2018 (Euro/a) | Clustering Result | Priority |
|---|---|---|---|---|---|---|---|---|
| 1 | An Giang | 28.2 | 7.6 | 6.3 | 30.8% | 1612.1 | 1 | 5 |
| 2 | Ba Ria-Vung Tau | 17.7 | 7.6 | 4.0 | 52.4% | 2210.3 | 2 | 3 |
| 3 | Bac Giang | 18.8 | 9.0 | 3.1 | 11.5% | 1562.3 | 3 | 4 |
| 4 | Bac Kan | 7.2 | 9.3 | 1.1 | 18.8% | 880.8 | 4 | 6 |
| 5 | Bac Lieu | 13.8 | 7.8 | 3.0 | 29.1% | 1222.2 | 5 | 2 |
| 6 | Bac Ninh | 17.6 | 8.9 | 2.9 | 28.3% | 2466.1 | 3 | 4 |
| 7 | Ben Tre | 23.5 | 7.7 | 5.3 | 10.8% | 1543.7 | 5 | 2 |
| 8 | Binh Dinh | 23.0 | 7.7 | 5.1 | 31.0% | 1369.4 | 5 | 2 |
| 9 | Binh Duong | 22.6 | 7.6 | 5.2 | 39.4% | 3089.7 | 1 | 5 |
| 10 | Binh Phuoc | 27.5 | 7.5 | 6.4 | 22.0% | 1632.0 | 1 | 5 |
| 11 | Binh Thuan | 19.1 | 7.3 | 4.6 | 78.2% | 1560.0 | 2 | 3 |
| 12 | Ca Mau | 24.5 | 7.9 | 5.2 | 22.7% | 1352.2 | 5 | 2 |
| 13 | Can Tho | 16.5 | 7.7 | 3.6 | 67.3% | 1979.3 | 2 | 3 |
| 14 | Cao Bang | 11.0 | 9.2 | 1.7 | 23.2% | 840.5 | 4 | 6 |
| 15 | Da Nang | 13.7 | 8.0 | 2.8 | 87.8% | 2493.3 | 2 | 3 |
| 16 | Dak Lak | 22.4 | 7.6 | 5.1 | 24.7% | 1244.4 | 5 | 2 |
| 17 | Dak Nong | 7.5 | 7.5 | 1.7 | 15.3% | 1372.1 | 5 | 2 |
| 18 | Dien Bien | 10.7 | 8.4 | 1.9 | 15.1% | 668.8 | 4 | 6 |
| 19 | Dong Nai | 43.8 | 7.6 | 9.9 | 35.6% | 2400.0 | 1 | 5 |
| 20 | Dong Thap | 24.9 | 7.6 | 5.7 | 17.8% | 1584.9 | 1 | 5 |
| 21 | Gia Lai | 19.3 | 7.6 | 4.3 | 30.9% | 1171.0 | 5 | 2 |
| 22 | Ha Giang | 13.2 | 9.3 | 2.0 | 15.1% | 781.1 | 4 | 6 |
| 23 | Ha Nam | 13.0 | 8.9 | 2.2 | 15.9% | 1633.8 | 3 | 4 |
| 24 | Ha Noi | 93.9 | 8.9 | 15.6 | 64.6% | 2741.4 | 6 | 1 |
| 25 | Ha Tinh | 27.4 | 8.9 | 4.6 | 18.7% | 1287.8 | 3 | 4 |
| 26 | Hai Duong | 24.7 | 8.9 | 4.2 | 25.3% | 1672.3 | 3 | 4 |
| 27 | Hai Phong | 19.2 | 8.8 | 3.4 | 46.8% | 2316.7 | 2 | 3 |
| 28 | Hau Giang | 11.9 | 7.9 | 2.5 | 25.4% | 1606.6 | 5 | 2 |
| 29 | Ho Chi Minh City | 110.0 | 7.6 | 24.8 | 80.5% | 2797.1 | 6 | 1 |
| 30 | Hoa Binh | 10.0 | 8.9 | 1.7 | 14.8% | 1039.2 | 4 | 6 |
| 31 | Hung Yen | 16.6 | 8.9 | 2.8 | 13.0% | 1740.2 | 3 | 4 |
| 32 | Khanh Hoa | 16.7 | 7.6 | 3.8 | 45.0% | 1564.5 | 5 | 2 |
| 33 | Kien Giang | 31.7 | 7.8 | 6.8 | 29.2% | 1711.2 | 1 | 5 |
| 34 | Kon Tum | 7.5 | 7.7 | 1.6 | 35.5% | 908.8 | 5 | 2 |
| 35 | Lai Chau | 9.5 | 8.6 | 1.6 | 17.3% | 676.1 | 4 | 6 |
| 36 | Lam Dong | 17.2 | 7.5 | 3.9 | 39.8% | 1648.8 | 5 | 2 |
| 37 | Lang Son | 14.6 | 9.1 | 2.3 | 20.3% | 926.9 | 4 | 6 |
| 38 | Lao Cai | 10.8 | 9.2 | 1.7 | 22.9% | 1052.4 | 4 | 6 |
| 39 | Long An | 29.6 | 7.6 | 6.8 | 18.0% | 1908.7 | 1 | 5 |
| 40 | Nam Dinh | 27.1 | 8.8 | 4.7 | 18.7% | 1532.4 | 3 | 4 |
| 41 | Nghe An | 45.4 | 8.6 | 8.1 | 15.1% | 1151.5 | 3 | 4 |
| 42 | Ninh Binh | 16.3 | 8.9 | 2.8 | 21.1% | 1191.4 | 4 | 6 |
| 43 | Ninh Thuan | 7.8 | 7.3 | 1.9 | 36.2% | 1710.8 | 5 | 2 |
| 44 | Phu Tho | 17.9 | 9.1 | 2.9 | 19.1% | 1309.6 | 4 | 6 |
| 45 | Phu Yen | 13.4 | 7.7 | 3.0 | 29.1% | 1284.7 | 5 | 2 |
| 46 | Quang Binh | 17.1 | 8.7 | 3.0 | 63.9% | 1207.2 | 2 | 3 |
| 47 | Quang Nam | 25.6 | 8.0 | 5.3 | 19.8% | 1315.9 | 5 | 2 |
| 48 | Quang Ngai | 18.3 | 7.8 | 3.9 | 30.3% | 1313.2 | 5 | 2 |
| 49 | Quang Ninh | 43.8 | 9.2 | 7.0 | 24.3% | 2163.2 | 3 | 4 |
| 50 | Quang Tri | 10.3 | 8.4 | 1.9 | 15.2% | 1151.5 | 4 | 6 |
| 51 | Soc Trang | 20.9 | 7.8 | 4.5 | 30.6% | 1654.2 | 5 | 2 |
| 52 | Son La | 19.7 | 8.5 | 3.5 | 13.7% | 671.5 | 4 | 6 |
| 53 | Tay Ninh | 24.5 | 7.4 | 5.8 | 22.6% | 1928.2 | 1 | 5 |
| 54 | Thai Binh | 26.9 | 8.9 | 4.6 | 10.5% | 1818.1 | 3 | 4 |
| 55 | Thai Nguyen | 16.5 | 9.3 | 2.6 | 35.3% | 1606.2 | 3 | 4 |
| 56 | Thanh Hoa | 42.8 | 8.7 | 7.5 | 17.3% | 1365.3 | 3 | 4 |
| 57 | Thua Thien Hue | 16.5 | 8.3 | 3.2 | 48.9% | 1396.5 | 2 | 3 |
| 58 | Tien Giang | 28.6 | 7.6 | 6.4 | 15.5% | 1804.1 | 1 | 5 |
| 59 | Tra Vinh | 16.8 | 7.7 | 3.7 | 18.3% | 1299.2 | 5 | 2 |
| 60 | Tuyen Quang | 11.7 | 9.3 | 1.8 | 13.9% | 1024.3 | 4 | 6 |
| 61 | Vinh Long | 16.5 | 7.7 | 3.6 | 25.0% | 1398.8 | 5 | 2 |
| 62 | Vinh Phuc | 18.9 | 9.0 | 3.1 | 17.0% | 1675.0 | 3 | 4 |
| 63 | Yen Bai | 13.1 | 9.2 | 2.1 | 20.7% | 1037.0 | 4 | 6 |
| ID | Province | FIT_2.0 (Euro cents/kWh) | Delta_1_1.0 (Euro cents/kWh) | Delta_1_2.0 (Euro cents/kWh) | Delta_1_2.1 (Euro cents/kWh) | Benefit_1.0 (10^6 Euro) | Benefit_2.0 (10^6 Euro) | Benefit_2.1 (10^6 Euro) |
|---|---|---|---|---|---|---|---|---|
| 1 | An Giang | 7.95 | 1.23 | 0.35 | 0.31 | 77.49 | 22.25 | 19.53 |
| 2 | Ba Ria-Vung Tau | 7.95 | 1.23 | 0.35 | 0.31 | 49.20 | 14.13 | 12.40 |
| 3 | Bac Giang | 10.32 | −0.17 | 1.32 | −1.09 | −5.27 | 40.90 | −33.79 |
| 4 | Bac Kan | 10.32 | −0.47 | 1.02 | −1.39 | −5.17 | 11.21 | −15.29 |
| 5 | Bac Lieu | 7.95 | 1.03 | 0.15 | 0.11 | 30.90 | 4.60 | 3.30 |
| 6 | Bac Ninh | 10.32 | −0.07 | 1.42 | −0.99 | −2.03 | 41.16 | −28.71 |
| 7 | Ben Tre | 7.95 | 1.13 | 0.25 | 0.21 | 59.89 | 13.42 | 11.13 |
| 8 | Binh Dinh | 7.95 | 1.13 | 0.25 | 0.21 | 57.63 | 12.91 | 10.71 |
| 9 | Binh Duong | 7.95 | 1.23 | 0.35 | 0.31 | 63.96 | 18.37 | 16.12 |
| 10 | Binh Phuoc | 7.95 | 1.33 | 0.45 | 0.41 | 85.12 | 29.01 | 26.24 |
| 11 | Binh Thuan | 7.48 | 1.53 | 0.18 | 0.61 | 70.38 | 8.47 | 28.06 |
| 12 | Ca Mau | 7.95 | 0.93 | 0.05 | 0.01 | 48.36 | 2.77 | 0.52 |
| 13 | Can Tho | 7.95 | 1.13 | 0.25 | 0.21 | 40.68 | 9.12 | 7.56 |
| 14 | Cao Bang | 10.32 | −0.37 | 1.12 | −1.29 | −6.29 | 19.03 | −21.93 |
| 15 | Da Nang | 8.88 | 0.83 | 0.88 | −0.09 | 23.24 | 24.61 | −2.52 |
| 16 | Dak Lak | 7.48 | 1.23 | −0.12 | 0.31 | 62.73 | −5.91 | 15.81 |
| 17 | Dak Nong | 7.95 | 1.33 | 0.45 | 0.41 | 22.61 | 7.70 | 6.97 |
| 18 | Dien Bien | 8.88 | 0.43 | 0.48 | −0.49 | 8.17 | 9.10 | −9.31 |
| 19 | Dong Nai | 7.95 | 1.23 | 0.35 | 0.31 | 121.77 | 34.97 | 30.69 |
| 20 | Dong Thap | 7.95 | 1.23 | 0.35 | 0.31 | 70.11 | 20.13 | 17.67 |
| 21 | Gia Lai | 7.48 | 1.23 | −0.12 | 0.31 | 52.89 | −4.98 | 13.33 |
| 22 | Ha Giang | 10.32 | −0.47 | 1.02 | −1.39 | −9.40 | 20.38 | −27.80 |
| 23 | Ha Nam | 10.32 | −0.07 | 1.42 | −0.99 | −1.54 | 31.22 | −21.78 |
| 24 | Ha Noi | 10.32 | −0.07 | 1.42 | −0.99 | −10.92 | 221.40 | −154.44 |
| 25 | Ha Tinh | 10.32 | −0.07 | 1.42 | −0.99 | −3.22 | 65.29 | −45.54 |
| 26 | Hai Duong | 10.32 | −0.07 | 1.42 | −0.99 | −2.94 | 59.61 | −41.58 |
| 27 | Hai Phong | 10.32 | 0.03 | 1.52 | −0.89 | 1.02 | 51.65 | −30.26 |
| 28 | Hau Giang | 7.95 | 0.93 | 0.05 | 0.01 | 23.25 | 1.33 | 0.25 |
| 29 | Ho Chi Minh City | 7.95 | 1.23 | 0.35 | 0.31 | 305.04 | 87.60 | 76.88 |
| 30 | Hoa Binh | 10.32 | −0.07 | 1.42 | −0.99 | −1.19 | 24.13 | −16.83 |
| 31 | Hung Yen | 10.32 | −0.07 | 1.42 | −0.99 | −1.96 | 39.74 | −27.72 |
| 32 | Khanh Hoa | 7.48 | 1.23 | −0.12 | 0.31 | 46.74 | −4.40 | 11.78 |
| 33 | Kien Giang | 7.95 | 1.03 | 0.15 | 0.11 | 70.04 | 10.42 | 7.48 |
| 34 | Kon Tum | 7.95 | 1.13 | 0.25 | 0.21 | 18.08 | 4.05 | 3.36 |
| 35 | Lai Chau | 10.32 | 0.23 | 1.72 | −0.69 | 3.68 | 27.51 | −11.04 |
| 36 | Lam Dong | 7.95 | 1.33 | 0.45 | 0.41 | 51.87 | 17.68 | 15.99 |
| 37 | Lang Son | 10.32 | −0.27 | 1.22 | −1.19 | −6.21 | 28.04 | −27.37 |
| 38 | Lao Cai | 10.32 | −0.37 | 1.12 | −1.29 | −6.29 | 19.03 | −21.93 |
| 39 | Long An | 7.95 | 1.23 | 0.35 | 0.31 | 83.64 | 24.02 | 21.08 |
| 40 | Nam Dinh | 10.32 | 0.03 | 1.52 | −0.89 | 1.41 | 71.40 | −41.83 |
| 41 | Nghe An | 10.32 | 0.23 | 1.72 | −0.69 | 18.63 | 139.26 | −55.89 |
| 42 | Ninh Binh | 10.32 | −0.07 | 1.42 | −0.99 | −1.96 | 39.74 | −27.72 |
| 43 | Ninh Thuan | 7.48 | 1.53 | 0.18 | 0.61 | 29.07 | 3.50 | 11.59 |
| 44 | Phu Tho | 10.32 | −0.27 | 1.22 | −1.19 | −7.83 | 35.36 | −34.51 |
| 45 | Phu Yen | 7.48 | 1.13 | −0.22 | 0.21 | 33.90 | −6.48 | 6.30 |
| 46 | Quang Binh | 10.32 | 0.13 | 1.62 | −0.79 | 3.90 | 48.58 | −23.70 |
| 47 | Quang Nam | 8.88 | 0.83 | 0.88 | −0.09 | 43.99 | 46.58 | −4.77 |
| 48 | Quang Ngai | 8.88 | 1.03 | 1.08 | 0.11 | 40.17 | 42.08 | 4.29 |
| 49 | Quang Ninh | 10.32 | −0.37 | 1.12 | −1.29 | −25.90 | 78.35 | −90.30 |
| 50 | Quang Tri | 8.88 | 0.43 | 0.48 | −0.49 | 8.17 | 9.10 | −9.31 |
| 51 | Soc Trang | 7.95 | 1.03 | 0.15 | 0.11 | 46.35 | 6.89 | 4.95 |
| 52 | Son La | 10.32 | 0.33 | 1.82 | −0.59 | 11.55 | 63.67 | −20.65 |
| 53 | Tay Ninh | 7.95 | 1.43 | 0.55 | 0.51 | 82.94 | 32.09 | 29.58 |
| 54 | Thai Binh | 10.32 | −0.07 | 1.42 | −0.99 | −3.22 | 65.29 | −45.54 |
| 55 | Thai Nguyen | 10.32 | −0.47 | 1.02 | −1.39 | −12.22 | 26.50 | −36.14 |
| 56 | Thanh Hoa | 10.32 | 0.13 | 1.62 | −0.79 | 9.75 | 121.44 | −59.25 |
| 57 | Thua Thien Hue | 8.88 | 0.53 | 0.58 | −0.39 | 16.96 | 18.52 | −12.48 |
| 58 | Tien Giang | 7.95 | 1.23 | 0.35 | 0.31 | 78.72 | 22.61 | 19.84 |
| 59 | Tra Vinh | 7.95 | 1.13 | 0.25 | 0.21 | 41.81 | 9.37 | 7.77 |
| 60 | Tuyen Quang | 10.32 | −0.47 | 1.02 | −1.39 | −8.46 | 18.35 | −25.02 |
| 61 | Vinh Long | 7.95 | 1.13 | 0.25 | 0.21 | 40.68 | 9.12 | 7.56 |
| 62 | Vinh Phuc | 10.32 | −0.17 | 1.32 | −1.09 | −5.27 | 40.90 | −33.79 |
| 63 | Yen Bai | 10.32 | −0.37 | 1.12 | −1.29 | −7.77 | 23.50 | −27.09 |
| ID | Province | Delta_2_2019 (Euro cents/kWh) | Delta_2_2025 (Euro cents/kWh) | Benefit_2019 (10^6 Euro) | Benefit_2025 (10^6 Euro) |
|---|---|---|---|---|---|
| 1 | An Giang | −0.40 | 1.10 | −25.20 | 69.30 |
| 2 | Ba Ria−Vung Tau | −0.40 | 1.10 | −16.00 | 44.00 |
| 3 | Bac Giang | −1.80 | −0.30 | −55.80 | −9.30 |
| 4 | Bac Kan | −2.10 | −0.60 | −23.10 | −6.60 |
| 5 | Bac Lieu | −0.60 | 0.90 | −18.00 | 27.00 |
| 6 | Bac Ninh | −1.70 | −0.20 | −49.30 | −5.80 |
| 7 | Ben Tre | −0.50 | 1.00 | −26.50 | 53.00 |
| 8 | Binh Dinh | −0.50 | 1.00 | −25.50 | 51.00 |
| 9 | Binh Duong | −0.40 | 1.10 | −20.80 | 57.20 |
| 10 | Binh Phuoc | −0.30 | 1.20 | −19.20 | 76.80 |
| 11 | Binh Thuan | −0.10 | 1.40 | −4.60 | 64.40 |
| 12 | Ca Mau | −0.70 | 0.80 | −36.40 | 41.60 |
| 13 | Can Tho | −0.50 | 1.00 | −18.00 | 36.00 |
| 14 | Cao Bang | −2.00 | −0.50 | −34.00 | −8.50 |
| 15 | Da Nang | −0.80 | 0.70 | −22.40 | 19.60 |
| 16 | Dak Lak | −0.40 | 1.10 | −20.40 | 56.10 |
| 17 | Dak Nong | −0.30 | 1.20 | −5.10 | 20.40 |
| 18 | Dien Bien | −1.20 | 0.30 | −22.80 | 5.70 |
| 19 | Dong Nai | −0.40 | 1.10 | −39.60 | 108.90 |
| 20 | Dong Thap | −0.40 | 1.10 | −22.80 | 62.70 |
| 21 | Gia Lai | −0.40 | 1.10 | −17.20 | 47.30 |
| 22 | Ha Giang | −2.10 | −0.60 | −42.00 | −12.00 |
| 23 | Ha Nam | −1.70 | −0.20 | −37.40 | −4.40 |
| 24 | Ha Noi | -1.70 | -0.20 | -265.20 | -31.20 |
| 25 | Ha Tinh | -1.70 | -0.20 | -78.20 | -9.20 |
| 26 | Hai Duong | -1.70 | -0.20 | -71.40 | -8.40 |
| 27 | Hai Phong | -1.60 | -0.10 | -54.40 | -3.40 |
| 28 | Hau Giang | -0.70 | 0.80 | -17.50 | 20.00 |
| 29 | Ho Chi Minh City | -0.40 | 1.10 | -99.20 | 272.80 |
| 30 | Hoa Binh | -1.70 | -0.20 | -28.90 | -3.40 |
| 31 | Hung Yen | -1.70 | -0.20 | -47.60 | -5.60 |
| 32 | Khanh Hoa | −0.40 | 1.10 | −15.20 | 41.80 |
| 33 | Kien Giang | −0.60 | 0.90 | −40.80 | 61.20 |
| 34 | Kon Tum | −0.50 | 1.00 | −8.00 | 16.00 |
| 35 | Lai Chau | −1.40 | 0.10 | −22.40 | 1.60 |
| 36 | Lam Dong | −0.30 | 1.20 | −11.70 | 46.80 |
| 37 | Lang Son | −1.90 | −0.40 | −43.70 | −9.20 |
| 38 | Lao Cai | −2.00 | −0.50 | −34.00 | −8.50 |
| 39 | Long An | −0.40 | 1.10 | −27.20 | 74.80 |
| 40 | Nam Dinh | −1.60 | −0.10 | −75.20 | −4.70 |
| 41 | Nghe An | −1.40 | 0.10 | −113.40 | 8.10 |
| 42 | Ninh Binh | −1.70 | −0.20 | −47.60 | −5.60 |
| 43 | Ninh Thuan | −0.10 | 1.40 | −1.90 | 26.60 |
| 44 | Phu Tho | −1.90 | −0.40 | −55.10 | −11.60 |
| 45 | Phu Yen | −0.50 | 1.00 | −15.00 | 30.00 |
| 46 | Quang Binh | −1.50 | 0.00 | −45.00 | 0.00 |
| 47 | Quang Nam | −0.80 | 0.70 | −42.40 | 37.10 |
| 48 | Quang Ngai | −0.60 | 0.90 | −23.40 | 35.10 |
| 49 | Quang Ninh | −2.00 | −0.50 | −140.00 | −35.00 |
| 50 | Quang Tri | −1.20 | 0.30 | −22.80 | 5.70 |
| 51 | Soc Trang | −0.60 | 0.90 | −27.00 | 40.50 |
| 52 | Son La | −1.30 | 0.20 | −45.50 | 7.00 |
| 53 | Tay Ninh | −0.20 | 1.30 | −11.60 | 75.40 |
| 54 | Thai Binh | −1.70 | −0.20 | −78.20 | −9.20 |
| 55 | Thai Nguyen | −2.10 | −0.60 | −54.60 | −15.60 |
| 56 | Thanh Hoa | −1.50 | 0.00 | −112.50 | 0.00 |
| 57 | Thua Thien Hue | −1.10 | 0.40 | −35.20 | 12.80 |
| 58 | Tien Giang | −0.40 | 1.10 | −25.60 | 70.40 |
| 59 | Tra Vinh | −0.50 | 1.00 | −18.50 | 37.00 |
| 60 | Tuyen Quang | −2.10 | −0.60 | −37.80 | −10.80 |
| 61 | Vinh Long | −0.50 | 1.00 | −18.00 | 36.00 |
| 62 | Vinh Phuc | −1.80 | −0.30 | −55.80 | −9.30 |
| 63 | Yen Bai | −2.00 | −0.50 | −42.00 | −10.50 |
References
- REN21. Renewables 2019—Global Status Report; 2019; ISBN 978-3-9818911-7-1. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2019_full_report_en.pdf (accessed on 31 January 2020).
- Khuong, M.P.; McKenna, R.; Fichtner, W. Multi-level decomposition of ASEAN urbanization effects on energy. Int. J. Energy Sect. Manag. 2019, 13, 1107–1132. [Google Scholar] [CrossRef]
- Moorthy, K.; Patwa, N.; Gupta, Y. Breaking barriers in deployment of renewable energy. Heliyon 2019, 5, e01166. [Google Scholar] [CrossRef]
- IRENA; OECD/IEA; REN21. Renewable Energy Policies in a Time of Transition; 2018; ISBN 978-92-9260-061-7. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2018/Apr/IRENA_IEA_REN21_Policies_2018.pdf (accessed on 31 January 2020).
- Hong, T.; Lee, M.; Koo, C.; Jeong, K.; Kim, J. Development of a method for estimating the rooftop solar photovoltaic (PV) potential by analyzing the available rooftop area using Hillshade analysis. Appl. Energy 2017, 194, 320–332. [Google Scholar] [CrossRef]
- Hofierka, J.; Kaňuk, J. Assessment of photovoltaic potential in urban areas using open-source solar radiation tools. Renew. Energy 2009, 34, 2206–2214. [Google Scholar] [CrossRef]
- Mansouri Kouhestani, F.; Byrne, J.; Johnson, D.; Spencer, L.; Hazendonk, P.; Brown, B. Evaluating solar energy technical and economic potential on rooftops in an urban setting: The city of Lethbridge, Canada. Int. J. Energy Environ. Eng. 2019, 10, 13–32. [Google Scholar] [CrossRef]
- Singh, R.; Banerjee, R. Estimation of rooftop solar photovoltaic potential of a city. Sol. Energy 2015, 115, 589–602. [Google Scholar] [CrossRef]
- Yan, J.; Yang, Y.; Elia Campana, P.; He, J. City-level analysis of subsidy-free solar photovoltaic electricity price, profits and grid parity in China. Nat. Energy 2019, 4, 709–717. [Google Scholar] [CrossRef]
- Sweerts, B.; Pfenninger, S.; Yang, S.; Folini, D.; van der Zwaan, B.; Wild, M. Estimation of losses in solar energy production from air pollution in China since 1960 using surface radiation data. Nat. Energy 2019, 4, 657–663. [Google Scholar] [CrossRef]
- Kappagantu, R.; Daniel, S.A. Challenges and issues of smart grid implementation: A case of Indian scenario. J. Electr. Syst. Inf. Technol. 2018, 5, 453–467. [Google Scholar] [CrossRef]
- Chaianong, A.; Bangviwat, A.; Menke, C.; Darghouth, N.R. Cost–Benefit Analysis of Rooftop PV Systems on Utilities and Ratepayers in Thailand. Energies 2019, 12, 2265. [Google Scholar] [CrossRef]
- Choi, Y.; Suh, J.; Kim, S.-M. GIS-Based Solar Radiation Mapping, Site Evaluation, and Potential Assessment: A Review. Appl. Sci. 2019, 9, 1960. [Google Scholar] [CrossRef]
- Hong, T.; Koo, C.; Park, J.; Park, H.S. A GIS (geographic information system)-based optimization model for estimating the electricity generation of the rooftop PV (photovoltaic) system. Energy 2014, 65, 190–199. [Google Scholar] [CrossRef]
- Jamal, T.; Ongsakul, W.; Singh, J.G.; Salehin, S.; Ferdous, S.M. Potential rooftop distribution mapping using Geographic Information Systems (GIS) for Solar PV Installation: A case study for Dhaka, Bangladesh. In Proceedings of the 2014 3rd International Conference on the Developments in Renewable Energy Technology (ICDRET), Dhaka, Bangladesh, 29–31 May 2014; pp. 1–6, ISBN 978−9843−3−7867−5. [Google Scholar]
- Margolis, R.; Gagnon, P.; Melius, J.; Phillips, C.; Elmore, R. Using GIS-based methods and lidar data to estimate rooftop solar technical potential in US cities. Environ. Res. Lett. 2017, 12, 74013. [Google Scholar] [CrossRef]
- Polo, J.; Bernardos, A.; Navarro, A.A.; Fernandez-Peruchena, C.M.; Ramírez, L.; Guisado, M.V.; Martínez, S. Solar resources and power potential mapping in Vietnam using satellite-derived and GIS-based information. Energy Convers. Manag. 2015, 98, 348–358. [Google Scholar] [CrossRef]
- Calcabrini, A.; Ziar, H.; Isabella, O.; Zeman, M. A simplified skyline-based method for estimating the annual solar energy potential in urban environments. Nat. Energy 2019, 4, 206–215. [Google Scholar] [CrossRef]
- Desthieux, G.; Carneiro, C.; Camponovo, R.; Ineichen, P.; Morello, E.; Boulmier, A.; Abdennadher, N.; Dervey, S.; Ellert, C. Solar Energy Potential Assessment on Rooftops and Facades in Large Built Environments Based on LiDAR Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 2018, 4, 2811. [Google Scholar] [CrossRef]
- Redweik, P.; Catita, C.; Brito, M. Solar energy potential on roofs and facades in an urban landscape. Sol. Energy 2013, 97, 332–341. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Pearce, J.M. Automated quantification of solar photovoltaic potential in cities. Int. Rev. Spat. Plan. Sustain. Dev. 2013, 1, 49–60. [Google Scholar] [CrossRef]
- Kodysh, J.B.; Omitaomu, O.A.; Bhaduri, B.L.; Neish, B.S. Methodology for estimating solar potential on multiple building rooftops for photovoltaic systems. Sustain. Cities Soc. 2013, 8, 31–41. [Google Scholar] [CrossRef]
- Lukač, N.; Seme, S.; Žlaus, D.; Štumberger, G.; Žalik, B. Buildings roofs photovoltaic potential assessment based on LiDAR (Light Detection And Ranging) data. Energy 2014, 66, 598–609. [Google Scholar] [CrossRef]
- Castellanos, S.; Sunter, D.A.; Kammen, D.M. Rooftop solar photovoltaic potential in cities: How scalable are assessment approaches? Environ. Res. Lett. 2017, 12, 125005. [Google Scholar] [CrossRef]
- Mainzer, K.; Fath, K.; McKenna, R.; Stengel, J.; Fichtner, W.; Schultmann, F. A high-resolution determination of the technical potential for residential-roof-mounted photovoltaic systems in Germany. Sol. Energy 2014, 105, 715–731. [Google Scholar] [CrossRef]
- Byrne, J.; Taminiau, J.; Kurdgelashvili, L.; Kim, K.N. A review of the solar city concept and methods to assess rooftop solar electric potential, with an illustrative application to the city of Seoul. Renew. Sustain. Energy Rev. 2015, 41, 830–844. [Google Scholar] [CrossRef]
- Bódis, K.; Kougias, I.; Jäger-Waldau, A.; Taylor, N.; Szabó, S. A high-resolution geospatial assessment of the rooftop solar photovoltaic potential in the European Union. Renew. Sustain. Energy Rev. 2019, 114, 109309. [Google Scholar] [CrossRef]
- Defaix, P.R.; van Sark, W.G.J.H.M.; Worrell, E.; de Visser, E. Technical potential for photovoltaics on buildings in the EU-27. Sol. Energy 2012, 86, 2644–2653. [Google Scholar] [CrossRef]
- Kabir, M.H.; Endlicher, W.; Jägermeyr, J. Calculation of bright roof-tops for solar PV applications in Dhaka Megacity, Bangladesh. Renew. Energy 2010, 35, 1760–1764. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. Rooftop Solar Photovoltaic Technical Potential in the United States: A Detailed Assessment. In U.S. Department of Energy; 2016. Available online: https://www.nrel.gov/docs/fy16osti/65298.pdf (accessed on 31 January 2020).
- Mainzer, K.; Killinger, S.; McKenna, R.; Fichtner, W. Assessment of rooftop photovoltaic potentials at the urban level using publicly available geodata and image recognition techniques. Sol. Energy 2017, 155, 561–573. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Tran, Q.-B.; Tran, D.-Q.; Reiter, S. An investigation on climate responsive design strategies of vernacular housing in Vietnam. Build. Environ. 2011, 46, 2088–2106. [Google Scholar] [CrossRef]
- Rosaclot, M.; Tina, G.M. Submerged and Floating Photovoltaic Systems. Modelling, Design and Case Studies; Academic Press: London, UK, 2018; ISBN 9780128121498. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley: Hoboken, NJ, USA, 2013; ISBN 9780470873663. [Google Scholar]
- World Bank Group. Solar Resource Mapping in Vietnam. Implementation Plan. 2017. Available online: http://documents.worldbank.org/curated/en/134421495707128537/Solar-resource-mapping-in-Vietnam-implementation-plan-selection-1231900 (accessed on 31 January 2020).
- Ciulla, G.; Lo Brano, V.; Moreci, E. Forecasting the Cell Temperature of PV Modules with an Adaptive System. Int. J. Photoenergy 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Neises, T.W.; Klein, S.A.; Reindl, D.T. Development of a Thermal Model for Photovoltaic Modules and Analysis of NOCT Guidelines. J. Sol. Energy Eng. 2012, 134. [Google Scholar] [CrossRef]
- Reinders, A.; Verlinden, P.; van Sark, W.; Freundlich, A. Photovoltaic Solar Energy. From Fundamentals to Applications; Reinders, A., Verlinden, P., van Sark, W., Freundlich, A., Eds.; John Wiley & Sons Ltd.: Chichester, West Sussex, UK; Hoboken, NJ, USA, 2017; ISBN 1118927486. [Google Scholar]
- Singh, P.; Ravindra, N.M. Temperature dependence of solar cell performance—An analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- World Bank Climate Change Knowledge Portal. Available online: https://climateknowledgeportal.worldbank.org/download-data (accessed on 9 May 2020).
- Jordan, D.C.; Kurtz, S.R. Photovoltaic Degradation Rates-an Analytical Review. Prog. Photovolt. Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- Konstantin, P. Praxisbuch Energiewirtschaft. Energieumwandlung, -Transport und -Beschaffung, Übertragungsnetzausbau und Kernenergieausstieg, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783662498224. [Google Scholar]
- Vietnam Electricity. EVN Annual Report 2018. 2019. Available online: https://www.evn.com.vn/userfile/User/tcdl/files/2019/8/EVNAnnualReport2018(1).pdf (accessed on 31 January 2020).
- Wiginton, L.K.; Nguyen, H.T.; Pearce, J.M. Quantifying rooftop solar photovoltaic potential for regional renewable energy policy. Comput. Env. Urban Syst. 2010, 34, 345–357. [Google Scholar] [CrossRef]
- Heckert Solar. Datenblatt NeMoM 60 2.0 Monokristallines PV-Modul dunkelblau. Available online: https://www.rw-energy.com/fileadmin/rwenergy/bilder/Downloads/Module/Heckert/NeMo_2.0_60_M_270-290_Watt.pdf (accessed on 22 April 2020).
- Heckert Solar NeMo 60P, 260W polykristallines Solarmodul. Available online: https://www.oeko-energie.de/shop1/de/Heckert-Solar-NeMo-60P--260W-polykristallines-Solarmodul-1429.html (accessed on 22 April 2020).
- General Statistics Office of Vietnam. General Statistics Office of Vietnam. Available online: https://www.gso.gov.vn/default_en.aspx?tabid=773 (accessed on 31 January 2020).
- Solar, V.P. [Bảng Giá 2019] So Sánh Tấm Pin Năng Lượng Mặt Trời Cao Cấp ở Việt Nam. Available online: https://vuphong.vn/danh-muc/tam-pin-nang-luong-mat-troi/ (accessed on 31 January 2020).
- Polo Martinez, J. Maps of Solar Resource and Potential in Vietnam; Ministry of Industry and Trade of Vietnam (MoiT): Hanoi, Vietnam, 2015.
- EVNHCMC. 3.923 Khách Hàng Lắp Điện Mặt Trời Trên Mái Nhà. Available online: http://www.tietkiemnangluong.vn/d6/news/EVNHCMC-3923-khach-hang-lap-dien-mat-troi-tren-mai-nha-111-135-12512.aspx (accessed on 9 March 2020).
- Vietnam Electricity. Regulations. Available online: https://en.evn.com.vn/c3/gioi-thieu-l/Regulations-2-10.aspx (accessed on 31 January 2020).
- Effigis Geo-Solutions. Assessment of Rooftop Photovoltaic Solar Energy Potential in Vietnam. 2018. Available online: https://effigis.com/en/case-studies/assessment-rooftop-photovoltaic-solar-energy-potential-vietnam/ (accessed on 9 March 2020).
- He, K.; Tang, R.; Jin, M. Pareto fronts of machining parameters for trade-off among energy consumption, cutting force and processing time. Int. J. Prod. Econ. 2017, 185, 113–127. [Google Scholar] [CrossRef]
- Kramp, K.H.; van Det, M.J.; Veeger, N.J.G.M.; Pierie, J.-P.E.N. The Pareto Analysis for Establishing Content Criteria in Surgical Training. J. Surg. Educ. 2016, 73, 892–901. [Google Scholar] [CrossRef] [PubMed]
- Spencer, T.; Mathur, A. Thomas Spencer and Ajay Mathur. Energy Transition in Emerging and Developing Countries: Promoting the New Paradigm. In Proceedings of the G20 2019 Japan, Osaka Summit, Osaka, Japan, 28–29 June 2019. [Google Scholar]
- Ministry of Industry and Trade of Vietnam. Legal Documents. Available online: https://moit.gov.vn/van-ban-phap-luat (accessed on 14 March 2020).
- Khuong, P. (Ed.) Boosting Residential Rooftop Solar by Using Financial Incentives—A Comparison Analysis. A Case Study in Vietnam. In Proceedings of the 4th AIEE Symposium on Current and Future Challenges to Energy Security, Rome, Italy, 10–12 December 2019. [Google Scholar]
- Nguyen, T.C.; Chuc, A.T.; Dang, L.N. Green Finance in Vietnam: Barriers and Solutions. ADBI Working Paper Series. 2018. Available online: https://www.adb.org/sites/default/files/publication/466171/adbi-wp886.pdf (accessed on 31 January 2020).
- Garg, V.; Bridle, R.; Clarke, K. Energy Pricing, Energy Supply and FDI Competitiveness in Viet Nam. An Assessment of Foreign Investor Sentiment. 2015. Available online: https://www.iisd.org/gsi/sites/default/files/ffs_vietnam_fdi.pdf (accessed on 14 March 2020).
- Kost, C.; Shivenes, S.; Verena, J.; Huyen-Tran, N.; Thomas, S. Levelized Cost of Electricity—Renewable Energy Technologies. 2018. Available online: https://www.ise.fraunhofer.de/content/dam/ise/en/documents/publications/studies/EN2018_Fraunhofer-ISE_LCOE_Renewable_Energy_Technologies.pdf (accessed on 31 January 2020).
- The International Renewable Energy Agency. Renewable Power Generation Costs in 2018. Available online: https://www.irena.org/publications/2019/May/Renewable-power-generation-costs-in-2018 (accessed on 31 January 2020).
- Reid, J.S.; Hyer, E.J.; Johnson, R.S.; Holben, B.N.; Yokelson, R.J.; Zhang, J.; Campbell, J.R.; Christopher, S.A.; Di Girolamo, L.; Giglio, L.; et al. Observing and understanding the Southeast Asian aerosol system by remote sensing: An initial review and analysis for the Seven Southeast Asian Studies (7SEAS) program. Atmos. Res. 2013, 122, 403–468. [Google Scholar] [CrossRef]
- Brennan, M.P.; Abramase, A.L.; Andrews, R.W.; Pearce, J.M. Effects of spectral albedo on solar photovoltaic devices. Sol. Energy Mater. Sol. Cells 2014, 124, 111–116. [Google Scholar] [CrossRef]
- Andrews, R.W.; Pearce, J.M. The effect of spectral albedo on amorphous silicon and crystalline silicon solar photovoltaic device performance. Sol. Energy 2013, 91, 233–241. [Google Scholar] [CrossRef]
- Liao, W.; Heo, Y.; Xu, S. (Eds.) Evaluation of Temperature Dependent Models for PV Yield Prediction. In Proceedings of the 4th Building Simulation and Optimization Conference, Cambridge, UK, 11–12 September 2018. [Google Scholar]
- Louwen, A.; de Waal, A.C.; Schropp, R.E.I.; Faaij, A.P.C.; van Sark, W.G.J.H.M. Comprehensive characterisation and analysis of PV module performance under real operating conditions. Prog. Photovolt: Res. Appl. 2017, 25, 218–232. [Google Scholar] [CrossRef]
- Appelbaum, J.; Maor, T. Dependence of PV Module Temperature on Incident Time-Dependent Solar Spectrum. Appl. Sci. 2020, 10, 914. [Google Scholar] [CrossRef]
- Chakraborty, S.; Kumar, R. Comparative analysis of NOCT values for mono and multi C-Si PV modules in Indian climatic condition. World J. Eng. 2015, 12, 19–22. [Google Scholar] [CrossRef]
- European Commission. JRC Photovoltaic Geographical Information System (PVGIS). Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 21 April 2020).
- IEA. World Energy Model. Available online: https://www.iea.org/reports/world-energy-model (accessed on 15 April 2020).

| Region | Detached House Roof Slope— (degrees) | Average of Relative Solar Irradiation— |
|---|---|---|
| North Vietnam | 25 | 0.95 |
| 32 | 0.93 | |
| Central Vietnam | 25 | 0.95 |
| 26 | 0.95 | |
| South Vietnam | 34 | 0.90 |
| 24 | 0.93 |
| Module | Type | Watt Price—I (Euros/W) | Maximum Power—E (W) | Efficiency of Module—STC (%) | Performance Coefficient—CT (%K) | Length—Lmod (mm) | Width—Wmod (mm) |
|---|---|---|---|---|---|---|---|
| Monocrystalline [45] | NeMo | 0.59 | 275 | 16.4 | −0.4 | 1670 | 1006 |
| Polycrystalline [46] | NeMo | 0.53 | 260 | 16 | −0.42 | 1640 | 991 |
| Uncertain Parameter | Variable | Symbol | Used Value (unit) [ref] | Variation Range |
|---|---|---|---|---|
| Geographical input | Utilization factor for flat roof | Μ | 50 (%) [16] | ±40% |
| Utilization factor for slanted roof | Μ | 58 (%) [25] | ±33% | |
| The average number of apartments on one floor of the building | 10 (-) [47] | ±60% | ||
| Added area to the ground floor area | b | 10 (%) [47] | ±50% | |
| Technological input | The azimuth of the slanted roof | ϒ | 90 (degrees) [32] | ±100% |
| Performance ratio | PR | 85 (%) [25] | ±10% | |
| Economic input | O&M cost | 0.036 (Euro/kWh) [48] | ±50% | |
| Capital cost | 0.59 (Euro/W) [48] | ±50% | ||
| Discount rate | 8 (%) [47] | ±50% |
| Subject | This Paper | Field Study [52] |
|---|---|---|
| Coverage | Whole country | Only urban areas of HCM and DN |
| Method to identify technical potential | Geostatistical analysis, GIS, Monte Carlo Simulation | Deep learning, Photogrammetry, GIS, Image processing, Digital surface, and elevation models |
| Production potential for the specific cities (TWh/a) | HCM: 23.4 (100% of the city area) DN: 2.7 (100% of the city area) | HCM: 18 (80% of the city area) DN: 2.3 (80% of the city area) |
| Priority | Cluster Name | Available Roof km2 | Average LCOE (euro cent/kWh) | Production Potential (TWh/a) | GDP per Capita (Euro) | Urban Rate | No. Province |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 101.95 | 8.25 | 20.20 | 2260.53 | 65% | 2 |
| 2 | 2 | 17.11 | 8.06 | 3.51 | 1558.96 | 51% | 7 |
| 3 | 1 | 29.04 | 7.59 | 6.59 | 1431.55 | 29% | 9 |
| 4 | 3 | 26.12 | 8.92 | 4.42 | 1307.08 | 22% | 13 |
| 5 | 5 | 17.03 | 7.69 | 3.74 | 1143.27 | 26% | 18 |
| 6 | 4 | 12.57 | 8.96 | 2.07 | 794.10 | 19% | 14 |
| Competitive Price | Metering Model | ||
|---|---|---|---|
| Business | Self-Consumption | ||
| >0 | >0 | x | x |
| >0 | <0 | x | - |
| <0 | >0 | - | x |
| <0 | <0 | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minh Khuong, P.; McKenna, R.; Fichtner, W. A Cost-Effective and Transferable Methodology for Rooftop PV Potential Assessment in Developing Countries. Energies 2020, 13, 2501. https://doi.org/10.3390/en13102501
Minh Khuong P, McKenna R, Fichtner W. A Cost-Effective and Transferable Methodology for Rooftop PV Potential Assessment in Developing Countries. Energies. 2020; 13(10):2501. https://doi.org/10.3390/en13102501
Chicago/Turabian StyleMinh Khuong, Phuong, Russell McKenna, and Wolf Fichtner. 2020. "A Cost-Effective and Transferable Methodology for Rooftop PV Potential Assessment in Developing Countries" Energies 13, no. 10: 2501. https://doi.org/10.3390/en13102501
APA StyleMinh Khuong, P., McKenna, R., & Fichtner, W. (2020). A Cost-Effective and Transferable Methodology for Rooftop PV Potential Assessment in Developing Countries. Energies, 13(10), 2501. https://doi.org/10.3390/en13102501




