Phasor Estimation for Grid Power Monitoring: Least Square vs. Linear Kalman Filter
Abstract
1. Introduction
- P-class that deals with the measurement applications and it is applied for fast and dynamic events.
- M-class refers to the applications that require a high estimation performances and requires a FE and smaller than 5 mHz and , respectively.
2. Power Quality Disturbances Characterization
- For individual events, magnitude and duration are investigated.
- For steady-state disturbances, only are magnitude.
- For intermittent disturbances, the frequency of occurrence is used as severity indices.
2.1. Three-Phase Signal Model
2.2. Phasor Model
3. Frequency and Phasor Estimation Methods
3.1. Frequency Estimator
- is a N matrix containing the three-phase recorded data and is given by
- is a that containing the noise samples and is defined as
- is a real-valued matrix and it is defined as
- is a real-valued matrix relying on the unknown phasors and it is defined as
- First, the estimation can be obtained by maximizing a 1-dimensional function.
- Second, the C estimation can be obtained by replacing with its estimate .
3.2. Phasor Estimation
Phasor Estimator-Based on Least Square Technique
3.3. Phasor Estimator-Based on Kalman Filter Technique
4. Simulation and Real Data-Based Validation
4.1. Simulation Results
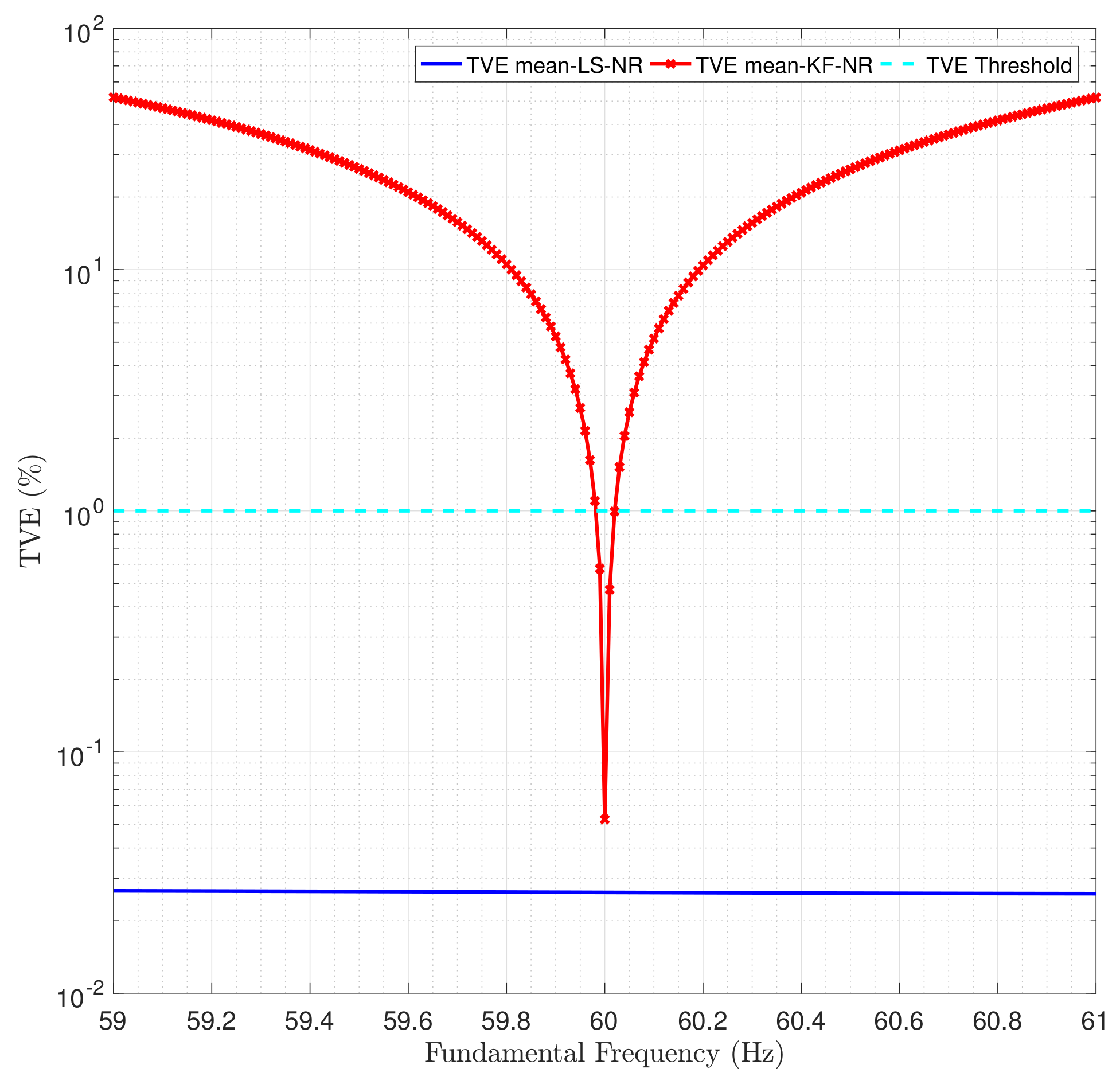
4.1.1. Off-Nominal Frequency Effect on the Phasor Estimators Performance
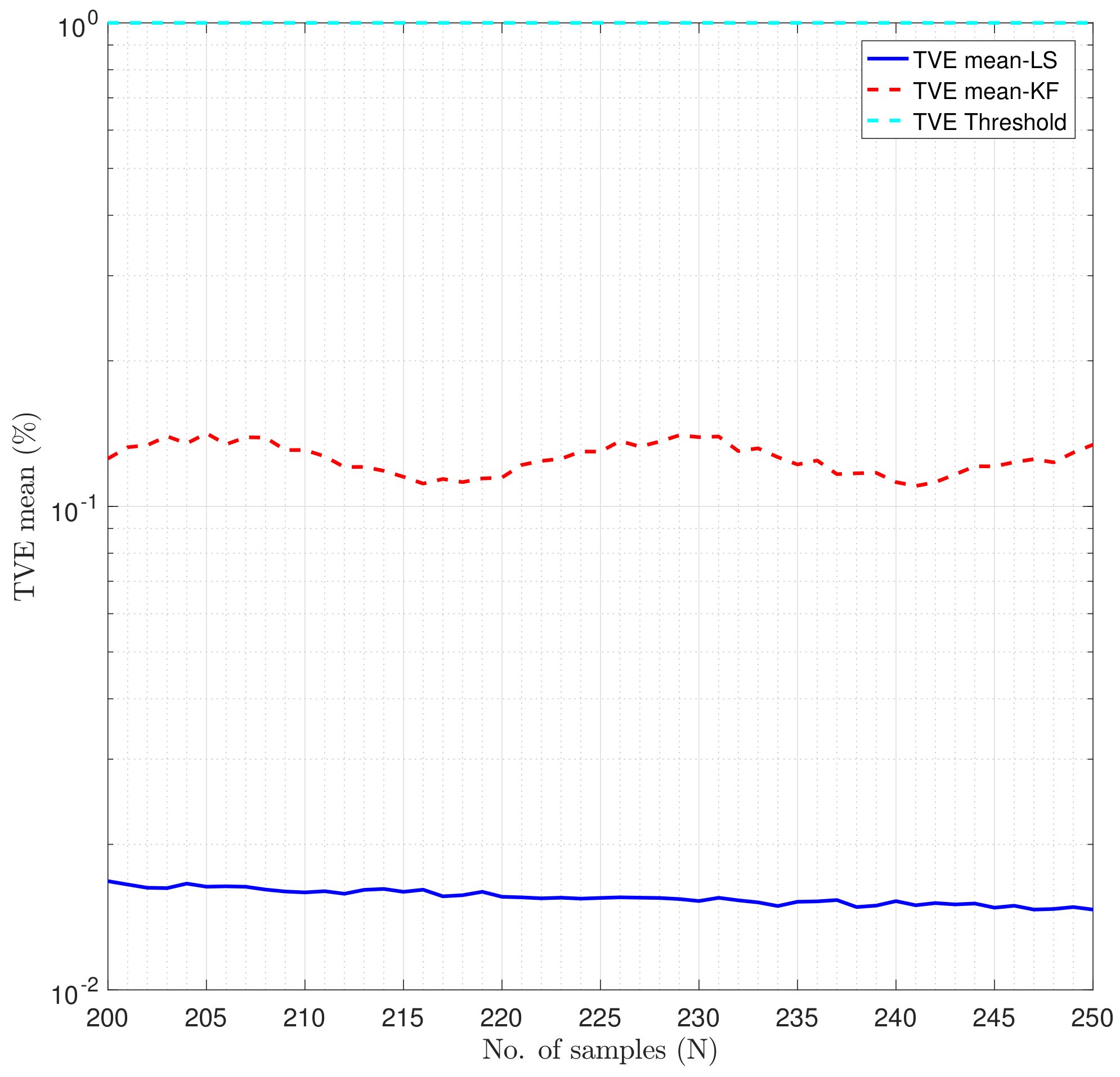
4.1.2. Number of Samples Effect on the Phasor Estimators Performance
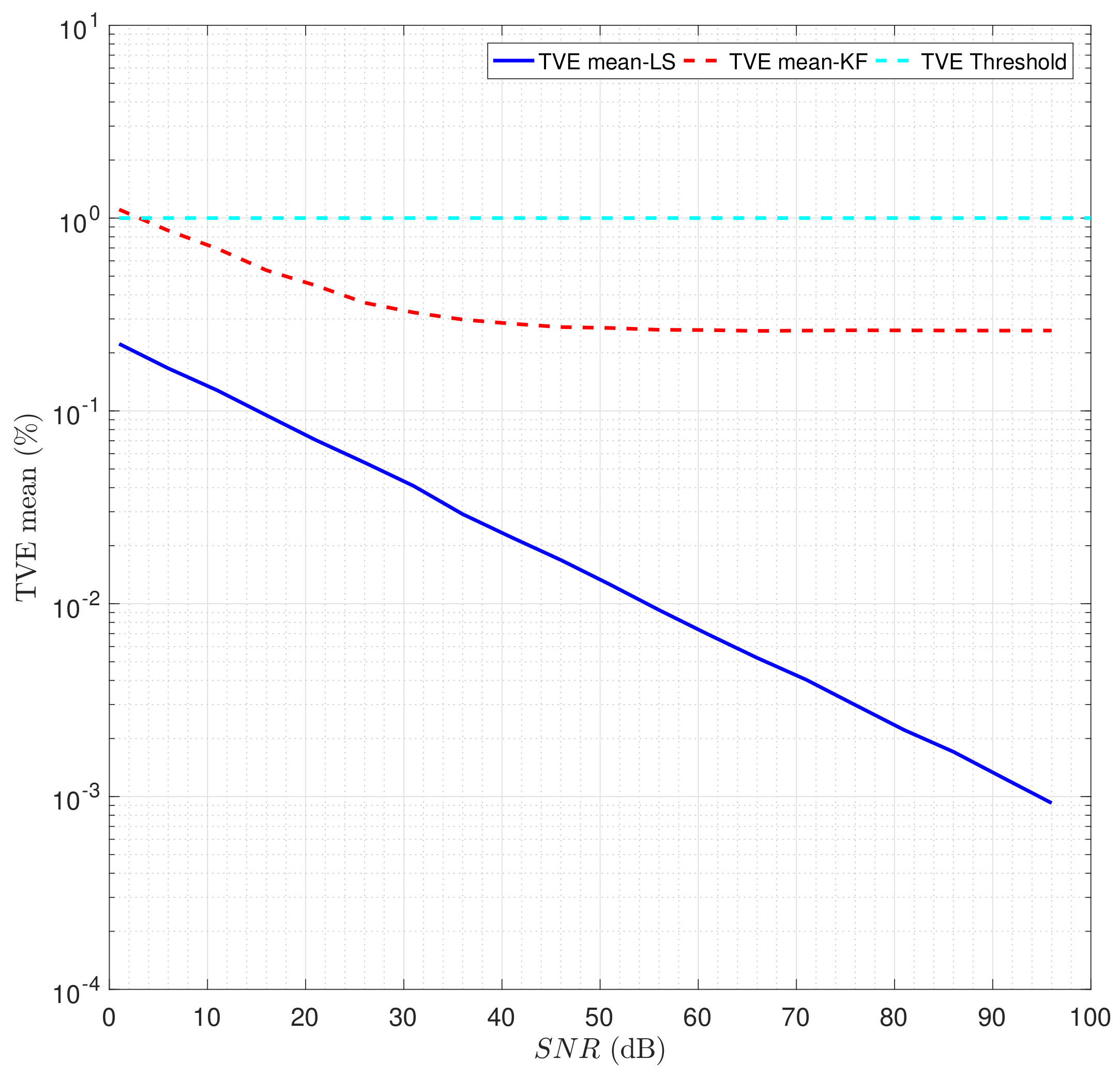
4.1.3. Noise Effect on the Phasor Estimators Performance
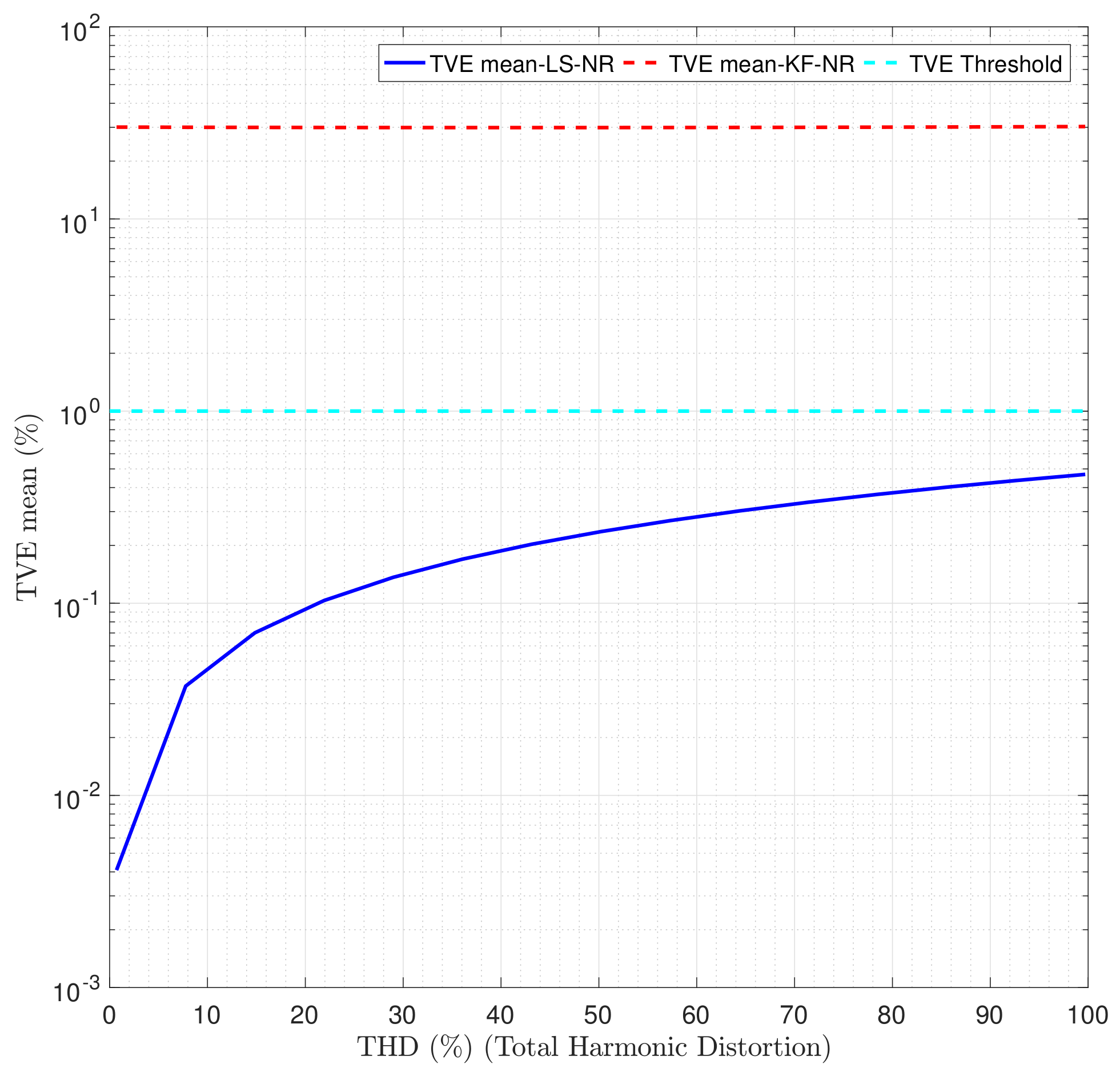
4.1.4. Harmonic Components Effect on the Phasor Estimators Performance
4.2. Performance Evaluation on Real World Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McBee, K.D.; Simoes, M.G. Utilizing a smart grid monitoring system to improve voltage quality of customers. IEEE Trans. Smart Grid 2012, 3, 738–743. [Google Scholar] [CrossRef]
- Banerjee, P.; Srivastava, S. An Effective Dynamic Current Phasor Estimator for Synchrophasor Measurements. IEEE Trans. Instrum. Meas. 2015, 64, 625–637. [Google Scholar] [CrossRef]
- Amin, S.; Wollenberg, B. Toward a smart grid: Power delivery for the 21st century. IEEE Power Energy Mag. 2005, 3, 34–41. [Google Scholar] [CrossRef]
- Amirat, Y.; Oubrahim, Z.; Benbouzid, M.E.H. On phasor estimation for voltage sags detection in a smart grid context. In Proceedings of the 2015 IEEE ISIE, Buzios-Rio de Janiero, Brazil, 3–5 June 2015; pp. 1351–1356. [Google Scholar]
- Hu, J.; Zhu, J.; Platt, G. Smart grid the next generation electricity grid with power flow optimization and high power quality. In Proceedings of the 2011 IEEE ICEMS, Beijing, China, 20–23 August 2011; pp. 1–6. [Google Scholar]
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2010, 8, 18–28. [Google Scholar] [CrossRef]
- Brown, M.A.; Zhou, S. Smart grid policies: An international review. Wiley Interdiscip. Rev. Energy Environ. 2013, 2, 121–139. [Google Scholar] [CrossRef]
- Bollen, M.H.; Gu, I. Signal Processing of Power Quality Disturbances; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 30. [Google Scholar]
- Khokhar, S.; Zin, A.A.B.M.; Mokhtar, A.S.B.; Pesaran, M. A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances. Renew. Sustain. Energy Rev. 2015, 51, 1650–1663. [Google Scholar] [CrossRef]
- Bollen, M.H.; Bahramirad, S.; Khodaei, A. Is there a place for power quality in the smart grid? In Proceedings of the 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 713–717. [Google Scholar]
- Ghanavati, A.; Lev-Ari, H.; Stanković, A.M. A Sub-Cycle Approach to Dynamic Phasors With Application to Dynamic Power Quality Metrics. IEEE Trans. Power Deliv. 2018, 33, 2217–2225. [Google Scholar] [CrossRef]
- Ahmed, H.; Bierhoff, M.; Benbouzid, M.E.H. Multiple Nonlinear Harmonic Oscillator-Based Frequency Estimation for Distorted Grid Voltage. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
- Bergen, A.R. Power Systems Analysis; Pearson Education India: Bengaluru, India, 2000. [Google Scholar]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2012, 14, 944–980. [Google Scholar] [CrossRef]
- Smith, J.C.; Hensley, G.; Ray, L. IEEE Recommended Practice for Monitoring Electric Power Quality. Revis. IEEE 2009. [Google Scholar] [CrossRef]
- Testing and Measurement Techniques–Power Quality Measurement Methods. In International Electrotechnical Commission Standard 61000-4-30; IEC: Geneva, Switzerland, 2015.
- Standard EN 50160. Voltage Characteristics of Electricity Supplied by Public Distribution Systems; Standard EN: Brussels, Belgium, 2002. [Google Scholar]
- Ribeiro, P.F.; Duque, C.A.; Ribeiro, P.M.; Cerqueira, A.S. Power Systems Signal Processing for Smart Grids; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bollen, M.H.J.; Gu, I.Y.H.; Santoso, S.; Mcgranaghan, M.F.; Crossley, P.A.; Ribeiro, M.V.; Ribeiro, P.F. Bridging the gap between signal and power. IEEE Signal Process. Mag. 2009, 26, 12–31. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.; Manikandan, M.S. Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected distributed generation system. IEEE Trans. Smart Grid 2016, 9, 3122–3132. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M.; Ahsan, M.; Albarbar, A.; Shahjalal, M. Frequency Adaptive Parameter Estimation of Unbalanced and Distorted Power Grid. IEEE Access 2020, 8, 8512–8519. [Google Scholar] [CrossRef]
- Zhang, L.; Bose, A.; Jampala, A.; Madani, V.; Giri, J. Design, testing, and implementation of a linear state estimator in a real power system. IEEE Trans. Smart Grid 2016, 8, 1782–1789. [Google Scholar] [CrossRef]
- Jain, S.K.; Jain, P.; Singh, S.N. A fast harmonic phasor measurement method for smart grid applications. IEEE Trans. Smart Grid 2016, 8, 493–502. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, Y.; Srivastava, A.K.; Wu, Y.; Banerjee, P. Ensemble-Based Algorithm for Synchrophasor Data Anomaly Detection. IEEE Trans. Smart Grid 2018, 10, 2979–2988. [Google Scholar] [CrossRef]
- Castello, P.; Muscas, C.; Pegoraro, P.; Sulis, S. PMU’s Behavior with Flicker-Generating Voltage Fluctuations: An Experimental Analysis. Energies 2019, 12, 3355. [Google Scholar] [CrossRef]
- IEEE Standard for Synchrophasor Measurements for Power Systems. In IEEE Standard C37.118.1-2011 (Revision IEEE Standard C37.118-2005); IEEE: Piscataway, NJ, USA, 2011.
- IEEE Standard for Synchrophasor Measurements for Power Systems Amendment 1: Modification of Selected Performance Requirements. In IEEE Standard C37.118.1a-2014 (Amendment to IEEE Standard C37.118.1-2011); IEEE: Piscataway, NJ, USA, 2014.
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Disturbances Classification Based on a Model Order Selection Method for Power Quality Monitoring. IEEE Trans. Ind. Electron. 2017, 64, 9421–9432. [Google Scholar] [CrossRef]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Maximum-Likelihood Frequency and Phasor Estimations for Electric Power Grid Monitoring. IEEE Trans. Ind. Inf. 2018, 14, 167–177. [Google Scholar] [CrossRef]
- Rouhani, A.; Abur, A. Linear phasor estimator assisted dynamic state estimation. IEEE Trans. Smart Grid 2016, 9, 211–219. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Application; Springer: Berlin, Germany, 2008. [Google Scholar]
- Oubrahim, Z. On Electric Grid Power Quality Monitoring Using Parametric Signal Processing Techniques. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2017. [Google Scholar]
- Fitzer, C.; Barns, M.; Green, P. Voltage sag detection technique for a dynamic voltage restorer. IEEE Trans. Ind. Appl. 2004, 40, 203–212. [Google Scholar] [CrossRef]
- De Carvalho, J.; Duque, C. A PLL-Based Multirate Structure for Time-Varying Power Systems Harmonic/Interharmonic Estimation. IEEE Trans. Power Deliv. 2009, 24, 1789–1800. [Google Scholar] [CrossRef]
- Amirat, Y.; Oubrahim, Z.; Feld, G.; Benbouzid, M.E.H. Phasor estimation for power quality monitoring: Least square versus Kalman filter. In Proceedings of the IECON 2017 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 4339–4343. [Google Scholar] [CrossRef]
- Ahmed, H.; Pay, M.L.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E. Hybrid estimator-based harmonic robust grid synchronization technique. Electr. Power Syst. Res. 2019, 177, 106013. [Google Scholar] [CrossRef]
- Ahmed, H.; Pay, M.L.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E. Gain normalized adaptive observer for three-phase system. Int. J. Electr. Power Energy Syst. 2020, 118, 105821. [Google Scholar] [CrossRef]
- Qi, J.; Taha, A.F.; Wang, J. Comparing Kalman filters and observers for power system dynamic state estimation with model uncertainty and malicious cyber attacks. IEEE Access 2018, 6, 77155–77168. [Google Scholar] [CrossRef]
- Zhao, J.; Mili, L. A robust generalized-maximum likelihood unscented Kalman filter for power system dynamic state estimation. IEEE J. Sel. Top. Signal Process. 2018, 12, 578–592. [Google Scholar] [CrossRef]
- Zhao, J.; Mili, L. A theoretical framework of robust H-infinity unscented Kalman filter and its application to power system dynamic state estimation. IEEE Trans. Signal Process. 2019, 67, 2734–2746. [Google Scholar] [CrossRef]
- Carquex, C.; Rosenberg, C.; Bhattacharya, K. State Estimation in Power Distribution Systems Based on Ensemble Kalman Filtering. IEEE Trans. Power Syst. 2018, 33, 6600–6610. [Google Scholar] [CrossRef]
- IEEE Working Group on Power Quality Data Analytics. Electrical Signatures Of Power Equipement Failures; Technical Report PES-TR73; IEEE Power & Energy Society: Piscataway, NJ, USA, 2009. [Google Scholar]
- IEEE. IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions; IEEE Press: Piscataway, NJ, USA, 2010; pp. 1–50. [Google Scholar]
- Laughton, M. Analysis of Unbalanced Polyphase Networks by the Method of Phase Co-ordinates. Part 2: Fault Analysis. Proc. Inst. Electr. Eng. 1969, 116, 857–865. [Google Scholar] [CrossRef]
- Bollen, M.H.J. Understanding Power Quality Problems; IEEE Press: New York, NY, USA, 1999; Volume 3. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory; Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- De Apráiz, M.; Diego, R.; Barros, J. An Extended Kalman Filter Approach for Accurate Instantaneous Dynamic Phasor Estimation. Energies 2018, 11, 2918. [Google Scholar] [CrossRef]
- Begovic, M.M.; Djuric, P.M.; Dunlap, S.; Phadke, A.G. Frequency tracking in power networks in the presence of harmonics. IEEE Trans. Power Deliv. 1993, 8, 480–486. [Google Scholar] [CrossRef]
- DOE/EPRI National Database Repository of Power System Events: Online. 2016. Available online: http://pqmon.epri.com/disturbance_library/ (accessed on 18 December 2016).
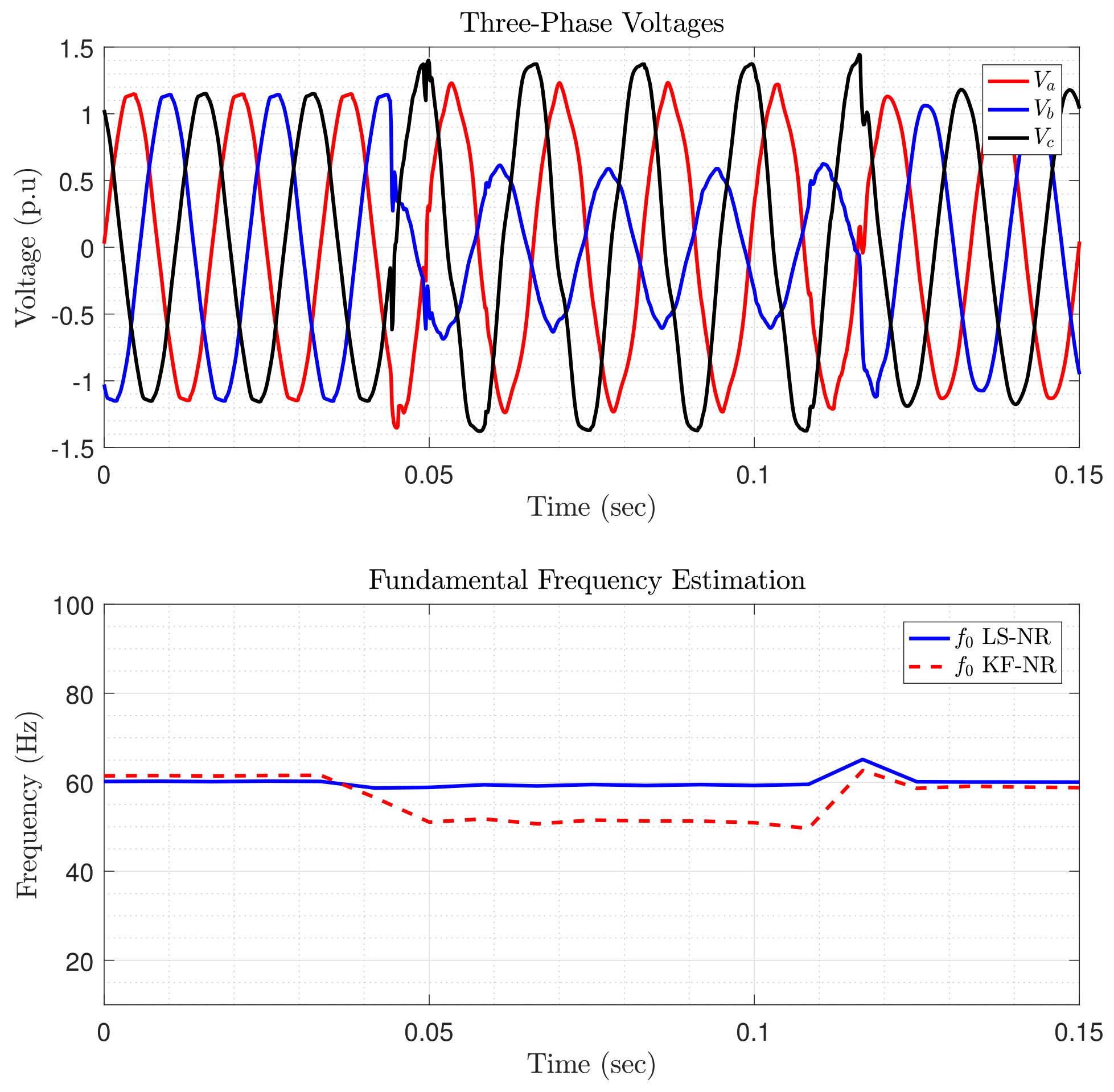




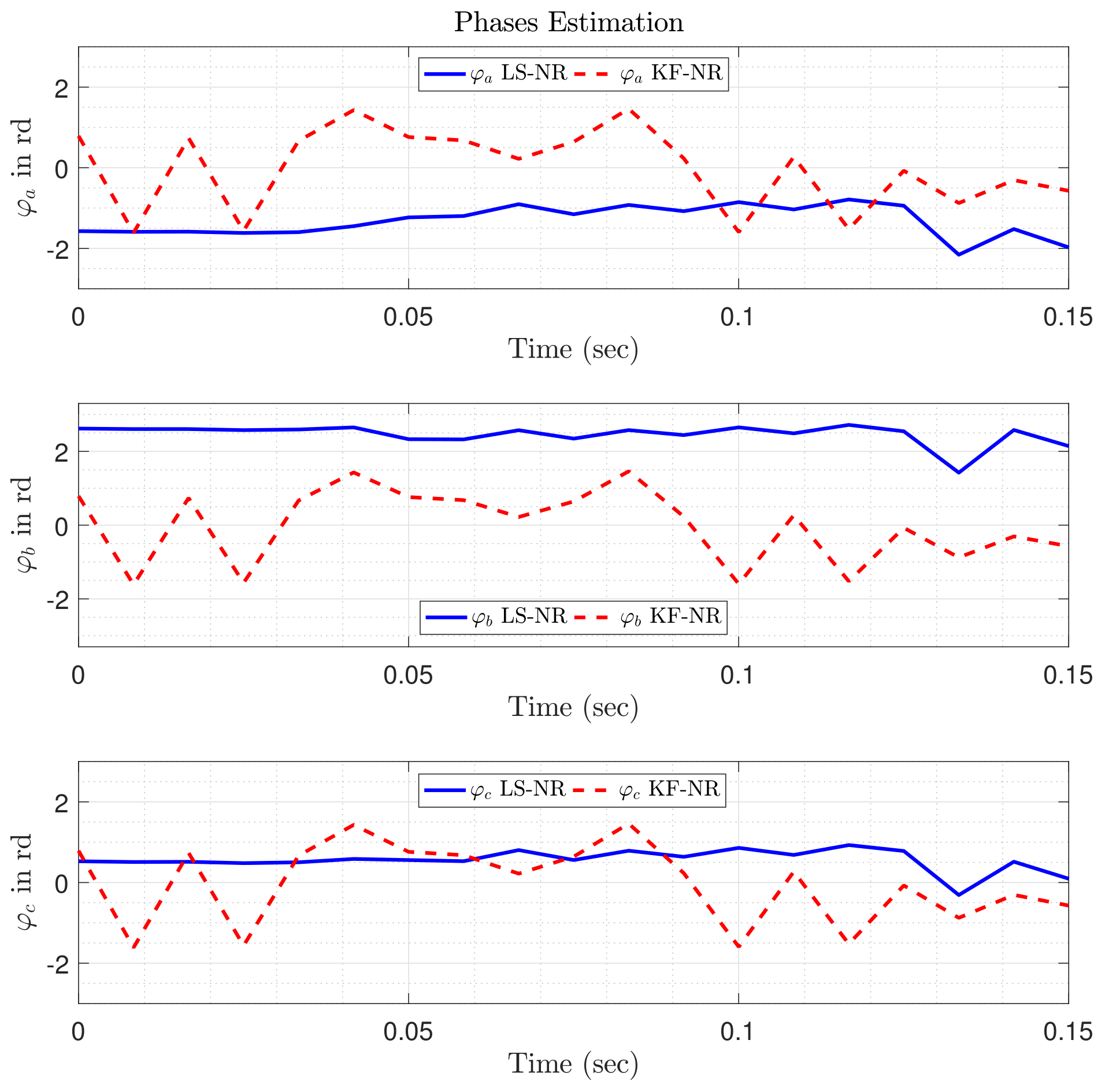
| 1 pu | 1 pu | 1 pu | 60 | 2880 |
| LSE | KFE | |
|---|---|---|
| Hz | 0.73 | 1.45 |
| Hz | 0.58 | 3.45 |
| Hz | 0.22 | 2.23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amirat, Y.; Oubrahim, Z.; Ahmed, H.; Benbouzid, M.; Wang, T. Phasor Estimation for Grid Power Monitoring: Least Square vs. Linear Kalman Filter. Energies 2020, 13, 2456. https://doi.org/10.3390/en13102456
Amirat Y, Oubrahim Z, Ahmed H, Benbouzid M, Wang T. Phasor Estimation for Grid Power Monitoring: Least Square vs. Linear Kalman Filter. Energies. 2020; 13(10):2456. https://doi.org/10.3390/en13102456
Chicago/Turabian StyleAmirat, Yassine, Zakarya Oubrahim, Hafiz Ahmed, Mohamed Benbouzid, and Tianzhen Wang. 2020. "Phasor Estimation for Grid Power Monitoring: Least Square vs. Linear Kalman Filter" Energies 13, no. 10: 2456. https://doi.org/10.3390/en13102456
APA StyleAmirat, Y., Oubrahim, Z., Ahmed, H., Benbouzid, M., & Wang, T. (2020). Phasor Estimation for Grid Power Monitoring: Least Square vs. Linear Kalman Filter. Energies, 13(10), 2456. https://doi.org/10.3390/en13102456









