1. Introduction
With the purpose of cooling or heating, transferred heat or excess heat from one region may be reused and contribute positively to the energy efficiency of a system; thus, heat exchangers are widely utilised. They can easily be found in chemical and petroleum plants, process engineering and civil heating system as well. Heat exchangers can be classified into several groups according to geometric configuration, although improving the heat transfer performance is the common goal. Over the last 50 years, the single-phase pipe exchanger has seen a variety of augmentation techniques, and the heat transfer capacity has been improved greatly [
1,
2,
3,
4,
5,
6,
7,
8]. Among various studies carried out on pipe flow enhanced technologies, adopting the insert inside a tube is a common approach.
Increasing the effective working surface can increase the heat flux in a relatively compact size and is often adopted as a practical way to improve heat transfer capacity. Open-cell foam is one kind of solid material with connected pores inside, which provide liquid with space and channels to flow through. With the advantage of large surface-to-volume ratio that can reach up to 10,000 m
2/m
3 in particular structure configurations [
9], it has been employed as a pipe insert to increase the effective surface in the heat exchanger. However, it is generally recommended for low-Reynolds-number fluids, as its high thermal performance is often offset by high head loss [
10,
11,
12]. Besides, uncontrollable size and diameter largely depend on the manufacturing process, which makes it hard to build solid theory. Lacroix et al. estimated the pressure drop of pipes using a simplified model for a cubic unit cell but with a good agreement with experimental results [
13]. With the advantage of 3D printing (3DP), the periodic cellular structure is regarded as a promising insert to enhance the heat transfer performance by two-fold advantages, such as large surface area and low-pressure drop. Busse et al. designed periodic open cellular structures (POCS) and carried out a comparative analysis with the randomly packed bed, open-cell foam and honeycomb [
14]. They studied material, morphology and wall coupling of POCS, and the result showed that POCS outperform others, particularly at a low flow rate. In reference to stochastic open-cell foams, another octet truss lattice (OTL) structure with a 12 node connection was proposed by Chaudhari et al. [
15]. They investigated the effect of porosity on thermal conductivity, permeability, inertial coefficient, friction factor and Nusselt number, and a correlation was also established. The experimental investigation proved that OTL is a possible alternative in heat exchanger/sink in consideration of low pressure drop.
Swirling flow has been verified as another effective method to increase the heat transfer capacity in convective systems, and some in-tube elements were designed to generate a swirling flow or vortex. A twisted strip inside a tube can function as a vortex generator and create a significant enhancement for turbulent or laminar flow in a single-phase convection process. Numerous studies have been carried out to investigate the thermal enhancement and the cost of swirling flow inside a tube. Adopting the performance evaluation criteria presented in [
16], Ji et al. [
17] compared different enhancement technologies and found that turbulence promoters have higher enhanced ratios than other passive technologies. The same result can be observed in [
18], and the enhancement ratio under the identical pressure drop criteria reached 2.8, which was nearly doubled that of other inserts. To improve the flow pattern and promote turbulence further, additional geometric patterns on tape surfaces have been investigated. Wijayanta et al. carried out numerical studies on the thermal improvement of pipe flow using tape with two-sided delta winglets or square cuts, and the results were encouraging [
19,
20]. Chang et al. discussed the pros and cons of repeated ribs on tape surfaces [
21]. They also investigated the effects that the number of twisted inserts had on frictional loss and augmentation ratio [
22]. Wongcharee and Eiamsa-ard clarified the influence of additional tape features like alternate axes and wings in different shapes [
23], while the performance of twisted tape with axial holes was reported by Thianpong et al. [
24]. Combining different enhancement technologies is also preferable; the characteristics of a corrugated tube with different forms of twisted tape inserts can be found in [
25], and it guaranteed a better overall performance compared to the single augmentation method.
The length and installation arrangement of twisted tapes have been studied by many researchers. Manglik and Bergles tested and recorded the friction factor and heat transfer enhancement of full-length twist tapes and presented correlation formulae suitable for transitional and fully developed flow [
26]. An expanded investigation was carried out by Hong et al., in which full and half-length twisted tape with different pitches were studied [
27]. Compared to smooth tubes, the encouraging results showed that both the Nusselt number and friction factor are strong functions of the twist ratio. In order to obtain a higher Nusselt number with a relatively small pressure drop, Saha et al. designed evenly spaced twisted-tape elements and discussed heat transfer and pressure drop characteristics in Reynolds numbers ranging from 500 to 2300 [
28]. However, a clear and assertive conclusion did not come out, as partially inserted twisted tape did not always have superior performance than the full-length one, and even the pumping power reduction could reach up to 40% at the fixed heat duty. Similar research can be found in [
29], and the correlation was proposed for practical application. Even though they provided direct evidence of its capacity in heat exchange augmentation and low pressure loss for this arrangement, they could not exclude the influence of the central rod used to connect single elements in a spaced twisted tape. On top of that, a loose fit between the inserts and the pipe wall could weaken the heat transfer ability [
30,
31]. In other words, their design freedom may be limited by manufacturing technology in the above-mentioned research. It is hard or even impossible for traditional manufacturing to fix one single insert inside a tube at the location as desired without a rod connection, and also the gap between insert and walls is uncontrollable. As a consequence, there are few publications about segmented twisted tape, and more detailed investigation is needed.
Adopting the idea of 3DP, the enhanced tube assembly conventionally consisting of pipes and inserts can be printed as a single part, and the insert element can be added at any location with controllable clearance but without any additional mechanical connection. Actually, there are some researchers utilising 3DP to realise a complex internal fluid guiding element and membrane in a compact heat exchanger, which are not applicable using conventional manufacturing methods [
32,
33]. Whereas there is limited research about the 3DP-optimized twisted tape insert, this article investigates the geometric features of a single insert element that is achievable by 3DP, and hopefully provides some reference for related research.
2. Geometric Model
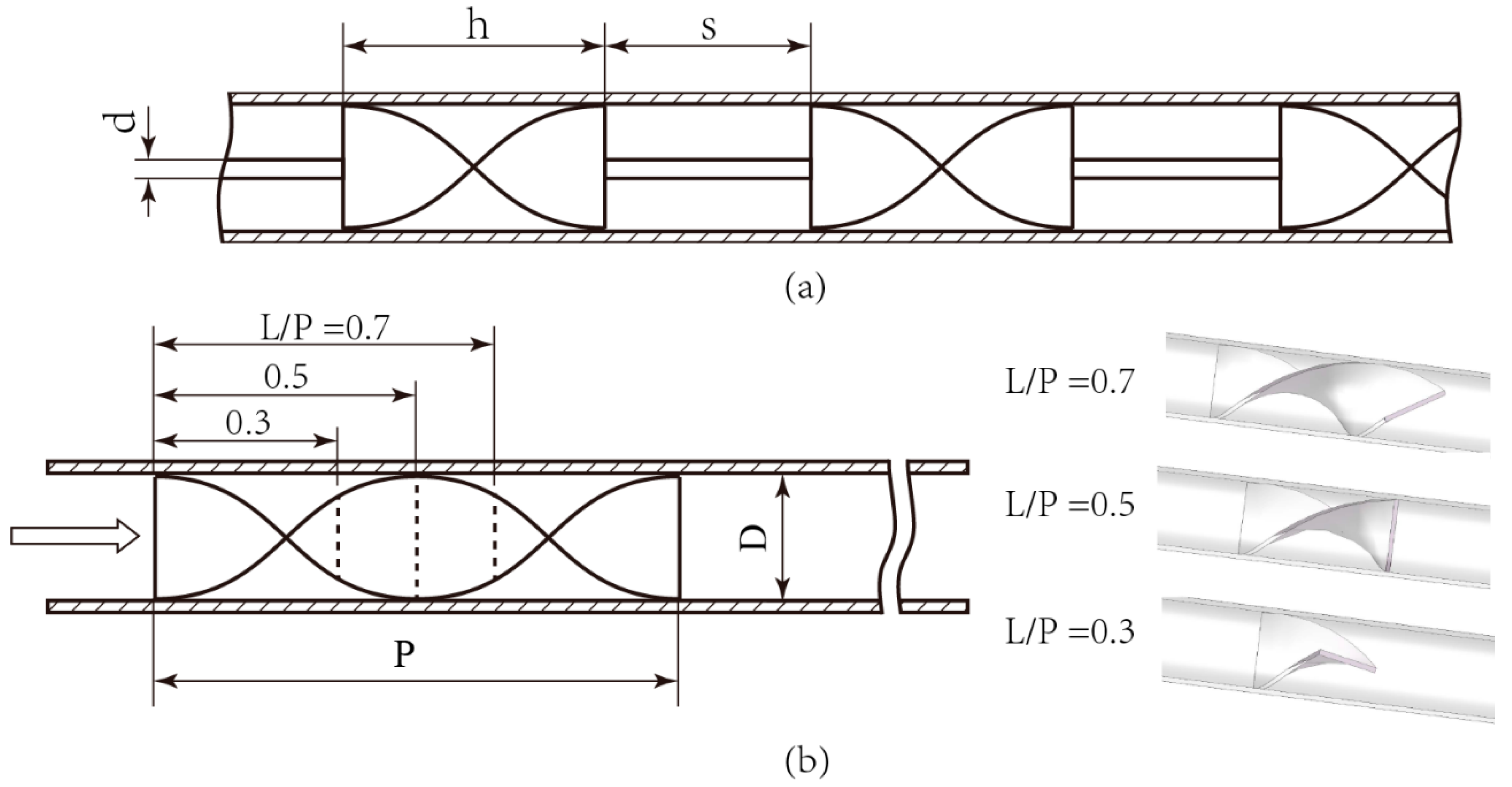
After being processed in a rolling operation, the twisted tape offers smooth and continuous curved surfaces inside a tube. For evenly distributed twisted tape shown in
Figure 1a, the single insert element is connected by a central rod, of which the diameter d is around 25% of the inner diameter of tube D. The length of twisted tape
h and free space
s are two main design parameters and the space lengths are usually constant among elements. As for the geometry under investigation in
Figure 1b, it puts much emphasis on the geometry design of single element and its consequential effect on heat transfer. Different from traditional design, a central rod is not necessary any longer to fix the insert to the wall at a specific location, because the 3DP can print them into one single part.
Twist ratio P/D and length ratio L/P are two geometric features of interest, where P denotes the length of a twisted unit and L presents the actual length of pipe insert. Setting D as 10 mm, three different twist ratios (P/D = 2.0, 3.3, 4.6) are designed, and three models with different length ratios (L/P = 0.3, 0.5, 0.7) are proposed at every P/D. A constant wall thickness of 0.67 mm is designed, and a smooth transition is added to the two tape ends. The tube in this research is 1000 mm long, and the segmented twisted tape is inserted 100 mm away from the inlet port, which can guarantee a fully developed flow.
3. Numerical Method
This research involves the investigation of flow state and heat transfer behaviour, so a finite difference method for turbulence is employed to solve the governing partial equations. It is necessary to make some fundamental assumptions before applying the universal flow equations and energy equation to the tube with vortex generators. The major assumptions include the following: (a) the fluid through the tube is incompressible, (b) the thermal–physical property is temperature independent and (c) the heat loss caused by radiation and natural convection is neglected.
On the basis of the stated assumptions, a proper governing equation is employed to describe the steady-state thermal condition and time-invariant fluid flow. The time-averaged impressible Navier–Stokes equations for three-dimensional models in Cartesian form can be expressed as follows:
A proper partial differential equation should be selected according to the complexity of the fluid domain, and generally, a balance between accuracy and computational cost is desired. The Navier–Stokes equation is widely accepted as it can reflect the actual fluid situation accurately in most cases, whereas this accuracy is offset by the cost of computational sources. Separating time-dependent turbulent velocity fluctuations from the mean flow velocity, a modified Reynolds Average Navier–Stokes (RANS) model makes it possible to simulate practical engineering flows. However, this will introduce Reynolds stresses that are related to fluctuation terms in the velocity field. Employing the Boussinesq hypothesis, the Reynolds stresses in Equation (2) can be expressed as Equation (5).
The turbulent viscosity term
μt in Equation (5) can be obtained in Equation (6).
In consideration of sudden geometry change within the tube, the incompressible Navier–Stokes equation along with the realisable k-ε turbulence model is discretized using the finite volume technique. Water is chosen as the working fluid, and the time-independent physical property of water at 20 °C is listed as follows: density 998.2 kg/m3, specific heat 4182 J/(kg·K), thermal conductivity 0.601 W/(m·K) and dynamic viscosity 1.003 mPa·s. To inspect the pressure distribution, the pressure–velocity coupling algorithm SIMPLE is selected. A second-order scheme is utilised in pressure, momentum, turbulent terms and energy, while a least-squares cell based spatial discretization is used in the gradient. The turbulent intensity is kept at 5% at the inlet while the hydraulic diameter is fixed at 10 mm. The residual constitutes one of the important parts in numerical simulation, and a tight convergence level at 10−6 is selected.
The discrimination of a continuum to a mesh model is one of the most important steps in computational analysis, which largely determines whether the simulation is successful or not. The commonly available mesh types include tetrahedra, polyhedra and hexahedra. Tetrahedra is the simplest volume element and is easy to generate automatically. However, high mesh quality near the long channel wall with small gaps is hard to obtain as tetrahedra cannot be stretched too much. A hybrid mesh consisting of tetrahedra and hexahedra is an alternative to discretize the complex geometry such as the fluid domain in this article but introducing a larger number of elements. The successful applications in [
34,
35] illustrated the advantages of polyhedral mesh. Less sensitive to stretching than tetrahedra, polyhedral cells can fit the boundary of complex geometry. Evidence from numerous comparison studies verifies the advantages over tetrahedral meshes at the identical computational accuracy level, in which three-fourths reduction of cells, half reduction of computer memory and nearly 80% reduction in calculation time can be achieved in polyhedra [
36]. As a result, the polyhedral mesh is adopted to describe the fluid domain, and the mesh conditions are shown in
Figure 2.
To achieve the balance between solution accuracy and calculation time, the independent verification of the grid is executed. For all cases in this research, the Nusselt number
Nu varies within the acceptable range of 3% when increasing the grid numbers, so the meshing technology corresponding to the moderate mesh number is chosen. Taking the complexity of the internal thermal and velocity field into consideration, the enhanced wall function method is adopted. After assessment of y+, the results correspond to the recommended value of ~1 for first near-wall nodes. Velocity inlet and pressure outlet are chosen for the fluid domain, and the temperature of hot fluid is 363 K while the wall temperature is fixed at 300 K [
37,
38]. The value of gauge pressure at the outlet is set as 0 Pa relative to a reference pressure.
4. Results and Discussion
Friction factor (
f), Nusselt number (
Nu) and performance evaluation factor (
η) are three main parameters of interest to describe the characteristics of frictional loss, heat transfer and overall performance enhancement. The friction factor can be defined using the following equation:
The calculation of Nusselt number is given by
The local convective heat transfer coefficient across a surface can be obtained by
Performance evaluation factor is defined as
where
Nu and
f present the Nusselt number and friction factor of inspected tubes, respectively, while the corresponding subscript 0 denotes the results of the plain tube.
The reliability of the simulation was verified by comparing the results to the value of empirical formulas. Due to the availability of rich research and strong reliability, a smooth tube was chosen as a valid reference. Suitable for high fluid viscosity, the improved Sieder–Tate empirical formula was adopted to assess the heat transfer performance [
39,
40] and is expressed as follows:
The empirical formula for the friction factor is the Blasius formula [
39]. The applicable Re for this formula is below 100,000.
Both the theoretical value and numerical results of the friction factor and Nusselt number were calculated according to Equations (7), (9), (12) and (13), and the errors between the empirical formulas and the simulation results were within an acceptable range, which can be found in
Figure 3.
4.1. Temperature and Velocity Field
Temperature and velocity distribution are displayed qualitatively in this section, giving some hints about the status of fluid through the tube. In consideration of the limited space in this paper, we cannot show every detail of every case in every parameter, so the tube with inserted twisted tape whose P/D = 3.3 and L/P = 0.5 was chosen as an example for simplicity.
The difference in temperature distribution between the smooth tube and tube with inserted tape can be clearly observed in
Figure 4. For the single-twisted-tape case, the heat exchange was sufficient near the tape element where the turbulence was violent, and the temperature showed a moderate variation in the cross profile. On the contrary, the smooth tube saw a much more even temperature distribution and the transition was smooth along the axial direction. Flowing through the twisted tape, the high-temperature fluid moved towards the wall where the temperature was set as 300 K, which was beneficial to dissipate heat to the wall. The temperature distribution in tape-inserted fluid went back to normal and became uniform with the low-temperature region dotted near the wall at around 500 mm. A shorter red region in the tube with inserts meant the fluid experienced an acute temperature drop, in comparison with the smooth tube, which demonstrated the positive effect of the segmented twisted tape.
Contour plots of streamlines through the tube with one single element are displayed in
Figure 5, which clearly depicts that various turbulence patterns were produced because of the abrupt appearance of the inserted tape, which was quite different from periodic patterns of full-length tapes. Depending on the relative attack angle between the fluid and twisted tape, the turbulence strength and formation region varied. Combining all these flow patterns, a complex flow status was formed, and the temperature distribution seen in
Figure 4 could find rationality from this.
4.2. Local Heat Transfer Coefficient
Along the axial direction, local heat transfer rate in terms of
hx through the cross-section of the fluid domain was calculated according to Equation (10) and the
hx over average value of the plain tube
h0 was plotted in
Figure 6,
Figure 7 and
Figure 8.
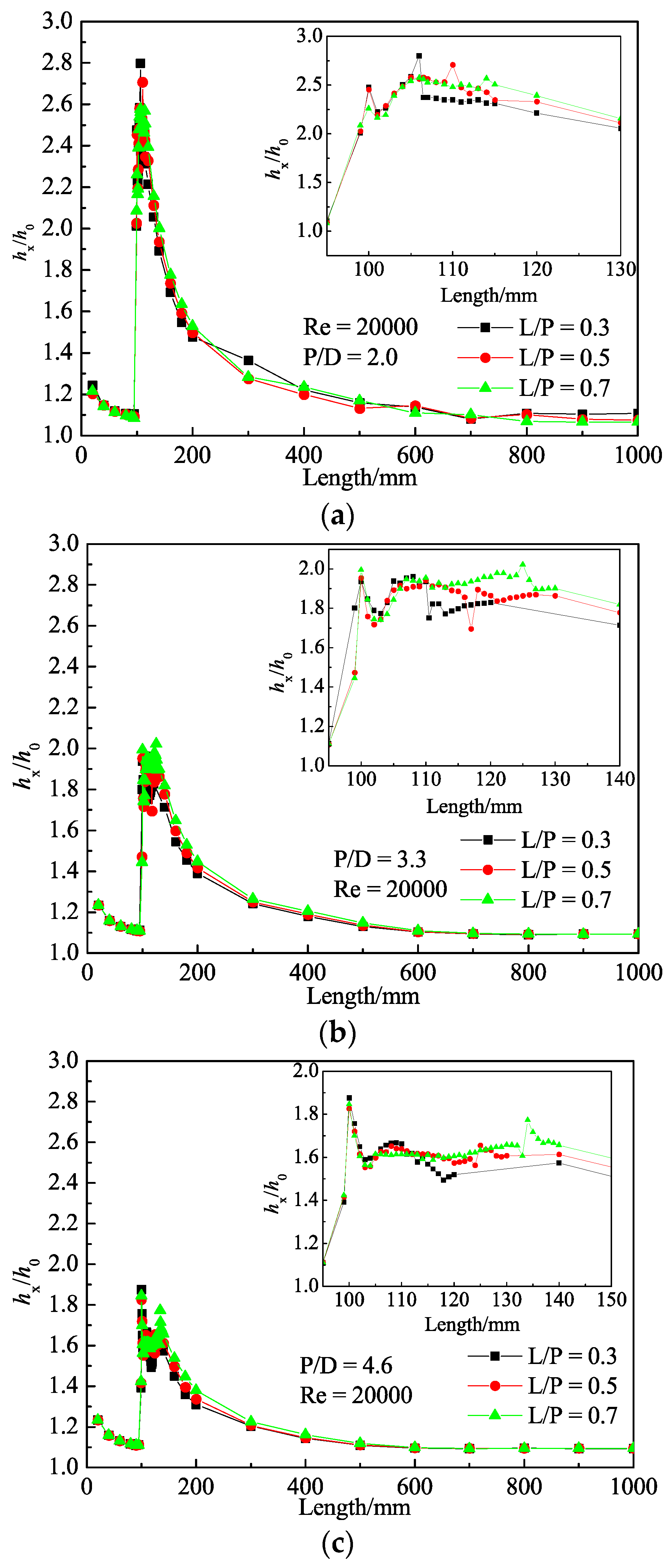
The difference in various operation conditions (different geometry configurations and Reynolds numbers) was numerically studied, and the results are plotted in
Figure 6. Generally,
hx/h0 experienced a sharp increase near 100 mm, where the segmented twisted tape is inserted. However, contrary to expectations, the Reynolds number seemed not to have a strong influence on the convective heat transfer coefficient. However, little different was observed in cases with the same
P/D and formed three distinctive group at different length ratios. The best performance observed in cases whose
P/D equalled 2.0 in every
L/P and
Re meant that the effect of the twist ratio (
P/D) surpassed the effect of the Reynolds number and dominated the overall range. The small discrepancy within a group may be explained by the following: The Reynolds number is calculated according to the condition at the inlet and may deviate from the actual fluid state in the local turbulent region. Thus, the acutely turbulent flow near the vortex generator could not be reflected accurately.
The investigation about the effect of length ratio (
L/P) at fixed
P/D on the local heat transfer coefficient was carried out and results at
Re = 20,000 are depicted in
Figure 7, in which a similar trend as in
Figure 6 is observed. As shown in the partially enlarged drawings, after peaking at the highest value,
hx/h0 reached a plateau and lasted until the end of the tape; then, a gradual decrease was observed. Smaller
L/P at fixed
P/D was witnessed by the earlier drop in the local heat transfer heat coefficient after the tape region, which could be read from the change of black dotted data points; even they experienced the same trend at first in accordance with the other twos. This difference can be explained by the early stoppage of the fierce turbulence region caused by twisted tape. In the following process, the tubes with longer tape generally had better performance, which meant the longer tape had positive impacts on heat transfer performance.
The influence of the length ratio with fixed
L/P on heat transfer enhancement is presented in
Figure 8. As shown in the pictures, the largest value, 2.8, was observed when
P/D equalled 2.0, while the lowest value was only 1.9 at point
P/D = 4.6. This local enhancement was better than that in [
38], even though only average data was available from that study. The smallest twist ratio (
P/D = 2.0) with constant length ratio (
L/P) witnessed the best performance, guaranteeing the highest value in the local region and along the rest of the tube. As discussed above, the length ratio had an influence on
hx/
h0, which caused the largest difference of about 0.2. However, the effect of the twist ratio still surpassed this effect, so it is safe to conclude that the twist ratio played a dominant role in heat transfer enhancement. One reason is that deviation around the
hx/
h0 was observed within a common range from 100 mm to 110 mm, in which all the different twisted tapes existed. Another is that after the common range, the deviation in all subplots could still be observed with the smallest twist ratio (
P/D = 2.0) remaining the largest.
4.3. Overall Heat Transfer Coefficient
The effect of twisted tapes in different twist ratios (
P/D) and length ratios (
L/P) on the heat transfer, friction factor and performance evaluation factor was studied and is presented in
Figure 9,
Figure 10 and
Figure 11. The outcomes of smooth tubes under the same Reynolds number were compared to the results in single-twisted-tape cases. As illustrated in
Figure 9, the dimensionless value of
Nu/Nu0 varied from 1.125 to 1.235, indicating the enhancement of segmented twisted tape in heat transfer. Displayed in different colours, three distinct zones in different twist ratios (
P/D) were observed, which means that a small twist ratio and large length ratio of inserted tape had positive impacts on the heat transfer enhancement. The quantitative results showed that the highest enhancement of mean heat transfer rate could reach up to 23.5% when
P/D = 2.0 and
L/P = 0.7. For specific cases with the fixed twist ratio, the longer the twisted tape was, the bigger the
Nu number was. This could be attributed to the fact that tape with a small twist ratio generated a strong swirl flow, causing a thinner thermal or hydrodynamic boundary layer and promoting heat exchange with the tube wall. Besides, the long smooth surface of twisted tapes contributed to the growth of swirl flow; thus, energy could be transferred fast and effectively across the boundary layer.
The frictional characteristic of twisted tapes is depicted in
Figure 10. Results show that the variance of friction factor
f became larger at specific Reynolds numbers when
P/D decreased, while a constant gap under different Reynolds numbers could be observed in the region highlighted in the same colour. The upward tendency was different from results given in other relevant works [
20,
31,
38], but as
P/D increased, the upward trend was weakened. This phenomenon may be attributed to the unique geometry features of the research interest.
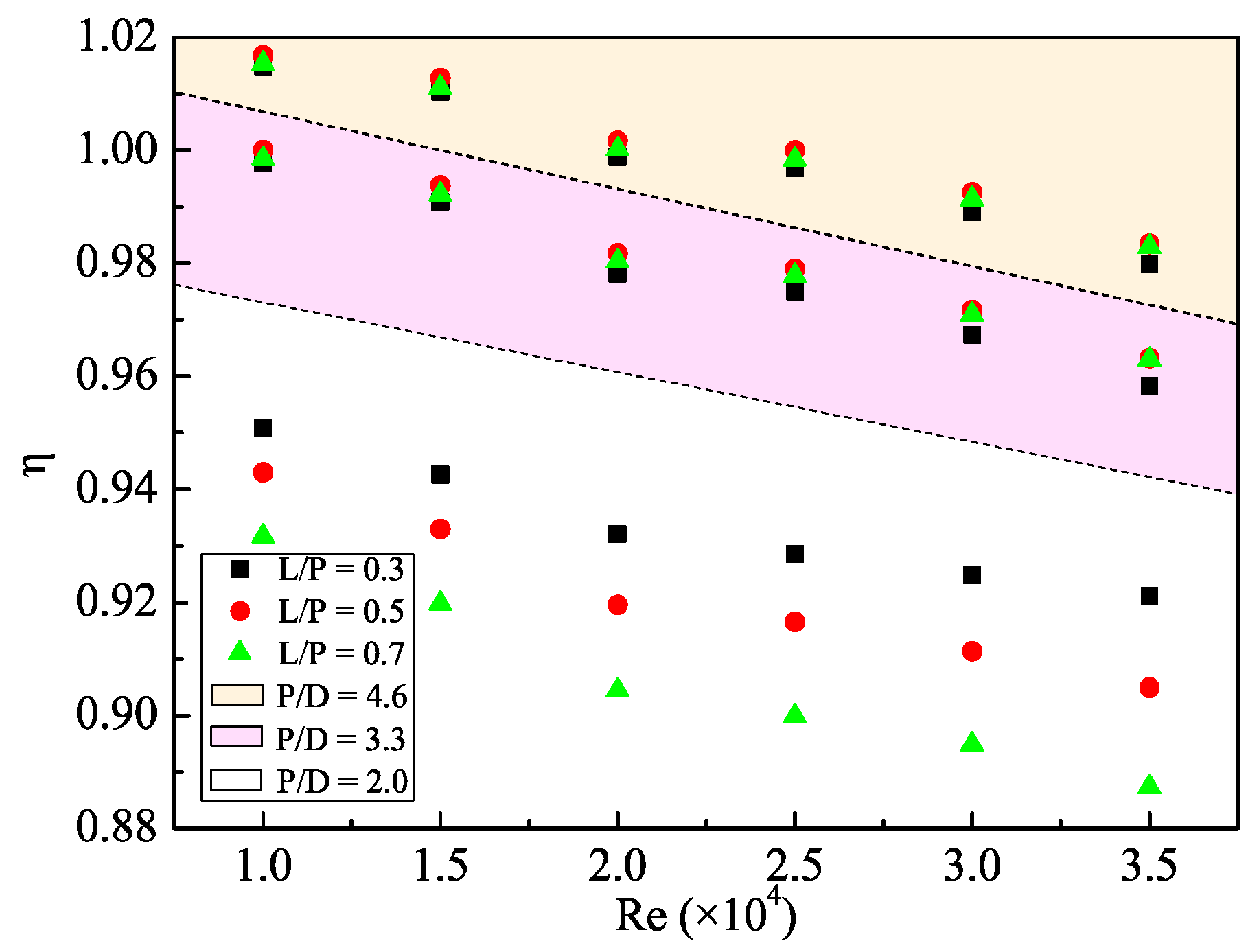
The performance evaluation factor of tubes with different twisted tapes obtained by computational simulation is given in
Figure 11, which shows the cost of saved energy. The best performance was obtained in tubes with tapes having twist ratio
P/D = 4.6 at small Reynolds numbers, with
η reaching slightly over 1, while the lowest value of
η at 0.887 was observed when
P/D = 2.0 when
Re = 35,000. It can be implied that low Reynolds number was friendlier to this design. This means that due to the increase of Reynolds number, the friction factor
f gradually became larger and began to dominate over the gain of heat transfer enhancement.