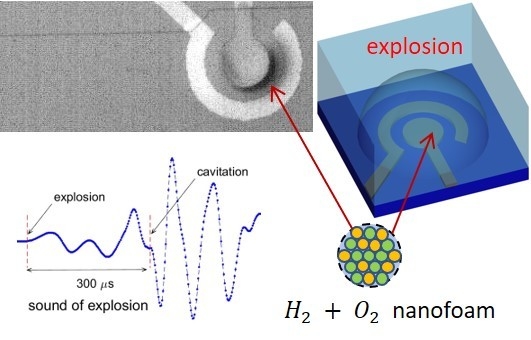
Explosion of Microbubbles Generated by the Alternating Polarity Water Electrolysis
Abstract
1. Introduction
2. Experiment
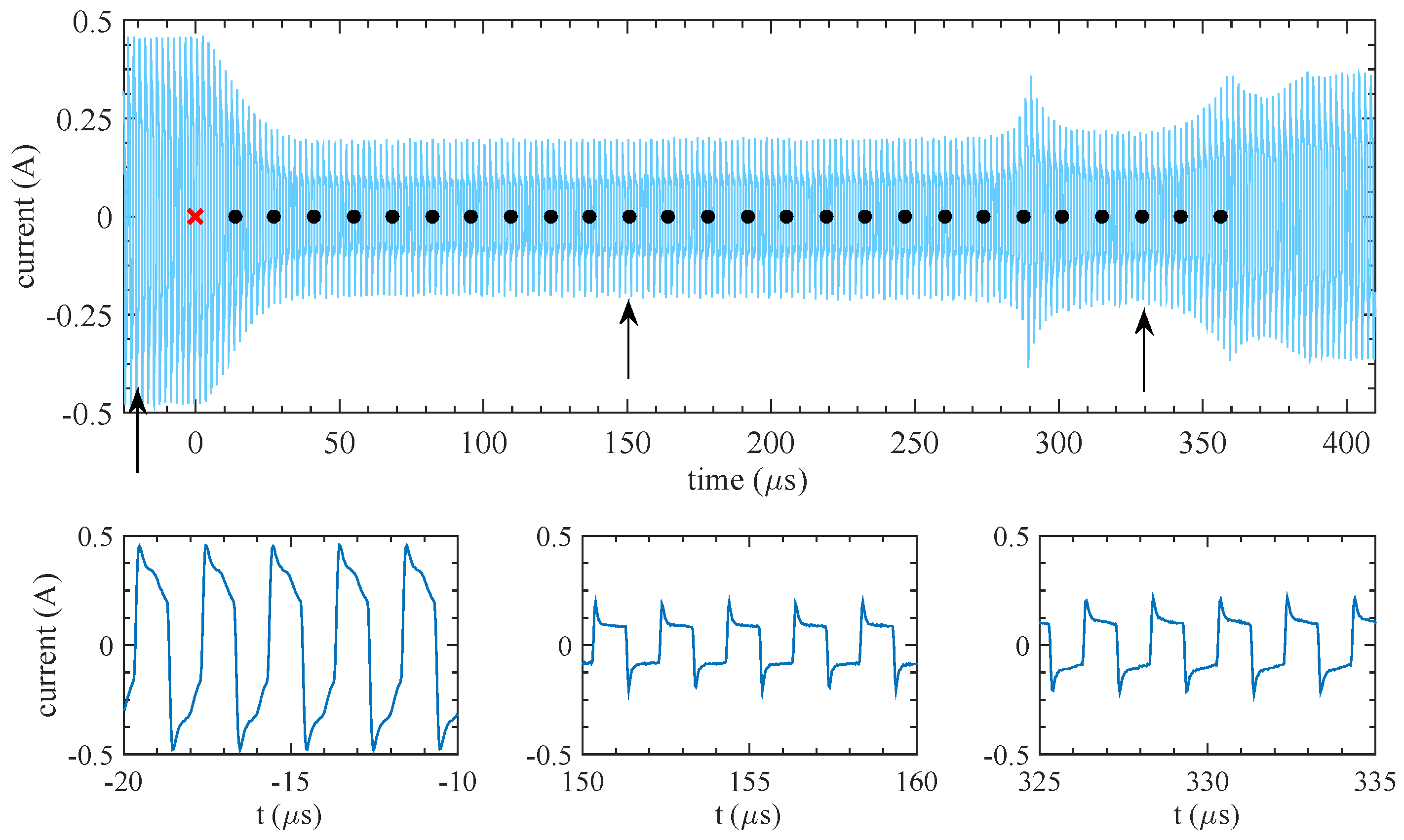
2.1. Materials and Methods
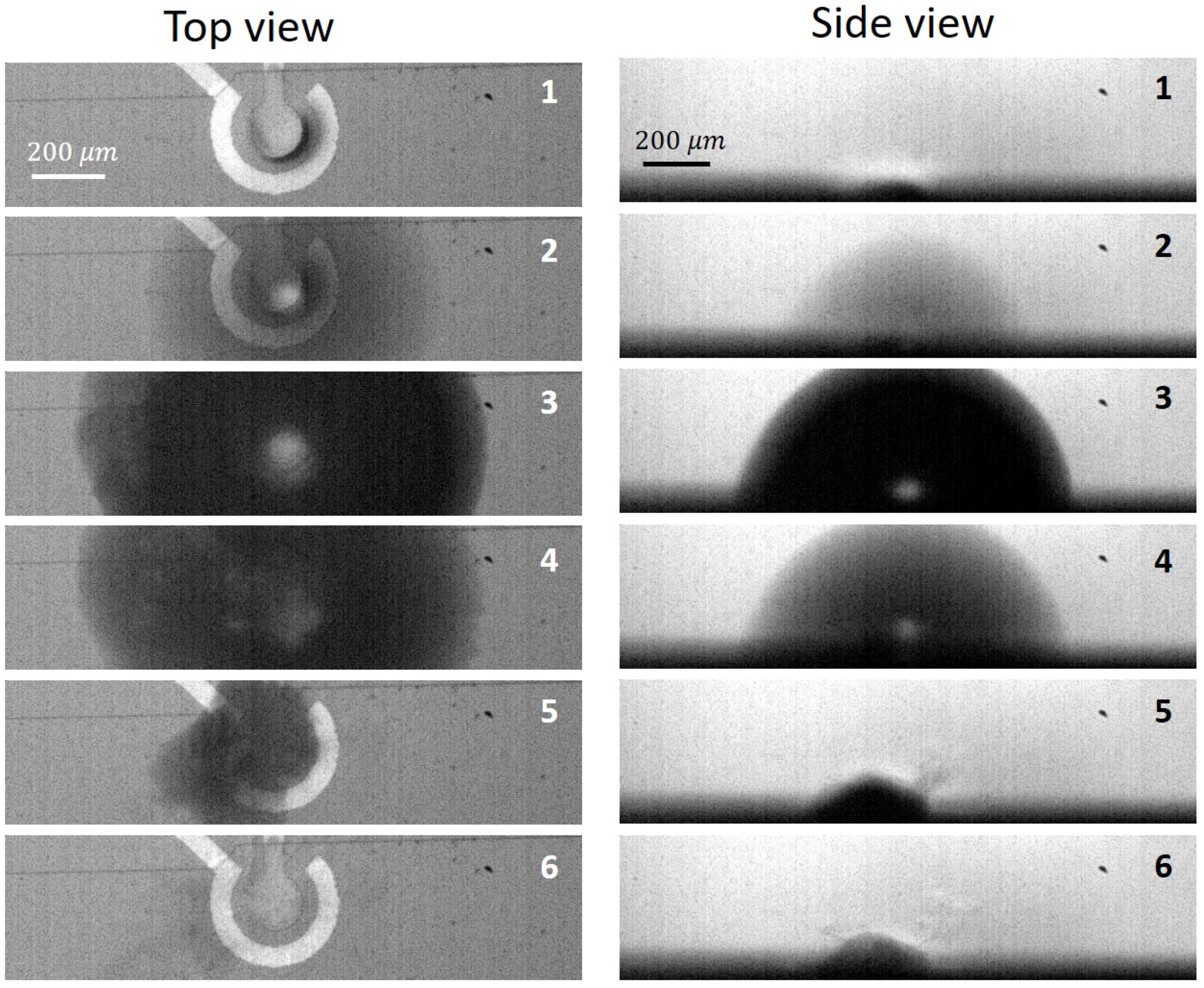
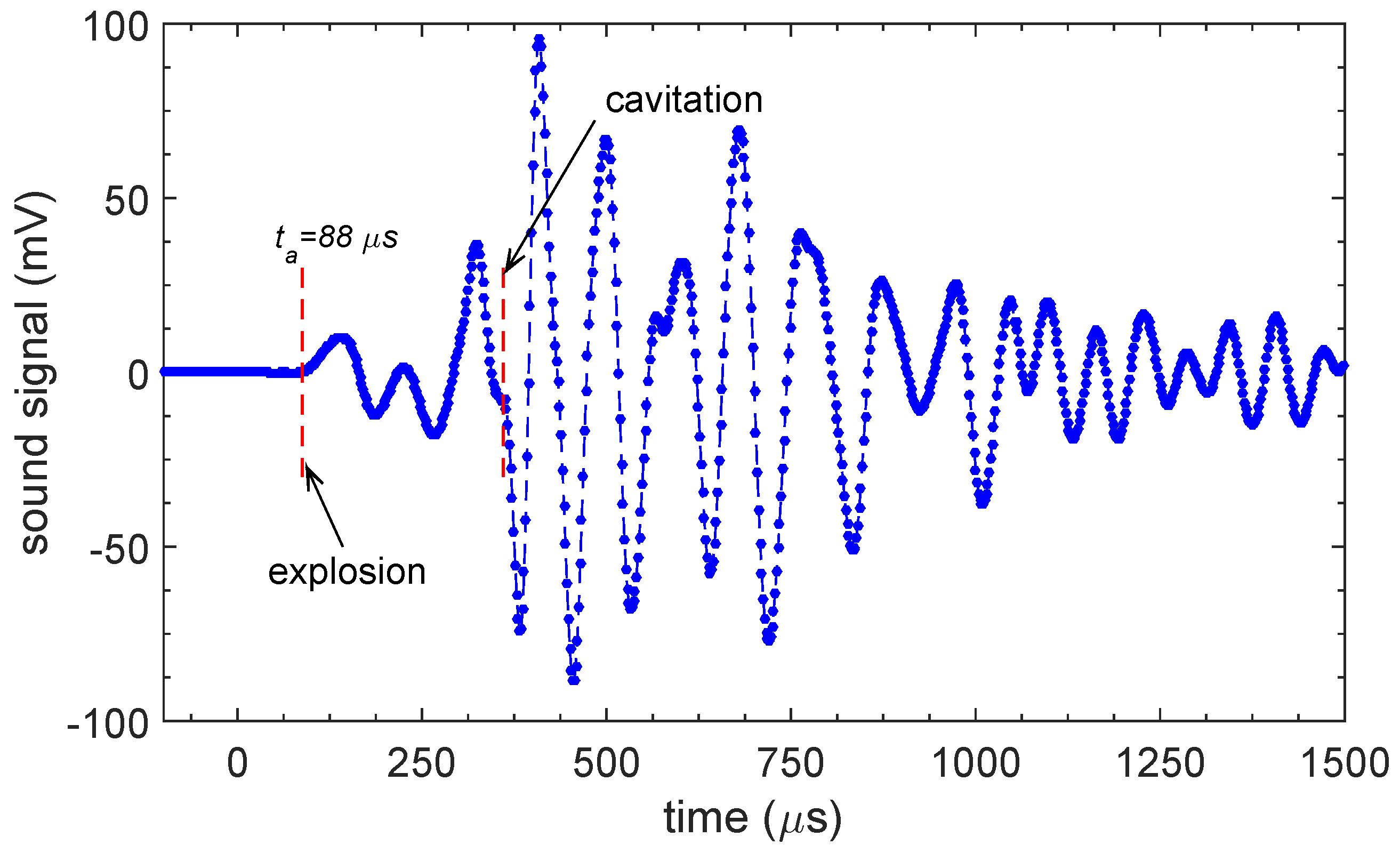
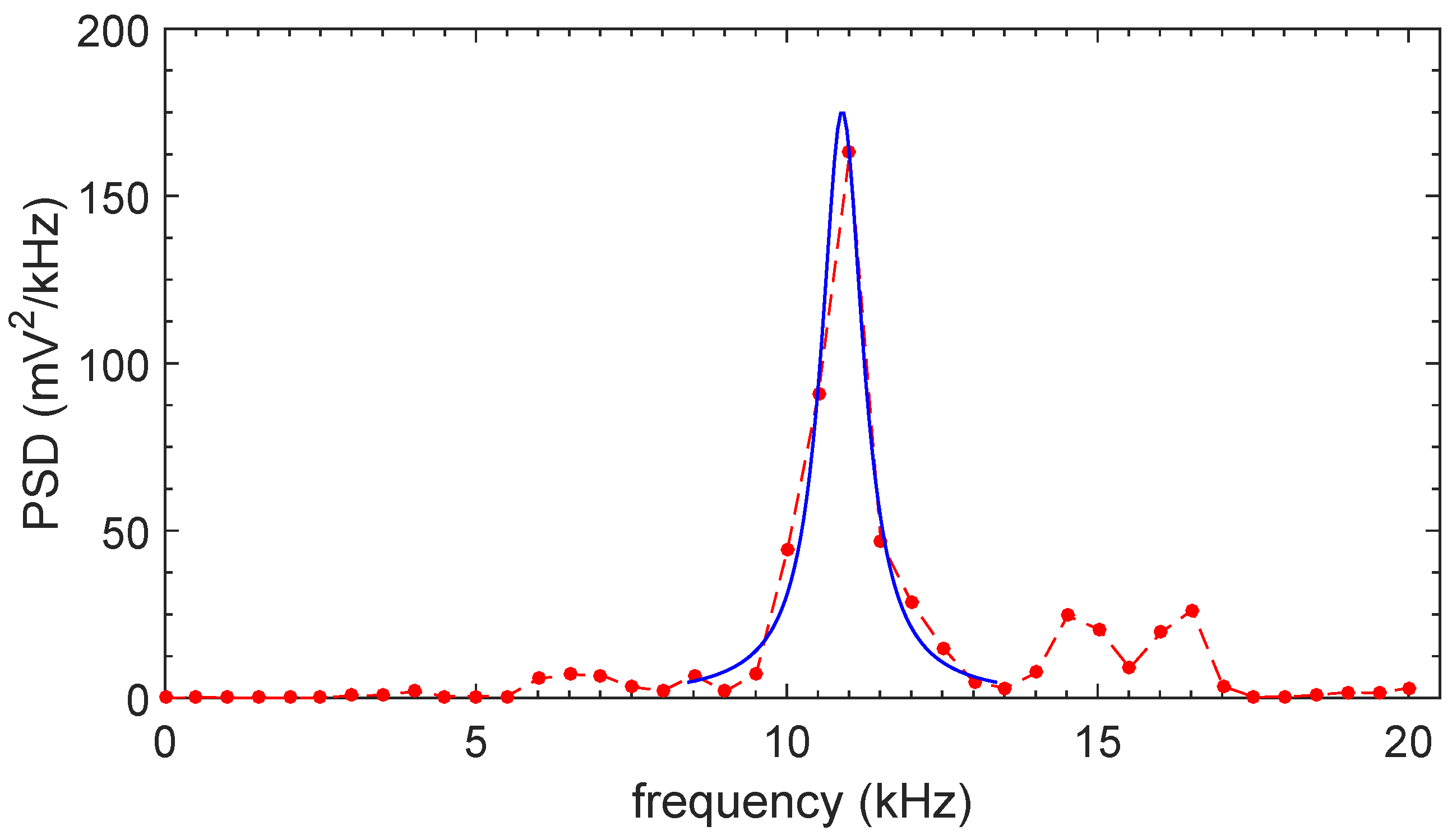
2.2. Results
3. Theory
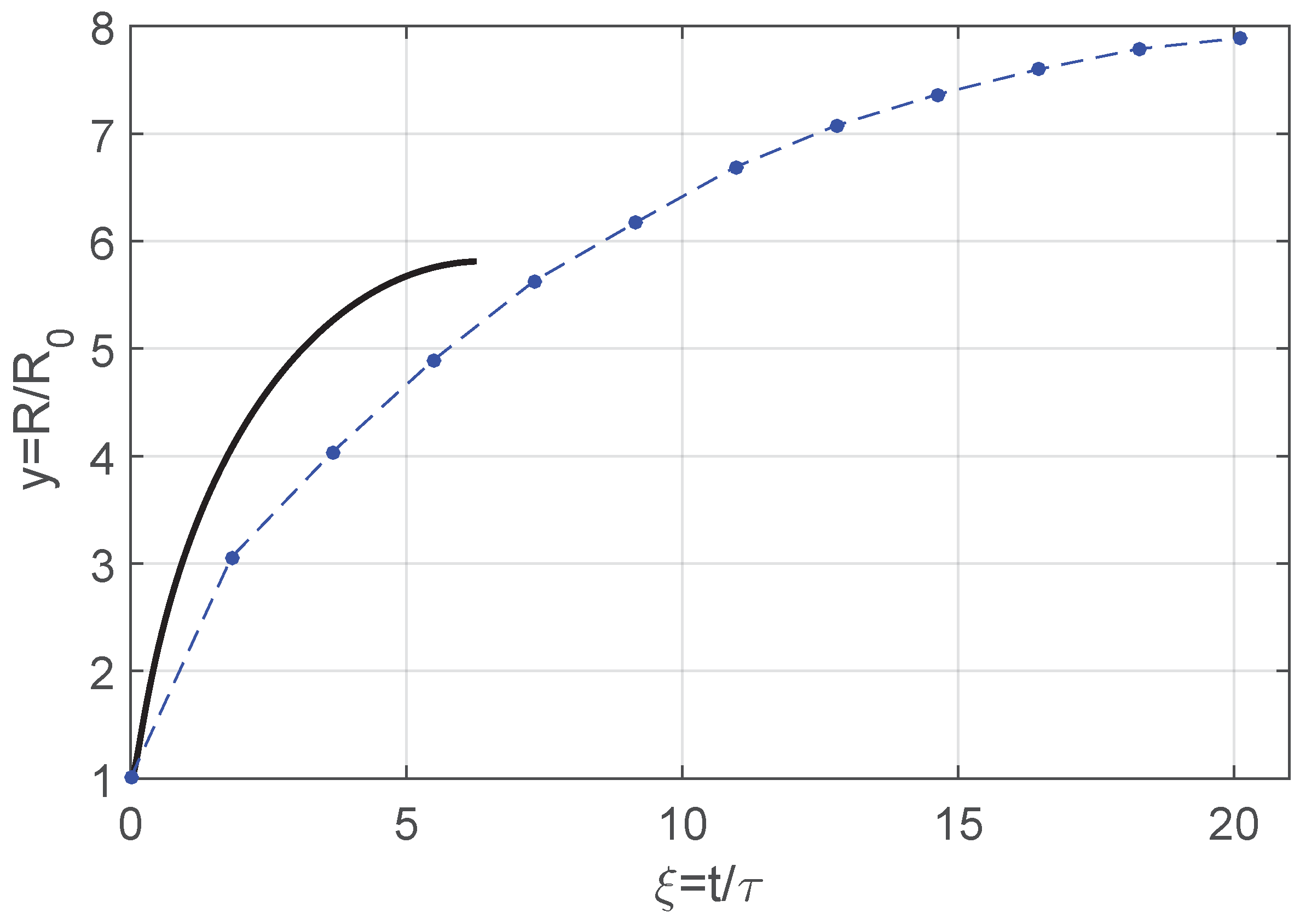
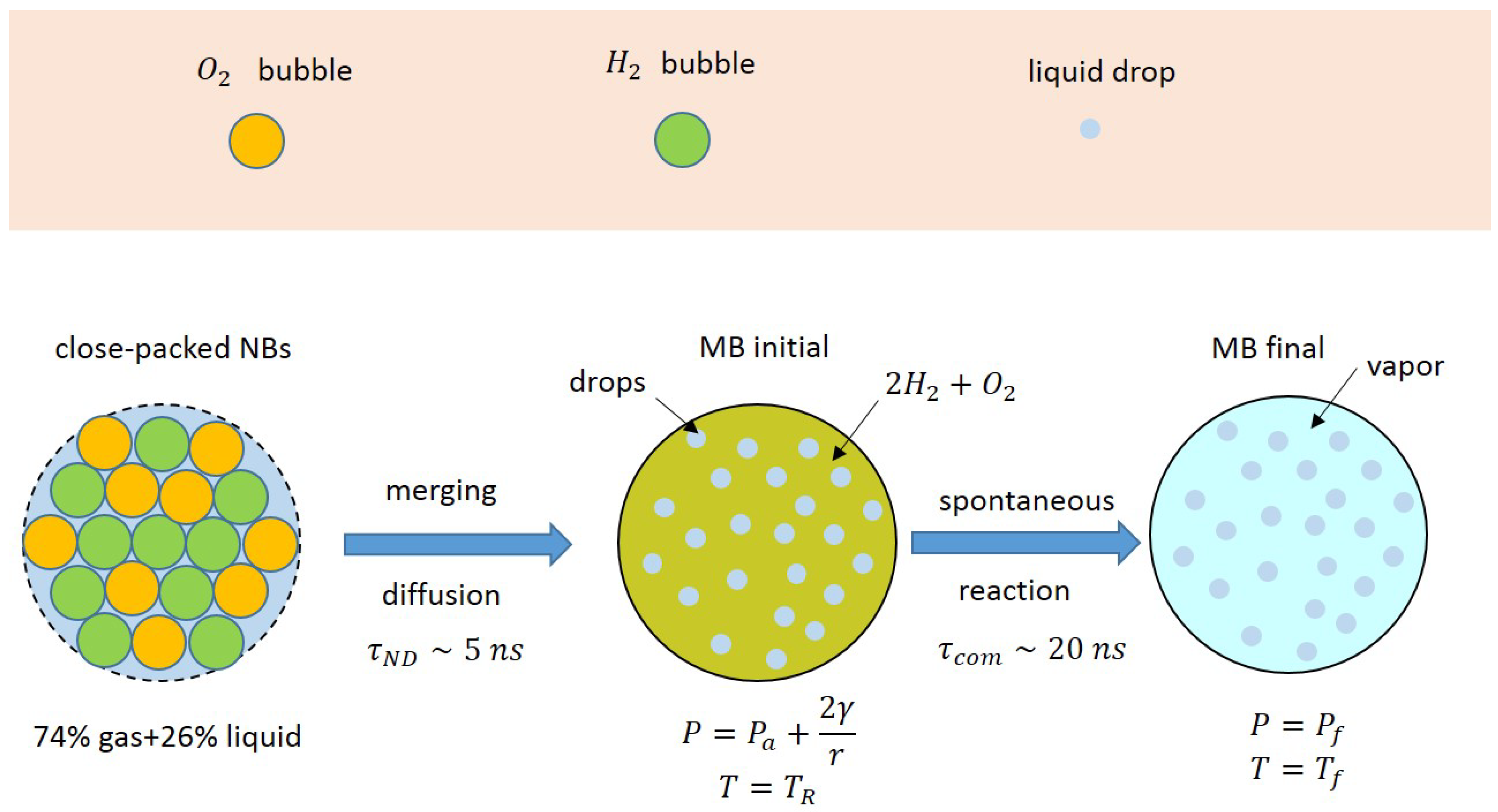
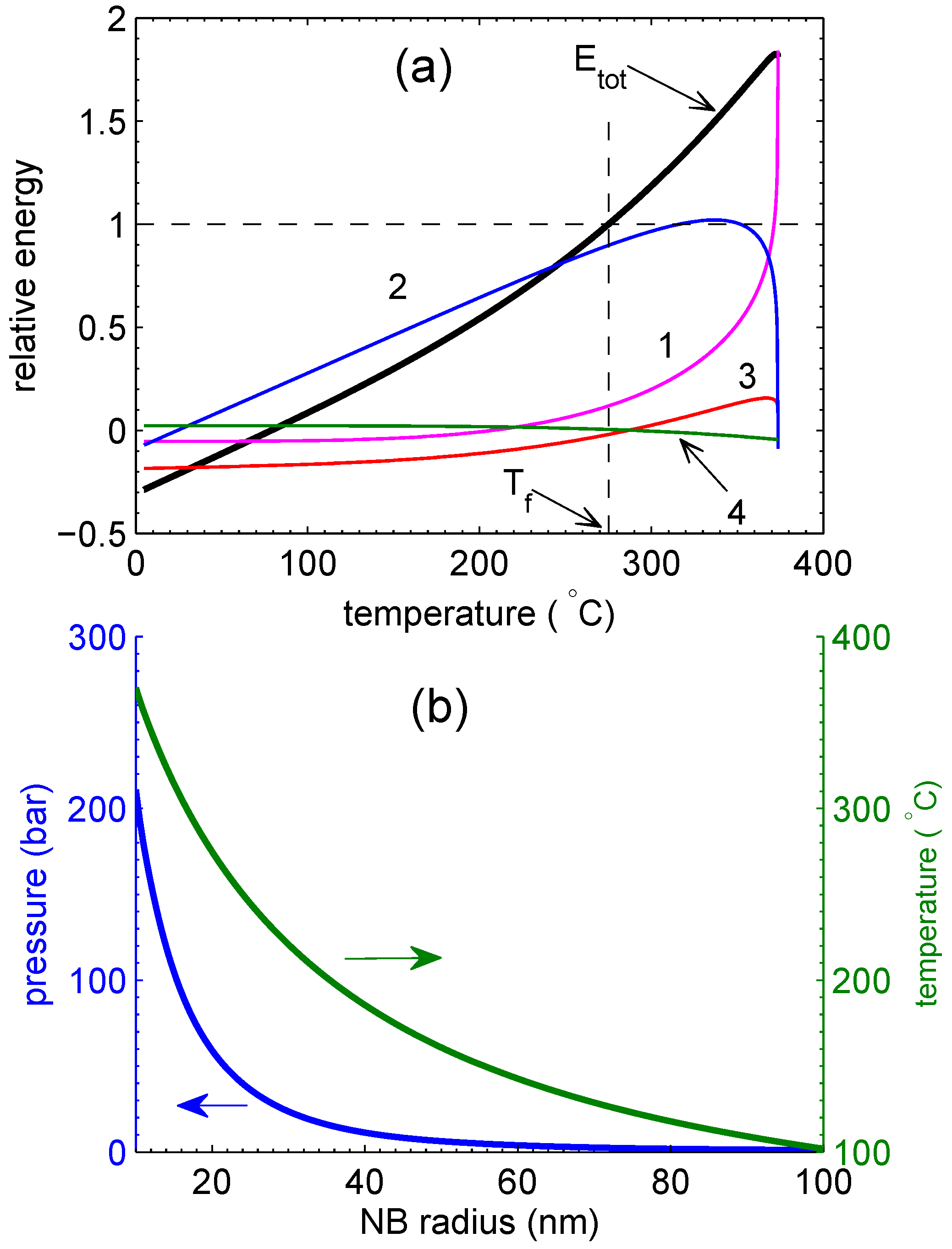
3.1. Qualitative Model
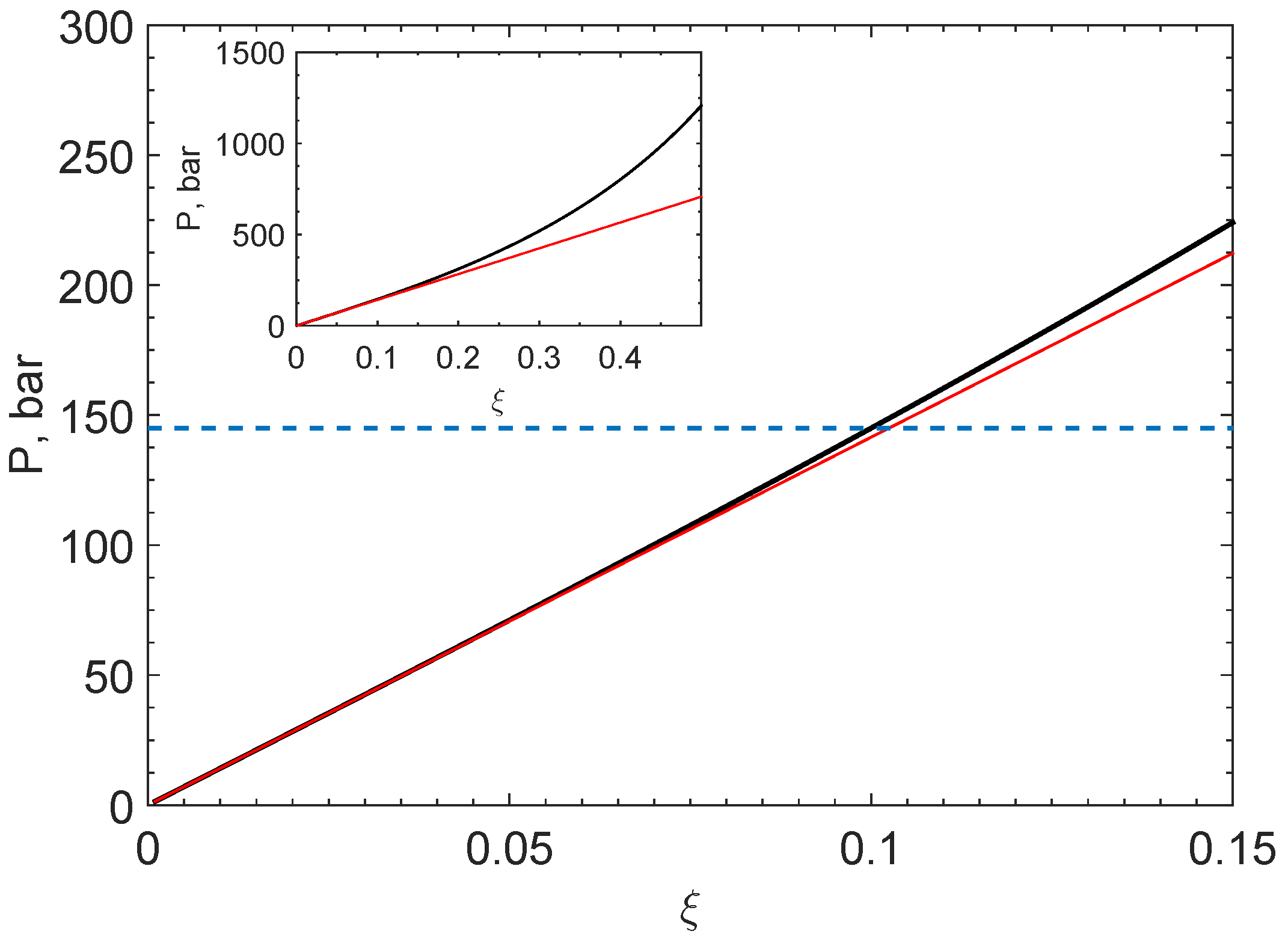
3.2. Energy Balance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Brandon, N.P.; Kelsall, G.H. Growth kinetics of bubbles electrogenerated at microelectrodes. J. Appl. Electrochem. 1985, 15, 475–484. [Google Scholar] [CrossRef]
- Matsushima, H.; Kiuchi, D.; Fukunaka, Y.; Kuribayashi, K. Single bubble growth during water electrolysis under microgravity. Electrochem. Commun. 2009, 11, 1721–1723. [Google Scholar] [CrossRef]
- Vogt, H.; Balzer, R. The bubble coverage of gas-evolving electrodes in stagnant electrolytes. Electrochem. Acta 2005, 50, 2073–2079. [Google Scholar] [CrossRef]
- Vogt, H. Interfacial supersaturation at gas evolving electrodes. J. Appl. Electrochem. 1993, 23, 1323–1325. [Google Scholar] [CrossRef]
- Hine, F.; Yasuda, M.; Nakamura, R.; Noda, T. Hydrodynamic Studies of Bubble Effects on the IR-Drops in a Vertical Rectangular Cell. J. Electrochem. Soc. 1975, 122, 1185–1190. [Google Scholar] [CrossRef]
- Vogt, H. The incremental ohmic resistance caused by bubbles adhering to an electrode. J. Appl. Electrochem. 1983, 13, 87–88. [Google Scholar] [CrossRef]
- Luo, L.; White, H.S. Electrogeneration of Single Nanobubbles at Sub-50-nm-Radius Platinum Nanodisk Electrodes. Langmuir 2013, 29, 11169–11175. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; Sanders, R.G.P.; Elwenspoek, M.C. Transient nanobubbles in short-time electrolysis. J. Phys. Condens. Matter 2013, 25, 184002. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; Sanders, R.G.P.; Lammerink, T.S.J.; Elwenspoek, M.C. Combustion of hydrogen-oxygen mixture in electrochemically generated nanobubbles. Phys. Rev. E 2011, 84, 035302. [Google Scholar] [CrossRef]
- Postnikov, A.V.; Uvarov, I.V.; Penkov, N.V.; Svetovoy, V.B. Collective behavior of bulk nanobubbles produced by alternating polarity electrolysis. Nanoscale 2018, 10, 428–435. [Google Scholar] [CrossRef]
- Seddon, J.R.T.; Lohse, D.; Ducker, W.A.; Craig, V.S.J. A Deliberation on Nanobubbles at Surfaces and in Bulk. Chem. Phys. Chem. 2012, 13, 2179–2187. [Google Scholar] [CrossRef] [PubMed]
- Lohse, D.; Zhang, X. Surface nanobubbles and nanodroplets. Rev. Mod. Phys. 2015, 87, 981–1035. [Google Scholar] [CrossRef]
- Alheshibri, M.; Qian, J.; Jehannin, M.; Craig, V.S.J. A History of Nanobubbles. Langmuir 2016, 32, 11086–11100. [Google Scholar] [CrossRef] [PubMed]
- Ohgaki, K.; Khanh, N.Q.; Joden, Y.; Tsuji, A.; Nakagawa, T. Physicochemical approach to nanobubble solutions. Chem. Eng. Sci. 2010, 65, 1296–1300. [Google Scholar] [CrossRef]
- Ushikubo, F.Y.; Furukawa, T.; Nakagawa, R.; Enari, M.; Makino, Y.; Kawagoe, Y.; Shiina, T.; Oshita, S. Evidence of the existence and the stability of nano-bubbles in water. Colloids Surf. A Physicochem. Eng. Asp. 2010, 361, 31–37. [Google Scholar] [CrossRef]
- Kikuchi, K.; Nagata, S.; Tanaka, Y.; Saihara, Y.; Ogumi, Z. Characteristics of hydrogen nanobubbles in solutions obtained with water electrolysis. J. Electroanal. Chem. 2007, 600, 303–310. [Google Scholar] [CrossRef]
- Jie, Q.; Zhenglei, Z.; Shuo, W.; Xingya, W.; Lei, W.; Yaming, D.; Hongwei, Z.; Lijuan, Z.; Jun, H. Formation and Stability of Bulk Nanobubbles Generated by Ethanol–Water Exchange. ChemPhysChem 2017, 18, 1345–1350. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Shkirin, A.V.; Ignatiev, P.S.; Chaikov, L.L.; Burkhanov, I.S.; Starosvetskij, A.V. Nanobubble clusters of dissolved gas in aqueous solutions of electrolyte. I. Experimental proof. J. Chem. Phys. 2012, 137, 054706. [Google Scholar] [CrossRef]
- Zhu, J.; An, H.; Alheshibri, M.; Liu, L.; Terpstra, P.M.J.; Liu, G.; Craig, V.S.J. Cleaning with Bulk Nanobubbles. Langmuir 2016, 32, 11203–11211. [Google Scholar] [CrossRef]
- Yurchenko, S.O.; Shkirin, A.V.; Ninham, B.W.; Sychev, A.A.; Babenko, V.A.; Penkov, N.V.; Kryuchkov, N.P.; Bunkin, N.F. Ion-Specific and Thermal Effects in the Stabilization of the Gas Nanobubble Phase in Bulk Aqueous Electrolyte Solutions. Langmuir 2016, 32, 11245–11255. [Google Scholar] [CrossRef]
- Postnikov, A.V.; Uvarov, I.V.; Lokhanin, M.V.; Svetovoy, V.B. Electrically controlled cloud of bulk nanobubbles in water solutions. PLoS ONE 2017, 12, e0181727. [Google Scholar] [CrossRef] [PubMed]
- Postnikov, A.V.; Uvarov, I.V.; Lokhanin, M.V.; Svetovoy, V.B. High concentration of H2 and O2 nanobubbles in water electrolytes and their collective optical effect. AIP Conf. Proc. 2017, 1884, 030003. [Google Scholar] [CrossRef]
- Postnikov, A.V.; Uvarov, I.V.; Lokhanin, M.V.; Svetovoy, V.B. Highly energetic phenomena in water electrolysis. Sci. Rep. 2016, 6, 39381. [Google Scholar] [CrossRef] [PubMed]
- Prokaznikov, A.; Tas, N.; Svetovoy, V. Surface Assisted Combustion of Hydrogen-Oxygen Mixture in Nanobubbles Produced by Electrolysis. Energies 2017, 10, 178. [Google Scholar] [CrossRef]
- Jain, S.; Qiao, L. Understanding Combustion of H2/O2 Gases inside Nanobubbles Generated by Water Electrolysis Using Reactive Molecular Dynamic Simulations. J. Phys. Chem. A 2018, 122, 5261–5269. [Google Scholar] [CrossRef]
- Uvarov, I.V.; Lokhanin, M.V.; Postnikov, A.V.; Melenev, A.E.; Svetovoy, V.B. Electrochemical membrane microactuator with a millisecond response time. Sens. Actuator B Chem. 2018, 260, 12–20. [Google Scholar] [CrossRef]
- Veser, G. Experimental and theoretical investigation of H2 oxidation in a high-temperature catalytic microreactor. Chem. Eng. Sci. 2001, 56, 1265–1273. [Google Scholar] [CrossRef]
- Fernandez-Pello, A.C. Micropower generation using combustion: Issues and approaches. Proc. Combust. Inst. 2002, 29, 883–899. [Google Scholar] [CrossRef]
- Schäfer, H.; Chatenet, M. Steel: The Resurrection of a Forgotten Water-Splitting Catalyst. ACS Energy Lett. 2018, 3, 574–591. [Google Scholar] [CrossRef]
- Shlepakov, P.S.; Uvarov, I.V.; Naumov, V.V.; Mazaletskiy, L.A.; Svetovoy, V.B. Degradation of Titanium Electrodes in the Alternating Polarity Electrolysis. Int. J. Electrochem. Sci. 2019, 14, 5211–5225. [Google Scholar] [CrossRef]
- Ceccio, S.L.; Brennen, C.E. Observations of the dynamics and acoustics of travelling bubble cavitation. J. Fluid Mech. 1991, 233, 633–660. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Churaev, N.V.; Muller, V.M. Surface Forces; Plenum Publishing Corporation: New York, NY, USA, 1987. [Google Scholar]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Elsevier: Oxford, UK, 1987. [Google Scholar]
- Postnikov, A.V.; Uvarov, I.V.; Prokaznikov, A.V.; Svetovoy, V.B. Observation of spontaneous combustion of hydrogen and oxygen in microbubbles. Appl. Phys. Lett. 2016, 108, 121604. [Google Scholar] [CrossRef]
- Eddi, A.; Winkels, K.G.; Snoeijer, J.H. Short time dynamics of viscous drop spreading. Phys. Fluids 2013, 25, 013102. [Google Scholar] [CrossRef]
- Vargaftik, N.B.; Vinogradov, Y.R.; Yargin, V.S. Handbook of Physical Properties of Liquids and Gases: Pure Substances and Mixtures, 3rd ed.; Begell House: New York, NY, USA, 1996. [Google Scholar]
- Beaton, C.F.; Hewitt, G.F. Physical Property Data for the Design Engineer; CRC Press: New York, NY, USA, 1988. [Google Scholar]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fund. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Pohl, S.; Jarczyk, M.; Pfitzner, M.; Rogg, B. Real gas CFD simulations of hydrogen/oxygen supercritical combustion. Prog. Propul. Phys. 2013, 4, 583–614. [Google Scholar]
- Azatyan, A.A.; Andrianova, Z.S.; Ivanova, A.N. Role of the HO2 radical in hydrogen oxidation at the third self-ignition limit. Kinet. Catal. 2010, 51, 337–347. [Google Scholar] [CrossRef]
- Wang, X.; Law, C.K. An analysis of the explosion limits of hydrogen-oxygen mixtures. J. Chem. Phys. 2013, 138, 134305. [Google Scholar] [CrossRef]
- Teslenko, V.S.; Manzhalei, V.I.; Medvedev, R.N.; Drozhzhin, A.P. Burning of Hydrocarbon Fuels Directly in a Water-Based Heat Carrier. Combust. Explos. Shock Waves 2010, 46, 486–489. [Google Scholar] [CrossRef]
- Takahashi, M.; Chiba, K.; Li, P. Free-Radical Generation from Collapsing Microbubbles in the Absence of a Dynamic Stimulus. J. Phys. Chem. B 2007, 111, 1343–1347. [Google Scholar] [CrossRef]
- Li, P.; Takahashi, M.; Chiba, K. Enhanced free-radical generation by shrinking microbubbles using a copper catalyst. Chemosphere 2009, 77, 1157–1160. [Google Scholar] [CrossRef]
- Beattie, J.K.; Djerdjev, A.M.; Warr, G.G. The surface of neat water is basic. Faraday Discuss. 2009, 141, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Vácha, R.; Marsalek, O.; Willard, A.P.; Bonthuis, D.J.; Netz, R.R.; Jungwirth, P. Charge Transfer between Water Molecules As the Possible Origin of the Observed Charging at the Surface of Pure Water. J. Phys. Chem. Lett. 2012, 3, 107–111. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svetovoy, V.B.; Prokaznikov, A.V.; Postnikov, A.V.; Uvarov, I.V.; Palasantzas, G. Explosion of Microbubbles Generated by the Alternating Polarity Water Electrolysis. Energies 2020, 13, 20. https://doi.org/10.3390/en13010020
Svetovoy VB, Prokaznikov AV, Postnikov AV, Uvarov IV, Palasantzas G. Explosion of Microbubbles Generated by the Alternating Polarity Water Electrolysis. Energies. 2020; 13(1):20. https://doi.org/10.3390/en13010020
Chicago/Turabian StyleSvetovoy, Vitaly B., Alexander V. Prokaznikov, Alexander V. Postnikov, Ilia V. Uvarov, and George Palasantzas. 2020. "Explosion of Microbubbles Generated by the Alternating Polarity Water Electrolysis" Energies 13, no. 1: 20. https://doi.org/10.3390/en13010020
APA StyleSvetovoy, V. B., Prokaznikov, A. V., Postnikov, A. V., Uvarov, I. V., & Palasantzas, G. (2020). Explosion of Microbubbles Generated by the Alternating Polarity Water Electrolysis. Energies, 13(1), 20. https://doi.org/10.3390/en13010020