A Novel Nonintrusive Load Monitoring Approach based on Linear-Chain Conditional Random Fields
Abstract
1. Introduction
1.1. Background
1.2. Literature Review and Motivation
1.3. Contributions
- We proposed a method called the linear-chain CRF model for load disaggregation and achieved accuracy of 96.04–99.94%. It is demonstrated that this method is effective for the NILM task.
- Because we relaxed the independent assumption required by HMM-based models and avoided the label bias problem, the performance is enhanced by 2.21% compared to existing models.
- We combined two promising features: current signals and real power measurements to build our model, which improved the accuracy of the model significantly.
2. Methodology
2.1. Probability Mass Functions
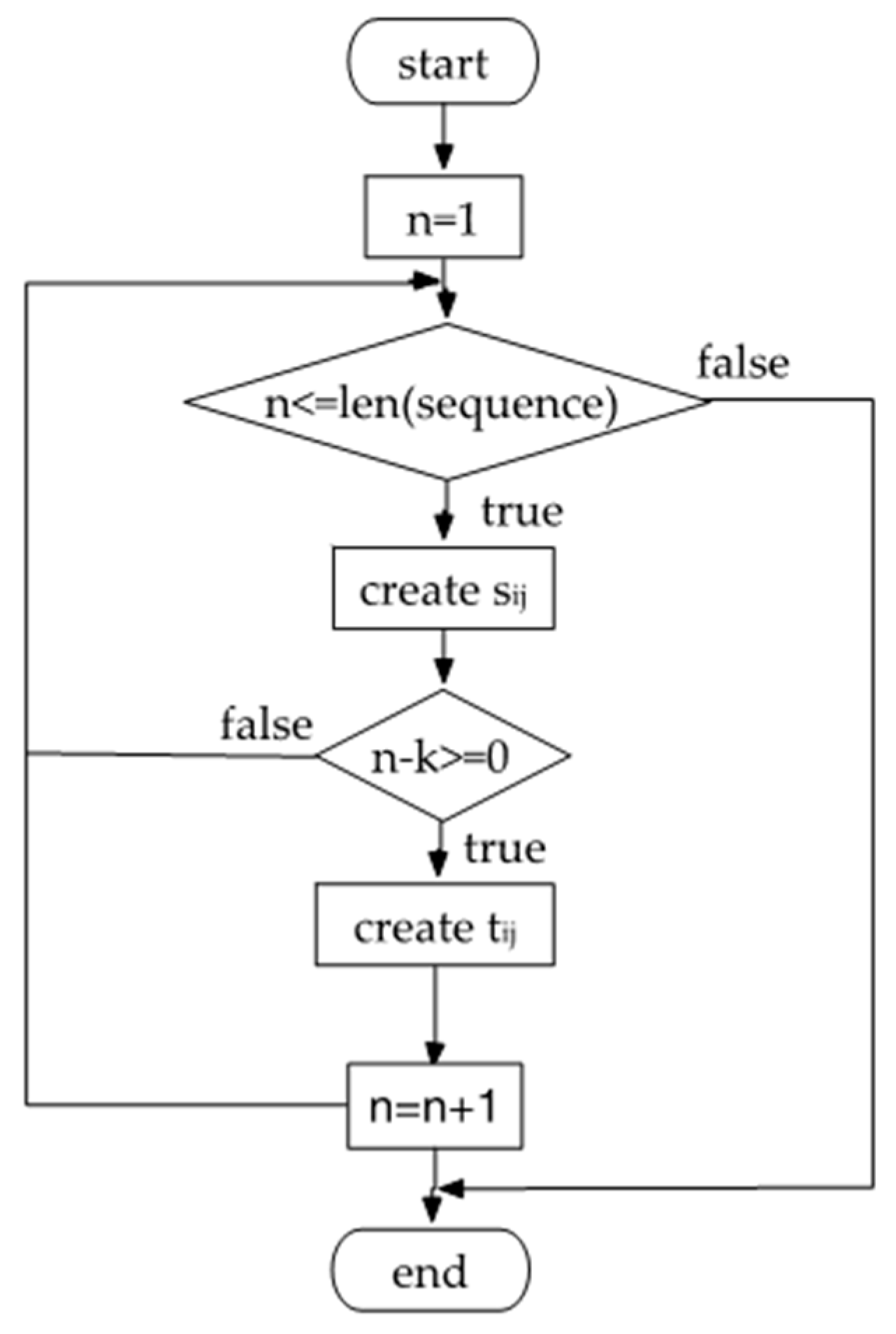
2.2. Segmenting Data
2.3. Extracting Features
2.4. Improved Iterative Scaling (IIS) Algorithm
| Algorithm 1. Improved iterative scaling algorithm. |
| 1: for k ∈ (1, M) |
| 2: ωk = 0 |
| 3: repeat |
| 4: for k ∈ (1, M) |
| 5: if k ∈ (1, M1) |
| 6: |
| 7: if k ∈ (M1 + 1, M) |
| 8: |
| 9: ωk ← ωk + δk |
| 10: until ωk converge |
2.5. Viterbi Algorithm
| Algorithm 2. Viterbi algorithm for CRF prediction. |
| 1: Step 1: initialization |
| 2: for j ∈ (1, m) |
| 3: |
| 4: Step 2: recursion |
| 5: for i ∈ (2, n) |
| 6: |
| 7: |
| 8: l = 1, 2, ..., m |
| 9: Step 3: terminate |
| 10: |
| 11: |
| 12: Step 4: traceback |
| 13: for i ∈ (n − 1, 1) |
| 14: |
3. Experiment and Analysis
3.1. Data
3.2. Experimental Setup
3.3. Evaluation Metrics
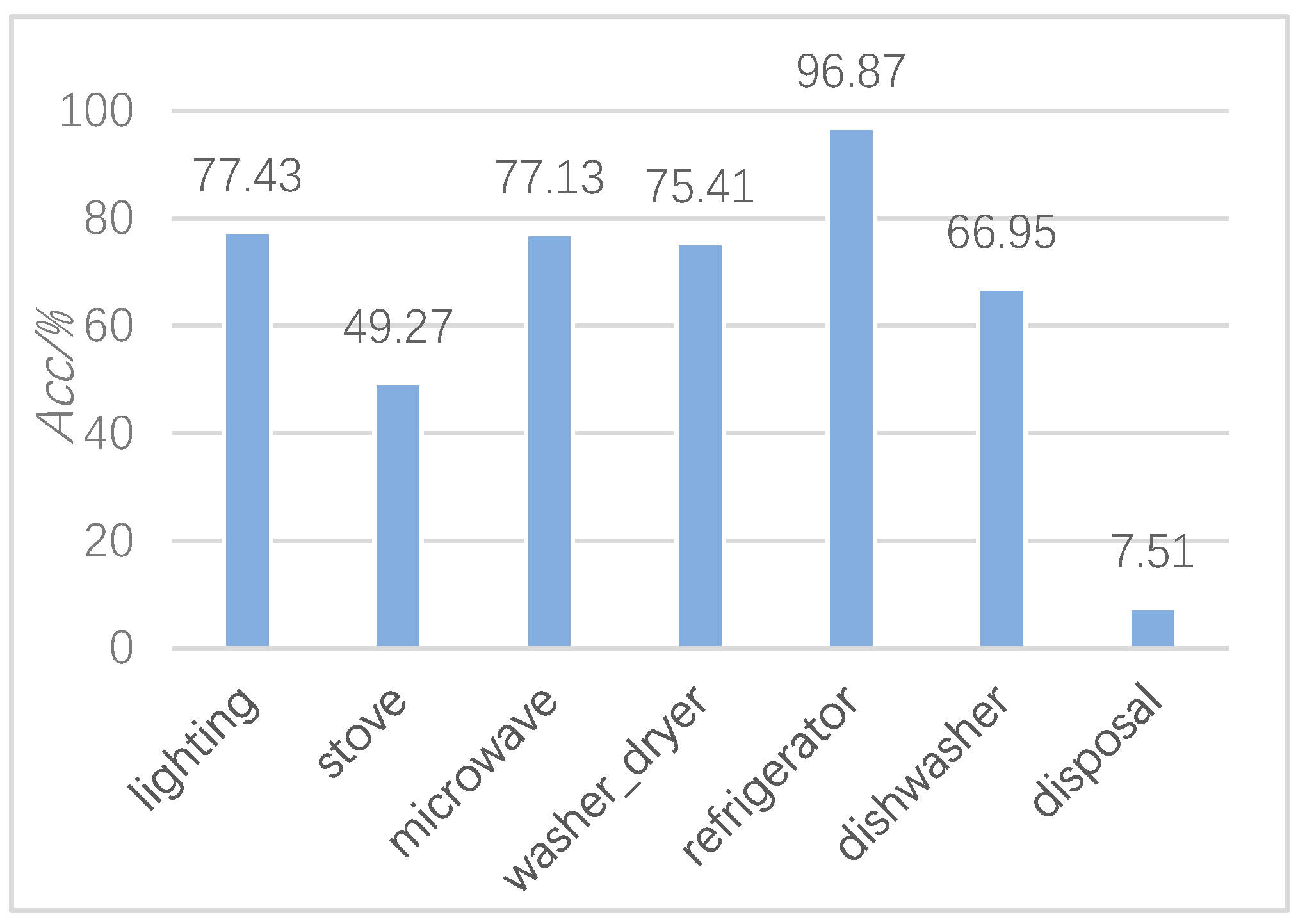
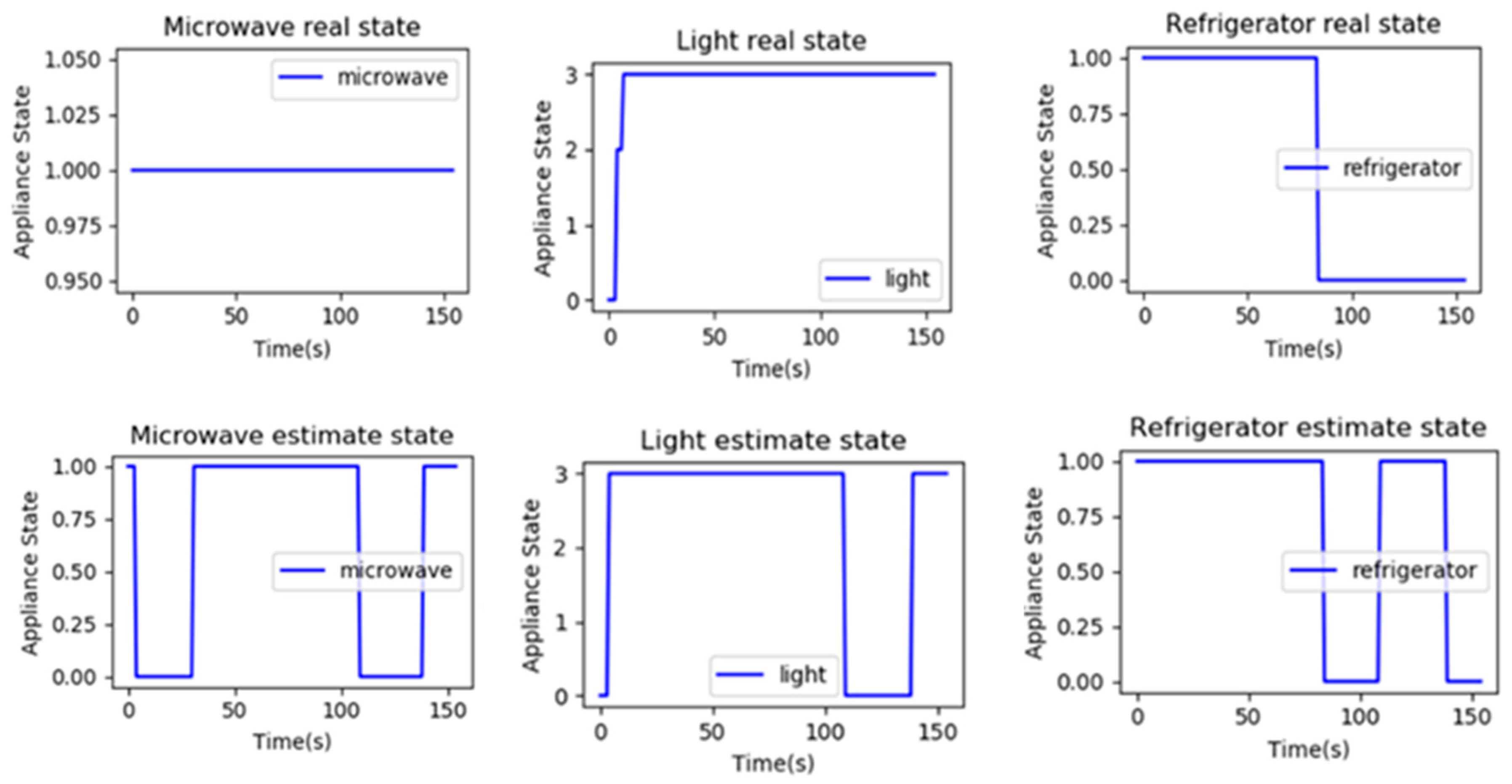
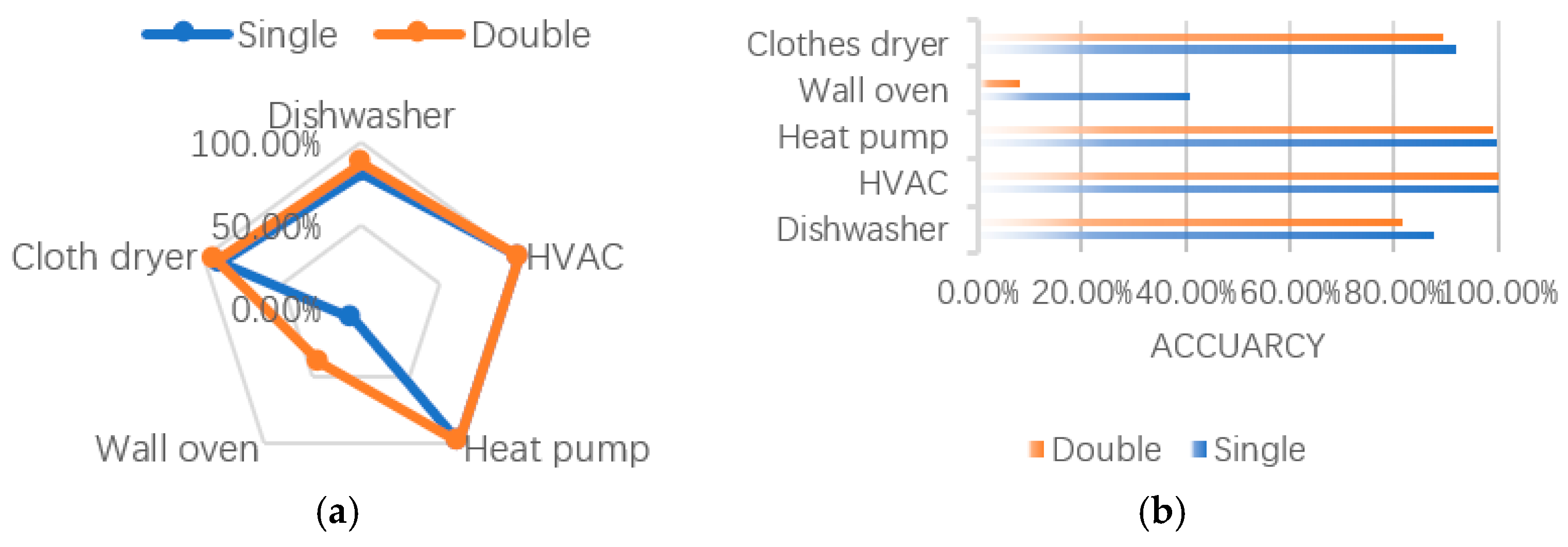
3.4. Experiment Results and Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hart, G.W. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Lin, G.; Lee, S.; Hsu, J.Y.; Jih, W. Applying power meters for appliance recognition on the electric panel. In Proceedings of the 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 2254–2259. [Google Scholar]
- Chui, K.T.; Lytras, M.D.; Visvizi, A. Energy Sustainability in Smart Cities: Artificial Intelligence, Smart Monitoring, and Optimization of Energy Consumption. Energies 2018, 11, 2869. [Google Scholar] [CrossRef]
- Lai, Y.X.; Lai, C.F.; Huang, Y.M.; Chao, H.C. Multi-appliance recognition system with hybrid SVM/GMM classifier in ubiquitous smart home. Inf. Sci. 2013, 230, 39–55. [Google Scholar] [CrossRef]
- Zia, T.; Bruckner, D.; Zaidi, A. A hidden Markov model-based procedure for identifying household electric loads. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 3218–3223. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Ma, J.; Zhao, J.H.; Luo, F.J. A Hierarchical Hidden Markov Model Framework for Home Appliance Modeling. IEEE Trans. Smart Grid 2018, 9, 3079–3090. [Google Scholar] [CrossRef]
- Kim, H.; Marwah, M.; Arlitt, M.; Lyon, G.; Han, J. Unsupervised Disaggregation of Low Frequency Power Measurements. In Proceedings of the 2011 SIAM International Conference on Data Mining, Mesa, AZ, USA, 28–30 April 2011; pp. 747–758. [Google Scholar]
- Kolter, J.Z.; Jaakkola, T. Approximate Inference in Additive Factorial HMMs with Application to Energy Disaggregation. Neural Inf. Process. Syst. 2010, 22, 1472–1782. [Google Scholar]
- Agyeman, K.A.; Han, S.; Han, S. Real-Time Recognition Non-Intrusive Electrical Appliance Monitoring Algorithm for a Residential Building Energy Management System. Energies 2015, 8, 9029–9048. [Google Scholar] [CrossRef]
- Wallach, H.M. Conditional Random Fields: An Introduction. Tech. Rep. 2004, 267–272. [Google Scholar]
- Lafferty, J.; McCallum, A.; Pereira, F. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. In Proceedings of the 18th International Conference on Machine Learning, Williams College, Williamstown, MA, USA, 28 June–1 July 2001; pp. 282–289. [Google Scholar]
- Heracleous, P.; Angkititrakul, P.; Kitaoka, N.; Takeda, K. Unsupervised energy disaggregation using conditional random fields. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–5. [Google Scholar]
- Makonin, S.; Popowich, F.; Bajic, I.V.; Gill, B.; Bartram, L. Exploiting HMM Sparsity to Perform Online Real-Time Nonintrusive Load Monitoring. IEEE Trans. Smart Grid 2016, 7, 2575–2585. [Google Scholar] [CrossRef]
- Makonin, S.; Popowich, F.; Bartram, L.; Gill, B.; Bajic, I.V. AMPds: A public dataset for load disaggregation and eco-feedback research. In Proceedings of the 2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 21–23 August 2013; pp. 1–6. [Google Scholar]
- Kolter, J.Z.; Johnson, M.J. REDD: A Public Data Set for Energy Disaggregation Research. Available online: http://redd.csail.mit.edu/kolter-kddsust11.pdf (accessed on 10 May 2019).
- Berger, A.L.; Pietra, V.J.D.; Pietra, S.A.D. A Maximum Entropy Approach to Natural Language Processing. Comput. Linguist. 1996, 22, 39–71. [Google Scholar]
- CRF++. Available online: https://www.findbestopensource.com/product/crfpp (accessed on 21 April 2019).

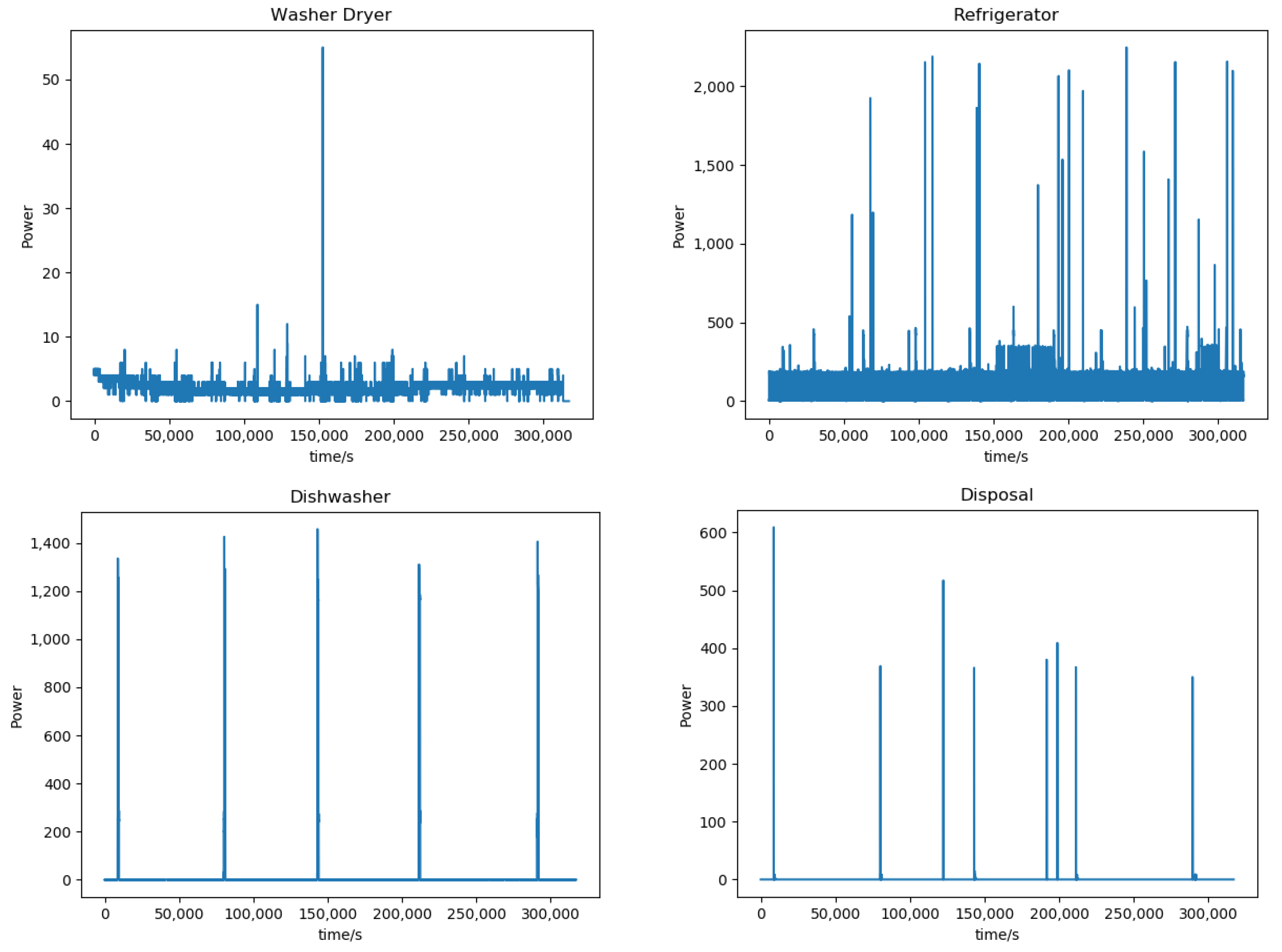

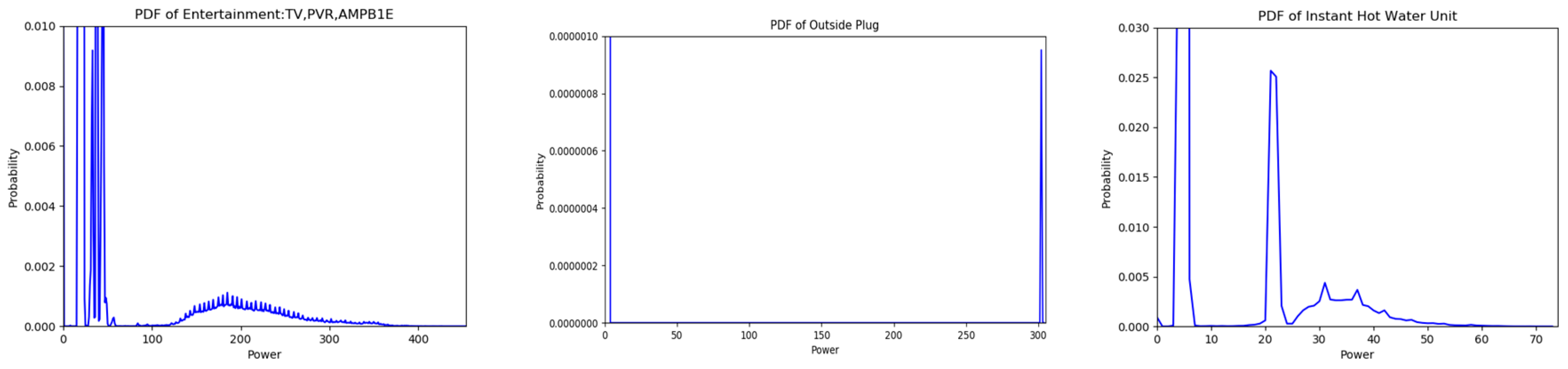
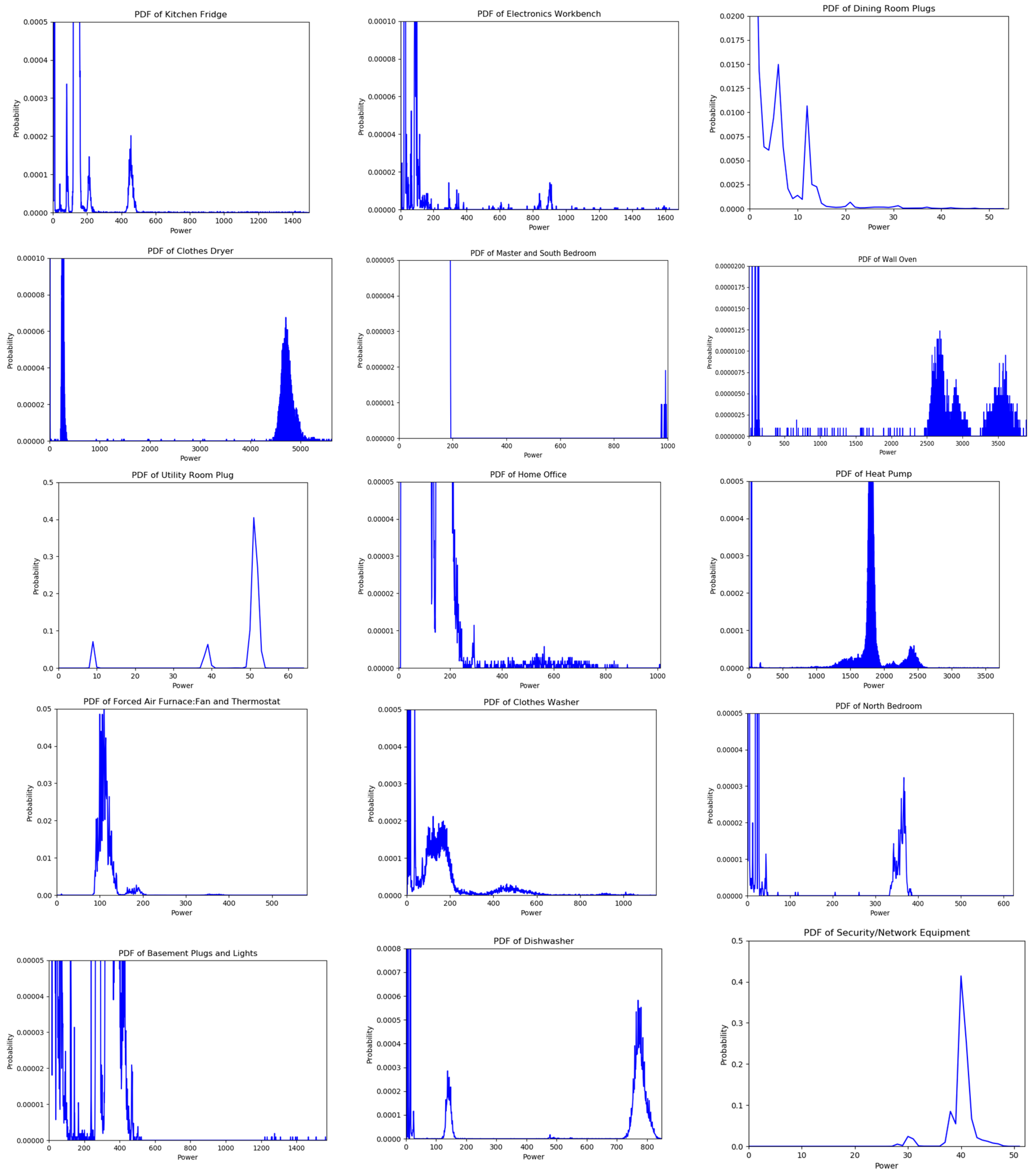

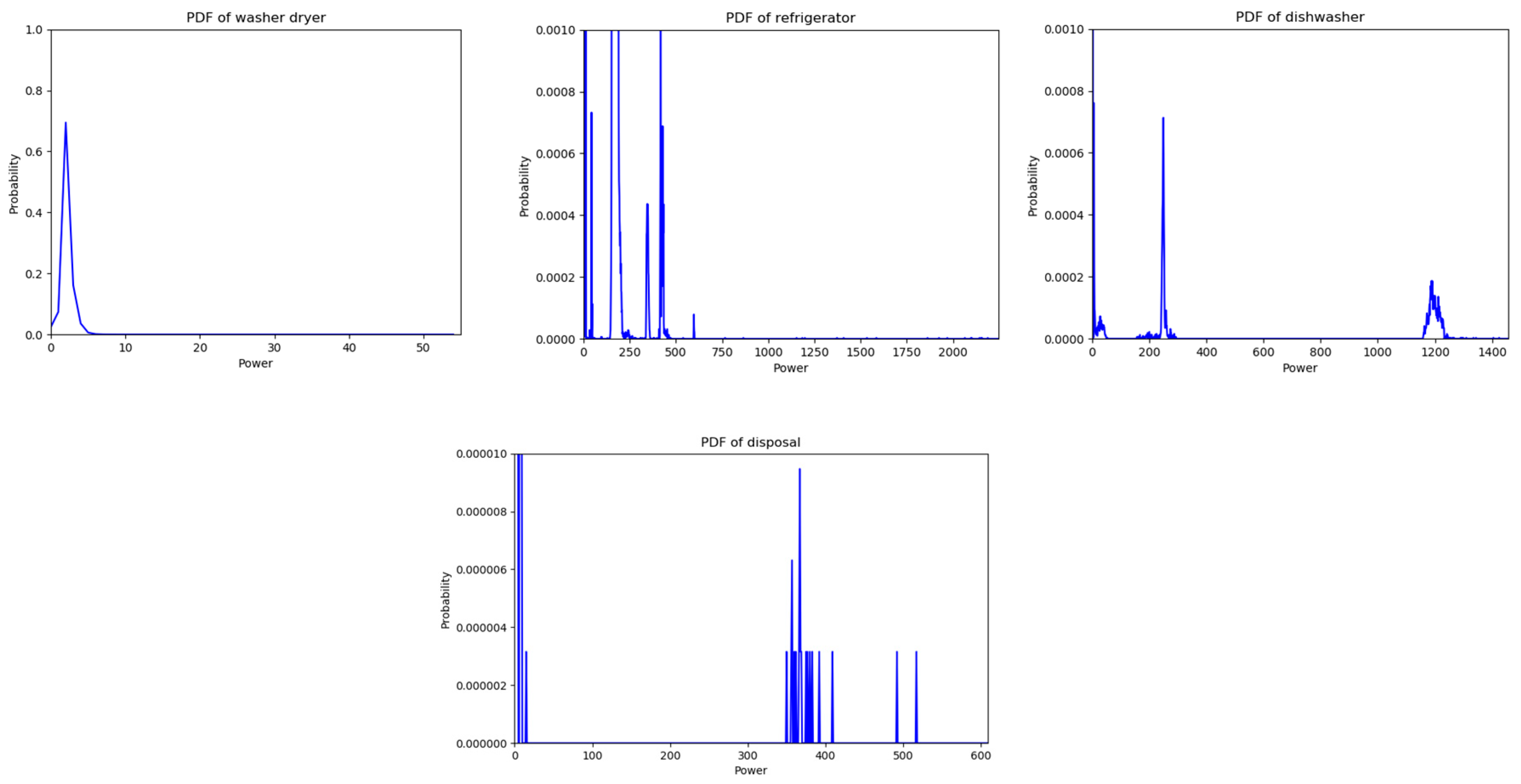

| Templates 1 | Templates 2 | Templates 3 | Meaning of the Template |
|---|---|---|---|
| current state | |||
| current state and previous state | |||
| current state and previous two states | |||
| / 1 | current state and previous three states | ||
| / | current state and previous four states | ||
| / | current state and previous five states | ||
| / | / | current state and previous six states | |
| / | / | current state and previous seven states | |
| / | / | current state and previous eight states |
| Appliance\Max power | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| B1E | 1 | 6 | 623 | \ |
| BME | 10 | 600 | 1571 | \ |
| DWE | 8 | 300 | 848 | \ |
| EQE | 20 | 34 | 52 | \ |
| FRE | 50 | 300 | 581 | \ |
| HPE | 500 | 2000 | 3701 | \ |
| UTE | 0 | 10 | 41 | 65 |
| WOE | 0 | 2300 | 3200 | 3896 |
| B2E | 9 | 200 | 1000 | \ |
| CDE | 7 | 1000 | 5614 | \ |
| FGE | 8 | 400 | 1497 | \ |
| OUE | 0 | 305 | \ 1 | \ |
| Appliance\Max power | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| B1E | 0 | 1 | 6 | 9999 |
| BME | 0 | 5 | 10 | 9999 |
| DWE | 0 | 4 | 8 | 9999 |
| EQE | 0 | 34 | 38 | 9999 |
| FRE | 0 | 100 | 107 | 9999 |
| HPE | 0 | 3 | 39 | 9999 |
| UTE | 0 | 10 | 41 | 9999 |
| WOE | 0 | 2 | 9999 | \ |
| B2E | 0 | 5 | 9 | 9999 |
| CDE | 0 | 7 | 9999 | \ |
| FGE | 0 | 3 | 8 | 9999 |
| OUE | 0 | 9999 1 | \ 2 | \ |
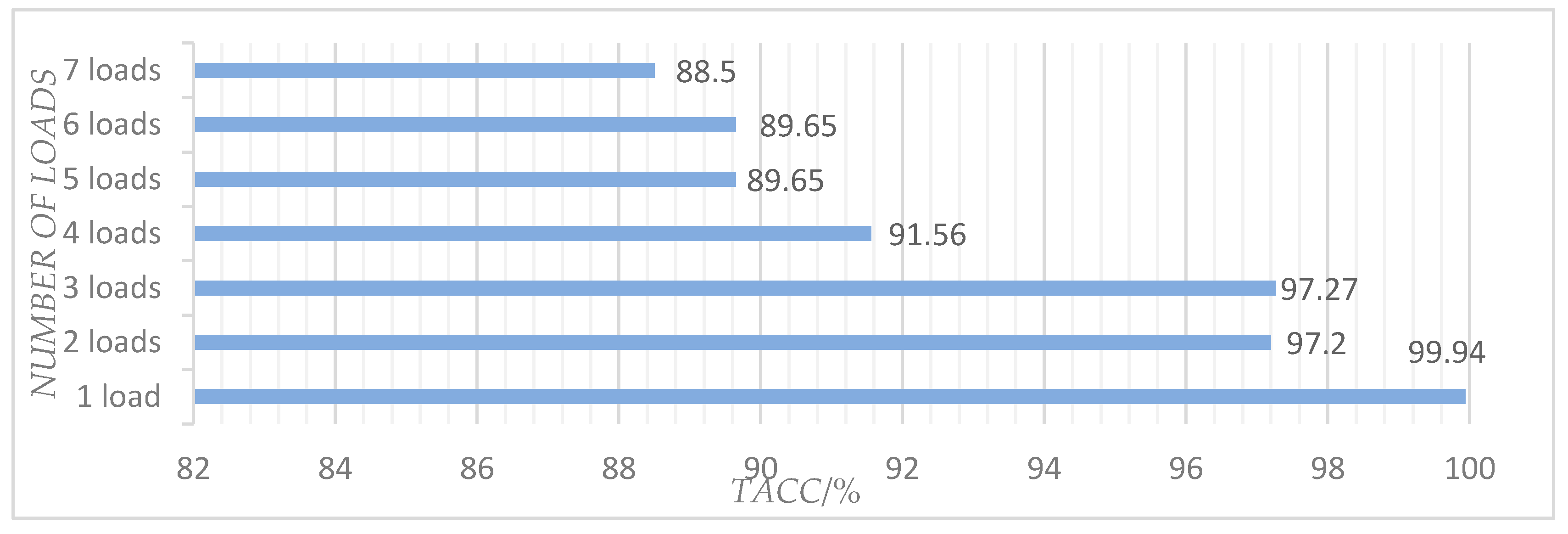
| Load\Acc (%) | Linear-Chain CRFs | Sparse HMM | SVM-rbf | SVM-Linear | SVM-Sigmoid |
|---|---|---|---|---|---|
| 1 load | 99.94 | 99.01 | 99.91 | 100 | 94.38 |
| 2 loads | 99.27 | 99.00 | 98.39 | 96.32 | 81.82 |
| 3 loads | 98.80 | 87.45 | 81.23 | 79.81 | 76.35 |
| 4 loads | 96.04 | 98.52 | 92.40 | 90.31 | 88.41 |
| 5 loads | 96.87 | 94.69 | 92.12 | 88.03 | 88.85 |
| 6 loads | 97.40 | 95.28 | 93.22 | 85.83 | 88.84 |
| 7 loads | 96.68 | 95.56 | 90.90 | 86.80 | 87.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Liu, Z.; Jiao, R.; Yan, G. A Novel Nonintrusive Load Monitoring Approach based on Linear-Chain Conditional Random Fields. Energies 2019, 12, 1797. https://doi.org/10.3390/en12091797
He H, Liu Z, Jiao R, Yan G. A Novel Nonintrusive Load Monitoring Approach based on Linear-Chain Conditional Random Fields. Energies. 2019; 12(9):1797. https://doi.org/10.3390/en12091797
Chicago/Turabian StyleHe, Hui, Zixuan Liu, Runhai Jiao, and Guangwei Yan. 2019. "A Novel Nonintrusive Load Monitoring Approach based on Linear-Chain Conditional Random Fields" Energies 12, no. 9: 1797. https://doi.org/10.3390/en12091797
APA StyleHe, H., Liu, Z., Jiao, R., & Yan, G. (2019). A Novel Nonintrusive Load Monitoring Approach based on Linear-Chain Conditional Random Fields. Energies, 12(9), 1797. https://doi.org/10.3390/en12091797




