A General Parameter Identification Procedure Used for the Comparative Study of Supercapacitors Models

Abstract

Supercapacitors with characteristics such as high power density, long cycling life, fast charge, and discharge response are used in different applications like hybrid and electric vehicles, grid integration of renewable energies, or medical equipment. The parametric identification and the supercapacitor model selection are two complex processes, which have a critical impact on the system design process. This paper shows a comparison of the six commonly used supercapacitor models, as well as a general and straightforward identification parameter procedure based on Simulink or Simscape and the Optimization Toolbox of Matlab^®. The proposed procedure allows for estimating the different parameters of every model using a different identification current profile. Once the parameters have been obtained, the performance of each supercapacitor model is evaluated through two current profiles applied to hybrid electric vehicles, the urban driving cycle (ECE-15 or UDC) and the hybrid pulse power characterization (HPPC). The experimental results show that the model accuracy depends on the identification profile, as well as the robustness of each supercapacitor model. Finally, some model and identification current profile recommendations are detailed.

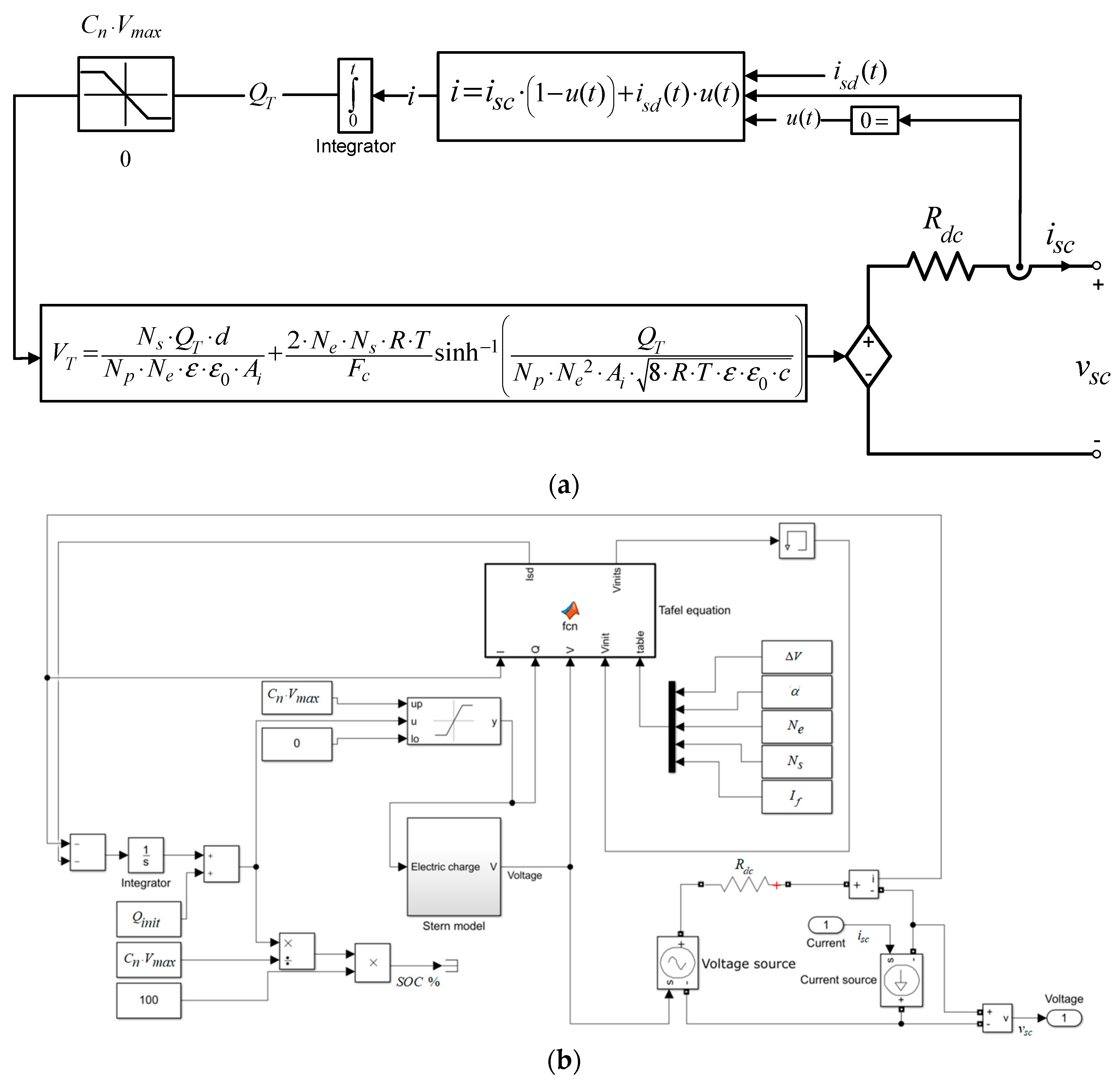
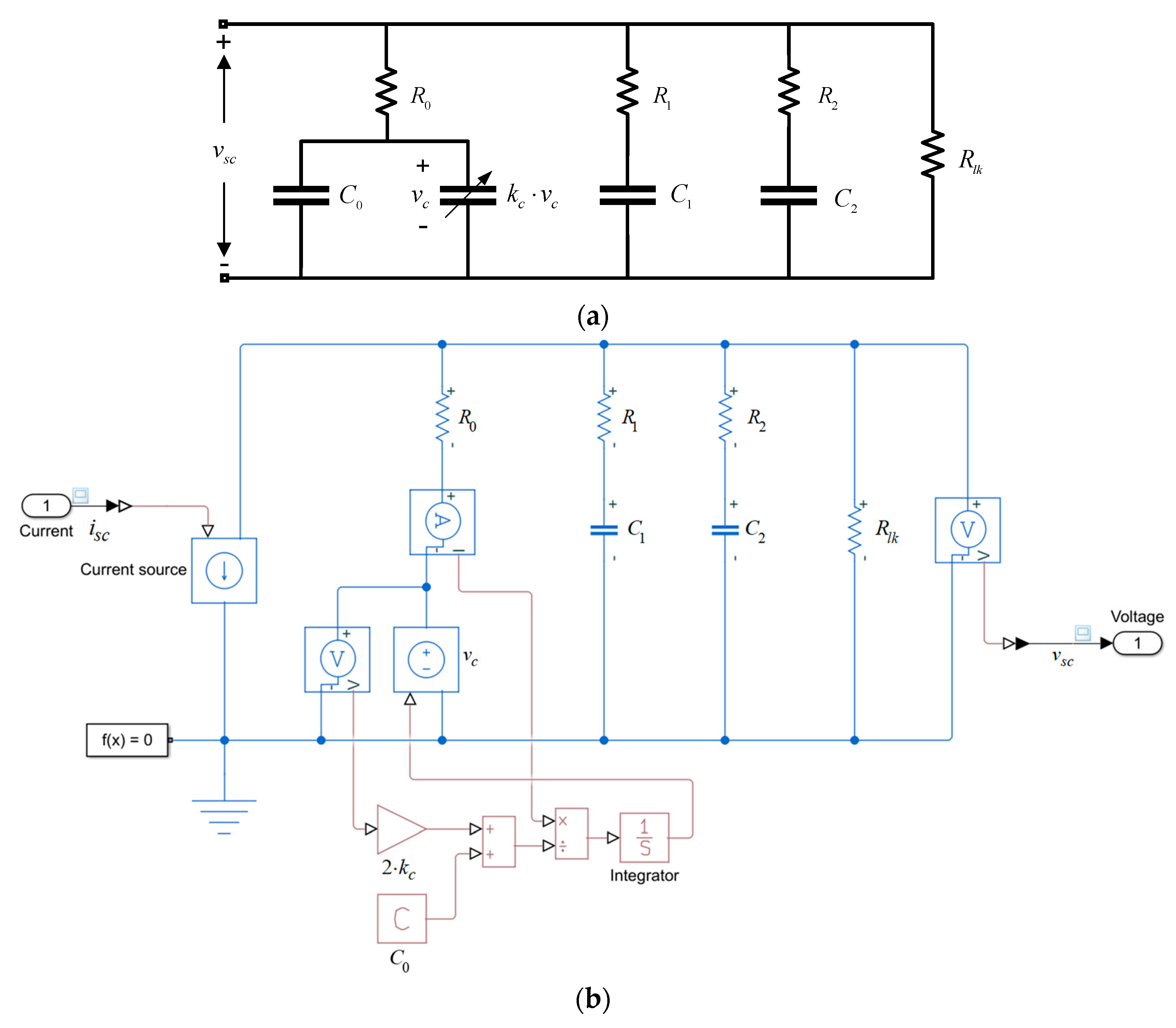
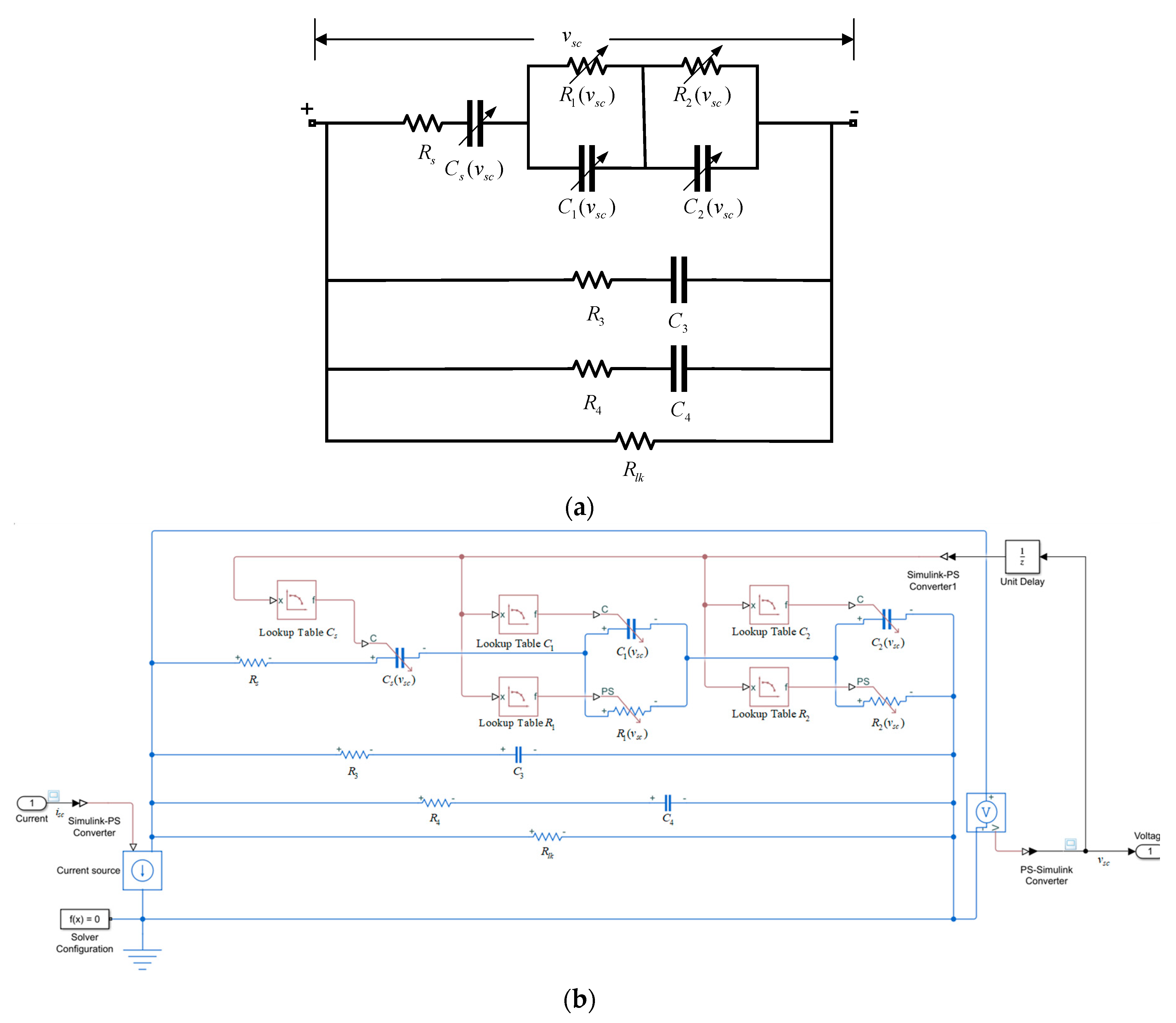
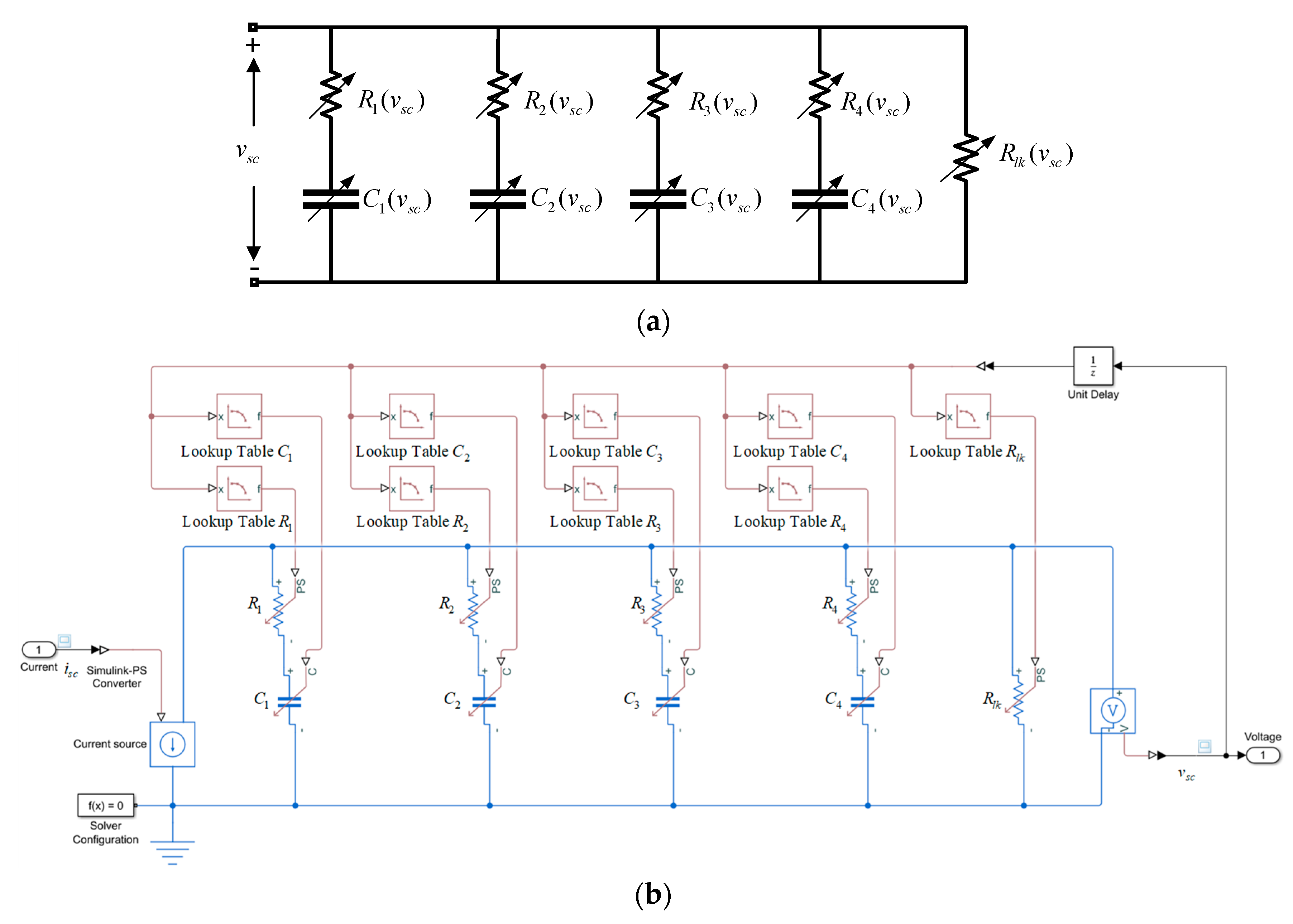
1. Introduction

Energy storage systems are essential in the industrial, medical, renewable or transportation sectors, as well as other sectors. Some characteristics like high power density, reliability and safety are critical in those sectors, this is why the electrochemical double layer capacitor or the supercapacitor play an important role [1].

Many application areas in which supercapacitors are used can be mentioned like magnetic resonance imaging (MRI) that needs very short pulses with high current [2] or fuel cell supercapacitor hybrid bus, where the supercapacitor satisfy the dynamic power demand [3]. In addition, the supercapacitor can be used for the integration of a photovoltaic power plant [4], grid integration of renewable energies [5] and the improvement of energy utilization for mine hoist applications [6]. However, many applications are limited by the self-discharge behavior in wireless sensor network applications [7], where the new techniques of chemical modification to suppress this phenomenon are shown in reference [8] and reference [9].

In general, the supercapacitors models classify into three categories: electrochemical, mathematical, and electrical. Electrochemical models consist of a set of partial differential-algebraic equations with many parameters. The estimation of the electrochemical model is very accurate [10]. However, the simulation of these models consumes many resources. Mathematical models are an alternative based on three dimensional ordered structures [11]. It can get a good fitting with experimental data but with a complex process to get the different parameters. Finally, circuit-based or electrical models are able to reproduce the electrical behavior of supercapacitors with equivalent circuits [12].

In the literature, there are some studies comparing supercapacitor models. Reference [13] reviews three types of equivalent circuits with linear components, with only an identification current profile and several verification current profiles. These models are the classic model, the multi-stage ladder model, and the dynamic model, which are used in electric vehicle applications. In this case, a genetic algorithm (GA) is used to estimate the different constant parameters of the resistors and capacitors (RC) circuits. Reference [14] analyzes three basic constant parameters RC networks models showing the relationship among them. However, as shown in reference [15], the model accuracy can be improved with a nonlinear equivalent circuit model. In reference [16], the authors compared three circuits models (Miller Model, Zubieta Model, and Thevenin Model) with a specific identification current profile for every model. In general, the papers found in the state-of-the-art compare some of the known supercapacitor models, applying different identification current profiles, and using different parameters identification procedures, as it is difficult to obtain reliable conclusions to identify the best model for every application.

The main contribution of this paper is the proposal of a general, practical and effective parameters identification procedure applied to supercapacitors models and obtained in offline mode. The parameters of this model can also be used as an initial estimation of the parameters in online supercapacitor models [17]. The numeric optimization is developed by means of the interactive interface provided by the Identification Toolbox of Matlab (Version R2018b, MathWorks, Natick, MA, USA), once the equivalent models are built in Simulink or Simscape. In addition, the paper shows the comparison of different identification current profiles applied to six kinds of models in order to obtain the best features of each model, as well as the best accurate vs. complexity model.

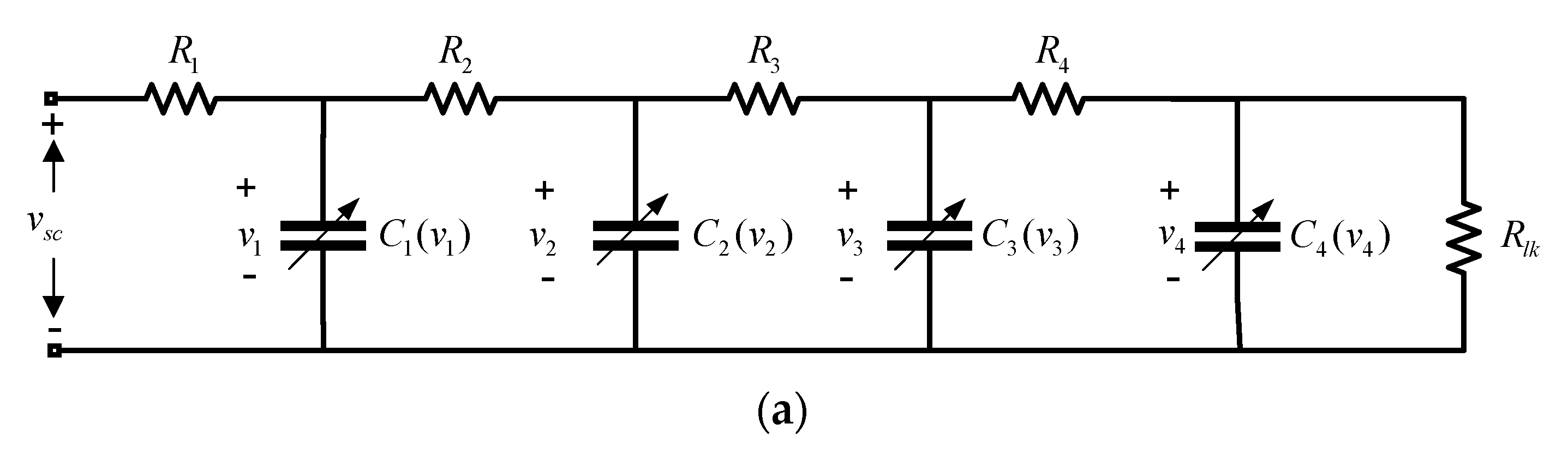
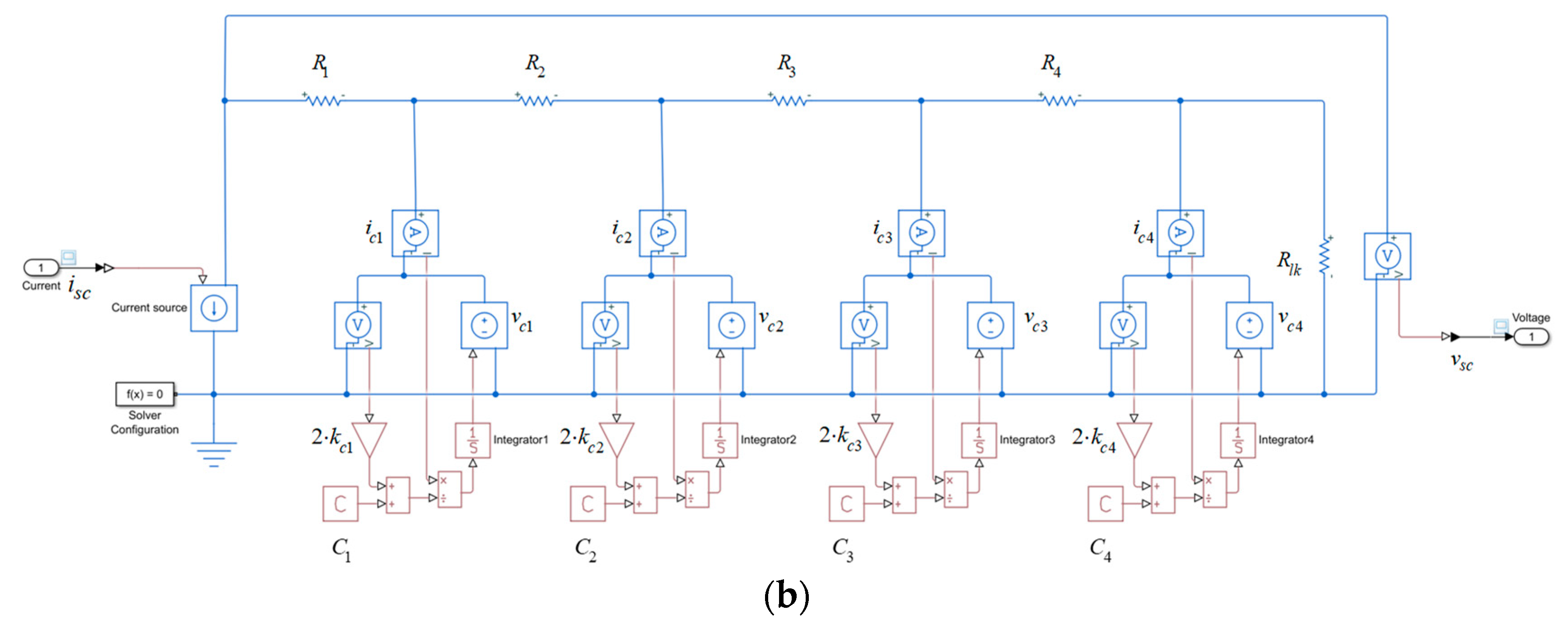
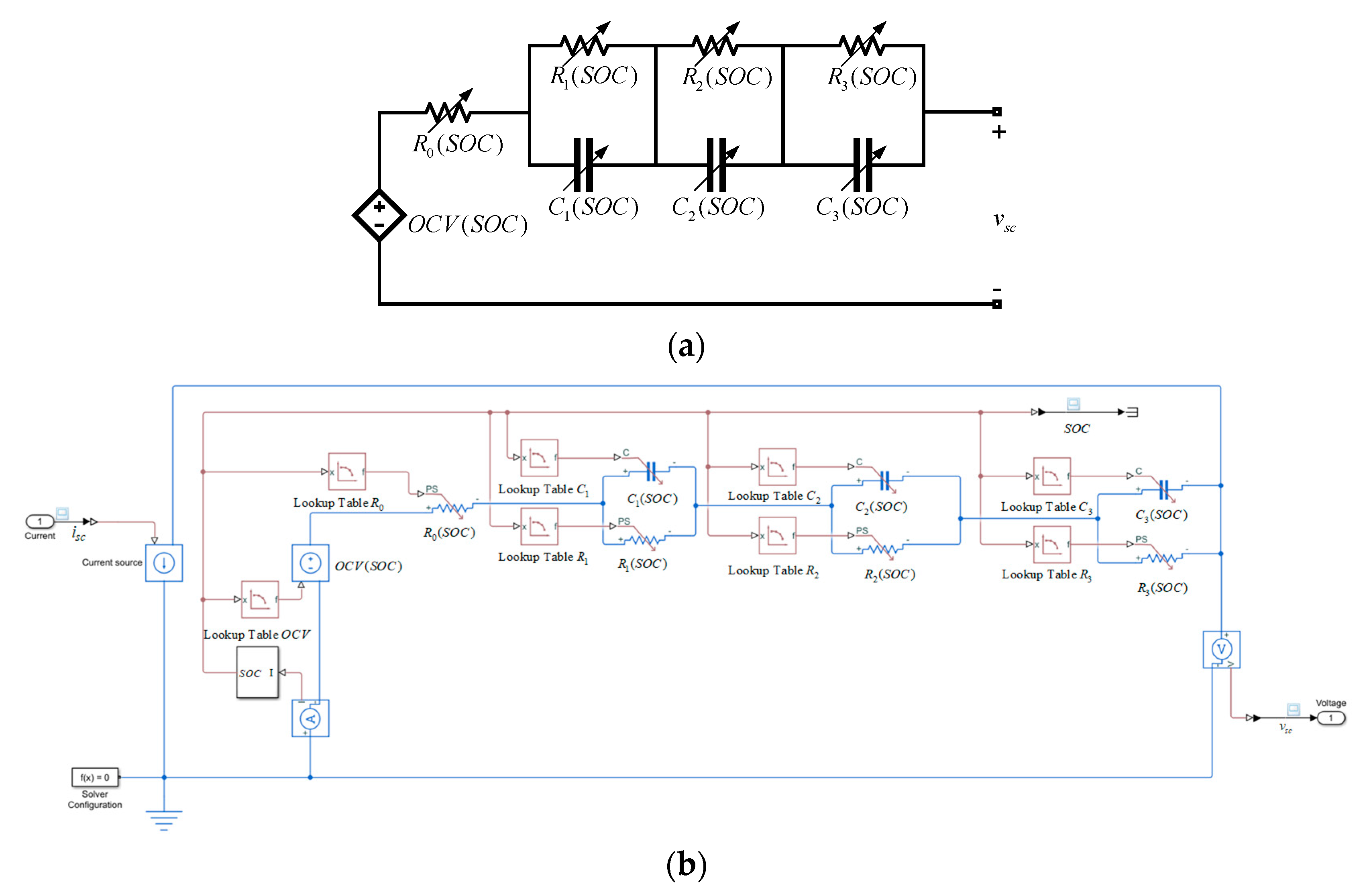
The next sections are organized as follows: Section 2 shows the six supercapacitor models selected to make the comparative study, as well as their circuits implemented in Simulink or Simscape. Section 3 describes the parameters estimation procedure. Section 4 depicted the different current profiles and the experimental setup to get the supercapacitor voltage and current responses. Section 5 shows the obtained statistical metrics using ECE15 and HPPC dynamic driving cycles, and the discussion about the experimental vs. simulation results. Finally, in Section 6, the main conclusions are presented.

2. Supercapacitors Models

In this section, six representative supercapacitor models are selected from the literature, which cover most of the typical applications. All of them are nonlinear models since this kind of models obtains better accuracy. The selected models are the Stern-Tafel Model [18], Zubieta Model [19], Series Model [20], Parallel Model [21], Transmission Line Model [22] and Thevenin Model [23]. In this section, the electrical equivalent circuit and the parameters of each model are reviewed.

2.1. Stern-Tafel Model

The supercapacitor proposed in reference [24] and reference [25] uses the Stern-Tafel model to describe the nonlinear capacitance. This electrochemical model reproduces the double layer capacitance (C_T) related to the nonlinear diffusion dynamics. To do this, the supercapacitor model combines both the Helmholtz’s capacitance (C_H) and Gouy-Chapman’s capacitance (C_GC) [26],

$$C_T=\frac{N_p}{N_s}·{\left(\frac{1}{C_H}+\frac{1}{C_{GC}}\right)}^{-1}$$

(1)

Being

$$C_H=\frac{N_e·\epsilon ·{\epsilon }_0·A_i}{d}$$

(2)

$$C_{GC}=\frac{F·Q_T}{2·N_e·R·T}sinh\left(\frac{Q_T}{N_e{}^2·A_i\sqrt{8·R·T·\epsilon ·{\epsilon }_0·c}}\right)$$

(3)

where N_p is the number of parallel supercapacitor cells, N_s is the number of series of supercapacitor cells, N_e is the number of layers of electrodes, d the molecular radius (m), c the molar concentration (mol.m⁻³), A_i is the interfacial area between electrode and electrolyte (m²), T is the operating temperature (K), F_c is the Faraday constant (C/mol), R is the ideal gas constant (J/(K·mol)), ε is the relative permittivity of the electrolyte material (F/m), and ε₀ is the free space permittivity (F/m) [18].

The model equivalent circuit has a controlled voltage source and an internal resistance, as shown in Figure 1a. This model depends on several parameters where C_n is the nominal capacitance (F), V_max is the maximum supercapacitor voltage (V), R_dc is the internal resistance (Ω), V_T is the total voltage (V), and i_sd is the self-discharge current (A) which is determined by the Tafel Equation (4) described in reference [27] as:

$$i_{sd}\left(t\right)=N_e·I_f·e^{\left(\frac{\alpha ·F_c·\left(\frac{V_{init}}{N_s}-\frac{V_{max}}{N_s}-\Delta V\right)}{R·T}\right)}$$

(4)

where I_f is the leakage current (A), V_init is the initial voltage (V), α is the charge transfer coefficient and ∆V is the over-potential (V). The capacitance of the electrochemical model requires only a few data from manufacturer datasheet and universal constant as described in reference [28]. The Simulink implementation is shown in Figure 1b.

2.2. Zubieta Model

The proposed model in reference [19] includes a circuit with three parallel RC time constant, Figure 2a. The first branch, with the elements R₀C₀, and the voltage-dependent k_c·v_c defines the response in seconds. The second branch R₁C₁ provides the response in the range of minutes. The branch R₂C₂ represents the response for a time longer than minutes. Finally, a resistor R_lk reproduces the leakage resistance.

A simplified equivalent circuit with two branches is shown in reference [29], with a simplified parameter identification procedure through the differential equation of the circuit. Similar studies are proposed in reference [30] in which the model parameters are easily obtained when the supercapacitor is discharged with constant power. In addition, reference [31] proposes a multivariable minimization function to find the parameters, they are validated with a current profile of a hybrid electric vehicle.

The total capacitance and current of the voltage-controlled capacitance implemented in Simscape are shown in Figure 2b, which are defined by (5) and (6):

$$C\left(v_c\right)=C_0+k_c·v_c$$

(5)

$$i_c=\frac{dQ}{dt}=\frac{d\left(C\left(v_c\right)·v_c\right)}{dt}=\left(C_0+2k_c·v_c\right)\frac{d{v}_c}{dt}$$

(6)

where C₀ is the initial linear capacitance which represents the electrostatic capacitance of the capacitor, and k_c a positive coefficient which represents the effects of the diffused layer of the supercapacitor.

2.3. Series Model

The series model is an equivalent circuit obtained through the AC impedance approach, which consists of two parallel RC circuit compound by R₁(vsc), C₁(vsc), R₂(vsc), C₂(vsc), connected in series with another RC circuit compound by R_s and C_s(vs), as described in references [20,32,33]. This equivalent circuit shows in the first branch of Figure 3a. In reference [34] a modified version of this circuit was presented, which includes the model proposed by Buller and Zubieta, in order to represent a complete model for a full frequency range. This complete model includes three branches in a parallel compound by R₃ and C₃, R₄ and C₄, and the leakage resistance R_lk, as shown in Figure 3a. Figure 3b shows the Simscape implementation of the modified series model.

2.4. Parallel Model

The basic parallel model with constant values is described in reference [35] and reference [36]. Reference [37] describes an approximation to calculate the parameters without data acquisition, only using the information provided by a supercapacitor datasheet, as well as the main basic equations to obtain the constant parameters using this information. A modified four parallel RC networks with voltage-dependent parameters are presented in reference [21], and it is shown in Figure 4a. This model is more complex, but it achieves better accuracy. Figure 4b shows the implementations of the modified parallel model in Simscape.

2.5. Transmission Line Model

Transmission line model is composed of nRC branches in order to reproduce the supercapacitor frequency response from 10 mHz to 1 kHz. This model was proposed for hybrid and electric vehicles, and it was described in reference [38] and reference [39]. This model consists of four parallel networks based on R₁, C₁(v₁), R₂, C₂(v₂), R₃, C₃(v₃) and R₄, C₄(v₄), and a parallel leakage resistance R_lk, as shown in Figure 5a. Reference [22] describes a procedure to estimate the parameters through time response and the equations of the circuit. Also, this model is used to evaluate the supercapacitor physical aging process [40], by estimating the uncertainties of the parameters. Reference [41] uses a different number of networks according to the simulation time step.

Figure 5b shows the model implemented in Simscape with the described Equations (5) and (6).

2.6. Thevenin Model

The equivalent electric circuit of the Thevenin model, which includes several parallel RC and a nonlinear state-of-charge (SOC) voltage-dependent source is described in reference [42]. The SOC is calculated by coulomb counting using (7):

$$SOC=\frac{Q_{init}-{{\displaystyle \int }}_0^{t}i\left(\tau \right)d\tau }{Q_T}$$

(7)

with Q_init being the initial supercapacitor charge, Q_T being the total supercapacitor charge and i(τ) as the supercapacitor current.

In this paper, three RC branches are used to get a better accuracy, where OCV represents the open circuit voltage, R₀ represents the internal resistance, and three parallel networks based on R₁, C₁, R₂, C₂, R₃, and C₃ reproduce the supercapacitor dynamic, as shown in Figure 6a. All parameters are state-of-charge dependent. The proposed model applied to a hybrid storage system for an electric vehicle gives a better agreement for a simulated vs. experimental response when 3-branches are used in the model [23]. Figure 6b shows the Simscape implementation.

3. Parameters Estimation Procedure

Parametric models explicitly contain differential equations, transfer function or block diagrams. The parameters update could be offline or online. For obtaining the parameters, in the offline mode, the data are stored to later process, on the other hand, in the online mode, the procedure is executed in parallel to the experiment [43]. In the literature, there are many proposed procedures to obtain the model parameters such as e.g., the unscented Kalman filter [44] or the Luenberger-style technique [17].

Taking into account the literature, this paper focuses on the proposal of a practical, interactive, simple and enough general offline procedures for estimating the model parameters.

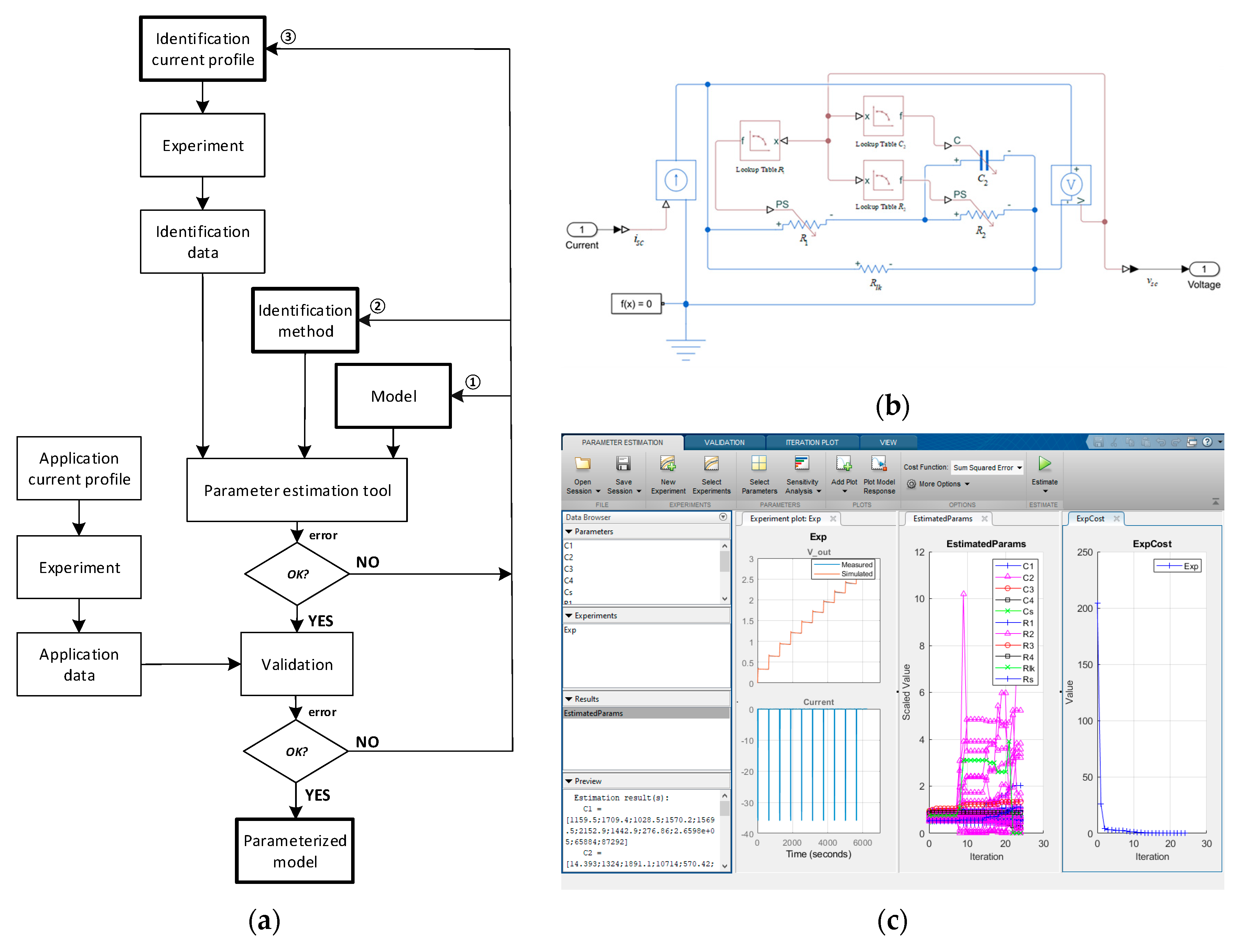
Figure 7a shows the proposed identification procedure block diagram. This procedure can be divided into several steps, shown and described in

Table 1. Parameter Estimation Steps.

Steps	Description
1	Apply the identification current profile to obtain supercapacitor current and voltage waveforms (identification data) from the experimental test. E.g., as shown in Section 4.2: current profiles and supercapacitor voltage response (a), (b) and (c).
2	Select and build the equivalent circuit model in Simulink or Simscape through a block diagram or circuit. E.g., as shown in Section 3: Figure 7b.
3	Create a new experiment in Simulink and to import the identification data. Simulate the model with the initial parameters and the identification current profile to obtain the simulation data. E.g., as shown in Section 3: Figure 7c.
4	Choose the variables and their limits to estimate their value. E.g., as shown in Section 3: Figure 7c.
5	Set up optimization options (optimization method, algorithm, and parameter and function tolerance). E.g., as shown in Section 3: Figure 8.
6	Run the parameter estimation process applying the selected optimization solver (E.g., sum-squared error) to match the identification data with the simulation data. E.g., as shown in Section 3: Figure 7c. If the error is not small enough, return to step 1 (①); or change the identification method and return to step 3 (②); or modify the current profile and return to step 2 (③), Figure 7a.
7	Once the model parameters have been obtained from the identification data, the next step is to verify the model response using the application current profile and the application data. For that, it is necessary to compare the application data with the new simulated data, using the obtained parameters in step 6, E.g., as shown in Section 4.2: Figure 9d,e. If the error is not small enough, return to step 1 (①); or change the identification method and return to step 3 (②); or modify the current profile and return to step 2 (③), Figure 7a.

.

In step 5, the optimization method has to be selected. This paper uses an offline parameters estimation based on the error minimization between the measured and simulated supercapacitor voltage. The iterative procedure tunes the supercapacitors model parameters (p) to get a simulated response (V_s) that tracks the measured response (V_m), with a finite number of samples (n). To do that, the solver minimizes the next cost function for each current profile:

$$F\left(p\right)=\underset{p}{\min }{\displaystyle \sum }_{i=0}^n{\left[V_{m_i}-V_{s_i}\left(p\right)\right]}^2$$

(8)

where p varies between zero and infinity (e.g., 0 to 10¹⁰).

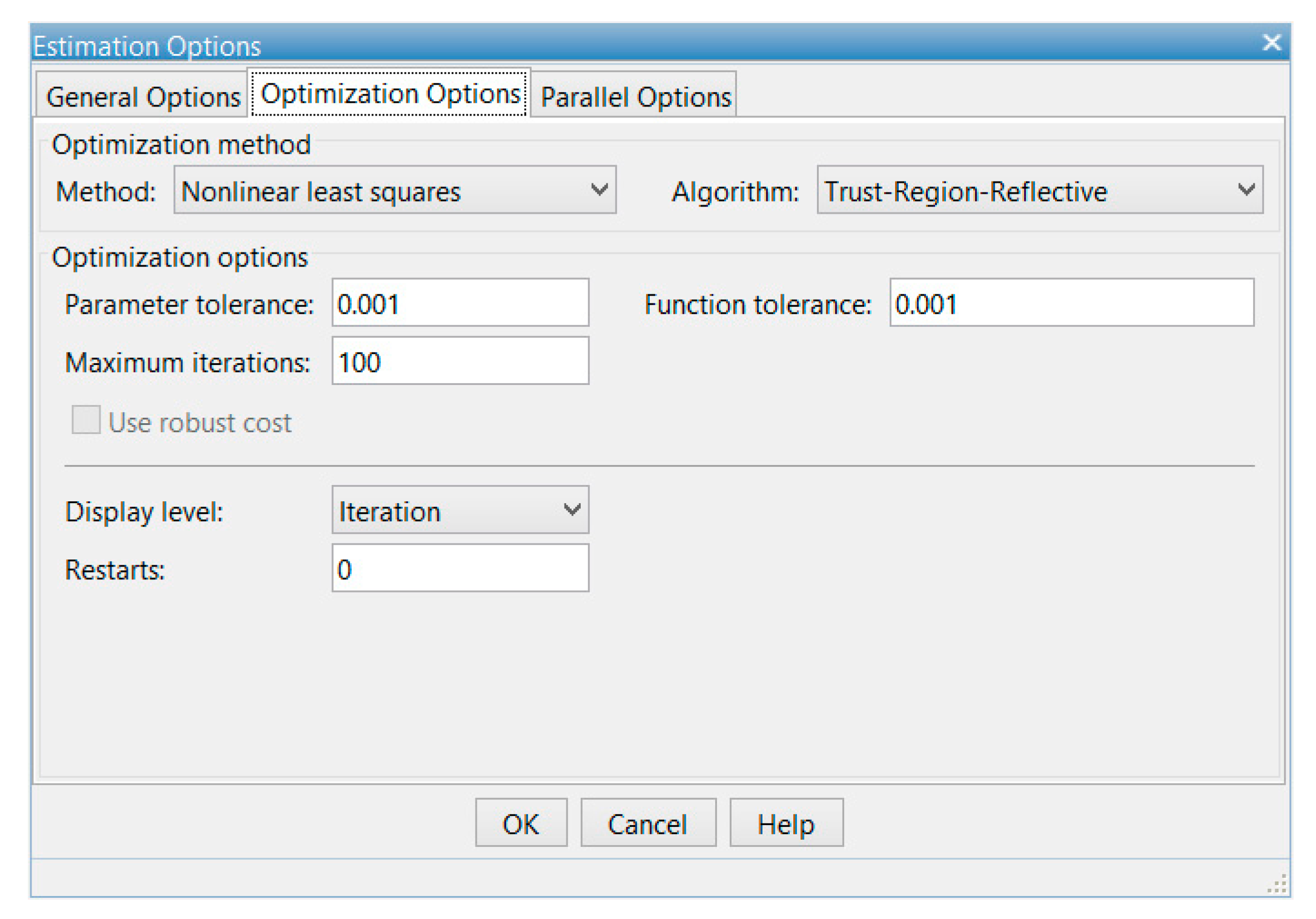
The minimization problem is carried out with Simulink^® Design Optimization™ of Matlab (Version R2018b, MathWorks, Natick, MA, USA). This toolbox provides an interactive interface that helps to minimize the square of the error between the measured and simulated supercapacitor voltage, using the nonlinear least squares method for parameters estimation. This method is selected in the user interface as shown in Figure 8.

This method uses the Simulink function named as lsqnonlin, that requires at least (2k + 1) simulations per iteration, where k is the number of parameters to be estimated [46]. The required CPU time and memory increase as a function of the numbers of parameters and their initial values. The offline runtime estimation is in the order of minutes.

If runtime estimation has to be reduced, other techniques based on the layered technique to break the global optimization into a smaller task [47], or based on differential mutation strategy [48], or based on genetic programming [49], among others, could be used, although the flexibility and simplicity provided by the Simulink user interface could be affected.

On the other hand, the algorithm selected is the Trust-Region-Reflective, which is based on a gradient process with a trial step by solving a trust region. Specific details of the algorithm can be found in reference [45]. Additional information is detailed in reference [50], in which the process of how to import, analyze, prepare and estimate model parameters in Simulink is described.

Using the proposed procedure, based on Simulink^® Design Optimization™ of Matlab, the most model can be built, from a practical point of view. Nevertheless, this procedure is limited by the optimization methods and algorithms included in Simulink.

4. Experimental Setup

4.1. Supercapacitor Testing System

The experimental setup includes a supercapacitor, a data acquisition system, a power source, and an electronic load, as shown in Figure 9. The supercapacitor used to develop the test has been the Maxwell BCAP3000. An equivalent bidirectional current source compound of the electronic load and the power source, connected in parallel, emulates the current profile. This equivalent current source includes the typical regenerative breaking present in automotive applications. The experimental current profile and the data acquisition system are conducted using the following set of equipment listed in

Table 2. Equipment and Components used in the Experimental Setup.

Component	Specifications	Use
Supercapacitor: Maxwell BCAP3000	2.7 V/3000 F	Cell under test
Datalogger: Agilent 34970A	100 nV–1000 V/500 kHz	Measure voltage
Power source: Sorensen SGI400/38	400 V/38 A	Current charge
Electronic load: Chroma 63206A-600	600 V/420 A	Current discharge
Shunt resistor: Newtons4th HF200	0.5m Ω/200 mA → 200 Arms	Measure current

:

All these elements have been synchronized with a computer running to manage the data logging and supervisory control using LabVIEW^® software.

4.2. Supercapacitor Test Schedule

The parameter identification procedure uses three different current profiles. The current profile i₁ is a current step, Figure 10a; the current profile i₂ are repetitive charging current steps applied until to reach the maximum supercapacitor voltage, Figure 10b; and the current profile i₃ is a dynamic charge-discharge current step modulated in amplitude and time applied until the middle value of the supercapacitor voltage range, [51], Figure 10c. From the modeling perspective, the validation current profile must be more dynamic in amplitude and frequency than the identification current profile, as shown in Figure 10d,e.

These identification current profiles apply to those models aforementioned in Section 2 to obtain their parameters. The current profile applied in every model is shown in

Table 3. Identification Current Profiles Used to Supercapacitor Parameters Estimation.

Model	Current Profile
	i1	i2	i3
Stern-Tafel	✓	–	–
Zubieta	✓	✓	✓
Series	–	✓	✓
Parallel	–	✓	✓
Transmission line	–	✓	✓
Thevenin	–	✓	✓

✓ = Applicable; – = Not applicable.

.

The robustness and accuracy of the supercapacitor models are evaluated by means of different standardized test profiles, which include the Hybrid Pulse Power Characterization (HPPC) test and European Urban Driving Cycle (ECE15) for long-time responses. Figure 9d shows the HPPC test that is described in the Freedom Car Battery Manual [52]. The ECE15 test, described in reference [53], is a more dynamic current profile, as shown in Figure 10e.

5. Experimental Results, Comparison, and Discussion

After obtaining the parameters for each model, detailed in Appendix A in

Table A1. Stern-Tafel Model Parameters with current profile i₁.

Parameter	Value
C (F)	3000
Rdc (mΩ)	2.1000
If (mA)	5.2000
Vn (V)	2.7000
Ns	1
Np	1
Ne *	2
d (nm) *	1.0115
α *	0.3200 (0 < α < 1)
∆V *	0.4100

* = Estimated parameters.

,

Table A2. Zubieta Model Parameters.

Parameter	Current Profile
	i1	i2	i3
R0 (mΩ) *	1.1080	0.8653	0.6504
C0 (F) *	2290.3000	2172.6000	2081.7000
kc (F/V) *	244.4400	240.5600	220.1800
R1 (Ω) *	16.9130	19.9280	10.5170
C1 (F) *	471.1500	368.1700	111.1500
R2 (Ω) *	0.6729	0.3773	3.5770
C2 (F) *	292.0100	176.3200	382.0700
Rlk (kΩ) *	171210	11023	51.4030

* = Estimated parameters.

,

Table A3. Series Model Parameters with current profile i₂.

Parameter	Voltage (V)
	0	0.330	0.6417	0.9295	1.1977	1.4522	1.6973	1.934	2.1622	2.3830	2.5948
Cs (kΩ) *	2.4655	2.3629	2.5419	2.6699	2.8260	2.8941	2.9450	2.962	3.0666	3.1518	3.5999
R1 (µΩ) *	581.02	470.26	563.94	546.61	540.87	507.120	544.94	238.4	0.0080	1.3731	1.6410
C1 (kF) *	1.1595	1.7094	1.0285	1.5702	1.5695	2.1529	1.4429	0.277	265.980	65.884	87.292
R2 (µΩ) *	0.120	58.126	14.810	25.842	43.970	108.870	0.0164	6.128	707.200	692.73	501.860
C2 (F) *	14.393	1324	1891.1	10714	570.42	34.5400	58.919	13.51	43.7690	161.84	54.3090
R3 (Ω) *	10.6610
C3 (kF) *	1.0877
R4 (Ω) *	14.4660
C4 (F) *	32.5750
Rlk (kΩ) *	5.5436

* = Estimated parameters.

,

Table A4. Series Model Parameters with current profile i₃.

Parameter	Voltage (V)
	1.4932	1.7931	2.0874	2.3761	2.6618
Cs (kΩ) *	2.8890	2.9626	3.0489	3.1745	3.1935
R1 (µΩ) *	192.3800	460.1300	428.0600	182.1800	437.5600
C1 (F) *	15.3320	923.8500	30.6020	9.3121	229.6200
R2 (µΩ) *	166.3700	1.4114	32.8880	303.2600	99.7610
C2 (kF) *	0.0309	0.2120	1.9380	1.9937	0.1050
R3 (Ω) *	7.6440
C3 (kF) *	1.2486
R4 (Ω) *	14.0350
C4 (F) *	110.7000
Rlk (kΩ) *	1584.4000

* = Estimated parameters.

,

Table A5. Parallel Model Parameters with current profile i₂.

Parameter	Voltage (V)
	0.0002	0.3301	0.6417	0.9295	1.1977	1.4522	1.6973	1.9337	2.1622	2.3830	2.5948
C1 (kF) *	11.494	56.47	86.826	0.2254	82.203	0.00353	100.120	219.83	125.880	182.96	170
R1 (Ω) *	18502	91.543	1980.4	15.8680	421.90	2545.4	51657	857.68	398.850	254.02	279.950
C2 (F) *	561.28	258.20	362.59	239.440	57.1310	65.969	56.8820	112.78	134.450	46.676	50.050
R2 (mΩ) *	0.00358	11.937	0.3757	1.9524	155.180	137.89	117.090	14.308	13.746	4622.1	500.020
C3 (F) *	1068.9	1780.7	0.3458	43.1960	47.3320	0.1059	665.260	8.367	12.691	30.798	25.003
R3 (mΩ) *	2.9311	5.5832	0.00014	0.6223	16.946	3.0161	5.6190	1.2579	0.01369	369.01	100
C4 (kF) *	1.8016	0.0452	2.4350	2.4355	2.7939	2.7622	2.4572	3.013	3.0641	3.3026	3.119
R4 (mΩ) *	6.4737	8.4052	0.1441	1.0450	0.5837	0.6355	0.6429	0.4083	0.3057	0.5758	0.199
Rlk (Ω) *	1.6786	15.397	13.829	25.6290	11.714	13.701	17.801	17.821	16.065	16.649	18.947

* = Estimated parameters.

,

Table A6. Parallel Model Parameters with current profile i₃.

Parameter	Voltage (V)
	1.4932	1.7931	2.0874	2.3761	2.6618
C1 (kF) *	21.1090	652.920	119.440	503.490	28.4650
R1 (Ω) *	0.3961	765.50	364.790	112.370	14.1460
C2 (F) *	59.1990	123.90	110.42	126.430	26.3940
R2 (Ω) *	9.1786	0.12605	0.11993	0.09205	0.01963
C3 (F) *	657.710	15.920	21.9840	17.6280	15.6860
R3 (mΩ) *	16.0070	4.7105	11.4340	0.0615	12.3470
C4 (kF) *	3.0746	2.867	2.9347	3.0351	3.1868
R4 (uΩ) *	507.890	657.90	689.490	470.030	850.340
Rlk (Ω) *	120.930	768.810	6150.30	585.340	303.670

* = Estimated parameters.

,

Table A7. Transmission Line Model Parameters.

Parameter	Current Profile
	i2	i3
R1 (µΩ) *	826.72	575.75
R2 (mΩ) *	115.67	2.7568
R3 (Ω) *	1.3558	0.0116
R4 (Ω) *	3.9621	1.5723
kc1 (F/V) *	209.20	85.715
kc2 (F/V) *	26.6080	21.482
kc3 (F/V) *	47.1510	13.4470
kc4 (F/V) *	11.8540	15.2340
C1 (F) *	2303.30	2408.90
C2 (F) *	0.1000	5.2926
C3 (F) *	21.2820	120.67
C4 (F) *	37.9010	55.4780
Rlk (kΩ) *	111.01	13.8080

* = Estimated parameters.

,

Table A8. Thevenin Model Parameters with i₂ Current Profile.

Parameter	SOC (%)
	0.01	10	20.04	29.96	39.95	49.86	59.89	69.77	70.77	89.67	99.64
OCV (V)	0.0002	0.330	0.6417	0.9295	1.1977	1.4522	1.6973	1.9337	2.162	2.3830	2.5953
C1 (F) *	17046	551.64	236.58	303.76	363.06	509.86	434.30	401.51	227.47	411.24	147.11
C2 (kF) *	119.28	29.58	35.427	30.323	39.527	22.579	20.577	771.57	11.614	94.522	19.695
C3 (kF) *	2943.8	498.12	248.36	205.07	541.22	449.09	844.16	97.252	2507.5	703.25	3.772
R0 (µΩ) *	723.2	431.02	0.2476	13.381	104.41	17.20	3.7923	213.26	115.96	23.528	372.15
R1 (mΩ) *	1.2436	0.9416	1.2504	1.1690	1.1998	1.3676	1.3495	1.2395	1.0854	1.1086	1.2487
R2 (mΩ) *	68.622	10.261	1.1819	35.648	3.3491	0.32405	0.4529	7.7754	14.9250	1.6529	186.44
R3 (Ω) *	33.592	22.765	0.9059	2.143	2.6865	1.9369	432.480	548140	29422	558.260	555

* = Estimated parameters.

and

Table A9. Thevenin Model Parameters with i₃ Current Profile.

Parameter	SOC (%)
	53.37	64.68	75.97	87.25	98.59
OCV (V)	1.4786	1.7794	2.0742	2.365	2.6499
C1 (F) *	0.070731	11.1610	11.1610	12.30	123.90
C2 (kF) *	7.2709	1.3362	0.7907	16.107	28.906
C3 (MF) *	1929.30	0.00769	0.00638	76.5800	9.8952
R0 (µΩ) *	6.5167	13.9100	39.4740	75.8540	53.527
R1 (µΩ) *	204.02	168.97	35.226	339.940	565.850
R2 (µΩ) *	684.340	486.780	512.330	352.520	284.940
R3 (µΩ) *	24.6710	4.8491	7.8730	74.0560	0.25154

* = Estimated parameters.

, using the procedure described in Section 3 and identification current profiles described in Section 4, the output voltage accuracy and robustness analysis for the six supercapacitor models described in Section 2 is performed based on statistical metrics, such as relative error and root-mean-square (RMS) error.

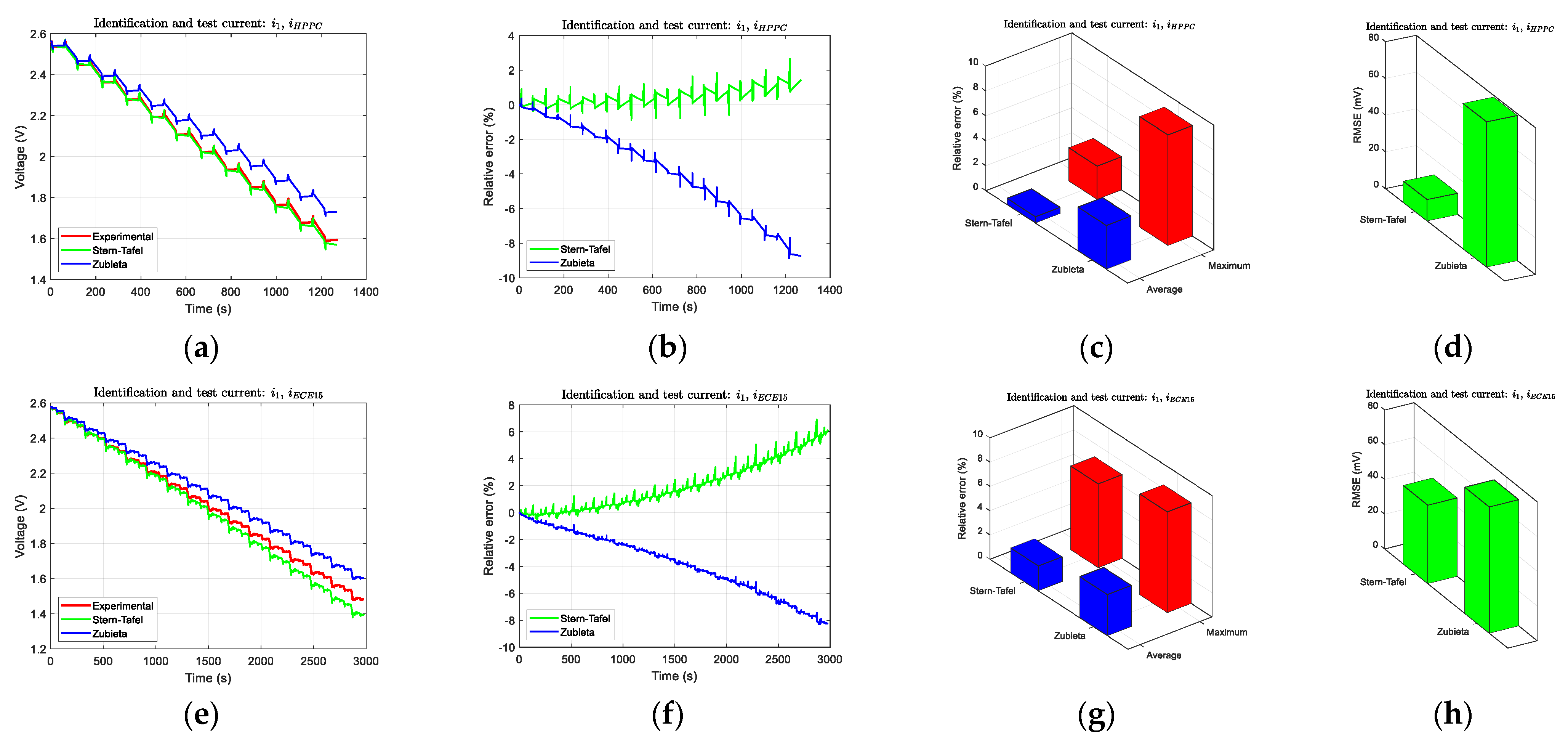
Comparative results with identification current profile i₁ are illustrated in Figure 11a–d for the HPPC test and Figure 11e–h for the ECE15 test. Figure 11a,e show the experimental supercapacitor voltage and the voltages provided by the Stern-Tafel and Zubieta models. Figure 11b,f show the relative error between these models and the experimental data.

Figure 11c,g represent the relative error in percentage. Figure 11d,h show the RMS error in mV. It shows that the Stern-Tafel model has lower error values in comparison with the Zubieta model. In any case, the relative error tendency with the time increase in both models, therefore the accuracy of both models identified with the i₁ current profile is not proper.

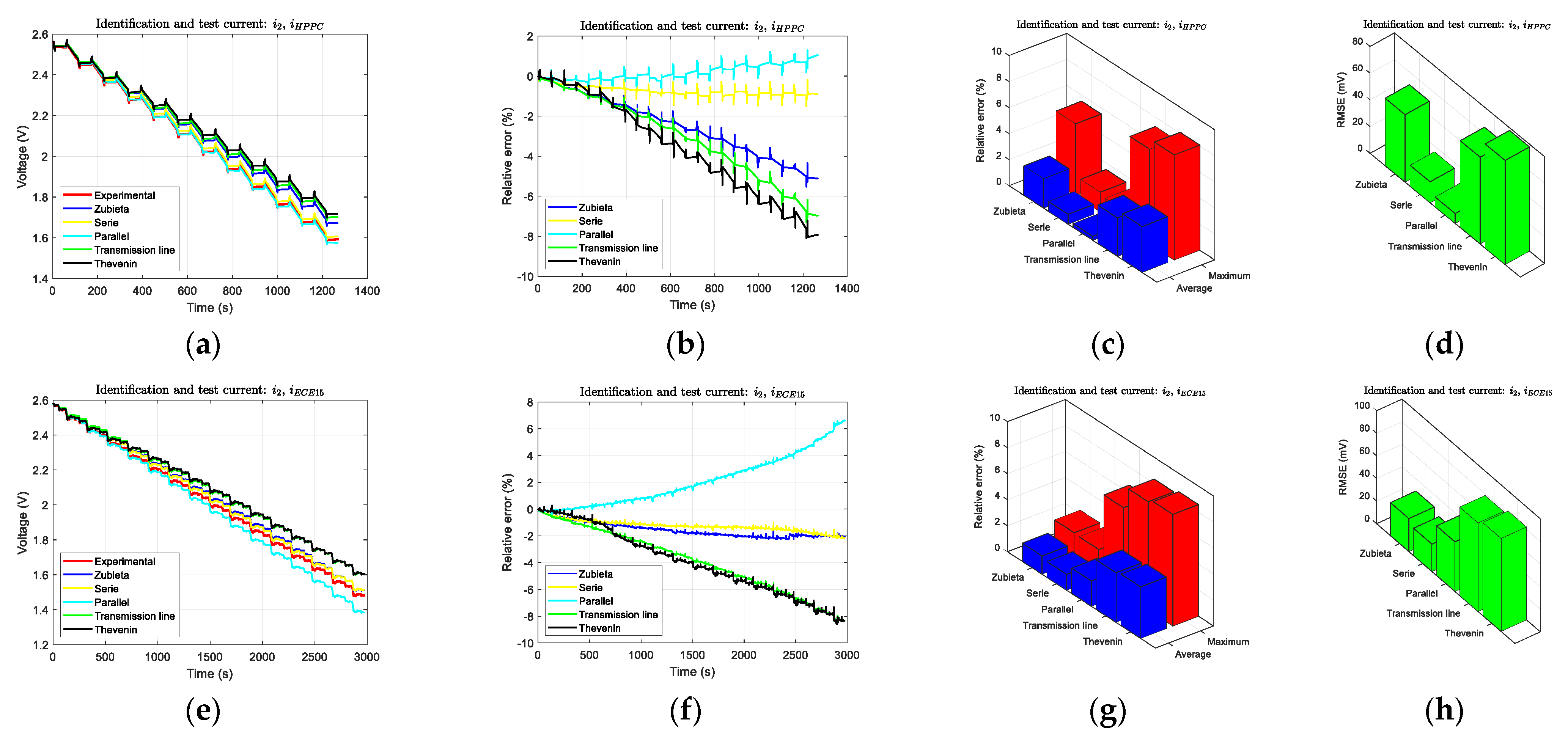
Similar information is shown when current profile i₂ is used to obtain the model parameters. Figure 12a–d depicted the obtained result for the HPPC test and Figure 12e–h for the ECE15 test. This current profile is applied to five out of the six models, with the exception of the Stern-Tafel model. In this case, the Series model is the best one, since it presents a reduced relative error that maintained with the time.

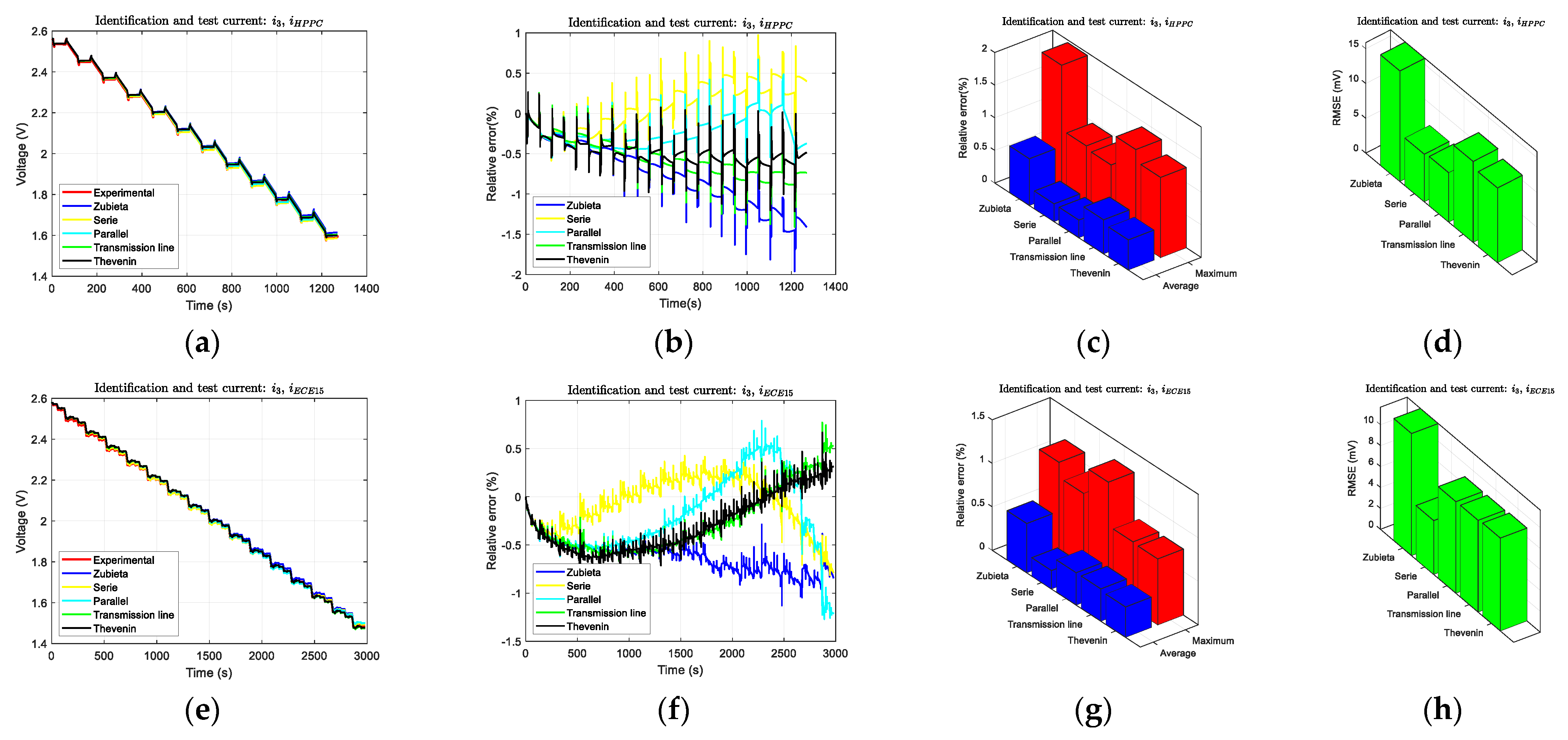
Finally, the result obtained with the current profile i₃, which is the most dynamic current profile, is depicted in Figure 13a–d for the HPPC test and Figure 13e–h for the ECE15 test. This current profile has been applied to the same models as current profile i₂. Again, the Serie Model has the best performance, and even the obtained relative error is lower than using the previous current profiles. Nevertheless, the Parallel model, Transmission Line model and Thevenin model get good behaviors.

The main conclusions obtained from these results are the following:

• The greater complex identification current profile i₃ gets greater accuracy for every model in which it can be applied.
• In most cases, the Series model provides the minimum relative error.
• If a simple and basic supercapacitor model has to be used, the best option is to use Zubieta model identified with the current profile i₃.

Table 4. The statistical metric with Current Profile i₁.

Model	HPPC			ECE15
	Maximum Relative Error (%)	Average Relative Error (%)	Root Mean Square Error (mV)	Maximum Relative Error (%)	Average Relative Error (%)	Root Mean Square Error (mV)
Stern-Tafel	2.6624	0.4975	11.6037	6.9044	2.0402	45.1645
Zubieta	8.8702	3.5055	79.0721	8.2994	3.3861	72.6719

,

Table 5. The statistical metric with Current Profile i₂.

Model	HPPC			ECE15
	Maximum Relative Error (%)	Average Relative Error (%)	Root Mean Square Error (mV)	Maximum Relative Error (%)	Average Relative Error (%)	Root Mean Square Error (mV)
Zubieta	5.5291	2.2657	50.5217	2.2409	1.4013	29.2705
Serie	1.5156	0.7592	15.7086	2.1871	1.2212	24.2654
Parallel	1.2932	0.2971	7.3963	6.6324	1.9509	43.9770
Transmission line	7.2856	2.9581	65.0135	8.3307	3.8223	78.3289
Thevenin	8.0835	3.5226	77.9992	8.5904	3.9647	82.2516

and

Table 6. The statistical metric with Current Profile i₃.

Model	HPPC			ECE15
	Maximum Relative Error (%)	Average Relative Error (%)	Root Mean Square Error (mV)	Maximum Relative Error (%)	Average Relative Error (%)	Root Mean Square Error (mV)
Zubieta	1.9602	0.7170	15.8874	1.1287	0.5673	11.6797
Serie	0.9718	0.2728	6.8365	0.9562	0.2119	5.1513
Parallel	0.9263	0.2714	7.0952	1.2706	0.3724	8.7621
Transmission line	1.4099	0.5227	11.6305	0.7700	0.3722	8.7803
Thevenin	1.2297	0.4617	10.7354	0.7593	0.3493	8.8829

include the numeric values for different current profiles identification and the response of each model for HPPC and ECE15 test. These values are those shown in Figure 10, Figure 11 and Figure 12.

6. Conclusions

This paper describes a parameter identification general procedure with a flexible and interactive interface used to build supercapacitor models in Simulink or Simscape. This procedure enables estimating the different models parameters based on the use of the Optimization Toolbox of Matlab^®. Once, the procedure steps are explained, the procedure is used to develop a comparative study of six commonly used supercapacitor models. In addition, the procedure enables using different identification current profiles, providing the possibility of analyzing the influence of three different identification current profiles in the accuracy and robustness of every model.

The experimental results obtained from the six models and three different identification current profiles, used to develop the study, show that both the model and the identification current profile are critical to obtaining good accuracy and robustness, which must be maintained over time.

From the comparison between the experimental results and the simulation results obtained using the model, it can be concluded that the greater complexity of the current identification profile, the greater accuracy and robustness of the model. In this case, the most complex identification current profile i₃ gets the best accuracy for every model in which it can be applied.

In a short simulation period, most models provide enough accuracy results. However, in a long simulation period the differences among models as well as among the current identification profiles increase, and models responses cumulate voltage errors and, in some cases, they cannot correctly represent the voltage of the supercapacitor. The Stern-Tafel model is proper for a short simulation and as a first approximation. However, in a long-time simulation, the Series Model represents a good performance, followed by the Parallel Model. In most cases, the Series model provides the minimum relative error. However, the Zubieta model provides a good compromise between complexity and accuracy. Then, if a simple and basic supercapacitor model has to be used, the best option is to use a Zubieta model identified by means of the current profile i₃.