Optimal Coordinated Bidding of a Profit Maximizing, Risk-Averse EV Aggregator in Three-Settlement Markets Under Uncertainty
Abstract
1. Introduction
- Development of a two-stage SD-MILP optimal coordinated bidding model for an aggregator who manages numerous storage units (stationary and EVs) and trades electric power in three-settlement markets, taking into account uncertainties in market price and fleet characteristics, as well as existing market rules. This model can be used for market exchange irrespective of (1) production or consumption technology and (2) mobile or stationary storage unit.
- Derivation of optimal coordinated charge (discharge) bids for day-ahead, intra-day and real-time markets with reasonable computation time using scenario-reduction techniques.
- Uncertainty modeling in all three market prices as well as of EV mobility parameters.
- Incorporation of the hourly CVaR (T-CVaR) to focus on the lower tails of the profits on hourly bases.
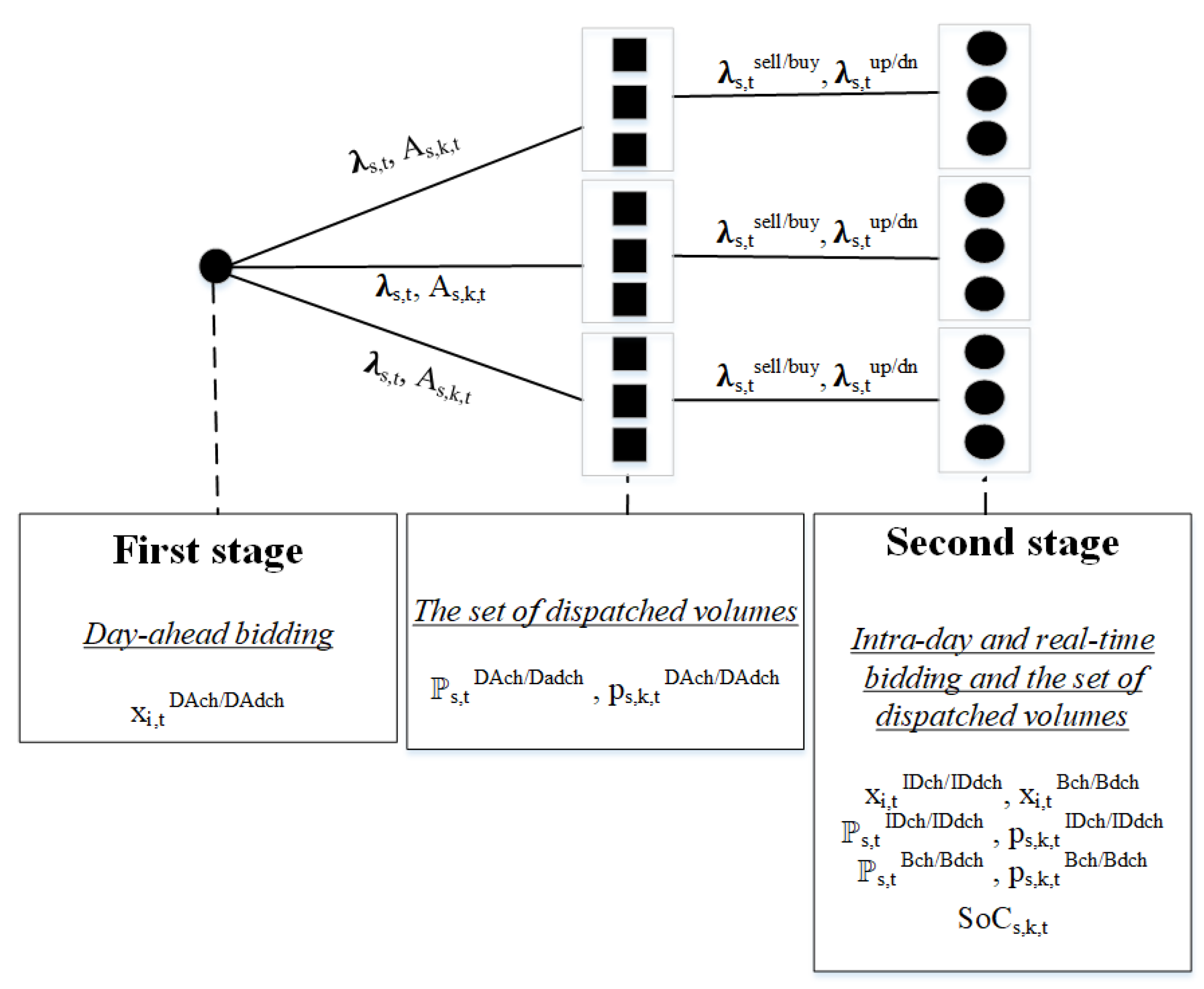
2. Decision Process Framework
- The daily bidding in day-ahead markets under the volatile day-ahead market prices, meanwhile allocating capacity in adjustment and regulating markets.
- The hourly/quarter-hourly intra-day selling/buying and balancing up/down-regulating positions driven by intra-day and real-time volatile market prices, and the strict requirements to satisfy driving needs of its fleet of EVs. These adjustments are necessary to address the errors stemming from the availability and price forecast.
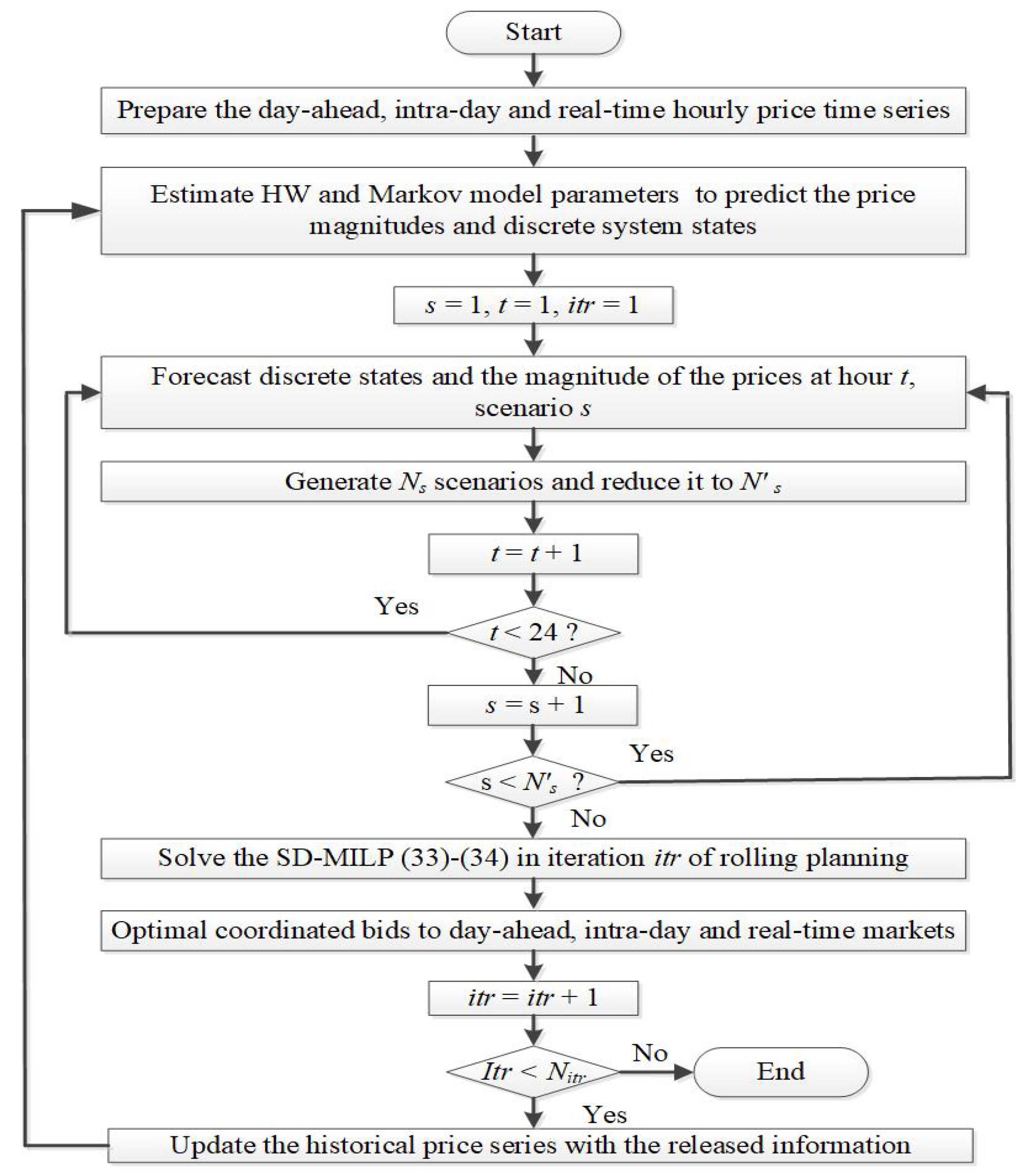
3. Scenario Generation
3.1. Market Places
3.2. Market Price Scenario Generation and Reduction
3.3. Availability Simulation
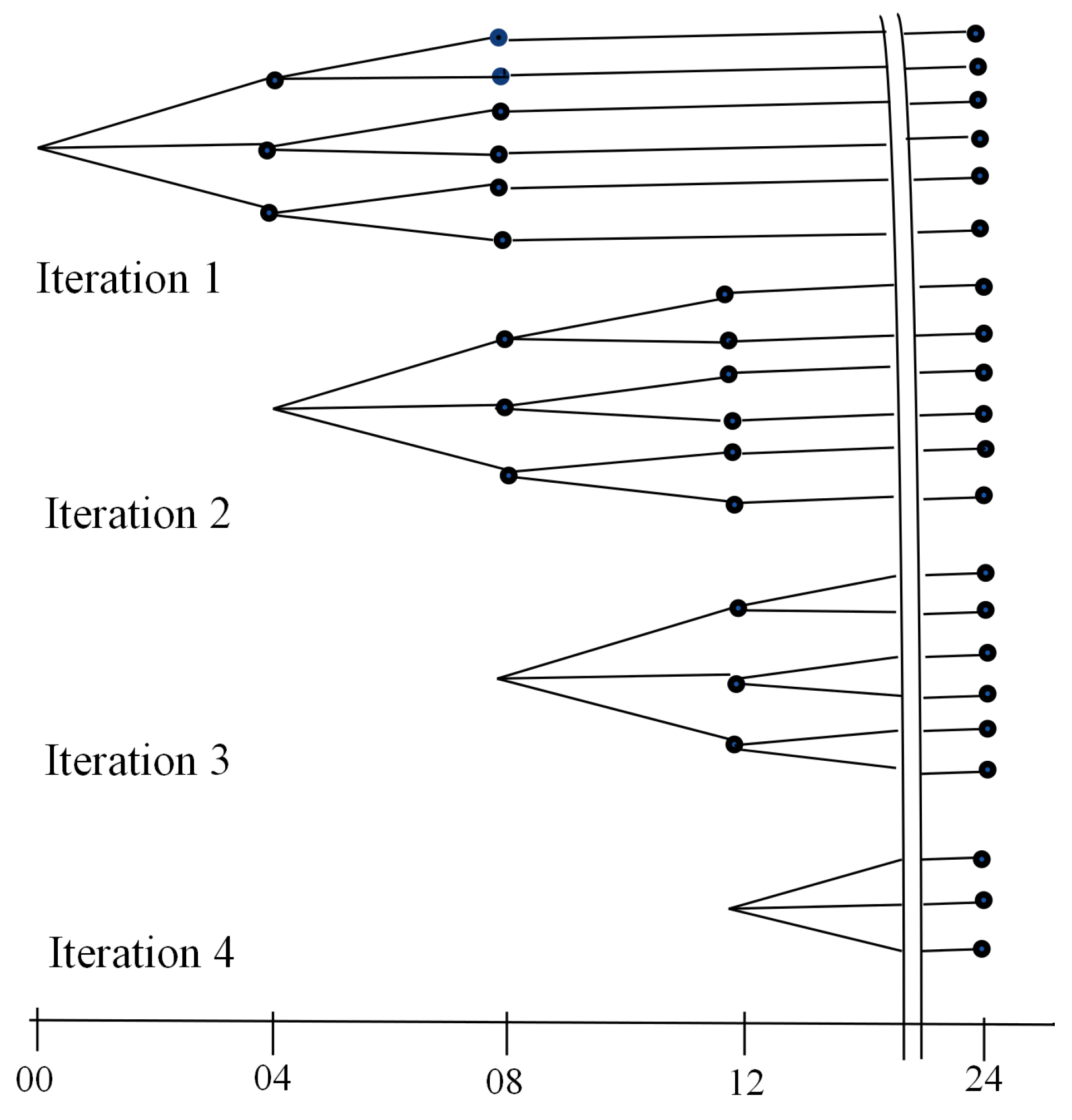
3.4. Rolling Planning
4. Mathematical Problem Formulation
Two-Stage Stochastic Optimal Strategy of an EV Aggregator
5. Case Study
5.1. Market Price Series
5.2. General Parameters
5.3. Simulation Results
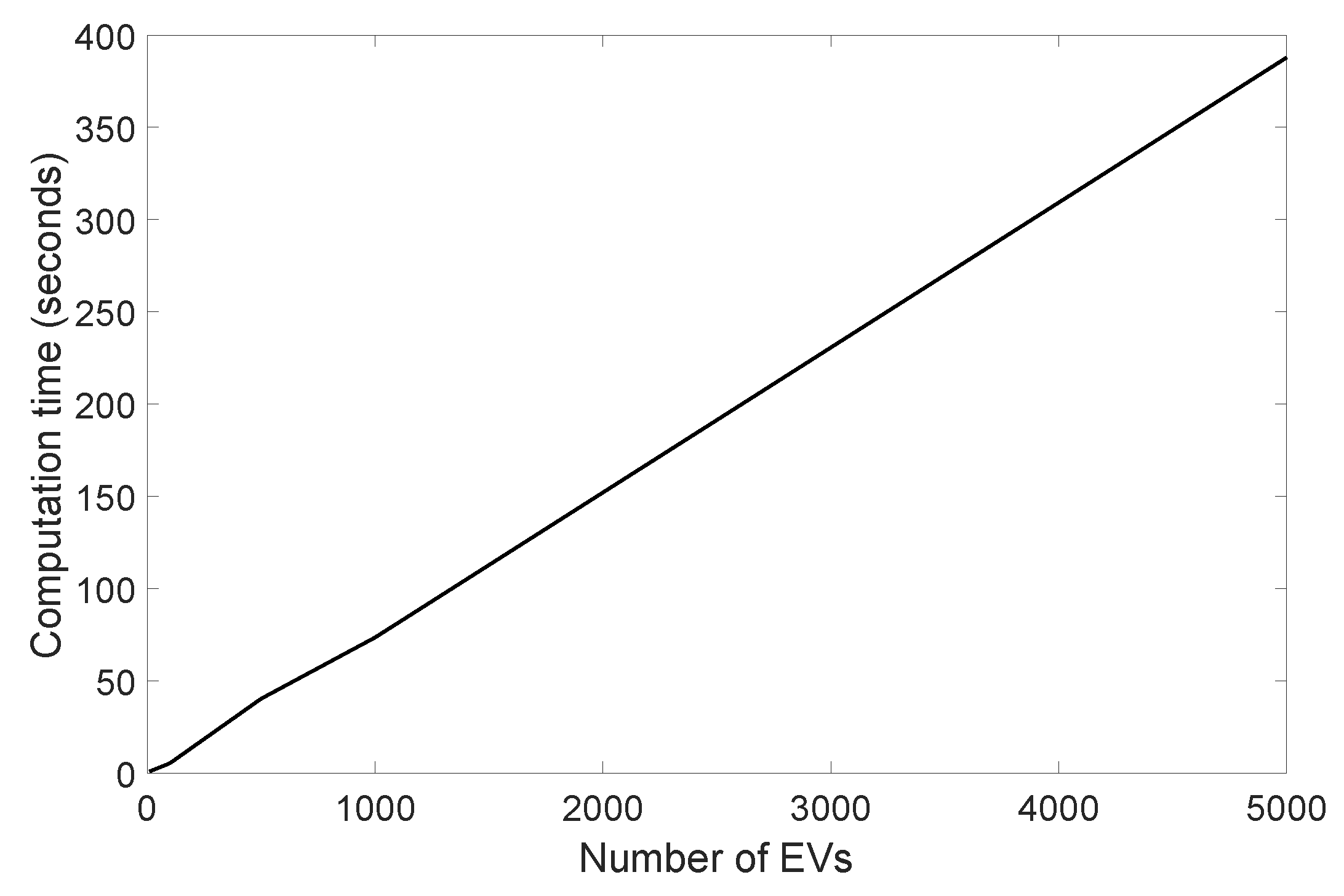
5.3.1. Tractability of the Solution
5.3.2. Rolling Planning Horizon
5.3.3. Controlling the Risk Measure T-CVaR
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| MILP | mixed integer linear program; |
| SD-MILP | stochastic dynamically updated MILP; |
| EV | electric vehicle; |
| T-CVaR | hourly CVaR; |
| DER | distributed energy resources; |
| PV | photovoltaic panel; |
| TCL | thermostatically controlled loads; |
| TSO | transmission system operator; |
| EES | electric energy storage; |
| RES | renewable energy source |
| Indices | |
| k | storage indices, ; |
| t | planning periods, ; |
| s | scenarios, ; |
| i | index for possible bid prices |
| Parameters | |
| probabilities associated with the scenarios; | |
| max/min storage rate of discharge/charge [kW]; | |
| max capacity of a storage [kWh]; | |
| scalar to calculate max/min SoC; | |
| charge, discharge efficiency of a storage; | |
| start storage level [kWh]; | |
| end storage level [kWh]; | |
| day-ahead market price scenario [€/MWh]; | |
| intra-day market price scenario [€/MWh]; | |
| real-time market price scenario [€/MWh]; | |
| fixed bid price for day-ahead market [€/MWh]; | |
| fixed bid price for intra-day market [€/MWh]; | |
| fixed bid price for real-time market [€/MWh]; | |
| aggregator’s offer to storage owner [€/MWh]; | |
| capital cost of a storage [€]; | |
| the slope of the linear approximation of the battery life as a function of the cycles; | |
| availability matrix indicating whether EV is available or not; | |
| average hourly driving distance of an EV [km]; | |
| driving efficiency of an EV; | |
| total energy spent on driving [kWh]; | |
| risk aversion level; | |
| significance level; | |
| profit in hour t and scenario s [€]; | |
| sufficiently big constants | |
| Variables | |
| charging/discharging dispatch level for kth storage in day-ahead market [kWh]; | |
| charging/discharging dispatch level for k-th storage in intra-day market [kWh]; | |
| charging/discharging dispatch level for k-th storage in real-time market [kWh]; | |
| energy as day-ahead buying/selling position [kWh]; | |
| buying/selling dispatch volume in intra-day market [kWh]; | |
| down/up-regulating dispatch volume in real-time market [kWh]; | |
| total cost of charging/discharging in day-ahead market [€]; | |
| total cost of charging/discharging in intra-day market [€]; | |
| total cost of charging/discharging in real-time market [€]; | |
| charging/discharging bid volume in day-ahead market [kWh]; | |
| charging/discharging bid volume in intra-day market [kWh]; | |
| charging/discharging bid volume in real-time market [kWh]; | |
| storage level at the end of time step t [kWh]; | |
| value-at-risk for a significance level ; | |
| auxiliary variable employed to calculate hourly CVaR |
References
- Global EV Outlook: Understanding the Electric Vehicle Landscape to 2020. Available online: http://www.iea.org/publications/globalevoutlook_2013.pdf (accessed on 12 October 2017).
- Ortega-Vazquez, M.A.; Bouffard, F.; Silva, V. Electric vehicle aggregator/System Operator coordination for charging scheduling and services procurement. IEEE Trans. Power Syst. 2013, 28, 1806–1815. [Google Scholar] [CrossRef]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Nickel Metal Hydride. In Proceedings of the 9th Iranian Conference on Electrical and Electronics Engineering, Gonabad, Iran, 28–29 August 2018. [Google Scholar]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Lead Acid. In Proceedings of the 9th Iranian Conference on Electrical and Electronics Engineering, Gonabad, Iran, 28–29 August 2018. [Google Scholar]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Lithium-ion. In Proceedings of the First International Conference on Modern Approaches in Engineering Sciences, Tbilisi, Georgia, 21 November 2018. [Google Scholar]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of electric vehicles in the electric power system. Proc. IEEE 2011, 99, 168–183. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A.; Soares, F.J.; Lopes, J.A.P. Optimized bidding of a EV aggregation agent in the electricity market. IEEE Trans. Smart Grid 2012, 3, 443–452. [Google Scholar] [CrossRef]
- Sarker, M.; Ortega-Vazquez, M.; Kirschen, D. Optimal coordination and scheduling of demand response via monetary incentives. IEEE Trans. Smart Grid 2015, 6, 1341–1352. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Global against divided optimization for the participation of an EV aggregator in the day-ahead electricity market. Part I: Theory. Electr. Power Syst. Res. 2013, 95, 309–318. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Global against divided optimization for the participation of an EV aggregator in the day-ahead electricity market. Part II: Numerical analysis. Electr. Power Syst. Res. 2013, 95, 319–329. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Bakirtzis, A.G. Optimal bidding strategy for electric vehicle aggregators in electricity markets. IEEE Trans. Power Syst. 2013, 28, 4031–4041. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal combined bidding of vehicle-to-grid ancillary services. IEEE Trans. Smart Grid 2012, 3, 70–79. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal scheduling of vehicle-to-grid energy and ancillary services. IEEE Trans. Smart Grid 2012, 3, 351–359. [Google Scholar] [CrossRef]
- Momber, I.; Siddiqui, A.; San Román, T.G.; Söder, L. Risk Averse Scheduling by a PEV Aggregator Under Uncertainty. IEEE Trans. Power Syst. 2015, 30, 882–891. [Google Scholar] [CrossRef]
- Sarker, M.R.; Dvorkin, Y.; Ortega-Vazquez, M.A. Optimal Participation of an Electric Vehicle Aggregator in Day-Ahead Energy and Reserve Markets. IEEE Trans. Power Syst. 2016, 31, 3506–3515. [Google Scholar] [CrossRef]
- Vardanyan, Y.; Banis, F.; Pourmousavi, S.; Madsen, H. Optimal coordinated bidding of a profit-maximizing EV aggregator under uncertainty. In Proceedings of the 5th IEEE International Energy Conference, Limassol, Cyprus, 3–7 June 2018. [Google Scholar]
- Ortega-Vazquez, M.A. Optimal scheduling of electric vehicle charging and vehicle-to-grid services at household level including battery degradation and price uncertainty. IET Gener. Transm. Distrib. 2014, 8, 1007–1016. [Google Scholar] [CrossRef]
- Korolko, N.; Sahinoglu, Z. Robust optimization of EV charging schedules in unregulated electricity markets. IEEE Trans. Smart Grid 2017, 8, 149–157. [Google Scholar] [CrossRef]
- Pantos, M. Exploitation of Electric-Drive Vehicles in Electricity Markets. IEEE Trans. Power Syst. 2012, 27, 682–694. [Google Scholar] [CrossRef]
- Al-Awami, A.; Sortomme, E. Coordinating Vehicle-to-Grid Services With Energy Trading. IEEE Trans. Smart Grid 2011, 3, 453–462. [Google Scholar] [CrossRef]
- Vardanyan, Y.; Hesamzadeh, M. The coordinated bidding of a hydropower producer in three-settlement markets with time-dependent risk measure. Electric Power Syst. Res. 2017, 51, 40–58. [Google Scholar] [CrossRef]
- Song, M.; Amelin, M.; Wang, X.; Saleem, A. Planning and operation models for an EV sharing community in spot and balancing market. IEEE Trans. Smart Grid 2019. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. A game theoretic approach to risk-based optimal bidding strategies for electric vehicle aggregators in electricity markets with variable wind energy resources. IEEE Trans. Sustain. Energy 2016, 7, 374–385. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Yamin, H.; Li, Z. Market Operations in Electric Power Systems: Forecasting, Scheduling and Risk Management; Willy-IEEE Press: Hoboken, NJ, USA, 2002. [Google Scholar]
- Taylor, J.W. Short-term electricity demand forecasting using double seasonal exponential smoothing. J. Oper. Res. Soc. 2003, 54, 799–805. [Google Scholar] [CrossRef]
- Nord Pool Database. Available online: http://www.nordpoolspot.com/ (accessed on 15 August 2017).
- Römisch, W. Scenario Reduction Techniques in Stochastic Programming; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar]
- Sundström, O.; Binding, C. Flexible Charging Optimization for Electric Vehicles Considering Distribution Grid Constraints. IEEE Trans. Smart Grid 2012, 3, 26–37. [Google Scholar] [CrossRef]
- Van Roy, J.; Leemput, N.; De Breucker, S.; Geth, F.; Tant, P.; Driesen, J. An Availability Analysis and Energy Consumption Model for a Flemish Fleet of Electric Vehicles. In Proceedings of the EEVC European Electric Vehicle Congress, Brussels, Belgium, 26–28 October 2011. [Google Scholar]
- Pesaran, A.; Markel, T.; Tataria, H.S.; Howell, D. Battery Requirements for Plug-In Hybrid Electric Vehicles—Analysis and Rationale. In Proceedings of the 23rd International Electric Vehicle Symposium, Anaheim, CA, USA, 2–5 December 2007. [Google Scholar]
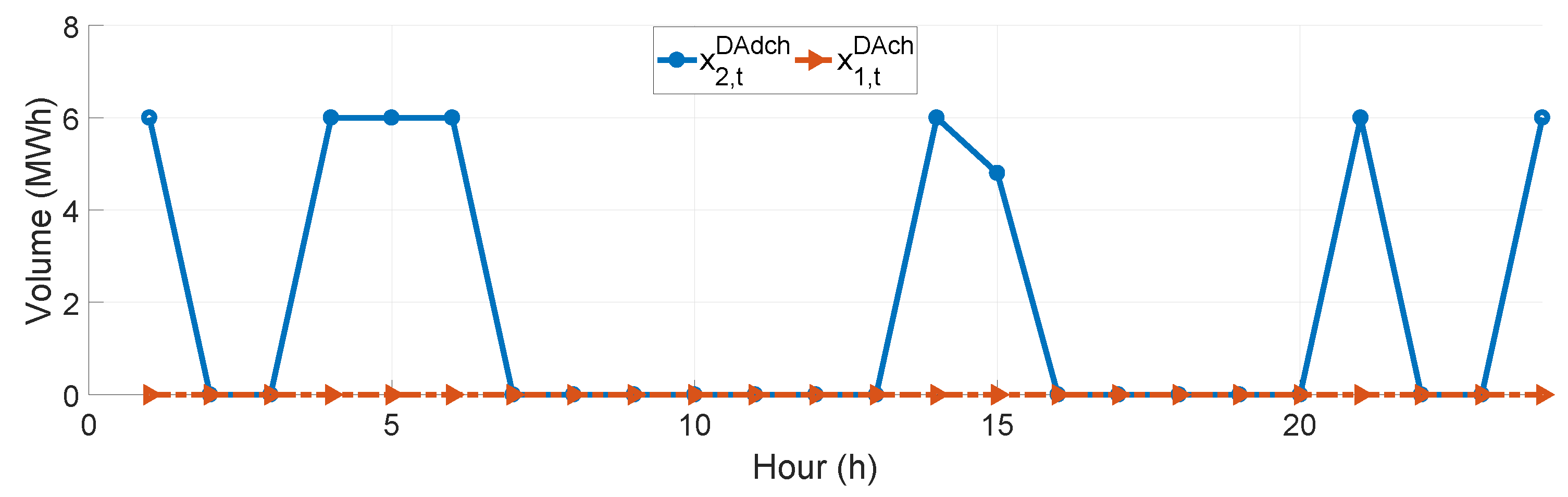
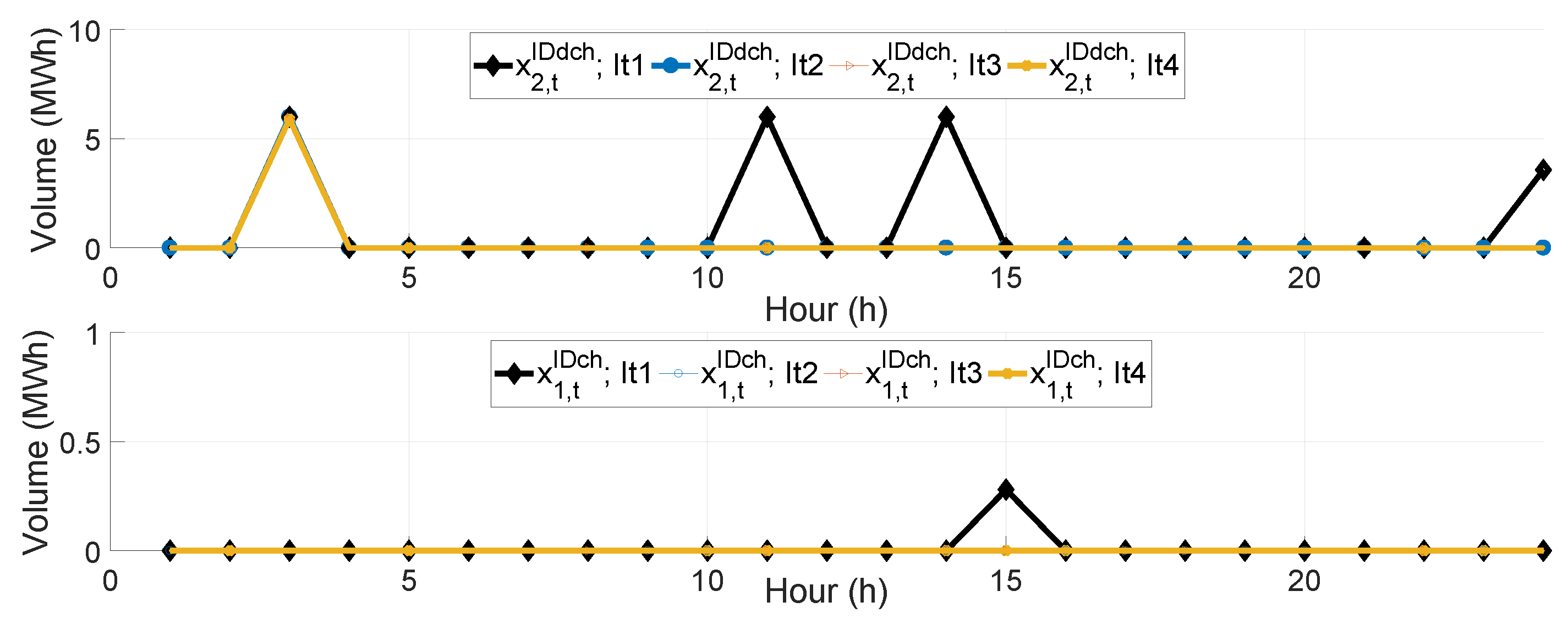
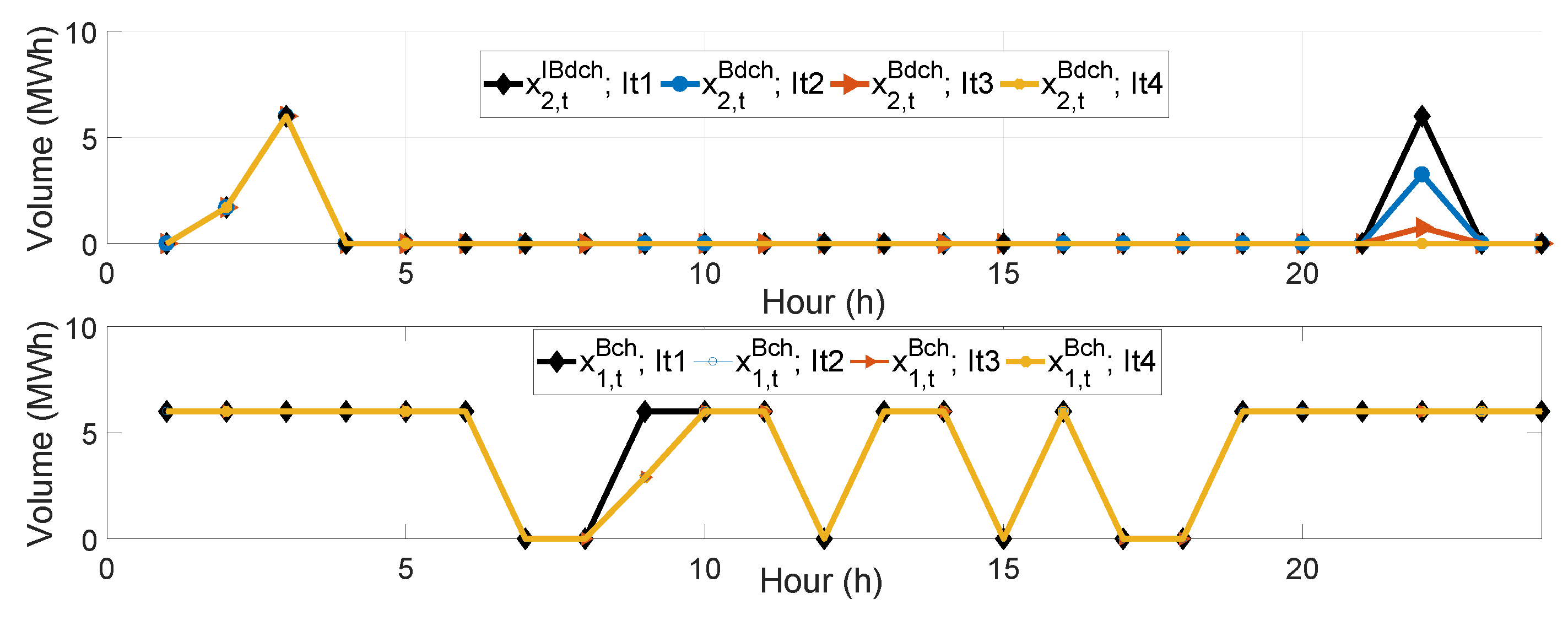
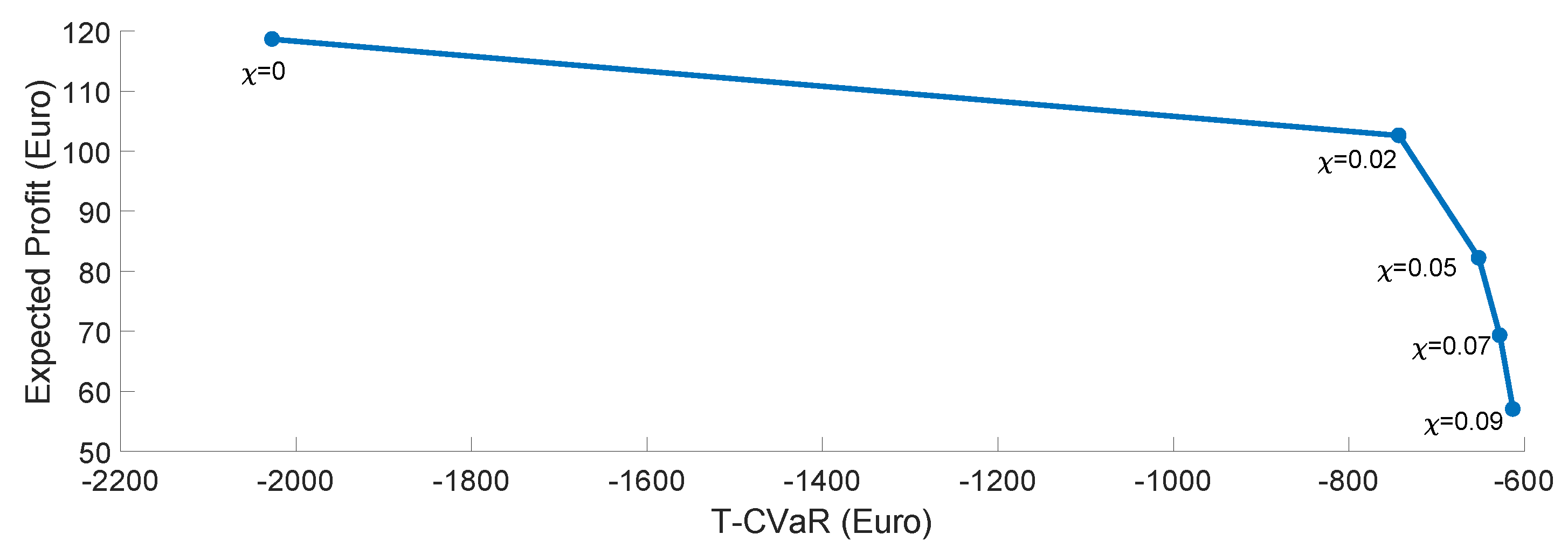
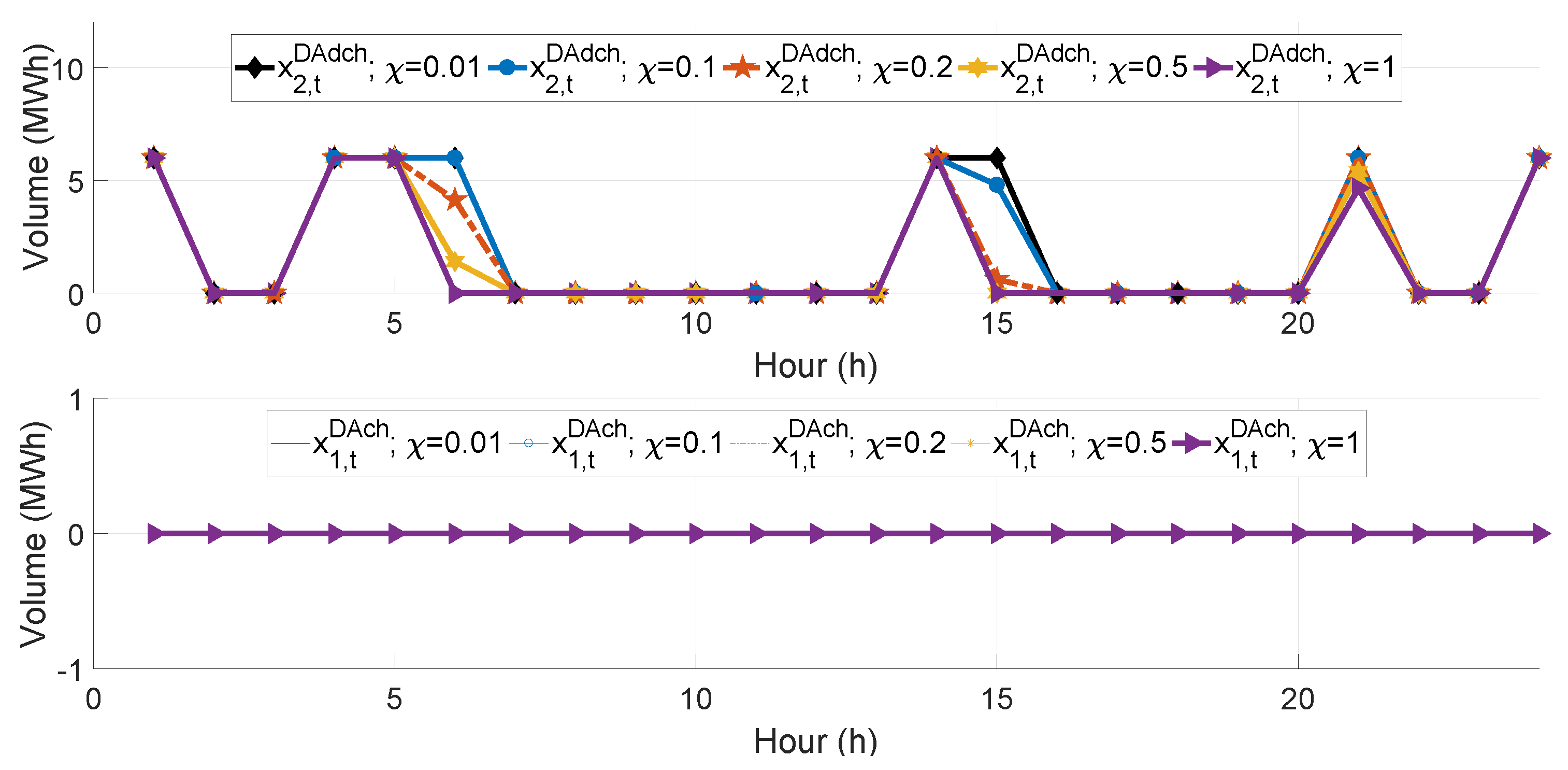
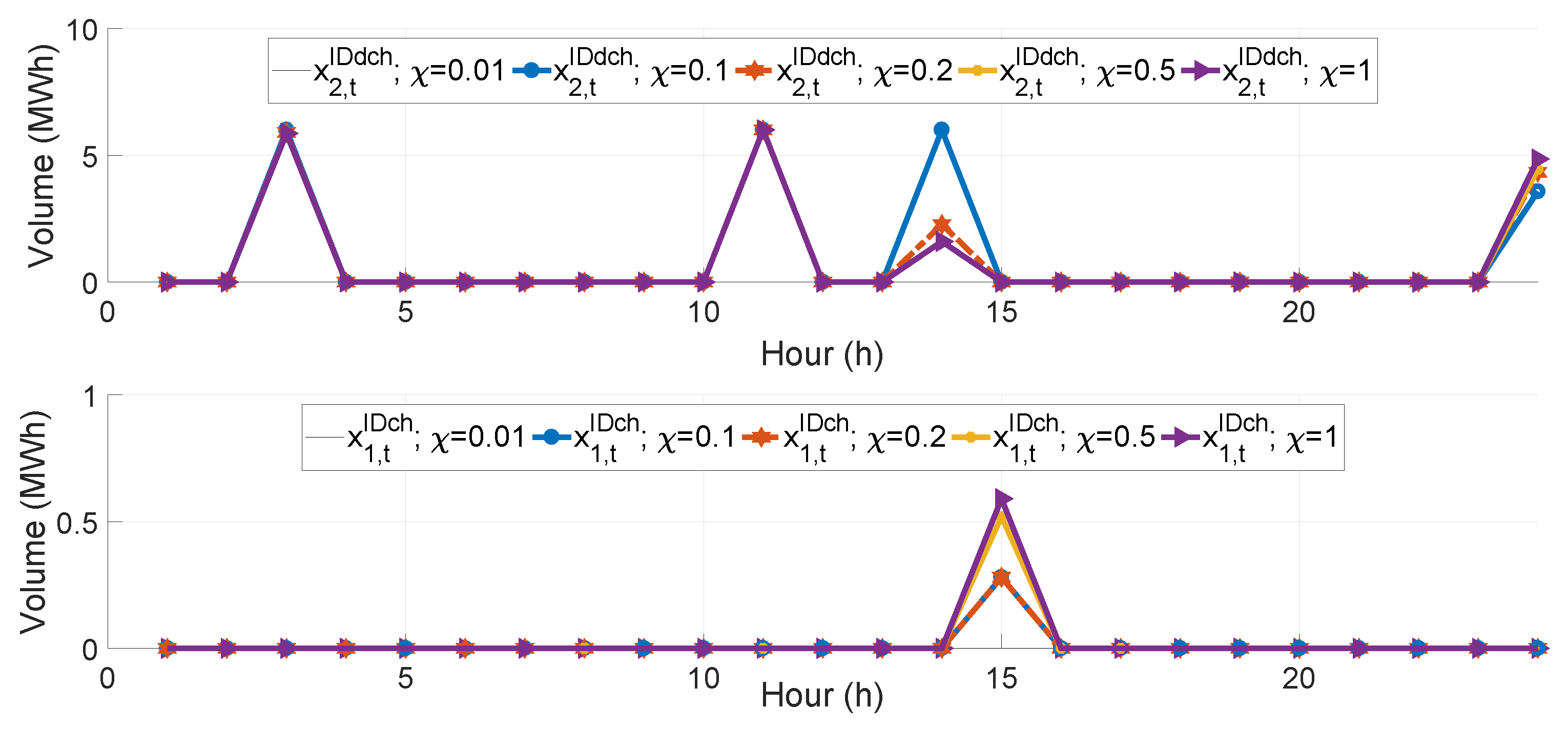
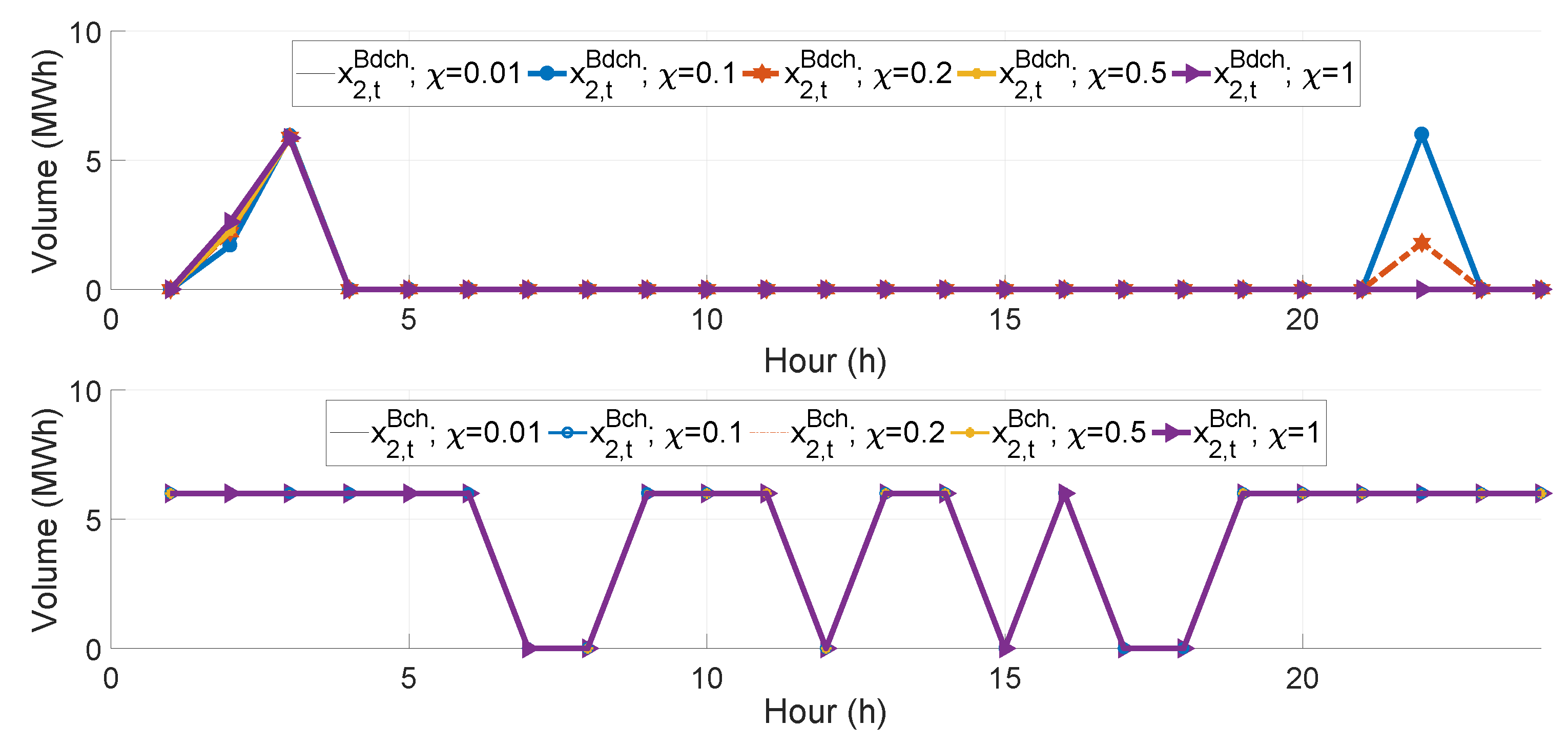
| Par. | Value | Units | Ref. | Par. | Value | Units | Ref. |
|---|---|---|---|---|---|---|---|
| 50 | KWh | [28] | 90% | [29] | |||
| 20 % | [30] | 93% | [29] | ||||
| 100% | [30] | 60% | |||||
| 6 | KW | [28] | 200 | € | [15] | ||
| 6 | KW | [28] | −[0.0013] | [15] |
| It. 1 | It. 2 | It. 3 | It. 4 | |
|---|---|---|---|---|
| (€) | 110.31 | 101.87 | 77.1 | 76.26 |
| Comp. time (second) | 68.34 | 58.3 | 59.56 | 63.76 |
| Number of EVs | 10 | 100 | 500 | 1000 | 5000 |
| Continuous variables | 73,177 | 526,777 | 2,542,777 | 5,062,777 | 25,150,802 |
| Discrete variables | 12,960 | 12,960 | 12,960 | 12,960 | 12,960 |
| Constraints | 115,921 | 569,521 | 2,585,521 | 5,105,521 | 25,205,521 |
| Comp. time (second) | 0.78 | 5.3 | 40.25 | 73.76 | 387.84 |
| Base Prices | Volatile Prices | Difference in % | |
|---|---|---|---|
| Day-ahead trading (€) | 183 | 9 | 95% decrease |
| Intra-day trading (€) | 64 | 413 | 85% increase |
| Real-time trading (€) | 1924 | 1983 | 3% increase |
| Hours | T-CVaR (€) | Hours | T-CVaR (€) | Hours | T-CVaR (€) |
|---|---|---|---|---|---|
| 1 | 9 | 0 | 17 | 0 | |
| 2 | 10 | 18 | 0 | ||
| 3 | * | 11 | 19 | * | |
| 4 | 12 | 20 | |||
| 5 | 13 | 21 | |||
| 6 | 14 | * | 22 | ||
| 7 | 0 | 15 | * | 23 | |
| 8 | 0 | 16 | 24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vardanyan, Y.; Madsen, H. Optimal Coordinated Bidding of a Profit Maximizing, Risk-Averse EV Aggregator in Three-Settlement Markets Under Uncertainty. Energies 2019, 12, 1755. https://doi.org/10.3390/en12091755
Vardanyan Y, Madsen H. Optimal Coordinated Bidding of a Profit Maximizing, Risk-Averse EV Aggregator in Three-Settlement Markets Under Uncertainty. Energies. 2019; 12(9):1755. https://doi.org/10.3390/en12091755
Chicago/Turabian StyleVardanyan, Yelena, and Henrik Madsen. 2019. "Optimal Coordinated Bidding of a Profit Maximizing, Risk-Averse EV Aggregator in Three-Settlement Markets Under Uncertainty" Energies 12, no. 9: 1755. https://doi.org/10.3390/en12091755
APA StyleVardanyan, Y., & Madsen, H. (2019). Optimal Coordinated Bidding of a Profit Maximizing, Risk-Averse EV Aggregator in Three-Settlement Markets Under Uncertainty. Energies, 12(9), 1755. https://doi.org/10.3390/en12091755





