Abstract
Periodic preventive maintenance of generators is required to maintain the reliable operation of a power system. However, generators under maintenance cannot supply electrical energy to the power system; therefore, it is important to determine an optimal generator maintenance schedule to facilitate efficient supply. The schedule should consider various constraints of the reliability-based demand response program, power system security, and restoration. Determining the optimal generator maintenance schedule is generally formulated as a non-linear optimization problem, which leads to difficulties in obtaining the optimal solution when the various power system constraints are considered. This study proposes a generator maintenance scheduling (GMS) method using transformation of mixed integer polynomial programming in a power system incorporating demand response. The GMS method is designed to deal with various system requirements and characteristics of demand response within a power system. A case study is conducted using data from the Korean power system to demonstrate the effectiveness of the proposed method for determining the optimal maintenance schedule. The results show that the proposed GMS method can be used to facilitate the efficient and reliable operation of a power system, by considering the applicable system constraints.
1. Introduction
Determining an optimal generator maintenance schedule is important for increasing the reliability [1,2] of a power system by ensuring the most appropriate amount of supply resources to meet the forecasted demand in the future. Various methods have been studied to determine optimal generator maintenance schedules for power system reliability. In [3], the sum of the loss of load probability (LOLP) was minimized. In [4], expected unserved energy (EUE) was used as reliability criteria for the generator maintenance scheduling (GMS) problem. In [5], the supply reserve margin was levelized for the GMS problem, which can lead to minimum fuel costs during power system operation [6]. Therefore, to satisfy the reliability requirement and reduce fuel costs, levelizing of the reserve margin is commonly used for the GMS problem. GMS problems are complex non-linear problems related to many factors such as resource characteristics and various system requirements [3,4,5,6,7]. It is particularly challenging to incorporate the demand response (DR) [8] within the GMS problem.
As such, very limited research has been conducted in the area of GMS algorithms incorporating DR programs. In [9], market-based DR was considered in the GMS problem and the impact of economic-based DR on the GMS problem was investigated in [10]. However, a reliability-based DR has not yet been considered in the GMS problem.
Reliability-based DR involves curtailing demands during the peak demand season or under emergency circumstances when resource inadequacy occurs in the power system. Reliability-based DR is therefore activated by a curtailment request from the independent system operator (ISO). Compared to incentive-based DR, the performances of reliability-based DR may be partly secured through considerable penalties. Its capacity can affect the results of the GMS problem by changing the supply reserves for power system reliability over the scheduling period. To efficiently ensure supply reserves in the power system, it is important to consider the characteristics of reliability-based DR, which differ from those of conventional generators in the GMS problem.
Hybrid renewable energy resources (HRES) and microgrids can also be used as resources for reliability-based DR. The increased penetration of renewable energy incorporating HRESs and distributed energy resources by microgrids can affect supply reserve requirements and stability under fault conditions [11,12] and dynamic operation [13]. This can lead to cause various problems in the power system such as voltage imbalance [14]. In order to maintain the security of the power system with high penetration of renewable energy and distributed energy resources, many must-run units may be required to be continuously on-line. However, if the must-run units are not considered in the GMS problem, several problems may arise in the power system due to a reduction of on-line must-run units.
Therefore, for reliable power system operation, a minimum number of must-run units are required in the power system. Furthermore, a minimum number of blackstart units should always be considered. In order to meet these requirements, it is necessary to prevent the simultaneous maintenance of generators to be used as blackstart units or must-run units. In [15], maintenance exclusion constraints were considered in the GMS problem to prevent the simultaneous maintenance of generators in a specific area. However, these constraints were formulated to consider locational supply reserve requirements in the GMS problem; thus, they do not take the characteristics of must-run and blackstart units into account.
This study presents a GMS method using transformation of mixed integer polynomial programming incorporating the reliability-based DR. The proposed method is based on levelizing the reserve margin. The characteristics of reliability-based DR, must-run units, and blackstart units are also formulated and considered as constraints for the GMS problem. The GMS problem can be formulated as a mixed integer non-linear programming (MINLP) problem because of the non-linear objective function, which is formulated as the sum of the squared supply reserves for levelizing the reserve margin. The nonlinear characteristics of the GMS problem can lead to a reduction in the convergence ratio of the GMS problem.
Various studies have been conducted on the non-linear GMS problem [3,4,5]. Due to the low convergence ratio and high computation time caused by the non-linear characteristics of the GMS problem, mathematical programming techniques such as the branch and bound algorithm and cutting plane algorithm, are considered as not particularly effective for GMS problems. Therefore, many heuristic-based approaches have been proposed to solve this non-linear GMS problem. In [16], a genetic algorithm (GA) was applied to find the solution of a GMS problem based on power system reliability. In [17,18], a simulated annealing method was applied to a GMS problem formulated with a reliability optimality criterion subject to a number of constraints. In [4,5,6,7], particle swarm optimization (PSO)-based approaches were presented to generate optimal schedule. Furthermore, [19] applied differential evolution to the GMS problem.
However, these heuristic-based approaches for the GMS problem can converge to a local optimal solution in a power system, unlike mathematical programming techniques. In this study, a mixed integer polynomial programming transformation technique [20,21] is adopted to transform the non-linear form of the GMS problem to a linear form and enable the use of the mathematical programming techniques.
The proposed GMS method is divided into a feasibility check stage for the constraints of the must-run and blackstart units and a maintenance scheduling stage. The feasibility check is performed based on an optimization problem with few constraints; i.e., the must-run and blackstart unit constraints and the maintenance schedule constraints. In the scheduling stage, the maintenance schedule is determined using the results of the feasibility check stage. Thus, the GMS problem is optimized subject to the constraints of the reliability-based DR, must-run units, and blackstart units.
The remainder of this paper is organized as follows. In Section 2, the formulation of the GMS problem considering the reliability-based DR, must-run units, and blackstart units is presented. In Section 3, the proposed GMS algorithm is presented. Finally, the results of a case study demonstrating the effectiveness of the proposed GMS method are presented in Section 4.
2. GMS Problem Incorporating Reliability-Based DR, Must-Run Units, and Blackstart Units
In this section, mathematical models of the reliability-based DR, must-run units, and blackstart units are proposed for the GMS problem. The GMS problem incorporating these factors is then formulated.
2.1. Reliability-Based DR Model for the GMS Problem
Reliability-based DR should only be used in the case of supply reserve deficiencies caused by generator maintenance or a high peak load. In this study, the supply reserve check constraint for load reduction of the reliability-based DR is formulated as follows:
where Pi,d is the capacity of generator i on day d; Xi,d is the binary variable for the maintenance status of generator i on day d, which is 1 if generator i is under maintenance on day d and 0 otherwise; Ld is the peak load on day d; R is the minimum supply reserve requirement for the power system; Yd is the binary variable for the check of the supply reserve deficiency and load reduction event occurrence; and K∞ is the upper bound of ∑Pi,d(1 − Xi,d) − Ld.
If Yd is 0, constraint (1) ensures that the supply reserve on day d is larger than R with constraint (2), which is redundant. If Yd is 1, constraint (2) ensures that the supply reserve on day d is lower than R with constraint (1), which is redundant.
The reliability-based DR is generally available for load reduction within a limited number of reduction events, which is predetermined in the scheduling period. In addition, even if the supply reserve is always larger than R during the scheduling period, a load reduction event may occur for performance testing. In this study, the constraints on the number of load reduction events for the reliability-based DR are expressed as follows:
where is the binary value for load reduction caused by the reliability-based DR performance test; and is the maximum number of load reduction events that can occur during the scheduling period.
2.2. Must-Run Unit Constraints for the Power System in the GMS Problem
In a power system, must-run units to maintain the security of power system are selected based on the analysis results for power system security [22]. Must-run units must always be on-line according to the required number of must-run units in the power system.
The number of generators that can be used as must-run units should always be greater than the number of required must-run units in the local power system. In order to incorporate this requirement within the GMS problem, the mathematical model for the number of must-run units is expressed as follows:
where g is the set of generators in the local power system that requires the must-run units; CCTg is the set of turbines of the combined cycle generator in g; Cg,n,d is the number of combined cycle generators considered as must-run units on day d, which is determined by the maintenance status of the turbines in the n-th combined cycle generator in g; and Ng is the number of required must-run units in g.
The combined cycle generator consists of several turbines whose maintenance can be performed separately. The capacity of the combined cycle generator varies depending on the maintenance schedule of each turbine in the generator. Therefore, the number of combined cycle generators considered as must-run units, Cg,n,d, should be determined by considering the maintenance schedule of each turbine. In this study, Cg,n,d is formulated based on the ratio of the capacity of the combined cycle generator to the predetermined reference capacity, as follows:
where CCTg,n is the set of turbines of the n-th combined cycle generator in g; and is a reference capacity used for calculating Cg,n,d.
2.3. Blackstart Unit Constraint for the Power System in the GMS Problem
In general, a power system contains both primary and backup blackstart units for use in the event of a wide-area blackout. Thus, simultaneous maintenance of the primary and backup blackstart units in a power system should be prevented. The maintenance exclusion constraint for blackstart units is expressed as follows:
where MBUh and SBUh are the sets of primary and backup blackstart units in area h, respectively; and is the number of backup blackstart units in h.
2.4. GMS Problem Formulation Considering Reliability-Based DR, Must-Run Units, and Blackstart Units
The objective when solving the GMS problem considered in this study is to determine maintenance schedules for all generators in a power system that minimize the supply reserve variation [3,4,5]. The reliability-based DR, must-run units, and blackstart units employed for power system reliability can affect the result of the GMS problem. Therefore, it is necessary to formulate the GMS problem considering the various constraints for these three factors. In this subsection, the GMS problem is formulated based on the proposed models (1)–(8) for the reliability-based DR, must-run units, and blackstart units and the formulation described in [3,4,5]. In this study, the historical aggregate hourly output from renewable generation is analyzed on a monthly basis to estimate the aggregate hourly output of renewable generation for the GMS problem.
The objective function [5] for the GMS problem is expressed as follows:
The optimization problem for determining the generator maintenance schedule should be solved subject to the following constraints:
- Supply reserve requirement constraintwhere PDR is the effective capacity of the reliability-based DR during the scheduling period, which represents the reliability-DR capacity adjusted by the historical performance data for the load reduction of the reliability-based DR.
- Maintenance window constraintswhere Mi,j is the time set in which the maintenance for the j-th schedule of generator i may be performed, termed an adjustable period in this paper; Xi,j,d is the binary variable for the status of the j-th maintenance schedule for generator i on day d; and OPi is the set of maintenance schedules of generator i.
- Maintenance outage duration constraintswhere Di,j is the maintenance outage duration in the j-th maintenance schedule for generator i; and si,j,d and fi,j,d are the binary variables for the beginning and end of the j-th maintenance schedule for generator i on day d, respectively.
- Maintenance exclusion constraintwhere gs is the set of generators for which simultaneous maintenance is impossible.
- Sequence and interval constraint for maintenance scheduleswhere gp is the set of maintenance schedules of the generators for which the sequence and interval for maintenance must be maintained; αk,l is the interval between the l-th maintenance schedule of generator k and the j-th maintenance schedule of generator i; and Ngp is the number of generators in gp.
- Must-run unit constraints
- Blackstart unit constraint
Equations (1)–(4) are regarded as constraints for the GMS problem considering the reliability-based DR, must-run units, and blackstart units.
The GMS problem is formulated as a mixed integer non-linear programming problem because of the quadratic terms in the objective function (9). The non-linearity can reduce the convergence rate of the GMS problem.
3. GMS Method Based on Transformation of Mixed Integer Polynomial Programming with Constraints for Reliability-Based DR, Must-Run Units, and Blackstart Units
The formulation of the GMS problem is non-linear due to the non-linear objective function. In this section, the GMS-problem objective function (9) is transformed into a linear form. In addition, a GMS algorithm is proposed that incorporates the various constraints for the reliability-based DR, must-run units, and blackstart units.
3.1. Formulation of the GMS Problem Objective Function Using the Transformation of Mixed Integer Polynomial Programming Method
The GMS problem is formulated as a non-linear programming problem owing to the non-linear objective function (9). However, as the non-linear formulation increases the problem complexity, a low-convergence problem is induced in the maintenance scheduling optimization.
In order to resolve this low-convergence problem, transformation of mixed integer polynomial programming [20,21] for linear transformation is used to convert the non-linear objective function (9) into a linear form. Specifically, slack variables are used for this purpose. The objective function reformulated using slack variables can be expressed as follows:
where Zi,d is the slack variable for linearization of the objective function.
In addition, the equivalency of Equations (9) and (23) is expressed by adding the constraints that define Zi,d in the maintenance scheduling problem, as follows:
where NG is the number of generators in the power system; and Kmin and Kmax are the lower and upper bounds for Pi,d∑Pm,dXm,d, respectively.
If Xi,d is 1, constraints (24) and (25) ensure that Zi,d = Pi,d∑Pm,dXm,d with constraint (26), which is redundant. If Xi,d is 0, constraint (26) ensures that Zi,d = 0 with constraints (24) and (25), which are redundant.
3.2. GMS Algorithm Considering Constraints for Reliability-Based DR and Power System
The GMS algorithm considering various constraints for the reliability-based DR and the power system is presented in this section. In the proposed algorithm, the input data include data for the maintenance schedule of each generator (including adjustable periods and maintenance outage duration), which are provided by the generator companies, a generator/transmission expansion plan, the capacity of each generator, the forecasted daily peak load, and historical data for peak load reduction due to the reliability-based DR and several power system constraints.
The generator maintenance schedule can be determined by performing optimization using the input data, the aforementioned mathematical model (1)–(4), and (10)–(22). However, if the maintenance scheduling problem is solved using only the aforementioned model, it can be difficult to confirm whether the maintenance schedules meet the constraints for the must-run or blackstart units. In order to clarify this point, feasibility checks for the must-run and blackstart unit constraints are performed before solving the GMS problem via the proposed algorithm.
The feasibility check is based on the optimization method and performed separately for each generator group, which consists of must-run or blackstart units. In the optimization problem for the feasibility check, the constant value “0” is used as the objective function, because the objective of the problem is to check the constraint feasibility, rather than that of the objective function. The feasibility check problems for the must-run and blackstart units should be solved subject to the following respective constraints:
- Feasibility check problem constraints for must-run units:
- Maintenance window constraints: (11), (12);
- maintenance outage duration constraints: (13)–(16);
- maintenance exclusion constraint: (17);
- sequence and interval constraint for maintenance schedules: (18);
- must-run unit constraints: (19)–(21).
- Feasibility check problem constraints for blackstart units:
- Maintenance window constraints: (11), (12);
- maintenance outage duration constraints: (13)–(16);
- maintenance exclusion constraint: (17);
- sequence and interval constraint for maintenance schedules: (18);
- blackstart unit constraints: (22).
A generator group that does not satisfy the must-run or blackstart unit constraints can be confirmed by solving the proposed feasibility check problem, with the scheduler then being notified of the results. The scheduler can revise the adjustable periods of the maintenance schedule for the generators in the group that do not satisfy the constraints, and perform the proposed feasibility check again. If the adjustable periods of the maintenance schedule are not revised, the must-run or blackstart unit constraints for the group of generators violating the constraints are not considered in the GMS optimization problem. This ensures the robustness of the proposed algorithm.
In order to obtain the optimal schedule, the GMS optimization based on a branch and cut algorithm [23] is performed by considering the results of the feasibility check for the must-run and blackstart units. First, is assumed to be 0. In the GMS optimization problem, Equation (23) is used as the objective function and Equations (1)–(4), (10)–(22), and (24)–(26) are used as the constraints. From the solutions of the GMS optimization problem, the value of to minimize the supply reserve variation can be derived using the following Equation (27) for the load reduction test. Then, with new , GMS optimization is re-performed to obtain the generator maintenance schedule.
The flowchart of the proposed GMS algorithm that considers the constraints for the reliability-based DR and the power system is shown in Figure 1.
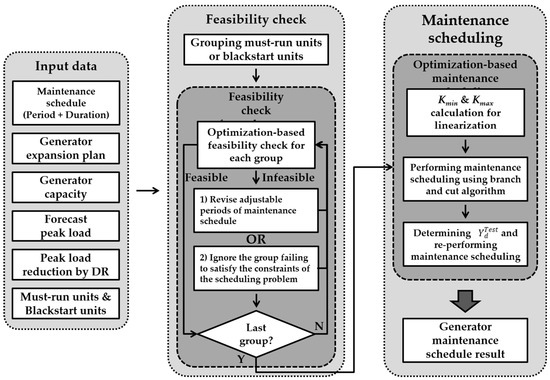
Figure 1.
Flowchart of proposed generator maintenance scheduling (GMS) algorithm.
4. Test Results
In this section, the results of a case study are presented to demonstrate the effectiveness of the proposed GMS method. The proposed method was applied to GMS of approximately 240 generators in the Korean power system, with the test year set to 2016. The generator scenario for the case study was based on the long-term generator expansion plan in Korea [24]. The data for the GMS, which included the initial schedule, the adjustable period, and the maintenance duration provided by the generator corporation, were obtained from Korea Power Exchange (KPX). The generator capacity data was based on historical data from 2014. The forecast daily load data for 2016 and the historical peak load reduction data for the reliability-based DR obtained from KPX were also considered in this case study. In addition, it was assumed that performance testing for the reliability-based DR was performed once in February and once in July. Table 1 shows the number and total capacity of generators, the effective capacity of the reliability-based DR PDR, and the minimum supply reserve requirement R in 2016. Figure 2 shows the forecasted daily system peak load data in 2016.

Table 1.
Data for generators, reliability-based demand response (DR), and supply reserve requirements.
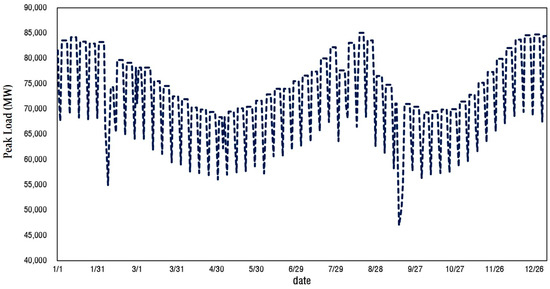
Figure 2.
Forecasted daily peak load.
A total of six must-run units were considered in this case study in order to provide security for the Korean power system. Their details are listed in Table 2. The must-run units were divided into two groups, depending on their locations and characteristics. In the case study, the number of required must-run units (Ng) for each group and the reference capacity () for the combined cycle generator in group 2 were 2 MW and 250 MW, respectively.

Table 2.
Must-run unit information.
The blackstart units were also considered in the case study. The test system was divided into seven areas for the blackstart service, with two primary blackstart units in each area. The number of backup blackstart units was three in two of the seven areas and two in the remaining five areas. In the case study, the fact that generators connected to the same bus and with similar characteristics as a blackstart unit could provide the blackstart service instead of the local blackstart units was also considered.
The following cases were compared to demonstrate the effectiveness of the proposed method.
- (1)
- Case 1: The maintenance schedule results for the 2016 Korean power system reported in [25] were used;
- (2)
- Case 2: The optimal maintenance schedule results for the 2016 Korean power system were determined using the generator maintenance scheduling method proposed in this study.
Table 3 and Table 4 show the results of the feasibility check of the must-run units performed by the proposed method. It is apparent that the initial adjustable maintenance periods (column 1 in both tables) for generators in both groups could not satisfy the must-run unit constraint for the GMS problem. Thus, in order to solve this problem, the maintenance scheduler revised the adjustable maintenance periods by obtaining new adjustable periods from the generator companies. The revised periods (column 2 in both tables) were used for the maintenance schedule determined by the proposed method.

Table 3.
Results of feasibility check for must-run units in Group 1.

Table 4.
Results of feasibility check for must-run units in Group 2.
Figure 3 shows the monthly average supply reserve in 2016, which indicates that the average supply reserve for the month with the lowest reserve is higher than that in Case 1. Moreover, the total supply reserves differ between Case 1 and Case 2 because of a change in the generator capacity due to temperature variations. Case 2 achieves a higher supply reserve than Case 1.
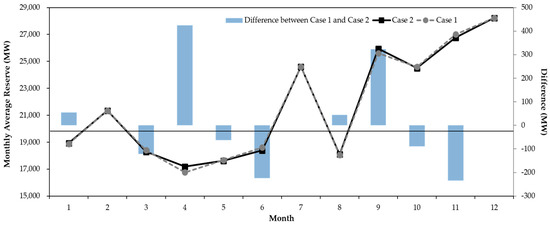
Figure 3.
Monthly average supply reserve results for Case 1 and Case 2.
In the peak period in Korea (January, February, July, August, and December), generator maintenance was rarely performed. During this peak period, the supply reserve obtained for Case 1 was similar to that for Case 2. In addition, after the peak period, a number of generator outages occurred for maintenance. In Case 1, most maintenance tended to be performed immediately after the peak period; for example, in March, April, and September. In Case 2, however, maintenance tended to be performed when the supply reserve was high.
Figure 4 shows the change in the supply reserve by reliability-based DR resources. It can be observed from the results in Figure 4 that the supply reserve increase occurs due to the reliability-based DR resources when the supply reserve was low during January and August. In addition, as January and August represent the peak period in Korea, only a few hydro unit maintenance schedules are adjusted. These results show that the GMS results considering the reliability-based DR resources had an impact on the minimization of supply reserve variation.
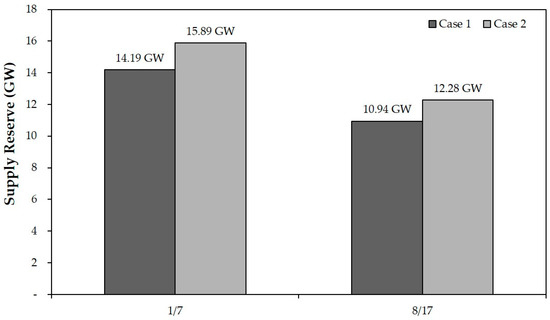
Figure 4.
Change in the supply reserve according to reliability-based DR resources.
Table 5 shows a comparison of the number of adjusted generator maintenance schedules in Cases 1 and 2, which indicates a greater number for Case 2. In addition, the number of adjusted maintenance schedules for the must-run and blackstart unit constraints was equal to that obtained for Case 1. The majority of maintenance schedules were adjusted to reduce the supply reserve variation. The number of adjusted maintenance schedules for coal-fired units increased from 10 (Case 1) to 16 (Case 2). The number of adjusted maintenance schedules for hydro units and combined cycle generator units also increased from 38 (Case 1) to 52 (Case 2).

Table 5.
Comparison of number of adjusted generator maintenance schedules for Cases 1 and 2.
In order to examine how the change in the forecasted daily peak load influenced the outcome of this study, another case study was conducted for the 5% reduced forecasted daily peak load. Figure 5 shows the monthly average supply reserve for the change in the forecasted daily peak load. For the 5% reduced forecasted daily peak load, it can be observed from the results shown in Figure 5 that the supply reserve variation was reduced and the supply reserve was approximately 10% higher than that of Case 2.
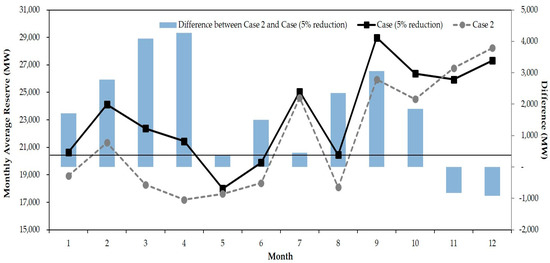
Figure 5.
Monthly average supply reserve results for Case 2 and Case with a 5% reduced forecasted daily peak load.
In order to examine how the transformation of the mixed integer polynomial programming method influenced the convergence of the GMS problem, the result obtained using the proposed method was compared with that obtained using the MINLP algorithm based on the branch-and-cut algorithm. Equation (9) was applied as an objective function of the GMS problem using the MINLP algorithm. Table 6 shows that the solution of the MINLP algorithm was infeasible because the maintenance exclusion constraint was violated, whereas a feasible solution satisfying all constraints was obtained by using the proposed method. Moreover, the computation time of the proposed method was faster than that of the MINLP algorithm.

Table 6.
Comparison of results obtained using the proposed method and the mixed integer non-linear programming (MINLP) algorithm.
From these results, it is apparent that the proposed method is effective for determining the optimal maintenance schedule to minimize the supply reserve variation.
5. Conclusions
A GMS method that incorporates reliability-based DR, must-run units, and blackstart units is required for the stable and efficient operation of a power system. Therefore, in this study, a GMS method was developed using transformation of mixed integer polynomial programming that considers several constraints related to reliability-based DR, must-run units, and blackstart units. Reliability-based DR can be incorporated into the GMS problem using the proposed reliability-based DR model, and an efficient maintenance schedule considering the capacity provided by the DR can be determined by the proposed method. In addition, the proposed GMS algorithm consists of two stages: A feasibility check stage for the must-run and blackstart unit constraints and a GMS stage employing the transformation of mixed integer polynomial programming. Generators that do not satisfy the must-run or blackstart unit constraints can be found by solving the proposed feasibility check problem. The proposed method is designed to resolve the low-convergence problem caused by the non-linear formulation of the GMS problem in a power system with a number of generators. The test results show that the proposed scheduling method has great potential for reducing the supply reserve variation.
The supply reserve requirements can be satisfied, and both the fuel cost and market price can be lowered by levelizing the supply reserve margin in the power system. Due to these advantages, GMS has been implemented in the Korean power system in order to levelize the reserve. However, the generator corporation may provide narrow adjustable periods for generator maintenance because the market price can be reduced by maintenance scheduling. This may reduce the effect of the proposed GMS method. Therefore, further study is required to consider this limitation on the GMS.
Author Contributions
H.-C.J. performed the research and wrote the paper. R.K. helped with the simulation and revised the paper. S.-K.J. provided guidance for the research and revised the paper.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. NRF-2017R1A2B2004259). This work was partially supported by “Human Resources program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) granted financial resource from the Ministry of Trade, Industry and Energy, Republic of Korea (No. 20174030201820).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, J.; Tran, T.; El-Keib, A.A.; Thomas, R.; Oh, H.; Billinton, R. A Method for Transmission System Expansion Planning Considering Probabilistic Reliability Criteria. IEEE Trans. Power Syst. 2005, 20, 1606–1615. [Google Scholar] [CrossRef]
- Leite da Silva, A.M.; Manso, L.A.F.; Flavio, S.A.; da Rosa, M.A.; Resende, L.C. Composite Reliability Assessment of Power Systems with Large Penetration of Renewable Sources. In Reliability and Risk Evaluation of Wind Integrated Power Systems; Billinton, R., Karki, R., Verma, A.K., Eds.; Springer: London, UK, 2013; Volume 1, pp. 107–128. [Google Scholar]
- Zurn, H.H.; Quintana, V.H. Several Objective Criteria for Optimal Generator Preventive Maintenance. IEEE Trans. Power Syst. 1977, 96, 984–992. [Google Scholar] [CrossRef]
- Kralj, B.; Rajakovic, N. Multiobjective Programming in Power System Optimization: New Approach to Generator Maintenance Scheduling. Int. J. Elec. Power Energ. Syst. 1994, 16, 211–220. [Google Scholar] [CrossRef]
- Yare, Y.; Venayagamoorthy, G.K. Optimal Maintenance Scheduling of Generators Using Multiple Swarms-MDPSO Framework. Eng. Appl. Artif. Intel. 2010, 23, 895–910. [Google Scholar] [CrossRef]
- Lindner, B.G. Bi-objective Generator Maintenance Scheduling for a National Power Utility. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2017. [Google Scholar]
- Suresh, K.; Kumarappan, N. Hybrid Improved Binary Particle Swarm Optimization Approach for Generation Maintenance Scheduling Problem. Swarm Evol. Comput. 2013, 9, 69–89. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, R.; Zhang, Y.; Wu, G.; Shi, J. An Optimal and Distributed Demand Response Strategy for Energy Internet Management. Energies 2018, 11, 215. [Google Scholar] [CrossRef]
- Mollahassani-pour, M.; Abdollahi, A.; Rashidinejad, M. Investigation of Market-Based Demand Response Impacts on Security-Constrained Preventive Maintenance Scheduling. IEEE Syst. J. 2015, 9, 1496–1506. [Google Scholar] [CrossRef]
- Mollahassani-pour, M.; Rashidinejad, M.; Abdollahi, A.; Forghani, M.A. Demand Response Resources’ Allocation in Security-Constrained Preventive Maintenance Scheduling via MODM Method. IEEE Syst. J. 2017, 11, 1196–1207. [Google Scholar] [CrossRef]
- Ou, T.C. A Novel Unsymmetrical Faults Analysis for Microgrid Distribution Systems. Int. J. Elec. Power Energ. Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Ou, T.C. Ground Fault Current Analysis with a Direct Building Algorithm for Microgrid Distribution. Int. J. Elec. Power Energ. Syst. 2013, 53, 867–875. [Google Scholar] [CrossRef]
- Ou, T.C.; Hong, C.M. Dynamic Operation and Control of Microgrid Hybrid Power Systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Ou, T.C.; Su, W.F.; Liu, X.Z.; Huang, S.J.; Tai, T.Y. A Modified Bird-Mating Optimization with Hill-Climbing for Connection Decisions of Transformers. Energies 2016, 9, 671. [Google Scholar] [CrossRef]
- Perez-Canto, S.; Rubio-Romero, J.C. A Model for the Preventive Maintenance Scheduling of Power Plants Including Wind Farms. Reliab. Eng. Syst. Safe. 2013, 119, 67–75. [Google Scholar] [CrossRef]
- Reihani, E.; Sarikhani, A.; Davodi, M.; Davodi, M. Reliability based Generator Maintenance Scheduling Using Hybrid Evolutionary approach. Int. J. Elec. Power Energ. Syst. 2012, 42, 434–439. [Google Scholar] [CrossRef]
- Satoh, T.; Nara, K. Maintenance Scheduling by Using Simulated Annealing Method. IEEE Trans. Power Syst. 1991, 6, 850–857. [Google Scholar] [CrossRef]
- Schlünz, E.B.; Van Vuuren, J.H. An Investigation into the Effectiveness of Simulated Annealing as a Solution Approach for the Generator Maintenance Scheduling Problem. Int. J. Elec. Power Energy Syst. 2013, 53, 166–174. [Google Scholar] [CrossRef]
- Balaji, G.; Balamurugan, R.; Lakshminarasimman, L. Mathematical Approach Assisted Differential Evolution for Generator Maintenance Scheduling. Int. J. Elec. Power Energy Syst. 2016, 82, 508–518. [Google Scholar] [CrossRef]
- Glover, F. Improved Linear Integer Programming Formulations of Nonlinear Integer Programs. Manag. Sci. 1975, 22, 455–460. [Google Scholar] [CrossRef]
- Westerlund, T.; Harjunkoski, I.; Isaksson, J. Solving a production optimization problem in a paper-converting mill with MILP. Comput. Chem. Eng. 1998, 22, 563–570. [Google Scholar] [CrossRef]
- Ou, T.C.; Lu, K.H.; Huang, C.J. Improvement of Transient Stability in a Hybrid Power Multi-System Using a Designed NIDC (Novel Intelligent Damping Controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Padberg, M.; Rinaldi, G. A Branch-and-cut Algorithm for the Resolution of Large-Scale Symmetric Traveling Salesman Problems. SIAM Rev. 1991, 33, 60–100. [Google Scholar] [CrossRef]
- Ministry of Knowledge Economy. The 6th Basic Plan for Long-Term Electricity Supply and Demand (2013–2017); Ministry of Knowledge Economy: Sejong, Korea, 2013. [Google Scholar]
- Korea Power Exchange. 2016–2017 Electricity Supply and Demand Outlook and Generator Maintenance Plan (Draft); Korea Power Exchange: Naju, Korea, 2015. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).