Weighted Regression-Based Extremum Response Surface Method for Structural Dynamic Fuzzy Reliability Analysis
Abstract
1. Introduction
2. Basic Theory on Dynamic Fuzzy Reliability Analysis
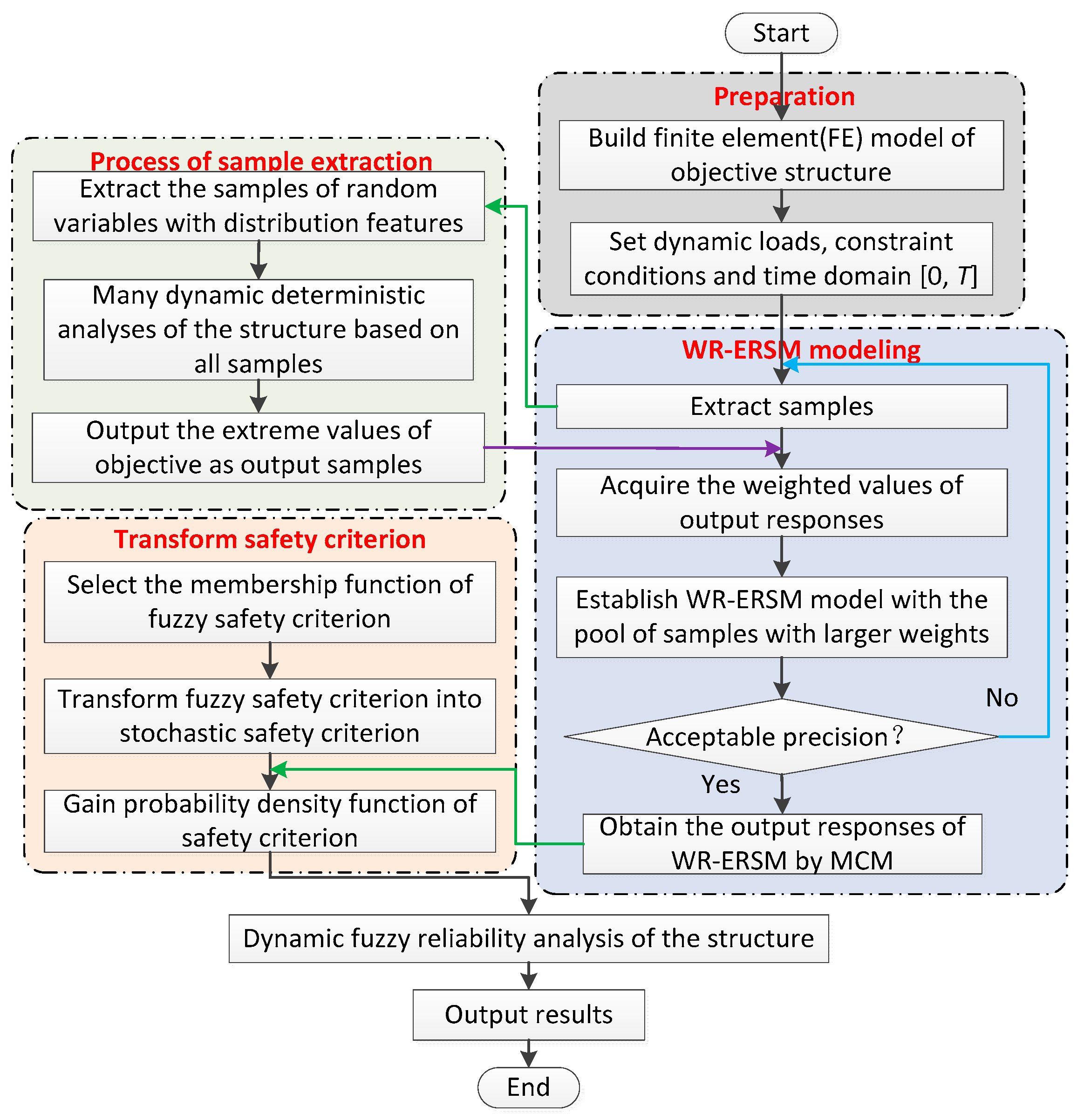
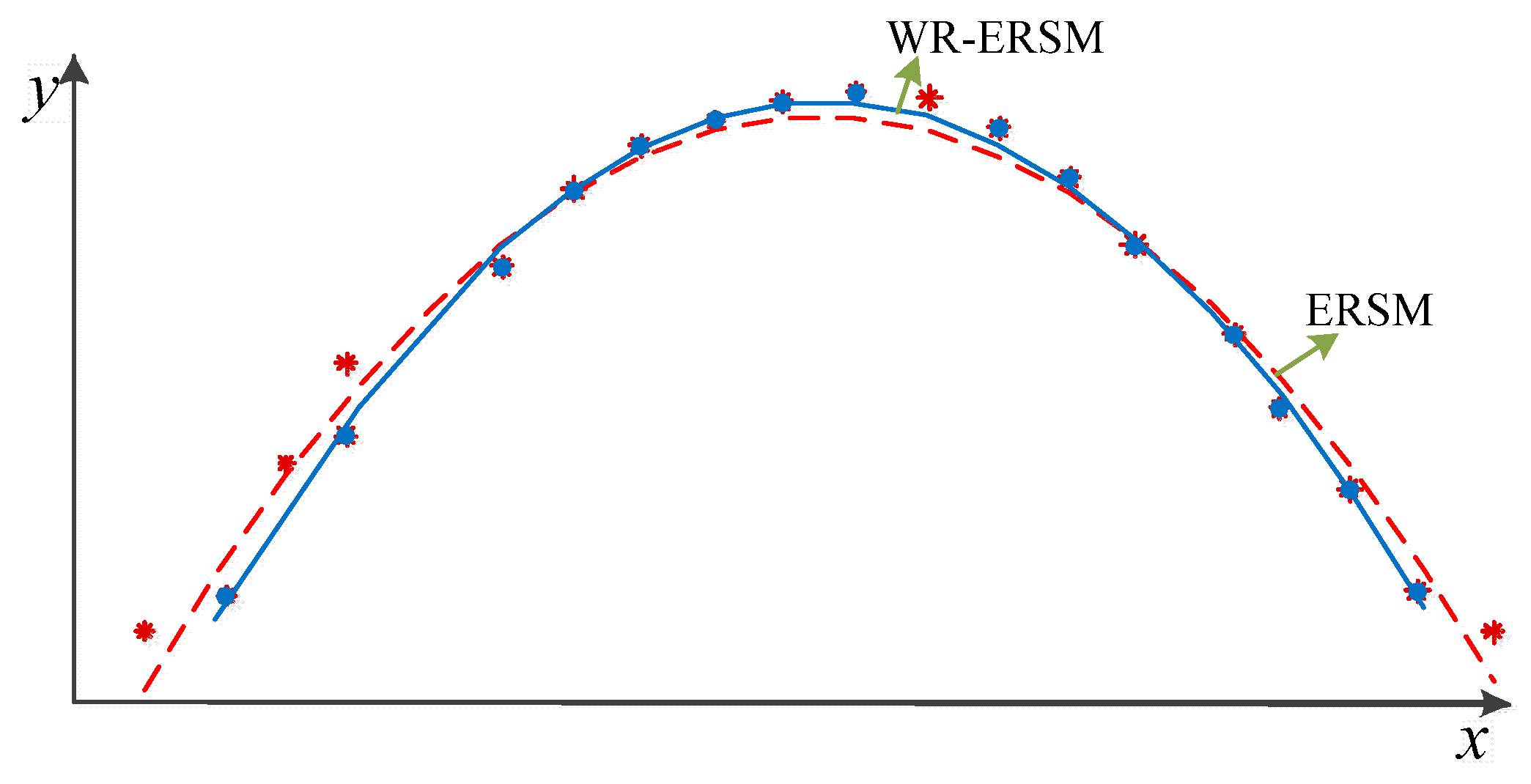
2.1. Weighted Regression Extremum Response Surface Method (WR-ERSM) Modeling
2.2. Safety Criterion Transformation
2.3. Structural Dynamic Fuzzy Reliability Analysis
3. Example Analysis
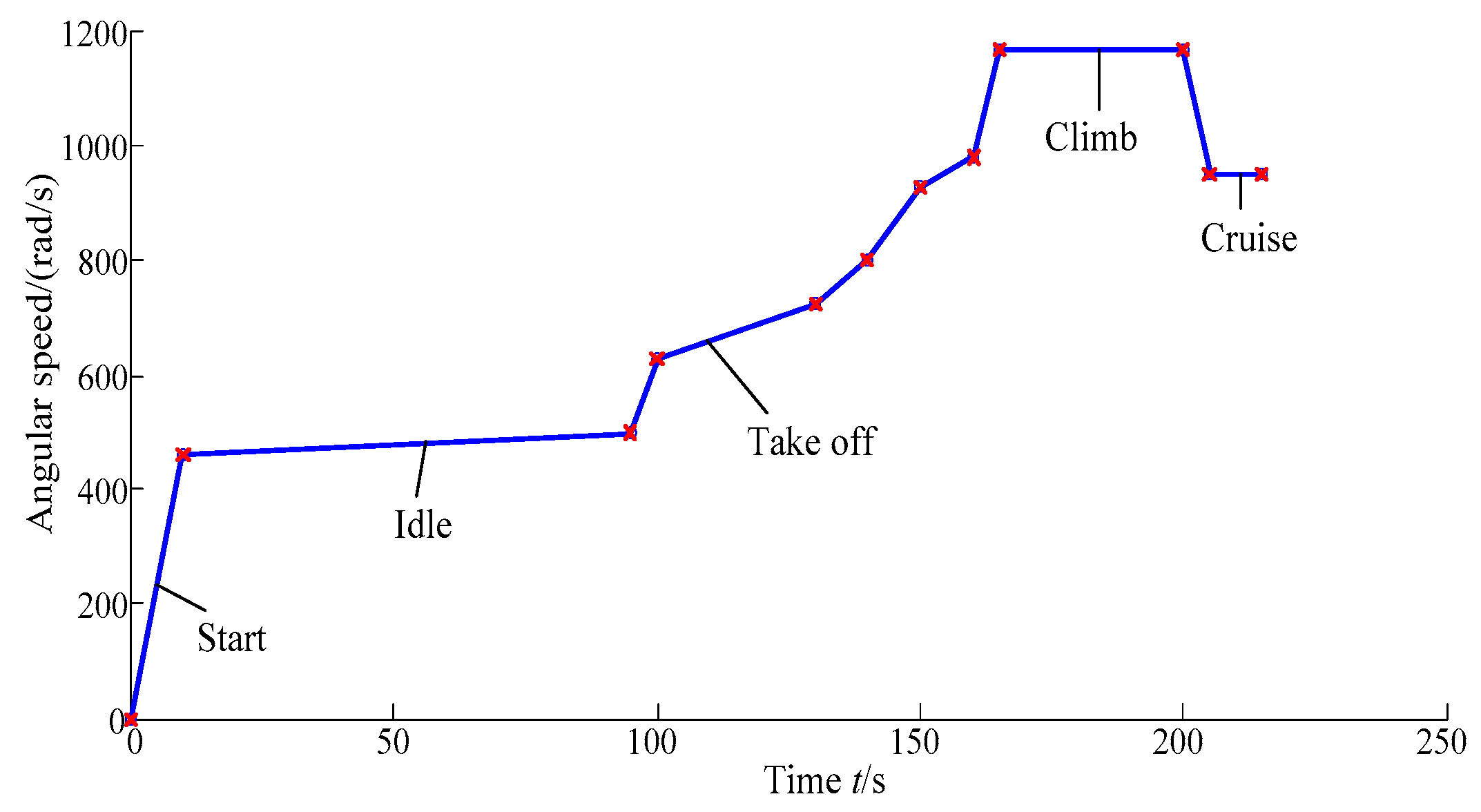
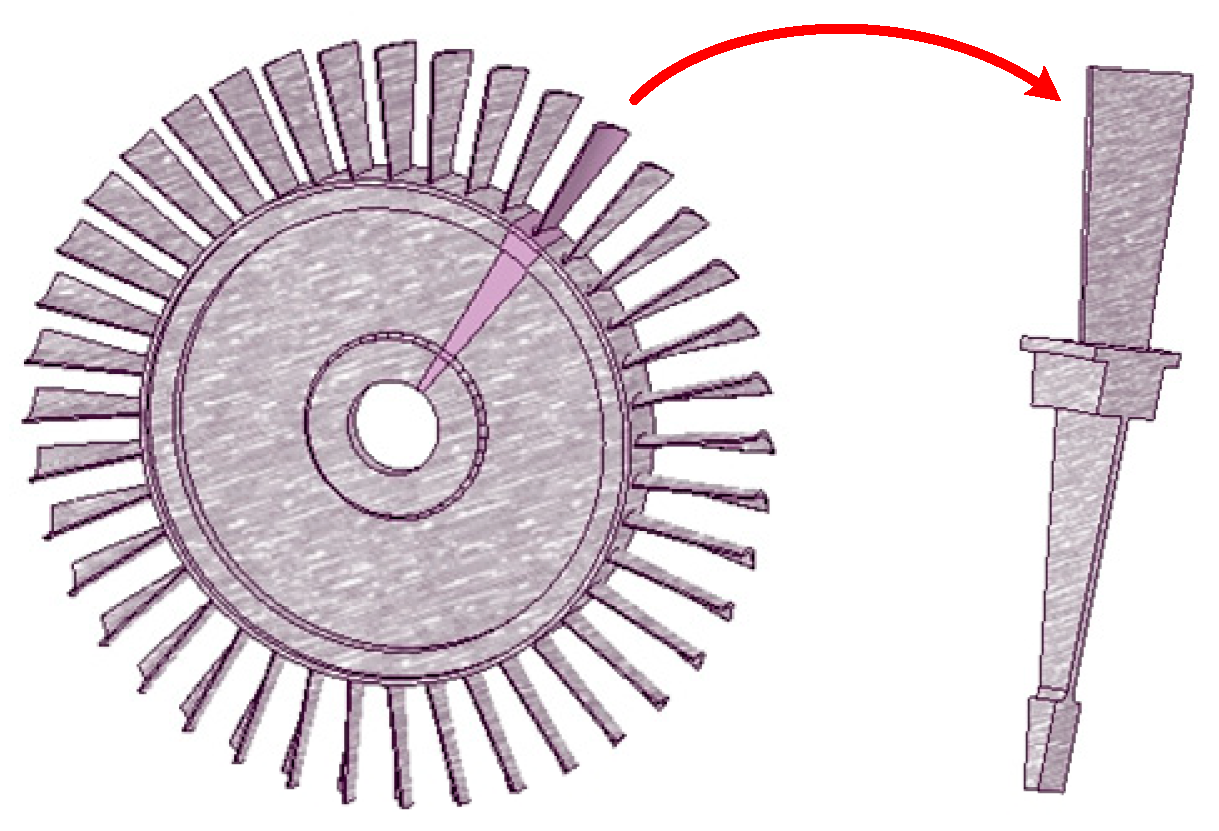
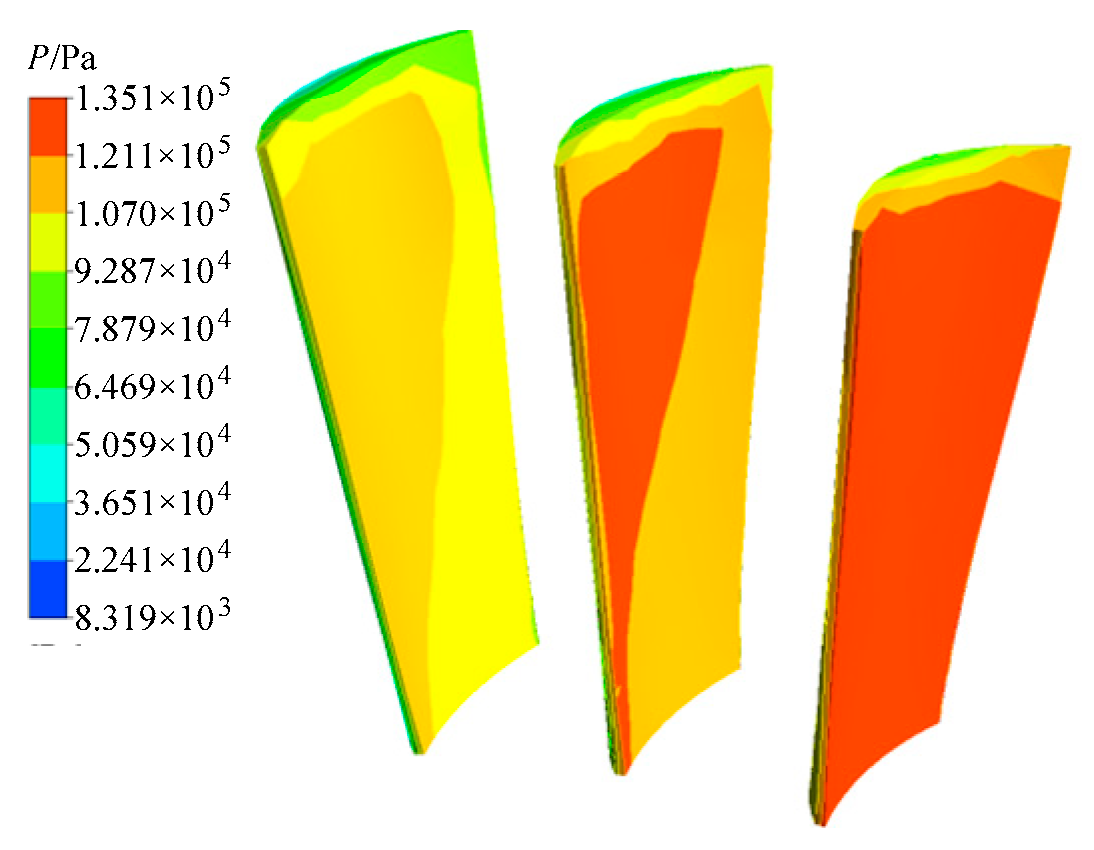
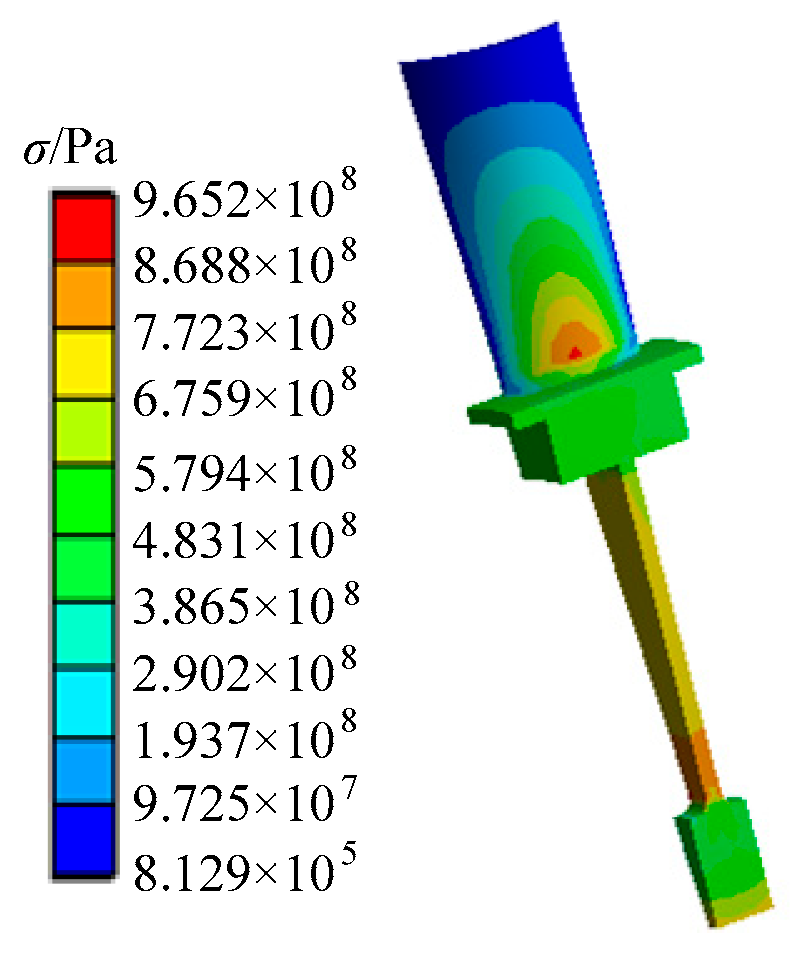
3.1. Deterministic Analysis for Turbine Blisk
3.2. The WR-ERSM Model of Turbine Blisk
3.3. Turbine Blisk Reliability Evaluation
4. WR-ERSM Verification Procedure
4.1. Model-Fitting Properties
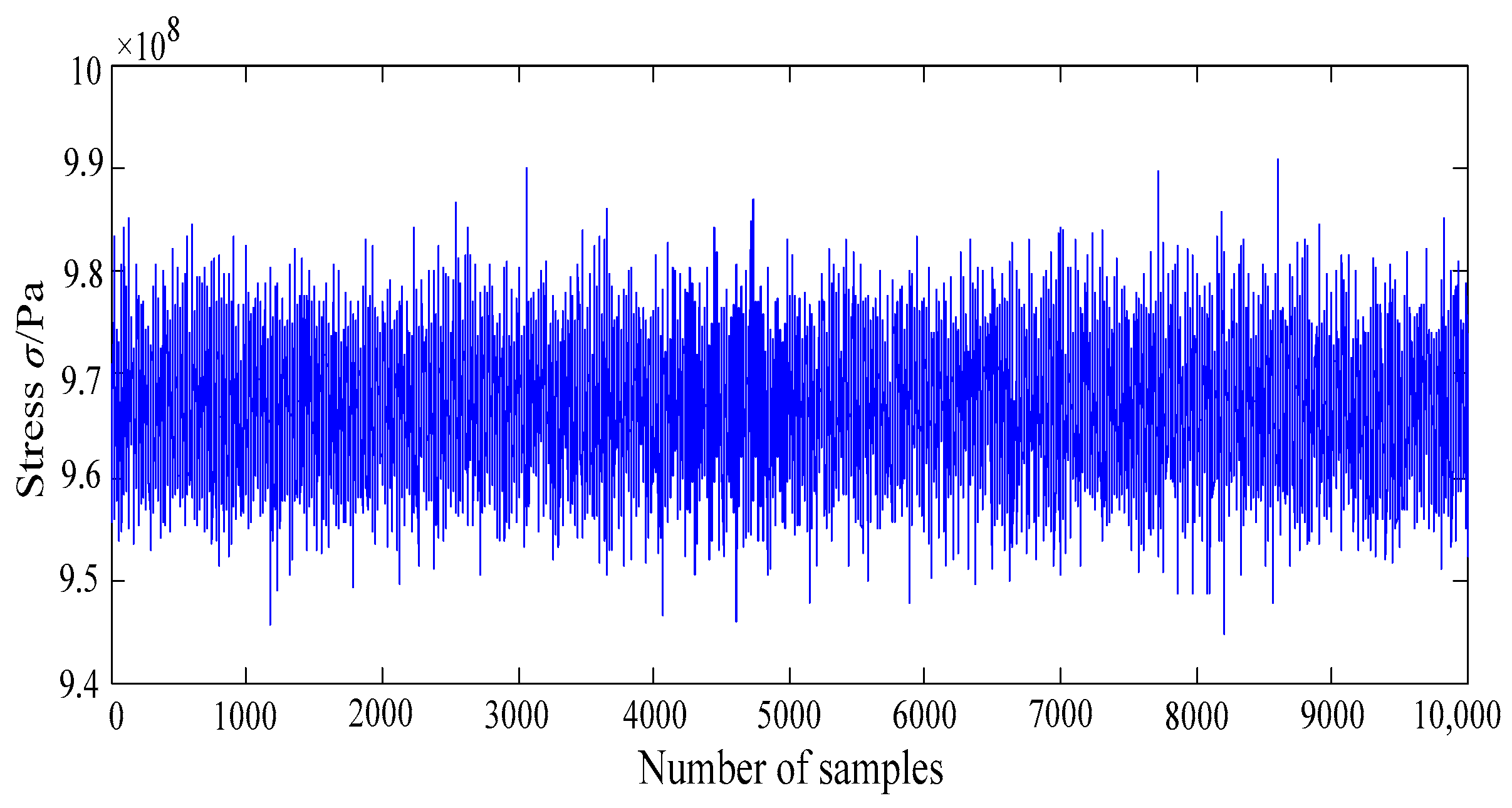
4.2. Simulation Performances for Dynamic Fuzzy Reliability Analysis of Turbine Blisk
5. Conclusions
- (1)
- The WR-ERSM is highly precise and efficient in structural dynamic reliability evaluation, since ERSM has the capacity of processing the transient problem;
- (2)
- The WR approach can improve modeling accuracy so that the proposed WR-ERSM possesses high fitting efficiency and accuracy, due to the requirement of small samples;
- (3)
- WR-ERSM possesses good simulation performance in structural dynamic fuzzy reliability evaluation, as the fuzzy safety criterion is considered to improve the precision;
- (4)
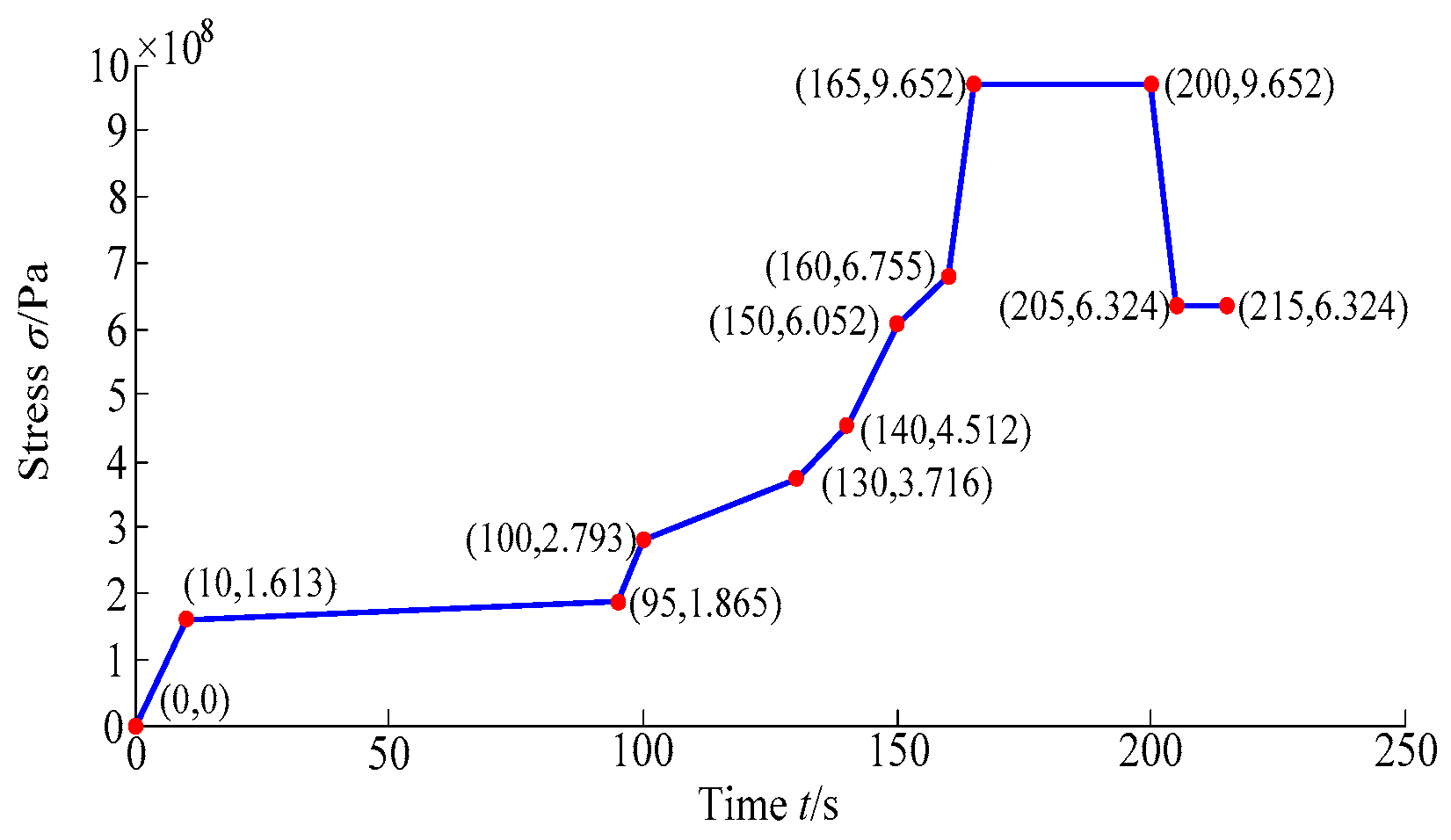
- The change rule of turbine blisk structural stress from start to cruise for an aircraft is acquired with the maximum value of structural stress at t = 165 s and the reliability degree (Pr = 0.997) of the turbine blisk.
- (5)
- The efforts of this study provide a promising method for the dynamic reliability analysis and evaluation of complex structures with respect to the working process.
Author Contributions
Funding
Conflicts of Interest
References
- Fei, C.W.; Choy, Y.S.; Hu, D.Y.; Bai, G.C.; Tang, W.Z. Dynamic probabilistic design approach of high-pressure turbine blade-tip radial running clearance. Nonlinear Dyn. 2016, 86, 205–223. [Google Scholar] [CrossRef]
- Liu, Y.; Meng, L.L.; Liu, K.; Zhang, Y.M. Chatter reliability of milling system based on first-order second-moment method. Int. J. Adv. Manuf. Technol. 2016, 87, 801–809. [Google Scholar] [CrossRef]
- Keshtegar, B. Conjugate finite-step length method for efficient and robust structural reliability analysis. Struct. Eng. Mech. 2018, 65, 415–422. [Google Scholar]
- Zhang, J.F.; Du, X.P. A second-order reliability method with first-order efficiency. J. Mech. Des. 2010, 132, 101006. [Google Scholar] [CrossRef]
- Huang, X.Z.; Li, Y.X.; Zhang, Y.M.; Zhang, X.F. A new direct second-order reliability analysis method. Appl. Math. Model. 2018, 55, 68–80. [Google Scholar] [CrossRef]
- Hu, Z.L.; Du, X.P. Efficient reliability-based design with second order approximations. Eng. Optim. 2019, 51, 101–119. [Google Scholar] [CrossRef]
- Nakamura, T.; Fujii, K. Probabilistic transient thermal analysis of an atmospheric reentry vehicle structure. Aerosp. Sci. Technol. 2006, 10, 346–354. [Google Scholar] [CrossRef]
- Martinez-Velasco, J.A.; Guerra, G. Reliability analysis of distribution systems with photovoltaic generation using a power flow simulator and a parallel Monte Carlo approach. Energies 2016, 9, 537. [Google Scholar] [CrossRef]
- Yang, X.J.; Yan, Y.L.; Xu, Z.Q.; Yan, X.Z. FEM simulation on the structural reliability of beam pumping unit based on the methods of Monte-Carlo. Appl. Mech. Mater. 2010, 34–35, 820–824. [Google Scholar] [CrossRef]
- Yang, Y.H.; Liu, D.; He, Z.Y.; Luo, Z.J. Optimization of preform shapes by RSM and FEM to improve deformation homogeneity in aerospace forgings. Chin. J. Aeronaut. 2010, 23, 260–267. [Google Scholar]
- Allaix, D.L.; Carbone, V.I. An improvement of the response surface method. Struct. Saf. 2011, 32, 165–172. [Google Scholar] [CrossRef]
- Kaymaz, I. Application of kriging method to structural reliability problems. Struct. Saf. 2005, 27, 133–151. [Google Scholar] [CrossRef]
- Zhao, Z.G.; Duan, X.J.; Wang, Z.M. A novel global method for reliability analysis with kriging. Int. J. Uncertain. Quantif. 2016, 6, 445–466. [Google Scholar] [CrossRef]
- Kishore, R.A.; Mahajan, R.L.; Priya, S. Combinatory finite element and artificial neural network model for predicting performance of thermoelectric generator. Energies 2018, 11, 2216. [Google Scholar] [CrossRef]
- Gondal, Z.U.R.; Lee, J. Reliability assessment using feed-forward neural network-based approximate meta-models. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2012, 226, 448–454. [Google Scholar] [CrossRef]
- Rocco, C.M.; Moreno, J.A. Fast Monte Carlo reliability evaluation using support vector machine. Reliab. Eng. Syst. Saf. 2002, 76, 237–243. [Google Scholar] [CrossRef]
- Guo, Z.W.; Bai, G.C. Classification using least squares support vector machine for reliability analysis. Appl. Math. Mech. 2009, 30, 853–864. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Bai, G.C. Extremum response surface method of reliability analysis on two-link flexible rotor manipulator. J. Cent. South Univ. 2012, 19, 101–107. [Google Scholar] [CrossRef]
- Fei, C.W.; Tang, W.Z.; Bai, G.C. Nonlinear dynamic probabilistic design of turbine disk-radial deformation using extremum response surface method-based support vector machine of regression. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 290–300. [Google Scholar] [CrossRef]
- Fei, C.W.; Tang, W.Z.; Bai, G.C. Dynamic probabilistic design for blade deformation with SVM-ERSM. Aircr. Eng. Aerosp. Technol. 2015, 87, 312–321. [Google Scholar] [CrossRef]
- Broadie, M.; Du, Y. Risk estimation via weighted regression. In Proceedings of the 2011 Winter Simulation Conference, Phoenix, AZ, USA, 11–14 December 2011; pp. 3859–3870. [Google Scholar]
- Kaymaz, I.; McMahon, C.A. A response surface method based on weighted regression for structural reliability analysis. Probabilistic Eng. Mech. 2005, 20, 11–17. [Google Scholar] [CrossRef]
- Guo, S.X.; Lu, Z.Z. Procedure for computing the possibility and fuzzy probability of failure of structures. Appl. Math. Mech. 2003, 24, 338–343. [Google Scholar]
- Hurtado, J.E.; Alvarez, D.A.; Ramirez, J. Fuzzy structural analysis based on fundamental reliability concepts. Comput. Struct. 2012, 112, 183–192. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Zhou, J.; Yu, Z.Y. Fatigue reliability assessment of turbine discs under multi-source uncertainties. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1291–1305. [Google Scholar] [CrossRef]
- Huang, H.Z. Structural reliability analysis using fuzzy sets theory. Eksploat. I Niezawodn. Maint. Reliab. 2012, 4, 284–294. [Google Scholar]
- Wang, Z.L.; Li, Y.F.; Huang, H.Z.; Liu, Y. Reliability analysis of structure for fuzzy safety state. Intell. Autom. Soft Comput. 2012, 18, 215–224. [Google Scholar] [CrossRef]
- Zhang, M.; Lu, S. A reliability model of blade to avoid resonance considering multiple fuzziness. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 641–652. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Peng, W.; Zhang, X.C. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int. J. Mech. Sci. 2018, 142–143, 502–517. [Google Scholar] [CrossRef]
- Lee, S.H.; Kwak, B.M. Response surface augmented moment method for efficient reliability analysis. Struct. Saf. 2006, 28, 261–272. [Google Scholar] [CrossRef]
- Afsan, B.M.U.; Basu, C.K. Fuzzy topological entropy of fuzzy continuous functions on fuzzy topological spaces. Appl. Math. Lett. 2011, 24, 2030–2033. [Google Scholar] [CrossRef]
- Markechova, D.; Riecan, B. Entropy of fuzzy partitions and entropy of fuzzy dynamical systems. Entropy 2016, 18, 19. [Google Scholar] [CrossRef]
- Fei, C.W.; Tang, W.Z.; Bai, G.C. Novel method and model for dynamic reliability optimal design of turbine blade deformation. Aerosp. Sci. Technol. 2014, 39, 588–595. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Lu, C.; Fei, C.W.; Liu, L.J.; Choy, Y.Z.; Su, X.G. Multiobject reliability analysis of turbine blisk with multidiscipline under multiphysical field interaction. Adv. Mater. Sci. Eng. 2015, 2015, 649046. [Google Scholar] [CrossRef]
- Li, L.Y.; Lu, Z.Z. Importance analysis for model with mixed uncertainties. Fuzzy Sets Syst. 2017, 310, 90–107. [Google Scholar] [CrossRef]
- Sun, J.; Luo, Y. Reliability-optimization design based on fuzzy entropy for cylinder head bolts. J. Appl. Sci. 2013, 13, 5198–5203. [Google Scholar] [CrossRef]
- Lattime, S.B.; Steinetz, B.M. Turbine engine clearance control systems: Current practices and future directions. J. Propuls. Power 2004, 20, 302–311. [Google Scholar] [CrossRef]
- Fei, C.W.; Choy, Y.S.; Hu, D.Y.; Bai, G.C.; Tang, W.Z. Transient probabilistic analysis for turbine blade-tip radial clearance with multiple components and multi-physics fields based on DCERSM. Aerosp. Sci. Technol. 2016, 50, 62–70. [Google Scholar] [CrossRef]
- Wang, H.B.; Wang, Z.G.; Sun, M.B.; Qin, N. Large eddy simulation of a hydrogen-fueled scramjet combustor with dual cavity. Acta Astronaut. 2015, 108, 119–128. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.W.; Fei, C.W.; Xue, X.F. Probabilistic analysis method of turbine blisk with multi-failure modes by two-way fluid-thermal-solid coupling. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2873–2886. [Google Scholar] [CrossRef]
- Liu, J.; Nan, Z.; Yi, P. Validation and application of three-dimensional discontinuous deformation analysis with tetrahedron finite element meshed block. Acta Mech. Sin. 2012, 28, 1602–1616. [Google Scholar] [CrossRef]
- Fei, C.W.; Bai, G.C. Extremum selection method of random variables for nonlinear dynamic reliability analysis of turbine blade deformation. Propuls. Power Res. 2012, 1, 58–63. [Google Scholar] [CrossRef]


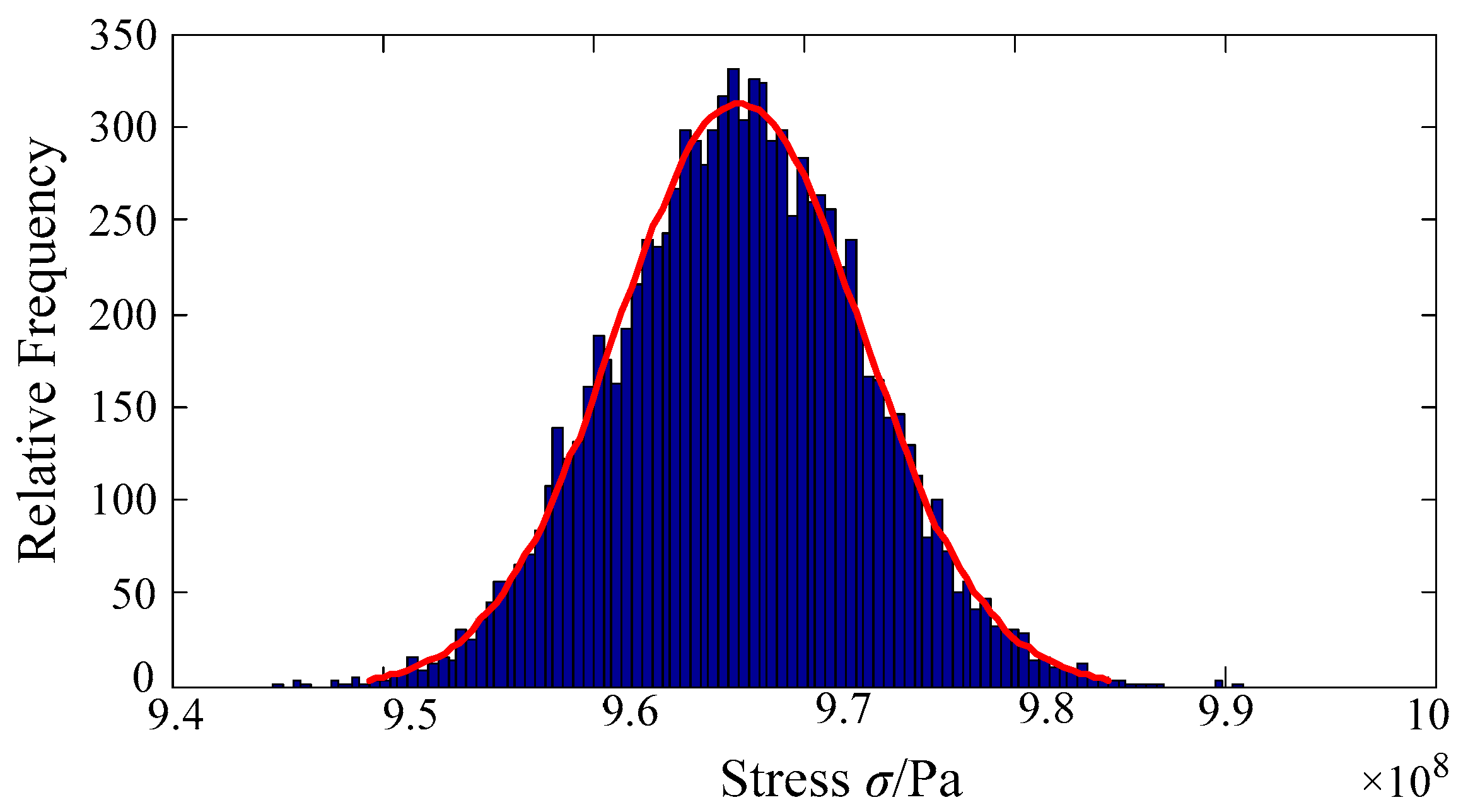
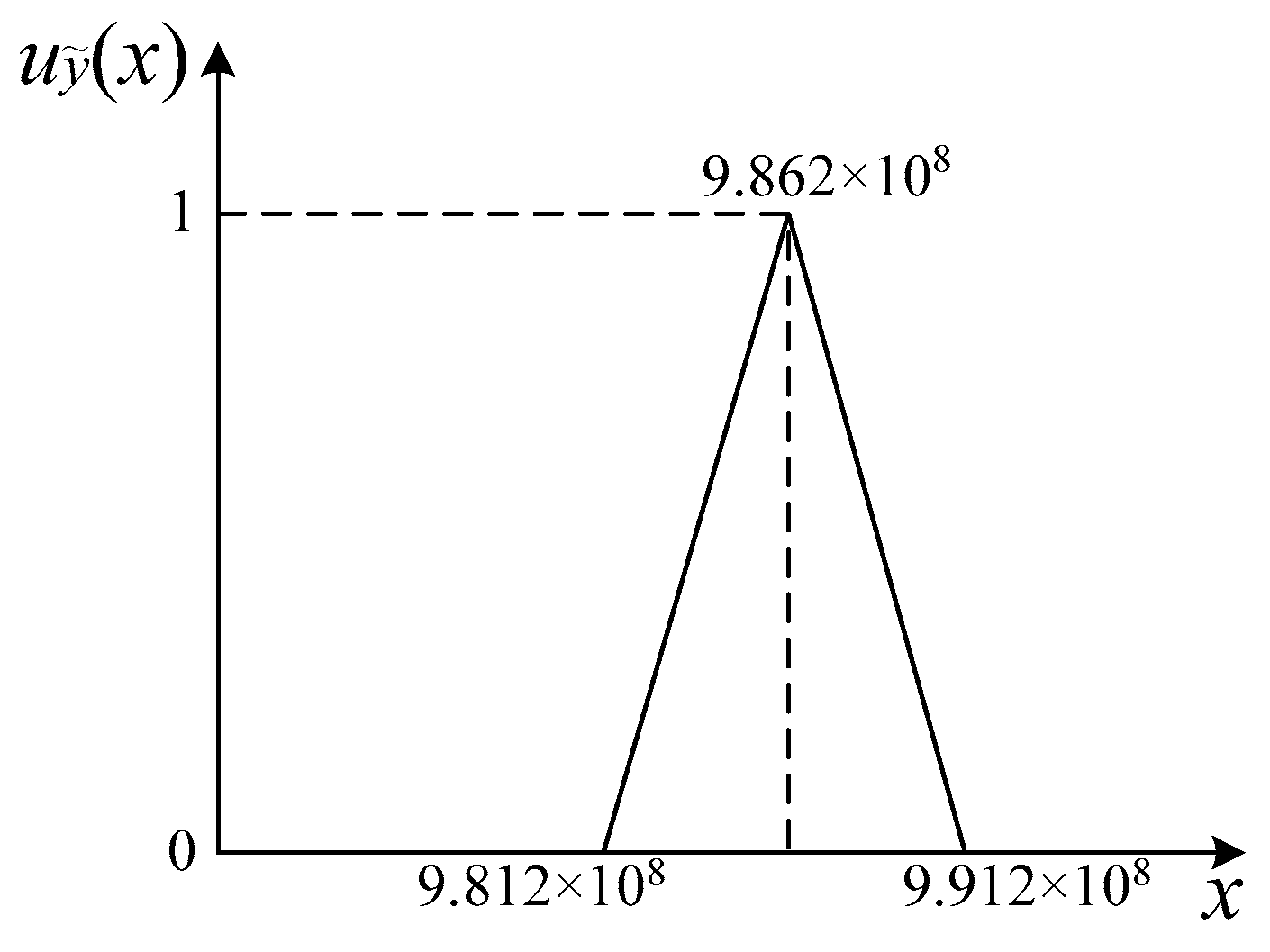
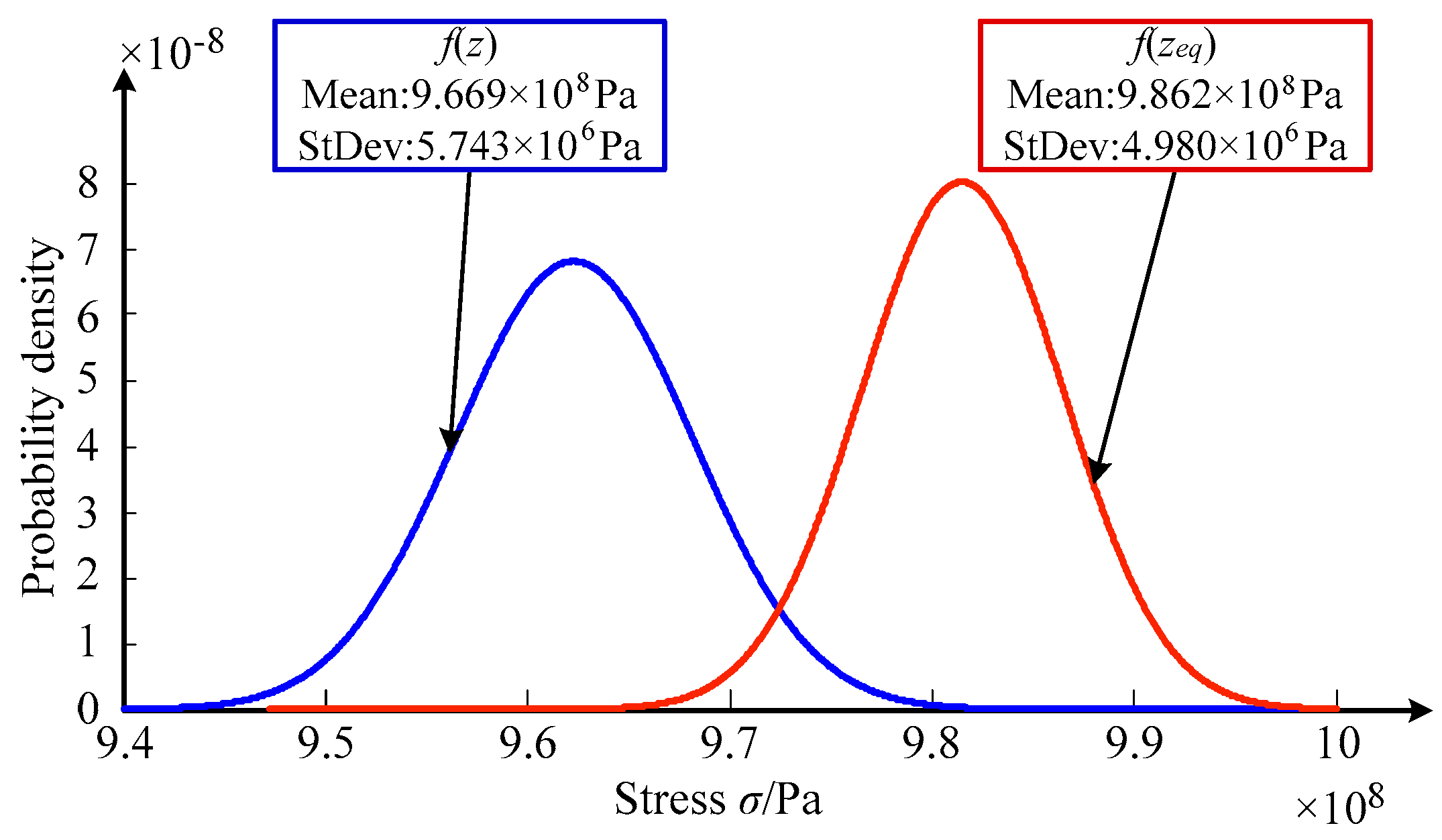
| Parameters | Variable | Distribution | Mean, μ | St.Dev., δ |
|---|---|---|---|---|
| Inlet velocity (m·s−1) | v | Normal | 168 | 5.04 |
| Inlet pressure (Pa) | P | Normal | 600,000 | 12,000 |
| Material density (kg·m−3) | ρ | Normal | 8210 | 246 |
| Angular speed (rad·s−1) | w | Normal | 1168 | 35 |
| Parameters and Weighted Coefficient | Parameters and Weighted Coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| v m·s−1 | P, ×105 Pa | ρ kg·m−3 | w rad·s−1 | σ × 108 Pa | W | v, m·s−1 | P, ×105 Pa | ρ, kg·m−3 | w, rad·s−1 | σ, ×108 Pa | W |
| 168.00 | 6.00 | 8210 | 1168 | 9.687 | 0.9105 | 173.04 | 6.00 | 8210 | 1133 | 9.098 | 0.9694 |
| 162.96 | 6.00 | 8210 | 1168 | 9.693 | 0.9099 | 168.00 | 6.12 | 8210 | 1133 | 9.105 | 0.9687 |
| 168.00 | 5.88 | 8210 | 1168 | 9.686 | 0.9106 | 168.00 | 6.00 | 7964 | 1133 | 8.827 | 0.9992 |
| 168.00 | 6.00 | 7964 | 1168 | 9.392 | 0.9391 | 173.04 | 5.88 | 7964 | 1168 | 9.385 | 0.9398 |
| 168.00 | 6.00 | 8210 | 1133 | 9.105 | 0.9687 | 173.04 | 5.88 | 8210 | 1133 | 9.098 | 0.9694 |
| 173.04 | 6.00 | 8210 | 1168 | 9.686 | 0.9391 | 162.96 | 6.12 | 7964 | 1168 | 9.398 | 0.9385 |
| 168.00 | 6.12 | 8210 | 1168 | 9.687 | 0.9105 | 162.96 | 6.12 | 8210 | 1133 | 9.111 | 0.9681 |
| 168.00 | 6.12 | 8210 | 1203 | 10.29 | 0.8576 | 168.00 | 6.00 | 8456 | 1203 | 10.59 | 0.8575 |
| 162.96 | 5.88 | 8210 | 1168 | 9.687 | 0.9105 | 168.00 | 6.12 | 7964 | 1133 | 8.829 | 0.9989 |
| 162.96 | 6.00 | 7964 | 1168 | 9.391 | 0.9392 | 162.96 | 6.00 | 8456 | 1133 | 9.389 | 0.9394 |
| 162.96 | 6.00 | 8210 | 1133 | 9.105 | 0.9687 | 168.00 | 5.88 | 8456 | 1133 | 9.383 | 0.9400 |
| 168.00 | 5.88 | 7964 | 1168 | 9.391 | 0.9392 | 173.04 | 6.12 | 7964 | 1168 | 9.385 | 0.9398 |
| 168.00 | 5.88 | 8210 | 1133 | 9.105 | 0.9687 | 173.04 | 6.12 | 8210 | 1133 | 9.098 | 0.9694 |
| 168.00 | 6.00 | 7964 | 1133 | 8.827 | 0.9992 | 173.04 | 6.00 | 8456 | 1133 | 9.376 | 0.9407 |
| 173.04 | 6.12 | 8210 | 1168 | 9.687 | 0.9105 | 168.00 | 6.12 | 8456 | 1133 | 9.383 | 0.9400 |
| 162.96 | 6.12 | 8210 | 1168 | 9.693 | 0.9099 | 162.96 | 5.88 | 7964 | 1168 | 9.398 | 0.9385 |
| 168.00 | 6.00 | 8210 | 1203 | 10.28 | 0.8576 | 173.04 | 6.00 | 8210 | 1203 | 10.28 | 0.8576 |
| 173.04 | 5.88 | 8210 | 1168 | 9.681 | 0.9111 | 162.96 | 5.88 | 8210 | 1133 | 9.111 | 0.9681 |
| 173.04 | 6.00 | 7964 | 1168 | 9.385 | 0.9398 | 162.96 | 6.00 | 7964 | 1133 | 8.827 | 0.9992 |
| 168.00 | 6.12 | 7964 | 1168 | 9.391 | 0.9392 | 168.00 | 5.88 | 7964 | 1133 | 8.826 | 0.9993 |
| Method | Fitting ERSM Model | Fitting Accuracy | ||
|---|---|---|---|---|
| Sample Number | Fitting Time, h | r2 | rmax | |
| WR-ERSM | 9 | 7.05 | 0.9984 | 0.0535 |
| ERSM | 29 | 22.39 | 0.9742 | 0.0834 |
| Methods | Pr | Errors | Precision, % |
|---|---|---|---|
| MC method | 0.9981 | - | - |
| ESTM | 0.9962 | 0.0019 | 99.81 |
| ERSM | 0.9937 | 0.0044 | 99.56 |
| WR-ERSM | 0.9970 | 0.0011 | 99.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Feng, Y.-W.; Fei, C.-W. Weighted Regression-Based Extremum Response Surface Method for Structural Dynamic Fuzzy Reliability Analysis. Energies 2019, 12, 1588. https://doi.org/10.3390/en12091588
Lu C, Feng Y-W, Fei C-W. Weighted Regression-Based Extremum Response Surface Method for Structural Dynamic Fuzzy Reliability Analysis. Energies. 2019; 12(9):1588. https://doi.org/10.3390/en12091588
Chicago/Turabian StyleLu, Cheng, Yun-Wen Feng, and Cheng-Wei Fei. 2019. "Weighted Regression-Based Extremum Response Surface Method for Structural Dynamic Fuzzy Reliability Analysis" Energies 12, no. 9: 1588. https://doi.org/10.3390/en12091588
APA StyleLu, C., Feng, Y.-W., & Fei, C.-W. (2019). Weighted Regression-Based Extremum Response Surface Method for Structural Dynamic Fuzzy Reliability Analysis. Energies, 12(9), 1588. https://doi.org/10.3390/en12091588






