Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders
Abstract
1. Introduction
2. Model Description
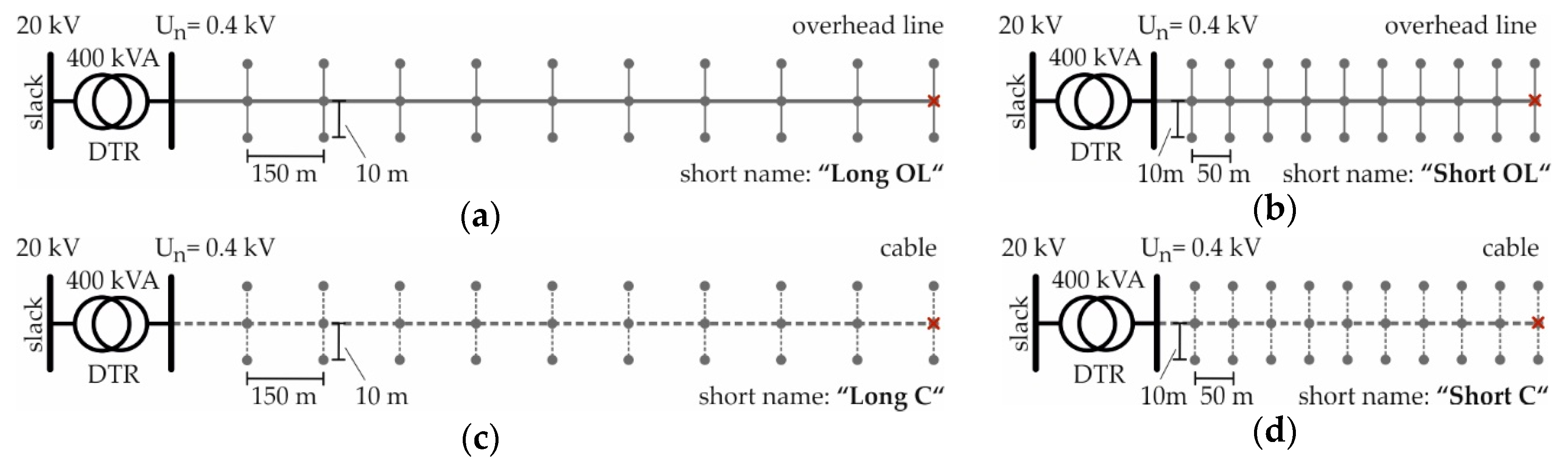
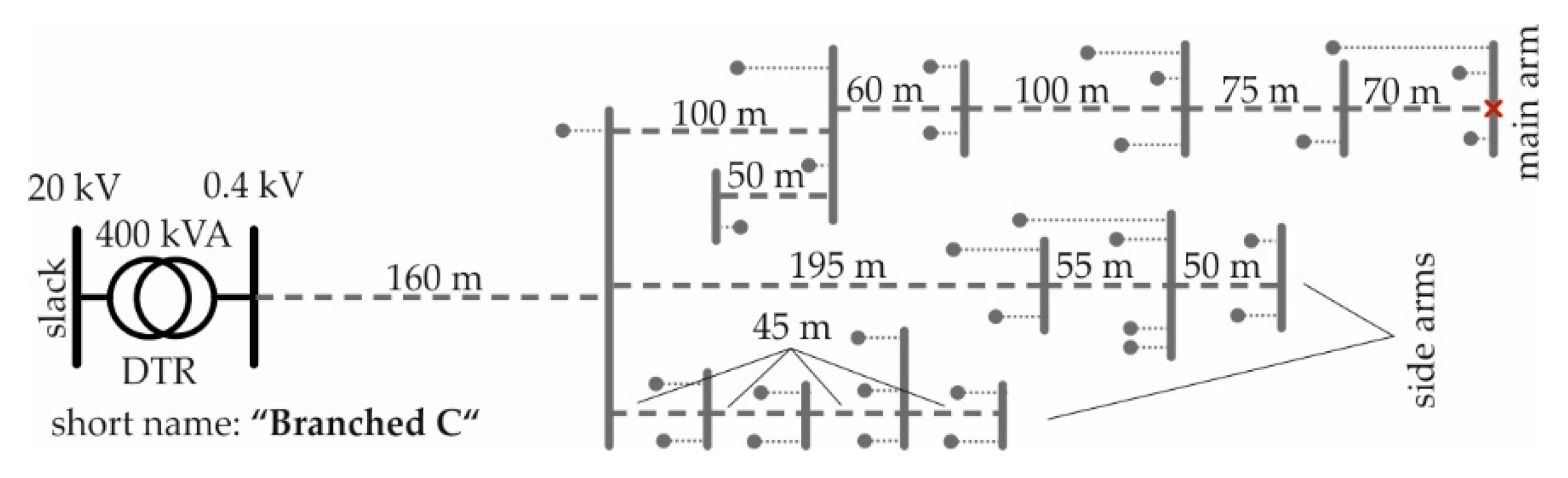
2.1. Low Voltage Test-Feeders
2.1.1. Theoretical LV Test-Feeders
2.1.2. Real LV Test-Feeder
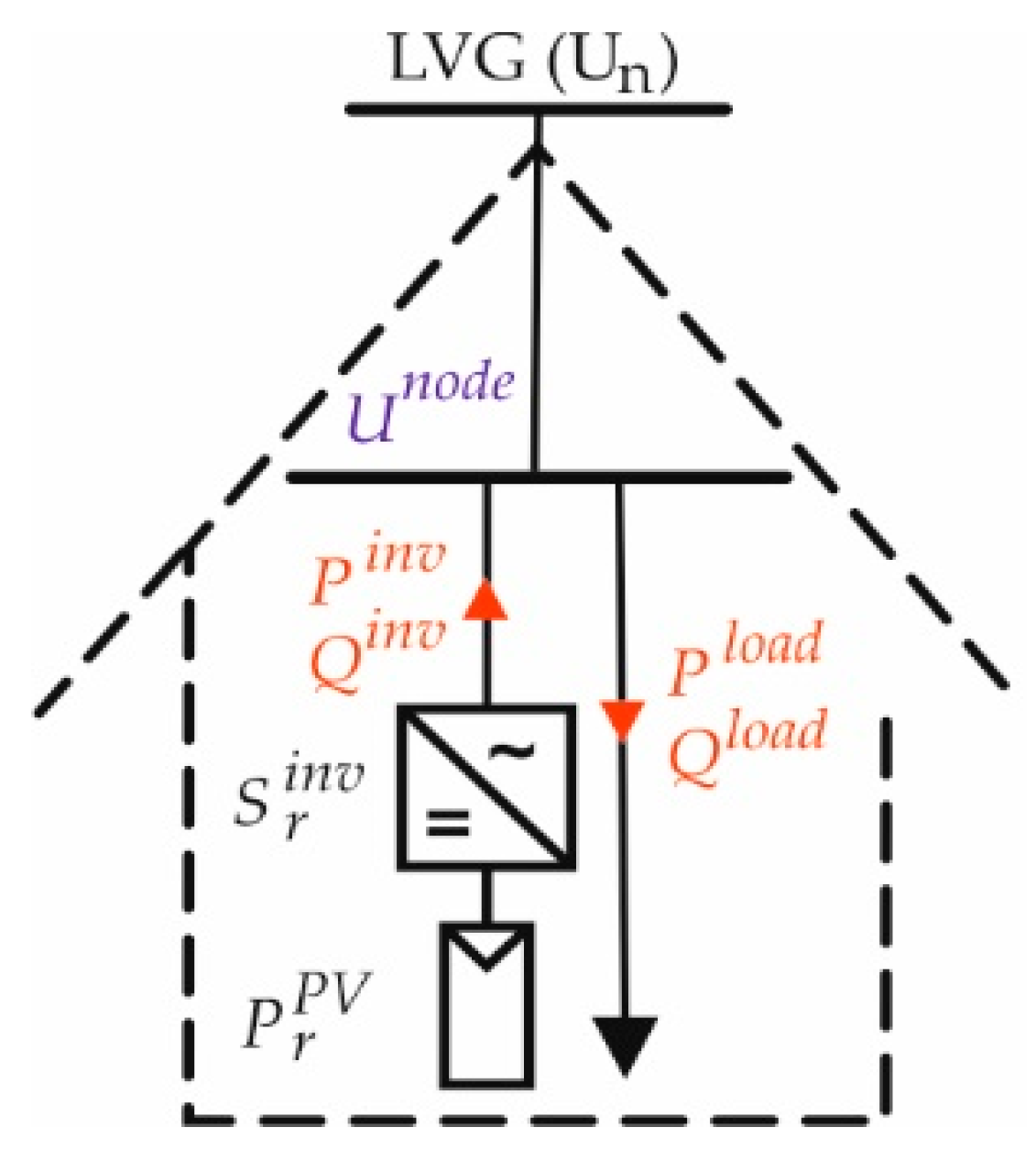
2.2. Prosumer Model
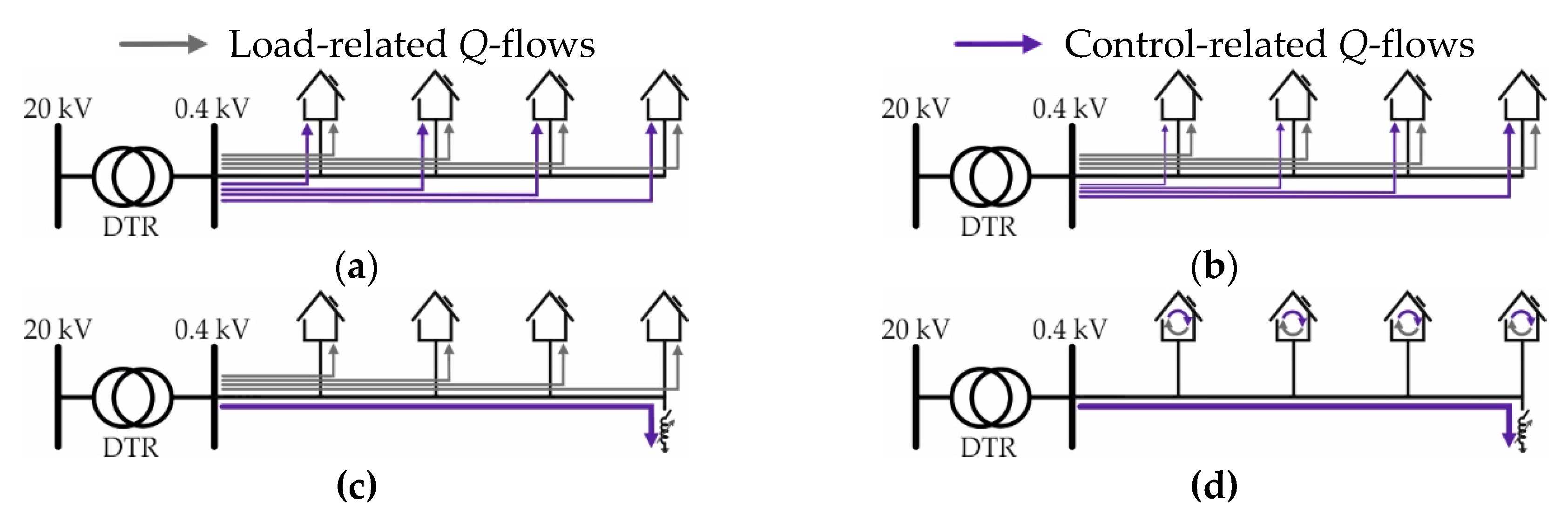
2.3. Control Strategies
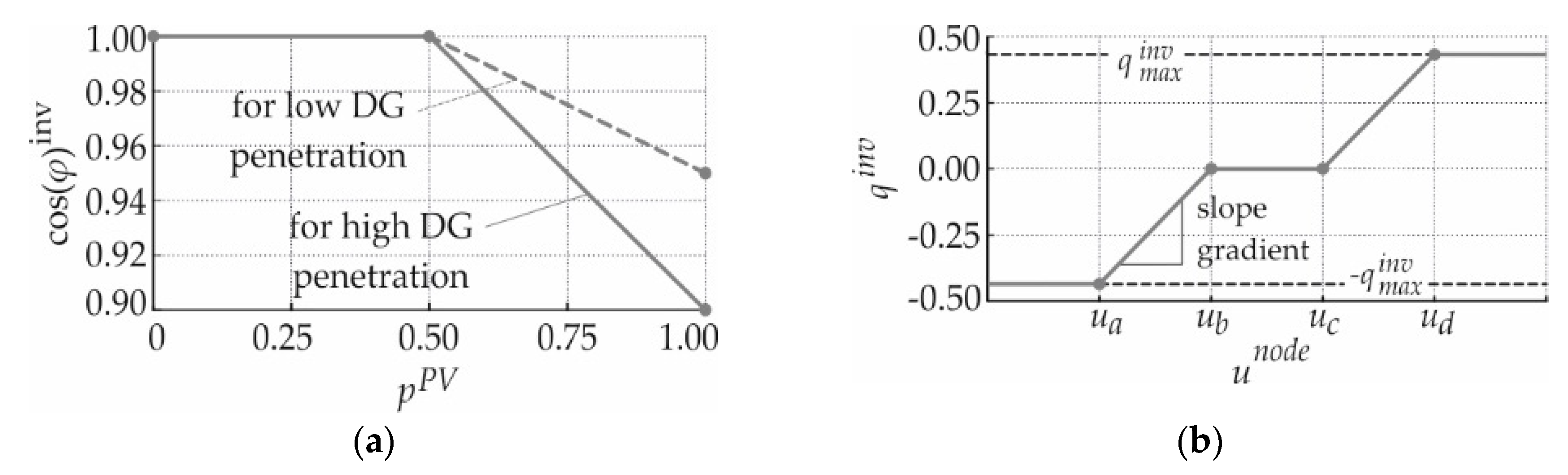
2.3.1. cosφ(P)-Control
2.3.2. Q(U)-Control
2.3.3. L(U)-Control
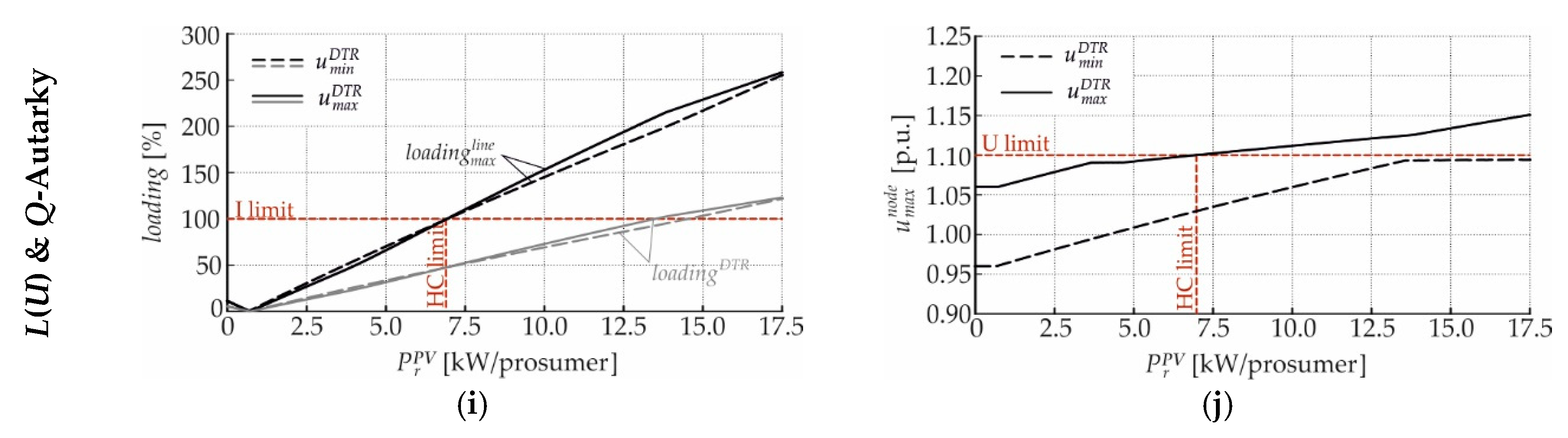
2.3.4. L(U)-Control Combined with Q-Autarkic Prosumers
3. Methodology
3.1. Scenario Definition
3.1.1. Load and Production
3.1.2. DTR Primary Voltage
3.1.3. Control Strategy
3.1.4. Test-Feeders
3.1.5. Scenario Overview
3.2. Control Parameterization
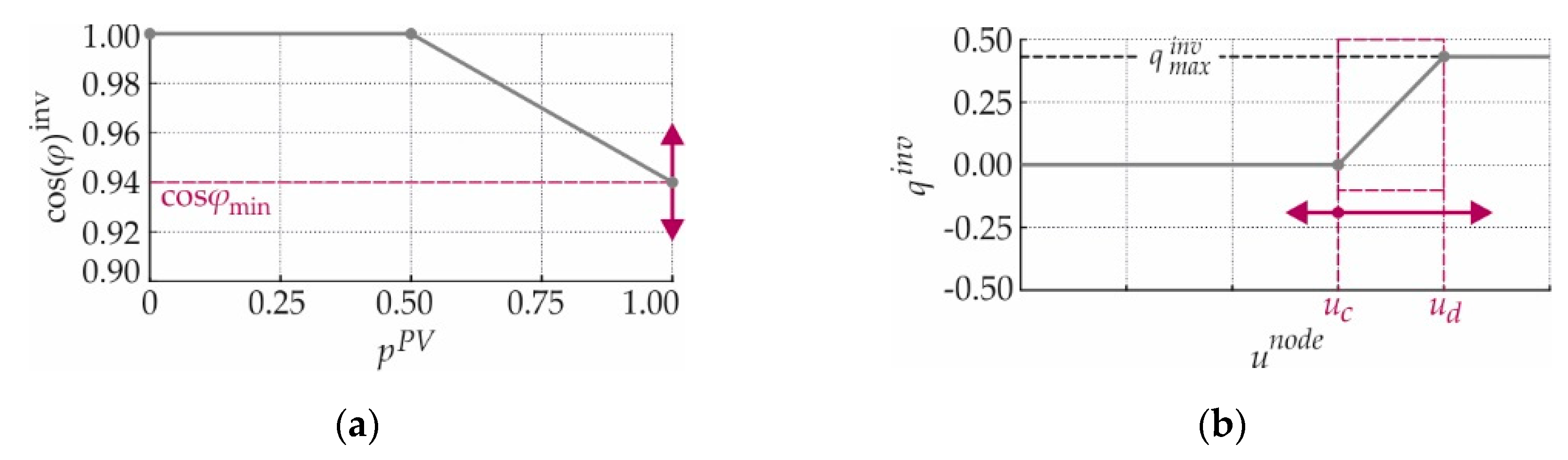
3.2.1. cosφ(P)-Control
3.2.2. Q(U)-Control
3.2.3. L(U)-Control
3.2.4. L(U)-Control Combined with Q-Autarkic Prosumers
3.3. Result Evaluation
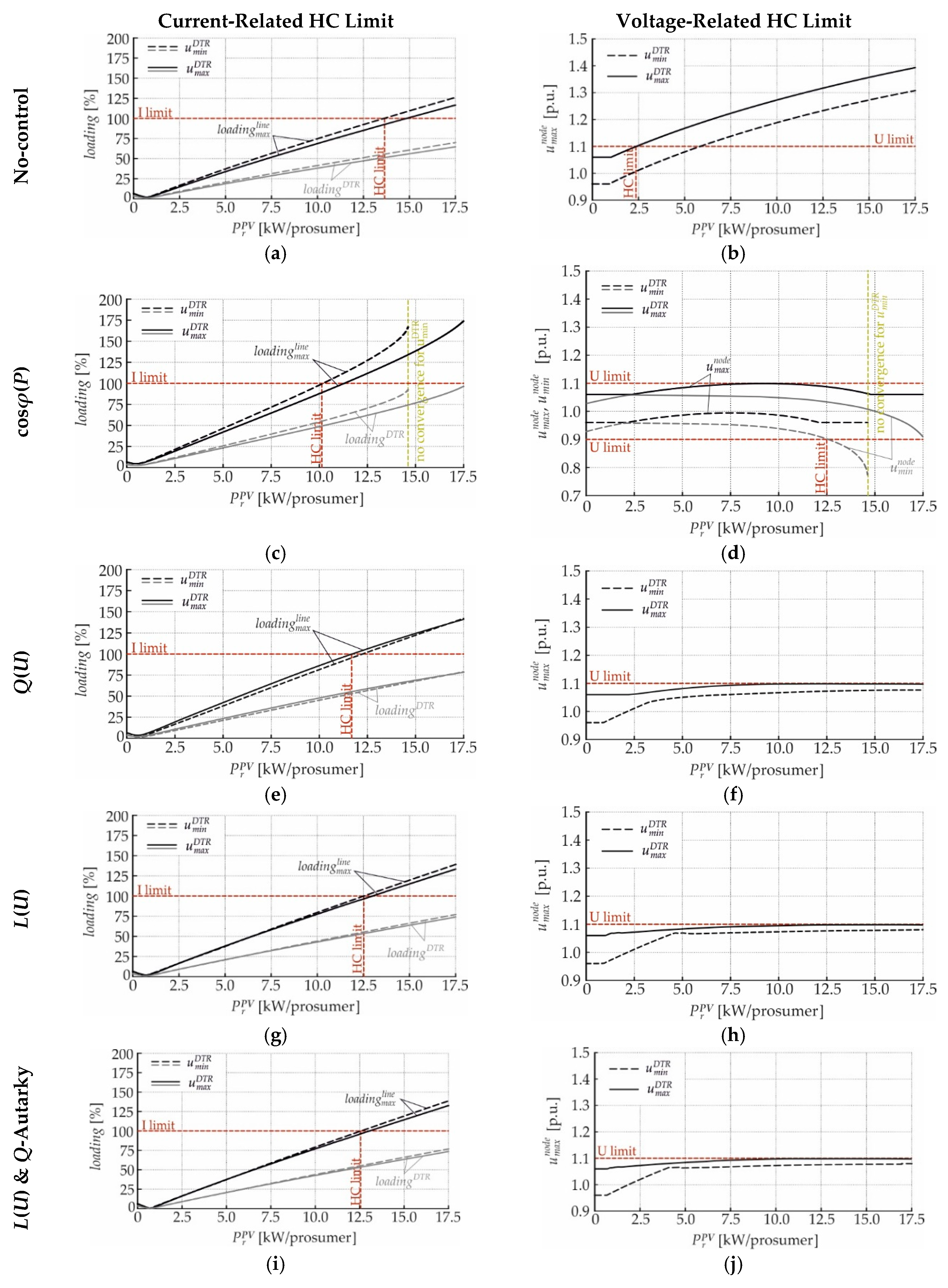
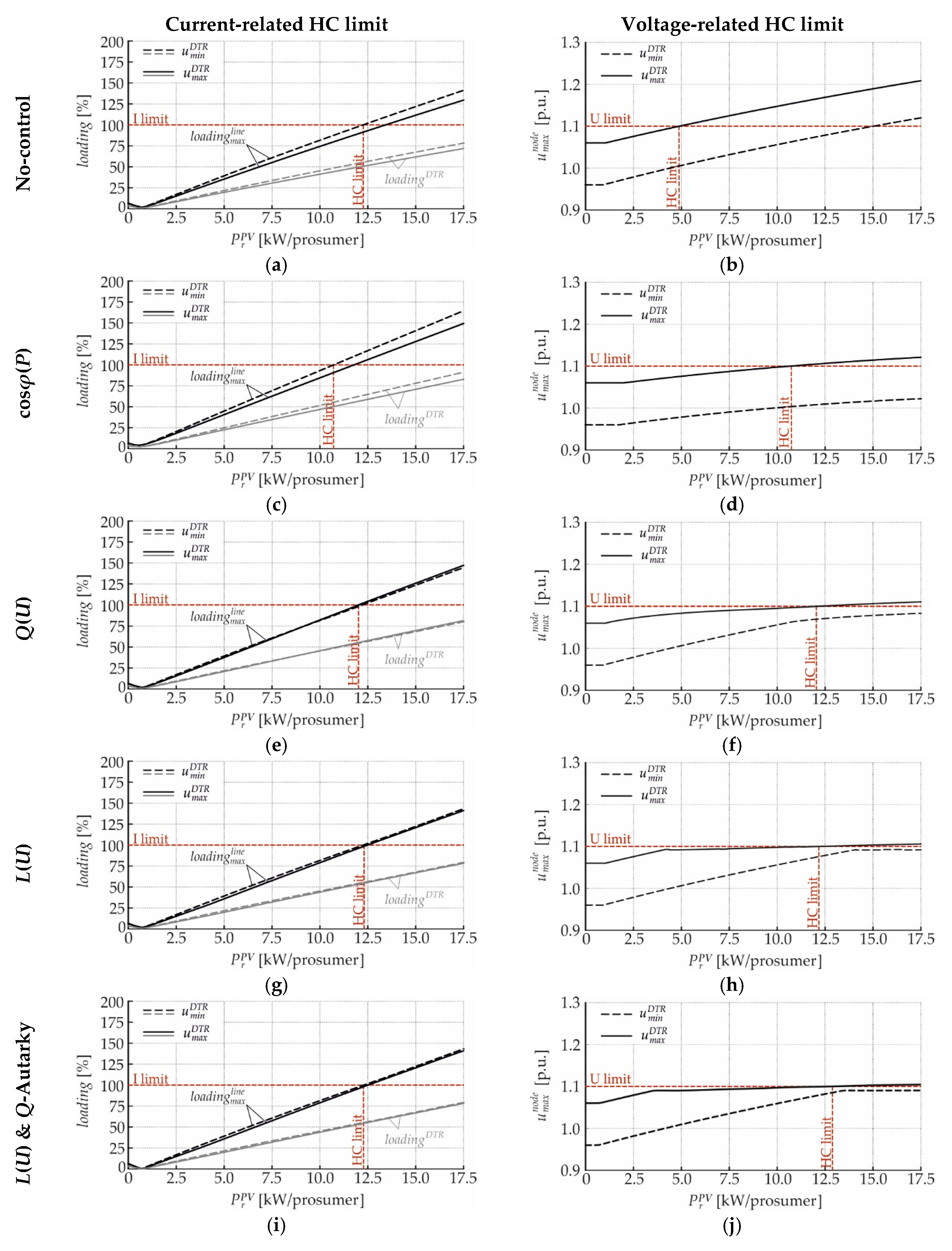
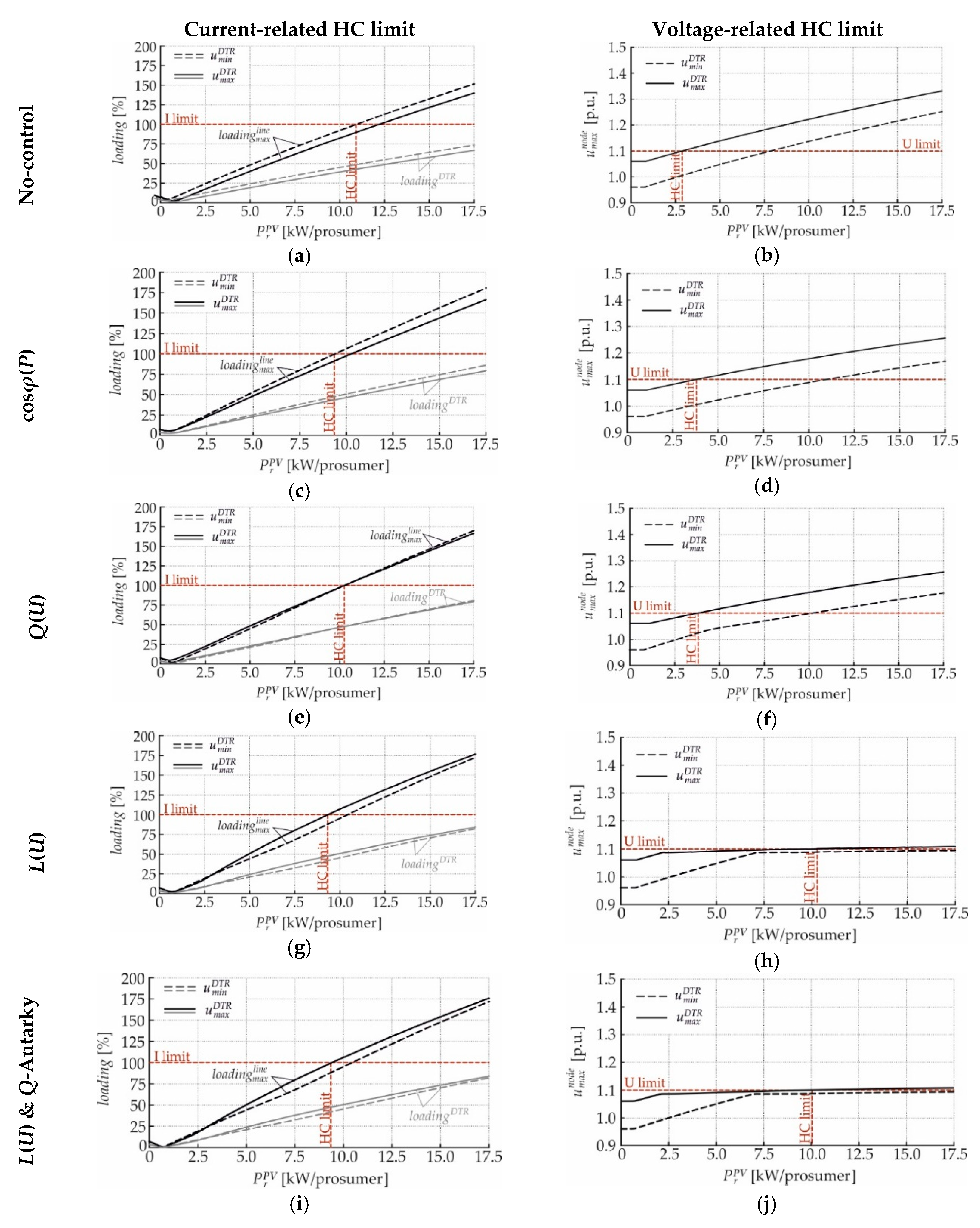
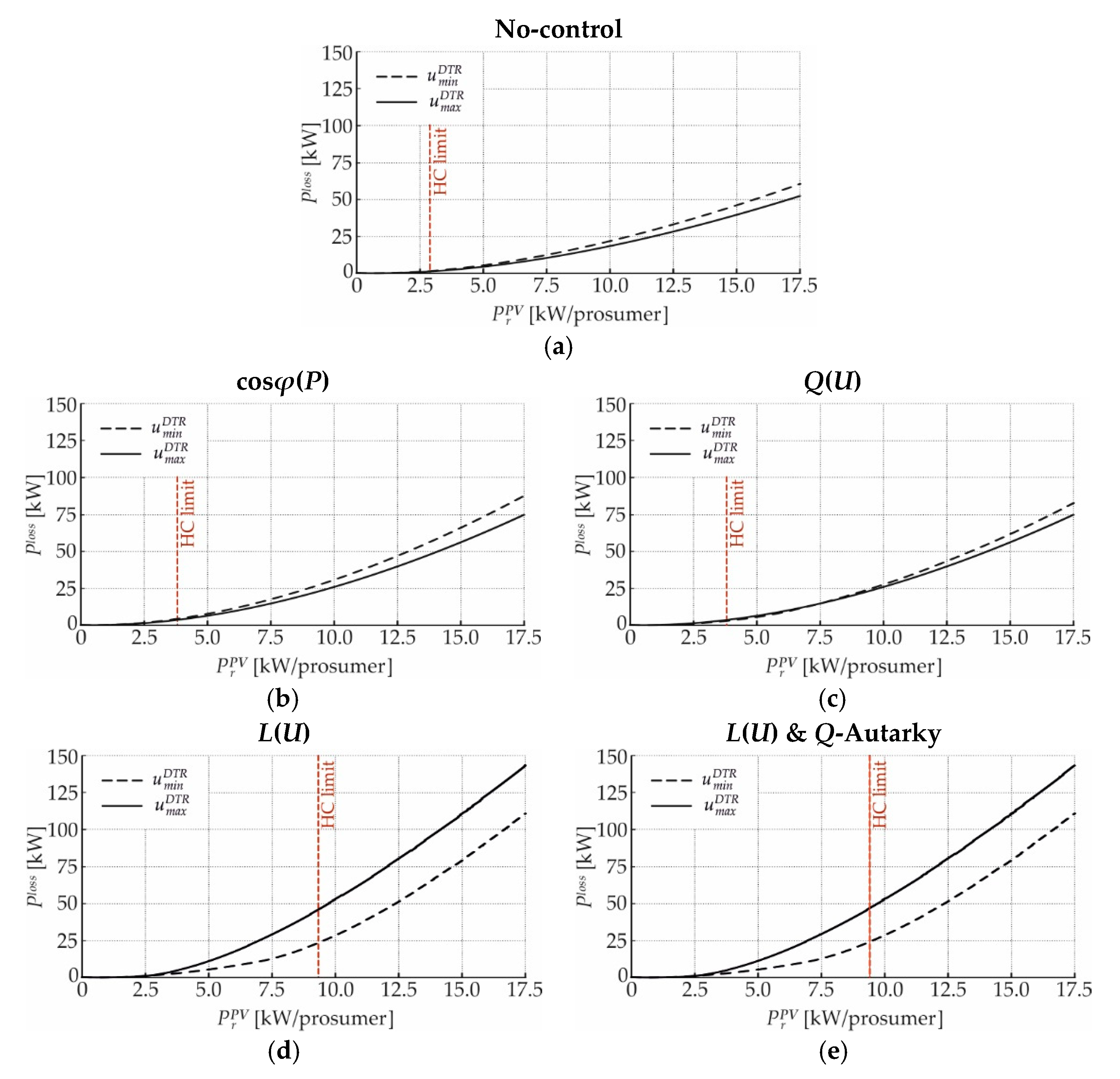
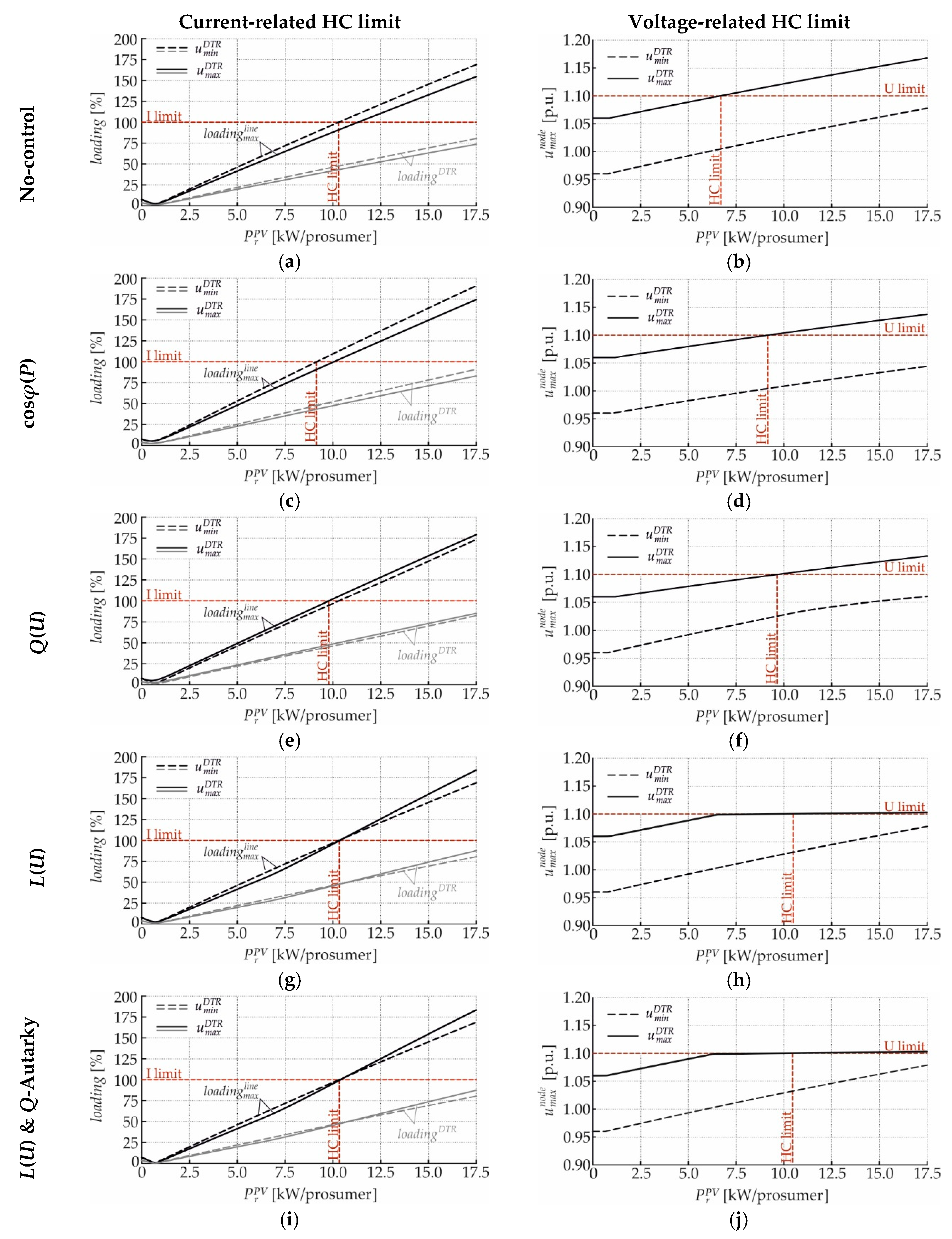
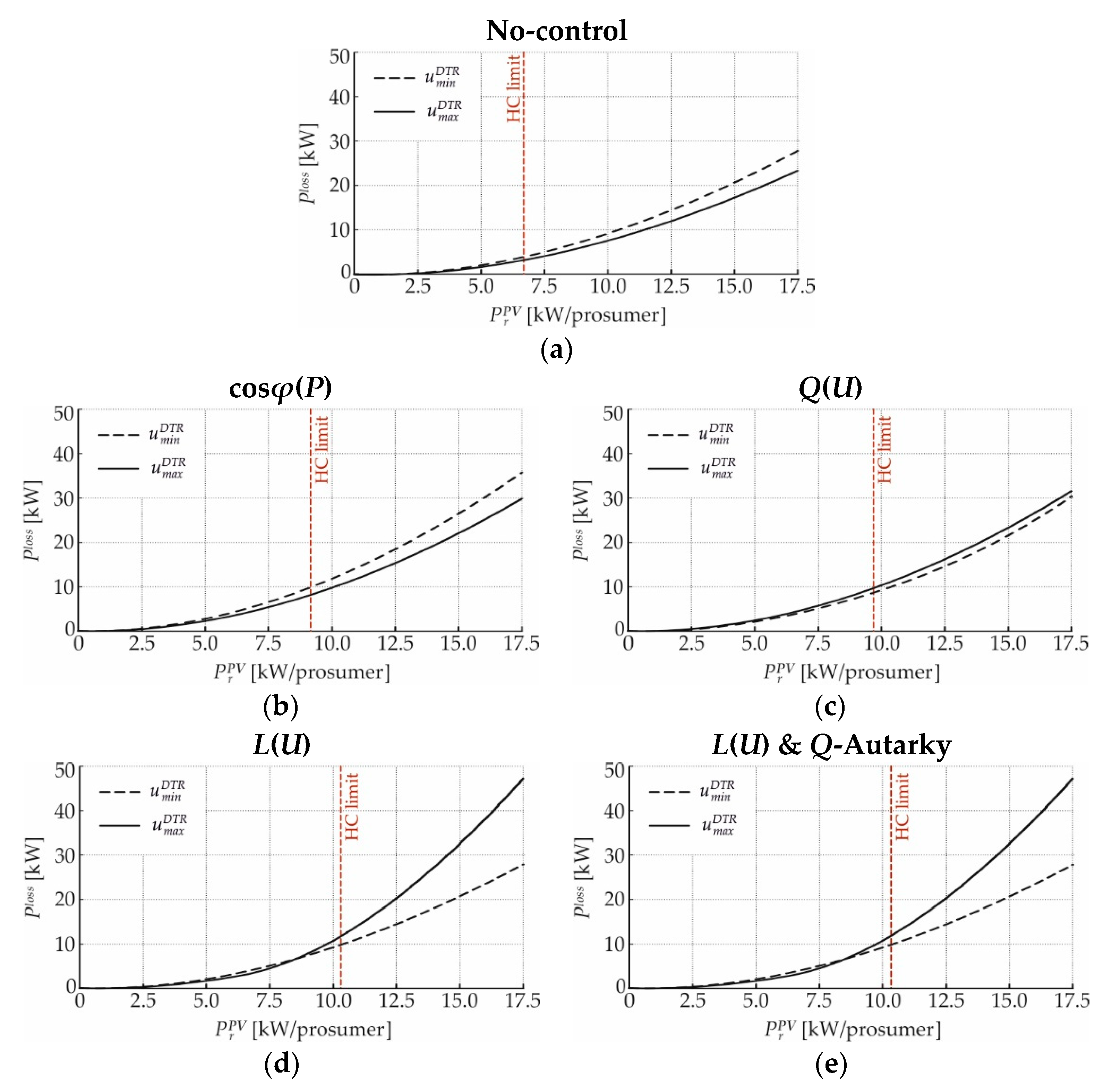
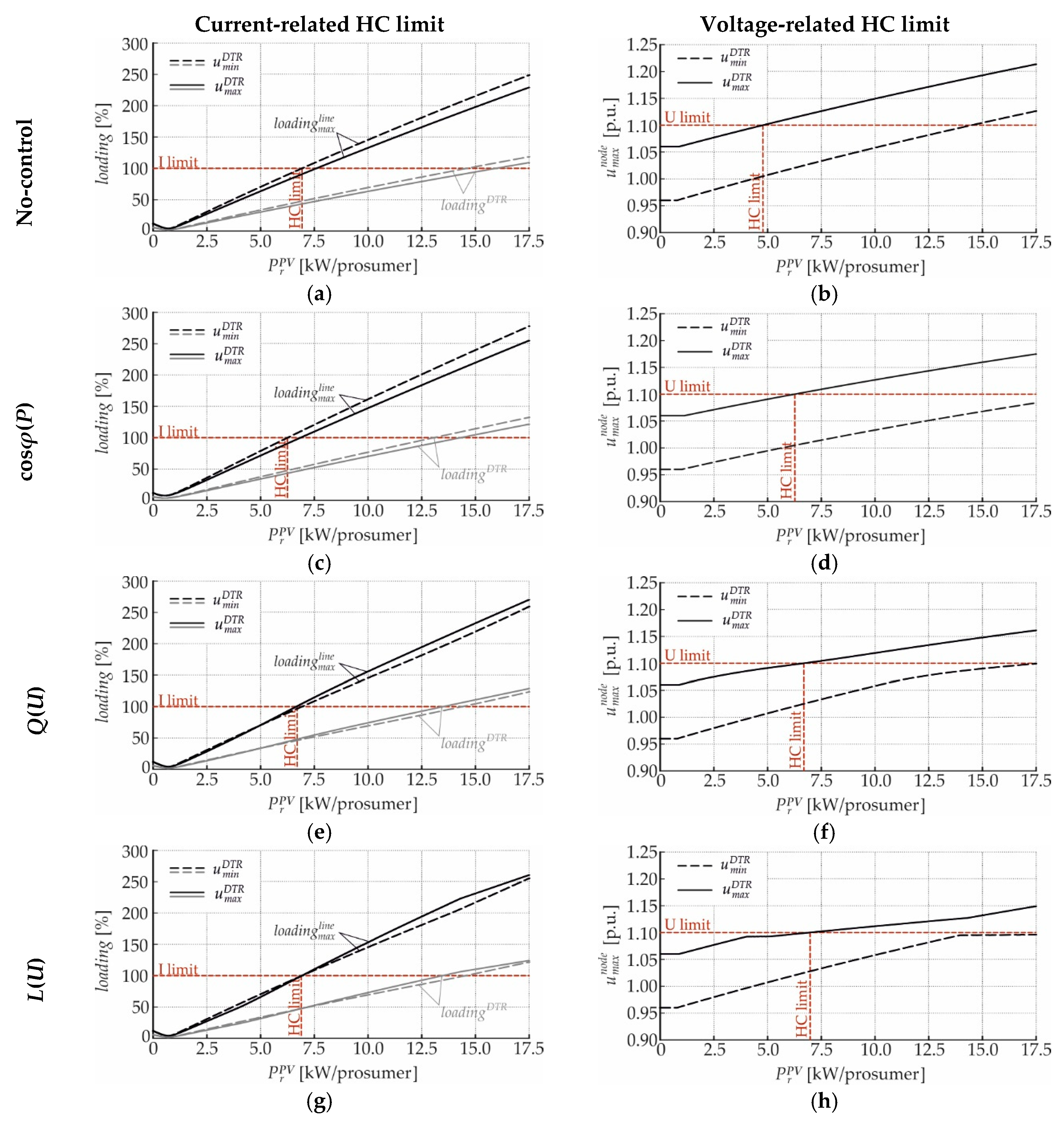
4. Hosting Capacity Enhancement by Local Reactive Power Control Strategies
4.1. Theoretical LV Test-Feeders
4.1.1. Long Overhead Line Test-Feeder
4.1.2. Short Overhead Line Test-Feeder
4.1.3. Long Cable Test-Feeder
4.1.4. Short Cable Test-Feeder
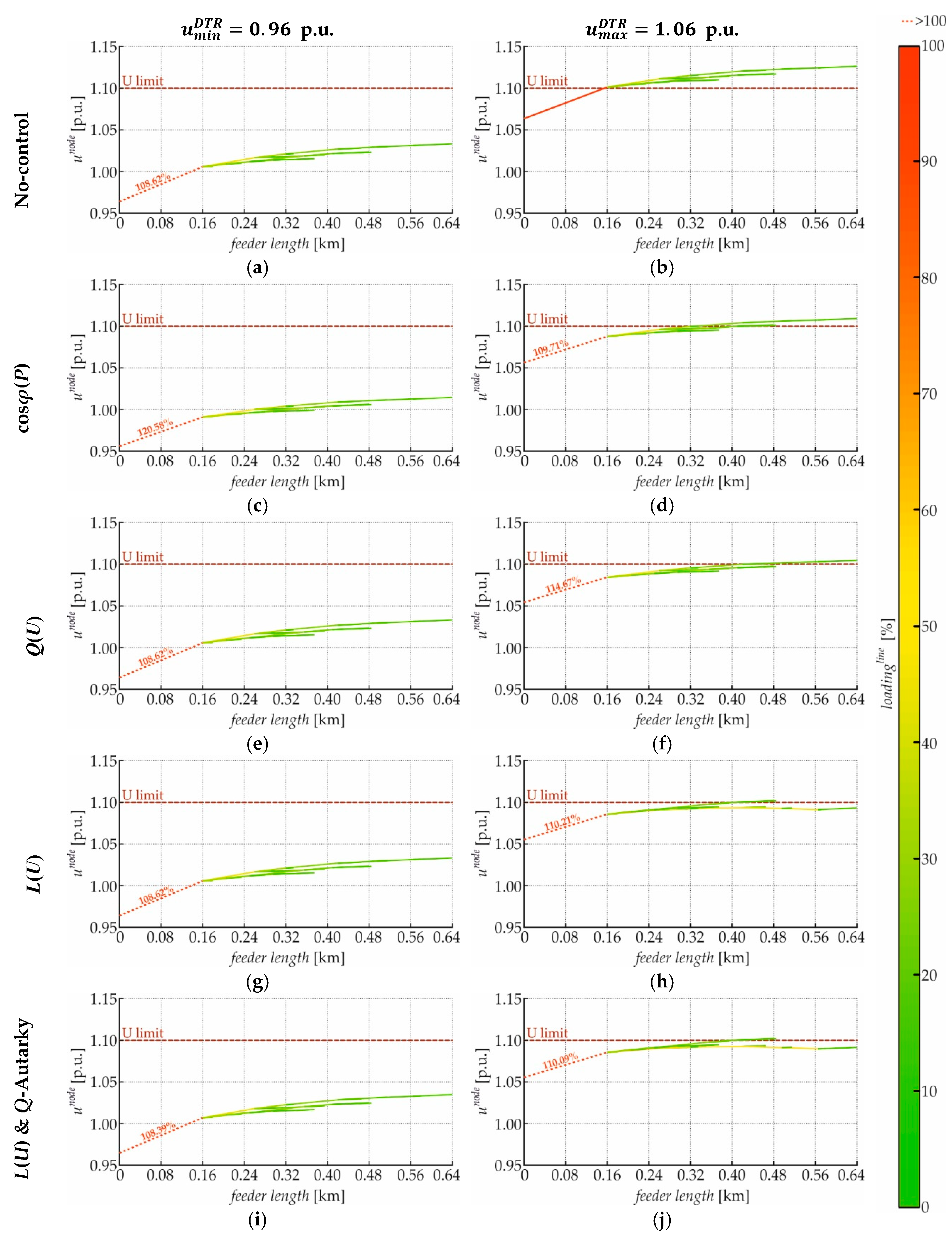
4.2. Real LV Test-Feeder
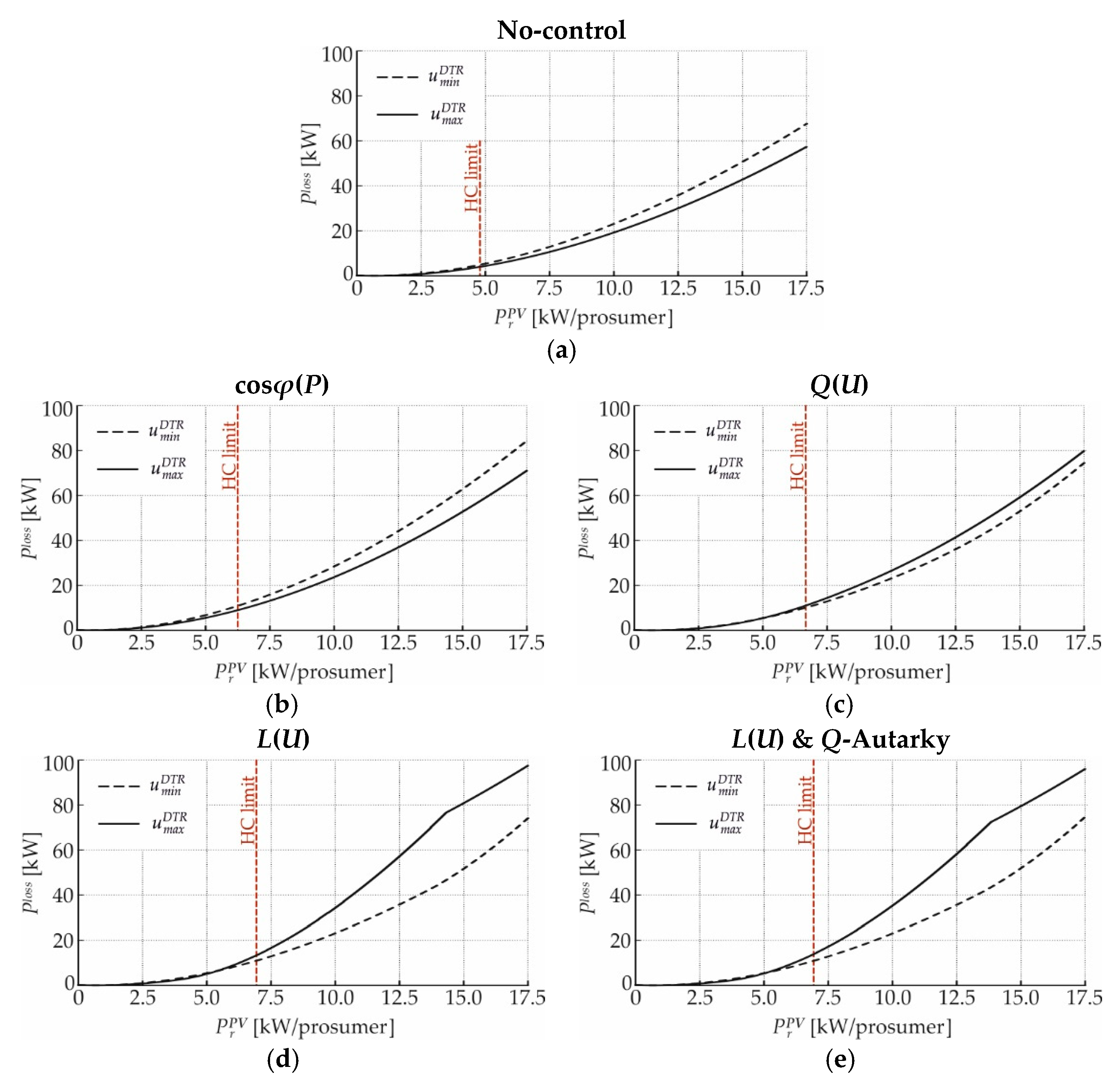
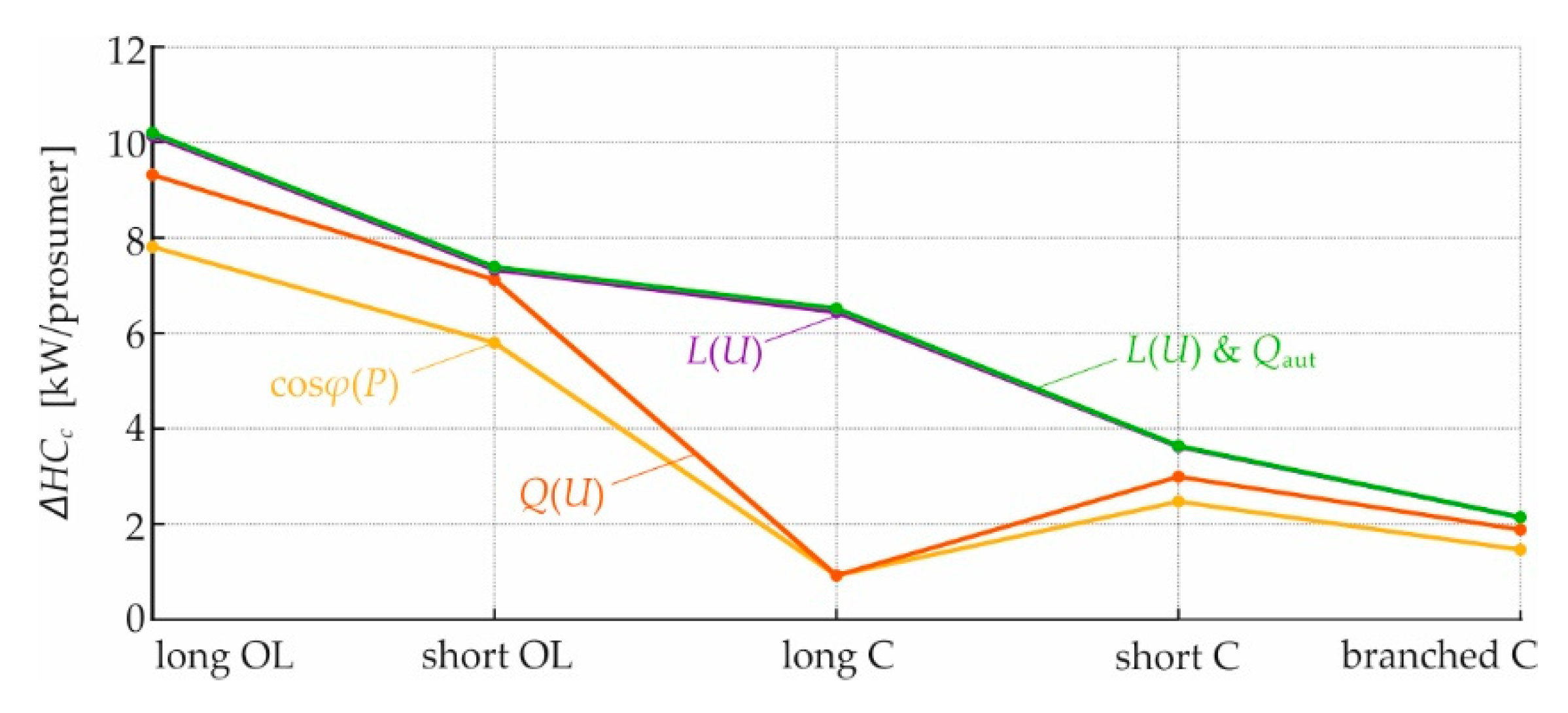
4.3. Overview
4.3.1. Current- and Voltage-Related Hosting Capacity Limits
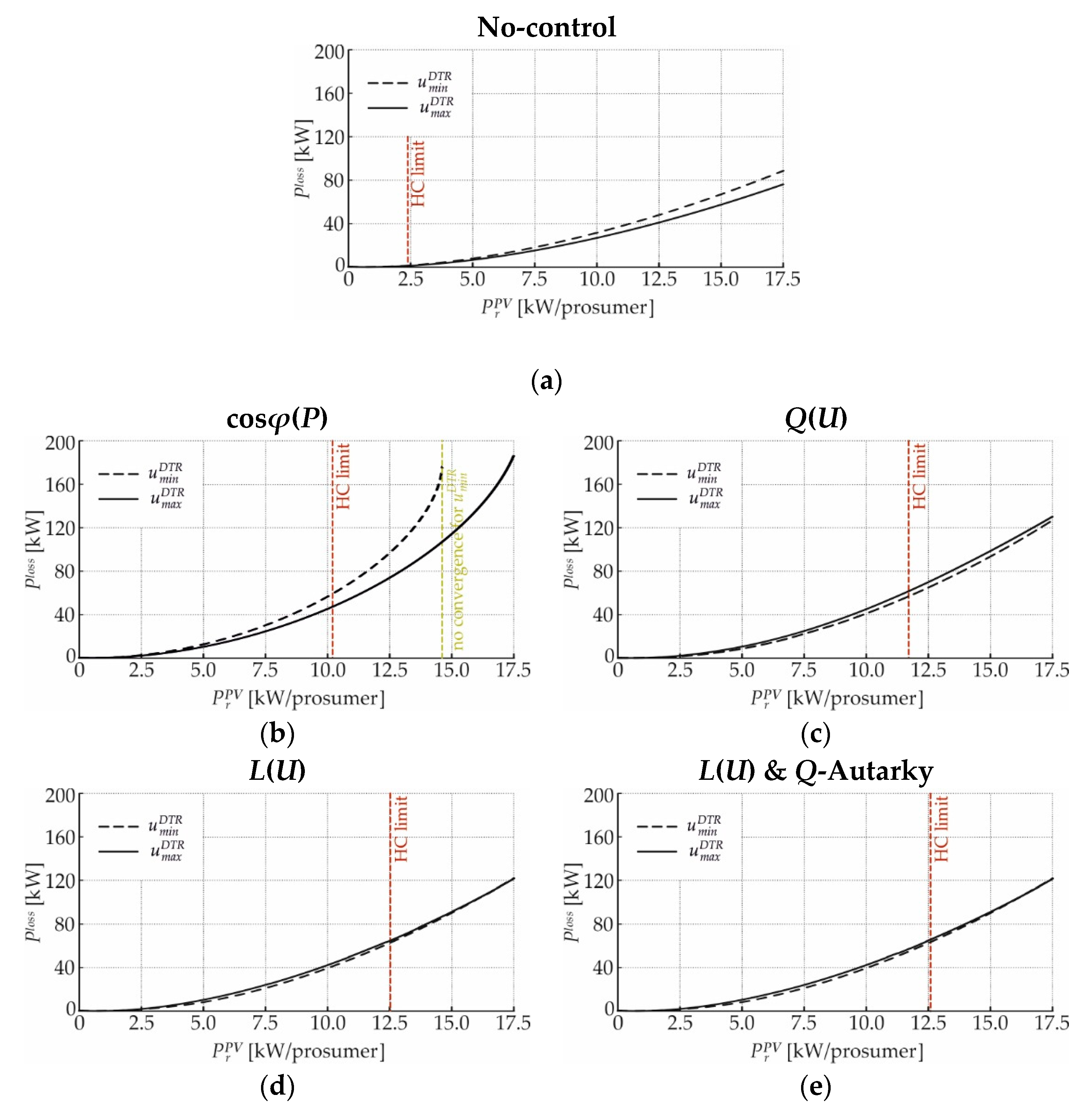
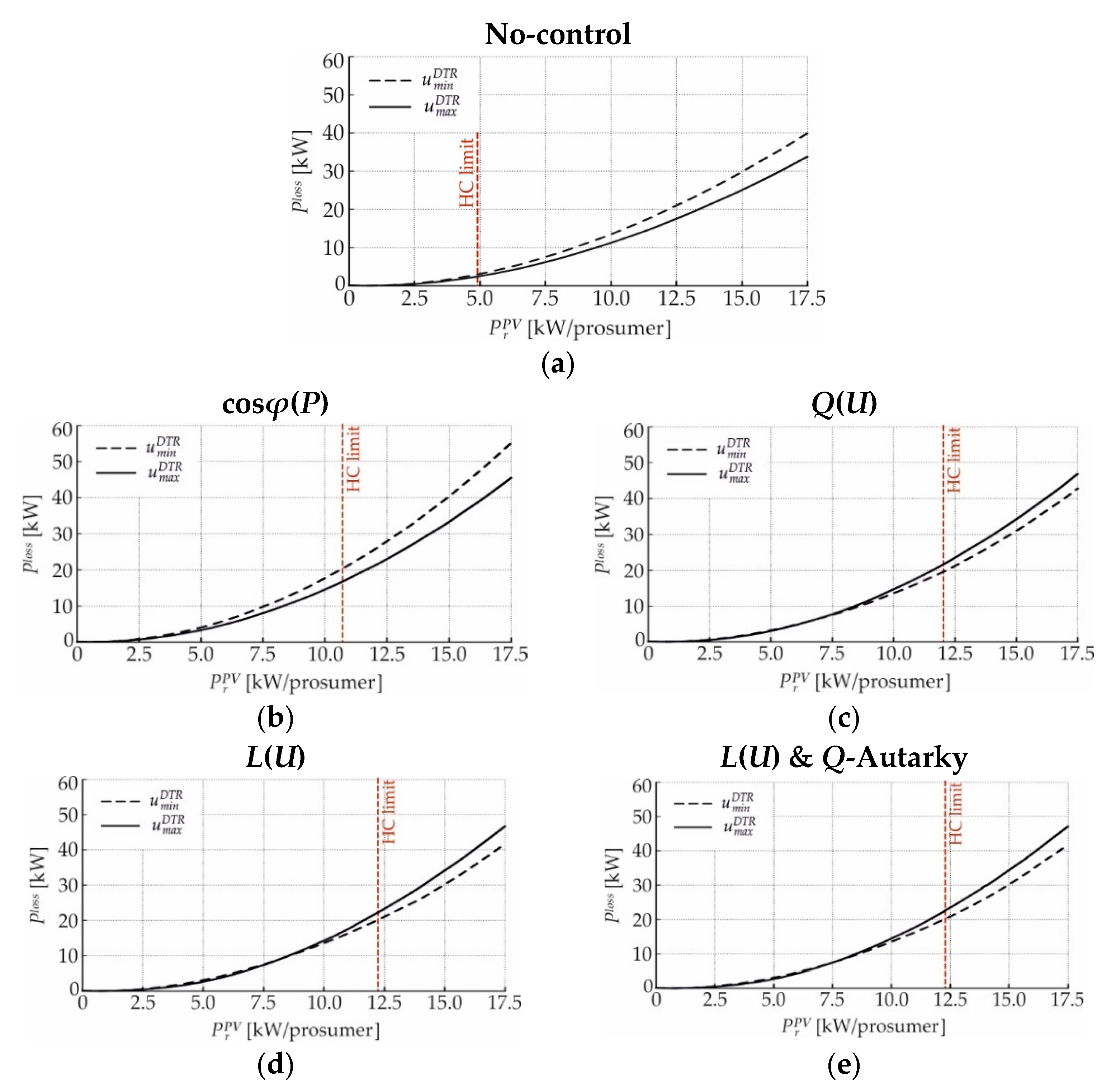
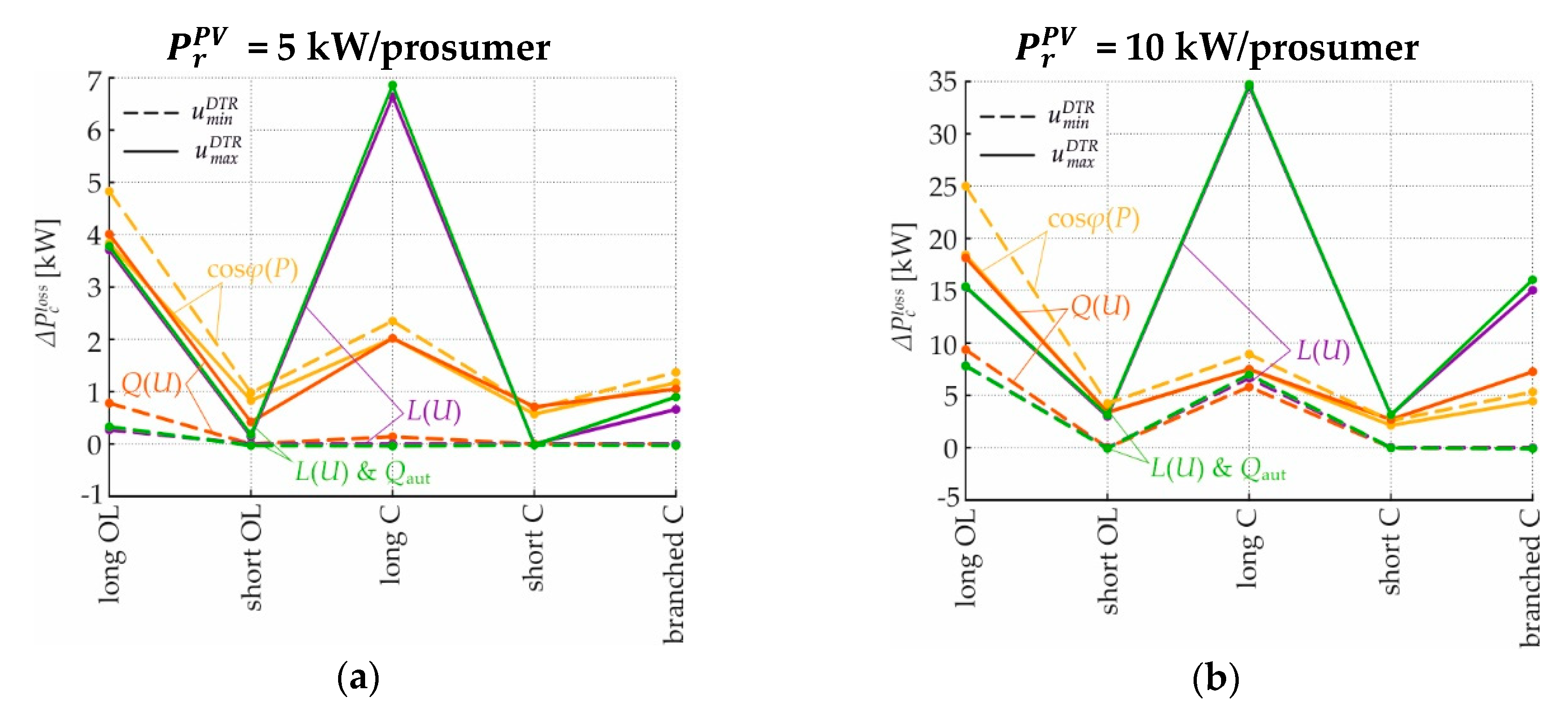
4.3.2. Grid Losses
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Line Type | Branch Type | Profile [mm2] | R′ [Ohm/km] | X′ [Ohm/km] | C′ [nF/km] | |
|---|---|---|---|---|---|---|
| Overhead line | Main branch | 95 | 0.3264 | 0.3557 | 0.0000 | 320 |
| Overhead line | Sub branch | 50 | 0.6152 | 0.3764 | 0.0000 | 210 |
| Cable | Main branch | 150 | 0.2060 | 0.0800 | 1040.0 | 275 |
| Cable | Sub branch | 50 | 0.6410 | 0.0850 | 720.00 | 145 |
Appendix B
| Test-Feeder | cosφ(P) cosφmin | Q(U) uc [%] | L(U) uset-point [%] | L(U) & Qaut uset-point [%] | |
|---|---|---|---|---|---|
| theoretical | Long OL | 0.905 | 103.20 | 106.70 | 106.40 |
| Short OL | 0.932 | 106.30 | 109.18 | 108.97 | |
| Long C | 0.900 | 103.00 | 108.70 | 108.60 | |
| Short C | 0.920 | 103.30 | 109.88 | 109.88 | |
| real | Branched C | 0.939 | 106.40 | 109.15 | 108.97 |
Appendix C
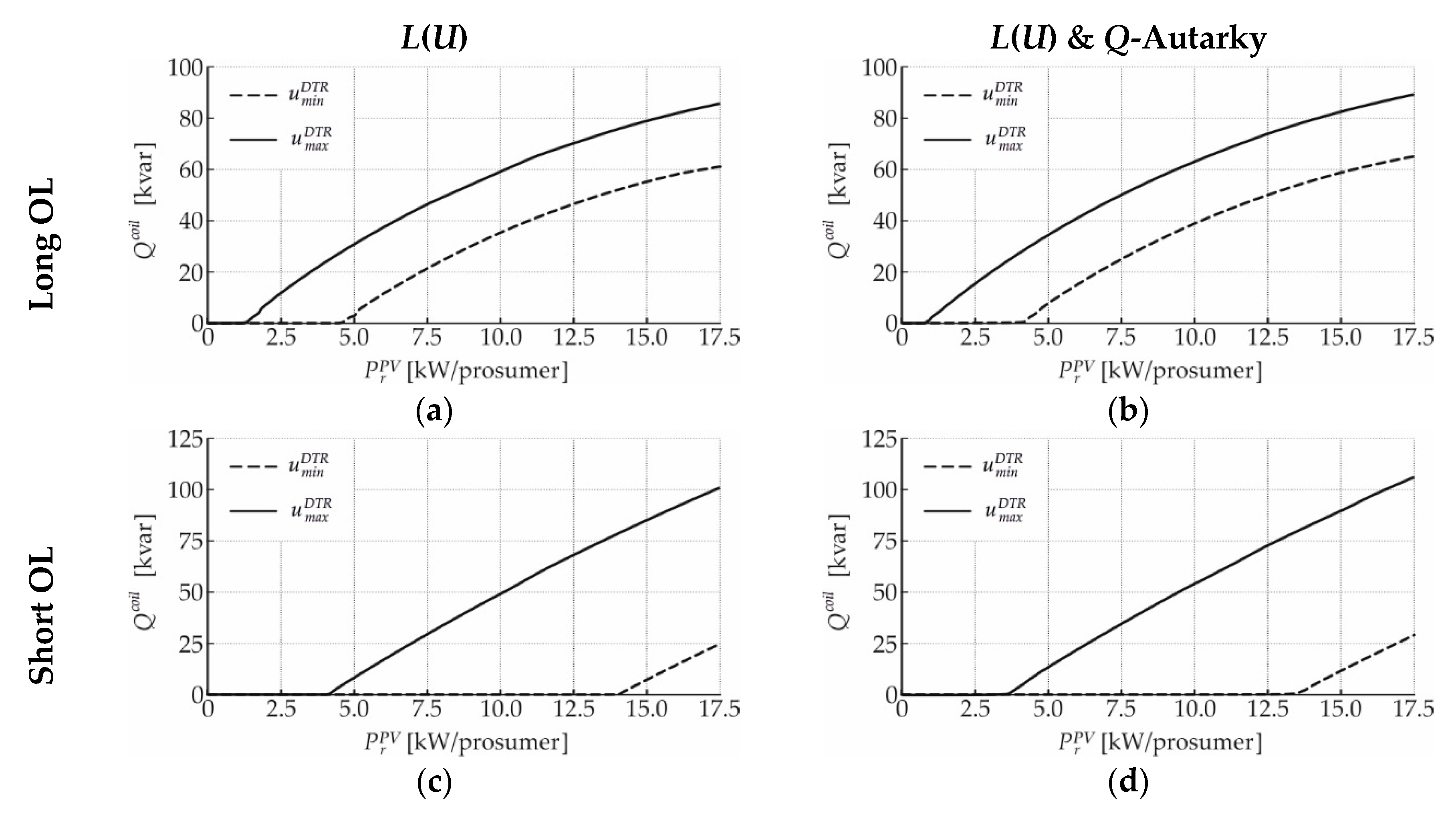
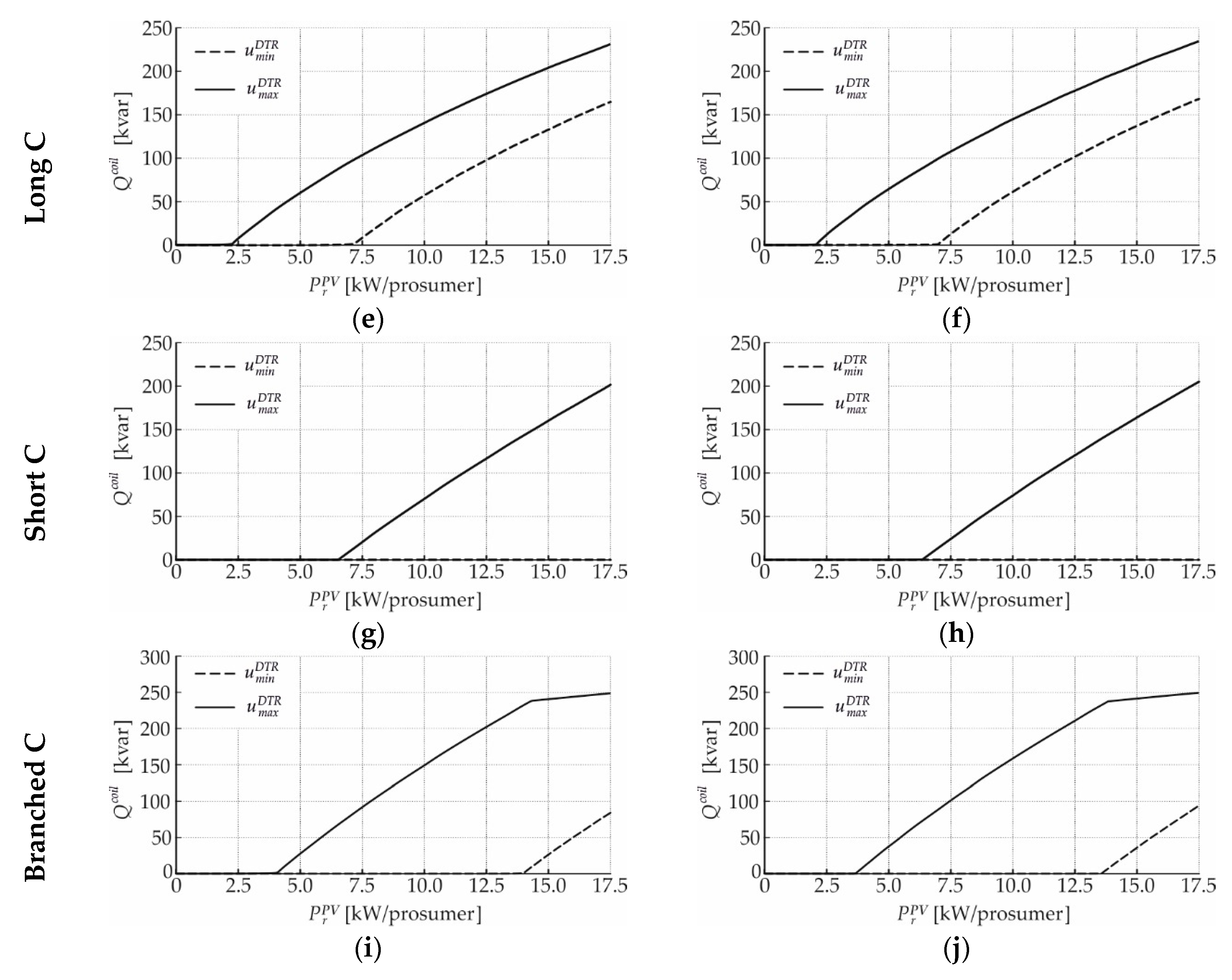
References
- Peças Lopes, J.A.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef]
- Manditereza, P.T.; Bansal, R. Renewable distributed generation: The hidden challenges—A review from the protection perspective. Renew. Sustain. Energy Rev. 2016, 58, 1457–1465. [Google Scholar] [CrossRef]
- Hatziargyriou, N.D.; Sakis Meliopoulos, A.P. Distributed energy sources: Technical challenges. In Proceedings of the IEEE Power Engineering Society Winter Meeting (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002; Volume 2, pp. 1017–1022. [Google Scholar] [CrossRef]
- Katiraei, F.; Aguero, J.R. Solar PV Integration Challenges. IEEE Power Energy Mag. 2011, 9, 62–71. [Google Scholar] [CrossRef]
- Navarro, B.B.; Navarro, M.M. A comprehensive solar PV hosting capacity in MV and LV radial distribution networks. In Proceedings of the ISGT-Europe, Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Bletterie, B.; Gorsek, A.; Uljanic, B.; Blazic, B.; Woyte, A.; Van, T.V.; Truyens, F.; Jahn, J. Enhancement of the network hosting capacity—Clearing space for/with PV. In Proceedings of the 5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010. [Google Scholar]
- Bollen, M.H.J.; Rönnberg, S.K. Hosting capacity of the power grid for renewable electricity production and new large consumption equipment. Energies 2017, 10, 1325. [Google Scholar] [CrossRef]
- Smith, J. Stochastic Analysis to Determine Feeder Hosting Capacity for Distributed Solar PV; Technical Update; EPRI: Knoxville, TN, USA, 2012. [Google Scholar]
- Bletterie, B.; Kadam, S.; Renner, H. On the classification of low voltage feeders for network planning and hosting capacity studies. Energies 2018, 11, 651. [Google Scholar] [CrossRef]
- Reese, C.; Buchhagen, C.; Hofmann, L. Voltage range as control input for OLTC-equipped distribution transformers. In Proceedings of the PES T&D, Orlando, FL, USA, 7–10 May 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Latif, A.; Gawlik, W.; Palensky, P. Quantification and mitigation of unfairness in active power curtailment of rooftop photovoltaic systems using sensitivity based coordinated control. Energies 2016, 9, 436. [Google Scholar] [CrossRef]
- Rossi, M.; Viganò, G.; Moneta, D.; Clerici, D.; Carlini, C. Analysis of active power curtailment strategies for renewable distributed generation. In Proceedings of the AEIT International Annual Conference, Capri, Italy, 5–7 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Marggraf, O.; Laudahn, S.; Engel, B.; Lindner, M.; Aigner, C.; Witzmann, R.; Schoeneberger, M.; Patzack, S.; Vennegeerts, H.; Cremer, M.; Meyer, M. U-control—Analysis of distributed and automated voltage control in current and future distribution grids. In Proceedings of the International ETG Congress, Bonn, Germany, 28–29 November 2017; pp. 1–6. [Google Scholar]
- Hashemi, S.; Østergaard, J. Methods and strategies for overvoltage prevention in low voltage distribution systems with PV. IET Renew. Power Gen. 2017, 11, 205–214. [Google Scholar] [CrossRef]
- Caldon, R.; Coppo, M.; Turri, R. Distributed voltage control strategy for LV networks with inverter-interfaced generators. Electr. Power Syst. Res. 2014, 107, 85–92. [Google Scholar] [CrossRef]
- Smith, J.W.; Sunderman, W.; Dugan, R.; Seal, B. Smart inverter volt/var control functions for high penetration of PV on distribution systems. In Proceedings of the IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, X.; Chang, X.; Fan, G.; Chen, L.; Wang, Q.; Tang, Y.; Dai, J. The reactive power voltage control strategy of PV systems in low-voltage string lines. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for control of reactive power by distributed photovoltaic generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- Ilo, A.; Schultis, D.-L.; Schirmer, C. Effectiveness of distributed vs. concentrated volt/var local control strategies in low-voltage grids. Appl. Sci. 2018, 8, 1382. [Google Scholar] [CrossRef]
- Schultis, D.-L.; Ilo, A.; Schirmer, C. Overall performance evaluation of reactive power control strategies in low voltage grids with high prosumer share. Electr. Power Syst. Res. 2019, 168, 336–349. [Google Scholar] [CrossRef]
- Ilo, A.; Schultis, D.-L. Low-voltage grid behaviour in the presence of concentrated var-sinks and var-compensated customers. Electr. Power Syst. Res. 2019, 171, 54–65. [Google Scholar] [CrossRef]
- Demirok, E.; González, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovol. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Bletterie, B.; Kadam, S.; Bolgaryn, R.; Zegers, A. Voltage control with PV inverters in low voltage networks—In depth analysis of different concepts and parameterization criteria. IEEE Trans. Power Syst. 2017, 32, 177–185. [Google Scholar] [CrossRef]
- “Benchmark Systems for Network Integration of renewable and Distributed Energy Resources”; Task Force C6.04; CIGRE: Paris, France, 2014; ISBN 978-285-873-270-8.
- E-Control, Technische und Organisatorische Regeln für Betreiber und Benutzer von Netzen, Besondere technische Regeln/Parallelbetrieb von Erzeugungsanlagen mit Verteilernetzen, Teil D/Hauptabschnitt D4, Version 2.3. 2016. Available online: https://www.e-control.at/documents/20903/388512/TOR_D4_V2.3+ab+1.7.2016.pdf/1fbc3aff-36a6-4eee-8de5-6027eaa53a89 (accessed on 11 March 2019).
- Bokhari, A.; Alkan, A.; Dogan, R.; Diaz-Aguiló, M.; De Leon, F.; Czarkowski, D.; Zabar, Z.; Birenbaum, L.; Noel, A. Experimental determination of the ZIP coefficients for modern residential, commercial, and industrial loads. IEEE Trans. Power Deliv. 2014, 29, 1372–1381. [Google Scholar] [CrossRef]
| DTR Primary Voltage | |
|---|---|
| 0.96 p.u | 1.06 p.u. |
| = 0.00 kW | = 0.00 kW |
| = 0.01 kW | = 0.01 kW |
| … | … |
| = 17.49 kW | = 17.49 kW |
| = 17.50 kW | = 17.50 kW |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultis, D.-L. Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders. Energies 2019, 12, 1560. https://doi.org/10.3390/en12081560
Schultis D-L. Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders. Energies. 2019; 12(8):1560. https://doi.org/10.3390/en12081560
Chicago/Turabian StyleSchultis, Daniel-Leon. 2019. "Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders" Energies 12, no. 8: 1560. https://doi.org/10.3390/en12081560
APA StyleSchultis, D.-L. (2019). Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders. Energies, 12(8), 1560. https://doi.org/10.3390/en12081560





