Uncertainty-Based Models for Optimal Management of Energy Hubs Considering Demand Response
Abstract
1. Introduction
1.1. Motivation and Problem Description
1.2. Literature Review
1.3. Paper Contributions
- Proposing a mixed integer nonlinear (MINLP) model for an EH based on a robust model.
- Proposing an IGDT model considering price and wind uncertainties.
- Proposing DR with IGDT simultaneously in the EH.
- Considering an energy storage system (ESS) in the IGDT-based problem.
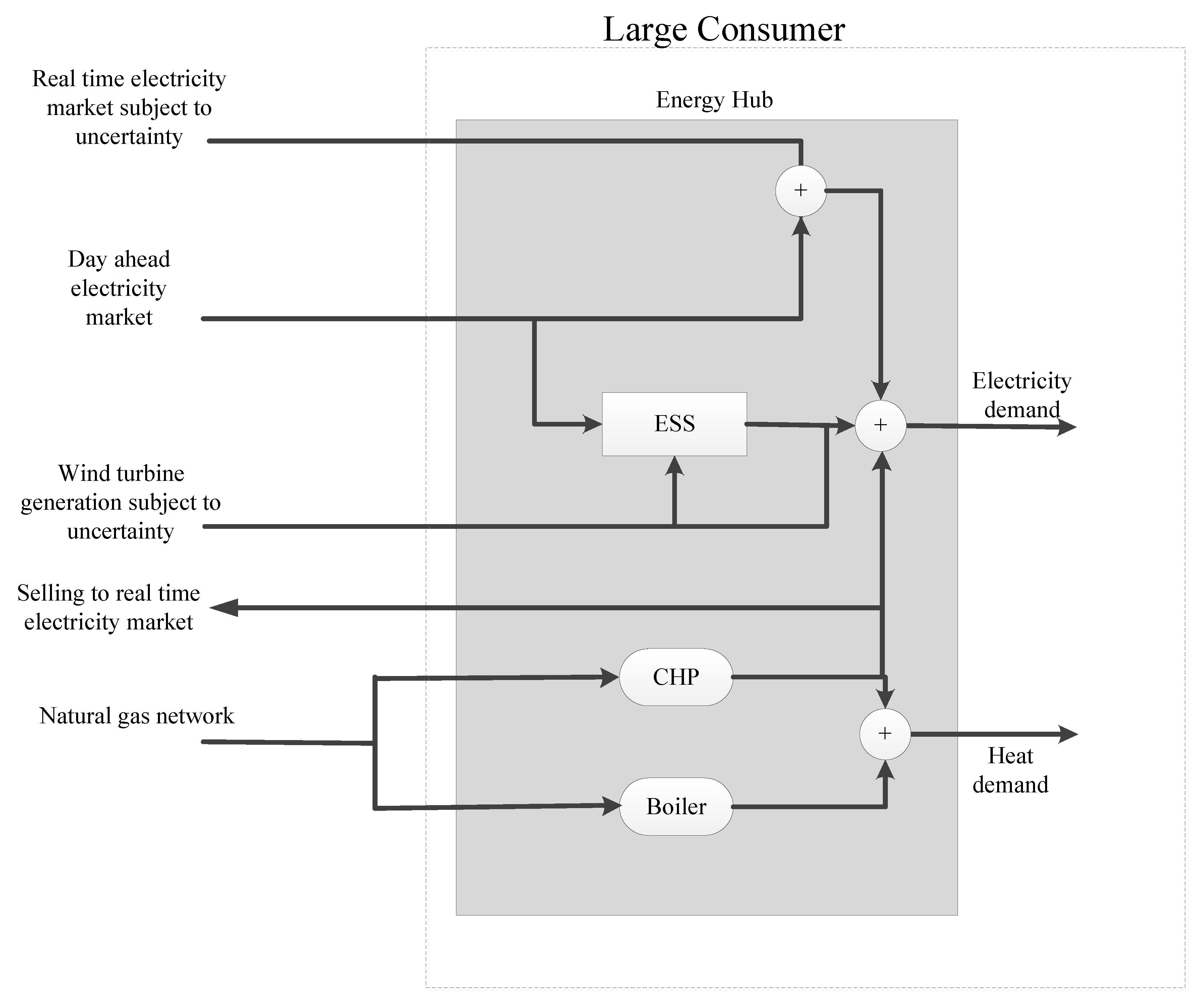
2. Robust Model of an Energy Hub
3. Problem Modeling
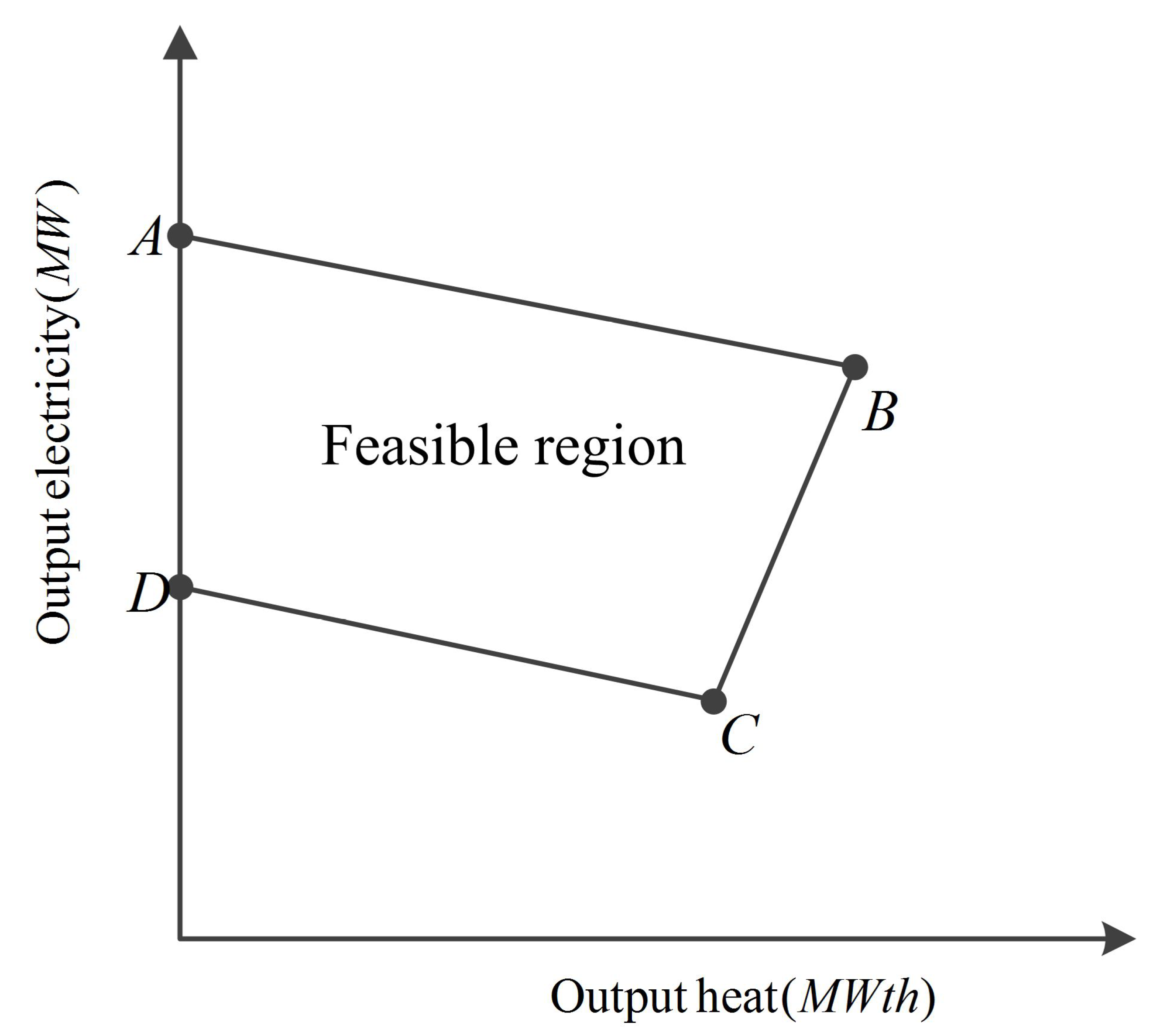
3.1. CHP and Boiler Models
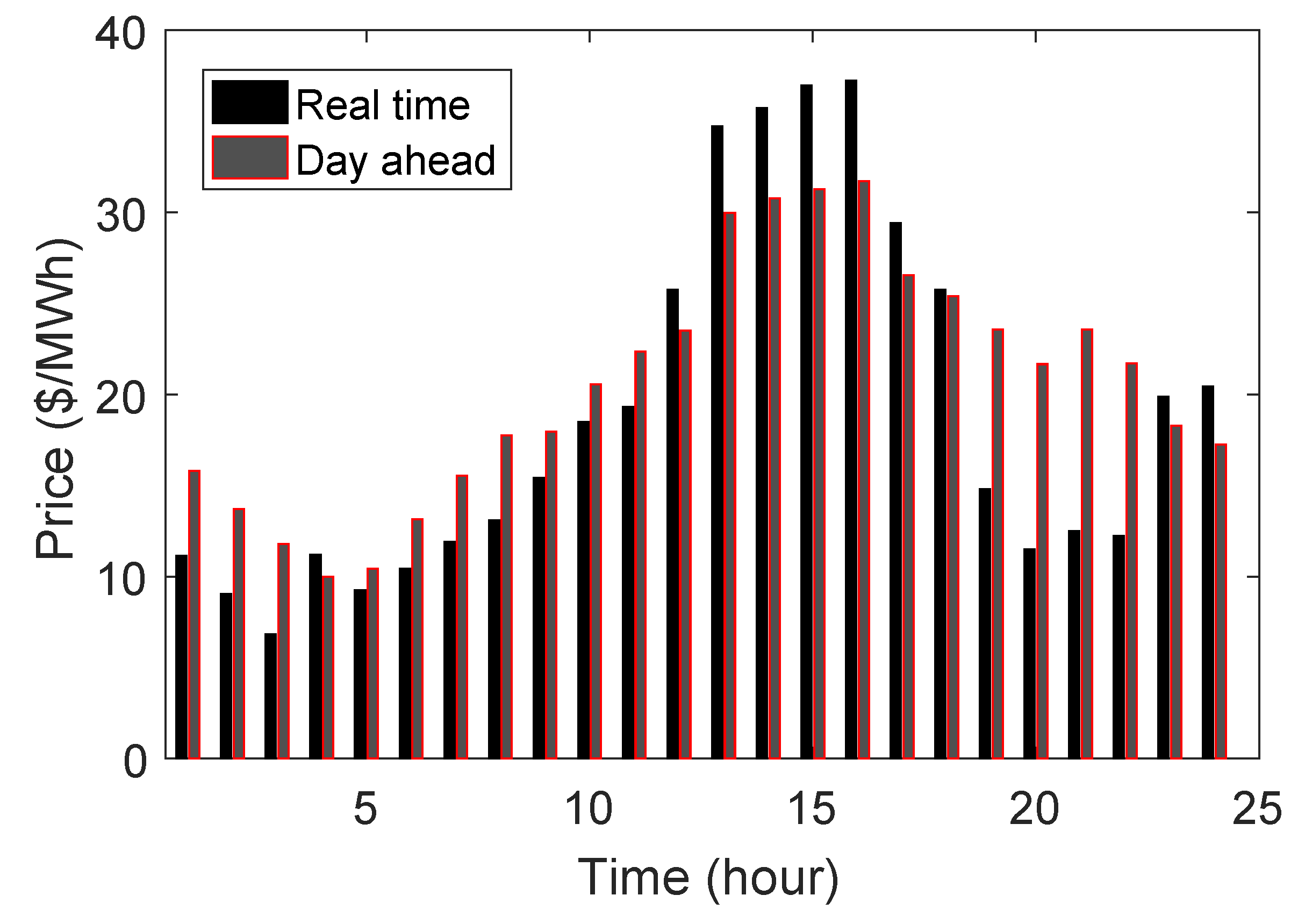
3.2. RT and DA Electricity Price Models
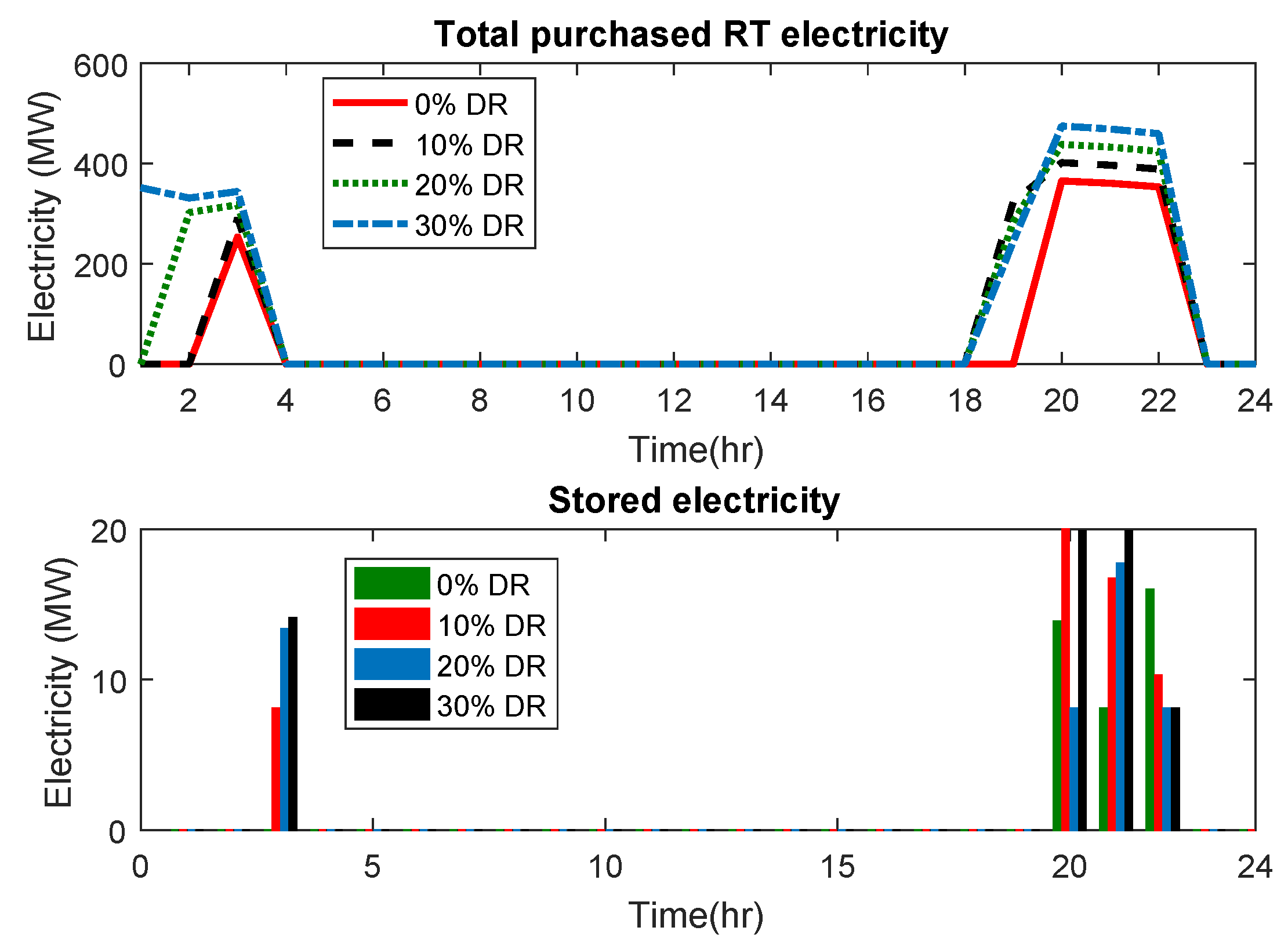
3.3. Energy Storage Modeling
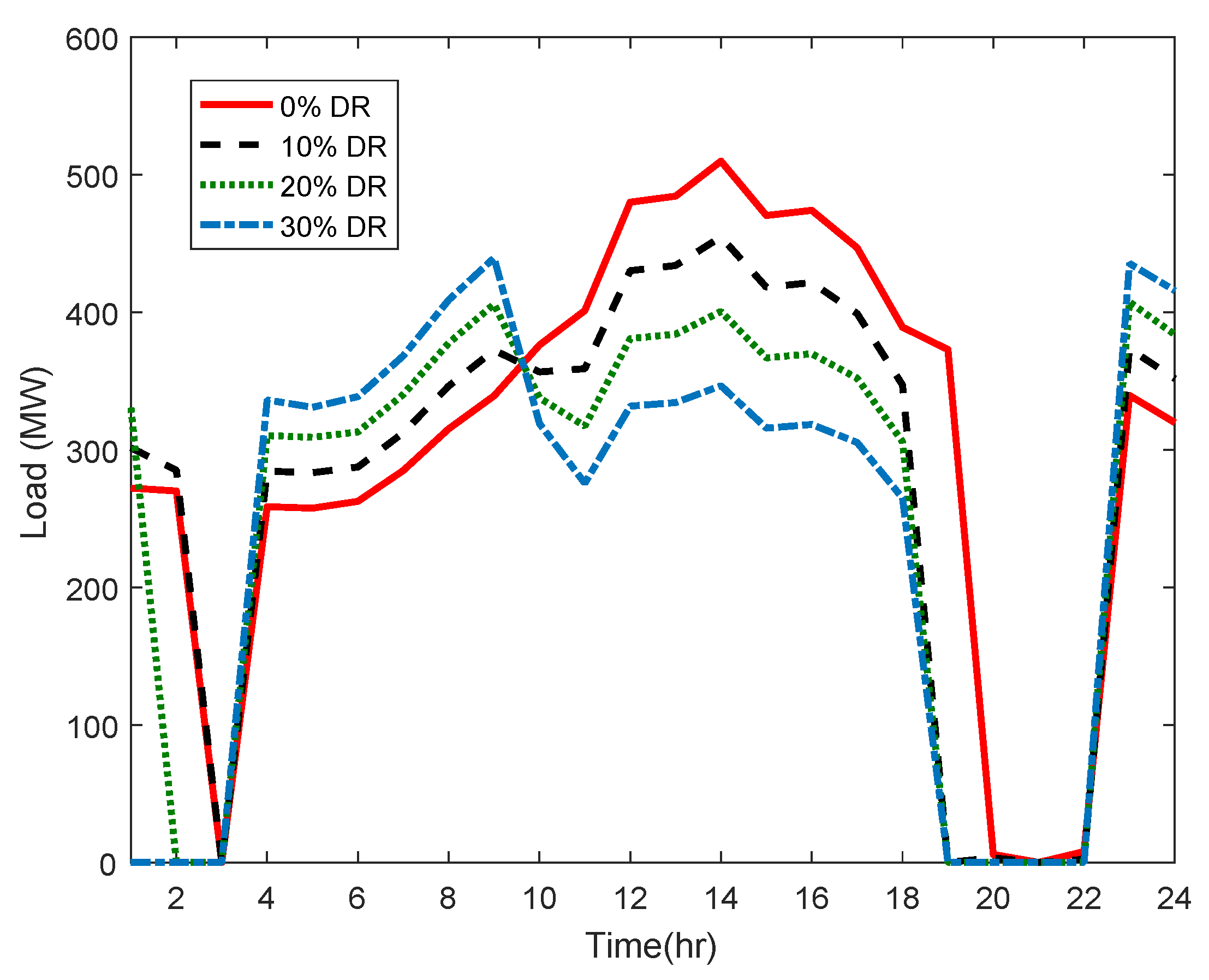
3.4. Wind Energy Modeling
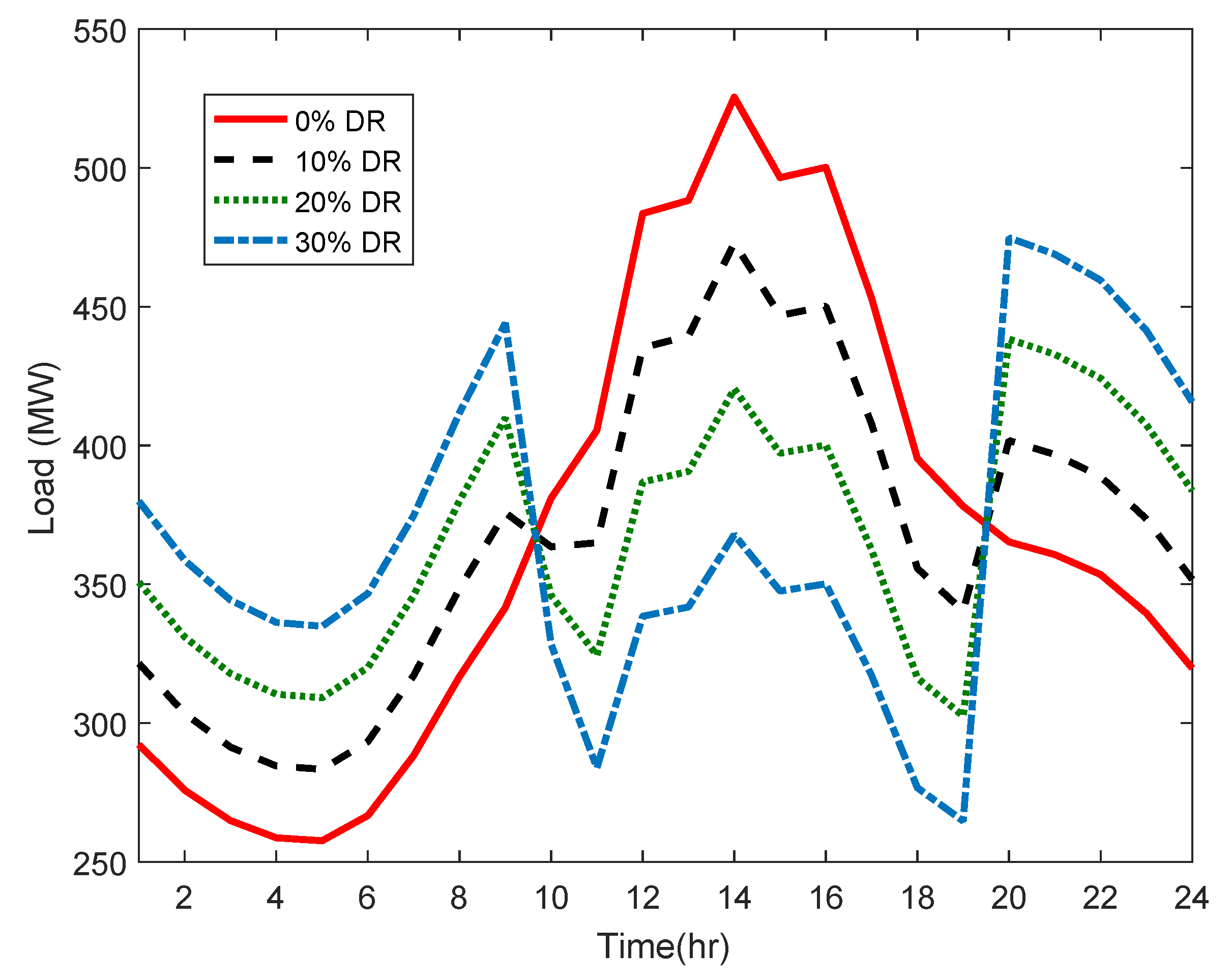
3.5. Demand Response Model
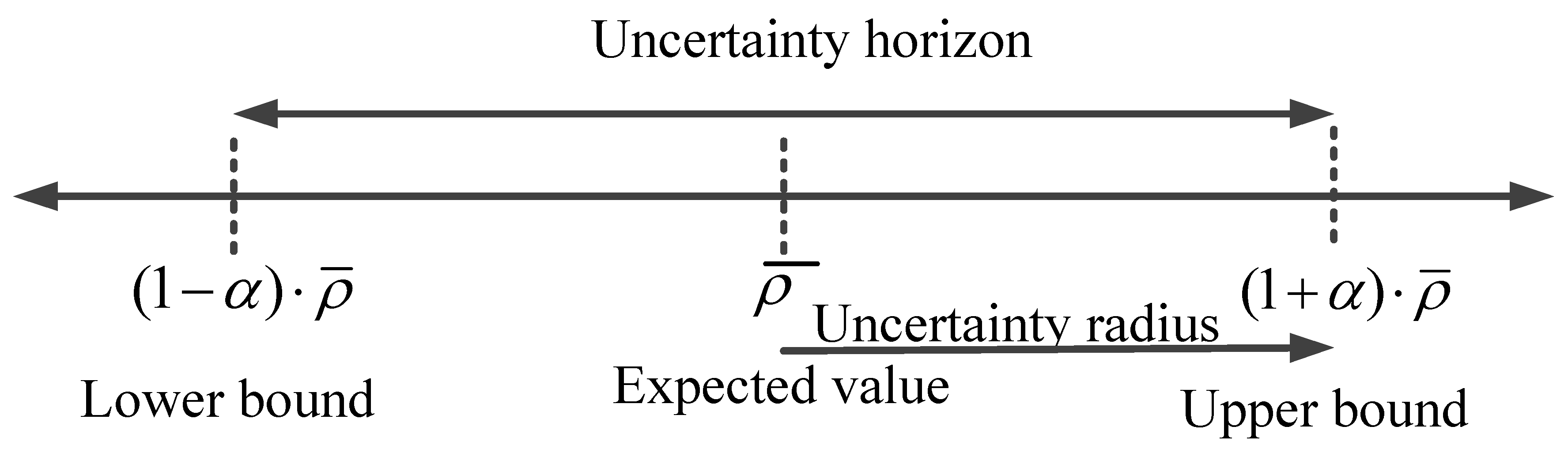
4. Information Gap Decision Theory
5. Problem Formulation
5.1. Energy Hub Management Formulation without Uncertainty
5.2. Robust Energy Hub Management Formulation
6. Numerical Results
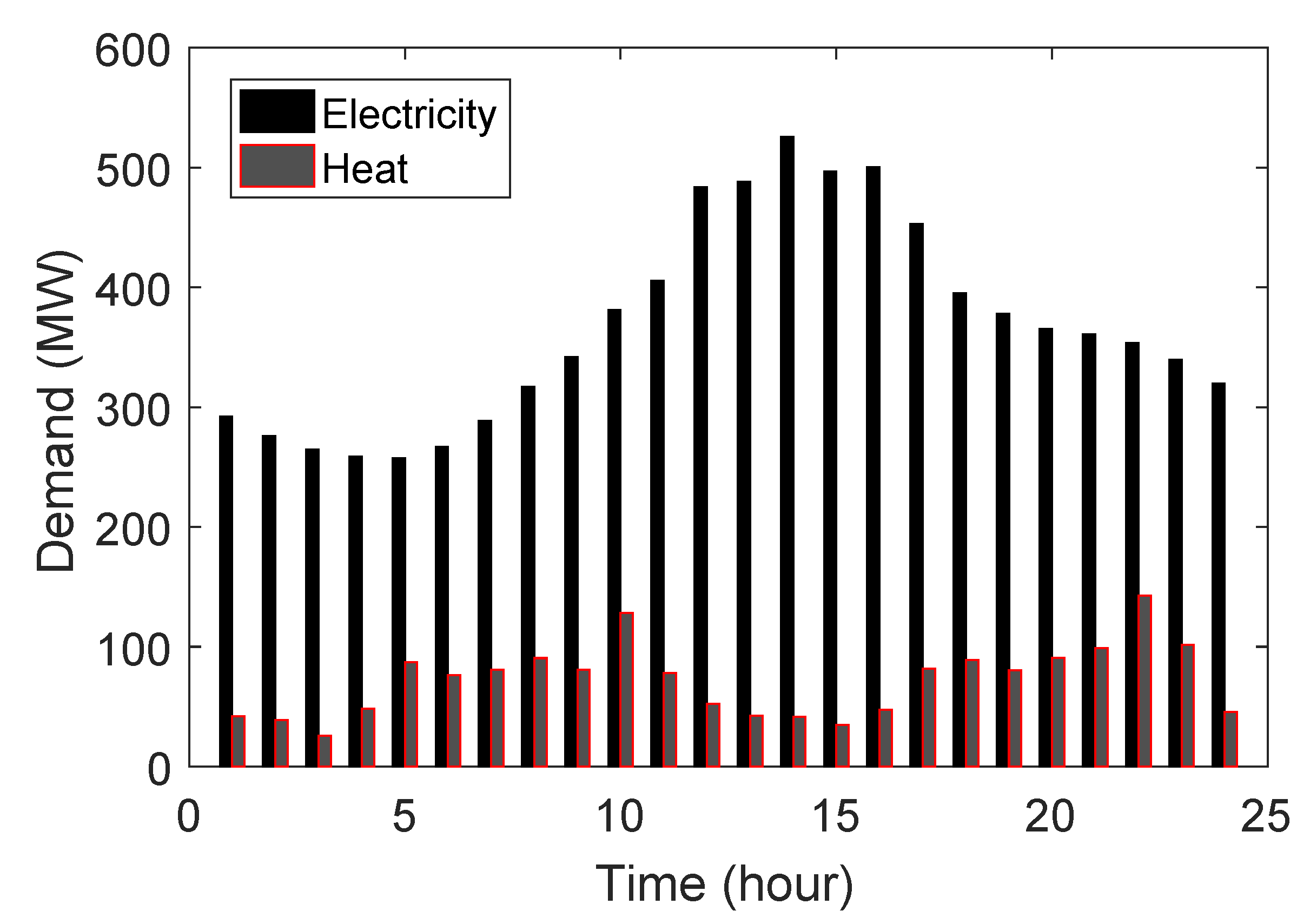
6.1. Case Study
6.2. Simulations and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| t | Time index |
| i | CHP index |
| j | Boiler index |
| Total cost of purchasing from the RT/DA markets ($) | |
| Energy purchased from the RT/DA markets (MWh) | |
| State of charge (SOC) (MWh) | |
| Discharging/charging power of the energy storage system (ESS) (MW) | |
| Electric/heat power produced by the combined heat and power (CHP) (MW) | |
| Electric power sold to the market by the combined heat and power (CHP) (MW) | |
| Electric power transferred to the load directly by the combined heat and power (CHP) (MW) | |
| Total cost of the CHP ($) | |
| Heat power produced by the boiler (MWth) | |
| Total cost of the boiler ($) | |
| Equivalent power of gas entering the CHP/ boiler (MW) | |
| Electric power demand after the DR program | |
| Deployed DR | |
| Shifted load in the DR program | |
| Increasing electricity demand in the DR program | |
| Uncertainty radius | |
| Uncertain parameter of the IGDT problem | |
| Cost obtained with deterministic parameters | |
| Forecasted electric power produced by a wind turbine (MW) | |
| Power purchased from the RT market to supply the load directly | |
| Electric power generated by the wind turbine to supply the load directly | |
| Power purchased from the RT market for charging the ESS | |
| Electric power generated by the wind turbine for charging the ESS | |
| Binary variable associated with the ON/OFF state of the CHP | |
| Binary variable associated with the ON/OFF state of charging/discharging | |
| Binary variable associated with decreasing electricity demand in the DR program | |
| Binary variable associated with increasing electricity demand in the DR program | |
| Parameters | |
| Maximum generation of the boiler | |
| Charging/discharging efficiency | |
| Maximum/minimum capacity of the ESS | |
| Maximum discharge of the ESS | |
| DA electricity market price ($/MWh) | |
| Expected RT market price ($/MWh) | |
| Maximum amount of increase in load in the DR program | |
| Maximum amount of reduced demand in the DR program | |
| Wind speed (m/s) | |
| Nominal wind speed (m/s) | |
| Cut-in/cut out wind speed (m/s) | |
| Nominal power of a wind turbine (MW) | |
| Base electricity demand | |
| Heat demand | |
| Risk parameter | |
| Critical value of the objective function | |
| Expected value of an uncertain parameter for IGDT modeling | |
| Gas price ($) | |
| Expected value of the power purchased from the RT market to supply the load directly | |
| Expected value of the electric power generated by a wind turbine to supply the load directly | |
| Expected value of the power purchased from the RT market for charging the ESS | |
| Expected value of the electric power generated by the wind turbine for charging the ESS | |
| Cost coefficients of the CHP | |
| T | Number of time periods |
| I | Number of CHP units |
| J | Number of boiler units |
References
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Ren, H.; Gao, W. A MILP model for integrated plan and evaluation of distributed energy systems. Appl. Energy 2010, 87, 1001–1014. [Google Scholar] [CrossRef]
- Kim, J.S.; Edgar, T.F. Optimal scheduling of combined heat and power plants using mixed-integer nonlinear programming. Energy 2014, 77, 675–690. [Google Scholar] [CrossRef]
- Wang, H.; Yin, W.; Abdollahi, E.; Lahdelma, R.; Jiao, W. Modelling and optimization of CHP based district heating system with renewable energy production and energy storage. Appl. Energy 2015, 159, 401–421. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R.; Niknam, T. A modified teaching learning based optimization for multi objective optimal power flow problem. Energy Convers. Manag. 2014, 77, 597–607. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Multi-objective operation management of a multi-carrier energy system. Energy 2015, 88, 430–442. [Google Scholar] [CrossRef]
- Adamek, F.; Arnold, M.; Andersson, G. On Decisive Storage Parameters for Minimizing Energy Supply Costs in Multicarrier Energy Systems. IEEE Trans. Sustain. Energy 2014, 5, 102–109. [Google Scholar] [CrossRef]
- Najafi, A.; Falaghi, H.; Contreras, J.; Ramezani, M. A Stochastic Bilevel Model for the Energy Hub Manager Problem. IEEE Trans. Smart Grid 2017, 8, 2394–2404. [Google Scholar] [CrossRef]
- Shahmohammadi, A.; Moradi-Dalvand, M.; Ghasemi, H.; Ghazizadeh, M.S. Optimal design of multicarrier energy systems considering reliability constraints. IEEE Trans. Power Deliv. 2015, 30, 878–886. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Mohammadi-Ivatloo, B.; Abapour, M.; Tohidi, S. Optimal Stochastic Design of Wind Integrated Energy Hub. IEEE Trans. Ind. Inform. 2017, 13, 2379–2388. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Farzin, H.; Fotuhi-Firuzabad, M.; Amrollahi, R. Generalized Analytical Approach to Assess Reliability of Renewable-Based Energy Hubs. IEEE Trans. Power Syst. 2017, 32, 368–377. [Google Scholar] [CrossRef]
- Hemmati, S.; Ghaderi, S.; Ghazizadeh, M. Sustainable energy hub design under uncertainty using Benders decomposition method. Energy 2018, 143, 1029–1047. [Google Scholar] [CrossRef]
- Zhang, N.; Yan, Y.; Xu, S.; Su, W. Game-theory-based electricity market clearing mechanisms for an open and transactive distribution grid. In Proceedings of the 2015 IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Rastegar, M.; Fotuhi-Firuzabad, M. Load management in a residential energy hub with renewable distributed energy resources. Energy Build. 2015, 107, 234–242. [Google Scholar] [CrossRef]
- Sheikhi, A.; Bahrami, S.; Ranjbar, A.M. An autonomous demand response program for electricity and natural gas networks in smart energy hubs. Energy 2015, 89, 490–499. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Zareipour, H.; Moeini-Aghtaieh, M. A Probabilistic Energy Management Scheme for Renewable-Based Residential Energy Hubs. IEEE Trans. Smart Grid 2017, 8, 2217–2227. [Google Scholar] [CrossRef]
- Roustai, M.; Rayati, M.; Sheikhi, A.; Ranjbar, A. A scenario-based optimization of Smart Energy Hub operation in a stochastic environment using conditional-value-at-risk. Sustain. Cities Soc. 2018, 39, 309–316. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Yazdankhah, A.S.; Mohammadi-Ivatloo, B.; Marzband, M.; Shafie-khah, M.; Ao, J.P.C. Stochastic network-constrained co-optimization of energy and reserve products in renewable energy integrated power and gas networks with energy storage systems. J. Clean. Prod. 2019, 223, 747–758. [Google Scholar] [CrossRef]
- Ashouri, A.; Fux, S.S.; Benz, M.J.; Guzzella, L. Optimal design and operation of building services using mixed-integer linear programming techniques. Energy 2013, 59, 365–376. [Google Scholar] [CrossRef]
- Brahman, F.; Honarmand, M.; Jadid, S. Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 2015, 90, 65–75. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Sichilalu, S.; Zhang, J. Residential load management in an energy hub with heat pump water heater. Appl. Energy 2017, 208, 551–560. [Google Scholar] [CrossRef]
- Barmayoon, M.H.; Fotuhi-Firuzabad, M.; Rajabi-Ghahnavieh, A.; Moeini-Aghtaie, M. Energy storage in renewable-based residential energy hubs. IET Gener. Transm. Distrib. 2016, 10, 3127–3134. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Roldán-Porta, C.; Álvarez-Bel, C. An optimisation algorithm for distributed energy resources management in micro-scale energy hubs. Energy 2017, 132, 126–135. [Google Scholar] [CrossRef]
- Davatgaran, V.; Saniei, M.; Mortazavi, S.S. Optimal bidding strategy for an energy hub in energy market. Energy 2018, 148, 482–493. [Google Scholar] [CrossRef]
- Ghasemi, G.; Noorollahi, Y.; Alavi, H.; Marzband, M.; Shahbazi, M. Theoretical and technical potential evaluation of solar power generation in Iran. Renew. Energy 2019, 138, 1250–1261. [Google Scholar] [CrossRef]
- Ghaffarpour, R.; Mozafari, B.; Ranjbar, A.M.; Torabi, T. Resilience oriented water and energy hub scheduling considering maintenance constraint market. Energy 2018, 158, 1092–1104. [Google Scholar] [CrossRef]
- Fan, S.; Li, Z.; Wang, J.; Piao, L.; Ai, Q. Cooperative Economic Scheduling for Multiple Energy Hubs: A Bargaining Game Theoretic Perspective. IEEE Access 2018, 6, 27777–27789. [Google Scholar] [CrossRef]
- Vahid-Pakdel, M.; Nojavan, S.; Mohammadi-ivatloo, B.; Zare, K. Stochastic optimization of energy hub operation with consideration of thermal energy market and demand response. Energy Convers. Manag. 2017, 145, 117–128. [Google Scholar] [CrossRef]
- Shafiee, S.; Zareipour, H.; Knight, A.M.; Amjady, N.; Mohammadi-Ivatloo, B. Risk-Constrained Bidding and Offering Strategy for a Merchant Compressed Air Energy Storage Plant. IEEE Trans. Power Syst. 2017, 32, 946–957. [Google Scholar] [CrossRef]
- Javadi, M.; Marzband, M.; Akorede, M.F.; Godina, R.; Al-Sumaiti, A.S.; Pouresmaeil, E. A centralized smart decision-making hierarchical interactive architecture for multiple home microgrids in retail electricity market. Energies 2018, 11, 3144. [Google Scholar] [CrossRef]
- Rodrigues, E.M.G.; Godina, R.; Marzband, M.; Pouresmaeil, E. Simulation and Comparison of Mathematical Models of PV Cells with Growing Levels of Complexity. Energies 2018, 11, 2902. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Akorede, M.F.; Elliott, I.D.; Godina, R.; Matias, J.; Pouresmaeil, E. Long-term decision on wind investment with considering different load ranges of power plant for sustainable electricity energy market. Sustainability 2018, 10, 3811. [Google Scholar] [CrossRef]
- Valinejad, J.; Barforoshi, T.; Marzband, M.; Pouresmaeil, E.; Godina, R.; Catalao, J.P.S. Investment Incentives in Competitive Electricity Markets. Appl. Sci. 2018, 8, 1978. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Rezaei, N.; Ahmadi, A.; Khazali, A.; Aghaei, J. Multi-objective Risk-Constrained Optimal Bidding Strategy of Smart Microgrids: An IGDT-based Normal Boundary Intersection Approach. IEEE Trans. Ind. Inform. 2019, 15, 1532–1543. [Google Scholar] [CrossRef]
- Kazemi, M.; Mohammadi-Ivatloo, B.; Ehsan, M. Risk-based bidding of large electric utilities using Information Gap Decision Theory considering demand response. Electr. Power Syst. Res. 2014, 114, 86–92. [Google Scholar] [CrossRef]
- Moradi-Dalvand, M.; Mohammadi-Ivatloo, B.; Amjady, N.; Zareipour, H.; Mazhab-Jafari, A. Self-scheduling of a wind producer based on Information Gap Decision Theory. Energy 2015, 81, 588–600. [Google Scholar] [CrossRef]
- Marzband, M.; Fouladfar, M.H.; Akorede, M.F.; Lightbody, G.; Pouresmaeil, E. Framework for smart transactive energy in home-microgrids considering coalition formation and demand side management. Sustain. Cities Soc. 2018, 40, 332–340. [Google Scholar] [CrossRef]
- Taherkhani, M.; Hosseini, S.H. IGDT-based multi-stage transmisison expansion planning model incorporating optimal wind farm integration. Electr. Power Syst. Res. 2014, 25, 2340–2358. [Google Scholar]
- Marzband, M.; Javadi, M.; Pourmousavi, S.A.; Lightbody, G. An advanced retail electricity market for active distribution systems and home microgrid interoperability based on game theory. Electr. Power Syst. Res. 2018, 157, 187–199. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Akorede, M.F.; Barforoshi, T.; Jovanović, M. Generation expansion planning in electricity market considering uncertainty in load demand and presence of strategic GENCOs. Electr. Power Syst. Res. 2017, 152, 92–104. [Google Scholar] [CrossRef]
- Marzband, M.; Ghazimirsaeid, S.S.; Uppal, H.; Fernando, T. A real-time evaluation of energy management systems for smart hybrid home Microgrids. Electr. Power Syst. Res. 2017, 143, 624–633. [Google Scholar] [CrossRef]
- Nikoobakht, A.; Aghaei, J. IGDT-based robust optimal utilization of wind power generation using coordinated flexibility resources. Electr. Power Syst. Res. 2017, 11, 264–277. [Google Scholar]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Rezaei, N.; Ahmadi, A.; Khazali, A.H.; Guerrero, J.M. Energy and Frequency Hierarchical Management System Using Information Gap Decision Theory for Islanded Microgrids. IEEE Trans. Ind. Electron. 2018, 65, 7921–7932. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Sepehr, A.; Pournazarian, B.; Marzband, M.; Catalao, J.P.S. Control technique for the operation of grid-tied converters with high penetration of renewable energy resources. Electr. Power Syst. Res. 2019, 166, 18–28. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Risk-Constrained Strategic Bidding of GenCos Considering Demand Response. IEEE Trans. Power Syst. 2015, 30, 376–384. [Google Scholar]
- Tavakoli, M.; Shokridehaki, F.; Marzband, M.; Godina, R.; Pouresmaeil, E. A two stage hierarchical control approach for the optimal energy management in commercial building microgrids based on local wind power and PEVs. Sustain. Cities Soc. 2018, 41, 332–340. [Google Scholar] [CrossRef]
- Soroudi, A.; Keane, A. Risk Averse Energy Hub Management Considering Plug-in Electric Vehicles Using Information Gap Decision Theory. In Plug In Electric Vehicles in Smart Grids; Springer: Singapore, 2016; pp. 107–127. [Google Scholar]
- Najafi, A.; Falaghi, H.; Contreras, J.; Ramezani, M. Medium-term energy hub management subject to electricity price and wind uncertainty. Appl. Energy 2016, 168, 418–433. [Google Scholar] [CrossRef]
- Shotorbani, A.M.; Mohammadi-Ivatloo, B.; Wang, L.; Marzband, M.; Sabahi, M. Application of finite-time control Lyapunov function in low-power PMSG wind energy conversion systems for sensorless MPPT. Int. J. Electr. Power Energy Syst. 2019, 106, 169–182. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rengaraj, R.; Salivahanan, S. Enhancement of combined heat and power economic dispatch using self adaptive real-coded genetic algorithm. Appl. Energy 2009, 86, 915–921. [Google Scholar] [CrossRef]
- Alipour, M.; Mohammadi-Ivatloo, B.; Zare, K. Stochastic risk-constrained short-term scheduling of industrial cogeneration systems in the presence of demand response programs. Appl. Energy 2014, 136, 393–404. [Google Scholar] [CrossRef]
- Karki, R.; Billinton, R. Cost-effective wind energy utilization for reliable power supply. IEEE Trans. Energy Convers. 2004, 19, 435–440. [Google Scholar] [CrossRef]
- Giorsetto, P.; Utsurogi, K.F. Development of a New Procedure for Reliability Modeling of Wind Turbine Generators. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 134–143. [Google Scholar] [CrossRef]
- Nojavan, S.; Ghesmati, H.; Zare, K. Robust optimal offering strategy of large consumer using IGDT considering demand response programs. Electr. Power Syst. Res. 2016, 130, 46–58. [Google Scholar] [CrossRef]
- Mehdizadeh, A.; Taghizadegan, N.; Salehi, J. Risk-based energy management of renewable-based microgrid using information gap decision theory in the presence of peak load management. Appl. Energy 2018, 211, 617–630. [Google Scholar] [CrossRef]
- Zare, K.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. Risk-Based Electricity Procurement for Large Consumers. IEEE Trans. Power Syst. 2011, 26, 1826–1835. [Google Scholar] [CrossRef]
- Zare, K.; Moghaddam, M.P.; Eslami, M.K.S.E. Electricity procurement for large consumers based on Information Gap Decision Theory. Energy Policy 2010, 38, 234–242. [Google Scholar] [CrossRef]
- NY ISO. Available online: http://www.nyiso.com (accessed on 31 July 2012).
- Homer Energy. Available online: http://www.homerenergy.com (accessed on 31 July 2012).
- North Dakota Agriculture Weather Network. Available online: http://ndawn.ndsu.nodak.edu/wind-speeds.html (accessed on 31 July 2012).
- Vestas. Available online: http://www.vestas.com (accessed on 31 July 2012).
- GAMS Software. Available online: https://www.gams.com (accessed on 31 July 2012).
- Baringo, L.; Conejo, A.J. Risk-Constrained Multi-Stage Wind Power Investment. IEEE Trans. Power Syst. 2013, 28, 401–411. [Google Scholar] [CrossRef]
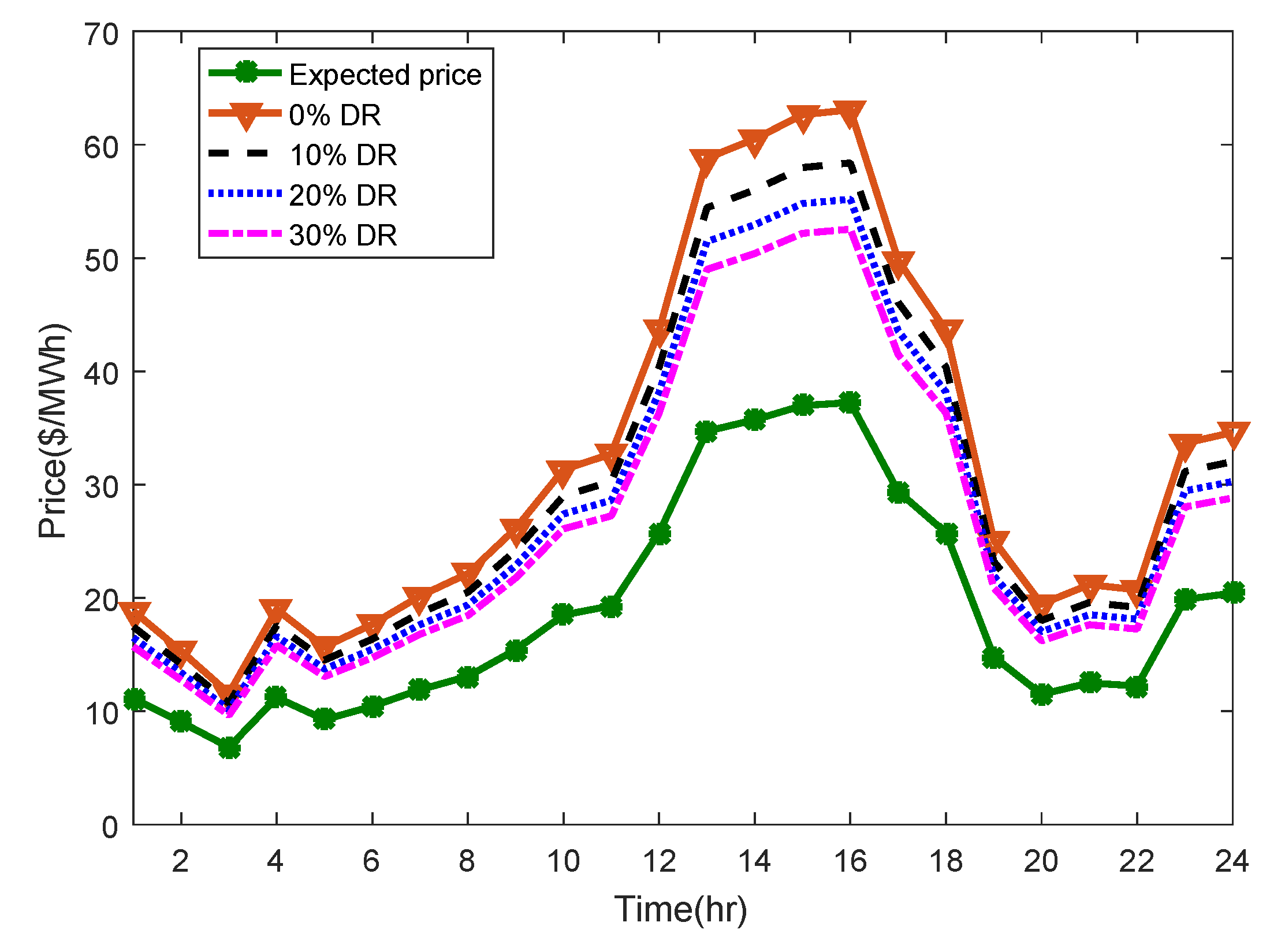
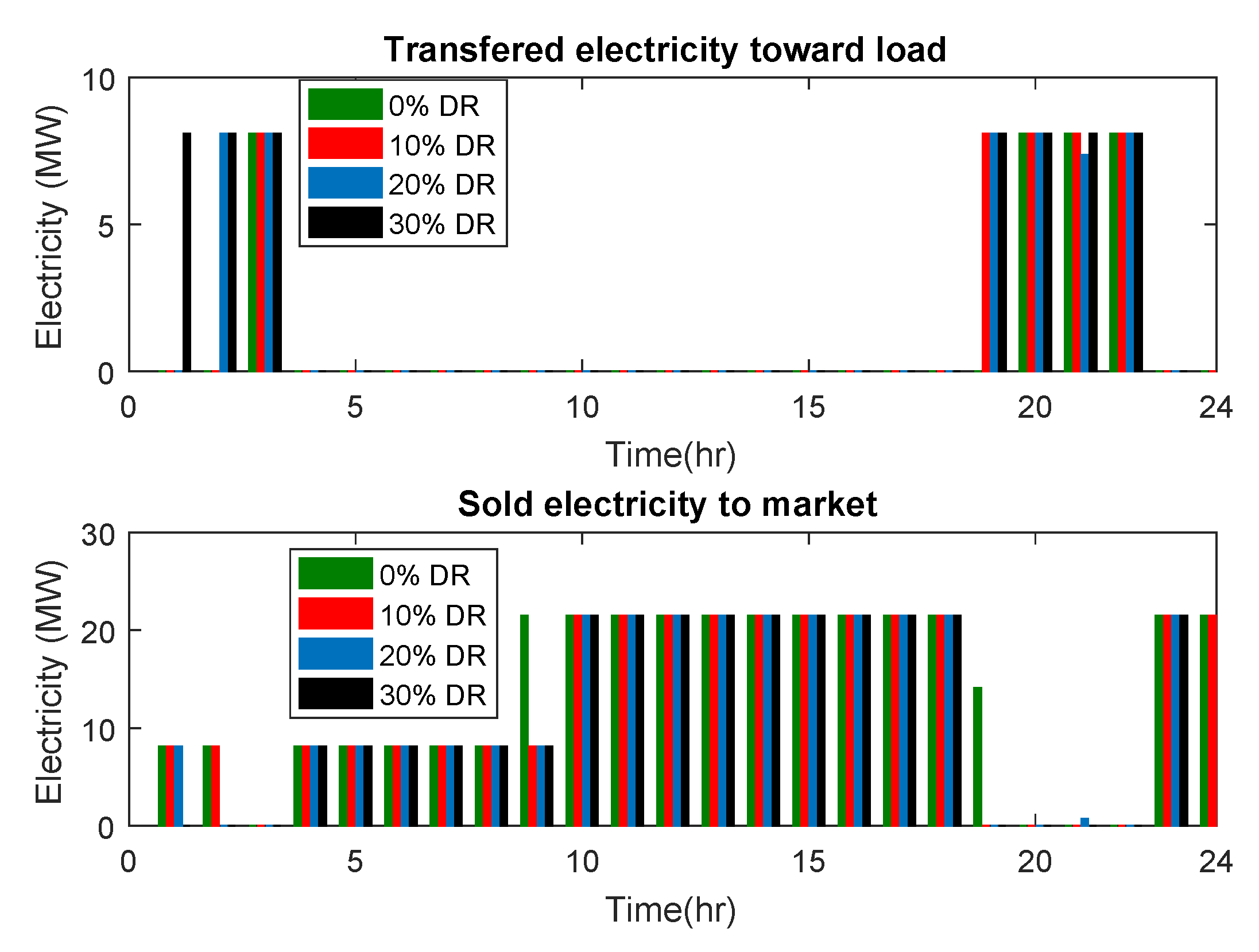
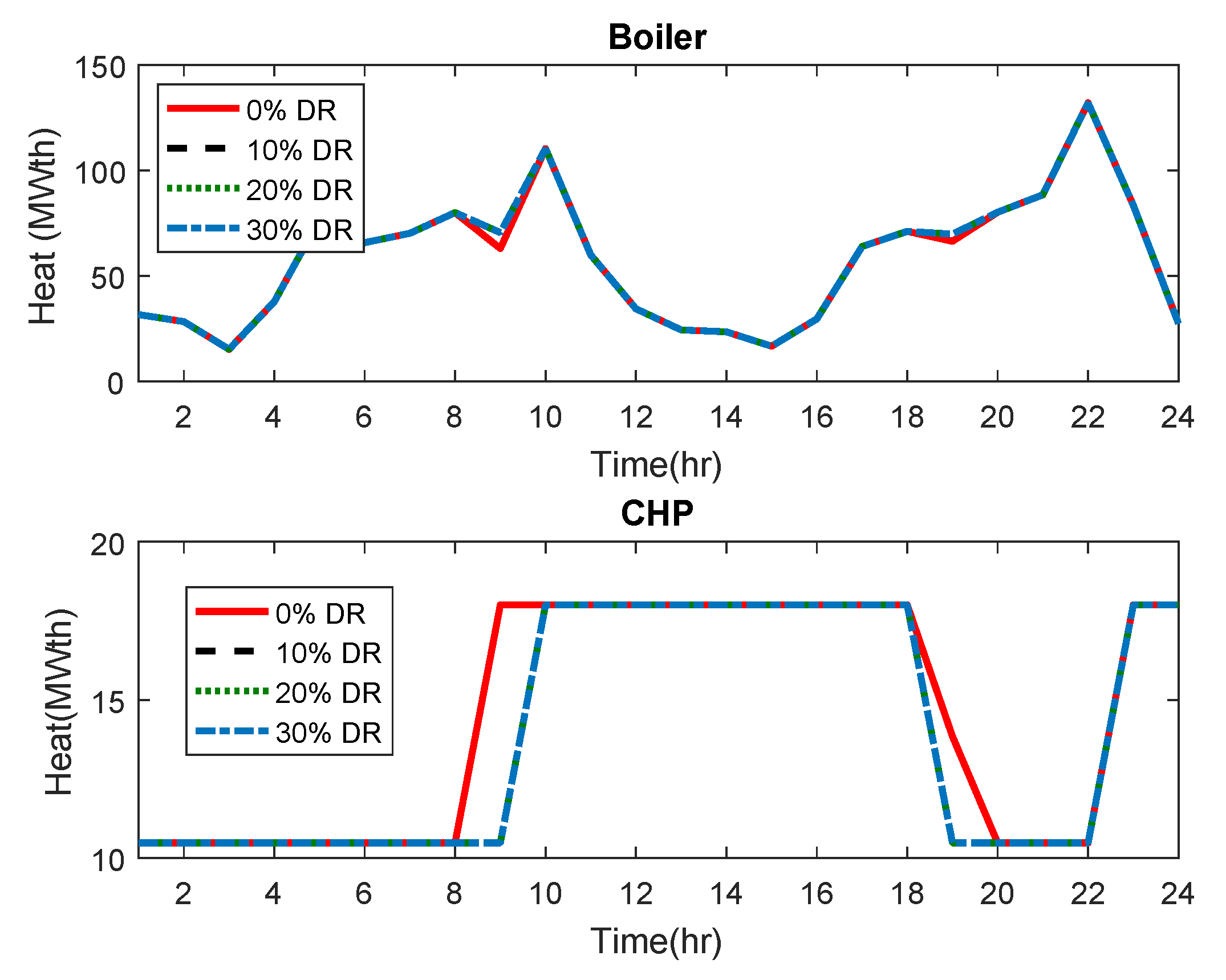
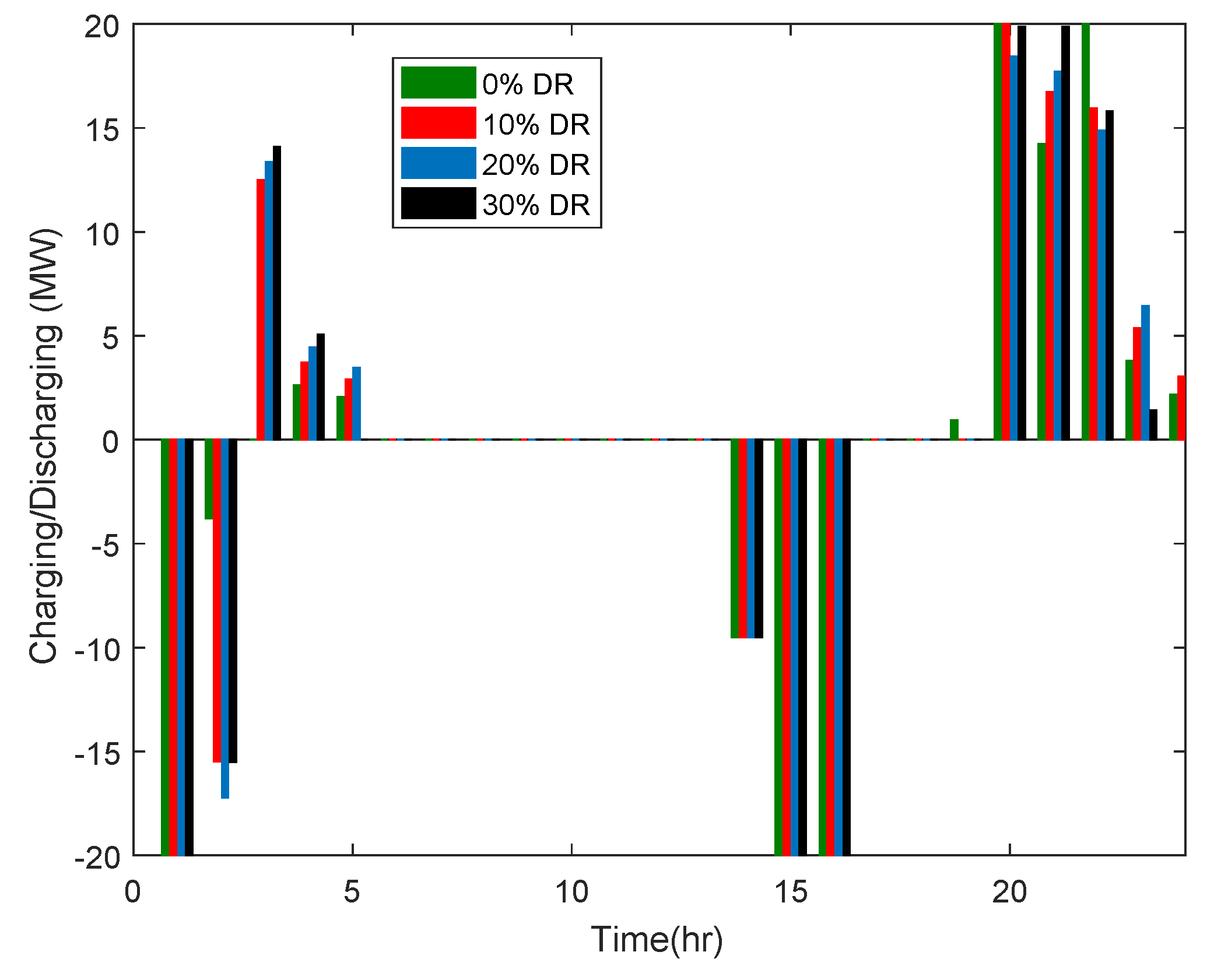
| Device (Coefficient) | Value |
|---|---|
| BSS maximum capacity | 55 MWh |
| Risk coefficient | 0.1 |
| Charging/discharging efficiencies | 0.9 |
| CHP FOR points | A(0, 24.7), B(18, 21.5), C(10.48, 8.1), and D(0, 9.88) |
| Wind power maximum output | 20 MW |
| Percent of DR (%) | 0 | 10 | 20 | 30 |
| 0.694 | 0.568 | 0.482 | 0.411 | |
| Expected cost ($) | 203,936 | 197,738 | 191,525 | 185,331 |
| Critical cost ($)() | 224,330 | 217,512 | 210,677 | 203,864 |
| Stochastic programming cost ($) | 201,342 | 194,737 | 188,132 | 181,528 |
| 0 % of DR | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | 0.12 | |
| 0.1 | 0.189 | 0.308 | 0.468 | 0.694 | 1 | ||
| 4348 | 3054 | 2535 | 1948 | 1333 | 1113 | ||
| 4073 | 5439 | 6002 | 6638 | 7338 | 7638 | ||
| 304 | 304 | 323 | 334 | 345 | 352 | ||
| 288 | 288 | 322 | 341 | 361 | 374 | ||
| 30 % of DR | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | 0.12 | |
| 0.081 | 0.14 | 0.214 | 0.3 | 0.448 | 0.559 | ||
| 5227 | 4670 | 4496 | 3510 | 2675 | 1995 | ||
| 3178 | 3769 | 3989 | 5016 | 5885 | 6628 | ||
| 304 | 304 | 306 | 322 | 333 | 334 | ||
| 288 | 288 | 292 | 320 | 342 | 342 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafi, A.; Marzband, M.; Mohamadi-Ivatloo, B.; Contreras, J.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Godina, R. Uncertainty-Based Models for Optimal Management of Energy Hubs Considering Demand Response. Energies 2019, 12, 1413. https://doi.org/10.3390/en12081413
Najafi A, Marzband M, Mohamadi-Ivatloo B, Contreras J, Pourakbari-Kasmaei M, Lehtonen M, Godina R. Uncertainty-Based Models for Optimal Management of Energy Hubs Considering Demand Response. Energies. 2019; 12(8):1413. https://doi.org/10.3390/en12081413
Chicago/Turabian StyleNajafi, Arsalan, Mousa Marzband, Behnam Mohamadi-Ivatloo, Javier Contreras, Mahdi Pourakbari-Kasmaei, Matti Lehtonen, and Radu Godina. 2019. "Uncertainty-Based Models for Optimal Management of Energy Hubs Considering Demand Response" Energies 12, no. 8: 1413. https://doi.org/10.3390/en12081413
APA StyleNajafi, A., Marzband, M., Mohamadi-Ivatloo, B., Contreras, J., Pourakbari-Kasmaei, M., Lehtonen, M., & Godina, R. (2019). Uncertainty-Based Models for Optimal Management of Energy Hubs Considering Demand Response. Energies, 12(8), 1413. https://doi.org/10.3390/en12081413











