1. Introduction
A recent projection predicted that primary energy consumption will rise by 48% in 2040 [
1]. The negative environmental impact of fossil resources has accelerated the shift toward renewable energy sources. In the development of renewable energy systems, energy storage has become an important part of renewable energy technology. Thermal energy storage (TES) is a technology that stocks thermal energy by heating or cooling so that the stored energy can be used for heating and cooling applications [
2] and power generations at later time. TES systems are used particularly in buildings and in industrial processes. Advantages of TES in energy systems include an increase in overall efficiency and better reliability. TES can also lead to better economics, reductions in investment and running costs, and less pollution of the environment, i.e., fewer carbon dioxide emissions [
3]. TES is becoming particularly important for electricity storage in combination with concentrating thermal power plants where heat can be stored for electricity production when operation is not economic. In Europe, it has been estimated that around 1.4 million GWh per year can be saved and 400 million tons of CO
2 emissions avoided, in buildings and in industrial sectors, by more extensive use of heat and cold storage [
4].
Storage density, in terms of the amount of energy per unit volume or mass, is important for optimizing the solar ratio (how much solar radiation is useful for the heating/cooling purposes), the efficiency of the appliances (solar thermal collectors and absorption chillers), and energy consumption for space heating/cooling consumption. Phase-change materials (PCMs) in solar systems are worth investigating. PCMs might be able to increase the energy density of small-sized water storage tanks, reducing solar storage volume for a given solar fraction or increasing the solar fraction for a given available volume [
5,
6]. Other studies [
7,
8] have been performed using advanced thermodynamic analysis for thermal storage. They found the optimal values of PCMs.
While heat storage on the hot side of thermal plants is always present because of heating and/or domestic hot water (DHW) production, cold storage is justified in larger plants. Cold storages are used not only for the economic advantages of lower electricity costs (in the case of electric compression chillers), depending on the time of day, but also to lower the installed cooling power and to allow more continuous operation of the chiller. The use of thermal storage could not provide effective backup but helped the system thermally stabilize. Since then, studying thermal energy storage technologies, as well as the usability and effects of both sensible and latent heat storage in numerous applications, has increased, leading to a number of reviews [
9]. These reviews focused only on one side (cold or hot), a component of the system or one of its integral mechanisms.
District heating and cooling (DHC) with thermal energy storage (TES) can enhance energy efficiency. DHC with TES can also help address global environmental problems. DHC systems are required to maintain comfortable thermal conditions for the occupants of commercial and office buildings. Traditional heating, ventilating, air-conditioning and cooling (HVAC) systems are high costs and contribute to peak demand [
10]. Thus, much research has been undertaken to reduce greenhouse gas (GHG) emissions using renewable energy and energy resources intelligently. DHC systems can use renewable energy and waste heat as a thermal energy source, and facilitate the intelligent integration of energy systems. The district heating system is a heating system that generates heat from large-scale heat source facilities such as cogeneration plants and supplies heat to nearby customers. Generally, the thermal energy storage system is equipped with a heat source system. TES systems can be generated with district heating (DH) equipment installed for the efficient operation of the heat source equipment for the district heating water (primary heating water). TES tanks in DHC systems, which store heating/cooling energy in the off-peak period for use in the peak period, can be used to offset peak time energy demand [
10,
11,
12].
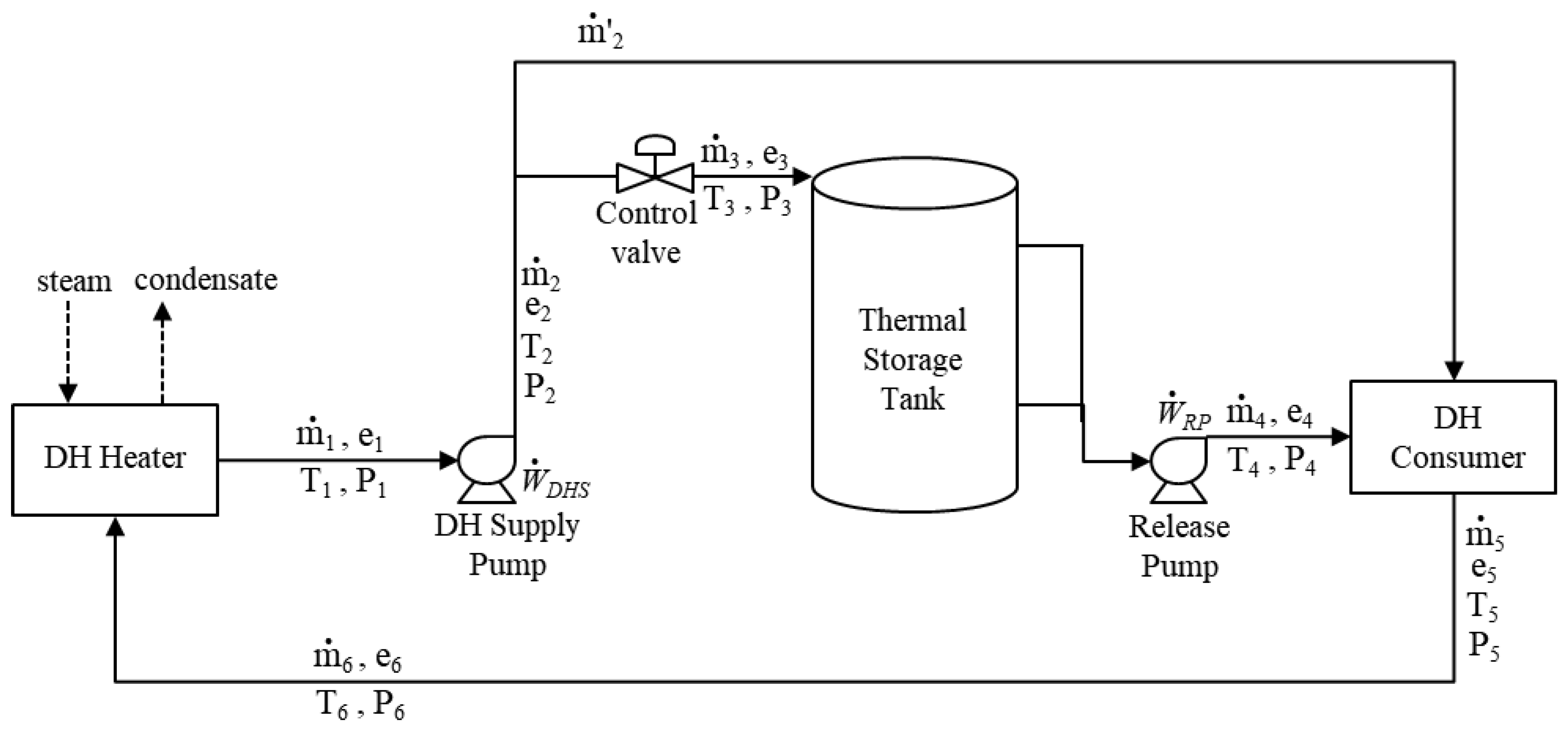
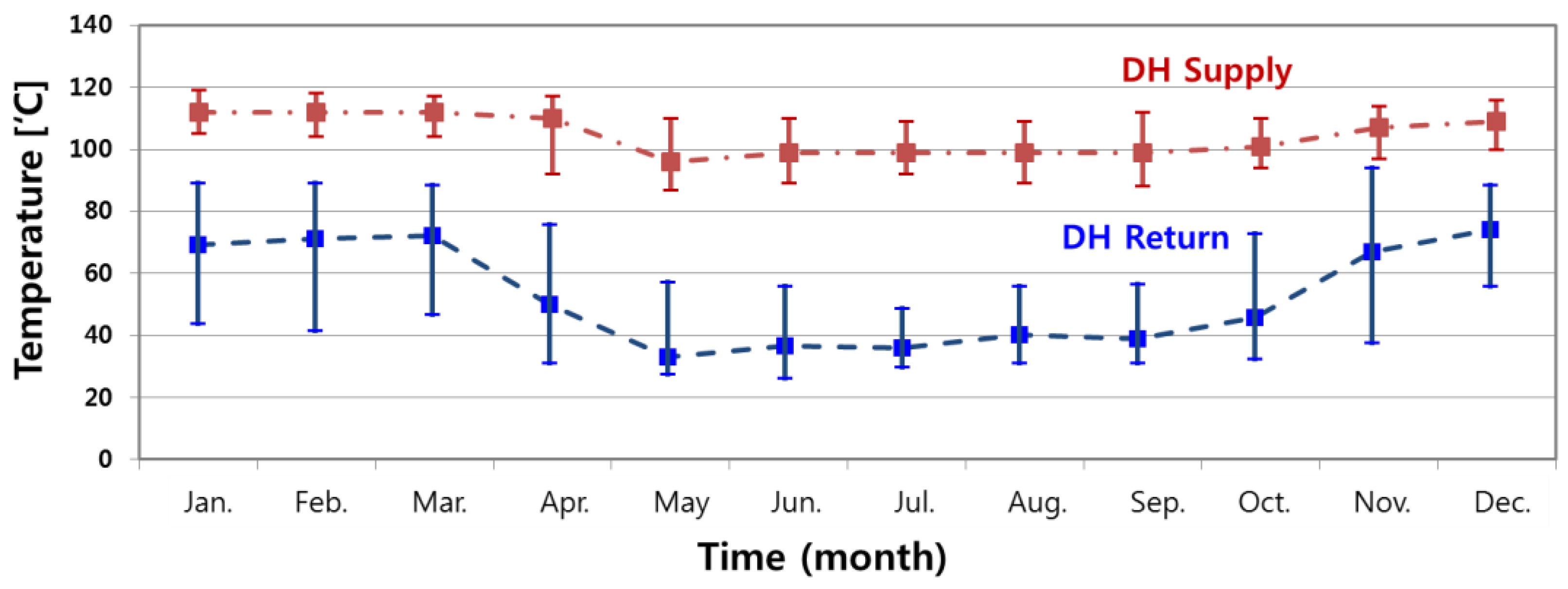
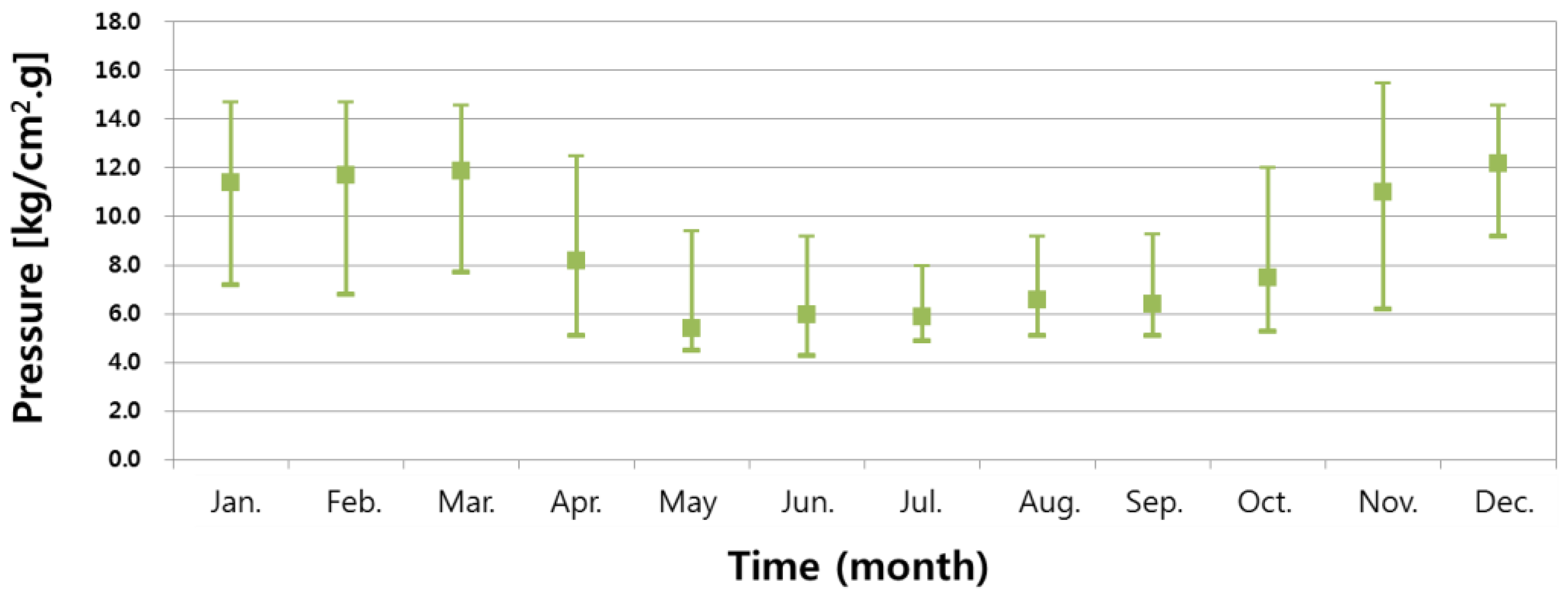
Since the heat storage system stores heat at atmospheric pressure, the primary heating water produced from the heat source equipment is stored at less than 100 °C (95~98 °C). If the temperature of the primary heating water is higher than the storage temperature, heat loss occurs. The stored DH water of 98 °C and 65 °C coexist in the TES tank. When the heat is stored, the 65 °C DH water in the tank is sent to heat the source equipment and then raise the temperature to the primary heating temperature. It is then stored in the TES system or supplied to the DH pipes. In addition, the primary heating water produced by the heat source equipment must maintain high pressure (more than 10 bar) to supply heat to long distance district heating customers. However, because the heat is stored at atmospheric pressure in the TES system, the pressure loss is generated in the heat-storage process. Therefore, there are two energy losses, heat loss and pressure loss, in the heat-storage process of a district heating system.
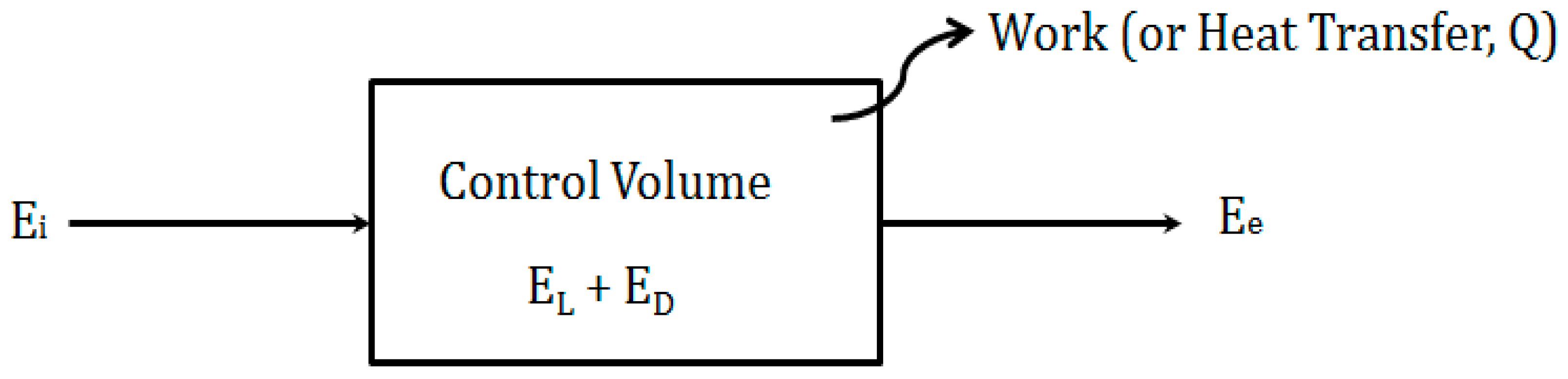
Exergy analysis deals with the quality of the energy based on the second law of thermodynamics. It is useful to identify the inefficiencies, their reasons, locations, and the amount of energy lost in the process of the energy system [
13]. As an analytical method for comparing and evaluating TES systems, the exergy analysis method can be a very reasonable and meaningful alternative to the energy analysis method. Exergy analysis provides efficiency, which means determining the actual value of how the performance of the system approaches the ideal values by determining the amount of thermodynamic loss, the cause and the location [
14]. Therefore, thermodynamic losses in the heat-storage process of the TES system are analyzable through exergy analysis. It is also possible to get substantial information and to obtain an optimum design for the improvement of the efficiency of the TES system.
A number of studies related to district heating systems have been undertaken. Rezaie et al. [
15,
16] analyzed the energy and exergy efficiency of the TES system in the district heating system. In the case of a district heating system including a solar panel, they explained that the TES system improves the effectiveness of the solar panel. Rosen and Dincer [
17] emphasized two important factors, the proper efficiency analysis method and the proper temperature in evaluation of heat storage systems, as results of the exergy analysis of closed TES systems. They have shown that the exergy analysis method can be usefully applied to the optimization of operation and the optimal design of the TES system.
Recently, many studies have been carried out to cope with climate change and to reduce greenhouse gas emissions. In the field of district heating, many researchers are trying to reduce greenhouse gas emissions via improvement of the efficiency, application of renewable energy and so on. Robins [
18] studied a variety of methods that could be practically applied to reduce GHG emissions. Rosen et al. [
19,
20,
21] proposed alternative energy sources that can replace fossil fuels. Dincer [
22] proposed environmentally friendly methods such as energy conservation, the application of renewable energy and clean energy technology.
Above all, the way to increase the utilization efficiency of energy sources is to use high-efficiency facilities or to recover lost or abandoned energy. Firstly, it is necessary to analyze the energy losses in temperature, pressure, electricity, or any other form, in a system, and then find ways to improve efficiency through energy recovery.
The previous studies have studied new TES system designs, new materials, and solar thermal storage systems. At present, however, many TES systems for storing hot water have been used at atmospheric pressure in industrial fields. This study investigated the energy loss that occurs in the process of storing heat in DH industries. A method for improving the efficiency of the TES system by utilizing the potential energy was studied. Using the exergy analysis method, the exergy values of the respective streams constituting the target system were calculated. The points where the exergy losses occurred and the amount of loss were also calculated in the TES system. In addition, the methods of reducing exergy losses in each process were proposed and additional generated energies were calculated.
3. Results and Discussion
3.1. Exergy Analysis of the Previous System
Table 5 and
Table 6 show the results of the exergy calculation and exergy balance for the TES system based on the operational data analysis.
As a result of the exergy analysis for each process of the TES system, in all processes, ①, ②, and ③, exergy loss was found. The largest exergy loss appeared in Process ②. Respectively, the losses in Processes ① and ③ occurred in the pumps, the DH supply pump and release pump. These processes lost power by boosting the pressure necessary for supplying the primary heating water from the TES system and the heat source plant to the DH customer. However, the boost was an essential process for supplying heat to all of the customers, especially the long distance customers. There was a pressure loss and depending on the distance and the gradient. Therefore, it was reasonable to regard the exergy losses in Processes ① and ③ as exergy consumption not exergy loss.
In Process ②, storing DH water, the primary heating water was stored without work. In this process exergy loss occurred due to pressure loss by the throttling of the control valve and heat loss by temperature drop. The amount of exergy loss was approximately 26.6% of the exergy inlet. Therefore, it was necessary to find proper ways to reduce the exergy loss in the TES system to reduce the overall exergy loss.
As explained in this section, thermal loss and pressure loss were the causes of exergy loss in Process ②. The two types of exergy loss were the most common types of loss in the thermal systems. However, there were many ways to recover the loss. In this study, an organic Rankine cycle to reduce heat loss and a hydraulic turbine to reduce pressure loss were applied. Exergy recovery was analyzed by the application of organic Rankine cycles and hydraulic turbines.
3.2. Reduction of Exergy Losses from Thermal Loss
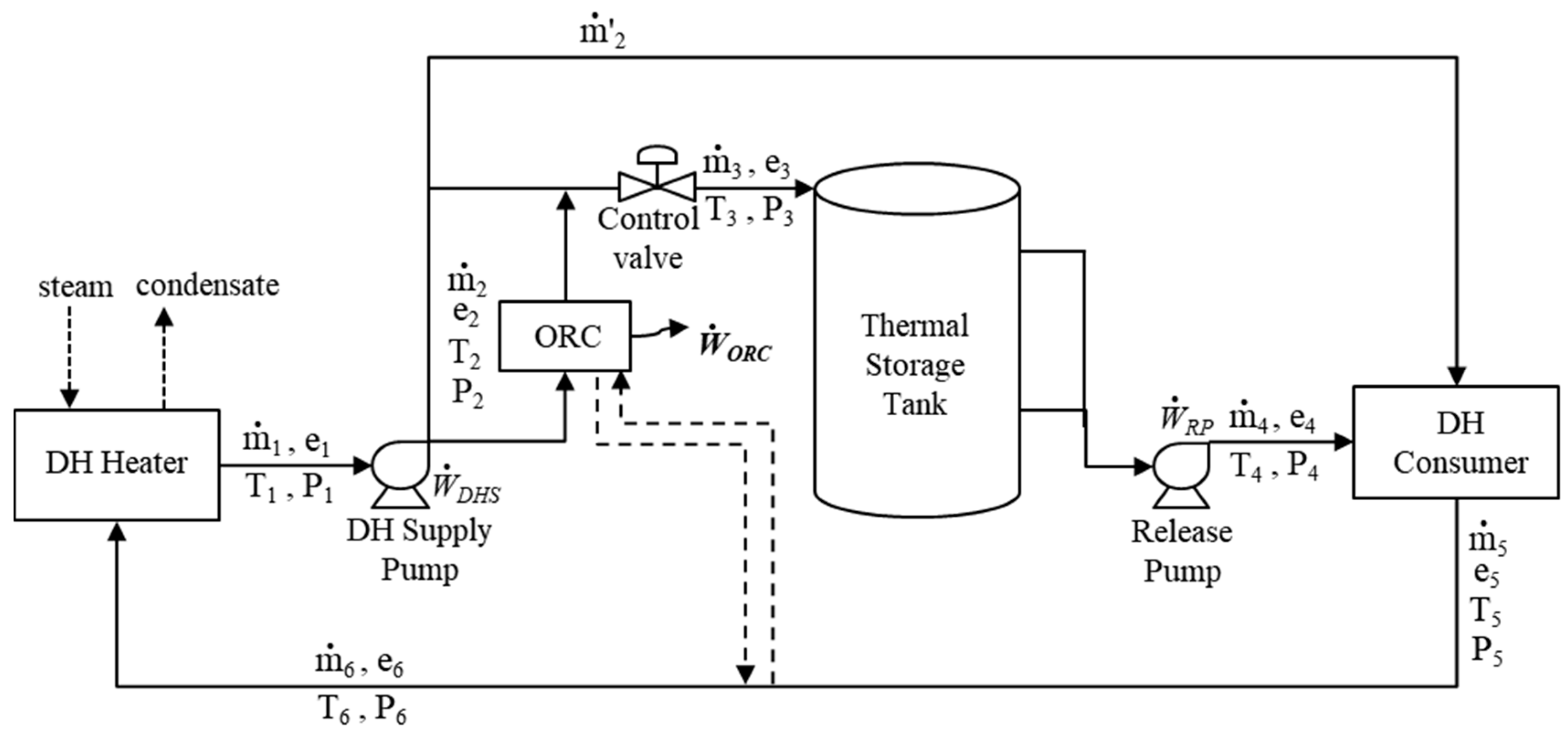
An organic Rankine cycle was applied to reduce exergy loss from temperature loss. The organic Rankine cycle uses organic material (hydrocarbon compound) as the working fluid, not water, and consists largely of the evaporator, condenser, pump and heat exchanger. Applying an organic Rankine cycle to reduce exergy loss can produce power through recovery of exergy loss. The organic Rankine cycle system can be introduced as shown in
Figure 5, based on the analysis of the operating state of the thermal storage system. The boundary conditions of the organic Rankine cycle are as follows:
- -
Amount of heat source water (primary heating water): 1500 m3;
- -
Temperature of heat source water: 110 °C;
- -
Temperature of condensing water (return DH water): 45 °C;
- -
Working fluid: R245fa (environment-friendly refrigerant).
As can be seen in
Figure 5, the organic Rankine cycle was applied to Process ②, in which maximum exergy loss in the thermal energy storage process occurred. The organic Rankine cycle uses the primary heating water stored in the TES tank as the heat source. The condenser cooling water is the return DH water from the district heating customer. If the return DH water is used as the cooling water, the condensation heat of the working fluid discharged from the organic Rankine cycle can be recovered and used for preheating the return DH water. Therefore, a more effective system can be configured to reduce the exergy loss of the TES system when the organic Rankine cycle is applied. By the boundary conditions of the organic Rankine cycle, the detailed design conditions were as shown in
Table 7.
When the organic Rankine cycle is applied to the TES system based on the design conditions of
Table 7, it is possible to produce 1150.5 kW of electricity from the organic Rankine cycle. In addition, the exergy loss of 3174.4 kW was recovered by increasing the temperature of the primary district heating return water by 5 °C. Thus, the total recovery of exergy loss was 4324.9 kW when using the organic Rankine cycle.
3.3. Reduction of Exergy Loss by Pressure Loss
Even if exergy loss due to thermal loss is reduced by applying an organic Rankine cycle, there is still exergy loss due to pressure loss. As previously analyzed, the total exergy loss in Process ② was 4879.6 kW. An organic Rankine cycle was applied to recover the exergy loss of 4324.9 kW but the exergy loss still remained at 554.7 kW. This exergy loss included the pressure loss from the throttling of the valve, the loss of the working fluid expander, internally present in the organic Rankine cycle, and the exergy loss from heat exchange between the working fluid and the cooling water in the condenser. This exergy loss was caused by the exergy loss of the device itself due to the exergy loss from the working fluid expander and the condenser. This is another way to increase the efficiency of the device or to reduce the exergy lost during the heat exchange process. Therefore, it is virtually impossible to recover until the development of more high-efficiency equipment or another way of reducing exergy loss in heat exchange processes. The present study does not discuss the exergy loss reduction problem stemming from the device itself.
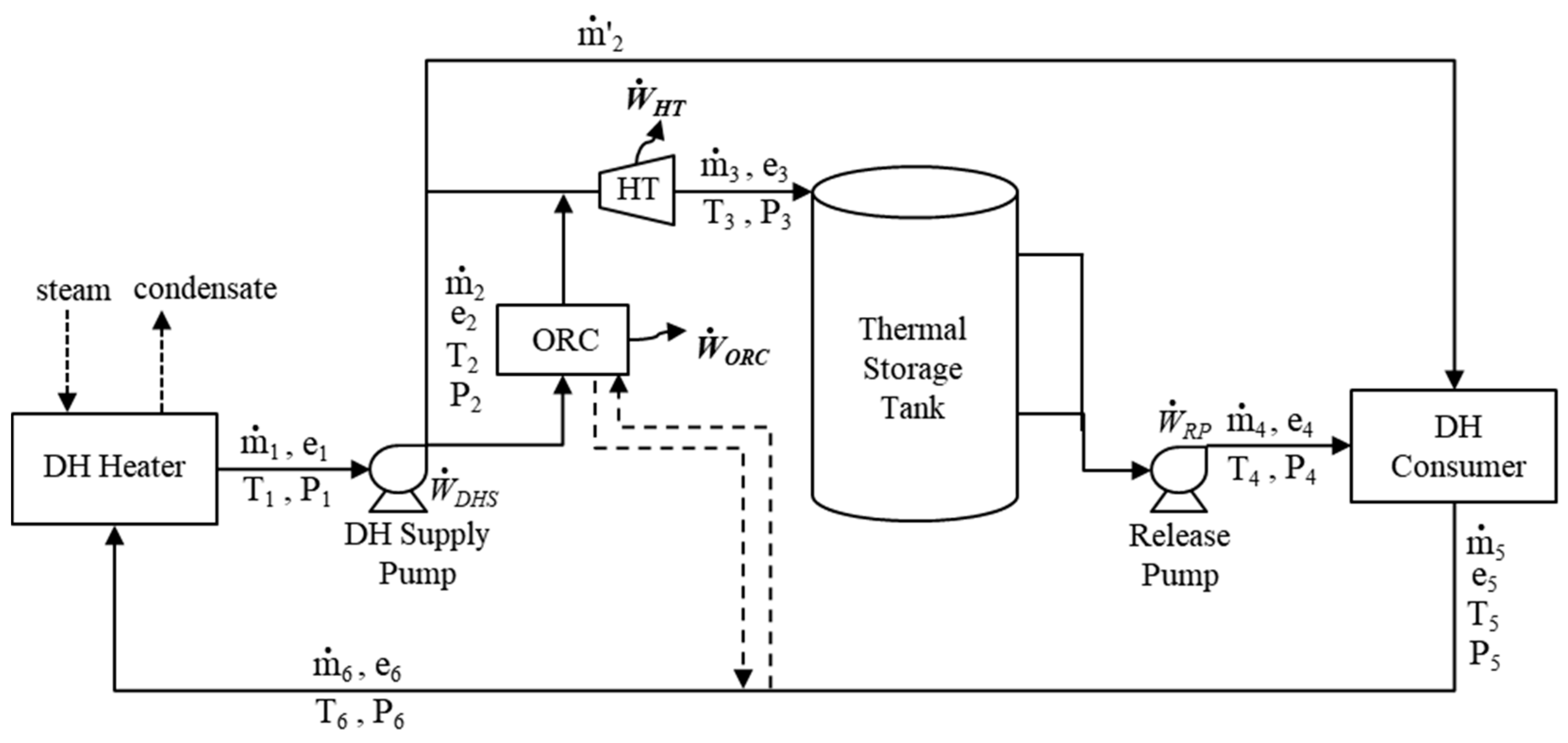
Hydraulic turbines have been applied to reduce residual exergy loss. The configuration of a combination of systems using an organic Rankine cycle and hydraulic turbines is shown in
Figure 6. The boundary conditions of hydraulic turbines are as follows:
- -
Flow rate of turbine inlet: 1500 m3;
- -
Pressure of turbine inlet: 11.6 kg/cm2g;
- -
Temperature of turbine inlet: 100 °C;
- -
Pressure of turbine outlet: 4.5 kg/cm2g.
According to the results of the analysis of the heating water supply pressure in
Table 3, the inlet pressure of the hydraulic turbine was applied to the average supply pressure and the turbine outlet pressure was based on
Table 5. From the analysis results, it was estimated that a power generation of 208.4 kW was possible with the hydraulic turbine. Hydraulic turbines can be a good alternative to pressure control by replacing the control valve with the reduction of the pressure lost by throttling in the heat storage system.
3.4. Economic Evaluation
For the above measures, proposed to reduce the exergy loss in the TES system, it was necessary to carry out an economic analysis to evaluate their applicability. Therefore, an economic analysis of the ORC and a hydraulic turbine was performed in this study.
The payback period method was used for the economic analysis. The payback period (PB) is defined as the time taken for the initial investment cost and product sales revenue to be equal (electric sales revenue in this study). This is defined by Equation (8). Here, C
0 denotes the initial investment cost and
i denotes the discount rate [
24,
25]. In this study, C
0 was obtained from the manufacturer’s proposal and
i was assumed to be 5%.
GM (Gross Margin) means the total revenue of the facility for a year and is defined by the following equation:
where PW (kWh) is the magnitude of electricity produced by each facility, PR (
$/kWh) is the unit price of electricity and C
OM (
$) denotes the relative operation and maintenance cost.
The electricity sales unit price applied for the economic analysis was based on the Korea Power Exchange’s average electricity trading price in 2018 [
26]. The maintenance cost was 3% of the facility investment cost.
It was considered appropriate to apply the capacity factor of the combined heat and power (CHP), a heat source facility, but it was necessary to make assumptions about the capacity factor because the acquisition of the capacity factor information for the heat source facility was limited. Thus, the capacity factor of the facility was assumed to be 80% in this study (
Table 8).
The results of economic analysis are shown in
Table 9.
As a result, the payback period of the ORC and hydraulic turbine will be 3.5 and 7.13 years, respectively, so that both measures can be practically applied as useful option to reduce exergy loss in TES system. However, the hydraulic turbine has a disadvantage in that the facility cost per unit power output and installation cost are high due to the civil engineering work. It is somewhat less economical than the ORC.
This study calculated the theoretical electricity production and economy based on the operating data of temperature and pressure. Although the results are economical, the actual case can affect the electricity production and economy as the site, space, and types of ORC and hydraulic turbine are selected. Therefore, it is necessary to judge the electricity production and economic efficiency through practical design or field demonstration.
4. Conclusions
The thermal energy storage (TES) system stores the district heating (DH) water which is primary heating water generated from a combined heat and power (CHP) plant when the thermal load is low. It then releases the district heating water when the thermal load is high. It is a system installed for the efficient operation of heat source facilities. In a general TES system, the high temperature water, 98 °C, and the low temperature water, 65 °C, are stored in the same tank. When heat is being stored, the low temperature water stored in the TES system is sent to the CHP plant (heat source facilities) and then to heated up to the DH supply temperature of 115 °C.
Since a TES system stores heat at atmospheric pressure, the primary heating water of 115 °C produced from a CHP plant has to be lowered to less than 100 °C. Therefore, the temperature of the primary heating water results in heat loss during storage. In addition, the primary heating water must have high pressure to supply heat to DH users a long distance from the CHP plant. When heat must be stored in the TES system a pressure drop in a throttling valve occurs. These losses occur in the thermal storage process of the TES system and can be analyzed by exergy analysis method to identify the locations, causes and the amount of loss. Exergy deals with the qualitative aspects of energy based on the second law of thermodynamics. Exergy analysis can provide a multitude of information to improve the efficiency of the process, identify problems and suggest a direction for improvement.
This study has evaluated the method on the efficiency improvement of a TES system using exergy analysis method in heat storage process. A power generation technology is also proposed using ORC and hydraulic turbine as a way to recover the exergy loss of the TES system. The exergy loss point and loss amount were identified through the point of view of second law of thermodynamics, and the exergy efficiency of the heat storage system was deep-dive analyzed when applying the power generation technology. The appropriate scale of ORC and hydraulic turbine for the heat storage system was suggested.
As a result, the ORC of 930 kW capacity and the hydraulic turbine of 270 kW capacity are considered to be suitable for the heat storage system that stores 3000 m3/h. In this case, each power generation facility is 50% of the thermal storage capacity, which is attributed to the variation of heat storage from the annual operating pattern analysis. Therefore, it is possible to produce 1200 kW of power by recovering 4533.3 kW exergy losses. In addition, economic analysis established that both facilities can reduce exergy losses in the TES system and be practically applicable.