1. Introduction
Small- and medium-capacity turbo-generator units in China’s power system have gradually been eliminated except for the power stations used for urban heat supply. Some 300 MW units, as well as large-capacity turbo-generator units of 600 MW, 1000 MW, or above, have been retained, which have been adopted at most thermal power stations and nuclear power stations. These units have large electromagnetic loads, especially the rotor windings, and they must bear large mechanical and thermal stresses under strong vibration conditions. If turn-to-turn insulation is weak, a turn-to-turn short circuit fault can easily occur.
The most troublesome problem for turbo-generator rotor windings caused by turn-to-turn short circuit faults is the deterioration that occurs in the vibration state. Sometimes, rotor grounding and shaft magnetization issues occur as well. Usually, 1–1.5 months are required to address and resolve this problem. This includes finding, processing, and repairing the turn-to-turn short circuit fault in the rotor winding. When this happens, serious economic losses are incurred by the power plants, including the loss of generating capacity, labor costs, and energy available for starting and stopping machines repeatedly, as well as service life loss. Therefore, serious problems caused by fault deterioration can be avoided if the turn-to-turn short circuit in the turbo-generator rotor winding can be assessed more accurately. If the short circuit can be found more effectively, timely warnings can be provided at the early stage so many problems can be avoided. Also, the accurate localization of a fault can reduce fault processing time and reduce economic losses to a great extent. In this case, work in this area has certain value and prospects [
1,
2,
3].
For turbo-generators, various kinds of online detection methods capable of detecting turn-to-turn short circuits in rotor windings have been proposed. For example, Mladen Šašić et al. [
4] detected the symmetry of each slot leakage flux in the rotor using a micro-probe. According to the symmetry, they determined if a turn-to-turn short circuit occurred. Rastko Fišer et al. [
5] proposed installing a small magnetic flux probe on the stator core “tooth unit”. This allowed users to confirm the short circuit’s position in the rotor winding using the difference in induced voltages on the probe according to the corresponding slots in the normal pole and the fault pole. In Li Yonggang et al. [
6], the turn-to-turn short circuit in rotor windings was judged by the relative deviation between the theoretical and actual values of the excitation current. In Wu Yucai, et al. [
7], turn-to-turn short circuits in rotor windings were judged by the deviation between the actual electromagnetic power and expected electromagnetic power. In Wu Yucai, et al. [
8], a detection method without the use of a sensor was proposed. Here, the turn-to-turn short circuit was judged by the induced voltage harmonic of piercing screw in the stator core. In addition, shaft voltage harmonics [
9,
10], no-load electromotive force deviation [
11], end leakage flux harmonics [
12], and parallel branch circulation in the stator winding [
13] have all been used to confirm whether the existence of a turn-to-turn short circuit fault in a rotor winding. For nearly half of these detection methods, excitation current data must be acquired from the turbo-generator including the excitation current method, virtual power method, and expected electromotive force method. These types of methods are inapplicable to large-capacity nuclear power units that use brushless excitation technology as a general rule. For the detection methods independent of excitation current, the detection coil method has been put into practical use. With this method, there is small interference under no-load or short circuit conditions in the turbo-generator and the detection effect is relatively good. When working under load, the output voltage waveform in the detection coil becomes insensitive to the turn-to-turn short circuit fault. This occurs due to the influence of the armature field, so the sensitivity drops sharply. Therefore, for this method, units are adjusted to a no-load or short circuit condition to finish the test after estimating that the turbo-generator is having a problem with a turn-to-turn short circuit in the rotor winding. In this case, online performance cannot be completely assessed, and though it is a method that can improve sensitivity, real-time evaluation is not possible. Wu Yucai et al. [
14] proposed installing a U-shaped magnetic field detection coil inside the turbo-generator. Then, the turn-to-turn short circuit fault in the rotor winding was judged using the even or fractional sub-harmonic in the induced voltage of U-shaped coil. This U-shaped detection coil method is based on the asymmetry of the north and south magnetic pole fields in the faulty turbo-generator. In this case, users are not limited by the excitation mode of the turbo-generator; however, t another fault like a turn-to-turn short circuit fault can occur in rotor windings. This is known as the rotor eccentricity fault, where the magnetic field asymmetry of the turbo-generator is caused by dynamic eccentricity, which is stronger on the small air gap side and weaker on the large air gap side. When the turn-to-turn short circuit for rotor windings are judged using the U-shaped coil method, the first step is to eliminate the interference of the dynamic eccentricity fault because dynamic eccentricity faults are common in turbo-generators. Here, success or failure depends on whether the eccentricity interference is eliminated.
In terms of the anti-interference performance, the same shortcomings generally exist for all detection methods based on using the magnetic field. When the operating state of a turbo-generator changes rapidly (the reactive power also changes rapidly), the induced voltage waveforms of the sensor are not comparable at different times. In this case, it is possible to receive a false alarm signal when operating in a normal state, so an unnecessary shutdown may occur. In addition, most of the detection sensors have only a single function and they can only be used to detect turn-to-turn short circuit faults for rotor windings. If turn-to-turn short circuits in rotor windings and dynamic eccentricity faults can be detected simultaneously using the same kind of sensor, the monitoring systems for turbo-generators will be perfected and capable of simplifying the structure of detection sensors.
In this study, the influence of turn-to-turn short circuits in rotor windings on the main magnetic field of a turbo-generator was deduced. Similarity comparisons with dynamic eccentricity faults were conducted, and an online detection method for turn-to-turn short circuits in rotor winding based on double U-shaped coils was designed. We used to numerical simulation to prove that the fault features of turn-to-turn short circuit faults extracted from the new signal acquisition method are not covered by dynamic eccentricity faults, and the fault location can be determined. After the turn-to-turn short circuit fault is eliminated, the new detection method can be used to judge the rotor for a dynamic eccentricity fault.
2. Principle of Detection Methods
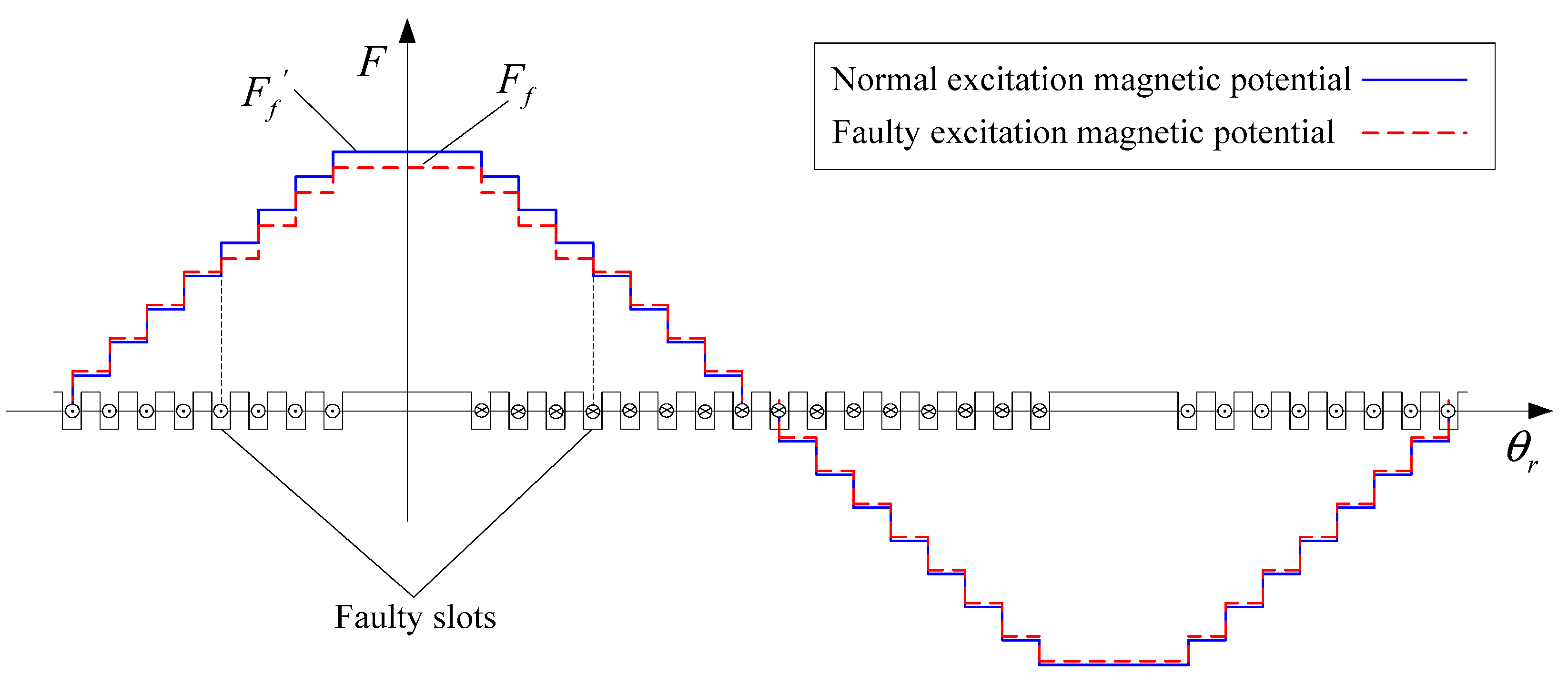
The rotor winding of a turbo-generator has a distributed structure. A certain number of excitation windings (generally 6–10 turns) are placed in each slot of the rotor and they are insulated by insulating layers, as shown in
Figure 1. According to ampere circuital theorem, the excitation magneto motive force in a turbo-generator is a stepped wave, as shown in
Figure 2. The amount of stepped wave in each slot of the rotor is related to the effective ampere turns of the slot. The larger the number of effective ampere turns, the larger the step amount. In the normal state of rotor winding, the number of winding turns for the rotor north and south poles is the same and the number of effective ampere turns is also the same. So, the excitation magnetic force is symmetrical. If a turn-to-turn short circuit fault occurs in a slot winding of the rotor, the current of the short circuited winding in the slot is zero, and the step amount of the excitation magnetic force in the slot decreases. In this case, the entire excitation magnetic force exists in an asymmetrical state.
where
Fi represents the amplitude of the
ith harmonic magnetic potential,
i is an odd number,
θr represents the spatial mechanical angle of the rotor,
p represents the pole pair of the turbo-generator,
ak represents the number of windings in the
kth slot,
γ is the angle at which the large gear of the rotor occupies the circumference of the rotor,
If represents the excitation current,
m is the number of short circuit slots, and
Q is the number of short circuit turns.
When the rotor winding is normal, the excitation magneto motive force waveform is symmetrical, and the stepped magnetic potential waveform contains only the fundamental wave and the odd harmonic after the Fourier decomposition. This is shown in Equation (1).
When the turn-to-turn short circuit in a rotor winding occurs, the asymmetric stepped excitation magnetic force contains even or fractional harmonics after the Fourier decomposition. The excitation magnetic force is shown in Equation (2) [
15]. Here, the blue item is the magnetic potential loss in the excitation winding which has short circuited. This is shown by the equation where
j = 1, 2, 3, 4...:
The eccentricity of the rotor can be expressed as:
where
g represents the largest or shortest air gap length of the turbo-generator and
g0 represents the average air gap length of the turbo-generator.
It is assumed that the air gap in the turbo-generator is uniform,
g(θr) =
g0 and that the air gap permeability is constant. Therefore, this can be expressed as:
where,
μ0 represents the permeability of the vacuum.
The excitation field of the turbo-generator can be expressed as Equation (5):
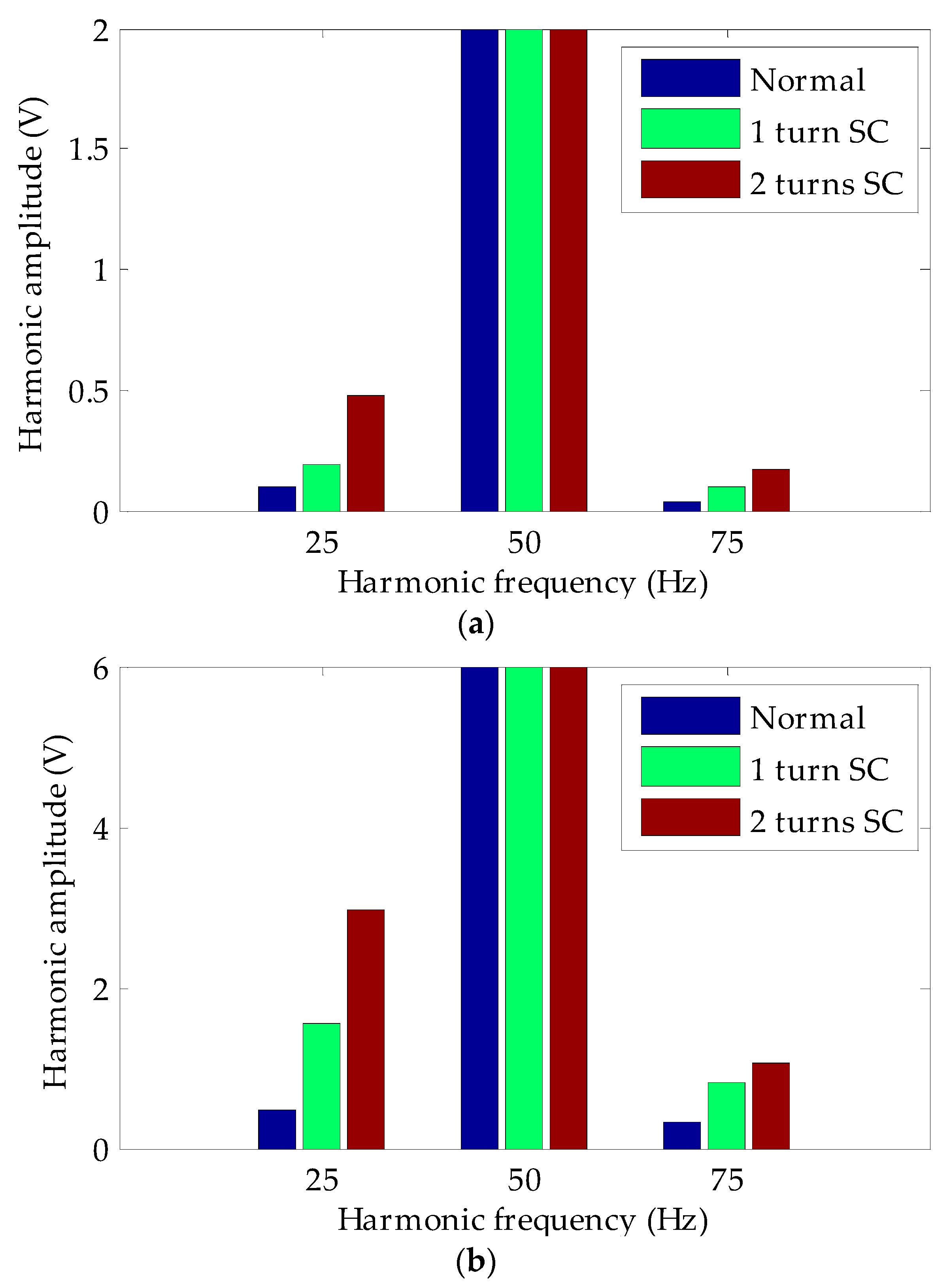
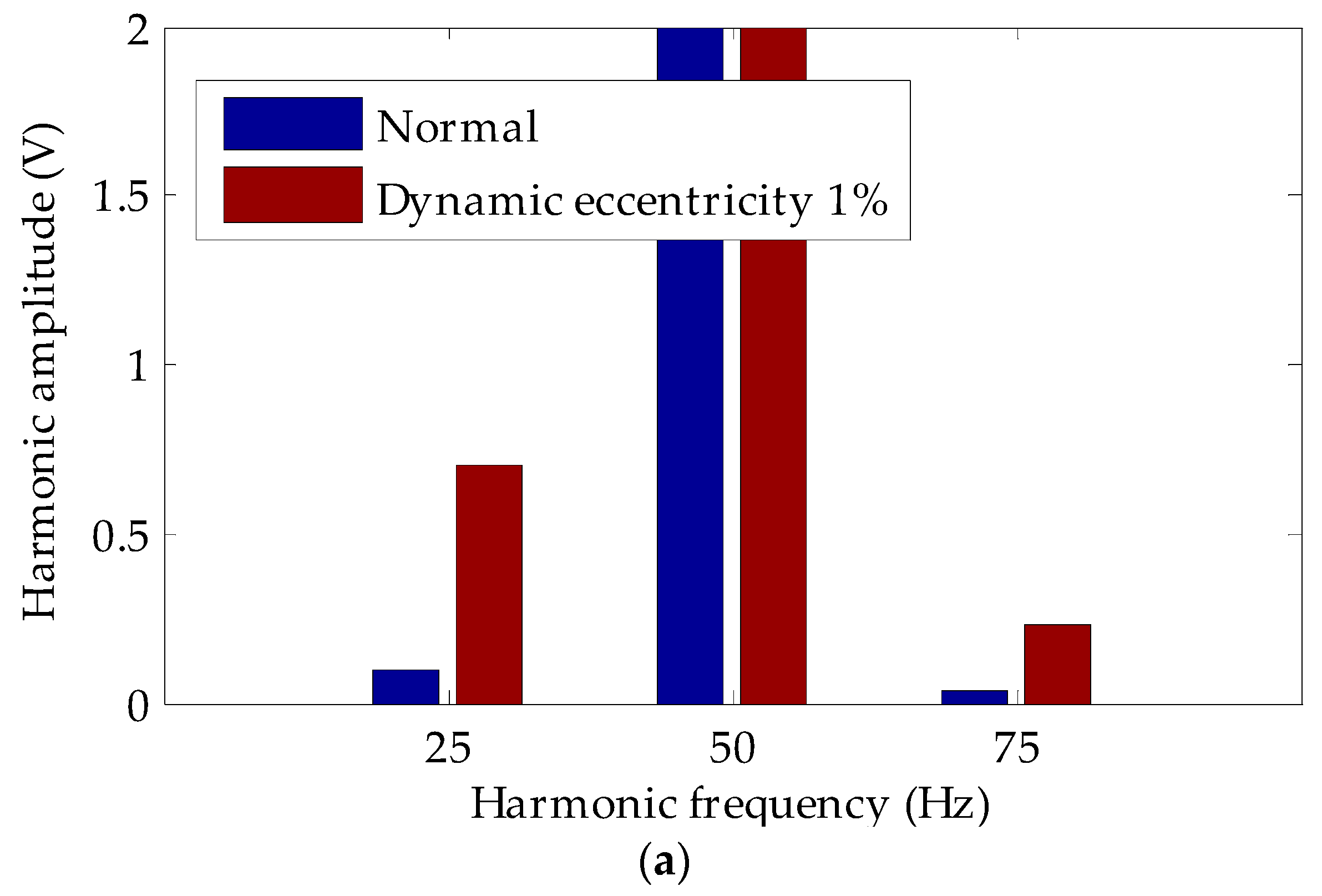
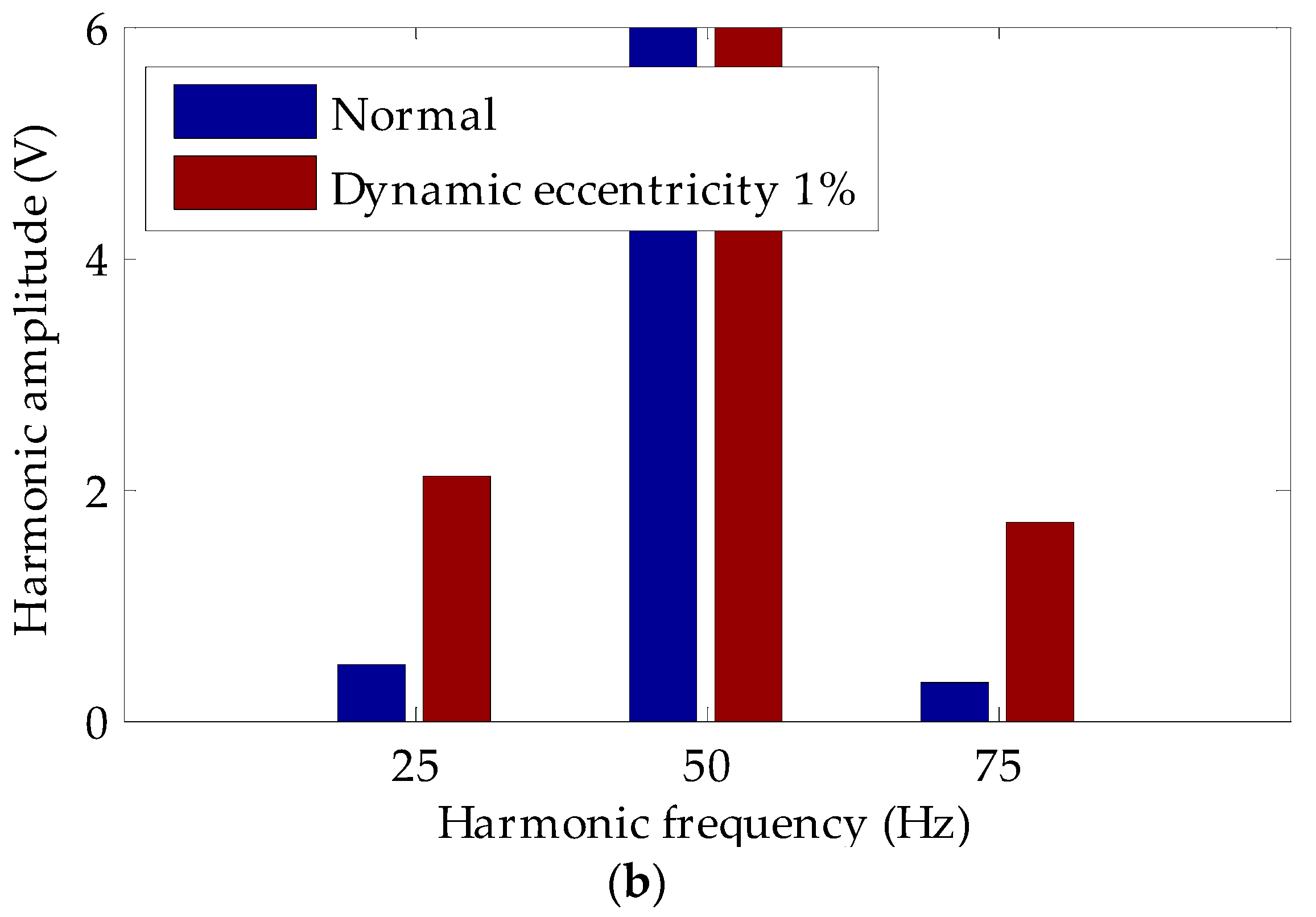
Equation (5) shows that some new harmonics appear in the excitation magnetic field after the turn-to-turn short circuit fault occurs in the turbo-generator rotor winding. For a 2-pole turbo-generator, even harmonics can occur 2, 4, and 6 times, and these will be generated in the excitation magnetic field; for the 4-pole turbo-generator, the 1/2, 3/2, 2, and 5/2 times harmonics do not exist when the rotor winding is normal.
The main magnetic field asymmetry of a turbo-generator can also be caused by the dynamic eccentricity of the rotor. In an abnormal state, the length of the air gap at any position changes periodically with time. If the slot effect, saturation effect, and higher harmonics are neglected, the length of the air gap in the synchronous rotating coordinate system can be expressed as [
16]:
where
β represents the angle between the shortest air gap and axis
d of the rotor.
Accordingly, the air gap permeance of the turbo-generator can be expressed as:
where
ε is the relative eccentric ratio.
The air gap synthetic magnetic potential of the turbo-generator is equal to the superposition of excitation magnetic potential and armature reaction magnetic potential, which contains only odd harmonics. According to the air gap magnetic permeance method, the main magnetic field can be expressed as Equation (8):
where
α1 and
α3 represent the phase of the fundamental and third harmonics magnetic potential, respectively; and
F1 and
F3 represent the amplitude of the fundamental and third harmonics magnetic potential, respectively.
The blue item in Equation (8) appears after the fault, including the p + 1, p − 1, 3p + 1, and 3p − 1 harmonic components, which rotate synchronously with the rotor. For a 2-pole turbo-generator (p = 1), there is no direct current component, and 2nd and 4th harmonics are in the magnetic field before the fault; for a 4-pole turbo-generator (p = 2), there are no 1/2, 3/2, 5/2, and 7/2 harmonics in the magnetic field before the fault.
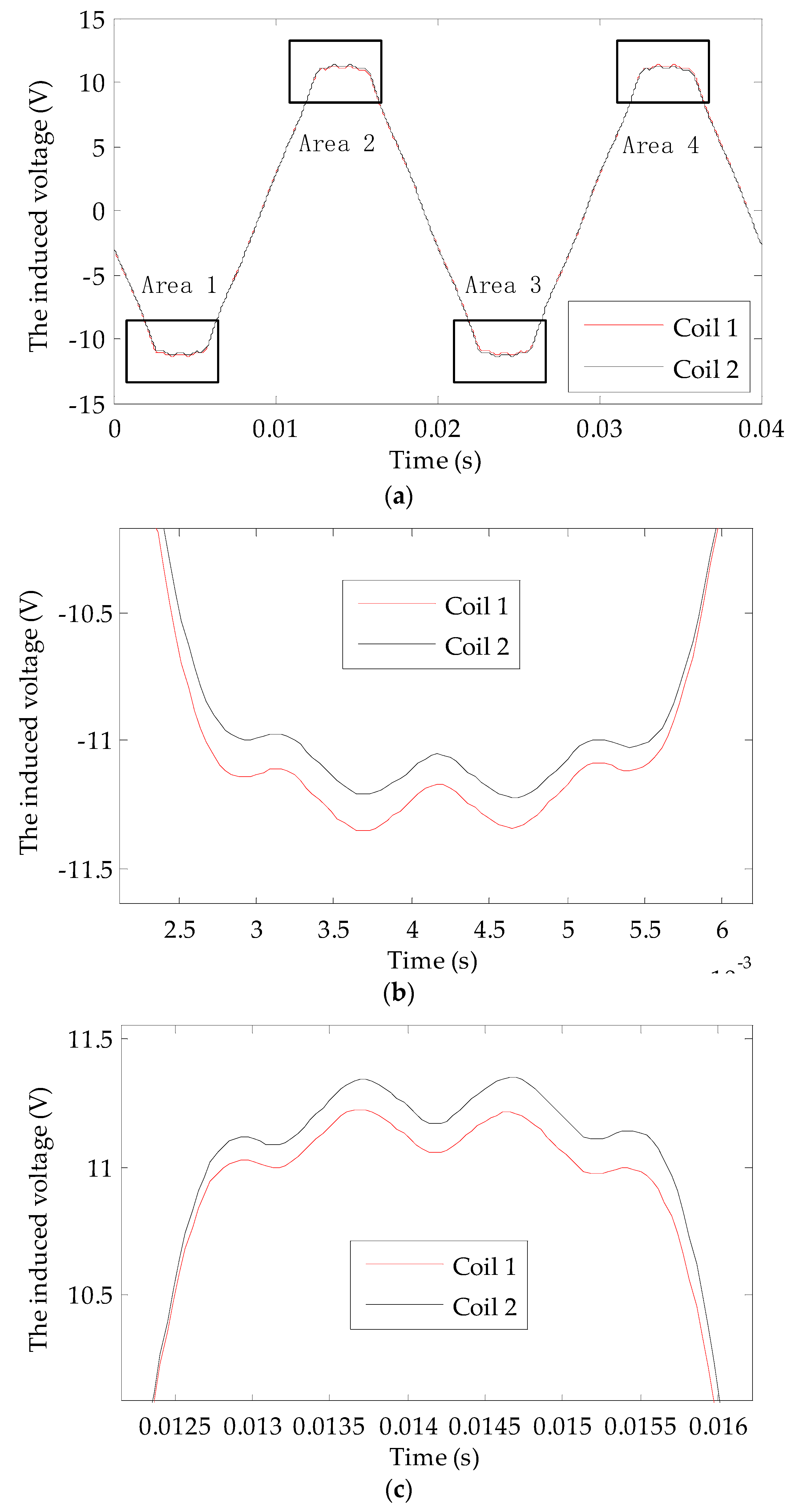
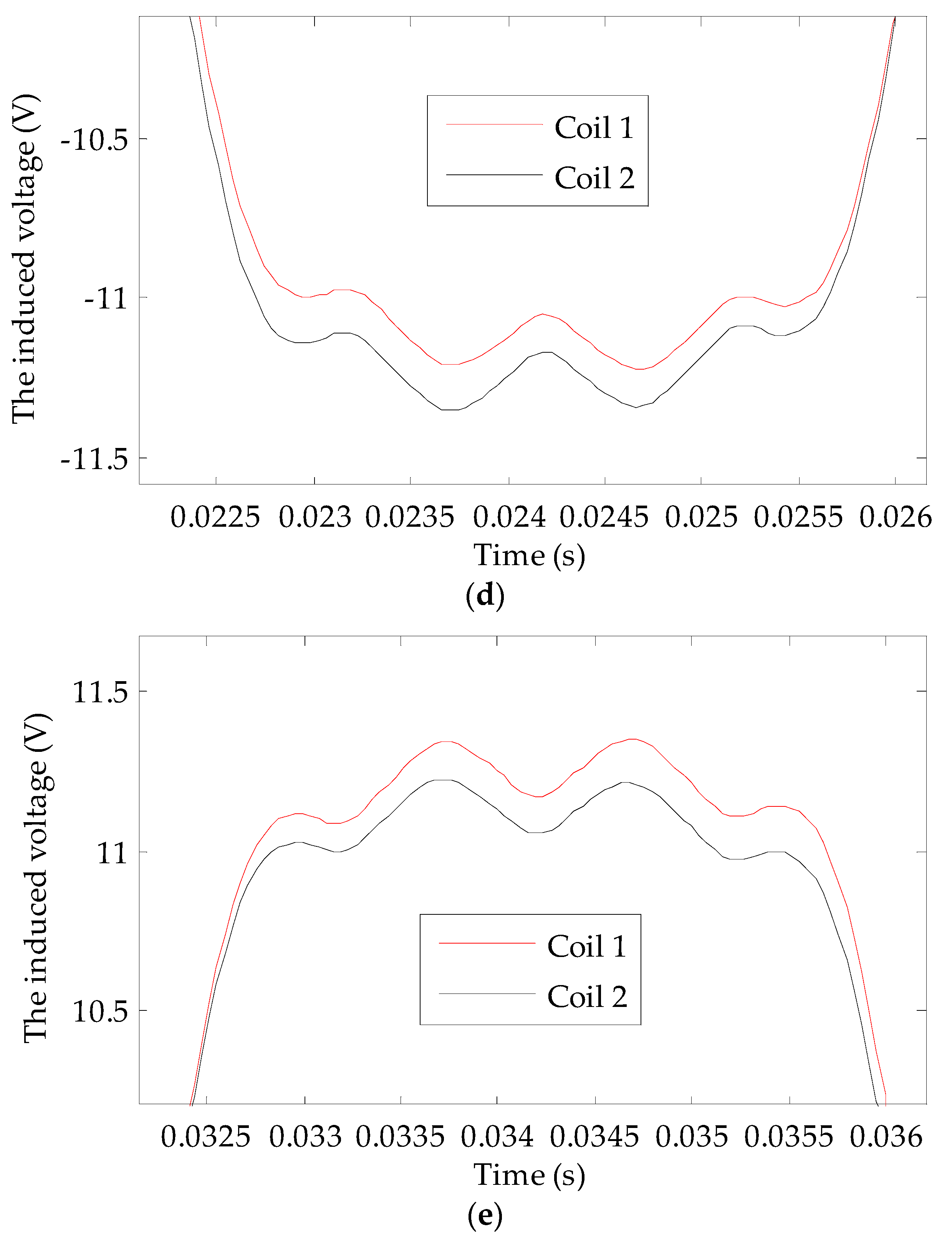
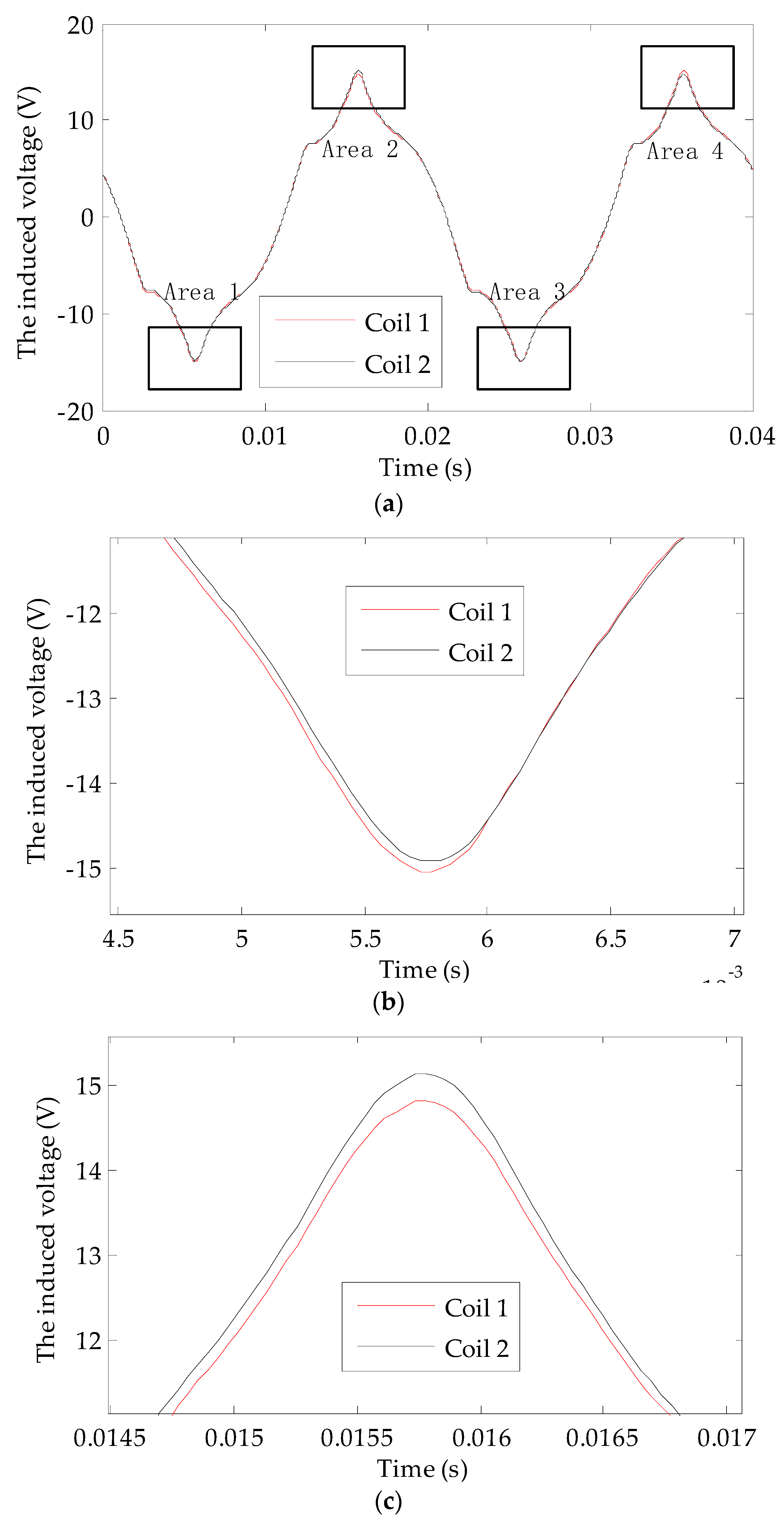
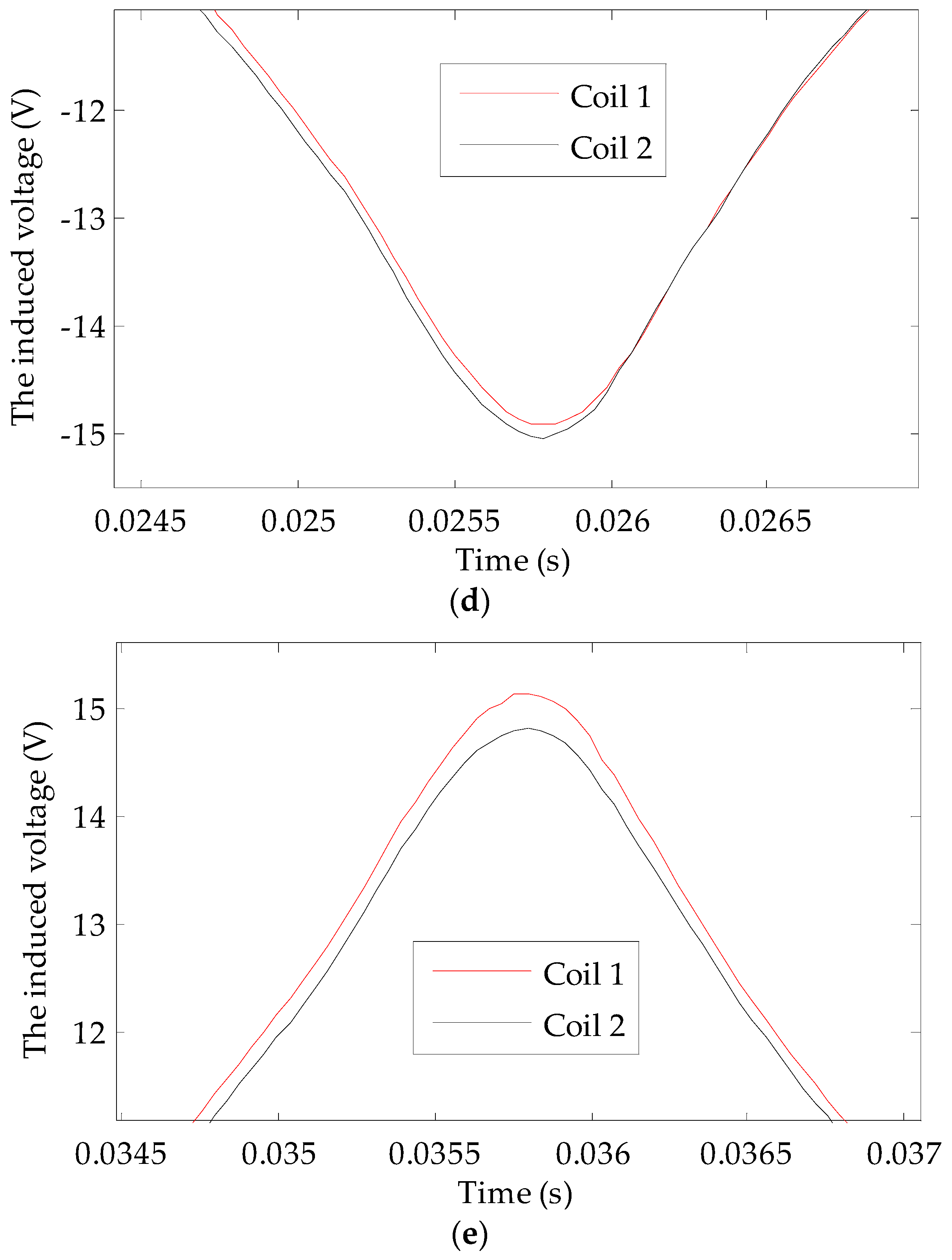
Compared with the magnetic field found with a turn-to-turn short circuit fault in the rotor winding, the frequency of the harmonics that appear in the main magnetic field of a turbo-generator are the same under dynamic eccentricity. It is impossible to judge a turn-to-turn short circuit fault in the rotor winding using the induced voltage spectrum of a single U-shaped coil. Even if these harmonics are detected, it is impossible to determine whether these harmonics are caused by dynamic eccentricity or by a turn-to-turn short circuit in the rotor winding. To address this shortcoming, we propose that two detection coils should be placed symmetrically at a circumferential distance of 180° in the turbo-generator. The principle of this type of detection system is shown in
Figure 3.
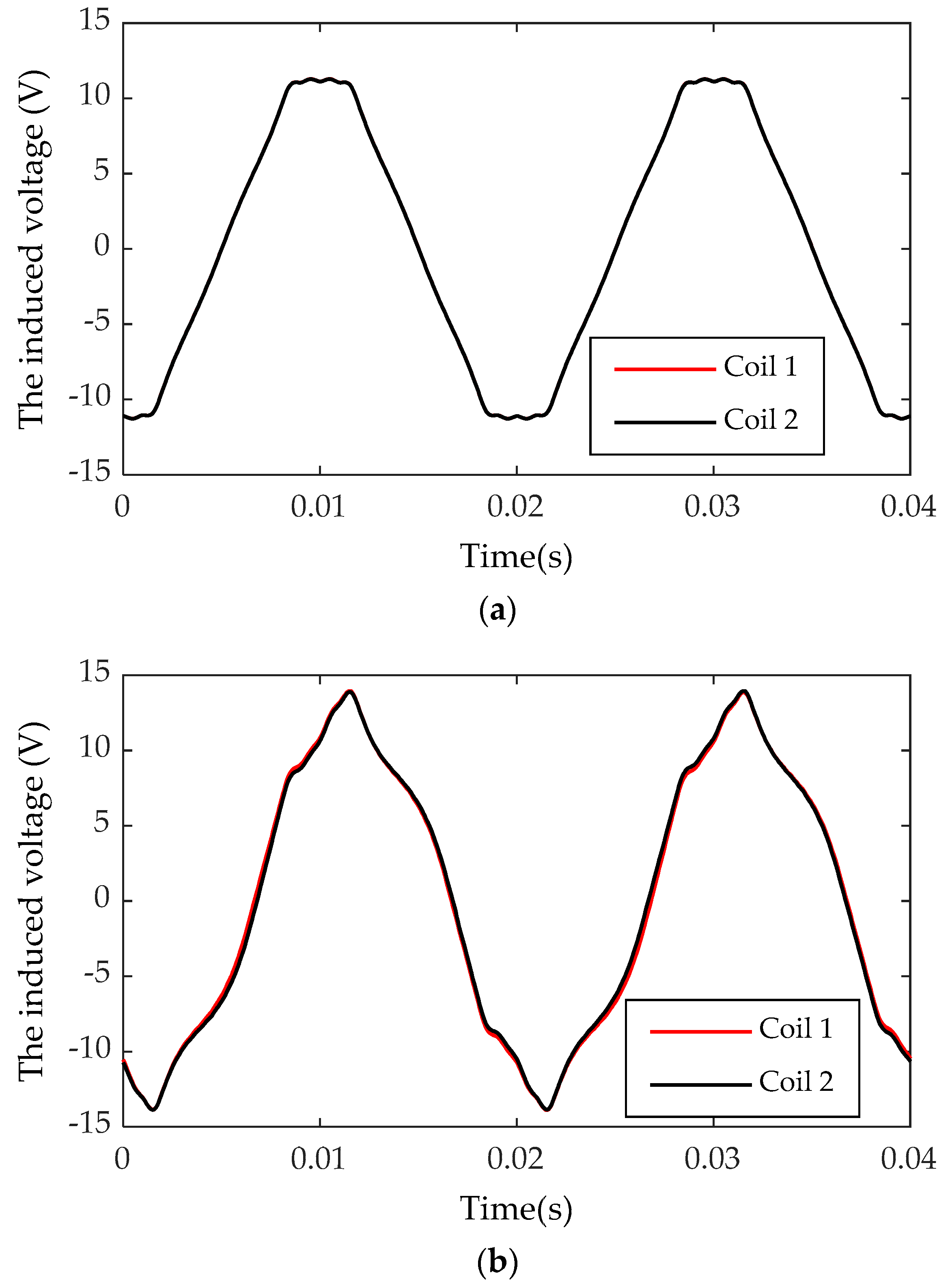
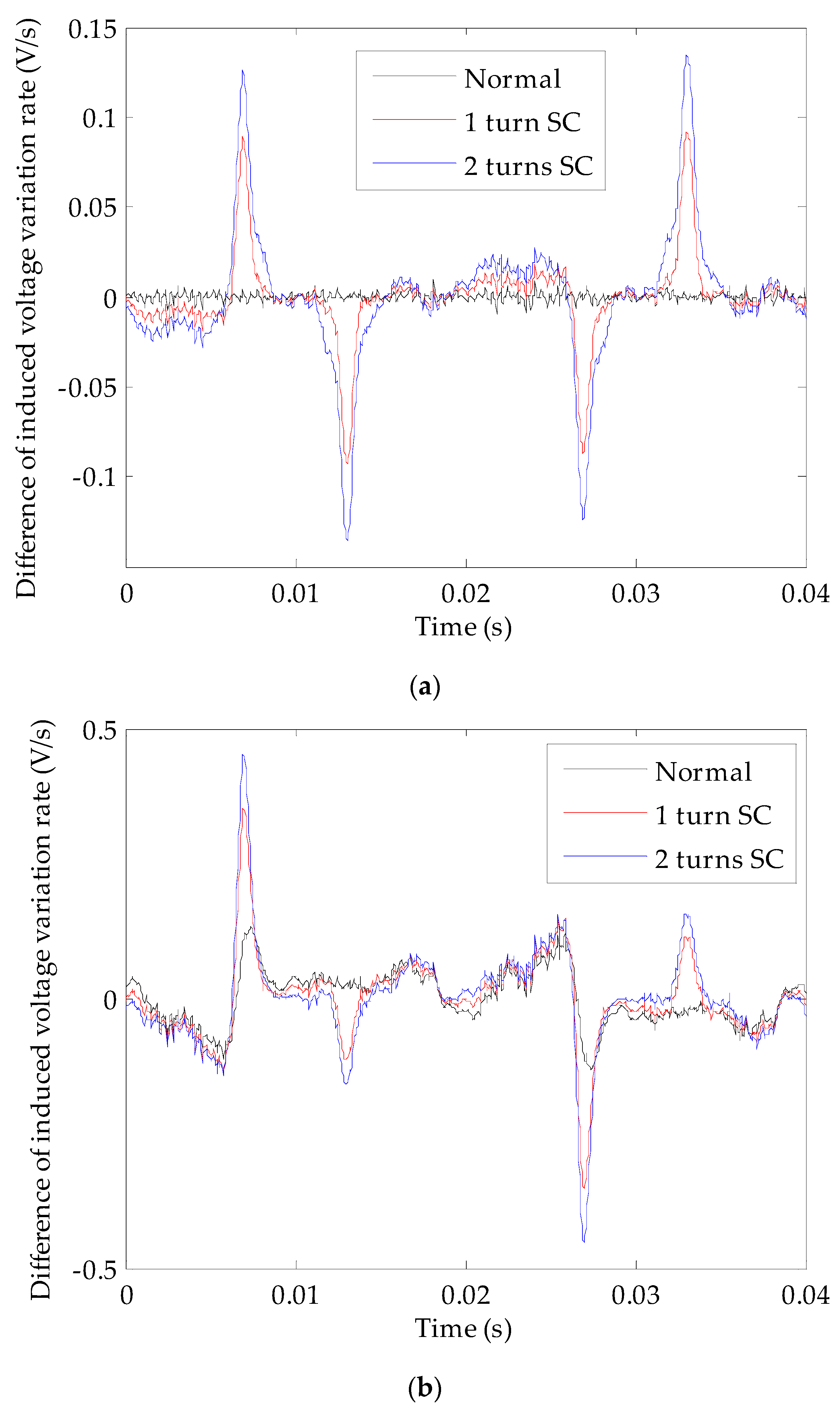
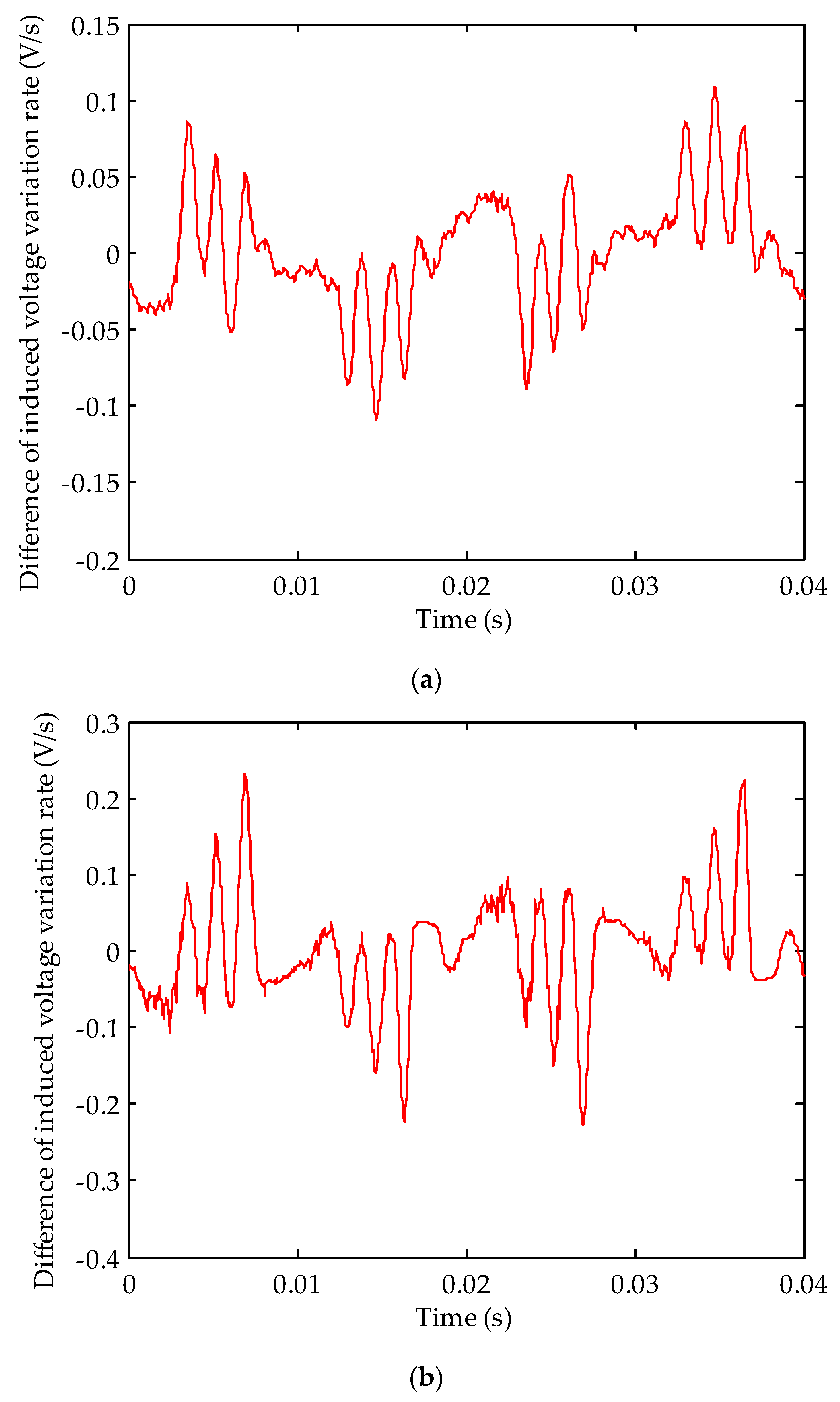
The voltages induced by the U-shaped coils can be expressed as e = BrLv = BrLωrR, where Br represents the radial component of the air gap flux density at the effective part of U-shaped coil, L is the effective part length of the U-shaped coil, v represents the moving speed of the radial magnetic field relative to the effective part of the U-shaped coil;, ωr is the mechanical angular speed of rotor rotation, and R is the distance between the effective part of the U-shaped coil and the center of the rotor. As L, ωr, and R are all constants, the induced voltage waveform of the U-shaped coil is similar to the radial component waveform of gap flux density at the effective part of the coil. Theoretically, during a fully symmetrical state of the turbo-generator air gap magnetic field, the induced voltages of both coils are the same. After decomposition, the harmonics with the faulty characteristics are not included. The result is zero if the induced voltage time domain waveforms of both coils are added together (two-pole generator) or subtracted (four-pole generator). If a turn-to-turn short circuit fault or dynamic eccentricity fault occurs, although the harmonic contents of the induced voltages for both coils are the same, the induced voltages are different due to the different positions of both detection coils. In this case, the voltage time domain waveform is not zero after operation. There is a significant advantage for adopting the use of double coils: the induced voltages of both coils change simultaneously with a change in the turbo-generator’s operating state. Under a normal state, the output voltage waveforms of both coils will always be the same (four-pole generator) or the opposite (two-pole generator); therefore, the double coil method has excellent anti-interference abilities, which helps to reduce the probability of misjudgment.